Иллюстрированный самоучитель по Maple 9 › Вычисление производных › Вычисление производных функций, заданных параметрически [страница — 41] | Самоучители по математическим пакетам
Вычисление производных функций, заданных параметрически
При вычислении производных функций, заданных параметрически, по сравнению с явно заданными функциями, принципиально ничего не меняется. Однако сама процедура вычисления производных (особенно высших порядков) становится несколько сложнее.
Рассмотрим пример.
Задача 2.7
Найти производную функции, заданной параметрически: x(t) = acos(t) и y(t) = bsin(t).
Переменной х присвоим значение.
Так же поступим и с переменной у.
Теперь х и у являются выражениями, которые зависят от переменной-параметра t; по этому параметру их можно дифференцировать. Поэтому остается только воспользоваться приведенной выше формулой для производной функции, заданной в параметрическом виде.
Построим график функции и ее производной с помощью процедуры plot().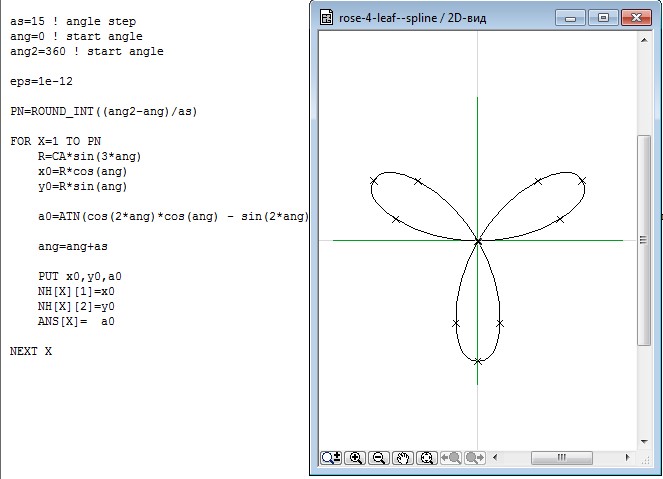
При построении графика только одной функции, заданной в параметрическом виде, первым параметром процедуры указывается список, элементами которого являются выражения, определяющие зависимость х и у от переменной-параметра, а также диапазон изменения параметра. Если нужно построить графики сразу нескольких параметрически заданных функций, то в качестве первого аргумента процедуры
Внимание!
Именно наличие третьего параметра в списке при отображении заданной в параметрическом виде функции является индикатором того, что строится график параметрической функции, а не графики двух разных функций.
Поскольку в исходных параметрических зависимостях х и у зависят от параметров а и b, при построении графиков эти зависимости следует поделить на соответствующие коэффициенты.
Следует обратить внимание на то, что при определении заголовка использовался символ перехода на новую строку (\n). Данный символ рекомендуется использовать при длинных заголовках, чтобы при отображении графика такой заголовок был виден целиком.
Процесс вычисления параметрической производной можно существенно автоматизировать. Подобный подход продемонстрирован в следующем примере.
Pers.narod.ru. Обучение. Лекции по MathCAD. Графика в MathCAD
Pers.narod.ru. Обучение. Лекции по MathCAD. Графика в MathCADЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
Для построения обратиться к пункту ВСТАВКА команда ГРАФИК (см. рисунок)
Основные
операции при построении графика.
При
построении графика необходимо выполнить следующие шаги:
· щелкнуть мышью в том месте, где нужно создать график;
· обратиться к пункту Вставка, командам График – Х-У Зависимость. В рабочем документе создается пустой график с шестью полями ввода;
Другие четыре поля используются для выбора границ на осях координат
Пример. В рабочем документе постройте график функции f(x)=x2+ x для x меняющимся от -10 до 10 с шагом 0.1.
Форматирование и редактирование графиков
Для изменения формата осей, способа их оцифровки, цвета графиков необходимо:
· щелкнуть мышью на графике, чтобы он заключился в синюю рамку;
· обратиться к появившемуся пункту X-Y-Plot, команде Format;
· используя закладки X-Y-оси, Графики, надписи выполнить форматирование
Построение нескольких графиков
Графическое представление вектора
Графики в полярной системе координат
Форматирование графика
График параметрической функции
Графики функций двух переменных (поверхностей)
Для создания трехмерного графика (графика функции двух
переменных) необходимо щелкнуть на одной из следующих кнопок палитры Графика с
изображением требуемого типа графика.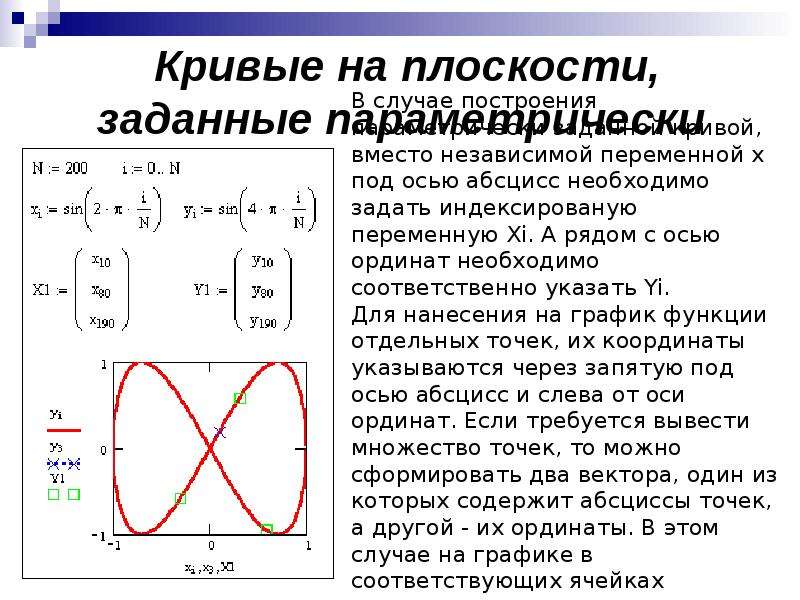
В документе появится шаблон графика с
тремя осями и пустым полем. В это поле вводится либо имя массива, либо имя
функции двух переменных.
В первом случае предварительно необходимо сформировать матрицу из значений функции в узлах прямоугольной сетке.
Во втором случае предварительно надо описать функцию от двух переменных.
Пример построения графика с формированием матрицы. Необходимо построить график функции
f(x,
5, 1.5]
Форматирование графика
Окно форматирования трехмерных графиков вызывается аналогично и имеет ряд вкладок:
· общие – установка общих параметров форматирования;
· ось – установка параметров форматирования координатных осей;· вид – установка вида графика;
· освещение – задание условий освещения и выбор схемы освещения;
· название – задание титульных надписей и их параметров;
· основание – установка параметров форматирования граней;
· особый – задание специальных эффектов форматирования;
· дополнительно – установка дополнительных параметров;
·
данные QuickPlot –
параметры быстрого построения графика.
Автоматическое формирование матрицы
Графики векторных полей
Для отрисовки векторного поля ( в каждой точке такого поля задается не скалярная величина, а вектор с двумя проекциями ) необходимо :
· вычислить две матрицы ( первая содержит проекции вектора на ось Х, вторая на ось У ) или сформировать комплексную матрицу;
· обратиться к пункту меню Graphics, команде Create Vector Field Plot ;
·
заполнить в нижней части
появившегося шаблона поле, введя туда имена двух вещественных массивов или имя
одного комплексного массива.
Пример
Схема построения графика заданной функции. Схема исследования плоских кривых
Схема построения графика функции
1. Найти область определения функции и значения (возможно бесконечные) этой функции в точках разрыва и граничных точках области определения.
2. Установить,
является ли функция четной, нечетной, периодической. При наличии симметрии или
периодичности выбрать подобласть области определения для дальнейшего исследования
(п.3-6 выполнять для выбранной подобласти).
3. Найти
асимптоты графика (вертикальные – в точках разрыва и граничных точках области
определения; наклонные или горизонтальные – если функция определена на
полупрямой или на всей числовой прямой).
4. Найти нули функции, т.е. решить уравнение .
5. Вычислить первую производную функции. Найти локальные экстремумы функции и промежутки ее возрастания и убывания.
6. Вычислить вторую производную. Найти промежутки сохранения направления выпуклости.
7. Определить характер особых точек кривой.
8. Построить таблицу (см. ниже).
9. Построить график функции. Если в п.2 была установлена симметрия или периодичность, то дорисовать функцию на всю область определения соответствующим образом.
Схема исследования плоских кривых, заданных параметрически.
x = x(t), y = y(t), tÎT
1. Найти общую часть областей определения функций x(t), y(t).
2. Установить,
обладает ли кривая симметрией (если кривая обладает симметрией, то можно
сократить выкладки, ограничив соответствующим образом исследуемую часть области
определения).
4Четыре основных случая симметрии:
, – симметрия относительно оси .
, – симметрия относительно оси .
, – симметрия относительно точки .
, – наложение ветвей графика. 3
3. Определить, не обладает ли данная кривая периодичностью на исследуемой части области определения.
4Условия периодичности:
Из того, что y(t) периодична, а x(t) – функция с неограниченной областью значений и периодичной производной, следует периодичность y(x), а из того, что x(t) периодична, а y(t) – функция с неограниченной областью определения и периодичной производной, следует периодичность x(y). 3
4. Найти асимптот графика функции y(x).
4Условия существования асимптот:
Если при , а , то – вертикальная асимптота кривой.
Если при , а , то – горизонтальная асимптота кривой.
Если при и , то возможна наклонная асимптота , где , , .
Отметим, что символ S может принимать следующие значения: , , где , , . 3
5. Найти нули функций x(t), y(t) и их области знакопостоянства.
6. Найти точки tk, в которых хотя бы одна из производных x′(t), y′(t) равна нулю или разрывна.
4Точки ti, найденные в пункте 4, и точки tk, найденные в этом пункте, разбивают множество T на промежутки знакопостоянства производных x′(t), y′(t), и, следовательно, данная система уравнений на интервале (tp, tp+1) задаёт параметрическую функцию вида , которая является одной из веток исходной кривой. 3
7. Найти вторую производную данной параметрической функции , где , и те точки tj, в которых .
8. Определить направление выпуклости каждой ветви графика функции.
4Если на интервале
существует вторая производная функции и если эта производная положительна
(отрицательна), то график этой функции на данном интервале имеет выпуклость,
направленную вниз (вверх).
3
9. Определить точки экстремума функции (вершины кривой).
4Для этого предварительно выделить точки возможного экстремума, то есть такие точки x(tp), где tp – одно из значений, найденных в пунктах 4,6 и 7 такое, что x′(t) сохраняет знак на интервале (tp-1, tp+1). Затем, рассмотрев изменение y на интервалах (tp-1, tp) и (tp, tp+1), выяснить, является ли x(tp) точкой экстремума. 3
10. Определить характер особых точек кривой.
11. Составить таблицу:
* | |||||||||||
Интервалы монотонности и точки экстремума | |||||||||||
Интервалы выпуклости и точки | |||||||||||
Особые точки графика и уравнения асимптот |
* Таблица строится только для
тех значений t, для которых определены обе функции – и .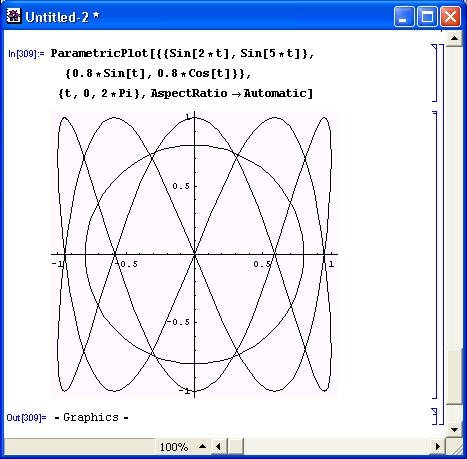
** Серым цветом отмечены те клетки таблицы, которые не заполняются;
***Для построения графика явно заданной функции используют аналогичную таблицу (в первой строке – интервалы и значения переменной x, а вторая строка отсутствует).
12. Пользуясь таблицей и сведениями об особых точках, построить ветви кривой, соответствующие промежуткам (tp, tp+1). Если была установлена симметрия или чётность, то дорисовать функцию на всю область определения соответствующим образом.
gnuplot / parametric (E)
В обычном двумерном построении в gnuplot координата Y выражается y=f(x), однако можно использовать параметрическое задание функции, использующее параметр t,
x = f(t) y = g(t)
С помощью этого выражения gnuplot может рисовать более сложные функции. Отметим, что 3D построения параметрической поверхности,
задаваемой параметрами u,v, дается в разделе построения сферических гармоник.
В первую очередь необходимо использовать команду set parametric, чтобы gnuplot определил параметрическую переменную для функции. Затем, команда plot, выполняющая построение функции f(t) координаты X и функцит g(t) для координаты Y, задается как plot f(t),g(t).
Чтобы провести простейшую вертикальную линию, не выражающуюся формой y=f(x), а заданную как x=const. Эта функция может быть определена как:
x=const y=t
с параметром t, когда t различен. Диапазон t контролируется командой set trange.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> const=3
gnuplot> set trange [1:4]
gnuplot> set xrange [0:5]
gnuplot> set yrange [0:5]
gnuplot> plot const,t
В данном случае вертикальная линия нарисованна в x=3.
Использование set
trange [1:4] , определило диапазон от 1 до 4.
Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы.
Параметрическое задание окружности:
x=sin(t) y=cos(t)
окружность может быть нарисована при изменении параметра t от 0 до 2pi. График принимает вид «квадрата» и диапазон t задается опцией команды plot.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> plot [0:2*pi] sin(t),cos(t)
Параметр t не изменяется непрерывно и фактически управляется значениями, установленными командой set
samples. По умолчанию значение равно 100. В случае set samples 8,
gnuplot вычисляет только 8 значений t от 0 до 2*pi, и график становиться семиугольником.
Если необходим построить N-угольник,
задается set samples N+1.
2D параметрическое представление удобно для рисования функции, которая находится в полярных координатах. 2D полярная координатаимеет 2 переменные: r и угловую theta. gnuplot выражает параметр t для theta, а радиус r выражается через функцию угла, а именно r(t). Координата (x,y) дается из:
x=r(t)*cos(t) y=r(t)*sin(t)
Окружность — особый случай, когда r(t)=const. Когда радиус пропорционален t, получается спираль.
gnuplot> set xrange [-10*pi:10*pi] gnuplot> set yrange [-10*pi:10*pi] gnuplot> plot [0:10*pi] t*sin(t),t*cos(t)
Следующий пример показывает график кардиоды r(t)=const*(1+cos(t)).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> r(t) = 1+cos(t)
gnuplot> plot [0:2*pi] r(t)*cos(t),r(t)*sin(t)
Обычная функция имеет вид y=f(x), но параметрическая позволяет делать график x=f(y).
Значения Y такие же как и t и значения x вычисляются функцией f(t).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> c=2*pi
gnuplot> set size square
gnuplot> set trange [-c:c]
gnuplot> set xrange [-c:c]
gnuplot> set yrange [-c:c]
gnuplot> plot c*sin(t),t with lines, t,c*cos(t) with impulses
Показаны 2 функции, одна (зеленые линии) y=2pi*cos(x), другая (красная толстая линия) x=f(t)=2pi*sin(y).
Опция with impulse рисует вертикальную линию от оси Y=0. Если используется with impulses для красной кривой x=2pi*sin(y), то получается вертикальная линия, не горизонтальная.
Модуль 23 — Параметрические уравнения
В этом уроке исследуются графики параметрических кривых. Обсуждаются параметры окна режима параметрического построения графиков и графически изображаются обратные параметрические отношения.
Сравнение функционального и параметрического режимов построения графиков
При отображении функций в режиме Function на вашем TI-89 независимая переменная составляет x , а зависимая переменная — y .Каждое значение, выбранное для x , дает уникальное значение для y , и они указывают точку на графике функции.
При построении уравнений в параметрическом режиме независимая переменная — t , а зависимые переменные — x и y . Другими словами, x и y являются функциями общего параметра t . Каждое значение t дает уникальную точку на графике.
График функции y = x 2 в режиме Function дает параболу. Эту же кривую также можно построить в параметрическом режиме, используя приведенные ниже уравнения.
x = т
y = t 2
Создание параметрических графиков
- Откройте меню Mode, нажав
- Выделите «2: ПАРАМЕТРИКА» в подменю «Графики».
2.
2.Ввод параметров окна
Для параметрического режима требуются начальное и конечное значения независимой переменной t , введенные как tmin и tmax , и величина изменения между последующими значениями t , введенная как tstep .График будет отображаться в окне, определяемом параметрами x и y .
- Откройте редактор окон, нажав
- Введите следующие значения
- Отобразите график, нажав
Управление внешним видом графика
В параметрическом режиме у вас больше контроля над внешним видом графика, чем в функциональном режиме.
23.1.1 Что произойдет с графиком, если вы позволите tmin = 0 в редакторе окон? Нарисуйте свой прогноз, затем внесите изменения на своем TI-89 и отобразите график с новым значением tmin . Нажмите здесь, чтобы получить ответ.
Сбросить значения окна на
| tmin = -3 | xmin = -3 | ymin = -3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tmax = 3 | xmax = 3 | ymax = 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tstep = 0. 2 yt1 = t и отобразите график, чтобы проверить свой прогноз.Нажмите здесь, чтобы получить ответ. Графические кривые, не являющиеся функциями Любую функцию y = f ( x ) можно изобразить в параметрическом режиме, положив x = t и y = f ( t ). Однако кривые, которые не являются функциями, также могут быть построены в параметрическом режиме. 23.1.3 Для 0 т 2 спрогнозировать кривую, которая создается параметрическими уравнениями x = cos t y = sin t Создайте график параметрических уравнений, чтобы проверить свой прогноз.Нажмите здесь, чтобы получить ответ. Построение графиков других параметрических кривых Параметрические уравнения часто представляют собой интересные графики, которые невозможно построить в режиме функций. Отобразите график параметрических уравнений x = 6sin t — sin 6 t y = 6cos t — cos 6 t в [0, 2 ] x [-10, 10] x [-10, 10] окно.Установите tstep = 0,1. Этот график называется эпициклоидой и имеет 5 «лепестков». 23.1.4 Замените каждую 6 в параметрических уравнениях на 7 и нанесите на график новые уравнения. Затем замените 7 на 8 и нанесите на график уравнения. Опишите влияние числа N на приведенный ниже график эпициклоиды. Подсказка: обратите внимание на количество лепестков на каждом графике. x = N sin t — sin Nt y = N cos t — cos Nt Нажмите здесь, чтобы получить ответ. Parametric Plots — Sage 9.4 Справочное руководство: 3D GraphicsВозвращает параметрическую трехмерную пространственную кривую или поверхность. Эту функцию можно вызвать четырьмя способами:
ВХОД:
Примечание
ПРИМЕРЫ: Мы демонстрируем каждый из четырех способов называть это функция.
Поверхность, но с сеткой: мудрец: u, v = var ('u, v')
sage: Parametric_plot3d ((cos (u), sin (u) + cos (v), sin (v)), (u, 0,2 * pi), (v, -pi, pi), mesh = True)
Объект Graphics3d
Увеличиваем количество точек на графике, делаем поверхность зеленой и прозрачный: sage: параметрический_plot3d ((cos (u), sin (u) + cos (v), sin (v)), (u, 0,2 * pi), (v, -pi, pi), ....: color = 'green', opacity = 0.1, plot_points = [30,30]) Объект Graphics3d Покрасить поверхность можно также с помощью функции окраски и цветовая карта следующим образом. Обратите внимание, что функция раскраски должна принимать значения в интервале [0,1]. мудрец: u, v = var ('u, v')
sage: def cf (u, v): return sin (u + v / 2) ** 2
мудрец: P = параметрический_площадь3d ((cos (u), sin (u) + cos (v), sin (v)),
....: (u, 0,2 * pi), (v, -pi, pi), color = (cf, colormaps.PiYG), plot_points = [60,60])
мудрец: P.show (viewer = 'tachyon')
Другой пример, цветная лента Мебиуса: шалфей: см = палитра.океан мудрец: def c (x, y): return sin (x * y) ** 2 sage: from sage.plot.plot3d.parametric_surface import MoebiusStrip sage: MoebiusStrip (5, 1, plot_points = 200, color = (c, см)) Объект Graphics3d Еще один цветной пример: sage: from sage.plot.plot3d.parametric_surface import ParametricSurface шалфей: cm = colormaps.autumn мудрец: def c (x, y): return sin (x * y) ** 2 sage: def g (x, y): return x, y + sin (y), x ** 2 + y ** 2 sage: ParametricSurface (g, (srange (-10,10,0.1), srange (-5,5.0,0.1)), цвет = (c, cm)) Объект Graphics3d Предупреждение Этот вид раскраски с помощью цветовой карты можно визуализировать.
с использованием Jmol, Tachyon (option Мы строим график, но смешиваем символьный ввод и целое число: мудрец: t = var ('t')
мудрец: параметрический_плот3d ((1, sin (t), cos (t)), (t, 0,3))
Объект Graphics3d
Мы указываем стиль границы, чтобы показать нам значения функции на ее экстремумы: мудрец: u, v = var ('u, v')
sage: параметрический_plot3d ((cos (u), sin (u) + cos (v), sin (v)), (u, 0, pi), (v, 0, pi),
....: border_style = {"color": "черный", "толщина": 2})
Объект Graphics3d
Мы можем построить векторов: мудрец: x, y = var ('x, y')
sage: Parametric_plot3d (вектор ([x-y, x * y, x * cos (y)]), (x, 0,2), (y, 0,2))
Объект Graphics3d
мудрец: t = var ('t')
мудрец: p = вектор ([1,2,3])
sage: q = vector ([2, -1,2])
мудрец: параметрический_плот3d (p * t + q, (t, 0,2))
Объект Graphics3d
Любые параметры, которые вы обычно используете для задания внешнего вида кривой,
действителен как записи в dict Узел-трилистник (статья в Википедии Trefoil_knot): мудрец: u, v = var ('u, v')
мудрец: f_x = (4 * (1 + 0,25 * sin (3 * v)) + cos (u)) * cos (2 * v)
мудрец: f_y = (4 * (1 + 0,25 * sin (3 * v)) + cos (u)) * sin (2 * v)
мудрец: f_z = sin (u) + 2 * cos (3 * v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi, pi), (v, -pi, pi), frame = False, color = "blue")
Объект Graphics3d
Зеленый галстук-бабочка: мудрец: u, v = var ('u, v')
мудрец: f_x = грех (и) / (sqrt (2) + грех (v))
мудрец: f_y = sin (u) / (sqrt (2) + cos (v))
мудрец: f_z = cos (u) / (1 + sqrt (2))
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi, pi), (v, -pi, pi), frame = False, color = "green")
Объект Graphics3d
Поверхность мальчика (статья в Википедии Boy% 27s_surface и https: // mathcurve.com / sizes / boy / boy.shtml): . мудрец: u, v = var ('u, v')
мудрец: K = cos (u) / (sqrt (2) - cos (2 * u) * sin (3 * v))
мудрец: f_x = K * (cos (u) * cos (2 * v) + sqrt (2) * sin (u) * cos (v))
мудрец: f_y = K * (cos (u) * sin (2 * v) -sqrt (2) * sin (u) * sin (v))
мудрец: f_z = 3 * K * cos (u)
мудрец: параметрический_плот3d ([f_x, f_y, f_z], (u, -2 * pi, 2 * pi), (v, 0, pi),
....: plot_points = [90,90], frame = False, color = "orange") # долгое время - около 30 секунд
Объект Graphics3d
Сова Мэдера, также известная как минимальная поверхность Бура (статья в Википедии Bour% 27s_minimal_surface): мудрец: u, v = var ('u, v')
мудрец: f_x = v * cos (u) - 0.1,5 * cos (3 * u / 2) / 3
мудрец: параметрический_плот3d ([f_x, f_y, f_z], (u, -2 * pi, 2 * pi), (v, 0,1),
....: plot_points = [90,90], frame = False, color = "purple")
Объект Graphics3d
Браслет: мудрец: u, v = var ('u, v')
мудрец: f_x = (2 + 0.2 * sin (2 * pi * u)) * sin (pi * v)
мудрец: f_y = 0,2 * cos (2 * pi * u) * 3 * cos (2 * pi * v)
мудрец: f_z = (2 + 0,2 * sin (2 * pi * u)) * cos (pi * v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0, pi / 2), (v, 0,3 * pi / 4), frame = False, color = "серый")
Объект Graphics3d
Зеленый кубок: мудрец: u, v = var ('u, v')
мудрец: f_x = cos (u) * cos (2 * v)
мудрец: f_y = sin (u) * cos (2 * v)
мудрец: f_z = грех (v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0, pi), frame = False, color = "green")
Объект Graphics3d
Забавная складчатая поверхность — с квадратным выступом: мудрец: u, v = var ('u, v')
мудрец: f_x = cos (u) * sin (2 * v)
мудрец: f_y = sin (u) * cos (2 * v)
мудрец: f_z = грех (v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0,2 * pi), frame = False, color = "green")
Объект Graphics3d
Поверхность вращения фигуры 8: мудрец: u, v = var ('u, v')
мудрец: f_x = cos (u) * sin (2 * v)
мудрец: f_y = sin (u) * sin (2 * v)
мудрец: f_z = грех (v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0,2 * pi), frame = False, color = "green")
Объект Graphics3d
Желтый зонт Уитни (статья в Википедии Whitney_umbrella): мудрец: u, v = var ('u, v')
мудрец: f_x = u * v
мудрец: f_y = u
мудрец: f_z = v ^ 2
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -1,1), (v, -1,1), frame = False, color = "желтый")
Объект Graphics3d
Cross cap (статья в Википедии Cross-cap): мудрец: u, v = var ('u, v')
мудрец: f_x = (1 + cos (v)) * cos (u)
мудрец: f_y = (1 + cos (v)) * sin (u)
мудрец: f_z = -tanh ((2/3) * (u-pi)) * sin (v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0,2 * pi), frame = False, color = "красный")
Объект Graphics3d
Скрученный тор: мудрец: u, v = var ('u, v')
мудрец: f_x = (3 + sin (v) + cos (u)) * cos (2 * v)
мудрец: f_y = (3 + sin (v) + cos (u)) * sin (2 * v)
мудрец: f_z = sin (u) + 2 * cos (v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0,2 * pi), frame = False, color = "красный")
Объект Graphics3d
Четыре пересекающихся диска: мудрец: u, v = var ('u, v')
мудрец: f_x = v * cos (u) - 0.1,5 * cos (3 * u / 2) / 3
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,4 * pi), (v, 0,2 * pi), frame = False, color = "красный", непрозрачность = 0,7)
Объект Graphics3d
Поверхность Штейнера / Поверхность Романа (см. Статья в Википедии Roman_surface и Статья в Википедии Steiner_surface): мудрец: u, v = var ('u, v')
мудрец: f_x = (sin (2 * u) * cos (v) * cos (v))
мудрец: f_y = (грех (и) * грех (2 * v))
мудрец: f_z = (cos (u) * sin (2 * v))
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi / 2, pi / 2), (v, -pi / 2, pi / 2), frame = False, color = "red")
Объект Graphics3d
Бутылка Клейна? (см. статью в Википедии Klein_bottle): мудрец: u, v = var ('u, v')
мудрец: f_x = (3 * (1 + sin (v)) + 2 * (1-cos (v) / 2) * cos (u)) * cos (v)
мудрец: f_y = (4 + 2 * (1-cos (v) / 2) * cos (u)) * sin (v)
мудрец: f_z = -2 * (1-cos (v) / 2) * sin (u)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, 0,2 * pi), (v, 0,2 * pi), frame = False, color = "green")
Объект Graphics3d
A Рисунок 8, врезка бутылки Клейна (см. 2 sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -2,2), (v, -2,2), frame = False, color = «красный») Объект Graphics3d Поверхность Хеннеберга (см. http: // xahlee.org / surface / gallery_m.html): мудрец: u, v = var ('u, v')
мудрец: f_x = 2 * sinh (u) * cos (v) - (2/3) * sinh (3 * u) * cos (3 * v)
мудрец: f_y = 2 * sinh (u) * sin (v) + (2/3) * sinh (3 * u) * sin (3 * v)
мудрец: f_z = 2 * cosh (2 * u) * cos (2 * v)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -1,1), (v, -pi / 2, pi / 2), frame = False, color = "red")
Объект Graphics3d
Спираль Дини: мудрец: u, v = var ('u, v')
мудрец: f_x = cos (u) * sin (v)
мудрец: f_y = sin (u) * sin (v)
мудрец: f_z = (cos (v) + log (tan (v / 2))) + 0,2 * u
мудрец: параметрический_плот3d ([f_x, f_y, f_z], (u, 0,12.4), (v, 0.1,2), frame = False, color = "red")
Объект Graphics3d
Каталонская поверхность (см. http://xahlee.org/surface/catalan/catalan.html): мудрец: u, v = var ('u, v')
мудрец: f_x = u - sin (u) * cosh (v)
мудрец: f_y = 1 - cos (u) * cosh (v)
мудрец: f_z = 4 * sin (1/2 * u) * sinh (v / 2)
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi, 3 * pi), (v, -2,2), frame = False, color = "красный")
Объект Graphics3d
Конхоид: мудрец: u, v = var ('u, v')
шалфей: k = 1,2; k_2 = 1,2; а = 1,5
мудрец: f = (k ^ u * (1 + cos (v)) * cos (u), k ^ u * (1 + cos (v)) * sin (u), k ^ u * sin (v) - а * к_2 ^ и)
sage: Parametric_plot3d (f, (u, 0,6 * pi), (v, 0,2 * pi), plot_points = [40,40], texture = (0,0.5,0))
Объект Graphics3d
Лента Мебиуса: sage: u, v = var ("u, v")
sage: параметрический_plot3d ([cos (u) * (1 + v * cos (u / 2)), sin (u) * (1 + v * cos (u / 2)), 0,2 * v * sin (u / 2 )],
....: (u, 0, 4 * pi + 0,5), (v, 0, 0,3), plot_points = [50,50])
Объект Graphics3d
Скрученная лента: мудрец: u, v = var ('u, v')
sage: параметрический_plot3d ([3 * sin (u) * cos (v), 3 * sin (u) * sin (v), cos (v)],
....: (u, 0,2 * pi), (v, 0, pi), plot_points = [50,50])
Объект Graphics3d
Эллипсоид: мудрец: u, v = var ('u, v')
sage: параметрический_plot3d ([3 * sin (u) * cos (v), 2 * sin (u) * sin (v), cos (u)],
.(0.5)],
....: (u, 0,001,1), (v, 0,1), plot_points = [70,70], color = 'красный')
мудрец: показать (p1 + p2)
Гипергеликоидальный: мудрец: u = var ("u")
мудрец: v = var ("v")
мудрец: f_x = (sinh (v) * cos (3 * u)) / (1 + cosh (u) * cosh (v))
мудрец: f_y = (sinh (v) * sin (3 * u)) / (1 + ch (u) * cosh (v))
мудрец: f_z = (cosh (v) * sinh (u)) / (1 + cosh (u) * cosh (v))
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi, pi), (v, -pi, pi), plot_points = [50,50], frame = False, color = "red")
Объект Graphics3d
Геликоид (линии, проходящие через спираль, Статья в Википедии Helix): мудрец: u, v = var ('u, v')
мудрец: f_x = sinh (v) * sin (u)
мудрец: f_y = -sinh (v) * cos (u)
мудрец: f_z = 3 * u
sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -pi, pi), (v, -pi, pi), plot_points = [50,50], frame = False, color = "red")
Объект Graphics3d
Поверхность Куена (http: // virtualmathmuseum.2)) мудрец: f_x = (2 * K * cosh (0,4 * u) * (- (K * cos (v) * cos (K * v)) — sin (v) * sin (K * v))) / G мудрец: f_y = (2 * K * cosh (0,4 * u) * (- (K * sin (v) * cos (K * v)) + cos (v) * sin (K * v))) / G шалфей: f_z = -u + (2 * 0,84 * ch (0,4 * u) * sinh (0,4 * u)) / G sage: Parametric_plot3d ([f_x, f_y, f_z], (u, -13.2,13.2), (v, -37.4,37.4), plot_points = [90,90], frame = False, color = «green») Объект Graphics3d Справка в Интернете — Справка OriginPD-Dialog-2DParaFunc-Tab
ПараметрПараметрУкажите параметр. ОчкиУкажите количество точек данных для отображения на графике функции. От и доУкажите начало и конец диапазона параметров. X (t) и Y (t)Введите здесь формулу параметра X и Y. Общие математические и статистические функции распределения доступны при нажатии кнопки треугольника справа от текстовых полей X (t) и Y (t) .Для получения подробной информации об этих функциях, пожалуйста, прочтите встроенные функции LabTalk. Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Вы также можете вызвать любую из встроенных функций Origin, даже если они недоступны из раскрывающегося меню треугольной кнопки или из любых функций, которые вы определили. Если вы нажмете кнопку «Показать в отдельном окне» под кнопкой треугольника, откроется новое диалоговое окно Y (x) = с более широким полем ввода и панелью предварительного просмотра.На панели предварительного просмотра отображается столбец, рассчитанный по заданной вами формуле. Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода. ОпределениеОпределите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом. Показать скрипт LabTalkУстановите этот флажок, чтобы определять переменные с помощью сценариев LabTalk. Если вы уже определили некоторые переменные в таблице Definition , установите этот флажок, чтобы отобразить эквиваленты этих определений в сценариях LabTalk. Помимо встроенных или определяемых пользователем функций, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Введенные здесь сценарии будут выполняться до определения формулы.
График функции выходаРаскрывающийся список опций в нижнем левом углу используется для указания способа вывода кривой функционального графика: Создать новый график , Добавить в активный график или Добавить в активный график и изменить масштаб .
3D-параметры с помощью Python и MatPlotLib | автор: Лиор Бен-ДавидПрежде чем мы сможем начать кодирование, мы сначала должны установить MatPlotLib, что мы можем сделать с помощью pip python -m pip install -U matplotlib MatPlotLib — это простая в использовании библиотека, которая имеет различные инструменты чтобы помочь визуализировать 2D и 3D данные. В верхней части нашего файла мы собираемся импортировать все необходимые инструменты из MatPlotLib, а также NumPy, математическую библиотеку, которая устанавливается вместе с MatPlotLib. import matplotlib.pyplot as plt Теперь давайте настроим 3D-графику. MatPlotLib делает это невероятно простым. Во-первых, мы собираемся создать оси нашего графика, которые мы укажем как 3D ax = plt.axes (projection = '3d') . рисовать пару точек в трехмерном пространстве. Чтобы построить график этих точек, мы собираемся создать массив координат для каждого измерения x = [0, 1, 2] Это будет хранить 3 точки: (0, 3, 1), (1, 4, 2) и (2, 4,3).MatPlotLib будет перебирать массивы, выбирая соответствующие координаты из 3 массивов. Наконец, чтобы построить значения по нашим осям, мы сделаем: ax.scatter (x, y, z) и создадим окно, чтобы показать нам наш красивый график: plt.show () Если мы запустим этот скрипт Python, мы должны увидеть окно со следующей диаграммой рассеяния: Теперь обратите внимание, что это только график точек, которые мы указали, но не рисует кривую между ними.Чтобы провести кривую между ними. Мы собираемся заменить нашу функцию ax.scatter () на: ax.plot (x, y, z) Затем мы видим: Прежде чем продолжить, наш код на этом этапе: import matplotlib. pyplot as plt Достаточно просто! А теперь давайте разберемся с графиком более интересным. Чтобы приступить к созданию нашей параметрической модели, мы собираемся импортировать те же вещи и таким же образом создавать наши оси.Однако, прежде чем мы определим наши массивы x, y и z, нам нужно создать нашу независимую переменную t, функциями которой будут координаты x, y и z. Для нашего первого примера мы собираемся построить график параметрической функции: Мы собираемся создать наши значения t с помощью функции linspace () NumPy, которая дает нам набор значений между границами, которые мы можем указать t = np. linspace (0,90,100) Это создаст массив t, который имеет 100 равномерно распределенных значений от 0 до 90. Затем давайте определим наши значения x, y и z в терминах нашего параметра t: x = np.sin (t / 5) Теперь у нас есть массивы x, y и z, которые MatPlotLib будет использовать для построения параметрического построения. После добавления двух функций для построения и отображения графика мы получаем: import matplotlib.pyplot as plt Запустив это, мы получаем: И вот и наша спираль! Чтобы сделать любой параметрический, просто замените определения x, y и z на нужные вам функции! Вот еще несколько интересных кривых, которые вы можете построить с помощью 3D-параметров: x = ln (t), y = sin (t), z = tcos (t) x = sin (t) cos (2.3t), y = sin (t) sin (2.3t), z = cos (t)Понимание параметрического построения графиков «Gnuplotting4 июня 2010 г. | 6 комментариев Если у кого-то есть система координат с n-мерностью, то одно из измерений может быть выражено n-1 другими измерениями, например.грамм. г = е (х, у). 2D футлярВ случае 2D у нас есть только одно свободное измерение: y = f (x) => x = fx (t), y = fy (t). На рис.1 мы видим связи между угловой координатой x = r cos (t) y = r cos (π / 2-t) = r sin (t) Используя результат выше, очень легко построить круг: установить параметрический установить trange [0: 2 * pi] # Параметрические функции для круга fx (t) = r * cos (t) fy (t) = r * sin (t) график fx (t), fy (t) 3D футлярВ трех измерениях мы имеем дело: z = f (x, y) => x = fx (u, v), y = fy (u, v), z = fz (u, v). На рис.3 мы видим связь между двумя угловыми переменными x = r cos (v) cos (u) y = r cos (v) sin (u) г = г грех (и) Используя параметрические переменные установить параметрический установить urange [0: 3.0 / 2 * pi] установить vrange [-pi / 2: pi / 2] # Параметрические функции для сферы fx (v, u) = r * cos (v) * cos (u) fy (v, u) = r * cos (v) * sin (u) fz (v) = r * sin (v) пятно fx (v, u), fy (v, u), fz (v) Результат показан на рис.4. Обратите внимание, что мы должны использовать 3.0 / 2, потому что 3/2 для Gnuplot равно 1! Нахождение параметрических уравнений для графикаНабор параметрических уравнений не уникален для данного графа. Например, следующие наборы параметрических уравнений приводят к одному и тому же прямоугольному уравнению и, таким образом, представляют один и тот же график.
Чтобы найти набор параметрических уравнений для графика, представленного как y = x 2 + 2 при t = x + 2, пусть t = x. Переключение ролей t и x в этом уравнении дает одно из параметрических уравнений: t = x + 2 → x = t + 2 Теперь подставьте выражение для x в прямоугольное уравнение y = x 2 + 2, чтобы получить второе параметрическое уравнение. y = x2 + 2 y = (t + 2) 2 + 2 y = t2 + 4t + 4 + 2 y = t2 + 4t + 6 Таким образом, набор параметрических уравнений для графика, представленного как y = x 2 + 2, имеет вид x = t + 2 y = t2 + 4t + 6 Теперь, когда определены оба параметрических уравнения, можно построить общий график с выбранными значениями параметра.
РУКОВОДСТВО ПО ПОИСКУ ПАРАМЕТРИЧЕСКИХ УРАВНЕНИЙ ДЛЯ ГРАФИКА: 1.Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. В результате получится одно параметрическое уравнение. 2. Подставьте выражение для переменной на шаге 1 в прямоугольное уравнение. В результате получится второе параметрическое уравнение. 3. Нарисуйте кривую. Попробуем пару примеров. Пример 1. Найдите набор параметрических уравнений для прямоугольного уравнения y = x 2 + 1, учитывая t = 2 — x.Затем нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой.
Пример 2: Найдите набор параметрических уравнений для прямоугольного уравнения y = 2×2 + 1 при t = x.Затем нарисуйте график с точками в точке t = {0,1,2,3,4} и укажите ориентацию кривой.
Параметрические кривые — определение, графики и примерыИзучение параметрических кривых даст нам еще одну со специальными атрибутами (время, чтобы быть конкретным). Бывают случаи, когда моделирование величин с помощью параметрических кривых более полезно, чем их графическое отображение в известных нам системах координат — прямоугольных и полярных системах координат. Вот почему так важно, чтобы мы научились строить и интерпретировать параметрические кривые. Параметрические кривые позволяют нам графически отображать отношения между двумя или более величинами и в то же время отображать направления или ориентации каждой величины. В этой статье мы оглянемся на то, что мы знаем о параметрических уравнениях до сих пор. Мы также установим основы, необходимые для параметризации и построения графиков параметрических кривых. К концу этого обсуждения у вас будет необходимый набор инструментов для построения графиков кривых общих плоскостей в их параметрической форме.Мы также покажем вам, как некоторые коники на плоской кривой могут быть определены более простыми параметрическими кривыми. Что такое параметрическая кривая?Параметрическая кривая — это , определяемая соответствующими параметрическими уравнениями : $ x = f (t) $ и $ y = g (t) $ в заданном интервале. Параметрические кривые подчеркивают ориентацию каждого набора величин относительно времени . В прямоугольной системе координат мы ограничены определением функций $ y = f (x) $, которые проходят проверку вертикальной линии.Если вы заметили, мы работали с графиками, такими как круг или эллипс, которые явно не проходят проверку вертикальной линии. Невозможность определить круги и другие пересекающиеся кривые (например, показанная выше) как одна функция становится проблематичной, когда мы позже разберемся со скоростью ее изменения. Вот почему так важно разработать новый подход к определению таких кривых. \ begin {выравнивание} x & = f (t) \\ y & = g (t) \ end {выравнивание} Мы начинаем с определения наших переменных $ x $ и $ y $ с помощью нового параметра — $ t $.Следовательно, два приведенных выше уравнения — это то, что мы называем параметрическими уравнениями. Точки $ (x, y) = (x (t), y (t)) $ — это точки, которые составляют график параметрической кривой . Как теперь $ t $ влияет на нашу кривую? Новый параметр $ \ boldsymbol {t} $, определяет направление кривой .
Чтобы побудить вас еще больше изучить эту тему, позвольте нам записать три основных преимущества использования параметрических кривых:
Теперь, когда мы установили важность параметрических кривых, а также их ключевых компонентов, давайте освежим наше понимание параметризации уравнений и их графиков. Как параметризовать кривую?Если задана плоская кривая, мы можем параметризовать ее до параметрической кривой, переопределив $ x $ и $ y $ как набор параметрических уравнений, определяемых параметром $ t $.Существует бесконечно много способов параметризации данной кривой — важно то, что их определение как плоская кривая остается прежним. Самый простой способ параметризовать кривую — установить $ x = t $.
Эта стратегия работает, когда мы хотим параметризовать линию. Мы просто используем $ x = t $ и $ y = mt + b $. Это позволяет нам наблюдать поведение кривой при увеличении $ t $. Однако бывают случаи, когда при выборе правильных параметрических уравнений лучше выработать стратегию. Позвольте нам показать вам стандартный способ переопределения уравнений окружностей с помощью параметрических уравнений:
Это две наиболее распространенные кривые, которые мы обычно параметризируем, и лучше всего, если вы освоите их общие параметрические формы, чтобы сэкономить ваше время в дальнейшем. Конечно, идея остается той же для остальных плоских кривых — пока наши определенные параметрические кривые по-прежнему представляют те же самые плоские кривые и $ t $ находится в заданной области. Мы также можем отменить процесс параметризации, удалив параметры . Мы просто применяем нашу алгебраическую технику к , удаляя $ \ boldsymbol {t} $ в уравнениях , $ x = f (t) $ и $ y = g (t) $.2 = 4 (x +16) $ — парабола с вершиной в точке $ (- 4, 0) $. Исключение параметров полезно, когда мы хотим понять или спрогнозировать форму параметрической кривой, используя наши знания о плоских кривых. Как построить параметрическую кривую?Теперь, когда мы знаем, как параметризовать кривые, пора определить шаги, необходимые для построения графиков параметрических кривых. Ниже приведены полезные рекомендации, которые следует помнить при графическом отображении параметрических кривых с учетом их параметрических уравнений:
Мы фактически показали примеры построения графиков параметрических кривых линейной функции и окружностей в связанных статьях. Взгляните на них, если вам нужны примеры построения графиков этих двух наиболее распространенных параметрических кривых.2 — 4 $ и $ y = 4t $, где $ t $ находится в пределах $ [- 4, 4] $. Сначала мы назначаем ключевые значения для $ t $. В идеале это значения, с которыми легко работать с нашими параметрическими уравнениями. 2 — 4 = -12 \ end {выровнено} | \ begin {выровнено} y = 4 (4) = 16 \ end {выровнено} | \ begin {Выровненный} (-12, 16) \ end {Выровненный} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Постройте эти точки на плоскости $ xy $, затем соедините их плавной кривой.Включите стрелки вдоль кривой, чтобы выделить направление кривой от $ t = -4 $ до $ t = 4 $.
Убедитесь, что упорядоченные пары построены в порядке от $ t = -4, (12, -16) $ до $ t = 4, (12, 16) $. Это поможет вам запомнить направление параметрической кривой и упростит нанесение меток на стрелки и выделение направления кривой.
Как мы и предсказывали, кривая уравнения представляет собой параболу с центром в точке $ (- 4, 0) $. Это подчеркивает важность знания того, как исключить параметры для прогнозирования формы параметрической кривой.{\ prime} (t)} \\ & = \ dfrac {4} {2t} \\ & = \ dfrac {2} {t} \ end {align}
Отсюда мы видим, что $ \ dfrac {dy} {dx} $ не определено, когда $ t = 0 $, поэтому критическая точка функции находится в $ t = 0 $. Используя таблицу значений из предыдущего раздела, мы можем видеть, что когда $ t = 0 $, $ (x, y) = (-4, 0) $, который является поворотной точкой параметрической кривой.
Когда мы знаем критические точки параметрической кривой, мы можем сохранить наши параметрические кривые для построения точек времени.Вместо этого мы можем использовать конечные и критические точки для построения параметрической кривой.
Не волнуйтесь, мы подготовили для вас больше задач, над которыми вы сможете поработать и проверить свои знания о параметрических кривых. Просмотрите статью еще раз, а когда будете готовы, переходите к следующему разделу!
Пример 1
Изобразите кривую, заданную параметрическими уравнениями $ x = 2 \ sqrt {t} $ и $ y = t- 2 $, где $ t \ geq 0 $. Включите стрелки, показывающие ориентацию результирующей параметрической кривой.
Решение
Мы начинаем с присвоения целочисленных значений $ t $, которые больше или равны $ 0 $. Оцените каждое из значений в $ x = 2 \ sqrt {t} $ и $ y = t- 2 $, чтобы найти несколько упорядоченных пар, которые помогут нам построить параметрическую кривую. Вот сводка наших вычислений, когда $ t = \ {0, 1, 4, 9, 16 \} $.
\ begin {align} \ boldsymbol {t} \ end {align} | \ begin {align} \ boldsymbol {x = 2 \ sqrt {t}} \ end {выравнивается} | \ begin {выравнивается} \ boldsymbol {y = t- 2} \ end {выравнивается} | \ begin {выравнивается} \ boldsymbol {(, y)} \ end {выравнивается} | |
\ begin {выравнивается} 0 \ end {выравнивается} | \ begin {выравнивается} x = 2 \ sqrt {0} = 0 \ end {выравнивается} | \ begin {выравнивается} y = 0 -2 = -2 \ end {выравнивается} | \ begin {выравнивается} (0, -2) \ end {выравнивается} | |
\ begin {выравнивается} 1 \ end {выравнивается} | \ begin {выравнивается } x = 2 \ sqrt {1} = 2 \ end {выровнен} | \ begin {выровнен} y = 1-2 = -1 \ end {выровнен} | \ begin {выровнен} (2, -1) \ end {выравнивается} | |
\ begin {выравнивается} 4 \ end {выравнивается} | \ begin {выравнивается} x = 2 \ sqrt {4} = 4 \ end {выравнивается} | \ begin {выравнивается} y = 4 -2 = 2 \ end {выравнивается} | \ begin {выравнивается} (4, 2) \ end {выравнивается} | |
\ begin {выравнивается} 9 \ end {выравнивается} | \ begin {выравнивается} x = 2 \ sqrt {9} = 6 \ end {выравнивается} | \ begin {выравнивается} y = 9 -2 = 6 выровнен} x = 2 \ sqrt {16} = 8 \ end {выравнивается} | \ begin {выравнивается} y = 16-2 = 14 \ end {выравнивается} | \ begin {выравнивается} (8, 14) \ end {align} |
Теперь нарисуйте пять упорядоченных пар на плоскости $ xy $, а затем соедините их плавной кривой.
Представляет параметрическую кривую, $ x = 2 \ sqrt {t} $ и $ y = t- 2 $, и не забудьте включить стрелки, чтобы выделить ориентацию кривой, когда.
Пример 2
Удалите параметр для параметрических уравнений, $ x = \ sec t $ и $ y = \ tan t $. Используйте полученное прямоугольное уравнение для построения плоской кривой. Включите стрелки, показывающие ориентацию результирующей параметрической кривой.
Решение
Нам будет проще исключить параметр, если возвести в квадрат оба параметрических уравнения.2 = 0 $. Фактически это гипербола с центром в $ (0, 0) $ и вершинами в $ (- 1, 0) $ и $ (1, 0) $.
Чтобы узнать направление плоской кривой, давайте оценим $ t $ при различных значениях, чтобы найти несколько упорядоченных пар от $ t = 0 $ до $ t = 2 \ pi $.
\ begin {align} \ boldsymbol {t} \ end {align} | \ begin {align} \ boldsymbol {x = \ sec t} \ end {align} | \ begin {Выровнен} \ boldsymbol {y = t- 2} \ end {Выровненный} | \ begin {Выровненный} \ boldsymbol {(, y)} \ end {Выровненный} |
\ begin {Выровненный} 0 \ end {выровнено} | \ begin {выровнено} x = \ sec 0 = 1 \ end {выровнено} | \ begin {выровнено} y = \ tan 0 = 0 \ end {выровнено} | \ begin {выравнивается} (1, 0) \ end {выравнивается} |
\ begin {выравнивается} \ dfrac {\ pi} {3} \ end {выравнивается} | \ begin {выравнивается } x = \ sec \ dfrac {\ pi} {3} = 2 \ end {align} | \ begin {align} y = \ tan \ dfrac {\ pi} {3} = \ sqrt {3} \ конец {выровненный} | \ begin {выровненный} (2, 1.73) \ end {выравнивается} |
\ begin {выравнивается} \ dfrac {2 \ pi} {3} \ end {выравнивается} | \ begin {выравнивается} x = \ sec \ dfrac {2 \ pi} {3} = -2 \ end {выравнивается} | \ begin {выравнивается} y = \ tan \ dfrac {2 \ pi} {3} = — \ sqrt {3} \ end {выравнивается} | \ begin {выравнивание} (-2, -1,73) \ end {выравнивание} |
\ начало {выравнивание} \ pi \ end {выравнивание} | \ начало {выровнено} x = \ сек \ пи = -1 \ конец {выровнено} | \ begin {выровнено} y = \ tan \ pi = 0 \ end {выровнено} | \ begin {выровнено} (-1, 0) \ end {Выровнено} |
\ begin {Выровнено} \ dfrac {4 \ pi} {3} \ end {Выровнено} | \ begin {Выровнено} x = \ sec \ dfrac {4 \ pi} { 3} = -2 \ end {выравнивается} | \ begin {выравнивается} y = \ tan \ dfrac {4 \ pi} {3} = \ sqrt {3} \ end {выравнивается} | \ begin {выровнено} (-2, 1.73) \ end {выравнивается} |
\ begin {выравнивается} \ dfrac {5 \ pi} {3} \ end {выравнивается} | \ begin {выравнивается} x = \ sec \ dfrac {5 \ pi} {3} = 2 \ end {выравнивается} | \ begin {выравнивается} y = \ tan \ dfrac {5 \ pi} {3} = — \ sqrt {3} \ end {выравнивается} | \ begin {выравнивание} (2, -1.73) \ end {выравнивание} |
Постройте эти упорядоченные пары и соедините их плавной кривой. Конечно, этот пример сложен, поскольку точки разбросаны по четырем квадрантам.Вот почему удаление параметров может быть полезным — мы воспользуемся тем фактом, что полученная плоская кривая представляет собой гиперболу, чтобы правильно построить кривую.
Это отличный пример параметризации конического сечения. Как видите, поиск упорядоченных пар с помощью параметрической формы проще, чем прямой поиск упорядоченных пар с использованием прямоугольной формы. Это становится более очевидным при работе с более сложными коническими сечениями.
Пример 3
Запишите два разных набора параметрических уравнений для параметризации уравнения, $ y = 3x + 5 $.
Решение
Прежде чем мы начнем, помните, что прямоугольные уравнения могут быть представлены несколькими наборами параметрических уравнений. Это означает, что мы можем показать наборы параметрических уравнений, отличные от тех, которые вы могли бы записать. Важно то, что ваш набор параметрических уравнений возвращает $ y = 3x + 5 $, когда мы удаляем параметр $ t $.
Для наших двух наборов параметрических уравнений мы положим 1) $ x $ равным $ t $ и 2) $ x $ равным $ t + 1 $. Мы подставим каждое из этих уравнений в прямоугольное уравнение.
\ begin {align} \ boldsymbol {x = t} \ end {align} | \ begin {align} \ boldsymbol {x = t + 1} \ end {align} |
\ begin {выравнивается} y & = 3 (t) + 5 \\ & = 3t + 5 \ end {выравнивается} | \ begin {выравнивается} y & = 3 (t +1) + 5 \\ & = 3t + 8 \ end {align} |
Это означает, что уравнение $ y = 3x + 5 $ может быть выражено в виде следующих наборов параметрических уравнений: $ x = t, y = 3t + 5 $ и $ x = t + 1, y = 3t + 8 $.
Ваш комментарий будет первым