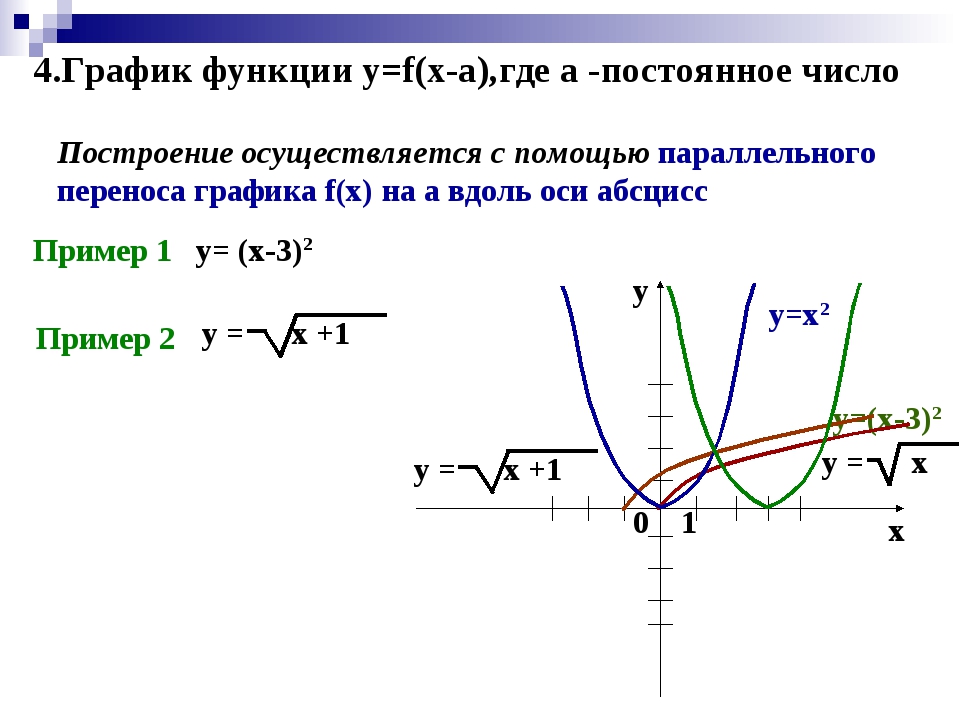
Универсальный калькулятор комплексных чисел онлайн
| Вы ввели следующее выражение |
| Окончательный результат выражения |
Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!
Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)
Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание.
Напомним как производятся эти операции:
Сложение двух комплексных чисел
Вычитание двух комплексных чисел
Умножение двух комплексных чисел
Деление двух комплексных чисел
Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты.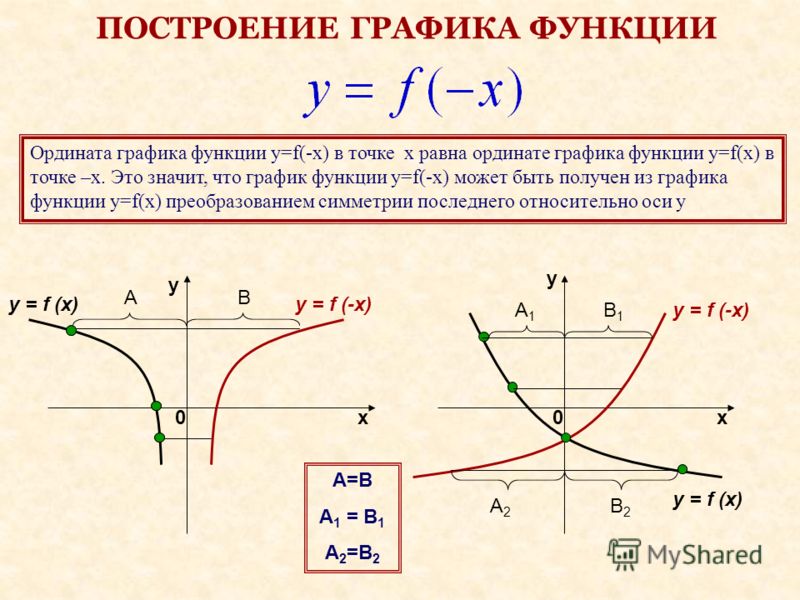
возведение в степень
синус(sin)
косинус(cos)
натуральный логарифм(ln)
тангенс(tan)
артангенс(atan)
арксинус(asin)
арккосинус(acos)
гиперболический синус(sinh)
гиперболический косинус(cosh)
гиперболический тангенс(tanh)
Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i
Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)
Примеры
(-4-1i)/((-5-2i)+7-1.2i)
или в более наглядном виде
Получаем
Наш запрос выглядит так как мы его и сформировали в самом начале
calc_i (-4-1i)/((-5-2i)+7-1.
(1/2))
Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734
Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.
- Уравнение пятой степени. Частное решение. >>
Калькулятор онлайн — Решение комплексных чисел: сумма, разность, произведение, частное, n-ая степень и корень n-ой степени (с подробным решением)
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Понятие комплексного числа
Определение.
Комплексными числами называют выражения вида \(а + bi\) где \(a\) и \(a\) — действительные числа, а \(i\) — некоторый символ, для которого
по определению выполняется равенство \( i^2=-1 \).
Название «комплексные» происходит от слова «составные» — по виду выражения \(а + bi\). Число \(а\) называется действительной частью
комплексного числа \(а + bi\), а число \(b\) — его мнимой частью. Число \(i\) называется мнимой единицей.
Например, действительная часть комплексного числа \(2-3i\) равна \(2\), мнимая часть равна \(-3\).
Запись комплексного числа в виде \(а + bi\) называют алгебраической формой комплексного числа.
Равенство комплексных чисел
Определение.
Два комплексных числа \(a + bi\) и \(c + di\) называются равными тогда и только тогда, когда \(a =c\) и \(b =d\), т. е. когда равны
их действительные и мнимые части.
Сложение и умножение комплексных чисел
Операции сложения и умножения двух комплексных чисел определяются следующим образом.
Определения.
Суммой двух комплексных чисел \(a+ bi\) и \(c + di\) называется комплексное число \( (a+c) + (b+d)i \), т.
2=-1 \).
Основные свойства сложения и умножения комплексных чисел
1. Переместительное свойство
\( z_1 + z_2 = z_2 + z_1 \),
\( z_1z_2 = z_2z_1 \)
2. Сочетательное свойство
\( (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) \),
\( (z_1z_2)z_3 = z_1(z_2z_3) \)
3. Распределительное свойство
\( z_1(z_2 + z_3) = z_1z_2 + z_1z_3 \)
Комплексно сопряженные числа
Определение.
Сопряженным с числом \(z = a + bi\) называется комплексное число \(a -bi\), которое обозначается \( \overline{z} \), т. е.
\( \overline{z} = \overline{a+bi} = a-bi \)
Например :
\( \overline{3 + 4i} = 3-4i \),
\( \overline{-2-5i} = -2+5i \),
\( \overline{i} = -i \)
Отметим, что \( \overline{a-bi} = a+bi \), поэтому для любого комплексного числа \(z\) имеет место равенство
\( \overline{(\overline{z})} = z \)
Равенство \( \overline{z} = z \) справедливо тогда и только тогда, когда \(z\) — действительное число.
2} \)
Из данной формулы следует, что \( |z| \geqslant 0 \) для любого комплексного числа \(z\), причем \(|z|=0\) тогда и только тогда, когда \(z=0\), т.е. когда \(a=0\) и \(b=0\).
Вычитание комплексных чисел
Определение.
Комплексное число \( (-1)z \) называется противоположным комплексному числу \(z\) и обозначается \(-z\).
Если \(z = a + bi\), то \(-z = -a — bi\)
Например : \( -(3-5i) = -3+5i \)
Для любого комплексного числа \(z\) выполняется равенство
\( z+(-z) = 0 \).
Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел \(z_1\) и
\(z_2\) существует, и притом только одно, число \(z\), такое, что
т.е. это уравнение имеет только один корень.
Деление комплексных чисел
Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел \( z_1 \) и
\( z_2 \neq 0 \) существует, и притом только одно, число \( z \), такое, что \( z \cdot z_2=z_1 \) т.
2_2}i $$
Геометрическая интерпретация комплексного числа.
Комплексная плоскость
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число \(a + bi\) можно рассматривать как пару действительных чисел \((a; b)\). Поэтому естественно комплексные числа изображать точками плоскости.
Пусть на плоскости задана прямоугольная система координат. Комплексное число \(z = a + bi\) изображается точкой плоскости с координатами \((a; b)\), и эта точка обозначается той же буквой \(z\).
Такое соответствие между комплексными числами и точками плоскости взаимно однозначно: каждому комплексному числу \(a + bi\)
соответствует одна точка плоскости с координатами \((a; b)\) и, наоборот, каждой точке плоскости с координатами \((a; b)\) соответствует
одно комплексное число \(a + bi\). Поэтому слова «комплексное число» и «точка плоскости» часто употребляются как синонимы. Так, вместо
слов «точка, изображающая число \(1 + i\)» говорят «точка \(1 + i\)».
Можно, например, сказать «треугольник с вершинами в точках \(i, \; 1+i, \; -i \)».
При такой интерпретации действительные числа \(a\), т.е. комплексные числа \(a+0i\), изображаются точками с координатами \((a; 0)\),
т.е. точками оси абсцисс. Поэтому ось абсцисс называют действительной осью.
Чисто мнимые числа \(bi = 0+bi\) изображаются точками с координатами \((0; b)\), т.е. точками оси ординат, поэтому ось ординат называют
Например, точка \((0; 1)\) обозначается \(i\), точка \((0; -1)\) — это \(-i\) , точка \((0; 2)\) — это точка \(2i\).
Начало координат — это точка \(O\).
Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью.
Отметим, что точки \(z\) и \(-z\) симметричны относительно точки \(O\) (начала координат), а точки \( z \) и \( \overline{z} \) симметричны
относительно действительной оси.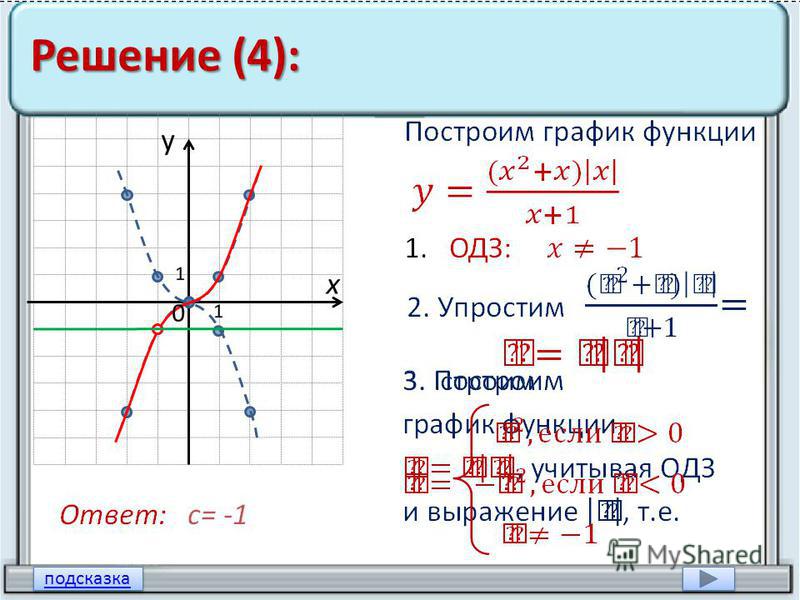
2} \) — модуль комплексного числа \(z\), \( \varphi \) — его аргумент. Запись комплексного числа в
виде (4), где \(r>0\), называют тригонометрической формой комплексного числа \(z\).
Умножение и деление комплексных чисел, записанных в тригонометрической форме
С помощью тригонометрической формы записи комплексных чисел удобно находить произведение и частное комплексных чисел
\(z_1\) и \(z_2\). Если два комплексных числа записаны в тригонометрической форме :
\( z_1z_2 = r_1r_2(\cos(\varphi_1+\varphi_2) +i\sin(\varphi_1+\varphi_2)) \)
Из этой формулы следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
Формула для нахождения частного комплексных чисел:
$$ \frac{z_1}{z_2} = \frac{r_1}{r_2}(\cos(\varphi_1-\varphi_2) +i\sin(\varphi_1-\varphi_2)) $$
Из этой формулы следует, что модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность
аргументов делимого и делителя является аргументом частного.
{-i\frac{\pi}{2}}.$
Представление синусоидальных величин с помощью векторов и комплексных чисел (Лекция N 3)
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии
осуществляется в основном на переменном токе.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем
| , | (1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
| , | (2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.
01¸10
Гц – в системах автоматического регулирования, в аналоговой вычислительной технике)
– до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны:
радиолокация, радиоастрономия). В РФ промышленная частота f
= 50Гц.
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е
— мгновенное значение ЭДС ;р— мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
— амплитуда тока;
— амплитуда напряжения;
— амплитуда ЭДС.
Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
| , | (3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при
помощи уравнений с тригонометрическими функциями, представить в виде векторов
на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2соответствуют уравнения:
.
Значения аргументов синусоидальных функций и называются фазами синусоид,
а значение фазы в начальный момент времени (t=0): и — начальной фазой
().
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2угол сдвига фаз:
.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю
амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой
стрелки (в ТОЭ данное направление принято за положительное) с угловой
частотой, равной w. Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат
равны мгновенным значениям ЭДС е1 и е2(рис. 3). Совокупность
векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют
векторными диаграммами. При построении векторных диаграмм векторы удобно
располагать для начального момента времени (t=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно
тому, что система декартовых координат сама вращается против часовой стрелки
со скоростью w.
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным
и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных
значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
и .
Результирующий ток также будет синусоидален:
.
Определение амплитуды и начальной фазы этого тока путем соответствующих
тригонометрических преобразований получается довольно громоздким и мало наглядным,
особенно, если суммируется большое число синусоидальных величин.
Значительно
проще это осуществляется с помощью векторной диаграммы.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями
с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической или
алгебраической — формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
.
Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
| , | (4) |
Комплексное число удобно представить в виде произведения двух комплексных чисел:
| , | (5) |
Параметр , соответствующий положению
вектора для t=0 (или на вращающейся со скоростью w
комплексной плоскости), называют комплексной амплитудой: , а параметр — комплексом мгновенного
значения.
Параметр является оператором поворота вектора на угол wt относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
| , | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
,
— то для записи ее в показательной форме, необходимо найти начальную фазу , т.
е. угол, который образует
вектор с положительной полуосью
+1:
.
Тогда мгновенное значение напряжения:
,
где .
При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)
| , | (7) |
а при (третий квадрант)
| (8) |
или
| (9) |
Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:
где ;
.
Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
.
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:
. |
(10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
.
Литература
1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2.
Какой практический смысл имеет представление синусоидальных величин с использованием
комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
5. На рис. 5 , а . Определить .
Ответ: .
Вычисляем гамма-функцию
Данный калькулятор сделан для вычисления гамма-функции. Давайте вспомним что такое гамма-функция. Это такая функция в мире математике, которая расширяет понятие факториала на поле комплексного или целого числа.
Есть не один способ вычисления гамма-функции, но в данном калькуляторе был использован метод аппроксимации Ланцоша. Подробней о данном методе можно прочитать просто зайдя по данной ссылке:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.
C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Комплексные числа и операции с ними
Содержание
Обнаружили ошибку? Выделите ее мышью и нажмитеВведение
Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для , а функция определена для .
Однако, ограниченная область определения функций на множестве вещественных чисел не означает,
что , или не имеют смысла.
Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том,
что не может быть представлено вещественным числом.
Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1),
на которой мы можем откладывать рациональные и иррациональные вещественные числа.
Но на этой прямой нет числа , значит его надо искать вне числовой прямой.
Таким образом мы должны расширить множество вещественных чисел до множества в котором значения ,
или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве,
как на множестве вещественных чисел.
Комплексная плоскость и мнимая единица
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .
Рисунок 1. Расширение множества вещественных чисел до множества комплексных числел
Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.
Для «навигации» по комплексной плоскости вводятся две прямые и ,
которые пересекаются в начале координат.
Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа.
Прямая называется мнимой осью и она перпендикулярна реальной оси .
Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.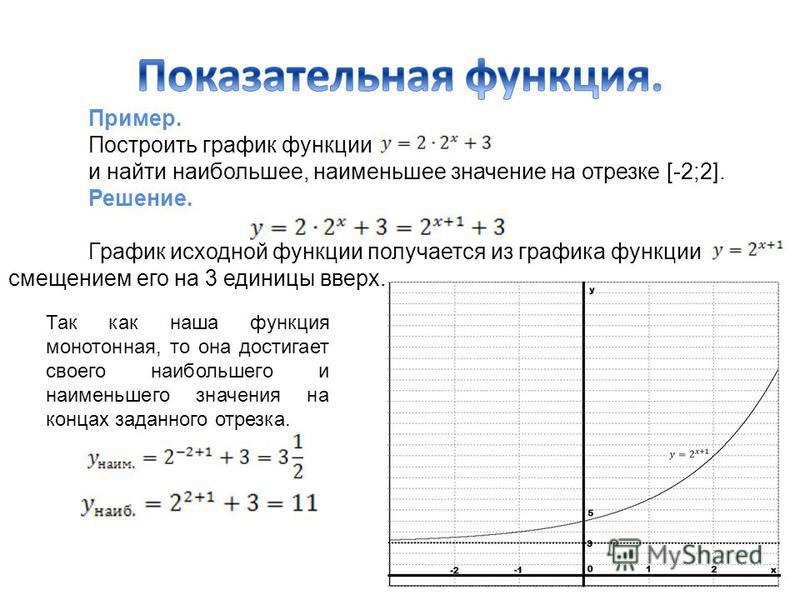
Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью и задает координату точки комплексной плоскости на мнимой оси .
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .
Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена
за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .
Если и , тогда число является действительным и располагается на реальной оси .
Если и , тогда число является чисто мнимым и располагается на мнимой оси .
Если и , тогда число располагается в одной из четвертей комплексной плоскости.
Модуль и фаза комплексного числа
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как
(1)
— неотрицательное вещественное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно реальной оси на некоторый угол , называемый фазой. Фаза комплексного числа может быть положительной или отрицательной, в зависимости от того в каком направлении относительно оси отсчитывать угол. Если угол поворота вектора на комплексной плоскости отсчитывать против часовой стрелки (как это показано на рисунке 1), то фаза будет принимать положительные значения, а если по часовой — то отрицательные.
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
(2)
Тогда комплексное число можно представить в тригонометрической форме:(3)
Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа, представленного в алгебраической форме:(4)
тогда(5)
где учитывает четверть комплексной плоскости в которой расположено число :(6)
Необходимость поправки возникает из-за того, что функция периодическая функция с периодом рад. В результате возвращает корректные значения только в интервале . Таким образом функция арктангенса не отличает четверть I от четверти III (в обоих случаях отношение положительное), а также не отличает четверть II от четверти IV (отношение отрицательное).На рисунке 2 показаны значения параметра , в зависимости от того в какой четверти комплексной плоскости расположено число.
Рисунок 2.
Значение поправки фазы комплексного числа в зависимости
от расположения на комплексной плоскости.
На рисунке 2а исходное комплексное число расположено в первой четверти комплексной плоскости и .
Тогда и значение фазы комплексного числа равно:
(7)
Рассмотрим случай, когда комплексное число расположено во второй четверти комплексной плоскости (рисунок 2б), т.е. и . В этом случае и угол также будет отрицательным (красная пунктирная линия). Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
(8)
Пусть комплексное число расположено в третьей четверти комплексной плоскости (рисунок 2в), т.е. и . В этом случае и угол будет положительным (красная пунктирная линия). Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
(9)
Если расположено в четвертой четверти комплексной плоскости (рисунок 2г),
т.
е. и , то в этом случае и угол
будет отрицательным и равным фазе комплексного числа без поправок ( рад):
(10)
Функция которая позволяет получить фазу комплексного числа c учетом четверти комплексной плоскости в которой расположено комплексное число называется функция арктангенс-2 и обозначается .Функция арктангенс-2 присутствует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.
Показательная форма комплексного числа. Формула Эйлера
Мы уже рассмотрели алгебраическую и тригонометрическую формы записи комплексного числа. Помимо алгебраической и тригонометрической формы существует также показательная форма комплексного числа:
(11)
связанная с тригонометрической формой формулой Эйлера:(12)
Cоотношение (12) легко доказать, если произвести разложение экспоненты в ряд Тейлора:
(13)
Представим ряд (13) в виде суммы четных и нечетных членов последовательности:(14)
Рассмотрим более подробно мнимую единицу в четной и нечетной степенях.
Из определения мнимой единицы можно сделать вывод, что , тогда , в свою очередь .
Таким образом, можно сделать вывод что .
Построим аналогичным образом соотношение для нечетных степеней: , тогда , в свою очередь и окончательно можно записать: . Тогда (14) можно представить как:
(15)
В выражении (15) первая сумма по четным степеням дает разложение в ряд Тейлора функции , а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции . Таким образом, получено доказательство справедливости формулы Эйлера (12).Необходимо отметить, что формула Эйлера является одной из важнейших в теории функций комплексного переменного. Так например при помощи формулы Эйлера можно связать математические константы и с использованием мнимой единицы :
(16)
Операции над комплексными числами. Комплексно-сопряженные числа
В данном параграфе мы кратко рассмотрим операции над комплексными числами.
Сумма двух комплексных чисел и представляет
собой комплексное число :
(17)
При сложении реальные и мнимые части комплексного числа также складываются. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3а).
Рисунок 3. Операции над комплексными числами
Разность двух комплексных чисел и представляет собой комплексное число
(18)
При вычитании реальные и мнимые части комплексного числа также вычитаются. На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов по правилу параллелограмма (рисунок 3б). На первом шаге из вектора формируется вектор (обозначенный пунктирной линией на рисунке 3б), после чего вектор складывается с вектором по правилу параллелограмма.Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:
(19)
Умножение комплексных проще выполнять если числа представлены в показательной форме:
(20)
При перемножении в показательной форме модули комплексных чисел перемножаются а фазы складываются.
Операция произведения комплексных чисел показано на рисунке 3в.
Введем понятие комплексно-сопряженного числа. Число является комплексно-сопряженным числу .
Комплексно-сопряженные числа отличаются знаком перед мнимой частью.
Графически комплексно-сопряженные числа показаны на рисунке 3г.
При этом можно заметить, что модули комплексно-сопряженных чисел равны , а фазы имеют противоположные знаки.
Произведение комплексно-сопряженных чисел
(21)
представляет собой действительное число равное квадрату модуля этих чисел.Из элементарных операций нам осталось рассмотреть лишь деление комплексных чисел. Рассмотрим результат деления комплексных чисел в показательной форме:
(22)
Таким образом, при делении комплексных чисел модуль частного равен частному модулей исходных чисел,
а фаза равна разности фаз исходных чисел.
При этом необходимо потребовать, чтобы был не равен нулю, иначе у нас появится деление на ноль при расчете модуля частного.
Рассмотрим теперь деление комплексных чисел в алгебраической форме:
(23)
Домножим и числитель и знаменатель на число, комплексно-сопряженное знаменателю:
(24)
Выводы
В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Введено понятие мнимой единицы.
Подробно рассмотрена комплексная плоскость и представление комплексных чисел в алгебраической, тригонометрической и показательной формах. Введены понятия модуля и фазы комплексного числа.
Рассмотрены основные арифметические операции над комплексными числами.
Показано как выполнять операции сложения, вычитания в алгебраической форме,
введено понятие комплексно-сопряженных чисел,
а также операции умножения и деления в показательной и алгебраической формах.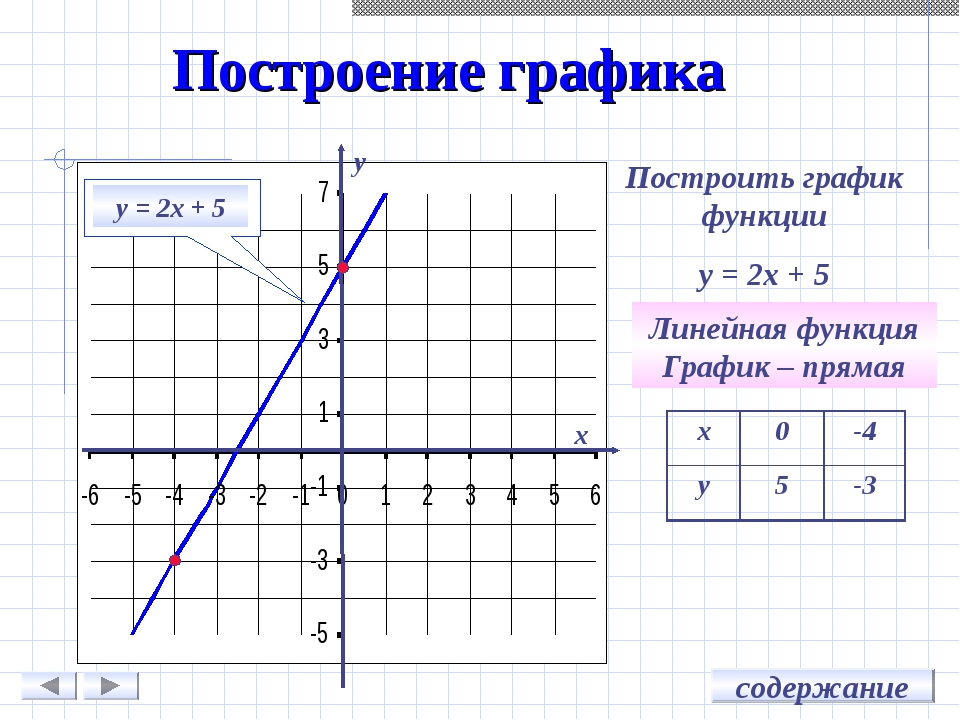
Мой мир
Вконтакте
Одноклассники
Список литературы
[1] Пантелеев А.В., Якимова А.С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. М: Высшая школа, 2011.
[2] Дубровин В.Т. Теория функций комплексного переменного. Теория и практика Казань: Казанский государственный университет, 2010. [PDF]
Последнее изменение страницы: 07.02.2021 (14:04:39)
Страница создана Latex to HTML translator ver. 5.20.11.14
Плоттер сложных функций
Вы можете использовать этот инструмент для построения графиков функций сложных, разделенных комплексных и двойных чисел, а также их обратных чисел в 2D и 3D.Основная цветовая схема и идея были полностью вдохновлены плоттером сложных функций Дэвида Бау, но моя цель состояла в том, чтобы моя версия работала быстрее (с использованием webgl) и имела больше функций (разделенные комплексные числа, двойные числа, трехмерное построение, инверсии) и более настраиваемый.
Базовое использование
Чтобы ввести функцию, наведите указатель мыши на нижнюю часть окна (или нажмите на мобильном устройстве) и щелкните 3 горизонтальные полосы, которые покажут вам интерфейс для ввода функций и настройки инструмента.В порядке чтения значки внизу экрана: справка, меню (три горизонтальные полосы, упомянутые выше), загрузка фонового изображения (это позволяет вам управлять изображением по вашему выбору с помощью введенной вами функции), загрузка и полноэкранный режим.
Переменная z предоставляет координаты x и y каждого пикселя в форме x + iy.
Любые другие переменные станут переключаемыми значениями в меню, которые вы можете использовать для управления программой.
Когда пользователь вводит функцию, каждая точка (x, y) окрашивается в соответствии с тем, где они приземляются под f (x + iy).Если вы хотите, чтобы точки были окрашены в зависимости от того, где они возникли, а не где они оказались, включите «инвертировать» в настройках, чтобы инвертировать функцию численно.
Это довольно дорого, поэтому подумайте об уменьшении AA или уменьшении окна, если у вас возникли проблемы (вы также можете настроить параметры инверсии в меню).Константы
eпи или π
i
Операторы и функции
Примечание: ниже u и v используются для представления любого выраженияГруппировка (u)
Величина | u | или ‖u‖
Conjuagte u *
Основная арифметика : u + v, u-v, u * v или u⋅v, u / v или u ÷ v
Для умножения вы также можете просто записать переменные рядом друг с другом i.v, ln (u), log (u), log (u, b) (аргумент b в журнале может использоваться для указания базы, по умолчанию e)
Факториал : u! (действительно гамма (u + 1))
Триггерные функции : sin (u), cos (u), tan (u)
Обратные триггерные функции : asin (u), acos (u), atan (u)
Гиперболические триггерные функции : sinh (u), cosh (u), tanh (u)
Угол : arg (u)
Получить действительные / мнимые компоненты : re (u), im (u)
Знак : sgn (u)
Шаг : шаг (u)
Квадратный корень : sqrt (z) или √ (z) (или просто использовать возведение в степень)
Гамма-функция : гамма (u) или Γ (u)
Дзета-функция : zeta (u) или ζ (z)
Итерированная функция {var = update, var = initial, итерация} (думайте о var = update как о теле цикла for, e .
г. {z ‘= z’ +1, z ‘= 0, 5} инициализирует z’ равным 0, а затем добавляет единицу к нему на каждой из 5 итераций). Значение var по умолчанию — z ‘, вам не нужно указывать «z’ =», если вы планируете использовать z ‘(так что {z’ +1, 0, 5} также работает), но если вы хотите использовать другую переменную, например «y», вам нужно будет указать ее ({y = y +1, y = 0, 5}). Итерации должны быть целым числом
Производная по z (u) ‘(производные можно вкладывать сколь угодно глубоко, но из-за ограничений арифметических операций с плавающей запятой результаты довольно быстро ухудшаются). Обратите внимание на скобки, z’ в повторяющейся функция не является производной от z.
Интеграл w.r.t z $ (u) или $ [нижний] (u) или $ [нижний, верхний] (u). Когда параметры нижней и верхней границы опущены, используются значения по умолчанию 0 и z соответственно. Интегрируется по линии от нижней к верхней границе. Вы также можете использовать $ [lower, upper, variable] (u), чтобы указать переменную для интегрирования по умолчанию z.
Используйте $ [lower, upper, variable, iter] (u), чтобы указать количество шагов, которые нужно предпринять при интегрировании. Вы можете использовать ∫ вместо $.
Сумма от 1 до | count |: Sum (u, count) или ∑ (u, count) e.z, 100н).
Прочие
Чтобы сгенерировать парсер для пользовательского ввода, я использовал peg.js. Сгенерированный файл парсера включен вместе с файлом грамматики, который я написал и использовал для генерации парсера.Wolfram | Примеры альфа: комплексный анализ
Другие примеры
Комплексные числаАнализировать свойства функций комплексной переменной или выполнять основную арифметику, находить корни или применять функции к комплексным числам.
Выполните простую арифметику над комплексными числами:
Примените функции к комплексным числам:
Еще примеры
Комплексные функции
Постройте функции комплексной переменной или вычислите и проанализируйте их свойства.
Вычислить свойства функции сложной переменной (используйте переменную z ):
Еще примеры
Поляки
Найдите полюса сложной функции в заданном домене или во всей комплексной плоскости.
Найдите полюса сложной функции:
Найдите полюса в указанном домене:
Еще примеры
Остатки
Вычислить остатки функций на комплексной плоскости в точке или в указанной области.
Вычислить остаток функции в точке:
Вычислить вычеты в полюсах функции:
Вычислить остатки на полюсах в указанном домене:
Еще примеры
Римановы поверхности
Вычисление и визуализация римановых поверхностей для сложных функций.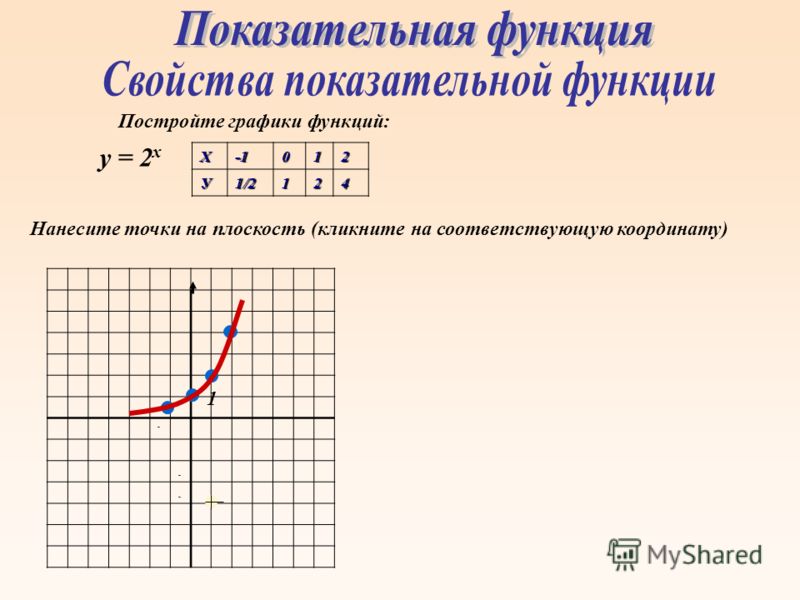
Визуализируйте риманову поверхность:
Еще примеры
Построение графиков комплексных чисел | Концепция, график и решенные примеры
Решенные примерыГ-жа Долма попросила своих учеников классифицировать следующие комплексные числа на основе квадранта, в котором они лежат.
Можете ли вы их классифицировать?
Решение
Давайте найдем точки, соответствующие каждому комплексному числу.
\ [\ begin {align} A & = 3 + 7i \; \; \; \; \; \; \; \ rightarrow (3,7) \\ [0,2 см] B & = 6-i \; \; \; \; \; \; \; \; \ rightarrow (6, -1) \\ [0,2 см] C & = — 2-4i \; \; \; \ rightarrow (-2, -4) \\ [0,2 см] D & = — 5 + 2i \; \; \; \ rightarrow (-5; 2) \ end {align} \]
Изобразим данные комплексные числа на комплексной плоскости.
Итак, данные комплексные числа можно классифицировать как:
| Квадрант 1 | 3 + 7i |
|---|---|
| Квадрант 2 | -5 + 2i |
| Квадрант 3 | -2-4i |
| Квадрант 4 | 6-я |
Итак, комплексные числа классифицируются. |
Дженни говорит Джолли, что точки \ (2-i, i \) и \ (2 + 3i \) образуют вершины прямоугольного треугольника.
Как вы думаете, она права? Обоснуйте свой ответ.
Решение
Допустим, что данные точки равны:
\ [\ begin {выровнено} A & = 2-я \; \; \; \; \ rightarrow (2, -1) \\ [0,2 см] B & = i \; \; \; \; \; \; \; \; \; \; \ rightarrow (0,1) \\ [0.2 \\ [0,3 см] 8 + 8 & = 16 \\ [0,3 см] 16 & = 16 \ конец {выровнено} \]
Таким образом, \ (A, B, \) и \ (C \) удовлетворяют теореме Пифагора.
Итак, \ (\ Delta ABC \) — прямоугольный треугольник.
Мы можем доказать то же самое, отметив все координаты на графике:
| \ (\ следовательно \) Данные точки образуют прямоугольный треугольник |
Город Лото нанесен на комплексную карту, как показано на рисунке.
Шоколадный домик находится в точке \ (3 + 7i \), а фабрика по производству тортов — в точке \ (- 1-3i \).
Главный въезд в город находится на полпути между шоколадным домом и кондитерской.
Вы можете рассчитать точку главного входа?
Решение
Комплексные числа \ (3 + 7i \) и \ (- 1-3i \) соответствуют точкам \ ((3, 7) \) и \ ((- 1, -3) \) на комплексной плоскости.
Чтобы вычислить точку главного входа, мы должны вычислить среднюю точку (3, 7) и (-1, -3).
Пусть \ (x_ {1} = 3 \), \ (y_ {1} = 7 \), \ (x_ {2} = — 1 \) и \ (y_ {2} = — 3 \)
Координаты главного входа рассчитываются как:
\ (\ begin {align} \! \! \ Left (\ dfrac {x_ {1} + x_ {2}} {2}, \ dfrac {y_ {1} + y_ {2}} {2} \ right ) \! \! & = \! \! \ left (\ dfrac {3 + (- 1)} {2}, \ dfrac {7 + (- 3)} {2} \ right) \\ & = \! \! \ left (\ dfrac {2} {2}, \ dfrac {4} {2} \ right) \\ & = \! \ left (1, 2 \ right) \ end {align} \)
\ (\ следовательно \) Главный вход находится в точке \ (1 + 2i \). |
Аналитический центр
| 1. | Диаметр окружности имеет концы 2-3i и -6 + 5i. |
| |
| Можете ли вы найти координаты центра этого круга? |
Вот несколько занятий для вас.Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции построения графиков комплексных чисел. Математическое путешествие по построению графиков сложных чисел начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах.
Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними.В этом заключается магия Куэмат.
Мы надеемся, что вы научились рисовать комплексные числа на комплексной плоскости и изображать мнимые числа в этом уроке по построению графиков комплексных чисел.
О компании CuemathВ Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в который мы, в Cuemath, верим.
Часто задаваемые вопросы о построении графиков комплексных чисел
1.
Для чего используется комплексная плоскость?Комплексная плоскость используется для нанесения комплексных чисел на график.
2. Как построить комплексное число на комплексной плоскости?
Выполните шаги, указанные ниже, чтобы построить комплексные числа на комплексной плоскости.
- Определите действительную и мнимую части данного комплексного числа. Например, для \ (z = x + iy \) действительная часть равна \ (x \), а мнимая часть — \ (y \).
- Сформируйте упорядоченную пару, в которой первый элемент — действительная часть, а второй элемент — мнимая часть. Например, для \ (z = x + iy \) упорядоченная пара равна \ ((x, y) \)
- Постройте точку \ ((x, y) \) на плоскости.
3. Что такое сложный граф?
Сложный граф — это граф, на котором представлены комплексные числа.
4. Как построить график комплексных чисел?
Выполните шаги, указанные ниже, чтобы построить комплексные числа на комплексной плоскости.
- Определите действительную и мнимую части данного комплексного числа. Например, для \ (z = x + iy \) действительная часть равна \ (x \), а мнимая часть — \ (y \).
- Сформируйте упорядоченную пару, в которой первый элемент — действительная часть, а второй элемент — мнимая часть. Например, для \ (z = x + iy \) упорядоченная пара равна \ ((x, y) \)
- Постройте точку \ ((x, y) \) на плоскости.
5. Где в реальной жизни используются комплексные числа?
Комплексные числа используются для решения квадратных уравнений.2 + 1 = 0 \) равно \ (z = i \).
6. Что такое Z * в комплексных числах?
\ (z * \) в комплексных числах — это сопряжение комплексного числа \ (z = x + iy \), заданного как \ (z * = x-iy \).
7. Как построить график i на комплексной плоскости?
Число \ (i \) соответствует точке \ (0,1 \) на графике.
8. Где на графике изображена действительная часть комплексного числа?
Действительная часть комплексного числа отложена на горизонтальной оси графика.
9.Где на графике изображена мнимая часть комплексного числа?
Мнимая часть комплексного числа отложена на вертикальной оси графика.
Визуализируйте сложные функции онлайн
(PRWEB) 14 января 2008 г.
Archimy http://www.archimy.com/ объявляет о выпуске совершенно новой службы визуализации данных для построения двумерных и трехмерных уравнений, которая позволяет студентам, учителям и энтузиастам математики визуализировать сложные математические функции в Интернете без необходимости загружать их. дополнительное программное обеспечение.
Визуальная математика играет важную роль в современных исследованиях и исследовании сложных математических функций. Визуальный подход помогает учителям лучше объяснять уравнения и поведение функций, независимо от их сложности, а также упрощает математические исследования и упрощает демонстрацию результатов.
Визуализируйте сложные математические функции онлайн без дополнительных загрузок! Расширьте свое представление о математических функциях, построив их графики в 2D или 3D! Одна картинка может объяснить студенту-математику или обычному читателю больше, чем экран, полный формул.Archimy позволяет рисовать любой мыслимый график в двух или трех измерениях в полярных или сферических координатах. Бесплатный онлайн-сервис строит графику и визуализацию в реальном времени, управляемую пользователем, по запросу, позволяя вращать функциональный график для лучшей визуализации. Archimy не ограничивается отрисовкой функций на http://www.archimy.com/; вы можете сгенерировать HTML-код для функции и использовать его на своих собственных веб-сайтах в качестве расширенного способа представления функций вашим посетителям.
Archimy позволяет вам определять график, задав формулу, описывающую координаты в пространстве (x, y, z).Задать поверхностную функцию только для двух переменных можно легко, зафиксировав координату «z» равной нулю.
Визуализация динамического поведения возможна с использованием простого языка сценариев. Параметрические функции поддерживаются за счет использования набора параметров для параметрического задания функции.
Расширьте возможности своей веб-страницы, сайта или математического блога с живыми графиками функций! Демонстрируйте идеи, динамически рисуя двумерные или трехмерные функциональные графики на вашем веб-сайте с помощью Archimy. Один щелчок мыши предоставляет вам небольшой HTML-код, который динамически отображает математические функции на вашем собственном веб-сайте.
Ученые всего мира использовали Java для рисования графиков функций в веб-браузерах. Многие пользователи компьютеров не имеют установленной Java в своих браузерах, и поэтому они не увидят графики при посещении вашего веб-сайта. Графики функций Archimy встраиваются в веб-страницы без использования Java. Archimy использует широко распространенный формат SWF Flash, поддерживаемый практически всеми веб-браузерами и устанавливаемый на компьютер каждого пользователя.
Использование SWF Flash приводит к получению высокосовместимого и чрезвычайно компактного кода, благодаря чему ваши страницы загружаются быстрее и выглядят лучше.
Archemy, безусловно, обладает всеми возможностями, которые вы ожидаете от службы научного построения графиков. Низкие системные требования, компактный код и использование популярного формата SWF Flash открывают путь популяризации сложной математики среди самой широкой аудитории.
Посетите http://www.archimy.com/ для получения дополнительных сведений.
Контакты:
Денис Козырь
+380 (50) 637-02-08
http://www.archimy.com/
###
Поделиться статьей в социальных сетях или по электронной почте:
Нанести комплексные числа на комплексную плоскость
Мы не можем нанести комплексные числа на числовую линию, как действительные числа.Однако мы все еще можем изобразить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа.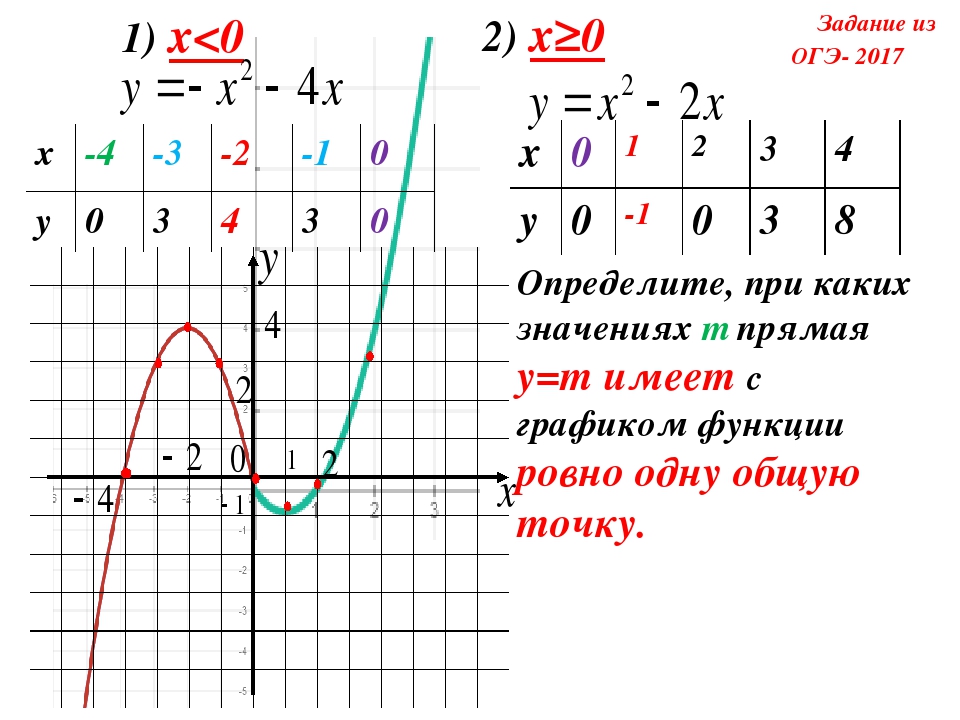
Мы используем комплексную плоскость , которая представляет собой систему координат, в которой горизонтальная ось представляет реальный компонент, а вертикальная ось представляет мнимый компонент. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар ( a , b ), где a представляет координату для горизонтальной оси, а b представляет координату для вертикальной оси.
Рисунок 2
Рассмотрим число [латекс] -2 + 3i \\ [/ latex]. Действительная часть комплексного числа –2, а мнимая часть — 3 i . Мы строим упорядоченную пару [латекс] \ left (-2,3 \ right) \\ [/ latex], чтобы представить комплексное число [latex] -2 + 3i \\ [/ latex] .
Общее примечание: сложная плоскость
Рисунок 3
В комплексной плоскости горизонтальная ось является действительной осью, а вертикальная ось — мнимой осью .
Как сделать: дано комплексное число, изобразите его компоненты на комплексной плоскости.
- Определите действительную и мнимую части комплексного числа.
- Двигайтесь по горизонтальной оси, чтобы показать действительную часть числа.
- Двигайтесь параллельно вертикальной оси, чтобы показать мнимую часть числа.
- Постройте точку.
Пример 2: Построение комплексного числа на комплексной плоскости
Постройте комплексное число [латекс] 3 — 4i \\ [/ latex] на комплексной плоскости.
Решение
Действительная часть комплексного числа равна 3, а мнимая часть — –4 i . Строим упорядоченную пару [латекс] \ left (3, -4 \ right) \\ [/ latex].
Рисунок 4
Попробуй 2
Постройте комплексное число [latex] -4-i \\ [/ latex] на комплексной плоскости.
Решение
Устройство графического отображения сложных функций
Устройство графического отображения сложных функцийГрафик сложных функций
| Этот апплет графически отображает сложные функции, в которых домен является базовая плоскость, модуль нанесен на график по вертикали, а цвет представляет аргументы.См. Текст справки для получения более подробной информации. |
Текст справки
Построить график сложной функции сложно, потому что вам нужно 2 (реальные) размеры для домена и 2 (реальные) измерения для диапазона — a всего 4 измерения. В этом апплете домен сложной функции на базовой плоскости. Диапазон нанесен на график с использованием полярных координаты. Модуль (величина) комплексной функции изображен на графике вертикальная ось. Аргумент (угол) отображается на графике с использованием различных цвета — голубой для позитивного реального, темно-синий (оттенок к пурпурному) для положительное воображаемое, красный для отрицательного действительного и желто-зеленый для отрицательного воображаемый., sqrt (), sin (), cos (), tan (), exp (), ln (), log () (синоним ln), sinh (), cosh (), abs (), mod () (синоним слова abs), arg (), con (), e, pi, я.Чтобы настроить область графика, щелкните правой кнопкой мыши (или щелкните, удерживая нажатой клавишу Shift, если у вас есть однокнопочная мышь) на графике. Редактор домена принимает только числовые вход, то есть 3,14 не пи.
Один судья попытался проверить личность с помощью этого апплета и обнаружил некоторые специфические эффекты, которые объясняются здесь.
Вернуться наверх
Типовые задания
Я обычно просматриваю пару графиков со студентами в классе в первую очередь раз я представлю этот апплет, чтобы быть уверенным они понимают, на что смотрят.Например, мы рассмотрим первые три перечисленные функции в соответствии с принципом аргумента ниже в классе. Я использую как вид сверху, так и сторона Просмотр изначально; впоследствии студенты часто используют оба представления, но иногда бывает достаточно одного просмотра для выполнения конкретного задания. Как только ученики освоятся с графиками, я их работать посмотрите на графики и обсудите их в парах, затем напишите краткие индивидуальные ответы о том, что они наблюдают, часто прося их проверить математически модели, которые они уведомление.2 + 1) / г- f (z) = sqrt (z)
- f (z) = -sqrt (z)
- f (z) = exp (pi * z) или альтернативно
- f (z) = exp (z) (изменить домен на -6,28
- Регулярные и гиперболические триггерные функции
- f (z) = cos (pi * z)
- f (z) = cosh (pi * z)
- В качестве альтернативы они могут посмотреть на cos (z) и cosh (z) с помощью
домены установлены на
-6.28 -2
Документация и исходный код
Документация была создана с помощью javadoc и предназначена для документирования использование классов, разработанных для этого апплета, для программистов, которые хотят использовать класс как есть в собственных проектах. Прокомментированный исходный код также предоставляется для программисты, которые хотят изменить эти классы, а также апплет сам (который в основном представляет собой пользовательский интерфейс). Код защищен авторским правом но может свободно использоваться в некоммерческих целях при условии, что оригинал источник указан, и автор проинформирован.Связаться с автором по адресу [email protected]Вернуться наверх
Пожалуйста, сообщайте о любых проблемах с этой страницей по адресу [email protected]
© 2001 Эндрю Дж. Беннетт
Визуализация сложных функций | Кевин ван Кессель
Комплексные числа
Пусть вас не пугает название: сложные числа понять легче, чем звучать. Комплексное число на самом деле состоит из двух чисел: действительного и мнимого числа. Действительное число — это то, к чему все привыкли, каждое значение от отрицательной бесконечности до бесконечности.2 = -1 \).
Причина, по которой эта константа важна, заключается в том, что с ее помощью идея извлечения квадратного корня или логарифма отрицательного числа может иметь смысл. Фактически, большинство функций имеют естественное расширение на комплексную область, например \ (\ sin () \). Они также предоставляют способ определения умножения и деления двумерных векторов наряду с обычным сложением и вычитанием.
Я вынужден указать, что они плохо названы. Боковое число Гаусса — гораздо лучшее название.Они существуют и так же полезны, как отрицательные числа, но вы не найдете ни того, ни другого в естественном мире.
Декартовы координаты
Вы складываете действительные и мнимые числа вместе, чтобы получить комплексное число. Это немного необычно для концепции числа, потому что теперь у вас есть два измерения информации вместо одного. Подобно тому, как можно представить себе действительные числа как точку на числовой прямой, можно представить комплексное число как точку на числовой плоскости. Ось X числовой плоскости представляет действительную составляющую, а ось Y — мнимую составляющую.Это декартова система координат.
\ [z = x + yi \]Полярные координаты
Хотя оси напрямую соответствуют каждому компоненту, на самом деле часто бывает проще представить комплексное число как величину (\ (r \)) и угол (\ (\ theta \)) от начала координат. Такой способ представления точки на плоскости называется полярной системой координат. Причина в том, что это проще, потому что когда вы умножаете два комплексных числа, величина результата является произведением двух исходных величин, а угол результата является суммой двух исходных углов.{2 \ theta i} \\ \ end {split} \]
Видите, насколько проще возвести квадрат в полярных координатах? Это не только проще, но и легко интерпретировать результат. Величина возводится в квадрат, а угол удваивается.
Графические сложные функции
Построить график сложной функции на удивление сложно. Реальная функция принимает одно измерение информации и выводит одно измерение информации. В сумме получается два удобных измерения, которые легко отобразить на экране компьютера или на бумаге.С другой стороны, сложные функции принимают два измерения информации и выводят два измерения, оставляя нам в общей сложности четыре измерения, которые нужно втиснуть в наш график. Это звучит почти невероятно, как, черт возьми, мы могли придумать способ визуализировать четыре измерения?
Один из способов — построить векторное поле. Векторное поле представляет собой набор маленьких стрелок. Каждая стрелка показывает, как функция преобразует точку, над которой они находятся. Это может сработать, но это не очень хорошо, поскольку для рисования каждой стрелки требуется пространство, которое можно было бы использовать для рисования стрелок меньшего размера.
К счастью, у нас есть хитрость в рукаве. Мы можем решить эту проблему, используя полярные координаты, указанные ранее. Как это помогает? Осталось построить всего четыре измерения. Важным отличием полярных координат от декартовых координат является угол. Углы отличаются от величин, потому что они периодичны. Полный оборот — это то же самое, что и полное отсутствие вращения. Цвет тоже периодичен. Вы можете переключаться между всеми оттенками: красным, желтым, зеленым, голубым, синим, пурпурным и обратно к красному.
У нас есть способ представить угол, а как насчет величины? Для этого мы можем использовать легкость. Чем меньше величина, тем она темнее, тем больше величина, тем светлее. Однако здесь есть очевидная проблема. Величина может быть от нуля до бесконечности, а яркость — от 0% до 100%. Чтобы учесть это, мы можем разбить эту величину на группы, каждая из которых имеет оттенок от темного к светлому, и каждый раз удваивать их размер. Например, один градиент от темного к светлому будет от 1 до 2.{\ theta i} \)). Оттенок пикселя отображается на новый угол (\ (\ theta \)), а яркость пикселя — на новую величину (\ (r \)). 2 \).Точки, где кажется, что контуры сходятся, я буду называть полюсами. Полюса — это место, где функция переходит в \ (0 \) или \ (\ pm \ infty \). В этой интерполяции вы можете увидеть, как полюс появляется вдоль отрицательной оси и сливается с исходным полюсом.
Куб
Куб з.Подобно квадрату, эта функция втрое увеличивает количество оттенков вокруг полюса и втрое плотность контуров. При интерполяции два дополнительных полюса объединяются в исходный, в результате чего получается три полюса.Что же произойдет, если мы возьмем отрицательные силы?
Обратный
Инверсия z.Здесь вы можете увидеть, как выглядит инверсия комплексной плоскости. Оттенки переворачиваются вдоль горизонтальной оси, и каждый контур теперь уменьшается вдвое, а не удваивается, потому что градиент яркости меняется на противоположный. В интерполяции можно увидеть, как два полюса вырываются из исходного полюса. Что следует по той же схеме, что и предыдущие два.
Обратный квадрат
Перевернутый квадрат zСнова по шаблону удаляются три полюса из оригинала.Это образует инверсию с двумя оттенками каждого и удваивает плотность контуров
Квадратный корень
Корень квадратный из z.Это немного странно. Подобно предыдущим, за исключением того, что полюса не движутся заметно, а вдоль отрицательной оси x имеется разрыв, называемый разветвлением. Разрез ветви означает, что функциональная поверхность становится слишком сложной для представления в двух измерениях, поэтому для простоты она усекается по отрицательной оси x. Уверяю вас, что если бы вы могли видеть четыре измерения, эта функция казалась бы непрерывной.
Обратный квадратный корень
Обратный квадратный корень из z.Этот похож на предыдущий, за исключением того, что два полюса удалены от оригинала под симметричными углами. Это проливает свет на предыдущую функцию. Я предполагаю, что предыдущая интерполяция также имела движущиеся полюса, но они были спрятаны за срезом ветки.
Мощность i
z в степень i.Теперь все становится напуганным. Если взять плоскость в степень \ (i \), похоже, она перевернется в другом смысле.{\ frac {2 \ pi} {6}} \ приблизительно 2.85 \) вместо \ (2 \), это приводит к тому, что контуры в преобразовании четко разделяют плоскость на \ (6 \) сегменты.
Мощность -i
z в степени -i.Аналогично предыдущему, но значения теперь удваиваются с углом и поворачиваются по часовой стрелке с увеличением. Мне интересно, что все интерполяции мощности включают слияние или разделение полюсов в разных направлениях.
Синус
Синус z.Это красивый и один из моих любимых.Полюса сливаются сверху и снизу только для того, чтобы сразу же снова разделиться, образуя красочную симметричную волну. Косинус похож, но сдвинут по горизонтали.
Гиперболический синус
Гиперболический синус z.Отношение Sine к его гиперболическому аналогу становится ясным из этих двух последних графиков.
Арксинус
Арксинус z.Это не кажется очень интересным, но мне любопытно посмотреть, что происходит за пределами сечения ветки.
Касательная
Касательная к z.Последовательность чередующихся обычных и обратных полюсов появляется вдоль горизонтали.
Синус обратной
Синус обратной величины z.Вспомните, как предел \ (\ sin (\ frac {1} {x}) \) не определен, когда \ (x \) приближается к \ (0 \)? Это потому, что синус начинает дико колебаться, не останавливаясь ни на каком значении. Теперь расширите эту концепцию до сложных значений, и вы получите эту странную особенность.
Тангенс обратной
Касательная к обратной z.Я даже не буду пытаться объяснять эту чушь.
Экспоненциальная
Число Эйлера в степени z.Столбы втягиваются справа налево, сглаживая контуры в четкую горизонтальную последовательность. Новая величина — это экспонента действительной составляющей, а новый угол — это мнимая составляющая в радианах.
Логарифм
Натуральный логарифм z.Трудно понять, что здесь происходит, но эта интерполяция разворачивается в бесконечную спираль за пределами сечения ветви. z \).
Softplus
Softplus з.Softplus также встречается как функция активации нейронных сетей. Кажется, что два полюса выходят из-под основной ветви, прорезанной справа от исходной точки, которая практически не меняется.
Гамма
Гамма-функция z.Гамма-функция — это непрерывная версия факториала. В частности, \ (\ Gamma (n) = (n — 1)! \). Это еще одна моя любимая функция, выглядит она довольно экзотично.
Экспоид
Экспоид з.Это функция, которую я придумал во время экспериментов, и в итоге она оказалась интересной. Я называю тебя экспоидной функцией. Черные области — это места, где вычисления выходят за пределы арифметики с плавающей запятой на моем компьютере, в противном случае эта область была бы заполнена еще более компактными колебаниями.
Кажется, что вплоть до самого последнего кадра столпы стабильности и нестабильности формируются на отрицательной реальной стороне сюжета. Кажется, что каждая колонна приближается к ширине \ (\ pi \). Это явление возникает потому, что, когда мнимая составляющая кратна пи, знак внутренней экспоненты становится положительным или отрицательным.Это приводит к тому, что внешняя экспонента взрывается или исчезает, вызывая один и тот же черный артефакт из-за того, как хранятся числа с плавающей запятой. Когда мнимая составляющая находится прямо между этими кратными, внутренняя экспонента становится чисто мнимым числом. Тогда внешняя экспонента только вращается, а не изменяет величину, поэтому эти области отображаются правильно.
Мягкая экспонента
Мягкая экспонента — довольно редкая функция активации, встречающаяся в машинном обучении.г \\ \ end {split} \]
Дзета-функция Римана
Дзета-функция z. Важные полюсы дзета-функции.Наконец, дедушка сложных функций: дзета-функция Римана. Почему эта функция так важна? Потому что это связано с распределением простых чисел, которое само по себе загадочно. Если вы сможете доказать гипотезу Римана, вы также получите ряд других результатов о распределении простых чисел, которые основаны на истинности гипотезы. Вы также выиграете миллион долларов, но это не так важно.
Какая именно гипотеза? Дело в том, что каждый нетривиальный нуль дзета-функции имеет действительную часть \ (\ frac {1} {2} \). Когда я говорю «тривиальные нули», это означает полюса на отрицательной действительной оси, которые вы можете видеть на изображениях выше. На втором изображении вы видите первые два нетривиальных нуля. Они лежат примерно в \ ((\ frac {1} {2} + 14.1i) \) и \ ((\ frac {1} {2} + 21.0i) \). Вроде есть закономерность, но пока никто не доказал ее с полной уверенностью.
Заключение
Математика прекрасна, а визуализация может помочь иностранным концепциям стать немного более интуитивно понятными.Я надеюсь, что это пробудит у кого-то интерес к изучению сложных систем счисления. Их бесконечно много, но они быстро усложняются, поэтому часто обсуждаются только первые несколько.
Что действительно интересно в них, так это то, что вы что-то теряете каждый раз, когда переходите к высшей алгебре.
Ваш комментарий будет первым