Построение графика функции, заданной в параметрической форме. — Студопедия
Государственное образовательное учреждение высшего профессионального образования
Московский авиационный институт
(национальный исследовательский университет)
РАДИОВУЗ МАИ
О.М.Данченко
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
МОСКВА
О.М. ДАНЧЕНКО
Методические указания по выполнению индивидуальных заданий по математическому анализу – М.; РАДИОВТУЗ, 2012г., — 36 с.
Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену.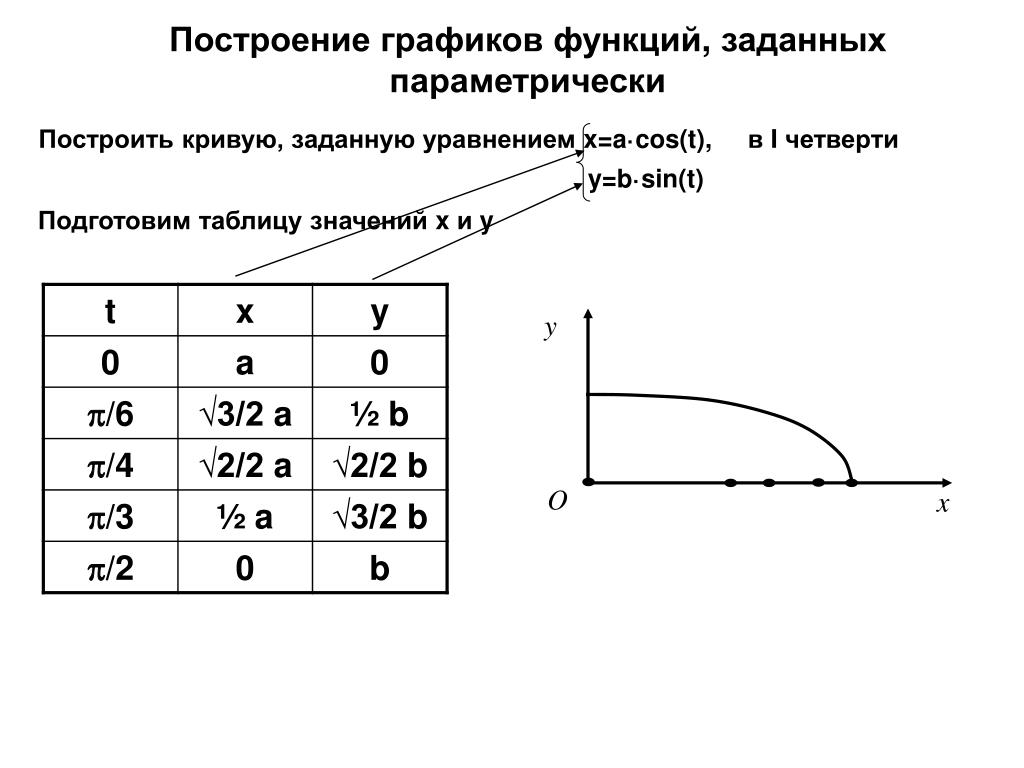
РАДИОВТУЗ 2012
Содержание
Введение…………………………………………………………………………….
Построение графиков функций, заданных в полярной системе координат или в параметрической форме……………………………………………………………
Вычисление пределов последовательностей и функций…………………………
Исследование функций на непрерывность………………………………………..
Вычисление производных………………………………………………………….
Исследование функций с помощью производных, построение графиков функций……………………………………………………………………………..
Задания на вычисление интегралов……………………………………………….
Приложения…………………………………………………………………………
Введение
В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи:
1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.
Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.
2. Вычисление пределов последовательностей и функций.
3. Исследование функций на непрерывность.
4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме.
5. Исследование функций с помощью производных, построение графика функции.
6. Вычисление неопределенного и определенного интегралов.
Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения.
Построение графиков функций, заданных в простой полярной системе координат.
Простая полярная система координат характеризуется следующим:
Положительные углы φотсчитываются от полярной оси (совпадающей с положительным направлением оси ОХ) против часовой стрелки, отрицательные – по часовой стрелке. При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий:
При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий:
а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φфункция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0;
б) найти область изменения функции;
в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ),то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0.После данных исследований следует построить кривую по точкам.
Пример: построить график функции в простой полярной системе координатρ=2cos2φ
Так как в простой полярной системе координат ρ≥0, то О.Д.З. будут являться только те углы φ,для которых cos2φ≥0,т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т. к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1).
к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1).
Построение графика функции, заданной в параметрической форме.
Пусть x=X(t)и y=Y(t), где параметр tизменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам.
Пример: x=t², y= t∙(t²-3)/3
а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости.
б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ.
в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0
при t= + и t= — y=0, а x(+ ) = 3 – т.е. это точки пересечения графика функции с осью ОХ. Для более точного построения графика функции достаточно добавить еще 2-3 точки, например при t=1 y(1)=-2/3, x(1)=1; при t=2 y(2)=2/3, x(2)=4; при t =3 y(3)=6, x(3)=9 (рис.2.).
рис. 1 рис. 2
Иллюстрированный самоучитель по Maple 9 › Вычисление производных › Вычисление производных функций, заданных параметрически [страница — 41] | Самоучители по математическим пакетам
Вычисление производных функций, заданных параметрически
При вычислении производных функций, заданных параметрически, по сравнению с явно заданными функциями, принципиально ничего не меняется. Однако сама процедура вычисления производных (особенно высших порядков) становится несколько сложнее.
Рассмотрим пример.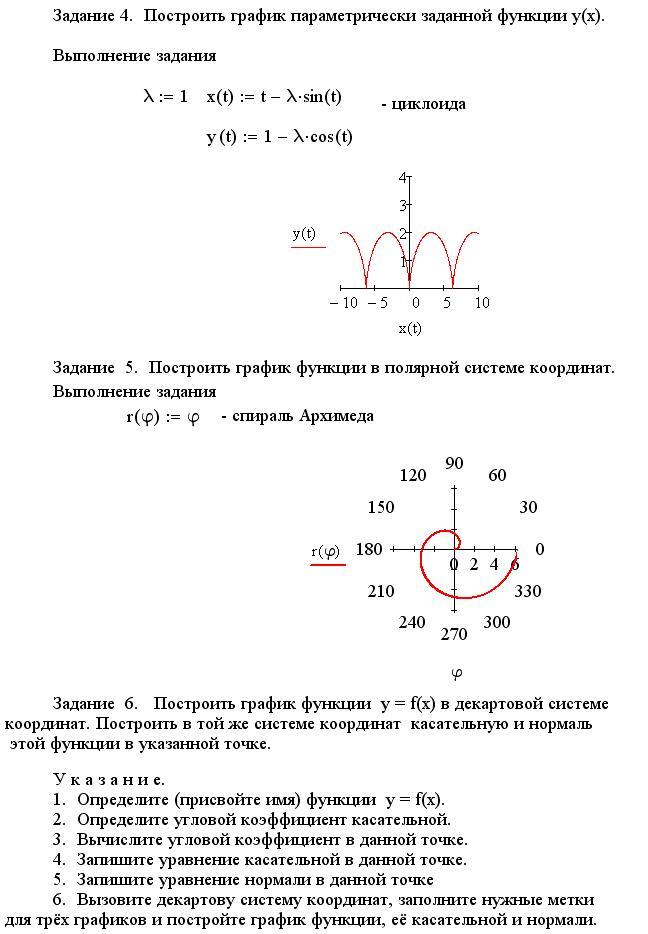
Задача 2.7
Найти производную функции, заданной параметрически: x(t) = acos(t) и y(t) = bsin(t).
Переменной х присвоим значение.
Так же поступим и с переменной у.
Теперь х и у являются выражениями, которые зависят от переменной-параметра t; по этому параметру их можно дифференцировать. Поэтому остается только воспользоваться приведенной выше формулой для производной функции, заданной в параметрическом виде.
Построим график функции и ее производной с помощью процедуры 
Внимание!
Именно наличие третьего параметра в списке при отображении заданной в параметрическом виде функции является индикатором того, что строится график параметрической функции, а не графики двух разных функций
Поскольку в исходных параметрических зависимостях х и у зависят от параметров а и b, при построении графиков эти зависимости следует поделить на соответствующие коэффициенты.
Следует обратить внимание на то, что при определении заголовка использовался символ перехода на новую строку (\n). Данный символ рекомендуется использовать при длинных заголовках, чтобы при отображении графика такой заголовок был виден целиком.
Процесс вычисления параметрической производной можно существенно автоматизировать. Подобный подход продемонстрирован в следующем примере.
gnuplot / parametric (E)
В обычном двумерном построении в gnuplot координата Y выражается y=f(x), однако можно использовать параметрическое задание функции, использующее параметр t,
x = f(t) y = g(t)
С помощью этого выражения gnuplot может рисовать более сложные функции.
В первую очередь необходимо использовать команду set parametric, чтобы gnuplot определил параметрическую переменную для функции. Затем, команда plot, выполняющая построение функции f(t) координаты X и функцит g(t) для координаты Y, задается как plot f(t),g(t).
Чтобы провести простейшую вертикальную линию, не выражающуюся формой y=f(x), а заданную как x=const. Эта функция может быть определена как:
x=const y=t
с параметром t, когда t различен. Диапазон t контролируется командой set trange.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> const=3
gnuplot> set trange [1:4]
gnuplot> set xrange [0:5]
gnuplot> set yrange [0:5]
gnuplot> plot const,t
В данном случае вертикальная линия нарисованна в x=3. Использование set
trange [1:4] , определило диапазон от 1 до 4.
Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы.
Использование set
trange [1:4] , определило диапазон от 1 до 4.
Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы.
Параметрическое задание окружности:
x=sin(t) y=cos(t)
окружность может быть нарисована при изменении параметра t от 0 до 2pi. График принимает вид «квадрата» и диапазон t задается опцией команды plot.
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> plot [0:2*pi] sin(t),cos(t)
Параметр t не изменяется непрерывно и фактически управляется значениями, установленными командой set
samples. По умолчанию значение равно 100. В случае set samples 8,
gnuplot вычисляет только 8 значений t от 0 до 2*pi, и график становиться семиугольником. Если необходим построить N-угольник,
задается set samples N+1.
Если необходим построить N-угольник,
задается set samples N+1.
2D параметрическое представление удобно для рисования функции, которая находится в полярных координатах. 2D полярная координатаимеет 2 переменные: r и угловую theta. gnuplot выражает параметр t для theta, а радиус r выражается через функцию угла, а именно r(t). Координата (x,y) дается из:
x=r(t)*cos(t) y=r(t)*sin(t)
Окружность — особый случай, когда r(t)=const. Когда радиус пропорционален t, получается спираль.
gnuplot> set xrange [-10*pi:10*pi] gnuplot> set yrange [-10*pi:10*pi] gnuplot> plot [0:10*pi] t*sin(t),t*cos(t)
Следующий пример показывает график кардиоды r(t)=const*(1+cos(t)).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> r(t) = 1+cos(t)
gnuplot> plot [0:2*pi] r(t)*cos(t),r(t)*sin(t)
Обычная функция имеет вид y=f(x), но параметрическая позволяет делать график x=f(y). Значения Y такие же как и t и значения x вычисляются функцией f(t).
Значения Y такие же как и t и значения x вычисляются функцией f(t).
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> c=2*pi
gnuplot> set size square
gnuplot> set trange [-c:c]
gnuplot> set xrange [-c:c]
gnuplot> set yrange [-c:c]
gnuplot> plot c*sin(t),t with lines, t,c*cos(t) with impulses
Показаны 2 функции, одна (зеленые линии) y=2pi*cos(x), другая (красная толстая линия) x=f(t)=2pi*sin(y).
Опция with impulse рисует вертикальную линию от оси Y=0. Если используется with impulses для красной кривой x=2pi*sin(y), то получается вертикальная линия, не горизонтальная.
Использование excel для построения графиков функций заданных в параметрическом виде или в полярных координатах и графиков объемных функций цели урока
Бут Людмила Александровна
учитель информатики лицея №14 г. Жуковский
Жуковский
Использование Excel для построения графиков функций, заданных в параметрическом виде или в полярных координатах и графиков объемных функций.
Цели урока:
Образовательная:
Научить учащихся применять современное программное обеспечение в решении нестандартных задач;
Сформировать представление учащихся о способах построения объемных изображений средствами Excel.
Развивающая:
Продолжить развивать умения учащихся применять компьютер для решения конкретных задач из конкретной предметной области;
Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений.
Воспитательная:
Задачи урока:
Воспитательная. Развитие познавательного интереса, воспитание информационной культуры.

Учебная. Изучить и закрепить основные навыки работы с электронными таблицами.
Развивающая. Развитие логического мышления, расширение кругозора.
Тип урока: Комбинированный — урок формирования и закрепления умений и навыков практического использования MS Excel.
План урока.
Организационная часть.
Повторение пройденного материала.
Обобщение и систематизация понятий для выполнения самостоятельной работы.
Самостоятельная работа.
Подведение итогов.
Домашнее задание.
Ход урока.
Вопросы для повторения:
Что такое относительная и абсолютная адресация?
Как протабулировать функцию, заданную в виде y=f(x)?
Как построить график функции, используя Мастер диаграмм?
На уроке мы рассмотрим особенности построения двух наиболее часто употребляемых в инженерной практике типов диаграмм – точечных (графиков) и поверхностных (или объемных).
Построение графиков функций, заданных в параметрическом виде или в полярной системе координат.
Параметрическое представление кривой на плоскости – это две функции, явно выражающие обе координаты x и y через значение некоторого производящего параметра:
Параметрические линии по форме могут быть более разнообразными, чем линии, описываемые одним уравнением. На них не распространяется ограничение по многозначности, поэтому линии могут быть самопересекающимися.
Для примера рассмотрим уравнение окружности с центром в начале координат и радиусом R.
.
Координаты точек окружности вычисляются по формулам:
.
Здесь центральный угол t является генерирующим параметром.
Для построения полной окружности радиуса R=100 составим таблицу, в которой значение параметра t меняется с шагом 0,1 от 0 до 2π.
Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная. Точечная диаграмма отображает взаимосвязь между числовыми значениями в нескольких рядах и представляет две группы чисел в виде одного ряда точек в координатах XY.
Получим диаграмму:
Полярные координаты и точки М на плоскости – это расстояние =ОМ от фиксированной точки О (полюса) до точки М и угол между лучами ОМ и ОР (полярная ось).
Полярные координаты являются наиболее употребительными после декартовых. Это нелинейные координаты. При построении кривых, заданных в полярных координатах, полярные координаты переводят в декартовы. Если полюс имеет координаты (x0, y0), то формулы преобразования таковы:
Для функций, заданных в полярных координатах формула имеет вид
, где – полярный угол.
Таблица должна содержать данные для построения кривой в полярной системе координат. Затем надо перевести данные из полярных координат в декартовы. Данные для построения точечного графика должны быть представлены в декартовой системе координат.
Рассмотрим Архимедову спираль, ее уравнение в полярных координатах:
ρ = aφ, где а — постоянная.
Составим таблицу для a=2, значение полярного угла меняется с шагом 0,1 от 0 до 6π. Такой диапазон выбран для того, чтобы увидеть несколько витков спирали.
Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная.
Получим диаграмму:
Задания для самостоятельной работы:
Построить графики замечательных кривых:
Астроида | Кардиоида X=acost(1+cost) Y=asint(1+cost) или ρ=a (1+cosφ) | ||
n- лепестковая роза ρ= asin mφ или ρ = a cos mφ | Лемниската Бернулли ρ2-a2cos(2φ)=0 |
Элементы диаграммы можно видоизменять при помощи контекстного меню, вызываемого правой кнопкой мыши. Видоизменение, как правило, состоит в определении другого цвета для какого-то элемента, нового типа линии или маркера. Внести изменения можно, выбрав в контекстном меню первый пункт – Формат соответствующего объекта и определив нужные параметры.
Видоизменение, как правило, состоит в определении другого цвета для какого-то элемента, нового типа линии или маркера. Внести изменения можно, выбрав в контекстном меню первый пункт – Формат соответствующего объекта и определив нужные параметры.
Построение графика объемной функции.
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей.
Поверхность будем рассматривать как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0.
Рассмотрим зависимость, которая описывает сферу радиуса R.
X2 +Y2+Z2=R2
Выразим z:
Поскольку z(x, y) является функцией двух переменных, то ее график будет объемным, т. к. по двум осям (x, y) будут откладываться значения аргументов, а по третьей (z) – вычисленные значения функции.
к. по двум осям (x, y) будут откладываться значения аргументов, а по третьей (z) – вычисленные значения функции.
Сначала нужно создать таблицу значений функции в заданных диапазонах аргументов.
Если бы мы попытались сделать это известными способами, то нам потребовалось бы ввести большое множество значений аргументов, т. к. для каждого значения x пришлось бы ввести все значения диапазона y. При этом таблица имела бы очень большие размеры в длину или ширину. Однако можно построить таблицу по другому – в виде массива(матрицы): по строке отложить значения переменной x, а по столбцу – переменной y, а вычисленные значения функции – в ячейках на пересечении соответствующих значений аргументов. Это компактный способ представления данных.
Рассмотрим пример такой таблицы для R=3.
Значение квадрата радиуса вводится в ячейку B1.
В ячейки A3:A15 введите числа от -3 до 3 с шагом 0,5. 2). Для того, чтобы все значения x брались из строки 2, а все значения y из столбца A нужно использовать абсолютную адресацию. Замена относительных адресов в формуле на абсолютные производится с помощью клавиши F4, которая при выборе очередной ячейки при вводе формулы нажимается несколько раз до появления нужного вида адреса. Распространяя формулы на диапазон B3:O19, получим следующую таблицу( в ней удалены сообщения об ошибке в ячейках, где происходило извлечение квадратного корня из отрицательного числа).
2). Для того, чтобы все значения x брались из строки 2, а все значения y из столбца A нужно использовать абсолютную адресацию. Замена относительных адресов в формуле на абсолютные производится с помощью клавиши F4, которая при выборе очередной ячейки при вводе формулы нажимается несколько раз до появления нужного вида адреса. Распространяя формулы на диапазон B3:O19, получим следующую таблицу( в ней удалены сообщения об ошибке в ячейках, где происходило извлечение квадратного корня из отрицательного числа).
Будем использовать стандартную объемную поверхностную диаграмму.
Поверхностные диаграммы отображают два или несколько рядов данных в виде поверхности.
В отличие от остальных диаграмм, в этом случае Excel применяет различные цвета для выделения значений, а не рядов данных.
Для построения графика выделим всю таблицу и выберем тип диаграммы Поверхность. Так как в таблице вычислены только положительные значения z , то на диаграмме будет изображена полусфера.
Получим объемный график.
Для видоизменения поверхностных диаграмм предоставляется больше возможностей. Вызвав через меню Диаграмма –Объемный вид диалоговое окно Формат трехмерной проекции, мы можем задать повороты в разных направлениях, перспективу, изменить высоту графика (задается в процентах от нормальной высоты), а также некоторые другие параметры.
Задания для самостоятельной работы:
Построить объемную диаграмму поверхностей второго порядка.
Эллиптический параболоид | ||
Гиперболический параболоид | ||
Вещественный конус | ||
Однополостной гиперболоид | ||
Двуполостной гиперболоид |
Требования к выполнению заданий.
Каждое задание выполняется на отдельном листе книги. Таблицы и диаграммы должны быть полностью оформлены. Файл сохранить в Личной папке.
Дифференцирование функций, заданных параметрически — Мегаобучалка
Пусть функция задана параметрически уравнениями
(1) — параметр.
Требуется найти производную .
Имеет место формула
или .
Пример
Найти производную функции, заданной параметрически: .
Решение
Найдем производные функций х и у по переменной t:
,
.
Согласно формуле , получим
.
Исследование функций и построение графиков функций
Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Определить четность, нечетность.
4. Найти точки разрыва функции и асимптоты графика функции.
5. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума.
6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба.
7. Построить график функции.
Пример
С помощью методов дифференциального исчисления исследовать и построить график функции .
Решение
1. Область определения функции находится из условия: , т.е. .
2. Точки пересечения графика функции с осями координат:
с осью Оу, , точка ,
с осью Ох, , точка .
3. Четность, нечетность.
Функция называется четной, если для любого х из области определения справедливо равенство . Функция называется нечетной, если для любого х из области определения справедливо равенство . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
В нашем случае, , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
4. Точки разрыва функции и асимптоты графика функции.
1) Вертикальные асимптоты. Прямая является вертикальной асимптотой графика функции , если хотя бы один из пределов
или
равен или . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
Заданная функция имеет две точки разрыва второго рода и , так как
, ,
, ,
следовательно, график функции имеет две вертикальных асимптоты и .
2) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда .
Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
.
Если эти пределы конечны и различны, то прямые будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен , то не существуют и соответствующие асимптоты.
Так как
,
то график функции имеет горизонтальную асимптоту .
3) Наклонные асимптоты. Пусть прямая является асимптотой графика функции . Такую асимптоту называют наклонной. Для того, чтобы график функции имел при наклонную асимптоту , необходимо и достаточно, чтобы существовали оба предела:
.
Аналогично находится асимптота при .
Так как , то наклонных асимптот нет.
5. Исследование функции на экстремум.
Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
.
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель к нулю:
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
_ _ _
х
-6 6 у
6.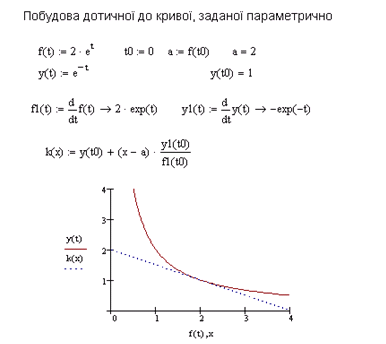 Исследование на выпуклость, вогнутость. Точки перегиба.
Исследование на выпуклость, вогнутость. Точки перегиба.
Вычислим производную второго порядка:
Необходимое условие точки перегиба: или не существует. Равенство выполняется при , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
_ + _ +
х
-6 0 6 у
Так как при переходе через точку вторая производная меняет знак, то точка с абсциссой является точкой перегиба. Итак, точка перегиба имеет координаты .
7. Построение графика функции.
11.6. Дифференцирование функции, заданной | Контрольные работы по матем
Дифференцирование функции, заданной gараметрически
Пусть даны два уравнения:
(11. 6)
Где параметр t Изменяется на некотором промежутке Т. Каждому фиксированному значению могут соответствовать одновременно значения x и y. Если при этом соответствие между x и y является функцией , то говорят, что эта функция задана параметрически системой уравнений (11.6). В том, что эта система не всегда задает функцию, можно убедиться на следующем примере. Пусть
Каждому фиксированному значению могут соответствовать одновременно значения x и y. Если при этом соответствие между x и y является функцией , то говорят, что эта функция задана параметрически системой уравнений (11.6). В том, что эта система не всегда задает функцию, можно убедиться на следующем примере. Пусть
Где .
Графически эти уравнения определяют окружность радиуса A с центром в начале координат, так как из соотношений:
Вытекает:
Но окружность не есть график функции. Более того, эта же окружность может быть задана и иначе:
,
Или же
Возможно и задание данной окружности в виде:
Но здесь параметр t изменяется в других границах.
Если параметр t удается исключить, как это было в случае с окружностью, то от так называемого параметрического задания кривой мы переходим к привычному заданию кривой в виде . Имеет место и обратная процедура. Она оправдана, если уравнения кривой после параметризации получают более простой вид. Например, линия
Имеет место и обратная процедура. Она оправдана, если уравнения кривой после параметризации получают более простой вид. Например, линия
,
Называемая АСТРОИДОЙ, в параметрическом виде может быть задана гораздо проще:
Докажите этот факт. |
А это позволяет значительно легче построить кривую, изменяя t от 0 до (рис. 11.3). Отметим, что астроида определяет траекторию точки M Окружности радиуса A/4, которая катится по внутренней стороне другой окружности радиуса A.
Рис. 11.3. Астроида. |
Далеко не всегда удается из системы уравнений, задающих функцию, исключить параметр t и записать эту функцию в виде . Поэтому возникает вопрос: можно ли для функции, заданной параметрически, найти производную и выразить ее через параметр T?
Будем предполагать, что функции И дифференцируемы, а функция имеет обратную . Тогда
Тогда
Дифференцируя y по x как сложную функцию и пользуясь свойством производной обратной функции:
Получим:
Постройте в системе координат xOy график функции , если , |
Итак,
Рассуждая аналогично, находим вторую производную, считая, что и существуют в T:
Таким образом, получаем:
| < Предыдущая | Следующая > |
|---|
1.2 Расчет параметрических кривых — том 3
Цели обучения
- 1.2.1 Определение производных и уравнений касательных для параметрических кривых.
- 1.2.2 Найдите площадь под параметрической кривой.
- 1.2.3 Используйте уравнение для длины дуги параметрической кривой.

- 1.2.4 Примените формулу площади поверхности к объему, полученному с помощью параметрической кривой.
Теперь, когда мы ввели концепцию параметризованной кривой, наш следующий шаг — научиться работать с этой концепцией в контексте исчисления.Например, если мы знаем параметризацию данной кривой, можно ли рассчитать наклон касательной к кривой? Как насчет длины дуги кривой? Или площадь под кривой?
Другой сценарий. Предположим, мы хотим изобразить положение бейсбольного мяча после того, как мяч покидает руку питчера. Если положение бейсбольного мяча представлено плоской кривой (x (t), y (t)), (x (t), y (t)), тогда мы сможем использовать математические вычисления, чтобы найти скорость мяч в любой момент времени.Кроме того, мы должны иметь возможность рассчитать, как далеко прошел этот шар, как функцию времени.
Производные от параметрических уравнений
Мы начинаем с вопроса, как рассчитать наклон прямой, касательной к параметрической кривой в точке.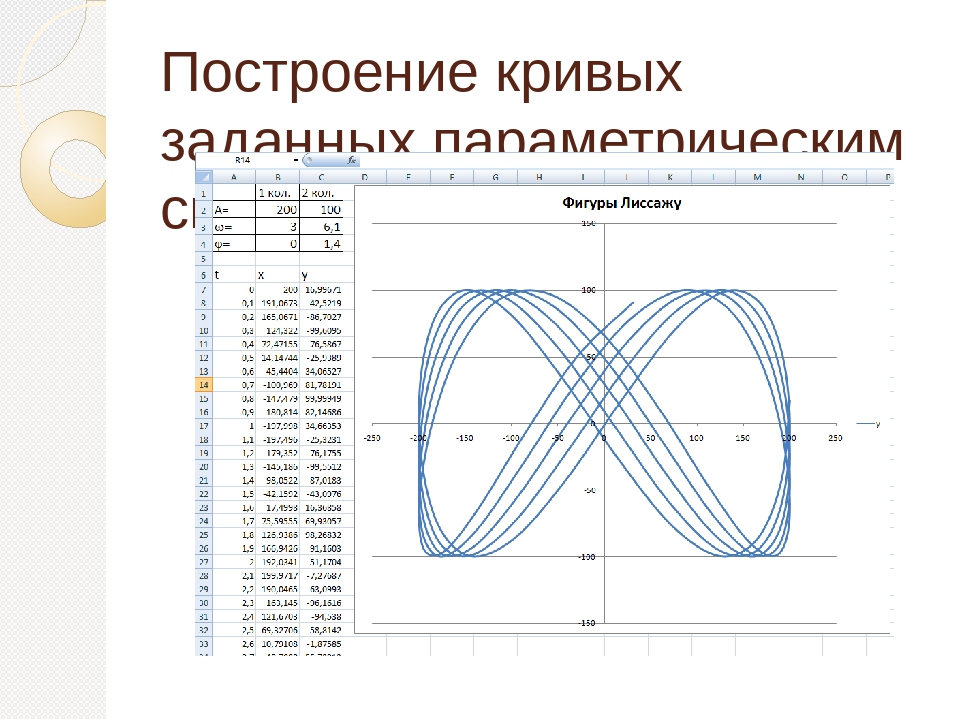 Рассмотрим плоскую кривую, заданную параметрическими уравнениями
Рассмотрим плоскую кривую, заданную параметрическими уравнениями
График этой кривой представлен на Рисунке 1.16. Это отрезок, начинающийся в (−1, −10) (- 1, −10) и заканчивающийся в (9,5).(9,5).
Рисунок 1.16 График отрезка прямой, описываемый заданными параметрическими уравнениями.
Мы можем исключить параметр, решив сначала уравнение x (t) = 2t + 3x (t) = 2t + 3 для t :
x (t) = 2t + 3x − 3 = 2tt = x − 32. x (t) = 2t + 3x − 3 = 2tt = x − 32.Подставляя это в y (t), y (t), получаем
y (t) = 3t − 4y = 3 (x − 32) −4y = 3×2−92−4y = 3×2−172.y (t) = 3t − 4y = 3 (x − 32) −4y = 3×2−92− 4у = 3х2−172. Наклон этой прямой равен dydx = 32.dydx = 32. Затем мы вычисляем x ′ (t) x ′ (t) и y ′ (t).y ′ (t). Это дает x ′ (t) = 2x ′ (t) = 2 и y ′ (t) = 3. y ′ (t) = 3. Обратите внимание, что dydx = dy / dtdx / dt = 32.dydx = dy / dtdx / dt = 32. Это не совпадение, как указано в следующей теореме.
Теорема 1.1
Производная параметрических уравнений
Рассмотрим плоскую кривую, определяемую параметрическими уравнениями x = x (t) x = x (t) и y = y (t) .y = y (t). Предположим, что x ′ (t) x ′ (t) и y ′ (t) y ′ (t) существуют, и предположим, что x ′ (t) ≠ 0.x ′ (t) ≠ 0. Тогда производная dydxdydx равна
dydx = dy / dtdx / dt = y ′ (t) x ′ (t).dydx = dy / dtdx / dt = y ′ (t) x ′ (t).1,1
Проба
Эту теорему можно доказать с помощью цепного правила. В частности, предположим, что параметр t может быть исключен, давая дифференцируемую функцию y = F (x) .y = F (x). Тогда y (t) = F (x (t)). Y (t) = F (x (t)). Дифференцируя обе части этого уравнения с помощью правила цепочки, получаем
y ′ (t) = F ′ (x (t)) x ′ (t), y ′ (t) = F ′ (x (t)) x ′ (t),так
F ′ (x (t)) = y ′ (t) x ′ (t). F ′ (x (t)) = y ′ (t) x ′ (t). Но F ′ (x (t)) = dydx, F ′ (x (t)) = dydx, что доказывает теорему.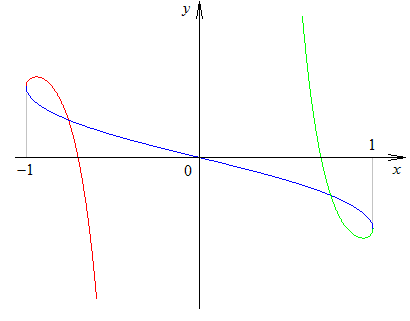
□
Уравнение 1.1 можно использовать для вычисления производных плоских кривых, а также критических точек. Напомним, что критической точкой дифференцируемой функции y = f (x) y = f (x) является любая точка x = x0x = x0 такая, что либо f ′ (x0) = 0f ′ (x0) = 0, либо f ′ (x0 ) f ′ (x0) не существует. Уравнение 1.1 дает формулу для наклона касательной к кривой, заданной параметрически, независимо от того, может ли кривая быть описана функцией y = f (x) y = f (x) или нет.
Пример 1.4
Нахождение производной параметрической кривой
Вычислите производную dydxdydx для каждой из следующих параметрически заданных плоских кривых и найдите любые критические точки на соответствующих графиках.
- x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4
- x (t) = 2t + 1, y (t) = t3−3t + 4, −2≤t≤5x (t) = 2t + 1, y (t) = t3−3t + 4, −2≤t ≤5
- x (t) = 5cost, y (t) = 5sint, 0≤t≤2πx (t) = 5cost, y (t) = 5sint, 0≤t≤2π
Решение
- Чтобы применить уравнение 1.
 1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = 2ty ′ (t) = 2. x ′ (t) = 2ty ′ (t) = 2.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 22tdydx = 1t.dydx = dy / dtdx / dtdydx = 22tdydx = 1t.
Эта производная не определена при t = 0. t = 0. Вычисление x (0) x (0) и y (0) y (0) дает x (0) = (0) 2−3 = −3x (0) = (0) 2−3 = −3 и y (0 ) = 2 (0) −1 = −1, y (0) = 2 (0) −1 = −1, что соответствует точке (−3, −1) (- 3, −1) на графике. График этой кривой представляет собой параболу, раскрывающуюся вправо, а точка (−3, −1) (- 3, −1) является ее вершиной, как показано.Рис. 1.17. График параболы, описываемый параметрическими уравнениями в части a.
- Чтобы применить уравнение 1.1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = 2y ′ (t) = 3t2−3.x ′ (t) = 2y ′ (t) = 3t2−3.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 3t2-32. dydx = dy / dtdx / dtdydx = 3t2-32.
Эта производная равна нулю, когда t = ± 1. t = ± 1. Когда t = −1t = −1, мы имеем
t = ± 1. Когда t = −1t = −1, мы имеем
x (−1) = 2 (−1) + 1 = −1andy (−1) = (- 1) 3−3 (−1) + 4 = −1 + 3 + 4 = 6, x (−1) = 2 (−1) + 1 = −1andy (−1) = (- 1) 3−3 (−1) + 4 = −1 + 3 + 4 = 6,
что соответствует точке (−1,6) (- 1,6) на графике. При t = 1t = 1 имеем
x (1) = 2 (1) + 1 = 3andy (1) = (1) 3−3 (1) + 4 = 1−3 + 4 = 2, x (1) = 2 (1) + 1 = 3andy (1) = (1) 3−3 (1) + 4 = 1−3 + 4 = 2,
что соответствует точке (3,2) (3,2) на графике.Точка (3,2) (3,2) является относительным минимумом, а точка (−1,6) (- 1,6) является относительным максимумом, как показано на следующем графике.Рис. 1.18 График кривой, описываемой параметрическими уравнениями в части b.
- Чтобы применить уравнение 1.1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = — 5sinty ′ (t) = 5cost.x ′ (t) = — 5sinty ′ (t) = 5cost.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 5cost − 5sintdydx = −cott.dydx = dy / dtdx / dtdydx = 5cost − 5sintdydx = −cott.
Эта производная равна нулю, когда cost = 0cost = 0, и не определена, когда sint = 0. sint = 0. Это дает t = 0, π2, π, 3π2 и 2πt = 0, π2, π, 3π2 и 2π в качестве критических точек для t. Подставляя каждый из них в x (t) x (t) и y (t), y (t), получаемtt х (т) х (т) г (т) г (т) 0 5 0 π2π2 0 5 ππ −5 0 3π23π2 0 −5 2π2π 5 0
Эти точки соответствуют сторонам, верху и низу круга, который представлен параметрическими уравнениями (рисунок 1. 19). На левом и правом краях круга производная не определена, а сверху и снизу производная равна нулю.
19). На левом и правом краях круга производная не определена, а сверху и снизу производная равна нулю. Рис. 1.19 График кривой, описываемой параметрическими уравнениями в части c.
КПП 1.4
Вычислить производную dy / dxdy / dx для плоской кривой, определяемой уравнениями
x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3и найдите критические точки на его графике.
Пример 1.5
Поиск касательной
Найдите уравнение касательной к кривой, определяемой уравнениями
x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4whent = 2. x (t) = t2−3, y (t) = 2t − 1, −3≤t≤ 4whent = 2.Решение
Сначала найдите наклон касательной с помощью уравнения 1.1, которое означает вычисление x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = 2ty ′ (t) = 2. x ′ (t) = 2ty ′ (t) = 2.Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 22tdydx = 1t. dydx = dy / dtdx / dtdydx = 22tdydx = 1t.
dydx = dy / dtdx / dtdydx = 22tdydx = 1t.Когда t = 2, t = 2, dydx = 12, dydx = 12, значит, это наклон касательной. Вычисление x (2) x (2) и y (2) y (2) дает
x (2) = (2) 2−3 = 1andy (2) = 2 (2) −1 = 3, x (2) = (2) 2−3 = 1andy (2) = 2 (2) −1 = 3,, что соответствует точке (1,3) (1,3) на графике (рисунок 1.20). Теперь используйте форму точки наклона уравнения прямой, чтобы найти уравнение касательной:
y − y0 = m (x − x0) y − 3 = 12 (x − 1) y − 3 = 12x − 12y = 12x + 52. y − y0 = m (x − x0) y − 3 = 12 (x− 1) y − 3 = 12x − 12y = 12x + 52. Рис. 1.20. Касательная к параболе, описываемой заданными параметрическими уравнениями при t = 2.т = 2.КПП 1.5
Найдите уравнение касательной к кривой, определяемой уравнениями
x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤10whent = 5. x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤ 10whent = 5.Деривативы второго порядка
Наша следующая цель — увидеть, как взять вторую производную функции, определенной параметрически. Вторая производная функции y = f (x) y = f (x) определяется как производная от первой производной; то есть
Вторая производная функции y = f (x) y = f (x) определяется как производная от первой производной; то есть
Поскольку dydx = dy / dtdx / dt, dydx = dy / dtdx / dt, мы можем заменить yy в обеих частях этого уравнения на dydx.dydx. Это дает нам
d2ydx2 = ddx (dydx) = (d / dt) (dy / dx) dx / dt. d2ydx2 = ddx (dydx) = (d / dt) (dy / dx) dx / dt.1,2
Если мы знаем dy / dxdy / dx как функцию от t, , то эту формулу легко применить.
Пример 1.6
Нахождение второй производной
Вычислить вторую производную d2y / dx2d2y / dx2 для плоской кривой, заданной параметрическими уравнениями x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4.x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4.
Решение
Из примера 1.4 мы знаем, что dydx = 22t = 1t.dydx = 22t = 1t. Используя уравнение 1.2, получаем
d2ydx2 = (d / dt) (dy / dx) dx / dt = (d / dt) (1 / t) 2t = −t − 22t = −12t3. d2ydx2 = (d / dt) (dy / dx) dx / dt = (d / dt) (1 / t) 2t = −t − 22t = −12t3.
d2ydx2 = (d / dt) (dy / dx) dx / dt = (d / dt) (1 / t) 2t = −t − 22t = −12t3.КПП 1.6
Вычислить вторую производную d2y / dx2d2y / dx2 для плоской кривой, определяемой уравнениями
x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3и найдите критические точки на его графике.
Интегралы, содержащие параметрические уравнения
Теперь, когда мы увидели, как вычислить производную плоской кривой, следующий вопрос: как найти площадь под кривой, заданной параметрически? Напомним циклоиду, определяемую уравнениями x (t) = t − sint, y (t) = 1 − cost.x (t) = t − sint, y (t) = 1 − cost. Предположим, мы хотим найти площадь заштрихованной области на следующем графике.
Рисунок 1.21 График циклоиды с выделенной аркой на [0,2π] [0,2π].Вывести формулу площади под кривой, определяемой функциями
x = x (t), y = y (t), a≤t≤b, x = x (t), y = y (t), a≤t≤b, мы предполагаем, что x (t) x (t) дифференцируема, и начинаем с равного разбиения интервала a≤t≤b. Рис. 1.22. Аппроксимация площади под параметрически заданной кривой. Мы используем прямоугольники для аппроксимации площади под кривой. Высота типичного прямоугольника в этой параметризации равна y (x (t – i)) y (x (t – i)) для некоторого значения t – it – i в подынтервале i , а ширину можно вычислить как x (ti) −x (ti − 1) .x (ti) −x (ti − 1). Таким образом, площадь прямоугольника и равна Тогда сумма Римана для площади равна Умножение и деление каждой площади на ti − ti − 1ti − ti − 1 дает Если принять предел, когда nn стремится к бесконечности, получаем Это приводит к следующей теореме. Теорема 1.2 Рассмотрим несамопересекающуюся плоскую кривую, определяемую параметрическими уравнениями и предположим, что x (t) x (t) дифференцируема. Площадь под этой кривой равна 1,3 Найдите площадь под кривой циклоиды, определяемой уравнениями Используя уравнение 1. КПП 1.7 Найдите площадь под кривой гипоциклоиды, определяемой уравнениями В дополнение к нахождению площади под параметрической кривой нам иногда необходимо найти длину дуги параметрической кривой. В случае линейного сегмента длина дуги равна расстоянию между конечными точками. Если частица перемещается из точки A в точку B по кривой, то расстояние, которое проходит частица, является длиной дуги. Рисунок 1.23 Аппроксимация кривой отрезками прямых. Для плоской кривой, определяемой функциями x = x (t), y = y (t), a≤t≤b, x = x (t), y = y (t), a≤t≤b, мы начните с разделения интервала [a, b] [a, b] на n равных подинтервалов: t0 = a Затем сложите их. Пусть s обозначает точную длину дуги, а snsn обозначает аппроксимацию n отрезков линии: Мы можем резюмировать этот метод в следующей теореме. Теорема 1.3 Рассмотрим плоскую кривую, заданную параметрическими уравнениями и предположим, что x (t) x (t) и y (t) y (t) — дифференцируемые функции от t. Тогда длина дуги этой кривой равна 1,5 На этом этапе боковой вывод приводит к предыдущей формуле для длины дуги. В частности, предположим, что параметр можно исключить, что приведет к функции y = F (x) .y = F (x). Тогда y (t) = F (x (t)) y (t) = F (x (t)) и цепное правило дает y ′ (t) = F ′ (x (t)) x ′ (t). Здесь мы предположили, что x ′ (t)> 0, x ′ (t)> 0, что является разумным предположением. Цепное правило дает dx = x ′ (t) dt, dx = x ′ (t) dt, и, полагая a = x (t1) a = x (t1) и b = x (t2) b = x (t2), мы получить формулу , которая представляет собой формулу для длины дуги, полученную во Введении в приложения интеграции. Найдите длину дуги полукруга, определяемую уравнениями Значения от t = 0t = 0 до t = πt = π очерчены красной кривой на рисунке 1. Обратите внимание, что формула для длины дуги полукруга равна πrπr, а радиус этой окружности равен 3.Это отличный пример использования исчисления для вывода известной формулы геометрической величины. КПП 1.8 Найдите длину дуги кривой, определяемой уравнениями А теперь вернемся к задаче, поставленной в начале раздела о том, что бейсбольный мяч выходит из руки питчера. Игнорируя эффект сопротивления воздуха (если это не криволинейный шар!), Мяч движется по параболической траектории.Предполагая, что рука питчера находится в начале координат, а мяч движется слева направо в направлении положительной оси x , параметрические уравнения для этой кривой можно записать как , где t — время. Затем запишем формулу длины дуги следующим образом: Переменная v действует как фиктивная переменная, которая исчезает после интегрирования, оставляя длину дуги как функцию времени t. Чтобы интегрировать это выражение, мы можем использовать формулу из Приложения A, Положим a = 140a = 140 и u = −32v + 2.и = −32v + 2. Это дает du = −32dv, du = −32dv, поэтому dv = −132du.dv = −132du. Следовательно, и Эта функция представляет расстояние, пройденное мячом, как функцию времени. Следовательно Через одну треть секунды после того, как мяч покидает руку питчера, расстояние, которое он проходит, равно Это значение составляет чуть более трех четвертей пути к исходной тарелке. Эта скорость соответствует примерно 95 милям в час — фастбол высшей лиги. Вспомните задачу о нахождении площади поверхности объема вращения. В разделах Длина кривой и Площадь поверхности мы вывели формулу для определения площади поверхности объема, созданного функцией y = f (x) y = f (x) от x = ax = a до x = b, x = b, вращается вокруг оси x : Теперь рассмотрим объем вращения, создаваемый вращением параметрически заданной кривой x = x (t), y = y (t), a≤t≤bx = x (t), y = y (t), a≤t ≤b вокруг оси x , как показано на следующем рисунке. Рис. 1.25 Поверхность вращения, образованная параметрически заданной кривой. Аналогичная формула для параметрически определенной кривой: 1,6 при условии, что y (t) y (t) не является отрицательным на [a, b]. Найдите площадь поверхности сферы радиусом r с центром в начале координат. Начнем с кривой, определяемой уравнениями Это создает верхний полукруг радиусом r с центром в начале координат, как показано на следующем графике. Рис. 1.26. Полукруг, образованный параметрическими уравнениями. Когда эта кривая вращается вокруг оси x , она образует сферу радиусом r . Чтобы вычислить площадь поверхности сферы, мы используем уравнение 1.6: Фактически, это формула для определения площади поверхности сферы. КПП 1.9 Найдите площадь поверхности, образованную плоской кривой, определяемой уравнениями вращается вокруг оси x . В следующих упражнениях каждый набор параметрических уравнений представляет собой линию.Не удаляя параметр, найдите наклон каждой линии. x = 3 + t, y = 1 − tx = 3 + t, y = 1 − t x = 4−3t, y = −2 + 6tx = 4−3t, y = −2 + 6t x = −5t + 7, y = 3t − 1x = −5t + 7, y = 3t − 1 Для следующих упражнений определите наклон касательной, а затем найдите уравнение касательной при заданном значении параметра. x = 3sint, y = 3cost, t = π4x = 3sint, y = 3cost, t = π4 x = стоимость, y = 8sint, t = π2x = стоимость, y = 8sint, t = π2 x = 2t, y = t3, t = −1x = 2t, y = t3, t = −1 x = t + 1t, y = t − 1t, t = 1x = t + 1t, y = t − 1t, t = 1 Для следующих упражнений найдите все точки кривой с заданным наклоном. x = 4cost, y = 4sint, x = 4cost, y = 4sint, наклон = 0,5 x = 2cost, y = 8sint, slope = −1x = 2cost, y = 8sint, slope = −1 x = t + 1t, y = t − 1t, наклон = 1x = t + 1t, y = t − 1t, наклон = 1 x = 2 + t, y = 2−4t, наклон = 0x = 2 + t, y = 2−4t, наклон = 0 Для следующих упражнений запишите уравнение касательной в декартовых координатах для данного параметра t . x = et, y = 1 − lnt2, t = 1x = et, y = 1 − lnt2, t = 1 x = tlnt, y = sin2t, t = π4x = tlnt, y = sin2t, t = π4 x = et, y = (t − 1) 2, при (1,1) x = et, y = (t − 1) 2, при (1,1) Для x = sin (2t), y = 2sintx = sin (2t), y = 2sint, где 0≤t <2π.0≤t <2π. Найдите все значения t , при которых существует горизонтальная касательная. Для x = sin (2t), y = 2sintx = sin (2t), y = 2sint, где 0≤t <2π.0≤t <2π. Найдите все значения t , при которых существует вертикальная касательная. Найдите все точки на кривой x = 4sin (t), y = 4cos (t) x = 4sin (t), y = 4cos (t), которые имеют наклон 0,50,5 Найдите dydxdydx для x = sin (t), y = cos (t). X = sin (t), y = cos (t). Найдите уравнение касательной к x = sin (t), y = cos (t) x = sin (t), y = cos (t) при t = π4.t = π4. Для кривой x = 4t, y = 3t − 2, x = 4t, y = 3t − 2 найдите наклон и вогнутость кривой при t = 3.t = 3. Для параметрической кривой, уравнение которой имеет вид x = 4cosθ, y = 4sinθ, x = 4cosθ, y = 4sinθ, найдите наклон и вогнутость кривой при θ = π4.θ = π4. Найдите наклон и вогнутость кривой, уравнение которой: x = 2 + secθ, y = 1 + 2tanθx = 2 + secθ, y = 1 + 2tanθ при θ = π6.θ = π6. Найдите все точки на кривой x = t + 4, y = t3−3tx = t + 4, y = t3−3t, в которых есть вертикальные и горизонтальные касательные. Найти все точки на кривой x = secθ, y = tanθx = secθ, y = tanθ, в которых существуют горизонтальные и вертикальные касательные. Для следующих упражнений найдите d2y / dx2.d2y / dx2. x = t4−1, y = t − t2x = t4−1, y = t − t2 x = sin (πt), y = cos (πt) x = sin (πt), y = cos (πt) x = e − t, y = te2tx = e − t, y = te2t Для следующих упражнений найдите точки на кривой, в которых касательная линия является горизонтальной или вертикальной. x = t (t2−3), y = 3 (t2−3) x = t (t2−3), y = 3 (t2−3) x = 3t1 + t3, y = 3t21 + t3x = 3t1 + t3, y = 3t21 + t3 Для следующих упражнений найдите dy / dxdy / dx в значении параметра. x = стоимость, y = синт, t = 3π4x = стоимость, y = синт, t = 3π4 x = t, y = 2t + 4, t = 9x = t, y = 2t + 4, t = 9 x = 4cos (2πs), y = 3sin (2πs), s = −14x = 4cos (2πs), y = 3sin (2πs), s = −14 Для следующих упражнений найдите d2y / dx2d2y / dx2 в заданной точке, не удаляя параметр. x = 12t2, y = 13t3, t = 2x = 12t2, y = 13t3, t = 2 x = t, y = 2t + 4, t = 1x = t, y = 2t + 4, t = 1 Найдите t интервалов, на которых кривая x = 3t2, y = t3 − tx = 3t2, y = t3 − t является вогнутой вверх и вогнутой вниз. Определите вогнутость кривой x = 2t + lnt, y = 2t − lnt.x = 2t + lnt, y = 2t − lnt. Нарисуйте и найдите площадь под одной аркой циклоиды x = r (θ − sinθ), y = r (1 − cosθ) .x = r (θ − sinθ), y = r (1 − cosθ). Найдите площадь, ограниченную кривой x = cost, y = et, 0≤t≤π2x = cost, y = et, 0≤t≤π2 и линиями y = 1y = 1 и x = 0. Найдите площадь, заключенную в эллипс x = acosθ, y = bsinθ, 0≤θ <2π.x = acosθ, y = bsinθ, 0≤θ <2π. Найдите площадь области, ограниченной x = 2sin2θ, y = 2sin2θtanθ, x = 2sin2θ, y = 2sin2θtanθ, для 0≤θ≤π2.0≤θ≤π2. Для следующих упражнений найдите площадь областей, ограниченных параметрическими кривыми и указанными значениями параметра. x = 2cotθ, y = 2sin2θ, 0≤θ≤πx = 2cotθ, y = 2sin2θ, 0≤θ≤π [T] x = 2acost − acos (2t), y = 2asint − asin (2t), 0≤t <2πx = 2acost − acos (2t), y = 2asint − asin (2t), 0≤t < 2π [T] x = asin (2t), y = bsin (t), 0≤t <2πx = asin (2t), y = bsin (t), 0≤t <2π («песочные часы») [T] x = 2acost − asin (2t), y = bsint, 0≤t <2πx = 2acost − asin (2t), y = bsint, 0≤t <2π («слеза») Для следующих упражнений найдите длину дуги кривой на указанном интервале параметра. x = 4t + 3, y = 3t − 2,0≤t≤2x = 4t + 3, y = 3t − 2,0≤t≤2 x = 13t3, y = 12t2,0≤t≤1x = 13t3, y = 12t2,0≤t≤1 x = cos (2t), y = sin (2t), 0≤t≤π2x = cos (2t), y = sin (2t), 0≤t≤π2 х = 1 + t2, y = (1 + t) 3,0≤t≤1x = 1 + t2, y = (1 + t) 3,0≤t≤1 x = etcost, y = etsint, 0≤t≤π2x = etcost, y = etsint, 0≤t≤π2 (выразите ответ в виде десятичной дроби с округлением до трех знаков) x = acos3θ, y = asin3θx = acos3θ, y = asin3θ на интервале [0,2π) [0,2π) (гипоциклоида) Найдите длину одной дуги циклоиды x = 4 (t − sint), y = 4 (1 − cost). X = 4 (t − sint), y = 4 (1 − cost). Найдите расстояние, пройденное частицей с положением (x, y) (x, y), поскольку t изменяется в заданном интервале времени: x = sin2t, y = cos2t, 0≤t≤3π.x = sin2t, y = cos2t, 0≤t≤3π. Найдите длину одной дуги циклоиды x = θ − sinθ, y = 1 − cosθ.x = θ − sinθ, y = 1 − cosθ. Покажите, что общая длина эллипса x = 4sinθ, y = 3cosθx = 4sinθ, y = 3cosθ равна L = 16∫0π / 21 − e2sin2θdθ, L = 16∫0π / 21 − e2sin2θdθ, где e = cae = ca и c = a2 − b2.c = a2 − b2. Найдите длину кривой x = et − t, y = 4et / 2, −8≤t≤3.x = et − t, y = 4et / 2, −8≤t≤3. Для следующих упражнений найдите площадь поверхности, полученную вращением данной кривой вокруг оси x . x = t3, y = t2,0≤t≤1x = t3, y = t2,0≤t≤1 x = acos3θ, y = asin3θ, 0≤θ≤π2x = acos3θ, y = asin3θ, 0≤θ≤π2 [T] Используйте CAS, чтобы найти площадь поверхности, созданную вращением x = t + t3, y = t − 1t2,1≤t≤2x = t + t3, y = t − 1t2,1≤t ≤2 относительно оси x .(Ответ с точностью до трех знаков после запятой.) Найдите площадь поверхности, полученную вращением x = 3t2, y = 2t3,0≤t≤5x = 3t2, y = 2t3,0≤t≤5 вокруг оси y . Найдите площадь поверхности, образованную вращением x = t2, y = 2t, 0≤t≤4x = t2, y = 2t, 0≤t≤4 вокруг оси x . Найдите площадь поверхности, образованную вращением x = t2, y = 2t2,0≤t≤1x = t2, y = 2t2,0≤t≤1 вокруг оси y . В прошлом мы работали с прямоугольными уравнениями, то есть уравнениями, включающими только x
и y, чтобы их можно было изобразить в декартовой (прямоугольной) системе координат. У нас также был пример зависимости высоты свободно падающего тела от времени в секундах t.
Эта функция была квадратичной функцией. Если объект не уронили или не бросили прямо в
воздух, также будет горизонтальная составляющая его положения. Горизонтальная составляющая — это
простая функция расстояния (d = rt). Путь падающего объекта y (t) = -16t 2 — v 0 t + y 0 х (т) = г т v 0 = начальная вертикальная скорость y 0 = начальная высота r = горизонтальная скорость t = время в секундах Обратите внимание, что обе эти функции, вертикальная высота и
горизонтальное расстояние зависит от времени. Это дает нам параметрические уравнения. Параметр просто
независимая переменная в функции. Плоская кривая получается, когда упорядоченные пары (x (t), y (t)) отображаются на графике для всех значений t на некотором
интервал. Один из способов нарисовать плоскую кривую — составить таблицу значений.Параметр t имеет несколько
значения, перечисленные для него, и соответствующие значения для x (t) и y (t) вычисляются. Затем заказали
пары построены, а кривая проведена между построенными парами. При построении плоской кривой «направление увеличения t» или «ориентация»
кривой обозначается маленькими стрелками, указывающими направление кривой
продвигается, когда стоимость
параметр t увеличивается. Графический калькулятор прекрасно справляется с графическим отображением параметрических уравнений.Вы должны,
однако сообщите калькулятору, что вы хотите графически отображать параметрические уравнения, а не обычные
функции. Для этого переведите калькулятор в параметрический режим, нажав [РЕЖИМ] и
выбирая опцию [PAR]. Не забудьте сбросить калькулятор обратно на [FUN] для функционального режима.
когда вы закончите с параметрическими уравнениями. Находясь в меню режима, вы можете
установите калькулятор в режим [РАДИАН] вместо режима [ГРАДУСЫ]. Они используются для
тригонометрические функции, которые мы не будем использовать, но они влияют на то, как клавиши масштабирования
работай. После настройки вашего калькулятора для параметрического режима, обратите внимание, что когда вы нажимаете клавишу Y =, вы не
больше у 1 =. Теперь у вас есть пара уравнений, x и y, которые являются функциями t.
Просто введите параметрические уравнения для x и y. Теперь у вас будет три дополнительных окна, которых у вас не было раньше.Tmin, Tmax и Tstep. Тмин является наименьшее значение для параметра, который вы
хотите использовать. Если у вас нет
хорошая причина, чтобы не (как домен говорит г> = 0), обязательно использовать отрицательные
значения Tmin. Tmax является наибольшим значением для параметра, который вы хотите
использовать. Если у вас есть веские причины не делать этого,
использовать положительное значение для Tmax. Другими словами, убедитесь, что T может взять на себя оба
положительные и отрицательные значения. Tstep — это изменение T и должно быть разумным.
для диапазона значений T
вы указали. TMin = -5, TMax = 5 и TStep = 0,1 обычно являются хорошими начальными значениями. Если
вы обнаружите, что график не отображается, вы
май
необходимость
чтобы изменить эти значения. Внимание! Zoom Standard сбросит настройки
на T. Если вы сделаете стандартное масштабирование, ваш T будет находиться в диапазоне от 0 до 2 пи (в
в радианах) на число пи / 24 и от 0 до 360 (в градусном режиме)
на 7,5. Ни один из них не содержит отрицательных значений и может не отображать весь
график. Направление увеличения t — это направление, в котором калькулятор рисует кривую.
в.Обозначьте это стрелками, направленными вдоль кривой. Другой способ нарисовать плоскую кривую — исключить параметр. Шаги к устранению
параметр прост. На шаге 1 вы должны решить относительно t в более простом уравнении. Легче решить
не всегда означает меньший показатель степени.Если у вас есть t 2 и t 3 ,
решить для t в t 3 (если возможно). Не всегда может быть необходимо полностью решить для t. Это ценно
когда один из членов появляется в других уравнениях. Удалите параметр из x = 3t 2 — 4 и y = 2t. Y определенно является более простой функцией для определения t, и когда вы это сделаете,
вы получите t = y / 2. Подставьте это в уравнение x для t, и вы получите x = 3 (y / 2) 2 —
4. Упростите, чтобы получить x = 3/4 y 2 — 4. Рассмотрим систему уравнений x = e t и y = e 3t . Если бы вы решили эту проблему, используя шаги, перечисленные выше, вы бы
x = e t уравнение и решите его относительно t, чтобы получить t = ln x. Затем подставьте
это в уравнение y = e 3t , чтобы получить y = e 3ln x .С помощью
свойства логарифмов, вы бы переместили 3 в степень на x
а затем функции e и ln инвертируют, оставляя вас с y =
х 3 . Теперь подумайте об этом. y = e 3t = (e t ) 3 .
Поскольку x = e t , замените e t на x. у = (х) 3 или просто y = x 3 . Не было необходимости спускаться до t. Еще одно замечание по поводу этой проблемы. Поскольку x и y являются экспоненциальными функциями,
диапазон на каждом из них — положительные реалы.2 = 1 $. Несколько вопросов, которые стоит задать себе: Теперь вы знаете , какие частей единичной окружности задаются параметрической кривой. Добавлен. Как и многие студенты на начальном этапе, вам кажется, что вы хотите построить несколько точек, а затем интерполировать; это не лучшая идея, потому что она полагается на то, что вы просто случайно попадете в нужные точки, чтобы получить точное представление о том, что происходит. Вы, , не хотите, это делать. Вместо этого вы хотите подумать о том, что делают эти функции. Один из способов, которым я считаю наиболее плодотворным размышление о параметрических уравнениях, — это думать о параметре как о дающем время , а об уравнениях как о движении точки; Представьте себе анимацию со светящейся точкой, движущейся по плоскости и оставляющей за собой «след» света.Этот след — параметрическая кривая, точка — это положение в «текущем $ t $». Вы хотите подумать о том, что делает эта точка, когда ваш параметр варьируется от своего начального значения до конечного значения (то есть, когда анимация идет от начала до конца). Итак, начнем с $ \ theta = 0 $, первого кадра вашей анимации. Ваша светящаяся точка будет в $ x (0) = \ sin (0) = 0 $ и $ y (0) = \ cos (0) = 1 $. Итак, вы начинаете с точки $ (0,1) $. Теперь нажмите кнопку А что насчет $ y $? Он начинается с 1 доллара США; он будет вести себя как график $ \ cos \ theta $. Когда вы нажмете Теперь объедините эти два движения: вы начнете с $ (0,1) $, вершины единичного круга. Затем, когда $ \ theta $ перемещается от $ 0 $ к $ \ pi / 2 $, светящаяся точка начинает двигаться вправо и вниз, всегда по единичной окружности, до тех пор, пока $ \ theta = \ pi / 2 $ не окажется в точке Хорошо, продолжить? Нажмите Все это время движение было без прыжков, колебаний или возвратов, потому что функции $ x = \ sin \ theta $ и $ y = \ cos \ theta $ имеют эти движения: без прыжков, без пропусков, без рывков, без колебаний , без возврата, просто плавное движение (представьте, что ваша рука рисует их графики).Эта светящаяся точка теперь проследила часть единичной окружности ровно один раз без возврата. Какая часть? Первое параметрическое уравнение Второе параметрическое уравнение Прямоугольное уравнение х = 4t2−4 у = т х = 4y2−4 х = t2−4 у = t2 2y = t х = (2у) 2 — 4 х = 4y2−4 Чтобы найти набор параметрических уравнений для графика, представленного как y = x 2 + 2 при t = x + 2, пусть t = x. Переключение ролей t и x в этом уравнении дает одно из параметрических уравнений: t = x + 2 → x = t + 2 y = x2 + 2 y = (t + 2) 2 + 2 y = t2 + 4t + 4 + 2 y = t2 + 4t + 6 x = t + 2 y = t2 + 4t + 6 т -2 -1 0 1 2 х = т + 2 0 1 2 3 4 у = т 2 + 4т + 6 2 3 6 11 18 РУКОВОДСТВО ПО ПОИСКУ ПАРАМЕТРИЧЕСКИХ УРАВНЕНИЙ ДЛЯ ГРАФИКА: 1. 2. Подставьте выражение для переменной на шаге 1 в прямоугольное уравнение. В результате получится второе параметрическое уравнение. 3. Нарисуйте кривую. Попробуем пару примеров. Пример 1. Найдите набор параметрических уравнений для прямоугольного уравнения y = x 2 + 1, учитывая t = 2 — x.Затем нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой. Шаг 1: Возьмите уравнение для параметра и поменяйте роли параметра и другой переменной. Пусть t = x и перепишем уравнение параметров, переключив t и x. т = 2 — х
Оригинал х = 2 — т
Переключить t и x Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение y = x2 + 1 Оригинал y = (2 − t) 2 + 1 Заменить y = (4−4t + t2) + 1 Квадрат y = 5−4t + t2 Добавить Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой. Прямоугольное уравнение:
у = х2 + 1 Параметрические уравнения:
х = 2 — т,
у = 5−4t + t2 т 0 1 2 3 Икс х = 2 — т 2 1 0 -1 у y = 5 — 4t + t 2 5 2 1 2 Пример 2: Найдите набор параметрических уравнений для прямоугольного уравнения y = 2×2 + 1 при t = x. Шаг 1: Возьмите уравнение для параметра и поменяйте роли параметра и другой переменной. t = xОригинал x = t Переключить t и x Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение y = 2×2 + 1 Оригинал y = 2t2 + 1 Заменить y = 2t + 1 квадрат Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками в t = {0, 1, 2, 3, 4} и укажите ориентацию кривой. Прямоугольное уравнение:
у = 2×2 + 1 Параметрические уравнения:
х = т, у = 2т + 1 т 0 1 2 3 4 Икс х = т 0 1 2 3 2 у у = 2т + 1 2 1 23 12 25 Обратите внимание, что область графика — x≥0, потому что область параметрического уравнения t = x ограничивает x значениями от нуля или выше. Синтаксис: Для 2-мерного построения параметрическая функция определяется парой параметрических
функции, работающие с параметром. Пример 2-мерной параметрической функции
будет plot sin (t), cos (t) , который рисует круг (если соотношение сторон
установить правильно — см. размер набора (стр. ). gnuplot отобразит сообщение об ошибке, если
обе функции не предусмотрены для параметрического графика . Для трехмерного построения поверхность описывается как x = f (u, v), y = g (u, v), z = h (u, v).
Поэтому требуется тройка функций. Пример 3-х мерного параметрического
функция будет иметь вид cos (u) * cos (v), cos (u) * sin (v), sin (u) , который рисует сферу. gnuplot отобразит сообщение об ошибке, если не все три функции
Предусмотрена параметрическая шлице . Полный набор возможных графиков — это надмножество простых графиков стиля f (x),
поскольку две функции могут описывать значения x и y для вычисления
раздельно.На самом деле графики типа t, f (t) эквивалентны тем
производится с помощью f (x), потому что значения x вычисляются с использованием тождества
функция. Точно так же трехмерные графики типа u, v, f (u, v) эквивалентны
f (х, у). Обратите внимание, что порядок задания параметрических функций — xfunction,
y-функция (и z-функция), и каждая из них работает с общим параметрическим
домен. Кроме того, заданная параметрическая функция предполагает новый диапазон значений. Параметрические уравнения определяют отношения как наборы уравнений.Изображение на графе называется
быть параметризованным, если набор координат (x, y) на изображении представлен
как функции переменной, обычно t (обычно используются параметрические уравнения
для представления движения объекта в любой момент времени t ). Любое уравнение может
быть параметризованным и представленным в виде набора параметрических уравнений.Обычно мы параметризуем следующие значения , где t — набор действительных чисел. Переменная t называется параметр и соотношение между переменными x , y ,
и t называются параметрическими уравнениями . Наоборот,
заданная пара параметрических уравнений, набор точек (f (t), g (t)) образуют кривую на графике.Вместо того, чтобы беспокоиться о двух входах
переменных (x и y), мы свели функцию к одной входной переменной. (1) Рассмотрим квадратное уравнение Параметризуя кривую, мы получили бы параметрические уравнения Если бы это было движущееся тело, и мы хотели бы найти положение через 3 секунды, мы
можно подключить t = 3 и получить нашу координату. Уравнения можно параметризовать по-разному. Взяв наш последний пример, мы могли бы
используйте следующие параметризации Следует отметить, что для разных параметрических уравнений одной и той же функции
координата (x, y) будет изменяться, однако график будет точно таким же. Здесь
представляет собой график параболы с четырьмя парами параметрических уравнений при t = 1 . Ориентация параметризованной кривой определяется увеличением
значения параметра. Иногда ориентация обозначается стрелками, нарисованными на
направление кривой. Полезно увидеть, как найти исходную функцию по параметрическим уравнениям.
чтобы понять связь. (2) Начнем с параметризованных кривых Найдите функцию y = f (x) , график которой дает параметрические уравнения. Начнем с решения x = 3t + 2 для t . Затем мы подставляем это во второе уравнение для y, что дает нам Это квадратное уравнение, которое образует открывающуюся вверх параболу с вершиной
(2,0).Мы еще не закончили, мы не можем забыть наш домен. Поскольку область определения нашего параметра — 0 ≤ t ≤ 5 , мы получаем новое неравенство
для области для x. (3) Отрезок линии между точками (2, -5) и (-3, 4) будет параметризован как Если мы хотим параметризовать всю строку, мы делаем то же самое, за исключением того, что t уходит с отрицательного
в положительную бесконечность Мы можем описать движение объекта по окружности с помощью параметрических уравнений
с тригонометрическими уравнениями.
Круги и эллипсы параметризованы с использованием тождества триггера Пифагора. Подменяем x (t) для x , y (t) для y , и помните, что cos 2 x + sin 2 x = 1 .
Напомним, что единичный круг можно записать как x 2 + y 2 = 1 .поэтому мы можем параметризовать единичную окружность как {cos (t), sin (t)} с t , идущим от [0,2Π] (4) Если мы хотим параметризовать окружность с центром (-3,2) радиусом 4, мы можем параметризовать
круг следующим образом То же самое и с эллипсами. Для параметризации эллипса Мы бы использовали Как правило, местоположение объекта в момент времени t зависит от ряда вещей. Местоположение объекта в момент времени t определяется по: Этот метод параметризации использует полярные координаты,
в котором используется другая графическая система, используемая в основном для кругов и более сложных кривых. Если у нас есть кривые, которые являются кусочными функциями или формами, мы можем параметризовать
каждую деталь по отдельности, а затем сместите параметризации, чтобы каждая деталь работала последовательно
и перерывов нет. (5) Учитывая это изображение квадрата, образованного следующими координатами, ориентированными
по часовой стрелке Если мы хотим обойти сторону в секунду, это займет 4 секунды. Наши параметры
равны 0 ≤t ≤ 4 . Поскольку это кусочная функция и каждая из наших частей является линиями, мы можем использовать
формулу для параметризации линий и разбить ее на четыре пары уравнений. Наша формула работает только для сегмента на интервале т: [0,1] , поэтому каждый
сегмент является компенсирующим для удовлетворения формулы. Введите параметрическую кривую. Используйте t в качестве переменной. ПОМОЩЬ Используйте предоставленную клавиатуру для ввода параметрических кривых.Используйте t в качестве переменной. Щелкните «PLOT», чтобы построить кривые, которые вы ввели. Вот несколько примеров того, что вы можете ввести. Вот как вы используете кнопки а≤t≤b. Предположим, что t0 = a
а≤t≤b. Предположим, что t0 = a 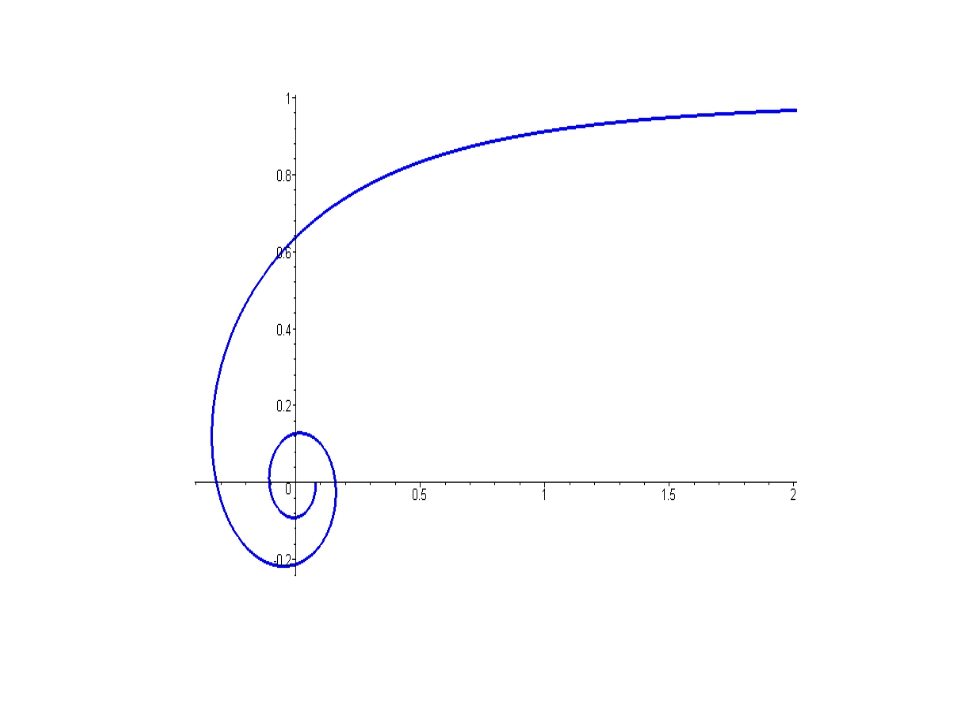 An = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) ti − ti − 1) (ti − ti − 1) = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) Δt) Δt.
An = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) ti − ti − 1) (ti − ti − 1) = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) Δt) Δt. Площадь под параметрической кривой
Пример 1.7
Нахождение площади под параметрической кривой
Решение
 3, получаем
3, получаем Длина дуги параметрической кривой
 Чтобы разработать формулу для длины дуги, мы начнем с аппроксимации отрезками линии, как показано на следующем графике.
Чтобы разработать формулу для длины дуги, мы начнем с аппроксимации отрезками линии, как показано на следующем графике. k) Δty (tk) −y (tk − 1) = y ′ (t ˜k) (tk − tk − 1) = y ′ (t˜k) Δt.k и t˜kt˜k содержатся в одном и том же постоянно сокращающемся интервале шириной Δt, Δt, поэтому они должны сходиться к одному и тому же значению.
k) Δty (tk) −y (tk − 1) = y ′ (t ˜k) (tk − tk − 1) = y ′ (t˜k) Δt.k и t˜kt˜k содержатся в одном и том же постоянно сокращающемся интервале шириной Δt, Δt, поэтому они должны сходиться к одному и тому же значению. Длина дуги параметрической кривой
 y ′ (t) = F ′ (x (t)) x ′ (t). Подставляя это в уравнение 1.5, получаем
y ′ (t) = F ′ (x (t)) x ′ (t). Подставляя это в уравнение 1.5, получаем Пример 1.8
Нахождение длины дуги параметрической кривой
Решение
 23. Чтобы определить его длину, используйте уравнение 1.5:
23. Чтобы определить его длину, используйте уравнение 1.5: Сначала мы вычисляем расстояние, которое проходит мяч, как функцию времени. Это расстояние представлено длиной дуги. Мы можем немного изменить формулу длины дуги. Сначала перепишите функции x (t) x (t) и y (t) y (t), используя v в качестве независимой переменной, чтобы избежать путаницы с параметром t :
Сначала мы вычисляем расстояние, которое проходит мяч, как функцию времени. Это расстояние представлено длиной дуги. Мы можем немного изменить формулу длины дуги. Сначала перепишите функции x (t) x (t) и y (t) y (t), используя v в качестве независимой переменной, чтобы избежать путаницы с параметром t :
 Для расчета скорости возьмите производную этой функции по т. Хотя это может показаться сложной задачей, можно получить ответ непосредственно из Фундаментальной теоремы исчисления:
Для расчета скорости возьмите производную этой функции по т. Хотя это может показаться сложной задачей, можно получить ответ непосредственно из Фундаментальной теоремы исчисления: Скорость мяча
Скорость мяча Площадь поверхности, созданная параметрической кривой
 [A, b].
[A, b]. Пример 1.9
Поиск площади поверхности
Решение
 S = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dt = 2π∫0πrsint (−rsint) 2+ (rcost) 2dt = 2π∫0πrsintr2sin2t + r2cos2tdt = 2π∫0πrsintr2 ( sin2t + cos2t) dt = 2π∫0πr2sintdt = 2πr2 (−cost | 0π) = 2πr2 (−cosπ + cos0) = 4πr2.
S = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dt = 2π∫0πrsint (−rsint) 2+ (rcost) 2dt = 2π∫0πrsintr2sin2t + r2cos2tdt = 2π∫0πrsintr2 ( sin2t + cos2t) dt = 2π∫0πr2sintdt = 2πr2 (−cost | 0π) = 2πr2 (−cosπ + cos0) = 4πr2. Раздел 1.2. Упражнения
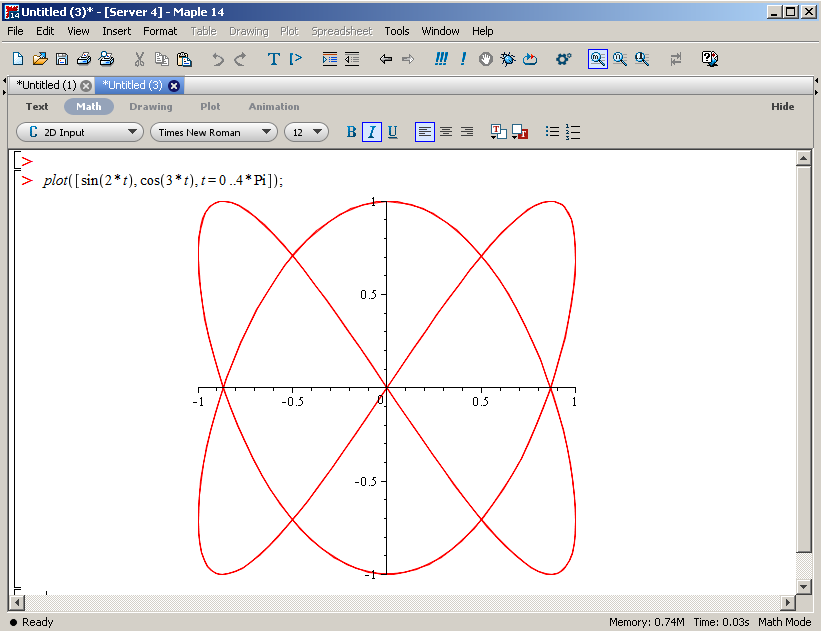



 x = 0.
x = 0.


8.3 — Параметрические уравнения
8.3 — Параметрические уравнения Итак, чтобы полностью
Чтобы описать путь объекта, нам понадобятся два уравнения. Один
для вертикального компонента и один для горизонтального
компонент. Обе эти функции являются функциями
третья переменная, т.
Итак, чтобы полностью
Чтобы описать путь объекта, нам понадобятся два уравнения. Один
для вертикального компонента и один для горизонтального
компонент. Обе эти функции являются функциями
третья переменная, т. Построение плоской кривой
Ориентация или направление

Графический калькулятор
 Обратите внимание, что ключ, который вы использовали для
X также обозначается T. В параметрическом режиме вместо X автоматически появляется буква T.
Обратите внимание, что ключ, который вы использовали для
X также обозначается T. В параметрическом режиме вместо X автоматически появляется буква T. Параметры окна

Удаление параметра
 При выполнении
Таким образом, вы избегаете положительной / отрицательной ситуации, когда извлекаете квадратный корень из t.
При выполнении
Таким образом, вы избегаете положительной / отрицательной ситуации, когда извлекаете квадратный корень из t. Пример 1
Пример 2

 Чтобы дать вам пример, если вы пытались построить график для функции $ y = \ sin (\ pi x) $ и попробовали несколько точек, скажем, $ x = 0 $, $ x = 1 $, $ x = 2 $, $ x = 3 $ и т. д., вы можете подумать, что ваша функция — это постоянная функция $ 0 $, потому что при выборе точек упускаются все важные вещи, которые происходят с $ y $.
Чтобы дать вам пример, если вы пытались построить график для функции $ y = \ sin (\ pi x) $ и попробовали несколько точек, скажем, $ x = 0 $, $ x = 1 $, $ x = 2 $, $ x = 3 $ и т. д., вы можете подумать, что ваша функция — это постоянная функция $ 0 $, потому что при выборе точек упускаются все важные вещи, которые происходят с $ y $.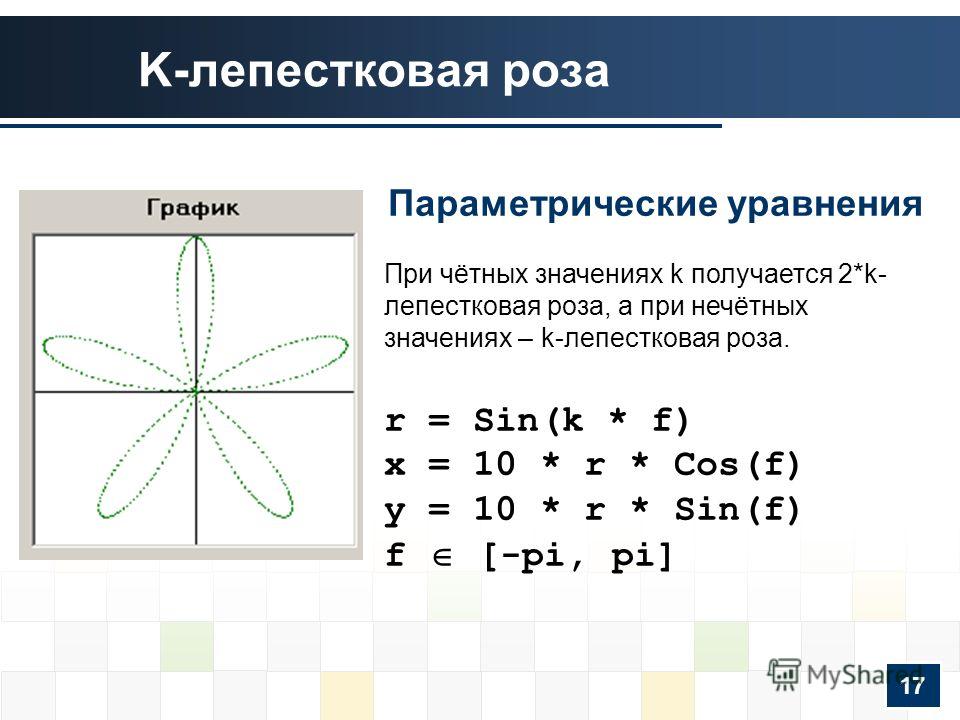
PLAY .Что происходит, когда $ \ theta $ начинает продвигаться от $ 0 $ к $ \ pi $? Координата $ x $ будет следовать графику $ y (\ theta) = \ sin (\ theta) $, поэтому сначала она повысится с $ 0 $ до $ 1 $ (при $ \ theta = \ frac {\ pi} {2 } $), а затем снова упасть с $ 1 $ на $ 0 $ (при $ \ theta = \ pi $). Это будет без скачков и перерывов. Итак, если вы смотрели только на «тень» нашей светящейся точки на оси $ x $, она начинается с $ x = 0 $, затем плавно перемещается вправо (без рывков, без прыжков, без пропусков ), пока он не достигнет $ 1 $ в середине фильма, а затем вернется к $ 0 $, пока не вернется к $ 0 $ в конце фильма. PLAY , он начнется с 1 доллара, а затем упадет до 0 долларов, снова плавно, без скачков, рывков и пропусков, пока не достигнет 0 долларов в середине фильма (при $ \ theta = \ frac {\ pi} {2} $). Затем продолжит движение в том же направлении, от $ 0 $ до $ -1 $, и достигнет $ -1 $ в конце «фильма» (когда $ \ theta = \ pi $). Итак, если вы посмотрите на «тень» светящейся точки на оси $ y $, она начнется с $ 1 $, затем опустится до $ 0 $ и продолжит снижаться до $ -1 $, и все это в целом гладко. манерой, без скачков, рывков, колебаний, откатов и т. д.
Затем продолжит движение в том же направлении, от $ 0 $ до $ -1 $, и достигнет $ -1 $ в конце «фильма» (когда $ \ theta = \ pi $). Итак, если вы посмотрите на «тень» светящейся точки на оси $ y $, она начнется с $ 1 $, затем опустится до $ 0 $ и продолжит снижаться до $ -1 $, и все это в целом гладко. манерой, без скачков, рывков, колебаний, откатов и т. д. <заполните поле> . Нажмите PAUSE на видео и подведите итоги. Где мы? Какую часть единичного круга мы проследили? Сколько раз? Любой возврат? Сколько времени вы проводите без движения? Было ли движение в целом «плавным»? PLAY еще раз, и наш $ \ theta $ начнет увеличиваться с $ \ pi / 2 $ в сторону $ \ pi $.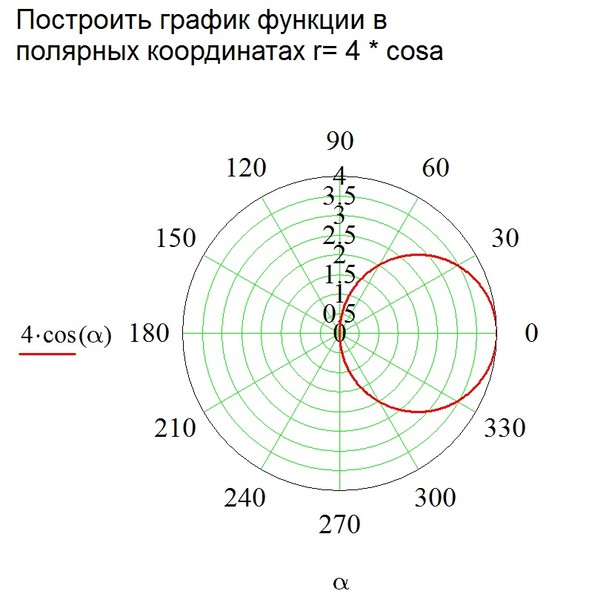 Эта светящаяся точка, представляющая $ (x (\ theta), y (\ theta)) $, перемещается, но теперь вниз и влево, всегда вдоль единичной окружности, пока, наконец, не $ \ theta = \ pi $, «конец фильм «, он достигает своего конечного пункта назначения в точке
Эта светящаяся точка, представляющая $ (x (\ theta), y (\ theta)) $, перемещается, но теперь вниз и влево, всегда вдоль единичной окружности, пока, наконец, не $ \ theta = \ pi $, «конец фильм «, он достигает своего конечного пункта назначения в точке <заполните другой бланк> . Нахождение параметрических уравнений для графика
Набор параметрических уравнений не уникален для данного графа. Например, следующие наборы параметрических уравнений приводят к тому же прямоугольному уравнению и, таким образом, представляют тот же график.
Однако с учетом прямоугольного уравнения и уравнения, описывающего параметр в терминах одной из двух переменных, можно определить набор параметрических уравнений.
Теперь подставьте выражение для x в прямоугольное уравнение y = x 2 + 2, чтобы получить второе параметрическое уравнение.
Таким образом, набор параметрических уравнений для графика, представленного как y = x 2 + 2, имеет вид
Теперь, когда определены оба параметрических уравнения, можно построить общий график с выбранными значениями параметра. Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. Это приведет к одному параметрическому уравнению.
Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. Это приведет к одному параметрическому уравнению. 
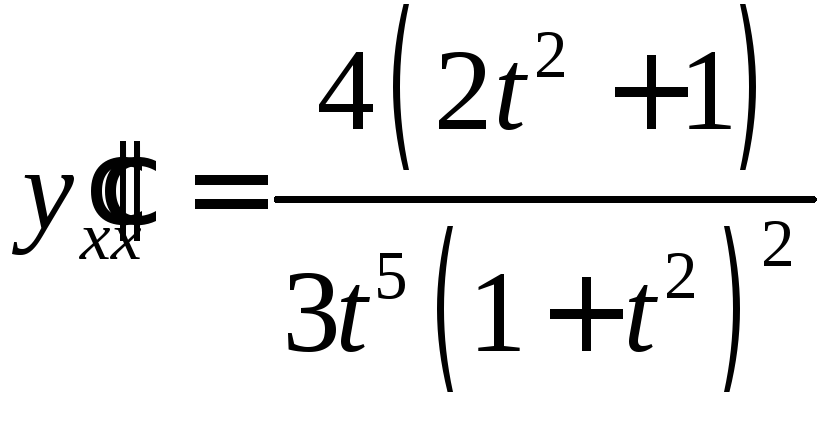 Затем нарисуйте график с точками в точке t = {0,1,2,3,4} и укажите ориентацию кривой.
Затем нарисуйте график с точками в точке t = {0,1,2,3,4} и укажите ориентацию кривой. 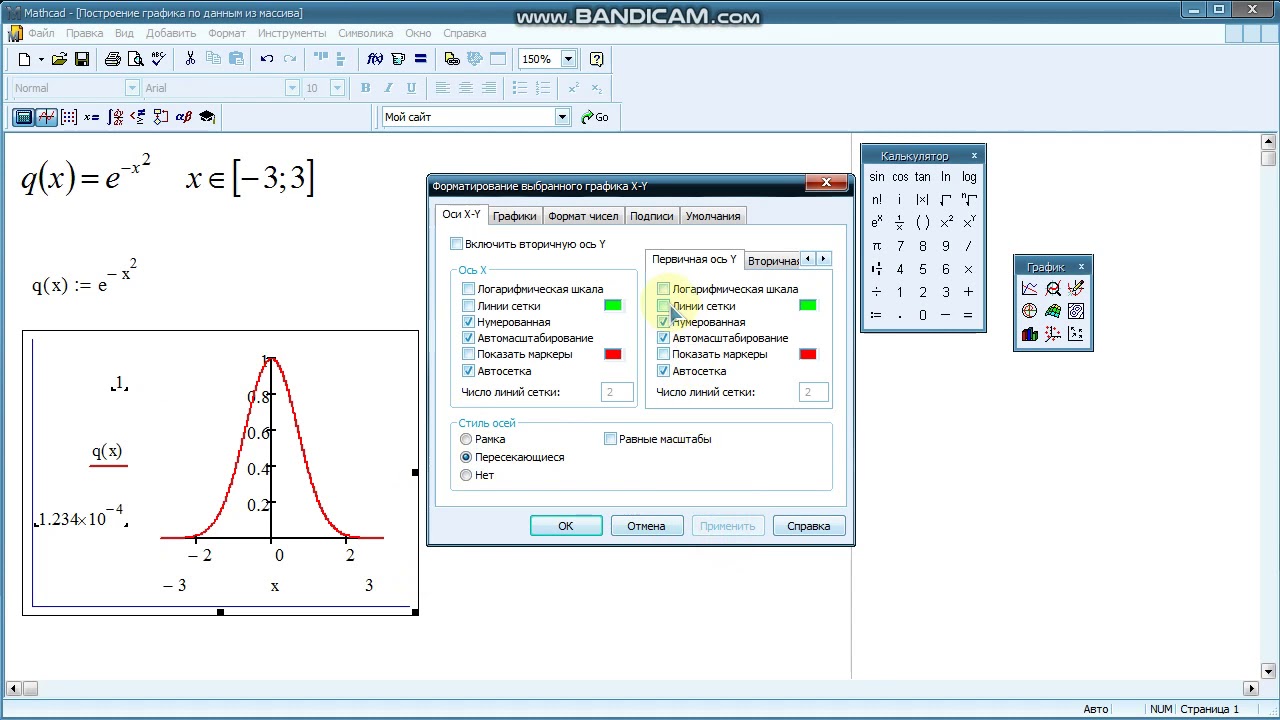

Параметрический
Параметрический
Следующая: Участок Up: Сет-шоу Предыдущий: Вывод Содержание Индекс
Параметрический Команда set параметрическая изменяет значение графика plot ( splot ) с
нормальные функции в параметрические функции. Команда снимает параметрический восстанавливает стиль рисования до обычного однозначного выражения.
установить параметрический
неустановленный параметрический
показать параметрический

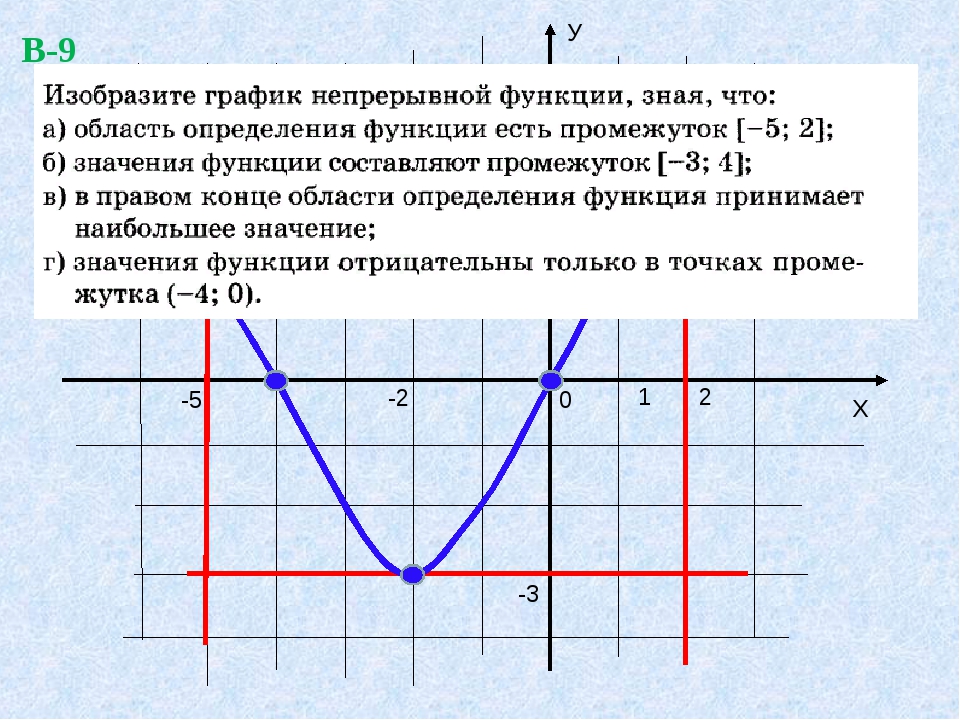 В то время как
при построении нормального стиля f (x) и f (x, y) предполагается, что xrange и yrange (и
zrange), параметрический режим дополнительно определяет trange, urange и
vrange.Эти диапазоны могут быть установлены напрямую с помощью set trange , set urange ,
и установите vrange , или указав диапазон на графике или splot команды. В настоящее время диапазон по умолчанию для этих параметрических переменных составляет
[-5: 5]. Ожидается установка диапазонов на что-то более значимое.
В то время как
при построении нормального стиля f (x) и f (x, y) предполагается, что xrange и yrange (и
zrange), параметрический режим дополнительно определяет trange, urange и
vrange.Эти диапазоны могут быть установлены напрямую с помощью set trange , set urange ,
и установите vrange , или указав диапазон на графике или splot команды. В настоящее время диапазон по умолчанию для этих параметрических переменных составляет
[-5: 5]. Ожидается установка диапазонов на что-то более значимое.
Следующая: Участок Up: Сет-шоу Предыдущий: Вывод Содержание Индекс Итан Мерритт
2007-03-03 параметрических уравнений | Ресурсы Wyzant
 Из одного входа мы можем найти оба
координаты точек с нашими параметрическими уравнениями.
Из одного входа мы можем найти оба
координаты точек с нашими параметрическими уравнениями. Нахождение исходной функции параметрических уравнений
Линии и сегменты
Как мы видели, есть много способов параметризации кривых. Для линий и сегментов
наиболее распространенный способ параметризации отрезка L между точками (a, b) и (c, d) является Круги и эллипсы
Различные кривые
— Open Omnia
См. Примеры
. УЧАСТОК Строит введенные кривые. ПРОЗРАЧНЫЙ Удаляет весь текст в текстовом поле. DEL Удаляет последний элемент перед курсором. триг Показывает тригонометрические функции. ◀ Переместите курсор влево. ▶ Переместите курсор вправо. ▲ Переместите курсор вверх. ▼ Переместите курсор вниз.{□} {□} долларов США N-й корень. (□) Скобка. журнал База 10. пер. Натуральное бревно (база е). | $ □ $ | Абсолютное значение.


 1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):  t = ± 1. Когда t = −1t = −1, мы имеем
t = ± 1. Когда t = −1t = −1, мы имеем 
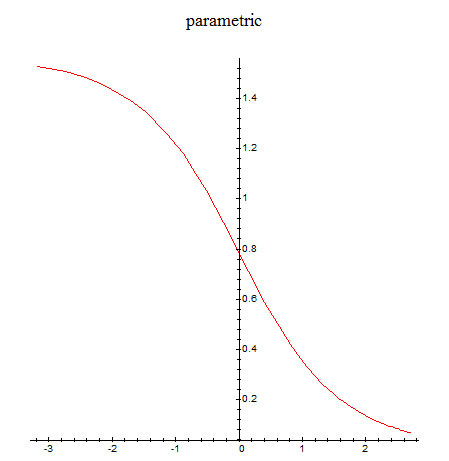 19). На левом и правом краях круга производная не определена, а сверху и снизу производная равна нулю.
19). На левом и правом краях круга производная не определена, а сверху и снизу производная равна нулю.
Ваш комментарий будет первым