График функции, построение графика, урок по алгебре за 10 класс, презентация
Дата публикации: .
Ребята, мы с вами построили много графиков функций, например, параболы, гиперболы, графики тригонометрических функций и другие. Давайте вспомним, как мы это делали. Мы выбирали точки на оси абсцисс, высчитывали значения ординат нашей функций и плавно соединяли наши ординаты на координатной плоскости. То есть, мы строили график по точкам. При построении многих графиков, точки нужно выбирать обдуманно. Теперь давайте обобщим наши знания и напишем общие правила построения графиков функций.
Что же такое график функции?
График функции – это множество точек, абсциссы которых являются значениями из области определения, а ординаты — значениями функции y= f(x). График любой функций строят по точкам. Но если мы точно не знаем, какой будет вид у графика, то точки надо выбирать обдуманно. Ребята, какие важные точки есть у функций?
Давайте, вспомним их:
а) Стационарные и критические точки Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.
Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.б) Точки экстремума. Точки максимума и минимума функций. Точки, возле которых определяется характер монотонности.
в) Точки пересечения графика с осью абсцисс и осью ординат. Значения, в которых функция y= f(x)= 0 – точки пересечения с осью абсцисс. А если вычислить f(0) – то эта точка пересечения с осью ординат.
г) Точки разрыва функций. Эти точки ищутся для не непрерывных функций.
Правило построения графиков функций
Ребята, давайте запишем основные правила построения графиков функций:
- Если функция y= f(x) непрерывна на всей числовой прямой, то надо найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек, в которых следует подсчитать значение нашей функции.

- Если функция y= f(x) определена не на всей числовой прямой, то начинать следует с нахождения области определения функции, с указания точек ее разрыва.
- Полезно исследовать функцию на чётность, поскольку графики четной или нечетной функций обладают симметрией (соответственно относительно оси y или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при x ≥ 0, а затем дорисовать симметричную ветвь.
- Если то прямая y= b является горизонтальной асимптотой нашего графика функции. Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения.
- Если f(x)=$\frac{p(x)}{q(x)}$; и при x= a знаменатель обращается в нуль, а числитель отличен от нуля, то x= a — это вертикальная асимптота.
Несколько правил, упрощающих построение графиков функций:
а) График функции y= f(x) + a получается из графика функции y= f(x) (график y= f(x) заранее известен), путем параллельного переноса графика y= f(x) на а единиц вверх, если а > 0; и на а единиц вниз, если аДля примера построим три графика: а) y= x2, б) y= x2 + 2, в) y= x2 — 3.
Графики наших функций:
б) График функции y= f(x + a) получается из графика функции y= f(x) (график y= f(x) заранее известен). Используем параллельный перенос графика y= f(x) на а единиц влево, если а > 0, и на а единиц вправо, если а
Для примера построим три графика: а) y= (x — 2) 2, б) y= (x + 1)2.
Графики наших функций получается из графика функции y= x2, путем его параллельного переноса: б) на две единицы вправо, в) на одну единицу влево.
Графики наших функций:
в) Для построения графика функции y= f(-x), следует построить график функции y= f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y= f(-x).
Для примера построим два графика: a) y= x3, б) y= (-x)3.
Графики нашей функций получается из графика функции y=x3, путем отражения относительно оси ординат.
г) Для построения графика функции y= -f(x) следует построить график функции y=f(x) и отразить его относительно оси абсцисс.
Для примера построим два графика: a) y= cos(x), б) y=-cos(x). Графики нашей функций получается из графика функции y= cos(x), путем отражения относительно оси абсцисс.
Ребята, теперь давайте построим графики функций, вид которых заранее не известен. Будем использовать правила, которые мы определили в начале.
Примеры на построение
I. Построить график функции: y= 2x2 + 4x — 5.
Решение:
1) Область определения: D(y)= (-∞; +∞).
2) Найдем стационарные точки:
y’= 4x + 4,
4x + 4 = 0,
x= -1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума. Найдем значение функции в точке x= -1
y(-1)= 2(-1)2 + 4(-1) — 5= -7.
Итак, наша функция убывает на промежутке =(-∞;-1), x= -1 – точка минимума, функция возрастает на промежутке (-1; +∞).
Вычислим значения функции в паре точек:
Построим график функции:
II. Построить график функции: y= 5x3 — 3x5.
Построить график функции: y= 5x3 — 3x5.
Решение:
1) Область определения: D(y)= (-∞;+∞).
y’= 15x2 — 15x4,
y’= 15x2(1 — x2)= 15x2(1 — x)(1 + x),
15x2(1 — x)(1 + x)= 0,
x= 0; ±1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума.
Точка x= 0 – точка перегиба, функция в этой точки так же возрастает, но вогнутость меняется в другую сторону.
Точка x= 1 – точка максимума.
Найдем значение функции в точке x= -1: y(-1)= 5(-1)3 — 3(-1)5= -2.
Найдем значение функции в точке x= 0: y(0)= 5(0)3 — 3(0)5= 0.
Найдем значение функции в точке x= 1: y(1)= 5(1)3 — 3 (1)5= 2
По определению функция нечетная, и график симметричен относительно начало координат.
Найдем горизонтальную асимптоту:
Прямая y= 1 – горизонтальная асимптота.
4) Найдем стационарные и критические точки: Критических точек у нашей функции нет, т.к. производная определена всюду на области определения нашей функции.5) Определим вид стационарной точки и характер монотонности: Точка x= 0 – точка максимума.
Итак, наша функция четная. Она возрастает на промежутке равном (-∞;0), x= 0 – точка максимума. Функция убывает на (0;+∞).
Прямая x= 2 – вертикальная асимптота. Прямая y= 1 – горизонтальная асимптота.
Вычислим значения функции в паре точек:
Т.к. функция четная построим сначала график для x ≥ 0.
Используя свойство четных функций, отразим график функции относительно оси ординат.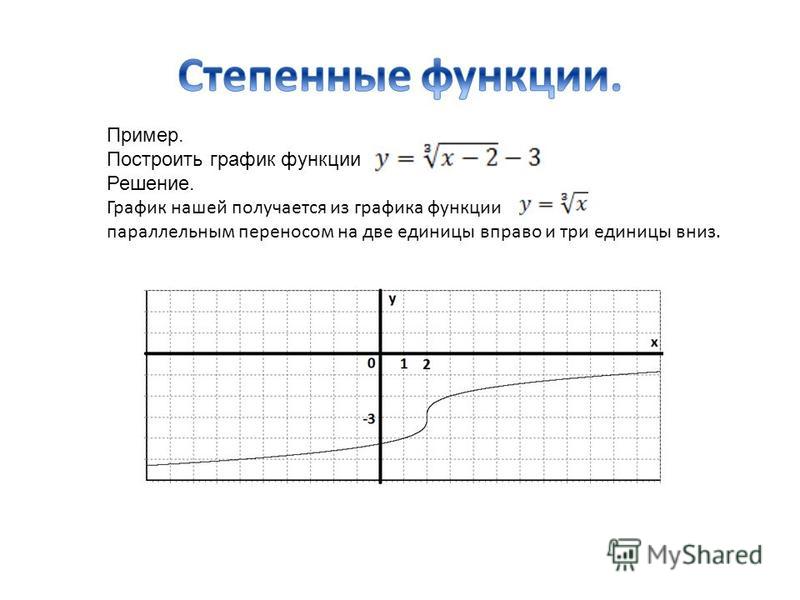 2+2)}$.
2+2)}$.Контрольная работа с решением Исследование функции и построение графика. 6) Экстремумы и монотонность. Вычисляем первую производную: ‘
ВЗФЭИ. Контрольная работа 1
ВЗФЭИ. Контрольная работа Задача. По формулам Крамера решить систему уравнений: 5 4 5 6 7 0, 0, 0. Решение. Перенесем свободные члены в правую часть системы: 4 7, 5, 5 6. Решим систему методом Крамера.
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
Урок на тему: Построение графиков.

Урок на тему: Построение графиков. Ребята, мы с вами строили уже не мало графиков функций, например параболы, гиперболы, тригонометрических функций и другие. Давайте вспомним, как мы это делали? Мы выбирали
ПодробнееКонтрольная работа T=3. Задание 1. [1, стр. 2]
Дана матрица Контрольная работа A 0 T= Задание [, стр ] Определите ее размерность Выпишите характеристики этой матрицы: прямоугольная, квадратная, симметричная, единичная, нулевая, треугольная, диагональная,
ПодробнееПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
М и н и с т е р с т в о о б р а з о в а н и я и н а у к и Р о с с и й с к о й Ф е д е р а ц и и Федеральное государственное автономное образовательное учреждение высшего профессионального образования Национальный
ПодробнееМатематический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Подробнее Построение графиков функций
Построение графиков функций 1. План исследования функции при построении графика 1. Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции:
План исследования функции при построении графика 1. Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции:
Математика (БкПл-100, БкК-100)
Математика (БкПл-100, БкК-100) М.П. Харламов 2009/2010 учебный год, 2-й семестр Лекция 5. Исследование функций с помощью производных 1 1. Понятие о производных высших порядков Опр. Пусть дана функция f(x)
Подробнее( )( )( ) ( )( ) ( ) ( ) ( ) ( )( )
МАТЕМАТИЧЕСКИЙ АНАЛИЗ. КОНТРОЛЬНАЯ РАБОТА Дифференциальное исчисление Задание. Найти пределы функций, не пользуясь правилом Лопиталя. 8 8 ; 8 8 ~ arcsi arcsi [ ] l l l l l l l l e Задание. Задана функция
Подробнее~ 1 ~ «Признаки монотонности функции»
~ 1 ~ «Признаки монотонности функции» Теорема: Для того чтобы функция f(x), дифференцируемая на a,b возрастала (убывала) на a,b необходимо и достаточно, чтобы x a,b выполнялось неравенство f (x) 0 (f (x)
Подробнее«ИССЛЕДОВАНИЕ ФУНКЦИЙ»
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И. М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
В.И. Иванов С.И. Васин
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
Подробнееприсутствие функций арксинуса вида arcsin f x
Практическая работа Полное исследование функции и построение графика Цель: закрепить навыки исследования функций и построения графиков Оборудование (приборы, материалы, дидактическое обеспечение): методические
Подробнее3. Производная функции
. Производная функции Актуальность темы Понятие производной одно из основных понятий математического анализа. В настоящее время понятия производной находит большое применение в различных областях науки
В настоящее время понятия производной находит большое применение в различных областях науки
ИССЛЕДОВАНИЕ ФУНКЦИЙ
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Введение в математический анализ Предел последовательности и функции. Раскрытие неопределенностей в пределах. Производная функции. Правила дифференцирования. Применение производной
Подробнее. Преобразуем функцию:, если x
Вариант Найти область определения функции : + + + Неравенство + выполняется всегда Поэтому область определения данной функции определяется следующими неравенствами:, те, и, те Решением системы этих неравенств
ПодробнееДифференциальное исчисление
ФГОУ СПО ЛТК МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ Дифференциальное исчисление Ст Ленинградская 00г Предисловие Настоящее пособие написано в соответствии с программой по математике для студентов средни профессиональны
ПодробнееИсследование функций и построение графиков
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Исследование функций и построение
Подробнее1.
 Производная функции в точке
Производная функции в точкеприращения аргумента Δ приращения Δ функции f производной функции точке f в Основные правила дифференцирования функций функции в точке Приращением аргумента Δ функции f называется разность между значением
Подробнее4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В результате изучения данной темы студент должен: уметь применять таблицу производных и правила дифференцирования для вычисления производных элементарных функций находить производные
Подробнееϕ, π ϕ и ϕ. В каждом интервале
Вариант + Найти область определения функции: y lg Область определения данной функции определяется неравенством + те Далее знаменатель не должен обращаться в нуль: lg или ± Кроме того аргумент логарифма
ПодробнееМатематический анализ.
 Лекция 3.4
Лекция 3.4Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Модуль 3. Дифференциальное исчисление функций одной переменной
ПодробнееИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКОЕ ВЫСШЕЕ АВИАЦИОННОЕ УЧИЛИЩЕ ГРАЖДАНСКОЙ АВИАЦИИ (ИНСТИТУТ)
ПодробнееКак построить график функции f(x) по результатам проведенного исследования
В этом посте мы наконец-то построим график функции по результатам проведенного ранее исследования.В серии постов, посвященной реализации общей схемы исследования функции одной переменной с применением Wolfram | Alpha, мы последовательно прошли целый ряд этапов, действуя так, как если бы мы проводили исследование функции «вручную». Wolfram | Alpha при этом мы использовали, как вспомогательный инструмент — своего рода калькулятор на все случаи жизни. Это позволило нам в значительной степени отвлечься от рутинных вычислений и сосредоточиться собственно на исследовании функции. Без Wolfram | Alpha некоторая часть необходимых вычислений оказалась бы слишком трудоемкой для ручных расчетов, и исследование данной функции показалось бы нам слишком сложной задачей.
Wolfram | Alpha при этом мы использовали, как вспомогательный инструмент — своего рода калькулятор на все случаи жизни. Это позволило нам в значительной степени отвлечься от рутинных вычислений и сосредоточиться собственно на исследовании функции. Без Wolfram | Alpha некоторая часть необходимых вычислений оказалась бы слишком трудоемкой для ручных расчетов, и исследование данной функции показалось бы нам слишком сложной задачей.
Именно это соображение — возможность, невзирая на объемность и трудоемкость рутинных вычислений исследовать любые функции, — главный резон в пользу использования Wolfram | Alpha при решении подобного рода задач. Фактически, без ограничения общности решается прежде всего методическое задание — изучить и научиться применять на практике общую схему исследования функции.
Однако, на практике, при решении прикладных задач, навряд ли кто-либо станет идти таким сложным и запутанным путем, если только имеются иные возможности. А они имеются. По ходу решения, эти возможности я систематически рассматривал, и пытался акцентировать на них ваше внимание: это специфические запросы Wolfram | Alpha, которые позволяют » в один клик» по мере надобности находить все отдельные свойства и характерные точки функции. Подробное изложение «практического» подхода к исследованию функции с помощью Wolfram | Alpha, в отличие от «теоретического», которому мы следовали все это время, будет представлено в одном из следующих постов.
Подробное изложение «практического» подхода к исследованию функции с помощью Wolfram | Alpha, в отличие от «теоретического», которому мы следовали все это время, будет представлено в одном из следующих постов.
Однако, вернемся к заключительному этапу классической общей схемы исследования функции. Это четвертый этап в общей схеме исследования функции. Цель этого этапа — построить по результатам проведенного выше исследования график функции:
Основные задания четвертого этапа состоят в следующем: используя результаты предыдущего исследования построить график функции f(x). Для этого нам понадобятся результаты всех предыдущих этапов исследования функции.
Это задание, особенно для самостоятельной работы учащихся, требует дальнейшей детализации в виде отдельных заданий:
16.1. Начертить систему координат, учитывая найденные ранее область определения данной функции (см. также: область определения функции в Wolfram | Alpha) и множество значений данной функции (см.
 также: множество значений функции в Wolfram | Alpha). Эти сведения на данном этапе нужны, чтобы начертить систему координат так, чтобы график функции расположился в ней крупным масштабом и по центру, а не как «очень одинокий петух» в поучительной детской книжке про Карлсона, который живет на крыше 🙂
также: множество значений функции в Wolfram | Alpha). Эти сведения на данном этапе нужны, чтобы начертить систему координат так, чтобы график функции расположился в ней крупным масштабом и по центру, а не как «очень одинокий петух» в поучительной детской книжке про Карлсона, который живет на крыше 🙂16.2. Обозначить на оси абсцисс точки разрыва функции. Сведения о точках разрыва были получены при исследовании области определения данной функции.
16.3. Обозначить точки пересечения графика функции с осью абсцисс и точки пересечения с осью ординат.
16.4. Начертить вертикальные, горизонтальные и наклонные асимптоты.
16.5. Обозначить на чертеже с помощью условных обозначений характер поведения функции возле вертикальных асимптот (см. также: изучение разрывных функций).
16.6. Обозначить точки пересечения графика функции с ее асимптотами.
16.7. Обозначить на чертеже точки экстремума функции, угловые точки графика функции (если они есть).
16.8. Обозначить на чертеже точки перегиба графика функции. 4)
4)
18. Осталось, пользуясь полученным графиком функции, проанализировать геометрические свойства построенного графика (симметрия относительно оси ординат и начала отсчета системы координат и др.) и сформулировать выводы относительно свойств четности-нечетности и периодичности данной функции f(x). Эту часть оставляю вам на самостоятельную проработку.
P.S.
Как я обещал в начале этого поста, в одном из следующих постов будет представлено подробное изложение «практического» подхода к исследованию функции с помощью Wolfram | Alpha, в отличие от «теоретического», которому мы следовали все это время.
Как построить график функции онлайн по уравнению с подробным решением
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Пример:
На рисунке мы видим график функции y = x. Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y. Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y.
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.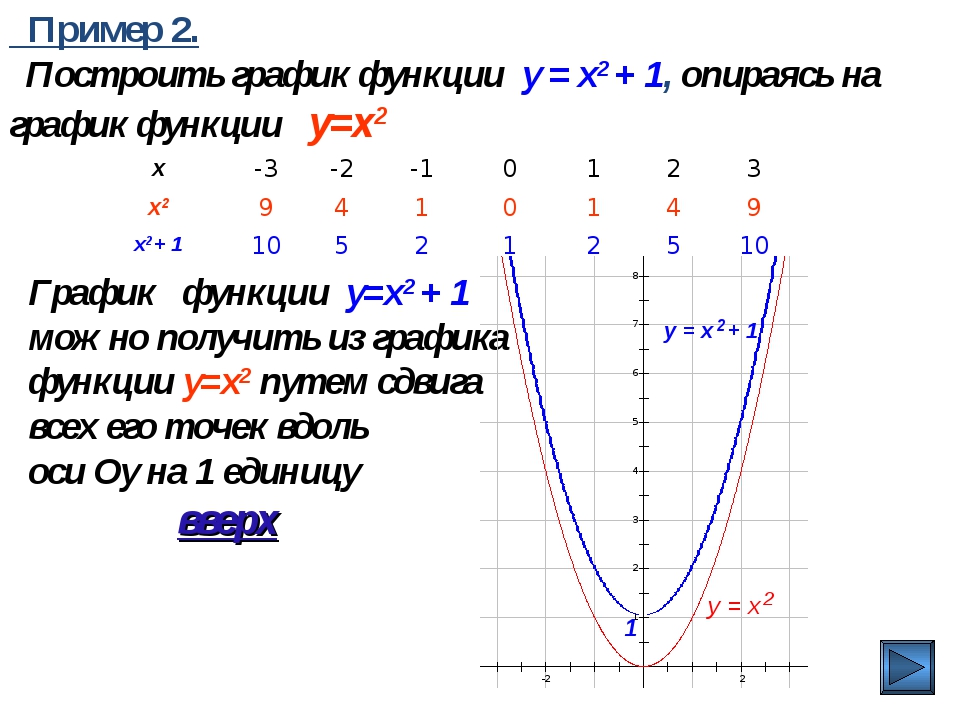
Umath.ru
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака =.
- Нажмите кнопку «Построить график».
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Перейти на официальный сайт Umath
Yotx.ru
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить».
Огромным плюсом этого сайта можно считать визуализацию графика. Удобно реализована возможность построения нескольких графиков на одной координатной плоскости: можно назначить каждому свой уникальный цвет, толщину линии.
Перейти на официальный сайт Yotx
Graph.reshish.ru
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:».
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Перейти на официальный сайт сервиса
Desmos.com
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Перейти на официальный сайт Desmos
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Загрузка…Применение производной к построению графиков функции
Если на некотором промежутке график функции представляет собой непрерывную линию, иными словами, такую линию, которую можно провести без карандаша от листа бумаги, то такая функция называется непрерывной на этом промежутке. Существуют также функции, которые непрерывными не являются. В качестве примера рассмотрим график функции, которая на промежутках [a; c] и [с; b] непрерывна, но в точке
х = с разрывна и поэтому на всем отрезке [a; b] не является непрерывной. Все функции, изучаемые нами в школьном курсе математики, – это функции непрерывные на каждом промежутке, на котором они определены.
Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.
Обратное утверждение является неверным. Функция, которая непрерывна на промежутке, может не иметь производной в некоторых точках этого промежутка. Например, функция
у = |log 2 x| непрерывна на промежутке х > 0, но в точке х = 1 не имеет производной, в силу того что в этой точке график функции касательной не имеет.
Рассмотрим построение графиков с помощью производной.
Задача 1.
Построить график функции f(x) = x3 – 2x2 + x.
Решение.
1) Эта функция определена при всех х € R.
2) Найдем промежутки монотонности рассматриваемой функции и ее точки экстремума с помощью производной. Производная равна f ‘(x) = 3x2 – 4x + 1. Найдем стационарные точки:
3x2 – 4x + 1 = 0, откуда х1 = 1/3, х2 = 1.
Для определения знака производной разложим квадратные трехчлен 3x2 – 4x + 1 на множители:
f ‘(x) = 3(х – 1/3)(х – 1). Следовательно, на промежутках х < 1/3 и х > 1 производная положительна; значит, функция возрастает на этих промежутках.
Следовательно, на промежутках х < 1/3 и х > 1 производная положительна; значит, функция возрастает на этих промежутках.
Производная отрицательна при 1/3 < х < 1; следовательно, функция убывает на этом интервале.
Точка х1 = 1/3 является точкой максимума, так как справа от этой точки функция убывает, а слева – возрастает. В этой точке значение функции равно f (1/3) = (1/3)3 – 2(1/3)2 + 1/3 = 4/27.
Точкой минимума является точка х2 = 1, так как слева от этой точки функция убывает, а справа возрастает; ее значение в этой точке минимума равняется f (1) = 0.
3) При построение графика обычно находят точки пересечения графика с осями координат. Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:
x3 – 2x2 + x = 0, х(x2 – 2х + 1) = 0, х(х – 1) 2 = 0, откуда х = 0, х = 1.
4) Для более точного построение графика найдем значения функции еще в двух точках: f(-1/2) = -9/8, f(2) = 2.
5) Используя результаты исследования (пункты 1 – 4), строим график функции у = x3 – 2x2 + x.
Для построения графика функции обычно сначала исследуют свойства этой функции с помощью ее производной по схеме, аналогичной схеме при решении задачи 1.
Таким образом, при исследовании свойств функции необходимо найти:
1) область ее определения;
2) производную;
3) стационарные точки;
4) промежутки возрастания и убывания;
5) точки экстремума и значения функции в этих точках.
Результаты исследования удобно записывать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.
Если же мы сталкиваемся с четной или нечетной функцией, то для построения ее графика достаточно исследовать свойства и построить ее график при х > 0, а затем отразить его симметрично относительно оси ординат (начала координат). Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
Для краткости решения задач на построение графиков функции большую часть рассуждений проводят устно.
Также отметим, что при решении некоторых задач мы можем столкнуться с необходимостью исследования функции не на всей области определения, а только на некотором промежутке, например, если нужно построить график, скажем, функции f(x) = 1 + 2x2 – x4 на отрезке [-1; 2].
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Графические линейные функции | Колледж алгебры
Результаты обучения
- Построение линейной функции по точкам
- Постройте линейную функцию, используя наклон и точку пересечения оси Y
- Построение линейной функции с помощью преобразований
Ранее мы видели, что график линейной функции представляет собой прямую линию. Мы также смогли увидеть точки функции, а также начальное значение на графике.
Мы также смогли увидеть точки функции, а также начальное значение на графике.
Есть три основных метода построения графиков линейных функций.Первый заключается в нанесении точек и затем проведении линии через точки. Второй — с использованием точки пересечения y- и наклона. Третий — применение преобразований к тождественной функции [латекс] f \ left (x \ right) = x [/ latex].
Построение графика функции по точкам
Чтобы найти точки функции, мы можем выбрать входные значения, оценить функцию по этим входным значениям и вычислить выходные значения. Входные значения и соответствующие выходные значения образуют пары координат.Затем мы наносим пары координат на сетку. В общем, мы должны оценивать функцию как минимум на двух входах, чтобы найти как минимум две точки на графике функции. Например, учитывая функцию [latex] f \ left (x \ right) = 2x [/ latex], мы могли бы использовать входные значения 1 и 2. Оценка функции для входного значения 1 дает выходное значение 2, которое представлен точкой (1, 2). Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4).Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что совершили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4).Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что совершили ошибку.
Как сделать: для данной линейной функции построить график с помощью точек.
- Выберите минимум два входных значения.
- Оцените функцию для каждого входного значения.
- Используйте полученные выходные значения для определения пар координат.
- Нанесите пары координат на сетку.
- Проведите линию через точки.
Пример: построение графика по точкам
График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] путем нанесения точек.
Показать решениеНачните с выбора входных значений. Эта функция включает дробь со знаминателем 3, поэтому давайте выберем в качестве входных значений числа, кратные 3. Мы выберем 0, 3 и 6.
Оцените функцию для каждого входного значения и используйте выходное значение для определения пар координат.
[латекс] \ begin {array} {llllll} x = 0 & & f \ left (0 \ right) = — \ frac {2} {3} \ left (0 \ right) + 5 = 5 \ Rightarrow \ left ( 0,5 \ right) \\ x = 3 & & f \ left (3 \ right) = — \ frac {2} {3} \ left (3 \ right) + 5 = 3 \ Rightarrow \ left (3,3 \ вправо) \\ x = 6 & & f \ left (6 \ right) = — \ frac {2} {3} \ left (6 \ right) + 5 = 1 \ Rightarrow \ left (6,1 \ right) \ end {array} [/ latex]
Постройте пары координат и проведите линию через точки.На приведенном ниже графике показана функция [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex].
Анализ решения
График функции представляет собой линию, как и ожидалось для линейной функции. Кроме того, график имеет наклон вниз, что указывает на отрицательный наклон. Это также ожидается от отрицательной постоянной скорости изменения уравнения для функции.
Попробуйте
График [латекс] f \ left (x \ right) = — \ frac {3} {4} x + 6 [/ latex] путем нанесения точек.
Построение линейной функции с использованием точки пересечения по оси Y и наклона
Другой способ построения графиков линейных функций — использование конкретных характеристик функции, а не точек.Первая характеристика — это точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти точку пересечения y- , мы можем установить [latex] x = 0 [/ latex] в уравнении.
Другой характеристикой линейной функции является ее наклон, м, , который является мерой ее крутизны. Напомним, что наклон — это скорость изменения функции. Наклон линейной функции равен отношению изменения выходов к изменению входов.Еще один способ думать о наклоне — разделить вертикальную разницу или подъем между любыми двумя точками на горизонтальную разницу или бег. Наклон линейной функции будет одинаковым между любыми двумя точками. Мы встретили точку пересечения y- и наклон в линейных функциях.
Рассмотрим следующую функцию.
[латекс] f \ left (x \ right) = \ frac {1} {2} x + 1 [/ latex]
Уклон [латекс] \ frac {1} {2} [/ latex]. Поскольку наклон положительный, мы знаем, что график будет наклоняться вверх слева направо.Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и перехват y . Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Начиная с нашего интервала y (0, 1) , мы можем подняться на 1, а затем на 2 или на 2 и затем на 1.Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано ниже.
Общее примечание: графическая интерпретация линейной функции
В уравнении [латекс] f \ left (x \ right) = mx + b [/ latex]
- b — это пересечение графика y и указывает точку (0, b ), в которой график пересекает ось y .

- м — это наклон линии, указывающий вертикальное смещение (подъем) и горизонтальное смещение (пробег) между каждой последовательной парой точек.Напомним формулу уклона:
[латекс] m = \ frac {\ text {изменение на выходе (подъем)}} {\ text {изменение на входе (запуск)}} = \ frac {\ Delta y} {\ Delta x} = \ frac { {y} _ {2} — {y} _ {1}} {{x} _ {2} — {x} _ {1}} [/ latex]
Вопросы и ответы
Все ли линейные функции имеют точки пересечения y ?
Да. Все линейные функции пересекают ось Y и, следовательно, имеют точки пересечения по оси Y. (Примечание: Вертикальная линия, параллельная оси y, не имеет точки пересечения оси y.Имейте в виду, что вертикальная линия — единственная линия, которая не является функцией.)
Практическое руководство. Имея уравнение для линейной функции, постройте график функции, используя точку пересечения
y и наклон.- Оцените функцию при нулевом входном значении, чтобы найти точку пересечения y-.

- Определите уклон.
- Постройте точку, представленную точкой пересечения y-.
- Используйте [latex] \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить еще как минимум две точки на линии.
- Проведите линию, проходящую через точки.
Пример: построение графика с использованием точки пересечения
y- и наклонаГрафик [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] с использованием точки пересечения и наклона y- .
Показать решениеОцените функцию при x = 0, чтобы найти точку пересечения y-. Выходное значение, когда x = 0, равно 5, поэтому график будет пересекать ось y в точке (0, 5).
Согласно уравнению для функции, наклон линии составляет [латекс] — \ frac {2} {3} [/ latex].Это говорит нам, что для каждого вертикального уменьшения «подъема» на [латекс] –2 [/ латекс] единиц, «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения y . От начального значения (0, 5) мы перемещаемся на 2 единицы вниз и на 3 единицы вправо. Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Теперь мы можем построить график функции, сначала построив точку пересечения y . От начального значения (0, 5) мы перемещаемся на 2 единицы вниз и на 3 единицы вправо. Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Анализ решения
График наклонен вниз слева направо, что означает, что он имеет отрицательный наклон, как и ожидалось.
Попробуйте
Найдите точку на графике, который мы нарисовали в примере: построение графика с использованием интервала y и угла наклона, имеющего отрицательное значение x .
Показать решениеВозможные ответы: [латекс] \ left (-3,7 \ right) [/ latex], [latex] \ left (-6,9 \ right) [/ latex] или [латекс] \ left (-9, 11 \ справа) [/ латекс].
Построение графика линейной функции с помощью преобразований
Другой вариант построения графиков — использовать преобразования для функции идентичности [latex] f \ left (x \ right) = x [/ latex]. Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Вертикальное растяжение или сжатие
В уравнении [латекс] f \ left (x \ right) = mx [/ latex], m действует как вертикальное растяжение или сжатие функции идентичности. Когда м отрицательное, также имеется вертикальное отражение графика. Обратите внимание, что умножение уравнения [латекс] f \ left (x \ right) = x [/ latex] на m растягивает график f на коэффициент m единиц, если m > 1, и сжимает график f с коэффициентом м единиц, если 0 < м <1.Это означает, что чем больше абсолютное значение м , тем круче наклон.
Вертикальные растяжки, сжатия и отражения на функции [латекс] f \ left (x \ right) = x [/ latex].
Вертикальный сдвиг
В [latex] f \ left (x \ right) = mx + b [/ latex], b действует как вертикальный сдвиг , перемещая график вверх и вниз, не влияя на наклон линии. Обратите внимание, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f всего на b единиц вверх, если b равно положительный и | b | единиц вниз, если значение b отрицательное.
Обратите внимание, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f всего на b единиц вверх, если b равно положительный и | b | единиц вниз, если значение b отрицательное.
Этот график иллюстрирует вертикальные сдвиги функции [латекс] f \ влево (x \ вправо) = x [/ латекс].
Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ определить различные типы линейных функций. Хотя это может быть не самый простой способ построить график функций такого типа, все же важно практиковать каждый метод.
Практическое руководство. Учитывая уравнение линейной функции, используйте преобразования, чтобы построить график линейной функции в виде [латекс] f \ left (x \ right) = mx + b [/ latex].
- График [латекс] f \ left (x \ right) = x [/ latex].
- Растянуть или сжать график по вертикали в м .

- Сдвинуть график вверх или вниз b единиц.
Пример: построение графиков с использованием преобразований
График [латекс] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex] с использованием преобразований.
Показать решениеУравнение для функции показывает, что [latex] m = \ frac {1} {2} [/ latex], поэтому функция идентичности сжимается по вертикали посредством [latex] \ frac {1} {2} [/ latex].Уравнение для функции также показывает, что [latex] b = -3 [/ latex], поэтому функция идентичности смещена по вертикали на 3 единицы.
Сначала нарисуйте функцию идентичности и покажите вертикальное сжатие.
Функция [latex] y = x [/ latex] сжата в [латекс] \ frac {1} {2} [/ latex] раз.
Затем покажите вертикальный сдвиг.
Функция [latex] y = \ frac {1} {2} x [/ latex] сдвинута на 3 единицы вниз.
Попробуйте
График [латекс] f \ left (x \ right) = 4 + 2x [/ latex], с использованием преобразований.
Вопросы и ответы
В примере: построение графиков с помощью преобразований, могли бы мы изобразить график, изменив порядок преобразований на противоположный?
Нет. Порядок преобразований соответствует порядку операций. Когда функция оценивается на заданном входе, соответствующий выход вычисляется в соответствии с порядком операций. Вот почему мы сначала выполнили сжатие. Например, следуя порядку операций, пусть на входе будет 2.
[латекс] \ begin {array} {l} f \ text {(2)} = \ frac {\ text {1}} {\ text {2}} \ text {(2)} — \ text {3} \ hfill \\ = \ text {1} — \ text {3} \ hfill \\ = — \ text {2} \ hfill \ end {array} [/ latex]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить страницуПодробнее
Алгебра — Графические функции
Хорошо, теперь, когда мы строим графики кусочных функций, мы действительно строим графики сразу нескольких функций, за исключением того, что мы собираемся строить графики только на очень определенных интервалах.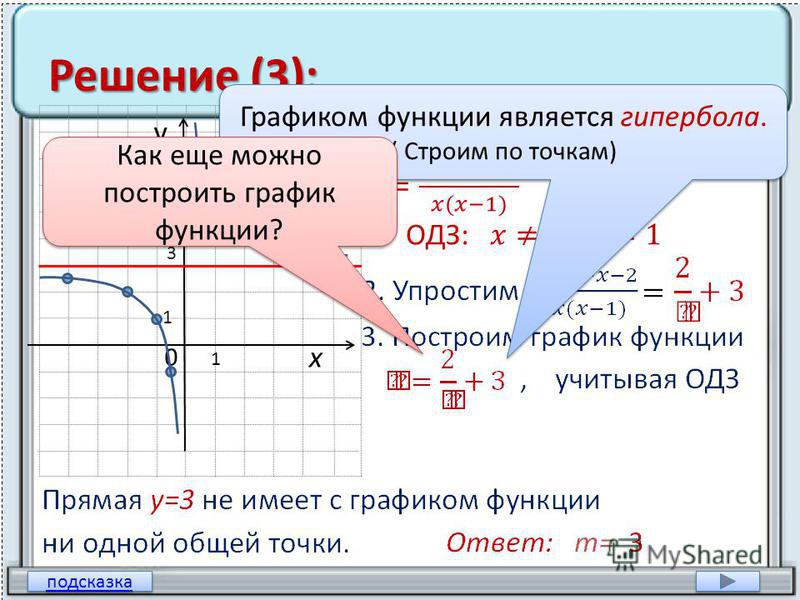 2} + 4 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 дюйма} x
2} + 4 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 дюйма} x
Нам нужно быть немного осторожнее с тем, что происходит прямо в \ (x = 1 \), поскольку технически это будет справедливо только для нижней функции. Однако мы разберемся с этим в самом конце, когда будем рисовать график. На данный момент мы будем использовать \ (x = 1 \) в обеих функциях.
Первое, что нужно сделать здесь, это получить таблицу значений для каждой функции в указанном диапазоне, и снова мы будем использовать \ (x = 1 \) в обоих, хотя технически это должно использоваться только с нижней функцией.2} + 4 \)
| \ (х \) | \ (2x — 1 \) | \ (\ left ({x, y} \ right) \) |
|---|---|---|
| 1 | 1 | \ (\ left ({1,1} \ right) \) |
| 2 | 3 | \ (\ слева ({2,3} \ справа) \) |
| 3 | 5 | \ (\ left ({3,5} \ right) \) |
Вот набросок графика и обратите внимание, как мы обозначили точки в \ (x = 1 \). Для верхней функции мы использовали открытую точку для точки в \ (x = 1 \), а для нижней функции мы использовали закрытую точку в \ (x = 1 \). Таким образом мы проясняем на графике, что только нижняя функция действительно имеет точку в \ (x = 1 \).
Для верхней функции мы использовали открытую точку для точки в \ (x = 1 \), а для нижней функции мы использовали закрытую точку в \ (x = 1 \). Таким образом мы проясняем на графике, что только нижняя функция действительно имеет точку в \ (x = 1 \).
Обратите внимание, что, поскольку два графика не пересекаются в точке \ (x = 1 \), мы оставили пустое место на графике. НЕ соединяйте эти две точки линией. Там действительно должен быть перерыв, чтобы показать, что две части не пересекаются в точке \ (x = 1 \).
Иногда в этих точках встречаются две части, а в других случаях — нет. Мы никогда не должны ожидать, что они встретятся или не встретятся, пока мы на самом деле не набросаем график.
Построение линейного уравнения с помощью таблицы значений
Построение графика линейного уравнения
Линейное уравнение — это уравнение с двумя переменными, которое при построении графика дает нам прямую линию. Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг — научиться составлять таблицу значений.
Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг — научиться составлять таблицу значений.
Что такое таблица значений
Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений. Таблица значений, как следует из названия, представляет собой графический способ определения значений, которые будут использоваться для создания вашего графика. Это место, где вы можете записать ответы, которые вы получите, когда найдете значения x и y. Вам нужно будет использовать как минимум 2 набора точек для построения линейного уравнения, но обычно вы делаете больше в таблице значений.
Таблица значений состоит из двух столбцов.В одном столбце перечислены значения x, а в одном столбце — соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.
Построение линейных уравнений с использованием таблицы значений
Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите построить графиком, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y.Представим, что у вас -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.
Выберите другое значение x, с которым вы хотите работать, и снова решите относительно y. Повторите столько раз, сколько хотите, чтобы выработать наборы значений для включения в вашу таблицу. Когда у вас есть сумма, которая вас устраивает или которую требует ваш вопрос, вы можете взять эти значения x и y и нанести их в виде координат на график, чтобы обозначить точки на линейном уравнении!
Примеры задач
Вопрос 1:
График следующей функции с использованием таблицы значений
г = 3х — 1
Раствор:
Сначала создайте таблицу значений для уравнения. Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одинаковым независимо от того, какие значения вы используете.
Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одинаковым независимо от того, какие значения вы используете.
Для x = -2
г = 3 (-2) — 1
г = -6 — 1
г = -7
Для x = -1
г = 3 (-1) — 1
г = -3 — 1
г = -4
Для x = 0
г = 3 (0) — 1
г = 0 — 1
г = -1
Для x = 1
г = 3 (1) — 1
г = 3 — 1
г = 2
Для x = 2
г = 3 (2) — 1
г = 6 — 1
г = 5
Теперь у нас есть полная таблица значений
Заполненная таблица значений x и yТеперь мы можем нанести упорядоченные пары на сетку
Построение данныхЗатем соедините точки прямой линией, и готово!
Связывание данных по прямойВопрос 2:
Изобразите следующую функцию, используя таблицу значений:
2x + 4y = 8
Раствор:
Во-первых, мы хотим упростить уравнение
2x + 4y = 8
х + 2у = 4
2у = -x + 4
y = −12 \ frac {-1} {2} 2−1 x + 2
Теперь у нас есть уравнение в форме пересечения наклона.
Затем создайте таблицу значений для уравнения. Используйте x, чтобы найти y.
Таблица x решает относительно yДля x = -2
y = −12 \ frac {-1} {2} 2−1 (-2) + 2
г = 1 + 2
г = 3
Для x = -1
y = −12 \ frac {-1} {2} 2−1 (-1) + 2
г = 0,5 + 2
г = 2,5
Для x = 0
y = −12 \ frac {-1} {2} 2−1 (0) + 2
г = 0 + 2
г = 2
Для x = 1
y = −12 \ frac {-1} {2} 2−1 (1) + 2
г = -0.5 + 2
г = 1,5
Для x = 2
y = −12 \ frac {-1} {2} 2−1 (2) + 2
г = -1 + 2
г = 1
Теперь у нас есть полная таблица значений
Таблица заполненных данныхМы можем нанести упорядоченные пары на сетку.
Координаты, построенные с использованием таблицы данныхЗатем соедините точки прямой линией, и готово!
Свяжите данные вместе прямой линией Хотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот для справки онлайн-калькулятор.
Далее, узнайте больше о таблице значений, как построить график линейных неравенств с двумя переменными и как построить график систем линейных неравенств. Вы также можете начать изучать введение в функции и способы их идентификации.
3.6 Графики функций — Промежуточная алгебра
Цели обучения
К концу этого раздела вы сможете:- Используйте тест вертикальной линии
- Определить графики основных функций
- Считать информацию с графика функции
Будьте готовы 3.6
Перед тем, как начать, пройдите тест на готовность.
- Оценить: 2323ⓑ 32,32.
Если вы пропустили эту проблему, просмотрите Пример 1.5. - Вычислить: ⓐ | 7 || 7 | ⓑ | −3 |. | −3 |.
Если вы пропустили эту проблему, просмотрите Пример 1.14. - Оцените: ⓐ 44ⓑ 16,16.
Если вы пропустили эту проблему, просмотрите Пример 1.41.
Используйте тест вертикальной линии
В последнем разделе мы узнали, как определить, является ли отношение функцией.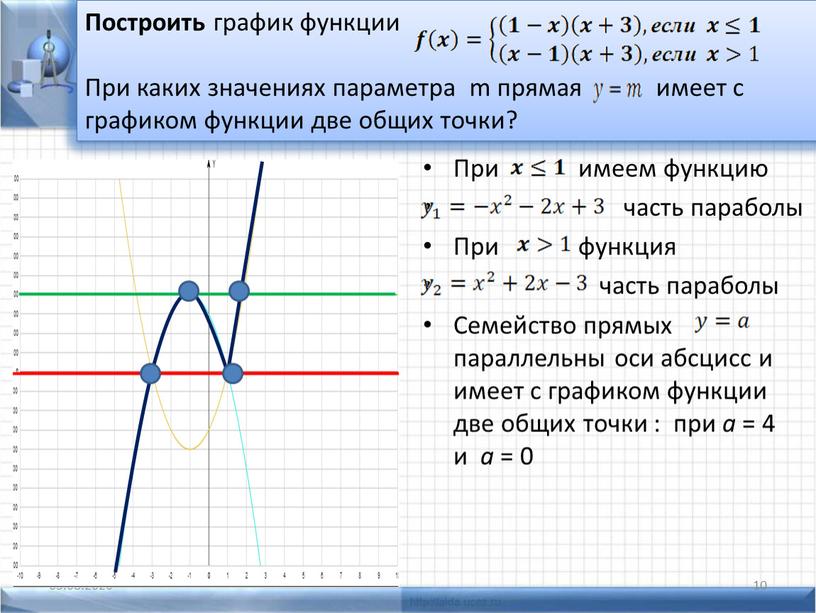 Рассматриваемые нами отношения были выражены в виде набора упорядоченных пар, отображения или уравнения. Теперь мы посмотрим, как определить, является ли график графиком функции.
Рассматриваемые нами отношения были выражены в виде набора упорядоченных пар, отображения или уравнения. Теперь мы посмотрим, как определить, является ли график графиком функции.
Упорядоченная пара (x, y) (x, y) — это решение линейного уравнения, если уравнение является истинным утверждением, когда x — и y -значения упорядоченной пары подставляются в уравнение .
График линейного уравнения — это прямая линия, где каждая точка на линии является решением уравнения, а каждое решение этого уравнения является точкой на этой линии.
На рисунке 3.14 мы видим, что на графике уравнения y = 2x − 3, y = 2x − 3 для каждого значения x существует только одно значение y , как показано в прилагаемой таблице. .
Рисунок 3.14
Отношение является функцией, если каждый элемент домена имеет ровно одно значение в диапазоне. Таким образом, отношение, определяемое уравнением y = 2x − 3y = 2x − 3, является функцией.
Если мы посмотрим на график, каждая вертикальная пунктирная линия пересекает линию только в одной точке.Это имеет смысл, как и в функции, для каждого значения x существует только одно значение y .
Если вертикальная линия дважды коснется графика, значение x будет сопоставлено с двумя значениями y , и поэтому график не будет представлять функцию.
Это приводит нас к тесту вертикальной линии. Набор точек в прямоугольной системе координат является графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке. Если какая-либо вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.
Тест вертикальной линии
Набор точек в прямоугольной системе координат является графиком функции, если каждая вертикальная линия пересекает график не более чем в одной точке.
Если какая-либо вертикальная линия пересекает график более чем в одной точке, график не представляет функцию.
Пример 3.51
Определите, является ли каждый график графиком функции.
ⓐ Поскольку любая вертикальная линия пересекает график не более чем в одной точке, график является графиком функции.
Ⓑ Одна из вертикальных линий, показанных на графике, пересекает его в двух точках. Этот график не представляет функцию.
Попробуйте 3.101
Определите, является ли каждый график графиком функции.
Попробуйте 3.102
Определите, является ли каждый график графиком функции.
Определить графики основных функций
Мы использовали уравнение y = 2x − 3y = 2x − 3 и его график при разработке теста вертикальной линии.Мы сказали, что отношение, определяемое уравнением y = 2x − 3y = 2x − 3, является функцией.
Мы можем записать это как в обозначении функции как f (x) = 2x − 3. f (x) = 2x − 3. Это по-прежнему означает то же самое. График функции — это график всех упорядоченных пар (x, y) (x, y), где y = f (x) .y = f (x). Таким образом, мы можем записать упорядоченные пары как (x, f (x)). (X, f (x)). Выглядит иначе, но график останется прежним.
f (x) = 2x − 3. Это по-прежнему означает то же самое. График функции — это график всех упорядоченных пар (x, y) (x, y), где y = f (x) .y = f (x). Таким образом, мы можем записать упорядоченные пары как (x, f (x)). (X, f (x)). Выглядит иначе, но график останется прежним.
Сравните график y = 2x − 3y = 2x − 3, ранее показанный на рисунке 3.14, с графиком f (x) = 2x − 3f (x) = 2x − 3, показанным на рисунке 3.15. Ничего не изменилось, кроме обозначений.
Рисунок 3.15
График функции
График функции — это график всех ее упорядоченных пар (x, y) (x, y) или с использованием обозначения функции (x, f (x)) (x, f (x)), где y = f (х) .у = е (х).
f имя функции x x координата упорядоченной пары f (x) координата y упорядоченной пары f имя функции x x координата упорядоченной пары f (x) координата y упорядоченной пары По мере продвижения нашего исследования полезно ознакомиться с графиками нескольких основных функций и уметь их идентифицировать.
Благодаря нашей предыдущей работе мы знакомы с графиками линейных уравнений. Процесс, который мы использовали, чтобы решить, является ли y = 2x − 3y = 2x − 3 функцией, применим ко всем линейным уравнениям. Все нелинейные линейные уравнения являются функциями. Вертикальные линии не являются функциями, поскольку значение x имеет бесконечно много значений y .
Мы написали линейные уравнения в нескольких формах, но для нас будет наиболее полезно использовать форму линейного уравнения с пересечением угла наклона. Форма линейного уравнения с угловым пересечением — y = mx + b.у = мх + Ь. В обозначении функции эта линейная функция принимает вид f (x) = mx + bf (x) = mx + b, где m, — наклон прямой, а b — интервал y .
Домен — это набор всех действительных чисел, а диапазон — это также набор всех действительных чисел.
Линейная функция
Мы будем использовать методы построения графиков, которые мы использовали ранее, для построения графиков основных функций.
Пример 3.52
График: f (x) = — 2x − 4.f (x) = — 2x − 4.
| f (x) = — 2x − 4f (x) = — 2x − 4 | |
| Мы признаем это линейной функцией. | |
| Найдите наклон и точку пересечения y . | м = −2м = −2 b = −4b = −4 |
График с использованием точки пересечения наклона.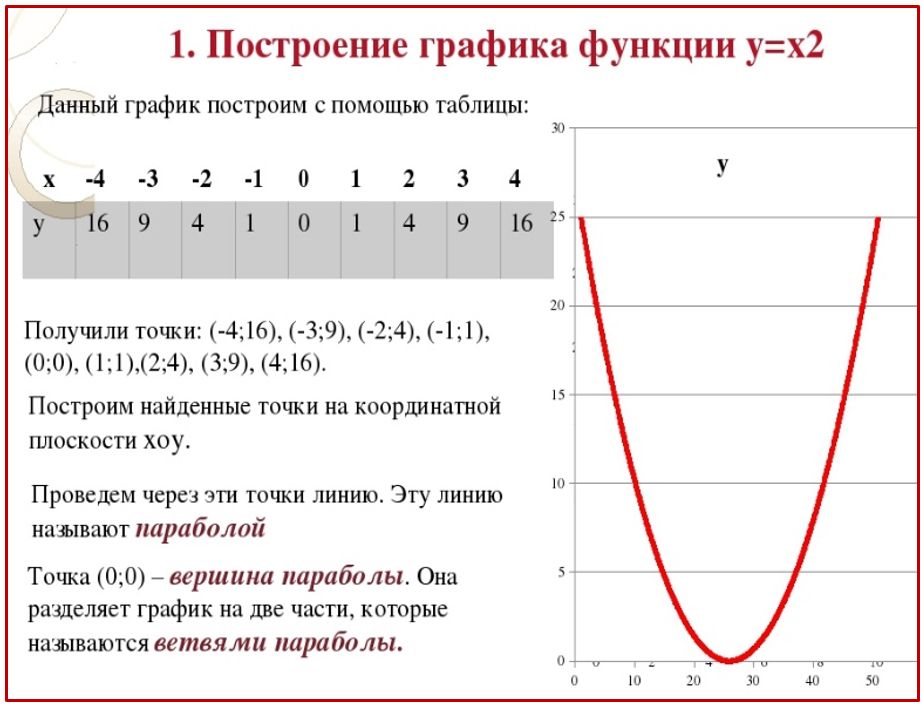 |
Попробовать 3.103
График: f (x) = — 3x − 1f (x) = — 3x − 1
Попробовать 3.104
График: f (x) = — 4x − 5f (x) = — 4x − 5
Следующая функция, график которой мы рассмотрим, называется постоянной функцией, и ее уравнение имеет вид f (x) = b, f (x) = b, где b — любое действительное число.Если мы заменим f (x) f (x) на y, мы получим y = b.y = b. Мы узнаем это как горизонтальную линию, пересечение которой y составляет b . График функции f (x) = b, f (x) = b также является горизонтальной линией, пересечение которой y составляет b .
Обратите внимание, что для любого действительного числа, которое мы вводим в функцию, значение функции будет b . Это говорит нам, что диапазон имеет только одно значение, b .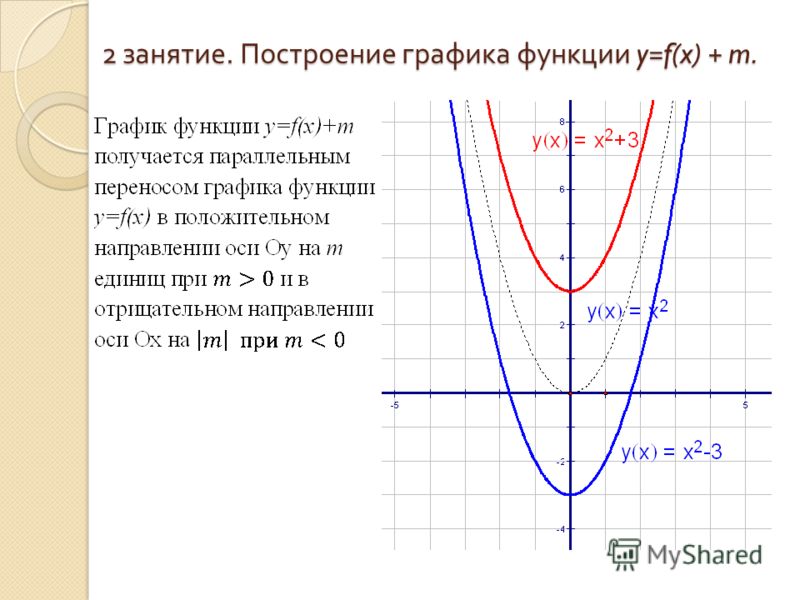
Постоянная функция
Пример 3.53
| f (x) = 4f (x) = 4 | |
| Мы признаем это постоянной функцией. | |
| График представляет собой горизонтальную линию, проходящую через (0,4). (0,4). |
Попробуйте 3.105
График: f (x) = — 2. f (x) = — 2.
Функция идентичности, f (x) = xf (x) = x, является частным случаем линейной функции. Если мы запишем это в линейной форме функции, f (x) = 1x + 0, f (x) = 1x + 0, мы увидим, что наклон равен 1, а интервал y равен 0.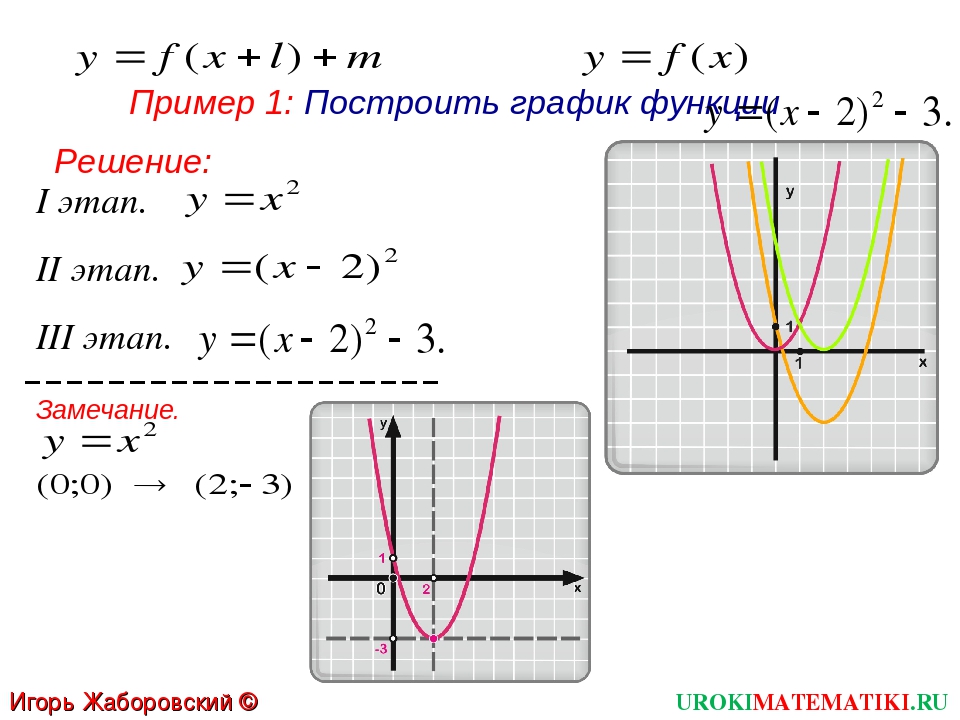
Функция идентификации
Следующая функция, которую мы рассмотрим, не является линейной функцией.Так что график не будет линией. Единственный метод построения графика этой функции — это точечный график. Поскольку это незнакомая функция, мы выбираем несколько положительных и отрицательных значений, а также 0 для наших значений x.
Пример 3.54
Выбираем х -значения. Мы подставляем их, а затем создаем диаграмму, как показано.
Глядя на результат в примере 3.54, мы можем суммировать особенности функции квадрата. Мы называем этот граф параболой.Когда мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как значение x . В домене все реальные числа.
Диапазон — это не все действительные числа. Обратите внимание, что график состоит из значений и , которые никогда не опускаются ниже нуля. Это имеет смысл, поскольку квадрат любого числа не может быть отрицательным. Итак, диапазон квадратной функции — это все неотрицательные действительные числа.
Это имеет смысл, поскольку квадрат любого числа не может быть отрицательным. Итак, диапазон квадратной функции — это все неотрицательные действительные числа.
Квадратная функция
Следующая функция, которую мы рассмотрим, также не является линейной функцией, поэтому график не будет линией.Снова мы будем использовать точечный график и обязательно выберем несколько положительных и отрицательных значений, а также 0 для наших значений x .
Пример 3.55
Выбираем х -значения. Подставляем их, а затем создаем диаграмму.
Попробовать 3.110
График: f (x) = — x3.f (x) = — x3.
Глядя на результат в примере 3.55, мы можем резюмировать возможности функции куба. Когда мы рассматриваем домен, обратите внимание, что любое действительное число может использоваться как значение x .В домене все реальные числа.
Диапазон состоит из действительных чисел. Это имеет смысл, поскольку куб любого ненулевого числа может быть положительным или отрицательным. Итак, диапазон функции куба — это все действительные числа.
Функция куба
Следующая функция, которую мы рассмотрим, не возводит в квадрат и не кубирует входные значения, а, скорее, извлекает квадратный корень из этих значений.
Давайте изобразим график функции f (x) = xf (x) = x, а затем резюмируем особенности функции. Помните, что мы можем извлекать квадратный корень только из неотрицательных действительных чисел, поэтому нашей областью будут неотрицательные действительные числа.
Пример 3.56
Выбираем х -значения. Поскольку мы будем извлекать квадратный корень, мы выбираем числа, которые являются точными квадратами, чтобы облегчить нашу работу. Подставляем их, а затем создаем диаграмму.
Попробовать 3. 112
112
График: f (x) = — x.f (x) = — x.
Функция квадратного корня
Наша последняя основная функция — это функция абсолютного значения, f (x) = | x | .f (x) = | x |. Имейте в виду, что абсолютное значение числа — это расстояние от нуля.Поскольку мы никогда не измеряем расстояние как отрицательное число, мы никогда не получим отрицательное число в диапазоне.
Пример 3.57
График: f (x) = | x | .f (x) = | x |.
Выбираем х -значения. Подставляем их, а затем создаем диаграмму.
Попробуйте 3.113
График: f (x) = | x | .f (x) = | x |.
Попробуйте 3.114
График: f (x) = — | x | .f (x) = — | x |.
Функция абсолютного значения
Чтение информации из графика функции
В науке и бизнесе данные часто собираются, а затем отображаются в виде графиков.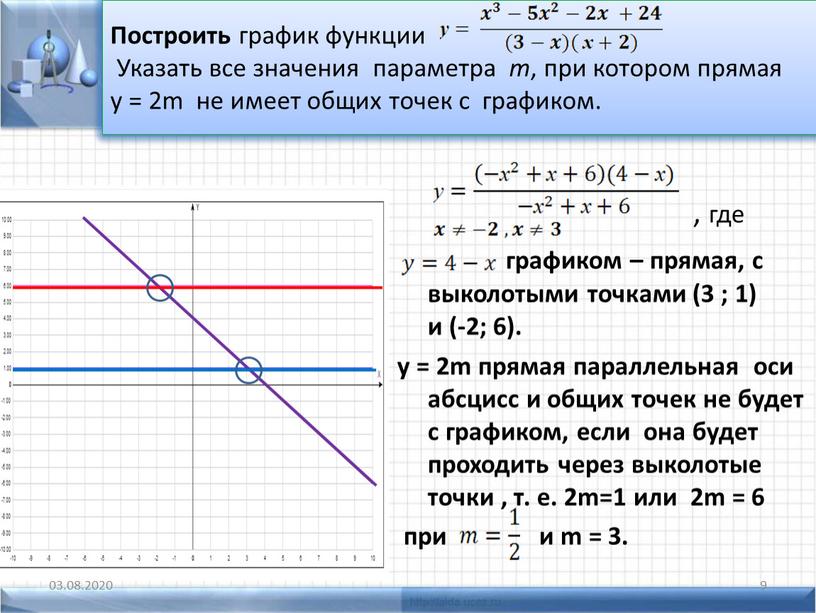 График анализируется, информация получается из графика, а затем часто на основе данных делаются прогнозы.
График анализируется, информация получается из графика, а затем часто на основе данных делаются прогнозы.
Мы начнем с чтения домена и диапазона функции по ее графику.
Помните, что домен — это набор всех значений x в упорядоченных парах функции. Чтобы найти домен, мы смотрим на график и находим все значения x , которым соответствуют соответствующие значения на графике. Следуйте за значением x вверх или вниз по вертикали.Если вы нажмете на график функции, тогда x находится в домене.
Помните, что диапазон — это набор всех значений y в упорядоченных парах функции. Чтобы найти диапазон, мы смотрим на график и находим все значения y , которым соответствуют соответствующие значения на графике. Следуйте значению y влево или вправо по горизонтали. Если вы нажмете на график функции, тогда y находится в диапазоне.
Если вы нажмете на график функции, тогда y находится в диапазоне.
Пример 3.58
Используйте график функции, чтобы найти ее домен и диапазон.Запишите домен и диапазон в виде интервалов.
Чтобы найти домен, мы смотрим на график и находим все значения x , которые соответствуют точке на графике. Домен выделен красным на графике. Домен [−3,3]. [- 3,3].
Чтобы найти диапазон, мы смотрим на график и находим все значения y , которые соответствуют точке на графике. Диапазон выделен синим цветом на графике. Диапазон составляет [−1,3]. [- 1,3].
Попробуй 3.115
Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
Попробуйте 3.116
Используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
Теперь мы собираемся прочитать информацию с графика, которую вы можете увидеть в будущих математических классах.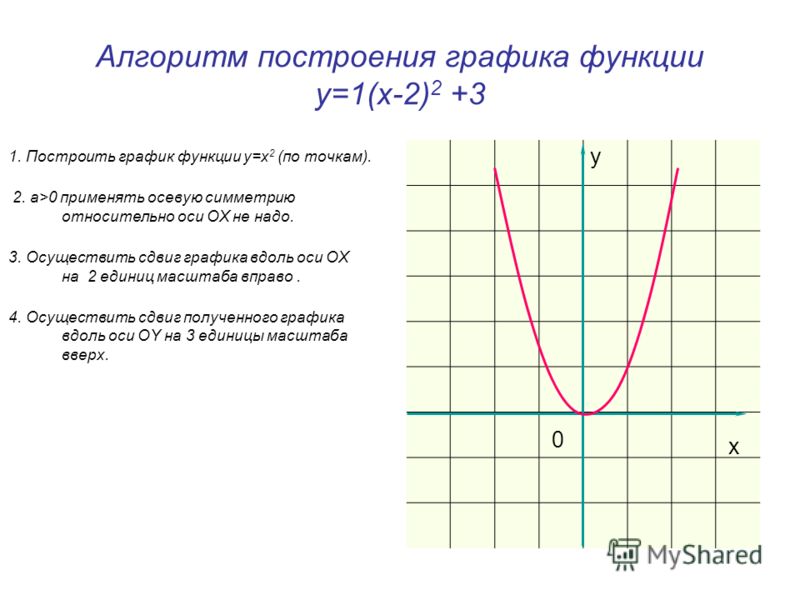
Пример 3.59
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (32π) .f (32π).
Ⓒ Найдите: f (−12π) .f (−12π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Когда x = 0, x = 0, функция пересекает ось y в точке 0. Итак, f (0) = 0. f (0) = 0.
Ⓑ Когда x = 32π, x = 32π, y -значение функции равно -1.−1. Итак, f (32π) = — 1. f (32π) = — 1.
Ⓒ Когда x = −12π, x = −12π, значение функции y равно −1. − 1. Итак, f (−12π) = — 1. f (−12π) = — 1.
Ⓓ Функция равна 0 в точках, (−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0).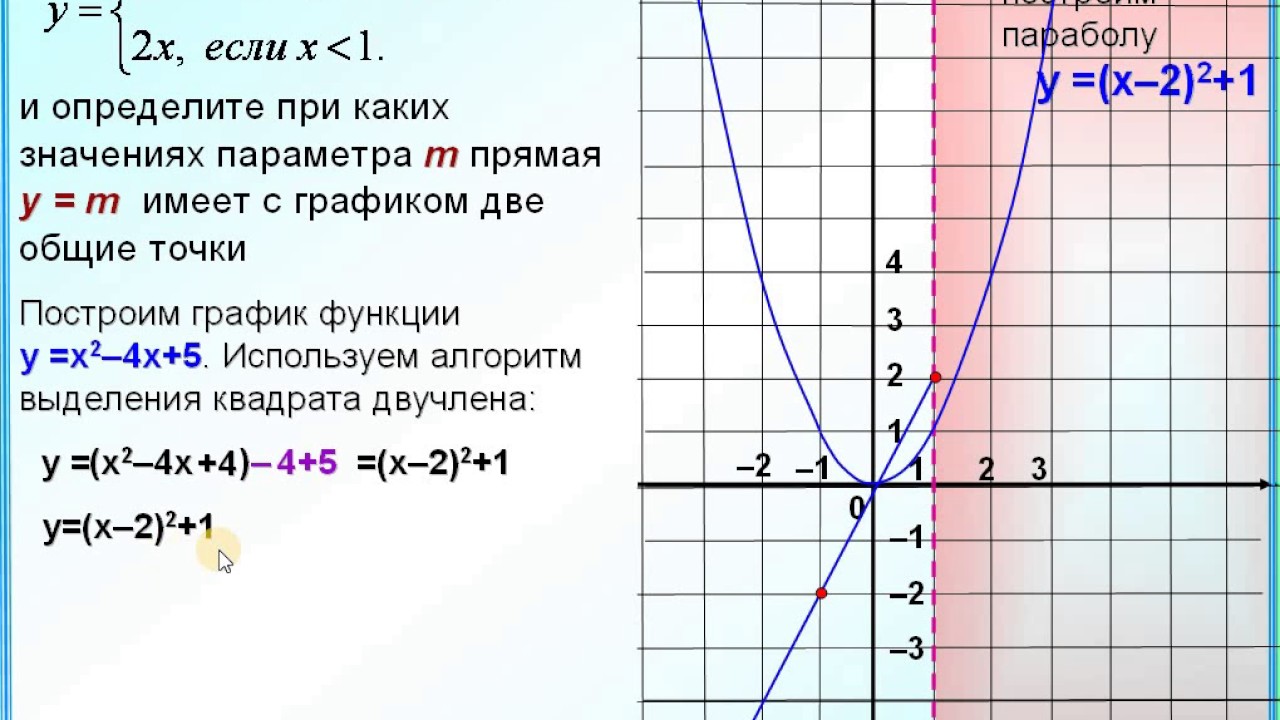 (- 2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0). Значения x при f (x) = 0f (x) = 0 равны −2π, −π, 0, π, 2π. − 2π, −π, 0, π, 2π.
(- 2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0). Значения x при f (x) = 0f (x) = 0 равны −2π, −π, 0, π, 2π. − 2π, −π, 0, π, 2π.
Ⓔ Перехват x происходит, когда y = 0. y = 0. Таким образом, перехват x происходит, когда f (x) = 0. f (x) = 0. x -перехваты: (−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0).(−2π, 0), (- π, 0), (0,0), (π, 0), (2π, 0).
Ⓕ Перехват y происходит, когда x = 0.x = 0. Таким образом, y -перехватывание происходят в f (0) .f (0). Перехват y равен (0,0). (0,0).
Ⓖ Эта функция имеет значение, когда x составляет от −2π − 2π до 2π,2π. Следовательно, область в обозначении интервалов равна [−2π, 2π]. [- 2π, 2π].
Ⓗ Значения этой функции, или y -значения, изменяются от -1-1 до 1. Следовательно, диапазон в обозначении интервала равен [-1,1]. [-1,1].
Следовательно, диапазон в обозначении интервала равен [-1,1]. [-1,1].
Попробуй 3.117
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (12π) .f (12π).
Ⓒ Найдите: f (−32π) .f (−32π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
Попробуйте 3.118
Используйте график функции, чтобы найти указанные значения.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (π) .f (π).
Ⓒ Найдите: f (−π) .f (−π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .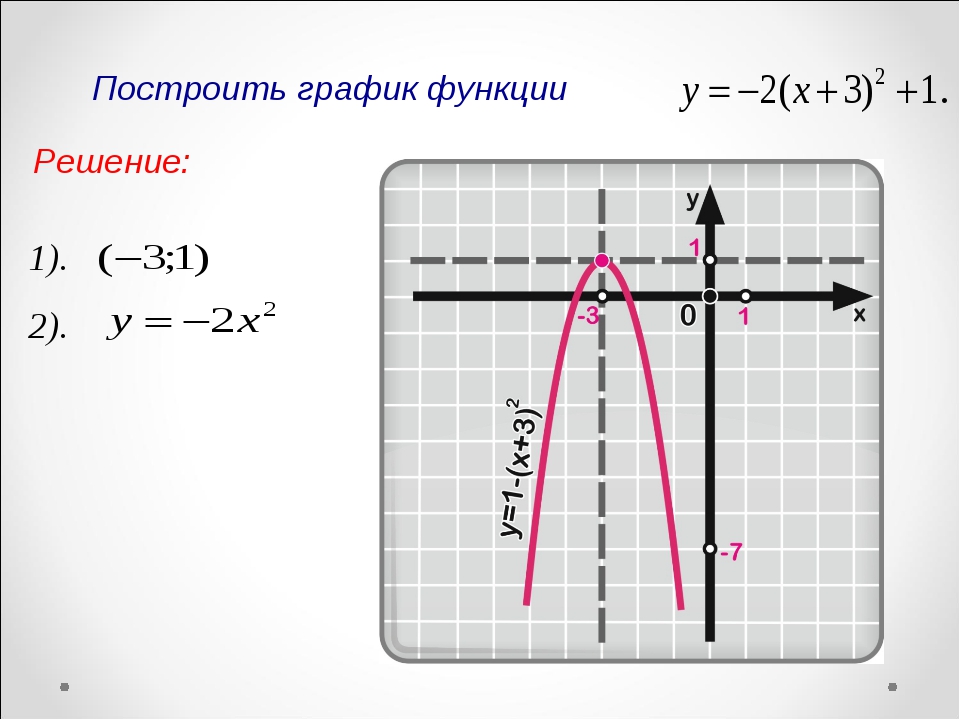
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
Раздел 3.6. Упражнения
Практика ведет к совершенству
Используйте тест вертикальной линии
В следующих упражнениях определите, является ли каждый график графиком функции.
338. ⓐ
ⓑ
ⓐ
ⓑ
Определение графиков основных функций
В следующих упражнениях ⓐ построите график каждой функции its укажите ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
343.f (x) = — x − 2f (x) = — x − 2
344.f (x) = — 4x − 3f (x) = — 4x − 3
Считывание информации из графика функции
В следующих упражнениях используйте график функции, чтобы найти ее домен и диапазон. Запишите домен и диапазон в виде интервалов.
Запишите домен и диапазон в виде интервалов.
В следующих упражнениях используйте график функции, чтобы найти указанные значения.
383. ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (12π) .f (12π).
Ⓒ Найдите: f (−32π) .f (−32π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (π) .f (π).
Ⓒ Найдите: f (−π) .f (−π).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.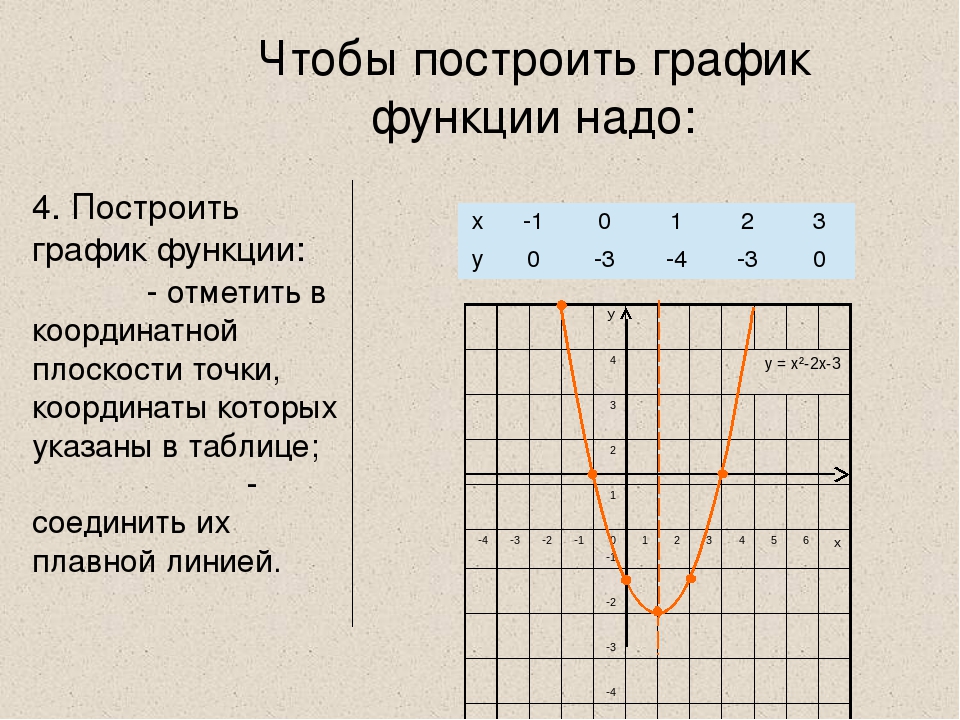
Ⓗ Найдите диапазон. Запишите его в обозначении интервала
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите: f (−3) .f (−3).
Ⓒ Найдите: f (3).f (3).
Ⓓ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓔ Найдите точки пересечения x .
Ⓕ Найдите точки пересечения и .
Ⓖ Найдите домен. Запишите это в интервальной записи.
Ⓗ Найдите диапазон. Запишите это в интервальной записи.
ⓐ Найдите: f (0) .f (0).
Ⓑ Найдите значения для x , когда f (x) = 0. f (x) = 0.
Ⓒ Найдите точки пересечения x .
Ⓓ Найдите точки перехвата и .
Ⓔ Найдите домен.Запишите это в интервальной записи.
Ⓕ Найдите диапазон. Запишите его в обозначении интервала
Письменные упражнения
387. Объясните своими словами, как найти домен по графику.
Объясните своими словами, как найти диапазон по графику.
389.Объясните своими словами, как использовать тест вертикальной линии.
390.Нарисуйте эскиз функций квадрата и куба. В чем сходство и различие графиков?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Решение PDE на Python — Учебное пособие FEniCS, том I
Цель этой главы — показать, как уравнение Пуассона самый простой из всех PDE, может быть быстро решен с помощью нескольких строк кода FEniCS. Мы представляем самые фундаментальные объекты FEniCS, такие какMesh,Function,FunctionSpace,TrialFunction, иTestFunction, и узнайте, как написать базовый решатель PDE, в том числе как сформулировать математическую вариационную задачу, применить граничные условия, вызвать решатель FEniCS и построить решение.2 u (\ x) & = f (\ x), \ quad && \ x \ mbox {in} \ Omega, \ tag {2.2} = f (x, y) \ tp \ tag {2.3} \ end {уравнение} $$ Неизвестное \ (u \) теперь является функцией двух переменных \ (u = u (x, y) \), определенных над двумерной областью \ (\ Omega \).
Уравнение Пуассона возникает во многих физических контекстах, включая теплопроводность, электростатика, диффузия веществ, скручивание упругие стержни, поток невязкой жидкости и волны на воде. Более того, уравнение появляется в стратегиях численного расщепления для более сложных системы УЧП, в частности уравнения Навье – Стокса.
Решение краевой задачи типа уравнения Пуассона в FEniCS состоит из следующих этапов:
Теперь мы подробно рассмотрим шаги 2–4. Ключевая особенность FEniCS заключается в том, что шаги 3 и 4 приводят к довольно короткому коду, в то время как аналогичная программа в большинстве других программных сред для PDE требует гораздо больше кода и технически сложного программирования.
- Определите вычислительную область (\ (\ Omega \)), PDE, ее граничные условия и исходные условия (\ (f \)).
- Переформулируйте УЧП как вариационную задачу конечных элементов.
- Напишите программу Python, которая определяет вычислительную область, вариационная задача, граничные условия и источник термины, используя соответствующие абстракции FEniCS.
- Позвоните в FEniCS для решения краевой задачи и, при необходимости, расширить программу для вычисления производных величин, таких как потоки и средние значения, и визуализировать результаты.
Что делает FEniCS привлекательной? Хотя многие программные фреймворки имеют действительно элегантный «Привет, мир!» пример для Уравнение Пуассона, FEniCS, насколько нам известно, является единственной структурой, в которой код остается компактным и красивым, очень близким к математическому формулировка, даже когда математическая и алгоритмическая сложность увеличивается и при переходе с ноутбука на высокопроизводительный вычислительный сервер (кластер).
Вариационная формулировка конечных элементов
FEniCS основана на методе конечных элементов, который является общим и эффективный математический аппарат для численного решения PDE.
Отправной точкой для методов конечных элементов является PDE выражается в вариационной форме . Читатели, не знакомые с вариационные задачи получат очень краткое введение в тему в этом учебном пособии, но читая подходящую книгу по конечным элементам метод дополнительно приветствуется.Раздел Метод конечных элементов содержит список рекомендуемых книг. Опыт показывает, что с FEniCS как инструмент для решения PDE даже без глубоких знаний метод конечных элементов, если вам кто-то поможет с формулировкой PDE в виде вариационной задачи.
Основной рецепт превращения PDE в вариационную задачу состоит в следующем: умножить УЧП на функцию \ (v \), проинтегрировать полученное уравнение по области \ (\ Omega \) и выполнить интегрирование по частям термов с производными второго порядка.Функция \ (v \), которая умножает PDE называется тестовой функцией . Неизвестная функция \ (u \) должна быть аппроксимация называется пробной функцией . Условия судебного разбирательства и Тестовые функции также используются в программах FEniCS.
Испытание и испытание функции принадлежат определенным так называемым функциональным пространствам , которые определяют свойства функций.
В данном случае сначала умножим уравнение Пуассона по тестовой функции \ (v \) и проинтегрируем по \ (\ Omega \): $$ \ begin {уравнение} \ tag {2.2 u) v \ dx = \ int_ \ Omega fv \ dx \ tp \ end {уравнение} $$ Обозначим здесь через \ (\ dx \) дифференциальный элемент для интегрирования по домен \ (\ Omega \). Позже мы будем обозначать дифференциал через \ (\ ds \) элемент для интегрирования по границе \ (\ Omega \).
Общее правило при выводе вариационных формулировок состоит в том, что мы пытаемся чтобы порядок производных от \ (u \) и \ (v \) оставался таким малым, как возможный. Здесь мы имеем пространственную производную второго порядка от \ (u \), которая может быть преобразована в первую производную от \ (u \) и \ (v \) с помощью применяя технику интеграции по частям.2 и) v \ dx = \ int_ \ Omega \ nabla u \ cdot \ nabla v \ dx — \ int _ {\ partial \ Omega} {\ partial u \ over \ partial n} v \ ds, \ end {уравнение} $$ где \ (\ frac {\ partial u} {\ partial n} = \ nabla u \ cdot n \) — производная \ (u \) по направлению нормали наружу \ (n \) на граница.
Еще одна особенность вариационных формулировок состоит в том, что пробная функция \ (v \) должна обращаться в нуль на частях граница, на которой известно решение \ (u \) (в книге [14] подробно объясняется, почему это требование необходимо).В настоящее время проблема, это означает, что \ (v = 0 \) на всей границе \ (\ partial \ Omega \). Второй член в правой части (2.5) поэтому обращается в нуль. Из (2.4) и (2.5) это Следовательно $$ \ begin {уравнение} \ int_ \ Omega \ nabla и \ cdot \ nabla v \ dx = \ int_ \ Omega fv \ dx \ tp \ tag {2.6} \ end {уравнение} $$ Если потребовать, чтобы это уравнение выполнялось для всех пробных функций \ (v \) в некоторое подходящее пространство \ (\ hat V \), так называемое тестовое пространство , мы получаем четко сформулированная математическая задача, которая однозначно определяет решение \ (u \), которое лежит в некотором (возможно, другом) функциональном пространстве \ (V \), так называемое пробное пространство .Мы ссылаемся на (2.
2 \) имеют конечные интегралы по \ (\ Omega \) (по сути означающие, что функции непрерывны).1 (\ Omega) \) допускает функции с разрывными производные. Это более слабое требование непрерывности \ (u \) в вариационной формулировке (2.7) в результате интеграция по частям, имеет большие практические последствия, когда дело доходит до к построению функциональных пространств конечных элементов. В частности, это позволяет использовать кусочно-полиномиальные функциональные пространства; т.е. функция пространства, построенные путем сшивания полиномиальных функций на простых такие области, как интервалы, треугольники или тетраэдры.
Вариационная задача (2.7) — это непрерывный проблема : она определяет решение \ (u \) в бесконечномерном функциональное пространство \ (V \). Метод конечных элементов для уравнения Пуассона находит приближенное решение вариационной задачи (2.7) заменой бесконечномерной функции пространства \ (V \) и \ (\ hat {V} \) по дискретным (конечномерным) пробным и тестовые пространства \ (V_h \ subset {V} \) и \ (\ hat {V} _h \ subset \ hat {V} \).
Дискретная вариационная задача гласит: найти \ (u_h \ in V_h \ subset V \) такая, что $$ \ begin {уравнение} \ tag {2.8} \ int _ {\ Omega} \ nabla u_h \ cdot \ nabla v \ dx = \ int _ {\ Omega} fv \ dx \ quad \ forall v \ in \ hat {V} _h \ subset \ hat {V} \ tp \ end {уравнение} $$
Эта вариационная задача вместе с подходящим определением функциональные пространства \ (V_h \) и \ (\ hat {V} _h \) однозначно определяют наши приближенные численное решение уравнения Пуассона (2.1). Примечание что граничные условия закодированы как часть проб и испытаний пробелы. Математическая структура может сначала показаться сложной взгляд, но хорошая новость заключается в том, что вариационный метод конечных элементов проблема (2.8) выглядит так же, как и непрерывный вариационная задача (2.7), а FEniCS может автоматически решать вариационные задачи типа (2.8)!
Что мы подразумеваем под обозначениями \ (u \) и \ (V \). В математической литературе по вариационным задачам написано \ (u_h \) для решение дискретной задачи и \ (u \) для решения непрерывная проблема.
Чтобы получить (почти) взаимно однозначное отношение между математической постановкой задачи и соответствующей программе FEniCS, мы опустим индекс \ (_h \) и воспользуемся \ (u \) для решения дискретной задачи.Мы будем использовать \ (\ uex \) для точного решение непрерывной задачи, , если нам нужно явно различать между двумя. Аналогично, обозначим через \ (V \) дискретную конечную элемент функционального пространства, в котором мы ищем наше решение.
Абстрактная вариационная формулировка методом конечных элементов
Оказывается, удобно ввести следующие канонические обозначение для вариационных задач: найти \ (u \ in V \) такое, что $$ \ begin {уравнение} a (u, v) = L (v) \ quad \ forall v \ in \ hat {V}.\ tag {2.9} \ end {уравнение} $$ Для уравнения Пуассона имеем: $$ \ begin {align} a (u, v) & = \ int _ {\ Omega} \ nabla u \ cdot \ nabla v \ dx, \ tag {2.10} \\ L (v) & = \ int _ {\ Omega} fv \ dx \ tp \ tag {2.11} \ end {align} $$ В математической литературе \ (a (u, v) \) известен как билинейная диаграмма .
образуют и \ (L (v) \) как линейную форму . Мы будем в каждой линейной задаче мы решаем, отождествляем члены с неизвестным \ (u \) и собираем их в \ (a (u, v) \), и аналогично собрать все члены только с известными функциями в \ (L (v) \).Формулы для \ (a \) и \ (L \) могут быть выражены непосредственно в наши программы FEniCS.
Для решения линейного уравнения в частных производных в FEniCS, такого как уравнение Пуассона, пользователь при этом необходимо выполнить всего два шага:
- Выберите пространства конечных элементов \ (V \) и \ (\ hat V \), указав область определения (сетка) и тип функционального пространства (полиномиальное степень и тип).
- Выразите PDE как (дискретную) вариационную задачу: найдите \ (u \ in V \) такое, что \ (a (u, v) = L (v) \) для всех \ (v \ in \ hat {V} \).
Выбор тестовой задачи
Задача Пуассона (2.1) — (2.2) имеет так далеко включал общую область \ (\ Omega \) и общие функции \ (\ ub \) для граничные условия и \ (f \) для правой части.
Для нашего первого реализации нам нужно будет сделать конкретный выбор для \ (\ Omega \), \ (\ ub \) и \ (f \). Будет разумно построить задачу с известным аналитическое решение, чтобы мы могли легко проверить, что вычисленное решение правильное. Решения, представляющие собой полиномы низшего порядка: основные кандидаты.2, $$ независимо от формы области, пока \ (\ uex \) предписано вдоль граница. Мы выбрали здесь для простоты домен должен быть единичным квадратом, $$ \ Omega = [0,1] \ times [0,1] \ tp $$ Этот простой, но очень мощный метод построения тестовых задач называется метод производства решений : выберите простой выражение для точного решения, подставьте его в уравнение, чтобы получить в правой части (исходный член \ (f \)), затем решите уравнение с эту правую часть и используя точное решение в качестве границы условие и попытайтесь воспроизвести точное решение.2 \) если \ (h \) — размер ячейки в сетке. Затем мы сравниваем ошибка на сетках с разными \ (h \) — значениями, чтобы увидеть, есть ли асимптотические поведение правильное.
Это очень мощная проверка метод и подробно объясняется в разделе Вычисление скорости сходимости. Однако, если у нас есть тестовая задача, для которой мы знаем, что ошибок аппроксимации быть не должно, мы знаем, что аналитическое решение задачи PDE следует воспроизвести в виде точность станка по программе. Вот почему мы подчеркиваем этот вид тестовых задач в этом руководстве.Обычно элементы степень \ (r \) может точно воспроизводить многочлены степени \ (r \), так что это является отправной точкой для построения решения без численных ошибки аппроксимации.
Полная программа
Программа FEniCS для решения нашей тестовой задачи для уравнения Пуассона в 2D с заданным выбором \ (\ Omega \), \ (\ ub \) и \ (f \) может выглядеть как следует:
из импорта феникс * # Создать сетку и определить функциональное пространство mesh = UnitSquareMesh (8, 8) V = FunctionSpace (сетка, 'P', 1) # Определить граничное условие u_D = Выражение ('1 + x [0] * x [0] + 2 * x [1] * x [1] », степень = 2) def Граница (x, on_boundary): return on_boundary bc = Дирихле BC (V, u_D, граница) # Определить вариационную задачу u = Пробная функция (V) v = TestFunction (V) f = Константа (-6.0) а = точка (град (и), град (в)) * dx L = f * v * dx # Вычислительное решение u = Функция (V) решить (a == L, u, bc) # Постройте решение и сетку сюжет (u) сюжет (сетка) # Сохранить решение в файл в формате VTK vtkfile = Файл ('poisson / solution.pvd') vtkfile << u # Ошибка вычисления в норме L2 error_L2 = errornorm (u_D, u, 'L2') # Вычислить максимальную ошибку в вершинах vertex_values_u_D = u_D.compute_vertex_values (сетка) vertex_values_u = u.compute_vertex_values (сетка) импортировать numpy как np error_max = np.max (np.abs (vertex_values_u_D - vertex_values_u)) # Ошибки печати print ('error_L2 =', error_L2) print ('error_max =', error_max) # Держать сюжет интерактивный ()
Этот пример программы можно найти в файле ft01_poisson.ру.
Запуск программы
Программа FEniCS должна быть доступна в виде простого текстового файла, написанного с текстовый редактор, такой как Atom, Sublime Text, Emacs, Vim или аналогичный. Есть несколько способов запустить программу Python, например ft01_poisson.
2 \) и будут напечатаны максимальные нормы.{-15} \). Если черчение включено в вашей установке FEniCS, тогда окно с простым графиком решения появится как на рисунке 1.
Spyder
Многие предпочитают работать в интегрированной среде разработки, которая предоставляет редактор для программирования, окно для выполнения кода, окно для просмотра объектов и т. д. Просто откройте файл ft01_poisson.py и нажмите кнопку воспроизведения, чтобы запустить его. Мы ссылаемся на учебник Spyder чтобы узнать больше о работе в среде Spyder.Spyder - это Настоятельно рекомендуется, если вы привыкли работать в графическом Среда MATLAB.
Ноутбуки Jupyter
Блокноты позволяют смешивать текст и исполняемый код в одном документ, но вы также можете просто использовать его для запуска программ в Интернете браузер. Запустите команду
jupyter notebookиз окна терминала, найдите раскрывающееся меню New в правом верхнем углу графического интерфейса, выбираем новую записную книжку на Python 2 или 3, пишем загрузка% ft01_poisson.в пустой ячейке записной книжки, затем нажмите Shift + Enter, чтобы выполнить ячейку. Затем файл ft01_poisson.py будет загружен в ноутбук. Повторно выполнить ячейку (Shift + Enter), чтобы запустить программу. Ты может разделить всю программу на несколько ячеек для изучения промежуточные результаты: поместите курсор в то место, где вы хотите разделить ячейку и выберите Edit - Split Cell . Для пользователей FEniCS Docker изображений, запустите командуpy
fenicsproject notebookи следуйте инструкции.Чтобы включить черчение, обязательно выполните команду% matplotlib inlineвнутри ноутбука.Теперь мы подробно разберем нашу программу FEniCS. Перечисленные FEniCS программа определяет сетку конечных элементов, функциональное пространство конечных элементов \ (V \) на этой сетке, граничные условия для \ (u \) (функция \ (\ ub \)), а также билинейная и линейная формы \ (a (u, v) \) и \ (L (v) \). После этого решение \ (u \) вычисляется. В конце программы сравниваем численные и точные решения.
Мы также строим решение, используя
plotи сохраните решение в файл для внешнего Постобработка.Важная первая линия
Первая строка в программе,
импортирует ключевые классы
UnitSquareMesh,FunctionSpace,Function, и так далее из библиотеки FEniCS. Все программы FEniCS для решение УЧП методом конечных элементов обычно начинается с этого линия.Создание простых сеток
Заявление
сетка = UnitSquareMesh (8, 8)определяет однородную сетку конечных элементов по единичному квадрату \ ([0,1] \ раз [0,1] \).Сетка состоит из ячеек , которые в 2D представляют собой треугольники. с прямыми сторонами. Параметры 8 и 8 указывают, что квадрат должен быть разделен на \ (8 \ умножить на 8 \) прямоугольников, каждый из которых разделен на пару треугольники. Таким образом, общее количество треугольников (ячеек) становится 128. Общее количество вершин в сетке \ (9 \ cdot 9 = 81 \).
В следующих главах вы узнаете, как создавать более сложные сетки.
Определение функционального пространства конечных элементов
Как только сетка создана, мы можем создать конечный элемент. функциональное пространство
V:V = FunctionSpace (сетка, 'P', 1)Второй аргумент
«P»указывает тип элемента.Тип элементом здесь является \ (\ mathsf {P} \), что подразумевает стандартное семейство Лагранжа элементы. Вы также можете использовать'Lagrange', чтобы указать этот тип элемент. FEniCS поддерживает все семейства симплексных элементов и обозначения определены в Периодической таблице конечных элементов [26].Третий аргумент
1указывает степень конечного элемента. В в данном случае стандартный \ (\ mathsf {P} _1 \) линейный элемент Лагранжа, который представляет собой треугольник с узлами в трех вершинах.Какой-то конечный элемент Практикующие называют этот элемент «линейным треугольником».В вычисленное решение \ (u \) будет непрерывным по элементам и линейно изменяющиеся в \ (x \) и \ (y \) внутри каждого элемента. Полином высшей степени аппроксимации по каждой ячейке тривиально получаются увеличением третий параметр
FunctionSpace, который затем сгенерирует функцию пространства типа \ (\ mathsf {P} _2 \), \ (\ mathsf {P} _3 \) и так далее. Изменение второй параметр«DP»создает функциональное пространство для разрывные методы Галеркина.Определение пробной и испытательной функций
В математике мы различаем пробное и тестовое пространства \ (V \) и \ (\ hat {V} \). Единственная разница в существующей проблеме - это граничные условия. В FEniCS мы не указываем границу условия как часть функционального пространства, поэтому достаточно работать с одним общим пространством
Vкак для пробных, так и для тестовых функций в программа:u = пробная функция (V) v = TestFunction (V)Определение граничных условий
Следующим шагом является определение граничного условия: \ (u = \ ub \) на \ (\ частичная \ Омега \).
Это делается
до н.э. = Дирихле BC (V, u_D, граница)где
u_D- выражение, определяющее значения решения на граница, аграница- функция (или объект), определяющая какие точки принадлежат границе.Граничные условия типа \ (u = \ ub \) известны как Дирихле. условия . Для настоящего метода конечных элементов для Пуассона задачи, они также называются существенными граничными условиями , поскольку они должны быть наложены явно как часть пробного пространства (в отличие от быть определенным неявно как часть вариационной формулировки).Естественно, класс FEniCS, используемый для определения границы Дирихле условия назван
DirichletBC.Переменная
u_Dотносится к объектуExpression, который используется для представляют собой математическую функцию. Типичная конструкцияu_D = Выражение (формула, степень = 1)где
формула- строка, содержащая математическое выражение.Формула должна быть написана с использованием синтаксиса C ++ и автоматически превратился в эффективную скомпилированную функцию C ++.
Выражения и точность. При определении
Выражениявторой аргументстепеньявляется параметр, указывающий, как следует обрабатывать выражение в вычисления. Для каждого локального элемента FEniCS будет интерполировать выражение в пространстве конечных элементов указанной степени. Для получения оптимального (порядок) точности вычислений, обычно это хороший выбор используйте ту же степень, что и для пространства \ (V \), которое используется для испытания и тестовые функции.Однако, если выражениеиспользуется для представления точное решение, которое используется для оценки точности вычисленного решение, необходимо использовать более высокую степень для выражения (один или два градусов выше).Выражение может зависеть от переменных
x [0]иx [1]соответствующие координатам \ (x \) и \ (y \).2 \) формула строка может быть записана как
1 + x [0] * x [0] + 2 * x [1] * x [1]:u_D = Выражение ('1 + x [0] * x [0] + 2 * x [1] * x [1] », степень = 2)Мы устанавливаем степень равной \ (2 \), так что
Строковые выражения должны иметь допустимый синтаксис C ++! Строковый аргумент объектаu_Dможет представлять точное квадратичное решение нашей тестовой задачи.Expressionдолжен подчиняться синтаксису C ++. Большая часть синтаксиса Python для математических выражений также является допустимым синтаксисом C ++, но степенные выражения составляют исключение:p ** aдолжно быть записано какpow (p, a)на C ++ (это также альтернативный синтаксис Python). Следующие математические функции могут использоваться напрямую в C ++ выражения при определенииExpressionобъектов:cos,sin,tan,acos,asin,atan,atan2,cosh,sinh,tanh,exp,frexp,ldexp,журнал,log10,modf,pow,sqrt,ceil,fabs,floorиfmod.2t} \ sin (\ pi k x) \) можно закодировать как
f = Выражение ('exp (-kappa * pow (pi, 2) * t) * sin (pi * k * x [0])', степень = 2, каппа = 1,0, t = 0, k = 4)В любой момент можно обновить параметры:
Функция
границауказывает, какие точки принадлежат часть границы, где должно применяться граничное условие:def Граница (x, on_boundary): return on_boundaryФункция, такая как
borderдля обозначения границы, должна возвращать логическое значение:Истинно, если данная точкаxлежит на Дирихле Граница иЛожьв противном случае.Аргументon_boundaryравенTrueеслиxнаходится на физической границе меша, поэтому в настоящем случай, где мы должны вернутьTrueдля всех точек на границе, мы можем просто вернуть предоставленное значениеon_boundary. В ГраницаФункциябудет вызываться для каждой дискретной точки в сетка, что означает, что мы можем определить границы, где \ (u \) также известно внутри домена, если это необходимо.Один из способов подумать о спецификации границ в FEniCS - это что FEniCS спросит вас (или скорее функция
border, которая вы реализовали), является ли конкретная точкаxчастью граница.FEniCS уже знает, принадлежит ли точка фактическая граница (математическая граница области) и любезно делится этой информацией с вами в переменнойon_boundary. Ты может использовать эту информацию (как мы здесь) или игнорировать ее полностью.Аргумент
on_boundaryтакже можно не указывать, но в этом случае нам потребуется для проверки значения координат вx:def Граница (x): вернуть x [0] == 0 или x [1] == 0 или x [0] == 1 или x [1] == 1Сравнение значений с плавающей запятой с использованием теста точного совпадения с
==не является хорошей практикой программирования, потому что небольшие ошибки округления при вычислениях значенийxможет получиться проверкаx [0] == 1становится ложным, даже еслиxлежит на границе.Лучше тест чтобы проверить равенство с допуском, либо явно
тол = 1Е-14 def Граница (x): return abs (x [0])или используя команду
nearв FEniCS:def Граница (x): вернуться около (x [0], 0, tol) или около (x [1], 0, tol) \ или около (x [0], 1, tol) или около (x [1], 1, tol)Никогда не используйте==для сравнения действительных чисел! Сравнение типаx [0] == 1никогда не следует использовать, еслиx [0]является действительным число, потому что ошибки округления вx [0]могут привести к сбою теста даже когда это математически правильно.Рассмотрим следующие расчеты в Python:>>> 0,1 + 0,2 == 0,3 Ложь >>> 0,1 + 0,2 0,30000000000000004Сравнение действительных чисел необходимо производить с допусками! В значения допусков зависят от размера чисел, участвующих в арифметические операции:
>>> абс (0,1 + 0,2 - 0,3) 5.551115123125783e-17 >>> абс (1,1 + 1,2 - 2,3) 0,0 >>> абс (10,1 + 10,2 - 20,3) 3,552713678800501e-15 >>> абс (100,1 + 100.{-16} \) можно использовать (Фактически, этот допуск известен как константа
DOLFIN_EPSв FEniCS). В противном случае необходимо использовать правильно масштабированный допуск.Определение источника
Перед определением билинейной и линейной форм \ (a (u, v) \) и \ (L (v) \) мы необходимо указать исходный термин \ (f \):
f = Выражение ('- 6', степень = 0)Когда \ (f \) постоянна по области,
fможет быть более эффективно представлено как константа:Определение вариационной задачи
Теперь у нас есть все ингредиенты, необходимые для определения вариационная задача:
a = точка (grad (u), grad (v)) * dx L = f * v * dxПо сути, эти две строки указывают PDE, которую нужно решить.Обратите внимание очень близкое соответствие между синтаксисом Python и математические формулы \ (\ nabla u \ cdot \ nabla v \ dx \) и \ (fv \ dx \).
Этот является ключевым преимуществом FEniCS: формулы в вариационном переводить непосредственно в очень похожий код Python, особенность что упрощает определение и решение сложных задач PDE. В язык, используемый для выражения слабых форм, называется UFL (Unified Form Language) [5] [1] и является неотъемлемой частью FEniCS.
Выражение внутренних продуктов. Внутренний продукт \ (\ int _ {\ Omega} \ nabla u \ cdot \ nabla v \ dx \) может быть выражено в FEniCS различными способами. Выше мы использовали обозначение
точка (grad (u), grad (v)) * dx. Точечный продукт в FEniCS / UFL вычисляет сумму (сокращение) по последнему индексу первого фактора и первого индекса второго фактора. В этом случае оба фактора являются тензорами первого ранга (векторами) и так что сумма чуть больше одного индекса обоих \ (\ nabla u \) и \ (\ nabla v \). Чтобы вычислить внутреннее произведение матриц (с два индекса) необходимо вместоточкииспользовать функциювнутренний.Для векторов
точкаивнутреннийэквивалентны.Построение и решение линейной системы
Определив вариационную задачу конечных элементов и границу условие, теперь мы можем попросить FEniCS вычислить решение:
u = Функция (В) решить (a == L, u, bc)Обратите внимание, что сначала мы определили переменную
uкакTrialFunctionи использовал его для представления неизвестного в формеa. После этого мы переопределеноuкак объектFunction, представляющий решение; я.е., вычисленная функция конечных элементов \ (u \). Это переопределение переменнаяuвозможна в Python и часто используется в FEniCS приложения для линейных задач. Два типа объектов, которыеиотносится к равным с математической точки зрения, и, следовательно, это естественно использовать одно и то же имя переменной для обоих объектов.Построение решения с помощью команды
plotПосле того, как решение было вычислено, его можно визуализировать с помощью команда
plot:участок (у) сюжет (сетка) интерактивный ()Обратите внимание на вызов функции
interactiveпосле командplot.Этот вызов позволяет взаимодействовать с графиками (вращать и масштабирование). Звонок на номер
interactiveобычно размещается в конце программа, создающая графики. На рисунке 1 показан два участка.Рисунок 1: График сетки и решение проблемы Пуассона, созданное с помощью встроенного инструмента визуализации FEniCS (команда
plot).Команда
plotполезна для отладки и начального научного расследования.Более сложные визуализации лучше создавать экспорт решения в файл и использование расширенной визуализации такой инструмент, как ParaView, как описано в следующем разделе.Щелкнув левой кнопкой мыши в окне графика, вы можете повернуть решение, а правая кнопка мыши используется для масштабирования. Точка наведите указатель мыши на текст
Helpв нижнем левом углу, чтобы отобразить список всех доступных команд быстрого доступа. Меню помощи может в качестве альтернативы можно активировать, набрав h в окне графика.В Команда
plotтакже принимает ряд дополнительных аргументов, например например, установка заголовка окна графика:plot (u, title = 'Конечно-элементное решение') plot (mesh, title = 'Сетка конечных элементов')Для получения подробной документации выполните команду
help (plot)в Python илиpydoc fenics.plotиз окна терминала.Встроенный график в Mac OS X и в Docker. Встроенное в FEniCS построение графиков может не работать должным образом, если работает в Mac OS X или внутри контейнера Docker FEniCS.FEniCS поддерживает печать с использованием команды
plotв Mac OS X. Однако сочетания клавиш могут не работать. работать. При запуске внутри контейнера Docker построение графиков не выполняется. поддерживается, поскольку Docker не взаимодействует с вашей оконной системой. Для пользователей Docker, которым требуется построение графиков, рекомендуется либо работать в записной книжке Jupyter / FEniCS (командаfenicsproject notebook) или полагайтесь на ParaView или другие внешние инструменты для визуализации.Построение решения с использованием ParaView
Простая команда
plotполезна для быстрой визуализации, но для Для более продвинутых визуализаций необходимо использовать внешний инструмент.В этом В разделе мы демонстрируем, как визуализировать решения в ParaView. ParaView - мощный инструмент для визуализации скалярных и векторных полей, в том числе вычислено FEniCS.Первым делом нужно экспортировать решение в формате VTK:
vtkfile = Файл ('poisson / solution.pvd') vtkfile << uСледующие шаги демонстрируют, как создать график решения. нашей проблемы Пуассона в ParaView. Полученный график показан на Фигура 2.
Для получения дополнительной информации мы обращаемся к Руководству ParaView [27] (доступен бесплатный PDF-файл), учебное пособие по ParaView и инструкция видео Введение в ParaView.
- Запустите приложение ParaView.
- Щелкните File – Open ... в верхнем меню и перейдите в каталог, содержащий экспортированное решение. Он должен находиться в подкаталоге с именем
poissonниже каталога, в котором была запущена программа Python FEniCS. Выберите файл с именемsolution.и нажмите OK .pvd
- Щелкните Применить на панели свойств слева. Это вызовет заговор решения.
- Чтобы построить трехмерный график решения, мы воспользуемся одним из многих фильтров ParaView .Щелкните Filters – Alphabetical – Warp By Scalar в верхнем меню, а затем Apply на панели свойств слева. Это создает приподнятую поверхность с высотой, определяемой значением решения.
- Чтобы отобразить исходный график под возвышенной поверхностью, щелкните значок маленького глаза слева от файла
solution.pvdна панели браузера конвейера слева. Также нажмите маленькую кнопку 2D в верхней части окна графика, чтобы изменить визуализацию на 3D. Это позволяет вам взаимодействовать с графиком путем вращения (левая кнопка мыши) и масштабирования (Ctrl + левая кнопка мыши).- Чтобы отобразить сетку конечных элементов, щелкните
solution.pvdв браузере конвейеров, перейдите к Представление на панели свойств и выберите Surface With Edges .Это должно сделать видимой сетку конечных элементов.
- Чтобы изменить соотношение сторон графика, щелкните WarpByScalar1 в обозревателе конвейеров и перейдите к Масштабный коэффициент на панели свойств. Измените значение на 0,2 и нажмите Применить .Это изменит масштаб искаженного сюжета. Мы также снимаем флажок Orientation Axis Visibility в нижней части панели свойств, чтобы удалить маленькие трехмерные оси в нижнем левом углу окна графика. Теперь вы должны увидеть что-то похожее на график на рисунке 2.
- Наконец, чтобы экспортировать визуализацию в файл, щелкните Файл – Сохранить снимок экрана ... и выберите подходящее имя файла, например
poisson.png.Рисунок 2: График сетки и решение проблемы Пуассона, созданное с помощью ParaView.
Вычисление ошибки
Наконец, мы вычисляем ошибку, чтобы проверить точность решения. Мы делаем это, сравнивая решение конечных элементов
ис точным решение, которое в этом примере совпадает с Выражениеu_Dиспользуется для задания граничных условий. Мы вычисляем ошибка двумя разными способами.1 \) норма. Введитеpydoc fenics.errornormв окне терминала. для подробностей.Мы также вычисляем максимальное значение ошибки во всех вершинах сетка конечных элементов. Как упоминалось выше, мы ожидаем, что эта ошибка быть нулевым с точностью до машинной точности для этого конкретного примера. К вычислить ошибку в вершинах, сначала мы просим FEniCS вычислить значение
u_Dиuво всех вершинах, а затем вычесть полученные результаты:vertex_values_u_D = u_D.compute_vertex_values (сетка) vertex_values_u = u.compute_vertex_values (сетка) импортировать numpy как np error_max = np.max (np.abs (vertex_values_u_D - vertex_values_u))
Здесь мы использовали функции максимального и абсолютного значения из
numpy, потому что они намного эффективнее для больших массивов (в 30 раз) чем встроенные в Python функцииmaxиabs.Как проверить, что ошибка исчезла. При неточной (с плавающей запятой) арифметике максимальное погрешность в вершинах не равна нулю, а должна быть небольшой.N U_j \ phi_j \ tag {2.13} \ tp \ end {уравнение} $$ Записав в программе
solution (a == L, u, bc), линейная система будет формируется из \ (a \) и \ (L \), и эта система решается для значения \ (U_1, \ ldots, U_N \). Значения \ (U_1, \ ldots, U_N \) известны как степеней свободы ("степеней свободы") или узловых значений \ (u \). Для Лагранжа элементы (и многие другие типы элементов) \ (U_j \) - это просто значение \ (u \) в узле с глобальным номером \ (j \). Расположение узлов и вершины ячеек совпадают для линейных элементов Лагранжа, а для элементов высшего порядка есть дополнительные узлы, связанные с грани, края, а иногда и внутренность ячеек.Имея
и, представленные как объектFunction, мы можем либо оценитьu (x)в любой точке сеткиx(дорогостоящая операция!), Или мы можем захватить все степени свободы вектора \ (U \) непосредственно с помощьюnodal_values_u = u.vector ()Результатом является объект
Vector, который по сути представляет собой инкапсуляцию. векторного объекта, используемого в пакете линейной алгебры, который используется решить линейную систему, возникающую из вариационной задачи.Поскольку мы программируем на Python, удобно преобразовать векторобъект в стандартный массивnumpyдля дальнейшей обработки:массив_u = nodal_values_u.array ()С
numpyмассивами мы можем написать MATLAB-подобный код для анализа данные. Индексирование выполняется в квадратных скобках:array_u [j], где индексjвсегда начинается с0.Если решение вычисляется с кусочно-линейные элементы Лагранжа (\ (\ mathsf {P} _1 \)), то размер массив
array_uравен количеству вершин, и каждаяarray_u [j]- это значение в некоторой вершине сетки.Однако градусы свободы не обязательно нумеруются так же, как вершины сетка. (Это обсуждается более подробно в разделе «Исследование степеней свободы»). Поэтому, если мы хотим знать значения в вершинах, нам нужно вызовите функциюu.compute_vertex_values . Эта функция возвращает значения во всех вершинах меша как массивnumpyс тем же нумерация как для вершин сетки, например:vertex_values_u = u.compute_vertex_values ()Обратите внимание, что для элементов \ (\ mathsf {P} _1 \) массивы
array_uиvertex_values_uимеют одинаковую длину и содержат одинаковые значения, хотя и в разном порядке.Графические полиномиальные функции
Графические полиномиальные функции
Полиномиальные функции вида f ( x ) = x n (где n - положительное целое число) образуют один из двух основных графиков, показанных на рисунке 1.
Рисунок 1. Графики многочленов
Графики многочленов.Каждый график имеет начало координат только в качестве точки пересечения x и точки пересечения y . Каждый граф содержит упорядоченную пару (1,1). Если полиномиальную функцию можно разложить на множители, можно сразу же найти ее перехваты x . Затем изучается, что происходит между этими перехватами слева от крайнего левого перехвата и справа от крайнего правого перехвата.
Пример 1
График f ( x ) = x 4 -10 x 2 + 9.
Нули этой функции - –1, 1, –3 и 3. То есть –1, 1, –3 и 3 являются интерцепциями x для этой функции.
Если x <–3, скажем, x = –4, тогда
Итак для x <–3, f ( x )> 0.
Если –1 < x <1, скажем, x = 0, тогда
Итак, для –1 < x <1, f ( x )> 0.
Аналогично видно, что
при x > 3, f ( x )> 0
при –3 < x <–1, f ( x ) <0
, если 1 < x <3, f ( x ) <0
Затем на графике есть точки в заштрихованных областях, как показано на рисунке 2.
Перехват y этой функции находится путем нахождения f (0).
f (0) = 9
, поэтому (0, 9) - это точка на графике. Чтобы завершить график, найдите и нанесите на карту несколько точек. Оцените f ( x ) для нескольких замен целых чисел; затем соедините эти точки, чтобы сформировать плавную кривую (см. рисунок 3).
Обратите внимание, что f ( x ) = x 4 -10 x 2 + 9 имеет ведущий член с четной степенью. Крайняя правая и крайняя левая части графика будут идти в одном направлении.Поскольку ведущий коэффициент положительный, обе стороны поднимутся вверх. Если бы ведущий коэффициент был отрицательным, обе стороны пошли бы вниз.
Рис. 2. График f (x).
Рисунок 3. Нули функции.
Пример 2
График f ( x ) = x 3 -19 x + 30.
f ( x ) = x 3 -19 x + 30 можно разложить на множители с помощью теоремы о рациональном нуле:
шт / кварт
1
0
–19
30
1
1
1
–18
12
–1
1
–1
–18
48
2
1
2
–15
0
f ( x ) теперь можно записать в факторизованной форме и дополнительно разложить на множители.
= ( x - 2) ( x - 3) ( x + 5)
Нули этой функции - 2, 3 и –5 (см. Рисунок 4).
Обратите внимание, что f ( x ) = x 3 -19 x + 30 имеет ведущий член с положительным коэффициентом и нечетным показателем. Эта функция всегда будет идти вверх в крайнее правое положение и вниз в крайнее левое положение. Если бы ведущий коэффициент был отрицательным с нечетной экспонентой, график шел бы вверх в крайнее левое положение и вниз в крайнее правое положение.
Рисунок 4. Кубическое уравнение.
Как построить график функции в Excel | Small Business
Математическая функция - это формула, которая принимает входные данные x, применяет к ним набор вычислений и производит выходные данные с именем y. Вычисляя функцию с большим количеством заданных интервалов, можно создать диаграмму рассеяния функции. В бизнесе это имеет множество применений. Например, вы можете построить график прибыли за вычетом затрат на различных уровнях продаж, или общие затраты можно оценить путем нанесения фиксированных затрат на различные приращения переменных затрат.
Создайте заголовки для таблицы данных. Введите входную переменную в ячейку A1 и выходную переменную в ячейку B1. Если хотите, вы можете использовать математические стандарты «x» и «y» или что-то более наглядное, например «продажи» и «прибыль».
Введите первый и второй интервалы входной переменной (например, «x» или «продажи»), которые вы будете использовать для построения графика функции. Например, если ваши интервалы представляют собой целые числа, вы можете начать с ввода «1» в ячейку A2 и «2» в ячейку A3.Выделите обе эти ячейки, а затем щелкните и перетащите маленький черный квадрат в правом нижнем углу области выбора вниз, пока у вас не будет столько значений, сколько вы хотите построить.
Введите знак равенства "=" в ячейку B2, а затем введите формулу сразу после него, не оставляя пробелов. Например, чтобы определить количество продаж определенного продукта для покрытия расходов, вы можете использовать:
= (A2 * 50) -3500
Замените «50» продажной ценой, а «3500» - ваши расходы.
Выберите ячейку B2 и затем перетащите, чтобы скопировать формулу вниз по столбцу тем же способом, который вы использовали на шаге 2. Убедитесь, что каждое из ваших значений x имеет соответствующую функцию справа от него. При этом столбец будет автоматически заполняться решениями для каждой функции на основе значения x в столбце A.
Выберите все ячейки, в которые вы ввели данные, включая заголовок.
Щелкните вкладку «Вставка», щелкните «Разброс» в области «Диаграммы», а затем щелкните нужный тип графика.График появится на вашем листе.
Биография писателя
Уоррен Дэвис пишет с 2007 года, уделяя особое внимание индивидуальным проектам для онлайн-клиентов, таких как PsyT и Институт коучинга. Это было параллельно с исследованиями, веб-дизайном и ведением блогов. Пользователь Linux и геймер, Уоррен занимается боевыми искусствами в качестве хобби. Он имеет степень бакалавра и магистра психологии, а также дополнительную квалификацию в области статистики и бизнес-исследований.

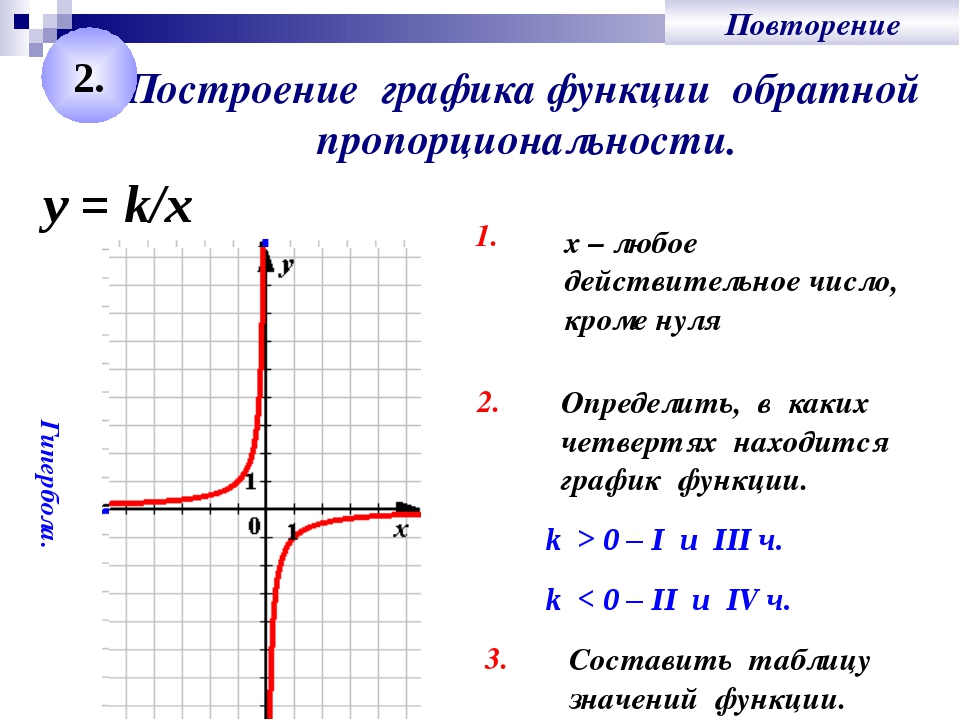
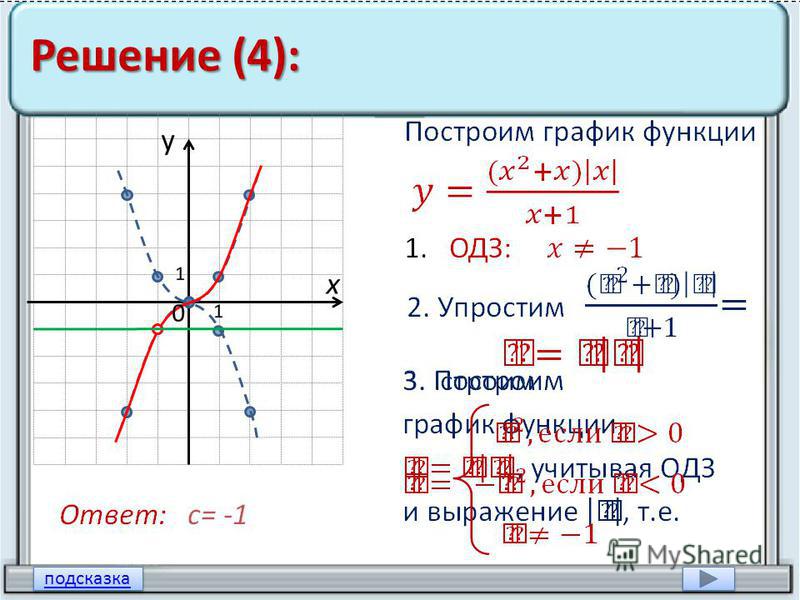
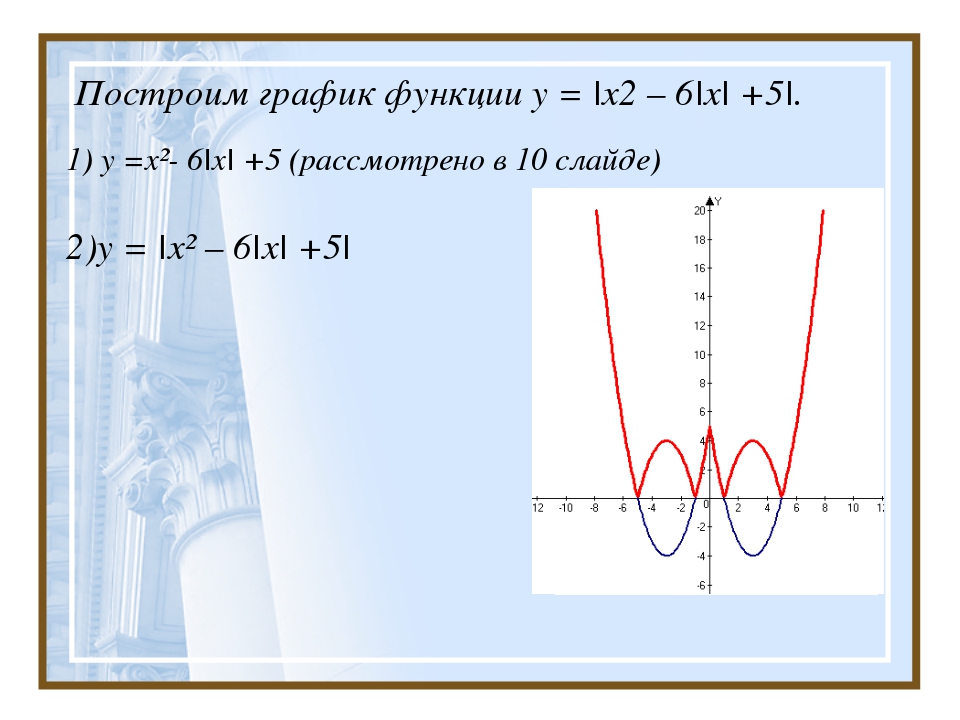
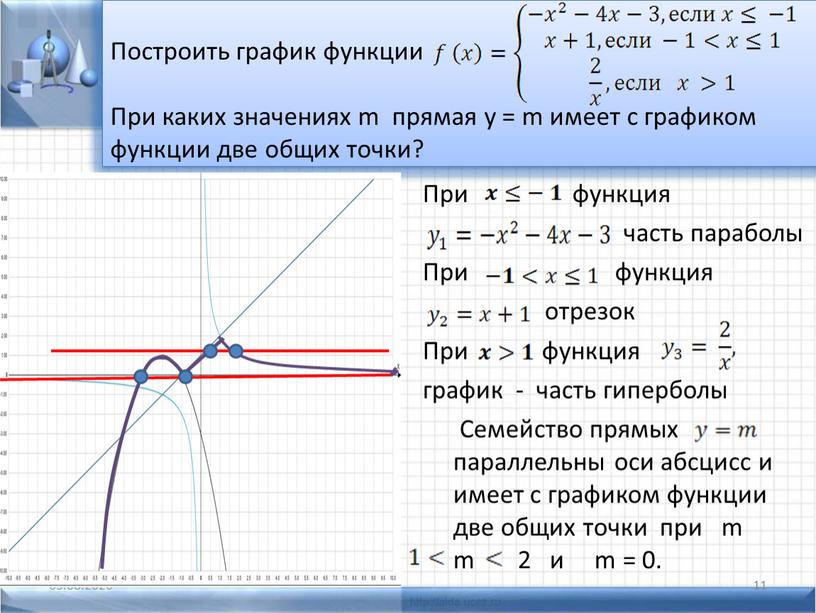 2 u (\ x) & = f (\ x), \ quad && \ x \ mbox {in} \ Omega,
\ tag {2.2} = f (x, y) \ tp
\ tag {2.3}
\ end {уравнение}
$$ Неизвестное \ (u \) теперь является функцией двух переменных \ (u = u (x, y) \), определенных
над двумерной областью \ (\ Omega \).
2 u (\ x) & = f (\ x), \ quad && \ x \ mbox {in} \ Omega,
\ tag {2.2} = f (x, y) \ tp
\ tag {2.3}
\ end {уравнение}
$$ Неизвестное \ (u \) теперь является функцией двух переменных \ (u = u (x, y) \), определенных
над двумерной областью \ (\ Omega \).
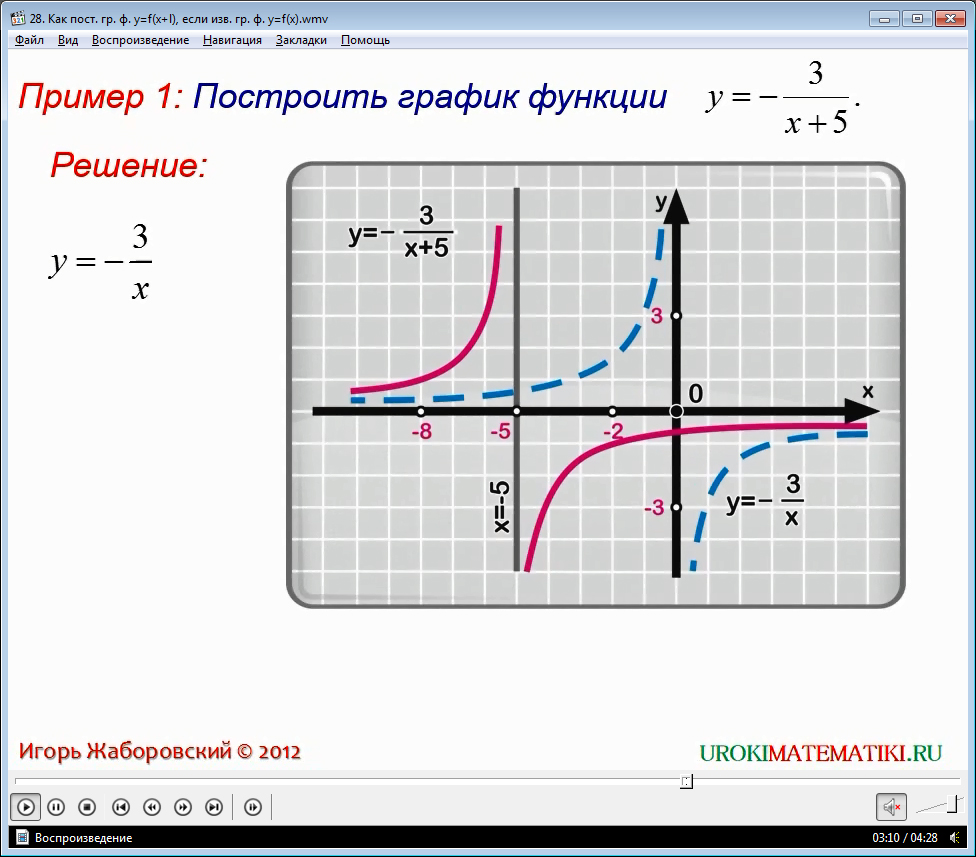 Отправной точкой для методов конечных элементов является PDE
выражается в вариационной форме . Читатели, не знакомые с
вариационные задачи получат очень краткое введение в тему
в этом учебном пособии, но читая подходящую книгу по конечным элементам
метод дополнительно приветствуется.Раздел Метод конечных элементов содержит
список рекомендуемых книг. Опыт показывает, что с
FEniCS как инструмент для решения PDE даже без глубоких знаний
метод конечных элементов, если вам кто-то поможет
с формулировкой PDE в виде вариационной задачи.
Отправной точкой для методов конечных элементов является PDE
выражается в вариационной форме . Читатели, не знакомые с
вариационные задачи получат очень краткое введение в тему
в этом учебном пособии, но читая подходящую книгу по конечным элементам
метод дополнительно приветствуется.Раздел Метод конечных элементов содержит
список рекомендуемых книг. Опыт показывает, что с
FEniCS как инструмент для решения PDE даже без глубоких знаний
метод конечных элементов, если вам кто-то поможет
с формулировкой PDE в виде вариационной задачи.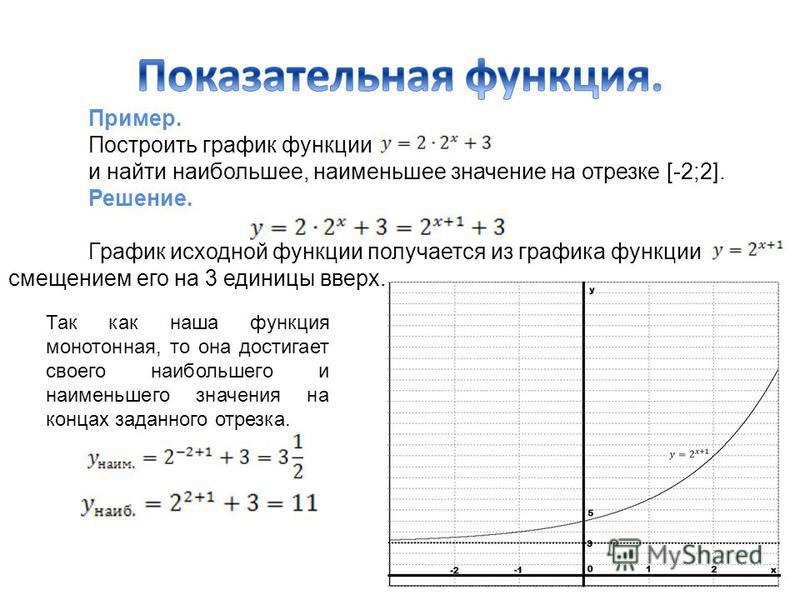 Испытание и испытание
функции принадлежат определенным так называемым функциональным пространствам , которые определяют
свойства функций.
Испытание и испытание
функции принадлежат определенным так называемым функциональным пространствам , которые определяют
свойства функций.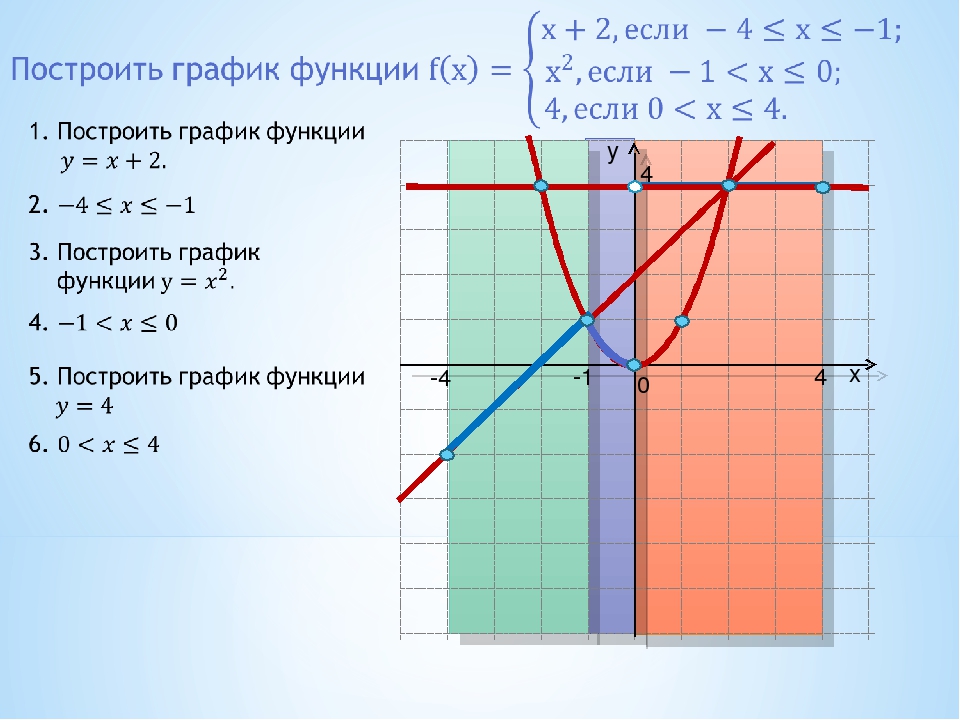
 2 \) имеют
конечные интегралы по \ (\ Omega \) (по сути означающие, что функции
непрерывны).1 (\ Omega) \) допускает функции с разрывными
производные. Это более слабое требование непрерывности \ (u \) в
вариационной формулировке (2.7) в результате
интеграция по частям, имеет большие практические последствия, когда дело доходит до
к построению функциональных пространств конечных элементов. В частности, это
позволяет использовать кусочно-полиномиальные функциональные пространства; т.е. функция
пространства, построенные путем сшивания полиномиальных функций на простых
такие области, как интервалы, треугольники или тетраэдры.
2 \) имеют
конечные интегралы по \ (\ Omega \) (по сути означающие, что функции
непрерывны).1 (\ Omega) \) допускает функции с разрывными
производные. Это более слабое требование непрерывности \ (u \) в
вариационной формулировке (2.7) в результате
интеграция по частям, имеет большие практические последствия, когда дело доходит до
к построению функциональных пространств конечных элементов. В частности, это
позволяет использовать кусочно-полиномиальные функциональные пространства; т.е. функция
пространства, построенные путем сшивания полиномиальных функций на простых
такие области, как интервалы, треугольники или тетраэдры. Дискретная вариационная задача гласит: найти \ (u_h \ in
V_h \ subset V \) такая, что $$
\ begin {уравнение} \ tag {2.8}
\ int _ {\ Omega} \ nabla u_h \ cdot \ nabla v \ dx =
\ int _ {\ Omega} fv \ dx
\ quad \ forall v \ in \ hat {V} _h \ subset \ hat {V} \ tp
\ end {уравнение}
$$
Дискретная вариационная задача гласит: найти \ (u_h \ in
V_h \ subset V \) такая, что $$
\ begin {уравнение} \ tag {2.8}
\ int _ {\ Omega} \ nabla u_h \ cdot \ nabla v \ dx =
\ int _ {\ Omega} fv \ dx
\ quad \ forall v \ in \ hat {V} _h \ subset \ hat {V} \ tp
\ end {уравнение}
$$ Чтобы получить (почти) взаимно однозначное отношение
между математической постановкой задачи и
соответствующей программе FEniCS, мы опустим индекс \ (_h \) и воспользуемся
\ (u \) для решения дискретной задачи.Мы будем использовать \ (\ uex \) для точного
решение непрерывной задачи, , если нам нужно явно различать
между двумя. Аналогично, обозначим через \ (V \) дискретную конечную
элемент функционального пространства, в котором мы ищем наше решение.
Чтобы получить (почти) взаимно однозначное отношение
между математической постановкой задачи и
соответствующей программе FEniCS, мы опустим индекс \ (_h \) и воспользуемся
\ (u \) для решения дискретной задачи.Мы будем использовать \ (\ uex \) для точного
решение непрерывной задачи, , если нам нужно явно различать
между двумя. Аналогично, обозначим через \ (V \) дискретную конечную
элемент функционального пространства, в котором мы ищем наше решение. образуют и \ (L (v) \) как линейную форму . Мы будем в каждой линейной задаче
мы решаем, отождествляем члены с неизвестным \ (u \) и собираем их в
\ (a (u, v) \), и аналогично собрать все члены только с известными функциями в
\ (L (v) \).Формулы для \ (a \) и \ (L \) могут быть выражены непосредственно в
наши программы FEniCS.
образуют и \ (L (v) \) как линейную форму . Мы будем в каждой линейной задаче
мы решаем, отождествляем члены с неизвестным \ (u \) и собираем их в
\ (a (u, v) \), и аналогично собрать все члены только с известными функциями в
\ (L (v) \).Формулы для \ (a \) и \ (L \) могут быть выражены непосредственно в
наши программы FEniCS. Для нашего первого
реализации нам нужно будет сделать конкретный выбор для \ (\ Omega \),
\ (\ ub \) и \ (f \). Будет разумно построить задачу с известным
аналитическое решение, чтобы мы могли легко проверить, что вычисленное
решение правильное. Решения, представляющие собой полиномы низшего порядка:
основные кандидаты.2, $$ независимо от формы области, пока \ (\ uex \) предписано вдоль
граница. Мы выбрали здесь для простоты
домен должен быть единичным квадратом, $$ \ Omega = [0,1] \ times [0,1] \ tp $$ Этот простой, но очень мощный метод построения тестовых задач
называется метод производства решений : выберите простой
выражение для точного решения, подставьте его в уравнение, чтобы получить
в правой части (исходный член \ (f \)), затем решите уравнение с
эту правую часть и используя точное решение в качестве границы
условие и попытайтесь воспроизвести точное решение.2 \)
если \ (h \) — размер ячейки в сетке. Затем мы сравниваем
ошибка на сетках с разными \ (h \) — значениями, чтобы увидеть, есть ли асимптотические
поведение правильное.
Для нашего первого
реализации нам нужно будет сделать конкретный выбор для \ (\ Omega \),
\ (\ ub \) и \ (f \). Будет разумно построить задачу с известным
аналитическое решение, чтобы мы могли легко проверить, что вычисленное
решение правильное. Решения, представляющие собой полиномы низшего порядка:
основные кандидаты.2, $$ независимо от формы области, пока \ (\ uex \) предписано вдоль
граница. Мы выбрали здесь для простоты
домен должен быть единичным квадратом, $$ \ Omega = [0,1] \ times [0,1] \ tp $$ Этот простой, но очень мощный метод построения тестовых задач
называется метод производства решений : выберите простой
выражение для точного решения, подставьте его в уравнение, чтобы получить
в правой части (исходный член \ (f \)), затем решите уравнение с
эту правую часть и используя точное решение в качестве границы
условие и попытайтесь воспроизвести точное решение.2 \)
если \ (h \) — размер ячейки в сетке. Затем мы сравниваем
ошибка на сетках с разными \ (h \) — значениями, чтобы увидеть, есть ли асимптотические
поведение правильное. Это очень мощная проверка
метод и подробно объясняется в разделе Вычисление скорости сходимости.
Однако, если у нас есть тестовая задача, для которой
мы знаем, что ошибок аппроксимации быть не должно, мы знаем, что
аналитическое решение задачи PDE следует воспроизвести в виде
точность станка по программе. Вот почему мы подчеркиваем этот вид
тестовых задач в этом руководстве.Обычно элементы
степень \ (r \) может точно воспроизводить многочлены степени \ (r \), так что это
является отправной точкой для построения решения без численных
ошибки аппроксимации.
Это очень мощная проверка
метод и подробно объясняется в разделе Вычисление скорости сходимости.
Однако, если у нас есть тестовая задача, для которой
мы знаем, что ошибок аппроксимации быть не должно, мы знаем, что
аналитическое решение задачи PDE следует воспроизвести в виде
точность станка по программе. Вот почему мы подчеркиваем этот вид
тестовых задач в этом руководстве.Обычно элементы
степень \ (r \) может точно воспроизводить многочлены степени \ (r \), так что это
является отправной точкой для построения решения без численных
ошибки аппроксимации. 0)
а = точка (град (и), град (в)) * dx
L = f * v * dx
# Вычислительное решение
u = Функция (V)
решить (a == L, u, bc)
# Постройте решение и сетку
сюжет (u)
сюжет (сетка)
# Сохранить решение в файл в формате VTK
vtkfile = Файл ('poisson / solution.pvd')
vtkfile << u
# Ошибка вычисления в норме L2
error_L2 = errornorm (u_D, u, 'L2')
# Вычислить максимальную ошибку в вершинах
vertex_values_u_D = u_D.compute_vertex_values (сетка)
vertex_values_u = u.compute_vertex_values (сетка)
импортировать numpy как np
error_max = np.max (np.abs (vertex_values_u_D - vertex_values_u))
# Ошибки печати
print ('error_L2 =', error_L2)
print ('error_max =', error_max)
# Держать сюжет
интерактивный ()
0)
а = точка (град (и), град (в)) * dx
L = f * v * dx
# Вычислительное решение
u = Функция (V)
решить (a == L, u, bc)
# Постройте решение и сетку
сюжет (u)
сюжет (сетка)
# Сохранить решение в файл в формате VTK
vtkfile = Файл ('poisson / solution.pvd')
vtkfile << u
# Ошибка вычисления в норме L2
error_L2 = errornorm (u_D, u, 'L2')
# Вычислить максимальную ошибку в вершинах
vertex_values_u_D = u_D.compute_vertex_values (сетка)
vertex_values_u = u.compute_vertex_values (сетка)
импортировать numpy как np
error_max = np.max (np.abs (vertex_values_u_D - vertex_values_u))
# Ошибки печати
print ('error_L2 =', error_L2)
print ('error_max =', error_max)
# Держать сюжет
интерактивный ()
 2 \) и
будут напечатаны максимальные нормы.{-15} \). Если черчение включено в вашей установке FEniCS,
тогда окно с простым графиком решения появится как
на рисунке 1.
2 \) и
будут напечатаны максимальные нормы.{-15} \). Если черчение включено в вашей установке FEniCS,
тогда окно с простым графиком решения появится как
на рисунке 1. py
py  Мы также строим решение, используя
Мы также строим решение, используя  В следующих главах вы узнаете, как создавать более сложные сетки.
В следующих главах вы узнаете, как создавать более сложные сетки. В
вычисленное решение \ (u \) будет непрерывным по элементам и линейно
изменяющиеся в \ (x \) и \ (y \) внутри каждого элемента. Полином высшей степени
аппроксимации по каждой ячейке тривиально получаются увеличением
третий параметр
В
вычисленное решение \ (u \) будет непрерывным по элементам и линейно
изменяющиеся в \ (x \) и \ (y \) внутри каждого элемента. Полином высшей степени
аппроксимации по каждой ячейке тривиально получаются увеличением
третий параметр 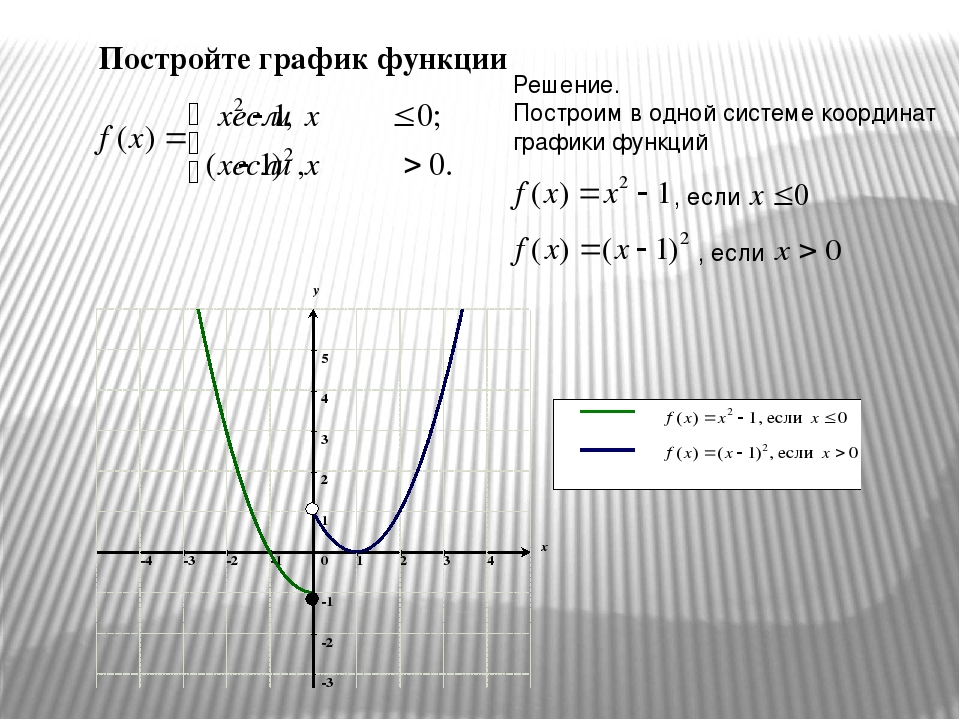 Это делается
Это делается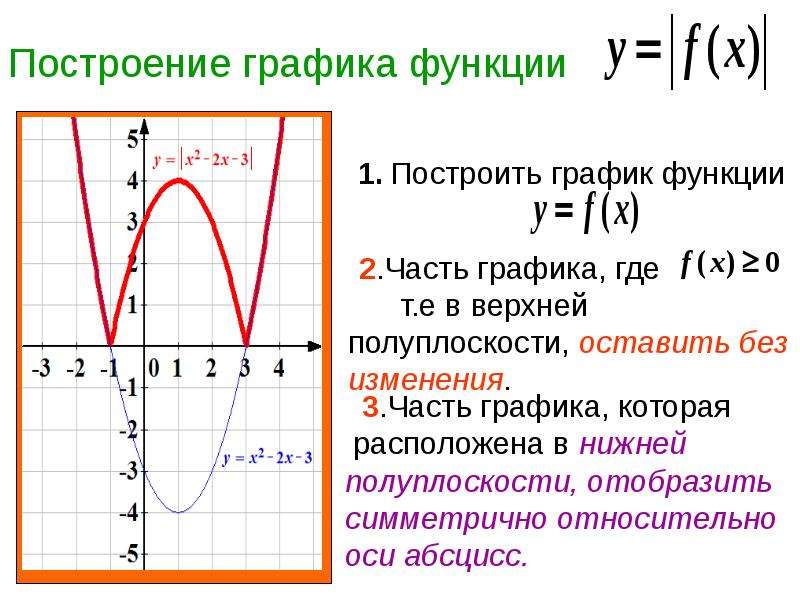 Формула должна быть написана с использованием синтаксиса C ++ и
автоматически превратился в эффективную скомпилированную функцию C ++.
Формула должна быть написана с использованием синтаксиса C ++ и
автоматически превратился в эффективную скомпилированную функцию C ++. 2 \) формула
строка может быть записана как
2 \) формула
строка может быть записана как  2t} \ sin (\ pi k x) \) можно закодировать как
2t} \ sin (\ pi k x) \) можно закодировать как
 Лучше тест
чтобы проверить равенство с допуском, либо явно
Лучше тест
чтобы проверить равенство с допуском, либо явно 551115123125783e-17
>>> абс (1,1 + 1,2 - 2,3)
0,0
>>> абс (10,1 + 10,2 - 20,3)
3,552713678800501e-15
>>> абс (100,1 + 100.{-16} \) можно использовать
(Фактически, этот допуск известен как константа
551115123125783e-17
>>> абс (1,1 + 1,2 - 2,3)
0,0
>>> абс (10,1 + 10,2 - 20,3)
3,552713678800501e-15
>>> абс (100,1 + 100.{-16} \) можно использовать
(Фактически, этот допуск известен как константа  Этот
является ключевым преимуществом FEniCS: формулы в вариационном
переводить непосредственно в очень похожий код Python, особенность
что упрощает определение и решение сложных задач PDE. В
язык, используемый для выражения слабых форм, называется UFL (Unified Form
Language) [5] [1] и является неотъемлемой частью FEniCS.
Этот
является ключевым преимуществом FEniCS: формулы в вариационном
переводить непосредственно в очень похожий код Python, особенность
что упрощает определение и решение сложных задач PDE. В
язык, используемый для выражения слабых форм, называется UFL (Unified Form
Language) [5] [1] и является неотъемлемой частью FEniCS. Для векторов
Для векторов  Этот вызов позволяет взаимодействовать с графиками (вращать и
масштабирование). Звонок на номер
Этот вызов позволяет взаимодействовать с графиками (вращать и
масштабирование). Звонок на номер  В
Команда
В
Команда 
 pvd
pvd  Это должно сделать видимой сетку конечных элементов.
Это должно сделать видимой сетку конечных элементов.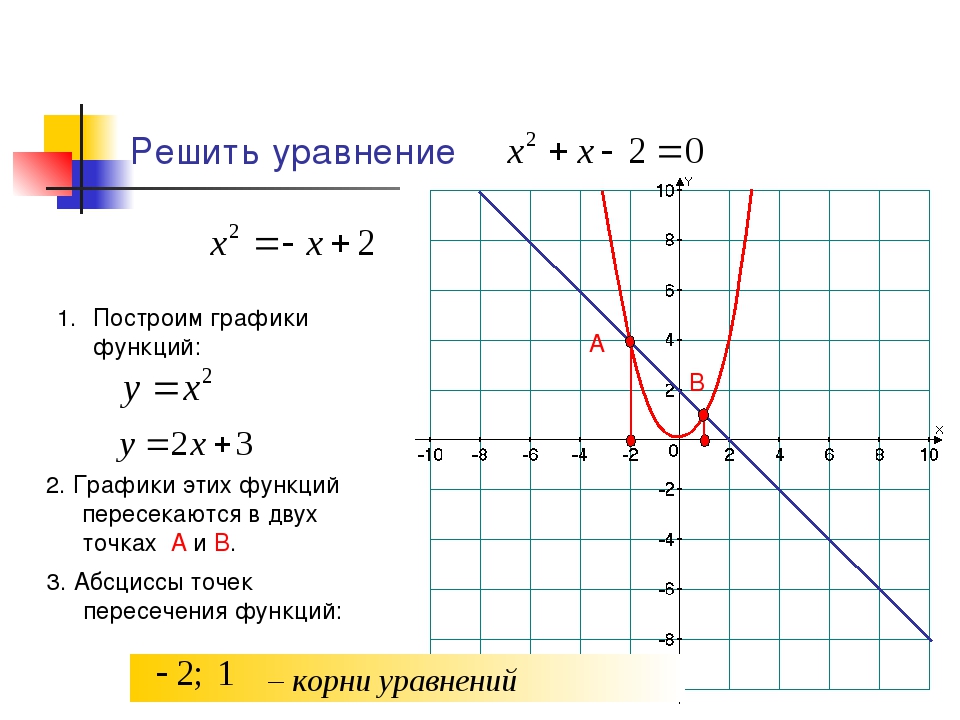
 max (np.abs (vertex_values_u_D - vertex_values_u))
max (np.abs (vertex_values_u_D - vertex_values_u))
 Если решение вычисляется с
кусочно-линейные элементы Лагранжа (\ (\ mathsf {P} _1 \)), то размер
массив
Если решение вычисляется с
кусочно-линейные элементы Лагранжа (\ (\ mathsf {P} _1 \)), то размер
массив 
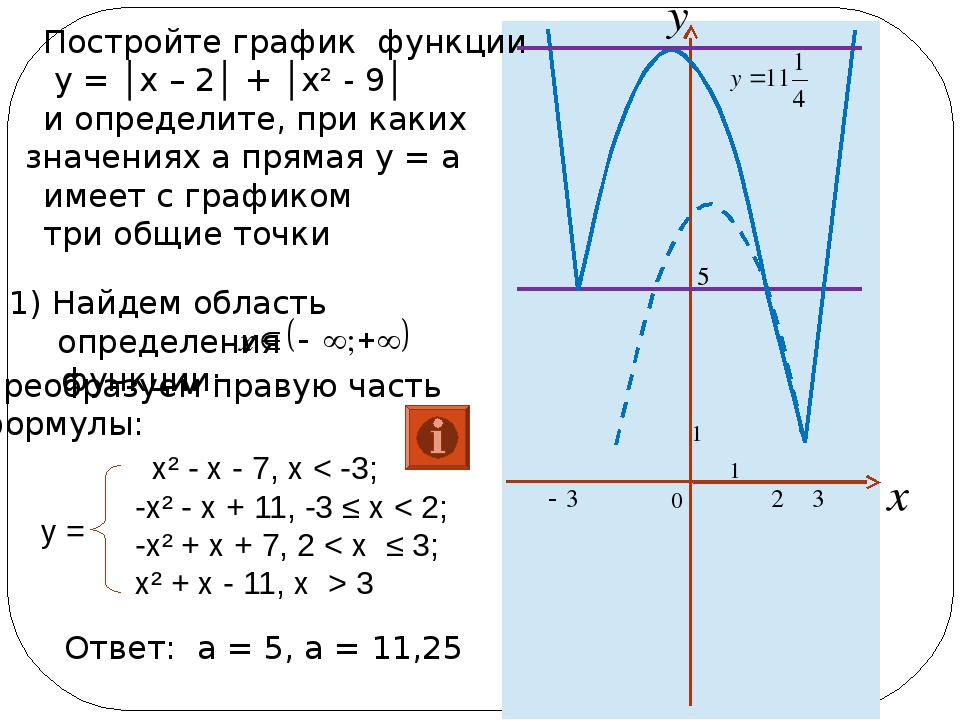




Ваш комментарий будет первым