Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Алгебра | Координатная плоскость |
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
| Преобразование | Описание | Рисунок |
y = f (x + c), | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
y = f (x) + c, | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
| y = – f (x) | График функции y = f (x) симметрично отражается относительно оси Ox. | |
| y = f ( – x) | График функции y = f (x) симметрично отражается относительно оси Oy. | |
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит растяжение графика функции | ||
В случае – 1 < k < 0 происходит растяжение графика функции | ||
В случае k < – 1 происходит | ||
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит | ||
В случае – 1 < k < 0 происходит | ||
В случае k < – 1 происходит | ||
| y = | f (x)| | Часть графика функции y = f (x), расположенная в области | |
| y = f (| x|) | Ось Oy является осью симметрии Часть графика функции y = f (x), расположенная в области |
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | | |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | | |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. | |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. | |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции | |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. | |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. | |
В случае k < – 1 происходит сжатие графика функции | |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. | |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. | |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
| Преобразование y = | f (x)| | |
Часть графика функции | |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции | |
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
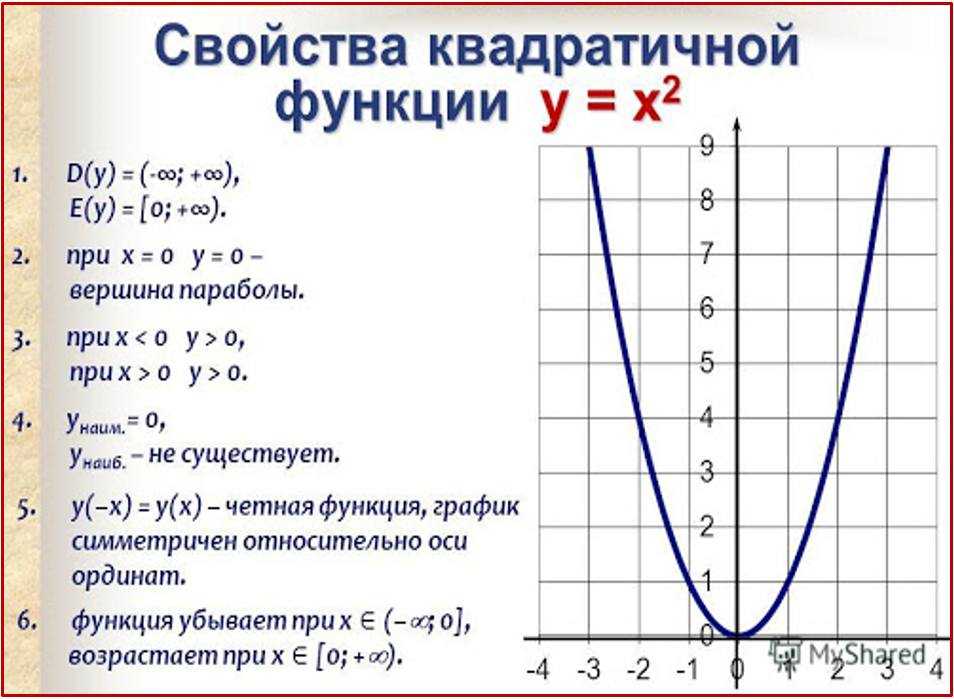
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
| Функция | График |
| y = x2 = f (x) | |
y = x2 + 4x + 4 = (x + 2)2 = = f (x + 2) | |
y = x2 – 4x + 4 = (x – 2)2 = = f (x – 2) | |
| y = x2 + 2 = f (x)+ 2 | |
| y = x2 – 2 = f (x) – 2 | |
| y = – x2 = – f (x) | |
| y = 2x2 = 2 f (x) |
Функция: y = x2 = f (x) График: |
Функция: y = x2 + 4x + 4 = График: |
Функция: y = x2 – 4x + 4 = График: |
Функция: y = x2 + 2 = График: |
Функция: y = x2 – 2 = График: |
Функция: y = – x2 = График: |
Функция: y = 2x2 = График: |
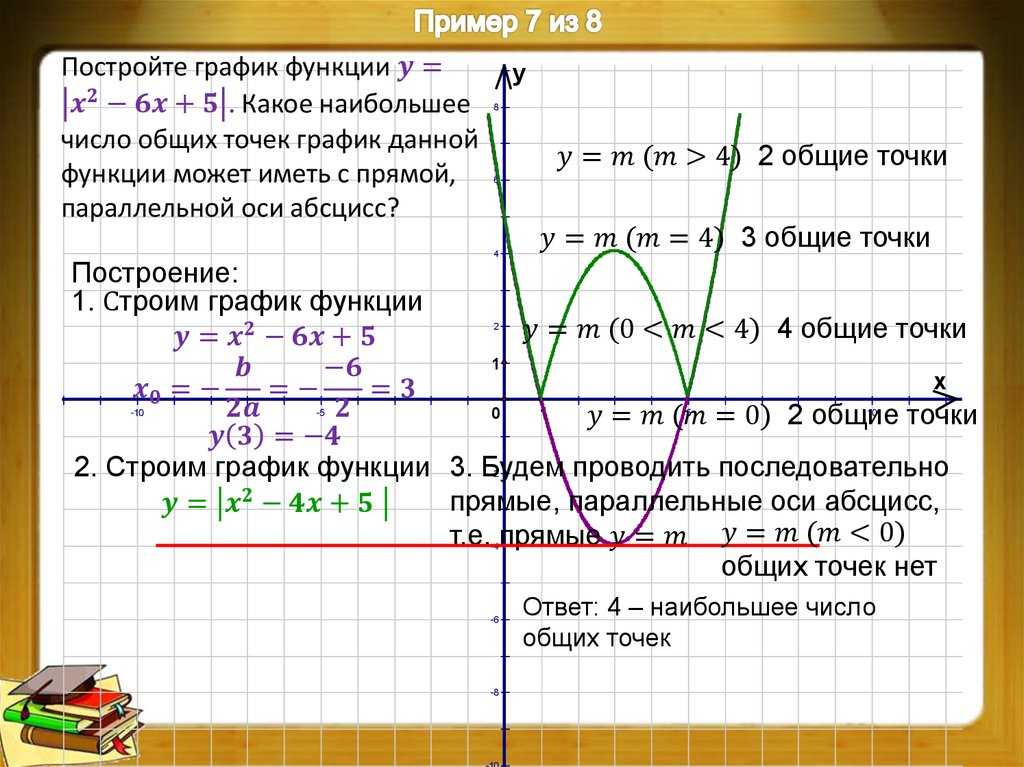
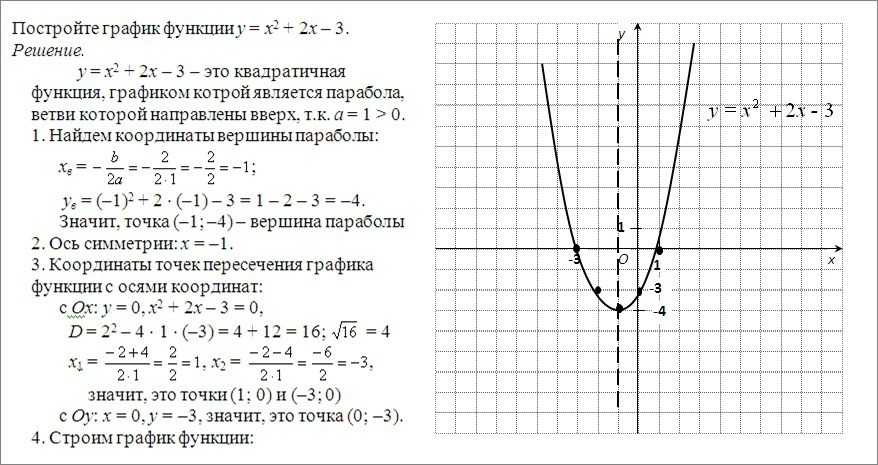
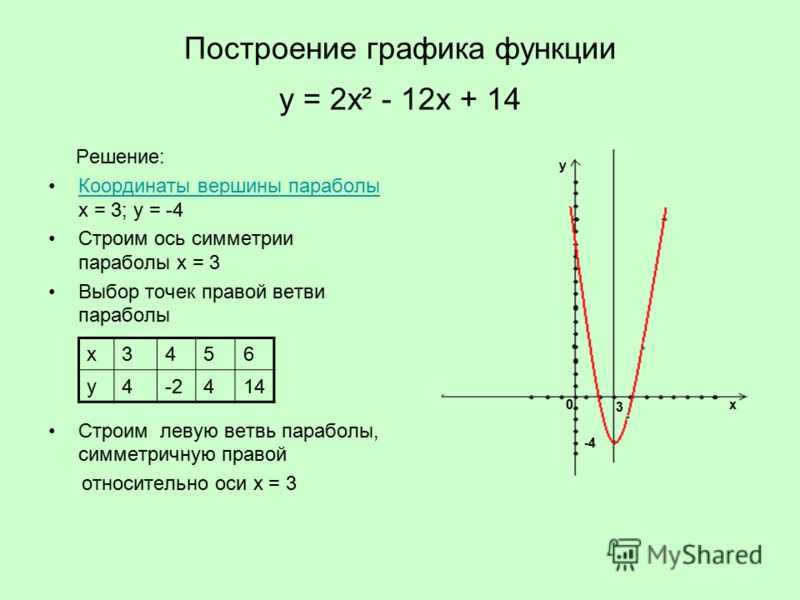
Примеры элементарных преобразований графика функции y = x2 – 6 x + 5 приведены в следующей таблице.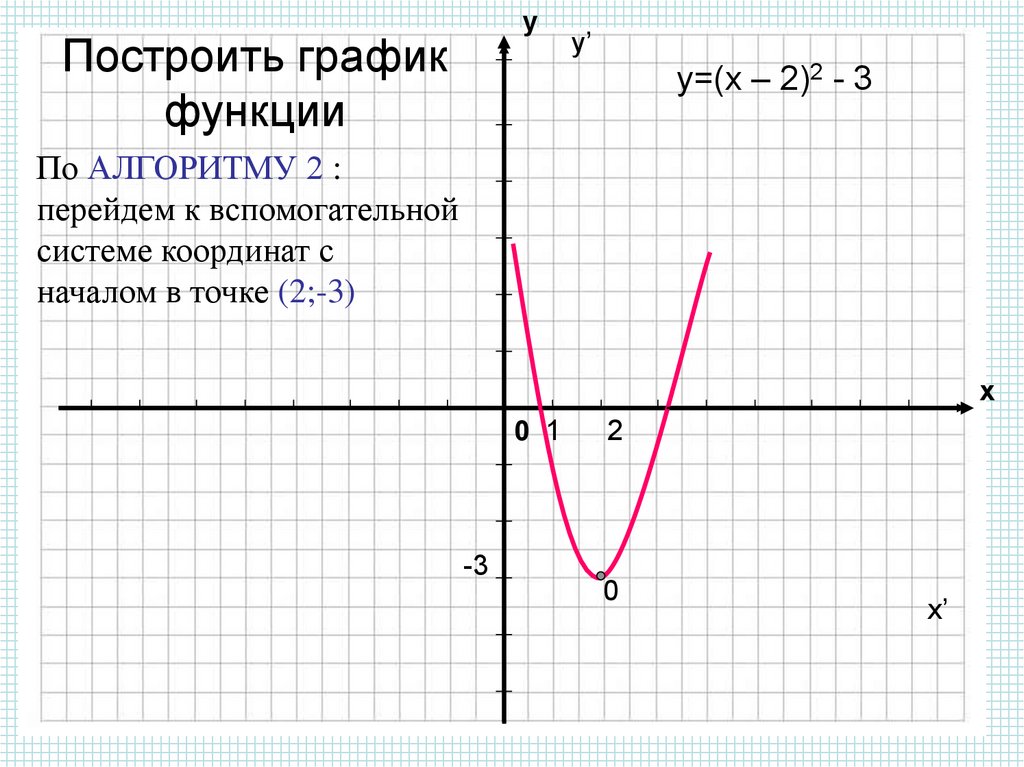
| Функция | График |
| y = x2 – 6x + 5 = = f (x) | |
| y = x2 + 6x + 5 = = f (– x) | |
| y = 4x2 – 12x + 5 = = f (2x) | |
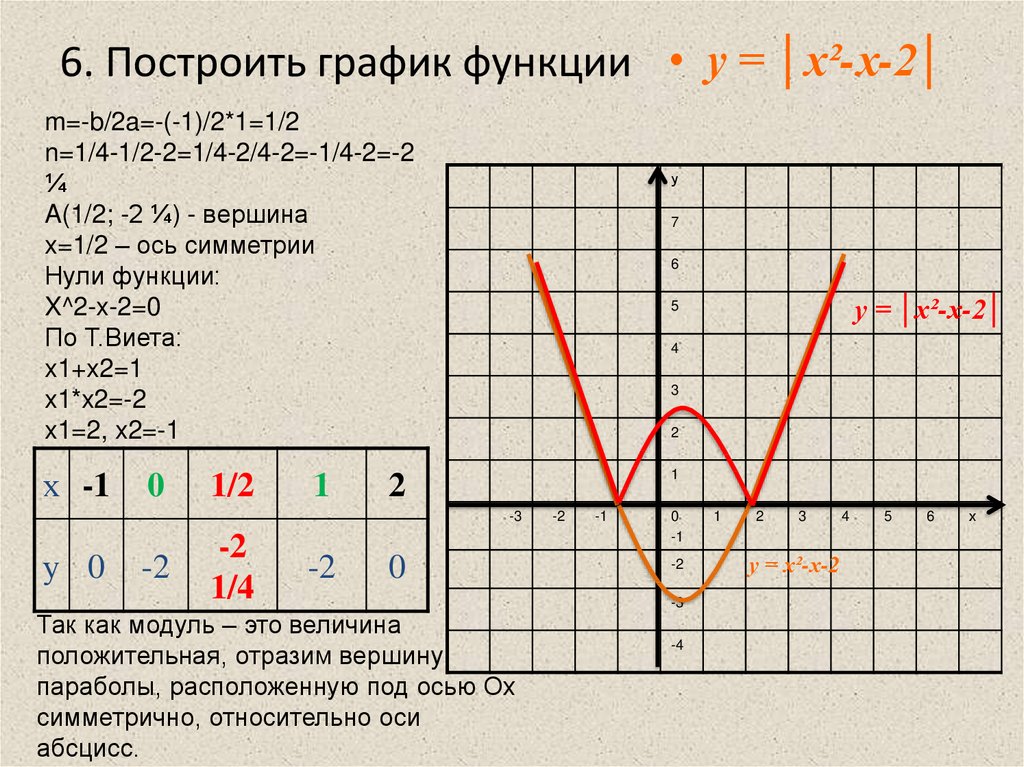
| y = | x2 – 6x + 5| = = | f (x)| | |
| y = x2 – 6 | x| + 5 = = f (| x|) |
Функция: y = x2 – 6x + 5 = График: |
Функция: y = x2 + 6x + 5 = График: |
Функция: y = 4x2 – 12x + 5 = График: |
Функция: y = | x2 – 6x + 5| = График: |
Функция: y = x2 – 6 | x| + 5 = График: |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Пять функций | NIST
В этом учебном модуле более подробно рассматриваются пять функций Cybersecurity Framework: идентификация, защита, обнаружение, реагирование и восстановление. Информация, представленная здесь, основывается на материалах, представленных в модуле «Компоненты платформы». Этот модуль исследует значение функций в рамках платформы и то, что включено в каждую функцию.
Введение в функции
Пять функций, включенных в ядро платформы:
- Идентифицировать
- Защита
- Обнаружить
- Ответить
- Восстановление
Функции — это высший уровень абстракции, включенный в платформу. Они действуют как основа ядра Framework, вокруг которого организованы все остальные элементы.
Эти пять функций были выбраны, потому что они представляют собой пять основных столпов успешной и целостной программы кибербезопасности. Они помогают организациям легко выражать свое управление рисками кибербезопасности на высоком уровне и позволяют принимать решения по управлению рисками.
Идентификация Функция идентификации помогает в разработке организационного понимания управления рисками кибербезопасности для систем, людей, активов, данных и возможностей. Понимание бизнес-контекста, ресурсов, поддерживающих критически важные функции, и связанных с ними рисков кибербезопасности позволяет организации сосредоточить усилия и расставить приоритеты в соответствии со своей стратегией управления рисками и потребностями бизнеса.
Примеры категорий результатов в рамках этой функции включают:
- Определение физических и программных активов в организации для создания основы программы управления активами
- Определение бизнес-среды, которую поддерживает организация, включая роль организации в цепочке поставок и место организации в секторе критической инфраструктуры
- Определение политик кибербезопасности, установленных в организации для определения программы управления, а также определение юридических и нормативных требований в отношении возможностей кибербезопасности организации
- Выявление уязвимостей активов, угроз для внутренних и внешних ресурсов организации и действий по реагированию на риски в качестве основы для оценки рисков организации
- Определение стратегии управления рисками для организации, включая установление допусков к риску
- Определение стратегии управления рисками цепочки поставок, включая приоритеты, ограничения, допуски к риску и допущения, используемые для поддержки решений о рисках, связанных с управлением рисками цепочки поставок
Функция защиты описывает соответствующие меры безопасности для обеспечения доставки критически важных инфраструктурных услуг. Функция защиты поддерживает возможность ограничения или сдерживания воздействия потенциального события кибербезопасности.
Функция защиты поддерживает возможность ограничения или сдерживания воздействия потенциального события кибербезопасности.
Примеры категорий результатов в рамках этой функции включают:
- Средства защиты для управления идентификацией и контроля доступа в организации, включая физический и удаленный доступ
- Расширение прав и возможностей сотрудников организации посредством повышения осведомленности и обучения, включая обучение на основе ролей и привилегированных пользователей
- Обеспечение защиты данных в соответствии со стратегией управления рисками организации для защиты конфиденциальности, целостности и доступности информации
- Внедрение процессов и процедур защиты информации для поддержания и управления защитой информационных систем и активов
- Защита ресурсов организации посредством обслуживания, включая дистанционное обслуживание, действия
- Управление защитными технологиями для обеспечения безопасности и отказоустойчивости систем и активов в соответствии с политиками, процедурами и соглашениями организации
Функция обнаружения определяет соответствующие действия для определения возникновения события кибербезопасности. Функция обнаружения позволяет своевременно обнаруживать события кибербезопасности.
Функция обнаружения позволяет своевременно обнаруживать события кибербезопасности.
Примеры категорий результатов в рамках этой функции включают:
- Обеспечение обнаружения аномалий и событий и понимания их потенциального воздействия
- Внедрение возможностей непрерывного мониторинга безопасности для мониторинга событий кибербезопасности и проверки эффективности защитных мер, включая сетевые и физические действия
- Поддержание процессов обнаружения для информирования об аномальных событиях
Функция реагирования включает в себя соответствующие действия для принятия мер в отношении обнаруженного инцидента кибербезопасности. Функция реагирования поддерживает возможность сдерживания воздействия потенциального инцидента кибербезопасности.
Примеры категорий результатов в рамках этой функции включают:
- Обеспечение выполнения процесса планирования реагирования во время и после инцидента
- Управление коммуникациями во время и после мероприятия с заинтересованными сторонами, правоохранительными органами, внешними заинтересованными сторонами по мере необходимости
- Анализ проводится для обеспечения эффективного реагирования и поддержки восстановительных мероприятий, включая криминалистический анализ и определение влияния инцидентов
- Действия по смягчению последствий выполняются для предотвращения распространения события и устранения инцидента
- Организация внедряет улучшения путем включения уроков, извлеченных из текущих и предыдущих действий по обнаружению/реагированию
Функция восстановления определяет соответствующие действия для поддержания планов устойчивости и восстановления любых возможностей или служб, которые были повреждены из-за инцидента кибербезопасности.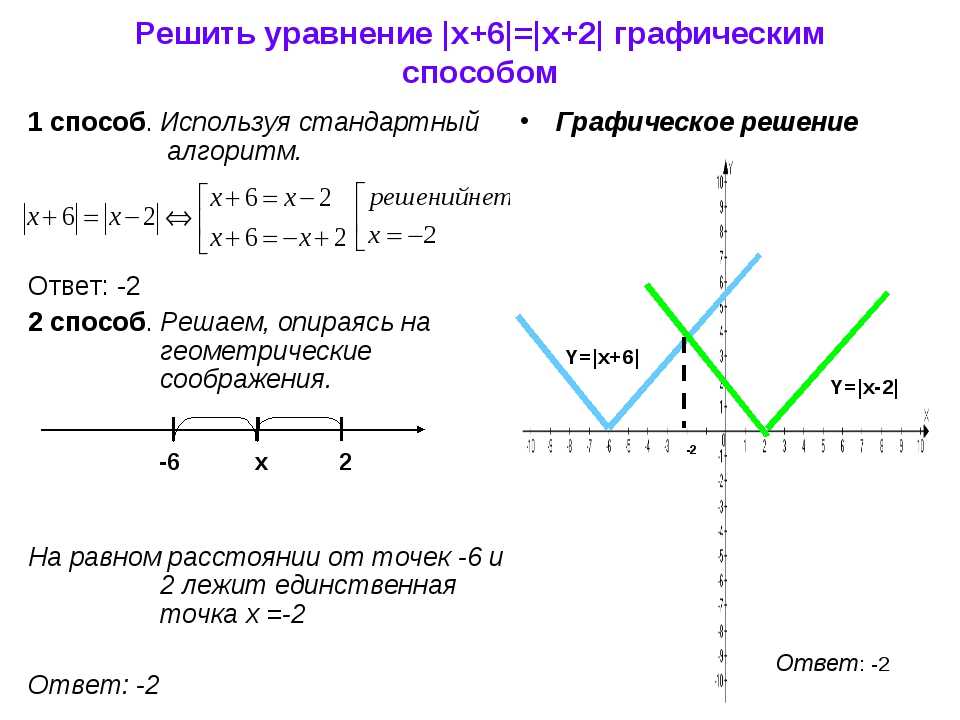 Функция восстановления поддерживает своевременное восстановление нормальной работы, чтобы уменьшить влияние инцидента кибербезопасности.
Функция восстановления поддерживает своевременное восстановление нормальной работы, чтобы уменьшить влияние инцидента кибербезопасности.
Примеры категорий результатов в рамках этой функции включают:
- Обеспечение внедрения организацией процессов и процедур планирования восстановления для восстановления систем и/или активов, затронутых инцидентами кибербезопасности
- Внедрение улучшений на основе извлеченных уроков и обзоров существующих стратегий
- Внутренние и внешние коммуникации координируются во время и после восстановления после инцидента кибербезопасности
Дополнительные ресурсы
The_Five_Functions.pptx (PPTX | 1 МБ)
Информационные технологии и кибербезопасность
Агрегированные функции в Tableau — Tableau
Применяется к: Tableau Cloud, Tableau Desktop, Tableau Public, Tableau Server
В этой статье представлены агрегатные функции и их использование в Tableau. Он также демонстрирует, как создать агрегатный расчет на примере.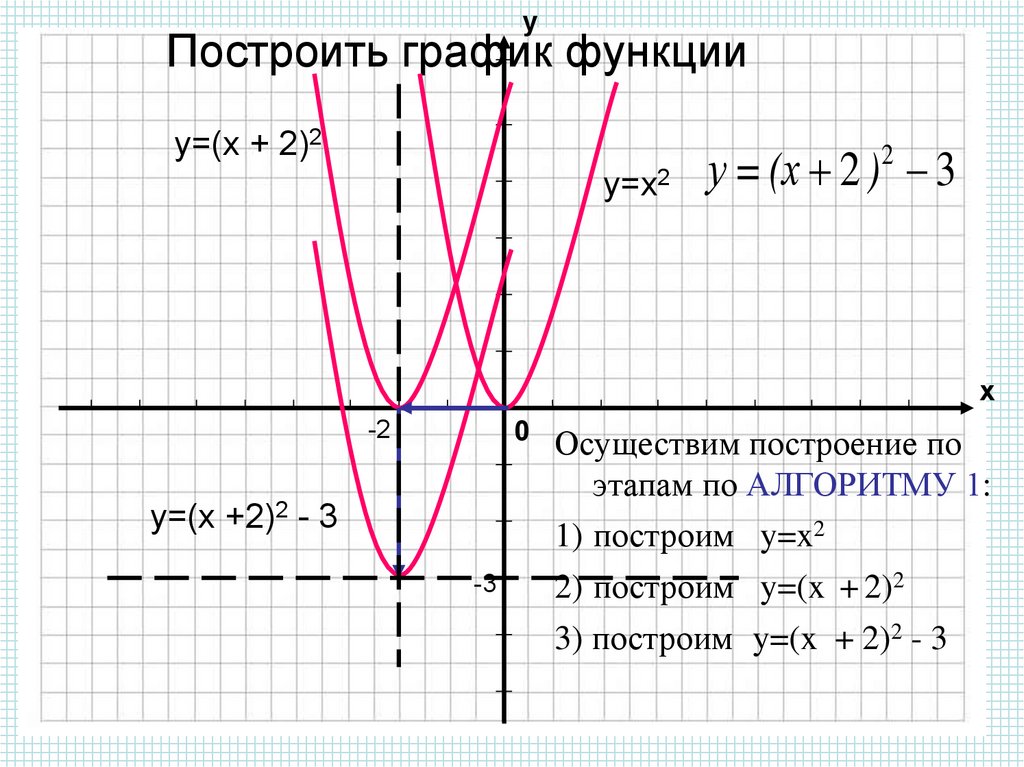
Зачем использовать агрегатные функции
Агрегированные функции позволяют обобщать или изменять степень детализации ваших данных.
Например, вы можете точно знать, сколько заказов было в вашем магазине за определенный год. Вы можете использовать функцию COUNTD, чтобы суммировать точное количество заказов, которые имела ваша компания, а затем разбить визуализацию по годам.
Расчет может выглядеть примерно так:
COUNTD(ID заказа)
Визуализация может выглядеть примерно так:
Функции агрегации, доступные в Tableau
Агрегации и арифметика с плавающей запятой : результаты некоторых агрегаций не всегда могут быть точно такими, как ожидалось. Например, вы можете обнаружить, что функция Sum возвращает значение, такое как -1,42e-14, для столбца чисел, которые, как вы знаете, должны в сумме давать ровно 0. Это происходит потому, что Институт инженеров по электротехнике и радиоэлектронике (IEEE) 754 с плавающей запятой Стандарт точки требует, чтобы числа хранились в двоичном формате, а это означает, что числа иногда округляются с чрезвычайно высокой степенью точности. Вы можете устранить это потенциальное отвлечение, используя функцию ОКРУГЛ (см. Функции чисел) или отформатировав число так, чтобы отображалось меньше знаков после запятой.
Это происходит потому, что Институт инженеров по электротехнике и радиоэлектронике (IEEE) 754 с плавающей запятой Стандарт точки требует, чтобы числа хранились в двоичном формате, а это означает, что числа иногда округляются с чрезвычайно высокой степенью точности. Вы можете устранить это потенциальное отвлечение, используя функцию ОКРУГЛ (см. Функции чисел) или отформатировав число так, чтобы отображалось меньше знаков после запятой.
Функция | Синтаксис | Определение |
АТТР | | Возвращает значение выражения, если оно имеет единственное значение для всех строк. |
СРЕДНИЙ | | Возвращает среднее значение всех значений в выражении. AVG можно использовать с числовыми полями. только. Нулевые значения игнорируются. |
СОБЕРИТЕ | | Агрегированный расчет, объединяющий значения в поле аргумента. Примечание : Функция COLLECT может использоваться только с пространственными полями. Пример: |
КОРРЕКЦИЯ | | Корреляция Пирсона измеряет линейную зависимость между двумя переменными. CORR доступен со следующими источниками данных:
Для других источников данных рассмотрите возможность извлечения данных или использования WINDOW_CORR. Примечание : Квадрат результата CORR эквивалентен значению R-квадрата для линейной модели линии тренда. См. Условия модели линии тренда. Пример: Вы можете использовать CORR для визуализации корреляции на дезагрегированном графике рассеяния. Способ сделать это — использовать выражение уровня детализации на уровне таблицы. Например: При выражении уровня детализации корреляция выполняется по всем строкам. Если вы использовали такую формулу, как См. таблицу |
СЧЕТ | | Возвращает количество предметы в группе. Нулевые значения не учитываются. |
СЧЕТ | | Возвращает число
отдельных предметов в группе. Нулевые значения не учитываются. Эта функция недоступна в следующих случаях: книги, созданные до Tableau Desktop 8.2, которые используют источники данных Microsoft Excel или текстовые файлы, книги, которые используют устаревшее соединение, и книги, которые используют источники данных Microsoft Access. Извлеките свой
данные в файл извлечения, чтобы использовать эту функцию. См. Извлечение ваших данных. Нулевые значения не учитываются. Эта функция недоступна в следующих случаях: книги, созданные до Tableau Desktop 8.2, которые используют источники данных Microsoft Excel или текстовые файлы, книги, которые используют устаревшее соединение, и книги, которые используют источники данных Microsoft Access. Извлеките свой
данные в файл извлечения, чтобы использовать эту функцию. См. Извлечение ваших данных. |
КОВАР | | Возвращает выборочную ковариацию двух выражений. Ковариация количественно определяет, как две переменные изменяются вместе. COVAR доступен со следующими источниками данных:
Для других источников данных рассмотрите возможность извлечения данных или использования WINDOW_COVAR. Пример: Следующая формула возвращает выборочную ковариацию продаж и прибыли. |
КОВАРП | | Возвращает ковариацию совокупности двух выражений. Ковариация количественно определяет, как две переменные изменяются вместе. COVARP доступен со следующими источниками данных:
Для других источников данных рассмотрите возможность извлечения данных или использования WINDOW_COVARP. Пример: Следующая формула возвращает ковариацию генеральной совокупности продаж и прибыли. |
МАКС | | Возвращает максимум из выражение во всех записях. Если выражение является строковым значением, эта функция возвращает последнее значение, где последнее определяется алфавитным заказ. |
МЕДИАНА | | Возвращает медиану
выражение во всех записях.
|
МИН | | Возвращает минимум выражение во всех записях. Если выражение является строковым значением, эта функция возвращает первое значение, где first определяется Алфавитный порядок. |
ПРОЦЕНТИЛЬ | | Возвращает значение процентиля из заданного выражения, соответствующего указанному числу. Эта функция доступна для следующих источников данных.
Для других типов источников данных вы можете извлечь данные в файл извлечения, чтобы использовать эту функцию. См. Извлечение ваших данных. |
СТАНДОТКЛОН | | Возвращает статистический
стандартное отклонение всех значений в данном выражении на основе
выборка населения. |
СТАНДОТКЛОН | | Возвращает статистический стандартное отклонение всех значений в данном выражении на основе предвзятое население. |
СУММА | | Возвращает сумму всех
значения в выражении. |
ВАР | | Возвращает статистический дисперсия всех значений в данном выражении на основе выборки населения. |
ВАРП | | Возвращает статистический
дисперсия всех значений в данном выражении на всей совокупности. |
Создание сводного расчета
Следуйте инструкциям ниже, чтобы узнать, как создать агрегатный расчет.
В Tableau Desktop подключитесь к сохраненному источнику данных Sample — Superstore , который поставляется с Tableau.
Перейдите к рабочему листу и выберите «Анализ» > «Создать вычисляемое поле».
В открывшемся редакторе расчетов выполните следующие действия:
Имя вычисляемого поля Margin.
Введите следующую формулу:
IIF(СУММ([Продажи]) !=0, СУММ([Прибыль])/СУММ([Продажи]), 0)Примечание .
 Справочник по функциям можно использовать для поиска и добавления агрегатных функций и других функций (таких как логическая функция IIF в этом примере) в формулу расчета. Дополнительные сведения см. в разделе Использование справочника функций в редакторе расчетов.
Справочник по функциям можно использовать для поиска и добавления агрегатных функций и других функций (таких как логическая функция IIF в этом примере) в формулу расчета. Дополнительные сведения см. в разделе Использование справочника функций в редакторе расчетов.Когда закончите, нажмите OK.
Новый совокупный расчет отображается в разделе Показатели на панели Данные . Как и другие ваши поля, вы можете использовать его в одной или нескольких визуализациях.
Примечание : Расчеты агрегации всегда являются мерами.
Когда Margin помещается на полку или на карточку рабочего листа, его имя изменено на AGG(Margin), что указывает, что это агрегированный расчет, и его дальнейшее агрегирование невозможно.

Правила расчета агрегатов
К расчету агрегатов применяются следующие правила:
Для любого агрегированного расчета нельзя комбинировать агрегированное значение и дезагрегированное значение. Например, SUM(Price)*[Items] не является допустимым выражением, поскольку SUM(Price) агрегируется, а Items — нет. Однако SUM(Price*Items) и SUM(Price)*SUM(Items) являются допустимыми.
Постоянные термины в выражении действуют как агрегированные или дезагрегированные значения в зависимости от ситуации. Например: СУММ(Цена*7) и СУММ(Цена)*7 являются допустимыми выражениями.
Все функции могут оцениваться по агрегированным значениям.




 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.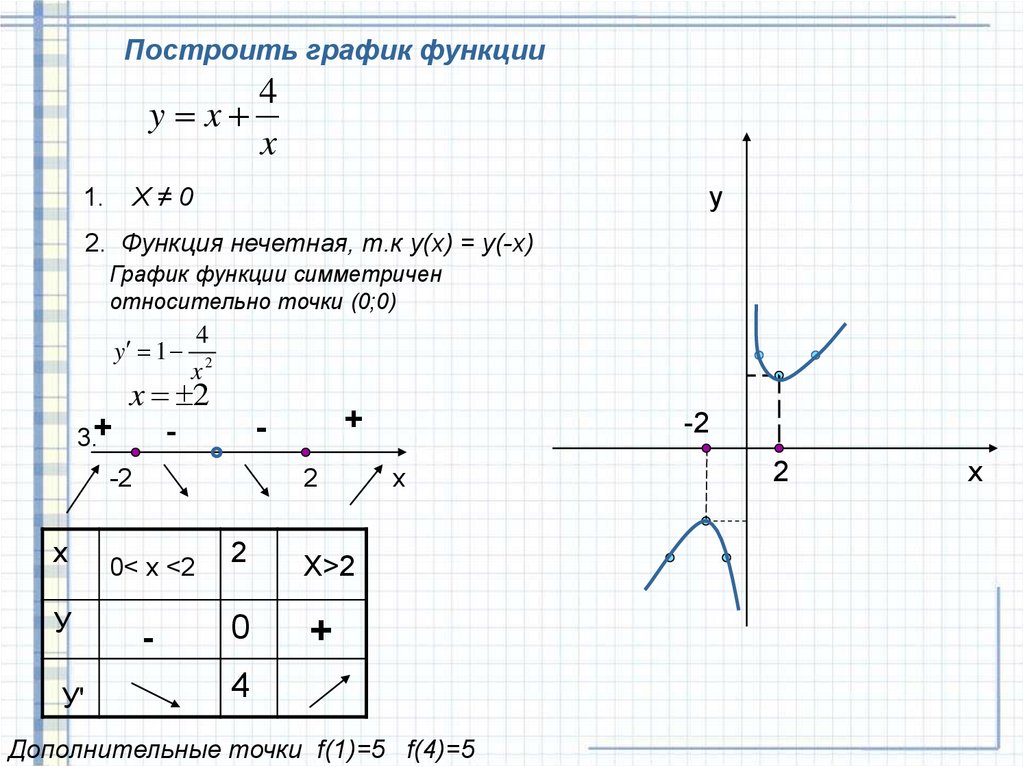

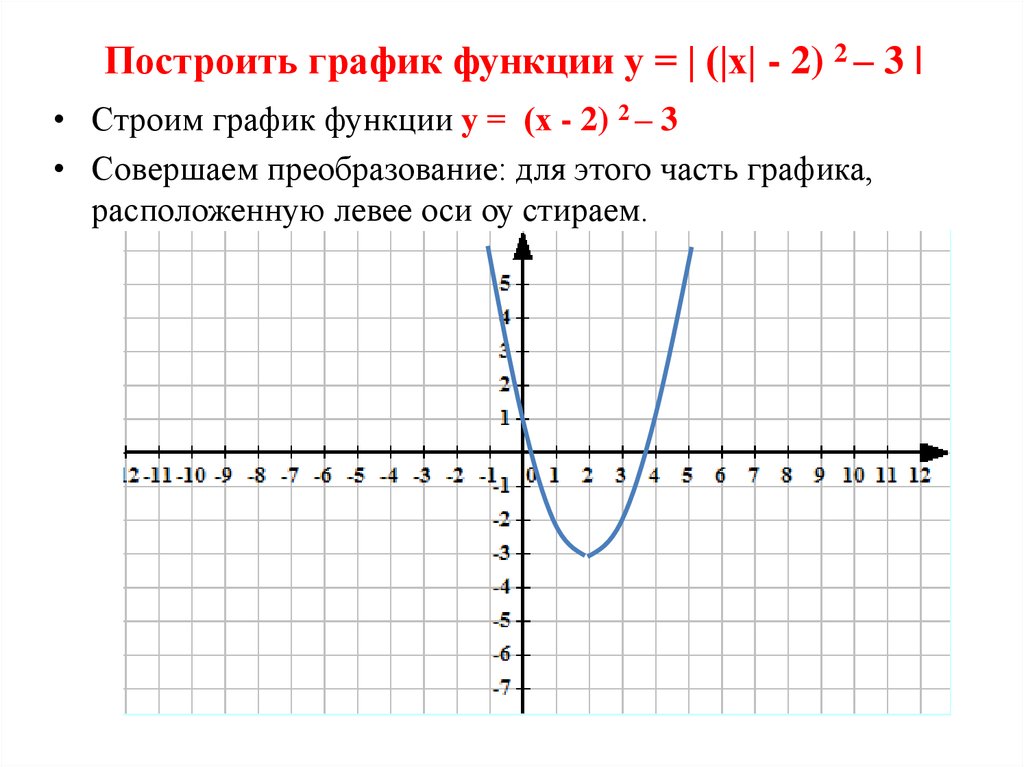 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
 Нулевые значения игнорируются.
Нулевые значения игнорируются. Результаты варьируются от -1 до +1 включительно, где 1 означает точную положительную линейную зависимость, например, когда положительное изменение одной переменной подразумевает положительное изменение соответствующей величины другой, 0 означает отсутствие линейной зависимости между дисперсией и -1 является точным отрицательным отношением.
Результаты варьируются от -1 до +1 включительно, где 1 означает точную положительную линейную зависимость, например, когда положительное изменение одной переменной подразумевает положительное изменение соответствующей величины другой, 0 означает отсутствие линейной зависимости между дисперсией и -1 является точным отрицательным отношением. См. Функции расчета таблицы.
См. Функции расчета таблицы. е. неопределенный.
е. неопределенный. Положительная ковариация указывает на то, что переменные имеют тенденцию двигаться в одном и том же направлении, например, когда большие значения одной переменной в среднем соответствуют большим значениям другой переменной. В выборочной ковариации для нормализации расчета ковариации используется количество ненулевых точек данных n – 1, а не n, которое используется ковариацией генеральной совокупности (доступно с функцией COVARP). Выборочная ковариация является подходящим выбором, когда данные представляют собой случайную выборку, которая используется для оценки ковариации для большей совокупности.
Положительная ковариация указывает на то, что переменные имеют тенденцию двигаться в одном и том же направлении, например, когда большие значения одной переменной в среднем соответствуют большим значениям другой переменной. В выборочной ковариации для нормализации расчета ковариации используется количество ненулевых точек данных n – 1, а не n, которое используется ковариацией генеральной совокупности (доступно с функцией COVARP). Выборочная ковариация является подходящим выбором, когда данные представляют собой случайную выборку, которая используется для оценки ковариации для большей совокупности.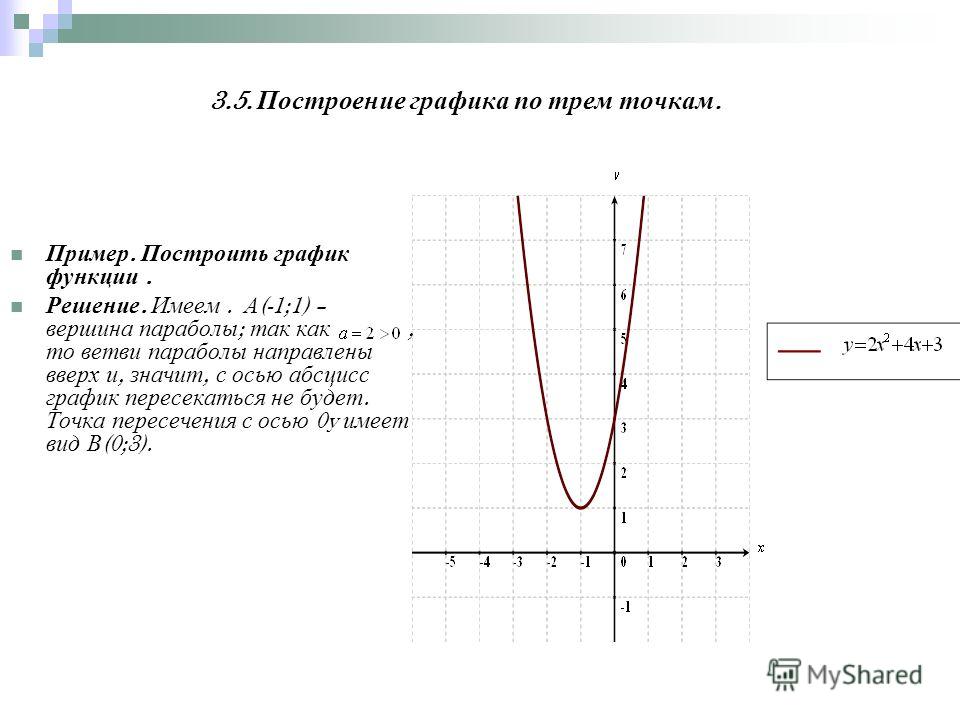 0 и выше)
0 и выше) 2.
2. Положительная ковариация указывает на то, что переменные имеют тенденцию двигаться в одном и том же направлении, например, когда большие значения одной переменной в среднем соответствуют большим значениям другой переменной. Ковариация генеральной совокупности представляет собой выборочную ковариацию, умноженную на (n-1)/n, где n — общее количество ненулевых точек данных. Ковариация генеральной совокупности является подходящим выбором, когда имеются данные по всем интересующим элементам, а не когда имеется только случайное подмножество элементов, и в этом случае уместна выборочная ковариация (с функцией COVAR).
Положительная ковариация указывает на то, что переменные имеют тенденцию двигаться в одном и том же направлении, например, когда большие значения одной переменной в среднем соответствуют большим значениям другой переменной. Ковариация генеральной совокупности представляет собой выборочную ковариацию, умноженную на (n-1)/n, где n — общее количество ненулевых точек данных. Ковариация генеральной совокупности является подходящим выбором, когда имеются данные по всем интересующим элементам, а не когда имеется только случайное подмножество элементов, и в этом случае уместна выборочная ковариация (с функцией COVAR).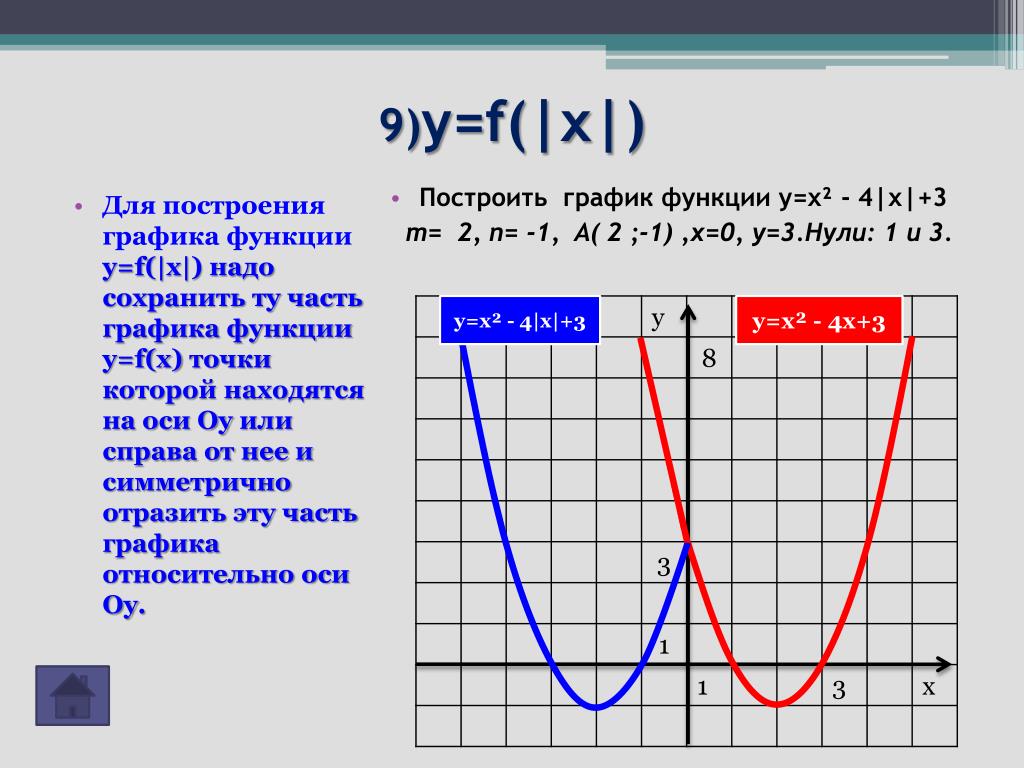 0 и выше)
0 и выше) 2.
2. Медиану можно использовать только с числовыми полями. Нулевые значения игнорируются. Эта функция недоступна для книг, созданных до Tableau Desktop 8.2 или использующих устаревшие подключения. Он также недоступен для соединений, использующих любой из следующих источников данных:
Медиану можно использовать только с числовыми полями. Нулевые значения игнорируются. Эта функция недоступна для книг, созданных до Tableau Desktop 8.2 или использующих устаревшие подключения. Он также недоступен для соединений, использующих любой из следующих источников данных: Число должно находиться в диапазоне от 0 до 1 (включительно), например 0,66, и должно быть числовой константой.
Число должно находиться в диапазоне от 0 до 1 (включительно), например 0,66, и должно быть числовой константой.
 SUM можно использовать только с числовыми полями. Нулевой
значения игнорируются.
SUM можно использовать только с числовыми полями. Нулевой
значения игнорируются.
 Справочник по функциям можно использовать для поиска и добавления агрегатных функций и других функций (таких как логическая функция IIF в этом примере) в формулу расчета. Дополнительные сведения см. в разделе Использование справочника функций в редакторе расчетов.
Справочник по функциям можно использовать для поиска и добавления агрегатных функций и других функций (таких как логическая функция IIF в этом примере) в формулу расчета. Дополнительные сведения см. в разделе Использование справочника функций в редакторе расчетов.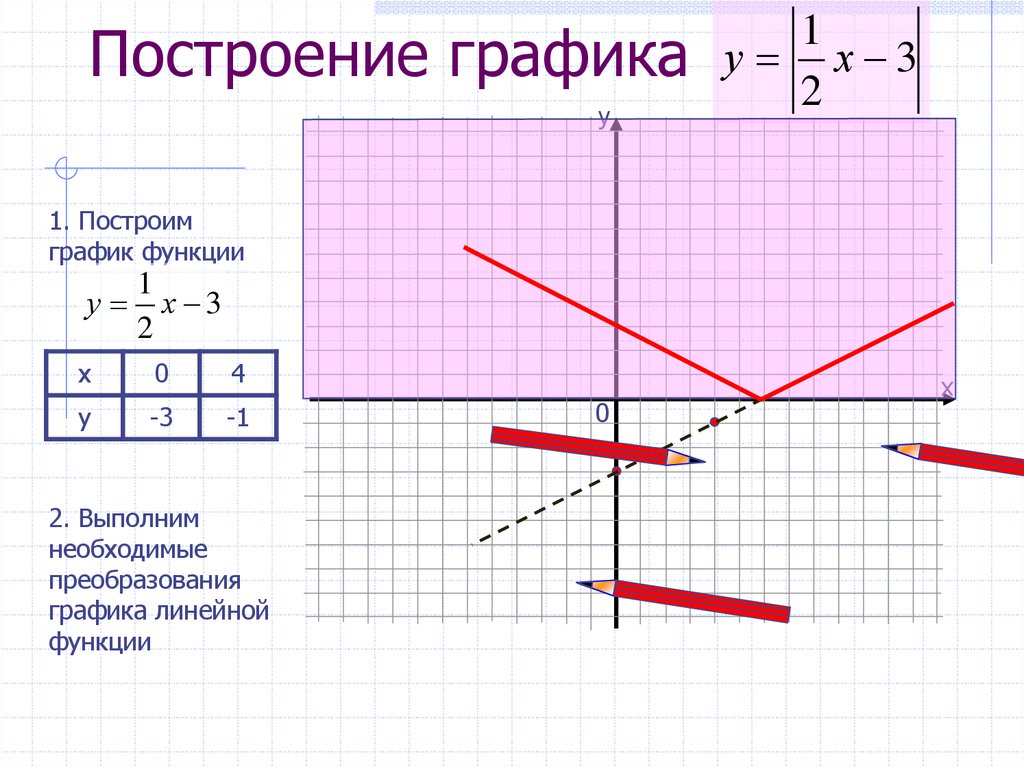
Ваш комментарий будет первым