Построение графиков со смещением: Смещение графиков функций. Изменение графиков функций.

Содержание

Смещение графика квадратичной функции y = (x

Дедерер Светлана Александровна, учитель математики

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (806 кБ)

Цели урока:

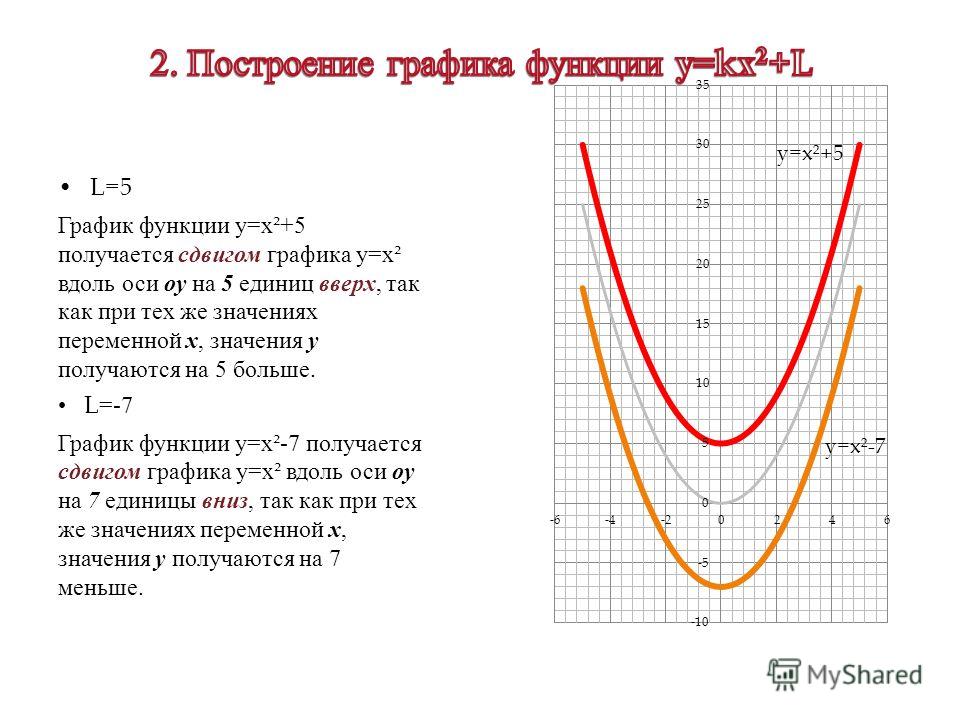
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c_.

Воспитательная: умение работать в группе, организованности.

Развивающая: навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.

Структура урока

Организационный момент – 3 минуты.
Исследовательская работа – 20 минут.
Закрепление изученного материала – 15 минут.
Рефлексия – 2 минут.
Итог урока – 3 минуты.
Домашнее задание – 2 минуты.

Ход урока

1. Организационный момент.

Цель урока провести исследовательскую работу. Объектом исследования будут квадратичные функции разного вида. Вам предстоит определить, как влияют коэффициенты b, c_{на график
функций вида y=x²+с, y=(x-b)², y=(x-b)²+c.}

Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).

Каждая группа получает план исследования <Приложение>, лист формата А3 для оформления результатов.

2. Исследовательская работа
.

Две группы (уровень А) исследуют функции вида y= x²+с, одна группа (уровень В) исследует функцию вида y=(x-b)², одна группа (уровень С) исследует функцию y=(x-b)²+c. Группа “Экспертов” исследует все функции.

	Функция	Результат
1 группа	у=x²+3;	<Рисунок 10>
2 группа	у=x²-5;	<Рисунок 11>
3 группа	у=(х-4)²;	<Рисунок 12>
4 группа	у=(х-2)²+3.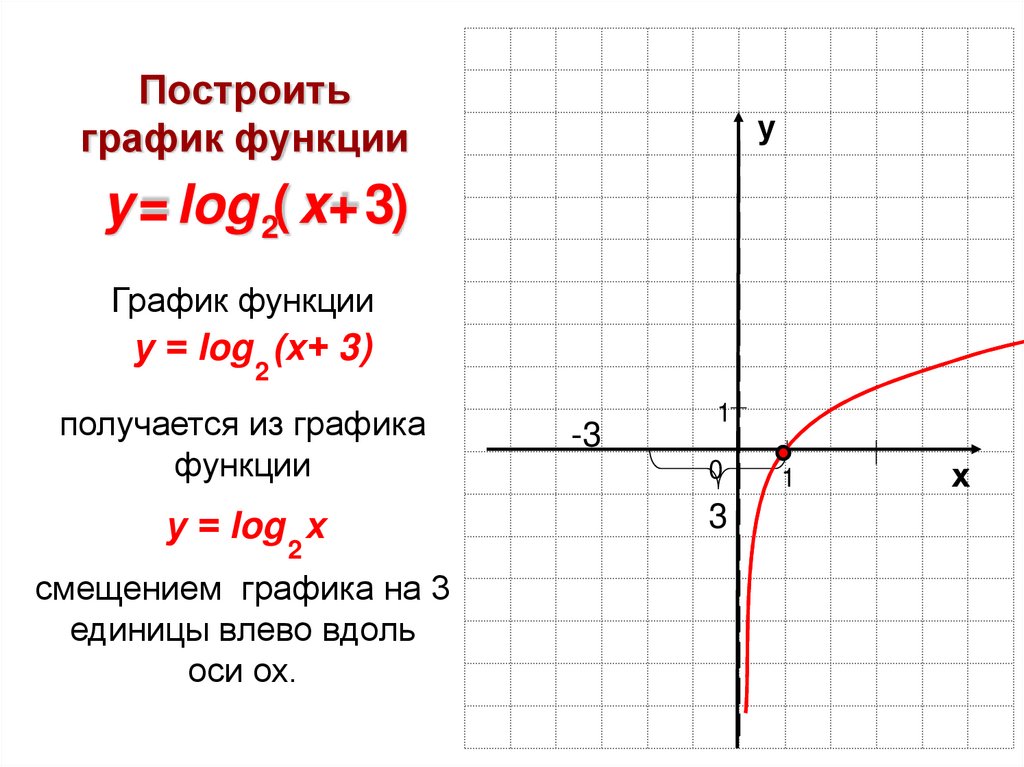	<Рисунок 13>

План работы

Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
Постройте график исследуемых функций (определите вершину параболы (х₀, y₀), задайте таблицей 4 точки).
Сравните получившийся график с контрольным образцом y=x².
Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).

Результаты оформите на листе формата А3 и представьте “экспертной” группе.

“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.

Сверка полученных результатов со слайдами №2-5.

Любую квадратичную функцию y=ax²+bx+c, можно записать в виде y=a(x-x₀)²+y_0,где x₀и y₀ выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x₀, c=y₀ являются координатами вершины параболы.

3. Закрепление изученного материала.

Фронтальная работа с классом.

1. Найти ошибку в графиках функций

(Слайды№6-9).

y=(х+6)²	у=х²-2
Коэффициент b	Нет ошибки
Рисунок 1	Рисунок 2

у=(х+5)²-1	у=(х-2)²+2
Коэффициент b и с	Коэффициент b
Рисунок 3	Рисунок 4

Результаты

<Рисунок 7>

<Рисунок 2>

<Рисунок 8>

<Рисунок 9>

Какой коэффициент вам помог найти ошибку?

2. Соотнесите графики функций согласно цветам (слайд №10).

Рисунок 5

y=(х-4)²-2	синий
y=-x²+5	красный
y=(x+1)²+3	зеленый
y=(x-3)²	фиолетовый

4. Рефлексия.

Группа “Экспертов” отвечают на вопросы:

– Какие ошибки допустили группы?

– Достигнута ли цель занятия?

– Соответствуют ли полученные результаты исследования поставленной гипотезе?

5. Итог урока (слайд №11)
:

На положение графика функции y=(x-b)²+c влияют коэффициенты b и c,

“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,

“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,

“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,

“-с” парабола сдвинута вниз по оси ординат на с единичных отрезков.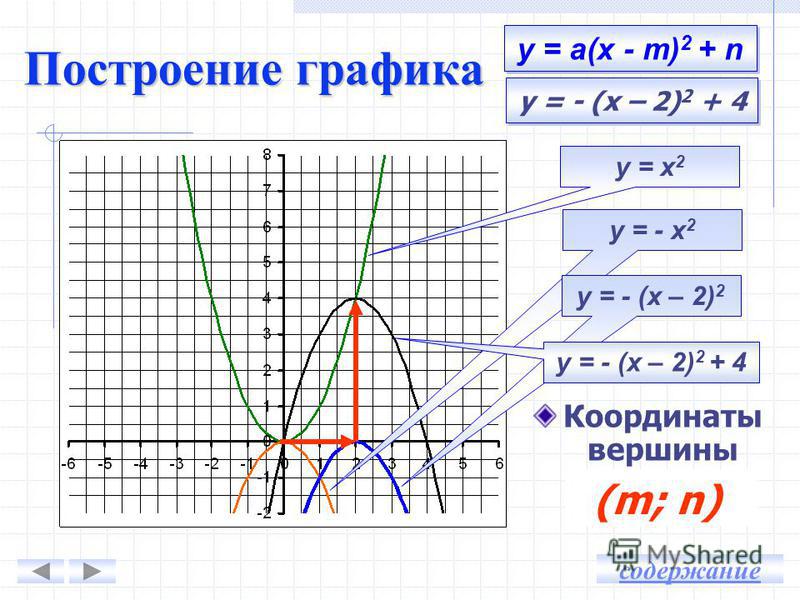

6. Домашнее задание

Построить график квадратичной функции, имеющую вершину в точке А(1;-2), коэффициент a=1.
Подумайте, в какой области можно использовать знания по данной теме (практическое применение).

Приложение

7.01.2012

растяжение и сжатие, параллельный перенос, общее уравнение синусоиды, тангенцоиды

Растяжение и сжатие графиков тригонометрических функций по оси OX
Растяжение и сжатие графиков тригонометрических функций по оси OY
Параллельный перенос графиков тригонометрических функций по оси OX
Параллельный перенос графиков тригонометрических функций по оси OY
Общее уравнение синусоиды
Общее уравнение тангенцоиды
Примеры

Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.

п.1. Растяжение и сжатие графиков тригонометрических функций по оси

Общие принципы растяжения и сжатия графиков по оси

OX:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π. Получаем следствие общих принципов:

При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ период второй функции уменьшается в p раз: $$ T_2=\frac{T_1}{p} $$

При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$

Например:

Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin2x,\ \ h(x)=sin\frac{x}{2} $$
Период колебаний функции $g(x)=sin2x$ в 2 раза меньше: $T_g=\frac{2\pi}{2}=\pi$.
Период колебаний функции $h(x)=sin\frac{x}{2}$ в 2 раза больше: $T_h=2\cdot 2\pi=4\pi$.

п.2. Растяжение и сжатие графиков тригонометрических функций по оси

Общие принципы растяжения и сжатия графиков по оси OY:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=Af(x),\ \ A\gt 1 $$ график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.

Общий принцип сжатия графиков:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=\frac{1}{A}f(x),\ \ A\gt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:

умножение на параметр $A\gt 1$ увеличивает амплитуду колебаний в $A$ раз;
деление на параметр $A\gt 1$ уменьшает амплитуду колебаний в $A$ раз.

Например:

1) Построим в одной системе координат три графика: $$ f(x)=cosx,\ \ g(x)=2cosx,\ \ h(x)=\frac{1}{2}cosx $$
Умножение на $A=2$ увеличивает амплитуду колебаний в 2 раза.
Область значений функции $g(x)=2cosx:\ y\in[-2;2]$. График растягивается по оси OY.
Деление на $A=2$ уменьшает амплитуду колебаний в 2 раза. Область значений функции $h(x)=\frac12 cosx:\ y\in\left[-\frac12; \frac12\right]$. График сжимается по оси OY.

2) Теперь построим $$ f(x)=tgx,\ \ g(x)=2tgx,\ \ h(x)=\frac{1}{2}tgx $$
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на $A=2$ служит поведение функции при $x=\frac\pi4$. $$ f\left(\frac\pi4\right)=tg\left(\frac\pi4\right)=1,\ \ g\left(\frac\pi4\right)=2tg\left(\frac\pi4\right)=2,\ \ h\left(\frac\pi4\right)=\frac12 tg\left(\frac\pi4\right)=\frac12 $$ Аналогично – для любого другого значения аргумента x.

п.3. Параллельный перенос графиков тригонометрических функций по оси

Общие принципы переноса по оси OX:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x+a),\ \ a\gt 0 $$ график второй функции смещается влево на a по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x-a),\ \ a\gt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций $y_1=f(x)$ и $y_2=f(x\pm a)$ говорят, что у второй функции сдвиг по фазе равен $\pm a$.

Например:

1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin\left(x+\frac\pi4\right),\ \ h(x)=sin\left(x-\frac\pi4\right) $$
Функция $g(x)=sin\left(x+\frac\pi4\right)$ сдвинута на $\frac\pi4$ влево по сравнению с $f(x)$
Функция $h(x)=sin\left(x-\frac\pi4\right)$ сдвинута на $\frac\pi4$ вправо по сравнению с $f(x)$

п.4. Параллельный перенос графиков тригонометрических функций по оси

Общие принципы переноса по оси OY:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)+a,\ \ a\gt 0 $$ график второй функции смещается вверх на a по оси OY по сравнению с графиком первой функции.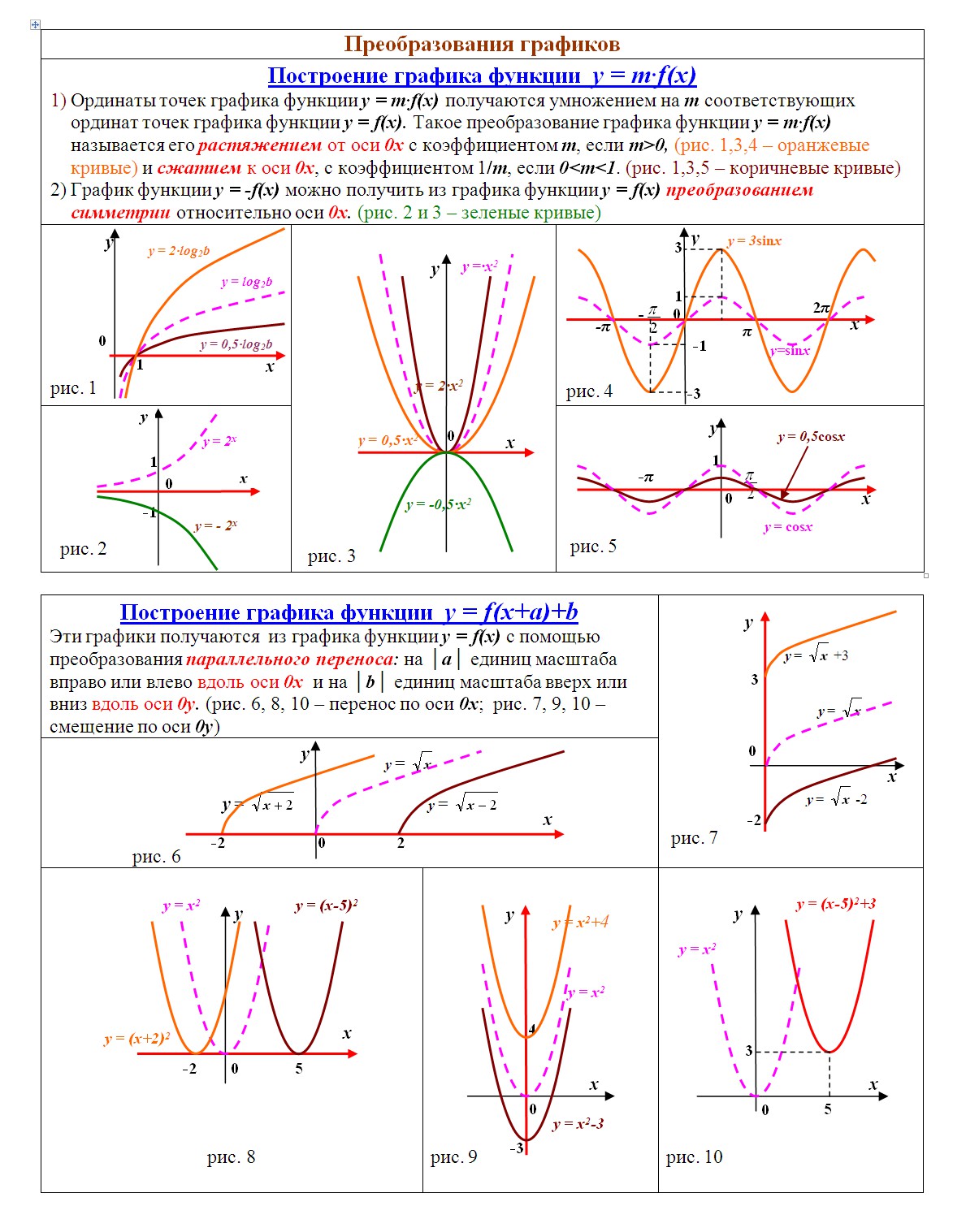

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)-a,\ \ a\gt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.

Например:

1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sinx+1,\ \ h(x)=sinx-1 $$
Функция $g(x)=sinx+1$ сдвинута на 1 вверх по сравнению c $f(x)$
Функция $h(x)=sinx-1$ сдвинута на 1 вниз по сравнению с $f(x)$

п.5. Общее уравнение синусоиды

Синусоида – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)

График $y(x)=Acos(cx+d)+B$ также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.

Например:

Построим график $g(x)=3sin\left(2x+\frac\pi2\right)-1$
По сравнению с $f(x)=sinx$:

$A=3$ — график растянут по оси OY в 3 раза
$c=2$ — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
$d=\frac\pi2$ – начальная фаза положительная, график сдвинут на $\frac{\pi}{2\cdot 2}=\frac\pi4$ влево
$B=-1$ — график сдвинут по оси OY на 1 вниз

п.6. Общее уравнение тангенцоиды

Tангенцоидa – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)

График $y(x)=Actg(cx+d)+B$ также называют тангенцоидой.

Например:

Построим график $g(x)=\frac12 tg\left(\frac{x}{2}-\frac\pi3\right)+1$
По сравнению с $f(x)=tgx$:

$A=\frac12$ — график сжат по оси OY в 2 раза
$c=\frac12$ — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
$d=-\frac\pi3$ – начальная фаза отрицательная, график сдвинут на $\frac{\pi}{3\cdot 1/2}=\frac{2\pi}{4}$ вправо
$B=1$ — график сдвинут по оси OY на 1 вверх

п.7. Примеры

Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx,\ \ g(x)=-sinx,\ \ h(x)=cosx $$ Найдите сдвиг по фазе для $g(x)$ и $h(x)$ в сравнении с $f(x)$.

Сдвиг по фазе удобно определять по главной арке синусоиды.
Для $f(x)=sin⁡x$ главная арка определена на отрезке $0\leq x\leq \pi$
Для $g(x)=-sin⁡x$ главная арка определена на отрезке $-\pi\leq x\leq 0$, т.е. сдвинута на π влево от $f(x)$. Это означает, что: $$ f(x)=g(x+\pi),\ \ sin⁡x=-sin⁡(x+\pi) $$ Для $h(x)=cos⁡x$ главная арка определена на отрезке $-\frac\pi2\leq x\leq \frac\pi2$, т.е. сдвинута на $\frac\pi2$ влево от $f(x)$. Это означает, что: $$ f(x)=h\left(x+\frac\pi2\right),\ \ sinx=cos\left(x+\frac\pi2\right) $$

Пример 2. Найдите наименьшие положительные периоды функций:
a) $y=sin5x$
Период синуса $2\pi$ уменьшается в 5 раз. Получаем: $T=\frac{2\pi}{5}$

б) $y=cos\pi x$
Период косинуса $2\pi$ уменьшается в $\pi$ раз. Получаем: $T=\frac{2\pi}{\pi}=2$

в) $y=tg\frac{x}{4}$
Период тангенса $\pi$ увеличивается в 4 раза. Получаем: $T=4\pi$

г) $y=tg\left(2x+\frac{\pi}{3}\right)$
Период тангенса $\pi$ уменьшается в 2 раза. Получаем: $T=\frac\pi2$

Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctg\left(3x+\frac\pi6\right) $$ По сравнению с $g(x)=tg⁡x$:

$A=2$ — график растянут по оси OY в 2 раза
$c=3$ — период меньше в 3 раза $T=\frac\pi3$, расстояние между асимптотами $\frac\pi3$, график сжат в 3 раза по оси OX
$d=-\frac\pi6$ – начальная фаза положительная, график сдвинут на $\frac{\pi}{6\cdot 3}=\frac{\pi}{18}$ влево

Расположение нулей: $$ tg\left(3x+\frac\pi6\right)=0\Rightarrow 3x+\frac\pi6=\pi k\Rightarrow 3x=-\frac\pi6+\pi k\Rightarrow x =-\frac{\pi}{18}+\frac{\pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.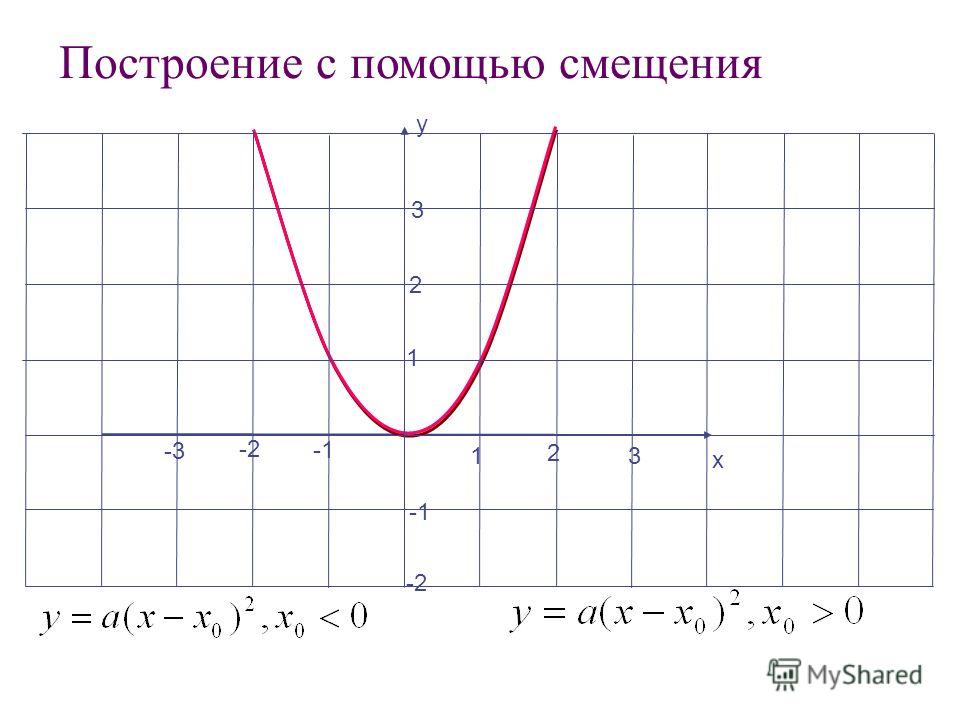
Расположение асимптот: $$ 3x+\frac\pi6\ne\frac\pi2+\pi k\Rightarrow 3x\ne\frac\pi3+\pi k\Rightarrow x\ne\frac\pi9+\frac{\pi k}{3} $$ Пересечение главной ветви с осью OY: $x=0,\ y=2tg\frac\pi6=\frac{2}{\sqrt{3}}$
С учетом периода $\frac\pi3$ получаем семейство дополнительных точек для построения графика $\left(\frac{\pi k}{3}; \frac{2}{\sqrt{3}}\right)$.

Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) $sinx=sin2x$ при $0\leq x\leq 3\pi$

Ответ: 7 корней

б) $cos\frac{x}{2}=cos2x$ при $-2\pi\leq x\leq 2\pi$

Ответ: 7 корней

python — Как построить несколько кривых со смещением на одном графике

Задавать вопрос

спросил 5 лет, 7 месяцев назад

Изменено 2 года, 11 месяцев назад

Просмотрено 7к раз

Я считываю сигнал с осциллографа. Форма волны разделена на 10 сегментов в зависимости от времени. Я хочу построить полную форму волны, один сегмент выше (или ниже) другого, так сказать, «с вертикальным смещением». Кроме того, цветовая карта необходима для отображения интенсивности сигнала. Я смог получить только следующий сюжет:

Как видите, все кривые накладываются друг на друга, что недопустимо. Можно было бы добавить смещение к данным y, но это не то, как я хотел бы это сделать. Наверняка есть более аккуратный способ отображения моих данных? Я пробовал несколько вещей, чтобы решить эту проблему с помощью pylab, но я даже не уверен, как действовать и правильно ли это.

Будем признательны за любую помощь.

 import readTrc #помогает считывать двоичные данные с осциллографа
импортировать matplotlib.pyplot как plt
fName = r"...trc"
datX, datY, m = readTrc.readTrc(fName)
segments = m['SUBARRAY_COUNT'] # количество сегментов
х, у = [], []
для i в диапазоне (сегменты + 1):
    x.append(datX[сегменты*i:сегменты*(i+1)])
    y. append(datY[сегменты*i:сегменты*(i+1)])
plt.plot(x,y)
plt.show()

питон
матплотлиб

График с смещением по вертикали звучит как частотный след.

Вот один из подходов, при котором делает просто корректировкой значения y.

Частотный след в MatPlotLib

Тот же самый график был также придуман как график радости/хребта. У Seaborn есть реализация, которая создает серию графиков (FacetGrid), а затем регулирует смещение между ними для получения аналогичного эффекта.

https://seaborn.pydata.org/examples/kde_joyplot.html

Пример использования линейного графика может выглядеть так:

 импортировать Seaborn как sns
импортировать matplotlib.pyplot как plt
импортировать numpy как np
импортировать панд как pd
сегменты = 10
точек_за_сегмент = 100
#ваша подготовка данных будет отличаться
x = np.tile (np.arange (points_per_segment), сегменты)
z = np.floor(np. arange(points_per_segment * segments)/points_per_segment)
у = np.sin (х * (1 + г))
        
    
df = pd.DataFrame({'x': x, 'y': y, 'z': z})
приятель = sns.color_palette()
g = sns.FacetGrid(df, row="z", hue="z", аспект=15, высота=0,5, палитра=pal)
g.map (plt.plot, 'х', 'у')
g.map(plt.axhline, y=0, lw=2, clip_on=False)
# Установите подграфики так, чтобы они перекрывались
g.fig.subplots_adjust(hspace=-.00)
g.set_titles("")
g.set(yticks=[])
g.despine (внизу = Истина, слева = Истина)
plt.show()

Исходящий:

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.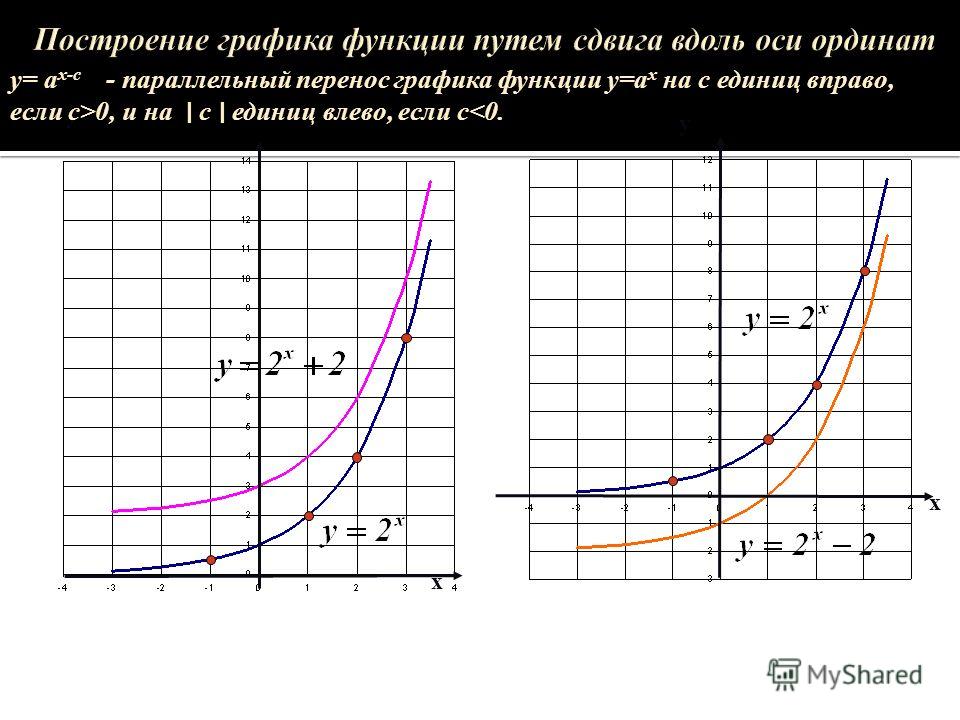

python — Как сместить ось x при построении линейного графика в matlibplot

спросил 3 года 11 месяцев назад

Изменено 3 года, 11 месяцев назад

Просмотрено 640 раз

Я пытаюсь построить график зависимости количества признаков от дисперсии для PCA. Я хотел бы выделить, когда дисперсия> 95% с использованием цвета линии

Пока у меня есть следующий код..

 pcaPlotData = {
    'r':var[np.argwhere(var < 95)],
    'g': var[np.argwhere(var >= 95)]
}
рис, топор = plt.subplots()
для k, v в pcaPlotData.items():
    ax.plot (v, цвет = k)
ax.set_ylabel('% объясненной дисперсии')
ax.set_xlabel('Количество объектов')
ax.set_title('Анализ PCA')
ax.set_ylim (var. min(), var.max()+1)
plt.show()

, который выводит следующий график:

Однако зеленая линия должна начинаться, когда заканчивается красная линия, как мне сместить зеленую линию?

питон
matplotlib

Если входными данными являются массивы NumPy, альтернативное решение может выглядеть следующим образом. Здесь вы создаете условную маску , а затем используете ~маска для доступа к элементам, которые не удовлетворяют условию. Это избавит вас от необходимости создавать маску дважды.

Ниже приведен полный исполняемый пример:

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
х = np.arange (40)
переменная = х**2
# Определяем условную маску
маска = (var<95)
plt.plot(x[маска], var[маска], 'r') # Данные, удовлетворяющие условию
plt.plot(x[~mask], var[~mask], 'g') # Данные не удовлетворяют условию
plt.show()

Просто это:

 x = np. argwhere(var < 95)
ax.plot(x, var[x], 'r')
х = np.arg, где (вар> = 95)
ax.plot(x, var[x], 'g')

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Смещение графика квадратичной функции y = (x

Презентация к уроку

Ход урока

1. Организационный момент.

2. Исследовательская работа

3. Закрепление изученного материала.

4. Рефлексия.

5. Итог урока (слайд №11)

6. Домашнее задание

растяжение и сжатие, параллельный перенос, общее уравнение синусоиды, тангенцоиды

п.1. Растяжение и сжатие графиков тригонометрических функций по оси

п.2. Растяжение и сжатие графиков тригонометрических функций по оси

п.3. Параллельный перенос графиков тригонометрических функций по оси

п.4. Параллельный перенос графиков тригонометрических функций по оси

п.5. Общее уравнение синусоиды

п.6. Общее уравнение тангенцоиды

п.7. Примеры

python — Как построить несколько кривых со смещением на одном графике

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

python — Как сместить ось x при построении линейного графика в matlibplot

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Ваш комментарий будет первым

Добавить комментарий Отменить ответ