Построение графиков функций с помощью графической системы Desmos.Com/Calculator — Математика — Каталог статей
Графики функций — одна из основных тем школьного курса алгебры. Умение строить графики как по точкам, так и с помощью геометрических преобразований является обязательным для каждого ученика средней школы.
В данной статье пойдет речь о том, как учителю с помощью компьютера и сети Интернет облегчить ученикам задачу восприятия материала, связанного с графиками функций в любом классе.
Содержание
«Графический калькулятор» Desmos
Рис.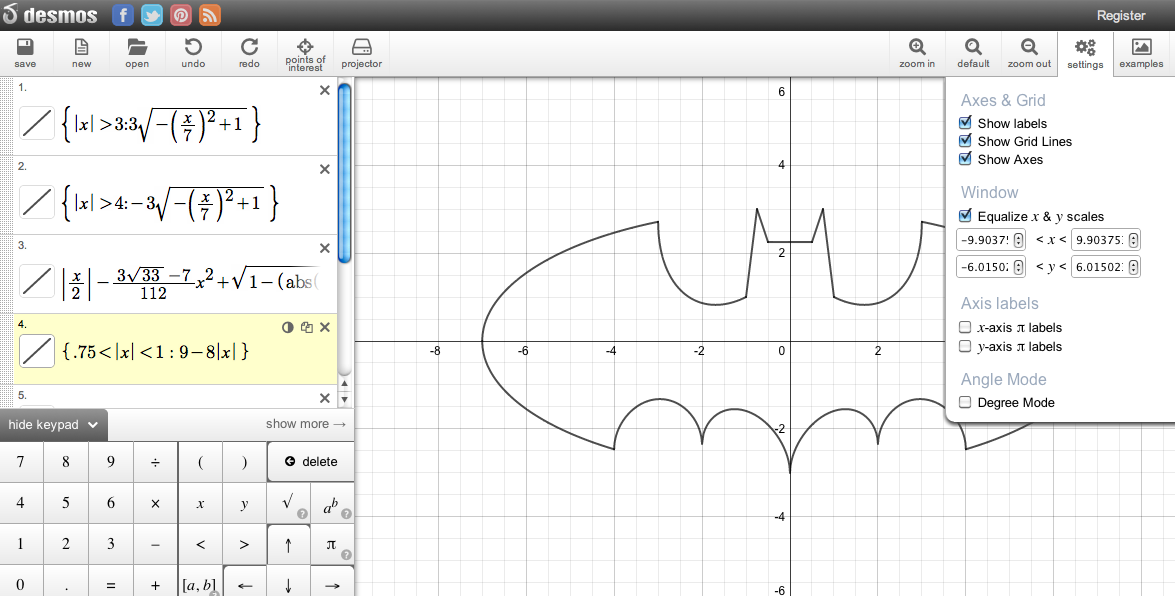
Нажав на большую зеленую кнопку Start Fresh, можно строить график «с чистого листа». Если Вы нажмете на один из трех квадратиков ниже, Вы сможете просмотреть пример построения графиков функций, изображенных на них.
Внимание! Для того, чтобы система у Вас запустилась и работала, необходимо, чтобы FlashPlayer был установлен в качестве плагина к Вашему браузеру. Иначе просто появится надпись «Flash Required» с иконкой Adobe Flash.
После нажатия Start Fresh окно графического калькулятора будет выглядеть так:
Рис. 2. Окно системы Desmos для построения графиков функций
Окно будет содержать в верхней части кнопки Undo (отменить последнее действие), Redo (повторить последнее действие), Clear (очистить все графики), Save and share
(сохранить и опубликовать), Examples (примеры), Graph Settings (графические настройки).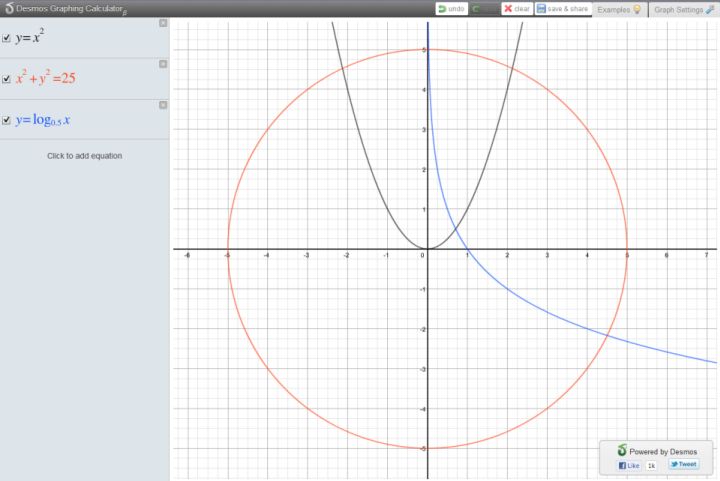
В правой части находится панель для ввода уравнений (функций), графики которых будут построены затем в области построения (то бишь на координатной плоскости). Область построения занимает большую часть экрана.
Чтобы изменить масштаб области построения, просто установите на нее курсор мыши, а затем подвигайте колесиком в ту или иную сторону.
Чтобы переместить область построения, просто захватите ее мышью и протащите.
Построение графика функции
1. Вставлять уравнение в поле ввода не получится. Можно только вводить вручную.
2. Символы y, x и другие должны набираться в английской раскладке клавиатуры. Вообще, данная система построения графиков англоязычная, но она очень проста для понимания.
3. (комбинация клавиш Shift+6). Курсор автоматически перейдет в верхний регистр.
(комбинация клавиш Shift+6). Курсор автоматически перейдет в верхний регистр.
Чтобы ввести основание логарифма (например, функцию y=log0.5x), введите символ «_» (подчеркивания). Курсор автоматически перейдет в нижний регистр.
Чтобы ввести модуль, используйте символ | (как обычно).
Вот пример построенных графиков функций и уравнений в системе Desmos:
Рис. 3. Примеры построенных графиков в системе Desmos
Точки экстремума и нули функции
Если просто навести мышью на любую точку уже построенного графика, то высветятся ее координаты. А к точкам экстремума и нулям функции курсор мышки вообще «примагничивается»:
Рис. 4. Точка максимума функции y=sin x (на нее навели мышкой)
Внимание! Для того, чтобы при наведении мыши на график показывались координаты точек, этот самый график нужно предварительно выделить, то есть просто щелкнуть мышью по самой линии графика.
Демонстрация геометрических преобразований
графиков функций
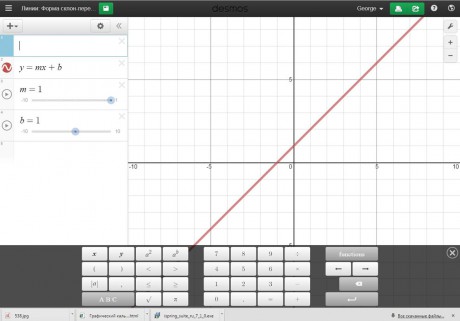
Система Desmos позволяет строить графики функций, которые содержат параметр. Например, можно в поле ввода ввести примерно следующее: y=(x — a)2. Вместо а может стоять любая буква, и функция может содержать несколько параметров, например,
Рис. 5. Построение графика функции с параметром
Как же можно демонстрировать геометрические преобразования графиков? Дело в том, что значение параметра а можно изменять. Если присмотреться, то снизу надписи «а=5» появляется ползунок под названием «adjust a«:
Если присмотреться, то снизу надписи «а=5» появляется ползунок под названием «adjust a«:
Рис. 6. Изменение параметра
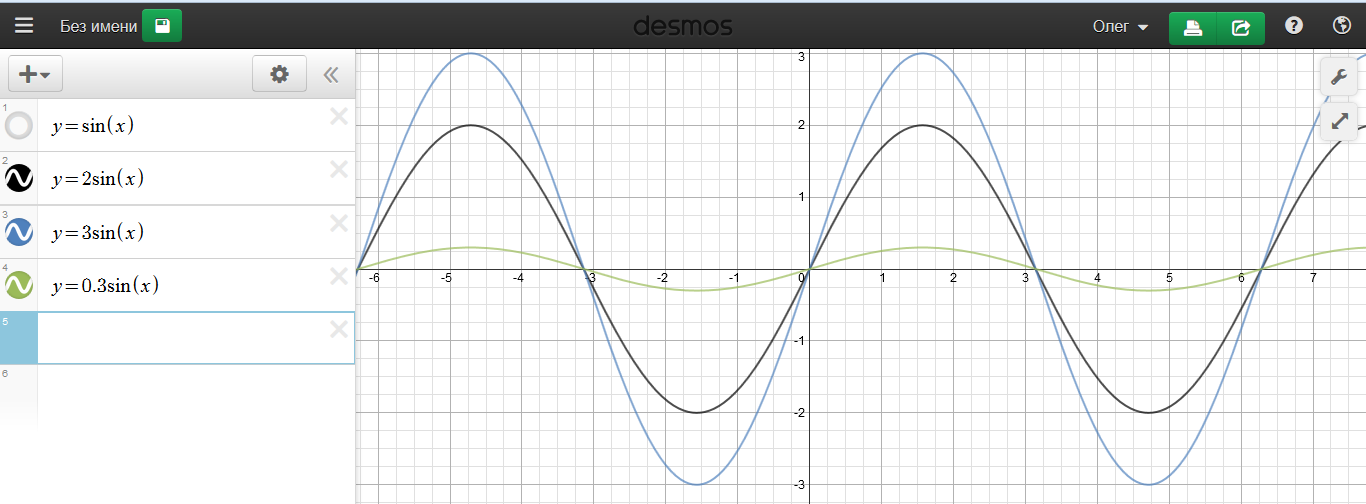
Так вот, если плавно перемещать ползунок в любую сторону, то график функции, уже построенный в координатной плоскости, начнет перемещаться вместе с ним (попробуйте!) Это дает возможность наглядной демонстрации различных геометрических преобразований графиков (особенно в сочетании с различными цветами):
Рис.7. Демонстрация геометрических преобразований
Таким образом можно продемонстрировать геометрические преобразования графиков любых функций школьного курса математики.
Как отметить точки и построить график по точкам
Чтобы отметить точку на координатной плоскости, можно просто ввести ее координаты x и y в скобках через запятую.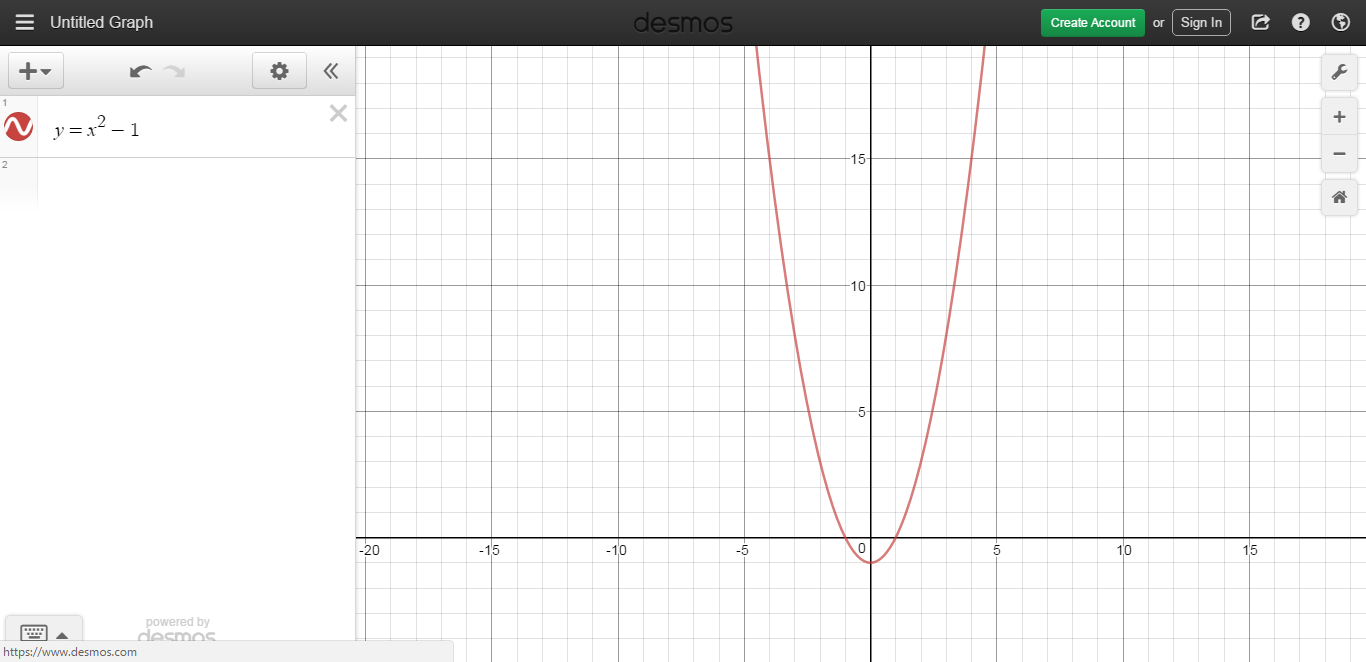 В одном поле ввода можно ввести несколько точек. Вот пример того, как можно построить график функции y=sqrt(x)
В одном поле ввода можно ввести несколько точек. Вот пример того, как можно построить график функции y=sqrt(x)
Рис. 8. Пример того, как можно отметить точки на координатной плоскости
Можно сказать, что данный пример иллюстрирует возможность имитации процесса построения графика на бумаге: сначала нанесли точки, а затем только провели график.
Кстати, чтобы ввести символ квадратного корня, нужно просто набрать комбинацию sqrt(
А можно просто возвести нужное число в степень 0,5.
Сохранение результатов в файл и в виде ссылки
Система позволяет сохранять построенный график функции в виде графического файла. Вы можете, например, вставить его в свою презентацию или распечатать в качестве раздаточного материала, если не имеете возможности посадить учеников за компьютеры.
 Внимание! В некоторых браузерах может наблюдаться «глюк», во избежание которого нажимать надо не на надпись «save & share», а на изображение дискеты.
Внимание! В некоторых браузерах может наблюдаться «глюк», во избежание которого нажимать надо не на надпись «save & share», а на изображение дискеты. При нажатии кнопки может появиться ошибка сохранения (timeout). Всё-таки графический калькулятор находится на этапе тестирования. В этом случае — ничего не поделаешь — график сохранить можно только с помощью снимка экрана (то бишь кнопочкой PrintScreen).
Если же ошибки не возникло, то появится такое окно:
Рис. 9. Окно сохранения построенного графика функции в Desmos
С помощью этого окна Вы можете:
1) поделиться Вашим графиком функции в Facebook или Twitter (кнопки Like, Send, Tweet)
3) сохранить график функции в виде картинки (для этого нажмите на самую нижнюю ссылку Save graph as image (opens in a new a window), см. рис. 9). Откроется новое окно, в котором отобразится только график построенной Вами функции. Щелкнув правой кнопкой по картинке, можно выбрать команду «Сохранить изображение» (в зависимости от того, каким браузером Вы пользуетесь, название этой команды может отличаться):
рис. 9). Откроется новое окно, в котором отобразится только график построенной Вами функции. Щелкнув правой кнопкой по картинке, можно выбрать команду «Сохранить изображение» (в зависимости от того, каким браузером Вы пользуетесь, название этой команды может отличаться):
Рис. 10. Сохранение графиков функций в виде графического файла
Таким способом можно делиться ссылками на свои графики, сохранять свои файлы с графиками функций, а также проверять работы учеников (например, ученик может на компьютере построить график и сдать Вам либо ссылку на него, либо распечатанный график, либо график функции в электронном виде).
Встроенные примеры построения графиков
 Ниже приводится перевод на русский язык почти всей панели Examples:
Ниже приводится перевод на русский язык почти всей панели Examples:Рис. 11. Панель Examples системы построения графиков Desmos
Рекомендую ознакомиться с панелью Examples и посмотреть примеры построения графиков функций перед началом использования системы для преподавания в учебном заведении.
Графические настройки
Рис. 12. Панель графических настроек системы Desmos.Com
С графическими настройками разобраться в принципе нетрудно, но необходимо прежде, чем использовать Desmos на уроках для демонстрации построения графиков. В следующем разделе отдельным пунктом разбирается важный вопрос графических настроек — как отобразить на осях координат числа (метки), выраженные через число pi.
Как сделать, чтобы по осям OX и OY отображались pi-координаты
Как правило, чтобы построить график тригонометрической функции, по оси ОХ удобно отмечать абсциссы, выраженные через число pi (т.е. pi/2, pi, 3pi/2, 2pi и т.д.). В случае же построения графика обратной тригонометрической функции (арксинус, арккосинус, арктангенс, арккотангенс) бывает удобно отложить ординаты, выраженные через pi.
Рис. 13. Нижний раздел панели графических настроек —
отображение pi-меток на осях
Вот примеры построенных графиков с pi-метками на осях:
Рис. 14. Графики тригонометрических функций с pi-метками на оси ОХ
Рис.
 15. Графики обратных тригонометрических функций
15. Графики обратных тригонометрических функций y=arcsin x и y=arccos x с pi-метками на оси ОY
Немного о keypad’e
Keypad (англ. — «клавиатура») в системе Desmos — это такая небольшая панель, которая вылезает каждый раз, когда вы пытаетесь ввести уравнение для построения графика или для проведения расчетов. Вот так она выглядит:
Рис. 16. Keypad
При желании можно пользоваться keypad’ом для ввода различных функций, констант или переменных. Мне лично хватает обычной клавиатуры, так что этой я не пользуюсь.
Если навести на некоторые кнопки keypad’a мышкой, появляется всплывающая подсказка, которая показывает, что можно ввести с клавиатуры вместо нажатия этой кнопки. Так, вместо нажатия кнопки ln можно ввести с клавиатуры ln( и т.д.
Итоги и выводы
Система Desmos для построения графиков на сегодняшний день является лучшей из тех, что попадались мне на глаза, для применения на уроках в школе. Она позволяет строить графики всех функций и уравнений из школьной программы, включая уравнения с модулем, тригонометрические функции и т.д. Система легко позволяет сохранять графики, в том числе в виде ссылок. Имеется большое количество примеров, по которым можно понять, как пользоваться системой, а также удобный и интуитивно понятный интерфейс управления.
Она позволяет строить графики всех функций и уравнений из школьной программы, включая уравнения с модулем, тригонометрические функции и т.д. Система легко позволяет сохранять графики, в том числе в виде ссылок. Имеется большое количество примеров, по которым можно понять, как пользоваться системой, а также удобный и интуитивно понятный интерфейс управления.
К некоторым недостаткам для применения в школах стран СНГ можно отнести во-первых, «англоязычность» системы, а во-вторых, «онлайновость». Использовать Desmos можно только в случае, если компьютер или компьютерный класс подключен к Интернету.
В случае наличия подключенного к Сети компьютерного класса ученики могут строить графики функций самостоятельно. В случае наличия одного компьютера, подключенного к Интернет, имеет смысл задействовать проектор и демонстрировать на нем построение графиков функции по точкам или геометрические преобразования.
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах.
| ||||
Страница не найдена — Информационные технологии в школе
На официальном интернет-ресурсе Минпросвещения России опубликован Календарь образовательных событий, приуроченных к государственным и национальным праздникам Российской Федерации, памятным датам и событиям российской истории и культуры, 2021/22 учебный год. 0.11MBКалендарь образовательных событий, приуроченных к государственным и национальным праздникам Росс […]
uCoz прекращает бесплатное обслуживание сайтов государственных и муниципальных учреждений и вводит льготный тариф «Образовательный» стоимостью 300р.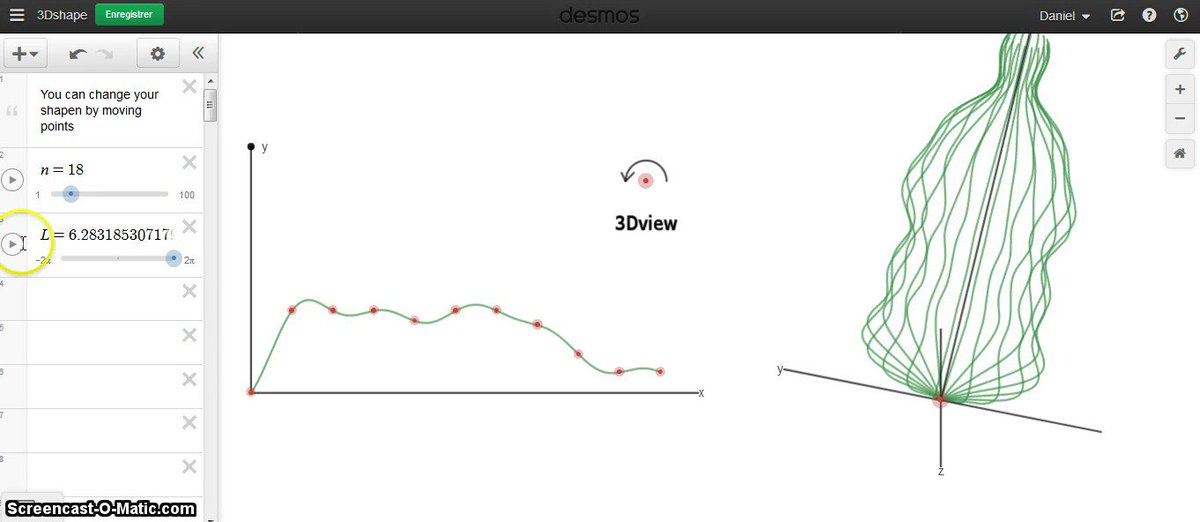 /мес. или 2880р./год. Тариф уже доступен в панели управления сайтом, его можно оплатить по безналичному расчёту Подробнее При оплате по безналичному расчету стоимость фиксируется в рублях. При оплате любым другим […]
/мес. или 2880р./год. Тариф уже доступен в панели управления сайтом, его можно оплатить по безналичному расчёту Подробнее При оплате по безналичному расчету стоимость фиксируется в рублях. При оплате любым другим […]
Предлагаю вашему вниманию новые сайты. Первый сайт Пушкаревой Ксении Юрьевны https://pushkareva-116.ucoz.net/, воспитателя муниципального бюджетного дошкольного образовательного учреждения детского сада общеразвивающего вида с приоритетным осуществлением деятельности по физическому развитию детей №116 «Светлячок» г. Брянска. CMS сайта — uCoz. uCoz — бесплатн […]
Как учителю создать эффективный личный сайт. Лучшие теоретические и практические советы специалистов. Личный сайт давно стал привычным инструментом для многих специалистов. Учителя не исключение. Кто-то создает одностраничный сайт-визитку, а кто-то владеет собственным образовательным ресурсом, кто-то вкладывает деньги в рекламу, а кто-то раскручивает сайт че […]
как создать и оформить страницу «Организация горячего питания» на школьном сайте, используя данные из шаблонного сайта → https://goo-gl. ru/IBCMU , если Вы используете конструктор ZabEdu.
ru/IBCMU , если Вы используете конструктор ZabEdu.
График функции y sin 2x. График функции y=sin x
«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см.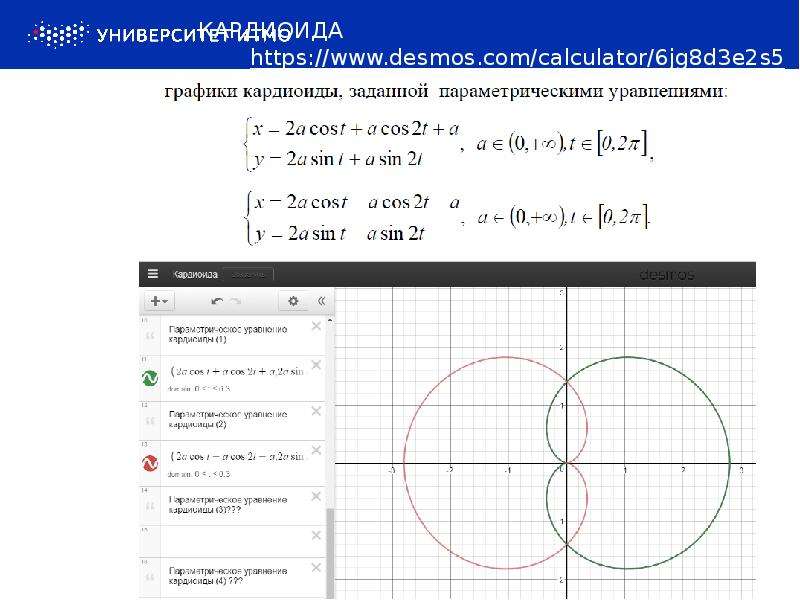 рисунок).
рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
DESMOS — замечательный инструмент для учителей математики — Дидактор
Не раз в Дидакторе обращалось внимание на научные калькуляторы, которые значительно облегчают рутинную работу и, наоборот, способствуют развитию творческого мышления. Математические калькуляторы по своему разнообразию наиболее многочисленны.
Однако даже на таком фоне сервис Desmos, уверен, удивит и учителей, и учеников. Этот калькулятор позволяет легко строить графики всех функций, создавать таблицы, добавлять ползунки, живую графику и многое другое.
Он позволяет построить различные типы графиков как в системах координат, так и с заданными параметрами.
Калькулятор имеет интерактивные инструменты. Прежде всего, это так называемый «ползунок».
Вы вводите его и сразу же получаете возможность изменять параметры как в ручном режиме, перетягивая «ползунок» или автоматическом, нажав значок play.
Второй инструмент: Масштабирование.
В любой момент можно увеличить или уменьшить изображение.
Третий инструмент: Выбор точки.
Нажимаете левой кнопкой мыши в любое место графика и узнаете координаты данной точки.
Вы можете вставить изображение для того, чтобы на примере какого-нибудь предмета построить систему координат.
Несмотря на то, что программа на английском языке, её интерфейс интуитивно понятен.
Все изображение перетаскивается по экрану. Полученный график можно распечатать.
К сожалению для многих пользователей, сервис онлайн.
Если же в вашем классе имеется доступ в Интернет, то весьма эффектно будет построение графиков на интерактивной доске. Для этого имеется режим «проектор», позволяющий увеличить толщину линий.
Если же доступ к сети имеют все ученики, то Desmos — это хороший инструмент для их творческой деятельности.
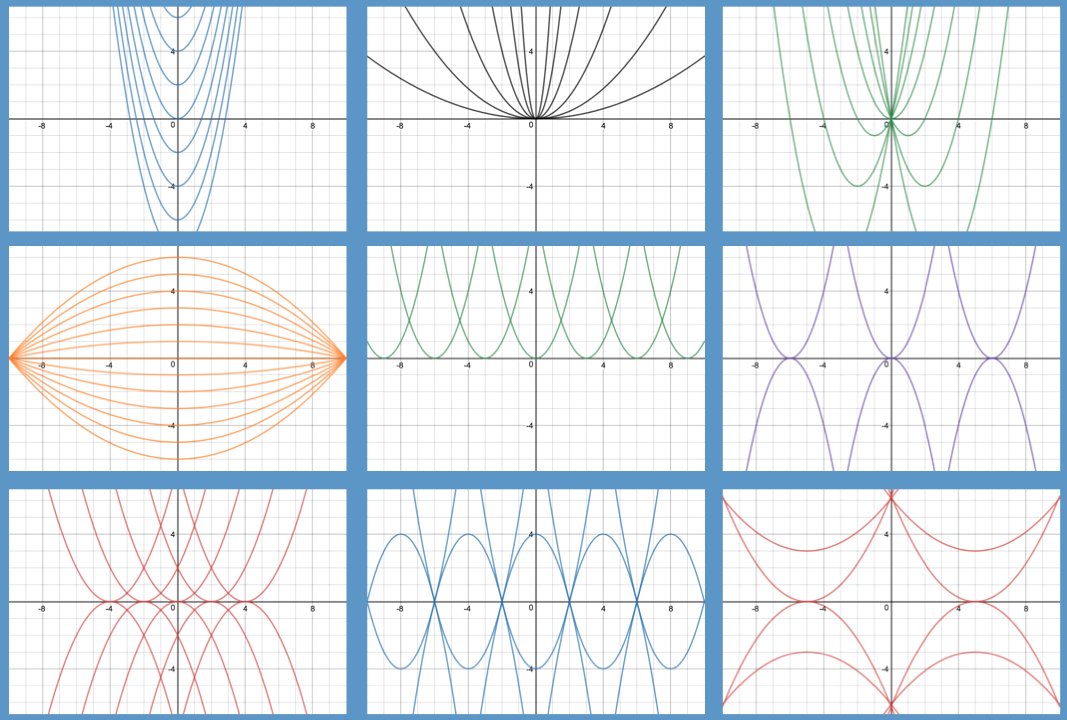
Постройте график функции y х2 3х 2. Квадратичная и кубическая функции
Разделы: Математика
Тема: “Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)
Цель.
- Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
- Развить навыки построения графика функции, содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.
Решение.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).
4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2
= 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Алгоритм построения графика квадратной функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
2.у = |х| + 1. График функции на рисунке 3.
3. у = |х + 1|. График функции рисунке 4.
Вывод.
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.
2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в группах.
Группа 1. Построить графики функций:
а) у = х 2 — 6|x| + 3,
б) у = |х 2 — 6х + 3|.
Решение.
1.Построить график функции у = х 2 -6х+3.
2. Отобразить его симметрично относительно оси Оу.
График на рисунке 5.
б) 1. Построить график функции у = х 2 — 6х + 3.
2. Отобразить его симметрично относительно оси Ох.
График функции на рисунке 6.
Вывод.
1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.
Решение.
1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.
2. Полученный график отображаем симметрично относительно оси Ох.
График функции на рисунке 7.
Вывод.
График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.
1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х 2 + 6x + 3 при х
График функции на рисунке 9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х 2 + 6х + 3 при х 6.
2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.
График на рис.10.
Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.
(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
Группа 4.
Построить график функции:
а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.
Решение.
а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:
Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:
Строим каждый график на соответствующем интервале.
График функции на рисунке 12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно оси Ох.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Вывод. Два модуля в предложенных
уравнениях существенно усложнили построение
общего графика, состоящего из трех отдельных
графиков.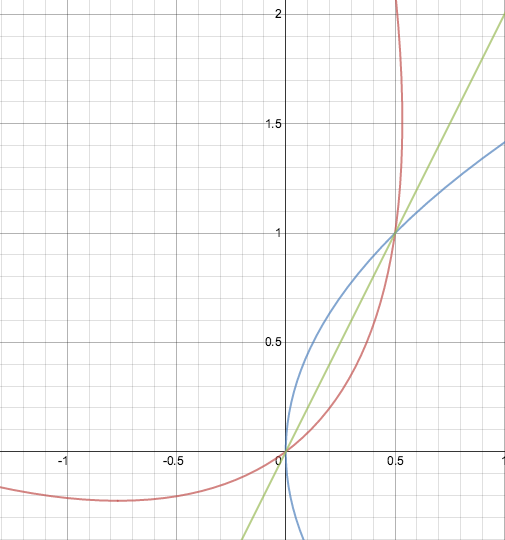
Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.
3. Задание на дом.
Построить графики функций с различным расположением модуля:
1. у = х 2 + 4х + 2;
2. у = — х 2 + 6х — 4.
4. Рефлексивно – оценочный этап.
1.Оценки за урок складываются из отметок:
а) за работу в группе;
б) за самостоятельную работу.
2. Какой момент был наиболее интересен на уроке?
3. Трудное ли домашнее задание?
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.
Преимущества построения графиков онлайн
- Визуальное отображение вводимых функций
- Построение очень сложных графиков
- Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
- Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
- Управление масштабом, цветом линий
- Возможность построения графиков по точкам, использование констант
- Построение одновременно нескольких графиков функций
- Построение графиков в полярной системе координат (используйте r и θ(\theta))
С нами легко в режиме онлайн строить графики различной сложности. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
X 2 5x 4 график. Строим график функций онлайн
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus. ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .

- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.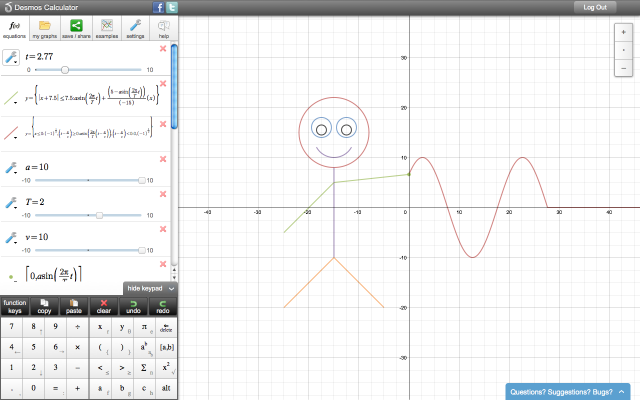 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Графический онлайн-калькулятор
Desmos — Freedom Scientific
Графический калькулятор Desmos — это бесплатный математический онлайн-инструмент, широко используемый учителями и учениками для построения уравнений и изучения математических понятий. Используйте его для построения графиков данных, функций графиков, оценки уравнений и создания классных занятий. Дополнительную информацию можно найти на странице Learn Desmos .
Используйте его для построения графиков данных, функций графиков, оценки уравнений и создания классных занятий. Дополнительную информацию можно найти на странице Learn Desmos .
Desmos доступен с помощью программы чтения с экрана JAWS и может использоваться с обновляемыми дисплеями Брайля.Посетите страницу Desmos Accessibility , чтобы узнать о встроенных настройках специальных возможностей и , чтобы настроить JAWS и Fusion .
Графические возможности
Графический калькулятор Desmos — это универсальный инструмент с обширными графическими функциями. Вот несколько примеров задач, которые вы можете выполнить, и шаги по их выполнению. Посетите страницу Learn Desmos Graphing для получения дополнительных сведений и ресурсов.
Создание и исследование графика
Для более плавного просмотра Desmos предлагает отключить эхо символов и установить режим форм на «полу».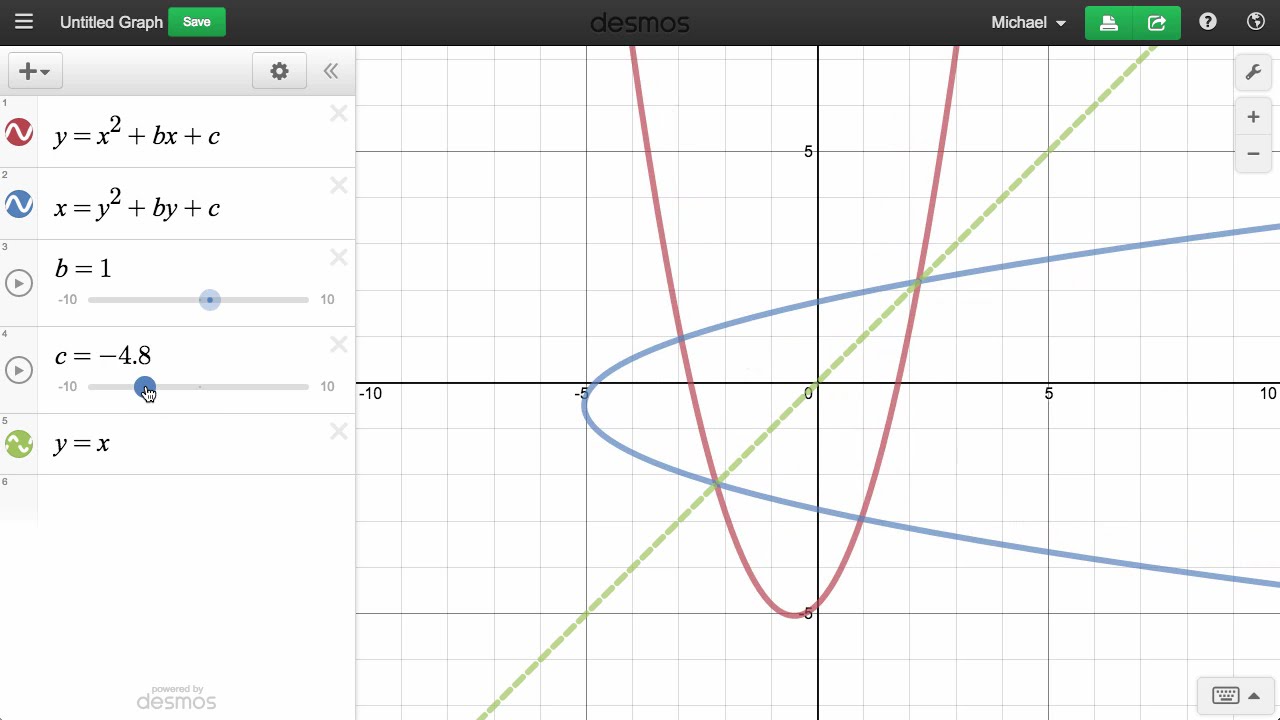 Настройки могут измениться с будущими обновлениями JAWS.
Настройки могут измениться с будущими обновлениями JAWS.
Чтобы создать и отследить график, выполните следующие действия:
- Посетите веб-сайт Desmos , затем найдите графический калькулятор .
- Запишите по одному уравнению в каждой строке в предусмотренных полях редактирования — «выражение 1», «выражение 2» и т. Д.Графики будут немедленно отображены.
- Нажмите ALT + T , затем H , чтобы построить график. Включится индикатор звуковой дорожки.
- Используйте клавиши со стрелками для изучения графика.
- Нажмите ALT + S , чтобы просмотреть список достопримечательностей. Эта сводка доступна как в режиме трассировки, так и вне его.
- В режиме трассировки нажмите ВКЛАДКА для навигации по интересующим точкам. Иногда вам нужно нажать SHIFT + TAB , чтобы их услышать.
- Нажмите ESC , чтобы выйти из режима трассировки.

Чтобы настроить параметры графика, выполните следующие действия:
- В поле редактирования дважды нажмите TAB , чтобы перейти в меню настроек графика, затем нажмите ПРОБЕЛ , чтобы активировать его.
Доступные настройки:
- Размер дисплея
- Обратный контраст
- Режим Брайля
- Сетка или без сетки
- Сетка или без сетки
- Декартова сетка
- Полярная сетка
- Стрелка
- Номера осей
- Незначительное линии сетки
- Показать или скрыть ось X
- Метка оси X
- Минимум оси X
- Максимум оси X
- Размер шага по оси X
- Те же параметры для оси Y
- Углы, радианы или градусы
Чтобы создать таблицу значений, выполните следующие действия:
- Перейдите в поля редактирования.

- Дважды нажмите SHIFT + TAB , чтобы перейти к «кнопке редактирования списка выражений», и выполните ее, нажав ПРОБЕЛ . JAWS должен указать, что «режим редактирования списка» включен.
- Трижды нажмите TAB , чтобы найти «преобразовать в таблицу», и нажмите ПРОБЕЛ .
- Нажмите TAB для навигации по значениям таблицы.Не используйте табличные команды.
- Чтобы найти конкретное значение, нажмите TAB или СТРЕЛКА ВНИЗ для перехода к строке с пустым полем редактирования и введите значение, которое вы хотите найти. Нажмите TAB, чтобы услышать результат.
- Чтобы вернуться к графику, нажмите SHIFT + TAB , пока JAWS не скажет «отменить». Нажмите ПРОБЕЛ , чтобы активировать кнопку.
- Очистите график и все выражения, нажав CTRL + O . Теперь вы готовы начать новый график.

Видеоурок по созданию и исследованию графика
Сравнить графики
Понимание свойств графиков имеет решающее значение, потому что это облегчит решение проблем как при продвинутой курсовой работе, так и при приеме на работу.2 будет отображаться.
Видеоруководство по сравнению графиков
Экспорт графика
Передача графиков коллегам или коллегам сегодня необходима. Возможность экспортировать четкий график позволяет правильно сдавать домашнее задание. На рабочем месте такой вид общения расширяет вашу способность работать с коллегами, особенно сейчас, когда командная работа настолько распространена. Коммуникация — ключ к успеху.
После построения графика функции экспортируйте график в Word:
- Нажмите SHIFT + TAB , чтобы найти «поделиться», и нажмите ENTER .
- Нажмите клавишу TAB несколько раз, пока не найдете кнопку «Загрузить».

- Или нажмите INSERT + F5 , чтобы просмотреть список полей формы, затем нажмите букву I, чтобы найти «загрузка изображения». Дважды нажмите ENTER . Это поместит фокус рядом с кнопкой «Загрузить», и для ее обнаружения потребуется меньшее количество нажатий клавиши TAB .
- Перейдите к документу Word.
- Вставьте изображение, нажав ALT + N , затем P , затем ENTER .
- Перейдите в адресную строку, нажав ALT + D и введите первые несколько букв слова «загрузить».
- Нажмите СТРЕЛКА ВНИЗ один раз, чтобы найти папку загрузок, и нажмите ENTER .
- Выполните команду «Найти файл», нажав ALT + N и набрав «des», чтобы найти файлы Desmos.
- Нажимайте СТРЕЛКА ВНИЗ , пока не найдете нужный файл, затем нажмите ENTER . Основное внимание будет уделено графику.
 Если вы потеряете фокус, нажмите CTRL + SHIFT + O , чтобы получить доступ к списку объектов, и выберите график, нажав ENTER .
Если вы потеряете фокус, нажмите CTRL + SHIFT + O , чтобы получить доступ к списку объектов, и выберите график, нажав ENTER . - Нажмите клавишу APPLICATIONS , а затем Z , чтобы перейти на вкладку размера.
- Нажмите ALT + A , чтобы убедиться, что установлен флажок «Заблокировать соотношение сторон».
- Нажимайте TAB , чтобы перемещаться по полям, пока не найдете абсолютную высоту и не наберете 2.5.
- Нажмите TAB , чтобы перейти к ширине и убедиться, что она изменилась. Если этого не произошло, снова перейдите к блокировке соотношения сторон, чтобы установить в этом поле правильную ширину и высоту. Нажмите ENTER , чтобы закрыть диалоговое окно.
Чтобы добавить и отредактировать замещающий текст, выполните следующие действия:
- Нажмите клавишу APPLICATIONS , а затем A , чтобы перейти к текстовому полю alt.
 Если в этом поле есть текст, нажмите CTRL + A , чтобы выделить текст и либо удалить его, либо введите новый замещающий текст, чтобы заменить существующее содержимое.
Если в этом поле есть текст, нажмите CTRL + A , чтобы выделить текст и либо удалить его, либо введите новый замещающий текст, чтобы заменить существующее содержимое. - Нажмите CTRL + ПРОБЕЛ , а затем C , чтобы закрыть меню навигации. Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению.Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста.
- Нажмите CTRL + END , а затем ENTER , чтобы продолжить запись документа на новой строке.
Экспорт графика Видеоурок
Быстрый экспорт графика в Word с помощью экрана печати
Экран Print screen работает лучше всего, когда ученик выполняет домашнее задание и ему нужно построить много графиков.
После создания графика выполните следующие действия:
- Нажмите PRINT SCREEN , чтобы скопировать график в буфер обмена.
- Перейдите к документу Word.
- Тип «1». (или # применительно к графику). Введите математическую задачу и нажмите ENTER .
- Вставьте график в Word, нажав CTRL + V .
- Ваш курсор будет помещен в конец вставленного материала. Нажмите SHIFT + СТРЕЛКА ВЛЕВО , чтобы выбрать график.Вы также можете нажать CTRL + SHIFT + O , чтобы перейти к списку объектов и перейти к концу списка, чтобы найти свой график. Оказавшись там, нажмите ENTER .
- Нажмите кнопку ПРИЛОЖЕНИЯ , затем нажмите СТРЕЛКА ВВЕРХ , чтобы найти «размер и положение». Нажмите ENTER , чтобы выбрать эту опцию. Либо нажмите Z после нажатия клавиши ПРИЛОЖЕНИЯ , чтобы открыть это диалоговое окно.

- Нажмите ALT + A , чтобы убедиться, что установлен флажок «Заблокировать соотношение сторон».Нажмите TAB , чтобы перемещаться по полям, найти абсолютную высоту и введите «2,5», затем нажмите TAB в поле ширины. Убедитесь, что он изменился. Если этого не произошло, снова перейдите к блокировке соотношения сторон, чтобы установить в этом поле правильную ширину и высоту. Нажмите ENTER , чтобы закрыть диалоговое окно.
Чтобы добавить и отредактировать замещающий текст, выполните следующие действия:
- Нажмите клавишу APPLICATIONS , а затем A , чтобы перейти к текстовому полю alt.Если в этом поле есть текст, нажмите CTRL + A , чтобы выделить его, и либо удалите текст, либо введите новый замещающий текст, чтобы заменить существующее содержимое.
- Нажмите CTRL + ПРОБЕЛ , а затем C , чтобы закрыть меню навигации.
 Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста.
Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста. - Нажмите CTRL + END , а затем ENTER , чтобы продолжить запись документа на новой строке.
Desmos: подробное руководство по построению графиков и вычислений
Думаете, вам нравится для построения графиков и для вычислений ? Большой! Возможно, вы помните эту штуку под названием Texas Instrument TI-83 из старых времен. Конечно, в то время как программируемые калькуляторы в целом все еще довольно популярны в наши дни, графические калькуляторы из 21 -го -го века также появляются волнами, пока мы говорим, потенциально разрушая рынок научных вычислений и образовательных технологий .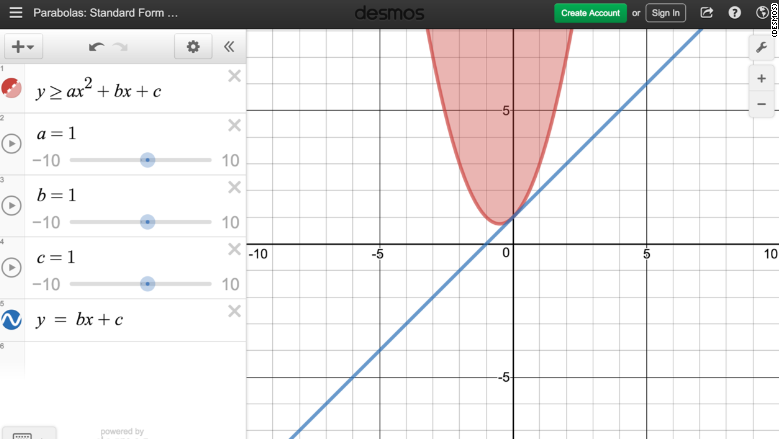
В частности, существует некий образовательный стартап , неустанно стремящийся перехватить наши интернет-браузеры и мобильные устройства в — так сказать — графическую феерию. И у него тоже забавное название: Desmos .
Ага. Вы все правильно поняли. Как звучит , вдохновленный греческой мифологией , Десмос на самом деле не имеет ничего общего с гигантским монстром, ответственным за превращение горы Олимп в руины из-за гнева адского пламени.Вместо этого он, вероятно, более известен как невинно выглядящий математический инструмент для людей с научным складом ума, делающий прикладную математику еще более приятной и интересной!
О. Не верите в могущественную силу Десмоса ? Молодец! Потому что тогда наш долг будет просить не согласиться и пытаться убедить вас в обратном. В самом деле, если в конце модуля вы все еще найдете объем функций Desmos непривлекательным , тогда — и только тогда — мы признаем поражение и вернемся в нашу башню из слоновой кости для более продвинутого обучения буддийской медитации! С другой стороны, если вам просто лень читать 12-страничное руководство пользователя Desmos , и вы ищете еще конкретных примеров , чтобы начать творческий процесс, то это тоже для вас!
О каком единственном слове думают люди, когда слышат онлайн-калькулятор с графиком ? Конечно же, графики! Действительно, Desmos делает это невероятно хорошо — несмотря на то, что пользовательский интерфейс кажется обманчиво простым. Далее мы увидим, как мы можем использовать Desmos для построения графиков уравнений , функций и неравенств различных форм, прежде чем вводить некоторые дополнительные функции, такие как сегментация графика , одновременное построение графиков и анимации !
Далее мы увидим, как мы можем использовать Desmos для построения графиков уравнений , функций и неравенств различных форм, прежде чем вводить некоторые дополнительные функции, такие как сегментация графика , одновременное построение графиков и анимации !
Уравнения
Когда дело доходит до построения графиков, уравнение — одно из первых слов, которое приходит на ум.С другой стороны, его также можно истолковать как общий термин , охватывающий множество математических объектов, таких как явных функций , неявных функций , параметрических уравнений и полярных кривых . Далее мы проиллюстрируем, как каждый из них может быть изобразен в Desmos — шаг за шагом.
Предварительные сведения
Однако, прежде чем строить графики, нам нужно сначала научиться печатать несколько математических символов, которые часто используются. С этой целью мы предоставили частичный список из общих символов , поддерживаемых в Desmos — вместе с их связанными командами :
С этой целью мы предоставили частичный список из общих символов , поддерживаемых в Desmos — вместе с их связанными командами :
- Символ умножения можно получить, набрав
*(Shift+8на клавиатурах США). - Разделительная линия можно получить, набрав
/(т.е. обратная косая черта). - $ \ pi $ можно получить, набрав
pi, а $ \ theta $ —theta.2 $), а ключ_(Shift+Дефисна клавиатуре США) для подстрочного индекса (например, 1 доллар в $ a_1 $). - Функция потолка на
ceil (), the функция пола наэтаж ()и функция знака на знак(). - Символ абсолютного значения на
|(т.е.Shift+\на клавиатурах США).
Для некоторых команд (например,g., деление, надстрочный индекс, подстрочный индекс), их ввод может переместить курсор в верхнюю или нижнюю область . В этом случае вы можете использовать клавиши со стрелками , чтобы помочь вам перемещаться по выражению и вводить то, что вы хотите. В других случаях вам может потребоваться использовать круглых скобок , чтобы сгруппировать некоторые из ваших выражений вместе, прежде чем они смогут быть правильно интерпретированы Desmos.
Определение функций
Традиционно наиболее популярными функциями являются функции, выраженные в $ x $, которые можно ввести в командной строке следующим образом:
\ begin {align *} y = \ text {некоторые алгебраические выражения в терминах} x \ end {align *}
Поменяв местами роли $ x $ и $ y $, функции в терминах $ y $ также могут быть введены в командную строку следующим образом:
\ begin { align *} x = \ text {некоторые алгебраические выражения в терминах} y \ end {align *}
Ага.Это аншлаг. Просто введите триггерные функции, используя указанные выше имена! Итак, какие функции поддерживаются в Desmos? По сути, все элементарные функции, о которых вы только можете подумать! К ним относятся 6 базовых тригонометрических функций , экспоненциальных / логарифмических функций (с помощью команд exp , ln и log ), полиномов и рациональных функций . Кроме того, 6 базовых обратных тригонометрических функций — наряду с 6 базовыми гиперболическими функциями — легко поддерживаются простым вводом имени функции.
Теперь, если функция в терминах $ x $ предназначена для повторного обращения, то ей можно присвоить имя , заменив $ y $ в левой части, скажем, на $ f (x) $. Аналогичным образом функции в терминах $ y $ также может быть присвоено имя, из которого мы можем определить и имя составную функцию в командной строке — без необходимости переписывать выражения снова и снова:
- $ y = 2f (3x-3) + e $
- $ g (y) = \ dfrac {\ pi} {f (y)} $
- $ f_1 (x) = 55f (x) + 43g (x) — 100 h (x) $
- $ y = g (x) ^ 2 \ cdot \ left (g (x) ^ {f (x)} \ right) $
- $ h (x) = 2 g (f (x)) + 3 g (f (x)) $
И, если вам интересно, полярные функции также поддерживаются в Desmos.2 $).
Полярные кривые и составные функции в действии!Функции, связанные с исчислением
Как оказалось, Desmos также замечательно восприимчив к выражениям, основанным на исчислении . Например, если задана функция в терминах $ x $, прикрепив перед ней $ \ dfrac {d} {dx} $, можно легко построить график ее производной функции — без необходимости прибегать к явная формула производной. Точно так же производную функции через $ y $ можно изобразить, добавив перед ней $ \ dfrac {d} {dy} $.Довольно аккуратно, правда?
В качестве альтернативы, если функции уже было присвоено имя, мы также можем использовать простое обозначение для обозначения ее производной функции (как в $ f ‘(x) $). Помимо простоты реализации, простая нотация также имеет то преимущество, что она может ссылаться на высшие производные , просто добавляя несколько дополнительных $ ‘$ (например, $ g ”$), что — по сравнению с повторным использованием $ \ dfrac {d} {dx} $ — определенно плюс.
Конечно, если Desmos хорош с производными функциями, то неудивительно, что он также поддерживает интегральные функции .Для записи, символ интегрального оператора $ \ int $ можно получить, набрав int в командной строке, после чего вы должны будете использовать клавиши со стрелками для навигации по нижнему / верхнему пределу и подынтегральному выражению .
Однако следует предостеречь: при настройке интегральной функции — особенно тех, которые включают несколько интегральных операторов — вы должны проявить особую осторожность, чтобы убедиться, что переменная интеграции отличается от переменной (переменных) в пределах.Поступая так, вы фактически избавляетесь от необходимости пробивать Desmos по-настоящему, в случае, если выражение не окажется точно Desmos-интерпретируемым . 🙂
Производные и интегральные функции. Между прочим, строки 2 и 3 относятся к одной и той же функции.Кусочные функции
Чтобы определить кусочную функцию в Desmos, мы можем использовать следующий синтаксис в командной строке:
\ begin {align *} y \ (\ text {или} x) = \ {\ text { condition 1}: \ text {определение 1}, \ text {condition 2}: \ text {определение 2}, \ ldots \} \ end {align *}
Как и в случае с другими функциями, кусочной функции также можно присвоить name, просто заменив крайнюю левую переменную именем функции.Таким образом, мы можем повторно использовать функцию без необходимости заново определять ее.
Например, предположим, что мы хотим определить функцию $ f $ как знаковую функцию . То есть:
\ begin {align *} f (x) = \ begin {cases} -1 & x <0 \\ 0 & x = 0 \\ 1 & x> 0 \ end {cases} \ end {align *}
, тогда это будет выражение, которое мы хотим ввести в командную строку:
\ begin {align *} f (x) = \ left \ {x <0: -1, x = 0: 0, x > 0: 1 \ right \} \ end {align *}
, что должно дать следующую цифру:
Знаковая функция.Обратите внимание, что строка 1 и строка 2 эквивалентны. В некоторых случаях может потребоваться использовать символы $ \ le $ и $ \ ge $ для точного определения функции. В этом случае просто знайте, что символ $ \ le $ можно получить, набрав < и = в этом порядке, а символ $ \ ge $, набрав > и = , снова в тот заказ.
Другие уравнения
Поскольку интерфейс Desmos по умолчанию имеет декартовых координатах , вполне естественно, что его можно будет использовать для построения уравнений, выраженных в терминах $ x $ и $ y $.Фактически, неявных функций , таких как окружности , эллипса или гиперболы , являются очень хорошими кандидатами для этого.
Однако менее ясно то, что Desmos также может интерпретировать параметрических уравнений , при условии, что мы вводим уравнения для $ x $ и $ y $, как если бы они были координатами точек (как в $ (2 \ cos t, 3 \ sin t) $), и что переменная $ t $ - обозначенная переменная для параметрических уравнений в Desmos - используется во всем выражении.По какой-то причине Desmos просто не будет использовать для этой цели другие переменные, такие как $ x $ или $ \ theta $.
С более оптимистичной точки зрения, если вам удастся правильно ввести параметрическое уравнение, то вы сможете увидеть неравенство в отношении домена, появляющееся прямо под командной строкой. Кстати, не принимайте это как должное, потому что именно здесь вы можете настроить диапазон переменной $ t $, которая, по сути, определяет часть параметрических уравнений, которая фактически отображается на графике.
Хорошо. Все идет нормально? Вот рисунок, иллюстрирующий, как неявные функции и параметрические уравнения работают в Desmos:
Неявные функции и параметрические уравнения - в основном набор из конических секций !Неравенства
Думаете, это уже был целый список уравнений? Знайте это: почти все уравнения можно превратить в неравенства , заменив знак $ = $ на $ <$, $> $, $ \ le $ или $ \ ge $, тем самым легко удвоив количество графов можно строить в Desmos.2 <4 $
И вот что произошло, когда мы добавили эти неравенства в Десмос.
Разнообразный спектр неравенств в Десмосе., что довольно круто. И это только начало!
Сегментация графика
Когда действительное уравнение / неравенство вводится в командную строку, Desmos по умолчанию строит свой график, предполагая, что полный домен , при котором уравнение / неравенство удовлетворяется. Однако это не всегда дает желаемый эффект, и бывают случаи, когда для этого предпочтительнее , а не .2 \, \ {x + y <5 \} \ {x> 0 \} \ end {align *}
Фактически, ограничение (я) могло составлять любое количество уравнений / неравенств , включая любое количество комбинация обозначенных переменных (например, $ x $, $ y $, $ r $, $ \ theta $), с оговоркой, что переменные в ограничениях должны быть совместимы с уравнением / неравенством они ограничивают в первую очередь (например, полярное уравнение может быть ограничено только с использованием полярных переменных $ r $ и $ \ theta $).
Звучит непонятно? Вот изображение для получения дополнительной информации:
Демонстрация сегментации графика. Обратите внимание, что в ограничительных предложениях можно использовать только соответствующие переменные.Одновременное построение графиков
Устали строить очень похожие графики один за другим ? Что ж, не отчаивайтесь, потому что выход есть, когда ты с Десмосом. Действительно, если уравнение / неравенство выражается в терминах некоторого параметра (ов), который сам определяется как список нескольких чисел, то несколько графиков могут быть созданы одновременно для каждого из этих чисел раз и навсегда.
Хм, о чем мы тут говорим? Вот сопроводительное изображение, которое нам поможет:
Woah! Что это!?Как вы можете видеть здесь, определив функцию с фиктивным параметром $ a $, который сам определяется как список с числами $ 1 $, $ 2 $, $ 3 $ и $ 4 $, мы смогли построить график всего четыре функции одновременно с двумя строками. Поговорим о лени и эффективности!
А если вы немного любите приключения, вы, безусловно, можете попробовать ввести уравнение / неравенство с несколькими параметрами , каждый из которых определяется как отдельный список с равными размерами .Фактически, этот метод «массового построения графиков» оказался грозной техникой для резкого замедления / парализации наших компьютеров и мобильных устройств!
Если серьезно, то если вы хотите использовать функциональные возможности Desmos в полной мере, это просто необходимо. не только автоматизирует процесс построения графиков, выполнение которого в противном случае было бы утомительно утомительно, но также не позволит нам изобретать колесо, когда шаблон для графиков уже доступен.О, вот еще один!
Фигура с 10 квадратичными функциями. Не наш отпечаток пальца.Анимация с неопределенными параметрами
Когда вы вводите строку математического выражения, содержащую неопределенный параметр , Desmos даст вам возможность включить ползунок для этого параметра, который позволяет вам регулировать его значение вручную - или еще лучше - создайте из него анимацию , разрешив значению параметра увеличиваться / уменьшаться автоматически .
В частности, ползунок позволит вам управлять диапазоном и размером приращения рассматриваемого параметра, а также скоростью и направлением , с которым изменяется параметр. И причина, по которой это имеет значение, заключается в том, что, имея ползунки, управляющие поведением наших интересующих параметров, мы можем создавать различные анимированные объекты , такие как подвижные точки , уравнения вращения и анимированные области / границы .
Например, чтобы смоделировать частицу, движущуюся по синусоидальной траектории , все, что нам нужно сделать, это встроить неопределенный параметр в координаты синусоидальной волны (как в $ (a, \ sin 2 \ pi a) + 3 $), прежде чем активировать ползунок для параметра с помощью кнопки «воспроизведение» . И если точка должна перемещаться по круговой траектории , вместо этого подойдет выражение типа $ (3 \ cos a - 5, 3 \ sin a + 6) $ в командной строке. 3 $ в три командные строки, активируйте ползунок и наблюдайте, как полиномы движутся в тандеме с гордостью!
Хотя интерфейс Desmos в основном состоит из графической сетки , , чем что-либо еще, факт остается фактом: он был построен в основном для вычислительных целей - и, вероятно, так будет всегда.Фактически, мы скоро увидим, что Desmos - очевидно, хорошо оснащенный для выполнения базовых вычислений - может быть перехвачен для выполнения целой кучи не связанных с графом вещей , таких как вычисление частичной суммы , оценивая коренит функции, определяя значение определенного интеграла или даже находя наибольших общих множителя из списка целых чисел!
Элементарные вычисления
В Desmos можно положить любое математическое выражение, включающее сложение , вычитание , умножение ( * ), деление (/) и возведение в степень ( ^ ). в командную строку, так что, если введенное выражение не содержит вообще никакой переменной, результат можно вычислить и вернуть обратно вам - обычно в мгновение ока.
Кроме того, если некоторые функции, такие как $ f $ и $ g $, уже были определены в командных строках, и мы хотим оценить выражение, включающее их значения функции (например, $ 4f (15) + 2g (0 ) + 5 $), то у нас есть гарантия ввести это же выражение в командную строку, после чего Desmos будет более чем счастлив выполнить наш запрос. Более того, используя простое обозначение , мы даже можем заставить Desmos оценить производную функции в определенной точке (например,г., $ f '(3) $).
По умолчанию, когда уравнение вводится в командную строку, Desmos дает нам возможность отобразить ключевых точек (например, пересекает , локальных максимумов , локальных минимумов ) на графике - всякий раз, когда применимый. {- 6} $ (т.е.е., наименьшее допустимое приращение ), то таким образом мы сможем получить несколько дополнительных десятичных знаков.
Кроме того, присвоив имя математическому выражению, которое мы хотим вычислить, мы можем передать результат вычисления в новую переменную, а затем использовать его для других более причудливых целей, таких как построение сложных вычислений или графическое отображение результатов вычислений. на фигурки и анимации .
Списки
Когда дело доходит до крупномасштабных вычислений, иногда более рентабельно потратить время на то, чтобы сначала составить список чисел , чем вручную записывать математические выражения одно за другим.В этом случае просто знайте, что в Desmos мы можем использовать ключей в квадратных скобках для создания списка, члены которого могут либо перечислить явно , либо неявно , набрав три точки (как в $ [7,8 , \ ldots, 22] $).
Фактически, можно также создать список, в котором элементы перечислены неявно, но с нетривиальным приращением (как в $ [2,7, \ ldots, 42] $), где приращение может быть как большой, как 5635 долларов США, или всего лишь 0,01 доллара США - гибкость, которая делает Desmos мощным инструментом для определения большого набора чисел.
Примечание
В Desmos клавиши в квадратных скобках специально предназначены для перечисления элементов списка. Для разделителей, которые служат для группировки алгебраических выражений, используйте скобки вместо .
Так почему именно мы вообще беспокоимся о создании списка? Потому что мы можем использовать его для выполнения «массовых вычислений» для каждого элементов в списке! И если мы намерены использовать список на постоянной основе, то мы можем назначить списку имя и передать имя в командные строки для еще более интересных целей, которые включают, среди прочего:
- Выполнение преобразование в списке.
- Одновременно графическое отображение нескольких функций одного семейства.
- Построение серии точек / линий / математических объектов на графике.
- Вычисление суммы списка - или любое другое вычисление, которое зависит от численного манипулирования элементами в списке.
Все из которых проиллюстрированы на рисунке ниже:
Определение списка, преобразование списка, одновременное построение графиков и вычисления, связанные со списком.В некоторых случаях вам может быть проще встроить листинг и вычисления в одну командную строку, но по мере роста сложности задачи вы можете захотеть записать их в несколько строк вместо этого, чтобы улучшить читаемость и облегчить будущие ссылки.
Вычислительные команды
В дополнение к стандартным функциям , предлагаемым научным калькулятором, Desmos также имеет несколько дополнительных команд, доступных для обычного программируемого калькулятора.Например, мы можем использовать Desmos для вычисления наибольшего общего множителя с помощью команды gcd - при условии, что мы придерживаемся следующего синтаксиса:
\ begin {align *} \ gcd (\ text {number 1}, \ ldots, \ text {number n}) \ end {align *}
Список различных функций, доступных из меню клавиатуры Desmos. Аналогичным образом мы также можем вычислить:
- Наименьшее общее кратное (через команда
lcm) - Минимум из кратных чисел (через команду
min) - Максимум (через команду
max) - Наименьший положительный остаток $ a $ под модулем $ b $ (введя
mod (a, b)) - Число комбинаций , доступных при выборе $ r $ объектов из $ n $ объектов (введя
nCr (n, r)) - Количество перестановок w При выборе $ r $ объектов из $ n $ (введя
nPr (n, r)) - Факториал для $ n $ (введя
n!)
Например, если ваш дедушка предлагает вам выбрать 5 гигантских мармеладных мишек из 15, которые он может предложить, то вы можете использовать Desmos, чтобы выяснить, сколькими способами вы можете выбрать мармеладки, набрав nCr (15,5) в командную строку, и будьте счастливы узнать, что у вас действительно есть выбор в размере 3003 долларов США, который вы можете свободно использовать.То есть выбор в 20+ раз больше, чем у жевательных конфет!
Что касается факториала, у нас есть для вас интересный факт: Desmos может вычислить факториал числа до $ 170! $, Что легко больше, чем двойной того, что может быть достигнуто с помощью TI-83 - или любой из его вариантов, если на то пошло!
На самом деле, с вычислительными командами мы еще не закончили. Вот еще пять интересных унарных операций - для вашего удовольствия:
-
ceil (): Функция потолка .Позволяет вернуть потолок ряда. -
этаж (): Функция пола . Возвращает пол числа. И потолок, и пол имеют отношение к зданию , лестница функции . -
round (): функция округления , которая округляет число до целого числа . -
abs (): Функция абсолютного значения . Использование клавиши с вертикальной чертой| Хотяпредпочтительнее. 2} \ end {align * }Для записи символ $ \ sum $ можно ввести с помощью команды
sum, после чего вам нужно будет использовать клавиши со стрелками , чтобы перемещаться и указывать нижних / верхних пределов .По умолчанию Desmos использует $ n $ (вместо, например, $ i $) в качестве основной переменной индекса , но вы всегда можете изменить ее на другую переменную по своему усмотрению - при условии, что вы выберете переменную, которая не является предопределено для других целей.Здесь, из любопытства, мы решили немного поиграть с верхним пределом и обнаружили, что Desmos, кажется, достигает максимума в 9 999 999 долларов - всего на одну единицу не хватает 10 миллионов долларов. Это поразительное улучшение по сравнению с возрастом программируемых калькуляторов !
Посмотрите, как Desmos выполняет молниеносные вычисления, которые ваш мозг никогда не сможет сделать!И становится еще лучше: используя неопределенный параметр в качестве верхнего предела и соответствующим образом настраивая ползунок.мы можем превратить результат вычислений в анимацию - как вы можете видеть на рисунке слева . Смотрите, как Desmos демонстрирует свою впечатляющую вычислительную мощь в режиме реального времени!
В качестве альтернативы, мы также можем оценить произведение последовательности с помощью команды
prodи, при необходимости, сложить столько суммирований и произведений, сколько захотим. Если вложить одного оператора в другой, мы также можем вычислить сложных математических выражений , таких как, например, двойное суммирование или тройное произведение.На самом деле, проявив немного воображения, мы можем даже превратить результат вычислений в анимированный график , преобразовав числа в анимированный линейный сегмент или, если мы этого предпочитаем, преобразовать числа в сравнительная диаграмма нам по душе!
Более того, команды
sumиprodтакже не ограничиваются вычислением чисел. Например, мы могли бы попробовать построить полиномы Тейлора $ n $ th -degree $ \ cos x $, оставив $ n $ как неопределенный параметр , так что как только мы включим ползунок с $ 1 $ как с размером шага , мы должны начать видеть множество функций, вспыхивающих как сумасшедшие!Определенные интегралы
Хотите вычислить площадь под странно выглядящей кривой? Пытаетесь смоделировать общее расстояние , пройденное надоедливой мухой ? Или, может быть, вы просто хотите спрогнозировать свой годовой доход в размере на следующий год? В любом случае, определенный интеграл должен вас охватить!
В Desmos интегральный символ $ \ int $ можно ввести с помощью команды
int, после чего вы можете использовать клавиши со стрелками для навигации и ввода верхнего / нижнего пределов .Конечно, при определении определенного интеграла необходимо включить дифференциал таким образом, чтобы переменная дифференциала соответствовала переменной в функции, которую вы хотите интегрировать.Подобно случаям с операторами суммирования и произведения , вы также можете складывать столько интегральных символов, сколько захотите, и использовать Desmos для вычисления, скажем, двойного интеграла (например, объем геометрической фигуры) или даже тройной интеграл (т.е.г., общей массой металлического стержня). Но в любом случае всегда полезно выработать привычку разумно использовать круглые скобки, чтобы Десмос правильно понимал ваше выражение на каждом этапе построения. В противном случае мы не виноваты, если Десмос откажется анализировать ваши выражения как сумасшедший!
Так что еще можно делать с интегральным оператором? Во-первых, вы можете попробовать смешать его с операторами суммирования и произведения, поскольку они все равно являются операторами одного и того же типа.В качестве альтернативы вы также можете использовать интегралы для определения уравнения или неравенства (например, интегральная функция ) и делать с ними всевозможные вещи, такие как проверка Первой фундаментальной теоремы исчисления !
Витрина тройного интеграла, интегральной функции и Первой фундаментальной теоремы исчисления!В дополнение к стандартным графическим / вычислительным функциям, доступным для большинства графических калькуляторов, Desmos также имеет некоторые изящные встроенные статистические функции для аналитически ориентированных и ориентированных на данные людей.Хотя это, безусловно, не замена специализированных статистических программ , таких как R или SPSS, его возможностей по созданию / управлению таблиц , вычислению статистических показателей и предоставлению моделей регрессии должно быть более чем достаточно, чтобы охватить основы для не -статисты среди нас!
Таблицы
В то время как список данных формирует основу одномерной статистики , наличие таблицы данных с несколькими столбцами открывает нам целый новый мир многомерной статистики , отрасль науки, которая является становится все труднее игнорировать в наши дни - большие данные и интеллектуальный анализ информации .
И хотя вы, скорее всего, , а не , будете использовать Desmos для обработки больших данных, включающих гигантские таблицы и причудливые метрики , факт остается фактом: вы все равно можете создать таблицу в Desmos через меню «добавить элемент» ( $ + $ в верхнем левом углу) и введите данные вручную по своему усмотрению. Являясь в первую очередь графическим калькулятором , Desmos, кажется, предпочитает по умолчанию представлять новую таблицу с двумя скромными столбцами : первый столбец $ x_1 $ предположительно для значений $ x $, а второй столбец $ x_2 $ - для $ y $ -значения.
Естественно, эта настройка привела бы к использованию таблицы как способа построения нескольких точек функции, сначала заполнив список из входных значений в столбце $ x_1 $, а затем переопределив имя второго столбца как функция от $ x_1 $ - так что Desmos может научиться автоматически заполнять второй столбец самостоятельно.
Pro-Tip
Если вы хотите, чтобы значения под первым столбцом были равномерно распределены, но вам лень вводить значения вручную, то вы можете автоматически заполнить первый столбец, нажав
Введитеповторно - после ввода первых двух значений в столбец.Фактически, создав столько столбцов, сколько мы хотим, мы можем расширить эту функцию построения точечных графиков до трех или четырех функций одновременно , Все, что нам нужно сделать, это убедиться, что «функциональные столбцы» помечены как функция от $ x_1 $, и наблюдайте, как Десмос автоматически заполняет оставшуюся часть таблицы и графика. Нет необходимости снова и снова переделывать значения $ x $!
Точечная печать со столом. Обратите внимание, что точки отображаются одновременно для каждой из трех функций.Значит ли это, что вам всегда приходилось создавать стол в Desmos с нуля? Не совсем. Фактически, если вы знакомы с любым программным обеспечением для работы с электронными таблицами , вы можете импортировать таблицу в Desmos с помощью простой комбинации клавиш для копирования и вставки (
Ctrl + Cдля копирования,Ctrl + Vдля вставки) . В то время как для небольшой таблицы с двумя столбцами импорт данных иногда может быть излишним. Для гигантской многомерной таблицы с десятком переменных ярлык копирования и вставки может быть настоящей спасательной машиной.Кстати, вы заметили кружок в верхней части большинства столбцов? Эти значки не только создаются каждый раз, когда мы создаем новый столбец, но они также являются нашим единственным способом настройки внешнего вида точек на графике. Щелкнув значок шестеренки , а затем соответствующий значок круга , Desmos предоставит нам возможность изменить цвет точек под всем столбцом. В качестве альтернативы, мы также можем настроить стиль графика между точками здесь, выбрав линейных сегментов или кривых , проходящих через них - функция, которая пригодится для рисования фигур или создания многоугольника участки .
Конечно, если вы назовете столбец как функция другого ранее существовавшего столбца, то значения в новом столбце будут определяться значениями в старом столбце. Однако, если вы решите пометить новый столбец как , новую переменную , то вы фактически сделаете возможным для записей под столбцом принять любое числовое значение .
(для записи, новая переменная не включает ни одной из предопределенных переменных , таких как $ x $ и $ y $.Однако, когда вы присоединяете новый индекс к заранее определенной переменной, в результате он становится новой переменной.)
Когда вы можете манипулировать данными, просто перетаскивая точки, статистика прекрасна.Более того, для каждого из столбцов, помеченных как новая переменная, вы можете сделать точки под ним перетаскиваемыми с помощью настройки перетаскивания (доступ снова через круглые значки и ). Настраивая точки так, чтобы их можно было перетаскивать в горизонтальных направлениях , вертикальных направлениях или в в каждом направлении , вы, по сути, даете себе возможность манипулировать данными визуально - что во многих случаях больше эффективнее, чем манипулирование данными численно .
Описательная статистика
Список функций статистики с клавиатуры Desmos.Каждый раз, когда нам дается набор чисел - либо в форме списка , либо в виде столбца из таблицы - мы можем вычислить на их основе около статистических показателей . Вот список собственных, унарных статистических команд, поддерживаемых в Desmos:
- Среднее : используйте команду
mean (), чтобы получить среднее арифметическое списка чисел, которое может быть определено явно (е.g., $ \ mathrm {mean} ([2.5,5.7,15,3]) $), или ссылка на него через имя переменной (например, $ \ mathrm {mean} (a_1) $). - Медиана : используйте команду
median (), чтобы вернуть среднее число (для набора с нечетным числом данных ) или среднее значение двух средних чисел (для набора с даже количество данных). - Стандартное отклонение : используйте команду
stdev ()для стандартного отклонения выборки иstdevp ()для стандартного отклонения генеральной совокупности . - Среднее абсолютное отклонение : используйте команду
mad (), чтобы найти среднее из всех абсолютных отклонений списка. - Дисперсия : используйте команду
var (), чтобы получить выборочную дисперсию . - Итого : используйте команду
total (), чтобы найти сумму всех чисел в списке. - Длина : используйте команду
length (), чтобы узнать номер данных в списке. - Extrema : используйте команду
min ()для минимума иmax ()для максимума .
Кроме того, вот список двоичных статистических команд, поддерживаемых в Desmos, с немного более тонким синтаксисом:
- Квантиль : Чтобы получить $ p $ -квантиль списка $ a $, введите
квантиль (a, p)в командную строку. Обратите внимание, что $ p $ должен быть представлен как десятичное число между $ 0 $ и $ 1 $. - Ковариация : чтобы получить образец ковариации между списками $ a $ и $ b $, введите в командной строке
cov (a, b)илиcov (b.a). - Корреляция : чтобы получить коэффициент корреляции Пирсона между списками $ a $ и $ b $, введите в командной строке
corr (a, b)илиcorr (b, a).
Безусловно, тот факт, что это почти единственные собственные команды, поддерживаемые в Desmos, не означает, что это единственные статистические измерения, которыми мы ограничены.Фактически, мы могли бы, например, оценить диапазон списка $ a $ с помощью команды
max (a) - min (a)и вычислить межквартильный диапазон , используя квантиль( a, 0,75) - квантиль (a, 0,25).На самом деле, проявив немного воображения и изобретательности, можно также разглядеть линейные диаграммы , и гистограммы, и в Desmos. Все, что требуется, - это некоторая способность рисовать несколько вертикальных полос и отрезков линии - и, возможно, способность делать это в нужных местах.Вот цифра, чтобы поддерживать идею визуализации данных в цикле!
Визуальная статистика в действии.В общем, создание диаграмм и диаграмм в Desmos - это больше искусство, чем настоящая наука! Щелкните, чтобы написать в Твиттере
Регрессия
При просмотре серии точек и связанной с ней диаграммы разброса вполне естественно, что мы стремимся глубже понять природу взаимосвязи - если таковая имеется - между двумя рассматриваемыми переменными. В этом случае имеет смысл использовать регрессионных моделей для объяснения и прогнозирования поведения одной переменной на основе другой.Фактически, если мы применим к данным «правильную» регрессионную модель, мы сможем - чаще всего - обнаружить удивительные идеи, которые было бы трудно получить в противном случае.
В Desmos, если у вас есть таблица даже с двумя столбцами - скажем, $ x_1 $ и $ y_1 $ - вы можете создать регрессионную модель для связанных точек, сколько вам угодно. Для линейной регрессионной модели просто введите $ y_1 \ sim mx_1 + b $ в новую строку, и Desmos будет более чем счастлив предоставить вам наиболее подходящую строку .2 + b x_1 + c $, и парабола должна быть готова для вас в мгновение ока. Кроме того, если вы предпочитаете вместо этого использовать полином более высокой степени или, может быть, вы просто считаете, что экспонента или логистическая модель более подходящая, тогда вы, безусловно, можете попробовать и их - если вы следуйте «синтаксису регрессии», описанному выше.
Более того, хотя графический интерфейс Desmos построен в основном для 2D-графика , это на самом деле не мешает нам выполнять многомерную регрессию .Действительно, если нам дана гигантская таблица с 4 столбцами - говорит $ x_1 $, $ x_2 $, $ x_3 $ и $ y_1 $ - тогда мы можем подогнать линейную модель для этих переменных, просто набрав что-нибудь в строке $ y_1 \ sim ax_1 + bx_2 + cx_3 + d $ в командную строку, так что даже если Desmos не оборудован должным образом для построения графиков, включающих несколько независимых переменных , мы можем продолжить выполнение многомерной регрессии, как будто ничего не произошло в первом место!
Pro-Tip
Хотя имя переменной обычно принимает форму одной буквы в Desmos, мы по-прежнему можем использовать столько индексов , сколько захотим.2 $ модели. Кроме того, мы также можем использовать серую кнопку «график» (под тегом «остатки»), чтобы включить остатков в как график, так и таблицу - и, если мы достаточно предприимчивы - передать остаточную переменную в снова командную строку для более детального анализа!
Регрессия в Десмосе. Обратите внимание, что многомерная регрессия все еще может выполняться - только не в виде графика.Хорошо. Теперь, когда большинство основных функций улажено, давайте перейдем к некоторым другим функциям, которые время от времени могут оказаться полезными.В частности, мы увидим, как использовать Desmos для настройки графика, настройки , создания заметок , организации линий в папок и использования save и с общими функциями !
Настройка графика
Если вы посмотрите в верхний правый угол пользовательского интерфейса Desmos, вы увидите значок с гаечным ключом на нем . Зачем надоедает? Потому что это место, где вы можете получить доступ к меню Graph Setting , которое содержит множество глобальных настроек , которые можно настроить для практических и не очень практичных целей . К ним, среди прочего, относятся:
- Переключение сетки с прямоугольной формы на круглой формы или полное отключение.
- Маркировка осей $ x $ и $ y $.
- Изменение размера шага каждой оси (например, использование $ \ dfrac {\ pi} {2} $ в качестве размера шага при построении графика тригонометрических функций ).
- Интерпретация углов в градусах или радианах .
Кроме того, под значком гаечного ключа вы должны увидеть значки $ + $ и $ - $. Как и следовало ожидать, эти значки используются для увеличения масштаба и уменьшения масштаба графика, соответственно, и когда одна из функций задействована, вы увидите под значком $ - $ дополнительный значок дома , который позволяет вернуться к уровню масштабирования по умолчанию . Подумайте об этом как о некой подстраховке на случай, если вы раздуваете график до непропорциональной степени (буквально)!
Примечания
Примечания - это именно то, что нужно: примечание для вас и других, смотрящих на ваш график и командные строки.Чтобы создать новую заметку, щелкните командную строку там, где вы хотите, чтобы заметка появилась, затем введите
"(то есть символ двойной кавычки ), чтобы превратить командную строку в строку для заметки. не вычислительная функция , примечание все еще можно использовать для включения любого комментария , инструкции или объяснения , которые считаются относящимися к графику и окружающим его вычислениям. Фактически, мы даже можем добавить несколько гиперссылок здесь и там, чтобы немного оживить обсуждение.Просто не забудьте начать ссылку с префиксаhttpилиhttps.Сворачиваемые / расширяемые папки
Пример папки в Desmos.Папка , в первую очередь косметическая, представляет собой неотъемлемый инструмент для организации ваших командных строк в согласованный набор групп, последняя из которых может быть свернута или развернута по запросу. Как и в случае с заметкой, папку можно создать, сначала щелкнув командную строку, в которой должна появиться папка, а затем зайдя в меню «Добавить элемент» через значок $ + $ в верхнем левом углу.После создания папки ей можно присвоить метку , после чего командную строку можно легко перетащить в или из из папки, а значок треугольной стрелки рядом с ней можно использовать для разверните / сверните папку по своему желанию.
Изображений
Хотя графические калькуляторы - отличные инструменты для создания геометрических фигур , бывают случаи, когда изображение выходит за рамки простой геометрии и его нужно импортировать откуда-то еще.К счастью, эта функция хорошо поддерживается в Desmos, где изображение может быть добавлено к графику так же, как папка добавляется в командную строку.
По умолчанию Desmos любит размещать изображение так, чтобы его центр располагался в исходной точке , хотя мы все равно можем перемещать / изменять размер изображения, перетаскивая его по центру или 8 граничным точкам , окружающим его . Кроме того, непрозрачность изображения может быть отрегулирована с помощью значка Gear Icon , а его размерные значения / координаты центра также могут быть сконфигурированы численно .Черт возьми, мы можем даже подкрасться к некоторым неопределенным параметрам в них, тем самым превратив статическое изображение в летающее изображение - где размер меняется от одного места к другому!
Сохранение / совместное использование графиков
Находите могущественную силу Desmos привлекательной и собираетесь широко использовать ее в ближайшем будущем? Тогда имеет смысл создать учетную запись и работать с графиками , войдя в учетную запись . Почему? Потому что тогда вы можете на самом деле сохранить этих графиков, а поделиться ими с другими единомышленниками!
Фактически, работа с графиком при входе в систему позволяет вам присвоить графику заголовок , так что если вы решите сохранить его на потом, подойдет простой
Меню Share Graph в Desmos. Почему бы не выбрать вариант рассмотрения вашего графика для подбора персонала и посмотреть, что произойдет? 😉Ctrl + S.С другой стороны, любой сохраненный график можно также удалить - при необходимости - нажав кнопку $ \ displaystyle \ times $ рядом с именем удаляемого графика.И если вы чувствуете себя достаточно щедрым, вы всегда можете поделиться своей работой с другими, создав ссылку для диаграммы - через зеленый значок Share Graph в правом верхнем углу.Помните, что Desmos - это, в конце концов, облачное приложение, а это означает, что каждый раз, когда вы сохраняете график и публикуете его где-нибудь в Интернете, вы фактически вносите свой вклад в постоянно растущую базу данных модулей Desmos - и все это во имя науки и технологий. !
Уф! Это немного для невинно выглядящего графического онлайн-калькулятора, не так ли? Кстати, если вам удалось зайти так далеко, вы уже настоящий герой на пути к тому, чтобы стать опытным пользователем Desmos! В конце концов, решите ли вы использовать Desmos для построения графиков , вычисления , статистики или для других целей , есть надежда, что вы найдете способ использовать эти функции и адаптировать их к своему собственному усмотрению. потребности.Кто знает, может быть, вы даже сможете превратить часть своего вдохновения в плодотворный творческий процесс - возможно, с небольшим техническим поворотом на этом пути!
Хорошо. Готовы к подведению итогов? Вот набитая до отказа интерактивная таблица о том, что мы уже рассмотрели:
Предварительные сведения
Умножение Деление греческие буквы \ , \ alpha, \ beta $) Корни ($ \ sqrt {}, \ sqrt [n] {x} $) Верхний индекс Функция потолка Функция пола Функция знака 000 000 000 000 000 Абсолютное значение Круглые скобки Определение функций
Функции (в x $) Функции (в долларах и долларах США) Триггерные функции Экспоненциальные функции 4
Логические 4
Логические функции Рациональные функции Обратные триггерные функции Гиперболические функции $ 7$ , $ - $, $ \ times $, $ \ div $, $ \ hat {} $ и $ \ circ $) Полярные функции Функции, связанные с вычислениями
Оператор производной Простое представление Оператор интеграла Нижний / верхний пределы (интеграл) Интегральное выражение Частичное синтаксис
80 80 9 Именование кусочных функций Знаковая функция $ \ le, \ ge $ Symbols 7
96969696969696Неявные уравнения (например,g., круг, эллипс, гипербола) Параметрические уравнения Обозначенная переменная 17317 9249 Плоскости Круги (внутри или снаружи) Полярные кривые (внутри или снаружи) 91 91 4 4 910 910 910 Пробел (между неявными функциями) Ограничение (синтаксис) Ограничение на $ x Ограничение на 18804 долларов США Ограничение, касающееся как $ x $, так и $ y $ Ограничение, касающееся других обозначенных переменных Использование нескольких параметров 915000 9100 9100 5 Параметр) Размер приращения (параметр) Скорость (параметр) Направление (воспроизведение параметров) 99 4 Кнопка «Ползунок» 99 4 Подвижная точка Множественные параметры (в командной строке) Общий параметр (в нескольких командных строках) 9184 23 8 9184 9187 9184 9184 9187 9184 9184 9187 9184 9184 9187 9188 Дополнение
Вычитание Умножение Разделение Exponentiation 0 9184 9184 9184 9189 ) Ключевые точки (точки пересечения, локальные максимумы, локальные минимумы) Отображение координат (ключевых точек) Поиск корня Выражения именования
3 3Создание списка Явное перечисление Неявное перечисление 9194 Преобразование списка Одновременное построение графиков (с использованием списка) Построение нескольких математических объектов (с использованием списка) 4 23
33 Наибольший общий множитель Наименьший общий кратный Минимум Максимум Перестановка (подсчет) Факториал Функция потолка Функция этажа 00 ction Функция абсолютного значения Знаковая функция $ \ sum $ (Оператор) Клавиши со стрелками (навигация) Фиктивная переменная Верхние / нижние пределы (суммирование) 7979Операторы вложения Анимированный график (серия) Многочлен Тейлора 91 9180
80 9199 918 23Дифференциал Двойные / тройные интегралы Интегральная функция Таблица vs.Список Создание таблицы Построение нескольких точек в функции (таблица) Создание нескольких столбцов (таблица) Регулировка цвета (для точек в таблице) Стиль графика (точки в таблице) Новая переменная (как название столбца) gg 04Статистические показатели Среднее значение Медиана 9118 Среднее отклонение 918 918 917 918 918 918 918 980 9199 Разница Всего Длина Минимум Максимум 9199 Корреляция Диапазон Межквартильный интервал Графики 918 918 918 918 918 919 918 919 919 919 Модель регрессии Линейная регрессия Квадратичная регрессия Модель Высшая полиномиальная модель Логистическая модель Многовариантная регрессия Использование индексов (именование переменных) 4-119803 Квадрат 0 4 3 4 3 Корреляция / $ r ^ 2 $ (линия наименьших квадратов) Остаточная величина (линия наименьших квадратов) Настройка сетки (прямоугольная vs.Круговой) Оси маркировки Настройка размера шага Настройка угла (градусы по сравнению с радианами) 6 3 9116 3 Уровень масштабирования по умолчанию Создание заметки (горячая клавиша) Создание папки 03
Создание папки 03
4 4 Добавление / удаление строк из папки Развертывание / свертывание папки Регулировка прозрачности 6 9184Координаты центраЗначения размеров Перемещение / изменение размера изображений (визуальное илиЧисленно) Встраивание неопределенных параметров
Создание учетной записи Заголовок (График) 03
97 03
97 03
97 Удаление графика Создание ссылки для графика На этом окончательное руководство по Desmos подошло к концу.Конечно, это не означает, что все еще закончено - есть еще один способ использования Desmos, который имеет большую эстетическую и педагогическую ценность, и это создание вычислительных чертежей !
Обзор Десмоса сообществом | Здравый смысл образование
Как я его использую
Desmos бесплатно предоставляет графический калькулятор всем вашим ученикам. Его текущая функциональность не может заменить полнофункциональный графический калькулятор Texas Instruments, поскольку Desmos не может выполнять все типы вычислений.Однако со временем можно было бы предположить, что к Desmos добавятся дополнительные функции. Недавнее обновление принесло добавление таблиц данных к одной из функций Desmos. Любой учитель математики может легко интегрировать использование Desmos в свой класс. Учащиеся могут работать над задачей на калькуляторе, сохранять свою работу и делиться ею с другими. Работу можно даже встроить в блог или поделиться через ссылку bit.ly. Одним из самых мощных элементов Desmos является то, что он создает график, когда вы вводите числа в программу.Если вы измените число, график будет быстро перерисован. Студенты могут вносить эти изменения и видеть влияние этих изменений в режиме реального времени. Эта немедленная обратная связь об изменении графика - очень эффективный способ изучения математики учащимися.Мой дубль
Подумайте о том, чтобы выбросить старый калькулятор. Десмос здесь. Desmos - это следующее поколение графического калькулятора. Калькулятор может строить множество различных уравнений, от линий до парабол и т. Д.Он может взять набор данных и построить график. Он поддерживает функции и неравенства; он может отображать экспоненты и журналы, триггерные функции, задачи предварительного и исчисления, а также статистику и вероятность. Использование Desmos неограниченно в математическом классе. Что делает Desmos еще более мощным, так это то, что он был разработан с использованием технологии HTML5. Это означает, что программа хорошо работает на любом компьютере или планшете, в том числе и на iPad. Все, что вам нужно, это веб-браузер. Desmos - это бесплатный ресурс, поэтому нет причин, по которым вы не должны проверять его на уроках математики.Захватывающие планы партнеров: Lumen + Desmos
Дебора Хур, менеджер по продукту платформы STEM
Как вы, возможно, видели в нашем совместном объявлении от 13 ноября, Lumen сотрудничает с Desmos, чтобы сделать построение графиков очень простым, увлекательным и интуитивно понятным, чтобы учащиеся могли сосредоточиться на математике и не изо всех сил пытаться использовать устаревшие технологии.
В этом сообщении в блоге рассказывается о наших планах, и вот три способа узнать еще больше и помочь сформировать будущее внутри OHM для вас и ваших учеников:
Почему стоит сотрудничать с Desmos?
В то время, когда я преподавал математику в колледже, семестр за семестром я изо всех сил пытался провести моего класса из 35 первокурсников колледжа с помощью всех нажатий клавиш, чтобы просто изобразить две функции в разумном графическом окне и найти точки интереса.К тому времени, когда у всех была отображена одна и та же информация, было трудно не упустить самую важную часть деятельности - интерпретацию результатов. Однако слишком часто к этому моменту внимание моих учеников ослабевало, потому что им приходилось так пристально сосредотачиваться на механике получения результатов.
Desmos меняет правила игры. Поскольку он интуитивно понятен и доступен, он сокращает время, затрачиваемое на работу с технологией графического калькулятора. Вместо этого он позволяет учителям и ученикам снова сосредоточиться на математических концепциях и интерпретации.
И еще есть важный вопрос доступности. Хотя OHM уже соответствует стандартам доступности для построения графиков, Desmos предлагает расширенные функции для поддержки доступности на уровне WCAG 2.1 AA. Его графический калькулятор включает поддержку программы чтения с экрана с интуитивно понятным языком и масштабированием с высоким разрешением. Он также включает отслеживание звука с запатентованной технологией Desmos, которая использует звук, чтобы помочь слабовидящим и слепым ученикам определить положение, размер и форму графического материала.Другие инструменты Desmos также поддерживают отображение Брайля, масштабирование с высоким разрешением, обратный контраст и другие комплексные функции, которые делают его решения эффективными для любого пользователя, особенно для людей с различными способностями.
Здесь, в Lumen, мы рады сотрудничать с Desmos, чтобы предоставить потрясающие возможности построения графиков, сохраняя при этом нашу приверженность низким ценам. Несмотря на то, что мы несем дополнительные расходы на каждого учащегося за добавление инструментов Desmos в OHM, цены на OHM не меняются. (Примечание: стандартная цена Lumen составляет 25 долларов США за одного студента на курс; s к некоторым учебным заведениям могут применяться специальные цены и условия оплаты, включая предоставление студентам бесплатных материалов курса.)
Что впереди?
Потрясающие интерактивы
Исследования показывают, что учащиеся наиболее эффективно учатся на практике. Как инструктор, мне всегда нравилось находить интересные способы применить знания в классе. Однако некоторые из моих любимых занятий по построению графиков занимали много времени, и если ученик пропустил урок, он пропустил ценное занятие.Из-за сложности традиционных графических калькуляторов им часто было трудно наверстать упущенное.
Чтобы обеспечить эффективные возможности активного обучения, мы рады запустить в OHM функцию под названием «Desmos Interactives». В этих настраиваемых интерактивных учебных мероприятиях используется технология Desmos, которая помогает учащимся на практике знакомиться с математическими концепциями и построением графиков. Desmos Interactives ускоряет время в классе для ознакомления с концепцией. Они также представляют задания в виде графиков с достаточным контекстом, чтобы учащиеся могли исследовать их самостоятельно - так что пропустить урок больше не будет катастрофой.
На следующем GIF-изображении показано, как учащиеся смогут видеть и взаимодействовать с учебными заданиями, созданными с помощью графического онлайн-калькулятора на базе Desmos в Lumen OHM.
Desmos Interactives скоро станет новым типом элементов в OHM. Они позволяют инструкторам создавать, копировать или редактировать интерактивные материалы, включая пояснительную информацию и инструкции, которые помогут студентам управлять каждым графиком Desmos. Преподаватели могут копировать и адаптировать готовые интерактивные материалы, созданные Lumen, или создавать их с нуля.В феврале 2020 года мы выпустим полный набор интерактивных материалов по алгебре колледжей и алгебры колледжей с поддержкой Corequisite (более 30 интерактивных материалов для каждого курса!). Вскоре появятся полные наборы интерактивных материалов по промежуточной алгебре (середина весны 2020 г.) и «Введение в статистику» (лето 2020 г.).
На этом снимке экрана показано, как учителя смогут добавлять новые интерактивные учебные мероприятия на базе Desmos в Lumen OHM
.Калькулятор при назначении
Своевременное и объединенное предоставление ресурсов помогает нашим студентам иметь легкий доступ ко всем необходимым им инструментам в одном месте.Выпуск в настоящее время запланирован на осень 2020 года, и мы рады предложить возможность использования калькуляторов Desmos непосредственно в тестах OHM, включая домашние задания, викторины и т. Д. Преподавательский состав будет контролировать, какие экзамены активируют инструмент калькулятора, а также к какому типу калькулятора (базовый, научный, графический или геометрический) студенты могут получить доступ в рамках экзамена.
Калькулятор: нерасширенный вид
Расширенный вид
Удивительные вопросы по построению графиков
Рассматривая нашу дорожную карту на 2021 год, мы с нетерпением ждем возможности изучить, как мы можем использовать Desmos для расширения существующего типа вопросов с градуированными графиками OHM, чтобы включить более надежную библиотеку графиков для автоматической оценки.Пока что наш короткий список включает полиномы более высокого порядка, рациональные функции, логистический рост и многое другое. У вас есть идеи для построения графиков вопросов, которые вы хотели бы видеть в нашем новом типе вопросов с градуированными графиками? Пожалуйста, поделитесь своим мнением, используя эту форму!
Оставайтесь на связи!
Следите за обновлениями, чтобы получить дополнительную информацию по мере того, как мы продвигаемся дальше по пути внедрения новых функций на базе Desmos в OHM. А пока обращайтесь с любыми вопросами или отзывами. Мы ценим вашу поддержку и возможность служить вам и вашим ученикам.
Smarter Balanced для встраивания графического калькулятора Desmos Online в математические тесты
Группа тестирования Smarter Balanced объявила сегодня о партнерстве с Desmos, компанией, которая создала бесплатный онлайн-калькулятор для построения графиков, который дает Texas Instruments возможность заработать деньги.
Со следующего года студенты в 15 штатах, которые проводят экзамены общего ядра Smarter Balanced, будут использовать калькулятор Desmos во время прохождения государственных математических тестов, а не давно используемые портативные калькуляторы.Фактически, в 10 из этих штатов учащиеся средних школ уже используют онлайн-инструмент в текущем сезоне тестирования.
Тони Альперт, исполнительный директор консорциума Smarter Balanced Assessment Consortium, сказал, что это решение было основано на необходимости сделать калькуляторы более доступными, особенно для слепых или слабовидящих студентов. По его словам, калькулятор Desmos будет поддерживать обновляемые дисплеи Брайля, которые переводят слова на мониторе компьютера в шрифт Брайля и подают звуковые сигналы для обозначения наклона и направления линии.
Но в совместном пресс-релизе решение рассматривается как направленное на экономическое неравенство. В нем говорится:
До недавнего времени школьникам и студентам-математикам приходилось полагаться почти исключительно на дорогие портативные графические калькуляторы стоимостью более 100 долларов. Учащиеся, которые не могли позволить себе эти дорогие калькуляторы, остались с ограниченными возможностями, как и многие школы, которые не могли позволить себе покупать калькуляторы от имени своих учеников. ... Smarter Balanced хотела, чтобы у учащихся была альтернатива дорогим портативным графическим калькуляторам для учащихся, сдающих экзамены по математике в средней и старшей школе.Для этого потребовался онлайн-калькулятор, который Smarter Balanced можно было встроить прямо в тест ...
Это правда, что одна компания - Texas Instruments - давно заблокировала бизнес по производству графических калькуляторов для школ. (Фактически, любой читающий это, кто ходил в среднюю или среднюю школу в 1990-х или позже, вероятно, в какой-то момент использовал одно из неуклюжих устройств.)
Экзамен Smarter Balanced всегда имел встроенный калькулятор, известный как уравнение редактор, который выполнял основные функции, но некоторые преподаватели жаловались, что им сложно пользоваться (хотя это и не является непреодолимой проблемой).«Компоновка более интуитивно понятная» с Desmos, - сказал Альперт.
Давид и Голиаф?
Появление Десмоса, особенно в свете этого партнерства с крупной испытательной компанией, может стать историей Давида и Голиафа компьютерного века.
Эли Люберофф начал разработку программного обеспечения для Desmos в 2007 году, когда он был в отпуске из Йельского университета, где он специализировался на математике и физике. Он официально основал компанию в 2011 году.
«Они внедрили этот калькулятор, сделав его практически« магазином для мам и пап », - сказал Альперт.
Онлайн-калькулятор бесплатен для всех и может использоваться на настольных компьютерах, ноутбуках, планшетах и смартфонах. Согласно пресс-релизу, у калькулятора есть «миллионы активных пользователей в месяц в 146 странах, которые ежедневно проводят на калькуляторе 300 000 часов».
Издатели, включая Pearson и College Board, также внедрили его в некоторые из своих продуктов.
По словам Альперта, Smarter Balanced заплатила около 460 000 долларов за трехлетний контракт с Desmos.Он отметил, что это дает шести миллионам студентов доступ к инструменту.
Калькулятор, который студенты будут использовать во время тестирования, имеет несколько ключевых отличий от онлайн-калькулятора; в частности, он не будет решать уравнения с решениями с одной переменной (например, x + 4 = 8) для студентов. Учащиеся младших классов будут иметь доступ к меньшей функциональности, чем учащиеся старшей школы.
Для получения дополнительных новостей и информации о чтении, математике и STEM:
И зарегистрируйтесь здесь, чтобы получать уведомления на свой электронный почтовый ящик, когда истории публикуются по вопросам учебной программы.
Поддержка калькулятораDesmos | Департамент образования штата Миссисипи
Бесплатный веб-семинар от MDE и Algebra Nation® для учителей на YouTube (45 минут) - щелкните здесь
Что такое Десмос?
Desmos - это онлайн-калькулятор, созданный Эли Люберофф. Desmos можно использовать онлайн через ваш интернет-браузер, выбрав раскрывающийся список Math Tools, чтобы выбрать версию своего калькулятора.
Вы также можете загрузить приложение Desmos в Google Play для устройств Android, Apple App Store для устройств Apple, таких как iPhone и iPad, и Интернет-магазин Chrome для Chromebook, все за БЕСПЛАТНО .
Преимущества Desmos?
Национальный совет учителей математики (NCTM) придерживается позиции, что « необходимо , чтобы учителя и ученики имели регулярный доступ к технологиям , которые поддерживают и продвигают математическое осмысление, рассуждение, решение проблем и общение. Эффективные учителя оптимизируют потенциал технологий для развития понимания учащихся, стимулирования их интереса и повышения их знаний по математике. Когда учителя стратегически используют технологии , они могут обеспечить больший доступ к математике для всех учеников ». (NCTM, 2011)
Desmos предоставляет учителям легкодоступных технологий , которые продвигают обучение на основе запросов для развития математических знаний у учащихся.(КНИЛТ, 2016)
Desmos и MAAP - Начиная с оценок Программы академической оценки штата Миссисипи (MAAP) на 2020-2021 годы, графический калькулятор Desmos (версия MAAP) теперь является встроенным графическим калькулятором в платформу доставки тестов Nextera для завершения курса (EOC). ) Алгебра I. Графический калькулятор Desmos (версия MAAP) также доступен в практическом тесте по алгебре I в конце курса (EOC). Как всегда, использование любого графического калькулятора (онлайн или портативного) - это выбор учащегося, основанный на его или ее классных инструкциях.Учащимся по-прежнему будет разрешено использовать свои портативные калькуляторы при условии, что калькуляторы соответствуют требованиям, изложенным в Политике MAAP в отношении калькуляторов.
Калькулятор версии Desmos
Обучение с использованием Desmos.
- Teacher Desmos - Создайте БЕСПЛАТНУЮ учетную запись учителя, чтобы находить или создавать задания Desmos для ваших учеников, чтобы практиковать материалы по математике.
- Algebra Nation Mississippi - Деятельность, созданная для использования с платформой Algebra Nation.
- Студент Десмос -Свободный доступ студента к заданию, назначенному учителем. Студенты могут создавать бесплатные учетные записи для сохранения работы.
- Gifmos Создавайте гифки из уроков Desmos. Начните с создания чего-нибудь динамичного и потрясающего в графическом калькуляторе Desmos! Вы можете сделать это прямо в GIFsmos или импортировать один из ваших сохраненных графиков с Desmos.com, вставив его URL-адрес в список выражений в GIFsmos, и он будет автоматически импортирован для вас.
- Desmos Дистанционное обучение Алгебре I Сборник заданий - Упражнения в этом сборнике разработаны Desmos для студентов, изучающих алгебру, и особенно полезны в условиях дистанционного обучения.
Desmos Professional Development
Desmos - Дана Хо - Блог в библиотеках Gottesman
Desmos - это мощный онлайн-калькулятор для построения графиков, предназначенный для построения любых уравнений, изучения преобразований, создания сложных таблиц и многого другого. Самое приятное в этом графическом калькуляторе то, что каждый может использовать его бесплатно. В настоящее время им пользуются студенты, преподаватели и исследователи более чем в 169 странах. Пользователи могут создать учетную запись для сохранения всех своих графиков, уравнений и таблиц или использовать ее по мере необходимости.Desmos также предлагает Function Carnival, уникальную обучающую модель для студентов, которым сложно визуализировать математические уравнения.
Плюсы:
Одним из самых больших преимуществ этого приложения является то, что это бесплатный ресурс. Графические калькуляторы могут стоить более 200 долларов, и для многих это расходы, которые они просто не могут себе позволить. Студенты и учителя могут использовать Desmos с любого устройства с доступом в Интернет бесплатно. Desmos также дает пользователям возможность создать учетную запись, позволяя им сохранять уравнения, графики, функции и даже изображения, которые они создали на своем «калькуляторе», для дальнейшего использования.Этот инструмент доступен более чем на 20 языках и работает так же, как обычный графический калькулятор, так что обучения практически не требуется. Веб-сайт также предлагает страницу комплексной поддержки для тех, кто нуждается в учебном пособии или хочет задать конкретный вопрос. На странице поддержки предлагаются краткие руководства по созданию таблиц данных, функциям построения графиков и созданию трехмерной графики.
Минусы:
Самым большим недостатком этого приложения является то, что, если у вас нет iPad, его нужно использовать в Интернете.В настоящее время инструмент предлагается только как приложение для Apple iPad, поэтому, если у пользователей нет iPad, доступа к Интернету или устройства, поддерживающего просмотр веб-страниц, они не могут использовать инструмент. Это также создает потенциальный риск потери данных при промежуточном использовании в случае возникновения проблем с сервером или сбоя питания.
Наш вынос:
Desmos - полезный инструмент для любого учителя, студента или энтузиаста математики, который хочет решать сложные уравнения, не ломая при этом деньги. В настоящее время приложение используется во всех штатах, а также в 169 странах, и команда Desmos работает над тем, чтобы сделать инструмент доступным на большем количестве языков.
- Среднее : используйте команду
 2/16=1)
2/16=1) Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».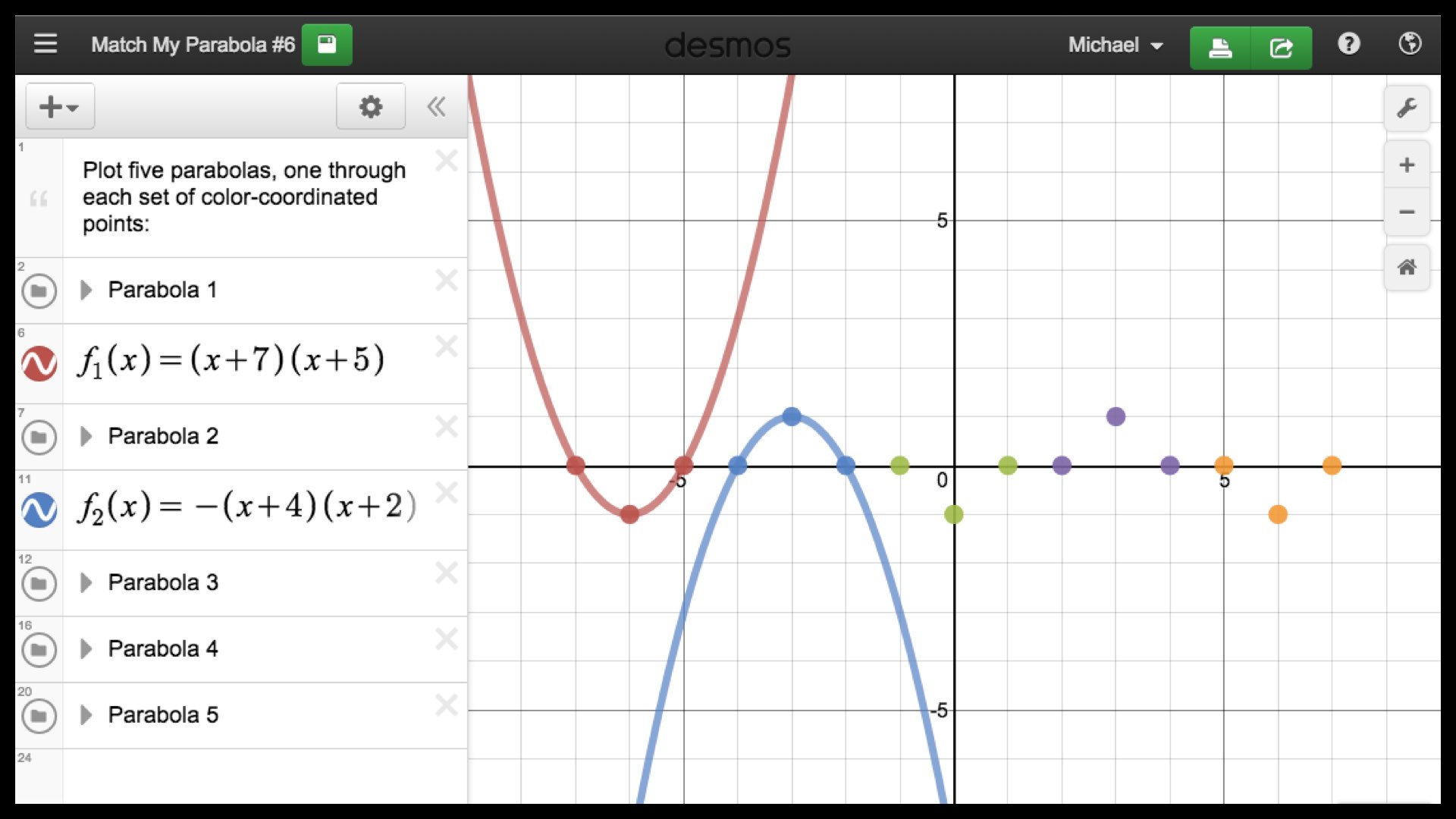 На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. Здесь пример для y = 2 x (a = 2 > 1).
Здесь пример для y = 2 x (a = 2 > 1). Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2
Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2

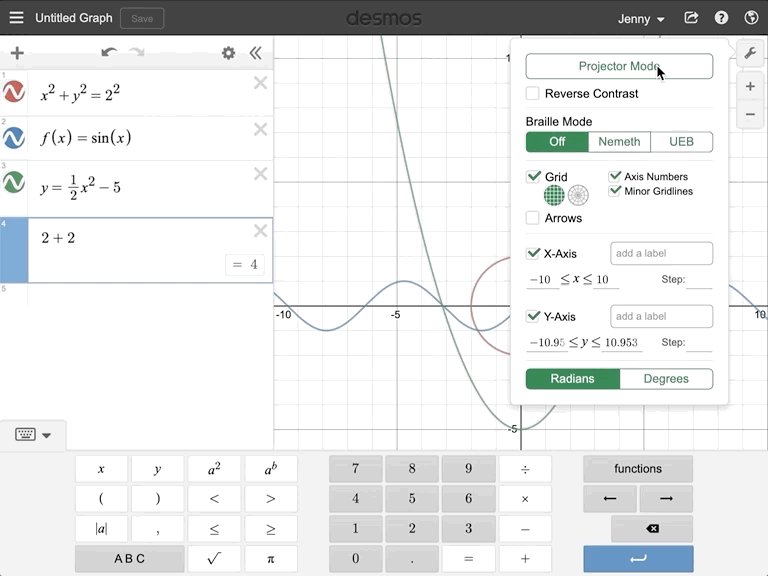 Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!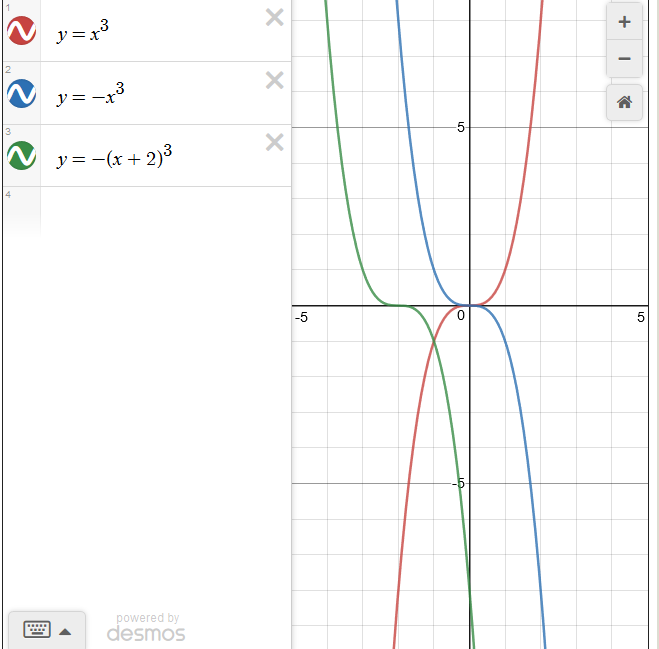
 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
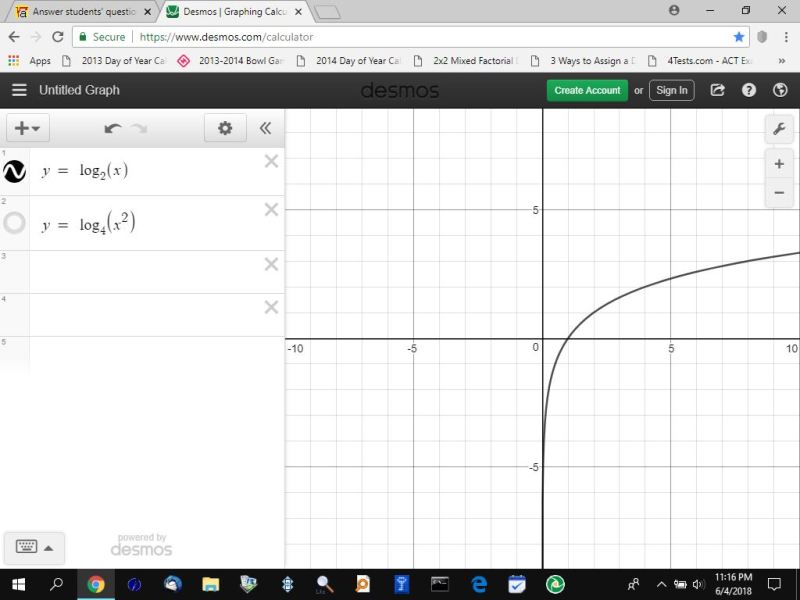 Изобразить график функции y = |-x 2 + 2|x| – 1|.
Изобразить график функции y = |-x 2 + 2|x| – 1|. 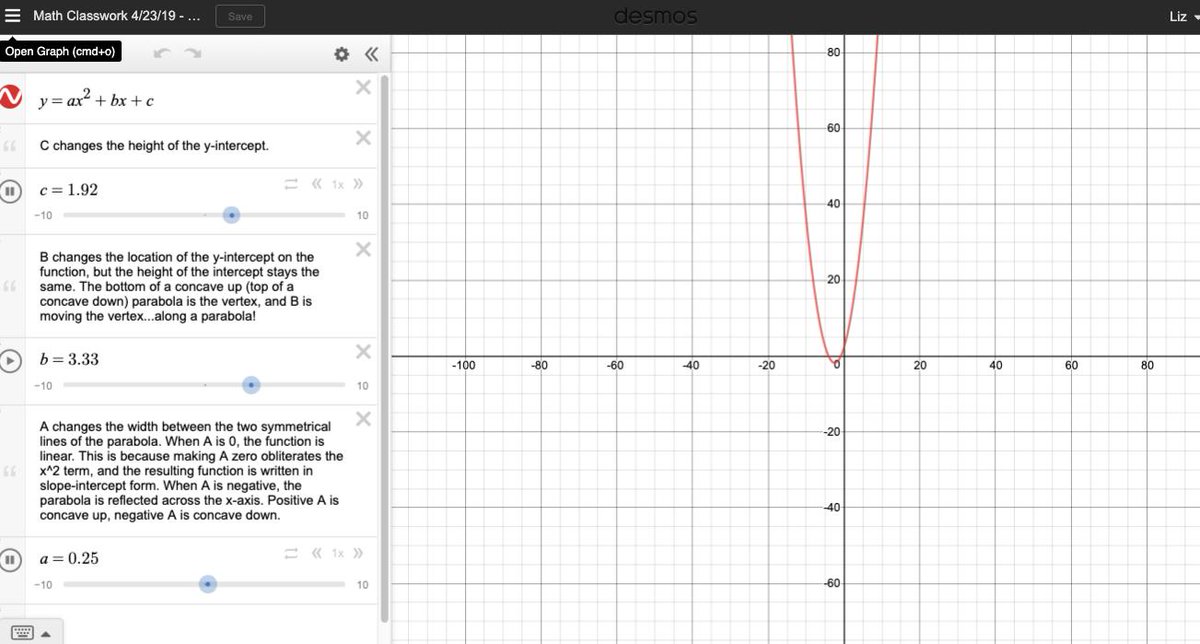 Для этого возвращаемся к алгоритму 2.
Для этого возвращаемся к алгоритму 2.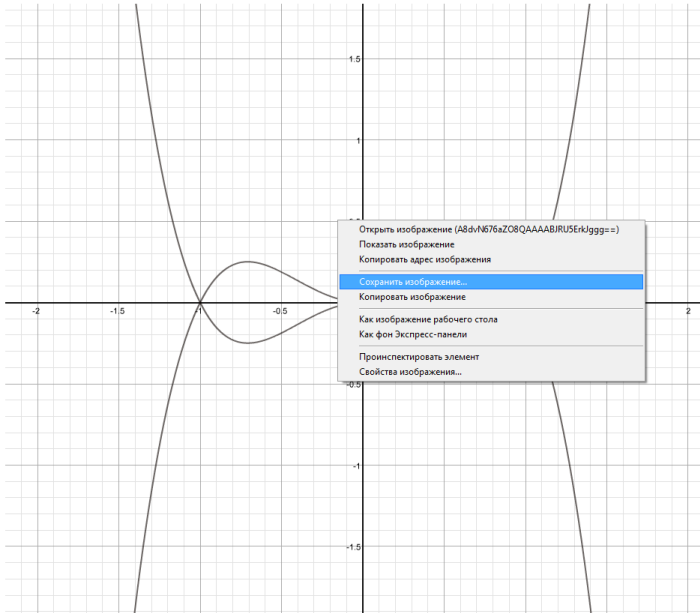
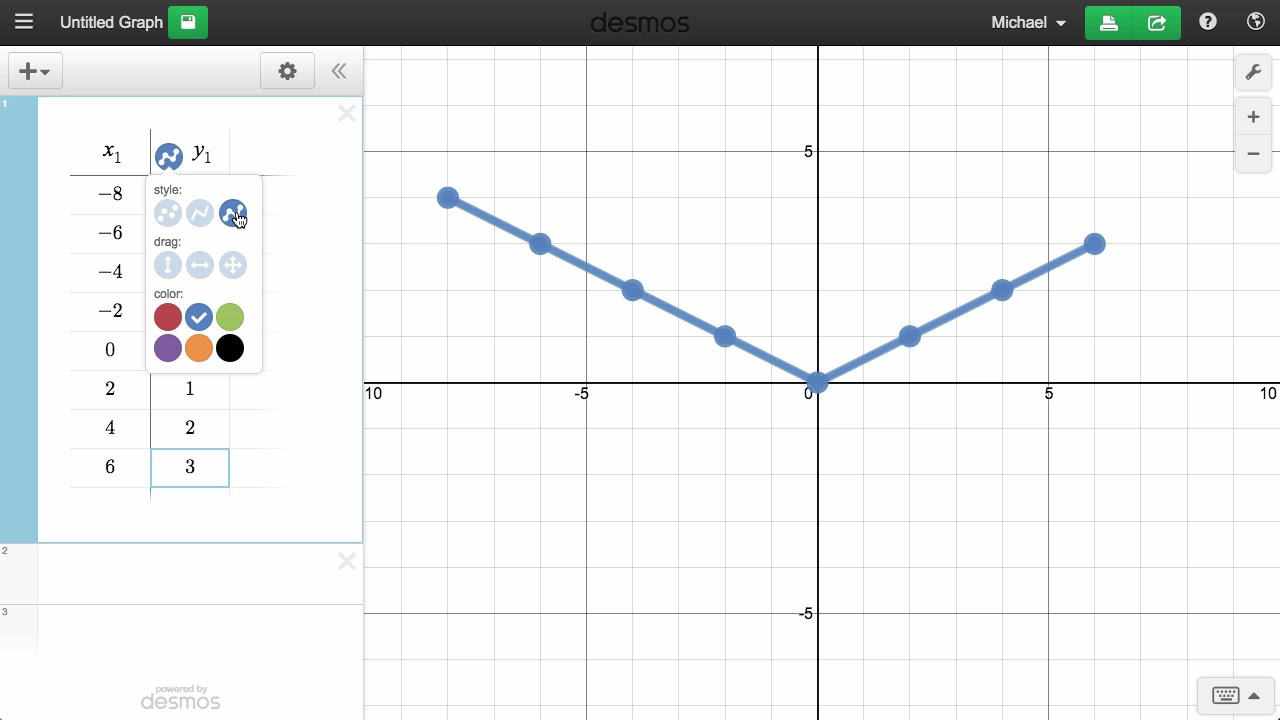 47).
47).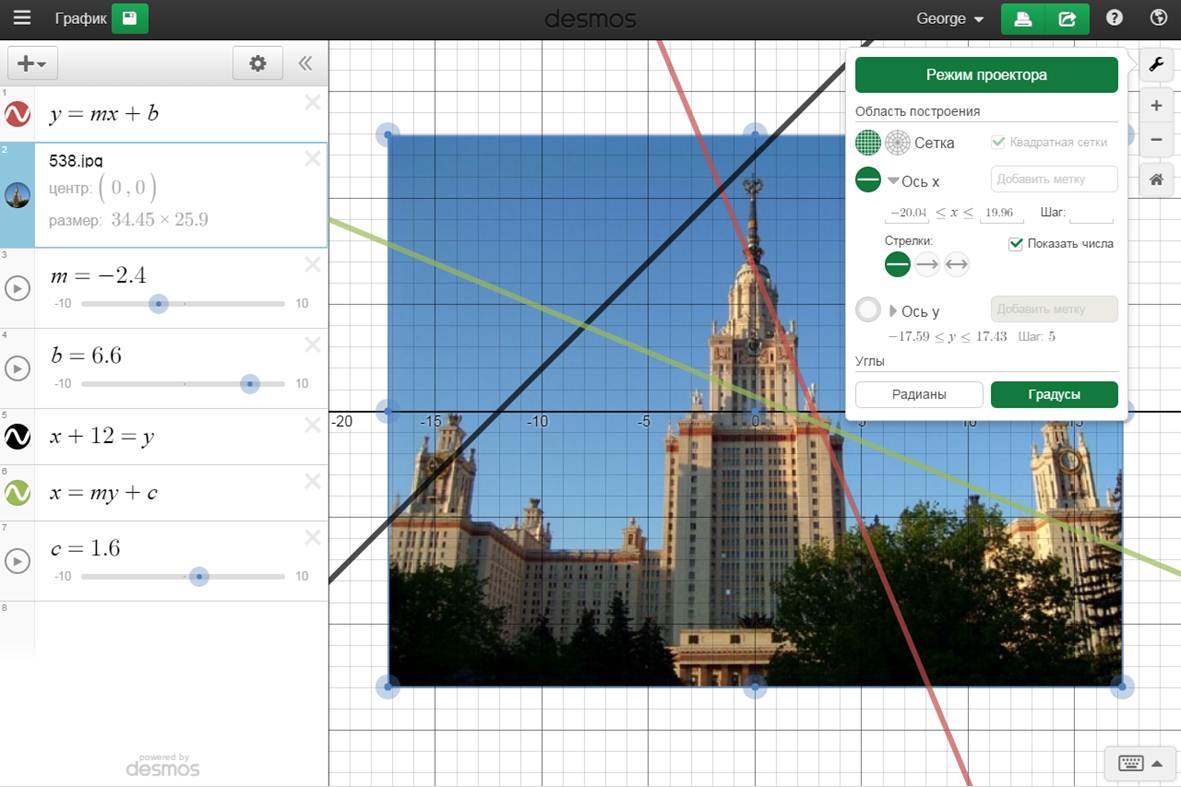
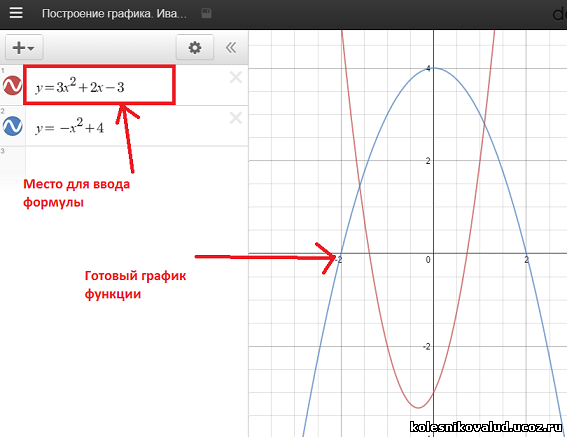

 В результате мы и получаем график функции у = |х| (рис. 50, б).
В результате мы и получаем график функции у = |х| (рис. 50, б).
 На рисунке методом сложения графиков построен график функции
На рисунке методом сложения графиков построен график функции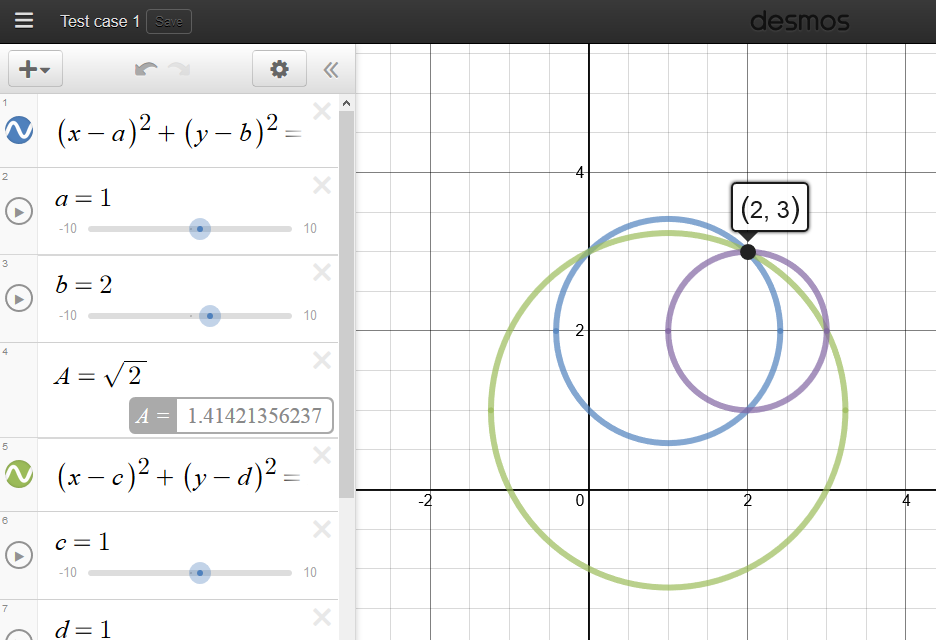
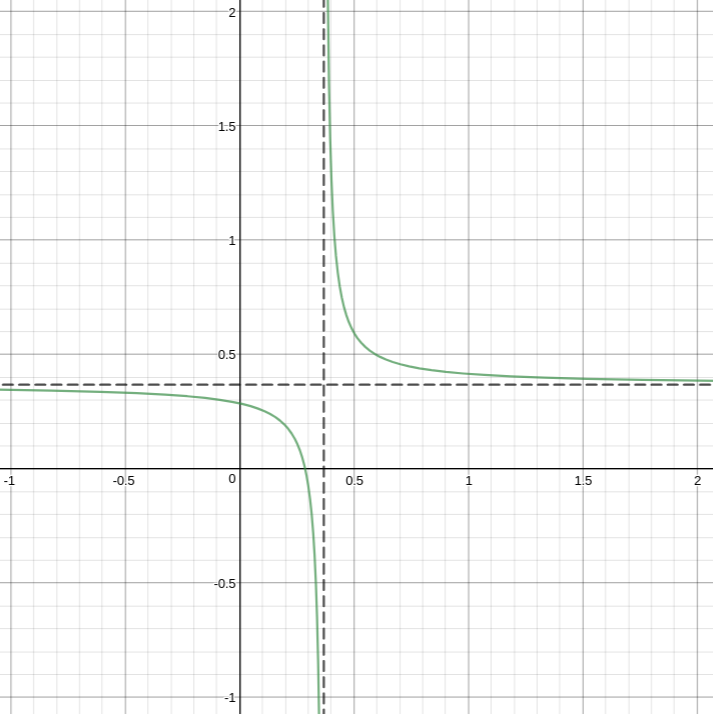

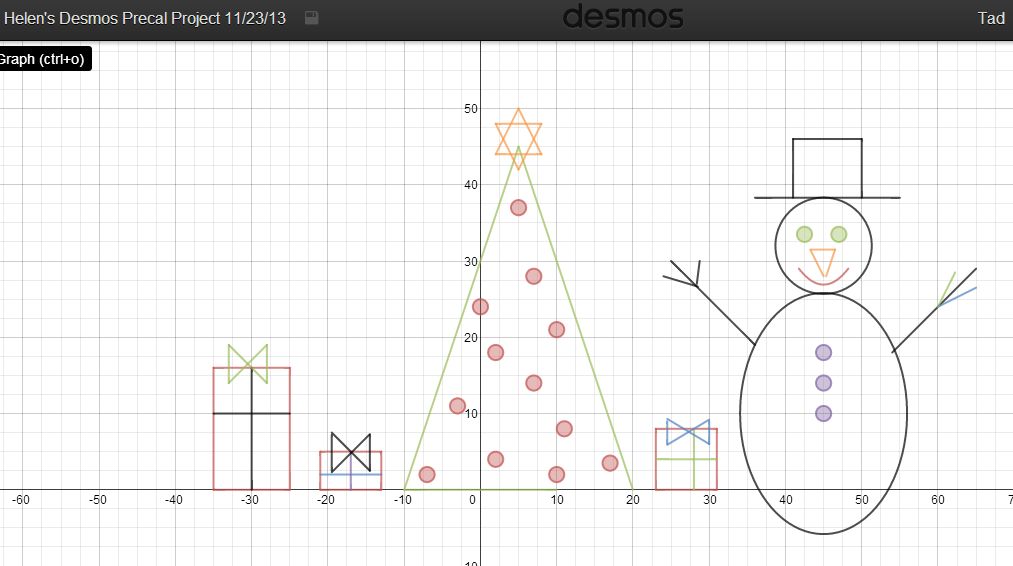
 Если вы потеряете фокус, нажмите CTRL + SHIFT + O , чтобы получить доступ к списку объектов, и выберите график, нажав ENTER .
Если вы потеряете фокус, нажмите CTRL + SHIFT + O , чтобы получить доступ к списку объектов, и выберите график, нажав ENTER . Если в этом поле есть текст, нажмите CTRL + A , чтобы выделить текст и либо удалить его, либо введите новый замещающий текст, чтобы заменить существующее содержимое.
Если в этом поле есть текст, нажмите CTRL + A , чтобы выделить текст и либо удалить его, либо введите новый замещающий текст, чтобы заменить существующее содержимое.
 Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста.
Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста.
Ваш комментарий будет первым