Исследовать функцию и построить график онлайн: Исследование функции и построение графика — Магазин Apple iPhone в Перми

Содержание

Исследование функции онлайн. Решение задач на построение графика и полное исследование функции он-лайн

Исследование функции производится по четкой схеме и требует от студента твердых знаний основных математических понятий таких, как область определения и значений, непрерывность функции, асимптота, точки экстремума, четность, периодичность и т.п. Студент должен свободно дифференцировать функции и решать уравнения, которые порой бывают очень замысловатыми.

То есть данное задание проверяет существенный пласт знаний, любой пробел в которых станет препятствием к получению правильного решения. Особенно часто сложности возникают с построением графиков функций. Эта ошибка сразу бросается в глаза преподавателю и может очень сильно подпортить вашу оценку, даже если все остальное было сделано правильно. Здесь вы можете найти задачи на исследование функции онлайн: изучить примеры, скачать решения, заказать задания.

Исследовать функцию и построить график: примеры и решения онлайн

Мы приготовили для вас множество готовых исследований функций, как платных в решебнике, так и бесплатных в разделе Примеры исследований функций.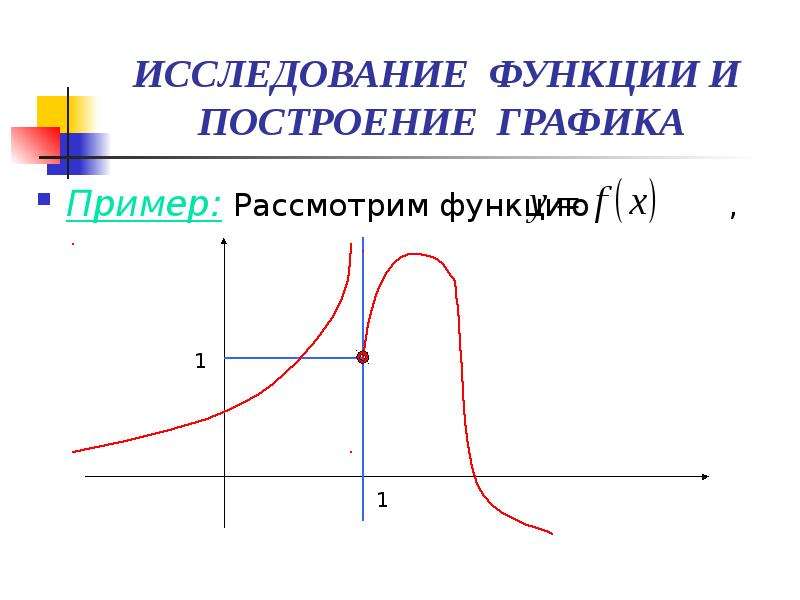

На основе этих решенных заданий вы сможете детально ознакомиться с методикой выполнения подобных задач, по аналогии выполнить свое исследование.

Мы предлагаем готовые примеры полного исследования и построения графика функции самых распространенных типов: многочленов, дробно-рациональных, иррациональных, экспоненциальных, логарифмических, тригонометрических функций. К каждой решенной задаче прилагается готовый график с выделенными ключевыми точками, асимптотами, максимумами и минимумами, решение ведется по алгоритму исследования функции.

Решенные примеры, в любом случае, станут для вас хорошим подспорьем, так как охватывают самые популярные типы функций. Мы предлагаем вам сотни уже решенных задач, но, как известно, математических функций на свете — бесконечное количество, а преподаватели — большие мастаки выдумывать для бедных студентов все новые и новые заковыристые задания. Так что, дорогие студенты, квалифицированная помощь вам не помешает.

Решение задач на исследование функции на заказ

На этот случай наши партнеры предложат вам другую услугу — полное исследование функции онлайн на заказ. Задание будет выполнено для вас с соблюдением всех требований к алгоритму решения подобных задач, что очень порадует вашего преподавателя.

Мы сделаем для вас полное исследование функции: найдем область определения и область значений, исследуем на непрерывность и разрывность, установим четность, проверим вашу функцию на периодичность, найдем точки пересечения с осями координат. Ну и, конечно же, дальше с помощью дифференциального исчисления: разыщем асимптоты, вычислим экстремумы, точки перегиба, построим сам график.

Представьте себе: вы получите готовое, гарантированно правильно решенное задание за скромную сумму! Может быть, вам осталось решить только один, самый сложный пример, с которым вы сами

никак не справитесь? Не затягивайте, закажите его или скачайте и сдавайте зачет на отлично!

Еще про задачи исследования функции:

Исследовать функцию и построить график

Краткая теория

Наиболее наглядное представление о ходе изменения функции дает ее график. Поэтому построение графика является заключительным этапом исследования функции, в котором используются все результаты ее исследования.

Схема исследования функции с последующим построением графика такова:

Исследование области определения функции.
Исследование функции на четность и нечетность.
Нахождение точек пересечения графика с осями координат
Исследование функции на точки разрыва. Нахождение вертикальных асимптот. Нахождение горизонтальных и наклонных асимптот.

Исследование функции на экстремум и интервалы монотонности функции.
Исследование функции на интервалы выпуклости и вогнутости графика функции. Нахождение точек перегиба графика функции.
Построение графика функции.

Полученные данные следует использовать для построения графика функции. Если исследуемая функция является четной или нечетной, то ее достаточно исследовать при неотрицательных значениях аргумента из множества ее задания и принять во внимание, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

Если, например, функция имеет период , то следует построить график на отрезке , а затем продолжить его периодически на всю числовую ось.

Кроме того, если полученных данных окажется недостаточно, то следует, воспользовавшись уравнением , найти дополнительные точки графика, в которых его изменение менее ясно.

Разумеется, в процессе исследования функции не обязательно придерживаться приведенной схемы, иногда порядок исследования полезно выбрать, исходя из конкретных особенностей данной функции.

Примеры решения задач

Задача 1

Исследовать функцию и построить ее график:

Решение

1) Область определения функции:

2) Исследуем функцию на четность-нечетность:

Функция является четной

3) Находим точки пересечения с осями координат:

График функции пересекает ось в точках и . Ось график функции не пересекает.

4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

В точке существует разрыв 2-го рода.

Прямая –вертикальная асимптота.

Для нахождения наклонной асимптоты вычисляем пределы:

–горизонтальная асимптота

5) Исследуем функцию на экстремум. Найдем производную функции.

Первая производная на области определения в нуль не обращается

-функция возрастает

-функция убывает

6) Исследуем функцию на интервалы выпуклости и вогнутости.

Вторая производная функции не равна нулю на всей области определения

–график функции вогнутый

– график функции вогнутый

7) График функции имеет вид:

Задача 2

Исследовать функцию и построить ее график:

Решение

1) Область определения функции:

2) Исследуем функцию на четность-нечетность:

Функция является нечетной

3) График функции оси координат не пересекает

4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:

В точке существует разрыв 2-го рода.

Прямая –вертикальная асимптота.

Для нахождения наклонной асимптоты вычисляем пределы:

–наклонная асимптота

5) Исследуем функцию на экстремум. Найдем производную функции.

Приравняем найденную производную к нулю и решим полученное уравнение:

-функция возрастает

-функция убывает

-функция возрастает

6) Исследуем функцию на интервалы выпуклости и вогнутости.

Вторая производная функции не равна нулю на всей области определения

–график функции выпуклый

– график функции вогнутый

7) График функции имеет вид:

Задача 3

Исследовать функцию и построить ее график.

Решение

1) Область определения функции:

2) Исследуем функцию на четность-нечетность:

Функция не обладает свойствами четности — нечетности

3) Находим точки пересечения с осями координат:

График пересекает ось в точке (-0618, 0) и (1.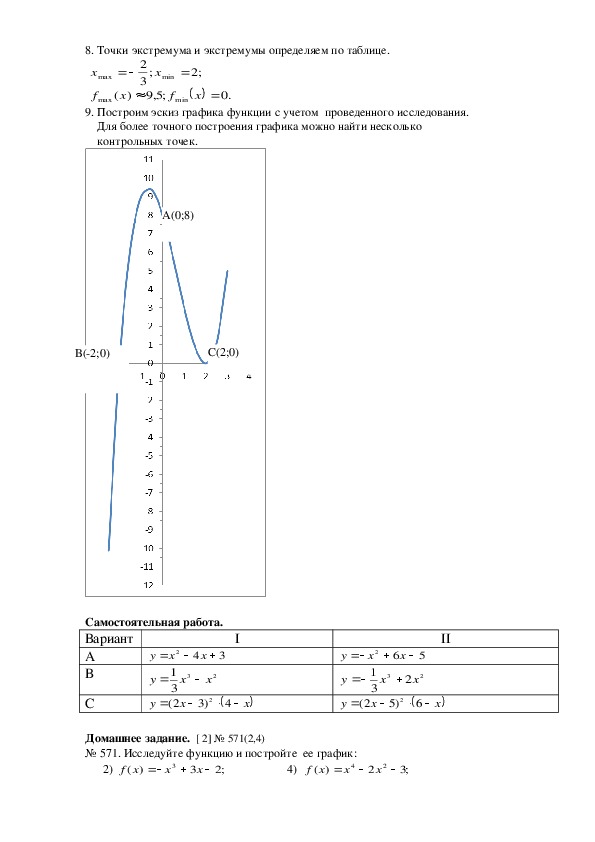 618, 0)

4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:

Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.

Для нахождения наклонной асимптоты вычисляем пределы:

Прямая –горизонтальная асимптота

5) Исследуем функцию на экстремум. Найдем производную функции.

Приравняем найденную производную к нулю и решим полученное уравнение:

Полученное уравнение действительных корней не имеет

– функция убывает

6) Исследуем функцию на интервалы выпуклости и вогнутости.

– график функции выпуклый

– график функции вогнутый

– график функции выпуклый

– график функции вогнутый

7) График функции имеет вид:

На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.

Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.

Полное исследование функции и построение графика, примеры решений

Задание. {\prime \prime}=0 : x=1$ ; при $x=0$ и $x=2$ вторая производная не существует.

Таким образом, на промежутках $(0 ; 1)$ и $(2 ;+\infty)$ функция вогнута, а на промежутках $(-\infty ; 0)$ и $(1 ; 2)$ — выпукла. Так как при переходе через точку $x=1$ вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Эскиз графика.

Исследование функций и построение графиков

Опорными точками при исследовании функций и построения их графиков служат характерные точки – точки разрыва, экстремума, перегиба, пересечения с осями координат. С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости и вогнутости графика, наличие асимптот.

Эскиз графика функции можно (и нужно) набрасывать уже после нахождения асимптот и точек экстремума, а сводную таблицу исследования функции удобно заполнять по ходу исследования.

Обычно используют следующую схему исследования функции.

1. Находят область определения, интервалы непрерывности и точки разрыва функции.

2. Исследуют функцию на чётность или нечётность (осевая или центральная симметрия графика.

3. Находят асимптоты (вертикальные, горизонтальные или наклонные).

4. Находят и исследуют промежутки возрастания и убывания функции, точки её экстремума.

5. Находят интервалы выпуклости и вогнутости кривой, точки её перегиба.

6. Находят точки пересечения кривой с осями координат, если они существуют.

7. Составляют сводную таблицу исследования.

8. Строят график, учитывая исследование функции, проведённое по вышеописанным пунктам.

Пример. Исследовать функцию

и построить её график.

Решение.

1. Область определения функции – вся числовая прямая. Множеством значений данной функции, как и всякой показательной функции, служит интервал ]0, +∞[. Поэтому график функции расположен выше оси Ox,

2. Напомним: из школьного курса известно, что функция y = f(x) называется чётной, если

для всех x, принадлежащих области определения функции.

.
График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y).
Функция y = f(x) называется нечётной, если
для всех x, принадлежащих области определения функции.
График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; -y).
Наша исследуемая функция чётная, так как
её график симметричен относительно оси Oy. Поэтому исследование можно выполнять только для ]0, +∞[.
3. Вертикальных асимптот у графика нет, поскольку функция непрерывна на всей числовой прямой. Горизонтальной асимптотой является ось Ox, так как
Поскольку кривая имеет двустороннюю горизонтальную асимптоту y = 0, у неё не может быть наклонных асиптот.
4. Находим . Из уравнения имеем .
Так как при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку .
5. Находим Из уравнения получаем т. е. .
Учитывая чётность функции, исследуем знаки в окрестности только точки .
Следовательно, при x = 1 кривая меняет выпуклость на вогнутость. Так как то — точка перегиба кривой. Угловой коэффициент касательной к кривой в этой точке . Поэтому в точке перегиба касательная образует с осью Ox тупой угол.
6. График не пересекает оси Ox, поскольку он расположен выше неё. Найдём точки пересечения кривой с осью Oy: полагая x=0, имеем
Тем самым получим точку (0; 1) графика, которая совпадает с точкой максимума.
7. Составим сводную таблицу исследования функции, куда внесём все характерные точки и интервалы между ними. Учитывая чётность функции, получаем следующую таблицу:

Особенности графика

[-1, 0[

+

—

Возрастает

Выпуклый

0

0

—

1

(0; 1) – точка максимума

]0, 1[

—

—

Убывает

Выпуклый

1

—

0

— точка перегиба, образует с осью Ox тупой угол

]1, +∞[

—

+

Убывает

Вогнутый

+∞

—

+

y = 0 – горизонтальная асимптота

8. Используя результаты исследования, строим график функции (см. рисунок).
Весь блок «Производная»
Исследование функции и построение графика с помощью производной
Пример 1.

Решение

1) Область определения функции

2) Чётность, нечётность функции:

Функция не является ни чётной, ни нечётной.

3) Точки разрыва функции :

— вертикальная асимптота

Найдём наклонные асимптоты функции :

- горизонтальная асимптота

4) Промежутки монотонности функции и точки экстремума:

              — критическая точка первого рода

Функция возрастает при и при .

Точек экстремума нет.

5) Промежутки выпуклости и вогнутости и точки перегиба:

             — критические точки второго рода

Функция выпукла при и вогнута при .

— точка перегиба

6) Точки пересечения с осями координат:

с : — точек пересечения с нет

с:

7) Построим график функции:

Пример 2.

Исследовать функцию и построить ее график:

Решение

1) Область определения функции

2) Чётность, нечётность функции:

Функция не является ни чётной, ни нечётной.

3) Точки разрыва функции :

— вертикальная асимптота

Найдём наклонные асимптоты функции :

- горизонтальная асимптота

4) Промежутки монотонности функции и точки экстремума:

              — критические точки первого рода

Функция возрастает при и убывает при и при.

— точка максимума

5) Промежутки выпуклости и вогнутости и точки перегиба:

             — критические точки второго рода

Функция выпукла при и и вогнута при .

— точка перегиба

6) Точки пересечения с осями координат:

с :

с:

7) Построим график функции:

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Схема исследования поведения функций, применяемая для построения графиков функций
Для построения графика функции y = f (x) желательно сначала провести исследование поведения функции y = f (x) по следующей схеме.
Найти область определения D ( f ).
Выяснить, является ли функция y = f (x) четной или нечетной.
Выяснить, является ли функция y = f (x) периодической.
Найти асимптоты графика функции.
Вычислить производную функции f ‘ (x) .
Найти критические точки функции y = f (x) .
Найти интервалы возрастания и убывания функции y = f (x) .
Найти экстремумы функции y = f (x) .
Найти точки пересечения графика функции y = f (x) с осями координат.
Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс Ox, то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.
Вычислить вторую производную функции f »  (x) .
Найти интервалы, на которых функция y = f (x) выпукла вверх, а также интервалы, на которых функция y = f (x) выпукла вниз.
Найти точки перегиба графика функции y = f (x) .
Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.
Примеры построения графиков функций
Пример 1. Построить график функции
y = x³ + 8x² + 16x + 128 (1)
Решение. Областью определения функции (1) является вся числовая прямая.
Функция (1) не является ни четной, ни нечетной.
Функция (1) не является периодической.
Вертикальных асимптот у графика функции (1) нет, так как для любого числа x₀
Проверим, есть ли у графика функции (1) наклонные асимптоты. Поскольку
то делаем вывод, что наклонных асимптот у графика функции (1) нет.
Теперь вычислим производную функции (1):
y’ (x) = 3x² + 16x + 16 .
Поскольку y’ (x) существует для всех , то все критические точки функции являются ее стационарными точками, то есть точками, в которых
y’ (x) = 0 .
Найдем стационарные точки функции (1), интервалы, на которых y’ (x) сохраняет знак, а также экстремумы функции. Для этого решим квадратное уравнение
3x² + 16x + 16 = 0.
Изобразим на рисунке 1 диаграмму знаков производной y’ (x)
Рис.1
На интервалах и производная y’ (x) положительна, значит, функция (1) возрастает. На интервале производная y’ (x) отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.
Рис.2
При переходе через точку x = – 4 производная функции y’ (x) меняет знак с «+» на «–» . Следовательно, точка x = – 4 является точкой максимума функции (1). При переходе через точку производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка является точкой минимума функции (1).
Найдем значения функции (1) в стационарных точках:
y (–4) = 256 ,
Теперь вычислим вторую производную функции (1):
y» (x) = (y’ (x))‘ = (3x² + 16x + 16)‘ = 6x + 16 .
y» (x) = (y’ (x))‘ =
= (3x² + 16x + 16)‘ =
= 6x + 16 .
Вторая производная y» (x) обращается в нуль при . Изобразим на рисунке 3 диаграмму знаков второй производной y» (x)
Рис.3
При переходе через точку вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, – точка перегиба графика функции (1). При функция (1) выпукла вверх, при функция (1) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).
Рис.4
Для того, чтобы найти точки пересечения функции (1) с осью Ox , решим уравнение
x³ + 8x² + 16x + 128 = 0 ,
x² (x + 8) + 16 (x + 8) = 0 ,
(x + 8) (x² + 16) = 0 .
Таким образом, точка (– 8; 0) является единственной точкой пересечения графика функции (1) с осью Ox . Точкой пересечения графика функции (1) с осью Oy будет точка (0; 128) .
На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).
Рис. 5
Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис.6):
Рис.6
Пример 2. Построить график функции
(2)
Решение. Областью определения функции (2) является вся числовая прямая, за исключением точки x = 0 , то есть .
Функция (2) не является ни четной, ни нечетной.
Функция (2) не является периодической.
Прямая x = 0 является вертикальной асимптотой графика функции (2), так как
Для того, чтобы выяснить, имеются ли у графика функции (2) наклонные асимптоты, представим правую часть формулы (2) в другом виде:
(3)
Из формулы (3) получаем равенство
откуда вытекает, что прямая
y = x + 3
является наклонной асимптотой графика функции (2), как при , так и при .
Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):
(4)
Для того, чтобы найти стационарные точки функции (2), преобразуем правую часть формулы (4):
Следовательно,
(5)
и стационарными точками функции (2) являются точки x = – 1 и x = 2 . Поскольку y’ (x) не существует при x = 0 , то критическими точками функции (2) являются точки
x = – 1 , x = 0, x = 2 .
Изобразим на рисунке 7 диаграмму знаков производной y’ (x)
Рис.7
На интервалах , и производная y’ (x) положительна, значит, функция (2) возрастает на этих интервалах. На интервале (0, 2) производная y’ (x) отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.
Рис.8
При переходе через точку x = – 1 производная функции y’ (x) знак не меняет, значит, в этой точке экстремума нет. При переходе через точку x = 2 производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка x = 2 является точкой минимума функции (2).
Найдем значения функции (1) в стационарных точках:
y (–1) = 0 ,
Теперь перейдем к вычислению второй производной функции (2). Проще всего это сделать, воспользовавшись формулой (4):
Вторая производная y» (x) обращается в нуль при x = – 1 . Изобразим на рисунке 9 диаграмму знаков второй производной y» (x)
Рис.9
При переходе через точку x = – 1 вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, x = – 1 – точка перегиба графика функции (2). При x < – 1 функция (2) выпукла вверх, при x > – 1 функция (2) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).
Рис.10
Найдем точки пересечения функции (2) с осями координат: точка (– 1; 0) является единственной точкой пересечения графика функции (2) с осью Ox , а точек пересечения графика функции (2) с осью Oy нет, поскольку x = 0 не входит в область определения функции (2).
На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).
Рис.11
Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис.12):
Рис.12
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Общая схема исследования функции и построения графиков (Лекция №11)
Найти ОДЗ и точки разрыва функции.

Найти точки пересечения графика функции с осями координат.

Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

Найти асимптоты графика функции: а) вертикальные, b) наклонные.

На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
. 1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=0.

Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
2. . Критические точки: x₁ = 1; x₂= –1.

3.
4. а) Вертикальных асимптот нет
б) . Асимптота – y = 0.

.
D(y)=(–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: .

.
а) Вертикальных асимптот нет
б).

Наклонных асимптот нет.

.
D(y)=(0; +∞). Функция непрерывна на области определения.

Пересечение с осью :

а) .
Вертикальная асимптота x = 0.

б).

Наклонная асимптота y = 0.

.
D(y)=( –∞;0)È(0;1)È(1;+∞).
Функция имеет две точки разрыва x= 0 и x= 1.

Точек пересечения с осями координат нет.

при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.

а)

Вертикальные асимптоты x = 0, x = 1.

б)

Наклонная асимптота y = x + 1.

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Во многих приложениях математического анализа встречаются комбинации показательных функций. Эти комбинации рассматриваются как новые функции и обозначаются:
– гиперболический синус.
– гиперболический косинус.
С помощью этих функций можно определить еще две функции.
– гиперболический тангенс.
– гиперболический котангенс.
Функции sh x, ch x, th x определены, очевидно, для всех значений x, т.е. их область определения (–∞; +∞). Функция же cthx определена всюду за исключением точки x = 0.
Между гиперболическими функциями существуют следующие соотношения, аналогичные соответствующим соотношениям между тригонометрическими функциями.
Найдем: .
Т.е. .
.
Итак, .
Следовательно, .
Найдем производные гиперболических функций
.
Аналогично можно показать .
.
Т.е. и .
Графики гиперболических функций. Для того чтобы изобразить графики функций
shx и chx нужно вспомнить графики функций y = e^x и y = e^—^x

Проведем исследования функции y = th x.
D(f) = (–∞; +∞), точек разрыва нет.

Точка пересечения с осями координат .

, функция возрастает на (–∞; +∞).

Вертикальной асимптоты нет.

.

y = cth x
D. Точка разрыва x = 0 cth x = 0 – нет

убывает на .

При x → +∞

Использование графических технологий для построения графиков функций
Графический калькулятор
Этот первый калькулятор существует уже несколько десятилетий. Это графический калькулятор . Это калькулятор с экраном и возможностью отображать ваши функции на графике для вас, как TI-85. Вы можете увеличивать и уменьшать масштаб графика. Эти калькуляторы могут отображать в виде графиков все виды функций за вас. Некоторые из более дорогих даже построят ваши 3D-функции.
Чтобы построить график на одном из этих калькуляторов, вы начнете с ввода функции y в единицах x . Если у вас есть калькулятор, способный строить трехмерные графики, вы можете ввести функцию с тремя переменными. После того, как вы закончите, вы затем нажмете кнопку, которая сообщает калькулятору о построении графика. Вы увидите график на своем экране. Затем вы можете использовать кнопки со стрелками для перемещения по графику. Переместите курсор туда, где ваш график пересекает ось x , и вы сможете увидеть, каковы ваши решения для функции.Это особенно полезно, если вам нужно решить сложную функцию.
Графические онлайн-калькуляторы
Еще одна технология, которую вы можете использовать, — это онлайн-графические калькуляторы. Вместо того, чтобы покупать физический графический калькулятор, теперь вы можете выйти в Интернет, посетить онлайн-графический калькулятор и ввести свою функцию для построения графика. И тогда вы увидите, что ваш график появится на экране. Вы можете использовать мышь, чтобы нажимать на разные точки на графике. С помощью этого метода вы сможете легко найти свои решения.
Например, вы хотите построить график этой функции.
Вы заходите в свой онлайн-калькулятор графиков, вводите свою функцию, а затем видите, как график появляется на вашем экране вот так.
Эти графические онлайн-калькуляторы позволяют легко находить важные моменты. Щелкните точки, и вы увидите их значения.
Единственным недостатком этих графических онлайн-калькуляторов является то, что для их использования требуется подключение к Интернету.
Программное обеспечение для построения графиков
Есть еще одна технология, которую вы можете использовать для построения графиков ваших функций. Вместо того, чтобы использовать онлайн-решение, вы можете фактически установить на свой компьютер математическое программное обеспечение, которое будет отображать функции для вас. Эта опция позволит вам графически отображать функции в любое время, когда вы используете свой компьютер.Для его использования не требуется подключение к Интернету. С ними более крутая кривая обучения, так как вам нужно немного изучить математическое программирование, чтобы использовать такое программное обеспечение.
Есть еще один тип графического программного обеспечения, которое вы можете использовать, для которого не требуется компьютер. Вместо этого требуется смартфон или планшет. Да, есть приложения для графического калькулятора, которые вы можете установить на свой телефон или планшет, которые позволят вам выполнять графические функции. Эти графические приложения позволяют создавать трехмерные графики с тремя переменными и на параметрических поверхностях.
Как и в случае с онлайн-калькуляторами для построения графиков, для построения графиков с помощью этих программ построения графиков вам необходимо ввести свою функцию, а затем указать программе, чтобы она построила график. Если у вас есть особые ограничения, их тоже нужно ввести. Затем вы можете увеличивать и уменьшать масштаб, чтобы увидеть, что делает график, и найти свои решения.
Итоги урока
Давайте рассмотрим.
Функции построения графиков никогда не были такими простыми. Это благодаря сегодняшним технологиям построения графиков.
Вот таблица, в которой перечислены технологии, упомянутые в этом уроке.
Технологии Описание
Графический калькулятор Калькулятор с экраном и возможностью построения графиков
Графический калькулятор онлайн Функции ввода и графиков с использованием компьютера с подключением к Интернету
Программное обеспечение для построения графиков График с использованием программного обеспечения для компьютера или смартфона / планшета
Изучение студентами функций и их графиков с помощью Desmos — Technology Tools for Teaching in Higher Education, The Practical Handbook Series
Ана Дафф
Графический калькулятор
Desmos — это открытый онлайн-инструмент с обширной числовой и визуальной универсальностью.Это позволяет пользователю строить и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, функции графиков и создавать модели регрессии из наборов данных, среди других возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент слайдера, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к конкретным компонентам.
Преимущества обучения с использованием Desmos
Открытый и бесплатный ресурс без регистрации или подписки
Позволяет статические и динамические графические демонстрации и количественный анализ двухмерных моделей
Можно предварительно организовать демонстрации и мероприятия
Требует от пользователей легко приобретаемых технических навыков
Позволяет легко делиться демонстрациями с другими пользователями
Ресурсы
Ноутбук или мобильное устройство (Android или iOS)
Интернет-браузер или приложение Desmos Graphing Calculator

Шаг 1.Создайте учетную запись на Desmos.com (необязательно)
Перейдите на сайт Desmos.com и перейдите по ссылке «Начать построение графиков». У вас есть возможность создать учетную запись и войти в систему, что позволит вам сохранять, называть и искать свою работу. Последующие шаги по реализации будут основаны на предположении, что вы вошли в свою учетную запись, чтобы воспользоваться этими функциями. Однако графические возможности Desmos не ограничиваются держателями учетных записей, и в этом случае можно сохранить доступ к своей работе, создав ссылку для общего доступа и сохранив ее на будущее.
Шаг 2. Откройте Графический калькулятор Desmos и создайте график
Щелкните График без названия и введите название графика (доступно только зарегистрированным пользователям). Введите краткое описание действия: поместите курсор в строку 1, нажмите +
(Добавить элемент), затем заметку «» и добавьте описание в строку 1.

Шаг 3. Укажите функцию, функциональные компоненты или данные, моделируемые функцией
Desmos позволяет пользователю явно указывать функцию (функции) и моделировать данные с помощью функции с использованием регрессии.Если вы используете упражнение как часть оценивания, попросите учащихся импортировать случайно сгенерированные данные (например, из документа Excel), чтобы в результирующих функциях была изменчивость.
Шаг 4. Создайте набор инструкций
Позвольте результатам обучения направлять ваш набор инструкций. Обратите внимание, что задачи могут включать статическое и динамическое исследование модели, включая визуализацию изменений с помощью ползунка. Для лучшего прогресса задачи можно организовать по папкам и руководствоваться примечаниями инструктора, встроенными в график Desmos.Оба могут быть добавлены, нажав
+ (Добавить элемент), затем папку или заметку.

Шаг 4. Предложите учащимся изучить руководства по графическим инструментам Desmos
Раздел справки предоставляет большой банк подробных и интерактивных учебных ресурсов для новых и опытных пользователей Desmos. Студенты могут научиться создавать ползунки и таблицы, определять ограничения домена и диапазона и выполнять регрессию, следуя простым интерактивным турам, предоставляемым Desmos. Библиотека видеоуроков обширна и легко доступна для поиска, а Руководство пользователя Desmos предоставляет базовое руководство по инструментам Desmos.

Шаг 5. Поделитесь графиком (ами) со своими учениками
Нажмите на инструмент «Поделиться своим графиком», расположенный в верхнем левом углу. Созданная ссылка отправит студентов на график и позволит каждому студенту просматривать и изменять его отдельно от других пользователей, не влияя на созданный вами график. Обратите внимание, что вы также можете использовать этот инструмент, чтобы сохранить изображение графика (за некоторыми исключениями) и встроить его в другие платформы.

Шаг 6. Включите Калькулятор Графа Десмоса в оценки
Включите результаты исследований учащихся и извлеченные уроки в оценки с помощью инструмента «Поделитесь своим графиком», с помощью которого учащиеся делятся ссылкой или изображениями своей работы внутри, непосредственно или как часть отдельного документа для отправки.Обратите внимание, что ссылка будет включать график в том виде, в котором он был на момент создания ссылки.
Избегайте путаницы, сводя к минимуму двусмысленность- Разработайте инструкции, соответствующие результатам обучения. Разбейте занятие на компоненты и распределите их по папкам. По мере необходимости направляйте учащихся к конкретным ресурсам в ходе упражнения по темам, которые могут нуждаться в разъяснении. Воспользуйтесь преимуществами обширной библиотеки обучающих видео от Desmos и его пользователей (доступных через любую поисковую систему с «выбранной темой Desmos +») в качестве ресурса для студентов по конкретным задачам.
Помните о времени и требуемых навыках. — Проверьте, сколько времени вам потребуется на выполнение задания, затем умножьте это время на три. На протяжении всего теста размышляйте о своих знаниях учеников, диапазоне их навыков, связанных с технологиями и контентом, и соответствующим образом корректируйте деятельность.
Поощряйте решение проблем и устранение неполадок с помощью одноранговой поддержки — Покажите учащимся, как делиться работой с помощью инструмента «Поделиться своим графиком», чтобы искать помощи у других во время упражнения.Наблюдая за работой учащегося, будет легче определить, где учащийся допустил ошибку или где он наткнулся на камень преткновения.
Цифровые ресурсы
Руководство пользователя Desmos
Примеры изучения функций через Desmos в действии:
Экичи, Селил и Плайли, Крис. «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Интернет.
Годин, Шон. «В чем проблема? Ищу лжецов.Бюллетень — Ассоциация математиков Онтарио 56.4 (2018): 11–13. Интернет.
Хойлс, Селия. «Преобразование математической практики учащихся и учителей с помощью цифровых технологий». Исследования в области математического образования. 20.3 1–20. Интернет.
Набб, Кейт и Муравска, Жаклин. «Мотивация расчетов с помощью одного вопроса». ПРИМУС 29.10 (2019): 1140–1153. Интернет.
Shahriari, Razieh et al. «Влияние использования технологий на понимание студентами математики и алгебры в колледже.”ProQuest Dissertations Publishing, 2019. Web.
Ана Дафф — научный сотрудник факультета бизнеса и информационных технологий Технического университета Онтарио, где она преподает математические курсы первого года обучения. Ее исследовательский опыт связан с математикой, в которой она имеет докторскую степень. из Университета Оттавы. До Технологического университета Онтарио она преподавала математику в Оттавском университете, Королевском военном колледже Канады и Международной школе Белграда в Сербии. Она также имеет обширный опыт разработки и управления крупномасштабными программами мобилизации и обучения сообществ в Канаде и за рубежом в неправительственном и государственном секторах.
Исследуйте математику с Desmos
Что такое Десмос?
Desmos — это бесплатный онлайн-калькулятор, позволяющий пользователям изучать математику новыми и увлекательными способами. Desmos хочет помочь каждому ученику выучить математику и полюбить ее. Графические функции, построение таблиц данных, оценка уравнений, изучение преобразований и многое другое — бесплатно!
ТОП 5 ПРИЧИН СЛЕДУЕТ ИСПОЛЬЗОВАТЬ ДЕСМО В КЛАССЕ
Это бесплатно !!! Для учителей и студентов.
Это графический калькулятор, который прекрасно работает в Интернете или как приложение для учащихся для моделирования с помощью математики — MP 4.
Когда вы регистрируетесь в качестве учителя, вы можете назначать занятия и игры (да, все они бесплатны, тоже) своим ученикам, и вы можете проверить их прогресс на странице своего учителя.
Вы можете легко создавать свои собственные занятия с помощью Activity Builder.
Доступ к нему можно получить в Интернете с компьютера или планшета, но есть также бесплатные приложения для iOS и Android, которые позволяют получить доступ к программе без использования Wi-Fi или данных.
Начните с калькулятора…
Как вы можете использовать эту функцию?
Учащиеся могут создавать графики
Учителя могут создавать графики для отображения и обмена с классом (режим проектора)
Учителя могут создавать графики и делать снимки экрана для использования в заданиях или экзаменах
Если вы вошли в систему, вы Вы можете сохранять созданные графики и возвращаться к ним в любое время.
Ползунки !!!
Загрузить картинки
Let’s Play!
Щелкните на большом красном поле с надписью «Начать построение графика»
или
щелкните здесь
Учитель Desmos
Учитель Desmos
Это набор заданий, созданных сотрудниками Desmos и классными учителями.Вы можете использовать эту часть сайта двумя способами:
Искать в теме и использовать задание как есть со своими учащимися
Создайте собственное задание и раздайте его своим учащимся
С чего начать?
Используйте одно из многих действий на полиграфе, разработанных Desmos (просто введите «Полиграф» в поисковую систему)
Если вы найдете то, что вам нравится, нажмите «начать новый сеанс» и поделитесь кодом в синем поле со своими учениками
Desmos позаботится обо всем остальном, и вы сможете наблюдать за тем, что делает каждый ученик
Если вы найдете занятие, которое вам нравится, но вы хотите внести несколько изменений, нажмите «продублировать это действие», и вы сможете внести изменения.
Студент Десмос
Student Desmos — это место, куда ваши ученики пойдут, чтобы получить доступ к занятиям.
Учащиеся увидят подсказку с просьбой ввести код (вы получите код, когда решите начать новый сеанс в Teacher Desmos).
Marbleslides
Игра, в которой вы должны трансформировать параболы, чтобы шарик летел к звездам.Это вызывает привыкание …
Marbleslides
Куда мне пойти в первую очередь?
Лучшее место, чтобы пойти, когда вы новый пользователь, — это Learn Desmos.
Вы найдете:
интерактивных занятий
коротких обучающих видео
примеров
вебинаров
4.График функции
График функции — это набор всех точек, координаты которых ( x , y ) удовлетворяют функции `y = f (x) `. Это означает, что для каждого значения x существует соответствующее значение y , которое получается, когда мы подставляем в выражение для `f (x)`.
Поскольку количество точек на графике функции не ограничено, сначала мы будем следовать этой процедуре:
Выберите несколько значений x (минимум 5)
Получить соответствующие значения функции и занести их в таблицу
Постройте эти точки, соединив их плавной кривой
Тем не менее, вам предлагается изучить общие формы некоторых общих кривых (таких как прямая линия, парабола, тригонометрические и экспоненциальные кривые, с которыми вы встретитесь в следующих главах).Это намного проще, чем рисовать точки, и гораздо полезнее на будущее!
Пример 1
Мужчина ростом «2 м» бросает мяч прямо вверх, и его высота в момент времени t (в s ) определяется выражением ч = 2 + 9 т — 4,9 т ² м.
Постройте график функции.
Ответ
Начнем с t = 0, поскольку отрицательные значения времени имеют практического смысла здесь нет.
Выбираем значения `0.С интервалом 5` (если бы мы использовали интервалы `t = 1 \» s «`, мы не увидели бы достаточно деталей на графике).
т 0 0,5 1 1,5 2
ч 2 5,3 6,1 4,5 0,4
График снаряда (парабола).
Эта форма называется параболой и является общепринятой. в приложениях математики.
ПРИМЕЧАНИЕ:
(1) На этом графике высота против времени. Мяч пошел прямо вверх, а не вперед. (Наш график может создать впечатление, что мяч двигался в направлении x , а также вверх, но это было не так.)
(2) Мы могли бы написать функцию в этом примере с h ( t ), а не просто h . Следующие два уравнения означают одно и то же.
ч = 2+ 9 т — 4.9 т ²
ч ( т ) = 2 + 9 т — 4,9 т ²
Пример 2
Скорость (в «м / с») мяча в Примере 1 во время т (в с ) дается по
v = 9 — 9,8 t
Нарисуйте график v — t . Что скорость при ударе мяча о землю?
Ответ
Это прямая линия, так как она имеет вид
y = м x + c
Подробнее на Straight Line.
Поскольку мы определили, что это прямая линия, нам нужно только построить 2 очка и присоединяйтесь к ним. Но мы находим 3 точки, просто чтобы убедиться, что у нас правильная линия.
График зависимости `v` от` t` — прямой.
Наш график начинается с t = 0 (поскольку отрицательные значения времени не имеют значения в этом примере).
В течение первых 0,918 «с» «мяч идет вверх (положительная скорость, то есть синяя линия находится выше оси t ), но замедляется.
После этого мяч приближается к земле и набирает скорость (участок, где синяя линия находится ниже оси t ).
Мяч падает на землю примерно за t = 2,04 с (мы можем см. это из примера 1). Скорость , когда мяч падает на землю с графика, который мы только что нарисовали, имеет значение `-11 \ «м / с» `. График останавливается на этом месте.
На нашем графике предполагается, что мяч приземляется в песок и не отскакивает.
Обычно, как мы сделали здесь, мы берем скорость в до направление быть положительным.
Пример 3
Постройте график функции y = x — x ².
Ответ
(a) Определите значения y- для типичного набора значений x и запишите их в таблицу.
x -2 -1 0 1 2 3
л −6 -2 0 0 -2 −6
(b) Так как y = 0 как для x = 0, так и для x = 1`, проверьте, что происходит между ними.2`, парабола.
Обратите внимание, что кривая продолжается за пределы того, что показано на графике. Это просто общий вопрос, и нет никаких практических ограничений для значений x или y .
Пример 4
Построить график функции `y = 1 + 1 / x`
Ответ
(a) Примечание: y не определено для `x = 0` из-за деление на `0`
Следовательно, `x = 0` не находится в области
(б) Составьте таблицу значений:
x «-4» `-3` `-2` `-1` `1` `2` `3` `4`
y `3/4` `2/3` `1/2` `0` `2` `3/2` `4/3` `5/4`
(c) Мы знаем, что что-то странное произойдет рядом с x = 0 (поскольку граф там не определен).Итак, мы проверяем, что происходит в некоторых типичных точках между `x = -1` и` x = 1`:
, когда `x = −0,5,` y = 1 + 1 / (- 0,5) = 1-2 = −1`
, когда `x = 0,5, \ y = 1 + 1 / (0,5) = 1 + 2 = 3`
(d) По мере приближения значения x к «0» точки становятся ближе к y — ось, правда ее не трогают. Ось y называется асимптотой кривой.
(Чтобы убедиться в этом, нанесите на график точки, где `x = 0.4, x = 0,3, x = 0,2, x = 0,1 и даже x = 0,01.)
График `y = 1 + 1 / x`, гипербола. Это прерывистая функция.
На этой кривой есть еще одна асимптота: y = 1, отмеченная пунктирной линией. Обратите внимание, что кривая не проходит через это значение.
Пример 5
Построить график функции `y = sqrt (x + 1)`
Ответ
(a) Примечание: y не определяется для значений x минус чем `-1`. (Попробуйте что-нибудь в своем калькуляторе, например, `x = −4`.)
(b) Мы определяем некоторые значения x и соответствующие значения y и записываем их в таблицу:
x -1 0 1 2 3 4 5
л 0 1 1,4 1,7 2 2.2`
Постройте зависимость мощности от сопротивления.
Ответ
(a) Отрицательные значения для R не имеют физического значимость, поэтому P не отображается для отрицательных значений из р.
(б) Составьте таблицу значений:
рэнд
0 1 2 3 4 5
пол 0 44.2`.
Обратите внимание, что оси имеют маркировку R (сопротивление) и P (мощность).
(d) Выводы:
(i) Максимальная мощность 50 Вт достигается при сопротивлении R = 0,5 Вт
(ii) P уменьшается по мере увеличения R выше 0,5 \ «W» `
Упражнения
Построить график заданных функций
1 кв. y = x ³— x ²
Ответ
(a) Нет никаких ограничений на значения, которые x может принимать в этом примере, поскольку это общий вопрос, не имеющий практического значения.
(б) Составьте таблицу значений:
x -1 0 1 2 3
л -2 0 0 4 18
Поскольку y = 0, когда x = 0 и x = 1, мы исследуем, что происходит между этими 2 значениями x :
Когда `x = 1/2, y = -1/8.`
Вот наш график:
График y = x ³ — x ², куб.
2 кв. `y = sqrt (x)`
Ответ
Мы можем извлечь квадратный корень только из положительного числа, поэтому `x ≥ 0`. Квадратный корень из числа может быть только положительным, поэтому `y ≥ 0`.
Этот график представляет собой половину параболы с горизонтальной осью.
График `y = sqrt (x)`, половина параболы.

Конический резервуар для воды
3 кв. ( Приложение ) Вода вытекает из резервуара в форме перевернутого конуса (т. Е. Вода течет через заостренный конец конуса и самую широкую часть конус находится наверху). Объем воды уменьшается при постоянная скорость.
Нарисуйте эскизный график высоты воды в конусе. против времени.
Ответ
Нам нужно смоделировать высоту в момент времени t на основе того, что мы знаем о конусах.(1 «/» 3) `.
Станки плоттерные (линейные)
6,3
ПОЛА КЕЛЛИ: Хорошо. Итак, мы собираемся взглянуть на то, как мы могли бы использовать наши функциональные машины, чтобы дать нам некоторые координаты. Итак, мы начнем с нашей функциональной машины. Мы умножим нашу на 3.
20,6
И наш ввод — может входить любое число. Какое бы число у нас ни было, мы умножаем его на 3. Итак, у нас есть 3x.
29.9
МАЙКЛ АНДЕРСОН: Итак, если бы мы начали, скажем, с отрицательными 2, умножьте это на 3. Это будет отрицательное 6.
39,7
ПОЛА КЕЛЛИ: Прекрасно. Очень хороший. Ага. Как вы думаете, какой будет разумный выбор в следующий раз?
45,6
МАЙКЛ АНДЕРСОН: Что ж, перейдем к отрицательному 1.
47
ПОЛА КЕЛЛИ: Хорошо. Сохраним выкройку.
50,2
МАЙКЛ АНДЕРСОН: И этот результат будет отрицательным 3.
53,6
ПОЛА КЕЛЛИ: Да. Хорошая — если у нас 0.
58,4
МАЙКЛ АНДЕРСОН: Ну, 0 умножить на 3, три лота из ничего, тоже 0.
61,6
ПОЛА КЕЛЛИ: Очень хорошо. И тогда мы можем заметить, что здесь мы получаем образец.
65.3
МАЙКЛ АНДЕРСОН: О, мы увеличиваем на 3 каждый раз, точно так же, как таблица умножения на 3. Итак, если бы мы выбрали 1 в качестве входа, на выходе было бы 3. 2 входит, а 6 выходит. А потом, может быть, 3 и 9.
81,6
ПОЛА КЕЛЛИ: И тогда мы могли бы продолжать так во веки веков.
85,2
МАЙКЛ АНДЕРСОН: Можно ли ввести какие-либо десятичные дроби? Итак, если мы введем 0,5 в качестве входных данных.
90.2
ПОЛА КЕЛЛИ: Совершенно верно. Это сработает.
93,2
МАЙКЛ АНДЕРСОН: И три лота по 0,5 равны 1 и 1/2, 1,5.
96,4
ПОЛА КЕЛЛИ: Очень хорошо.
97,6
МАЙКЛ АНДЕРСОН: И я полагаю, мы могли бы снова добавить 100.
100,1
ПОЛА КЕЛЛИ: Любое число. Ничего вообще.
102,5
МАЙКЛ АНДЕРСОН: 100 умноженное на 3 даст нам 300.
105,6
PAULA KELLY: Итак, теперь у нас много входов и выходов. Сейчас они действительно полезны, потому что мы можем их использовать — вместо входов и выходов мы собираемся использовать их в качестве некоторых координат.
118
МАЙКЛ АНДЕРСОН: Итак, у нас есть несколько предварительно нарисованных топоров. Это горизонтальный, который мы обозначили x, и он будет нашими входными данными.И мы обозначили вертикальную ось y, которая будет нашими выходами, то есть теми 3x, то есть тем, что мы умножаем на 3.
134,4
ПОЛА КЕЛЛИ: Прекрасно. Итак, если мы собираемся нарисовать эту функцию на этом графике, нам нужно знать, куда поместить эти координаты. Итак, у нас есть 10 квадратов, и мы можем занести их в таблицу как 1, 2, 3, 4.
145,1
МАЙКЛ АНДЕРСОН: Да. Итак, если это начало отсчета, это 0, 0.
150,8
МАЙКЛ АНДЕРСОН: Итак, на каждый квадрат, который мы пересекаем, приходится одна единица. Итак, я мог сказать, ну вот, это 1, 2, 3, 4, 5, и продолжать. Это будет 6, 7, 8, 9, а затем мы дойдем до 10. Я собираюсь сэкономить немного времени и, возможно, не буду писать их все. , так что здесь будет 1, 2, 3, 4, 5. А потом 6, 7, 8, 9, 10 здесь. А что насчет того, что внизу или там тоже?
184.4
ПОЛА КЕЛЛИ: И снова то же самое. Как термометр, он ушел бы в наши отрицательные значения. Мы могли бы просто пометить наш минус 5.
190,7
МАЙКЛ АНДЕРСОН: Итак, мы продолжаем отсчет вниз, так что будет 0, отрицательный 1, отрицательный 2, отрицательный 3, отрицательный 4, отрицательный 5. И отрицательный 6, 7, 8, 9, отрицательный 10. То же самое и в этом случае. , так что 1, 2, 3, 4, 5, но это будет отрицательно. И тогда я предполагаю, что это тоже отрицательное 10.Давай просто проверим. 6, 7, 8, 9, 10.
218,7
ПОЛА КЕЛЛИ: Прекрасно. Так что мы могли бы их пометить. Мы могли бы, чтобы каждый из этих квадратов имел значение 2 и увеличивалось до 20. В этом случае у нас такой же масштаб для горизонтальной оси, как и для вертикальной. Нам это не обязательно было бы.
234,1
МАЙКЛ АНДЕРСОН: Итак, я каждый раз считал по одной, но мы могли довольно легко перебрать 2, 4, 6, 8, причем каждый квадрат стоил две единицы, при условии, что это достаточно стабильно.И мы могли бы сделать любой аналогичный масштаб по оси Y.
246,5
ПОЛА КЕЛЛИ: Да. Он должен соответствовать вашей горизонтали. Ваша вертикаль — если она постоянна в пределах оси, каждая из них может стоить 10 единиц, если хотите.
257,1
МАЙКЛ АНДЕРСОН: Да, но пока пробелы есть, потому что я знаю, что многие мои ученики слегка путаются при рисовании и маркировке этих осей.
264,1
ПОЛА КЕЛЛИ: Да. А также соблазн обозначить середину квадрата, но вы правильно отметили здесь свои топоры. Итак, давайте поместим некоторые из этих координат на наш график. Итак, у нас есть отрицательный 2 и отрицательный 6. Итак, мы идем по коридору к отрицательному 2, складываем до — вниз, а не к отрицательному 6. Очень хорошо. Опять же, мы собираемся поставить крест, а не точку, потому что самая точная точка находится прямо в середине этого креста.
291.1
МАЙКЛ АНДЕРСОН: Значит, эти значения говорят нам, куда мы движемся от исходной точки, влево или вправо. И эти ценности скажут нам, идем мы вверх или вниз. Итак, мы переходим к отрицательному 2, а затем к отрицательному 6.
303,8
ПОЛА КЕЛЛИ: Идеально. Таким же образом, от отрицательного 1 до отрицательного 3. Я поставлю крестик. 0, 0 — это наша исходная точка. И мы видим, что здесь мы начинаем закономерность.
318.8
МАЙКЛ АНДЕРСОН: Да. Они выглядят как прямая линия. Не знаю, совпадение это или нет. Так что, может быть, нарисуйте еще несколько моментов и посмотрите.
325,9
ПОЛА КЕЛЛИ: Совершенно верно. Итак, у нас есть 1 и 3, так что дальше от 1 до 3. 2 и 6. Далее до 2, до 6. 3 и 9. И поднимаемся до 9.
341,5
МАЙКЛ АНДЕРСОН: Да, они определенно выглядят на этой прямой.Итак, для наших более сложных примеров, 0,5 вошло в функциональную машину, а 1,5 вышло. Я полагаю, это означает, что нам нужно пройти половину квадрата в поперечнике, что было бы примерно там, а затем на 1 и 1/2 квадрата вверх. Так что я попробую обозначить это. Если мы пойдем на 1/2 квадрата вверх и на 1 и 1/2 квадрата там, где-то там. И хотя это десятичная дробь, похоже, она лежит на той линии, которую мы как бы нанесли на карту.
370,7
ПОЛА КЕЛЛИ: Да, очевидно, это должно быть на нашей линии.И мы увидим, что это за правило. Как вы сказали, трудно быть абсолютно точным.
377,6
МАЙКЛ АНДЕРСОН: При условии точной оценки.
378,5
ПОЛА КЕЛЛИ: Да, это приблизительная оценка. Когда мы подходим к нашим 100 и 300 —
382,6
МАЙКЛ АНДЕРСОН: Ну…
383,8
ПОЛА КЕЛЛИ: — мы можем бороться.
384,9
МАЙКЛ АНДЕРСОН: Должны ли мы оставить это, потому что оно зашкаливает?
386,9
ПОЛА КЕЛЛИ: За пределами шкалы. Но если мы продолжим эту фразу…
388,7
МАЙКЛ АНДЕРСОН: Значит, это где-то там.
389,5
ПОЛА КЕЛЛИ: — это будет продолжаться. Итак, мы проведем линию через все эти координаты.Если мы правильно разместили их на нашей сетке, они должны проходить через центр всех этих крестов. Я собираюсь продлить линию, потому что на самом деле эта линия будет продолжаться бесконечно. А затем, чтобы мы знали, какую линию мы на самом деле нарисовали, нам нужно пометить ее нашей функцией. Итак, мы собираемся вызвать нашу функцию, чтобы найти наш результат, наше значение y — у нас есть три партии любого значения x.
419,7
МАЙКЛ АНДЕРСОН: Итак, прямая y равна 3x.
422,5
ПОЛА КЕЛЛИ: Идеально.
423,4
МАЙКЛ АНДЕРСОН: И что интересно, я заметил, что здесь проходит именно этот момент. И когда я считываю значения, то есть когда наше значение x отрицательное 3, значение y отрицательное 9, что имеет смысл, потому что, если входит отрицательное 3, мы умножаем его на 3 и получаем отрицательное 9 как значение ay. Итак, для всех этих координатных точек, где бы мы ни выбрали точку на линии, значение y будет в 3 раза больше, чем значение x.
451,9
ПОЛА КЕЛЛИ: Совершенно верно. Мы могли бы думать об этом наоборот. Каким бы ни было наше значение x, оно будет 1/3 нашего значения y.
460
МАЙКЛ АНДЕРСОН: Да, в этом есть смысл.
3 Визуализация данных | R для науки о данных
Введение
«Простой график предоставил аналитикам больше информации. чем любое другое устройство.»- Джон Тьюки
Эта глава научит вас визуализировать данные с помощью ggplot2. В R есть несколько систем построения графиков, но ggplot2 — одна из самых элегантных и универсальных. ggplot2 реализует грамматику графики , согласованную систему для описания и построения графиков. С ggplot2 вы можете сделать больше быстрее, изучив одну систему и применив ее во многих местах.
Если вы хотите узнать больше о теоретических основах ggplot2, прежде чем начать, я бы порекомендовал прочитать «Многослойная грамматика графики», http: // vita.had.co.nz/papers/layered-grammar.pdf.
Предпосылки
В этой главе основное внимание уделяется ggplot2, одному из основных членов тидиверсии. Чтобы получить доступ к наборам данных, страницам справки и функциям, которые мы будем использовать в этой главе, загрузите тидиверс, запустив этот код:
Библиотека (tidyverse) #> ── Присоединение пакетов ──────────────────────────────────────── tidyverse 1.3.0 ─ ─ #> ✔ ggplot2 3.3.2 ✔ мурлыкать 0.3.4 #> ✔ tibble 3.0.3 ✔ dplyr 1.0.2 #> ✔ тидыр 1.1.2 ✔ стрингер 1.4.0 #> ✔ readr 1.4.0 ✔ forcats 0.5.0 #> ── Конфликты ─────────────────────────────────────────── tidyverse_conflicts () ── #> ✖ dplyr :: filter () маскирует stats :: filter () #> ✖ dplyr :: lag () маски stats :: lag ()
Эта одна строка кода загружает основной тидиверс; пакеты, которые вы будете использовать практически при каждом анализе данных. Он также сообщает вам, какие функции из тидиверса конфликтуют с функциями в базовом R (или из других пакетов, которые вы могли загрузить).
Если вы запустите этот код и получите сообщение об ошибке «Нет пакета с именем« tidyverse »», вам нужно сначала установить его, а затем снова запустить library () .
Вам нужно установить пакет только один раз, но вам нужно перезагружать его каждый раз, когда вы начинаете новый сеанс.
Если нам нужно точно указать, откуда берется функция (или набор данных), мы воспользуемся специальной формой package :: function () . Например, ggplot2 :: ggplot () явно сообщает вам, что мы используем функцию ggplot () из пакета ggplot2.
Первые шаги
Давайте воспользуемся нашим первым графиком, чтобы ответить на вопрос: автомобили с большими двигателями потребляют больше топлива, чем автомобили с маленькими двигателями? Вероятно, у вас уже есть ответ, но постарайтесь дать точный ответ. Как выглядит взаимосвязь между объемом двигателя и топливной экономичностью? Это положительно? Отрицательный? Линейный? Нелинейный?
Кадр данных
миль на галлон Вы можете проверить свой ответ с помощью фрейма данных mpg , найденного в ggplot2 (он же ggplot2 :: mpg ).Фрейм данных представляет собой прямоугольную коллекцию переменных (в столбцах) и наблюдений (в строках). миль на галлон содержит наблюдения, собранные Агентством по охране окружающей среды США на 38 моделях автомобилей.
миль на галлон #> # Таблица: 234 x 11 #> модель производителя displ год cyl trans drv cty hwy fl class #> #> 1 audi a4 1.8 1999 4 авто (l5) f 18 29 p компа… #> 2 audi a4 1.8 1999 4 механика (m5) f 21 29 p compa… #> 3 audi a4 2 2008 4 механика (m6) f 20 31 p compa… #> 4 audi a4 2 2008 4 auto (av) f 21 30 p compa… #> 5 audi a4 2.8 1999 6 auto (l5) f 16 26 p compa… #> 6 audi a4 2.8 1999 6 механика (m5) f 18 26 p compa… #> #… С еще 228 строками
Среди переменных в миль на галлон следующие:
displ — объем двигателя автомобиля в литрах.
hwy , топливная экономичность автомобиля на шоссе, в милях на галлон (миль на галлон). Автомобиль с низкой топливной экономичностью потребляет больше топлива, чем автомобиль с высокой топливной экономичностью. топливная экономичность, когда они едут на одинаковое расстояние.
Чтобы узнать больше о mpg , откройте страницу справки, запустив ? Mpg .
Создание графика ggplot
Чтобы построить миль на галлон , запустите этот код, чтобы поместить displ на ось x и hwy на ось y:
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy))
График показывает отрицательную взаимосвязь между объемом двигателя ( displ ) и топливной экономичностью ( hwy ).Другими словами, автомобили с большими двигателями потребляют больше топлива. Подтверждает ли это или опровергает вашу гипотезу о топливной экономичности и объеме двигателя?
С помощью ggplot2 вы начинаете построение графика с помощью функции ggplot () . ggplot () создает систему координат, в которую вы можете добавлять слои. Первый аргумент ggplot () — это набор данных для использования в графике. Итак, ggplot (data = mpg) создает пустой график, но это не очень интересно, поэтому я не собираюсь его здесь показывать.
Вы завершаете свой график, добавляя один или несколько слоев в ggplot () . Функция geom_point () добавляет слой точек к вашему графику, который создает диаграмму рассеяния. ggplot2 поставляется с множеством функций geom, каждая из которых добавляет к графику разные типы слоев. В этой главе вы узнаете о них целую кучу.
Каждая функция geom в ggplot2 принимает аргумент сопоставления . Это определяет, как переменные в вашем наборе данных сопоставляются с визуальными свойствами.Аргумент сопоставления всегда связан с aes () , а аргументы x и y aes () указывают, какие переменные сопоставлять с осями x и y. ggplot2 ищет сопоставленные переменные в аргументе данных , в данном случае миль на галлон .
Графический шаблон
Давайте превратим этот код в шаблон многократного использования для построения графиков с помощью ggplot2. Чтобы построить график, замените заключенные в скобки разделы в приведенном ниже коде набором данных, функцией geom или набором сопоставлений.
ggplot (data = ) + (отображение = aes ())
Остальная часть этой главы покажет вам, как дополнить и расширить этот шаблон для создания различных типов графиков. Начнем с компонента .
Упражнения
Выполнить ggplot (данные = миль на галлон) . Что ты видишь?
Сколько рядов в миль на галлон ? Сколько столбцов?
Что описывает переменная drv ? Прочтите справку для ? миль на галлон, чтобы найти вне.
Создайте диаграмму рассеяния hwy и cyl .
Что произойдет, если построить диаграмму рассеяния класса и drv ? Почему сюжет не полезен?
Эстетические карты
«Самая большая ценность картины — это когда она заставляет нас замечать то, что мы никогда не ожидал увидеть. — Джон Тьюки
На графике ниже одна группа точек (выделена красным), кажется, выходит за пределы линейного тренда.Эти автомобили имеют больший пробег, чем можно было ожидать. Как вы можете объяснить эти машины?
Предположим, что автомобили — гибриды. Один из способов проверить эту гипотезу — посмотреть на значение класса для каждого автомобиля. Переменная class набора данных миль на галлон классифицирует автомобили на такие группы, как компактные, среднеразмерные и внедорожники. Если отдаленные точки являются гибридами, их следует классифицировать как компактные или, возможно, малолитражные автомобили (имейте в виду, что эти данные были собраны до того, как гибридные грузовики и внедорожники стали популярными).
Вы можете добавить третью переменную, например class , к двумерной диаграмме рассеяния, сопоставив ее с эстетикой . Эстетика — это визуальное свойство объектов на вашем участке. Эстетика включает такие вещи, как размер, форма или цвет ваших очков. Вы можете отображать точку (как показано ниже) по-разному, изменяя значения ее эстетических свойств. Поскольку мы уже используем слово «значение» для описания данных, давайте использовать слово «уровень» для описания эстетических свойств.Здесь мы меняем уровни размера, формы и цвета точки, чтобы сделать точку маленькой, треугольной или синей:
Вы можете передать информацию о ваших данных, сопоставив эстетику вашего графика с переменными в вашем наборе данных. Например, вы можете сопоставить цвета ваших точек с переменной class , чтобы показать класс каждого автомобиля.
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy, color = class))
(Если вы предпочитаете британский английский, например Hadley, вы можете использовать цвет вместо цвета .)
Чтобы сопоставить эстетику переменной, свяжите имя эстетики с именем переменной внутри aes () . ggplot2 автоматически назначит уникальный уровень эстетики (здесь уникальный цвет) каждому уникальному значению переменной, процесс, известный как масштабирование . ggplot2 также добавит легенду, объясняющую, какие уровни каким значениям соответствуют.
По цветам видно, что многие из необычных вещей представляют собой двухместные автомобили. Эти автомобили не похожи на гибриды, а на самом деле являются спортивными автомобилями! Спортивные автомобили имеют большие двигатели, такие как внедорожники и пикапы, но маленькие кузова, такие как среднеразмерные и компактные автомобили, что позволяет сократить расход топлива.Оглядываясь назад, вряд ли эти автомобили были гибридами, поскольку у них были большие двигатели.
В приведенном выше примере мы сопоставили класс с эстетикой цвета, но мы могли бы сопоставить класс с эстетикой размера таким же образом. В этом случае точный размер каждой точки покажет ее классовую принадлежность. Здесь мы получаем предупреждение , потому что сопоставление неупорядоченной переменной (, класс ) с упорядоченной эстетикой (, размер ) не является хорошей идеей.
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy, size = class)) #> Предупреждение: не рекомендуется использовать размер дискретной переменной.
Или мы могли бы сопоставить class с эстетикой alpha , которая контролирует прозрачность точек, или с эстетикой формы, которая управляет формой точек.
# Left ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy, alpha = class)) # Правильно ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy, shape = class))
Что случилось с внедорожниками? ggplot2 будет использовать одновременно только шесть фигур.По умолчанию при использовании эстетики формы дополнительные группы не отображаются.
Для каждой эстетики вы используете aes () , чтобы связать имя эстетики с отображаемой переменной. Функция aes () собирает вместе все эстетические сопоставления, используемые слоем, и передает их аргументу сопоставления слоя. Синтаксис подчеркивает полезную информацию о x и y : положения x и y точки сами по себе являются эстетикой, визуальными свойствами, которые вы можете сопоставить с переменными для отображения информации о данных.
После того, как вы нанесете на карту эстетику, ggplot2 позаботится обо всем остальном. Он выбирает разумный масштаб для использования с эстетикой и строит легенду, объясняющую соответствие между уровнями и значениями. Для эстетики x и y ggplot2 не создает легенду, но создает осевую линию с делениями и меткой. Линия оси действует как легенда; он объясняет соответствие между местоположениями и ценностями.
Вы также можете установить эстетические свойства геометрии вручную.Например, мы можем сделать все точки на нашем графике синими:
ggplot (данные = миль на галлон) + geom_point (mapping = aes (x = displ, y = hwy), color = "blue")
Здесь цвет не передает информацию о переменной, а только изменяет внешний вид графика. Чтобы установить эстетику вручную, задайте эстетику по имени в качестве аргумента вашей функции geom; то есть идет за пределами из aes () . Вам нужно будет выбрать уровень, соответствующий этой эстетике:
Название цвета в виде строки символов.
Размер точки в мм.
Форма точки в виде числа, как показано на Рисунке 3.1.
Рисунок 3.1: R имеет 25 встроенных форм, которые обозначены номерами. Есть некоторые кажущиеся дубликаты: например, 0, 15 и 22 — все квадраты. Разница заключается во взаимодействии цветов и , заполняющих эстетику . Полые формы (0–14) имеют границу, определяемую цветом ; сплошные фигуры (15–20) залиты цветом ; закрашенные фигуры (21–24) имеют границу цвета и заполнены заливкой .
Упражнения
Что случилось с этим кодом? Почему точки не синие?
ggplot (данные = миль на галлон) + geom_point (mapping = aes (x = displ, y = hwy, color = "blue"))
Какие переменные в миль на галлон являются категориальными? Какие переменные непрерывны? (Подсказка: введите ? Mpg , чтобы прочитать документацию по набору данных). Как Вы можете увидеть эту информацию, когда запустите миль на галлон ?
Сопоставьте непрерывную переменную с цветом , размером и формой .Как эти эстетики ведут себя по-разному для категориального и непрерывного переменные?
Что произойдет, если сопоставить одну и ту же переменную с несколькими эстетиками?
Что делает эстетика ходовой части ? С какими формами он работает? (Подсказка: используйте ? Geom_point )
Что произойдет, если вы сопоставите эстетику с чем-то другим, кроме переменной имя, например aes (color = displ <5) ? Обратите внимание: вам также необходимо указать x и y.
Общие проблемы
При запуске кода R вы, вероятно, столкнетесь с проблемами. Не волнуйтесь - это случается со всеми. Я писал код на R в течение многих лет, и каждый день я все еще пишу код, который не работает!
Начните с тщательного сравнения кода, который вы запускаете, с кодом в книге. R чрезвычайно разборчив, и неуместный персонаж может иметь решающее значение. Убедитесь, что каждый ( совпадает с ) и каждый " сопряжен с другим " .Иногда вы запускаете код, но ничего не происходит. Посмотрите на левую часть консоли: если это + , это означает, что R не думает, что вы набрали полное выражение, и ждет, когда вы его закончите. В этом случае обычно легко снова начать с нуля, нажав ESCAPE, чтобы прервать обработку текущей команды.
Одной из распространенных проблем при создании графики ggplot2 является размещение + не в том месте: он должен стоять в конце строки, а не в начале.Другими словами, убедитесь, что вы случайно не написали такой код:
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy))
Если вы все еще не знаете, что делать, попробуйте помощь. Вы можете получить справку по любой функции R, запустив ? Имя_функции в консоли или выбрав имя функции и нажав F1 в RStudio. Не волнуйтесь, если помощь не покажется такой полезной - вместо этого перейдите к примерам и поищите код, соответствующий тому, что вы пытаетесь сделать.
Если это не помогло, внимательно прочтите сообщение об ошибке. Иногда там и закопают ответ! Но когда вы новичок в R, ответ может быть в сообщении об ошибке, но вы еще не знаете, как это понять. Еще один отличный инструмент - Google: попробуйте поискать в Google сообщение об ошибке, так как, вероятно, кто-то другой столкнулся с такой же проблемой и получил помощь в Интернете.
Грани
Один из способов добавить дополнительные переменные - это эстетика. Другой способ, особенно полезный для категориальных переменных, - разделить график на фасетов , подзаголовки, каждый из которых отображает одно подмножество данных.
Чтобы огранить ваш график одной переменной, используйте facet_wrap () . Первым аргументом facet_wrap () должна быть формула, которую вы создаете с ~ , за которой следует имя переменной (здесь «формула» - это имя структуры данных в R, а не синоним «уравнения»). Переменная, которую вы передаете в facet_wrap () , должна быть дискретной.
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_wrap (~ класс, nrow = 2)
Чтобы обработать график на основе комбинации двух переменных, добавьте facet_grid () к вызову графика.Первый аргумент facet_grid () также является формулой. На этот раз формула должна содержать два имени переменных, разделенных ~ .
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_grid (DRV ~ Cyl)
Если вы предпочитаете не фасетировать измерение строк или столбцов, используйте . вместо имени переменной, например + facet_grid (. ~ Cyl) .
Упражнения
Что произойдет, если вы фасетите непрерывную переменную?
Что означают пустые ячейки на графике с facet_grid (drv ~ cyl) ? Как они относятся к этому сюжету?
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = drv, y = cyl))
Какие графики создает следующий код? Что значит . делать?
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_grid (drv ~.) ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_grid (. ~ cyl)
Возьмите первый граненый график в этом разделе:
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + facet_wrap (~ класс, nrow = 2)
Каковы преимущества использования огранки вместо эстетики цвета? Какие недостатки? Как мог бы измениться баланс, если бы у вас был больший набор данных?
Прочитать ? Facet_wrap .Что делает nrow ? Что делает ncol ? Какие еще варианты управления компоновкой отдельных панелей? Почему не facet_grid () имеет аргументы nrow и ncol ?
При использовании facet_grid () обычно следует помещать переменную с дополнительными уникальные уровни в столбцах. Почему?
Геометрические объекты
Чем похожи эти два графика?
Оба графика содержат одну и ту же переменную x, одну и ту же переменную y, и оба описывают одни и те же данные.Но сюжеты не идентичны. Каждый график использует разные визуальные объекты для представления данных. В синтаксисе ggplot2 мы говорим, что они используют разные геометрии .
geom - это геометрический объект, который график использует для представления данных. Люди часто описывают сюжеты по типу геометрии, которую они используют. Например, гистограммы используют геометрию гистограмм, линейные диаграммы используют геометрию линий, диаграммы коробчатой диаграммы используют геометрию диаграммы и так далее. Диаграммы рассеивания ломают тренд; они используют точечную геометрию. Как мы видим выше, вы можете использовать разные геометрии для построения одних и тех же данных.График слева использует точечную геометрию, а график справа использует гладкую геометрию, плавную линию, подогнанную к данным.
Чтобы изменить геометрию вашего графика, измените функцию geom, которую вы добавляете в ggplot () . Например, чтобы построить графики выше, вы можете использовать этот код:
# осталось ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) # верно ggplot (данные = миль на галлон) + geom_smooth (отображение = aes (x = displ, y = hwy))
Каждая функция geom в ggplot2 принимает аргумент отображения .Однако не всякая эстетика подходит для всех геометрических фигур. Вы можете задать форму точки, но не можете задать «форму» линии. С другой стороны, вы могли бы установить тип линии. geom_smooth () будет рисовать разные линии с разными типами линий для каждого уникального значения переменной, которую вы сопоставляете с типом линии.
ggplot (данные = миль на галлон) + geom_smooth (отображение = aes (x = displ, y = hwy, linetype = drv))
Здесь geom_smooth () разделяет автомобили на три строки на основе их значения drv , которое описывает трансмиссию автомобиля.Одна линия описывает все точки со значением 4 , одна линия описывает все точки со значением f , а одна линия описывает все точки со значением r . Здесь 4 обозначает полный привод, f - передний привод и r - задний привод.
Если это звучит странно, мы можем сделать это более понятным, наложив линии поверх необработанных данных, а затем раскрасив все в соответствии с drv .
Обратите внимание, что этот график содержит две геометрии на одном графике! Если это вас возбуждает, пристегнитесь. Очень скоро мы узнаем, как разместить несколько геометрических фигур на одном участке.
ggplot2 предоставляет более 40 геометрий, а пакеты расширений предоставляют еще больше (см. Https://exts.ggplot2.tidyverse.org/gallery/ для выборки). Лучший способ получить исчерпывающий обзор - это шпаргалка по ggplot2, которую вы можете найти по адресу http://rstudio.com/resources/cheatsheets. Чтобы узнать больше о каком-либо отдельном geom, воспользуйтесь справкой: ? Geom_smooth .
Многие geom, например geom_smooth () , используют один геометрический объект для отображения нескольких строк данных. Для этих геометрических фигур вы можете установить эстетику группы как категориальную переменную для рисования нескольких объектов. ggplot2 будет рисовать отдельный объект для каждого уникального значения группирующей переменной. На практике ggplot2 автоматически группирует данные для этих геометрических фигур всякий раз, когда вы сопоставляете эстетику дискретной переменной (как в примере с типом линий ). На эту особенность удобно полагаться, потому что эстетика группы сама по себе не добавляет к геометрии легенды или отличительных особенностей.
ggplot (данные = миль на галлон) + geom_smooth (отображение = aes (x = displ, y = hwy)) ggplot (данные = миль на галлон) + geom_smooth (отображение = aes (x = displ, y = hwy, group = drv)) ggplot (данные = миль на галлон) + geom_smooth ( отображение = aes (x = displ, y = hwy, color = drv), show.legend = ЛОЖЬ )
Чтобы отобразить несколько геометрий на одном графике, добавьте несколько функций геометрии в ggplot () :
ggplot (данные = миль на галлон) + geom_point (отображение = aes (x = displ, y = hwy)) + geom_smooth (отображение = aes (x = displ, y = hwy))
Однако это приводит к некоторому дублированию в нашем коде.Представьте, что вы хотите изменить ось Y, чтобы отобразить cty вместо hwy . Вам нужно будет изменить переменную в двух местах, и вы можете забыть обновить одно. Вы можете избежать такого повторения, передав набор сопоставлений в ggplot () . ggplot2 будет рассматривать эти сопоставления как глобальные сопоставления, которые применяются к каждому объекту geom в графе. Другими словами, этот код создаст тот же график, что и предыдущий код:
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_point () + geom_smooth ()
Если вы разместите сопоставления в функции geom, ggplot2 будет рассматривать их как локальные сопоставления для слоя.Он будет использовать эти сопоставления для расширения или перезаписи глобальных сопоставлений только для этого уровня . Это позволяет отображать разную эстетику на разных слоях.
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_point (отображение = aes (цвет = класс)) + geom_smooth ()
Вы можете использовать ту же идею, чтобы указать разные данные для каждого слоя. Здесь наша плавная линия отображает только подмножество набора данных миль на галлон — малолитражные автомобили.Аргумент локальных данных в geom_smooth () переопределяет аргумент глобальных данных в ggplot () только для этого слоя.
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_point (отображение = aes (цвет = класс)) + geom_smooth (data = filter (mpg, class == "subcompact"), se = FALSE)
(Вы узнаете, как работает filter () , в главе о преобразовании данных: пока просто знайте, что эта команда выбирает только малолитражные автомобили.)
Упражнения
Какой геометрический объект вы бы использовали для построения линейной диаграммы? Коробчатый сюжет? Гистограмма? Диаграмма с областями?
Запустите этот код в уме и предскажите, как будет выглядеть результат. Затем запустите код на R и проверьте свои прогнозы.
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy, color = drv)) + geom_point () + geom_smooth (se = FALSE)
Что показывает .legend = FALSE делает? Что будет, если его убрать?
Как вы думаете, почему я использовал его ранее в этой главе?
Что делает аргумент se для geom_smooth () ?
Эти два графика будут выглядеть по-разному? Почему, почему нет?
ggplot (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_point () + geom_smooth () ggplot () + geom_point (данные = миль на галлон, отображение = aes (x = displ, y = hwy)) + geom_smooth (данные = миль на галлон, отображение = aes (x = displ, y = hwy))
Восстановите код R, необходимый для создания следующих графиков.
Статистические преобразования
Теперь давайте взглянем на гистограмму. Гистограммы кажутся простыми, но они интересны, потому что раскрывают что-то тонкое в графиках. Рассмотрим простую гистограмму, нарисованную с помощью geom_bar () . На следующей диаграмме показано общее количество бриллиантов в наборе данных бриллиантов , сгруппированных по огранкам . Набор данных алмазов входит в ggplot2 и содержит информацию о ~ 54 000 бриллиантов, включая цену , карат , цвет , чистоту и огранку каждого алмаза.Таблица показывает, что доступно больше алмазов с огранкой высокого качества, чем с огранкой низкого качества.
ggplot (данные = бриллианты) + geom_bar (отображение = aes (x = вырезано))
По оси X на диаграмме отображается огранки , переменная из бриллиантов . По оси Y отображается количество, но количество не является переменной в бриллиантах ! Откуда берется счет? Многие графики, например диаграммы рассеяния, отображают необработанные значения вашего набора данных. Другие графики, например гистограммы, вычисляют новые значения для построения:
гистограммы, гистограммы и частотные многоугольники объединяют ваши данные а затем нанесите на график количество точек, которые попадают в каждую ячейку.
сглаживания подбирают модель к вашим данным, а затем строят прогнозы на основе модель.
Коробчатые диаграммы
вычисляют надежную сводку распределения, а затем отображают специально отформатированный ящик.
Алгоритм, используемый для вычисления новых значений для графика, называется stat , сокращение от статистического преобразования. На рисунке ниже показано, как этот процесс работает с geom_bar () .
Вы можете узнать, какой стат использует geom, проверив значение по умолчанию для аргумента stat .Например, ? Geom_bar показывает, что значением по умолчанию для stat является «count», что означает, что geom_bar () использует stat_count () . stat_count () задокументирован на той же странице, что и geom_bar () , и если вы прокрутите вниз, вы найдете раздел под названием «Вычисляемые переменные». Это описывает, как он вычисляет две новые переменные: count и prop .
Обычно вы можете использовать геометрию и статистику как взаимозаменяемые.Например, вы можете воссоздать предыдущий график, используя stat_count () вместо geom_bar () :
.
ggplot (данные = бриллианты) + stat_count (mapping = aes (x = cut))
Это работает, потому что у каждой геометрии есть стат по умолчанию; и каждый стат имеет геометрию по умолчанию. Это означает, что вы обычно можете использовать геометрию, не беспокоясь о лежащей в основе статистической трансформации. Есть три причины, по которым вам может потребоваться явное использование статистики:
Вы можете изменить статистику по умолчанию.В приведенном ниже коде я меняю статистика geom_bar () от счетчика (по умолчанию) до идентификатора. Это позволяет Я сопоставляю высоту столбцов с необработанными значениями переменной \ (y \). К сожалению, когда люди небрежно говорят о гистограммах, они могут относится к этому типу гистограммы, где высота столбца уже равна присутствует в данных, или на предыдущей гистограмме, где высота столбца генерируется путем подсчета строк.
демо <- tribble ( ~ вырезать, ~ частота, «Ярмарка», 1610 г., г. «Хорошая», 4906, г. «Очень хорошо», 12082, г. «Премиум», 13791, г. «Идеал», 21551 ) ggplot (данные = демонстрация) + geom_bar (mapping = aes (x = cut, y = freq), stat = "identity")
(Не беспокойтесь, что вы раньше не видели <- или tribble () .Вы, возможно уметь угадывать их значение из контекста, и вы точно узнаете что они скоро сделают!)
Вы можете захотеть переопределить отображение по умолчанию из преобразованных переменных эстетике. Например, вы можете отобразить гистограмму пропорция, а не количество:
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = cut, y = stat (prop), group = 1))
Чтобы найти переменные, вычисляемые с помощью статистики, обратитесь к разделу справки. под названием «вычисляемые переменные».
Возможно, вы захотите привлечь больше внимания к статистическому преобразованию в вашем коде. Например, вы можете использовать stat_summary () , который суммирует значения y для каждого уникального значения x, чтобы нарисовать Обратите внимание на сводку, которую вы вычисляете:
ggplot (данные = бриллианты) + stat_summary ( mapping = aes (x = вырез, y = глубина), fun.min = min, fun.max = max, веселье = медиана )
ggplot2 предоставляет вам более 20 статистических данных.Каждая статистика - это функция, поэтому вы можете получить помощь обычным способом, например ? Stat_bin . Чтобы увидеть полный список статистики, попробуйте шпаргалку ggplot2.
Упражнения
Какая геометрия по умолчанию связана с stat_summary () ? Как мог вы переписываете предыдущий график, чтобы использовать эту функцию geom вместо stat функция?
Что делает geom_col () ? Чем он отличается от geom_bar () ?
Большинство геометрических фигур и статистики попадают в пары, которые почти всегда используются в концерт.Прочтите документацию и составьте список всех пары. Что у них общего?
Какие переменные вычисляет stat_smooth () ? Какие параметры контролируют его поведение?
В нашей гистограмме пропорций нам нужно установить group = 1 . Почему? В другом словами в чем проблема с этими двумя графиками?
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = cut, y = after_stat (prop))) ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, fill = color, y = after_stat (prop)))
Регулировка положения
Есть еще одно волшебство, связанное с гистограммами.Вы можете раскрасить гистограмму, используя эстетику цвета или, что более полезно, заливку :
ggplot (данные = бриллианты) + geom_bar (отображение = aes (x = вырезать, цвет = вырезать)) ggplot (данные = бриллианты) + geom_bar (отображение = aes (x = вырезать, заполнить = вырезать))
Обратите внимание, что произойдет, если вы сопоставите эстетику заливки с другой переменной, например с четкостью : полосы автоматически складываются. Каждый цветной прямоугольник представляет собой комбинацию огранки и ясности .
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, заполнить = четкость))
Укладка выполняется автоматически с помощью регулировки положения , заданной аргументом позиция . Если вам не нужна столбчатая диаграмма с накоплением, вы можете использовать один из трех других вариантов: «идентификатор» , «уклонение» или «заполнить» .
position = "identity" разместит каждый объект именно там, где он падает. контекст графика.Это не очень полезно для баров, потому что перекрывает их. Чтобы увидеть это перекрытие, нам нужно сделать полосы слегка прозрачным, установив альфа на малое значение, или полностью прозрачный, установив fill = NA .
ggplot (данные = ромбы, отображение = aes (x = вырезка, заливка = четкость)) + geom_bar (альфа = 1/5, position = "identity") ggplot (данные = бриллианты, отображение = aes (x = огранка, цвет = чистота)) + geom_bar (fill = NA, position = "identity")
Регулировка положения идентичности более полезна для 2d геометрии, например точек, где это значение по умолчанию.
position = "fill" работает как наложение, но делает каждый набор наборных полос такой же высоты. Это упрощает сравнение пропорций между группы.
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, заполнить = четкость), position = "fill")
position = "dodge" помещает перекрывающиеся объекты прямо рядом с одним Другой. Это упрощает сравнение отдельных значений.
ggplot (данные = бриллианты) + geom_bar (mapping = aes (x = вырезать, заполнить = четкость), position = "dodge")
Есть еще один тип корректировки, который бесполезен для гистограмм, но может быть очень полезен для диаграмм рассеяния. Вспомните нашу первую диаграмму рассеяния. Вы заметили, что на графике отображается только 126 точек, хотя в наборе данных 234 наблюдения?
Значения hwy и displ округлены, поэтому точки появляются на сетке, и многие точки перекрывают друг друга.Эта проблема известна как , перекрывающая . Такое расположение затрудняет понимание того, где находится масса данных. Распределены ли точки данных равномерно по графику, или существует одна особая комбинация hwy и displ , которая содержит 109 значений?
Вы можете избежать этой сетки, установив регулировку положения на «дрожание». position = "jitter" добавляет небольшое количество случайного шума к каждой точке. Это раздвигает границы, потому что никакие две точки вряд ли получат одинаковое количество случайного шума.
ggplot (данные = миль на галлон) + geom_point (mapping = aes (x = displ, y = hwy), position = "jitter")
Добавление случайности кажется странным способом улучшить ваш график, но, хотя это делает ваш график менее точным в малых масштабах, оно делает ваш график более показательным в больших масштабах. Поскольку это очень полезная операция, в ggplot2 есть сокращение для geom_point (position = "jitter") : geom_jitter () .
Чтобы узнать больше о корректировке положения, просмотрите страницу справки, связанную с каждой корректировкой: ? Position_dodge , ? Position_fill , ? Position_identity , ? Position_jitter и ? Position_stack .
Упражнения
В чем проблема этого участка? Как бы вы могли это улучшить?
ggplot (данные = миль на галлон, отображение = aes (x = cty, y = hwy)) + geom_point ()
Какие параметры в geom_jitter () управляют величиной дрожания?
Сравните и сопоставьте geom_jitter () с geom_count () .
Какая настройка положения по умолчанию для geom_boxplot () ? Создавать визуализация набора данных миль на галлон , который демонстрирует это.
Системы координат
Системы координат, вероятно, самая сложная часть ggplot2. Системой координат по умолчанию является декартова система координат, в которой положения x и y действуют независимо, чтобы определить положение каждой точки. Иногда могут быть полезны и другие системы координат.
corre_flip () переключает оси x и y. Это полезно (например), если вам нужны горизонтальные коробчатые диаграммы.Это также полезно для длинных ярлыков: это их сложно подогнать без перекрытия по оси абсцисс.
ggplot (данные = миль на галлон, отображение = aes (x = класс, y = hwy)) + geom_boxplot () ggplot (данные = миль на галлон, отображение = aes (x = класс, y = hwy)) + geom_boxplot () + Coord_flip ()
corre_quickmap () правильно устанавливает соотношение сторон для карт. Это очень важно, если вы строите пространственные данные с помощью ggplot2 (что, к сожалению, у нас нет места для освещения в этой книге).
nz <- map_data ("nz") ggplot (nz, aes (long, lat, group = group)) + geom_polygon (fill = "white", color = "black") ggplot (nz, aes (long, lat, group = group)) + geom_polygon (fill = "white", color = "black") + Coord_quickmap ()
corre_polar () использует полярные координаты. Полярные координаты показывают интересная связь между гистограммой и диаграммой Кокскомба.
бар <- ggplot (data = diamonds) + geom_bar ( отображение = aes (x = вырезать, заполнить = вырезать), показать.легенда = ЛОЖЬ, ширина = 1 ) + тема (aspect.ratio = 1) + labs (x = NULL, y = NULL) бар + corre_flip () бар + координата_полярной ()
Упражнения
Превратите гистограмму с накоплением в круговую диаграмму с помощью ordin_polar () .
Чем занимается labs () ? Прочтите документацию.
В чем разница между corre_quickmap () и corre_map () ?
Что сюжет ниже рассказывает вам об отношениях между городами и шоссе на галлон? Почему так важен corre_fixed () ? Что значит geom_abline () делать?
ggplot (данные = миль на галлон, отображение = aes (x = cty, y = hwy)) + geom_point () + geom_abline () + Coord_fixed ()
Многослойная грамматика графики
В предыдущих разделах вы узнали гораздо больше, чем о том, как создавать диаграммы рассеяния, гистограммы и коробчатые диаграммы.Вы узнали фундамент, который можно использовать для построения любого типа графика с помощью ggplot2. Чтобы убедиться в этом, давайте добавим корректировки положения, статистику, системы координат и фасетирование в наш шаблон кода:
ggplot (data = ) + ( отображение = aes (<КАРТЫ>), stat = , position = <ПОЛОЖЕНИЕ> ) + +
Наш новый шаблон принимает семь параметров, слова в квадратных скобках, которые появляются в шаблоне.На практике вам редко нужно указывать все семь параметров для построения графика, потому что ggplot2 предоставит полезные значения по умолчанию для всего, кроме данных, сопоставлений и функции geom.
Семь параметров в шаблоне составляют грамматику графики, формальную систему построения графиков. Грамматика графики основана на понимании того, что вы можете однозначно описать любой график как комбинацию набора данных, геометрии, набора сопоставлений, статистики, корректировки положения, системы координат и схемы фасетирования.
Чтобы увидеть, как это работает, подумайте, как вы можете построить базовый график с нуля: вы можете начать с набора данных, а затем преобразовать его в информацию, которую вы хотите отобразить (со статистикой).
Затем вы можете выбрать геометрический объект для представления каждого наблюдения в преобразованных данных. Затем вы можете использовать эстетические свойства геометрии для представления переменных в данных. Вы бы сопоставили значения каждой переменной с уровнями эстетики.
Затем вы должны выбрать систему координат для размещения геометрии.Вы можете использовать расположение объектов (которое само по себе является эстетическим свойством) для отображения значений переменных x и y. В этот момент у вас будет полный график, но вы можете дополнительно настроить положения геометрии в системе координат (корректировка положения) или разбить график на подзаголовки (фасетирование). Вы также можете расширить график, добавив один или несколько дополнительных слоев, где каждый дополнительный слой использует набор данных, геометрию, набор сопоставлений, статистику и корректировку положения.
Вы можете использовать этот метод для построения любого сюжета , который вы себе представляете. Другими словами, вы можете использовать шаблон кода, который вы изучили в этой главе, для построения сотен тысяч уникальных графиков.
Графический анализ данных с программированием на R - подробное руководство!
В этой статье мы проведем вас через комплексный тур по графическому анализу данных с помощью R. Мы исследуем типы графиков, доступные в R, и научимся создавать их с помощью функций и примеров реализации.
Также мы рассмотрим сохранение графики в файл в R и выбор соответствующего графика. Итак, приступим к изучению тура.
Что такое графический анализ данных с помощью R?
Большая часть статистического анализа основана на численных методах, таких как доверительных интервалов , проверка гипотез , регрессионный анализ и так далее. Во многих случаях эти методы основаны на предположениях об используемых данных. Одним из способов определить, подтверждают ли данные эти предположения, является анализ графических данных с использованием R, в виде графика, который может предоставить много информации о свойствах построенного набора данных.
Графики полезны для нечисловых данных, таких как цвета, вкусы, названия брендов и т. Д. Когда числовые меры трудно или невозможно вычислить, важную роль играют графики.
Статистические вычисления выполняются с целью получения высококачественной графики.
Различные типы графиков, нарисованных в программировании R:
Графики с одной переменной - Вы можете построить график для одной переменной.
Графики с двумя переменными - Вы можете построить график с двумя переменными.
Графики с несколькими переменными - Вы можете построить график с несколькими переменными.
Special Plots - R имеет графические возможности низкого и высокого уровня.
Прежде чем продолжить, вы должны пройти Учебное пособие по графическим моделям
1. Графики с одной переменной
Возможно, вам понадобится построить график для одной переменной в графическом анализе данных с помощью программирования R. Например - График, показывающий ежедневные объемы продаж определенного продукта за определенный период времени.Вы также можете построить временной ряд для продаж по месяцам.
Выбор графиков более ограничен, когда у вас есть только одна переменная для графика. В R:
есть различные функции построения графиков для отдельных переменных.
hist (y) - Гистограммы для отображения частотного распределения.
plot (y) - Мы можем получить значения y в последовательности с помощью графика.
plot.ts (y) - Графики временных рядов.
pie (x) - Композиционные графики в виде круговых диаграмм.
Типы участков, доступных в R:
Гистограммы - Используется для отображения режима, распространения и симметрии набора данных.
Index Plots - Здесь график принимает единственный аргумент. Этот вид графика особенно полезен для проверки ошибок.
Графики временных рядов - По истечении определенного периода времени график временных рядов можно использовать для соединения точек в упорядоченном наборе значений y.
Круговые диаграммы - Полезно для иллюстрации пропорционального состава образца в презентациях.
Распространенная ошибка новичков - путать гистограммы и гистограммы. Гистограммы имеют переменную отклика на оси x, а ось y показывает частоту различных значений отклика. Напротив, гистограмма имеет переменную отклика на оси y и категориальную независимую переменную на оси x.
Получите глубокое понимание гистограммы и гистограммы в программировании на языке R
1.1 Гистограммы
Гистограммы отображают режим, разброс и симметрию набора данных. Функция R hist () используется для построения гистограмм.
Делится ось x, по которой распределяются и затем подсчитываются значения переменной ответа. Это называется бункерами. Гистограммы сложны, потому что это зависит от субъективных суждений о том, где именно разместить поля бункера и на какой график вы будете смотреть. Широкие интервалы дают одно изображение, узкие интервалы дают другое изображение, а неравные интервалы создают путаницу.
Маленькие ячейки создают мультимодальность (комбинацию звукового, текстового и визуального режимов), тогда как широкие ячейки создают унимодальность (содержат одномодовый режим). При разной ширине бункера по умолчанию в R используется преобразование отсчетов в плотности.
В языке R принято использовать квадратные и круглые скобки для отображения границ ячеек, так что:
[a, b) означает «больше или равно a, но меньше b» [квадрат, чем круглый).
(a, b) означает «больше a, но меньше или равно b» (круглое, чем квадратное).
Вам необходимо позаботиться о том, чтобы в лотках можно было разместить как минимальные, так и максимальные значения.
Функция cut () берет непрерывный вектор и разрезает его на интервалы, которые затем можно использовать для подсчета.
Функция hist () в R не принимает во внимание ваши советы относительно количества полосок или ширины полосок. Это помогает одновременно просматривать несколько гистограмм с одинаковым диапазоном. Для небольших целочисленных данных у вас может быть одна ячейка для каждого значения.
В R параметр k отрицательного биномиального распределения известен как размер , а среднее значение известно как mu .
Построение гистограмм непрерывных переменных является более сложной задачей, чем независимые переменные. Эта проблема зависит от оценки плотности, что является важным вопросом для статистиков. Чтобы справиться с этой проблемой, вы можете приблизительно преобразовать непрерывную модель в дискретную модель, используя линейное приближение для оценки плотности в указанных точках.
Выбор полосы пропускания - это компромисс между удалением незначительных ударов и реальных пиков.
Пора освоить концепцию биномиального и пуассоновского распределения в программировании на языке R
1.2 Индексные участки
Для построения отдельных выборок можно использовать индексные диаграммы. Функция построения графика принимает единственный аргумент. Это непрерывная переменная, значения которой отображаются на оси Y, причем координата x определяется положением числа в векторе.Графики индекса особенно полезны для проверки ошибок.
1.3 График временных рядов
График временного ряда можно использовать для соединения точек в упорядоченном наборе значений y по истечении определенного периода времени. Проблемы возникают, когда во временном ряду отсутствуют значения (например, если значения продаж за два месяца отсутствуют в течение последних пяти лет), особенно группы отсутствующих значений (например, если значения продаж за два квартала отсутствуют в течение последних пяти лет). пять лет), и в течение этого периода мы обычно ничего не знаем о поведении временного ряда.
ts.plot и plot.ts - две функции для построения графика данных временных рядов в R.
1,4 Круговая диаграмма
Вы можете использовать круговые диаграммы, чтобы проиллюстрировать пропорциональный состав образца в презентациях. Здесь функция pie берет вектор чисел и превращает их в пропорции. Затем он делит круг на основе этих пропорций.
Чтобы обозначить каждый сегмент пирога, необходимо использовать этикетку.Метка предоставляется как вектор символьных строк, здесь он называется data $ names .
Если список имен содержит пробелы, вы не можете использовать read.table с текстовым файлом, разделенным табуляцией, для ввода данных. Вместо этого вы можете сохранить файл с именем piedata как файл с разделителями-запятыми с расширением «.csv» и ввести данные в R, используя read.csv вместо read.table.
#Author DataFlair данные <- read.csv ("/ home / dataflair / data / piedata.csv ") данные
Выход:
Круговая диаграмма может быть создана с помощью следующей команды:
пирог (данные $ суммы, метки = as.character (данные $ имена))
Выход:
Вы обязательно должны взглянуть на числовые и символьные функции в R
2. Графики с двумя переменными
Два типа переменных, используемых в графическом анализе данных с помощью R:
Переменная ответа
Объясняющая переменная
Переменная ответа представлена на оси y , а пояснительная переменная представлена на оси x . Характер объясняющей переменной определяет вид создаваемого графика. Когда независимая переменная является непрерывной переменной, такой как длина, вес или высота, подходящим графиком для использования является диаграмма рассеяния.
Когда независимая переменная является категориальной, например генотип, цвет или пол, подходящим графиком является либо график с ячейками и усами, либо гистограмма.
Мы можем представить наборы числовых данных с помощью прямоугольного и усового графика, который использует квартили и зависит от минимального и максимального значений, а также от верхнего и нижнего квартилей.
Гистограмма обеспечивает графическое представление данных в виде гистограмм.
Наиболее часто используемые функции построения графиков для двух переменных в R:
график (x, y): График рассеяния y против x
график (фактор, y): Прямоугольный график y на каждом уровне фактора.
barplot (y): Высоты из вектора значений y (одна полоса на уровень фактора).
Типы участков, доступных в R:
Диаграммы рассеяния - Когда независимая переменная является непрерывной переменной.
Ступенчатые линии - Используется для четкого отображения данных и обеспечения четкого обзора.
Коробчатые диаграммы - Коробчатые диаграммы показывают расположение, разброс данных и указывают на асимметрию.
Гистограмма - Показывает высоту средних значений для различных обработок.
2,1 Диаграммы рассеяния
Диаграммы рассеяния показывают графическое представление взаимосвязи между двумя пронумерованными наборами. Функция построения графика рисует ось и добавляет диаграмму рассеяния точек.Вы также можете добавить дополнительные точки или линии к существующему графику, используя функции, точку и линии.
Функции точек и линий можно указать двумя способами:
Декартова диаграмма (x, y) - Декартова координата определяет положение точки в двумерной плоскости с помощью двух перпендикулярных векторов, которые называются осью. Начало декартовой системы координат - это точка, в которой две оси пересекают друг друга, а положение этой точки - (0,0).
График формулы (y, x) - График на основе формулы относится к представлению взаимосвязи между переменными в графической форме. Например - Уравнение y = mx + c показывает прямую линию в декартовой системе координат.
Преимущество графика на основе формулы состоит в том, что функция построения графика и соответствие модели выглядят одинаково. Декартовы графики строят графики с использованием « x , затем y », в то время как подгонка модели использует «y , затем x ».
Функция построения графика использует следующие аргументы:
Имя независимой переменной.
Имя переменной ответа.
Основной синтаксис диаграммы рассеяния следующий:
график (x, y, main, xlab, ylab, xlim, ylim, оси)
, где x - данные, представленные в горизонтальных координатах.
y - это данные, представленные на вертикальной оси.
main представляет название нашего сюжета.
xlab - метка, обозначающая горизонтальную ось.
ylab - метка для вертикальной оси.
xlim - это пределы x для построения графика.
ylim - пределы y для построения графика.
осей указывают на то, что обе оси должны присутствовать на графике.
Для создания диаграммы рассеяния мы будем использовать набор данных mtcars, который присутствует в библиотеке данных R. Мы строим график между метками «wt» и «mpg».
данных («mtcars») scatter_data <- mtcars [, c ('вес', 'миль на галлон')] # Присвоение имени файлу png (file = "DataFlair_scatterplot.png") # Создание нашей диаграммы рассеяния график (x = scatter_data $ wt, y = scatter_data $ mpg, xlab = "Вес", ylab = "Milage", xlim = c (2,5,5), ylim = c (15,30), main = "Вес по сравнению с пробегом" ) dev.off () # Сохраняем файл
Выход:
Лучший способ идентифицировать несколько человек на диаграммах рассеяния - использовать комбинацию цветов и символов.Полезный совет - использовать в качестве числового , чтобы преобразовать фактор группирования в цвет и / или символ.
Подождите! Вы проверили - Обобщенные линейные модели в программировании на R
2.2 Ступенчатые линии
Ступенчатые линии могут быть построены в виде графического представления, отображаемого в R. Эти графики четко отображают данные, а также обеспечивают четкое представление различий в рисунках.
При нанесении прямоугольных краев между двумя точками необходимо решить, идти ли поперек, а затем вверх, или вверх, а затем поперек.Предположим, что у нас есть два вектора от 0 до 10. Построим эти точки следующим образом:
х = 0:10 у = 0:10 сюжет (x, y)
Выход:
Мы можем нарисовать прямую линию с помощью следующей команды:
> #Author DataFlair > сюжет (x, y) > строки (x, y, col = "красный")
Выход:
Также сгенерируйте строку, используя заглавную букву «S», как показано ниже:
> lines (x, y, col = "green", type = 'S')
Выход:
2.3 Участок с ящиками и усами
График в виде прямоугольников и усов - это графическое средство представления наборов числовых данных с использованием квартилей. Он основан на минимальном и максимальном значениях, а также на верхнем и нижнем квартилях.
Boxplots обобщает имеющуюся информацию. Вертикальные пунктирные линии называются «усами». Коробчатые диаграммы также отлично подходят для выявления ошибок в данных. Крайние выбросы представляют собой эти ошибки.
2,4 Штриховая диаграмма
Гистограмма - это альтернатива прямоугольной диаграмме для отображения высот средних значений для различных обработок. Функция tapply вычисляет высоту стержней. Таким образом, он определяет средние значения для каждого уровня категориальной объясняющей переменной.
Давайте создадим игрушечный набор данных температур за неделю. Затем мы построим гистограмму с метками.
температура <- c (28, 35, 31, 40, 29, 41, 42) days <- c («Вс», «Пн», «Вт», «Ср», «Чт», «пт», «сб») barplot (temperature, main = "Максимальные температуры через неделю", xlab = "Дни", ylab = "Степень Цельсия", имена.arg = дни, col = "darkred")
Выход:
Есть сомнения в графическом анализе данных с помощью R до сих пор? Прокомментируйте свои запросы ниже.
3. Графики с несколькими переменными
Первоначальная проверка данных с использованием графиков еще более важна, когда есть много переменных, в любой из которых могут быть ошибки или упущения. Основными функциями графика, представляющими несколько переменных, являются:
Функция пар - Для матрицы диаграмм рассеяния каждой переменной относительно друг друга.
Функция Coplot - Для графиков кондиционирования, где y отображается в зависимости от x для различных значений z.
При работе со строками и столбцами фреймов данных лучше использовать более специализированные команды.
3.1 Функция пар
Для двух или более непрерывных независимых переменных полезно проверить наличие тонких зависимостей между независимыми переменными. Строки представляют переменные ответа, а столбцы - независимые переменные.
Каждая переменная во фрейме данных находится на оси Y по отношению ко всем другим переменным на оси X с использованием графиков парных функций. Для функции пар требуется только имя всего фрейма данных в качестве первого аргумента.
Давайте вернемся к теме аргументов в языке программирования R
3.2 Функция Coplot
Связь между двумя переменными может быть скрыта из-за влияния других процессов в многомерных данных. Когда вы рисуете двумерный график зависимости y от x, тогда все эффекты других независимых переменных отображаются на плоскости бумаги.В простейшем случае у нас есть одна переменная ответа и всего две независимые переменные.
Панели коплота упорядочены слева направо снизу вверх, связанные со значениями переменной кондиционирования на верхней панели слева направо.
Coplot включает в себя "черепицу", показанную на верхнем поле, что является ее самым большим недостатком. Наложение черепицы показывает степень перекрытия между одной панелью и следующей панелью по отношению к количеству общих точек данных между ними.
4. Специальные графики в графическом анализе данных с R
R имеет обширные возможности для создания графиков. Он также имеет графические возможности низкого и высокого уровня в соответствии с требованиями.
Низкоуровневая графика - это базовые строительные блоки, с помощью которых можно строить графики шаг за шагом, в то время как высокоуровневые средства предоставляют множество предварительно собранных графических дисплеев.
Помимо обсуждаемых различных видов графических графиков, R поддерживает следующие специальные графики:
Графики дизайна - Эффективные размеры в запланированных экспериментах могут быть визуализированы с помощью графиков дизайна.Графики дизайна можно построить с помощью функции plot.design - plot.design (Скорость роста ~ Вода * Моющее средство * Дафния)
Пузырьковые графики - Полезно для иллюстрации вариации третьей переменной в разных местах x – y.
Графики со многими идентичными значениями - Иногда две или более точки с данными подсчета попадают в одно и то же место на диаграмме рассеяния. В результате повторяющиеся значения y скрываются одно под другим.
Добавление других фигур на участок
Используя следующие функции, мы можем добавить дополнительные графические объекты в графики:
rect - Для построения прямоугольников - rect (xleft, ybottom, xright, ytop)
Используя функцию локатора, мы можем получить координаты углов прямоугольника. Но функция rect не принимает локатор в качестве аргумента.
стрелки - Для построения стрелок и полос с направлением - Синтаксис функции стрелок заключается в рисовании линии от точки (xO, yO) до точки (x1, y1) с помощью стрелки, по умолчанию , на «втором» конце (x1, y1) .
стрелки (xO, yO, xl, yl)
Добавление кода = 3 дает горизонтальную двустороннюю стрелку от (2,1) до (9,8) , например:
участок (x, y) стрелки (2,1,9,8, код = 3) #Author DataFlair
Выход:
Сохранение графики в файл за R
Вы, вероятно, захотите сохранить каждый из ваших графиков как файл PDF или PostScript для графики качества публикации.Это делается путем указания «устройства» перед черчением и последующего выключения устройства после завершения.
Экран компьютера является устройством по умолчанию, с которого мы можем получить приблизительную копию графика, используя следующую команду:
данных <- таблица чтения (имя файла, заголовок = T) прикрепить (данные)
Существует множество опций для функций PDF и Postscript, но ширину и высоту вы захотите изменять чаще всего. Размеры указаны в дюймах. Вы можете указать любые аргументы не по умолчанию, которые вы хотите изменить, используя функции pdf.опции и ps.options перед вызовом PDF или postscript.
Выбор подходящего графика в
рэндов
Вы узнали о разных типах графиков. Теперь вы можете легко нарисовать эти графики в R. Также важно выбрать соответствующий тип графика в соответствии с требованиями.
Вот некоторые общие графики и их использование:
Линейный график - Отображается за период времени. Обычно он ведет учет записей как за долгий, так и за краткосрочный период в соответствии с требованиями.В случае небольшого изменения, линейный график встречается чаще, чем гистограмма. В некоторых случаях на линейных графиках также сравниваются изменения среди разных групп за один и тот же период времени.
Круговая диаграмма - Отображает сравнение внутри группы. Например - Вы можете сравнивать студентов в колледже на основе их направлений, таких как искусство, наука и торговля, с помощью круговой диаграммы. Нельзя использовать круговую диаграмму для отображения изменений за период времени.
Гистограмма - Подобно линейной диаграмме, гистограмма обычно сравнивает различные группы или отслеживает изменения за определенный период времени.Таким образом, разница между двумя графиками заключается в том, что линейный график отслеживает небольшие изменения, а гистограмма - большие изменения.
График с областями - График с областями отслеживает изменения за определенный период времени для одной или нескольких групп, относящихся к аналогичной категории.
График X-Y - График X-Y отображает определенную взаимосвязь между двумя переменными. В этом типе переменных ось X измеряет одну переменную, а ось Y - другую. С одной стороны, если значения обеих переменных увеличиваются одновременно, между переменными существует положительная связь.С другой стороны, если значение одной переменной уменьшается во время увеличения значения другой переменной, между переменными существует отрицательная связь. Также возможно, что две переменные не связаны между собой. В этом случае построение графика не имеет смысла.
Сводка
Мы обсудили полную концепцию графического анализа данных с помощью R Programming. Мы также поняли, как создавать различные типы графиков и сохранять графику в файл в R, и как выбрать подходящий график.
Следующая статья в нашем учебнике по R DataFlair Series - Top Graphical Models Applications
Тем не менее, если у вас есть какие-либо вопросы, связанные с анализом графических данных с помощью R, не стесняйтесь поделиться с нами.
Published in Разное
Предыдущая запись Не слышно звука на ноутбуке: Пропал звук на ноутбуке: причины и их решение
Следующая запись Как сделать скриншот с айфона: Как сделать снимок экрана или запись экрана на iPhone
Ваш комментарий будет первым
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя*
Email*
Веб-сайт

Боковая панель
Поиск
Рубрики
Видео
Дешев
Дорогая
Комплектующ
Комплектующие
Конфигурац
Конфигурация
Питание
ПК
Проц
Процессор
Разное
Рекомендации по сборке
Самостоят
Сборка
Своими руками
Собрать
Совет
Советы
© 2019 iApple-59.ru

				Особенности графика
[-1, 0[	+	—	Возрастает	Выпуклый
0	0	—	1	(0; 1) – точка максимума
]0, 1[	—	—	Убывает	Выпуклый
1	—	0		— точка перегиба, образует с осью Ox тупой угол
]1, +∞[	—	+	Убывает	Вогнутый
+∞	—	+		y = 0 – горизонтальная асимптота

Технологии	Описание
Графический калькулятор	Калькулятор с экраном и возможностью построения графиков
Графический калькулятор онлайн	Функции ввода и графиков с использованием компьютера с подключением к Интернету
Программное обеспечение для построения графиков	График с использованием программного обеспечения для компьютера или смартфона / планшета

x	«-4»	`-3`	`-2`	`-1`	`1`	`2`	`3`	`4`
y	`3/4`	`2/3`	`1/2`	`0`	`2`	`3/2`	`4/3`	`5/4`