Исследование функции и построение графика онлайн калькулятор: Построение графика функции методом дифференциального исчисления

Содержание

Построение графика функции методом дифференциального исчисления

Существует способ построения графика функции, основанный на аналитическом исследовании функции. Исследование проводится по следующей примерной схеме:
1) выяснение области определения функции;
2) решается вопрос о четности или нечетности функции;
3) исследуется периодичность функции;
4) находят точки пересечения кривой с осями координат;
5) находят точки разрыва функции и определяют их характер;
6) проводят исследования на экстремум, находят экстремальные значения функции;
7) ищутся точки перегиба и интервалы выпуклости и вогнутости кривой;
8) отыскание асимптот кривой;
9) полученные результаты наносят на чертеж и получают график исследуемой функции.

Построить график без исследования функции (получить просто рисунок) можно с помощью этого сервиса.

Решение онлайн
Видеоинструкция
Оформление Word

Правила ввода функции

Примеры
≡ x^2/(x+2)
cos²(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Пример №1. Провести полное исследование функции и построить ее график.

1) Функция определена всюду, кроме точек .

2) Функция нечетная, так как f(-x) = -f(x), и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.

3) Функция не периодическая.

4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.

5) Функция имеет разрыв второго рода в точке , причем , . Попутно отметим, что прямая – вертикальная асимптота.

6) Находим и приравниваем ее к нулю: , откуда x₁ = -3, x₂ = 0, x₃ = 3. На экстремум надо исследовать только точку x=3 (точку x₂=0 не исследуем, так как она является граничной точкой промежутка [0, +∞)).

В окрестности точки x₃=3 имеет: y’>0 при x<3 и y ’<0 при x>3, следовательно, в точке x₃ функция имеет максимум, y_max(3)=-9/2.

Найти первую производную функции

Для проверки правильности нахождения минимального и максимального значения.

7) Находим . Видим, что y’’=0 только при x=0, при этом y”<0 при x<0 и y”>0 при x>0, следовательно, в точке (0,0) кривая имеет перегиб. Иногда направление вогнутости может измениться при переходе через разрыв кривой, поэтому следует выяснить знак y” и около точек разрыва функции. В нашем случае y”>0 на промежутке (0, ) и y”<0 на (, +∞), следовательно, на (0, ) кривая вогнута и выпукла на (, ∞).

Найти вторую производную функции

8) Выясним вопрос об асимптотах.

Наличие вертикальной асимптоты установлено выше. Ищем горизонтальные: , следовательно, горизонтальных асимптот нет.

Найдем наклонные асимптоты: , , следовательно, y=-x – наклонная двусторонняя асимптота.

9) Теперь, используя полученные данные, строим чертеж:

Построить график функции

Пример №2. Построить график функции .
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем
; .
4. Точки разрыва x=0, причем ; следовательно, x=0 является вертикальной асимптотой графика.
Найдем наклонные асимптоты:
;
.
Наклонная асимптота имеет уравнение y=x.
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем . Существует единственная критическая точка

x=2. В промежутках x∈(-∞ ;0)∪(2; +∞) y’>0, следовательно, функция возрастает; в промежутке x∈(0;2) y'<0, функция убывает. Далее, находим ; y»(2)>0, следовательно, x=2 – точка минимума y_min=3.
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.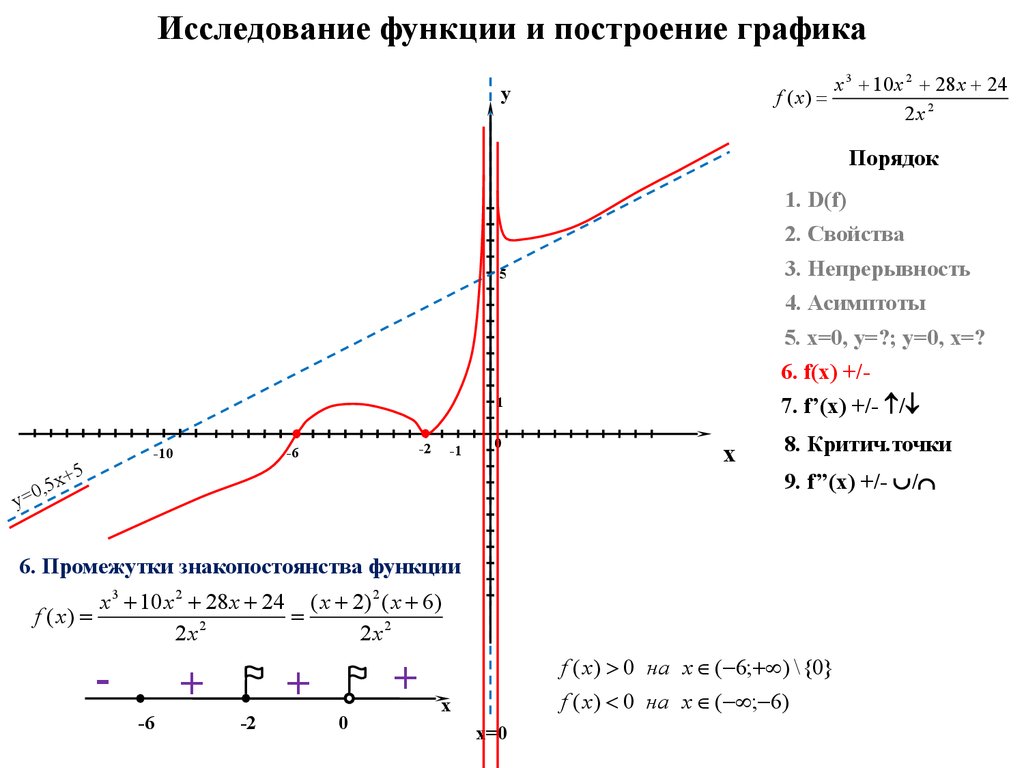

2)(1/5 x +1/6))’, и этот калькулятор сделает следующее упрощение функций для вас.

После того, как вы ввели действительную функцию в соответствующую форму, вам нужно просто нажать кнопку «Рассчитать», чтобы получить построенный график.

Работа с график функции может помочь вам понять его основные свойства. Действительно, наличие график функции может рассказать вам в конечном итоге все, что нужно, о поведении функции: возрастает ли она? Уменьшается ли она? Пересекает ли она ось x? Имеет ли она какую-либо симметрию?

Что такое график функции?

График функции f(x)- это множество точек (x, f(x)).

При построении по осям x-y это выглядит как «кривая» (может быть линией), которая течет слева направо.

Теперь у этого потока слева направо есть одно очень специфическое свойство: он проходит тест на вертикальную линию, который показывает, что график функции при пересечении с любой вертикальной линией будет иметь не более одной точки пересечения. Например, график ниже соответствует графику функции, потому что он проходит тест на вертикальную линию.

С другой стороны, график ниже не соответствует графику функции, потому что мы видим вертикальную линию, пересекающую кривую в двух точках.

Каковы этапы нахождения графика функции?

Шаг 1: Определите функцию, график которой вы хотите построить. Путем осмотра оцените, является ли функция действительной
Шаг 2: Если функция является допустимым выражением, найдите потенциальные точки, в которых функция не может быть оценена (деление на ноль или квадратные корни из отрицательных чисел)
Шаг 3: Упростите как можно больше, чтобы представить функцию в ее простейшей форме

Шаг 4: Попытайтесь выявить известные закономерности. Является ли функция в своей простейшей форме многочленом? Полиномы имеют определенную форму. Является ли функция тригонометрической функцией? Они также имеют очень хорошо известную и характерную форму
Шаг 5: Если у вас нет простой, узнаваемой модели или известной функции, создайте таблицу точек (x, f(x)), столько точек, сколько это практически возможно
Шаг 6: Постройте точки из таблицы на плоскости XY.
2\) (простая парабола) или \(f(x) = x\) (простая линия), но у вас могут быть переводы масштабированных версий этих основных версий. Действительно, например, любой квадратичная функция может быть помещена в Вершинная форма , что помогает определить кривую как простую параболу, которая переводится.
Каковы этапы выполнения преобразований графиков функций?
- Шаг 1: Определите функцию, график которой вы хотите построить
- Шаг 2: Упрощайте как можно больше, избегая ловушки деление на ноль и извлечение квадратного корня из отрицательных значений
- Шаг 3: Используя простейшую версию функции, посмотрите, можно ли распознать какие-либо элементарные функции
- Шаг 4: Если нет, посмотрите, есть ли преобразования обычных функций (полиномов, линий, триггерные функции и т.
  д.) могут быть идентифицированы, поскольку их тоже легко изобразить на графике
- Шаг 5: Если все вышеперечисленное не помогает, просто постройте таблицу со значениями (x, f(x)) и вручную проследите форму графика
Конечно, вам не обязательно строить график вручную, вы можете использовать следующее график функции онлайн инструмент для получения точного и аккуратного графика.
Почему вы хотите узнать о типах графиков функций?
График функции может рассказать о ней практически все.
2\), который был сдвинут влево на 4 единицы, сдвинут вниз на \(\frac{5}{6}\) и повторно масштабирован.
Пример: еще один пример графика функции
Вычислите график \( f(x) = \displaystyle \frac{\sin(x)}{x}\).
Отвечать: Была предоставлена следующая функция: \(\displaystyle f(x) = \frac{\sin\left(x\right)}{x}\), тогда получается следующий график, интервал \([-10, 10]\):
Другие функциональные калькуляторы
Получив функцию, вы должны быть в состоянии упростить функцию , если выразить это в простейшей форме. Мы уже видели, что полезно определить более простым способом потенциальное преобразование графика функции от базовых функций, которые там могут быть.
Онлайн-калькулятор графиков — Рисование онлайн-кривой — Онлайн-график
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель , это онлайн-график , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. Построитель кривых особенно подходит для функционального исследования , позволяет получить графическое представление функции из уравнения кривой, его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
Операторы для использования в 9Для питания
/ Для отдела

Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :

абс (абсолютное значение), график абсолютного значения
арккос (арккосинус), арккосинус участка
арксинус (арксинус), арксинус графика
арктангенс (арктангенс), арктангенс графика
ch (гиперболический косинус), построить гиперболический косинус
cos (косинус), график косинус
cosec (косеканс), косеканс участка
котан (котангенс), котангенс участка
coth (гиперболический котангенс), построить гиперболический котангенс
cube_root (кубический корень), построить кубический корень
опыта (экспоненциальный), экспоненциальный график
ln (напировский логарифм), построить напьеровский логарифм
(логарифм), логарифм графика
сек (секанс), секущая участка
ш (гиперболический синус), построить гиперболический синус
sin (синус), график синуса
sqrt (квадратный корень), участок квадратный корень
тангенс (тангенс), участок касательной
-й (гиперболический тангенс), построить гиперболический тангенс

Графические функции онлайн

Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно , просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .

Переменная, которая будет использоваться для представления функций, — «x».

Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.

Кривые можно удалить из плоттера:

Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.

Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.

Онлайн-построитель кривых имеет несколько опций, позволяющих настроить график. Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов, чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.

Проведение касательной функции к точке

Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.

График производной функции

Онлайн-плоттер позволяет вам построить производную функции для этого, вы просто рисуете нужную функцию, затем после того, как функция нарисована, нажмите на меню, на параметры, затем на появившуюся производную кнопку, затем строится производная функции.

9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).

Построить параметрическую кривую онлайн

Плоттер позволяет рисовать параметрическую кривую , для этого вам просто нужно ввести абсциссу, ординату как функцию от t, затем нажмите кнопку «Построить параметрическую кривую», кривая автоматически отображается с двумя курсорами для отображения нужных точек.

Построить полярную кривую онлайн

Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.

Переместите курсор на кривую

Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.

Доступные варианты графики

Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.

Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это, используйте область в правом нижнем углу графиков.

Кнопка + позволяет увеличить масштаб кривых,
— позволяет уменьшить масштаб кривых,
Стрелки используются для перемещения кривых,

Экспорт кривых

Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков. Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение, также возможно скопировать изображение. Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.

Онлайн-калькулятор Desmos | Департамент образования штата Вирджиния

Онлайн-калькулятор по математике Стандарты оценки успеваемости

Начиная с 2022–2023 учебного года учащиеся будут использовать калькулятор Desmos Virginia только в TestNav во время онлайн-оценки роста или теста SOL. Ручные калькуляторы будут использоваться только учащимися, прошедшими бумажный тест, или учащимися с ограниченными возможностями, у которых есть IEP или приспособление 504, требующее использования ручного калькулятора. По вопросам, касающимся других сценариев, в которых учащийся может использовать портативный калькулятор, обращайтесь к директору отдела тестирования 9 вашего подразделения.0015

Обзор и реализация

Онлайн-калькуляторы Desmos, которые включают в себя четырехфункциональный, научный и графический калькулятор, доступны для всех бесплатно. Доступ к онлайн-калькуляторам можно получить с компьютера, планшета или другого персонального устройства.

Начиная с проведения теста ОСЕНЬЮ 2022 г., Оценки роста и Стандарты обучения, оценивающие стандарты обучения по математике 2016 года, проводимые онлайн, будут включать доступ к версиям онлайн-калькуляторов Desmos Virginia. Тесты по математике для 4 и 5 классов будут иметь четырехфункциональный калькулятор Desmos Virginia на панели инструментов для активных элементов теста. В тестах по математике для 6 и 7 классов научный калькулятор Desmos Virginia появится на панели инструментов для активных элементов теста, а в тесте по математике для 8 класса научный калькулятор Desmos Virginia будет отображаться на панели инструментов для всего теста. Для тестов по математике в конце курса (EOC) будет доступен графический калькулятор Desmos Virginia для всего теста. Кроме того, в 2022-2023 годах онлайн-оценки роста по математике больше не будут иметь отдельных разделов без калькулятора и с калькулятором. Это же изменение коснется и онлайн-тестов по математике Standards of Learning (SOL), начиная с весны 2023 года. Поскольку больше не будет отдельных разделов, не связанных с калькулятором, и разделов с калькулятором, для всех онлайн-оценок развития математики в 3-8 классах и онлайн-весны 2023 года Тесты SOL по математике учащимся будет предоставлен доступ к соответствующему калькулятору Desmos Virginia на панели инструментов программного обеспечения для онлайн-тестирования (TestNav) для тех тестовых заданий, где можно использовать калькулятор. Калькулятор Desmos Virginia не будет отображаться на панели инструментов для тех тестовых заданий, где калькулятор нельзя использовать. По вопросам, касающимся различных сценариев, включающих онлайновые и бумажные тесты, размещение калькулятора и доступ к соответствующему калькулятору, обращайтесь к директору отдела тестирования вашего подразделения. Все тесты Science SOL, измеряющие 2010 и 2018 Научные стандарты обучения будет включать доступ к онлайн-калькулятору Desmos Virginia с осени 2022 года.

Стандартные онлайн-калькуляторы Desmos

Четырехфункциональный калькулятор Desmos
Научный калькулятор Desmos
Графический калькулятор Desmos

Онлайн-калькуляторы Desmos Virginia

Четырехфункциональный калькулятор Desmos Virginia
Научный калькулятор Desmos Virginia
Графический калькулятор Desmos, Вирджиния

Калькуляторы Desmos Virginia (четыре функции, научный и графический), которые будут встроены в приложение TestNav, будут эмулировать многие возможности бесплатных стандартных версий, доступных на веб-странице Desmos, с некоторыми отличиями. Учителям и учащимся рекомендуется использовать калькуляторы Desmos Virginia и ознакомиться с ними.

Калькулятор Desmos для Вирджинии – раздаточный материал (PDF) содержит список функций, отключенных в тестовых версиях калькуляторов Desmos для Вирджинии.

Версии научного и графического калькулятора Desmos для стандартной версии и версии для Вирджинии также доступны в виде приложений, которые позволяют пользователям получать доступ к калькулятору без использования Wi-Fi или данных. (iOS) )

Приложения для калькуляторов Desmos Virginia

Научный калькулятор Desmos Virginia (iOS)

Графический калькулятор Desmos Virginia (iOS)

Преимущества Desmos

Использование Desmos в качестве встроенного калькулятора в среде тестирования создает стандартизированную и согласованную платформу тестирования учащийся будет использовать тот же калькулятор при оценке стандартов обучения. Графический калькулятор Desmos позволяет пользователям одновременно просматривать несколько представлений и управлять ими, способствуя более глубокому концептуальному пониманию математики. В Desmos есть функции, которые стимулируют студенческий поиск и помогают учащимся понять богатые связи и сложность математики. Современные студенты подключены к технологиям с помощью смартфонов, планшетов и других устройств. Возможность использовать Desmos как форму учебной технологии, которая сочетается с текущими способами доступа учащихся к информации, может привести к более активному участию учащихся и более содержательным математическим исследованиям.
Desmos в настоящее время доступен для оценок в ряде штатов и теперь включен в качестве встроенного инструмента в часть калькулятора нового цифрового SAT, PSAT 10 и PSAT 8/9. Совет колледжей создал предварительный просмотр цифрового теста для учащихся, который включает ссылку на графический калькулятор Desmos, а также варианты доступных функций тестирования.

Desmos и специальное образование

Команды Индивидуальной программы обучения (IEP) продолжат определять право учащегося использовать калькулятор для предметов, не связанных с калькулятором, с помощью формы Критерии адаптации калькулятора, а также использовать форму Критерии адаптации калькулятора, чтобы определить, учащийся требует использования портативного калькулятора вместо онлайн-калькулятора Desmos. Если учащемуся требуется использование портативного калькулятора, приложения-калькулятора или программного обеспечения, выходящего за рамки того, что предлагает калькулятор Desmos Virginia, необходимо подать в Департамент оценки учащихся, подотчетность Запрос на специальное оценивание и заполненную форму Критерии приспособления к калькулятору. , и программы ESEA.

Часто задаваемые вопросы

В документе «Часто задаваемые вопросы: специальное образование и Desmos» рассматриваются часто задаваемые вопросы, касающиеся реализации Desmos и специального образования.

Ресурсы VDOE

Департамент образования штата Вирджиния, в рамках своей работы по поддержке внедрения Стандартов обучения математике 2016 года, предоставляет ресурсы и веб-семинары, которые включают Desmos в качестве обучающего технологического инструмента на уроках математики.

Вебинары

VDOE DESMOS Обзор калькулятора графического калькулятора

VDOE Desmos Обзор научного калькулятора

VDOE Algebra I: копание глубже в калькулятор Desmos Graphing

VDOE: Копаем глубже в средней школе — Desmos Графический калькулятор

VDOE: Знакомство с Desmos Activity Builder для средней школы

VDOE: Знакомство с Desmos Activity Builder для старшей школы

VDOE: Вовлечение учащихся с помощью Desmos

VDOE: Вовлечение учащихся в Desmos — PowerPoint (PPT)

VDOE: Изменение и создание заданий Desmos

VDOE: Изменение и Создание заданий Desmos – PowerPoint (PPT)

. Кроме того, Desmos предоставляет множество бесплатных онлайн-руководств и ресурсов для учителей и учащихся.

Практические предметы

2016 Элементы практики SOL по математике в программном обеспечении для онлайн-тестирования TestNav8 предоставляют доступ к соответствующему калькулятору Desmos Virginia. Школьным подразделениям рекомендуется использовать Desmos в обучении математике.

Журнал занятий Desmos в классе: обновлено осенью 2021 г. Desmos разработал банк учебных занятий по математике, расположенный в Desmos Classroom Activity, которые поддерживают и улучшают методы обучения в классе с использованием калькуляторов Desmos.

Многие из существующих заданий, созданных Desmos, а также задания, созданные педагогами Вирджинии, были пересмотрены и приведены в соответствие со Стандартами обучения математике 2016 года и включены в журнал действий Desmos Департамента образования Вирджинии. Этот журнал, электронная таблица Excel, содержит вкладку для каждого уровня класса/математического курса от детского сада до алгебры II. Лист каждого уровня включает список заданий Desmos, связанных с SOL, с кратким описанием и прямой ссылкой на задание на веб-сайте Desmos.

Инструкции по использованию

Чтобы использовать эти занятия в своих классах, учителям необходимо войти на сайт teacher.desmos.com, используя существующую учетную запись Google или создав собственную учетную запись Desmos Classroom Activity. Действия из этих журналов могут быть сохранены в их учетных записях, где они могут использовать действия как есть или копировать и редактировать действия в соответствии со своими потребностями. Учителя также могут создавать коды для своих классов, чтобы иметь возможность использовать многие встроенные функции, такие как панель управления учителя и беседы в классе. Подробную информацию о функциях и использовании см. в разделе Занятия в Desmos Classroom.

Благодарность

Департамент образования штата Вирджиния благодарит команду преподавателей штата Вирджиния, которые рассмотрели, создали и привели занятия в соответствие со Стандартами обучения математике штата Вирджиния 2016 года. Выражаем особую благодарность государственным школам Хэмптон-Сити и государственным школам округа Фредерик за то, что они поделились своими планами деятельности Desmos, на которые ссылались при создании этого документа VDOE. Важно отметить, что, хотя этот журнал содержит множество действий, не все Стандарты обучения имеют соответствующее действие Desmos.

Ресурсы Desmos

Учебные пособия

Desmos предоставляет множество бесплатных онлайн-учебников и ресурсов, которые позволяют учителям и учащимся узнать больше о функциях каждого калькулятора Desmos.

Learn Desmos: Четыре функции

Вводное видео: Четыре функции калькулятора

Learn Desmos: Scientific

Вводное видео: Scientific Calculator

Learn Desmos: Graphing

0261

Доступны дополнительная поддержка и руководства пользователя. Руководства пользователя для графического калькулятора доступны для оказания учебной помощи учащимся. Доступен пакет профессионального развития, который включает заметки и слайды презентаций, помогающие преподавателям и учащимся в обучении.