5.2. Построение графиков в полярной системе координат при помощи MathCad
Для того чтобы построить график в полярной системе координат при помощи MathCAD, необходимо:
Определить как дискретную переменную (в пределах области определения).
Задать функцию () .
Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» PolarPlot (Полярный график).
В появившемся шаблоне напечатать в нижнем поле, напечатать () в левом поле.
Щелкнуть мышью вне графика.
Пример
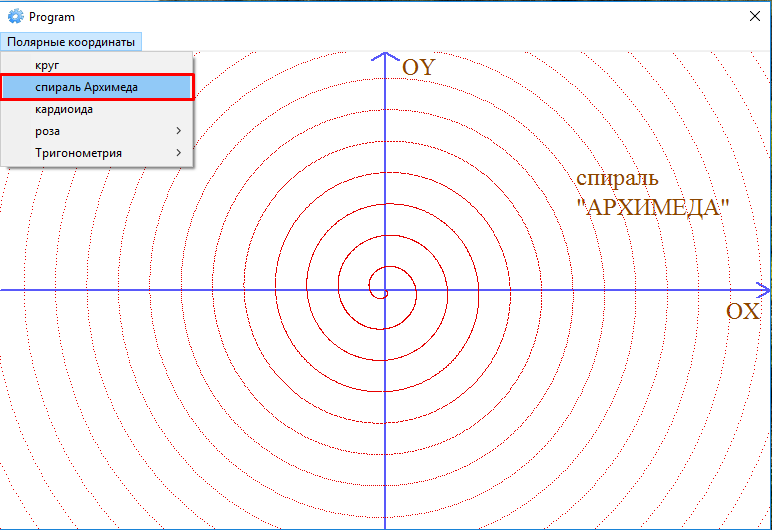
2. Построим
график функции
(спираль Архимеда) при помощиMathCAD.
Решение.
График в полярных координатах можно форматировать.
Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
5.3. Задания для самостоятельного решения
1. Построить (в тетради) в полярной системе координат линию по точкам, придавая значения от 0 до с шагом (для вычисления значений можно использовать возможности MathCAD):
1. | ,, | 11. | , , |
2. | , , | 12. | , , |
3. | , , | 13. | , , |
4. | , , | 14. | , , |
5. | , , | 15. | ,, |
6. | , , | 16. | , , |
7. | , , | 17. | , , |
8. | , , | 18. | , , |
9. | , , | 19. | , , |
10. | , , | 20. | , , |
2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:
1. | 11. | ||
2. | 12. | ||
3. | 13. | ||
4. | 14. | ||
5. | 15. | ||
6. | 16. | ||
7. | 17. | ||
8. | |||
9. | 19. | ||
10. | 20. |
Лабораторная работа № 6 Тема: Символьные вычисления
Цель
работы: Научиться
производить символьные вычисления:
преобразовывать выражения, вычислять
пределы.
MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.
Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).Знак символьного равенства представляет собой стрелку вправо () и набирается сочетанием клавиш [Ctrl] и [.], либо с палитры «Преобразования».
Чтобы произвести символьные вычисления, необходимо:
Ввести выражение, которое надо вычислить или преобразовать.

Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.
Щелкнуть мышью вне выражения.
Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим двумя способами:
Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.
При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.
Исследовательская работа «Построение кривых в полярной системе координат» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Построение кривых в полярной системе координат»
Автор: Джикибаев Данияр Хакимович
Место работы/учебы (аффилиация): СОШ № 10 г. Экибастуз Павлодарской области Республики Казахстан, 11 класс
Экибастуз Павлодарской области Республики Казахстан, 11 класс
Научный руководитель:
Зубко Светлана Алексеевна, учитель математикиЦель исследования – показать принцип построения кривых в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Выявить преимущества полярной системы координат.
Гипотеза — если для построения кривых, заданных уравнениями третьей (и выше) степеней с двумя переменными ввести новые переменные и новую систему координат и использовать при этом компьютерные программы, то это даст возможность рассмотреть большое количество примеров на построение различных кривых с минимальными усилиями.
Этапы исследования — изучение и анализ теоретических сведений по данной теме, обзор литературы, сбор материала, наблюдение, систематизация материала.
Задачи исследования:
- Ознакомиться с историей появления полярной системы координат;
- Изучить переход от декартовой системы координат к полярной и обратно;
- Исследовать изменения вида кривой, в зависимости от параметров входящих в её уравнение;
- Познакомиться с некоторыми замечательными кривыми известных математиков.

- Выяснить, какие кривые встречаются в окружающем нас мире;
- Познакомиться с компьютерными программами, необходимыми для построения графиков кривых;
- Построить графики кривых с помощью компьютерных программ;
- Подготовить презентацию по теме проекта
Научная новизна. Особенность работы состоит в том, что в ней рассматривается механизм построения кривых, заданных уравнениями третьей (и выше) степеней с двумя переменными, в полярной системе координат с помощью компьютерных программ, что представляет интерес для учащихся, увлекающихся математикой и информатикой, так как в школьных учебниках механизм построения таких кривых не оговаривается.
Объектом исследования является полярная система координат, предметом — полярные уравнения кривых и их построение с помощью программ Microsoft Excel и Visual Basic.
Практическая ценность данной работы заключается в том, что использование компьютерных программ для построения графиков функций, изучения их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями.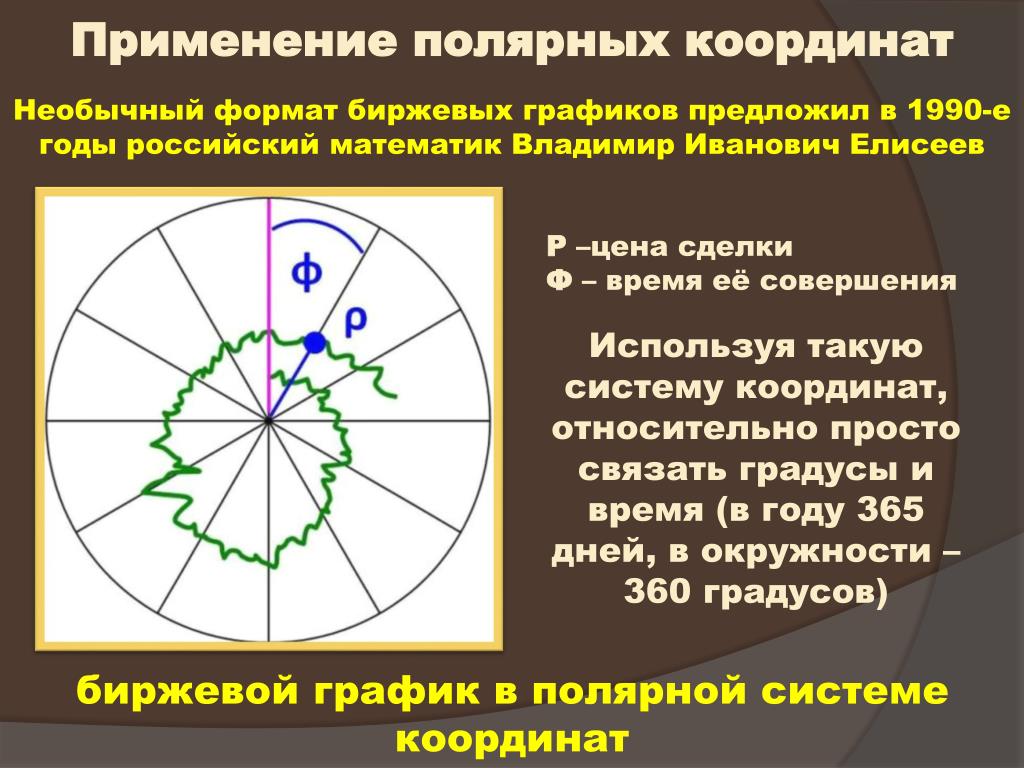
Результат работы: обобщение материала, написание программы построения кривых в среде Microsoft Excel и Visual Basic.
.
Физико-математические дисциплины
Исследовательская работа «Связь математики с экологией»
Наш дом – планета Земля. Она красива, она богата, в ее недрах и на поверхности содержатся огромные сокровища. Но не все люди, к сожалению, по-настоящему любят и берегут природные богатства. Однажды я обратил внимание, что в школьном мусорном ведре оч…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Школьный прогноз погоды»
Гипотеза: возможно создать собственную метеорологическую станцию из подручных средств, которая будет описывать и прогнозировать погоду на данной местности. Цели: создать метеорологическую станцию, используя подручные средства; описывать и прогнозиров. ..
..
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Создание домашнего термоса»
Доступна к просмотру полнотекстовая версия работы
Я люблю смотреть познавательную программу «Галилео». В ней рассказывают о различных явлениях, окружающих человека, научных фактах, технике. В одной из передач говорили про такой предмет, как термос. И здесь я узнал, что его можно применять не только…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа по математике «Финансовая математика. Вклады»
Доступна к просмотру полнотекстовая версия работы
В современном мире люди проводят миллионы банковских операций. С развитием технологий можно управлять своими средствами через гаджеты, стали возможны переводы средств другому человеку/организации и т. д., Online инвестиции, вклады, расчеты пенсии. Воз…
д., Online инвестиции, вклады, расчеты пенсии. Воз…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Компьютерные вирусы и борьба с ними»
В настоящее время компьютер прочно вошел в повседневную жизнь. Его возможности используются в школе, на работе, при проведении досуга, в быту и других сферах жизни человека. Несмотря на принятые во многих странах законы о борьбе с компьютерными прест…
Посмотреть работу
Технические дисциплины, Физико-математические дисциплины
Исследовательская работа «Три телефона, созданные в домашних условиях»
Летние каникулы я провела у бабушки и дедушки. Мое внимание привлек их домашний телефон. Он был с необычной трубкой и диском. Такого я еще никогда не видела. У нас дома тоже есть домашний телефон. Он немного похож на мобильный, с ним можно легко пере.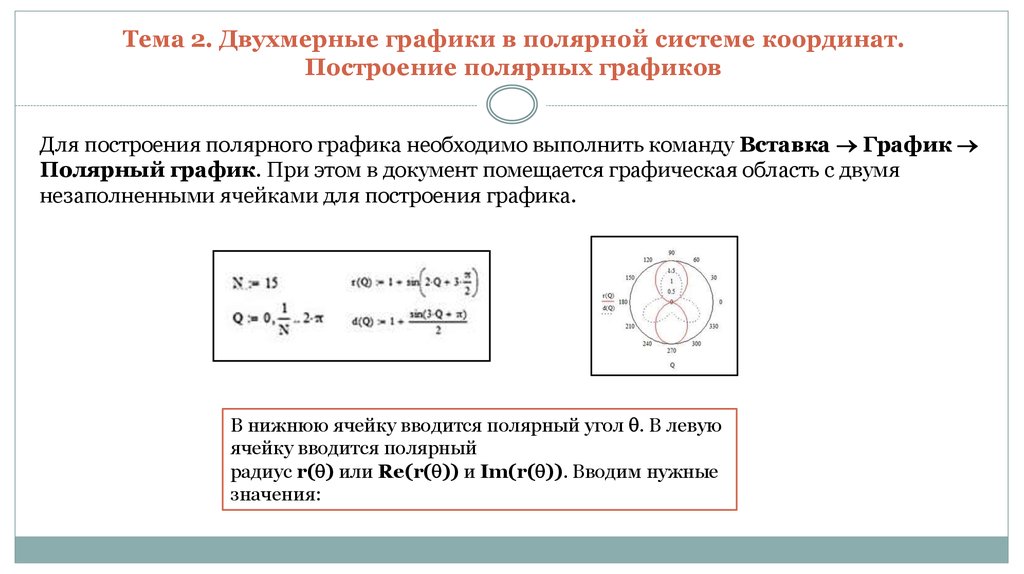 ..
..
Посмотреть работу
Мероприятие завершено
. Способный анимировать полярный график процесса наиболее подходящим образом, он показывает, как полярный график функции строится постепенно в своей области. Вы также можете график данный функция в декартовой системе координат на сняв флажок Polar .Добро пожаловать в самый передовой в мире декартовый и полярный функциональный граф ! Граф
полярных функций представляет собой граф функций , который рисует график функции в заданной области в полярной системе координат. Такой граф называется полярным графом или полярная кривая данной функции. Процесс построения графика в полярной системе координат и его визуализация с использованием функционального графического калькулятора принципиально отличается от построения графика в декартовой системе координат .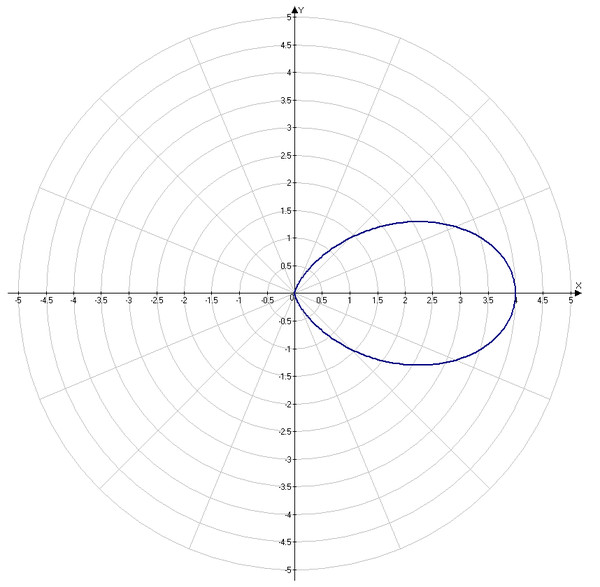 Это связано с тем, что полярный граф необходимо рисовать постепенно, чтобы можно было визуализировать, как полярный граф представляет собой построенный в своей области.
Это связано с тем, что полярный граф необходимо рисовать постепенно, чтобы можно было визуализировать, как полярный граф представляет собой построенный в своей области.
Этот функциональный граф , использующий самую сложную декартову и полярную системы координат , является единственным известным графическим инструментом, который может отображать неперпендикулярную декартову систему координат , а также помогает правильно визуализировать полярную кривую постепенно создается с помощью анимации полярной графики. Таким образом, вы можете наблюдать, как шаг за шагом рисуются все ваши крутых полярных графика .
Вы можете использовать эту чрезвычайно полезную функцию, нажав ► в нижней части графического калькулятора функций (если он скрыт, сначала нажмите кнопку Animate ).
Запускает анимацию процесса построения полярных графиков функции в фокусе . График построен последовательно от начального значения θ₁ до конечного значения θ₂ радиальной оси . Анимированный полярный график показывает вращения угловых осей ( радиальных осей ) и радиальных расстояний .
Затем вы можете нажать ‖ до приостановить анимацию или нажать Готово до остановить это. Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите кнопку Animate в верхней части полярного графа.
Вы также можете изменить скорость анимации полярной графики с помощью ползунка предоставленного
Этот бесплатный онлайн-калькулятор для построения графиков полярных функций также рисует полярных графиков с повернутой полярной осью .
Советы: по мере ввода:
- ..t заменяется на θ . ( Вы также можете использовать x или t. Они внутренне заменены на θ ).
- пи заменяется на π .
- inf ( бесконечность ) заменяется на ∞ .
Для построения графика кусочно-определенных функций введите каждую часть с соответствующим подынтервалом как одиночную функцию .
Самый быстрый способ ввести dom=(0, 2π) или dom=(-∞, ∞) — это полностью удалить домен, включая dom= .
МышьМатикс! Вы можете использовать мышь до Поворот осей , Перемещение и Изменение масштаба
В дополнение к вводу данных — сначала нажав кнопку шестеренки — вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивного графического редактора функций , как описано выше. ниже.
ниже.
- Щелкните по оси (или рядом с ней) и переместите мышь. Это будет вращать ось . график(ы) перерисовываются в неперпендикулярных Декартова система координат или обобщенная полярная система координат . Нажмите еще раз, чтобы освободить ось.
- Перетащите мышь на , переместите систему координат вместе с графиками.
- Дважды щелкните холст, чтобы переместить исходную точку туда, где был сделан щелчок.
- Удерживая клавишу Alt, щелкните по оси, чтобы изменить масштаб (увеличение в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.
Анимация вращения оси: Икс у ► ⬛
сообщение
f(x) =
?
f( ) =
⌨
4 Десятичные разряды
FinenessGraph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)
Метка осей ось x: ось y: Повернуть оси Ось x°: Ось Y°:⚙
РезультатыСкрыть
Наложение Прозрачный
Функции
Линии
1 х+1 2x
92-4)Прочие графики
√(4sin(2x)) √(4cos(2x))
Функции — Полярный
Линии
2csc(θ) 2сек(θ) 1/(sin(θ) — cos(θ))
Круги
1 2 6sin(θ) 8cos(θ)
Спирали
θ θ/5 дом=(0, 10π) √(θ) дом=(0, 10π) 1/θ дом=(0, 10π)
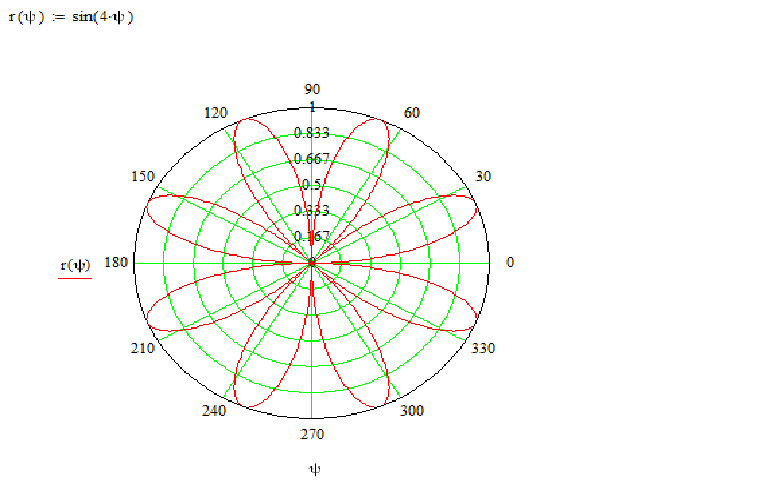
Розы
4sin(3θ) 4sin(2θ) 4sin(5θ) 4sin(4θ)
Эллипсы
1/(1-. 8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
Параболы
1/(1-sin(θ)) 1/(1+cos(θ)) 1/(1+sin(θ)) 1/(1-cos(θ))
Гипербола
1/(1+2cos(θ)) 4/(1+2sin(θ)) 1/(1-2cos(θ)) 4/(1-2sin(θ)) 95 дом = (0, 12π)
РАД Полярный
🔍+ 1 🔍−
время построения графика (с)
Калькулятор загружается.
Пожалуйста, подождите….
Сделайте это прозрачным
Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осей…
Медленный Быстро
Показать угловые оси Сделанный
подпись Отключить программную клавиатуру
Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.
это интерактивная полярная функция Grapher была разработана для построения графиков, и, в частности, для демонстрации с помощью анимации того, как график функции создается в полярной системе координат . Полярные кривые могут быть очень сложными и могут иметь много петель. Все остальные полярные графы
(до этого графического калькулятора полярных функций — недавно некоторые другие графографы в партнерстве с Google и Microsoft начали следовать этому правилу) отображают полярную диаграмму функции, не показывая, где начинается или заканчивается кривая, а также прослеживаются ли петли, если таковые имеются, и как. Этот уникальный калькулятор построения графиков полярных функций представляет правильный способ построения графиков функций в полярных системах координат . А именно, он начинает строить график с начального значения угловой координаты θ₁ и постепенно показывает процесс построения графика до конечного значения θ₂, показывая, повторяются ли петли или какая-либо часть кривой. Более того, этот графограф полярных функций позволяет изменять скорость процесса построения полярных графиков.
Более того, этот графограф полярных функций позволяет изменять скорость процесса построения полярных графиков.
Легко использовать декартовых или полярных графических функций ; введите функцию в любое поле выражения , например, f(x) или r(θ) . График функций отображается при вводе (по умолчанию) в выбранной системе координат . (Не беспокойтесь о том, какую переменную вы используете, функция автоматически изменяет переменные в соответствии с выбранным система координат.)
- В график две или более функции на одной и той же декартовой или полярной системе координат Панель с несколькими графиками состоит из панелей выражений , которые можно добавить или удалить по желанию, нажав + или × .
 на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график. - Для удобства графопостроитель полярных функций или графопостроитель декартовых функций добавляет подходящий интервал, dom = (0, 2π) или dom = (-∞, ∞), соответственно, к функциональным выражениям и графикам на указанных домен. При желании можно изменить конечные точки . Конечные точки должны быть конечными для построения полярного графика. Устройство графического отображения полярных функций автоматически изменяет бесконечности, если таковые имеются, на конечные значения.
- Полярные графики или декартовы графики отображаются сразу же после ввода. Вы можете Анимировать процесс построения полярного графика, как описано выше.
- Можно установить тонкость декартовой или полярной кривых , выбрав нужный вариант из раскрывающегося списка Graph Fineness .
 В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций. - Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графиком функций . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
- Чтобы оценить функцию , введите число или числовое (постоянное) выражение в соответствующем поле; функциональный граф отображает рассчитанные значения функции с количеством знаков после запятой, которое можно указать с помощью предоставленного ползунка.
Интересные кривые : Нарисуйте любое из выражений в разделе Интересные графики , а также отобразите несколько классных полярных графиков , выбрав его. Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness как «+1» или выше.
Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness как «+1» или выше.
Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.
- Измените толщину из графиков с помощью предоставленного ползунка.
- Выберите режим угла ( радиана – по умолчанию , градуса или градуса ).
- Если вы отмените выбор График при вводе параметра , вам придется нажать График выбранных выражений , который затем появится в нижней части калькулятора, чтобы обновлять графики всякий раз, когда вы вносите какие-либо изменения в выражения или координаты. плоскость (т. е. переместить начало координат, повернуть оси и т. д.).
- При необходимости отобразите элементы управления в верхней части графического редактора функций , которые позволяют запускать/приостанавливать и останавливать вращение любой или всех осей.

- Графический редактор функций запоминает функциональные выражения , которые вы вводите, и извлекает их между посещениями. Вы можете очистить их, нажав кнопку Сброс калькулятора .
Для эффективного использования этого онлайн-калькулятора функций используйте последние версии браузеров Chrome , Microsoft Edge , Firefox , Opera или Safari . В противном случае некоторые компоненты графического редактора функций могут не отображаться или работать.
Вставка 1 St производная Вставка 2 и производная от
Графики в полярных координатах — онлайн? — Двойное наблюдение за звездами
#1 Коттс
Размещено 21 марта 2017 г. — 16:54
Я ищу инструмент для построения графиков в полярных координатах, желательно онлайн, который позволит мне ввести PA (0-360 градусов) и расстояние/радиус отдельных точек, чтобы увидеть, какую кривую я могу получить. Я бы ввел точки данных из файла Excel…
Я бы ввел точки данных из файла Excel…
Единственные графы полярных координат, которые я могу найти, просят ввести функцию, и она покажет результирующую кривую — не то, что мне нужно…
Для фона Я хочу иметь возможность отображать исторические измерения пары, а затем отображать свои измерения, чтобы увидеть, как они соответствуют историческим данным…….
У кого-нибудь есть что-нибудь?
спасибо
Дэйв
- Наверх
#2 кузнец
Опубликовано 21 марта 2017 г. — 17:30
Дэйв —
Вот ссылка на подключаемый модуль полярного графика Excel. Возможно, это сработает для вас.
http://www.andypope…./polarplot3.htm
- Наверх
#3 Эд Уайли
Размещено 21 марта 2017 г. — 19:42
— 19:42
Дэйв,
Я конвертирую свои данные в декартовы, и это значительно упрощает задачу, так как я могу просто переносить историю наблюдений, конвертировать и затем строить графики. Напишите мне.
Эд
- Наверх
#4 Редбеттер
Размещено 21 марта 2017 г. — 20:47
Дэйв, 9 лет0031
Когда я недавно обдумывал это, я пришел к выводу, что для меня было бы проще преобразовать его в x y и построить таким образом.
Я не рассматривал последствия сокращения данных, так как я просто выполняю визуальные и приблизительные измерения, а не разрабатываю отчетные показатели. Однако мне приходит в голову, что (по иронии судьбы) полярная диаграмма, вероятно, лучше подходит для того, как выполняются визуальных измерений, поскольку ошибки будут выравниваться по полярным координатам.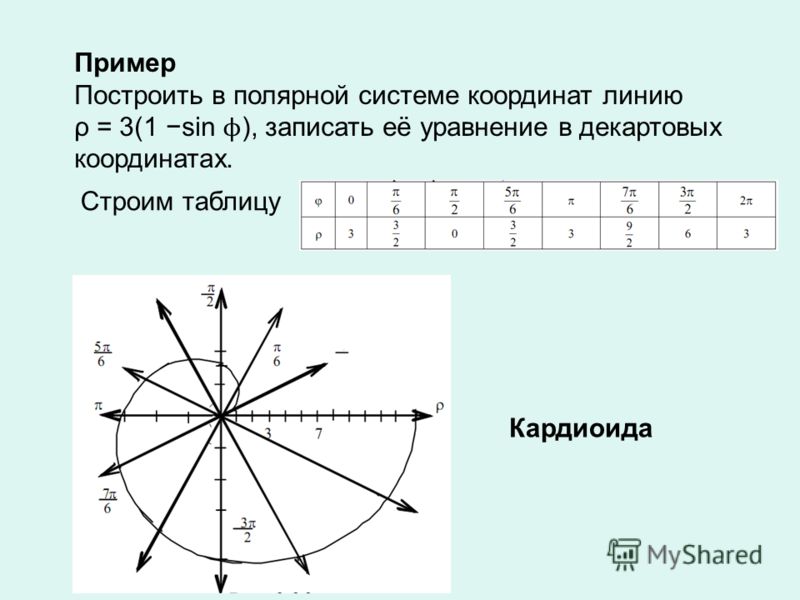 С другой стороны, проверка ошибок измерений, сделанных с помощью изображений, может привести к декартовым графикам.
С другой стороны, проверка ошибок измерений, сделанных с помощью изображений, может привести к декартовым графикам.
- Наверх
#5 OJS
Опубликовано 22 марта 2017 г. — 10:58
Как насчет этого?
https://www.desmos.c…ator/g8acfji4oy
Первые два графика полярных точек отображают точки (нарисуйте эту фразу, пожалуйста), которые слишком велики, но полярный->прямоугольный единицы (r cos (тета), r sin (тета)), ниже, меньше, и похоже, что вы можете построить сотни. У меня было выше 200.
Отредактировано OJS, 22 марта 2017 г. — 13:16.
- Наверх
#6 дроллер
Опубликовано 07 апреля 2017 г. — 09:38
тригонометрию легко сделать внутри excel. используйте функции SIN и COS, а PA преобразуется непосредственно в декартовы x, y со знаком.
x = -rho*SIN(РАДИАНЫ(PA))
y = rho*COS(РАДИАНЫ(PA))
если вы опустите «-» в x, PA будет увеличиваться по часовой стрелке, а не против нее .
поскольку первичная звезда всегда находится точно в начале координат, вся ошибка наблюдения проявляется как разброс во вторичной, как и должно быть.
кстати, вам нужно будет делать поправку на прецессию угла небесного севера для эпохи каждого наблюдения, если это еще не сделано. вы можете найти математику для этой операции в Интернете здесь и там, и снова она отлично работает в Excel.
Отредактировал drollere, 07 апреля 2017 г. — 09:40.
- Наверх
#7 Коттс
Размещено 08 апреля 2017 г. — 08:57
Спасибо, Брюс. Навскидку знаете ли вы, исправлена ли прецессия в исторических данных WDS Theta/Rho?
Дэйв
- Наверх
#8 Эд Уайли
Размещено 08 апреля 2017 г. — 09:19
— 09:19
Привет, Дэйв:
Это не так, вам нужно выполнить расчет самостоятельно.
Эд
- Наверх
#9Коттс
Размещено 08 апреля 2017 г. — 15:00
Наука СЛОЖНА!!!!!!!!
Дэйв
- Наверх
#10 WRAK
Размещено 11 апреля 2017 г. — 16:53
Может быть, это поможет: Несколько лет назад у нас была длинная ветка на этой доске о разделении Gam Equ, тем временем урегулированная новым измерением 2014 года. Чтобы получить представление о том, как может выглядеть потенциальная орбита Gam Equ, я сделал электронную таблицу для визуализации перечисленных измерений — добавленное позже измерение 2014 года полностью подтвердило идею, которую я получил из полученного графика, несмотря на неизбежный разброс данных.
 на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.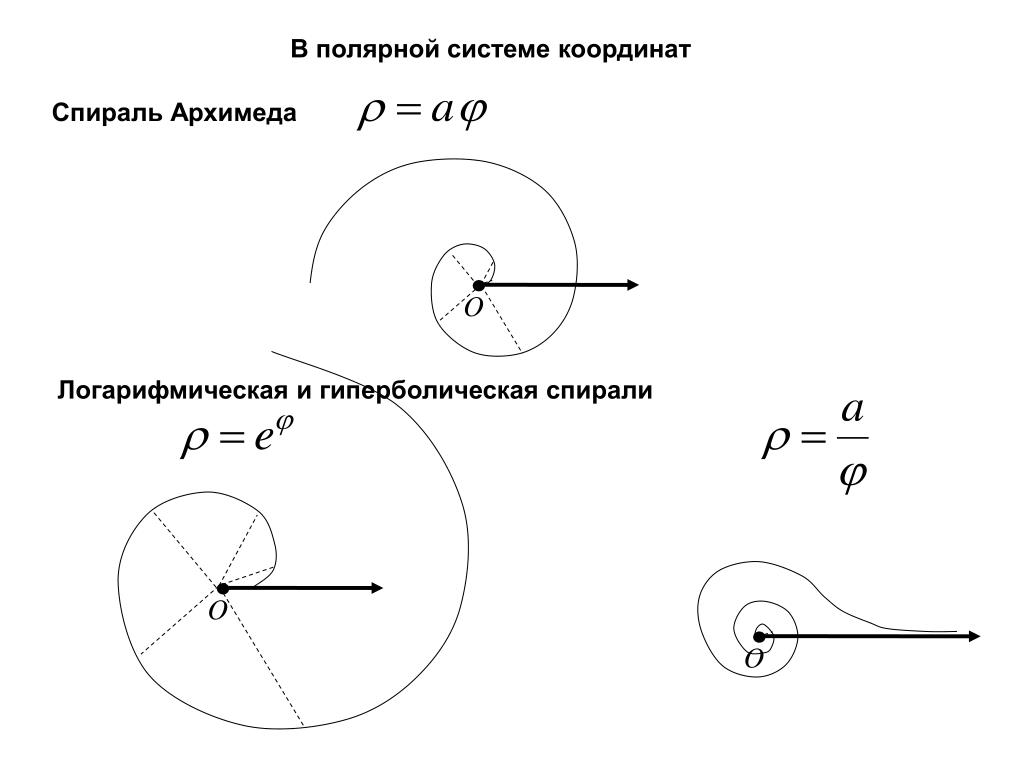 В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
Ваш комментарий будет первым