Касательная плоскость к поверхности онлайн
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0). Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Решение онлайн
- Видеоинструкция
z = f(x,y)
в точке M0(;)Функция задана в неявном виде f(x,y,z)
F(x,y,z) =
в точке M(;;)Дополнительно находить уравнение нормали
Правила ввода функций:
Правила ввода функций:
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
z – z0 = f’x(x0,y0)(x – x 0) + f’y(x0,y0)(y – y0)
Вектор называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1). 3+5*y:
3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f’x
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример.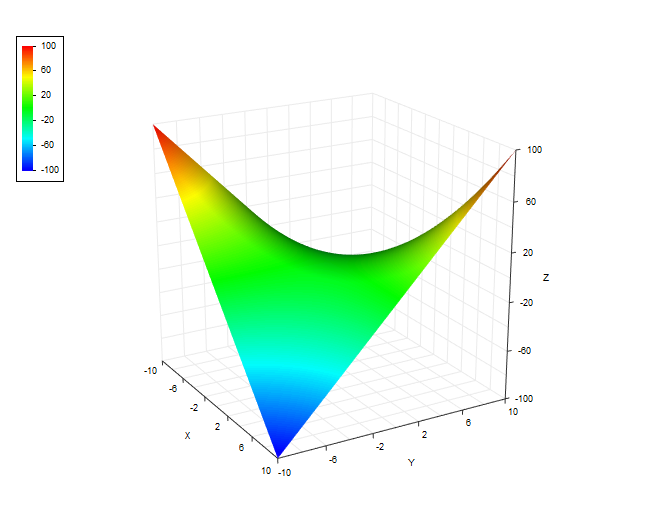 Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z= y/x + xy – 5x3
z0 = 2/(-1) + (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y +4 15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
f’x(x,y) = (x2+3•x•y•+y2)’x = 2•x+3•y3
f’x(x,y) = (x2+3•x•y•+y2)’y = 9•x•y2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение
MathCAD — это просто! Часть 6. Графики поверхностей
В прошлый раз мы с вами говорили о системах нелинейных алгебраических уравнений — точнее, не столько о них самих, сколько о методах их решения с использованием такого замечательного программного продукта, как MathCAD. И остановились на подборе начальных условий для приближенного (численного) решения систем нелинейных алгебраических уравнений с помощью построения графиков уравнений.
График функции z = f(x; y)
Для того, чтобы начать работу с графиками, для начала запустите MathCAD.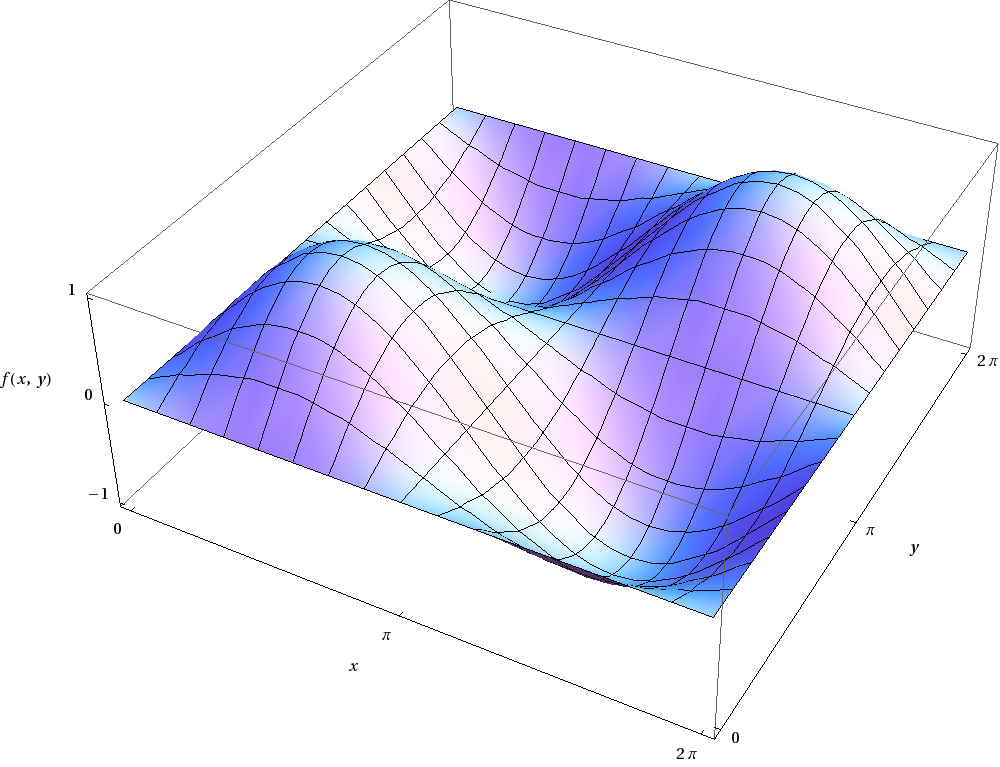 Мы с вами начнем, пожалуй, с самого простого случая трехмерных графиков, а именно с построения графика для того случая, когда z имеет функциональную зависимость от x и y. К уравнениям такие графики, правда, имеют довольно опосредованное отношение, но начинать всегда лучше с простого. Для начала нужно определить функцию, график которой мы будем строить. Лично я для примера (см. соответствующий скриншот) взял f(x, y) := sin(x) / cos(y). В отличие от двумерных графиков, где мы могли задавать зависимости переменных x и y друг от друга прямо на графике, для построения графиков в трех измерениях нужно использовать именно запись функции. Почему? Об этом чуть-чуть ниже. После того, как вы определили функцию, график которой мы будем получать, найдите на панели Graph кнопку Surface Plot и щелкните по ней мышью. На экране появится пустой график, очень похожий на тот, который мы с вами уже вполне успешно (и не раз) использовали для визуализации двумерных функций и уравнений. Только здесь всего одна область для ввода — она находится внизу под координатной сеткой.
Мы с вами начнем, пожалуй, с самого простого случая трехмерных графиков, а именно с построения графика для того случая, когда z имеет функциональную зависимость от x и y. К уравнениям такие графики, правда, имеют довольно опосредованное отношение, но начинать всегда лучше с простого. Для начала нужно определить функцию, график которой мы будем строить. Лично я для примера (см. соответствующий скриншот) взял f(x, y) := sin(x) / cos(y). В отличие от двумерных графиков, где мы могли задавать зависимости переменных x и y друг от друга прямо на графике, для построения графиков в трех измерениях нужно использовать именно запись функции. Почему? Об этом чуть-чуть ниже. После того, как вы определили функцию, график которой мы будем получать, найдите на панели Graph кнопку Surface Plot и щелкните по ней мышью. На экране появится пустой график, очень похожий на тот, который мы с вами уже вполне успешно (и не раз) использовали для визуализации двумерных функций и уравнений. Только здесь всего одна область для ввода — она находится внизу под координатной сеткой.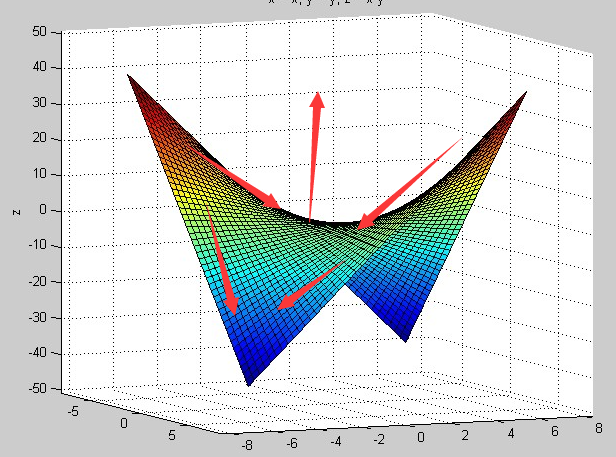
В ней нужно написать просто f. Почему не f(x, y)? Вопрос, безусловно, уместный и очень грамотный. Дело в том, что MathCAD, вообще говоря, не умеет строить трехмерные графики для функций или уравнений. Он умеет отображать в виде графика только массив точек — именно его та часть среды, которая отвечает за построение графиков, и ожидает увидеть на этом месте. Если мы запишем вместо массива функцию без указания аргументов, то MathCAD автоматически построит на ее основе нужный ему массив, который успешно будет отображен на графике. Если же мы укажем для функции аргументы, то MathCAD выдаст сообщение об ошибке. Не верите — можете сами попробовать и убедиться.
В общем, если вы правильно все сделали, а сделать что-то неправильно при внимательном чтении будет сложно, то на экране у вас должен появиться такой же график, как на скриншоте к статье. На этом мы пока остановимся и посмотрим, как и что для этого графика можно настроить.
Настройка графика
Если дважды щелкнуть по графику мышью, то появится окно его настроек. Уже по количеству различных вкладок в нем видно, что настраивать графики поверхностей в MathCAD’е можно долго и упорно, и можно, что называется, донастраиваться. Обо всех этих настройках у нас с вами сейчас поговорить, конечно, не получится, потому что объем газетной статьи, сами понимаете, имеет некоторые ограничения. Да и вряд ли, говоря откровенно, подробный рассказ о каждой галочке в этом окне сильно облегчит кому-либо жизнь. Поэтому лучше обратимся к самым часто употребляемым из них.
Уже по количеству различных вкладок в нем видно, что настраивать графики поверхностей в MathCAD’е можно долго и упорно, и можно, что называется, донастраиваться. Обо всех этих настройках у нас с вами сейчас поговорить, конечно, не получится, потому что объем газетной статьи, сами понимаете, имеет некоторые ограничения. Да и вряд ли, говоря откровенно, подробный рассказ о каждой галочке в этом окне сильно облегчит кому-либо жизнь. Поэтому лучше обратимся к самым часто употребляемым из них.
Первая интересная настройка задает положение «камеры» относительно графика функции, который мы с вами только что успешно построили. Объединены они в группу View на вкладке General и помогают при правильном подходе гораздо лучше рассмотреть все особенности построенной на графике поверхности. Настройки эти задают поворот и наклон наблюдателя относительно графика, а также увеличение в том случае, если нужно рассмотреть график подробнее или, напротив, «общим планом». Чтобы научиться хорошо настраивать эти параметры, придется потратить немало времени, а сначала при их изменении графики будут выглядеть, скорее всего, не лучше, а гораздо хуже, чем до этих изменений.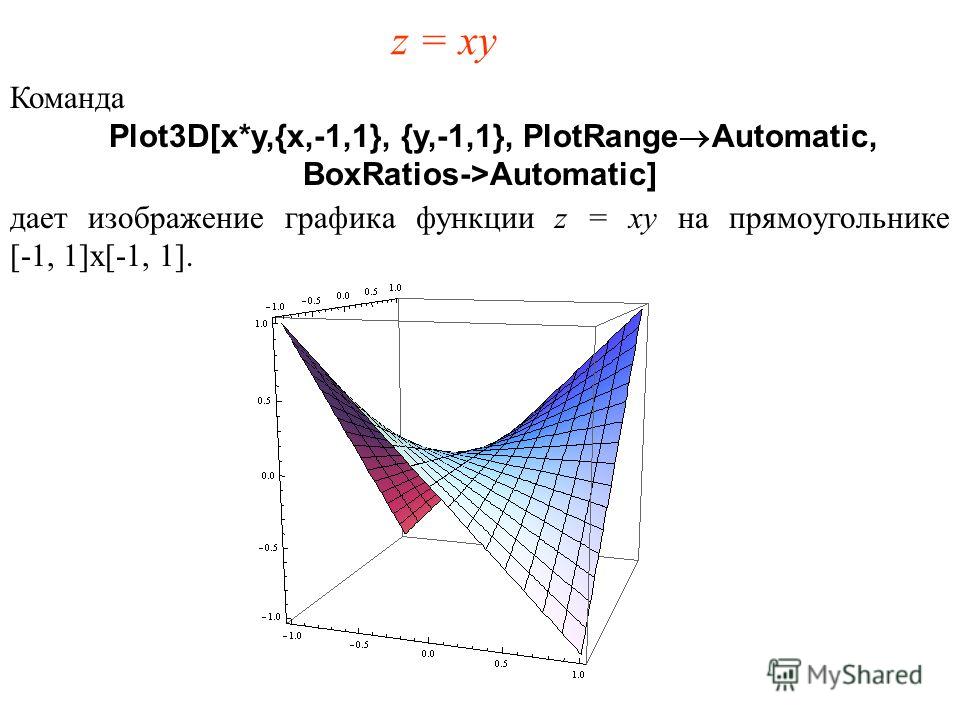 Но здесь, как говорится, терпение и труд все перетрут.
Но здесь, как говорится, терпение и труд все перетрут.
Отдельного упоминания стоят настройки для координатных осей, расположившиеся на закладке Axes. На этой вкладке для каждой из осей по отдельности можно включить или выключить подписи в виде чисел, настроить цвет, задать поясняющую надпись (полезно, если за поверхностью, которую вы строите, стоит какой-либо физический или, например, экономический процесс — тогда можно ось Z назвать «распределение температуры», а X и Y — «длина бруска» и «ширина бруска» соответственно).
При настройке внешнего вида графика вам пригодится и вкладка Appearance. Если вам нужно раскрасить поверхность градиентной заливкой, то выберите переключатель Fill Surface из группы Fill Options, а в группе Colour Options установите в активное положение переключатель Colormap. Если вы хотите вовсе отключить любую заливку поверхности (а вам вполне может понадобиться и такое), то в группе Fill Options выберите No Fill. Аналогичным образом можно настраивать и линии, которые отображаются по контуру графика для его лучшей видимости. Хотя лично мне кажется, что с ними график, во-первых, и выглядит как-то эстетичнее, и, во-вторых, более легко воспринимается, но вы, само собой, вправе со мной не согласиться и их, если они вам мешают, напрочь отключить. В целом обращаться с этими линиями ничуть не сложнее, чем с заливкой — их, кстати, тоже можно сделать градиентными. Если нужно, можно также включить отображение точек, которые лежат в основе графиков, которые строит MathCAD — тех самых точек, массив которых нужен для построения трехмерного графика. Для этих точек можно менять цвет аналогично тому, как это можно делать для самой поверхности и ее контурных линий, а также настраивать размер точек — для этого служит поле Size, расположенное в группе Point Options. Также можно менять символ, обозначающий на графике точки — это может быть круг, ромб, два разных крестика или квадрат. В общем и целом, как можно увидеть на соответствующем скриншоте, с использованием вкладки Appearance можно преобразовать полученный график так, что его родной отец или мать (то есть вы) не узнает.
Хотя лично мне кажется, что с ними график, во-первых, и выглядит как-то эстетичнее, и, во-вторых, более легко воспринимается, но вы, само собой, вправе со мной не согласиться и их, если они вам мешают, напрочь отключить. В целом обращаться с этими линиями ничуть не сложнее, чем с заливкой — их, кстати, тоже можно сделать градиентными. Если нужно, можно также включить отображение точек, которые лежат в основе графиков, которые строит MathCAD — тех самых точек, массив которых нужен для построения трехмерного графика. Для этих точек можно менять цвет аналогично тому, как это можно делать для самой поверхности и ее контурных линий, а также настраивать размер точек — для этого служит поле Size, расположенное в группе Point Options. Также можно менять символ, обозначающий на графике точки — это может быть круг, ромб, два разных крестика или квадрат. В общем и целом, как можно увидеть на соответствующем скриншоте, с использованием вкладки Appearance можно преобразовать полученный график так, что его родной отец или мать (то есть вы) не узнает.
Для еще более тонкой настройки внешнего вида графика можно воспользоваться источниками света, добавить которые можно на вкладке Lighting все того же диалога настройки трехмерных графиков. По умолчанию все источники света для любого трехмерного графика отключены, и включить их можно установкой в активное положение переключателя Enable Lighting. Всего на каждом графике может быть до восьми источников света, но реально вам вряд ли когда понадобится иметь их больше, чем три. Для каждого источника можно настроить его положение или, если этот источник расположен на бесконечности, то направление света. Также можно настроить цвет освещения, которое создается на поверхности этим источником. Также присутствуют пять стандартных схем освещения, выбрать которые можно в списке, расположенном слева внизу диалогового окна. Следует отметить, что графики с градиентной заливкой для любого стандартного освещения смотрятся не слишком привлекательно.
О вкладке Title долго говорить не будем — это просто заголовок графика, который можно разместить сверху или снизу относительно самого изображения. Для настройки плоскостей, которые могут помочь более наглядно отобразить ход графика, применяется вкладка Backplanes. На ней доступны настройки для трех плоскостей: X-Y, X-Z и Y-Z. Конечно, для каждой из них все возможности настройки абсолютно идентичны. По умолчанию все задние плоскости не отображаются. Для того, чтобы включить их отображение, нужно активировать переключатель Fill Backplane и выбрать цвет, щелкнув по квадратику рядом со словом Color. По умолчанию в нем выставлен белый цвет, который будет не виден на белом фоне графика. Если вы хотите, чтобы на задней плоскости, ко всему прочему, еще и отображалась координатная сетка, то нужно активировать переключатели Draw Lines в группах X Axis и Y Axis группы Grid. Первый переключатель задает отображение линий по оси X, второй — по оси Y. Если плоскость, которую вы настраиваете, это, например, X-Z, то и оси будут не X и Y, а X и Z. Можно также добавить промежуточную сетку — для этого настраивать нужно опции в группе Sub-Grid.
Для настройки плоскостей, которые могут помочь более наглядно отобразить ход графика, применяется вкладка Backplanes. На ней доступны настройки для трех плоскостей: X-Y, X-Z и Y-Z. Конечно, для каждой из них все возможности настройки абсолютно идентичны. По умолчанию все задние плоскости не отображаются. Для того, чтобы включить их отображение, нужно активировать переключатель Fill Backplane и выбрать цвет, щелкнув по квадратику рядом со словом Color. По умолчанию в нем выставлен белый цвет, который будет не виден на белом фоне графика. Если вы хотите, чтобы на задней плоскости, ко всему прочему, еще и отображалась координатная сетка, то нужно активировать переключатели Draw Lines в группах X Axis и Y Axis группы Grid. Первый переключатель задает отображение линий по оси X, второй — по оси Y. Если плоскость, которую вы настраиваете, это, например, X-Z, то и оси будут не X и Y, а X и Z. Можно также добавить промежуточную сетку — для этого настраивать нужно опции в группе Sub-Grid.
Вкладку Special этого окна мы с вами пока что отложим до лучших времен — в ближайшее время ее настройка нам не понадобится. Поэтому сразу перейдем к вкладке Advanced. Переключатель Enable Fog в активном состоянии включает на графике «туман», который может сделать график существенно более приятным для глаз. Переключатель Perspective позволяет включить для графика эффект перспективы. Также на этой вкладке можно выбрать одну из наиболее подходящих градиентных окрасок в группе Coloumap. По умолчанию ставится радужная окраска, что далеко не всегда удобно.
Поэтому сразу перейдем к вкладке Advanced. Переключатель Enable Fog в активном состоянии включает на графике «туман», который может сделать график существенно более приятным для глаз. Переключатель Perspective позволяет включить для графика эффект перспективы. Также на этой вкладке можно выбрать одну из наиболее подходящих градиентных окрасок в группе Coloumap. По умолчанию ставится радужная окраска, что далеко не всегда удобно.
Вкладка Quick Data Plot позволяет настроить несколько очень важных параметров графика — в первую очередь, координатную систему, которую MathCAD будет использовать при выводе графика на экран. Доступны прямоугольная (декартова), сферическая и цилиндрическая координатные системы, что хватает для решения львиной доли практических задач. Там же можно задать диапазон изменения значений переменной, которая отображается по этой шкале — правда, в приведенном выше примере вполне хватит и автоматически выставляемого диапазона от -5 до +5. Шаг сетки тоже задается именно там — по умолчанию предусматривается по 20 точек на каждую ось, но если такой точности вам не хватает, никто не запрещает увеличить это число.
Шаг сетки тоже задается именно там — по умолчанию предусматривается по 20 точек на каждую ось, но если такой точности вам не хватает, никто не запрещает увеличить это число.
Возможно, Вам показалось, что я излишне подробно рассказывал обо всех настройках для трехмерных графиков, которых разработчики MathCAD щедрой рукой отсыпали пользователям. Однако на самом деле это имело смысл — однажды рассказав об этих настройках, к ним после можно будет уже не возвращаться, а просто говорить: «настройте то-то и то-то». А как настраивать, вы уже знаете. Хочу еще раз подчеркнуть, что, несмотря на немалое число рассмотренных выше настроек, здесь я охватил далеко не все из них, однако, в общем-то, ничего страшного в этом нет. Для человека, владеющего худо-бедно (но лучше, конечно, хорошо владеющего) английским языком, все оставшиеся неразобранными в данной статье настройки будут прозрачны и понятны, так что волноваться по этому поводу совершенно не стоит.
Искренне надеюсь, что в следующей статье цикла мы с вами уже успешно закончим разбираться с графиками поверхностей, хотя, говоря откровенно, стопроцентно обещать этого я не могу — тема, как я уже не один раз говорил, очень и очень объемная, а также очень полезная на практике, так что это извиняет в некотором роде излишнюю детальность данной статьи. 2
2
Ось Z должна представлять функцию f(x,y)
У меня есть следующая функция:
def fnc(X):
возврат (Х[0] - Х[1]) ** 2
Здесь X — массив numpy с первым параметром X и вторым параметром Y. Мне конкретно нужно, чтобы так было. Поэтому, пожалуйста, не предлагайте мне изменить подпись. 😉
Я попробовал следующее из этого решения:
fig = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = fnc1([np.linspace(-5,5,100) , np.linspace(-6,6,100)])
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
plt.show()
Однако я ошибаюсь в сюжете.
- python
- numpy
- matplotlib
- mplot3d
Ваш fnc неверен. Получите свою поверхность так же, как Z=(X-Y)**2 . Это лучшее решение, потому что все вычисления Z будут векторизованы.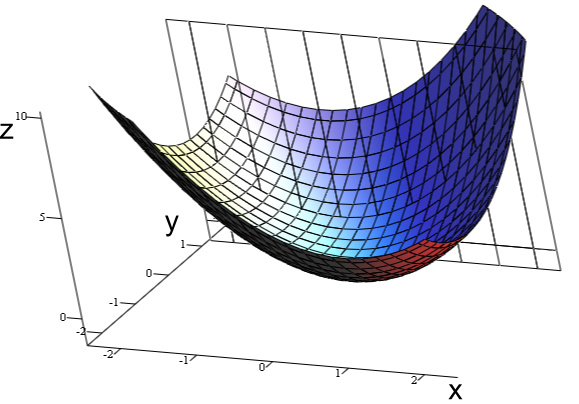
импортировать matplotlib.pylab как plt
из mpl_toolkits.mplot3d импортировать Axes3D
импортировать numpy как np
рис = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = (XY)**2
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
plt.show()
3
Построенный массив Z должен быть двумерным массивом, точно так же, как X и Y являются двумерными массивами, так что для каждой пары значений из X и Y вы получаете ровно одну точку в З . Поэтому имеет смысл использовать эти массивы X и Y в качестве входных данных для вашей функции fnc , Z = fnc([X,Y])
Полный код будет выглядеть так:
импортировать numpy как np импортировать matplotlib.pylab как plt из mpl_toolkits.mplot3d импортировать Axes3D защита fnc(X): возврат (Х[0] - Х[1]) ** 2 рис = plt.figure() топор = fig.add_subplot(111, проекция=Axes3D.name) х = у = np.linspace (-5,5,100) X, Y = np.meshgrid(x, y) Z = fnc([X,Y]) ax.plot_surface (X, Y, Z) ax.set_xlabel('Ярлык X') ax.set_ylabel('Ярлык Y') ax.set_zlabel('Ярлык Z') ax.view_init (высота = 15, азим = -118) plt.show()
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
python — построение поверхности и кривой в 3D и кривой в плоскости xy, все на одном графике
Чтобы проиллюстрировать проблему оптимизации, я хочу, чтобы все это было на одном и том же трехмерном графике:
- Поверхность.

- Кривая в плоскости xy.
- Кривая/путь на поверхности, которая отмечает точки на поверхности, лежащие непосредственно над кривой в плоскости xy.
Пока это мой код:
импортировать matplotlib.pyplot как plt
из matplotlib импорт см
из matplotlib.ticker импортировать LinearLocator
импортировать numpy как np
из mpl_toolkits импортировать mplot3d
рис, топор = plt.subplots(subplot_kw={"проекция": "3d"})
X = np.linspace(-5,5,100)
Y = Х
X, Y = np.meshgrid(X, Y)
Z = 50 - X**2 - Y**2
#Построение кривой на поверхности
топор = plt.axes (проекция = '3d')
yline = np.linspace(-5,5,100)
xline = -np.sqrt(4/(2+yline**2)) #значения x кривой в плоскости xy
zline = 50 - xline**2 - yline**2
ax.plot3D (xline, yline, zline, «черный»)
прибой = ax.plot_surface (X, Y, Z, cmap = cm.coolwarm)
топор.set_zlim (0, 50)
#Построение кривой в плоскости xy
а = 5
г = 1 - 2*Х - Х*У**2
plt.contour(X,Y,g, [a], смещение=0)
plt.show()
Вот сюжет с двух разных точек зрения:
Некоторые проблемы:
- Во-первых, кажется, что оси пронумерованы дважды.
 Это потому, что я делаю сетку, а потом использую ax.plot3D? Что я использую два разных способа построения чего-то и, как следствие, делаю 3D-пространство дважды?
Это потому, что я делаю сетку, а потом использую ax.plot3D? Что я использую два разных способа построения чего-то и, как следствие, делаю 3D-пространство дважды? - Путь на поверхности выглядит слабо. Есть ли способ сделать путь более заметным?
- На картинке в перспективе птицы мы видим, что путь не лежит прямо над кривой в плоскости xy. Было бы проще, если бы в Python была встроенная функция, которая могла бы проецировать кривую в плоскости xy прямо на поверхность. Я что-то упустил здесь? Кто-нибудь знает о такой функции?
Эти вопросы могут быть фиктивными, но ответы и советы приветствуются!
- python
- plot
- 3d
- проекция
- кривая
Код создает объекты с двумя осями (оба назначены на 900 13 x переменная) на том же рисунке. Это не требуется и приводит к двойным отметкам.
Чтобы сделать путь на поверхности более заметным, начертите его с более высоким порядком.

 pylab как plt
из mpl_toolkits.mplot3d импортировать Axes3D
защита fnc(X):
возврат (Х[0] - Х[1]) ** 2
рис = plt.figure()
топор = fig.add_subplot(111, проекция=Axes3D.name)
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = fnc([X,Y])
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
ax.view_init (высота = 15, азим = -118)
plt.show()
pylab как plt
из mpl_toolkits.mplot3d импортировать Axes3D
защита fnc(X):
возврат (Х[0] - Х[1]) ** 2
рис = plt.figure()
топор = fig.add_subplot(111, проекция=Axes3D.name)
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = fnc([X,Y])
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
ax.view_init (высота = 15, азим = -118)
plt.show()
 Это потому, что я делаю сетку, а потом использую ax.plot3D? Что я использую два разных способа построения чего-то и, как следствие, делаю 3D-пространство дважды?
Это потому, что я делаю сетку, а потом использую ax.plot3D? Что я использую два разных способа построения чего-то и, как следствие, делаю 3D-пространство дважды?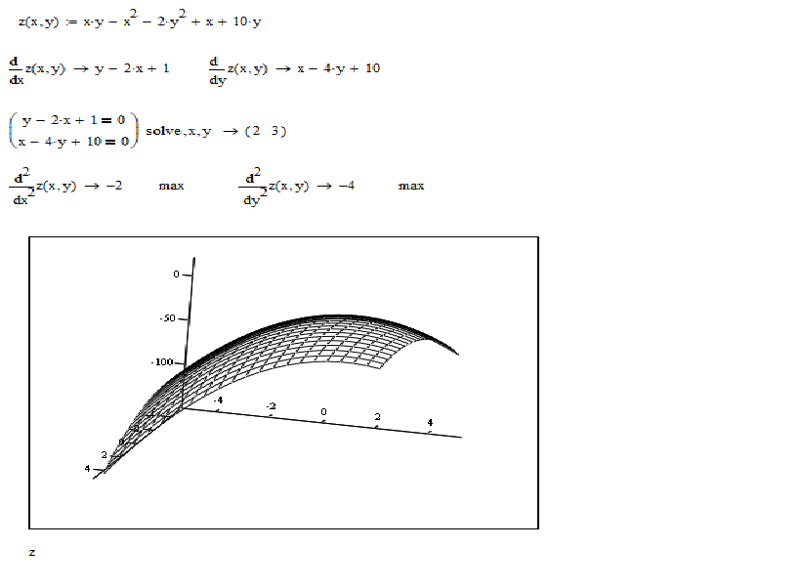
Ваш комментарий будет первым