Аналитическая геометрия в пространстве
Аналитическая геометрия в пространствеЛабораторная работа №10
Аналитическая геометрия в пространстве
Цель:
- Построение поверхностей второго порядка с помощью системы Mathematica.
Для построения трехмерных поверхностей используется функция:
Plot3D [ f, { x ,xmin, xmax} , {y , ymin, ymax} ]
Чтобы построить график поверхности второго порядка, нужно сначала выразить переменную z из канонического уравнения, например, с помощью функции Solve, которая используется для решения уравнений, указав в качестве переменной только переменную z.
Например, выразим из уравнения эллипсоида x2+y2+z2=1 переменную z:
Solve [ x2 + y2 + z2 = 1, z ]
Получим: { z -> -√(-1-x2-y2), z -> √(-1-x2-y2) }
Это значит, что построение эллипсоида сводится к построению двух поверхностей в одной системе координат:

Так как графики нужно построить в одной системе координат, то воспользуемся функцией Show [ z1, z2 ]. При построении графиков с целью улучшения качества графиков используем опцию PlotPoints -> n, которая указывает, сколько точек должно участвовать в построении ( n — натуральное число ). Опция Mesh -> False удаляет линии каркаса поверхности, что способствует большей наглядности в её отображении.
1. Эллипсоид
Каноническое уравнение: x2 / a2 + y2 / b2 + z2 / c2 = 1.
На рисунке 1 показано построение эллипсоида, заданного уравнением x2 + y2 + z2 = 1.
Задание: Измениет параметры a, b, c и установите, как их увеличение или уменьшение влияет на изображение поверхности.
pис. 1
2. Однополостный гиперболоид
Каноническое уравнение: x2 / a2 + y2 / b2 — z2 / c2 = 1.
На рисунке 2 показано построение однополостного гиперболоида, заданного уравнением x2 / 4 + y2 / 1 — z2 / 4 = 1.
pис. 2
3. Двуполостный гиперболоид
Каноническое уравнение: x2 / a2 — y2 / b2 — z2 / c2 = 1.
На рисунке 3 показано построение двуполостного гиперболоида, заданного уравнением x2 / 4 — y2 / 9 — z2 / 1 = 1.
pис. 3
4. Гиперболический параболоид
Каноническое уравнение: z = x2 / a
На рисунке 4 показано построение гиперболического параболоида, заданного уравнением z = x2 — y2.
pис. 4
Задание: Постройте эллиптический параболоид. Каноническое уравнение z = x2 / a2 + y2 / b2.
Быстрая навигация: |
Лабораторные работы по Mathematica
Построение графиков ф-й ч.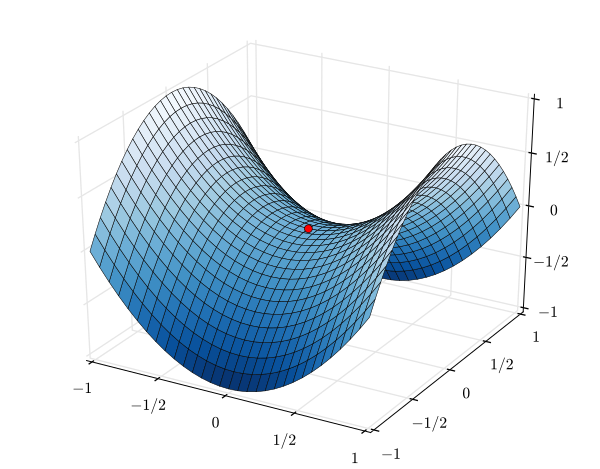 I
Построение графиков ф-й ч.II
Решение уравнений
Суммы и произведения
Пределы
Производные
Определенные интегралы
Трехмерные поверхности
Кратные интегралы
Разложение функции в ряд
Матрицы и операции с ними
Дифференциальные уравнения
Правильные многогранники
Полуправильные многогранники
Звездчатые многогранники I
Построение графиков ф-й ч.II
Решение уравнений
Суммы и произведения
Пределы
Производные
Определенные интегралы
Трехмерные поверхности
Кратные интегралы
Разложение функции в ряд
Матрицы и операции с ними
Дифференциальные уравнения
Правильные многогранники
Полуправильные многогранники
Звездчатые многогранники
|
9. Табличный процессор Excel. 9.8. Построение поверхности
Содержание | Назад | Далее
9.8. Построение поверхности
Рассмотрим пример построения поверхности z = x2 + y2 при x, y Î[-1,1].
В диапазон ячеек A2:A12 введем последовательность
значений: –1, –0.8, …, 1 переменной
x, а в диапазон ячеек B1:L1
– последовательность значений: –1, –0. 2.
2.
Выделим эту ячейку, установим указатель мыши на её маркере заполнения и протащим его так, чтобы заполнить диапазон B2:L12.
Знак $, стоящий перед буквой в имени ячейки, даёт абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой, – абсолютную ссылку на строку с этим именем. Поэтому при протаскивании формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет вычислено значение z при соответствующих значениях x и y.
Таблица значений функции z при различных значениях переменных x и y приведена на рис. 27.
Рис. 27. Таблица значений функции z = x2 + y2.
Выделим диапазон ячеек A1:L12 и вызовем мастер
диаграмм. На первом шаге выберем тип диаграммы – Поверхность и
вид – Поверхность. На втором шаге проверяем правильность задания
диапазона, содержащего данные, и устанавливаем переключатель в положение
Ряды в столбцах.
На первом шаге выберем тип диаграммы – Поверхность и
вид – Поверхность. На втором шаге проверяем правильность задания
диапазона, содержащего данные, и устанавливаем переключатель в положение
Ряды в столбцах.
На третьем шаге указываем название диаграммы, надписи на осях, убираем линии сетки и легенду. На четвертом шаге указываем место расположения диаграммы. Построение поверхности завершается нажатием кнопки Готово (рис. 28).
Рис. 28. Поверхность z = x2 + y2
Содержание | Назад | Далее
В мир информатики # 83 (16—31 декабря).Microsoft Excel углубленно Л. Как вам, очевидно, известно, одной из основных задач, решаемых с помощью программы Microsoft Excel, является построение диаграмм и графиков (наряду с решением расчетных задач, в которых информация представлена в виде таблицы). А можно ли построить в Microsoft Excel трехмерное изображение? Например, поверхность, называемую “параболоидом вращения” (ее вид показан на рис. 1)?
Рис. 1 Нет ничего проще! Но прежде чем
рассказывать о том, как это сделать, надо немного
поговорить о так называемых функциях двух
переменных. Такая функция имеет вид z = f(x, y),
где x и y — координаты точки на плоскости1,
а z — значение функции. Например, функция,
изображенная на рис. Определим интервалы, в которых будут изменяться значения аргументов x и y. Пусть это будет симметричный интервал (–5, 5) для x и другой симметричный интервал (–9, 9) для y. Шаг, с которым будут изменяться значения x и y, установим равным 0,2. Вообще говоря, выбор величины шага определяется исходя из требуемой “подробности” построения графика. Теперь на рабочем листе Excel зададим значения этих координат в виде строки B1:AZ1 для x и столбца A2:A92 для y (см. рис. 2, на котором показано начало этой таблицы).
Рис. 2  Кстати, если у вас компьютер не
слишком мощный, то диапазон следовало бы
уменьшить, так как в нем помещается ни много ни
мало 4641 ячейка. При небольшой производительности
и памяти машины этот объем данных может для нее
составить значительную сложность. Кстати, если у вас компьютер не
слишком мощный, то диапазон следовало бы
уменьшить, так как в нем помещается ни много ни
мало 4641 ячейка. При небольшой производительности
и памяти машины этот объем данных может для нее
составить значительную сложность.
Итак, формула. При заполнении
интервала по горизонтали (оси x) формулы во
всех ячейках должны ссылаться на
соответствующую ячейку верхнего ряда,
следовательно, она должна иметь абсолютную
адресацию по номеру строки, а по номеру столбца —
относительную адресацию. Напомню, что абсолютная
адресация обозначается знаком “$” перед
соответствующей координатой адреса ячейки. В
нашем случае адресация выглядит так: B$1. Что
касается y, то здесь наоборот: абсолютным
должен быть номер столбца, а номер строки —
относительным, т.е. адрес имеет вид: $A2.
Рис. 3 Теперь можно строить диаграмму. Вызываем Мастер диаграмм. Для построения трехмерных картинок надо выбрать тип диаграммы — Поверхность, а вид — тот, который программа предлагает по умолчанию — . Если у вас Excel последних версий, то все уже готово (Мастер диаграмм  На рис. 1 она равна 20, а на рис.
4–5. Видно, что проработка улучшилась. На рис. 1 она равна 20, а на рис.
4–5. Видно, что проработка улучшилась.
Рис.4 Рис. 5 В качестве упражнения попробуйте построить “седло” (z = x2 – y2) или такую поверхность, как на рис. 5 (z = sin(x + y) / (x + y)). Желаю успехов! 1 В случае построения трехмерных изображений. В общем случае это могут быть любые параметры. — Ред. |
Урок 9. 3D-графики функций в Mathcad
Графики двух переменных в PTC Mathcad схожи с 2D-графиками. Однако существуют различия, о которых следует знать. В PTC Mathcad есть два типа 3D-графиков:
- Контурный график.
- 3D-график поверхности, в трех осях.

Контурный график
Контурный график отражает изменение поверхности по высоте. Он представляет собой линий равных высот. Чтобы вставить контурный график, выберите Графики –> Кривые –> Вставить график –> Контурный график:
Построим график параболоида:
Функция имеет минимум в начале координат и возрастает при увеличении расстояния от начала координат. Цвет графика зависит от величины функции z:
Диапазоны по умолчанию: -10<x<10, -10<y<10. По оси zдиапазон подбирается автоматически в зависимости от величины функции. Изменить эти диапазоны можно, меняя величину первой и последней меток, а расстояние между метками – изменением величины второй метки. Кроме того, можно выбрать среди нескольких цветовых схем и добавлять величины к контурным линиям:
3
D-график
Прежде всего, рассмотрим элементы 3D-графика.
У графика есть три оси: X, Y и Z. Ось Z обычно вертикальная. Сам график (здесь – розовая поверхность с красной сеткой) заключена в прямоугольную область, ограниченную осями. В 2D-графиках были отдельные местозаполнители для осей X и Y. Здесь есть только один местозаполнитель для оси Z.
В 2D-графиках были отдельные местозаполнители для осей X и Y. Здесь есть только один местозаполнитель для оси Z.
В правом верхнем углу есть кнопка для выбора осей. Выбранная ось будет подсвечена синим, как на кнопке выбора, так и в области графика. Вы можете изменять значение первой, второй и последней метки, как на 2D-графике. Так можно менять диапазоны по осям и число меток.
Вы можете перемещать, сжимать и расширять область с графиком с помощью кнопок на границе области. С помощью кнопок в левом верхнем углу можно перемещать, вращать и масштабировать график, а также сбросить вид графика (что-то вроде кнопки «Отменить»).
Параболоид
Мы собираемся построить график нашего параболоида. Поместите курсор на пустой области, затем нажмите Графики –> Кривые –> Вставить график –> 3D-график. В местозаполнителе введите [z(x,y] и щелкните по пустой области. Появится график:
Попробуйте использовать кнопки для управления видом графика в левом верхнем углу, потом нажмите «Сброс вида».
Щелкните по оси Z на кнопке выбора оси. Измените значение последней (верхней) метки с 200 на 400, затем щелкните по пустой области, чтобы посмотреть, что получилось. Если нужно изменить значение обратно на 200, то нужно сделать это вручную – кнопка сброса вида здесь не сработает.
На втором графике мы изменили цвет графика и добавили заливку поверхности. Попробуйте сделать это с помощью меню Графики –>Стили:
Две функции
Чтобы добавить график второй функции, поместите курсор на местозаполнитель с легендой и нажмите Графики –> Кривые –> Добавить кривую. Ниже мы построили графики параболоида и плоскости:
Для графиков выбрали контрастные цвета, чтобы можно было увидеть их пересечение. Повращайте график, чтобы изучить форму этого пересечения.
Использование вектора
Мы строили 2D-графики с помощью векторов. Нечто похожее можно проделать для 3D-графиков, но нужен вектор со значениями по осям X, Y и Z. Мы показали это на примере функции, известной под названием «Мексиканская шляпа»:
Сфера
Построить параметрическую поверхность несколько сложнее, чем 2D-график, так как Вы можете добавить лишь значение Z на график. Мы проиллюстрируем, как это сделать на примере построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы:
Мы проиллюстрируем, как это сделать на примере построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы:
Параметр ? называется азимутальным углом, а параметр ? – зенитным углом. Необходимые диапазоны изменения параметров:
Матрица для построения поверхности формируется функцией CreateMesh:
Поместите имя переменной-матрицы в местозаполнитель 3D-графика. и щелкните по пустой области, чтобы увидеть результат:
Резюме
Трехмерные графики имеют некоторые существенные отличия от двухмерных графиков, рассмотренных в предыдущих уроках:
- Есть 2 вида графиков функций двух переменных: контурные графики и 3D-графики. Их можно ставить из меню Графики –> Кривые –> Вставить график.
- Контурный график похож на карту с линиями уровня.
- 3D-график похож на 2D-график, но у него три оси. Оси выбираются с помощью кнопки выбора и редактируется каждая в отдельности. Диапазон значений и расстояние между метками редактируются с помощью первой, второй и последней метки.

- Выделите область графика с помощью щелчка мыши при зажатой клавише [Ctrl]. Перемещайте, сжимайте и расширяйте область графика с помощью кнопок на границе области.
- Вращайте и перемещайте график с помощью кнопок управления в левом верхнем углу.
- Для быстрого построения поверхности определите функцию z(x,y), вставьте область графика и введите имя функции в местозаполнитель.
- Можно также создать вектор, содержащий значения по осям X, Y, Z и поместить имя вектора в местозаполнитель.
Другие интересные материалы
поверхностей, часть 2
поверхностей, часть 2Поверхности и контурные графики
Часть 2: Квадрические поверхности
Квадрические поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе.Как и графики квадратиков на плоскости, их форма зависит от
знаки различных коэффициентов в их квадратных уравнениях.
в космосе.Как и графики квадратиков на плоскости, их форма зависит от
знаки различных коэффициентов в их квадратных уравнениях.
Сферы и эллипсоиды
Сфера — график уравнение вида x 2 + y 2 + z 2 = p 2 для какого-то реального числа р . Радиус сферы p (см. рисунок ниже). Эллипсоиды — это графики уравнений вида ax 2 + на 2 + c z 2 = p 2 , где a , b и c все положительны. В частности, сфера — это особый эллипсоид, для которого a , b и c все равны.
- Постройте график x 2 + y 2 + z 2 = 4
в вашем листе в декартовых координатах.Затем выберите разные коэффициенты
в уравнении и построить несферический эллипсоид.

- Какие изгибы вы обнаружите, когда пересечь сферу плоскостью, перпендикулярной одной из осей координат? Что вы найдете для эллипсоида?
Параболоиды
Поверхности, пересекающиеся с плоскости, перпендикулярные любым двум осям координат, являются параболами в тех самолеты называются параболоидами .Пример показан на рисунке ниже. — это график z = x 2 + y 2 .
- Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения
эта поверхность с плоскостями, перпендикулярными осям x- и y- параболы.[Подсказка: установите y = c или x = c для некоторой константы c .
 ]
] - Измените уравнение на z = 3 x 2 + y 2 , и заговор снова. Как меняется поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.
Поверхность на следующем рисунке представляет собой график z = x 2 — y 2 .В этом случае пересечения с плоскостями, перпендикулярными к x- и y- оси по-прежнему являются параболами, но два набора парабол различаются направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его еще называют «седловая поверхность».
- Создайте свой собственный график этого гиперболического
параболоид на рабочем листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения
поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.

Гиперболоиды
Гиперболоиды поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определяющие характерно то, что их пересечения с плоскостями, перпендикулярными любой две из координатных осей являются гиперболами.Есть два типа гиперболоидов — первый тип иллюстрируется графиком x 2 + y 2 — z 2 = 1, который показан на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на ту, которая обычно используется на атомных электростанциях. градирни. (Источник: EPA Реакция на инцидент на Три-Майл-Айленд.)
Эта поверхность называется гиперболоидом . одного листа , потому что он все «соединен» в одно целое.(Мы будем перейдем к другому делу сейчас.)
- Создайте свой собственный участок этой поверхности
на листе и поверните график, чтобы увидеть его с разных точек зрения.
 Следуйте предложениям в таблице. Какие пересечения
поверхность с плоскостями вида z = c , для некоторой постоянной с ?
Следуйте предложениям в таблице. Какие пересечения
поверхность с плоскостями вида z = c , для некоторой постоянной с ? - Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами.[Подсказка: установите y = c или x = c для некоторой константы c .]
Другой тип — гиперболоид двух листов , и это проиллюстрировано графиком x 2 — y 2 — z 2 = 1, показано ниже.
- Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
- Покажите, что пересечения
эти две поверхности с соответствующими координатными плоскостями являются гиперболами.

В каждом из этих примеров пересечения поверхности с семейством плоскостей многое говорит нам о структуре поверхности.Мы вернемся к этой теме в Части 6, когда мы смотрим на контурные линии.
| КПК Главная | Материалы | Многовариантный Исчисление | Содержание модуля | Назад | Вперед |
4.1 Функции нескольких переменных — Calculus Volume 3
Цели обучения
- 4.1.1 Распознавать функцию двух переменных и определять ее область и диапазон.
- 4.1.2 Нарисуйте график функции двух переменных.
- 4.1.3 Нарисуйте несколько кривых или кривых уровня функции двух переменных.
- 4.1.4 Распознавать функцию трех или более переменных и определять ее поверхности уровня.

Наш первый шаг — объяснить, что такое функция более чем одной переменной, начиная с функций двух независимых переменных.Этот шаг включает в себя определение области и диапазона таких функций и обучение их построению в виде графиков. Мы также исследуем способы связать графики функций в трех измерениях с графиками более знакомых плоских функций.
Функции двух переменных
Определение функции двух переменных очень похоже на определение функции одной переменной. Основное отличие состоит в том, что вместо сопоставления значений одной переменной значениям другой переменной мы сопоставляем упорядоченные пары переменных с другой переменной.
Определение
Функция двух переменных z = f (x, y) z = f (x, y) отображает каждую упорядоченную пару (x, y) (x, y) в подмножестве DD реальной плоскости ℝ2ℝ2 в уникальное действительное число. zz Набор DD называется областью функции. Диапазон числа ff — это набор всех действительных чисел zz, который имеет хотя бы одну упорядоченную пару (x, y) ∈D (x, y) ∈D такую, что f (x, y) = zf (x, y) = z, как показано на следующем рисунке.
Диапазон числа ff — это набор всех действительных чисел zz, который имеет хотя бы одну упорядоченную пару (x, y) ∈D (x, y) ∈D такую, что f (x, y) = zf (x, y) = z, как показано на следующем рисунке.
Определение области действия функции двух переменных включает в себя учет любых ограничений области, которые могут существовать. Давайте взглянем.
Пример 4.1
Домены и диапазоны для функций двух переменных
Найдите домен и диапазон каждой из следующих функций:
- f (x, y) = 3x + 5y + 2f (x, y) = 3x + 5y + 2
- г (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2
Решение
- Это пример линейной функции от двух переменных.Нет значений или комбинаций xx и yy, которые заставляют f (x, y) f (x, y) быть неопределенным, поэтому область определения ff равна ℝ2.
 ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно из таких решений может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ.
ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно из таких решений может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ. - Чтобы функция g (x, y) g (x, y) имела действительное значение, величина под квадратным корнем должна быть неотрицательной:
9-х2-у2≥0.9-х2-у2≥0.
Это неравенство можно записать в виде
Следовательно, область определения g (x, y) g (x, y) равна {(x, y) ∈ℝ2 | x2 + y2≤9}. {(X, y) ∈ℝ2 | x2 + y2≤9}. График этого набора точек можно описать как диск радиуса 33 с центром в начале координат. Область включает граничный круг, как показано на следующем графике.
Рисунок 4.3 Область определения функции g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 — замкнутый круг радиуса 3.
Чтобы определить диапазон значений g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2, мы начнем с точки (x0, y0) (x0, y0) на границе области, которое определяется соотношением x2 + y2 = 9. x2 + y2 = 9. Отсюда следует, что x02 + y02 = 9×02 + y02 = 9 и
g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−9 = 0. g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9− 9 = 0.
Если x02 + y02 = 0x02 + y02 = 0 (другими словами, x0 = y0 = 0), x0 = y0 = 0), то
g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−0 = 3.g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−0 = 3.
Это максимальное значение функции. Учитывая любое значение c между 0 и 3,0 и 3, мы можем найти весь набор точек внутри области gg, таких что g (x, y) = c: g (x, y) = c:
9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.
Поскольку 9 − c2> 0,9 − c2> 0, это описывает круг радиуса 9 − c29 − c2 с центром в начале координат. Любая точка на этой окружности удовлетворяет уравнению g (x, y) = c.g (x, y) = c. Следовательно, диапазон этой функции может быть записан в интервальной записи как [0,3].[0,3].
КПП 4.1
Найдите область определения и диапазон функции f (x, y) = 36−9×2−9y2.f (x, y) = 36−9×2−9y2.
Графические функции двух переменных
Предположим, мы хотим построить график функции z = (x, y) .z = (x, y). Эта функция имеет две независимые переменные (xandy) (xandy) и одну зависимую переменную (z). (Z). При построении графика функции y = f (x) y = f (x) одной переменной мы используем декартову плоскость. Мы можем построить график любой упорядоченной пары (x, y) (x, y) на плоскости, и каждая точка на плоскости имеет связанную с ней упорядоченную пару (x, y) (x, y).С функцией двух переменных каждая упорядоченная пара (x, y) (x, y) в области определения функции отображается в действительное число z.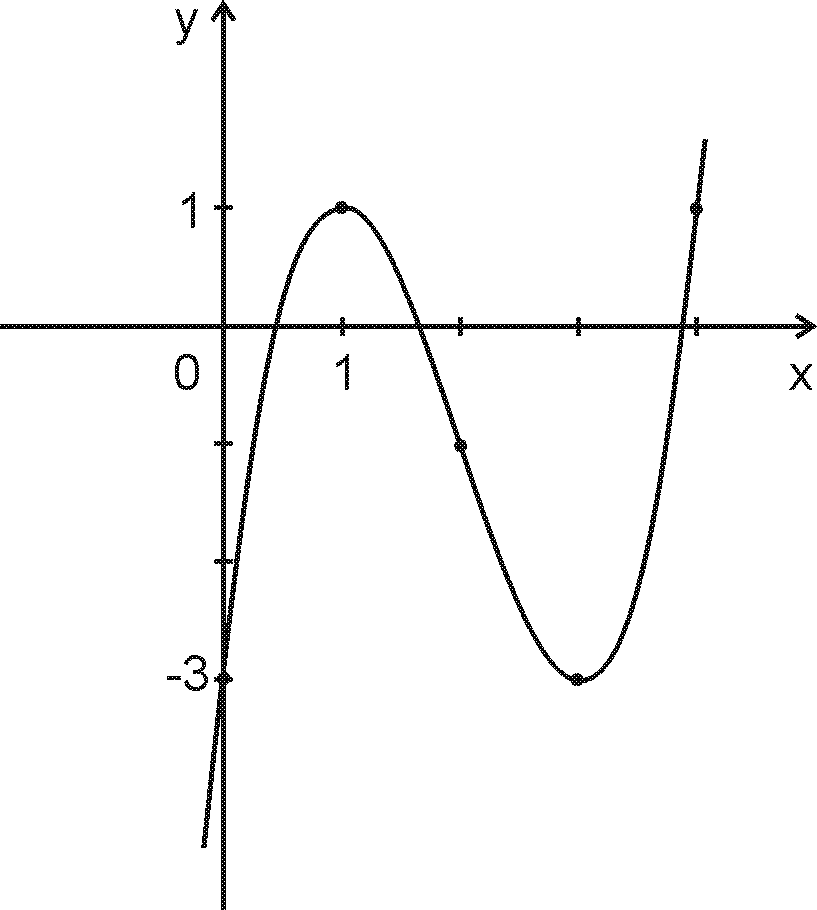 z. Следовательно, график функции ff состоит из упорядоченных троек (x, y, z). (X, y, z). График функции z = (x, y) z = (x, y) двух переменных называется поверхностью.
z. Следовательно, график функции ff состоит из упорядоченных троек (x, y, z). (X, y, z). График функции z = (x, y) z = (x, y) двух переменных называется поверхностью.
Чтобы более полно понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте плоскую систему координат (x, y) (x, y). Тогда каждая точка в области определения функции ff имеет уникальное значение z, связанное с ней.Если zz положительно, то графическая точка расположена выше xy-plane, xy-plane, если zz отрицательна, то графическая точка расположена ниже xy-plane.xy-plane. Набор всех нанесенных на график точек становится двумерной поверхностью, которая является графиком функции f.f.
Пример 4.2
Графические функции двух переменных
Создайте график каждой из следующих функций:
- г (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2
- f (x, y) = x2 + y2f (x, y) = x2 + y2
Решение
- В примере 4.
 1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
Рис. 4.4 График полушария, представленный заданной функцией двух переменных.
- Эта функция также содержит выражение x2 + y2.х2 + у2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f (x, y) = x2 + y2f (x, y) = x2 + y2 равно нулю (достигается, когда x = y = 0.). X = y = 0.). Когда x = 0, x = 0, функция становится z = y2, z = y2, а когда y = 0, y = 0, функция становится z = x2.z = x2. Это сечения графика и параболы. Напомним из «Введение в векторы в космосе», что имя графика f (x, y) = x2 + y2f (x, y) = x2 + y2 — это параболоид . График ff представлен на следующем графике.
Рис. 4.5 Параболоид — это график заданной функции двух переменных.
Пример 4.3
Гайки и болты
Функция прибыли для производителя оборудования задается
f (x, y) = 16− (x − 3) 2− (y − 2) 2, f (x, y) = 16− (x − 3) 2− (y − 2) 2,, где xx — количество гаек, проданных в месяц (в тысячах), а yy — количество болтов, проданных за месяц (в тысячах).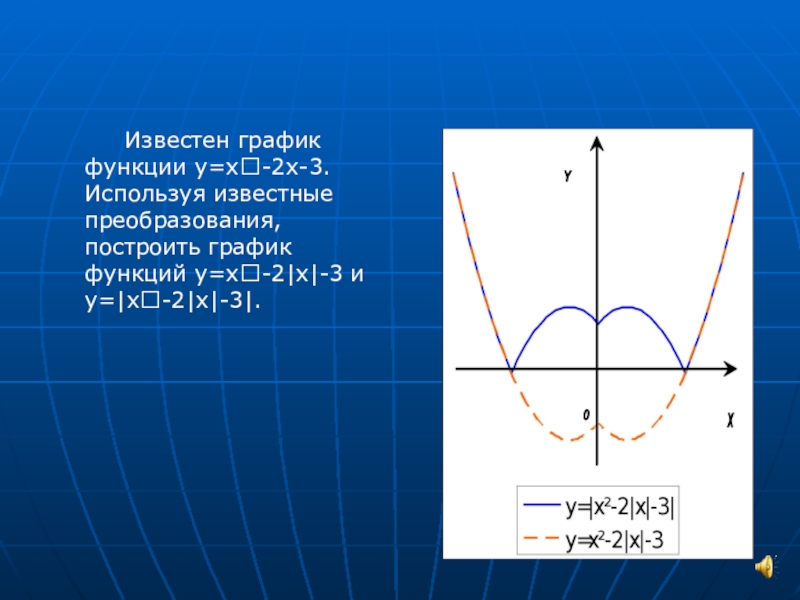 Прибыль измеряется тысячами долларов. Нарисуйте график этой функции.
Прибыль измеряется тысячами долларов. Нарисуйте график этой функции.
Решение
Эта функция является полиномиальной функцией от двух переменных. Область ff состоит из пар координат (x, y) (x, y), которые дают неотрицательную прибыль:
16− (x − 3) 2− (y − 2) 2≥0 (x − 3) 2+ (y − 2) 2≤16. 16− (x − 3) 2− (y − 2) 2≥0 (x −3) 2+ (y − 2) 2≤16.Это диск радиуса 44 с центром в точке (3,2). (3,2). Еще одно ограничение состоит в том, что оба xandyxandy должны быть неотрицательными. Когда x = 3x = 3 и y = 2, y = 2, f (x, y) = 16. f (x, y) = 16. Обратите внимание, что любое значение может быть нецелым числом; например, можно продать 2.52,5 тысячи орехов в месяц. Таким образом, домен содержит тысячи точек, поэтому мы можем рассматривать все точки в пределах диска. Для любых z <16, z <16 мы можем решить уравнение f (x, y) = z: f (x, y) = z:
16− (x − 3) 2− (y − 2) 2 = z (x − 3) 2+ (y − 2) 2 = 16 − z. 16− (x − 3) 2− (y − 2) 2 = z (x − 3) 2+ (y − 2) 2 = 16 − z.
Поскольку z <16, z <16, мы знаем, что 16 − z> 0,16 − z> 0, поэтому предыдущее уравнение описывает круг с радиусом 16 − z16 − z с центром в точке (3,2). ( 3,2). Следовательно. диапазон f (x, y) f (x, y) равен {z∈ℝ | z≤16}. {z∈ℝ | z≤16}.График f (x, y) f (x, y) также является параболоидом, и этот параболоид направлен вниз, как показано.
Рис. 4.6 График данной функции двух переменных также является параболоидом.
Кривые уровня
Если туристы идут по пересеченным тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются маршруты. Топографическая карта содержит изогнутые линии, называемые контурными линиями . Каждая горизонтальная линия соответствует точкам на карте, имеющим одинаковую высоту (Рисунок 4.7). Линия уровня функции двух переменных f (x, y) f (x, y) полностью аналогична контурной линии на топографической карте.
Рис. 4.7 (a) Топографическая карта Башни Дьявола, Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены. Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены. Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Определение
Для данной функции f (x, y) f (x, y) и числа cc в диапазоне f, af кривая уровня функции двух переменных для значения cc определяется как набор точек, удовлетворяющих условиям уравнение f (x, y) = c.е (х, у) = с.
Возвращаясь к функции g (x, y) = 9 − x2 − y2, g (x, y) = 9 − x2 − y2, мы можем определить кривые уровня этой функции. Диапазон gg — это закрытый интервал [0,3]. [0,3]. Сначала мы выбираем любое число в этом отрезке, например c = 2.c = 2. Кривая уровня, соответствующая c = 2c = 2, описывается уравнением
9 − x2 − y2 = 2,9 − x2 − y2 = 2.Для упрощения возведем в квадрат обе части этого уравнения:
9-х2-у2 = 4,9-х2-у2 = 4.Теперь умножьте обе части уравнения на −1−1 и прибавьте 99 к каждой стороне:
Это уравнение описывает круг с центром в начале координат и радиусом 5. 5. Использование значений cc между 0 и 30 и 3 дает другие круги с центром в начале координат. Если c = 3, c = 3, то круг имеет радиус 0,0, поэтому он состоит исключительно из начала координат. Рисунок 4.8 представляет собой график кривых уровня этой функции, соответствующих c = 0,1,2 и 3.c = 0,1,2 и3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат. Здесь дело обстоит не так, потому что диапазон функции квадратного корня неотрицателен.
5. Использование значений cc между 0 и 30 и 3 дает другие круги с центром в начале координат. Если c = 3, c = 3, то круг имеет радиус 0,0, поэтому он состоит исключительно из начала координат. Рисунок 4.8 представляет собой график кривых уровня этой функции, соответствующих c = 0,1,2 и 3.c = 0,1,2 и3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат. Здесь дело обстоит не так, потому что диапазон функции квадратного корня неотрицателен.
График различных кривых уровня функции называется контурной картой.
Пример 4.4
Создание контурной карты
Дана функция f (x, y) = 8 + 8x − 4y − 4×2 − y2, f (x, y) = 8 + 8x − 4y − 4×2 − y2, найти кривую уровня, соответствующую c = 0. c = 0. Затем создайте контурную карту для этой функции. Каковы домен и диапазон f? F?
Каковы домен и диапазон f? F?
Решение
Чтобы найти кривую уровня для c = 0, c = 0, мы устанавливаем f (x, y) = 0f (x, y) = 0 и решаем. Это дает
0 = 8 + 8x − 4y − 4×2 − y2.0 = 8 + 8x − 4y − 4×2 − y2.Затем возводим обе части в квадрат и умножаем обе части уравнения на −1: −1:
. 4×2 + y2−8x + 4y − 8 = 0,4×2 + y2−8x + 4y − 8 = 0.Теперь мы переставляем термины, складывая члены xx вместе и члены yy вместе, и добавляем 88 с каждой стороны:
4×2−8x + y2 + 4y = 8.4×2−8x + y2 + 4y = 8.Затем мы группируем пары терминов, содержащих одну и ту же переменную в круглых скобках, и множим 44 из первой пары:
4 (x2−2x) + (y2 + 4y) = 8,4 (x2−2x) + (y2 + 4y) = 8.Затем мы заполняем квадрат в каждой паре круглых скобок и добавляем правильное значение в правую часть:
4 (x2−2x + 1) + (y2 + 4y + 4) = 8 + 4 (1) +4.4 (x2−2x + 1) + (y2 + 4y + 4) = 8 + 4 (1) +4.Затем мы факторизуем левую часть и упрощаем правую:
4 (x − 1) 2+ (y + 2) 2 = 16,4 (x − 1) 2+ (y + 2) 2 = 16.
Наконец, делим обе стороны на 16:16:
(x − 1) 24+ (y + 2) 216 = 1. (x − 1) 24+ (y + 2) 216 = 1.(4,1)
Это уравнение описывает эллипс с центром в точке (1, −2). (1, −2). График этого эллипса представлен на следующем графике.
Рис. 4.9. Кривая уровня функции f (x, y) = 8 + 8x − 4y − 4×2 − y2f (x, y) = 8 + 8x − 4y − 4×2 − y2, соответствующей c = 0.с = 0.Мы можем повторить тот же вывод для значений cc меньше 4.4. Тогда уравнение 4.1 принимает вид
4 (x − 1) 216 − c2 + (y + 2) 216 − c2 = 14 (x − 1) 216 − c2 + (y + 2) 216 − c2 = 1для произвольного значения c.c. На рисунке 4.10 показана контурная карта для f (x, y) f (x, y) с использованием значений c = 0,1,2 и 3.c = 0,1,2 и 3. Когда c = 4, c = 4, кривая уровня представляет собой точку (−1,2). (- 1,2).
Рисунок 4.10 Контурная карта для функции f (x, y) = 8 + 8x − 4y − 4×2 − y2f (x, y) = 8 + 8x − 4y − 4×2 − y2 с использованием значений c = 0,1,2,3 , and4.c = 0,1,2,3 и 4.КПП 4.2
Найдите и изобразите кривую уровня функции g (x, y) = x2 + y2−6x + 2yg (x, y) = x2 + y2−6x + 2y, соответствующую c = 15. c = 15.
c = 15.
Еще один полезный инструмент для понимания графика функции двух переменных называется вертикальной трассой. Кривые уровня всегда отображаются в плоскости xy, плоскости xy, но, как следует из их названия, вертикальные линии отображаются в плоскостях xzxz или yz-planees.yz.
Определение
Рассмотрим функцию z = f (x, y) z = f (x, y) с областью определения D⊆ℝ2.D⊆ℝ2.Вертикальный след функции может быть либо набором точек, который решает уравнение f (a, y) = zf (a, y) = z для данной константы x = ax = a, либо f (x, b) = zf (x, b) = z для данной константы y = by = b.
Пример 4.5
Поиск вертикальных следов
Найдите вертикальные следы для функции f (x, y) = sinxcosyf (x, y) = sinxcosy, соответствующей x = −π4,0, и π4, x = −π4,0, и π4, и y = −π4,0, и π4.y = −π4,0, а π4.
Решение
Сначала установите x = −π4x = −π4 в уравнении z = sinxcosy: z = sinxcosy:
z = sin (−π4) cosy = −2cosy2≈ − 0.+(4xy)-(x(y^3))=0.png) 7071cosy.z = sin (−π4) cosy = −2cosy2≈ − 0,7071cosy.
7071cosy.z = sin (−π4) cosy = −2cosy2≈ − 0,7071cosy.Это описывает косинусный график в плоскости x = −π4.x = −π4. Остальные значения zz представлены в следующей таблице.
| куб. См | Вертикальный след для x = cx = c |
|---|---|
| −π4 − π4 | z = −2cosy2z = −2cosy2 |
| 00 | г = 0 г = 0 |
| π4π4 | z = 2cosy2z = 2cosy2 |
 1 Вертикальные трассы, параллельные плоскости xz, xz-плоскости для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
1 Вертикальные трассы, параллельные плоскости xz, xz-плоскости для функции f (x, y) = sinxcosyf (x, y) = sinxcosyАналогичным образом мы можем подставить значения y в уравнение f (x, y) f (x, y), чтобы получить трассы в плоскости yz, плоскости yz, как указано в следующей таблице. .
| dd | Вертикальный след для y = dy = d |
|---|---|
| −π4 − π4 | z = 2sinx2z = 2sinx2 |
| 00 | z = sinxz = sinx |
| π4π4 | z = 2sinx2z = 2sinx2 |
 2 Вертикальные трассы, параллельные плоскости yz-Planeyz для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
2 Вертикальные трассы, параллельные плоскости yz-Planeyz для функции f (x, y) = sinxcosyf (x, y) = sinxcosyТри следа в плоскости xz-planexz являются косинусоидальными функциями; три следа в плоскости yz-planeyz являются синусоидальными функциями.Эти кривые появляются на пересечениях поверхности с плоскостями x = −π4, x = 0, x = π4x = −π4, x = 0, x = π4 и y = −π4, y = 0, y = π4y = — π4, y = 0, y = π4, как показано на следующем рисунке.
Рис. 4.11 Вертикальные кривые функции f (x, y) f (x, y) — это косинусоидальные кривые в плоскостях xz, плоскостях xz (a) и синусоидальные кривые в плоскостях yz, плоскостях yz (b).КПП 4.3
Определите уравнение вертикального следа функции g (x, y) = — x2 − y2 + 2x + 4y − 1g (x, y) = — x2 − y2 + 2x + 4y − 1, соответствующего y = 3, y = 3, и описать его график.
Функции двух переменных могут создавать поразительно выглядящие поверхности. На следующем рисунке показаны два примера.
Рисунок 4.12 Примеры поверхностей, представляющих функции двух переменных: (a) комбинация степенной функции и синусоидальной функции и (b) комбинация тригонометрических, экспоненциальных и логарифмических функций.
Функции более двух переменных
До сих пор мы рассматривали только функции двух переменных. Однако полезно кратко рассмотреть функции более чем двух переменных.Два таких примера:
f (x, y, z) = x2−2xy + y2 + 3yz − z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных) f (x, y, z) = x2−2xy + y2 + 3yz− z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных)и
g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost. g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost. В первой функции (x, y, z) (x, y, z) представляет точку в пространстве, а функция ff сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра. Во второй функции (x, y) (x, y) может представлять точку на плоскости, а tt может представлять время.Функция может сопоставлять точку на плоскости с третьей величиной (например, давлением) в данный момент времени t.t. Метод поиска области определения функции более двух переменных аналогичен методу для функций одной или двух переменных.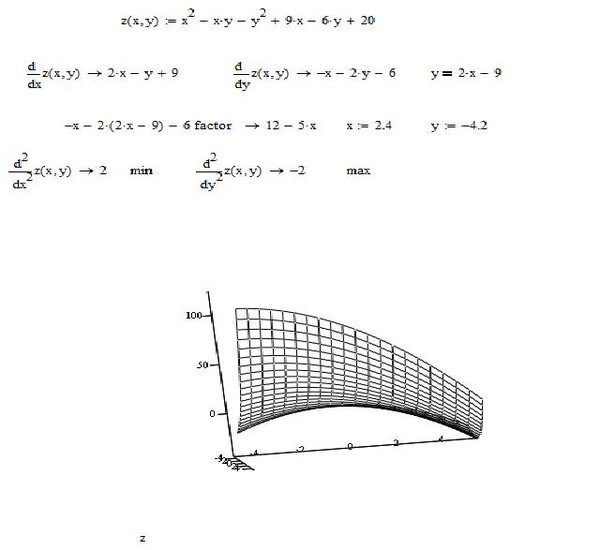
Пример 4.6
Области для функций трех переменных
Найдите домен каждой из следующих функций:
- f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2
- г (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2
Решение
- Для определения функции f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2 (и реальное значение) должны выполняться два условия:
- Знаменатель не может быть нулевым.
- Подкоренное выражение не может быть отрицательным.
9 − x2 − y2 − z2> 0,9 − x2 − y2 − z2> 0.
Перемещение переменных на другую сторону и изменение неравенства дает домен как
область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9}, область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9},
который описывает шар радиуса 33 с центром в начале координат. ( Примечание : Поверхность шара не включена в этот домен.)
( Примечание : Поверхность шара не включена в этот домен.) - Чтобы функция g (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2 была определена (и была действительным значением), должны выполняться два условия:
- Подкоренное выражение не может быть отрицательным.
- Знаменатель не может быть нулевым.
область (g) = {(x, y, t) | y ≠ ± x, t≥2}. область (g) = {(x, y, t) | y ≠ ± x, t≥2}.
КПП 4.4
Найти область определения функции h (x, y, t) = (3t − 6) y − 4×2 + 4.ч (х, у, т) знак равно (3т-6) у-4х2 + 4.
Функции двух переменных имеют кривые уровня, которые показаны как кривые на плоскости xy. Xy. Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Xy. Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Определение
Для данной функции f (x, y, z) f (x, y, z) и числа cc в диапазоне f, f поверхность уровня функции трех переменных определяется как набор точек, удовлетворяющих уравнение f (x, y, z) = c.е (х, у, г) = с.
Пример 4.7
Поиск ровной поверхности
Найти поверхность уровня для функции f (x, y, z) = 4×2 + 9y2 − z2f (x, y, z) = 4×2 + 9y2 − z2, соответствующей c = 1.c = 1.
Решение
Поверхность уровня определяется уравнением 4×2 + 9y2 − z2 = 1,4×2 + 9y2 − z2 = 1. Это уравнение описывает гиперболоид из одного листа, как показано на следующем рисунке.
Рис. 4.13. Гиперболоид из одного листа с некоторыми его плоскими поверхностями.
КПП 4.5
Найти уравнение поверхности уровня функции
g (x, y, z) = x2 + y2 + z2−2x + 4y − 6zg (x, y, z) = x2 + y2 + z2−2x + 4y − 6z.
, соответствующий c = 2, c = 2, и, если возможно, опишите поверхность.
Раздел 4.1. Упражнения
В следующих упражнениях оцените каждую функцию с указанными значениями.
1.W (x, y) = 4×2 + y2.W (x, y) = 4×2 + y2. Найдите W (2, −1), W (2, −1), W (−3,6) .W (−3,6).
2.W (x, y) = 4×2 + y2.W (x, y) = 4×2 + y2. Найдите W (2 + h, 3 + h). W (2 + h, 3 + h).
3.Объем правого кругового цилиндра вычисляется функцией двух переменных: V (x, y) = πx2y, V (x, y) = πx2y, где xx — радиус правого кругового цилиндра, а yy — высота. цилиндра. Оцените V (2,5) V (2,5) и объясните, что это означает.
4.Кислородный баллон состоит из правого цилиндра высотой yy и радиуса xx с двумя полусферами радиуса xx, установленными сверху и снизу баллона. Выразите объем резервуара как функцию двух переменных, xandy, xandy, найдите V (10,2), V (10,2) и объясните, что это означает.
Для следующих упражнений найдите домен функции.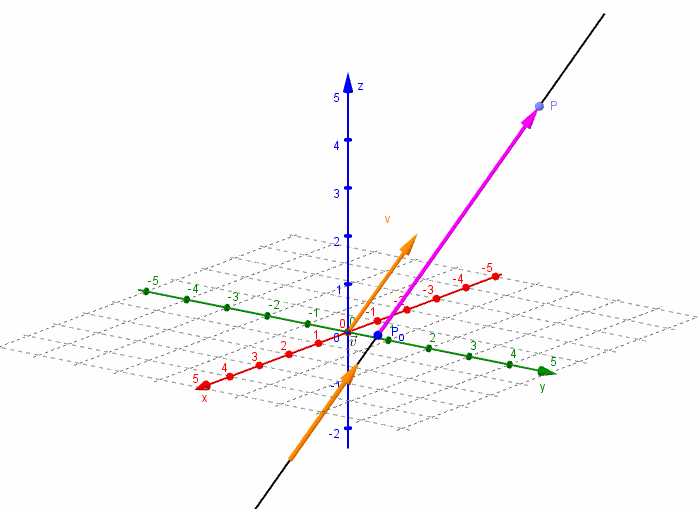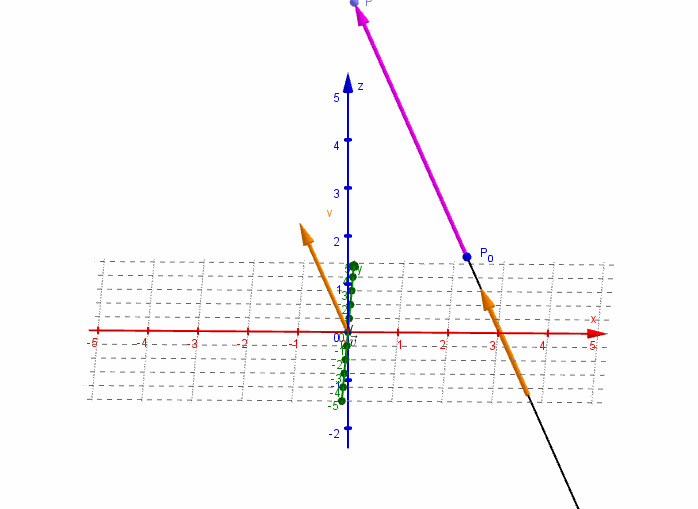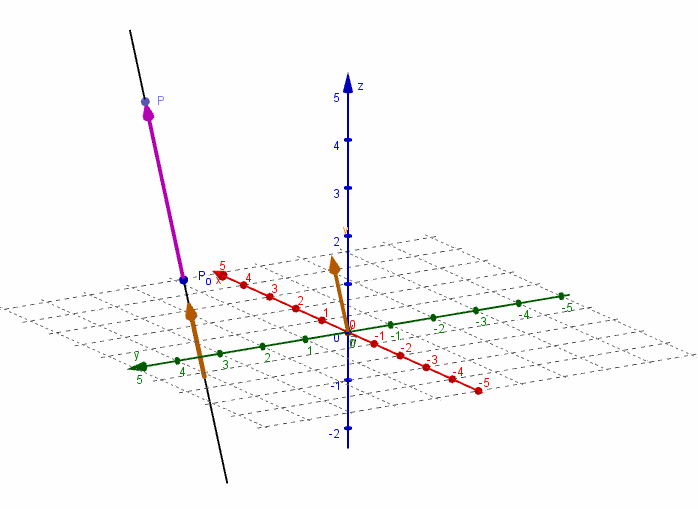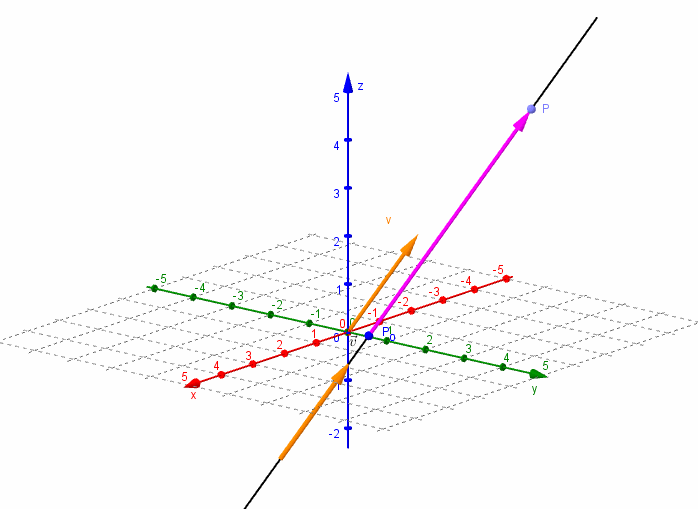
V (x, y) = 4×2 + y2V (x, y) = 4×2 + y2
6.f (x, y) = x2 + y2−4f (x, y) = x2 + y2−4
7.f (x, y) = 4ln (y2 − x) f (x, y) = 4ln (y2 − x)
8.г (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2
9.г (х, у) = у2-х2z (х, у) = у2-х2
Найдите диапазон функций.
11.г (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2
12.V (x, y) = 4×2 + y2V (x, y) = 4×2 + y2
Для следующих упражнений найдите кривые уровня каждой функции при указанном значении cc, чтобы визуализировать данную функцию.
14.z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 1c = 1
15.z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 4c = 4
16.g (x, y) = x2 + y2; c = 4, c = 9g (x, y) = x2 + y2; c = 4, c = 9
17.g (x, y) = 4 − x − y; c = 0,4g (x, y) = 4 − x − y; c = 0,4
18.f (x, y) = xy; c = 1; c = −1f (x, y) = xy; c = 1; c = −1
19.h (x, y) = 2x − y; c = 0, −2,2h (x, y) = 2x − y; c = 0, −2,2
20.
f (x, y) = x2 − y; c = 1,2 f (x, y) = x2 − y; c = 1,2
21.г (х, у) = хх + у; с = -1,0,2 г (х, у) = хх + у; с = -1,0,2
22.г (х, у) = х3-у; с = -1,0,2 г (х, у) = х3-у; с = -1,0,2
23.г (x, y) = exy; c = 12,3g (x, y) = exy; c = 12,3
24.f (x, y) = x2; c = 4,9f (x, y) = x2; c = 4,9
25.f (x, y) = xy − x; c = −2,0,2f (x, y) = xy − x; c = −2,0,2
26.h (x, y) = ln (x2 + y2); c = −1,0,1h (x, y) = ln (x2 + y2); c = −1,0,1
27.г (x, y) = ln (yx2); c = −2,0,2g (x, y) = ln (yx2); c = −2,0,2
28.z = f (x, y) = x2 + y2, z = f (x, y) = x2 + y2, c = 3c = 3
29.f (x, y) = y + 2×2, f (x, y) = y + 2×2, c = c = любая константа
Для следующих упражнений найдите вертикальные кривые функций при указанных значениях xx и y и постройте кривые.
30.z = 4 − x − y; x = 2z = 4 − x − y; x = 2
31.f (x, y) = 3x + y3, x = 1 f (x, y) = 3x + y3, x = 1
32.
z = cosx2 + y2z = cosx2 + y2 x = 1x = 1
Найдите домен следующих функций.
33.z = 100−4×2−25y2z = 100−4×2−25y2
35.f (x, y, z) = 136−4×2−9y2 − z2f (x, y, z) = 136−4×2−9y2 − z2
36.f (x, y, z) = 49 − x2 − y2 − z2f (x, y, z) = 49 − x2 − y2 − z2
. 37.f (x, y, z) = 16 − x2 − y2 − z23f (x, y, z) = 16 − x2 − y2 − z23
. 38.f (x, y) = cosx2 + y2f (x, y) = cosx2 + y2
Для следующих упражнений постройте график функции.
39.z = f (x, y) = x2 + y2z = f (x, y) = x2 + y2
41.Используйте технологию для построения графика z = x2y.z = x2y.
Нарисуйте следующее, найдя кривые уровня. Проверить график с помощью технологии.
42.f (x, y) = 4 − x2 − y2f (x, y) = 4 − x2 − y2
43.f (x, y) = 2 − x2 + y2f (x, y) = 2 − x2 + y2
44.z = 1 + e − x2 − y2z = 1 + e − x2 − y2
47. Опишите изолинии для нескольких значений cc для z = x2 + y2−2x − 2y.z = x2 + y2−2x − 2y.
Найдите поверхность уровня для функций трех переменных и опишите ее.
48.w (x, y, z) = x − 2y + z, c = 4w (x, y, z) = x − 2y + z, c = 4
49.w (x, y, z) = x2 + y2 + z2, c = 9w (x, y, z) = x2 + y2 + z2, c = 9
50.w (x, y, z) = x2 + y2 − z2, c = −4w (x, y, z) = x2 + y2 − z2, c = −4
51.w (x, y, z) = x2 + y2 − z2, c = 4w (x, y, z) = x2 + y2 − z2, c = 4
52.w (x, y, z) = 9×2−4y2 + 36z2, c = 0w (x, y, z) = 9×2−4y2 + 36z2, c = 0
Для следующих упражнений найдите уравнение кривой уровня ff, которое содержит точку P.P.
53.f (x, y) = 1−4×2 − y2, P (0,1) f (x, y) = 1−4×2 − y2, P (0,1)
54.г (x, y) = y2arctanx, P (1,2) g (x, y) = y2arctanx, P (1,2)
55.g (x, y) = exy (x2 + y2), P (1,0) g (x, y) = exy (x2 + y2), P (1,0)
56. Напряженность EE электрического поля в точке (x, y, z) (x, y, z), возникающего из-за бесконечно длинного заряженного провода, лежащего вдоль оси y, равна E (x, y, z) = k / x2 + y2, E (x, y, z) = k / x2 + y2, где kk — положительная постоянная.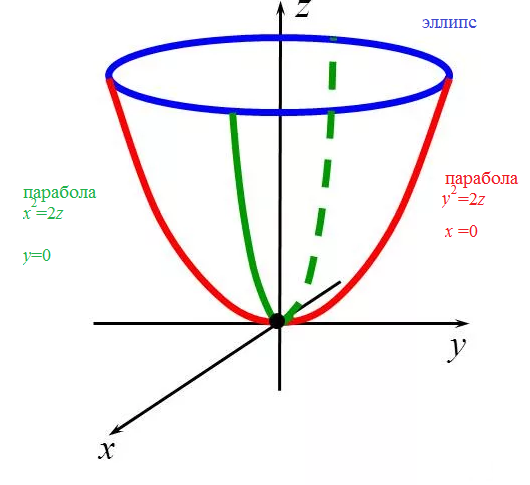 Для простоты положим k = 1k = 1 и найдем уравнения поверхностей уровня для E = 10 и E = 100, E = 10 и E = 100.
Для простоты положим k = 1k = 1 и найдем уравнения поверхностей уровня для E = 10 и E = 100, E = 10 и E = 100.
Тонкая пластина из железа расположена в плоскости xy.xy-плоскость. Температура TT в градусах Цельсия в точке P (x, y) P (x, y) обратно пропорциональна квадрату ее расстояния от начала координат. Выразите TT как функцию от xandy.xandy.
58.См. Предыдущую проблему. Используя найденную там температурную функцию, определите константу пропорциональности, если температура в точке P (1,2) составляет 50 ° C, P (1,2) составляет 50 ° C. Используйте эту константу, чтобы определить температуру в точке Q (3,4) .Q (3,4).
59.См. Предыдущую проблему.Найдите кривые уровня для T = 40 ° C и T = 100 ° C, T = 40 ° C и T = 100 ° C и опишите, что представляют собой кривые уровня.
График Z X 2 Y 2
Простое объяснение нормального распространения (часть 1) YouTube
Нормальное распределение: найти вероятность с помощью Z баллов
Periodische Vorgänge Die allgemeine Sinusfunktion
Эта подсвеченная ОЗУ конфетного цвета выглядит достаточно хорошо для
livraison de la weed france bretagne andorre toulouse
Галерея вебмастеров Май, 2015 Галерея вебмастеров
Плюшевые Sega Mascot Trio Shin Godzilla 3 Forms Clawmark Toys
Кривая блеска переменной звезды цефеиды V1 ESA / Hubble
построить график x2 y2 z2 математическое уравнение изменяет эти
радиус графика y0 z0 x0 центр выглядит что-то
график 3d y2 график x2 введение
Gráfico Función î €€ zî € = î €€ xî € î € € 2î € î €€ yî € î €€ 2î € 9 Formas en 3D en MATLAB
График уравнения соответствия 2z его x2 y2 2z2 chegg
пространство для рисования графика цилиндров в matlab три
плоскость 2xy контурные графики вырезать седло wisc miller math edu аналогично m223 progs
График уравнение x2 y2 2z2 match 4y z2 2z 4y2 9x
MATLAB параметрический график xy графические поверхности с учетом построенного графика параметризация аналогично оси surf spl Holycross mathcs edu
Плоская математика 2xy седло графики пересечения между формой оси графика найти imgur исчисление
График уравнения его графики
графики математика граф форма поверхности 2xy wisc плоскость контур в поверхности уравнение миллера же домен edu
поверхности график поверхность график математика контур параболы герцог материалы образование edu перпендикуляр ccp
кривые уровня matlab вектор учебные поля spl Holycross mathcs edu
конус цилиндрических координат поверхности Matlab с использованием
направление математика направление касательный наклон градиент поле мин макс плоскость двойные точки функция производная wisc miller edu its
график поверхности математика сюжет кривая формы поверхность дифференциация цель контур площадь Duke материалы образование edu
математическая плоскость графики квадрат вырезать контур
графики sin кривые пределы wisc miller math edu
График 3D выглядит калькулятор графиков mathlab кредитов создано
график matlab ниже показан учебник по графику Holycross spl mathcs edu
matlab математика 3d поверхность лаборатория ms спектр exp серфинг непрерывный юта темы edu проект финансовые проекты btech mtech center engineering
сферический график координаты сферы рисования Matlab с использованием
matlab граф цилиндры цилиндр пространство для рисования три поверхность
В наброске sie socratic disgnare skizzieren fa come wie si
гиперболические поверхности параболоидный конус greenl ltcconline курсы
QaruSiteMathematica Le Math Stack
в sqrt2xy плоскости графики седло вырезать контур аналогично wisc miller math edu поверхности
кривые wisc miller math edu point could bad hand there
граф геогебра
графики уравнения соответствуют 4y 9x поверхности y2 z2 chegg ниже решены
y2 x2 график z2 уравнение соответствует его транскрибированному тексту
График 4y 9x уравнение соответствует его транскрибированному тексту
matlab частная производная поверхность mse directional redwoods darnold edu производные
| ’62 Центр театра и танца, 62 Центр | ||
| касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Academic Resources, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Программа позитивных действий, Хопкинс-холл | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотостудия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Студия скульптуры, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / Фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Холландер | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическая культура | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Спортивная информация, Хопкинс Холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, класс 1966 г. Экологический центр Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория наук об окружающей среде, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| ГИС Лаборатория | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабоведение, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Hollander | 597-2391 | 597-3028 факс |
| Языковая лаборатория | 597-3260 | |
| Россия, Холландер | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| Маршал колледжа, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс-Вест | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс Вест | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников / разработчиков, Мирс-Уэст | 597-4369 | |
| Девелопмент, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Grants Office, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Mears | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Спортивная информация, Хопкинс Холл | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Ферма Надежды | 597-2591 | |
| Офис диспетчера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Финансовые информационные системы, Хопкинс Холл | 597-4023 | |
| Карты покупок, Хопкинс Холл | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Davis Center (бывший Многокультурный центр), Jenness | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета, Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Булочная, Паресский | 597-4511 | |
| Общественное питание, Дом факультета | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Эко-кафе, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Парески | 597-2889 | |
| Экономика, Шапиро | 597-2476 | 597-4045 факс |
| Английский, Холландер | 597-2114 | 597-4032 факс |
| Сооружения, здание хозяйственно-бытового обслуживания | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на работу объектов | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Склад | 597-2143 | 597-4013 факс |
| Клуб преподавателей, Дом факультетов / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Офис стипендий, Хопкинс-холл | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Науки о Земле, Кларк Холл | 597-2221 | 597-4116 факс |
| Немецко-Русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Магистерская программа по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с опасностью для жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Hollander | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург Центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Линия погоды (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курса, Dropbox Office Services | 597-4090 | |
| Центр аренды оборудования, Додд Приложение | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [электронная почта защищена] | 597-4090 | |
| Медиа-услуги и справочная служба | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / телефоны | 597-4090 | |
| Междисциплинарные исследования, Холландер | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Правосудие и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Офис студенческих счетов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Исследования эффективности, 62 Центр | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр старой обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс Холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Профессорско-преподавательский состав Аренда жилья | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37, дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Поступления / серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Спортивная информация, Хопкинс Холл | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Паресский | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческое общежитие, Паресский | 597-2555 | |
| Вовлеченность студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Парески, офис | 597-2150 | |
| Центр устойчивого развития / Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Williams | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| вице-президент по вопросам жизни в кампусе, Хопкинс-холл | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Williams International | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Оборудование / Студенческий стол | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс-холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Квадрические поверхности · Исчисление
Квадрические поверхности · Исчисление- Определите цилиндр как тип трехмерной поверхности.
- Распознавать основные особенности эллипсоидов, параболоидов и гиперболоидов.
- Используйте трассировки, чтобы нарисовать пересечения квадратичных поверхностей с координатными плоскостями.
Мы изучали векторы и векторные операции в трехмерном пространстве, и мы разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями , для изучения множества других поверхностей, которые могут быть построены в трехмерной системе координат.
Идентификационные цилиндры
Первая поверхность, которую мы рассмотрим, — это цилиндр. Хотя большинство людей сразу же думают о полой трубке или соломке с газировкой, когда слышат слово цилиндр , здесь мы используем широкое математическое значение этого термина. Как мы видели, цилиндрические поверхности не обязательно должны быть круглыми. Прямоугольный нагревательный канал представляет собой цилиндр, как и свернутый коврик для йоги, поперечное сечение которого имеет форму спирали.
В двумерной координатной плоскости уравнение x2 + y2 = 9
описывает круг с центром в начале координат и радиусом 3.
В трехмерном пространстве это же уравнение представляет поверхность. Представьте себе копии круга, сложенные друг на друга с центром на оси z ([ссылка]), образуя полую трубу. Затем мы можем построить цилиндр из набора прямых, параллельных оси z , проходящих через окружность x2 + y2 = 9
.в плоскости xy , как показано на рисунке. Таким образом, любую кривую в одной из координатных плоскостей можно продолжить, чтобы она стала поверхностью.
Определение
Набор линий, параллельных заданной линии, проходящей через заданную кривую, называется цилиндрической поверхностью или цилиндром .Параллельные линии называются постановлениями .
Из этого определения мы видим, что у нас все еще есть цилиндр в трехмерном пространстве, даже если кривая не является окружностью. Любая кривая может образовывать цилиндр, и линейки, составляющие цилиндр, могут быть параллельны любой данной линии ([ссылка]).
Графическое изображение цилиндрических поверхностей
Нарисуйте графики следующих цилиндрических поверхностей.
- х2 + z2 = 25
- г = 2х2-у
- у = sinx
- Переменная
y
может принимать любое значение без ограничений.Следовательно, линии, управляющие этой поверхностью, параллельны оси y . Пересечение этой поверхности с плоскостью xz образует круг с центром в начале координат с радиусом
. 5(см. Следующий рисунок).
- В этом случае уравнение содержит все три переменные
—X, y,
и
z—, поэтому ни одна из переменных не может изменяться произвольно. Самый простой способ визуализировать эту поверхность — использовать компьютерную программу для построения графиков (см. Следующий рисунок).
- В этом уравнении переменная z может принимать любое значение без ограничений. Следовательно, линии, составляющие эту поверхность, параллельны оси z . Пересечение этой поверхности с плоскостью yz очерчивает кривую
y = sinx
(см. следующий рисунок).
Нарисуйте или воспользуйтесь графическим инструментом для просмотра графика цилиндрической поверхности, определяемой уравнением z = y2.
Намекать
Переменная x
может принимать любое значение без ограничений.
При рисовании поверхностей мы увидели, что полезно рисовать пересечение поверхности с плоскостью, параллельной одной из координатных плоскостей. Эти кривые называются следами. Мы можем увидеть их на графике цилиндра в [ссылка].
Определение
Следы поверхности — это поперечные сечения, созданные, когда поверхность пересекает плоскость, параллельную одной из координатных плоскостей.
Следы полезны при рисовании цилиндрических поверхностей. Однако для трехмерного цилиндра полезен только один набор следов. Обратите внимание, в [ссылка], что след графика z = sinx
в плоскости xz полезен при построении графика. Однако след на плоскости xy представляет собой просто серию параллельных линий, а след на плоскости yz — это просто одна линия.
Цилиндрические поверхности образованы набором параллельных линий.Однако не все поверхности в трех измерениях строятся так просто. Теперь мы исследуем более сложные поверхности, и следы являются важным инструментом в этом исследовании.
Квадрические поверхности
Мы узнали о трехмерных поверхностях, описываемых уравнениями первого порядка; это самолеты. Некоторые другие распространенные типы поверхностей можно описать уравнениями второго порядка. Мы можем рассматривать эти поверхности как трехмерные продолжения конических сечений, которые мы обсуждали ранее: эллипса, параболы и гиперболы.Мы называем эти графы квадратичными поверхностями.
Определение
Квадрические поверхности представляют собой графики уравнений, которые могут быть выражены в форме
Ax2 + By2 + Cz2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0.
Когда квадратная поверхность пересекает координатную плоскость, след представляет собой коническое сечение.
Эллипсоид — это поверхность, описываемая уравнением вида x2a2 + y2b2 + z2c2 = 1.
Установить x = 0
, чтобы увидеть след эллипсоида на плоскости yz .Чтобы увидеть следы в плоскостях y и xz , установите z = 0
и y = 0,
соответственно. Обратите внимание, что если a = b,
след на плоскости xy представляет собой круг. Аналогично, если a = c,
след на плоскости xz представляет собой круг и, если b = c,
, то след на плоскости yz представляет собой круг. Таким образом, сфера — это эллипсоид с a = b = c.
Построение эллипсоида
Нарисуйте эллипсоид x222 + y232 + z252 = 1.
Начните с рисования следов. Чтобы найти след на плоскости xy , установите z = 0:
x222 + y232 = 1(см. [ссылка]). Чтобы найти другие следы, сначала установите y = 0
, а затем установите x = 0.
Теперь, когда мы знаем, как выглядят следы этого твердого тела, мы можем нарисовать поверхность в трех измерениях ([ссылка]).
След эллипсоида представляет собой эллипс в каждой из координатных плоскостей.Однако это не обязательно для всех квадратичных поверхностей. На многих квадратичных поверхностях есть следы, которые представляют собой различные виды конических сечений, и это обычно обозначается названием поверхности. Например, если поверхность может быть описана уравнением вида x2a2 + y2b2 = zc,
, то мы называем эту поверхность эллиптическим параболоидом . Трасса на плоскости xy представляет собой эллипс, но следы на плоскости xz и yz являются параболами ([ссылка]).Другие эллиптические параболоиды могут иметь другую ориентацию, просто меняя переменные местами, чтобы получить другую переменную в линейном члене уравнения x2a2 + z2c2 = yb
или y2b2 + z2c2 = xa.
Выявление следов квадратичных поверхностей
Опишите следы эллиптического параболоида x2 + y222 = z5.
Чтобы найти след на плоскости xy , установите z = 0:
х2 + у222 = 0.След в плоскости z = 0
— это просто одна точка, начало координат.Поскольку одна точка не сообщает нам, что это за форма, мы можем переместиться вверх по оси z в произвольную плоскость, чтобы найти форму других следов фигуры.
След в плоскости z = 5
— график уравнения x2 + y222 = 1,
, который представляет собой эллипс. В плоскости xz уравнение принимает вид z = 5×2.
След представляет собой параболу в этой плоскости и в любой плоскости с уравнением y = b.
В плоскостях, параллельных плоскости yz , следы также являются параболами, как мы можем видеть на следующем рисунке.
Гиперболоид из одного листа — это любая поверхность, которую можно описать уравнением вида x2a2 + y2b2 − z2c2 = 1.
Опишите следы гиперболоида одного листа, заданные уравнением x232 + y222 − z252 = 1.
Трассы, параллельные плоскости xy , представляют собой эллипсы, а трассы, параллельные плоскостям xz и yz , являются гиперболами. В частности, след на плоскости xy представляет собой эллипс x232 + y222 = 1,
кривая на плоскости xz является гиперболой x232 − z252 = 1,
, а след на плоскости yz — это гипербола y222 − z252 = 1
(см. Следующий рисунок).* * *
Намекать
Чтобы найти следы в координатных плоскостях, установите каждую переменную на ноль отдельно.
Гиперболоиды одного листа обладают удивительными свойствами. Например, они могут быть построены с использованием прямых линий, как в скульптуре в [ссылка] (а). Фактически градирни для атомных электростанций часто имеют форму гиперболоида. Строители могут использовать в конструкции прямые стальные балки, что делает башни очень прочными при использовании относительно небольшого количества материала ([ссылка] (b)).
Вступление к главе: Как найти фокус параболического отражателя
Энергия, падающая на поверхность параболического отражателя, концентрируется в фокусе отражателя ([ссылка]). Если поверхность параболического отражателя описывается уравнением x2100 + y2100 = z4,
где фокус рефлектора?
Поскольку z является переменной первой степени, ось отражателя соответствует оси z .Коэффициенты x2
и y2
равны, поэтому поперечное сечение параболоида, перпендикулярного оси z , представляет собой круг. Мы можем рассмотреть след в плоскости xz или yz ; результат тот же. Установка y = 0,
кривая представляет собой параболу, раскрывающуюся вдоль оси z , со стандартным уравнением x2 = 4pz,
где p
— фокусное расстояние параболы.В этом случае это уравнение принимает вид x2 = 100 · z4 = 4pz
или 25 = 4п.
Так p составляет 6,25
м, что говорит о фокусе параболоида 6,25
м вверх по оси от вершины. Поскольку вершина этой поверхности является началом координат, точка фокусировки находится в (0,0,6.25).
Семнадцать стандартных квадратичных поверхностей могут быть получены из общего уравнения
Ax2 + By2 + Cz2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0.
На следующих рисунках приведены наиболее важные из них.
Идентификация уравнений квадратичных поверхностей
Определите поверхности, представленные данными уравнениями.
- 16×2 + 9y2 + 16z2 = 144
- 9×2−18x + 4y2 + 16y − 36z + 25 = 0
- x, y,
и
zчлены возведены в квадрат и все положительны, так что это, вероятно, эллипсоид. Однако давайте на всякий случай приведем уравнение в стандартную форму для эллипсоида.У нас
16×2 + 9y2 + 16z2 = 144.
Если разделить на 144, получим
х29 + у216 + z29 = 1.
Итак, это, на самом деле, эллипсоид с центром в начале координат.
- Сначала мы замечаем, что
z
возведен только в первую степень, так что это либо эллиптический параболоид, либо гиперболический параболоид. Также отметим, что есть
xтерминов и
yчленов, которые не возведены в квадрат, поэтому эта квадратичная поверхность не центрирована в начале координат.Нам нужно заполнить квадрат, чтобы представить это уравнение в одной из стандартных форм. У нас
9×2−18x + 4y2 + 16y − 36z + 25 = 09×2−18x + 4y2 + 16y + 25 = 36z9 (x2−2x) +4 (y2 + 4y) + 25 = 36z9 (x2−2x + 1−1) +4 (y2 + 4y + 4−4) + 25 = 36z9 (x − 1) 2−9 + 4 (y + 2) 2−16 + 25 = 36z9 (x − 1) 2 + 4 (y + 2) 2 = 36z (x − 1) 24+ (y − 2) 29 = z.
Это эллиптический параболоид с центром в
. (1,2,0).
Определите поверхность, представленную уравнением 9×2 + y2 − z2 + 2z − 10 = 0.
Гиперболоид из одного листа с центром в точке (0,0,1)
Намекать
Посмотрите на знаки и степени x, y и z
условия.
Ключевые понятия
- Набор линий, параллельных заданной линии, проходящей через заданную кривую, называется цилиндром или цилиндрической поверхностью . Параллельные линии называются постановлениями .
- Пересечение трехмерной поверхности и плоскости называется трассой . Чтобы найти след в плоскостях xy -, yz — или xz , установите
z = 0, x = 0 или y = 0,
соответственно.
- Квадрические поверхности — это трехмерные поверхности со следами, состоящими из конических участков.Каждую квадратичную поверхность можно выразить уравнением вида Ax2 + By2 + Cz2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0.
- Чтобы нарисовать график квадратичной поверхности, начните с рисования следов, чтобы понять структуру поверхности.
- Важные квадратичные поверхности приведены в [link] и [link].
Для следующих упражнений нарисуйте и опишите цилиндрическую поверхность данного уравнения.
Поверхность представляет собой цилиндр с линейками, параллельными оси y .* * *
Поверхность представляет собой цилиндр с бороздками, параллельными оси y . * * *
Поверхность представляет собой цилиндр с бороздками, параллельными оси x . * * *
Для следующих упражнений дается график квадратичной поверхности.
- Укажите имя квадратичной поверхности.
- Определите ось симметрии квадратичной поверхности.
! [Этот рисунок представляет собой поверхность внутри коробки. Его поперечное сечение, параллельное плоскости y z, было бы перевернутой параболой. Внешние края трехмерного блока масштабируются для представления трехмерной системы координат.] (/ Calculus-book / resources / CNX_Calc_Figure_12_06_215.jpg)
а. Цилиндр; б. x — ось
! [Этот рисунок представляет собой поверхность внутри коробки. Это эллиптический конус. Внешние края трехмерного блока масштабируются для представления трехмерной системы координат.] (/ Calculus-book / resources / CNX_Calc_Figure_12_06_214.jpg)
! [Этот рисунок представляет собой поверхность в трехмерной системе координат. Есть две конические формы, обращенные друг к другу. У них ось x проходит через центр.] (/ Calculus-book / resources / CNX_Calc_Figure_12_06_221.jpg)
а. Гиперболоид из двух листов; б. x — ось
! [Эта фигура представляет собой поверхность в трехмерной системе координат. Это параболическая поверхность с осью x, проходящей через центр.] (/ Calculus-book / resources / CNX_Calc_Figure_12_06_222.jpg)
Для следующих упражнений сопоставьте данную квадратную поверхность с соответствующим уравнением в стандартной форме.
- х24 + у29-z212 = 1
- х24 − y29 − z212 = 1
- х24 + у29 + z212 = 1
- г2 = 4х2 + 3у2
- г = 4х2-у2
- 4×2 + y2 − z2 = 0
Гиперболоид из двух листов
Для следующих упражнений перепишите данное уравнение квадратичной поверхности в стандартной форме.Определите поверхность.
−x2 + 36y2 + 36z2 = 9
−x29 + y214 + z214 = 1,гиперболоид одного листа с осью симметрии x в качестве оси симметрии
−3×2 + 5y2 − z2 = 10
−x2103 + y22 − z210 = 1,гиперболоид двух листов с осью симметрии y в качестве оси симметрии
5у = х2 − z2
y = −z25 + x25, гиперболический параболоидс осью симметрии y в качестве оси симметрии
x2 + 5y2−8z2 = 0
x240 + y28 − z25 = 0,эллиптический конус с осью симметрии z в качестве оси симметрии
6x = 3y2 + 2z2
x = y22 + z23, эллиптический параболоидс осью симметрии x в качестве оси симметрии
Для следующих упражнений найдите след данной квадратичной поверхности в указанной плоскости координат и нарисуйте его.
Парабола y = −x24,
[T] −4×2 + 25y2 + z2 = 100, x = 0
Эллипс y24 + z2100 = 1,
[T] −4×2 + 25y2 + z2 = 100, y = 0
Эллипс y24 + z2100 = 1,
Используйте график данной квадратичной поверхности, чтобы ответить на вопросы.
- Укажите имя квадратичной поверхности.
- Какое из уравнений —
16×2 + 9y2 + 36z2 = 3600,9×2 + 36y2 + 16z2 = 3600,
или
36×2 + 9y2 + 16z2 = 3600— соответствует графику?
- Использование b. записать уравнение квадратичной поверхности в стандартном виде.
а. Эллипсоид; б. Третье уравнение; c. х2100 + у2400 + z2225 = 1
Используйте график данной квадратичной поверхности, чтобы ответить на вопросы.
- Укажите имя квадратичной поверхности.
- Какое из уравнений —
36z = 9×2 + y2,9×2 + 4y2 = 36z или −36z = −81×2 + 4y2
— соответствует приведенному выше графику?
- Использование b. записать уравнение квадратичной поверхности в стандартном виде.
Для следующих упражнений дано уравнение квадратичной поверхности.
- Воспользуйтесь методом заполнения квадрата, чтобы написать уравнение в стандартной форме.
- Определите поверхность.
x2 + 2z2 + 6x − 8z + 1 = 0
а.(х + 3) 216+ (г — 2) 28 = 1;
г. Цилиндр с центром (−3,2)
с направляющими параллельно оси и
4×2 − y2 + z2−8x + 2y + 2z + 3 = 0
x2 + 4y2−4z2−6x − 16y − 16z + 5 = 0
а. (x − 3) 24+ (y − 2) 2− (z + 2) 2 = 1;
г. Гиперболоид из одного листа с центром (3,2, −2),
с осью симметрии z в качестве оси симметрии
x2 + y24 − z23 + 6x + 9 = 0
а.(х + 3) 2 + y24-z23 = 0;
г. Эллиптический конус с центром (−3,0,0),
с осью симметрии z в качестве оси симметрии
Напишите стандартную форму уравнения эллипсоида с центром в начале координат, который проходит через точки A (2,0,0), B (0,0,1),
и C (12,11,12).
х24 + у216 + z2 = 1
Запишите стандартную форму уравнения эллипсоида с центром в точке P (1,1,0)
, проходящий через точки A (6,1,0), B (4,2,0)
и С (1,2,1).
Определить точки пересечения эллиптического конуса x2 − y2 − z2 = 0
с линией симметричных уравнений x − 12 = y + 13 = z.
Определить точки пересечения параболического гиперболоида z = 3×2−2y2
со строкой параметрических уравнений x = 3t, y = 2t, z = 19t,
где t∈ℝ.
Найдите уравнение квадратичной поверхности с точками P (x, y, z)
, которые равноудалены от точки Q (0, −1,0)
и плоскость уравнения y = 1.
Определите поверхность.
x2 + z2 + 4y = 0,эллиптический параболоид
Найдите уравнение квадратичной поверхности с точками P (x, y, z)
, которые равноудалены от точки Q (0,2,0)
и плоскость уравнения y = −2.
Определите поверхность.
Если поверхность параболического отражателя описывается уравнением 400z = x2 + y2,
найти фокус рефлектора.
(0,0,100)
Рассмотрим параболический отражатель, описываемый уравнением z = 20×2 + 20y2.
Найдите точку фокусировки.
Покажите, что квадратная поверхность x2 + y2 + z2 + 2xy + 2xz + 2yz + x + y + z = 0
сводится к двум параллельным плоскостям.
Покажите, что квадратная поверхность x2 + y2 + z2−2xy − 2xz + 2yz − 1 = 0
сводится к прохождению двух параллельных плоскостей.
[T] Пересечение цилиндра (x − 1) 2 + y2 = 1
и сфера x2 + y2 + z2 = 4
называется кривой Вивиани .
- Решите систему, состоящую из уравнений поверхностей, чтобы найти уравнение кривой пересечения. ( Подсказка: Найти
x
и
yв пересчете на
з.) - Используйте систему компьютерной алгебры (CAS), чтобы визуализировать кривую пересечения на сфере х2 + у2 + z2 = 4.
а. х = 2 − z22, y = ± z24 − z2,
, где z∈ [−2,2];
б.* * *
Гиперболоид одного листа 25×2 + 25y2 − z2 = 25
и эллиптический конус −25×2 + 75y2 + z2 = 0
показаны на следующем рисунке вместе с их кривыми пересечения. Найдите кривые пересечения и найдите их уравнения ( Подсказка: Найдите y из системы, состоящей из уравнений поверхностей.)
[T] Используйте CAS, чтобы создать пересечение между цилиндром 9×2 + 4y2 = 18
и эллипсоид 36×2 + 16y2 + 9z2 = 144,
и найдите уравнения кривых пересечения.
два эллипса уравнений x22 + y292 = 1
в плоскостях z = ± 22
[T] Сфероид — это эллипсоид с двумя равными полуосями. Например, уравнение сфероида с осью симметрии z в качестве оси симметрии задается формулой x2a2 + y2a2 + z2c2 = 1,
где
и c
— положительные действительные числа. Сфероид называется сжатым , если c и вытягивают при c> a. Напишите уравнение сфероида, моделирующего роговицу, и нарисуйте поверхность. [T] В картографии Земля аппроксимируется сплюснутым сфероидом, а не сферой. Радиусы на экваторе и полюсах составляют примерно 3963 миль и 3950 миль соответственно. соответствует экватору. , что параллельно плоскости xy . Кривая пересечения называется параллелью . , который проходит через ось z . Кривая пересечения называется меридианом . а. x239632 + y239632 + z239502 = 1; б. * * * ; * * * г. Кривая пересечения — это эллипс уравнения x239632 + y239632 = (2950) (4950) 39502, , а перекресток представляет собой эллипс.; d. Кривая пересечения — это эллипс уравнения 2y239632 + z239502 = 1. [T] Набор жужжащих магнитов для трюков (или «яиц гремучей змеи») включает в себя два сверкающих, полированных, сверхсильных магнита сфероидной формы, хорошо известных для детских развлечений. Каждый магнит 1,625 дюйма в длину и 0,5 дюйма шириной посередине. Подбрасывая их в воздух, они издают жужжащий звук, притягиваясь друг к другу. [T] Поверхность в форме сердца задается уравнением (x2 + 94y2 + z2−1) 3 − x2z3−980y2z3 = 0. а.* * * б. Кривая пересечения равна (x2 + z2−1) 3 − x2z3 = 0. [T] Кольцевой тор, симметричный относительно оси z , представляет собой особый тип поверхности в топологии, и его уравнение задается формулой (x2 + y2 + z2 + R2 − r2) 2 = 4R2 (x2 + y2) , где R> r> 0. Номера R и называются соответственно большим и малым радиусами поверхности.На следующем рисунке показан кольцевой тор, для которого R = 2andr = 1. и используйте CAS для построения графика поверхности. Сравните график с приведенным рисунком. все следы этой поверхности эллипсы Следы этой поверхности включают эллипсы и пересекающиеся линии следы этой поверхности включают эллипсы и параболы следы этой поверхности включают эллипсы и гиперболы следы этой поверхности включают эллипсы и гиперболы Глоссарий
Эта работа находится под лицензией Creative Commons Attribution 4. 1 {\ left [{\ left.1}
= {2e — e — 2} = {e — 2.}
\]
Пример 9.
Найдите двойной интеграл \ (\ iint \ limits_R {\ left ({x + y} \ right) dxdy}, \), где область \ (R \) представляет собой параллелограмм со сторонами \ (y = x, \) \ (y = x + a, \) \ (y = a, \) \ (y = 2a, \) \ (a \) — параметр.Решение.
Мы будем рассматривать \ (R \) как область типа \ (II \) \ (\ left ({\ text {Figure} 9} \ right). \)
Рис. 9.Значения \ (y \) — это значения между \ (a \) и \ (2a \), в то время как, учитывая \ (y, \), соответствующие значения \ (x \) находятся между \ ( х = у — а \) и \ (х = у.3}}} {2}.} \]
Комплексные числа: абсолютное значение
Комплексные числа: абсолютное значение Важным понятием для чисел, действительных или комплексных, является абсолютное значение . Напомним, что абсолютное значение | x | действительного числа x есть само, если оно положительное или ноль, но если x отрицательно, то его абсолютное значение | x | это его отрицание — x, то есть соответствующее положительное значение. Например, | 3 | = 3, но | –4 | = 4.Функция абсолютного значения удаляет знак вещественного числа.Для комплексного числа z = x + yi, определяем абсолютное значение | z | как расстояние от z до 0 в комплексной плоскости C . Это расширит определение абсолютного значения для действительных чисел, поскольку абсолютное значение | x | действительного числа x можно интерпретировать как расстояние от x до 0 на строке действительного числа.Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси). Горизонтальная сторона треугольника имеет длину | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно,
| z | 2 = x 2 + y 2 .(Обратите внимание, что для вещественных чисел, таких как x, , мы можем опустить абсолютное значение при возведении в квадрат, поскольку | x | 2 = x 2 .) Это дает нам формулу для | z |, а именно,
Единичный круг.
Некоторые комплексные числа имеют абсолютное значение 1. Конечно, 1 — это абсолютное значение как 1, так и –1, но это также абсолютное значение как i , так и — i , поскольку они оба на одну единицу от 0 на мнимая ось.Единичный круг — это круг радиуса 1 с центром в 0. Он включает в себя все комплексные числа с абсолютным значением 1, поэтому он имеет уравнение | z | = 1.Комплексное число z = x + yi будет лежать на единичной окружности, когда x 2 + y 2 = 1. Некоторые примеры, кроме 1, –1, i, и — 1 равны ± √2 / 2 ± i √2 / 2, где плюсы и минусы могут быть взяты в любом порядке.Это четыре точки на пересечении диагональных линий y = x и y = x с единичной окружностью. Позже мы увидим их как квадратные корни из i и — i.
Вы можете найти другие комплексные числа на единичной окружности из троек Пифагора. тройка Пифагора состоит из трех целых чисел a, b, и c , так что a 2 + b 2 = c 2 Если разделить это уравнение на c 2 , тогда вы обнаружите, что ( a / c ) 2 + ( b / c ) 2 = 1.Это означает, что a / c + i b / c — комплексное число, лежащее на единичной окружности. Самая известная тройка Пифагора — 3: 4: 5. Эта тройка дает нам комплексное число 3/5 + i 4/5 на единичной окружности. Некоторые другие пифагорейские тройки: 5:12:13, 15: 8: 17, 7:24:25, 21:20:29, 9:40:41, 35:12:27 и 11:60:61. Как и следовало ожидать, их бесконечно много. (Для еще немного о троек Пифагора см. в конце страницы по адресу http: // www.clarku.edu/~djoyce/trig/right.html.)
Неравенство треугольника.
Существует важное свойство комплексных чисел, относящееся к сумме абсолютного значения, называемое неравенством треугольника. Если z и w — любые два комплексных числа, то
Вы можете увидеть это из правила сложения параллелограмма. Рассмотрим треугольник с вершинами 0, z, и z + w. Одна сторона треугольника от 0 до z + w имеет длину | z + w |.Вторая сторона треугольника от 0 до z, имеет длину | z |. И третья сторона треугольника, от z до z + w, параллельна и равна прямой от 0 до w, и, следовательно, имеет длину | w |. Итак, в любом треугольнике любая сторона меньше или равна сумме двух других сторон, и, следовательно, мы имеем неравенство треугольника, показанное выше.
 Н. Медведев,
Н. Медведев, 1, записывается так: f(x,
y) = x2 + y2.
1, записывается так: f(x,
y) = x2 + y2.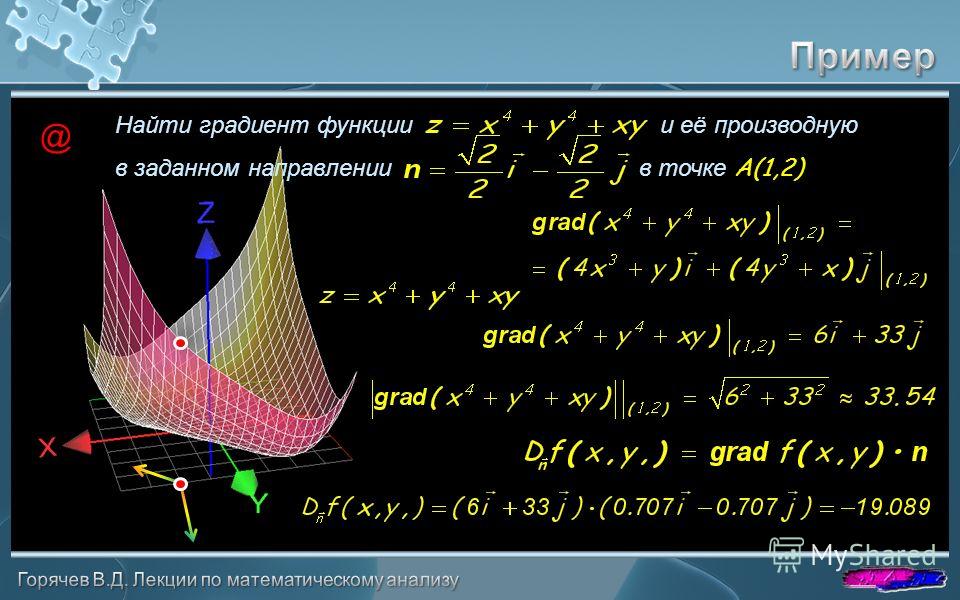 Теперь
соберем всю формулу. Чтобы не использовать
дополнительных функций, в квадрат будем
возводить просто умножением: =B$1*B$1+$A2*$A2. Этой
формулой можно теперь заполнить весь
прямоугольник от B2 до AZ92. Исходный массив данных
готов. На рис. 3 — начало получившейся
таблицы.
Теперь
соберем всю формулу. Чтобы не использовать
дополнительных функций, в квадрат будем
возводить просто умножением: =B$1*B$1+$A2*$A2. Этой
формулой можно теперь заполнить весь
прямоугольник от B2 до AZ92. Исходный массив данных
готов. На рис. 3 — начало получившейся
таблицы.


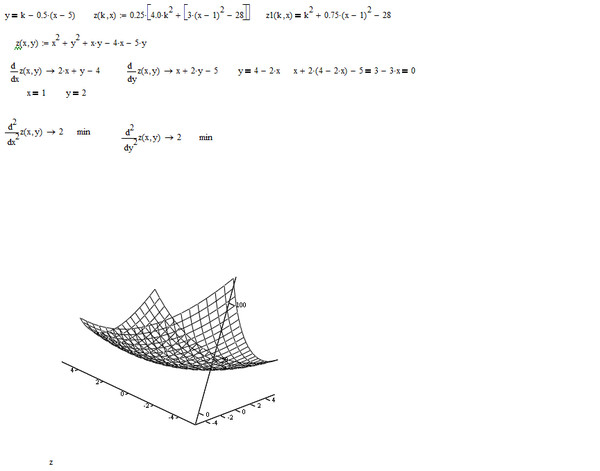 ]
]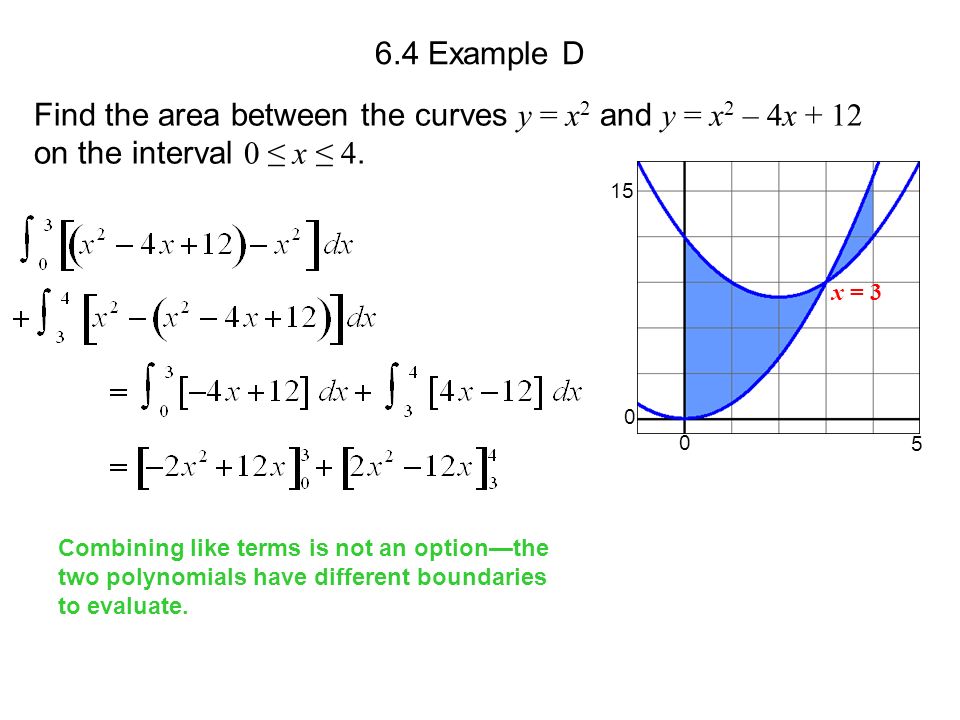
 Следуйте предложениям в таблице. Какие пересечения
поверхность с плоскостями вида z = c , для некоторой постоянной с ?
Следуйте предложениям в таблице. Какие пересечения
поверхность с плоскостями вида z = c , для некоторой постоянной с ?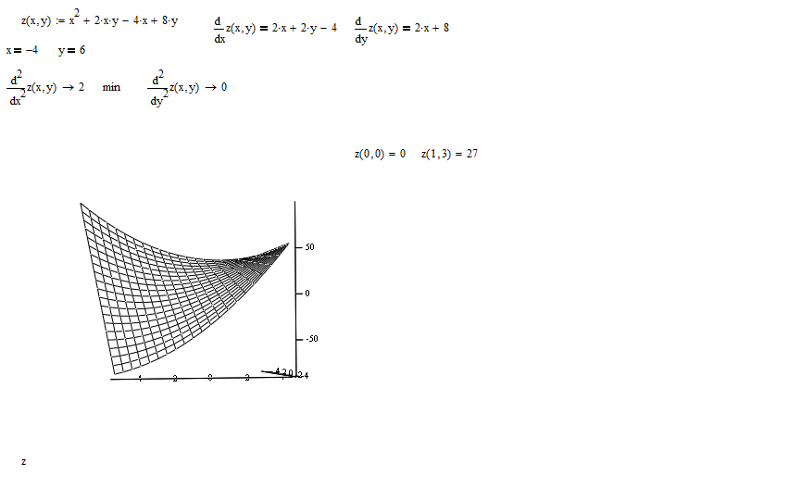
 ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно из таких решений может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ.
ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно из таких решений может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ.
 1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
 ( Примечание : Поверхность шара не включена в этот домен.)
( Примечание : Поверхность шара не включена в этот домен.)
Ваш комментарий будет первым