X2 y2 0 график: Постройте графики уравнения x^2+y^2=0 и x^2-y^2=0 — Магазин Apple iPhone в Перми

Содержание

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения

Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
Выбрать платежную систему.

Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Построить график у x 2 3 x 2: Mathway

Решение.

Функция степенная без каких-либо ограничений, поэтому область определения будет вся числовая прямая. Значения функции — вся числовая прямая.
Четная или нечетная функция.

Подставим вместо переменной х значение —х и по результату сделаем вывод:

В результате получили, что функция не является ни четной, ни нечетной.

Функция должна пересекаться с координатными осями. Вычислим точки пересечения функции с ними.

Для вычисления точек пересечения с осью Ох, подставим в функцию вместо переменной х число 0:

Функция пересекается с осью Ох в точке с координатами (0; 0).
Вычислим точку пересечения с осью Оу. Для этого подставим вместо переменной у значение 0 и решим полученное уравнение:

или
или
Функция пересекается с осью Оу в двух точках, первая— это пересечение с осью Ох, так как это начало координат — (0; 0). У второй точки координаты (1; 0).

Поскольку функция степенная, то должна иметь экстремумы. Вычислим их, рассчитав производную:

Запишем производную, как равную нулю, и вычислим корни уравнения:

или
или
Проверим полученные точки на экстремум. Для этого возьмем какую-нибудь точку из каждого полученного промежутка между найденными точками и найдем знак производной на всех полученных промежутках.
Первый промежуток от минус бесконечности до 0. Возьмем точку —1 и рассчитаем для нее производную:

— функция возрастает.
Второй промежуток от 0 до 2/3. Выберем точку 0,5 и вычислим от нее производную:
— функция убывает.

Третий промежуток от 2/3 до + бесконечности. Возьмем точку 1 и вычислим от нее производную:
— функция возрастает на этом промежутке.
Когда функция переходит через точку с абсциссой 0, она изменяет знак производной с + на —. Значит, это точка максимума, а при переходе через точку 2/3 знак производной меняется с — на +, значит, это точка минимума.
Вычислим координаты максимума и минимума:

Максимум — точка (0; 0)
Минимум — точка .

Урок 6. решение уравнений графическим способом — Алгебра — 8 класс

Тема: Решение уравнений графическим способом

Содержание модуля (краткое изложение модуля):

Решим графическим способом уравнение:

x² = −3x

Решить уравнение – значит найти такие значения x, при которых выполняется равенство x² = −3x
Построим в одной системе координат два графика:
график функции y = x² и график функции y = −3x.
Для каждого графика составим таблицы значений
y = x² – на рисунке синий график

x	0	1	2	3	−1	−2	−3
y	0	1	4	9	1	4	9

y = −3x – на рисунке красный график

x	0	1	2	3	−1	−2	−3
y	0	−3	−6	−9	3	6	9

Заметим, что графики пересекаются в двух точках: точке с координатами (0 ; 0) и в точке с координатами (–3 ; 9). Это значит, что при x = 0 и при x = –3 функции y = x² и y = −3x имеют одинаковые значения.
Таким образом получаем, что при x = 0 и при x = –3 выполняется равенство x² = −3x.
Значит значения x = 0 и x = –3 являются корнями уравнения x² = −3x.
Корни, найденные графическим способом – приближённые. Чтобы доказать точность значений корней, надо каждый из них подставить в решаемое уравнение и проверить: выполняется ли полученное равенство.
Подставим в уравнение x² = −3x значение x = 0.

0² = −3•0

0 = 0 – верное равенство, значит x = 0 – точный корень уравнения

x² = −3x.
Подставим в уравнение x² = −3x значение x = –3.

(−3)2 = −3•(−3)

9 = 9 – верное равенство, значит x = −3 – точный корень уравнения x² = −3x.
Подведём итог.
Чтобы решить уравнение f₁(x) = f₂(x) графическим способом, необходимо:
1) Построить в одной системе координат графики функций y = f₁(x) и y = f₂(x).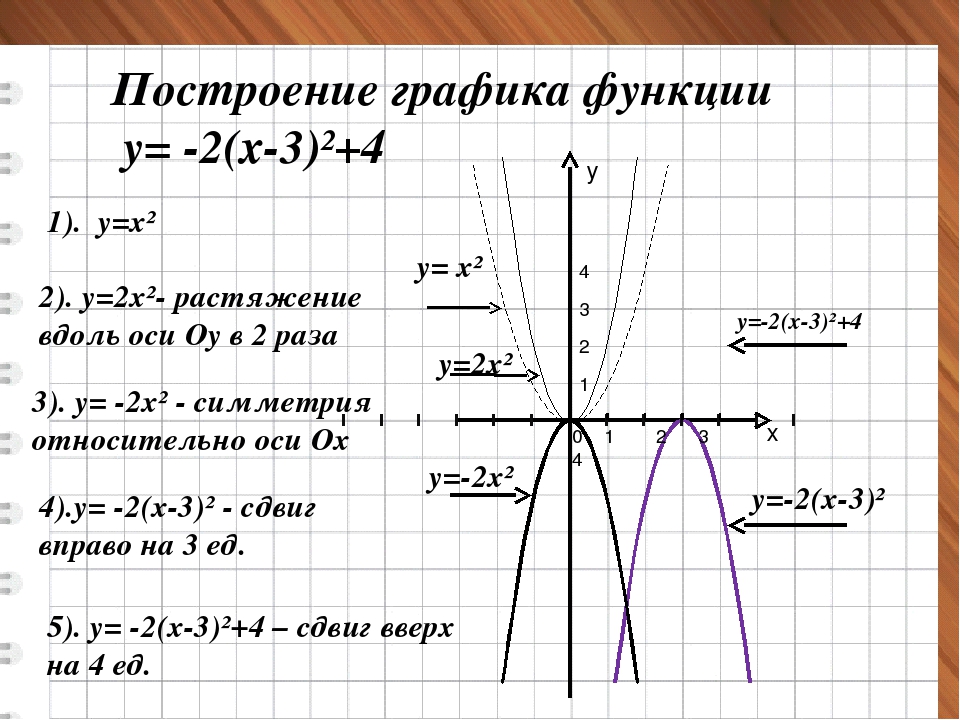 Абсциссы точек пересечения – это приближённые корни уравнения f₁(x) = f₂(x).
2) Необходимо подставить каждый приближённый корень в уравнение f₁(x) = f₂(x). Те корни, при которых получается верное равенство будут являться точными корнями уравнения f₁(x) = f₂(x).

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

График функции с модулем | Алгебра

Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.

Рассмотрим примеры таких заданий.

1) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

x-2=0, x=2.

Найдём значение функции при x=2.

y(2)=5·0-2²+5∙2-3∙0-6=0.

Получили точку (2;0).

2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.

Если x-2>0, то есть при x>2, |х-2|=x-2,

y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.

y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

Координаты вершины параболы

то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).

3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.

Если x-2<0, то есть при x<2, |х-2|=-(x-2),

y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.

y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.

Координаты вершины параболы

то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².

Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:

График функции с модулем можно рассматривать и как график кусочной функции:

Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:

Ответ: 0; 4.

2) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.

y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).

Координаты вершины параболы

Так как a=1, от вершины (3;-10) строим график y=x².

|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.

y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.

Координаты вершины параболы

от вершины (-3;-8) строим график y=x².

Или:

Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:

Ответ: -8; 1/36.

3) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x=0, y=|0|·0+3·|0|-5·0=0.

2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.

y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).

Координаты вершины параболы

От вершины (1;-1) строим параболу y=x² (так как a=1).

3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.

y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).

Координаты вершины параболы

От вершины (-4;16) строим параболу y=-x² (так как a=-1).

Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:

Альтернативный вариант:

Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:

Ответ: -1; 16.

4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

Область определения функции D(y): x∈R.

Построим график функции y=x²+2x-3.

Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.

Координаты вершины параболы

, то есть вершина параболы — точка (-1;-4).

От вершины строим график функции y=x²:

График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.

Или y=|x²+2x-3|

Вершина параболы (-1;-4) при этом переходит в точку (-1;4):

Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).

Ответ: 4.

Построить график функции у=-x²+2x+8 (парабола) – решение и ответ

Формулировка задания: Построить график функции у = -x² + 2x + 8.

Решение:

Для построения графика параболы нужно построить таблицу значений x и y.

Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:

x = 0 ⇒

y = -0² + 2 ⋅ 0 + 8 = 8

Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:

y = 0 ⇒

-x² + 2x + 8 = 0

a = -1, b = 2, c = 8

D = 2² – 4 ⋅ (-1) ⋅ 8 = 36

x₁ = (-2 + 6) / (-2) = -2

x₂ = (-2 – 6) / (-2) = 4

Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:

Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:

x = 1 ⇒

y = -1² + 2 ⋅ 1 + 8 = 9

x = -1

y = -(-1)² + 2 ⋅ (-1) + 8 = 5

Таблица значений теперь выглядит следующим образом:

Отметим полученные точки на координатной плоскости:

Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними. Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):

(4 – (-2)) / 2 = 6 / 2 = 3

x_в = -2 + 3 = 1

Точка с таким значением x уже есть в таблице значений. Осталось построить график:

Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Построение графиков уравнений, содержащих модули

Тип урока: Урок формирования новых знаний.

Цели урока:

Формировать умение строить графики уравнений содержащих модули.
Развитие логического мышления, познавательного интереса.
Развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.

Оборудование: мультимедиа проектор, доска.

Ход урока

I. Орг. момент.

II. Устный счет.

Вычислите. (слайд 1)
Решите уравнение. (слайд 2)

III.

Объяснение нового материала.

1. Построить график уравнения (слайд 3)

Решение. (слайд 4)

По определению модуля имеем:

Построим график уравнения: (слайд 5)

х=2у, если у≥0
х=0, если у<0
Получили график уравнения

2. Построить график уравнения .(слайд 6)

Решение. (слайд 7)

По определению модуля имеем:

Если у=0, то х – любое.

Выполним построение. (слайд 8)

х = 1, если у>0;
x = — 1, если у<0;

3. Построить график уравнения (слайд 9)

Решение. (слайд 10)

По определению модуля имеем:

При х≥0, у≥0, уравнение х+у=4;
При х≥0, у<0, уравнение х-у=4;
При х<0, у≥0, уравнение –х+у=4;
При х<0, у<0, уравнение –х-у=4.

(слайд 11)

Построить график уравнения (слайд 12)

Решение. (слайд 13)

По определению модуля имеем:

При х≥0, у≥0, уравнение х-у=4;
При х≥0, у<0, уравнение х+у=4;
При х<0, у≥0, уравнение –х-у=4;
При х<0, у<0, уравнение –х+у=4.

(слайд 14)

IV.

Закрепление. Решение задач.
Построить график уравнения. (слайд 15)
а) |x|+|y|=2;
б)|x|-|y|=3.
Проверка (слайд ) (слайд 16)
(слайд 17)
V. Итог урока.
Домашнее задание. (слайд 18)
Построить графики уравнений: а) |y|=1-|x|; б)|y|=|x|+3.
Расширение команды не всегда ведет к росту производительности
Когда появляется желание ускорить процесс разработки, первое, что приходит в голову – надо нанять больше людей. Допустим, в данный момент у нас над проектом работает один разработчик. Пусть теперь их станет двое.
Отлично. Если предположить, что после обучения навыки у нового разработчика будут примерно на том же уровне, что и у старого, то общая производительность должна практически удвоиться. Возможно, немного временных затрат придется заложить на обсуждение и все прочее, но тем не менее, объем кода, который будет выдаваться за единицу времени, определенно возрастет в существенной мере.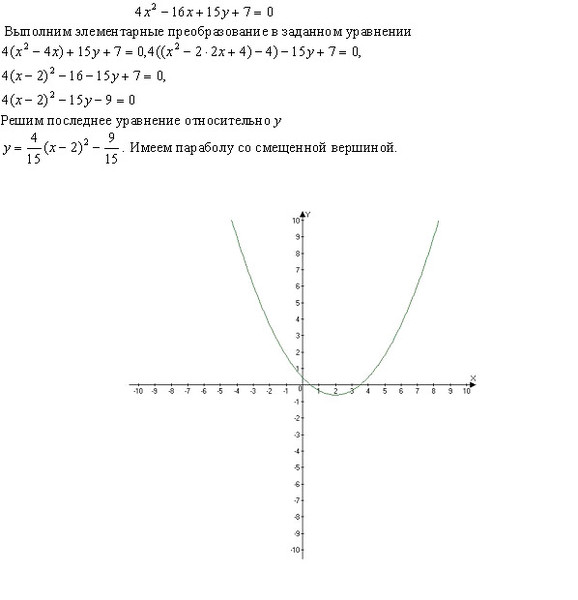
Если нас в первую очередь интересует качество, можно организовать сеансы парного программирования, что позволит усовершенствовать код. Тогда объем кода не возрастет в той же мере, но мы всё-таки получим выгоду от пополнения в команде в виде более качественного итогового продукта.

Само собой, придет момент, когда снова станет нужно развивать проект активнее, и нам автоматически придет в голову нанять еще сколько-то разработчиков. Ну ладно, давайте добавим одного или двоих.
С появлением третьего и четвёртого разработчиков мы по-прежнему наблюдаем прирост в производительности, однако в процентном отношении эффект уже не так велик, как было со вторым. Почему?
Как вы можете заметить, на рисунке сверху я соединил работников линиями со стрелками на обоих концах. Они обозначают всю коммуникацию, которая происходит при работе в команде. Каждое изменение в коде, каждое решение нужно обсудить, а потом держать коллег в курсе по ходу дела, чтобы никто не выпал из процесса.
Команда из четверых человек, в целом, пока еще представляет собой здоровую структуру – здесь кроется много возможностей для обмена знаниями и так далее. Если все участники вписываются в командную культуру, то в таком составе людям будет комфортнее работать, чем вдвоем.
Под давлением необходимости развивать проект очень легко попасть в ловушку и продолжать нанимать всё больше и больше сотрудников, чтобы распределить между ними работу. Давайте посмотрим, что будет, если добавить еще от одного до четверых разработчиков – размер команды, таким образом, будет составлять от пяти до восьми человек.
Как видите, чем больше сотрудников мы вводим, тем более сложной и разветвлённой становится система коммуникации. Всем нужно взаимодействовать со всеми.
В математическом выражении число направлений коммуникации возрастает по схеме, показанной на графике ниже.
2 человека = 1 x 2 = 2 связи 3 человека = 3 x 2 = 6 связей 4 человека = 6 x 2 = 12 связей 5 человек = 10 x 2 = 20 связей 6 человек = 15 x 2 = 30 связей 7 человек = 21 x 2 = 42 связей 8 человек = 28 x 2 = 56 связей
Издержки, связанные с коммуникацией, начинают тормозить процесс разработки.
Ресурс времени на написание кода сокращается, по мере того как возрастают временные затраты на собрания, обсуждения и планирование. Синхронизация обходится команде всё дороже и дороже.
Так как все работают на одном и том же проекте, люди всё чаще непредумышленно наступают друг другу на ноги.
При таком раскладе каждый дополнительно нанятый разработчик будет не повышать суммарную производительность, а служить помехой для неё.
Масштабирование не сводится к умножению числа разработчиков
Корень проблемы, к которой мы пришли в итоге вышесказанного, не в том, что мы нанимали разработчиков, а в том, что мы предварительно не выстроили структуру, способную выдержать возрастающее число людей.
Вместо того чтобы просто добавлять новых и новых сотрудников, нам следовало в первую очередь задуматься, не нужно ли для начала разбить структуру кода на модули и четко прописать для каждого модуля соответствующий набор обязанностей.
Давайте попробуем разбить наш крупный, единый, модулярный проект на два модуля и разделить разработчиков поровну между ними. Таким образом, каждому разработчику будет уже не нужно ни принимать участие в работе над чужим модулем, ни отслеживать процессы по нему – исключение составляет только особый представитель группы.
На графике ниже эта схема представлена яснее.
В математическом выражении мы свели число связей к гораздо меньшему значению: вместо 56 связей теперь насчитывается 26. Сокращение более чем в два раза!
(Группа1) + (Группа2) + (Коммуникация между группами) => 12 связей + 12 связей + 2 связи = 26 связей
Это дает нам много преимуществ:
Требуется меньше синхронизации – теперь всем не нужно быть в курсе всего. Значит, больше времени можно тратить на написание кода.
Объем информации, с которым приходится работать каждому из разработчиков, уменьшается, и это упрощает им жизнь.
Из-за разделения ответственности по модулям, снижается риск того, что кто-то вторгнется на чужую территорию.
Если вкратце
Масштабирование проектов по созданию ПО – это не только бесконечный наем сотрудников. Необходима более тщательная предварительная подготовка к расширению, в частности, создание подходящей для роста структуры команды. Соответственно, разделение на модули представляет собой крайне важную составляющую масштабирования. Хотя сама идея, конечно, не нова – она применяется даже при делении клетки у живых организмов.
Обзор и тестирование ноутбука Acer Predator Helios 300 Ph515-54 на базе процессора Core i7-11800H и видеокарты GeForce RTX 3070
В мае компания Intel презентовала производительные процессоры семейства Tiger Lake-h55. Увеличенный до 45 Вт тепловой пакет и 8 ядер Willow Cove обеспечивают максимум быстродействия для игровых ноутбуков нового поколения. И компания Acer уже предлагает ряд моделей с такими процессорами. В их числе обновленный лэптоп Acer Predator Helios 300, с которым мы познакомимся в данном обзоре.
Acer Predator Helios 300 Ph515-54
В семействе игровых «хищников» Acer ноутбуки Predator Helios 300 представляют сбалансированный класс. Это отличный вариант для тех, кому нужна производительность и практичность без дизайнерских изысков и каких-то уникальных атрибутов. При этом рассматриваемая версия Predator Helios 300 Ph515-54-73XF представляет топовый вариант в рамках своей серии. Это 8-ядерный Intel Core i7-11800H c частотой до 4,6 ГГц в Boost-режиме, большой объем памяти 32 ГБ и мощная игровая видеокарта NVIDIA GeForce RTX 3070. Установлено два быстрых SSD-накопителя NVMe M.2 Samsung 1 ТБ в режиме RAID 0 и жесткий диск на 2 ТБ в качестве дополнительного хранилища данных. Используется быстрый Full HD экран 144 Гц диагональю 15,6 дюймов. Все это упаковано в корпус габаритами 363 x 255 x 23 мм. Согласно измерениям в самой толстой части с учетом ножек высота 29 мм. Также ноутбук обладает широким набором портов, включая три USB 3.2, видеоинтерфейсы HDMI и DisplayPort. Есть полноценный Ethernet, который часто отсутствует в тонких ноутбуках.
Полные характеристики представлены в таблицах.
Модель ноутбука Acer Predator Helios 300 Ph515-54-73XF
Страница продукта Predator Helios 300
Процессор Intel Core i7-11800H 2,3 ГГц (до 4,6 ГГц в Boost-режиме)
Оперативная память 32 ГБ, DDR4-3200
Дисплей 15,6″, 1920×1080, 144 Гц, IPS (LG LP156WFG-SPF3)
Видеокарта NVIDIA GeForce RTX 3070 8 ГБ
Дисковая подсистема RAID 0 2x SSD NVMe M. 2 Samsung MZVL21T0HCLR-00B07 1ТБ
HDD SATA III WD20SPZX-21UA7TO 2 ТБ
Порты ввода/вывода 3x USB-A 3.2 Gen2 Type A, Thunderbolt 4 USB Type-C, HDMI 2.0, mini-DisplayPort 1.4, Ethernet, комбинированный аудиоразъем
Коммуникации Gigabit Ethernet (Killer 2600), Wi-Fi 6 802.11ax (Killer 1650i), Bluetooth 5.2
Мультимедиа Веб-камера 720p, стереодинамики, встроенный микрофон
Безопасность Замок Kensington
Аккумулятор, мА•ч 3720 – 3815
Адаптер питания, Вт 230
Размеры, мм 363 x 255 x 23
Масса, кг 2,3
Стоимость н/д
Acer Predator Helios 300 на базе Intel Core i7-11800H могут сочетаться с GeForce RTX 3060 и иметь другую конфигурацию накопителей.
Комплект поставки
Ноутбук поставляется в черной картонной коробке.
Внутри он уложен в дополнительную жесткую коробку. Комплектуется блоком питания и двумя кабелями под разный тип розеток.
Источник питания Chicony A17-230P1A рассчитан на нагрузку в 230 Вт.
Внешний вид
Ноутбук выполнен в стандартном дизайне и не отличается от прошлого поколения Acer Predator Helios 300. Это сочетание строгих форм и агрессивных очертаний задней части. С учетом выпирающих элементов полные габариты 363 x 260 x 23 мм при весе 2,3 кг.
Ноутбук выполнен в черно-синих тонах. Производитель называет это цветовое исполнение Abyssal Black. Внешние панели из металла, дно из пластика. Поверхность гладкая, не сильно маркая, но отпечатки видны.
На крышке есть стилизованный логотип Predator с подсвечиваемыми контурами. Боковые декоративные полосы подсветки не имеют.
На дне сделаны отверстия для притока воздуха. Основные отверстия расположены над вентиляторами. Резиновые ножки обеспечивают надежную фиксацию на поверхности и немного приподнимают корпус для доступа воздуха.
Система охлаждения предусматривает выдув горячего воздуха в задней части и по бокам. С левой стороны корпуса расположено два порта USB 3.2 Type A, LAN и комбинированный аудиоразъем 3,5 мм.
С правой стороны расположены порты Thunderbolt 4, USB 3.2 с функцией зарядки, HDMI 2.0 и mini-DisplayPort 1.4.
Экран с двумя угловыми шарнирами откидывается на широкий угол.
В верхней части крышки над экраном расположена веб-камера и несколько микрофонов.
Рабочая поверхность выполнена в одной цветовой гамме с внешним корпусом. Клавиши с белой окантовкой приятно разбавляют строгий дизайн.
Клавиатура островного типа. Есть цифровой блок.
Кнопка включения расположена в общем ряду клавиш. С непривычки возможны случайные нажатия. В цифровом блоке расположена кнопка быстрого вызовы программы PredatorSense.
Кнопки WASD и стрелки имеют более крупную окантовку голубого цвета. Благодаря визуальному и тактильному выделению пользователю легче ориентироваться при быстром нажатии клавиш. Это один из элементов удобства для геймеров.
В левом углу расположена дополнительная кнопка Turbo для активации ускоренного режима с максимальным охлаждением. Также стоит отметить наличие небольшой перфорации корпуса над клавиатурой для дополнительного притока воздуха.
Клавиатура имеет 4-зональную RGB-подсветку. По умолчанию клавиши светятся голубым цветом, что отлично сочетается с темным корпусом. Есть эффекты поэтапной активации зон подсветки при включении и выключении. Доступна быстрая регулировка яркости с кнопок на клавиатуре.
Тачпад с кнопками выполнен в виде единой панели с серебристой окантовкой.
Экран
У Acer Predator Helios 300 матовый экран диагональю 15,6 дюймов с антибликовым покрытием.
Используется IPS-матрица LG LP156WFG-SPF3 разрешением 1920×1080, частота обновления 144 Гц.
Согласно измерениям охват цветового пространства sRGB 92 % и Adobe RGB 65 %. Цветовая температура близка к 7100К-7200K, гамма немного сдвинута в сторону холодных тонов.
Яркость регулируется в диапазоне от 25 кд/м² до 361 кд/м². Коэффициент контрастности стабилен на уровне 720:1.
Экран показывает высокую точность цветопередачи с низким отклонением. Средний коэффициент отклонения DeltaE на уровне 2 единиц, максимальное отклонение 5 единиц.
У матрицы хорошие, но не выдающиеся для топового сегмента характеристики. Экран обеспечивает качественную цветопередачу и широкие углы обзора. Частота обновления в 144 Гц позволяет достичь комфортной плавности в динамичных играх. Это оптимальное сочетание характеристик для игрока. На рынке есть лэптопы с более быстрой матрицей и с лучшими параметрами контраста, но они относятся к более дорогим моделям.
Внутреннее устройство
Разберем ноутбук. Нижняя часть корпуса имеет много опорных точек, чтобы избежать деформации. Центральные отверстия закрыты дополнительной решеткой. Предусмотрены радиаторы для накопителей NVMe M.2, контакт осуществляется через термопрокладки.
Внутренняя компоновка стандартная, общая конструкция не изменилась со времен Acer Predator Helios 300 Ph515-52. Основной объем занимает плата и охлаждающая система с двумя «турбинами».
Нижнее пространство делят аккумулятор и жесткий диск.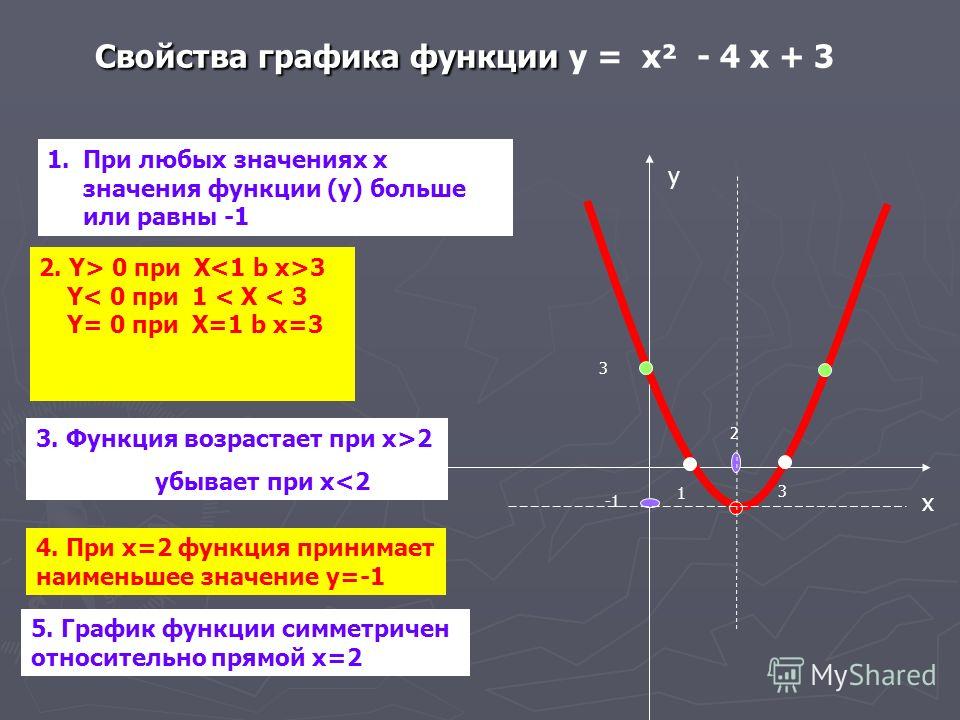 Это вынудило производителя немного сэкономить на батарее и установить аккумулятор на 58,7 Вт·ч.
Система охлаждения использует три тепловые трубки, одна из которых общая для процессора и видеокарты. Солидно выглядят пластины, которые накрывают чипы, силовые элементы и память — это толстые радиаторы с дополнительными ребрами.
Используются специальные вентиляторы AeroBlade 3D с тонкими лопастями особой формы, с зазубринами на краях и стабилизационным кольцом. Вентилятор охлаждающего блока видеокарты имеет все особенности данного дизайн, а вентилятор процессорного блока чуть проще.
В два слота памяти установлены планки DDR4-3200 от Samsung.
Установлены два накопителя NVMe M.2. Samsung MZVL21T0HCLR-00B07 объемом 1 ТБ. Они работают в режиме RAID 0 для повышения производительности.
В качестве дополнительного хранилища данных задействован жесткий диск Western Digital WD20SPZX-21UA7TO объемом 2 ТБ.
Игровой статус ноутбука подчеркивается применением специализированных сетевых контроллеров Killer. Работу беспроводных интерфейсов Wi-Fi 6 802.11ax и Bluetooth 5.2 обеспечивает Killer 1650i (Intel AX210NGW), а Gigabit Ethernet реализован на базе Killer 2600.
В нижних углах корпуса привычно расположены звуковые динамики. Поддерживаются эффекты объемного звучания DTS: X Ultra.
Полные характеристики ноутбука представлены на скриншоте утилиты HWiNFO.
Процессор Intel Core i7-11800H является младшей моделью в линейке 8-ядерных мобильных CPU нового поколения с TDP 45 Вт. Он выполнен по технологии 10 нм SuperFin и насчитывает 8 ядер на архитектуре Willow Cove, которые обрабатывают 16 потоков данных. Кэш-память L3 увеличена до 24 МБ. Максимальная частота в Boost-режиме может достигать 4,6 ГГц. 32 ГБ памяти DDR4-3200 работают в двухканальном режиме с задержками 22-22-22-52-1T.
Процессор имеет встроенное графическое ядро Intel UHD, которое задействовано в простых задачах. В 3D-режиме ноутбук переключается на игровую видеокарту NVIDIA GeForce RTX 3070. Ее графический чип по активным блокам идентичен десктопным GeForce RTX 3070, но порезан по частотам. По характеристикам видеокарта близка к сверхэкономичной версии RTX 3070 — базовая частота GPU 780 МГц при среднем Boost Clock 1290 МГц, память GDDR6 работает на частоте 12000 МГц, но заявлен высокий TGP 110 Вт. Используется 8 линий PCI-E 4.0. Подробнее о разных версиях мобильных видеокарт NVIDIA в этой заметке.
Видеокарта GeForce RTX 3070 поддерживает все преимущества архитектуры NVIDIA Ampere с аппаратным ускорением трассировки лучей и режимом NVIDIA DLSS. В ноутбуке уже активна технология Resizable BAR, которая позволяет процессору обращаться ко всей видеопамяти. В некоторых играх это обеспечит небольшое повышение производительности.
Программное обеспечение
Ключевой программой для пользователя является Acer PredatorSense. Она предоставляет функции мониторинга температуры, загрузки и прочих параметров. Есть переключение рабочих режимов, где вместо стандартного «По умолчанию» можно выбрать тихий режим, экстремальный и «Турбо». Последние два предполагают некоторое ускорение за счет повышения лимитов мощности, но основное их преимущество в лучшем охлаждении, что повышает стабильность на высоких частотах.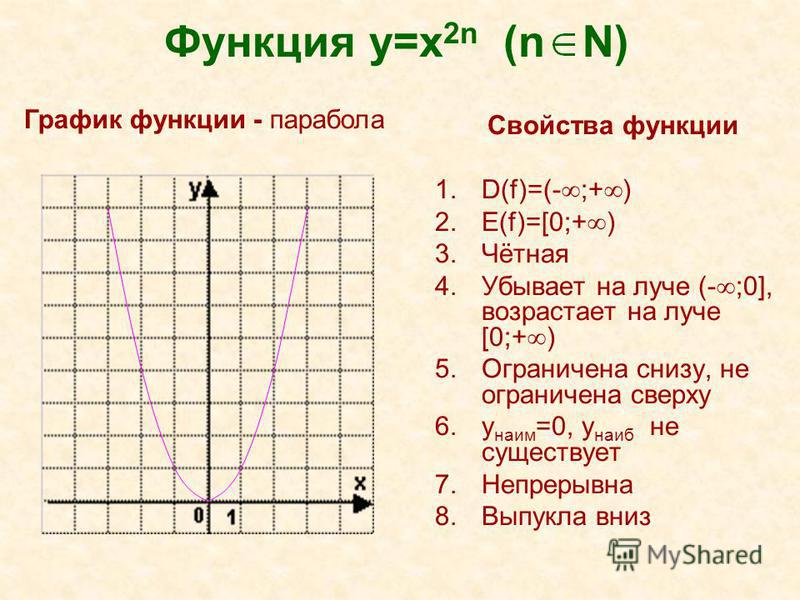 Turbo-режим переключает вентиляторы на 100%, он же активируется кнопкой с клавиатуры.
Есть отдельные настройки управления скоростью вентиляторов, где можно раздельно указывать фиксированную скорость каждого вентилятора. Полезная функция в случае эксплуатации в жестких температурных условиях и при разгоне.
На отдельной вкладке есть настройки подсветки отдельно по четырем зонам.
Acer PredatorSense позволяет сохранять любые настройки в профили для конкретного приложения игры. Вы можете назначить ускоренный режим и индивидуальный режим подсветки только под нужные игры.
Дополнительно пользователи Acer Predator Helios 300 получают видеоредактор Power Director 14 и графический редактор Photo Director.
Установлена пробная 30-дневная версия Express VPN и Norton Security Ultra.
Для гибкой настройки звука и звуковых эффектов используются приложения X Ultra и DTS Sound Unbound.
Эффективность системы охлаждения и уровень шума
Теперь поговорим о температурном режиме. Ноутбук тестировался в помещении с температурой 25-26 °С.
Для воссоздания длительной игровой нагрузки запускался зацикленный стресс-тест 3DMark Time Spy Extreme.
По итогам 20-минутного прогрева средняя температура ядер CPU была ниже 70 °С, хотя пиковые значения могли превышать 80 °С. Частота ядер уверенно держалась на уровне 4,4 ГГц, что близко к максимуму. GPU нагрелся до 71 °С при рабочем диапазоне Boost 1200-1250 МГц. Показания самой горячей точки кристалла GPU Hotspot выше примерно на 10 °С. Скорость вентиляторов достигла 4000-4700 об/мин.
Оценим возможности охлаждения при экстремальной нагрузке в стрессс-тесте AIDA64, который одновременно нагружал процессор, графику и память.
Вначале процессор стартует с высоких частот, достигая пиковых температур в 94-95 °С. Постепенно частоты снижаются до 2,8-3 ГГц при рабочих температурах около 80 °С. Графический процессор прогревается до 71 °С. Скорость вентиляторов 4000-4700 об/мин.
Нагрев корпуса ощущается в центральной части.
Производитель уделил особое внимание охлаждению видеокарты и это обеспечило скромный нагрев в 71 °С. Рабочие температуры процессора ниже того, что мы привыкли видеть в прошлом поколении мобильных Сore. Уровень шума стандартный.
Разгон видеокарты GeForce RTX 3070
Хорошее охлаждение и невысокие рабочие частоты наводят на мысли о разгоне видеокарты. Для обеспечения максимальной производительности и максимального охлаждения мы включили режим Turbo, а далее подбирали рабочую конфигурацию частот.
В нашем случае удалось повысить частоту GPU на 170 МГц, достигнув базового значения 950 МГц при Boost Clock 1460 МГц. Память стабильно работала на частотах до 13100 МГц.
Реальный Boost в играх возрос до 1400-1500 МГц. Температура не превысила 69 °С при максимальной скорости вентиляторов. Но при 5100-5700 об/мин шум безусловно высокий. Для практического применения нужно подбирать меньшие частоты и вручную выбирать оптимальный режим вентиляторов. Но общий потенциал для разгона радует. Мы получили хорошее ускорение относительно начальных частот, что должно обеспечить серьезный рост быстродействия в играх.
Результаты тестирования
Общая производительность
PCMark 8
В старом PCMark ноутбук показывает высокие результаты во всех тестах.
PCMark 10
На графике приведен общий результат расширенного теста и результаты отдельных групп тестов в составе этого бенчмарка.
Интересно сравнить показатели с системой на процессоре Intel Core i7-10870H (MSI GE66 Raider 10UG). Новый процессор оказывается быстрее во всех специализированных тестах.
CPU-Z Benchmark
Общий результат Core i7-11800H на 20% выше показателей Core i7-10870H.
Cinebench
Более 30% выигрывает новый процессор у предшественника в старой версии Cinebench и 13% в новой версии. Также можно констатировать небольшое преимущество Intel Core i7-10870H над процессором Ryzen 7 5800H (Acer Nitro 5 AN515-45).
Geekbench 5
Многопоточный результат Intel Core i7-10870H на 29% выше результата Intel Core i7-10870H и на 15% выше показателей AMD Ryzen 9 5900HX (ASUS ROG Strix Scar 15 G533).
x264 HD Benchmark
С обработкой видео в Full HD новый процессор Core i7-11800H справился на 28% быстрее Core i7-10870H, в 4K разница 10%. И эти результаты лишь немного ниже уровня AMD Ryzen 7 5800H.
Дисковая подсистема
В системе установлено два NVMe-накопителя Samsung MZVL21T0HCLR из серии PM9A1, которая является аналогом топовых накопителей Samsung 980 PRO. Два быстрых SSD с интерфейсом PCI Express 4.0 в RAID 0 обеспечивают рекордные показатели чтения/записи во всех специализированных тестах.
Итоговый результат в тесте накопителя PCMark 10 достиг 2731 баллов, что очень много.
Для наглядности мы приводим также результаты жесткого диска WD20SPZX в CrystalDiskMark. Его быстродействие стандартно для таких устройств, но и требования к нему ниже, поскольку диск используется в качестве дополнительного хранилища данных.
Игровые приложения
Тестирование в играх проведено в стандартном режиме и с разогнанной видеокартой GeForce RTX 3070.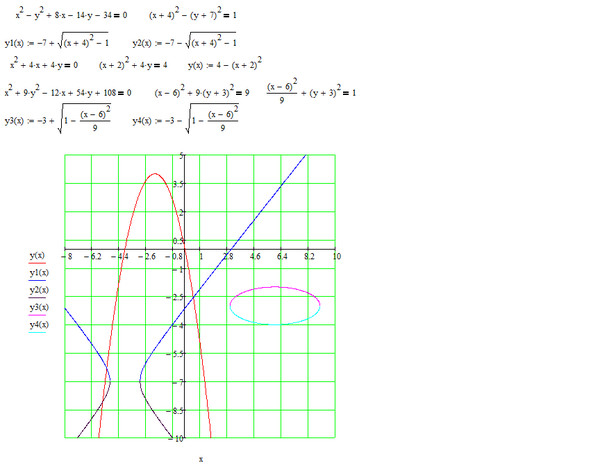
На графиках указаны следующие параметры: 1% low, минимальный fps, средний fps.
3DMark
Вначале приведены результаты в тесте Time Spy при стандартных частотах, потом в разгоне.
Общие показатели соответствуют невысоким частотам энергоэффективной версии GeForce RTX 3070. GPU Score на 21% ниже результата GeForce RTX 3070 в ноутбуке MSI GE66 Raider 10UG. Разгон добавляет к результату 11%.
В тесте с трассировкой ускорение от разгона менее 4%.
Assassin’s Creed Valhalla
В Valhalla ноутбук обеспечивает 60 кадров в Ultra-режиме. Разгон ускоряет на 8%.
Control
Максимальные настройки графики с трассировкой среднего уровня.
Acer Predator Helios 300 снова выдает около 60 кадров. Разгон повышает производительность на 12%.
Crysis Remastered
Вместо бенчмарка повторялась определенная последовательность действий на первой локации, после рассвета.
В реальной игре ноутбук не выдает стабильные 50 кадров даже с активной технологией DLSS. Разгон минимально сказывается на результатах. Небольшое снижение настроек позволит частично исправить ситуацию.
Cyberpunk 2077
В обычном режиме в городской сцене вы получите до 50 кадров, что весьма неплохо.
Трассировка высокого уровня и DLSS позволяют достичь 40 кадров, что маловато для комфортного игрового процесса. Поскольку трассировка среднего уровня не дает красивые отражения, оптимальным решением будет использовать обычную графику без Ray Tracing. Повышение частот видеокарты GeForce RTX 3070 позволяет поднять производительность на 6-12%.
Ghostrunner
Технология DLSS позволяет комфортно играть с эффектами на базе трассировки. Разгон дает неожиданно большое ускорение в 15% и выше.
Horizon Zero Dawn
Acer Predator Helios 300 легко обеспечивает комфортную производительность в стандартном рабочем режиме.
Mafia: Definitive Edition
В этой игре тоже все отлично, и даже без разгона производительность около 80 кадров.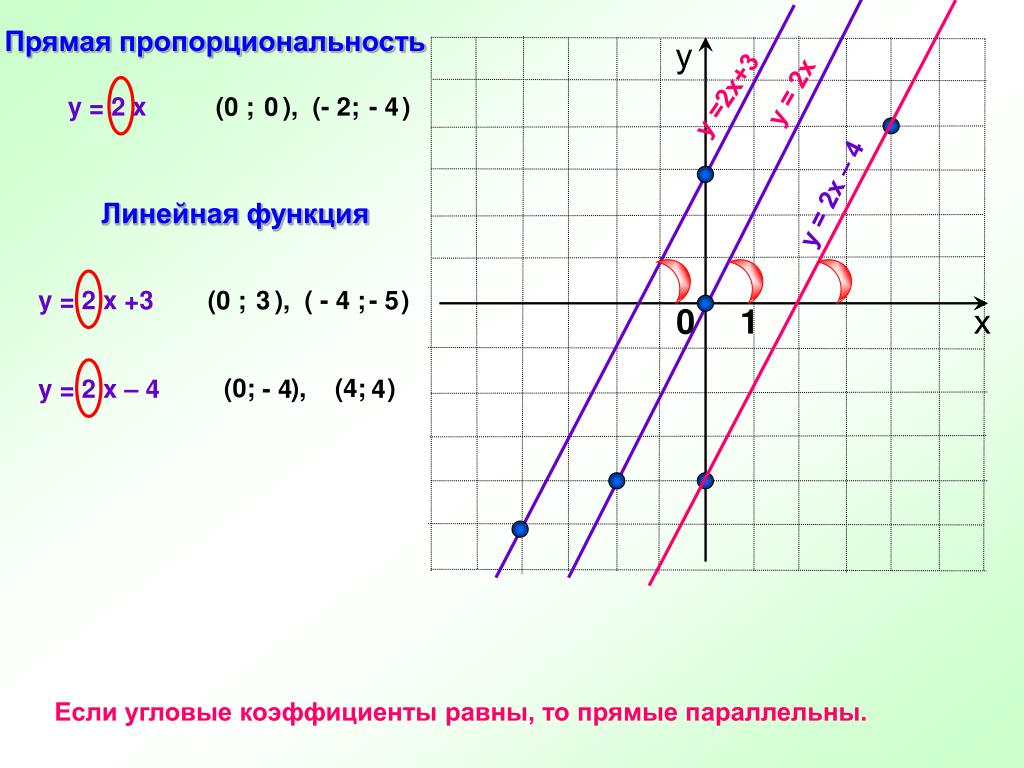
Red Dead Redemption 2
Последняя сцена встроенного бенчмарка. Стандартный профиль Ultra-качества без дополнительной коррекции второстепенных параметров.
В нативном разрешении Full HD ноутбук выдает до 60 кадров, разгон ускоряет на 7%. Недавнее обновление добавило в игру технологию DLSS, что позволит дополнительно поднять производительность и избавит от просадок в тяжелых сценах.
Resident Evil: Village
Максимальное качество всех параметров при трассировке лучей высокого уровня. Тестирование проводилось во время первой прогулки по деревне.
Acer уверенно выдает более 60 кадров в тяжелой сцене, обеспечивая еще больший fps в закрытых локациях. Разгон повышает результаты на 14%.
The Outer Worlds
Высокая производительность даже без разгона.
The Medium
Тестовая сцена — прибытие в дом отдыха «Нива», прогулка по сторожке и окрестностям. Тяжелый момент, сопоставимый по нагрузке со сценами двойной реальности.
Крайне требовательная игра, где даже 50 кадров — отличный результат.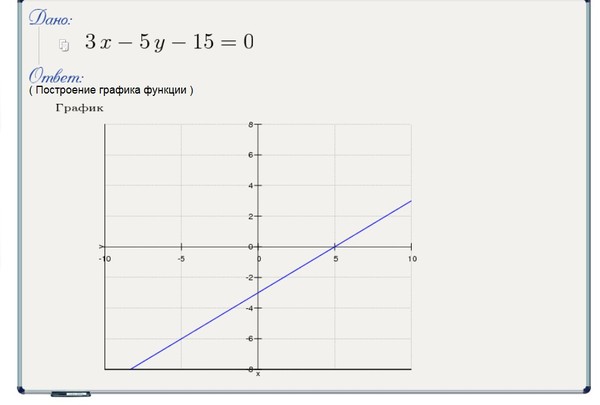 На такую производительность в тяжелых сценах можно рассчитывать при активных эффектах трассировки с DLSS высокого качества.
The Witcher 3: Wild Hunt
Вы сможете наслаждаться «Ведьмаком» с максимальными настройками графики. В тестовой сцене ноутбук легко выдает 80 кадров, разгон ускоряет на 12%.
Tom Clancy’s The Division 2
Средний результат около 80 кадров при Ultra-графике.
Watch Dogs: Legion
При обычном Ultra-качестве в Watch Dogs ноутбук выдает до 55 кадров, разгон дает небольшое ускорение менее 5%.
Трассировка лучей дается с большими потерями. Активации сбалансированного режима DLSS позволяет выйти на среднюю производительность в 50 кадров
Время автономной работы
Чтобы проверить время работы от аккумулятора, мы провели испытания с помощью специализированного набора тестов PCMark 10 Modern Office, которые симулируют комбинированную офисную нагрузку. Яркость экрана зафиксирована на 120 кд/м² (20% от максимума) для сравнения показателей с другими ноутбуками.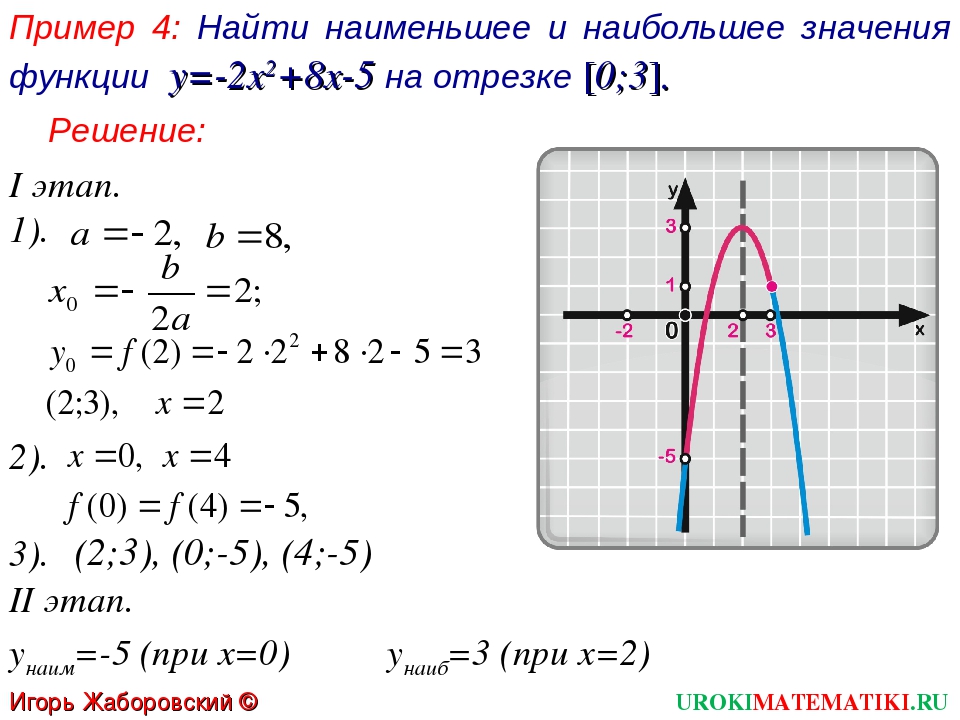
В таких условиях Acer отработал менее 4 часов. Повышение яркости экрана и более серьезная нагрузка могут серьезно уменьшить это время. При игровой нагрузке ноутбук выдержит около часа с пониженной производительности в условиях отсутствия внешнего питания.
Выводы
Acer Predator Helios 300 Ph515-54 — это производительный современный ноутбук для игр. Он построен на новом процессоре Intel Core i7-11800H, который в специализированных тестах на 10-30% быстрее Intel Core i7-10870H из прошлого поколения при сопоставимых результатах с 8-ядерными AMD Ryzen. Большой объем оперативной памяти в 32 ГБ обеспечит комфортную работу самых требовательных приложений. А RAID 0 из двух быстрых накопителей NVMe превращают систему в «ракету» при работе с большими объемами данных. Наличие предустановленных редакторов для видео и фото намекает, что такой ноутбук отлично подойдет для работы с таким контентом. Дополнительный жесткий диск позволяет хранить большие объемы данных. И в рамках мобильного сегмента Acer Predator Helios 300 может стать оптимальным выбором для пользователя, который кроме игр заинтересован в работе с видеоконтентом и какими-то профессиональными приложениями. Экран обладает хорошей цветопередачей и частотой 144 Гц, хотя в сегменте топовых игровых ноутбуков есть и более качественные матрицы. Неоднозначные впечатления вызывает видеокарта GeForce RTX 3070, поскольку используется экономичная версия с низкими рабочими частотами. Но при помощи разгона можно поднять ее производительность на 10-15%, что является отличным ускорением для мобильного устройства. И даже такая версия GeForce RTX 3070 в большинстве игр она легко справляется с родным разрешением Full HD. Ноутбук использует качественную систему охлаждения с тремя тепловыми трубками и большими теплосъемными пластинами, что обеспечивает невысокие рабочие температуры видеокарты. Предусмотрены радиаторы для накопителей NVMe. Шум высоковат, но тихих игровых ноутбуков не бывает. Опытный пользователь может настроить рабочие параметры и скорость вентиляторов под свои предпочтения с помощью программы Acer PredatorSense. Также стоит отметить большой набор портов и наличие Ethernet, от которого начинают избавляться в тонких лэптопах. У Acer Predator Helios 300 небольшое время автономной работы, что для игрового ноутбука не критично, поскольку это замена домашнего ПК. И по совокупности характеристик Acer Predator Helios 300 станет хорошим мощным ноутбуком при условии умеренной стоимости.
2 + k , где (h, k) = вершина и ось симметрии x = h .
Уравнение y = (x — 7) (x + 3).
Записываем уравнение в виде y = x ² — 4x — 21.
Вышеприведенное уравнение представляет собой параболу.
Запишите уравнение в стандартной форме уравнения параболы.
Чтобы преобразовать выражение [x ² — 4x — 21] в трехчлен полного квадрата , сложите и вычтите (половина коэффициента x ) ²
Здесь x коэффициент = — 4.2 + k , где (h, k) = вершина и ось симметрии x = h .
Вершина (h, k) = (2, — 25) и ось симметрии x = 2.
Составьте таблицу значений, чтобы найти упорядоченные пары, удовлетворяющие уравнению.
Выберите значения для x и найдите соответствующие значения для y .
х
y = (x — 2) ²-25
(х, у)
— 4 y = (- 4-2) ²-25 = (- 6) ²-25 = 36-25 = 11 (- 4, 11)
— 3
y = (- 3 — 2) ² — 25 = (- 5) ² — 25 = 25 — 25 = 0
(- 3, 0)
— 2
y = (- 2 — 2) ² — 25 = (- 4) ² — 25 = 16 — 25 = — 9
(- 2, — 9)
— 1
y = (- 1-2) ²-25 = (- 3) ²-25 = 9-25 = — 16
(- 1, — 16)
0
y = (0 — 2) ² — 25 = (- 2) ² — 25 = 4 — 25 = — 21
(0, — 21)
2
y = (2 — 2) ² — 25 = (0) ² — 25 = — 25
(2, — 25)
4 y = (4-2) ²-25 = (2) ²-25 = 4-25 = — 21 (4, — 21)
6 y = (6-2) ²-25 = (4) ²-25 = 16-25 = — 9 (6, — 9)
8 y = (8-2) ²-25 = (6) ²-25 = 36-25 = 11 (8, 11)
Графические уравнения, система уравнений с программой «Пошаговое решение математических задач»
Описание
Команда plot генерирует график практически любой функции или отношения, обнаруживаемого в математике средней школы и колледжа. Он будет отображать функции, заданные в форме y = f (x), например y = x ² или y = 3x + 1, а также отношения вида f (x, y) = g (x, y) , например x ² + y ² = 4.
Чтобы использовать команду построения графика, просто перейдите к основному
страницу графика, введите свое уравнение (в терминах x и y), введите набор
значения x и y, для которых должен быть построен график, и нажмите «График»
кнопка. Ваше уравнение будет автоматически построено, и будет показан ответ.
в вашем браузере в течение нескольких секунд.2 = 1 от x = -2 до x = 2, y = -1,8 до y = 1,8
Параметры (только расширенная страница)
Деления
Значения: отмечено или не отмечено
По умолчанию: отмечено
Если установлен флажок «Отметки», на осях графика будут отображаться отметки и числовые шкалы.
Линии сетки
Значения: установлен или не установлен
По умолчанию: не установлен
Если установлен флажок Линии сетки, на график будет наложена синяя сетка.
Оси
Значения: Нет или Автоматическая исходная точка или Исходная точка в (#, #)
По умолчанию: Автоматическая исходная точка
Параметр «Оси» управляет внешним видом и расположением осей на графике. Если отмечено «Нет», оси не будут отображаться вообще. Когда установлен флажок «Автоматическое начало координат», будут отображаться оси. Две оси обычно пересекаются в точке (0,0), но иногда эта точка пересечения может быть расположена в другом месте. Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке.
Соотношение сторон
Значения: Один к одному или Золотое сечение или #: #
По умолчанию: Один к одному
Параметр Соотношение сторон управляет отношением высоты графика к его ширине. Когда установлен флажок «Один к одному», соотношение составляет 1: 1, и масштабы на двух осях будут идентичными. Это гарантирует, что круги, например, действительно будут отображаться на экране круглыми.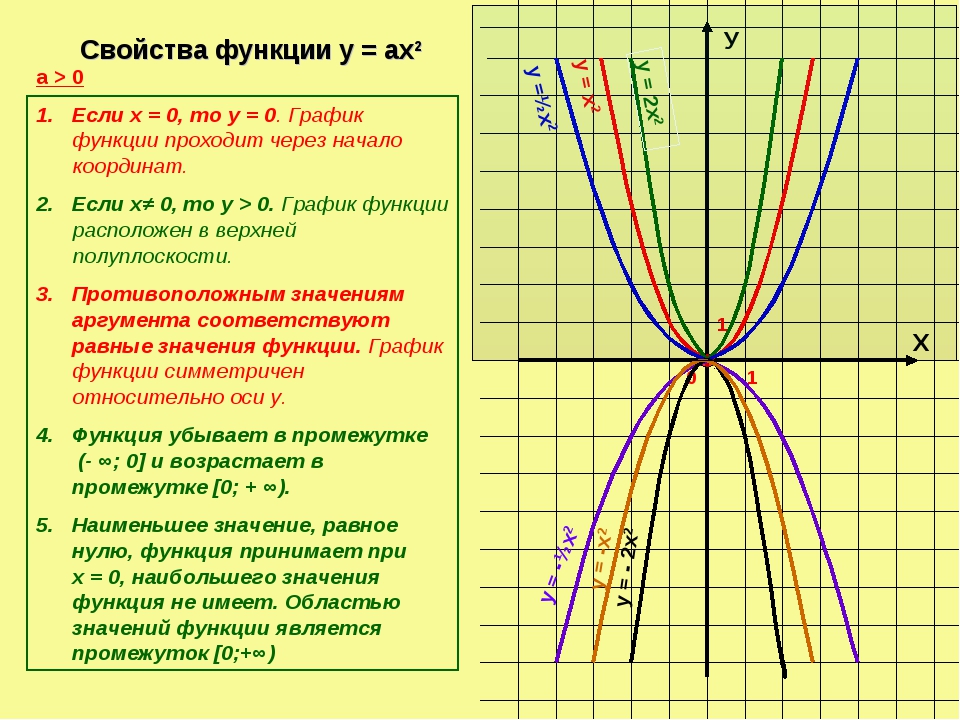 Когда выбрано золотое сечение, соотношение сторон составляет 1: 1 / г, где g — золотое сечение (приблизительно 1.6180). Это якобы дает соотношение высоты к ширине, которое особенно «приятно» для глаз. Когда выбрано #: # и введены два значения, будет применяться указанное соотношение сторон. Это полезно, если сюжет сильно сжат в одном или другом направлении и его нужно «растянуть», чтобы сделать его более четким.
Решение линейно-квадратичных систем
Вы, наверное, решили системы линейных уравнений. Но как насчет системы двух уравнений, в которой одно уравнение является линейным, а другое — квадратичным?
Мы можем использовать вариант метода подстановки для решения систем этого типа.
Помните, что уравнение прямой имеет вид y = mx + b, а стандартная форма уравнения параболы с вертикальной осью симметрии — y = ax2 + bx + c, a ≠ 0.
Чтобы избежать путаницы с переменными, запишем линейное уравнение в виде y = mx + d, где m
наклон и d
является точкой пересечения оси Y линии.
Подставляем выражение для y
из линейного уравнения в квадратное уравнение. То есть подставляем mx + d
для тебя
в y = ax2 + bx + c
.
мх + д = ах2 + Ьх + с
Теперь перепишите новое квадратное уравнение в стандартной форме.
Вычесть
mx + d
с обеих сторон.
(mx + d) — (mx + d) = (ax2 + bx + c) — (mx + d) 0 = ax2 + (b − m) x + (c − d)
.
Теперь у нас есть квадратное уравнение с одной переменной, решение которого можно найти с помощью формулы корней квадратного уравнения.
Решения уравнения ax2 + (b − m) x + (c − d) = 0
даст x-координаты точек пересечения графиков прямой и параболы.Соответствующие координаты y могут быть найдены с помощью линейного уравнения.
Другой способ решения системы — построить график двух функций на одной и той же координатной плоскости и определить точки пересечения.
Пример 1:
Найдите точки пересечения прямой y = 2x + 1
и парабола y = x2−2.
Замена 2x + 1
для y в y = x2−2.
2x + 1 = x2−2
Запишите квадратное уравнение в стандартной форме.
2x + 1−2x − 1 = x2−2−2x − 10 = x2−2x − 3
Используйте формулу корней квадратного уравнения, чтобы найти корни квадратного уравнения.
Здесь a = 1, b = −2, c = −3.
x = — (- 2) ± (−2) 2-4 (1) (- 3) 2 (1) = 2 ± 4 + 122 = 2 ± 42 = 3, −1
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
x = 3⇒y = 2 (3) +1 = 7x = −1⇒y = 2 (−1) +1 = −1
Следовательно, точки пересечения равны (3,7)
и (−1, −1).
Постройте параболу и прямую линию на координатной плоскости.
Аналогичный метод можно использовать для поиска точек пересечения прямой и окружности.
Пример 2:
Найдите точки пересечения прямой y = −3x
и окружность x2 + y2 = 3.
Заменитель −3x
для тебя
в x2 + y2 = 3
.
x2 + (- 3x) 2 = 3
Упростить.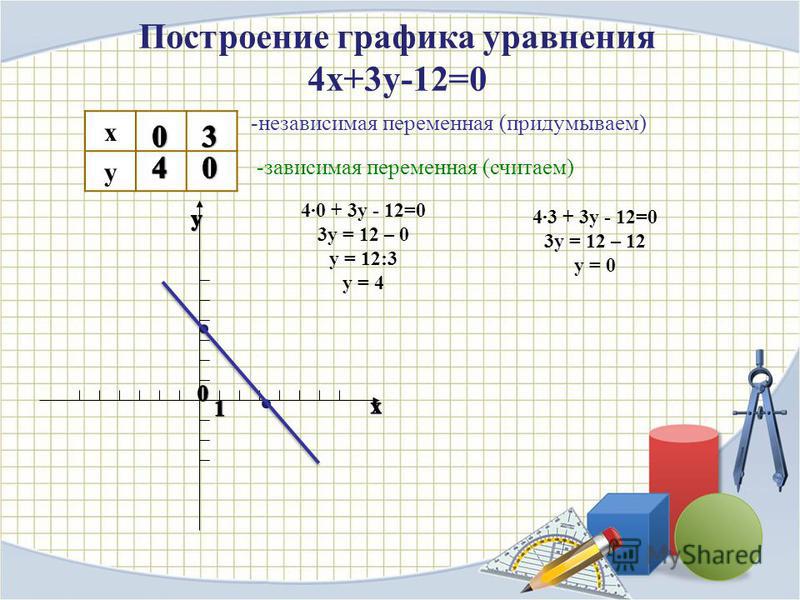
x2 + 9×2 = 310×2 = 3×2 = 310
Извлечение квадратного корня, x = ± 310.
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
x = 310⇒y = −3 (310) = −3310x = −310⇒y = −3 (−310) = 3310
Следовательно, точки пересечения (310, −3310)
и (-310, 3310).
Постройте окружность и прямую линию на координатной плоскости.
… или линия и эллипс.
Пример 3:
Решите систему уравнений y = −5
и x29 + y24 = 1.
Заменитель −5
для тебя
в −5.
x29 + (- 5) 24 = 1
Упростить.
x29 + (- 5) 24 = 14×236 + 9 (25) 36 = 14×2 + 225 = 364×2 = −189×2 = −1894
Здесь у нас есть отрицательное число как квадрат числа. Итак, два уравнения не имеют реальных решений.
Постройте эллипс и прямую линию на координатной плоскости.
Мы видим, что они не пересекаются.
преобразований квадратичных функций | Колледж алгебры
Результаты обучения
График вертикальных и горизонтальных сдвигов квадратичных функций
График вертикального сжатия и растяжения квадратичных функций
Напишите уравнение преобразованной квадратичной функции, используя форму вершин
Определить вершину и ось симметрии для данной квадратичной функции в форме вершины
Стандартная форма квадратичной функции представляет функцию в форме
[латекс] f \ left (x \ right) = a {\ left (x-h \ right)} ^ {2} + k [/ latex]
где [латекс] \ left (h, \ text {} k \ right) [/ latex] — вершина.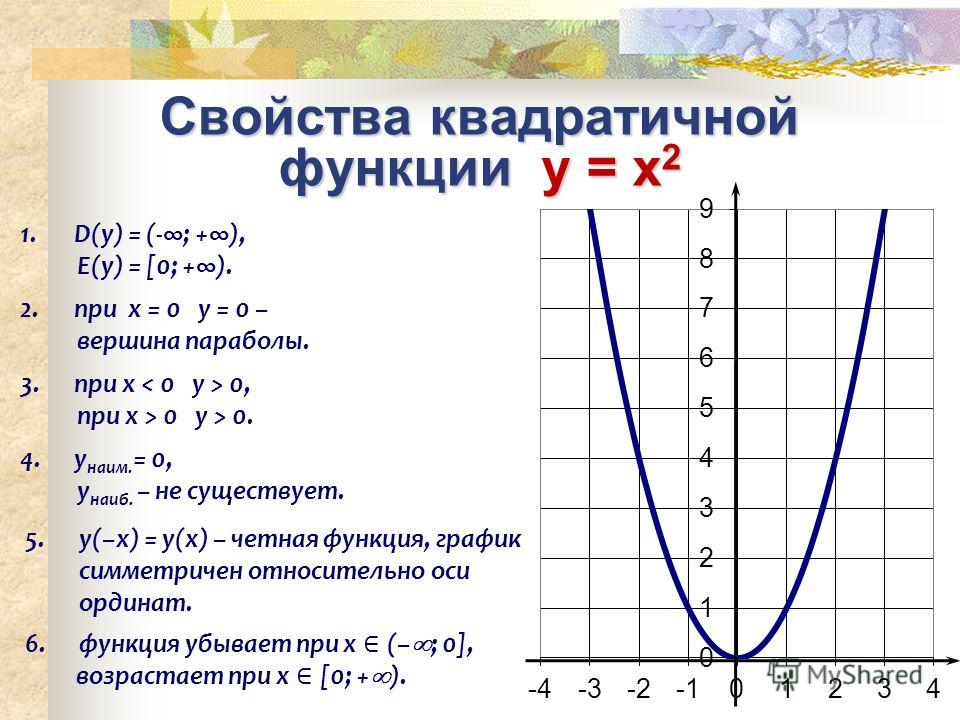 2 [/ латекс]
Величина [латекс] а [/ латекс] указывает на растяжение графика. Если [latex] | a |> 1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается дальше от оси [latex] x [/ latex] –, поэтому график кажется, становится уже, и появляется вертикальная растяжка. Но если [latex] | a | –, поэтому график кажется шире, но на самом деле есть вертикальное сжатие.{2}} {4a} \ end {align} [/ latex]
На практике, однако, обычно легче запомнить, что [latex] h [/ latex] является выходным значением функции, когда входным значением является [latex] h [/ latex], поэтому [latex] f \ left (h \ right) = f \ left (- \ dfrac {b} {2a} \ right) = k [/ latex].
Попробуй
Сетка координат наложена на квадратную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение пути мяча. Стрелок забивает корзину?
(кредит: модификация работы Дэна Мейера)
Показать решение
Путь проходит через начало координат и имеет вершину в [latex] \ left (-4, \ text {} 7 \ right) [/ latex], поэтому [latex] \ left (h \ right) x = — \ frac { 7} {16} {\ left (x + 4 \ right)} ^ {2} +7 [/ латекс]. Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Построение функции y = f (x) в Python (с Matplotlib)
В нашем предыдущем уроке мы узнали, как построить прямую линию или линейные уравнения типа $ y = mx + c $.
Здесь мы узнаем, как построить определенную функцию $ y = f (x) $ в Python через указанный интервал.2 здесь
у = х ** 2
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘ноль’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’)
# построить функцию
plt.plot (x, y, ‘r’)
# показать сюжет
plt. {3} $.3 здесь
у = х ** 3
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’)
# построить функцию
plt.plot (x, y, ‘g’)
# показать сюжет
plt.show ()
Тригонометрические функции
Здесь мы строим тригонометрическую функцию $ y = \ text {sin} (x) $ для значений $ x $ между $ — \ pi $ и $ \ pi $.У метода linspace () интервал установлен от $ — \ pi $ до $ \ pi $.
импортировать matplotlib.pyplot как plt импортировать numpy как np # 100 чисел с линейным интервалом x = np.linspace (-np.pi, np.pi, 100) # функция, которая здесь y = sin (x) у = np.sin (х) # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines ['влево']. set_position ('центр') ax.spines ['дно']. set_position ('центр') топор.шипы ['право']. set_color ('нет') ax.spines ['вверху']. set_color ('нет') ax.xaxis.set_ticks_position ('снизу') ax.yaxis.set_ticks_position ('влево') # построить функцию plt.plot (x, y, 'b') # показать сюжет plt.show ()
Построим его вместе с еще двумя функциями, $ y = 2 \ text {sin} (x) $ и $ y = 3 \ text {sin} (x) $. На этот раз мы помечаем функции.
import matplotlib.pyplot как plt импортировать numpy как np # 100 чисел с линейным интервалом x = np.linspace (-np.pi, np.pi, 100) # функция, которая здесь y = sin (x) у = np.sin (х) # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines ['влево']. set_position ('центр') ax.spines ['дно']. set_position ('центр') ax.spines ['правильно']. set_color ('нет') ax.spines ['вверху']. set_color ('нет') ax.xaxis.set_ticks_position ('снизу') топор.yaxis.set_ticks_position ('влево') # построить график функций plt.plot (x, y, 'b', label = 'y = sin (x)') plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)') plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)') plt.legend (loc = 'верхний левый') # показать сюжет plt.show ()
И здесь мы строим вместе как $ y = \ text {sin} (x) $, так и $ y = \ text {cos} (x) $ через один и тот же интервал от $ — \ pi $ до $ \ pi $.
import matplotlib.pyplot как plt импортировать numpy как np # 100 чисел с линейным интервалом x = np.linspace (-np.pi, np.pi, 100) # здесь функции y = sin (x) и z = cos (x) у = np.sin (х) z = np.cos (х) # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines ['влево']. set_position ('центр') ax.spines ['дно']. set_position ('центр') ax.spines ['правильно']. set_color ('нет') ax.spines ['вверху']. set_color ('нет') ax.xaxis.Икс') plt.legend (loc = 'верхний левый') # показать сюжет plt.show ()
3D поверхностный плоттер | Academo.org
Эта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет
вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности.
График можно увеличивать с помощью прокрутки мышью и вращать с помощью перетаскивания. Щелчок по графику покажет значения x, y и z в этой конкретной точке.
В таблице ниже перечислены функции, которые можно вводить в поле выражения.
Выражение Описание
sin (x) Синус x в радианах
cos (x) Косинус x в радианах
желто-коричневый (x) Тангенс x в радианах
asin (x), acos (x), atan (x) Обратная из трех тригонометрических функций, перечисленных выше
sqrt (x) Квадратный корень из x (только для положительного x)
журнал (x) Натуральный логарифм x
pow (x, y) Степень x к y
Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше \ (y \), и \ (x \) во всех областях, где x равен , а не больше, чем y.
Ползунок разрешения можно использовать для увеличения количества точек данных, отображаемых на графике, что дает более плавный конечный результат, но поскольку для этого требуется больше вычислительной мощности, вы можете заметить небольшое снижение частоты кадров при взаимодействии с графиком.
Каждый раз, когда вы нажимаете кнопку «Рассчитать», URL-адрес обновляется с вашими текущими настройками, что означает, что вы можете поделиться ссылкой прямо на график по вашему выбору, не набирая значения в настройках.
Обратите внимание: если ваша поверхность содержит комплексные числа, будет отображена только действительная часть.
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.
Графические линейные уравнения с двумя переменными — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
Определите взаимосвязь между решениями уравнения и его графиком.
Постройте линейное уравнение, нанеся точки.
График вертикальных и горизонтальных линий.
Прежде чем начать, пройдите тест на готовность.
Оценить, когда.
Если вы пропустили эту проблему, просмотрите (рисунок).
Решите в общем.
Если вы пропустили эту проблему, просмотрите (рисунок).
Распознать связь между решениями уравнения и его графика
В предыдущем разделе мы нашли несколько решений уравнения. Они перечислены на (Рисунок).Итак, упорядоченные пары, и являются некоторыми решениями уравнения. Мы можем построить эти решения в прямоугольной системе координат, как показано на (Рисунок).
Обратите внимание, как точки идеально совпадают? Соединяем точки линией, чтобы получился график уравнения. См. (Рисунок). Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой.Пункты , а не на линии, не являются решениями.
Обратите внимание, что точка с координатами находится на линии, показанной на (Рисунок). Если вы подставите и в уравнение, вы обнаружите, что это решение уравнения.
Итак, дело в решении уравнения. (Фраза «точка с координатами» часто сокращается до «точка».)
Значит, это не решение уравнения. Следовательно, дело не в контуре.См. (Рисунок). Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам всех решений уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения.
График линейного уравнения
График линейного уравнения представляет собой линию.
Каждая точка на линии является решением уравнения.
Каждое решение этого уравнения — точка на этой прямой.
Используйте график, чтобы решить, будет ли каждая упорядоченная пара:
решение уравнения.
на линии.
ⓐ ⓑ
ⓐ да, да ⓑ да, да
Используйте график, чтобы определить, составляет ли каждая заказанная пара:
решение уравнения
по линии
ⓐ ⓑ
ⓐ нет, нет ⓑ да, да
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения.Метод, который мы использовали для построения графиков, называется построением точек или методом построения точек.
Как построить уравнение по точкам
Постройте уравнение, нанеся точки.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Действия, которые необходимо предпринять при построении линейного уравнения с помощью точек, приведены ниже.
Постройте линейное уравнение, нанеся точки.
Найдите три точки, координаты которых являются решениями уравнения.Разложите их в виде таблицы.
Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек — хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения.Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).
Приведем еще один пример. На этот раз мы покажем последние два шага в одной сетке.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Здесь, опять же, легче выбрать значения для.Вы понимаете почему?
Перечислим точки на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Когда уравнение включает дробь в качестве коэффициента, мы все равно можем подставлять любые числа вместо. Но математика будет проще, если мы сделаем «правильный» выбор значений.Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь является коэффициентом, мы будем тщательно выбирать значения. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов. Почему значения, кратные 2, являются хорошим выбором?
Точки показаны на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Изобразите уравнение.
Изобразите уравнение.
До сих пор все уравнения, которые мы построили на графике, были выражены в терминах. Теперь изобразим уравнение с одной и той же стороной и на одной стороне. Посмотрим, что получится в уравнении. Если в чем ценность?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем построить график этой точки, трудно быть точным, указав дроби. Помните, что в этом примере мы тщательно выбирали значения для, чтобы вообще не отображать дроби.Если мы решим уравнение для, будет легче найти три решения уравнения.
Решения для, и показаны на (Рисунок). График представлен на (Рисунок).
Можете ли вы определить точку, которую мы нашли, пропустив на линии?
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают!
Уравнение на (Рисунок) было записано в стандартной форме, с обеими и на одной и той же стороне.Мы решили это уравнение всего за один шаг. Но для других уравнений в стандартной форме это не так просто решить, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения, позволяя и решая для. Мы можем построить вторую точку, позволив, а затем решив для. Затем мы построим третью точку, используя другое значение для или.
Изобразите уравнение.
Решение
Мы перечисляем упорядоченные пары на (Рисунок). Нанесите точки, убедитесь, что они совпадают, и проведите линию.См. (Рисунок).
Изобразите уравнение.
Изобразите уравнение.
Вертикальные и горизонтальные линии графика
Можно ли построить уравнение только с одной переменной? Просто и нет, или просто без? Как мы составим таблицу значений, чтобы получить точки для построения?
Рассмотрим уравнение. Это уравнение имеет только одну переменную,. Уравнение говорит, что всегда равно , поэтому его значение не зависит от. Независимо от того, что есть, ценность всегда есть.
Итак, чтобы составить таблицу значений, впишите все значения. Затем выберите любые значения для. Поскольку не зависит от, вы можете выбрать любые номера, которые вам нравятся. Но чтобы уместить точки на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Постройте точки из (Рисунок) и соедините их прямой линией. Обратите внимание на (Рисунок), что мы построили вертикальную линию .
Вертикальная линия
Вертикальная линия — это график уравнения вида.
Линия проходит через ось x в точке.
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Что делать, если в уравнении есть, но нет? Давайте изобразим уравнение в виде графика. На этот раз значение y — является константой, поэтому в этом уравнении не зависит от. Заполните 4 для всех (рисунок), а затем выберите любые значения для. Мы будем использовать 0, 2 и 4 для координат x .
График представляет собой горизонтальную линию, проходящую через ось y в точке 4. См. (Рисунок).
Горизонтальная линия
Горизонтальная линия — это график уравнения вида.
Линия проходит по оси y в точке.
Постройте уравнение
Изобразите уравнение.
Изобразите уравнение.
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа В чем разница между уравнениями и?
Уравнение содержит и.Значение зависит от значения. Координата y изменяется в зависимости от значения. Уравнение имеет только одну переменную. Значение постоянно. Координата y всегда равна 4. Она не зависит от значения. См. (Рисунок).
Обратите внимание, что на (Рисунок) уравнение дает наклонную линию, а дает горизонтальную линию.
График и в той же прямоугольной системе координат.
Решение
Обратите внимание, что в первом уравнении есть переменная, а во втором — нет.См. (Рисунок). Два графика показаны на (Рисунок).
График и в той же прямоугольной системе координат.
График и в той же прямоугольной системе координат.
Ключевые понятия
Построение линейного уравнения по точкам
Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают.Если нет, внимательно проверьте свою работу!
Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Повседневная математика
Стоимость дома на колесах. Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обходится им в 594 фунта плюс 0,32 фунта за милю, поэтому линейное уравнение дает стоимость проезда на несколько миль. Рассчитайте стоимость аренды за 400, 800 и 1200 миль, а затем нарисуйте линию.
? 722,? 850,? 978
Еженедельный заработок. В художественной галерее, где он работает, Сальвадору платят 200 фунтов в неделю плюс 15% от продаж, которые он совершает, поэтому уравнение дает сумму, которую он зарабатывает на продаже произведений искусства в долларах. Подсчитайте сумму, которую Сальвадор зарабатывает от продажи 900, 1600 и 2000 фунтов стерлингов, а затем изобразите эту линию.
Письменные упражнения
Объясните, как выбрать три значения x -, чтобы составить таблицу для построения графика линии.
В чем разница между уравнениями вертикальной и горизонтальной линии?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
.
Matplotlib. Урок 4.1. Визуализация данных. Линейный график
Линейный график – это один из наиболее часто используемых видов графика для визуализации данных. Он использовался нами для демонстрации возможностей Matplotlib в предыдущих уроках, в этом уроке мы более подробно рассмотрим возможности настройки его внешнего вида.
Построение графика
Для построения линейного графика используется функция plot(), со следующей сигнатурой:
plot([x], y, [fmt], *, data=None, **kwargs)
plot([x], y, [fmt], [x2], y2, [fmt2], …, **kwargs)
Если вызвать функцию plot() с одним аргументом – вот так: plot(y), то мы получим график, у которого по оси ординат (ось y) будут отложены значения из переданного списка, по по оси абсцисс (ось x) – индексы элементов массива.
Рассмотрим аргументы функции plot():
x, x2, …: array
Набор данных для оси абсцисс первого, второго и т.д. графика.
y, y2, …: array
Набор данных для оси ординат первого, второго и т.д. графика.
fmt: str
Формат графика, задается в виде строки: ‘[marker][line][color]’.
**kwargs – свойства класса Line2D, которые предоставляют доступ к большому количеству настроек внешнего вида графика, отметим наиболее полезные:
Свойство Тип Описание
alpha float Прозрачность
color или c color Цвет
fillstyle {‘full’, ‘left’, ‘right’, ‘bottom’, ‘top’, ‘none’} Стиль заливки
label object Текстовая метка
linestyle или ls {‘-‘, ‘–‘, ‘-.’, ‘:’, ”, (offset, on-off-seq), …} Стиль линии
linewidth или lw float Толщина линии
marker matplotlib.markers Стиль маркера
markeredgecolor или mec color Цвет границы маркера
markeredgewidth или mew float Толщина границы маркера
markerfacecolor или mfc color Цвет заливки маркера
markersize или ms float Размер маркера
Параметры аргумента fmt
marker: str
Определяет тип маркера, может принимать одно из значений, представленных в таблице ниже
Символ Описание
‘.’ Точка (point marker)
‘,’ Пиксель (pixel marker)
‘o’ Окружность (circle marker)
‘v’ Треугольник, направленный вниз (triangle_down marker)
‘^’ Треугольник, направленный вверх(triangle_up marker)
‘<‘ Треугольник, направленный влево (triangle_left marker)
‘>’ Треугольник, направленный вправо (triangle_right marker)
‘1’ Треугольник, направленный вниз (tri_down marker)
‘2’ Треугольник, направленный вверх(tri_up marker)
‘3’ Треугольник, направленный влево (tri_left marker)
‘4’ Треугольник, направленный вправо (tri_right marker)
‘s’ Квадрат (square marker)
‘p’ Пятиугольник (pentagon marker)
‘*’ Звезда (star marker)
‘h’ Шестиугольник (hexagon1 marker)
‘H’ Шестиугольник (hexagon2 marker)
‘+’ Плюс (plus marker)
‘x’ Х-образный маркер (x marker)
‘D’ Ромб (diamond marker)
‘d’ Ромб (thin_diamond marker)
‘|’ Вертикальная линия (vline marker)
‘_’ Горизонтальная линия (hline marker)
line: str
Стиль линии/ Может принимать одно из следующих значений:
Символ Описание
‘-‘ Сплошная линия (solid line style)
‘–‘ Штриховая линия (dashed line style)
‘-.’ Штрих-пунктирная линия (dash-dot line style)
‘:’ Штриховая линия (dotted line style)
color
Цвет графика. В рамках аргумента fmt цвет задается значением из следующей таблицы:
Символ Описание
‘b’ Синий
‘g’ Зеленый
‘r’ Красный
‘c’ Бирюзовый
‘m’ Фиолетовый (пурпурный)
‘y’ Желтый
‘k’ Черный
‘w’ Белый
Реализуем возможности plot() на примере:
x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [4, 3, 1, 8, 12] plt.figure(figsize=(12, 7)) plt.plot(x, y1, 'o-r', alpha=0.7, label="first", lw=5, mec='b', mew=2, ms=10) plt.plot(x, y2, 'v-.g', label="second", mec='r', lw=2, mew=2, ms=12) plt.legend() plt.grid(True)
Рассмотрим различные варианты использования линейного графика.
Заливка области между графиком и осью
Для заливки областей используется функция fill_between(). Сигнатура функции:
fill_between(x, y1, y2=0, where=None, interpolate=False, step=None, *, data=None, **kwargs)
Основные параметры функции:
x : массив длины N
Набор данных для оси абсцисс.
y1 : массив длины N или скалярное значение
Набор данных для оси ординат – первая кривая.
y2 : массив длины N или скалярное значение
Набор данных для оси ординат – вторая кривая.
where: массив bool элементов (длины N), optional, значение по умолчанию: None
Задает заливаемый цветом регион, который определяется координатами x[where]: интервал будет залит между x[i] и x[i+1], если where[i] и where[i+1] равны True.
step: {‘pre’, ‘post’, ‘mid’}, optional
Определяет шаг, если используется step-функция для отображения графика (будет рассмотрена в одном из следующих уроков).
**kwargs
Свойства класса Polygon
Создадим набор данных для эксперимента:
import numpy as np x = np.arange(0.0, 5, 0.01) y = np.cos(x*np.pi)
Отобразим график с заливкой:
plt.plot(x, y, c = "r") plt.fill_between(x, y)
Изменим правила заливки:
plt.plot(x, y, c = "r") plt.fill_between(x, y, where = (y > 0.75) | (y < -0.75))
Используя параметры y1 и y2 можно формировать более сложные решения.
Заливка области между 0 и y, при условии, что y >= 0:
plt.plot(x, y, c = "r") plt.fill_between(x, y, where = (y > 0))
Заливка области между 0.5 и y, при условии, что y >= 0.5:
plt.plot(x, y, c = "r") plt.grid() plt.fill_between(x, 0.5, y, where=y>=0.5)
Заливка область между y и 1:
plt.plot(x, y, c = "r") plt.grid() plt.fill_between(x, y, 1)
Вариант двухцветной заливки:
plt.plot(x, y, c = "r") plt.grid() plt.fill_between(x, y, where=y>=0, color="g", alpha=0.3) plt.fill_between(x, y, where=y<=0, color="r", alpha=0.3)
Настройка маркировки графиков
В начале этого раздела мы приводили пример использования маркеров при отображении графиков. Сделаем это ещё раз, но уже в упрощенном виде:
x = [1, 2, 3, 4, 5, 6, 7] y = [7, 6, 5, 4, 5, 6, 7] plt.plot(x, y, marker="o", c="g")
В наборе данных, который создает код:
import numpy as np x = np.arange(0.0, 5, 0.01) y = np.cos(x*np.pi)
количество точек составляет 500, поэтому подход, представленный выше уже будет не применим:
plt.plot(x, y, marker="o", c="g")
В этой случае нужно задать интервал отображения маркеров, для этого используется параметр markevery, который может принимать одно из следующих значений:
None – отображаться будет каждая точка;
N – отображаться будет каждая N-я точка;
(start, N) – отображается каждая N-я точка начиная с точки start;
slice(start, end, N) – отображается каждая N-я точка в интервале от start до end;
[i, j, m, n] – будут отображены только точки i, j, m, n.
Ниже представлен пример, демонстрирующий работу с markevery:
x = np.arange(0.0, 5, 0.01) y = np.cos(x*np.pi) m_ev_case = [None, 10, (100, 30), slice(100,400,15), [0, 100, 200, 300], [10, 50, 100]] fig, ax = plt.subplots(2, 3, figsize=(10, 7)) axs = [ax[i, j] for i in range(2) for j in range(3)] for i, case in enumerate(m_ev_case): axs[i].set_title(str(case)) axs[i].plot(x, y, "o", ls='-', ms=7, markevery=case)
Обрезка графика
Для того, чтобы отобразить только часть графика, которая отвечает определенному условию используйте предварительное маскирование данных с помощью функции masked_where из пакета numpy.
x = np.arange(0.0, 5, 0.01) y = np.cos(x*np.pi) y_masked = np.ma.masked_where(y < -0.5, y) plt.ylim(-1, 1) plt.plot(x, y_masked, linewidth=3)
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Функции и их графики. Задание №23
1. Функции и их графики Задание №23
x 2
1. Постройте график функции y 1 2
x 2x
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x 2
y 1 2
x 2x
x 2
x 2
1
1 2
1
1
x 2x
x x 2
x
при условии х 0 и х 2 0
D y ; 2 2; 0 0; .
х 0 и х 2.
у
1
Решение. y 1
x
х 2; х 0.
1 точка
3
1,5
у = 1,5
1
у=1
1 точка
-3
-2
0
-1
-1
1
2
1 точка
Ответ: m = 1; m = 1,5.
3
х
x x
2. Постройте график функции y 1
x x2
и определите, при каких значениях т прямая у = т
имеет с графиком две общие точки.
4
3
Решение.
x 4 x3
y 1
2
x x
4
3
3
x x
x x 1
2
1
1
1
x
x x2
x x 1
при условии х 0 и х 1 0
D y ; 1 1; 0 0; .
х 0 и х 1.
у
2
Решение. y 1 x
х 1; х 0.
2 точки
1 точка
2 точки
0 точек
1
-3 -2 -1
-1
0 1
2
3
-2
-3
-4
2 точки
-5
-6
-7
Ответ: m
х
3. Постройте график функции
x 5 x 2 5 x 4
y
x 4
и определите, при каких значениях т прямая у = т
имеет с графиком ровно одну общую точку.
Решение.
x 5 x 2 5 x 4
y
x 4
x 5 x 2 5x 4 x 5 x 4 x 1 x 5 x 1
x 4
x 4
2
2
x 6x 5 x 3 4
при условии х 4 0 х 4.
D y ; 4 4; .
Решение.
y x 3 4
2
у
х 4.
2 точки
4
3
2
2 точки
1
-6 -5 -4 -3 -2 -1
0 1
2
-1
-2
у(-4) = -3
у(-3) = -4
х
3
-3
-4
-5
Ответ: m = ‒ 4; m = ‒ 3.
2 точки
1 точка
1 точка
4. Постройте график функции y x 2 x 2
Какое наибольшее число общих точек график данной функции
может иметь с прямой, параллельной оси абсцисс?
Решение.
y x2 x 2
y1 x 2 x 2
2
b 1
1
1 1
xв
; yв 2 2 .
2a 2
4
2 2
x
y
0
-2
1
-2
-1
0
2
0
3
4
-2
4
у
Решение. y1 x 2 x 2
y x2 x 2
4
2 точки
3
3 точки
2
4 точки
2 точки
1
-6 -5 -4 -3 -2 -1
0 1
2
3
-1
-2
-3
-4
-5
Ответ: наибольшее
число точек
пересечения равно 4 при 0
х
5. Постройте график функции y x 2 6 x 8
Какое наибольшее число общих точек график данной функции
может иметь с прямой, параллельной оси абсцисс?
Решение.
2
y x 6 x 8
y x 6 x 8, т.к . x x
2
2
y1 x 2 6 х 8
b
xв
3; yв 32 6 3 8 1.
2a
x
y
0
8
6
8
1
3
5
3
2
0
4
0
2
у
Решение. y1 x 2 6 х 8
y x 6 x 8
2
2 точки
8
3 точки
4 точки
4
3
4 точки
2
1
0 1
-6 -5 -4 -3 -2 -1
-1
2
3
4
5
6
7
2 точки
Ответ: наибольшее
число точек
-2
пересечения равно 4 при – 1
х
x
y
x 6 x2 4x 5
6. Постройте график функции
2
x 2x 3
и определите, при каких значениях т прямая у = т
имеет с графиком ровно одну общую точку.
Решение.
2
2
x x 6 x 4x 5
y
x2 2x 3
2
2
x x 6 x 4 x 5 x 3 x 2 x 1 x 5
2
x 1 x 3
x 2x 3
2
2
x 2 x 5 x 3x 10 х 1,5 12,25.
при условии х 1 0, х 3 0 х 1 и х 3.
D y ; 1 1; 3 3; .
2
у
0 1
-4 -3 -2 -1
Решение.
2
y x 1,5 12,25
х 1; х 3.
2
3
4
5
6
-2 1
2 точки
-4
у(-1) = -6
1 точка
-6
1 точка
-8
2 точки
-10
у(3) = -10
2 точки
1 точка
-12
Ответ: m = ‒ 12,25; m = ‒ 10; m = ‒ 6.
х
x 2 4 x 6, если х 1,
7. Постройте график функции y
3х, если х 1
и определите, при каких значениях т прямая у = т
имеет с графиком ровно две общие точки.
Решение.
x 2 4 x 6, если х 1,
y
3х, если х 1
y1 x 2 4 х 6
y2 3x
b
xв
2;
2a
yв 2 2 4 2 6 2.
x
y
0
0
-2
-6
Решение.
2
y1 x 4 х 6, х 1
у
9
8
y2 3x, х 1
7
1 точка
6
5
4
3 точки
2 точки
3
2
1 точка
2 точки
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: m = 2; m = 3.
4
5
6
7
х
8. Найдите все значения k, при каждом из которых прямая y = kx
имеет с графиком функции y = x2 + 4 ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение.
Другими словами, нужно найти все значения k, при каждом из
которых система имеет одно решение:
y x 2 4,
y kx;
kx x 2 4 ,
y kx;
kx x 2 4
x 2 kx 4 0
D k 2 16
1 корень D 0 k 2 16 0 k 4.
у
Решение.
2
y x 4
y1 4 x
y2 4 x
9
8
7
6
5
4
3
2
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
-2
Ответ: k = 4; k = ‒ 4.
4
5
6
7
х
9. Найдите все значения k, при каждом из которых прямая y = kx
имеет с графиком функции y = ‒ x2 – 1 ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение.
Другими словами, нужно найти все значения k, при каждом из
которых система имеет одно решение:
y x 2 1,
kx x 2 1,
y kx;
y kx;
kx x 2 1
x 2 kx 1 0
D k2 4
1 корень D 0 k 2 4 0 k 2.
у
Решение.
1
0 1
-6 -5 -4 -3 -2 -1
2
3
-1
y x2 1
y1 2 x
y2 2 x
-2
-3
-4
-5
-6
-7
-8
Ответ: k = 2; k = ‒ 2.
4
5
6
7
х
10. Найдите p и постройте график функции y = x2 + p если
известно, что прямая y = 6x имеет с этим графиком ровно одну
общую точку.
Решение.
Другими словами, нужно найти все значения p, при каждом из
которых система имеет одно решение:
y x2 p,
y 6 x;
6 x x 2 p ,
y 6 x;
6x x2 p
x2 6x p 0
D 36 4 p
1 корень D 0 36 4 p 0
p 9.
у
Решение.
y x2 9
y 6x
18
16
14
12
10
8
6
4
2
-6 -5 -4 -3 -2 -1
0 1
2
-1
-2 p = 9.
Ответ:
3
4
5
6
7
х
11. Постройте график функции
x
y
2
x x
x 1
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x2 x x
y
x 1
x 2 , если х 0;
x 2 x x x x 1 x
xx 2
x 1
x 1
х , если х 0.
при условии х 1 0
D y ; 1 1; .
х 1.
у
Решение.
y1 x 2 , х 0
2
y2 x , х 0
х 1.
5
4
3
1 точка
2
1
0 1
-6 -5 -4 -3 -2 -1
2
3
4
5
6
7
-1
-2
0 точек
-3
-4
1 точка
-5
-6
Ответ: m = ‒ 1.
х
Открытая Математика. Функции и Графики. Решение систем уравнений и неравенств
Уравнение g (x, y) = 0 задает на координатной плоскости некоторую кривую, каждая точка M (x; y) которой удовлетворяет этому уравнению.
Некоторые кривые являются графиками функций y = f (x), что означает равносильность уравнений g (x, y) = 0 и y = f (x). К таковым, например, относится кривая, задаваемая уравнениями x + y – 1 = 0 или y – x² = 0. Другим не соответствуют никакие функции, например, x2+y2-1=0 (в данном случае каждому значению x∈(-1; 1) соответствуют два значения y).
Окружность с центром в точке (-2; 1) Гипербола, задаваемая уравнением x² – y² = 1.
Уравнением окружности с центром в точке (a; b) и радиусом r > 0 является (x – a)² + (y – b)² = r².
Уравнение (x – a)² + (y – b)² = 0 задает точку с координатами (a; b), уравнение x² – y² = a² – гиперболу.
Уравнение вида f (x, y) · g (x, y) = 0 задает на плоскости объединение линий f (x, y) = 0 и g (x, y) = 0. Каждая точка этой фигуры является решением совокупности уравнений [fx, y=0;gx, y=0.
Система уравнений с двумя переменными
Пусть задана система уравнений {fx, y=0,gx, y=0. Ее решением является совокупность пар чисел (x_i; y_i), подстановка которых в каждое из уравнений превращает его в верное равенство. Построим на координатной плоскости кривые, задаваемые уравнениями f (x, y) = 0 и g (x, y) = 0. Тогда можно сказать, что геометрически решением системы уравнений является совокупность всех точек M_i (x_i; y_i), в которых пересекаются кривые, задаваемые этими уравнениями.
Если кривые не пересекаются, то система уравнений решений не имеет. В этом случае говорят, что система несовместна.
Систему {fx, y=0,gx, y=0,hx, y=0, геометрически можно представить как совокупность точек, в которых пересекаются три кривые f (x, y) = 0, g (x, y) = 0 и h (x, y) = 0. Если не существует точки, в которой пересекаются все три кривые, то система также несовместна.
Аналогичным образом уравнение f (x, y, z) = 0 задает поверхность в трехмерной декартовой системе координат. Геометрически решением системы уравнений {fx, y, z=0,gx, y, z=0,hx, y, z=0, будет совокупность координат точек M_i (x_i; y_i; z_i), в которых пересекаются поверхности, задаваемые этими уравнениями.
Так, уравнения x² + y² + z² = 1, y = 0, z = 0 задают в пространстве сферу единичного радиуса с центром в начале координат и две координатные плоскости, перпендикулярные соответственно оси ординат и оси аппликат. Плоскость z = 0 пересекает сферу по окружности x² + y² = 1, лежащей в плоскости z = 0. Плоскость y = 0 пересекает эту окружность в двух точках с координатами M₁ (–1; 0; 0) и M₂ (1; 0; 0). Таким образом, решением системы уравнений {x2+y2+z2=1,y=0,z=0, являются две тройки чисел (±1; 0; 0).
Иногда при решении задач графики могут ввести в заблуждение. Так, на эскизе кажется, что графики функций y = (1/16)^x и y = log_1/16 x пересекаются только в одной точке, лежащей на биссектрисе первого координатного угла. И только при более внимательном рассмотрении у уравнения (1/16)x = log_1/16 x находятся еще два корня x = 1/2 и x = 1/4. Увеличьте масштаб графика, чтобы убедиться в этом
Кривая f (x, y) = 0 делит координатную плоскость на несколько областей, внутри каждой из которых функция f сохраняет знак. Для решения неравенства f (x, y) > 0 графическим методом необходимо в каждой из таких областей взять пробную точку и вычислить ее знак, после чего отобрать области, в которых функция f принимает положительные значения. Присоединяя к полученному решению саму кривую, получим решение неравенства f (x, y) ≥ 0.
Чтобы решить графически систему {fx, y>0gx, y>0, нужно изобразить на координатной плоскости решения каждого из неравенств f (x, y) > 0, g (x, y) > 0, а затем найти их пересечение. Аналогичным образом поступают, если неравенств больше двух.
поверхностей, часть 2
поверхностей, часть 2
Поверхности и контурные графики
Часть 2: Квадрические поверхности
Квадрические поверхности — это графики квадратных уравнений с тремя декартовыми переменными. в космосе.Как и графики квадратиков на плоскости, их форма зависит от знаки различных коэффициентов в их квадратных уравнениях.
Сферы и эллипсоиды
Сфера — график уравнение вида x ² + y ² + z ² = p ² для какого-то реального числа р . Радиус сферы p (см. рисунок ниже). Эллипсоиды — это графики уравнений вида ax ² + на ² + c z ² = p ², где a , b и c все положительны. Особенно, сфера — это особый эллипсоид, для которого a , b и c все равны.
Постройте график x ² + y ² + z ² = 4 в вашем листе в декартовых координатах.Затем выберите разные коэффициенты в уравнении и построить несферический эллипсоид.
Какие изгибы вы обнаружите, когда пересечь сферу плоскостью, перпендикулярной одной из осей координат? Что вы найдете для эллипсоида?
Параболоиды
Поверхности, пересекающиеся с плоскости, перпендикулярные любым двум осям координат, являются параболами в тех самолеты называются параболоидами .Пример показан на рисунке ниже. — это график z = x ² + y ².
Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- параболы.[Подсказка: установите y = c или x = c для некоторой константы c .]
Измените уравнение на z = 3 x ² + y ², и заговор снова. Как меняется поверхность? В частности, что происходит с кривые пересечения с горизонтальными плоскостями.
Поверхность на следующем рисунке представляет собой график z = x ² — y ².В этом случае пересечения с плоскостями, перпендикулярными к x- и y- оси по-прежнему являются параболами, но два набора парабол различаются направление, в котором они указывают. По причинам, которые мы увидим, эта поверхность называется гиперболический параболоид — и по понятным причинам его еще называют «седловая поверхность».
Создайте свой собственный график этого гиперболического параболоид на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ? Объясните обе части имени.
Гиперболоиды
Гиперболоиды поверхности в трехмерном пространстве аналогично гиперболам на плоскости. Их определяющие характерно то, что их пересечения с плоскостями, перпендикулярными любой две из координатных осей являются гиперболами.Есть два типа гиперболоидов — первый тип иллюстрируется графиком x ² + y ² — z ² = 1, который показан на рисунке ниже. Как показано на рисунке справа, эта форма очень похожа на ту, которая обычно используется на атомных электростанциях. градирни. (Источник: EPA Реакция на инцидент на Три-Майл-Айленд.)
Эта поверхность называется гиперболоидом . одного листа , потому что он все «соединен» в одно целое.(Мы будем перейдем к другому делу сейчас.)
Создайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения. Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
Покажите, что пересечения эта поверхность с плоскостями, перпендикулярными осям x- и y- являются гиперболами.[Подсказка: установите y = c или x = c для некоторой константы c .]
Другой тип — гиперболоид двух листов , и это проиллюстрировано графиком x ² — y ² — z ² = 1, показано ниже.
Сделайте свой собственный участок этой поверхности на листе и поверните график, чтобы увидеть его с разных точек зрения.Следуйте предложениям в таблице. Какие пересечения поверхность с плоскостями вида z = c , для некоторой постоянной с ?
Покажите, что пересечения эти две поверхности с соответствующими координатными плоскостями являются гиперболами. 2 = 1, ближайшие к (0,2)
Если вы рассмотрите график x ² — y ² = 1, это гипербола, и если вы наложите точку (0, 2), вы получите что-то вроде этого:
Очевидно, единственная часть графика нам нужно беспокоиться о верхней части (над осью x).Эту часть графика можно записать, решив график для y и взяв только положительную часть.
x ² — y ² = 1
x ² — 1 = y ²
y = ± √ (x ² — 1), но, взяв только положительную часть, мы получаем y = √ (x ² — 1)
Формула расстояния d = √ [(x ₂ — x ₁) ² + (y ₂ — y ₁) ²] и пусть (x ₂, y ₂) будет точкой (0, 2), поэтому формула расстояния станет d = √ [(0 _{— x ₁) ² + (2 — y ₁) ²]}
Теперь давайте просто отбросим суффикс «1» от x и y, чтобы упростить и упростить получение: d = √ [x ² + 4 — 4y + y ²] где (x, y) находится на графике x ² — y ² = 1
Теперь мы знаем, что y = √ (x ² — 1), поэтому мы можем подставить «√ (x ² — 1) «в уравнение везде, где мы видим» y «, составляющую уравнение расстояния: d = √ [x ² + 4 — 4√ (x 9003 5 2 — 1) + (√ (x ² — 1)) ²]
Если мы упростим, а затем запишем как функцию от x, мы получим:
d (x) = √ (2x ² — 4√ (x ² — 1) + 3) или d (x) = [2x ² — 4 (x ² — 1) ^1/2 + 3] ^1/2
Для минимизации возьмите производную и установите ее равной нулю
d ‘(x) = 1/2 (2x ² — 4√ (x ² — 1) + 3) ^-1/2 • (4x — 2 (x ² — 1) ^-1/2 • 2x)
Единственный способ, которым это может быть равно нулю, — это если числитель равен нулю, поэтому:
4x — 4x / (x ²-1) ^1/2 = 0
4x (1 — 1 / (x ²-1) ^1/2) = 0, поэтому x = 0 или 1 — 1 / (x ² -1) ^1/2) = 0
1 = 1 / (x ²-1) ^1/2
(x ²-1) ^1/2 = 1
x ² — 1 = 1
x ² = 2
x = ± √ 2
Когда x = √2, тогда y = √ ((√2) ²-1) = √ (2-1) = √1 = 1, поэтому точка равна (√2, 1).Соответствующая точка на другой стороне (-√2, 1)
Круговые уравнения
Круг сделать легко:
Нарисуйте кривую на расстоянии
«радиуса» от центральной точки.
А так:
Все точки находятся на одинаковом расстоянии
от центра.
На самом деле определение круга — это
Круг на графике
Нарисуем на графике окружность радиуса 5:
Теперь давайте определим именно , где находятся все точки.
Делаем прямоугольный треугольник:
А затем используйте Пифагор:
x ² + y ² = 5 ²
Таких точек бесконечное количество, вот несколько примеров:
x y x ² + y ²
5 0 5 ² + 0 ² = 25 + 0 = 25
3 4 3 ² + 4 ² = 9 + 16 = 25
0 5 0 ² + 5 ² = 0 + 25 = 25
−4 −3 (−4) ² + (−3) ² = 16 + 9 = 25
0 −5 0 ² + (−5) ² = 0 + 25 = 25
Во всех случаях точка на окружности подчиняется правилу x ² + y ² = радиус ²
Мы можем использовать эту идею, чтобы найти пропущенное значение
Пример:
x значение 2 и радиус из 5
Начать с: x ² + y ² = r ²
Известные нам значения: 2 ² + y ² = 5 ²
Переставить: y ² = 5 ² — 2 ²
Квадратный корень с обеих сторон: y = ± √ (5 ²-2 ²)
Решить: y = ± √21
у ≈ ± 4.58 …
( ± означает, что есть два возможных значения: одно с + , другое с — )
А вот две точки:
Более общий случай
Теперь поместим центр на (а, б)
Итак, круг — это всех точек (x, y) , которые находятся на расстоянии «r», от центра (a, b) .
Теперь давайте определим, где находятся точки (используя прямоугольный треугольник и Пифагор):
Это та же идея, что и раньше, но нам нужно вычесть a и b :
И это «Стандартная форма» для уравнения круга!
Он сразу показывает всю важную информацию: центр (a, b) и радиус r .
Пример: круг с центром в точке (3,4) и радиусом 6:
Начать с:
(x − a) ² + (y − b) ² = r ²
Вставьте (a, b) и r:
(x − 3) ² + (y − 4) ² = 6 ²
Затем мы можем использовать наши навыки алгебры, чтобы упростить и изменить это уравнение, в зависимости от того, для чего оно нам нужно.
Попробуйте сами
«Общая форма»
Но вы можете увидеть уравнение круга, а не знать его !
Потому что это может не быть в аккуратной «Стандартной форме» выше.
В качестве примера давайте поместим некоторые значения в a, b и r, а затем расширим их
Начать с: (x − a) ² + (y − b) ² = r ²
Пример: a = 1, b = 2, r = 3: (x − 1) ² + (y − 2) ² = 3 ²
Развернуть: x ² — 2x + 1 + y ² — 4y + 4 = 9
Соберите как термины: x ² + y ² — 2x — 4y + 1 + 4-9 = 0
И в итоге получаем:
x ² + y ² — 2x — 4y — 4 = 0
Это уравнение круга, но «замаскировано»!
Итак, когда вы видите что-то подобное, подумайте: «хм… что может быть круг! «
Фактически, мы можем записать его в «Общая форма» , поместив константы вместо чисел:
x ² + y ² + Ax + By + C = 0
Примечание. Общая форма всегда имеет x ² + y ² для первых двух терминов .
Переход от общей формы к стандартной
Теперь представьте, что у нас есть уравнение в общей форме :
x ² + y ² + Ax + By + C = 0
Как мы можем поместить его в стандартную форму вот так?
(x − a) ² + (y − b) ² = r ²
Ответ: пройдите квадрат (прочтите об этом) дважды… один раз для x и один раз для y :
Пример: x
² + y ² — 2x — 4y — 4 = 0
Начать с: x ² + y ² — 2x — 4y — 4 = 0
Совместите x s и y s: (x ² — 2x) + (y ² — 4y) — 4 = 0
Константа справа: (x ² — 2x) + (y ² — 4y) = 4
Теперь завершите квадрат для x (возьмите половину −2, возведите ее в квадрат и прибавьте к обеим сторонам):
(x ² — 2x + (−1) ²) + (y ² — 4y) = 4 + (−1) ²
И завершите квадрат y (возьмите половину −4, возведите ее в квадрат и прибавьте к обеим сторонам):
(x ² — 2x + (−1) ²) + (y ² — 4y + (−2) ²) = 4 + (−1) ² + (−2) ²
Убрать:
Упростить: (x ² — 2x + 1) + (y ² — 4y + 4) = 9
Наконец: (x — 1) ² + (y — 2) ² = 3 ²
И он у нас в Стандартном Бланке!
(Примечание: здесь использовался предыдущий пример a = 1, b = 2, r = 3, так что мы все поняли правильно!)
Единичный круг
Если мы поместим центр круга в (0,0) и установим радиус равным 1, то получим:
(x − a) ² + (y − b) ² = r ²
(x − 0) ² + (y − 0) ² = 1 ²
x ² + y ² = 1
Какое уравнение представляет собой единичный круг
Как построить круг вручную
1.Участок центр (а, б)
2. Нанесите 4 точки «радиусом» от центра вверх, вниз, влево и вправо.
3. Нарисуйте это!
Пример: График (x − 4)
² + (y − 2) ² = 25
Формула для круга: (x − a) ² + (y − b) ² = r ²
Итак, центр находится в (4,2)
И r ² это 25 , поэтому радиус √25 = 5
Итак, мы можем построить:
Центр: (4,2)
Вверх: (4,2 + 5) = (4,7)
Вниз: (4,2−5) = (4, −3)
Слева: (4−5,2) = (−1,2)
Справа: (4 + 5,2) = (9,2)
А теперь нарисуйте круг как можно лучше!
Как нарисовать круг на компьютере
Нам нужно изменить формулу так, чтобы мы получили «y =».
У нас должно получиться два уравнения (верхнее и нижнее обведенные кружком), которые затем можно построить.
Пример: График (x − 4)
² + (y − 2) ² = 25
Итак, центр находится в (4,2), а радиус √25 = 5
Переставьте, чтобы получить «y =»:
Начать с: (x − 4) ² + (y − 2) ² = 25
Переместите (x − 4) ² вправо: (y − 2) ² = 25 — (x − 4) ²
Извлеките квадратный корень: (y − 2) = ± √ [25 — (x − 4) ²]
(обратите внимание на ± «плюс / минус»…
может быть два квадратных корня!)
Переместите «−2» вправо: y = 2 ± √ [25 — (x − 4) ²]
Итак, когда мы построим эти два уравнения, у нас должен быть круг:
y = 2 + √ [25 — (x − 4) ²]
y = 2 — √ [25 — (x − 4) ²]
Попробуйте построить график этих функций в графическом редакторе функций.
Также можно использовать Equation Grapher, чтобы сделать все это за один раз.
линий графика
линия графика
Графическое изображение линейных уравнений
График уравнения с двумя переменными представляет все возможные комбинации x и y , которые удовлетворяют уравнению. Другими словами, точки на графике имеют координаты ( x , y ), которые делают утверждение уравнения верным. В зависимости от природы уравнения и показателей переменных каждое уравнение имеет свой график.
График любого уравнения, имеющего две переменные, у которых обе имеют степень один, не умножаются друг на друга и не входят в знаменатель каких-либо дробей, представляет собой прямую линию.
Например, график 2y — x + 4 = 0 представляет собой линию. Это означает, что если мы найдем все возможные комбинации x и y, которые работают в уравнении, и построим их в системе координат, результатом будет линия. Поскольку две точки определяют линию, если мы распознаем уравнение как линейное уравнение, нам понадобятся только два набора x и y (точек), которые удовлетворяют уравнению для графика.Есть много способов найти эти точки, и их бесконечное количество. Мы рассмотрим графики линий, используя их точки пересечения по оси x и оси y. Это точки, в которых линия пересекает ось x и ось y соответственно. Мы выбираем эти точки потому, что с ними легче работать. Пересечение линии по оси x является точкой на оси x и, следовательно, имеет нулевую координату y. А точка пересечения линии y — это точка на оси y, имеющая нулевую координату x .Мы собираемся использовать эти факты, чтобы найти недостающие координаты каждой точки.
Сначала мы подставим ноль для y и найдем соответствующее x , а затем подставим ноль для x и найдем соответствующее y .
Пример 1) График 2 y — x + 4 = 0
Если мы подставим 0 для x , мы получим:
2 y — 0 + 4 = 0 Мы вычтем 4 с обеих сторон:
2 y = -4 и разделив на 2, получим y = -2, поэтому у нас есть (0, -2), это перехват y .
Затем мы подставим ноль для y :
2 (0) — x + 4 = 0 Мы вычтем 4 с обеих сторон:
— x = -4 или x = 4, получим наша вторая точка (4,0), это пересечение x
. Теперь мы строим точки и соединяем их. Результирующая линия представляет все комбинации x, y , которые работают в данном уравнении.
Каждая линия имеет крутизну, которая обозначается как уклон . Крутизна линии или ее наклон — это отношение подъема линии (насколько далеко вверх или вниз мы должны пройти, чтобы достичь другой точки) к ее пробегу (насколько далеко вперед или назад нам нужно пройти).Для приведенной выше линии наклон равен 2/4 или 1/2, так как нам нужно подняться на 2 единицы, а затем на 4 единицы, чтобы перейти от одной точки к другой. Мы также можем найти наклон, сначала решив наше уравнение для y . Тогда наклон будет коэффициентом x (а оставшееся число будет пересечением по оси Y):
Сначала мы прибавим x к обеим сторонам и вычтем 4: 2 y = x — 4
Затем мы разделим обе стороны на 2: y = x /2 — 2 (это называется формой пересечения угла наклона линии)
Таким образом, наклон равен 1/2, а точка пересечения оси Y равна -2.Эта информация может быть полезна в некоторых случаях.
Пример 2) График 4y + 5x = 20
Подставляя ноль для x, мы получаем:
4y = 20 или y = 5
Таким образом, мы получаем точку пересечения с y (0,5)
Подставляя ноль для y, получаем:
5x = 20 или x = 4
Итак, пересечение по оси x равно (4,0)
Обратите внимание, что наклон этой линии равен -5/4, так как нам нужно спуститься на 5 единиц вниз и вперед на 4 единицы, чтобы перейти от одной точки к другой.
И если мы решим для y (изменим форму на наклон-пересечение ), мы сначала должны вычесть 5x с обеих сторон:
4y = -5x + 20, а затем разделить на 4:
y = -5/4 x + 5
Который также показывает, что наклон равен -5/4, а точка пересечения по оси Y равна 5.
Особые случаи:

Иногда нам может потребоваться графическое отображение уравнений только с одной переменной в системе координат.
Например, y = 4 или x = -2 — это уравнения, которые содержат только одну переменную, но их можно построить в виде линий.
В случае y = 4, набор точек, удовлетворяющих уравнению, — это все точки, которые имеют y значение 4 (с любым возможным значением x). Эти точки могут быть представлены горизонтальной линией y = 4.В целом график всех уравнений вида y = C, где C — число, представляет собой горизонтальную линию в точке C.
В случае x = -2, график представляет собой набор всех точек со значением x -2, которое может быть представлено вертикальной линией с отметкой -2. Обычно график всех уравнений в форме x = C представляет собой вертикальную линию в точке C.
Вернуться к линейным функциям
Гиперболы:
Гиперболы:
Гипербола — это множество точек, в которых абсолютное значение разницы между двумя фиксированными точками, называемыми фокусами, является постоянным ценить.
Гиперболы имеют две симметричные половины. У них есть два вершины, которые являются самыми внутренними точками. У них есть два очага, как указано в определение, и у них есть две асимптоты, которые пересекаются друг с другом в центре гиперболы.
Если гипербола открывается в горизонтальном направлении, уравнение гиперболы в стандартной форме выглядит как
Обратите внимание на вычитание между термины.Если термин y используется после вычитания гипербола открывается в стороны.
Если гипербола открывается вверх и вниз, стандартная форма уравнения составляет
. x -член теперь вычитается.
Внутри гиперболы помещается ящик. В асимптоты пересекают углы этого прямоугольника. Вы найдете эту коробку перемещение влево и вправо от центра a расстояние от до и вверх и вниз от центра на расстояние b .Центр гиперболы — это центр этого прямоугольника. В прямоугольник имеет размеры 2 a на 2 b .
c ² = a ² + b ² для гиперболы, где a, b и c связывают фокусы и вершины.
Самая базовая гипербола — это x ² y ² = 1 или y ² x ² = 1. С центром в точке (0,0).
Эксцентриситет гиперболы — это эксцентриситет. = c / a, а эксцентриситет на больше 1 для гиперболы. Чем больше эксцентриситет, тем шире гипербола.
Еще раз завершив квадрат, можно написать уравнения гипербол к стандартной форме, чтобы легко определить его график и связанные с ним точки и асимптоты.
Пример:
Обратите внимание, эта гипербола открывается боком.Член x ² равен положительный.
Есть прямоугольник с центр гиперболы как ее центр. Длина стороны прямоугольника в направлении x составляет 2 (5) = 10. Длина стороны в y направление 2 (12) = 24.
Диагональные линии через центр гиперболы и углы бокса — асимптоты кривая гиперболы. Эти строки: y = 12x / 5 и y = -12x / 5.
c ² = a ² + b ² = 25 + 144 = 169 с = 13. Вы перемещаетесь на 13 делений вправо и влево от центра, чтобы найти фокусы. Фокусы — (-13, 0) и (13, 0).
В общем виде эта гипербола имеет уравнение формы 144x ² 25y ² 3600 = 0. Обратите внимание, что коэффициенты x ² и y ² имеют противоположные знаки, в отличие от эллипсы и круги.
Другой Пример:

Обратите внимание, эта гипербола открывается вверх и вниз. Член x ² равен отрицательный.
Есть прямоугольник с центр гиперболы как ее центр. Длина стороны прямоугольника в направлении x составляет 2 (3) = 6.Длина стороны в направлении y равно 2 (3).
Диагональные линии через центр гиперболы и углы бокса — асимптоты гиперболы изгиб. Эти строки
y = (3x) / 3 и y = — (3x) / 3.
В общем виде эта гипербола имеет уравнение формы 9y ² x ² 9 = 0. Обратите внимание, что коэффициенты равны x ² и y ² имеют противоположные знаки, в отличие от эллипсов и окружностей.
Другой Пример:

или в общем виде x ² 16 лет ² 6x 32 года 21 = 0
Центр
равен (3, -1) a ² = 16 a = 4, б ² = 1, б = 1
c ² = a ² + b ² = 17 с = 17
Сейчас вы тренируетесь:
1.Учитывая , найдите следующее элементы этой гиперболы и нарисуйте график, пометив все важные элементы.
Находка: a. Центр б. В основные вершины c. Углы внутренний прямоугольник e. В асимптоты f. Очаги
2. Для найдите следующее элементы этой гиперболы и нарисуйте график, пометив все важные элементы.
Находка: a.Центр б. В основные вершины c. Углы внутренний прямоугольник e. В асимптоты f. Очаги
3. Дано x ² y ² = 1 найдите следующие элементы этой гиперболы и нарисуйте график, маркировка всех важных элементов.
Находка: a. Центр б. В основные вершины c. Углы внутренний прямоугольник e. В асимптоты f.Очаги
4. Завершите квадрат, чтобы переписать эту гиперболу в эталон. форма
. Затем найдите центр, основные вершины, углы внутренний прямоугольник, асимптоты и фокусы. Нарисуйте диаграмму, обозначающую важные элементы.
5лет ² — 2x ² + 50лет + 4х + 73 = 0
5. Завершите квадрат, чтобы переписать эту гиперболу в стандартную форма
.Затем найдите центр, основные вершины, углы внутренний прямоугольник, асимптоты и фокусы. Нарисуйте диаграмму, обозначающую важные элементы.
72x ² y ² + 16лет 100 = 0
6. Решите относительно y, чтобы получить верхняя и нижняя функции, представляющие эту параболу. Изобразите это на своем калькулятор, чтобы проверить свой график на 1.
7. Что такое домен и диапазон верхняя функция в 6.
8. Решите относительно y, чтобы получить верхняя и нижняя функции, представляющие эту параболу. Изобразите это на своем калькулятор, чтобы проверить свой график на 2.
9. Укажите домен и диапазон нижняя функция в 8.
10. Решите x ² y ² = 1 относительно y, чтобы получить верхнюю и нижние функции, представляющие эту параболу. Изобразите их на своем калькуляторе, чтобы проверьте свой график на 2.
11. Укажите домен и диапазон нижняя функция в 10.
12. Для каждого уравнения ниже укажите представляет ли он круг, эллипс, параболу или гиперболу.
а. 9x ² 15 лет ² + 7x 3г + 20 = 0
г. х ² + 4г ² 12x + 9y + 14 = 0
г. y ² -4,5y + 3x 2,5 = 0
г.х ² + у ² 19x + 25y + 4 = 0
e. 2х ² + 2лет ² 5x 9лет + 3 = 0
ф. х ² у ² 8х 2у + 8 = 0
13. Заполните страницы с №1 по №6. 551
14. Завершить № 7 стр. 551
15. Завершить № 10 стр. 551
16. Завершить № 35 и № 36 стр. 552
17.Завершить # 40 стр. 552
18. Завершить # 52 стр. 552
Сдать домашнее задание Оценка:

2., 3., 5., 8., 12., 15. и 17.
Кратчайшее расстояние между точкой и окружностью
Какое расстояние между кругом C с уравнением Икс 2 + у 2 знак равно р 2 с центром в начале координат и в точке п ( Икс 1 , у 1 ) ?
Луч О п → , начиная с начала координат О и проходя через точку п , пересекает круг в точке, ближайшей к п .Таким образом, расстояние между кругом и точкой будет разницей расстояния точки от начала координат и радиуса круга.
С помощью Формула расстояния , кратчайшее расстояние между точкой и окружностью равно | ( Икс 1 ) 2 + ( у 1 ) 2 — р | .
Обратите внимание, что формула работает независимо от того, п находится внутри или вне круга.
Если круг не центрирован в начале координат, но имеет центр, скажите ( час , k ) и радиус р , кратчайшее расстояние между точкой п ( Икс 1 , у 1 ) и круг | ( Икс 1 — час ) 2 + ( у 1 — k ) 2 — р | .
Пример 1:
Какое кратчайшее расстояние между кругом Икс 2 + у 2 знак равно 9 и точка А ( 3 , 4 ) ?
Круг с центром в начале координат и имеет радиус 3 .
Итак, кратчайшее расстояние D между точкой и кругом задается
D знак равно | ( 3 ) 2 + ( 4 ) 2 — 3 | знак равно | 25 — 3 | знак равно | 5 — 3 | знак равно 2
То есть кратчайшее расстояние между ними составляет 2 единицы.
Пример 2:
Какое кратчайшее расстояние между кругом Икс 2 + у 2 знак равно 36 и точка Q ( — 2 , 2 ) ?
Круг с центром в начале координат и имеет радиус 6 .
Итак, кратчайшее расстояние D между точкой и кругом задается
D знак равно | ( — 2 ) 2 + ( 2 ) 2 — 6 | знак равно | 8 — 6 | знак равно 6 — 2 2 ≈ 3.17
То есть кратчайшее расстояние между ними составляет около 3,17 единицы.
Пример 3:
Какое кратчайшее расстояние между кругом ( Икс + 3 ) 2 + ( у — 3 ) 2 знак равно 5 2 и точка Z ( — 2 , 0 ) ?
Сравните данное уравнение со стандартной формой уравнения круга,
( Икс — час ) 2 + ( у — k ) 2 знак равно р 2 куда ( час , k ) это центр и р это радиус.
Данный круг имеет центр в ( — 3 , 3 ) и имеет радиус 5 единицы.
Тогда кратчайшее расстояние D между точкой и кругом задается
D знак равно | 5 — ( — 3 — ( — 2 ) ) 2 + ( 3 — 0 ) 2 | знак равно | 5 — 1 + 9 | знак равно | 5 — 10 | ≈ 1.84
То есть кратчайшее расстояние между ними составляет около 1,84 единицы.
Пример 4:
Какое кратчайшее расстояние между кругом Икс 2 + у 2 — 8 Икс + 10 у — 8 знак равно 0 и точка п ( — 4 , — 11 ) ?
Перепишем уравнение круга в виде ( Икс — час ) 2 + ( у — k ) 2 знак равно р 2 куда ( час , k ) это центр и р это радиус.
Икс 2 + у 2 — 8 Икс + 10 у — 8 знак равно 0 Икс 2 — 8 Икс + 16 + у 2 + 10 у + 25 знак равно 8 + 16 + 25 ( Икс — 4 ) 2 + ( у + 5 ) 2 знак равно 49 ( Икс — 4 ) 2 + ( у + 5 ) 2 знак равно 7 2
Итак, круг имеет центр в ( 4 , — 5 ) и имеет радиус 7 единицы.
Тогда кратчайшее расстояние D между точкой и кругом задается
D знак равно | ( — 4 — 4 ) 2 + ( — 11 — ( — 5 ) ) 2 — 7 | знак равно | 64 + 36 — 7 | знак равно 100 — 7 знак равно 3
То есть кратчайшее расстояние между ними составляет 3 единицы.

College Algebra
Урок 34: Графики квадратичных функций
Цели обучения
После изучения этого руководства вы сможете:
Найдите вершину квадратичной функции.
Определите, является ли вершина максимальной или минимальной точкой квадратичного функция.
Постройте квадратичную функцию.
Введение

В этом уроке мы рассмотрим графики квадратичных функций. График квадратичной функции называется параболой и имеет искривленную форму. форма. Одна из основных точек параболы — ее вершина. Это самая высокая или самая низкая точка на графике. Ты можешь думать как конечная точка параболы.Я покажу вам, как найти вершина, а также ось симметрии, проходящая через эту точку. Я также освежу вашу память о том, как найти x — и y — перехватывает. Если вам нужен обзор Чтобы узнать, что такое перехват на графике, см. Учебное пособие по 26: Уравнения линий. При нахождении x -перехватов, вам придется решать квадратное уравнение. если ты нужен обзор решения квадратных уравнений, см. Учебное пособие 17: Квадратичные уравнения. Если вы изучаете алгебру в колледже класса, работа с квадратичными функциями неизбежна, даже если это против твоя религия. Так что, думаю, тебе лучше начать.
Учебник

Квадратичная функция
Квадратичная функция — это функция, которую
можно записать в виде
где a , b , и c
константы и

Обратите внимание, что в квадратичной функции на вашей независимой переменная, и это наивысшая степень.

Стандартная форма
Квадратичная функция

Иногда квадратичная функция записывается в стандартной форме. Можно оставить его в этой форме при работе с вашей проблемой. Я покажу вам, как построить параболу, используя любую форму.

График квадратичной функции

График квадратичной функции называется параболой . Это в основном представляет собой изогнутую форму, открывающуюся вверх или вниз.

Если у вас есть квадратичная функция в любой форме, ИЛИ,
если a > 0, , то парабола открывается с на ,
если a <0, , то парабола открывается на вниз на .

Вершина — самая низкая или самая высокая точка (в зависимости от направления) на графике квадратичной функции.
Нахождение вершины по форме ,:

Если квадратичная функция имеет вид ,, затем

вершина = .
В основном вы найдете значение x для сначала вершина, а затем просто вставьте это значение в функцию, чтобы получить y или функциональное значение вершины.
Нахождение вершины по форме:

Если ваша квадратичная функция имеет вид, затем
вершина = ( h , k ).

Каждая парабола симметрична относительно вертикальной линии, называемой осью. симметрии. Эта вертикальная линия проходит через вершину.
Думайте об этом как о зеркальном изображении этой вертикальной линии.

Следующие три графика иллюстрируют различные аспекты графика. квадратичной функции или параболы.

График функции:
Я хочу, чтобы вы отметили несколько моментов по этому поводу график:

Прежде всего, посмотрите, как вершина является самая низкая точка на графике.Он будет либо самым низким, либо высшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . На самом деле это не так часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, что есть , один y -перехват но нет x — перехват . Квадратичный функция может иметь один или два перехвата x .

График функции:
Я хочу, чтобы вы отметили несколько моментов по этому поводу график:

Прежде всего, посмотрите, как вершина является самая низкая точка на графике.Он будет либо самым низким, либо высшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . На самом деле это не так часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, что есть один y -перехват и один x — перехват . Квадратичный функция может иметь один или два перехвата x .

График функции:
Я хочу, чтобы вы отметили несколько моментов по этому поводу график:

Прежде всего, посмотрите, как вершина является высшая точка на графике.Он будет либо самым низким, либо высшая точка на графике квадратичной функции.
Во-вторых, посмотрите на ось симметрии . На самом деле это не так часть самого графика, но важна тем, что парабола создает зеркальное изображение об этом. Обратите внимание, как он симметричен относительно оси симметрии. Также обратите внимание, как он проходит через вершину.
В-третьих, обратите внимание, что есть , один y -перехват и два x -перехват . Квадратичный функция может иметь один или два перехвата x .

Пример 1 : Найдите координаты вершины. Без построения графиков определите, является ли вершина точкой максимума или минимума квадратичной функции.

* Стандартная форма квад. функция

Начиная с ( h , k ) это вершина в стандартном виде, как вы думаете, что наша вершина для этого проблема?
Если вы сказали (1, -3), вы правы.
Будьте осторожны со своими признаками этой проблемы. Это действительно соблазнительно сказать, что вершина равна (1, 3). Однако внимательно посмотрите на стандартная форма. Обратите внимание, что знак перед h — минус, а знак перед k — положительный. Итак, h — это число, которое мы вычитаем из x , который в нашем случае равен 1. k — это число мы добавляем в конце, в нашем случае мы добавляем отрицательное число 3.

Максимум или минимум?
Далее мы хотим определить, есть ли вершина, мы обнаружили, что (1, -3) является точкой максимума или минимума, без построения графиков.
Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.
Так как a = 4 и 4 больше 0, эта парабола раскрылась бы.
Значит ли это, что вершина является максимальной или минимальной? точка?
Если вы сказали минимум, вы правы.
Итак, наша вершина (1, -3) является точкой минимума.

Пример 2 : Найдите координаты вершины. Без построения графиков определите, является ли вершина точкой максимума или минимума квадратичной функции.

* Определить a , b , и c
* Вставить значения в форму вершины. для a , b , и c
* Подключите -5/4 для x , чтобы найти значение y вершины

Вершина будет.

Максимум или минимум?
Далее мы хотим определить, есть ли вершина, мы нашли« является максимумом или точка минимума, без построения графика.
Если мы знаем, в каком направлении открывается кривая, то может помочь нам ответить на этот вопрос.
Так как a = -2, и -2 меньше 0, эта парабола раскрылась бы вниз.
Значит ли это, что вершина является максимальной или минимальной? точка?
Если вы сказали максимальный балл, вы правы.
Итак, наша вершина — это максимальная точка.

Построение квадратичной функции

Шаг 3: Найдите точки перехвата.

Шаг 4: Постройте параболу.

Постройте точки, найденные на шагах 2 и 3, и проведите изогнутую линию через их.

Пример 3 : Используйте вершину и точки пересечения, чтобы нарисовать график квадратичная функция. Найдите уравнение для оси симметрии этой функции.

Поскольку a = -1 и -1 <0, то это выглядит как и , он будет изгибаться вниз.
Это дает нам хороший ориентир, чтобы знать, что мы идем в правильном направлении.

* Стандартная форма квадроцикла.функция

Начиная с ( h , k ) это вершина в стандартной форме, как вы думаете, что это за вершина?
Если вы сказали (-1, 4), вы правы.
Будьте осторожны со своими признаками этой проблемы. Обратите внимание, как знак перед h — минус, но один перед k положительный.Так что это число, которое мы вычитаем из x , что в нашем случае -1. k — это номер, который мы добавляем в конце, в нашем случае мы добавляем 4.

y -перехват
Напоминаем, что перехват y всегда где график пересекает ось y , что означает x = 0:

* Заменить x на 0

Перехват y — (0, 3).
x — интервал
Напоминаем, что перехват x всегда где график пересекает ось x , что означает y = 0:

Преобразование x — это (-3, 0) и (1, 0).

Ось симметрии
Как показано на графике, ось симметрии составляет x = -1.

Пример 4 : Используйте вершину и точки пересечения, чтобы нарисовать график квадратичная функция. Найдите уравнение для оси симметрии этой функции.

Поскольку a = 1 и 1> 0, то это выглядит как it собирается изогнуться.
Это дает нам хороший ориентир, чтобы знать, что мы идем в правильном направлении.

* Определить a , b , и c
* Вставить значения в форму вершины. для a , b , и c
* Подключите -1 для x , чтобы найти значение y вершины

Итак, вершина равна (-1, 1).

y -перехват
Напоминаем, что перехват y всегда где график пересекает ось y , что означает x = 0:

* Заменить x на 0

Перехват y — (0, 2).
x — интервал
Напоминаем, что перехват x всегда где график пересекает ось x , что означает y = 0:

* Заменить y (или f (x)) с 0

Обратите внимание, что это не фактор. Попробуем решить, используя квадратная формула:

Обратите внимание, как мы получили отрицательное число под квадратным корнем. Это означает, что вещественных чисел не существует. Это также означает, что НЕТ x -перехватов.

Ось симметрии
Как показано на графике, ось симметрии составляет x = -1.

Практические задачи

Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает как и все в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.
Чтобы получить максимальную отдачу от них, вы должны решить проблему на свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1a — 1b: Найти координаты вершины заданного квадратичная функция.Без построения графиков определите, является ли вершина точка максимума или минимума квадратичной функции.
Published in Разное
Предыдущая запись Устранение неполадок windows 8 при запуске долго: Запуск Windows 8 (8.1) в безопасном режиме
Следующая запись Как делать скриншот на asus: Три способа сделать скриншот на ZenFone
Ваш комментарий будет первым
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя*
Email*
Веб-сайт

Боковая панель
Поиск
Рубрики
Видео
Дешев
Дорогая
Комплектующ
Комплектующие
Конфигурац
Конфигурация
Питание
ПК
Проц
Процессор
Разное
Рекомендации по сборке
Самостоят
Сборка
Своими руками
Собрать
Совет
Советы
© 2019 iApple-59.ru

Модель ноутбука	Acer Predator Helios 300 Ph515-54-73XF
Страница продукта	Predator Helios 300
Процессор	Intel Core i7-11800H 2,3 ГГц (до 4,6 ГГц в Boost-режиме)
Оперативная память	32 ГБ, DDR4-3200
Дисплей	15,6″, 1920×1080, 144 Гц, IPS (LG LP156WFG-SPF3)
Видеокарта	NVIDIA GeForce RTX 3070 8 ГБ
Дисковая подсистема	RAID 0 2x SSD NVMe M. 2 Samsung MZVL21T0HCLR-00B07 1ТБ HDD SATA III WD20SPZX-21UA7TO 2 ТБ
Порты ввода/вывода	3x USB-A 3.2 Gen2 Type A, Thunderbolt 4 USB Type-C, HDMI 2.0, mini-DisplayPort 1.4, Ethernet, комбинированный аудиоразъем
Коммуникации	Gigabit Ethernet (Killer 2600), Wi-Fi 6 802.11ax (Killer 1650i), Bluetooth 5.2
Мультимедиа	Веб-камера 720p, стереодинамики, встроенный микрофон
Безопасность	Замок Kensington
Аккумулятор, мА•ч	3720 – 3815
Адаптер питания, Вт	230
Размеры, мм	363 x 255 x 23
Масса, кг	2,3
Стоимость	н/д

х	y = (x — 2) ²-25	(х, у)
— 4	y = (- 4-2) ²-25 = (- 6) ²-25 = 36-25 = 11	(- 4, 11)
— 3	y = (- 3 — 2) ² — 25 = (- 5) ² — 25 = 25 — 25 = 0	(- 3, 0)
— 2	y = (- 2 — 2) ² — 25 = (- 4) ² — 25 = 16 — 25 = — 9	(- 2, — 9)
— 1	y = (- 1-2) ²-25 = (- 3) ²-25 = 9-25 = — 16	(- 1, — 16)
0	y = (0 — 2) ² — 25 = (- 2) ² — 25 = 4 — 25 = — 21	(0, — 21)
2	y = (2 — 2) ² — 25 = (0) ² — 25 = — 25	(2, — 25)
4	y = (4-2) ²-25 = (2) ²-25 = 4-25 = — 21	(4, — 21)
6	y = (6-2) ²-25 = (4) ²-25 = 16-25 = — 9	(6, — 9)
8	y = (8-2) ²-25 = (6) ²-25 = 36-25 = 11	(8, 11)

Выражение	Описание
sin (x)	Синус x в радианах
cos (x)	Косинус x в радианах
желто-коричневый (x)	Тангенс x в радианах
asin (x), acos (x), atan (x)	Обратная из трех тригонометрических функций, перечисленных выше
sqrt (x)	Квадратный корень из x (только для положительного x)
журнал (x)	Натуральный логарифм x
pow (x, y)	Степень x к y

Свойство	Тип	Описание
alpha	float	Прозрачность
color или c	color	Цвет
fillstyle	{‘full’, ‘left’, ‘right’, ‘bottom’, ‘top’, ‘none’}	Стиль заливки
label	object	Текстовая метка
linestyle или ls	{‘-‘, ‘–‘, ‘-.’, ‘:’, ”, (offset, on-off-seq), …}	Стиль линии
linewidth или lw	float	Толщина линии
marker	matplotlib.markers	Стиль маркера
markeredgecolor или mec	color	Цвет границы маркера
markeredgewidth или mew	float	Толщина границы маркера
markerfacecolor или mfc	color	Цвет заливки маркера
markersize или ms	float	Размер маркера

Символ	Описание
‘.’	Точка (point marker)
‘,’	Пиксель (pixel marker)
‘o’	Окружность (circle marker)
‘v’	Треугольник, направленный вниз (triangle_down marker)
‘^’	Треугольник, направленный вверх(triangle_up marker)
‘<‘	Треугольник, направленный влево (triangle_left marker)
‘>’	Треугольник, направленный вправо (triangle_right marker)
‘1’	Треугольник, направленный вниз (tri_down marker)
‘2’	Треугольник, направленный вверх(tri_up marker)
‘3’	Треугольник, направленный влево (tri_left marker)
‘4’	Треугольник, направленный вправо (tri_right marker)
‘s’	Квадрат (square marker)
‘p’	Пятиугольник (pentagon marker)
‘*’	Звезда (star marker)
‘h’	Шестиугольник (hexagon1 marker)
‘H’	Шестиугольник (hexagon2 marker)
‘+’	Плюс (plus marker)
‘x’	Х-образный маркер (x marker)
‘D’	Ромб (diamond marker)
‘d’	Ромб (thin_diamond marker)
‘\|’	Вертикальная линия (vline marker)
‘_’	Горизонтальная линия (hline marker)

Символ	Описание
‘-‘	Сплошная линия (solid line style)
‘–‘	Штриховая линия (dashed line style)
‘-.’	Штрих-пунктирная линия (dash-dot line style)
‘:’	Штриховая линия (dotted line style)

Символ	Описание
‘b’	Синий
‘g’	Зеленый
‘r’	Красный
‘c’	Бирюзовый
‘m’	Фиолетовый (пурпурный)
‘y’	Желтый
‘k’	Черный
‘w’	Белый

x	y	x ² + y ²
5	0	5 ² + 0 ² = 25 + 0 = 25
3	4	3 ² + 4 ² = 9 + 16 = 25
0	5	0 ² + 5 ² = 0 + 25 = 25
−4	−3	(−4) ² + (−3) ² = 16 + 9 = 25
0	−5	0 ² + (−5) ² = 0 + 25 = 25