X y 0 график: математика — Как построить график функции f(x,y) = 0? — Магазин Apple iPhone в Перми

Коэффициенты k и b | 7 класс | Алгебра

Содержание

На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.

Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.

Например,

$y = \textcolor{blue}{5}x + \color{green}{10}$ – линейная функция
$\color{blue} k = 5$
$\color{green} b = 10$.

График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.

Коэффициент k

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

При $k > 0$ угол между графиком и осью $Ox$ меньше $90 \degree$ (острый)

При $k < 0$ угол между графиком и осью $Ox$ больше $90 \degree$ (тупой)

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.

Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.

Если $b > 0$, график сдвинут вверх,
если $b < 0$, то график сдвинут вниз.

На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

Частные случаи. b = 0

Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.

Подставим в формулу $x = 0$, получим: $$y = k \times 0$$

Значит, график будет проходить через начало координат $O(0;0)$.

Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.

{
    "questions": [{
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 2,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=2x$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 1,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=x$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0.  5,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=0.5x$[[graph]]"
    }]
}

k = 0

Если коэффициент $k = 0$, угол наклона также будет равен $0$.

Функция при этом принимает вид $y = 0 \times x + b$, то есть $y = b$.

Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.

{
    "questions": [{
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 2
                }
            }
        },
        "content": "Постройте график функции $y=2$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 1.
  5
                }
            }
        },
        "content": "Постройте график функции $y=1.5$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 0,
                    "b": 0
                }
            }
        },
        "content": "Постройте график функции $y=0$[[graph]]"
    }]
}

Таблица

Оценить урок

Поделиться уроком →

Что можно улучшить?

Изложение материала

Непонятное объяснение

Урок неполный, не хватает информации

Урок перегружен, слишком много информации

Тесты плохого качества

Тестов недостаточно

Тестов слишком много

Тесты слишком легкие

Тесты слишком сложные

Изображения

Изображения плохого качества

Изображений недостаточно

Изображений слишком много

Другое

Войдите, чтобы оценивать уроки

Что нужно исправить?

Спасибо, что помогаете нам стать лучше!

Проверим знания по теме?

Построение графиков функции y = kx

Комментарии

11.

Главная » 11 класс. Алгебра. » 11.3.1. Показательная функция, ее свойства и график

Показательная функция — одна из основных функций, изучаемая в школе и в ВУЗе. Познакомимся с основными понятиями и свойствами показательной функции, построим ее график.

Функцию вида y=a^x, где а > 0, a≠1, х – любое число, называют показательной функцией.
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R₊ — множество всех положительных чисел.
Показательная функция y=a^x возрастает при a > 1.
Показательная функция y=a^x убывает при 0 .

Справедливы все свойства степенной функции:

а⁰=1 Любое число (кроме нуля) в нулевой степени равно единице.
а¹=а Любое число в первой степени равно самому себе.
a^x∙a^y=a^x⁺^y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
a^x:a^y=a^x-^y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(a^x)^y=a^xy При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)^x=a^x∙b^y При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)^x=a^x/b^yПри возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
а^-х=1/a^x
(a/b)^-x=(b/a)^x.

Рассмотрим несколько примеров.

Содержание

Пример 1

1) Построить график функции y=2^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=2⁰=1; Точка А.

x=1, y=2¹=2; Точка В.

x=2, y=2²=4; Точка С.

x=3, y=2³=8; Точка D.

x=-1, y=2^-1=¹/₂=0,5; Точка K.

x=-2, y=2^-2=¹/₄=0,25; Точка M.

x=-3, y=2^-3=¹/₈=0,125; Точка N.

Большему значению аргумента х соответствует и большее значение функции у. Функция y=2^x возрастает на всей области определения D (y)=R, так как основание функции 2 > 1.

Пример 2

2) Построить график функции y=(¹/₂)^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=(½)⁰=1; Точка A.

x=1, y=(½)¹=½=0,5; Точка B.

x=2, y=(½)²=¼=0,25; Точка C.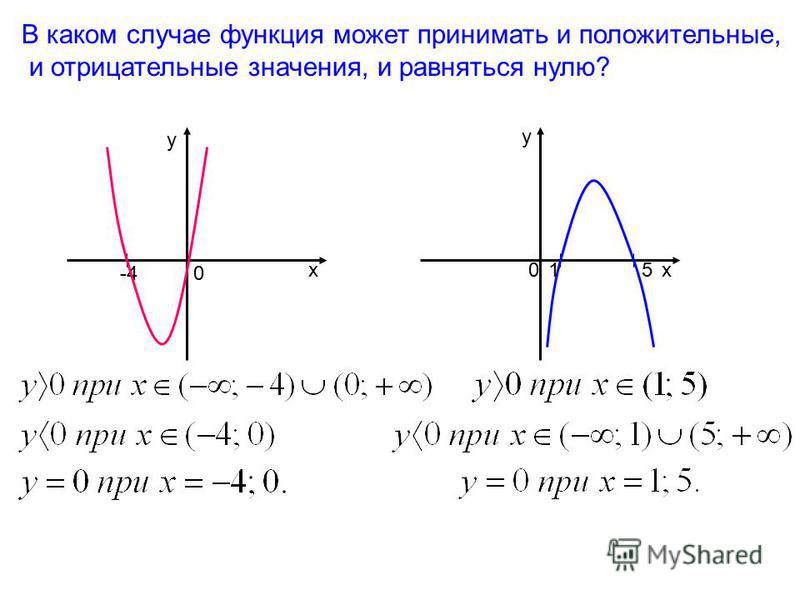

x=3, y=(½)³=1/8=0,125; Точка D.

x=-1, y=(½)^-1=2¹=2; Точка K.

x=-2, y=(½)^-2=2²=4; Точка M.

x=-3, y=(½)^-3=2³=8; Точка N.

Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(¹/₂)^xубывает на всей своей области определения: D (y)=R, так как основание функции 0 1/₂) .

Пример 3

3) В одной координатной плоскости построить графики функций:

y=2^x, y=3^x, y=5^x, y=10^x. Сделать выводы.

График функции у=2^х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R₊).

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a > 1) показательной функции у=а^х, тем ближе расположена кривая к оси Оу.

Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

Пример 4

4) В одной координатной плоскости построить графики функций:

y=(¹/₂)^x, y=(¹/₃)^x, y=(¹/₅)^x, y=(¹/₁₀)^x. Сделать выводы.

Смотрите построение графика функции y=(¹/₂)^x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.

Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R₊.

Чем меньше основание а (при 0 х, тем ближе расположена кривая к оси Оу.

Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Решить графически уравнения:

1) 3^x=4-x.

В одной координатной плоскости построим графики функций: у=3^х и у=4-х.

Графики пересеклись в точке А(1; 3).

Ответ: 1.

2) 0,5^х=х+3.

В одной координатной плоскости строим графики функций: у=0,5^х

(y=(¹/₂)^x )

и у=х+3.

Графики пересеклись в точке В(-1; 2).

Ответ: -1.

Найти область значений функции: 1) y=-2^x; 2) y=(¹/₃)^x+1; 3) y=3^x+1-5.

Решение.

1) y=-2^x

Область значений показательной функции y=2^x – все положительные числа, т.е.

0 x

— ∞ x

Ответ: Е(у)=(-∞; 0).

2) y=(¹/₃)^x+1;

0 1/₃)^x1, получаем:

0+1 1/₃)^x+1 1;

1 1/₃)^x+1

Ответ: Е(у)=(1; +∞).

3) y=3^x⁺¹-5.

Запишем функцию в виде: у=3^х∙3-5.

0 x 3:

0∙3 x∙3 3;

0 x∙3 5:

0-5 x∙3-5 -5;

— 5 x∙3-5

Ответ: Е(у)=(-5; +∞).

Смотрите Карту сайта, и Вы найдете нужные Вам темы!

Как построить график $x-y=0$?

Последняя обновленная дата: 20 марта 2023 г.

•

Общее представление: 239,4K

•

Просмотр сегодня: 5,17K

Ответ

Проверено

239,4K+ виды

HINT: 9003 данное уравнение даст точки пересечения x и y прямой $x- y=0$. Мы изменим его на форму $\dfrac{x}{p}+\dfrac{y}{q}=1$, чтобы найти точку пересечения x и точку пересечения y линии как $p$ и $q$ соответственно.
Затем расставляем точки по осям и оттуда проводим линию на графике.

Полное пошаговое решение:
Мы используем общее уравнение прямой, чтобы понять наклон и форму пересечения прямой
$x-y=0$.
Мы переходим от уравнения $x-y=0$ к $y=x$.
Данное уравнение имеет вид $y=mx+k$. м — уклон линии. Наклон линии равен 1.
Нам нужно найти точку пересечения по осям x и y линии $x-y=0$.
Для этого преобразуем данное уравнение в вид $\dfrac{x}{p}+\dfrac{y}{q}=1$. Из формы мы получаем, что точки пересечения x и y линии будут равны $p$ и $q$ соответственно. Точки будут $\left( p,0 \right),\left( 0,q \right)$.
Данное уравнение равно $x-y=0$. Преобразуя в вид $\dfrac{x}{p}+\dfrac{y}{q}=1$,
получаем
$\begin{align}
& x-y=0 \\
& \Rightarrow \dfrac {x}{0}+\dfrac{y}{0}=1 \\
\end{align}$
Мы не находим пересечений, так как форму создать невозможно. Это означает, что линия пересекает оси в одной и той же точке. Мы видим, что линия проходит через начало координат $\left( 0,0 \right)$. Прямая $x-y=0$ пересекает оси в точке $\left( 0,0 \right)$.

Примечание: Линия, параллельная оси X, не пересекает ось X ни на каком конечном расстоянии. Следовательно, мы не можем получить какой-либо конечный x-отрезок такой прямой. То же самое касается линий, параллельных оси Y. В случае наклона линии диапазон наклона составляет от 0 до $\infty $.

Недавно обновленные страницы

Рассчитать изменение энтропии, связанное с преобразованием 11 класса химии JEE_Main

Закон, сформулированный доктором Нернстом, является первым законом термодинамики 11 класса химии JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении А класс 11 химии JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химии JEE_Main

Для реакции rm2Clg в rmCrmlrm2rmg знаки перехода 11 класса 9 JEE_Main жидкой воды 11 класс химии JEE_Main

Рассчитать изменение энтропии при преобразовании 11 класса химии JEE_Main

Закон, сформулированный доктором Нернстом, является первым законом термодинамики 11 класс химии JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении А класс 11 химии JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химии JEE_Main

Для реакции rm2Clg в rmCrmlrm2rmg знаки перехода 11 класса 9 JEE_Main жидкой воды класс 11 химия JEE_Main

Актуальные сомнения

Решение уравнений вида xy = 0

Очень важным типом уравнения является уравнение вида ‘$\,xy = 0\,$’. В этом типе уравнения ноль с одной стороны (обычно правая сторона), и

вещи умножаются на с другой стороны.
Как предложение такой формы может быть истинным? Чтобы ответить на этот вопрос, рассмотрим следующее. Предположим, я сказал бы вам:
Я думаю о двух числах. Когда я перемножаю эти числа вместе, я получаю ноль.
Можете ли вы сказать мне что-нибудь о числах, о которых я думаю? Действительно! Единственный способ, которым числа могут умножаться, чтобы дать ноль, это если хотя бы одно из чисел равно нулю:

$3\cdot 0 = 0$ $0\cdot\frac12 = 0$ $0\cdot 0 = 0$ $(3. 7)\cdot 0 = 0$ и так далее $\ldots$
То есть для приговора ‘$\,xy = 0\,$’, чтобы быть правдой, или $\,x\,$ должны равняться $\,0\,$ или $\,y\,$ должны равняться $\,0\,$ или оба должны быть равны нулю.
«Официальное» заявление об этом свойство называется законом нулевого фактора. Не беспокойтесь прямо сейчас, если формальное заявление ниже не имеет смысла для вас. Вы научитесь «переводить» его на предстоящие разделы.

Закон нулевого фактора
Пусть $\,x\,$ и $\,y\,$ — действительные числа. Затем: $$ \cssId{s30}{xy = 0}\ \ \ \ \cssId{s31}{\text{эквивалентно}}\ \ \ \ \cssId{s32}{(x = 0\ \text{ или }\ y = 0)} $$
Имея в виду эту идею, рассмотрим уравнение:

$\,х(х-1) = 0\,$
Вещи умножаются на левая сторона это:
$\,x\,$ и $\,x-1\,$
Чтобы уравнение было верным, либо:
$\,x = 0\,$ или $\,x-1 = 0\,$
Следовательно, единственными числами, которые делают уравнение верным, являются $\,0\,$ и $\,1\,.$
Примечание
При представлении уравнения типа ‘$\,х(х-1) = 0\,$’ или ‘$\,(x-2)(x+3) = 0\,$’, первая реакция многих людей чтобы начать умножать левую часть.
ПРОТИВ ЭТОГО ИСКУШЕНИЯ! Умножение дает абсолютно бесполезно (за исключением, возможно, предоставления потренироваться с умножением многочленов).
Правильный мыслительный процесс: Ах ха! У меня вещи УМНОЖАЮТСЯ что равно НОЛЬ. Итак… одно из умножаемых вещей должно равен нулю!
Пример
Вопрос:
Определите значения $\,x\,$, для которых верно предложение: $(х-1)(х+3) = 0$

Решение:
Что делает $\,x-1\,$ равным нулю? Ответ: $\,1$
Что делает $\,x + 3\,$ равным нулю? Ответ: $\,-3$
Таким образом, значения $\,x\,$, для которых предложение истинно: $\,1,-3$
Практика
В веб-упражнении вы должны:
Расположите решения в порядке слева направо в уравнении;
Поставьте запятую между цифрами;
Перечислите повторяющиеся ответы каждый раз, когда они встречаются.

X y 0 график: математика — Как построить график функции f(x,y) = 0?