Таблица для построения графика функции: Построение графиков в Excel по данным таблицы

Функции. Графики функций. Диаграммы 9 класс онлайн-подготовка на Ростелеком Лицей

Вставка формул в таблицу, мастер форм

Мы уже знаем, что в электронных таблицах можно вводить в ячейки выражения и вычислять их значение. В ячейки также можно вводить функции, в том числе и стандартные, это удобно делать с помощью мастера. Мастер – это удобное средство для прохождения всех этапов создания документа или его фрагмента в диалоговом режиме.

На первом этапе мастер откроет окно «Мастер функций», в котором мы можем выбрать категорию функции, саму функцию и посмотреть, какие у этой функции аргументы и каково ее назначение. В этом диалоговом окне мы увидим формат функции, то есть правило ее записи. Формат определяет, какие у функции аргументы, какие между аргументами разделители и в каком порядке эти аргументы следует записать. Следует отметить, что разделители очень важны и их нужно строго соблюдать, т. к. если поставить, например, запятую вместо точки с запятой, функция не будет корректно работать.

На втором этапе мастер поможет правильно подобрать аргументы и ввести их.

При записи функции также важно соблюдать количество скобок. Количества закрывающих и открывающих скобок должны быть равны. Это несложно отследить, так как пары скобок обычно бывают разных цветов.

Кроме того, важно правильно указать название функции. Например, если написать «Сумма» вместо стандартного «sum», результат не будет получен, т. к. название «Сумма» отсутствует в списке стандартных функций.

Если при записывании формулы допущены ошибки, появится окно с сообщением об ошибках и советами по их исправлению. Если ошибки исправить не удалось, лучше удалить формулу, составить и записать ее заново, так как допущенные ошибки не дадут продолжить работу и сохранить документ.

Построение и форматирование круговой диаграммы

Для наглядного представления результатов вычислений удобно использовать графики и диаграммы. Строить их можно с помощью мастера или команды Вставка главного меню программы.

Для примера построим диаграмму распределения населения Петербурга в 1869 году по сословиям. Построим соответствующую таблицу (рис. 1):

Рис. 1. Таблица с данными

Выделяем столбец с названиями сословий и столбец с кол-вом населения, выполняем данное действие, удерживая клавишу Ctrl (рис. 2):

Рис. 2. Выделение данных

Теперь во вкладке «вставка» выбираем круговую диаграмму (рис. 3):

Рис. 3. Выбор типа диаграммы

Получен результат (рис. 4):

Рис. 4. Диаграмма распределения населения

На полученной диаграмме можно выполнять форматирование, причем как всей диаграммы, так и отдельных ее элементов. Отформатируем один сектор. Для этого щелкнем по нему правой кнопкой мыши и выберем Формат точки данных. В открывшемся диалоговом окне выбираем пункт «заливка», далее «сплошная заливка» и изменяем цвет произвольно (рис. 5):

Рис. 5. Форматирование диаграммы

Теперь выберем все сектора, щелкнем правой кнопкой мыши и выберем Добавить подписи данных (рис. 6):

Рис. 6. Форматирование диаграммы

Изменим формат подписей. Выберем не значение, а проценты (рис. 7):

Рис. 7. Форматирование диаграммы

Размещение на листе электронной таблицы диаграммы приведет к появлению на ленте вкладок Конструктор и Макет. Они видны, когда диаграмма выделена.

Здесь расположены команды для форматирования и редактирования диаграмм (рис. 8).

Рис. 8. Дополнительные вкладки

Построение и форматирование гистограммы

Построим столбчатую диаграмму (гистограмму) соотношения мужчин и женщин в дворянском сословии. Выделяем данные, выбираем соответствующую диаграмму и получаем результат (рис. 9):

Рис. 9. Построение гистограммы

Вид диаграммы нас не вполне устраивает. Выполним форматирование (рис. 10). Для начала щелкнем правой кнопкой мыши по диаграмме и выберем Выбор данных.

Рис. 10. Форматирование гистограммы

В появившемся диалоговом окне меняем местами строки и столбцы нажатием на соответствующую кнопку. Далее в поле подписи горизонтальной оси нажимаем Изменить и вводим нужное нам название – дворяне. Получена гистограмма (рис. 11):

Рис. 11. Гистограмма распределения мужчин и женщин

Построение графика функции

Теперь рассмотрим построение графиков функций. Построим график функции . Сначала вводим нужные значения в табличку. Столбец значений аргумента заполним вручную. Для заполнения значений функции введем формулу. Для этого выбираем нужную ячейку, пишем знак равно, далее нажимаем на ячейку с соответствующим значением аргумента, вставляем значок возведения в степень и показатель степени 3 (рис. 12):

Рис. 12. Заполнение таблицы

Теперь мы можем скопировать формулу и вставить ее во все остальные поля. Для этого на поле с формулой нажимаем правой кнопкой мыши и выбираем «копировать». Далее на следующем поле нажимаем правой кнопкой мыши, выбираем «специальная вставка» и вставляем формулы. Но можно поступить проще: берем ячейку с формулой за правый нижний угол и растягиваем на весь столбец. Так, получена таблица (рис. 13):

Рис. 13. Таблица значений для построения графика функции

Отметим, что при копировании ссылка изменилась в соответствии с номером строки, в которой находится ячейка с формулой. Такая ссылка называется относительной.

Для построения графика выделяем данные, переходим на вкладку вставка, выбираем график и его тип (рис. 14):

Рис. 14. Построение графика функции

Получен график (рис. 15):

Рис. 15. График функции

На полученном графике ось абсцисс подписана неверно. Щелкнем по графику правой кнопкой мыши и выберем Выбрать данные. В появившемся диалоговом окне в поле Подписи по горизонтальной оси нажимаем Изменить, выбираем нужные нам значения в столбце х и получаем график (рис. 16):

Рис. 16. График функции

Итак, мы рассмотрели некоторые возможности электронных таблиц, а именно построение диаграмм и графиков функций. На следующем уроке мы продолжим рассматривать возможности электронных таблиц.

 

Список литературы

1. Угринович Н.Д. Информатика-9. – М.: БИНОМ. Лаборатория знаний, 2012.
2. Гейн А.Г., Юнерман Н.А. Информатика-9. – М.: Просвещение, 2012.
3. Соловьёва Л.Ф. Информатика и ИКТ. Учебник для 9 класса. – СПб.: БХВ-Петербург, 2007.

 

Домашнее задание

1. Построить график функции: А) Б) В)
2. Построить круговую диаграмму для распределения территории Украины по природным зонам (степь, лесостепь и т. д.)
3. Построить гистограмму численности населения Великобритании за 2005–2010 гг.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Teachexcel.ru (Источник).
2. Интернет-портал Support.office.microsoft.com (Источник).

075. Способы построения графиков функций

Анализ графиков элементарных функций показывает, что если известен график функции , то при помощи геометрических преобразований можно построить график более сложной функции.

Рассмотрим некоторые способы построения графиков при помощи геометрических преобразований.

1. График функции получается из графика увеличением всех ординат этого графика в раз, если и уменьшение ординат графика в раз, если (рис. 5.47).

Пример 3. Постройте график функции .

Решение. Сначала построим график функции .

Увеличим все ординаты этого графика в 2 раза и получим график функции (рис. 5.48).

Ответ. График функции показан на рис. 5.48 сплошной линией.

2. График функции получается из графика сжатием графика вдоль оси , если и растяжением графика вдоль оси , если .

Пример 4. Постройте графики функций и .

Решение

. Составим таблицу некоторых значений функций и (табл. 5.3).

Таблица 5.3 – Значения функций , ,

Для функции основным периодом будет . Тогда основной период функции равен , а основной период функции равен .

По данным таблицы 5.3 построим графики всех трех функций (рис. 5.49).

Вывод. Из графика функции сжатием его вдоль оси получается график функции , а график функции получается растяжением графика функции вдоль оси

Ответ. График функции показан на рис. 5.49 точечной линией. График функции показан на рис. 5.49 пунктирной линией.

3. График функции Получается сдвигом графика вдоль оси на величину влево (в отрицательном направлении оси ), если и вправо (в положительном направлении оси ), если .

Пример 5. Постройте графики функций и .

Решение

. Составим таблицу некоторых значений функций и (табл. 5.4).

Таблица 5.4 – Значения функций , ,

	–4	–3	–2	–1	0	1	2	3	4
	36	25	16	9	4	1	0	1	4
	16	9	4	1	0	1	4	9	16
	4	1	0	1	4	9	16	25	36

Построим графики этих функций по данным таблицы 5.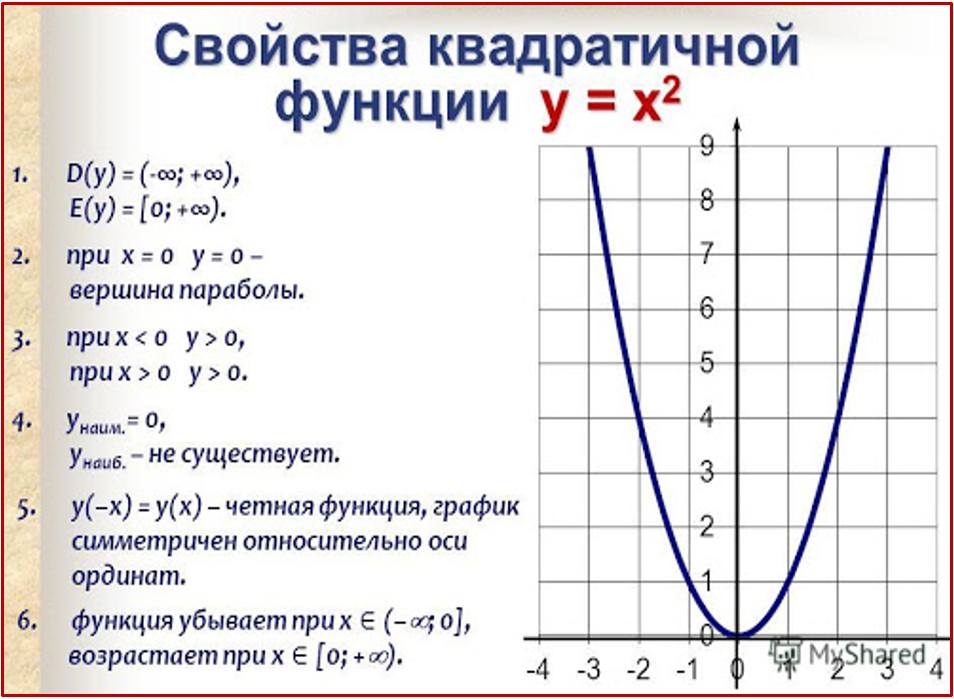 4 (рис. 5.50).

Вывод. График функции получается сдвигом графика на 2 единицы вдоль оси влево (в отрицательном направлении оси ), а график функции получается сдвигом графика на 2 единицы вдоль оси вправо (в положительном направлении оси ).

Ответ. График функции показан на рис. 5.50 точечной линией. График функции показан на рис. 5.50 пунктирной линией.

Пример 6. Постройте график функции .

Решение. Сначала построим график функции . Сдвинем его на 3 единицы влево (по правилу построения графика функции ). При этом вертикальная асимптота гиперболы тоже сдвинется на 3 единицы влево. Следовательно, график функции имеет две асимптоты: и . Найдем координаты точки пересечения графика с осью : ; .

Ответ. График функции показан на рис. 5.51 сплошной линией.

4. График функции Получается сдвигом графика на величину в положительном направлении оси (вверх), если и в отрицательном направлении оси (вниз), если .

Пример 7. Постройте графики функций и .

Решение. Составим таблицу некоторых значений функций , и (табл. 5.5).

Таблица 5.5 – Значения функций , ,

	–3	–2	–1	0	1	2	3
	7	2	-1	-2	-1	2	7
	9	4	1	0	1	4	9
	11	6	3	2	3	6	11

Построим графики этих функций по данным таблицы 5.5 (рис. 5.52).

Вывод. График функции получается сдвигом графика на 2 единицы вниз вдоль оси а график функции получается сдвигом графика на 2 единицы вверх вдоль оси .

Ответ. График функции показан на рис. 5.52 пунктирной линией. График функции показан на рис. 5.52 точечной линией.

Пример 8. Постройте график функции .

Решение. Сначала построим график функции . Сдвинем его на 2 единицы вниз (по правилу построения графика функции ). При этом горизонтальная асимптота гиперболы тоже сдвинется на 2 единицы вниз. Следовательно, график функции имеет две асимптоты: и . График функции пересекает ось .

При получим: , т. е. (рис. 5.53).

Ответ. График функции показан на рис. 5.53 сплошной линией.

5. График функции Получается симметричным отображением графика функции относительно оси .

Пример 9. Постройте графики функций и .

Решение. Составим таблицу некоторых значений этих функций (табл. 5.6).

Таблица 5.6 – Значения функций та

	1	2	3	4	5
	6	3	2	3	6
	-6	-3	-2	-3	-6

Построим графики этих функций по данным таблицы 5.6 (рис. 5.54).

Вывод. График функции получается симметричным отображение графика относительно оси .

Ответ. График функции показан на рис. 5.54 сплошной линией. График функции показан на рис. 5.54 пунктирной линией.

Пример 10. Постройте график функции .

Решение. Построим одну полуволну графика функции . Произведем ее сжатие вдоль оси с коэффициентом 3 и растяжение вдоль оси с коэффициентом 2, а затем симметричное преобразование относительно оси Получим график функции (рис. 5.55 а).

На рисунке 5.55 а показана одна полуволна графика, а на рисунке 5.55 б – весь график.

Ответ. График функции показан на рис. 5.55 (б) сплошной линией.

6. График функции получается симметричным отображением графика функции относительно оси .

Пример 11. Постройте графики функций и .

Решение. Составим таблицу некоторых значений этих функций (табл. 5.7).

Таблица 5.7 – Значения функций та

	–3	–2	–1	0	1	2	3
				1	2	4	9
	9	4	2	1

Построим графики этих функций по данным табл.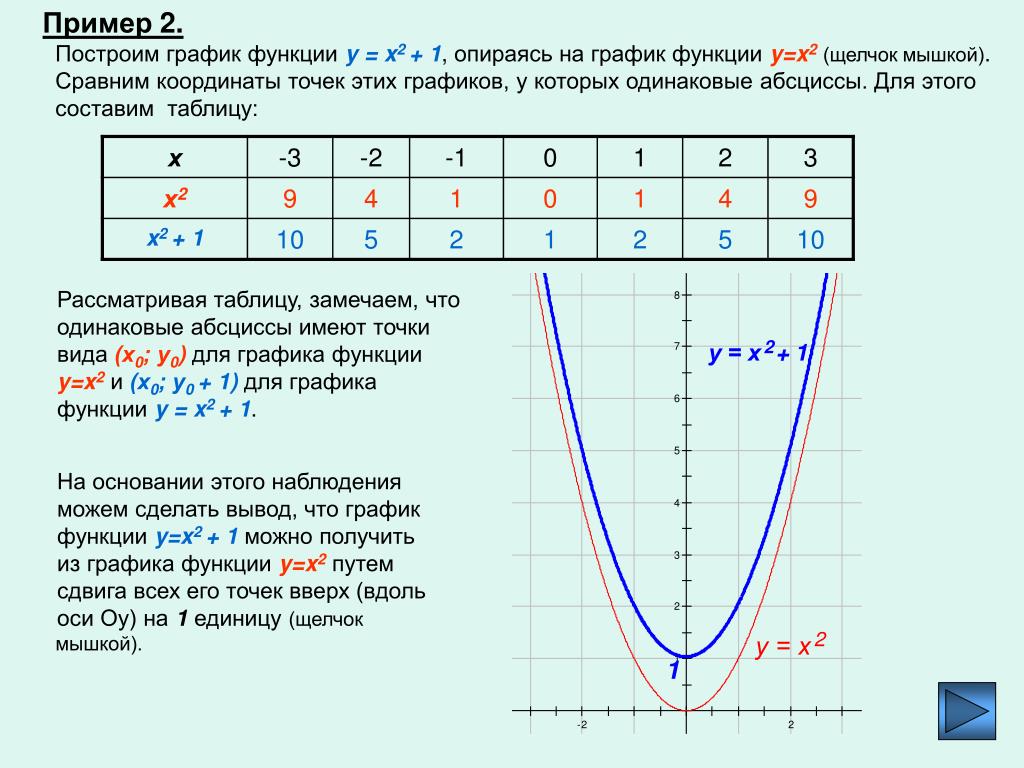 5.7 (рис. 5.56).

Вывод. График функции получается симметричным отображение графика относительно оси .

Ответ. График функции показан на рис. 5.56 сплошной линией. График функции показан на рис. 5.56 пунктирной линией.

Пример 12. Постройте график функции .

Решение. Строим график функции и симметрично отображаем его относительно оси .

Ответ. График функции показан на рис. 5.57 сплошной линией.

7. График функции получается из графика функции симметричным отображением относительно оси части графика, которая лежит под осью (). Часть графика над осью () остается без изменений.

Пример 13. Постройте график функции .

Решение. Составим таблицу некоторых значений функции (табл. 5.8).

Таблица 5.8 – Значения функции

	0	1	2	3	4
	3	0	-1	0	3

Из решения уравнения находим, что нулями функции будут два значения: и .

Найдем координаты вершины параболы:

; .

По полученным результатам построим график функции (рис. 5.58).

Интервалами положительности для этой функции будут интервалы . Интервалом отрицательности будет .

Из определения модуля функции запишем:

На интервале значения функций и совпадают и по величине и по знаку, а на интервале значения функций совпадают по величине, но противоположны по знаку.

Вывод. График функции получается из графика функции симметричным отображением относительно оси той части графика, которая лежит ниже оси .

Ответ. График функции показан на рис. 5.58 сплошной линией.

8. График функции получается из графика функции так: график функции сохраняется только при , и отображается симметрично относительно оси (рис. 5.59).

Пример 14. Постройте график функции .

Решение. Учитывая определение модуля, функцию можно записать так:

Составим таблицу значений функции по этим формулам на соответствующих интервалах (табл. 5.9).

Таблица 5.9 – Значения функции

	-3	-2	-1	0	1	2	3
	4	1	0	1	0	1	4

По данным этой таблицы построим график функции (рис. 5.60).

Вывод. Как видно из рис. 5.60 график функции получается из графика функции симметричным отображение части графика при относительно оси .

Ответ. График функции показан на рис. 5.60 сплошной линией.

Пример 15. Постройте график функции .

Решение. Заданная функция содержит как модуль аргумента, так и модуль функции.

Перепишем формулу заданной функции в виде: .

Построим параболу квадратичной функции без модуля аргумента. Это будет график функции , смещенный на 1 вправо вдоль оси и на 4 вниз вдоль оси . Осью симметрии графика будет прямая . Координатами вершины параболы будут и (рис. 5.61).

График функции будет получен из графика симметричным отображением части графика при относительно оси (рис. 5.62).

График модуля функции получается симметричным отображением относительно оси части графика функции , которая находится под осью (рис. 5.63).

Ответ. График функции показан на рис. 5.63 сплошной линией.

< Предыдущая		Следующая >

Table View – GeoGebra

Автор:

GeoGebra Team

Тема:

Функции, График функций

Что такое Table View?

Создайте таблицу значений для функции, используя табличное представление графического калькулятора GeoGebra ! С Table View вы можете. ..

• создать таблицу значений в указанном диапазоне
• показать/скрыть сгенерированные точки в Graphics View
• изменить функцию
• изменить диапазон значений

Изучите таблицу значений функций, открыв табличное представление . Затем следуйте инструкциям, чтобы шаг за шагом научиться использовать табличное представление .

Исследуйте конструкцию…

Инструкции

1.		Введите в строке ввода и нажмите Введите . Функция будет автоматически помечена как f(x) и отображается в графическом представлении .
2.		Откройте контекстное меню, нажав кнопку Еще справа от строки, содержащей f(x) .
3.		Выбрать Таблица значений .
4.		Откроется диалоговое окно, в котором вы можете определить Начальное значение для x , Конечное значение для x и Шаг . Нажмите OK для подтверждения настроек.
5.		Таблица открывается автоматически, поэтому вы можете сразу увидеть значения.
6.		Вернитесь к Algebra View , введите в строку ввода и нажмите Enter . Функция будет автоматически помечена как g(x) и отображена в графическом представлении 9.0018 .
7.		Откройте контекстное меню, нажав кнопку Еще справа от строки, содержащей g(x) .
8.		Выбрать Таблица значений .
		 Примечание: На этот раз диалоговое окно для определения начального и конечного значений не будет отображаться, поскольку вы уже установили эти значения на шаге 4. Вы можете изменить значения позже.
10.		Таблица открывается автоматически, поэтому вы можете сразу увидеть значения.

Попробуйте сами…

Параметры

Переключитесь на Табличное представление , чтобы изменить следующие параметры. Изменить диапазон значений

1.		Откройте контекстное меню, нажав кнопку Еще рядом с x. 
2.		Выбрать Редактировать .
3.		Откроется диалоговое окно, в котором вы можете изменить Начальное значение для x , Конечное значение для x и Шаг . Нажмите OK для подтверждения настроек.

Показать/скрыть точки в Графический вид

1.		Откройте контекстное меню, нажав кнопку Еще рядом с функцией, для которой вы хотите скрыть точки, например. ф(х) . 
2.		 Выберите Скрыть точки .
 3.		 Точки теперь не отображаются в графическом виде . Чтобы показать их снова, откройте контекстное меню, нажав кнопку Кнопка «Дополнительно» и выберите Показать точки.

Редактировать функцию

1.		Откройте контекстное меню, нажав кнопку Еще рядом с функцией, которую вы хотите изменить, например. ф(х) . 
2.		Выбрать Редактировать .
3.		Algebra View открывается автоматически. Теперь вы можете редактировать функцию.

Удалить столбец

1.		Откройте контекстное меню, нажав кнопку Еще рядом с функцией, которую вы хотите удалить из табличного представления , например. ф(х) .  
2.		Выбрать Удалить столбец .
3.		Теперь столбец удален из Table View . Примечание: Сама функция не удаляется из Algebra View . Вы можете снова сгенерировать таблицу значений, следуя приведенным выше инструкциям.

Расширение табличного представления

Если вам не нужно графическое представление , вы можете расширить табличное представление на весь экран, чтобы у вас было больше места для ввода и исследований.

Рисование графиков с помощью SciDAVis

Двухмерный график основан на кривых, которые определяются значениями Y как функциями значений X. Существует два способа получения 2D-графика в зависимости от способа определения значений (X,Y):

SciDAVis создаст новое окно графика, и график будет вставлен в новый слой

После создания графика , вы можете настроить все графические элементы графика с помощью команд меню «Формат». Вы можете добавлять новые элементы (текстовые метки, линии или стрелки, новую легенду, изображения) на график с помощью команд меню График.

Данные должны храниться в таблице. Есть несколько возможностей вставить ваши значения (X,Y) в таблицу: вы можете написать их прямо с клавиатуры или прочитать их из файла. Здесь мы будем использовать первое решение, обратитесь к команде Import ASCII , чтобы использовать второе.

Первым шагом является создание пустого проекта с помощью команды New -> New Project из меню File, также можно использовать клавишу Ctrl-N или значок на панели инструментов File. Затем создайте новую таблицу с Создать -> Новая таблица из меню Файл или с помощью Ctrl-T или с помощью значка на панели инструментов Файл.

При создании таблица имеет два столбца (один для X и один для Y) и 32 строки. Вы можете добавлять строки и столбцы, выбирая строку или столбец и используя правую кнопку мыши, вы также можете изменить количество строк и столбцов с помощью команды строк и команды столбцов из меню Таблица.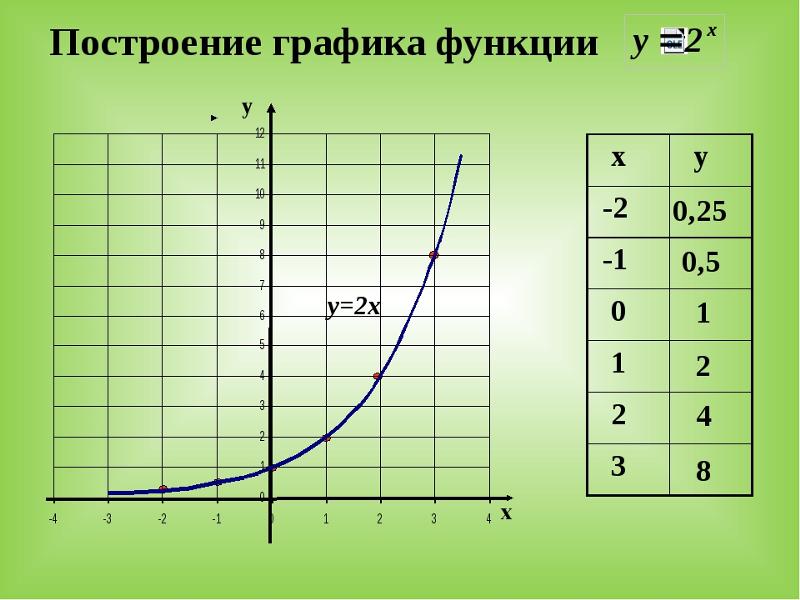 Вы вводите свои значения и получаете эту таблицу:

Рис. 2-1. Простой 2D-график: таблица.

Вы должны выбрать два столбца и построить свой график (здесь простой 2D-разброс) с помощью команды Scatter из контекстного меню, или щелкнув соответствующий значок на панели инструментов График или с помощью кнопки Команда Scatter из меню Plot. Создается график, который использует параметры по умолчанию для всех элементов. Вы можете настроить эти параметры по умолчанию в диалоговом окне настроек. С параметрами по умолчанию вы получите следующий график:

Рис. 2-2. Простой 2D-график: график по умолчанию.

Затем вы можете настроить свой график. Двойным щелчком по точкам открывается диалоговое окно Пользовательские кривые, которое используется для изменения символов. Затем двойной щелчок по осям открывает диалоговое окно общих параметров графика, и вы можете изменить масштабы, шрифты для меток осей и т. д. Вы также можете добавить линии сетки на оси X или Y и т. д. Наконец, двойной щелчок на каждом текстовом элементе (заголовок X, заголовок Y, заголовок сюжета) позволяет изменить текст и представление этих элементов. Окончательный сюжет:

Рис. 2-3. Простой 2D-сюжет: сюжет закончен.

Наконец, вы должны сохранить свой проект в файле ‘.sciprj’ с помощью команды Сохранить проект из меню Файл или с помощью Ctrl-S или с помощью значка на панели инструментов Файл. В зависимости от вашего приложения вы можете экспортировать свой график в стандартный файл изображения с помощью команды Export Graph -> Current из меню File (или с помощью кода клавиши Alt-G).

Существует несколько типов графиков, которые можно построить из таблицы. Они представлены в меню График

Для данных можно использовать до четырех осей:

Рисунок 2-4. Двухмерный график с двумя осями Y.

В дополнение к уже описанной настройке оси, которые используются для каждой кривой, были определены с помощью диалогового окна «Пользовательские кривые», а две стрелки были добавлены с помощью команды Draw Arrow .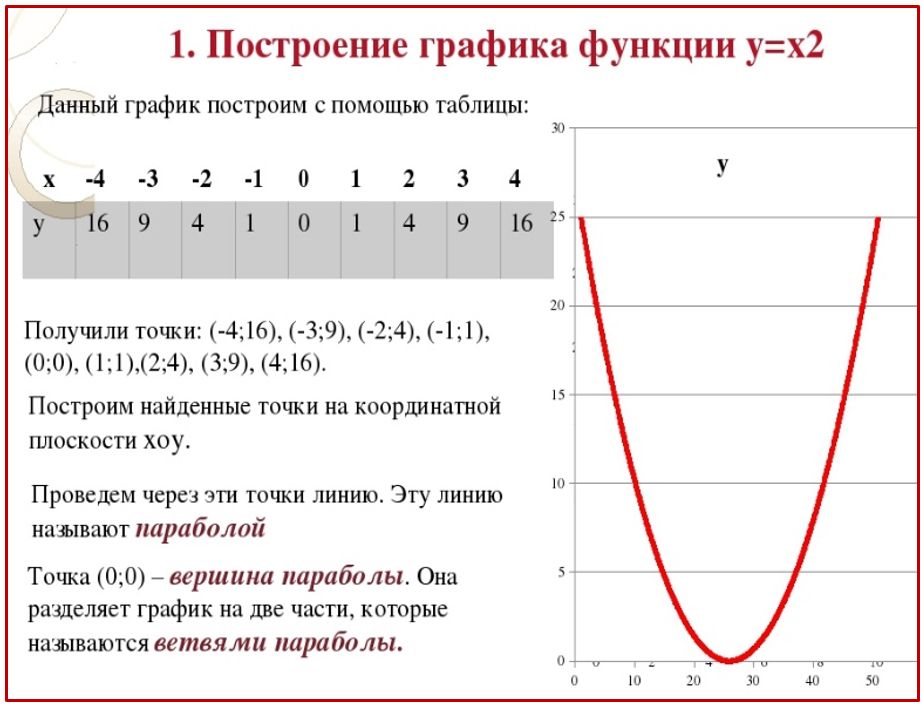

Есть два способа получить такой график: вы можете построить график непосредственно функции или заполнить таблицу значениями, рассчитанными по этой функции, прежде чем строить график классическим способом.

Прямой график функции.

Если вы просто хотите построить график функции, вы можете использовать команду New -> New Function Plot из меню File или с помощью Ctrl-F или значка на панели инструментов File.

Эта команда открывает диалоговое окно «Добавить кривую функции». Затем вы можете ввести выражение вашей математической функции, диапазон X, используемый для графика, и количество точек, используемых в этом диапазоне X. Помимо классических функций Y=f(X), могут быть определены параметрические и полярные функции.

Рис. 2-5. Прямой график функции.

Заполнение таблицы значениями функции.

Если вы просто хотите работать не только с графиком, но и с данными, вы можете создать новую таблицу, как описано в предыдущем разделе.