Преобразование графиков функций — подготовка к ЕГЭ по Математике
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
1. Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
2. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
3. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если
4. Растяжение (сжатие) по вертикали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.
5. Отражение по горизонтали.
График функции симметричен графику функции относительно оси Y.
6. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
7. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике.
Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1.
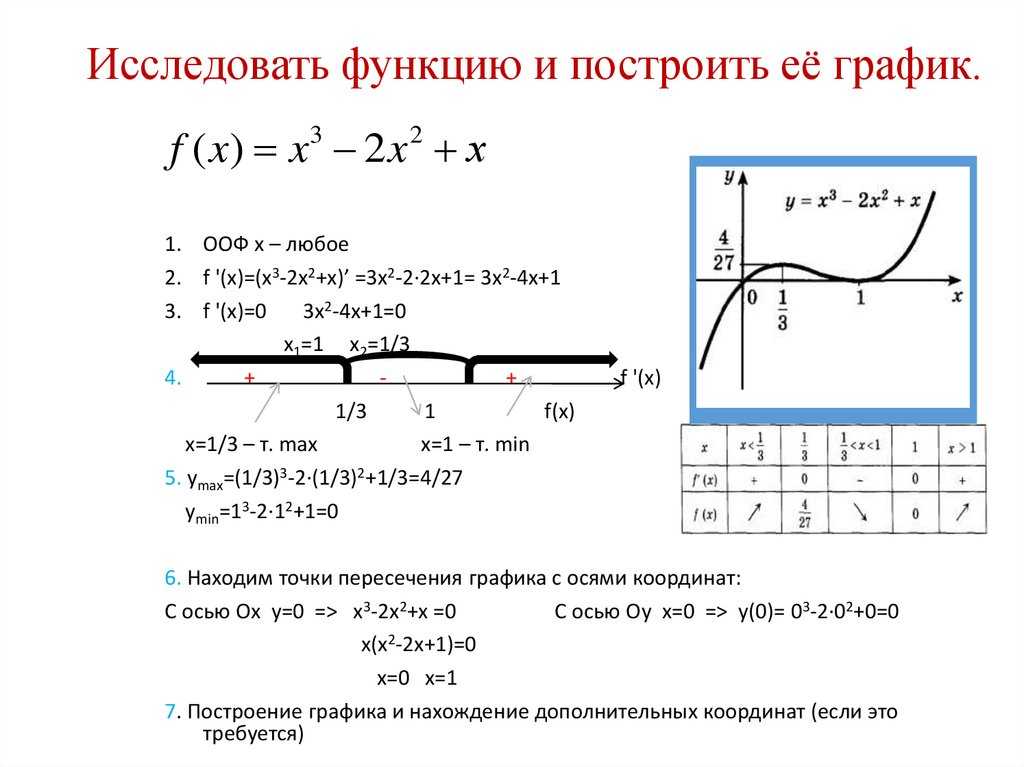Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
Продолжение — в статье «Построение графиков функций».
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Преобразование графиков функций» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
06.
02.2023
Построение графика функции с помощью производной, сопутствующие задачи 10 класс онлайн-подготовка на Ростелеком Лицей |
Введение
Методика исследования функции, построение ее графика, включает в себя 2 этапа:
1. исследование без производной;
2. исследование с помощью производной.
Построение графика и исследование функции без производной
При исследовании функции без производной нахождение интервалов знакопостоянства и определение знаков функции на них выполнить очень затруднительно. Однако некоторые свойства данной функции можно узнать:
1. Область определения функции – это множество всех действительных чисел.
2. Если x стремится к , то и данная функция стремится к . Следовательно, множество значений функции – это вся числовая ось.
3.
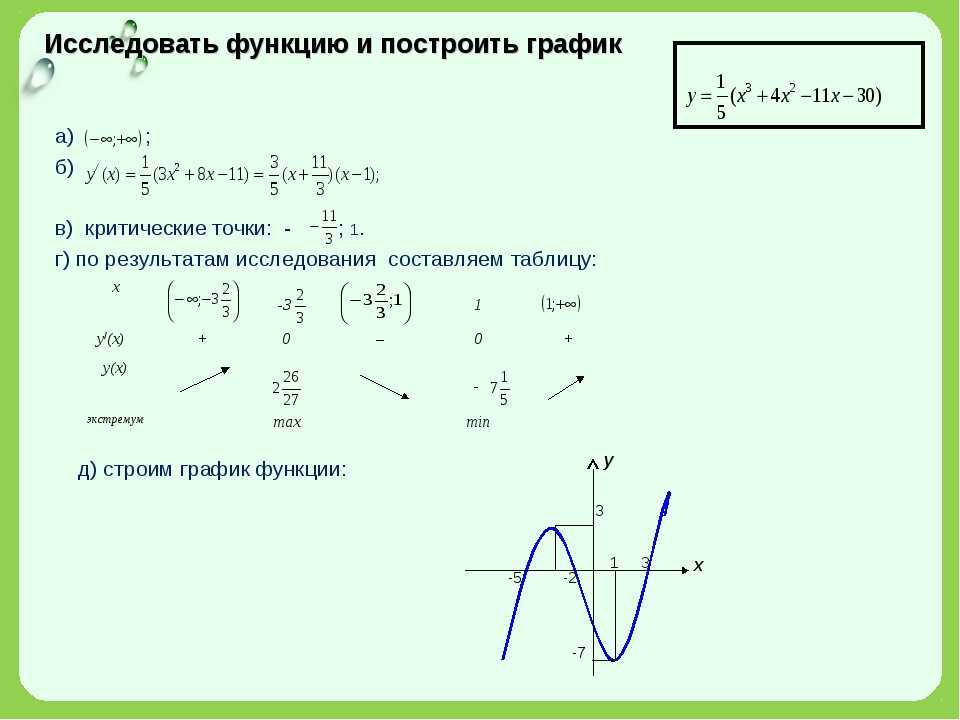График этой функции симметричен относительно точки .
Пояснение
Рассмотрим функцию
Эта функция позволяет найти интервалы знакопостоянства и построить эскиз графика (см. Рис. 1).
Эта функция нечетная:
График нечетной функции симметричен относительно точки с координатами .
Рис. 1. График функции
При прибавлении 4 к функции график сдвинется на 4 единицы вверх по оси (см. Рис. 2): корни и пропадают, а корень сдвигается влево. Следовательно, график функции будет симметричен относительно точки .
Рис. 2. Схематичное изображение графиков функции и
Нам удалось установить, что функция имеет как минимум один корень, который меньше чем .
Построение графика и исследование функции с помощью производной
Приравниваем производную к 0 и находим критические точки:
– критические точки
Выделим интервалы знакопостоянства производной, которые определяют интервалы монотонности самой функции (см.
Рис. 3).
До точки функция возрастала (производная была положительна), после этой точки функция убывает (производная отрицательная), следовательно, – это точка максимума.
До точки функция убывала, после этой точки функция возрастает, следовательно, – это точка минимума.
Рис. 3. График производной функции
Найдем значения функции в точках минимума и максимума:
Можно сделать вывод, что функция возрастает от до 6 и от 2 до ; функция убывает от 6 до 2.
На рисунке 4 показан график функции . Этот график читается следующим образом:
Если аргумент возрастает от до , то функция возрастает от до 6; если аргумент от до 1, то функция убывает от 6 до 2; если аргумент возрастает от 1 до , то функция возрастает от 2 до .
Рис. 4. График функции
Результаты исследования функции
1.
при и при
2. при
3. – т. max
– т. min
3. . Наибольшего и наименьшего значения функции не существует.
Задача
Найти число корней уравнения в зависимости от параметра .
Решение
1. Перенесем в правую часть уравнения:
2. Построим график функции (см. Рис. 5) (как построить график этой функции см. выше).
Рис. 5. Иллюстрация к задаче
3. Рассечем этот график семейством прямых , при разных . Найдем точки пересечения этих прямых с графиком функции (см. Рис. 6).
Рис. 6. Иллюстрация к задаче
Уравнение имеет один корень при каждом из множества , а также из множества .
Уравнение имеет два корня при и при .
Уравнение имеет три корня при всех из множества .
Ответ: 1 корень:
2 корня: ; ;
3 корня: .
Частные случаи для задачи
1. Найти все значения параметра , при каждом из которых данное уравнение имеет ровно два различных корня.
Ответ: уравнение имеет два корня при и при .
2. Найти наибольшее натуральное значение параметра a, при котором уравнение имеет три различных корня.
Решение
Уравнение имеет три корня при всех из множества . В это множество входят такие натуральные числа: 3, 4, 5. Наибольшее из них – это 5.
Ответ: .
Общий план построения графика и исследования функции
Общий план состоит из двух этапов:
1. Этап А: исследование без производной.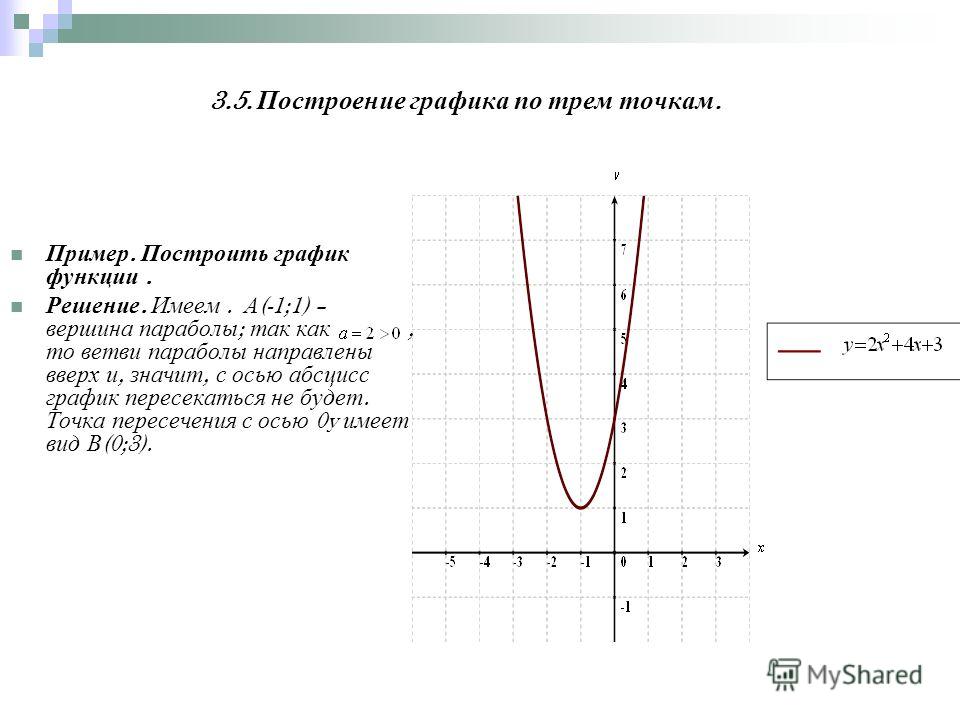
2. Этап Б: исследование с производной.
Этап А
1. Найти область определения функции .
2. Выделить интервалы знакопостоянства функции и определить знаки функции на них (для этого нужно приблизительно оценить расположение корней или точно найти их).
3. Найти точку пересечения графика с осью , для этого приравнять и вычислить .
4. Выяснить специфику функции:
— четность, нечетность, периодичность;
— наличие центра или оси симметрии.
5. Построить эскиз графика в окрестностях каждого корня (в окрестностях корня функция может возрастать, убывать, иметь точку максимума или минимума (см. Рис. 7)).
Рис. 7. Эскиз графиков в окрестностях корня
6. Построить эскиз графика функции в окрестностях точек разрыва области определения . Точки разрыва – это, как правило, корни знаменателя.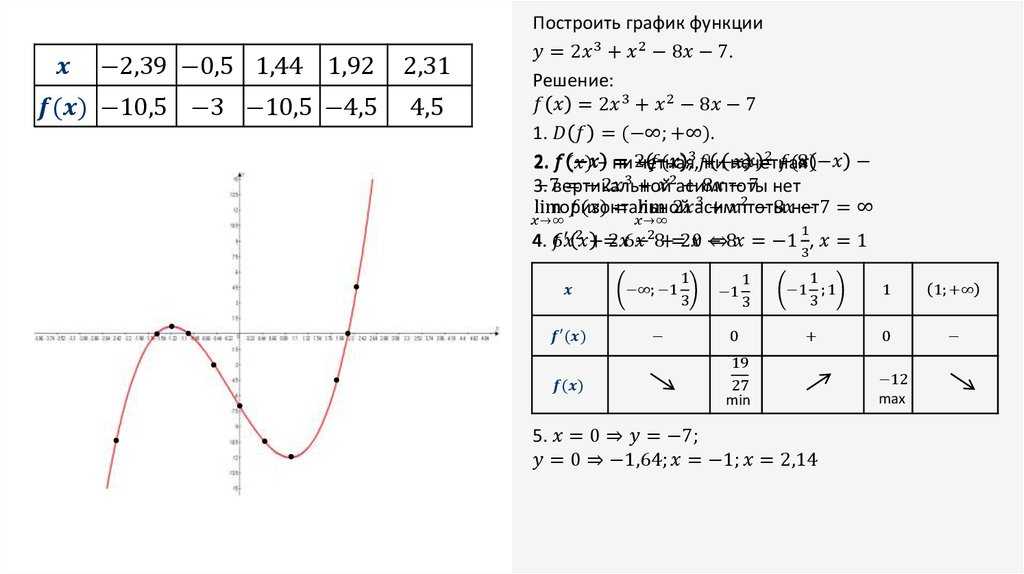
Они могут определять вертикальные асимптоты.
7. Построить график функции в окрестностях бесконечно удаленных точек: .
Этап Б
1. Найти производную функции .
2. Найти интервалы знакопостоянства производной и определить знаки производной на них. Эти интервалы определяют интервалы монотонности самой функции.
3. Найти критические точки, исследовать их на экстремум.
4. Построить и описать график функции .
Предложенная схема работает особенно хорошо для функций вида: , где и – многочлены.
Список литературы
1. Мордкович А.Г., Семенов П. В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
2. Мордкович А.Г. Алгебра и начала математического анализа, 10 класс.
В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
4. Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт «Вся элементарная математика» (Источник)
3. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Задание 45.13, 45.15(а), 45.3 (б) (стр.
265) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)
2. Исследуйте функцию и постройте ее график .
Math Help: Графические функции — Руководство по использованию графического калькулятора
Графические функции: Руководство по графическому калькулятору
Математика пробуждает в вас художника!
В то время как трудолюбивый студент может просто достать графический калькулятор, чтобы нарисовать графические функции, вычисление функций старомодным способом может быть довольно увлекательным. Не имея ничего, кроме карандаша и листа бумаги, разделенного на маленькие квадраты, мы можем создавать линии и заставлять их танцевать под кривую формы пересечения склона. О да, помните, что вы можете нанять онлайн-репетитора по математике в Studygate!
Мы все знали, что математика — милое маленькое число, но вот где мы это доказываем!
Возьмем простое уравнение:
y = mx + b
Это довольно простой формат для построения графика.
У нас есть ось Y, которая напрямую связана с осью X. Соотношение между Y и X определяется M.
Давайте добавим несколько чисел и посмотрим, что получится:
y = 2x + 6
Это очень просто. Давайте составим график:
Начнем с простого, с x = 0.
Итак, мы знаем, что когда X равно 0, Y равно 6. «2» — это отношение между X и Y. Если X равно 1, то просто умножьте X x 2 + 6 = 8.
Мы можем построить быструю диаграмму между X и Y. Не забывайте, что мы также можем использовать отрицательные значения для X и Y!
| Х | Д |
| -4 | -2 |
| -3 | 0 |
| -2 | 2 |
| -1 | 4 |
| 0 | 6 |
| 1 | 8 |
| 2 | 10 |
| 3 | 12 |
| 4 | 14 |
| 5 | 16 |
| 6 | 18 |
| 7 | 20 |
Затем нанесите точки и соедините их, чтобы сформировать линию!
Симпатично, да?
****БЫСТРЫЙ СОВЕТ: вернитесь к уравнению
Мы можем разбить M, чтобы представить изменение над Y над изменением над X.
Если бы это была дробь, это выглядело бы как это : изменение над Y ÷ изменение над X
Поскольку 2 в основном равно 2÷1, мы можем просто сказать, что при каждом изменении X мы перемещаем Y на 2 позиции вверх! Посмотрите на график и посчитайте. Посмотри, как это работает?
Что М было дробь? Это все еще работает:
Это означает, что для каждого значения X, которое у нас есть, Y увеличивается на . Диаграмма будет выглядеть так:
| X | Д |
| -4 | -1 |
| -3 | -.25 |
| -2 | .5 |
| -1 | 1,25 |
| 0 | 2 |
| 1 | 2,75 |
| 2 | 3,5 |
| 3 | 4,25 |
| 4 | 5 |
| 5 | 5,75 |
| 6 | 6,5 |
| 7 | 7,25 |
Графики с дробью M выглядят менее крутыми, чем графики с целым числом M.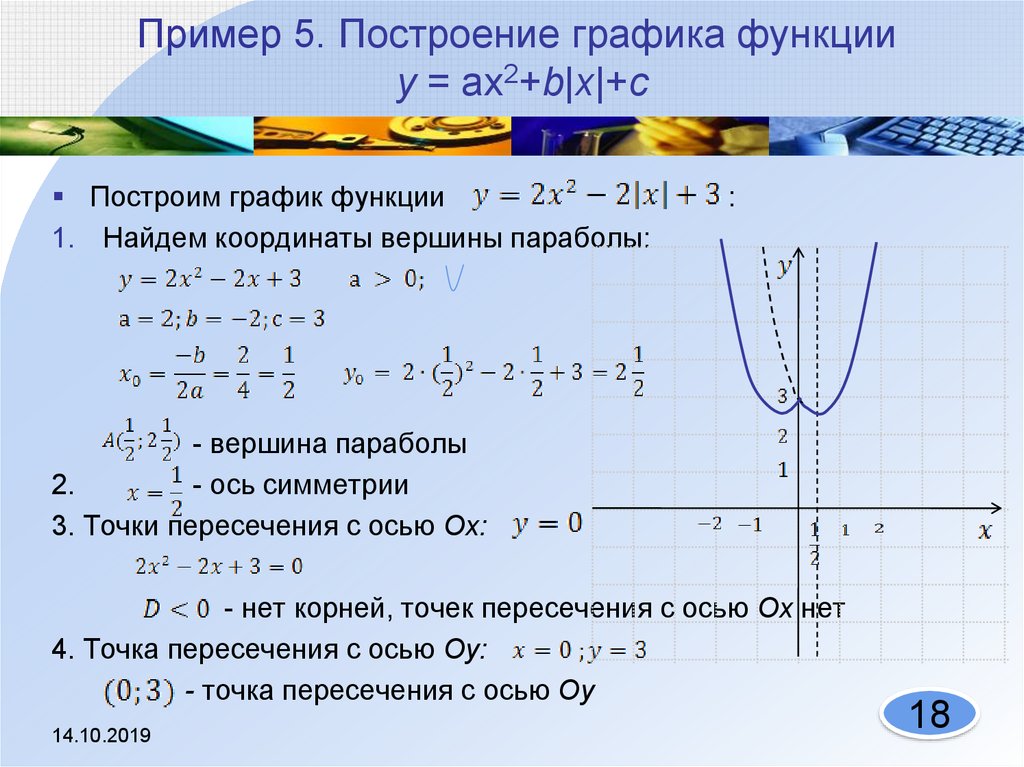
Но что это дает нам с графическими функциями?
Это очень просто: это практически одно и то же!
ƒ(x) = x 2 + 2
В этом случае Y = F(x). Поскольку уравнение возведено в квадрат, при изменении точки пересечения Y с положительной на отрицательную будут некоторые кривые. Но процедура такая же.
Итак, давайте добавим несколько значений X и посмотрим, что у нас получится! Вы также можете связаться с онлайн-репетитором по математике, чтобы выполнить этот шаг.
| Х | Д |
| -5 | 23 |
| -4 | 18 |
| -3 | 11 |
| -2 | 6 |
| -1 | 3 |
| 0 | 2 |
| 1 | 3 |
| 2 | 6 |
| 3 | 11 |
| 4 | 18 |
| 5 | 23 |
Как видите, у нас кривая!
Представьте себе возможности: цифрами можно нарисовать что угодно!
Для получения дополнительных математических советов поможет наше руководство по решению квадратной формулы.
Graph Maker: легко создавайте графики и диаграммы в Интернете
Graph Maker: легко создавайте графики и диаграммы в Интернете | FotorИзысканные шаблоны графиков на выбор
В онлайн-генераторе графиков Fotor есть много наборов готовых шаблонов графиков, с помощью которых вы можете напрямую создавать графики. Найдите нужный набор шаблонов диаграмм, нажмите на диаграмму и графики и введите свои данные во всплывающем окне, чтобы точно подобрать лучший эффект диаграммы. Вы можете переключаться между различными типами диаграмм в одном наборе шаблонов, такими как столбчатые, линейные и круговые диаграммы. После этого вы можете экспортировать напрямую, чтобы сформировать отчет об анализе данных.
Создайте график сейчас
Добавьте свои данные с помощью Chart Maker в клики
На основе ваших данных онлайн-конструктор графиков Fotor работает как математический калькулятор для создания бесплатных онлайн-графиков данных.
После выбора нужного типа и стиля диаграммы нажмите «Редактировать данные диаграммы» в верхней части столбца навигации. Введите данные, связанные с осями X и Y, во всплывающую таблицу, как вы обычно это делаете в Excel или Google Sheets. Калькулятор графиков Fotor внутри средства быстрого создания графиков автоматически преобразует ваши данные в диаграмму.
Создайте график сейчас
Реализуйте визуализацию данных с помощью графиков
Список данных может не приветствоваться в отчете, поэтому визуализация данных является одним из наиболее важных аспектов анализа. Онлайн-конструктор графиков Fotor уже учёл это для вас. После импорта данных вы можете бесплатно получить соответствующую диаграмму, будь то гистограмма, круговая диаграмма или линейная диаграмма. При создании графика легко получить графические уравнения, потому что графические инструменты Fotor поддерживаются мощными и логичными алгоритмами преобразования диаграммы.
Создайте график сейчас
Настройте графики и диаграммы, чтобы они выглядели красиво
Теперь доступны привлекательные стили графиков и диаграмм.
Каждая диаграмма Fotor позволяет вам представлять свои данные, уделяя особое внимание эстетике ваших диаграмм. Вы можете получить логический набор настраиваемых графиков в онлайн-создателе графиков Fotor. У вас есть максимальная гибкость в настройке дизайна графика от стиля структуры фреймов до текста описания. Вы можете изменить цвет изображения, настроить размер шрифта текста, добавить значки для фокусировки и многое другое. Красивые графики у вас под рукой с Fotor.
Создайте график сейчас
Вставьте онлайн-графики в любой отчет
Загрузите созданные вами красивые графики бесплатно. Графика онлайн-диаграмм Fotor доступна для загрузки в высоком разрешении в различных форматах, включая PNG, JPG и PDF. Вы можете встраивать свои онлайн-графики в презентации или файлы отчетов в соответствии с вашими намерениями использования, а также делиться ими напрямую по электронной почте или распечатывать.
Сделать график сейчас
Как сделать график?
- Нажмите кнопку «Создать график сейчас», чтобы начать.
Ваш комментарий будет первым