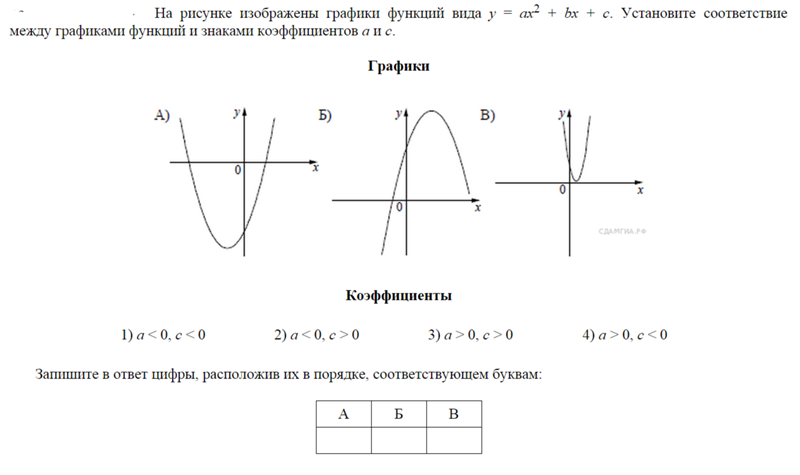
Свойства и графики тригонометрических функций. Профильный уровень 10 класс онлайн-подготовка на Ростелеком Лицей |
Тригонометрические функции числового аргумента
Основное отличие науки от искусства в том, что результат научного опыта, воспроизведенный разными людьми, будет одинаковым (если соблюдены основные условия проведения такого опыта). Произведение искусства каждый понимает по-своему, и единого правильного мнения о таком произведении быть не может.
Русский язык позволяет нам описать процессы, которые происходят вокруг: птица летит и машет крыльями, дерево согнулось под порывом ветра. Поэт может и более изящно воспользоваться языком: «…летят серебряные птицы, седые птицы – журавли…». Это описание помогает нам воспринимать окружающий мир, вдохновляться ним.
Но для более практичных вопросов такого описания недостаточно. Почему летит птица? Можем ли мы это использовать и построить аппарат для полетов? При каких условиях дерево сломается? Можно ли это предотвратить? Для ответа на эти вопросы нужен другой язык – математический. Мы строим математическую модель процесса, описываем его на математическом языке. И в дальнейшем эти расчеты позволяют создавать самолеты и строить небоскребы, которые защищены от ураганов и землетрясений.
Мы строим математическую модель процесса, описываем его на математическом языке. И в дальнейшем эти расчеты позволяют создавать самолеты и строить небоскребы, которые защищены от ураганов и землетрясений.
Множество процессов, которые окружают нас – периодически повторяющиеся. Это и различные колебания, о которых вы знаете из курса физики («Механические колебания», «Механические волны. Звук»), и периодические спады и подъемы в экономике.
Конечно, в реальном мире не существует идеальных периодических процессов. Да, зима наступает каждый год, но мы не можем предсказать заранее, в какой именно день выпадет снег, когда станет холодно и т. д. С другой стороны, зная, что зима все равно наступит, мы покупаем пальто, заготавливаем дрова на даче (не знаем, в какой именно день будем их сжигать, но знаем, что они, скорее всего, пригодятся). Тот же маятник обязательно затухает, если не сообщать ему дополнительную энергию.
Но, как мы уже знаем, точность решения задачи определяется целью.
Чтобы построить математическую модель всех этих повторяющихся событий, нужен определенный инструмент – тригонометрические функции. С этим инструментом мы уже немного знакомы: умеем вычислять значения тригонометрических функций и упрощать выражения, которые их содержат. Но чтобы полноценно использовать тригонометрические функции для построения математической модели периодических процессов, нам еще нужно изучить свойства и графики этих функций, а также научиться решать уравнения и неравенства, которые их содержат.
Об уравнениях речь пойдет позже, а сегодня мы займемся свойствами и графиками тригонометрических функций.
Мы определили тригонометрические функции как функции, которые ставят в соответствие углу поворота координаты (или их отношение) соответствующей точке на окружности (см. рис. 1):
Рис. 1. Единичная окружность
1. Единичная окружность
Понятно, что при повороте на полный оборот значения тригонометрических функций начинают повторяться (мы каждый день наблюдаем это на примере часов: прошло 12 часов, и стрелки снова на своих местах). Поэтому тригонометрические функции будут периодическими – их значения после изменения значения аргумента на определенное число будут повторяться. Периодических функций можно ввести много, самых разных. Мы рассмотрим свойства базовых, с помощью комбинаций которых можно выразить остальные. Звуки – это механические колебания, их вокруг нас великое множество. Но при этом все их с той или иной степенью точности можно математически описать с помощью набора базовых тригонометрических функций.
Мы выделили и изучили свойства некоторых видов функций: линейной, квадратичной, функции квадратного корня и других («Свойства функций. Базовые функции»). Воспользуемся готовой схемой изучения свойств функций для тригонометрических функций:
Правда, есть небольшая загвоздка: мы изучали числовые функции – в них числу ставится в соответствие число. В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например,
В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например,
Аналогично и для косинуса, тангенса и котангенса.
Как исследовать числовые функции, мы уже знаем. Можно построить их графики и рассмотреть различные характеристики:
- область определений и область значений;
- промежутки монотонности: возрастания и убывания;
- четность;
- периодичность.
Про четность и периодичность тригонометрических функций, на самом деле, мы уже знаем. Вспомним, что функция называется четной, если для всех ее допустимых аргументов выполняется соотношение:
А для нечетных функций выполняется соотношение:
Мы знаем, что , а . Соответственно, функция является четной функцией; – нечетной.
Соответственно, функция является четной функцией; – нечетной.
Для тангенса и котангенса выполнены следующие соотношения:
Значит, функции и также являются нечетными.
Теперь про периодичность. Вспомним, что функция называется периодической, если для всех ее аргументов выполняется соотношение:
Величина называется периодом функции. Мы знаем соотношения:
Значит, все тригонометрические функции являются периодическими. Причем синус и косинус имеют период , а тангенс и котангенс – период .
Об остальных свойствах и характеристиках тригонометрических функций, а также об их графиках мы поговорим далее в уроке.
Синус и косинус
Начнем с построения графика функции синуса:
Мы знаем значения синуса для некоторых углов:
|
Градусы |
|||||
|
Радианы |
|||||
По ним мы можем составить таблицу значений для нашей функции. Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Отметим эти точки на графике и соединим плавной линией (см. рис. 2).
Рис. 2. Соединенные точки
Обратите внимание на масштаб оси . Ранее мы изучали такие функции, в которых аргументом удобно было брать целые значения. Поэтому и цену деления было удобно брать целым числом. У тригонометрических же функций мы знаем значения для аргументов, пропорциональных . Поэтому и выбираем соответствующий масштаб.
Далее воспользуемся соотношением:
Его можно получить из формул приведения:
Это соотношение означает, что для аргументов, лежащих слева и справа от на равном расстоянии, значения синусов будут одинаковы. Получаем следующий график (см. рис. 3).
Рис. 3. Полученный график
Теперь воспользуемся тем, что синус – нечетная функция. Графики нечетных функций симметричны относительно начала координат. Отражаем график. Мы получили график функции на промежутке от (см. рис. 4).
рис. 4).
Рис. 4. График функции на промежутке от
Далее пользуемся периодичностью. Период синуса равен , значит, прибавив к аргументу , мы получим те же значения функции. Прибавляя еще или вычитая , мы будем получать те же значения. Наш кусочек функции будет как бы «копироваться» влево и вправо бесконечное количество раз. Полученная линия и будет являться графиком функции (см. рис. 5). Эту кривую еще называют синусоидой.
Рис. 5. График функции
Теперь отметим характеристики и свойства функции.
1. Областью определения являются все действительные числа:
Мы расширили понятие угла так, что его величина может быть любым числом. А величина угла в радианах – и есть аргумент функции.
2. Область значений:
Мы определяли синус как ординату точки на единичной окружности. Соответственно, значения синуса могут лежать только в пределах от до .
3. Нули функции – это решения уравнения .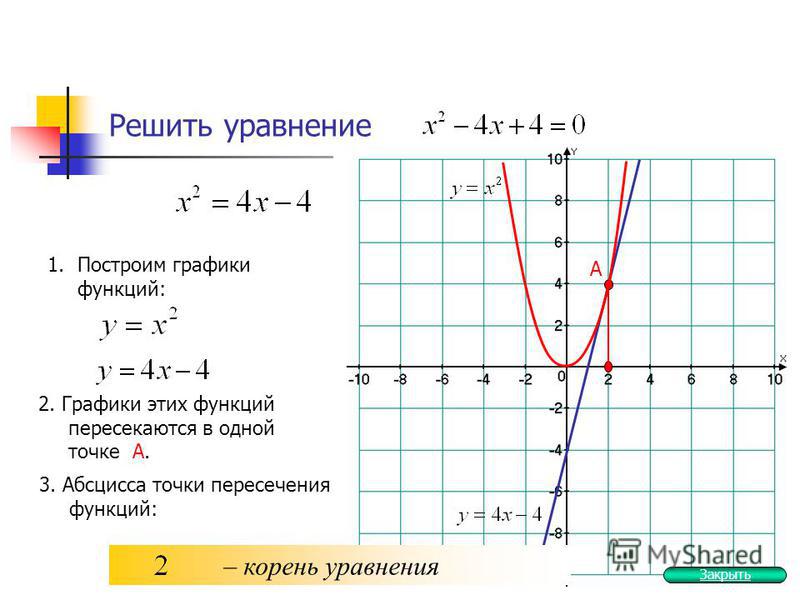 С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.
С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.
4. Промежутки знакопостоянства также отметим по графику. От до функция принимает положительные значения; от до – отрицательные. Это же поведение мы видим и на других участках графика. В общем виде:
5. По графику также можно определить промежутки монотонности. От до функция возрастает; от до – убывает. На других участках графика то же самое. Тогда в общем виде:
Теперь перейдем к косинусу. Его график легко построить, воспользовавшись соотношением, которое мы уже сегодня доказывали:
Т. е. график функции совпадает с графиком функции . А этот график мы можем построить с помощью преобразования . Оно соответствует сдвигу графика на единиц влево. Значит, для построения график функции достаточно сдвинуть график синуса на влево.
Рис. 6. График функции
Видим, что область определения и область значений у косинуса такие же, как и у синуса:
А вот нули функции, промежутки знакопостоянства и монотонности сдвинутся вместе с графиком на влево. Нули:
Положительные и отрицательные значения:
Функция возрастает и убывает при:
Тангенс и котангенс
Теперь перейдем к тангенсу и котангенсу. Начнем строить график тангенса по точкам.
|
Радианы |
||||
Соответственно, таблица значений:
Тангенс не определен, ведь , а деление на ноль не определено. Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Рис. 7. Соединенные точки
будет приближаться к , – приближаться к , а значение дроби будет становиться все больше и больше. Т. е. значение тангенса будет все расти и расти. Но график никогда не пересечет прямую , ведь при этом значении аргумента функция не определена. Подобную ситуацию мы видели на графике функции (см. рис. 8).
Рис. 8. График функции
При приближении аргумента к нулю значение функции неограниченно убывало. При этом график не пересекал прямую . Вспомним, что подобная прямая называется асимптотой графика. Соответственно, асимптотой графика будет прямая .
Мы построили часть графика тангенса. Теперь воспользуемся тем, что эта функция нечетная. Значит, график симметричен относительно начала координат. Далее пользуемся периодичностью функции. Период тангенса равен , значения функции будут повторяться через этот промежуток.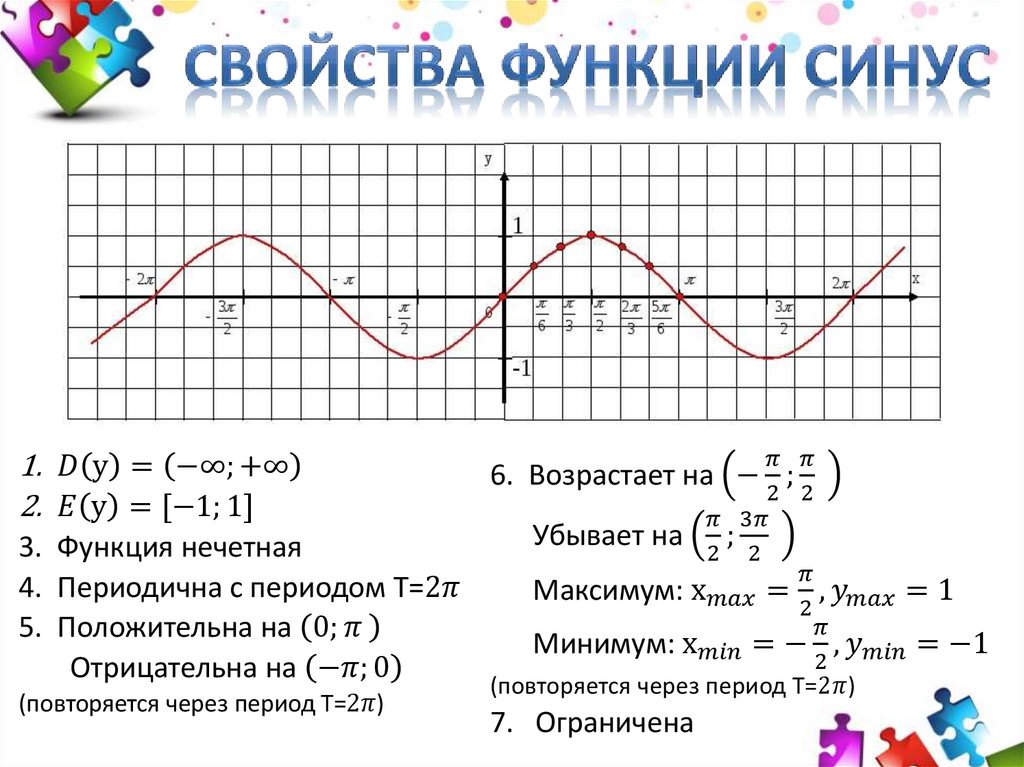 Получили график функции (см. рис. 9).
Получили график функции (см. рис. 9).
Рис. 9. График функции
Видим, что этот график имеет множество асимптот, уравнения которых в общем виде можно описать так:
Эти асимптоты разбивают график на отдельные части, которые еще называют ветками тангенса. Ветка, которая проходит через начало координат, называют главной веткой.
По графику определим характеристики функции.
1. Область определения:
2. Область значений:
3. Нули функции: . В общем виде все их можно описать так:
Несложно понять, почему они совпадают с нулями синуса, если вспомнить, что тангенс – отношение синуса и косинуса, а дробь равна только тогда, когда ее числитель равен .
4. В общем виде:
5. На каждой своей ветке функция возрастает:
При этом корректно говорить, что функция возрастает на каждом из этих интервалов. Но нельзя сказать, что она возрастает на всей области определения, ведь при переходе через асимптоту функция меняет значение с положительного на отрицательное. Т. е. значение уменьшается.
Т. е. значение уменьшается.
Теперь, наконец, рассмотрим функцию . Для ее построения удобно воспользоваться формулой приведения:
Т. е. нам достаточно построить график функции . В этом нам помогут преобразования графиков. Сначала строим – график тангенса отражается симметрично относительно оси . Затем сдвигаем его на влево. Получаем график функции , он же будет графиком функции .
Рис. 10. График функции
Отметим характеристики.
1. Область определения:
2. Область значений:
3. Нули функции (совпадают с нулями косинуса, объясните сами, почему):
4. В общем виде:
5. На каждой своей ветке функция убывает:
Преобразования графиков тригонометрических функций
Мы рассмотрели характеристики и графики тригонометрических функций , , и . Но при моделировании процессов обычно встречаются более сложные функции, например:
Чтобы исследовать подобные функции, достаточно применить преобразования графиков к уже изученным. Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
- Прибавление числа к функции сдвигает график вдоль оси .
- Прибавление числа к аргументу сдвигает график вдоль оси .
- Умножение значения функции на число растягивает или сжимает график вдоль оси . Если , то еще и симметрично отражает график относительно оси .
- Умножение аргумента на число растягивает или сжимает график вдоль оси x. Если , то еще и симметрично отражает график относительно оси .
Соответственно, чтобы построить график функции , необходимо:
1. Построить график функции (см. рис. 11).
Рис. 11. График функции
2. Сжать его вдоль оси в раз, получив график (см. рис. 12).
Рис. 12. График функции
3. Растянуть его вдоль оси (см. рис. 13), а затем симметрично отразить относительно оси . В итоге получим график функции (см. рис. 14).
В итоге получим график функции (см. рис. 14).
Рис. 13. График функции
Рис. 14. График функции
По построенному графику функции можно указать все ее свойства. В частности, стоит обратить внимание, что у данной функции изменилась область значений и период по сравнению с функцией . Область значений данной функции: .
Период был , после сжатия вдоль оси он уменьшился в раз:
В общем случае про изменение области значений и периода функций можно сказать следующее.
- При преобразованиях вида и соответствующим образом изменяется область значений: сдвигается на или расширяется/сужается в раз.
- При преобразовании вида период функций увеличивается или уменьшается в раз.
- При преобразовании вида период функции и ее область значений остается прежней.
Итак, применяя различные преобразования графиков, мы можем исследовать тригонометрические функции вида , где – некоторые числа. Аналогично и для косинусов, тангенсов и котангенсов. Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Тогда выражение для кинетической энергии принимает вид:
Константы и деление на можем объединить в одну положительную константу . Получим функцию кинетической энергии от времени: , где – некоторые числа. Как видите, здесь мы столкнулись с квадратом тригонометрической функции. Как же ее исследовать? Здесь нам поможет известный нам математический прием: свести нашу задачу к той, решение которой мы знаем.
Для начала перейдем к более привычным обозначениям:
Теперь используем формулу понижения степени:
Получаем:
А уже эту функцию мы уже знаем, как исследовать. Здесь нам помогут преобразования графиков. Базовая функция (см. рис. 15):
Рис. 15. График функции
Умножаем аргумент на :
При этом график сожмется вдоль оси в раз (см. рис. 16).
рис. 16).
Рис. 16. График функции
Период функции станет в раз меньше:
Далее умножаем функцию на :
График растягивается вдоль оси в раз и отражается симметрично относительно оси (см. рис. 17).
Рис. 17. График функции
При этом область значений расширяется в раз: было , станет:
И наконец, прибавляем :
График поднимается на (см. рис. 18).
Рис. 18. График функции
Область значений также смещается на :
Таким образом, мы смогли исследовать функцию, содержащую квадрат тригонометрической функции. Посмотрели, какой будет ее область значений и ее период.
Список литературы
- Алимов Ш.А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Семенов П.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс.
 Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019. - Никольский С.М., Потапов М.К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал ru.solverbook.com
- Интернет-портал math34.ru
Домашнее задание
- Определить промежутки возрастания (убывания) функции на промежутке .
- Найти множество значений функции , если .
- Построить график функции:
Тригонометрические функции
В школьной программе изучаются четыре тригонометрических функции — синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.
1. Начнем с построения графика функции y = sin x.
Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда — одна клеточка, — две клетки.
По оси X: три клетки примем за (это примерно полтора). Тогда — одна клеточка, — две клетки.
По оси Y: две клетки примем за единицу.
Область определения функции y = sin x — все действительные числа, поскольку значение sin α можно посчитать для любого угла α.
Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
| x | 0 | ||||
| sin x | 0 |
Можем добавить, для большей плавности графика, точки и В них значение синуса равно
Соединим полученные точки плавной кривой.
Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.
Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть
Это значит, что функция y = sin x является периодической. Мы уже построили участок графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Мы уже построили участок графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Синусоида построена.
Перечислим основные свойства функции y = sin x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее — минус единице.
3) Функция y = sin x — нечетная. Ее график симметричен относительно нуля.
4) Функция y = sin x — периодическая. Ее наименьший положительный период равен 2π.
2. Следующий график: y = cos x. Масштаб — тот же. Отметим на графике точки, в которых косинус является рациональным числом:
| x | 0 | ||||
| cos x | 1 | 0 |
Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.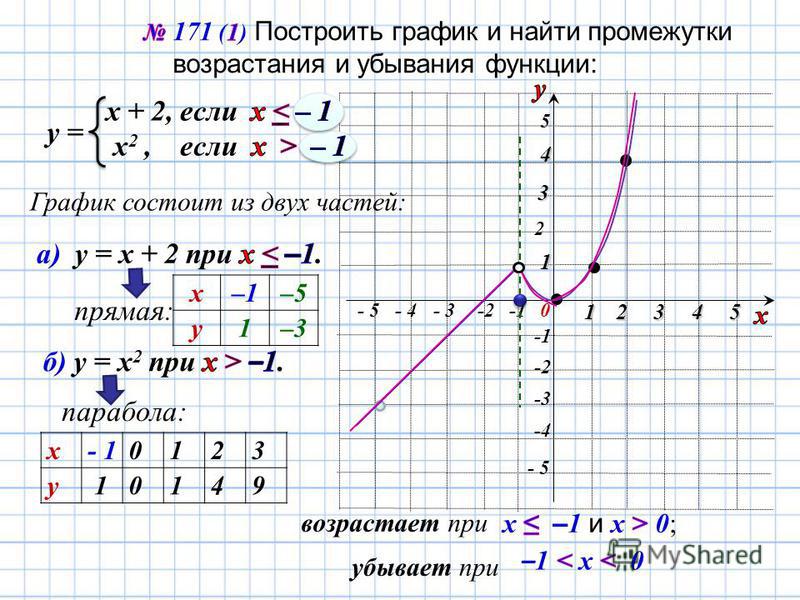
Функция y = cos x — тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. «Копируем» участок графика, который уже построили, и повторяем периодически.
Перечислим основные свойства функции y = cos x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее — минус единице.
3) Функция y = cos x — четная. Ее график симметричен относительно оси Y.
4) Функция y = cos x — периодическая. Ее наименьший положительный период равен 2π.
Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть — по одной из формул приведения,.
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны.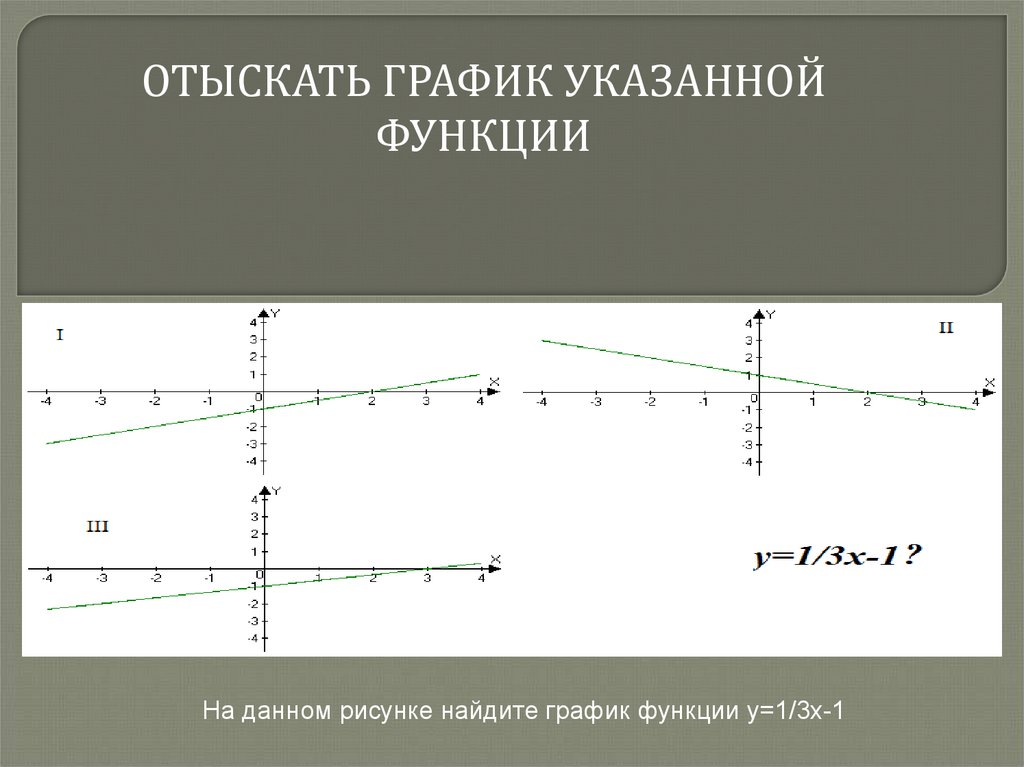 Да, это и есть волны!
Да, это и есть волны!
Функции синус и косинус идеально подходят для описания колебаний и волн — то есть процессов, повторяющихся во времени.
По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.
3. Перейдем к графику функции y = tg x.
Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.
Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.
Непонятно только, как быть с точкой Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к то есть к 90 градусам?
Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .
Синус угла — это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.
Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к ), значение функции y = tg x стремится к бесконечности.
Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности.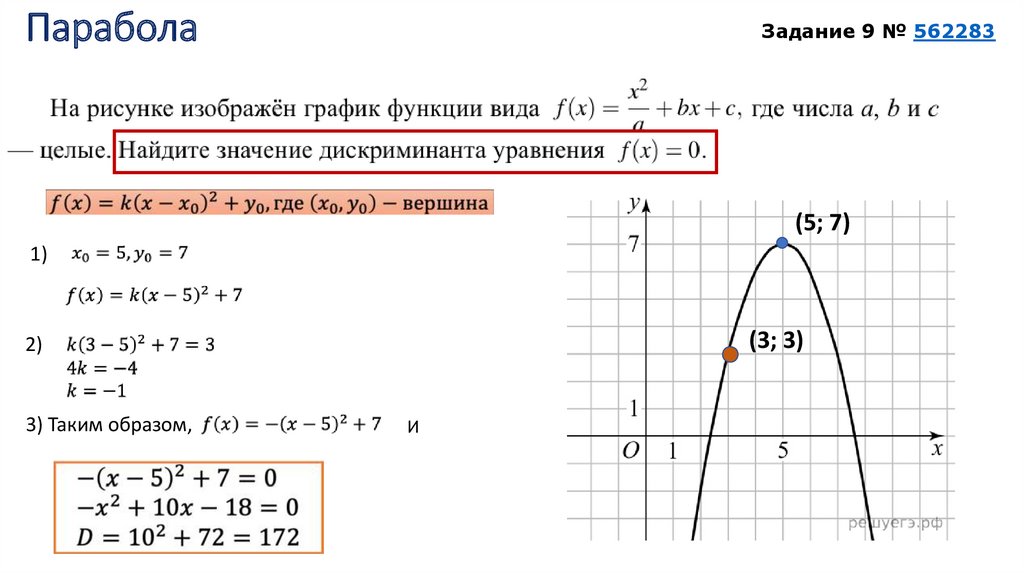
Осталось только «скопировать» этот участок графика и повторить его с периодом π.
Перечислим свойства функции y = tg x.
1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = tg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = tg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = tg x возрастает при , то есть на каждом участке, на котором она непрерывна.
4. График функции y = ctg x строится аналогично. Вот он:
1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = сtg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = сtg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = сtg x убывает при , то есть на каждом участке, на котором она непрерывна.
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Тригонометрические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 06.02.2023
Taculator Graphing Calculator в App Store
Описание
TACULATOR ГРАФИЧЕСКИЙ КАЛЬКУЛЯТОР
• Ваш графический калькулятор для старшеклассников и студентов колледжей.
• Включает в себя все команды и функции для продвинутой математики, списков, статистики, распределения, статистических графиков и т. д.
• Используйте клавиши со стрелками или пальцы для навигации внутри приложения.
• Охватывает все, что вам нужно: предварительная алгебра, алгебра 1 и 2, предварительное исчисление, исчисление, статистика…
ЭТО ДАЖЕ ЛУЧШЕ, ЧЕМ НАСТОЯЩИЙ КАЛЬКУЛЯТОР
• Такулятор в 100 раз быстрее, так как он использует огромную вычислительную мощность вашего iPhone/iPad, в то время как карманные калькуляторы часто работают медленно.
• Графическое окно с высоким разрешением: Создавайте четкие и красивые графики.
• Ваш новый калькулятор ничего не весит и всегда готов к работе в вашем телефоне.
• Поделитесь своими расчетами с друзьями в виде текстового сообщения или электронной почты.
◉ Математические функции
• Научный калькулятор со всеми основными арифметическими и расширенными функциями.
• Возможность прокручивать историю и копировать предыдущие расчеты.
• Комплексные числа поддерживают
• Функции вероятности, такие как nPr, nCr, факториал, случайные числа.
• Легко вводите дроби.
• Преобразование углов и использование формата DMS.
◉ Графические функции
• Нарисуйте график каждой функции, которую вы хотите, и проследите для значений X и Y.
• Вычислите пересечение, ноль, минимум, максимум, интеграл и производную.
• Переключение между полноэкранными графиками и обычным режимом.
• Увеличивайте и уменьшайте масштаб пальцами и настраивайте параметры окна.
• Графики статистических графиков, таких как гистограмма, коробчатая диаграмма, точечная диаграмма, линейная диаграмма xy
• Нарисуйте вертикаль, горизонталь, касательную, окружность.
◉ Калькулятор матриц
• Сохраняйте матрицы и повторно используйте их, используя сочетания клавиш, такие как [A], [B], [C],…
• Выполняйте матричные арифметические операции: скалярное умножение, сложение и вычитание, умножение, степень матрицы .
• Вычислить транспонирование, определитель, размерность, обратную матрицу, эшелонированную форму строк, уменьшенную форму эшелонирования строк, единичную матрицу, кумулятивную сумму.
◉ Список, статистика и распределение
• Используйте редактор списка статистики для ввода значений списка.
• Выполнить статистику с 1 и 2 переменными.
• Используйте списки для расчета минимума, максимума, среднего, медианы, суммы, произведения, стандартного отклонения, дисперсии.
• Найдите наиболее подходящие регрессии: LinReg (ax+b), LinReg (a+bx), QuadReg, CubicReg, QuartReg, LnReg, ExpReg, PwrReg, Logistic, SinReg.
• Выполнение статистических тестов: Z-тест, T-тест, 2-SampleZTest, 2-SampleTTest, 1-PropZTest, 2-PropZTest, ZInterval, TInterval, 2-SampleZInterval, 2-SampleTInterval, 1PropZInterval.
• Расчет различных распределений: Normalpdf/cdf, invT, Tpdf/cdf, χ2pdf/cdf, Fpdf/cdf, Poissonpdf/cdf, Binompdf/cdf, Geometpdf/cdf.
◉ Справка по каталогу команд и синтаксису
• Получите помощь по всем командам в нашем интегрированном разделе «Каталог и справка».
• Предоставляет справку по синтаксису, примеры и возможные сообщения об ошибках.
• Введите команду, и приложение покажет вам правильный синтаксис рядом с курсором.
ПОДДЕРЖКА
Свяжитесь с нами по адресу [email protected]
—
Чтобы получить расширенные возможности, такие как более сложные вычисления и функции, приобретите членство в Taculator Pro.
Условия автоматического продления подписки:
Вы можете выбрать один из трех вариантов подписки:
• Ежемесячная подписка;
• Годовая подписка;
• Пожизненная подписка, оплачиваемая разовым авансовым платежом.
• Оплата будет снята с учетной записи iTunes при подтверждении покупки;
• Подписка продлевается автоматически, если автоматическое продление не будет отключено по крайней мере за 24 часа до окончания текущего периода;
• С аккаунта будет взиматься плата за продление в течение 24 часов до окончания текущего периода, и укажите стоимость продления;
• Пользователь может управлять подписками, а автоматическое продление можно отключить, перейдя в настройки учетной записи пользователя после покупки;
• Любая неиспользованная часть бесплатного пробного периода, если она предлагается, будет аннулирована, когда пользователь приобретет подписку на эту публикацию, где это применимо;
• Цены указаны в долларах США, могут отличаться в других странах, кроме США, и могут быть изменены без предварительного уведомления.
Условия обслуживания:
https://www.taculator.com/terms-of-service.html
Политика конфиденциальности:
https://www.taculator.com/privacy-policy.html
Версия 1.0.3
Крупнейшее обновление такулятора в 2020 году!
+ Исправлена ошибка, из-за которой уравнения Y= не сохранялись и не отображались на графике. Теперь он снова работает нормально.
+ Новое боковое меню со ссылками быстрого доступа. Откройте его, проведя слева направо в меню расчета.
+ Переработано меню Y=. Теперь вы можете раскрасить графики в свои любимые цвета.
+ Поддержка построения графиков кусочных функций.
Доступны новые команды Taculator!
+ Med-Med
+ randNorm
+ randBin
+ Matrix-List
+ List-Matrix
+ DrawInv
+ 2-PropZ-Interval
+ Chi²-Test
+ Chi²GOF-Test
+ LinRegT-5 + LinRegT-Test
Interval
+ ANOVA
Предыдущие улучшения:
+ Функции трассировки теперь более точны.
+ Во время трассировки вы можете ввести значение x, и Taculator покажет значение y. Нажмите кнопку TRACE и введите любое значение.
+ Используйте команды nDeriv и fnInt в меню Y= для построения графика производной или интегральной функции.
+ Теперь вы можете графически отображать семейства функций, используя следующий синтаксис: {1,2,3}X.
Рейтинги и обзоры
501 Рейтинг
Я скачал его по причине
Это приложение имеет очень чистый и профессиональный вид, очень приятно для глаз, а всплывающее окно имеет хороший размер. Настройка цвета в начале выглядит немного ненужной, но это тоже круто. Все эти вещи великолепны, и это было бы идеальным приложением для моей школьной работы.
За исключением….
Функция построения графиков не работает.

Я действительно разочарован,
Я ненавижу переключаться между вкладками в моем браузере и неловко нажимать на каждое из отдельных полей в графических онлайн-калькуляторах.
Если вам нужен обычный научный калькулятор, который выглядит красиво, то это идеальное приложение для вас.
Что касается меня, то я воспользуюсь для этого своим физическим калькулятором.
Действительно, я скачал его только для функции построения графиков.
Я мог бы дать этому приложению три звезды, несмотря на это, но на логотипе явно есть вводящий в заблуждение график, и в описании нет ничего, говорящего о том, что вам нужно заплатить, чтобы иметь возможность ГРАФИЧЕСКОГО калькулятора.
Я имею в виду, что я понимаю, разработчики приложений для калькуляторов тоже должны зарабатывать на жизнь, но, по крайней мере, информировать своих потребителей.В любом случае главное:
ГРАФИК НЕ РАБОТАЕТ
НО ЭТО ВСЕ ЕЩЕ АТХЕТИЧЕСКИЙ ОБЫЧНЫЙ КАЛЬКУЛЯТОР
ОБНОВЛЕНИЕ: ошибка исправлена в последнем обновлении v1.
0.1. Мы будем рады, если вы снова попробуете приложение и обновите свой отзыв 🙂
Спасибо за ваш отзыв и сообщение о проблеме с графикой. Графики можно использовать в Taculator бесплатно, но в настоящее время существует ошибка, из-за которой уравнение не сохраняется.
Мы делаем все возможное, чтобы исправить это как можно скорее 🙂А пока, вот обходной путь для построения графика:
В меню Y= введите уравнение как обычно. Затем нажмите клавишу со стрелкой ВВЕРХ или ВНИЗ на клавиатуре калькулятора. Затем нажмите ГРАФИК. Не нажимайте GRAPH или ENTER после ввода уравнения, иначе оно будет потеряно (из-за ошибки). Мы надеемся, что это поможет, пока мы не исправим это.
Приносим извинения за неудобства.
Не стоит денег
Сначала я подумал, что это приложение — отличный калькулятор, и мне понравилось, что его можно настраивать, я получил бесплатную пробную версию и не смог отменить ее, когда мой телефон перестал работать на неделю, когда я уронил его в воду, поэтому я получил заряд.
Я не был слишком расстроен, что я случайно купил его в течение года до сих пор. Раньше я использовал графические функции для своего математического класса, но теперь, когда я использую их для показателей степени, это часто дает мне неправильные вычисления. Для моего урока химии нам нужен калькулятор во время занятий и для тестов, и мои окончательные расчеты были неправильными. Я показал своему учителю, что я ввожу, и все мои шаги верны, и это приложение иногда дает неправильные расчеты. Это происходит не всегда, но очень расстраивает то, что я заплатил за калькулятор, который не гарантирует, что я всегда буду получать правильные точные расчеты. Я искренне верил, что приложение-калькулятор станет отличной заменой, которую я бы порекомендовал, но оно ненадежно, и по этой причине я бы не стал рекомендовать его другим на 100%.
Мех
Я заплатил 29 долларов, чтобы иметь это навсегда.
И по сравнению с игрой на 100$ за настоящую, это очень хорошая сделка. но у меня возникли некоторые проблемы с калькулятором. В частности, при решении длинных уравнений он никогда не несет отрицательное значение через проблему. Например, если бы я подставил -3•4, то получил бы -12, но затем я умножил свой ответ на 8 (-12•8), и это дало бы мне положительное число 96, а не -96. Это вызвало у меня несколько проблем с некоторыми заданиями, но как только я понял, что происходит, мне было довольно легко продолжить. Мне также трудно смотреть на графики, когда я рисую их. Я помещу свои уравнения в Y=, и он будет хорошо отображаться, но я никогда не смогу увидеть полный график, и из-за этого я не могу найти пересечения и все такое. Кроме того, он работает довольно хорошо, я просто пытаюсь использовать его для более простых вещей, которые не может сделать калькулятор моего телефона.
Спасибо за отзыв.

Мы попытались воспроизвести ваш расчет проблемы с отрицательным знаком.
После того, как мы умножим -12 на 8 в следующей строке (то есть будет -12, а затем в следующей строке будет *8), калькулятор даст нам -96.
Можете ли вы прислать нам снимок экрана вашего калькулятора, чтобы мы могли его подробнее изучить?
Для построения графика вы можете увидеть полный график, изменив настройки окна или воспользовавшись одной из команд масштабирования, например, «zoomFit» должен работать, чтобы показать весь график.
Мы будем рады помочь вам с этим более подробно. Вы можете написать нам на [email protected]
Подписки
Taculator Pro — Ежегодно
Разблокируйте более 100 функций и команд PRO
Бесплатная пробная версия
Разработчик Di Venisco UG (haftungsbeschrankt) указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:
- Данные об использовании
- Диагностика
Данные, не связанные с вами
Могут быть собраны следующие данные, но они не связаны с вашей личностью:
- Данные об использовании
- Диагностика
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Узнать больше
Информация
- Продавец
- Ди Вениско УГ (haftungsbeschrankt)
- Размер
- 26,7 МБ
- Категория
- Образование
- Возрастной рейтинг
- 4+
- Авторское право
- © 2019-2020 Такулятор
- Цена
- Бесплатно
- Тех. поддержка
- политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
графическое представление функции log(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- косек (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- exp (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- th (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- косек (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- exp (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- th (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер кривых имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0258 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого,
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.
 Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
 0.1. Мы будем рады, если вы снова попробуете приложение и обновите свой отзыв 🙂
0.1. Мы будем рады, если вы снова попробуете приложение и обновите свой отзыв 🙂 Я не был слишком расстроен, что я случайно купил его в течение года до сих пор. Раньше я использовал графические функции для своего математического класса, но теперь, когда я использую их для показателей степени, это часто дает мне неправильные вычисления. Для моего урока химии нам нужен калькулятор во время занятий и для тестов, и мои окончательные расчеты были неправильными. Я показал своему учителю, что я ввожу, и все мои шаги верны, и это приложение иногда дает неправильные расчеты. Это происходит не всегда, но очень расстраивает то, что я заплатил за калькулятор, который не гарантирует, что я всегда буду получать правильные точные расчеты. Я искренне верил, что приложение-калькулятор станет отличной заменой, которую я бы порекомендовал, но оно ненадежно, и по этой причине я бы не стал рекомендовать его другим на 100%.
Я не был слишком расстроен, что я случайно купил его в течение года до сих пор. Раньше я использовал графические функции для своего математического класса, но теперь, когда я использую их для показателей степени, это часто дает мне неправильные вычисления. Для моего урока химии нам нужен калькулятор во время занятий и для тестов, и мои окончательные расчеты были неправильными. Я показал своему учителю, что я ввожу, и все мои шаги верны, и это приложение иногда дает неправильные расчеты. Это происходит не всегда, но очень расстраивает то, что я заплатил за калькулятор, который не гарантирует, что я всегда буду получать правильные точные расчеты. Я искренне верил, что приложение-калькулятор станет отличной заменой, которую я бы порекомендовал, но оно ненадежно, и по этой причине я бы не стал рекомендовать его другим на 100%.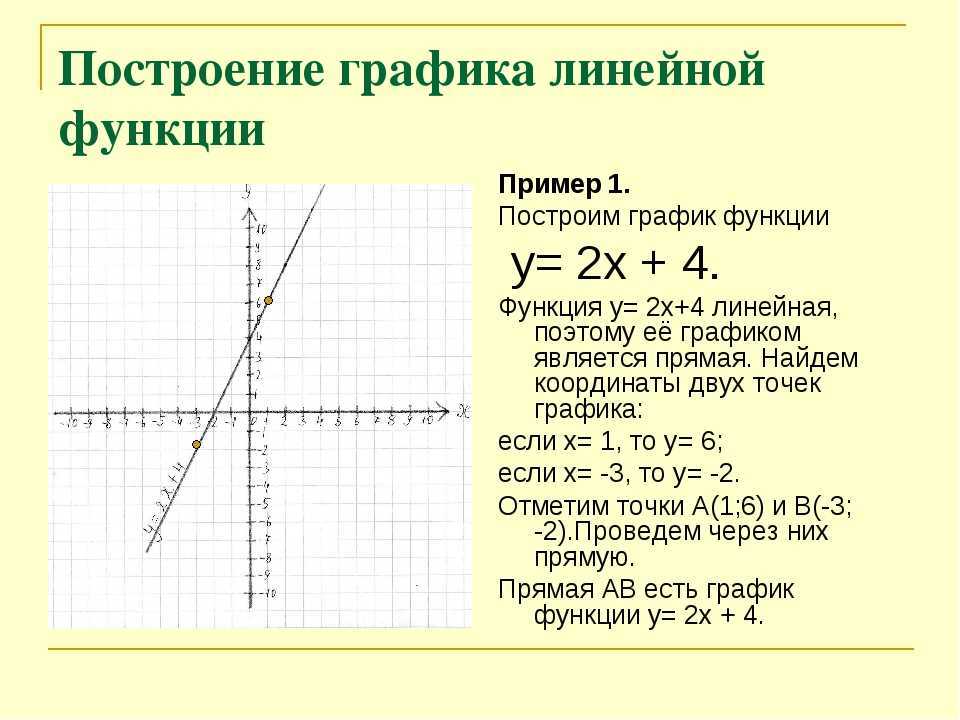 И по сравнению с игрой на 100$ за настоящую, это очень хорошая сделка. но у меня возникли некоторые проблемы с калькулятором. В частности, при решении длинных уравнений он никогда не несет отрицательное значение через проблему. Например, если бы я подставил -3•4, то получил бы -12, но затем я умножил свой ответ на 8 (-12•8), и это дало бы мне положительное число 96, а не -96. Это вызвало у меня несколько проблем с некоторыми заданиями, но как только я понял, что происходит, мне было довольно легко продолжить. Мне также трудно смотреть на графики, когда я рисую их. Я помещу свои уравнения в Y=, и он будет хорошо отображаться, но я никогда не смогу увидеть полный график, и из-за этого я не могу найти пересечения и все такое. Кроме того, он работает довольно хорошо, я просто пытаюсь использовать его для более простых вещей, которые не может сделать калькулятор моего телефона.
И по сравнению с игрой на 100$ за настоящую, это очень хорошая сделка. но у меня возникли некоторые проблемы с калькулятором. В частности, при решении длинных уравнений он никогда не несет отрицательное значение через проблему. Например, если бы я подставил -3•4, то получил бы -12, но затем я умножил свой ответ на 8 (-12•8), и это дало бы мне положительное число 96, а не -96. Это вызвало у меня несколько проблем с некоторыми заданиями, но как только я понял, что происходит, мне было довольно легко продолжить. Мне также трудно смотреть на графики, когда я рисую их. Я помещу свои уравнения в Y=, и он будет хорошо отображаться, но я никогда не смогу увидеть полный график, и из-за этого я не могу найти пересечения и все такое. Кроме того, он работает довольно хорошо, я просто пытаюсь использовать его для более простых вещей, которые не может сделать калькулятор моего телефона.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения
Ваш комментарий будет первым