python — Программа для рисования графиков функций, введенных пользователем или заданных в виде строк
Всем привет. Как создать программу, которая рисует графики функций в MatplotLib. Я тут набросал кое-что:
# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
import math
import pylab
from matplotlib import mlab
print("Строитель графиков")
f = input ('f(x)=')
code = """
def func (x):
return %s
""" % f
exec(code)
xmin = -20.0
xmax = 20
dx = 0.01
xlist = mlab.frange (xmin, xmax, dx)
ylist = [func (x) for x in xlist]
plt.axis([-20, 20, -20, 20])
plt.xlabel('x')
plt.ylabel('y')
plt.title('График функции(x)')
plt.grid(True)
pylab.plot (xlist, ylist)
pylab.show()
Всё нормально. Но как начинаю трогать:
code = """
def func (x):
return %s
""" % f
пишет, что есть лишний отступ, но вопрос: где? Я хочу вставить сюда ещё и while, чтобы бесконечно можно было строить графики функций, но не могу из-за этого.
Подскажите, как сделать так, чтобы я мог бесконечно строить графики функций?:)
У кого какие варианты?
- python
- numpy
- matplotlib
- pyqt
1
UPDATE: строим графики сразу всех функций.
Функции у которых отсутствует переменная x (например f(x) = 5 + 20) будут преобразованы к виду: f(x) = x/x * (5 + 20)
# -*- coding: utf-8 -*-
import numexpr as ne
import matplotlib.pyplot as plt
from matplotlib import mlab
plt.style.use('ggplot')
xmin = -20.0
xmax = 20
dx = 0.01
x = mlab.frange(xmin, xmax, dx)
funcs = ["x**2 * sin(x)", "x**2", "15", "12 + 34"]
# преобразовуем функции, в которых отсутствует переменная `x` к виду: `x/x * (5)`
new_funcs = [f if 'x' in f else 'x/x * ({})'.format(f) for f in funcs]
[plt.plot(x, ne.evaluate(f), linewidth=1.5) for f in new_funcs]
plt.title('Графики функций')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(funcs)
plt.show()
Преобразованные функции:
In [25]: new_funcs Out[25]: ['x**2 * sin(x)', 'x**2', 'x/x * (15)', 'x/x * (12 + 34)']
PS надо бы еще добавить обработку исключений, но мне лень…
Предыдущий ответ:
Воспользуйтесь модулем numexpr:
# -*- coding: utf-8 -*- import numexpr as ne import matplotlib.pyplot as plt from matplotlib import mlab plt.style.use('ggplot') xmin = -20.0 xmax = 20 dx = 0.01 x = mlab.frange(xmin, xmax, dx) # f = input ('f(x)=') f = "x**2 * sin(x)" plt.plot(x, ne.evaluate(f), linewidth=1.5) plt.xlabel('x') plt.ylabel('y') plt.legend(['График функции: f(x) = {}'.format(f)]) plt.show()
pyplot as plt
from matplotlib import mlab
plt.style.use('ggplot')
xmin = -20.0
xmax = 20
dx = 0.01
x = mlab.frange(xmin, xmax, dx)
# f = input ('f(x)=')
f = "x**2 * sin(x)"
plt.plot(x, ne.evaluate(f), linewidth=1.5)
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['График функции: f(x) = {}'.format(f)])
plt.show()
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Построение графиков функций при помощи геометрических преобразований | Презентация к уроку:
Слайд 1
Построение графиков функций при помощи геометрических преобразований
Слайд 2
Цель занятия: Научиться строить графики сложных функций путем геометрических преобразований графиков элементарных функций Задачи: Рассмотреть возможные направления преобразований графиков функций.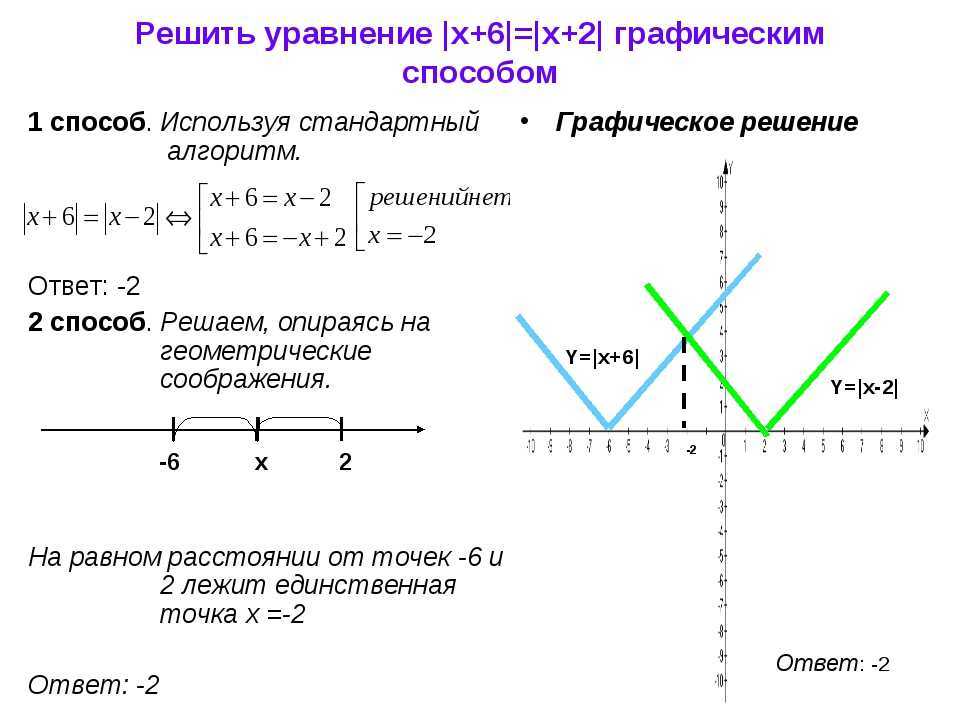
Изучить, к каким изменениям в графиках функций приводит появление числовых слагаемых, коэффициентов, знаков модуля в записи формулы функции. Научиться использовать теоретические сведения об изменениях формы графиков для решения практических задач. Исследовать нетипичные способы геометрических преобразований для построения графиков функций. Выработать критерии выбора способа построения графика функции.
Слайд 3
Направления преобразований графиков Преобразования вдоль оси ординат Преобразования вдоль оси абсцисс x y x y
Слайд 4
y=f(x) Преобразования графика функции f(x) +b параллельный перенос на | b | единиц: — вверх , если b >0 — вниз , если b
Слайд 5
преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k — растяжение вдоль oY у k раз, если k >1 x y y=2f(x) y=f(x) 4 8
Слайд 6
преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k x y y=f(x) y= 1/2 f(x) 2 4 — сжатие вдоль oY в k раз, если 0
Слайд 7
преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) k — симметричное отображение относительно оси абсцисс , если k =-1 x y y=f(x) -4 4 y= — f(x)
Слайд 8
преобразования вдоль оси ординат y= f(x) преобразования графика функции f(x) | | 1) сохранение частей , которые лежат над осью oX x y y=|f(x)| y=f(x) 2) симетричное отображение частей , которые лежат ниже оси oX
Слайд 9
преобразования вдоль оси абсцис y=f(x ) преобразования графика функции f(x) + a паралельный перенос на | a | единиц: — влево , если a >0 — вправо , если a
Слайд 10
преобразования вдоль оси абсцис y=f( x) преобразования графика функции f(x) k — сжатие вдоль oX в k раз, если k >1 x y y=f(2x) y=f(x)
Слайд 11
преобразования вдоль оси абсцис y=f( x) преобразования графика функции f(x) k — растяжение вдоль oX в k раз, если 0
Слайд 12
преобразования графика функции f(x) — симметричное отображение относительно оси ординат , если k =-1 x y y=f(x) y= f( — x) y=f( x) k преобразования вдоль оси абсцис
Слайд 13
y=f ( x ) преобразования графика функции f(x) | | 1) отбрасывание части , которая лежит левее oY x y y=f(|x|) y=f(x) 2) сохранение и симметричное отображение части , которая лежит правее oY преобразования вдоль оси абсцис
Слайд 14
Примеры построения графиков функций при помощи геометрических преобразований
Слайд 15
Пример 1 При помощи геометрических преобразований графика функции y=x 2 постройте график функции y=-2(x-3) 2 +7 1 шаг параллельный перенос на 3 единицы вправо 2 шаг симметричное отображение относительно oX 3 шаг растяжение в 2 раза вдоль oY 4 шаг параллельный перенос на 7 единиц вверх — 2 +7 -3
Слайд 16
Пример 1 Построение графика y=x 2 1 шаг: y= ( x -3 ) 2 2 шаг: y= — ( x -3) 2 3 шаг: y= — 2 ( x -3) 2 4 шаг: y= -2( x -3) 2 +7 параллельный перенос вправо на 3 единицы симметричное отображение относительно oX растяжение в 2 раза вдоль oY параллельный перенос вверх на 7 единиц x y y= -2( x -3) 2 +7 y=-2(x-3) 2 +7
Слайд 17
Пример 2 При помощи геометрических преобразований графика функции y=x 2 постройте график функции y=|x 2 -6x+4| Выделим полний квадрат из квадратного трехчлена: |x 2 -6x+4| = |(x 2 -2 .
x . 3+3 2 )-3 2 +4|=|(x-3) 2 -5| Следовательно необходимо построить график функции y=| (x-3) 2 -5 |
Слайд 18
Пример 2 Построение графика y=x 2 1 шаг: y= (x -3 ) 2 2 шаг: y= (x-3) 2 -5 3 шаг: y= | (x-3) 2 -5 | параллельный перенос вправо на 3 единицы параллельный перенос вниз на 5 единиц сохранение частей, которые лежат над осью oX ; симметричное отображение частей, которые лежат ниже оси oX x y y=| ( x -3) 2 -5| y=| (x-3) 2 -5 |
Слайд 19
Пример 3 При помощи геометрических преобразований графика функции y=√x постройте график функции 1 шаг параллельный перенос на 1 единицу влево 2 шаг растяжение в 3 раза вдоль oY 3 шаг параллельный перенос на 4 единицы вниз 4 шаг отбрасывание части, которая лежит левее oY сохранение и симметричное отображение части, которая лежит правее oY.
Слайд 20
Пример 3 Построение графика 1 шаг: 2 шаг: 3 шаг: 4 шаг: параллельный перенос влево на 1 единицу растяжение в 3 раза вдоль oY параллельный перенос вниз на 4 единицы отбрасывание части, которая лежит левее oY сохранение и симметричное отображение части, которая лежит правее oY x y
Слайд 21
Отдельные случаи построения графиков при помощи геометрических преобразований
Слайд 22
Сложение графиков Постройте график функции y=|x+1|+|x-1| 1 шаг: построим график функции y=|x+1| 2 шаг: построим график функции y=|x-1| 3 шаг: y =|x+1|+|x-1| Ординату искомого графика получаем сложением ординат двух построенных графиков в той самой точке x y y =|x+1|+|x-1|
Слайд 23
Деление графиков Постройте схематически график функции y=1/f(x) , если известен график функции y=f(x) 1 шаг: Предположим, график функции y=f(x) имеет такой вид 2 шаг: Построим вертикальные асимптоты для графика y=1/f(x) .
Они будут проходить через точки пересечения графика y=f(x) и оси oX . 3 шаг: Точки графика y=f(x) с ординатами y=1 и y=-1 будут общими для обоих графиков. y = 1/ f(x) 4 шаг: Для точек графика y=f(x) с положительными ординатами соответствующие точки графика y=1/f(x) будут иметь также положительные ординаты, а для отрицательных – отрицательные. Чим больше по модулю ордината точки графика y=f(x) , тем в большей мере график y=1/f(x) приближается к оси oX и наоборот. x y
Слайд 24
Сравнение методов сложения и деления графиков построим методом сложения и методом деления график функции и сравним результаты Выполним преобразования выражения для сложения графиков для деления графиков y = y 1 + y 2 y = 1/ y 3
Слайд 25
Сложение графиков построим график функции 1 шаг: построим график функции y=x 2 шаг: построим график функции y=1/x 3 шаг: Ординату искомого графика получим сложением ординат построенных графиков в той самой точке x y Построенный график имеет две асимптоты: — вертикальную x=0 ; — наклонную y=x .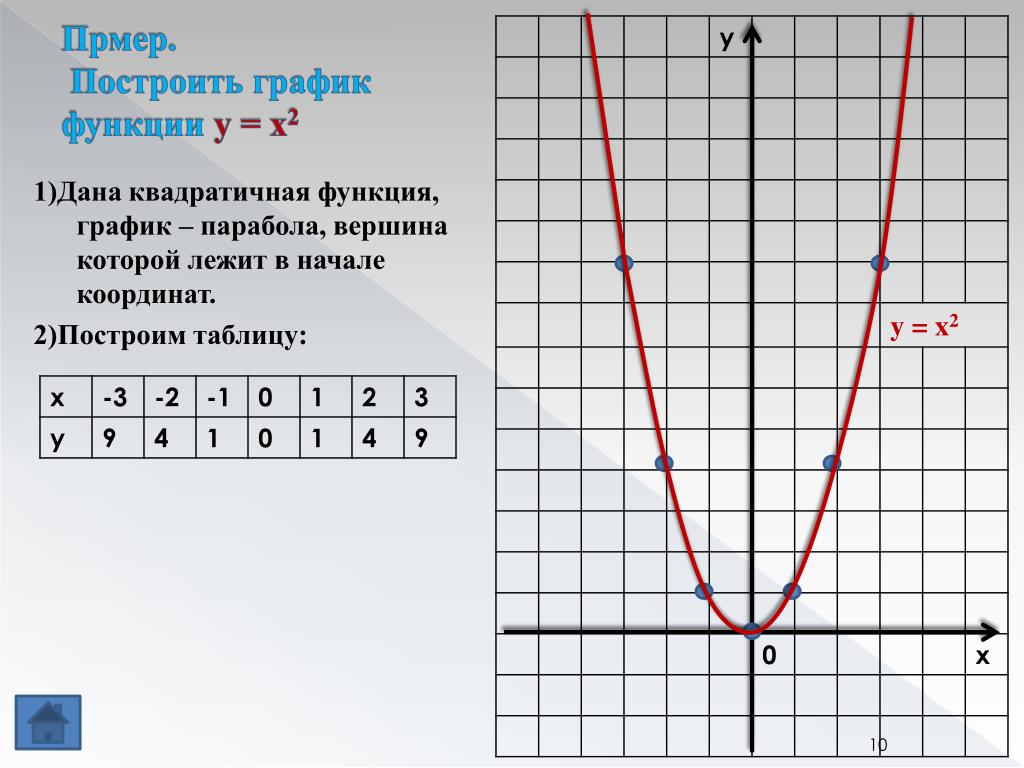
Слайд 26
Деление графиков построим график функции 1 шаг: Предположим, нам известен график функции 2 шаг: построим вертикальную асимптоту для графика y=1/y 3 . Она будет проходить через точку пересечения графика y 3 =f(x) с осью oX . 3 шаг: график y 3 =f(x) не имеет точек с ординатами y=1 и y=-1 . Следовательно, общие точки графиков функций y 3 =f(x) и y=1/y 3 отсутствуют. 4 шаг: Для точек графика y 3 =f(x) с положительными ординатами соответствующие точки графика y=1/y 3 будут иметь также положительные ординаты, а для отрицательных – отрицательные. Чем больше по модулю ордината точки графика y 3 =f(x) , тем больше график y=1/y 3 приближается к оси oX и наоборот x y y — 1 / 2 -2 1 / 2 2
Слайд 27
Сложение графиков x y Сравнение результатов Деление графиков x y — 1 / 2 -2 1 / 2 2 1)Графики идентичны, но график, который построен сложением, точно определяет еще и наклонную асимптоту. 2)Суммировать ординаты легче, чем оценивать пропорции их изменения. Вывод : Для построения графика выбираем тот способ, который обеспечивает более информативный результат и является более удобным в применении.
Слайд 28
Успехов в изучении математики!
Слайд 29
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики (основные приемы ) 7-е изд., стереотипное.—М.: МЦНМО, 2006. — 120 с. Гурский И. П.Функции и построение графиков. Пособие для учителей. Изд. 3-е, испр . и доп. М., «Просвещение», 1968. — 215 с . Дороднов А. М., Острецов И. Н., Петросов В. А., Приходов В. Ю., Сафонов И. Б.. Графики функций. Учеб. пособие для поступающих в вузы. М., « Высш . школа», 1972, — 104 с . Ершов Л. В., Райхмист Р. Б. Построение графиков функций: Кн. для учителя М.: Просвещение, 1984, — 80 с . Список использованных информационных ресурсов
Алгебра — Графические функции
Онлайн-заметки Пола
Главная
/
Алгебра
/
Графики и функции
/ Графические функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3.5: Графические функции
93} + 1\).Показать решение
Теперь, как мы говорили ранее в этой главе, когда впервые рассматривали построение графиков, нам нужно выбрать значения \(x\) для подстановки, а знание того, какие значения следует выбирать, на самом деле приходит только с опытом. Поэтому не беспокойтесь так о значениях \(x\), которые мы здесь используем. К концу этой главы вы также сможете правильно выбирать эти значения.
Вот оценки функций.
| \(х\) | \(ф(х)\) | \(\влево({х,у}\вправо)\) |
|---|---|---|
| -1 | -7 | \(\слева( { — 1, — 7} \справа)\) |
| 0 | 0 | \(\влево( {0,0} \вправо)\) |
| 1 | 1 | \(\влево({1,1} \вправо)\) |
| 2 | 2 | \(\влево( {2,2} \вправо)\) |
| 3 | 9 | \(\влево( {3,9} \вправо)\) |
Вот набросок графика.
Итак, построение графиков функций очень похоже на построение графиков уравнений. 92} + 4 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 дюйма} x < 1 \\ 2x - 1 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 in}x \ge 1\end{align*}\]
Нам нужно быть немного осторожными с тем, что происходит прямо в точке \(x = 1\), так как технически это справедливо только для нижней функции. Однако мы займемся этим в самом конце, когда будем строить график. Сейчас мы будем использовать \(x = 1\) в обеих функциях.
Первое, что нужно сделать здесь, это получить таблицу значений для каждой функции в указанном диапазоне, и снова мы будем использовать \(x = 1\) в обоих случаях, хотя технически его следует использовать только с нижней функцией. 92} + 4\)
| \(х\) | \(2x — 1\) | \(\влево({х,у}\вправо)\) |
|---|---|---|
| 1 | 1 | \(\влево({1,1} \вправо)\) |
| 2 | 3 | \(\влево( {2,3} \вправо)\) |
| 5 | \(\влево( {3,5} \вправо)\) |
Вот набросок графика и обратите внимание, как мы обозначили точки \(x = 1\).
Для верхней функции мы использовали открытую точку для точки \(x = 1\), а для нижней функции мы использовали закрытую точку для \(x = 1\). Таким образом, на графике становится ясно, что только нижняя функция действительно имеет точку \(x = 1\).
Обратите внимание: поскольку два графика не пересекались в точке \(x = 1\), мы оставили на графике пустое место. НЕ соединяйте эти две точки линией. Там действительно должен быть разрыв, чтобы показать, что две части не встречаются в точке \(x = 1\).
Иногда две части встречаются в этих точках, а иногда нет. Мы не должны ожидать, что они встретятся или не встретятся, пока мы не набросаем график.
Давайте рассмотрим еще один пример кусочной функции. 92}}&{{\mbox{if}} — 2 \le x < 1}\\{ - x + 2}&{{\mbox{if}}\,x \ge 1}\end{массив}} \верно.\]
Показать решение
В этом случае мы будем строить графики трех функций в диапазонах, указанных выше. Итак, как и в предыдущем примере, мы будем получать значения функций для каждой функции в указанном диапазоне и будем включать конечные точки каждого диапазона в каждое вычисление.
Когда мы рисуем график, мы подтвердим, к какой функции на самом деле принадлежит конечная точка, используя закрытую точку, как мы делали ранее. Кроме того, верхняя и нижняя функции являются линиями, поэтому нам действительно не нужно больше двух точек для этих двух. Мы получим еще пару баллов за среднюю функцию.
| \(х\) | \(х + 3\) | \(\влево({х,у}\вправо)\) |
|---|---|---|
| -3 | 0 | \(\влево( { — 3,0} \вправо)\) |
| -2 | 1 | \(\влево( { — 2,1} \вправо)\) |
| \(х\) 92}\) | \(\влево({х,у}\вправо)\) | |
|---|---|---|
| -2 | 4 | \(\влево( { — 2,4} \вправо)\) |
| -1 | 1 | \(\влево( { — 1,1} \вправо)\) |
| 0 | 0 | \(\влево({0,0} \вправо)\) |
| 1 | 1 | \(\влево({1,1} \вправо)\) |
| \(х\) | \(- х + 2\) | \(\влево({х,у}\вправо)\) |
|---|---|---|
| 1 | 1 | \(\влево({1,1} \вправо)\) |
| 2 | 0 | \(\влево( {2,0} \вправо)\) |
Вот набросок графика.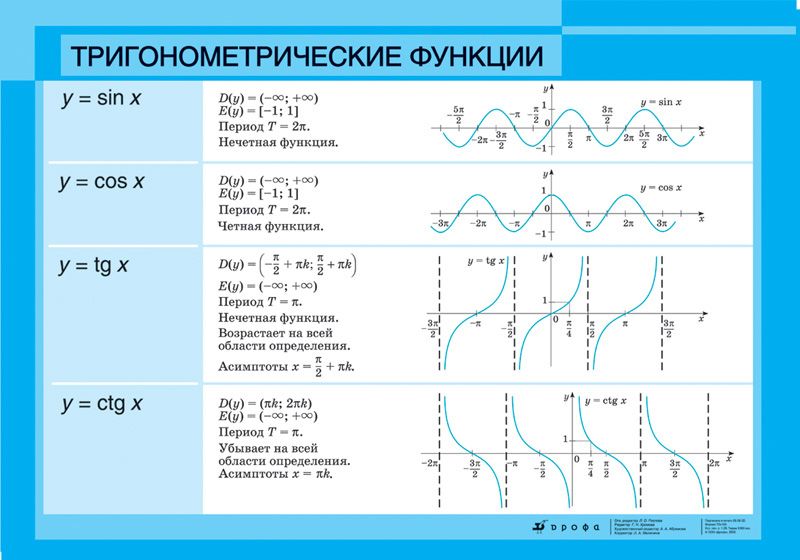
Обратите внимание, что в этом случае две части встретились в точке разрыва \(x = 1\), а в другой точке разрыва, \(x = — 2\), они не встретились. Как отмечалось в предыдущем примере, иногда они встречаются, а иногда нет.
Технология построения графиков функций
Технология построения графиков функций Графические функции Учащиеся всех уровней алгебры и математических расчетов находят это интересным
и полезно иметь возможность быстро построить график многих функций. Вы можете использовать графику
калькуляторы или компьютерные программы для этого. Какой-нибудь бесплатный или недорогой компьютер
доступны программы и графические калькуляторы по цене от 50 до 50 долларов.
Можно использовать 150 долларов. Каждая программа и калькулятор работает немного по-своему, поэтому
вероятно, проще всего выбрать один и выполнить всю свою работу над ним. Они должны
получить студента от алгебры через курс исчисления первого семестра.
(см. комментарии
под списками.)
Начало работы | Где найти их на ACC
Графические калькуляторы:
- В ACC инструкторы используют Техас Калькуляторы инструментов. (около 100 долларов и выше). Некоторые комментарии см. ниже.
- Несколько полезных советов от Аризонского университета. программы для различных графических калькуляторов
Графическое программное обеспечение для ПК:
- Winplot от Peanut Software (Бесплатно. Необходимо установить. Инструкции см. ниже.)
- Графический калькулятор 3.2 от Pacific Tech (Студенческая версия стоит 40 долларов США по состоянию на 30.12.07. Посмотрите «Тур».)
Графическое программное обеспечение для компьютеров Mac:
- Графический калькулятор 3.2 от Pacific
Tech (Внимательно проверьте веб-сайт. Возможно, он уже есть на вашем компьютере. )
- Различные программы для Mac (бесплатное и условно-бесплатное ПО)
)Графическое программное обеспечение веб-браузера:
- Функциональный граф (Бесплатно, и вам не нужно устанавливать его. Просто используйте его. См. некоторые комментарии ниже. Не отображает полярные функции или параметрические уравнения, которые используются в конце курса тригонометрии, а иногда и в курсах более высокого уровня)
Комментарии:
Программное обеспечение для ПК:
Я много лет пользуюсь Winplot, и он мне нравится. Единственная трудность заключается в том, что не очевидно, как начать, когда вы его установите. Информация «помощь» в
само программное обеспечение не очень полезно. Различные люди написали некоторые дополнительные
справочная информация. Мой бриф
введение | дольше
введение | Ориентация
программы (это для более ранних версий, но я думаю, что базовая функциональность почти такая же.
)
Я видел демонстрацию более ранней версии программы Pacfic Tech, которая был NuCalc 2.0, и это было ОЧЕНЬ ХОРОШО! Это дало впечатляющие трехмерные графики. Он будет делать такие сложные вещи, как параметрические неравенства в полярных координатах. и в демо есть некоторые неравенства, которые создают очень интересные закономерности. я думаю, что Graphing Calculator 3.2 является обновлением этого.
Программное обеспечение для компьютеров Mac:
Джон Томасон — профессор ACC, использующий Mac. Посмотрите на его страницу, чтобы увидеть, что он в настоящее время рекомендует.
Программное обеспечение браузера:
Этот апплет Java предоставляет простой способ построения графика функции без установки
что-либо. Джон Томасон, порекомендовавший мне это, говорит:
следующий. «У него есть несколько особенностей. Чтобы ввести функцию, не набирайте «y=» или «f(x)=»;
просто введите формулу функции. Кроме того (по крайней мере, на моем Mac) функция трассировки
описанное не было доступно.
И нет функции печати. Если вы хотите распечатать
график, вам сначала нужно сделать снимок экрана или сделать экран печати. Другой
более того, это довольно быстро и очень удобно».0004
Графические калькуляторы:
В ACC есть калькуляторы TI.
Для любого калькулятора вам обязательно нужен доступ к Руководству . Если вы потеряли руководство , найдите его в Интернете. Онлайн-руководства TI доступны здесь. Выберите Загрузки > Путеводители.
Обычно на веб-сайте TI есть сравнительный справочник, где можно легко сравнить возможности всех выпускаемых в настоящее время моделей.
TI 84 — новейшая версия самого популярного калькулятора для курсов по математическому анализу. Клавиатура и основные возможности такие же, как у старых 83, 82 и 81. Каждая новая версия имеет больше возможностей, чем предыдущая, но любой из них подходит для наших курсов. Новые калькуляторы этой линейки стоят от 100 до 140 долларов, в зависимости от расширенных функций.
ТИ-89 (около 150 долларов США) — это совсем другой тип, поскольку он включает в себя возможности системы компьютерной алгебры (CAS) и обычно считается калькулятором, более подходящим для курсов более высокого уровня. Он включает в себя трехмерную графику. Из-за этих расширенных возможностей учащимся с меньшей вероятностью разрешат использовать его на тестах, чем калькуляторы более низкого уровня.
Возможности Voyage 200 аналогичны TI-89.
В настоящее время существует несколько калькуляторов TI-Nspire с различными возможностями. Некоторые из них имеют возможности системы компьютерной алгебры (CAS), аналогичные более продвинутому TI-89, а другие — нет. Они стоят около 150-170 долларов. Сила этой линейки в основном заключается в более существенных возможностях редактирования, сохранении заметок и связи с другими электронными устройствами, чем в других графических калькуляторах TI. Все эти расширенные возможности «совместного использования» могут привести к тому, что учителя не захотят разрешать учащимся использовать их во время тестов.
По состоянию на август 2010 года даже самый продвинутый TI-Nspire не включает трехмерные графики, настраиваемые пользовательские меню и органайзер, которые включены в TI-89.и Вояж 200.
TI-86 является модернизацией более старого TI-85, который был рекомендован для уроков математики более высокого уровня и даже классов инженерии. Он был заменен калькулятором TI-89, но калькулятор TI-86 или 85 по-прежнему более чем подходит для наших курсов.
TI-74 также является графическим калькулятором, но не подходит для курсов математического анализа.
У Casio есть несколько более дешевых графических калькуляторов, чем у TI. я мало что знаю о их.
Если у вас уже есть графический калькулятор любой марки или модели, не покупайте
другой, пока вы не определите, действительно ли вам нужны дополнительные функции
более новый. Если у вас нет Руководства для , выполните поиск в Интернете и найдите электронную версию Руководства для , чтобы вы могли найти инструкции, когда вам это нужно.
Ваш комментарий будет первым