Задание 5. Построение графиков функций
Провести полное исследование функции , построить ее график, а также графики ее производных: .
1. . 2. . |
3. . 4. . |
5. . 6. . |
7. . 8. . |
9. . 10. . |
11. . 12. . |
13. . 14. |
15. . 16. . |
17. . 18. . |
19. . 20. . |
21. . 22. . |
23. . 24. . |
25. . 26. . |
27. . 28. . |
29. . 30. . |
31.
. 32. . |
33. . 34. . |
35. . 36. . |
37. . 38. . |
39. . 40. . |
41. . 42. . |
43. . 44. . |
45. . 46. . |
48. . |
49. 50. . |
Все задачи решаются по одной схеме. Пусть дана функция .
1. Находим область определения .
2. Находим точки разрыва функции. Определим характер разрыва, уточнив поведение функции в окрестности точки разрыва . Для этого найдем . Если — точка разрыва второго рода, то прямая будет вертикальной асимптотой графика функции.
3. Находим точки пересечения графика с осями координат, для чего решаем системы уравнений: .
4. Проверяем условия четности функции: и нечетности
. Если функция четная (или нечетная), то все последующие исследования проводим при .
5. Аналогично: если — периодическая функция с периодом Т, то исследование проводим при .
6. Находим первую
и вторую производные
.
Эту работу надо
выполнять очень аккуратно, иначе график будет построен неверно.
7. Находим экстремумы и промежутки монотонности функции.
8. Находим точки перегиба и промежутки выпуклости и вогнутости графика функции.
9. Находим наклонные асимптоты , где ; . Каждый из случаев: надо рассмотреть отдельно (асимптоты могут быть различными).
10. По результатам исследования составляем сводную таблицу и строим график функции.
11. По графику функции строим графики ее первой и второй производных.
Замечание 1. Построение графика функции рекомендуется проводить параллельно с исследованием.
Замечание 2. Если полученной в результате
исследований информации недостаточно
для построения графика функции, можно
построить несколько точек графика,
придавая аргументу х допустимые
значения.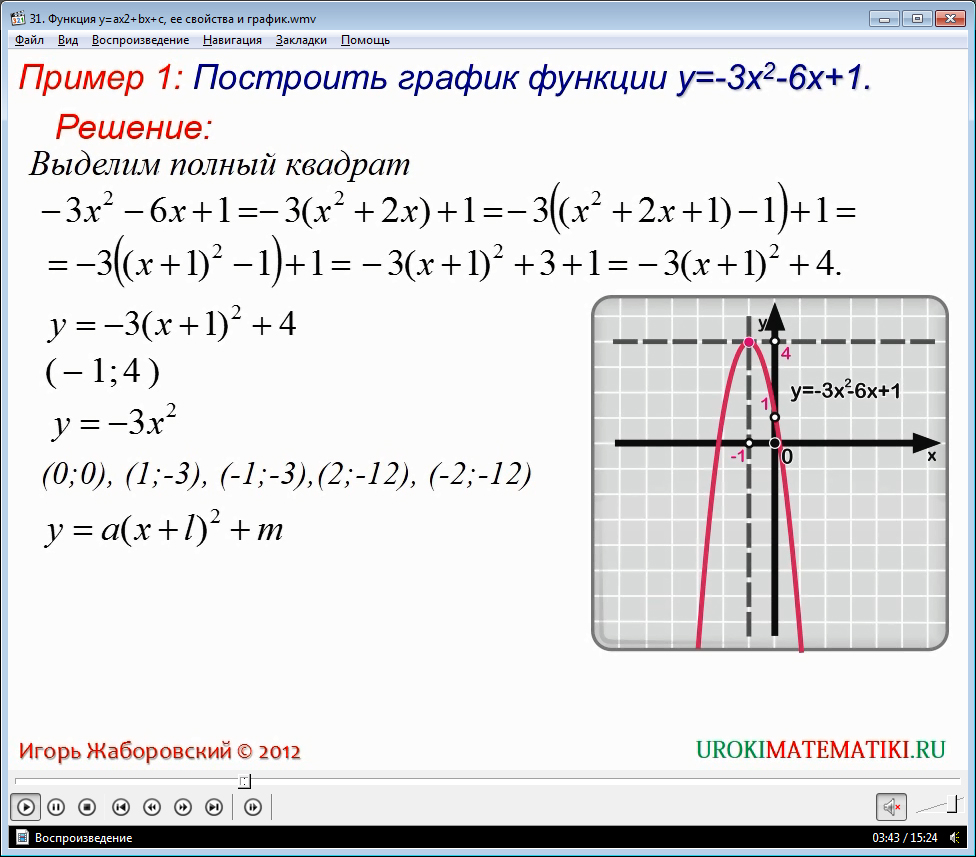
Пример 1. Исследовать функцию и построить ее график (рис.4).
Решение. 1. .
2. Функция терпит разрыв второго рода в точках , так как , и , . Следовательно, — уравнения вертикальных асимптот. Строим эти асимптоты.
3. Находим точки пересечения графика с осью ОХ, для чего решаем систему уравнений . Кривая пересекает ось ОХ в точках и .
Замечание. Если решение уравнения вызывает большие затруднения, то этого можно не делать. Для построения графика нужно выбрать несколько дополнительных точек.
Аналогично . Получаем точку .
4. . Функция четная, поэтому исследуем ее поведение в области .
5. Функция непериодическая.
6. Находим производные функции .
7. Находим
экстремумы функции.
Для этого найдем
сначала критические точки. Из уравнения следует, что
.
Так как вторая производная известна,
то характер экстремума определяем по
второму правилу. ,
поэтому при
функция имеет максимум, равный .
Итак, точка —
точка максимума. не существует при ,
но .
На функция убывает, на функция убывает.
8. Находим точки перегиба графика из уравнения , у нас , следовательно, кривая не имеет точек перегиба. В промежутке , следовательно, кривая выпуклая. В промежутке , поэтому кривая вогнута.
9. Находим уравнение наклонной асимптоты.
;
. Итак, — горизонтальная асимптота кривой.
10. В свободную таблицу вносят точки, полученные при исследовании функции в порядке возрастания аргумента х, а также дополнительные точки, если полученных недостаточно для построения графика функции:
х | 0 | 1 | 2 | 3 | 4 | |||
у | 0 | |||||||
Примечание | Точка макси-мума, точка пересечения с ОУ | Точка пересе- чения с ОХ | Точка разрыва | |||||
Строим график
функции в промежутке .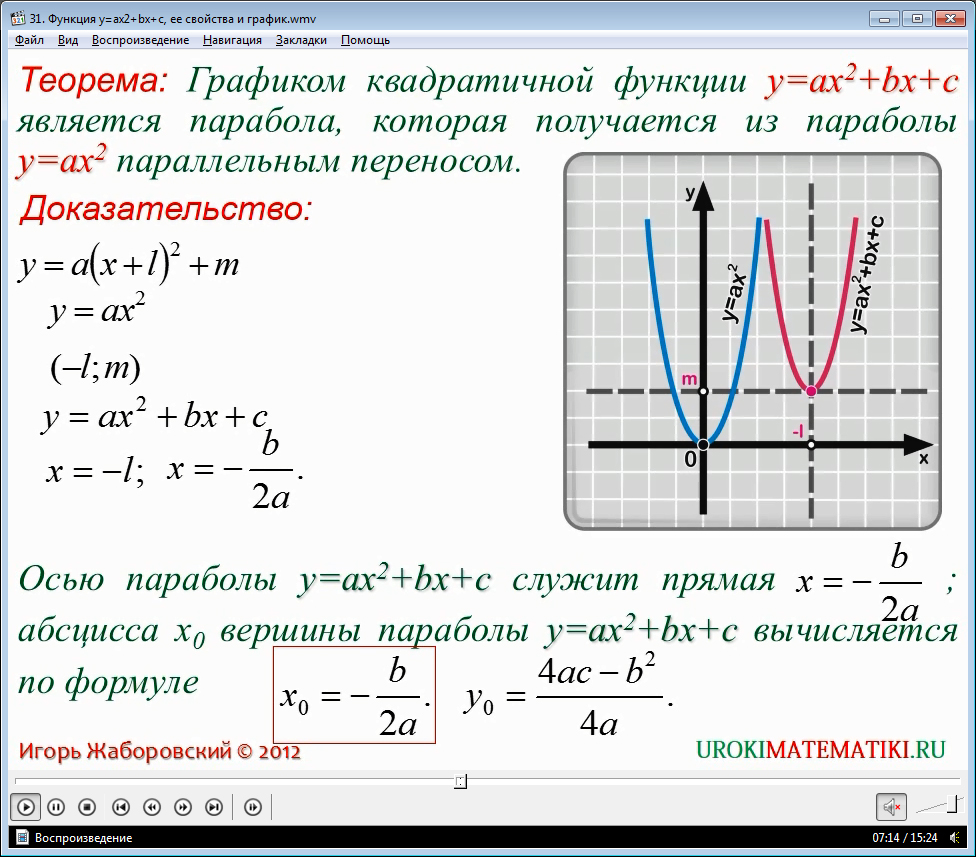
Так как функция четная, то в про-межутке ее график строим по симметрии относительно
оси ОУ (см. рис.4).
Пример 2. Исследовать функцию , построить график функции, а также графики и (рис.5).
Решение. 1. , то есть .
2. Функция всюду непрерывна, следовательно, не имеет точек разрыва, а также вертикальных асимптот.
3. Точки пересечения с осями координат
Получаем точки , , .
4. .
Функция нечетная, ее график симметричен относительно . Дальнейшее исследование проводим на промежутке .
5. Функция непериодическая.
6. Производные функции , .
Итак, ; .
7. Находим
экстремумы функции. Из уравнения
, .
Из уравнения следует, что .
Таким образом, получаем три критические
точки: .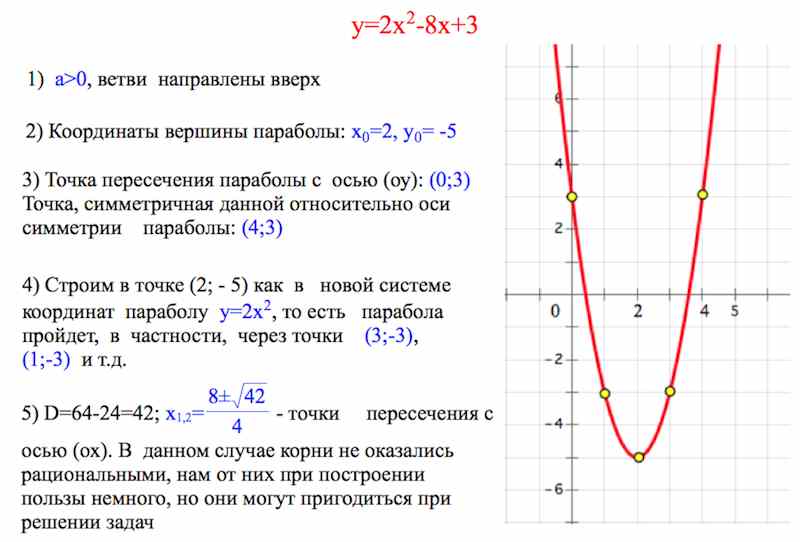
а) При не существует, поэтому экстремума нет.
б) При , следовательно, в этой точке функция имеет минимум, равный . Получаем точку минимума . Так как функция нечетная, то будет точкой максимума.
8. Находим точки перегиба. . В промежутке , здесь кривая выпукла. В промежутке , здесь кривая вогнута. Итак, — точка перегиба.
9. Находим уравнение наклонной асимптоты.
.
. Так как не существует, то график функции
асимптот не имеет.
у
1
0 х
x
0
0 x
-1/2
Рис.
4
у
4
0 х
-8
Рис. 5
10. Составим таблицу значений в промежутке
х | 0 | 1 | 2 | 3 | 4 | 8 | 13 | |
у | 0 | -8 | 0 | 4,8 | ||||
Примечание | Точка пересечения с осями координат | Дополнительные точки | Точка минимума | Дополнительная точка | Точка пересечения с ОХ | Дополнительная точка | ||
Замечание.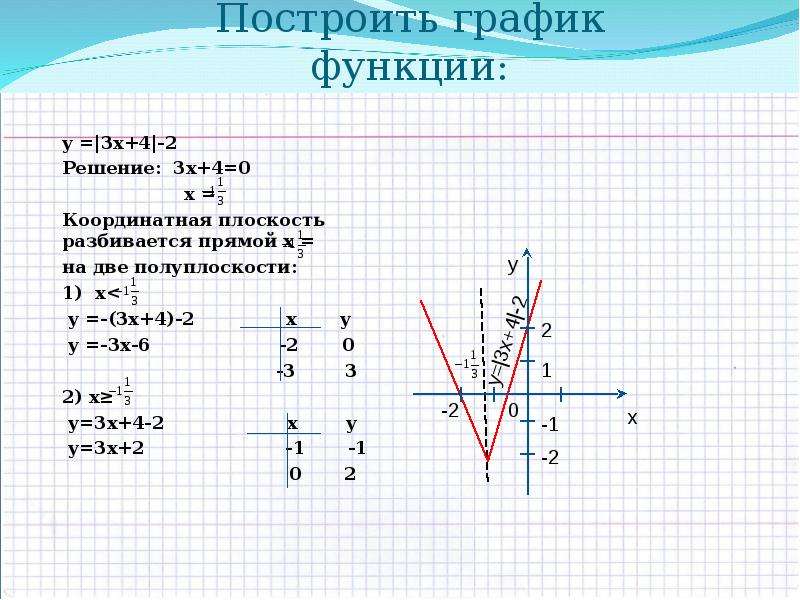
Ось ОУ является касательной к графику
в точке О (0; 0) (почему?).
Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел.  7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами.  29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47.  3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени.  130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения.  149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными.  169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188.  Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21.  Производная и ее применения209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22.  Простейшие задачи на построение.23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники.  49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76.  Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
2.4: Решение уравнений и неравенств с помощью графиков
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19688
- Дэвид Арнольд
- College of the Redwoods
В этой главе основное внимание уделялось функциям и интерпретации их графиков.
В этом разделе мы продолжаем в том же духе и обратимся к решению уравнений и неравенств с помощью графиков. Уравнения будут иметь вид \(f(x) = g(x)\), а неравенства будут иметь вид \(f(x) < g(x)\) и/или \(f(x) > g (Икс)\).
Вы можете удивиться, почему мы не упомянули неравенства вида \(f(x) \leq g(x)\) и \(f(x) \geq g(x)\). Причиной этого упущения является тот факт, что решение неравенства \(f(x) \leq g(x)\) есть просто объединение решений \(f(x) = g(x)\) и \(f(x) Мы начнем со сравнения значений двух функций f и g при различных значениях x в их областях определения. Предположим, что мы оцениваем две функции f и g при определенном значении x. Возможен один из трех исходов. Либо \[f(x)=g(x), \quad \text { или } \quad f(x)>g(x), \quad \text { или } \quad f(x) Довольно просто сравнить два значения функции по конкретному значению, если для каждой функции заданы правила. Мы также можем сравнивать значения функций при определенном значении x, изучая графики функций. Например, рассмотрим графики двух функций f и g на рисунке \(\PageIndex{1}\). Рисунок \(\PageIndex{1}\) Далее предположим, что мы проводим пунктирную вертикальную линию через точку пересечения графиков f и g, затем выбираем значение x, лежащее слева пунктирной вертикальной линии, как показано на рисунке \(\PageIndex{2}\)(a). Поскольку график f лежит над графиком g для всех значений x, лежащих слева от пунктирной вертикальной линии, будет иметь место, что \(f(x) > g(x)\) для всех таких x (см. рисунок \(\PageIndex{2}\)(a)). С другой стороны, график f лежит ниже графика g для всех значений x, лежащих справа от пунктирной вертикальной линии. Следовательно, для всех таких x будет иметь место \(f(x) < g(x)\) (см. рисунок \(\PageIndex{2}\)(b)). Рисунок \(\PageIndex{2}\). Наконец, если мы выберем значение x точки пересечения графиков f и g, то для этого значения x будет так, что f(x) и g(x) равны; то есть \(f(x) = g(x)\) (см. рисунок \(\PageIndex{3}\)). Рисунок \(\PageIndex{3}\). Значения функций f(x) и g(x) равны там, где графики функций f и g пересекаются. Подведем итоги. Резюме Давайте рассмотрим пример. Пример \(\PageIndex{2}\) Имея графики f и g на рисунке \(\PageIndex{4}\)(a), используйте построитель множеств и нотацию интервала для описания решения неравенство f(x) < g(x). Затем аналогичным образом найдите решения неравенства f(x) > g(x) и уравнения f(x) = g(x). Решение Чтобы найти решение f(x) < g(x), мы должны найти, где график f лежит ниже графика g. Проведем пунктирную вертикальную линию через точку пересечения графиков f и g (см. рис. \(\PageIndex{4}\)(b)), затем заметим, что график f лежит ниже графика g до точки пересечения. слева от этой пунктирной линии. Следовательно, решением неравенства f(x) < g(x) является совокупность всех x, лежащих левее пунктирной линии. Этот набор заштрихован красным (или более толстой линией при просмотре в черно-белом режиме) по оси x на рисунке \(\PageIndex{4}\)(b). Рисунок \(\PageIndex{4}\). Сравнивая f и g. Обратите внимание, что заштрихованные точки на оси x имеют значения x меньше 2. Следовательно, решение f(x) < g(x) есть \[(-\infty, 2)=\{x : x <2\}\] Аналогичным образом, решение f(x) > g(x) находится путем определения того, где график f лежит над графиком g, и заштриховывания соответствующих значений x на x- оси (см. рисунок \(\PageIndex{5}\)(a)). Чтобы найти решение f(x) = g(x), отметьте, где график f пересекает график g, затем заштрихуйте значение x этой точки пересечения на оси x (см. рисунок \( \PageIndex{5}\)(б)). Следовательно, решение f(x) = g(x) есть \(\{x : x = 2\}\). Это не интервал, поэтому нецелесообразно описывать это решение интервальной нотацией. Рисунок \(\PageIndex{5}\). Дальнейшие сравнения. Давайте посмотрим на другой пример. Пример \(\PageIndex{3}\) Имея графики f и g на рисунке \(\PageIndex{6}\)(a), используйте как построитель множеств, так и нотацию интервала для описания решения неравенства f(x) > g(x). Затем аналогичным образом найдите решения неравенства f(x) < g(x) и уравнения f(x) = g(x). Рисунок \(\PageIndex{6}\). Сравнивая f и g. Решение Чтобы найти решение f(x) > g(x), мы должны найти, где график f находится над графиком g. Обратите внимание, что точки, заштрихованные на оси x на рисунке \(\PageIndex{6}\)(b), имеют значения x от −2 до 3. Следовательно, решение f(x) > g(x) равно \[(-2,3)=\{x :-2 Аналогичным образом решение f(x) < g(x) находится, отмечая, где график f лежит ниже графика g и заштриховывает соответствующие значения x на оси x (см. рис. 7(a)). Таким образом, решение f(x) < g(x) равно \[(-\infty,-2) \cup(3, \infty)=\{x : x<-2 \text { или } x >3\}\] Чтобы найти решение f(x) = g(x), обратите внимание, где график f пересекает график g, и заштрихуйте значение x каждой точки пересечения на оси x (см. Рисунок \(\PageIndex{7}\). Дальнейшие сравнения. Теперь мы знаем, что решением f(x) = g(x) является множество всех x, для которых пересекаются графики f и g. Поэтому графический калькулятор становится незаменимым помощником при решении уравнений. Пример \(\PageIndex{4}\) Используйте графический калькулятор, чтобы решить уравнение Примечание что уравнение (6) имеет вид f(x) = g(x), где \[f(x)=1,23 x-4,56 \quad \text { и } \quad g(x)=5,28-2,35 x \] Таким образом, наш подход будет состоять в том, чтобы нарисовать графики f и g, а затем найти значение x точки пересечения. Сначала загрузите f(x) = 1,23x − 4,56 в Y1 и g(x) = 5,28 − 2,35x в Y2 в меню Y= графического калькулятора (см. Рисунок \(\PageIndex{8}\). Рисуем графики f(x) = 1,23x−4,56 и g(x) = 5,28−2,35x. Решением уравнения (6) является значение x точки пересечения графиков f и g на рисунке (\PageIndex{8}\)(b). Мы воспользуемся утилитой intersect в меню CALC графического калькулятора, чтобы определить координаты точки пересечения. Действуем следующим образом: Рисунок \(\PageIndex{9}\). Использование утилиты пересечения. Результат этой последовательности шагов показан на рисунке \(\PageIndex{10}\). Координаты точки пересечения приблизительно равны (2,7486034, −1,179218). Значение x этой точки пересечения является решением уравнения (6). То есть решение \(1,23x — 4,56 = 5,28 — 2,35x\) примерно равно \(x \приблизительно 2,7486034\). Рисунок \(\PageIndex{10}\). Координаты точки пересечения. Резюме Рекомендации. Вам нужно будет обсудить ожидания со своим учителем, но мы ожидаем, что наши ученики резюмируют свои результаты следующим образом. 1. Настройте систему координат.6 Пометьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. 2. Скопируйте изображение в окне просмотра в свою систему координат. Подпишите каждый график его уравнением. 3. Проведите пунктирную вертикальную линию через точку пересечения. 4. Заштрихуйте и обозначьте решение уравнения на оси x. 9{2}-3\) и \(g(x)=1,23 x+1,25\) в Y1 и Y2 в меню Y= соответственно, как показано на рисунке \(\PageIndex{12}\)(a). Выберите 6:ZStandard в меню ZOOM, чтобы создать графики, показанные на рисунке \(\PageIndex{12}\)(b). Чтобы найти точки пересечения графиков f и g, мы выполняем ту же последовательность шагов, что и в примере \(\PageIndex{4}\), до точки, где калькулятор просит вас сделать предположение (т. е. 2nd CALC, 5: пересечение, ввод первой кривой, ввод второй кривой). Поскольку есть две точки пересечения, когда калькулятор попросит вас 9{2}-3\) и \(g(x) = 1,23x + 1,25\). сделать предположение, вы должны переместить курсор (с помощью клавиш со стрелками) так, чтобы он был ближе к точке пересечения, которую вы хотите найти, чем к другой точке пересечения. Рисунок \(\PageIndex{13}\). Точки пересечения графиков функций f и g. Приблизительные координаты первой точки пересечения (−1,626682, −0,7508192). Вторая точка пересечения имеет приблизительные координаты (3.0737411, 5.0307015). Важно помнить, что каждый раз, когда вы берете в руки калькулятор, вы получаете только приблизительное значение. Возможно, вы получите несколько иной результат для точек пересечения. Например, вы можете получить (-1,626685, -0,7508187) для точки пересечения. Основываясь на положении курсора, когда вы отмечали кривые и делали предположения, вы можете получить немного разные приближения. Обратите внимание, что это второе решение очень близко к тому, которое мы нашли, отличаясь только несколькими последними десятичными знаками, и вполне приемлемо в качестве ответа. 9{2} − 3 > 1,23x + 1,25\) приблизительно равно \[(-\infty,-1,626682] \cup[3,0737411, \infty)=\{x : x \leq-1,626682 \text { или } x \geq 3. Когда мы оцениваем функцию f при определенном значении x, возможен только один из трех результатов. Либо \[f(x)=0, \quad \text { или } \quad f(x)>0, \quad \text { или } \quad f(x)<0\] То есть, либо f(x) равно нулю, либо f(x) положительно, либо f(x) отрицательно. Других возможностей нет. Мы могли бы начать заново, используя совершенно новый подход, или мы можем опираться на то, что уже знаем. Мы выбираем последний подход. Предположим, нас попросили сравнить f(x) с нулем? Равно ли оно нулю, больше нуля или меньше нуля? Положим g(x) = 0. Теперь, если мы хотим сравнить функцию f с нулем, нам нужно только сравнить f с g, что мы уже умеем делать. Чтобы найти, где f(x) = g(x), отметим, где пересекаются графики f и g, чтобы найти, где f(x) > g(x), отметим, где график f лежит над графиком g , и, наконец, чтобы найти, где f(x) < g(x), мы просто отмечаем, где график f лежит ниже графика g. Однако график g(x) = 0 представляет собой горизонтальную линию, совпадающую с осью x. резюме Например: Рисунок \(\PageIndex{15}\). Сравнение функции f с нулем. Далее мы определим некоторые важные термины. Определение Если f(a) = 0, то a называется нулем функции f. График f пересекает ось x в точке \((a, 0)\), точке, называемой точкой пересечения x графика f. 9{2}-1,24 х-3,84\). Наша стратегия будет заключаться в том, чтобы нарисовать график f, а затем определить, где график f лежит ниже или на оси x. Действуем следующим образом: Рисунок (\PageIndex{16}\). Нахождение точки пересечения с нулем или х с помощью калькулятора. Последним шагом является интерпретация результатов и запись нашего решения на нашем домашнем листе. Ссылаясь на рекомендации Summary 7, мы приходим к графику, показанному на рисунке (\PageIndex{18}\). 9{2}-1,24 х-3,84\), заметим: \[[-2. Предполагать
ф
(
Икс
)
и
г
(
Икс
)
две функции, которые принимают на вход действительное число и выводят действительное число. Тогда точки пересечения
ф
(
Икс
)
и
г
(
Икс
)
это те числа
Икс
для которого
ф
(
Икс
)
«=»
г
(
Икс
)
. Иногда точные значения можно легко найти, решив уравнение
ф
(
Икс
)
«=»
г
(
Икс
)
алгебраически. Пример 1: Каковы точки пересечения функций
ф
(
Икс
)
и
г
(
Икс
)
если
ф
(
Икс
)
«=»
Икс
+
6
и
г
(
Икс
)
«=»
−
Икс
? Точки пересечения
ф
(
Икс
)
и
г
(
Икс
)
это те числа
Икс
для которого
ф
(
Икс
)
«=»
г
(
Икс
)
. То есть,
Икс
+
6
«=»
−
Икс
. Решить для
Икс
. Икс
+
6
«=»
−
Икс
2
Икс
+
6
«=»
0
2
Икс
«=»
−
6
Икс
«=»
−
3 Теперь вы можете использовать значение
Икс
найти соответствующий
у
-координата точки пересечения. Подставьте значение
Икс
в любой из двух функций. г
(
−
3
)
«=»
−
(
−
3
)
«=»
3 Уравнения также можно решить графически, нанеся две функции на координатную плоскость и указав точку их пересечения. В других случаях точные значения найти сложно. Возможно, вам придется использовать технологию для их оценки. Пример 2: Найдите точку (точки) пересечения двух функций. ф
(
Икс
)
«=»
|
Икс
−
5
|
г
(
Икс
)
«=»
бревно
Икс Здесь решить алгебраически не так просто. Решения уравнения
|
Икс
−
5
|
«=»
бревно
Икс
не являются красивыми рациональными числами. График функций на
координатная плоскость
. Вы можете использовать графическую утилиту, чтобы найти, что координаты точек пересечения приблизительно
(
4,36
,
0,64
)
и
(
5,76
,
0,76
)
. Сравнение функций
9{2}=9 \quad \text { и } \quad g(3)=2(3)+3=9\] так что ясно, \(f(3) = g(3)\).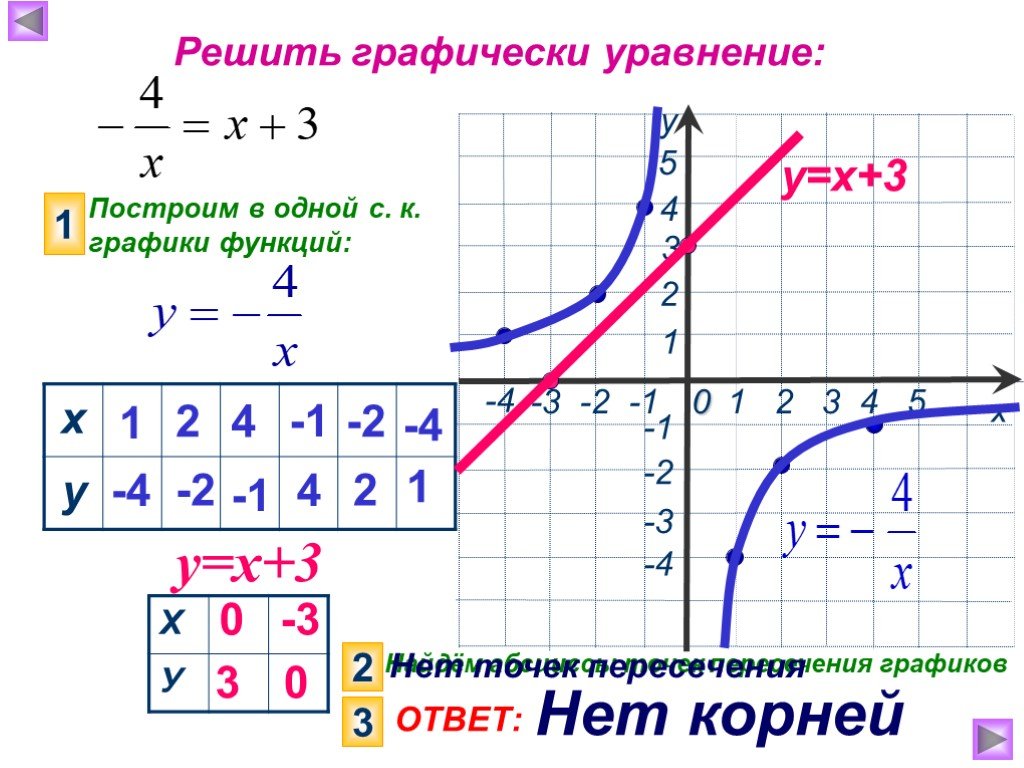
Сравнивая f и g.
Решением f(x) > g(x) является \((2, \infty)\) или, альтернативно, \(\{x : x>2\}\).
Проведите пунктирные вертикальные линии через точки пересечения графиков f и g (см. рисунок \(\PageIndex{6}\)(b)), затем обратите внимание, что график f лежит над графиком g между пунктирной вертикалью только что нарисованные линии. Следовательно, решением неравенства f(x) > g(x) является совокупность всех x, лежащих между пунктирными вертикальными линиями. Мы заштриховали эту коллекцию по оси X красным цветом (или более толстыми линиями для тех, кто просматривает черно-белые изображения) на рисунке \(\PageIndex{6}\)(b).
рисунок \( \PageIndex{7}\)(б)). Таким образом, решение f(x) = g(x) равно \(\{x : x=-2\) или \(x=3\}\). Поскольку этот набор решений не является интервалом, было бы неуместно описывать его интервальной нотацией. Решение уравнений и неравенств с помощью графического калькулятора
рисунок \(\PageIndex{8}\)( а)). Выберите 6:ZStandard в меню ZOOM, чтобы создать графики на рисунке \(\PageIndex{8}\)(b).
С помощью этой техники получаются две точки пересечения, изображенные на рисунках \(\PageIndex{13}\)(a) и (b).
0737411\}\] Сравнение функций с нулем
Действительно, g(x) = 0 — это уравнение оси x. Это рассуждение приводит к следующим ключевым результатам.
Таким образом, решением f(x) < 0 является \((-\infty, 1)=\{x : x<1 \}\).
Нажмите ENTER, чтобы записать этот «левый предел».
Обратите внимание, что координата x точки пересечения приблизительно равна −2,157931.
157931,7.1179306]=\{x :-2.157931 \leq x \leq 7.1179306\}\] На этой странице нет тегов.
Функции: графики и пересечения
Горячая математика
Ваш комментарий будет первым