Решение графиков функций онлайн: Построение графика функции онлайн

Содержание

Дмитрий Кудрец — Исследование графиков функций читать онлайн бесплатно

Исследование графиков функций

Дмитрий Кудрец

ISBN 978-5-0051-8240-1

Создано в интеллектуальной издательской системе Ridero

Понятие графика функции

Графиком функции называется множество всех точек (х; f (х)) на координатной плоскости.

По оси Ох (оси абсцисс) откладываются значения аргумента х.

По оси Оу (оси ординат) откладываются значения функции у (f (x)).

Графики функций широко используются в математике, физике, химии.

В отличие от табличных данных графики дают более наглядное представление о происходящих явлениях и процессах.

Исследование графиков функций

При исследовании графиков функций следует учесть, что графики дают приближенные значения аргумента и функции, зависящие от точности построения графика, выбора единичного отрезка, масштаба и т.

п. В таких случаях при решении указывается не точное, а приближенное значение функции или аргумента.

Пример 1. По графику функции, изображенному на рисунке, найдите значение функции при значении аргумента х=2.

Решение. Через точку оси Ох с абсциссой 2 проведем перпендикуляр. Точка пересечения этого перпендикуляра с графиком функции имеет координаты (2; 3), значит, при значении аргумента х=2 значение функции f (x) равно 3.

Ответ: f (x) =3

Задание 1. Найдите по графику значение функции, соответствующее значению аргумента – 4; – 2; 0; 2; 4.

Пример 2. По графику функции, изображенному на рисунке, найдите значение аргумента х, при котором значение функции равно 4.

Решение. Проведем через точку оси Оу с ординатой 4 прямую, параллельную оси

Ох.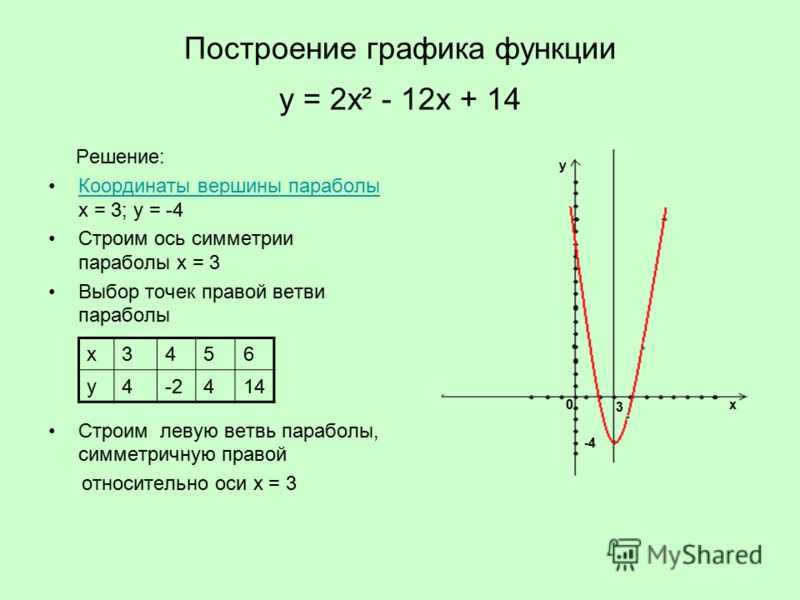

Эта прямая пересекает график в точке с координатами (2; 4). Значит, функция принимает значение, равное 4, при х=2.

Ответ: х=2

Задание 2. Найдите по графику значение аргумента, при котором функция принимает значения – 3; 0; 2.

Пример 3. В ходе химической реакции количество вещества, которое не вступило в реакцию, со временем уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося вещества (в граммах). Определите по графику, сколько граммов вещества вступило в реакцию за три минуты?

Решение. В начале реакции количество вещества составило 20 г. через три минуты его осталось 8 г. Следовательно, за три минуты в реакцию вступило 20 – 8=12 г вещества.

Ответ: 12 г

Задание 3. На графике показана зависимость силы тока в цепи от сопротивления. На оси абсцисс отложено сопротивление (в Омах), на оси ординат – сила тока в Амперах. На сколько уменьшится сила тока при увеличении сопротивления с 0,5 Ом до 3 Ом?

Задание 4. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат – пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте.

Область определения и область значений функции

Областью определения функции называется множество значений аргумента х, при котором функция

f (x) определена, т.е. функция в этих точках имеет значения. Область определения обозначается D (f).

Областью значений функции называется множество значений, которые может принимать f

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

8 Построение графиков функций

8.1 Построение двумерного графика функции

Для построения графиков в декартовых координатах выбираем меню Добавить — подменю Графики — Х-У график или нажимаем кнопки Shift +

В ячейке, расположенной под осью абсцисс, необходимо задать независимую переменную х, а в ячейке, находящейся рядом с осью ординат — f(x). Границы графика определяются автоматически в зависимости от промежутка изменения х. Независимую переменную х необходимо определить заранее как переменную, принимающую значения из промежутка, в виде: х := хmin, хmin + х.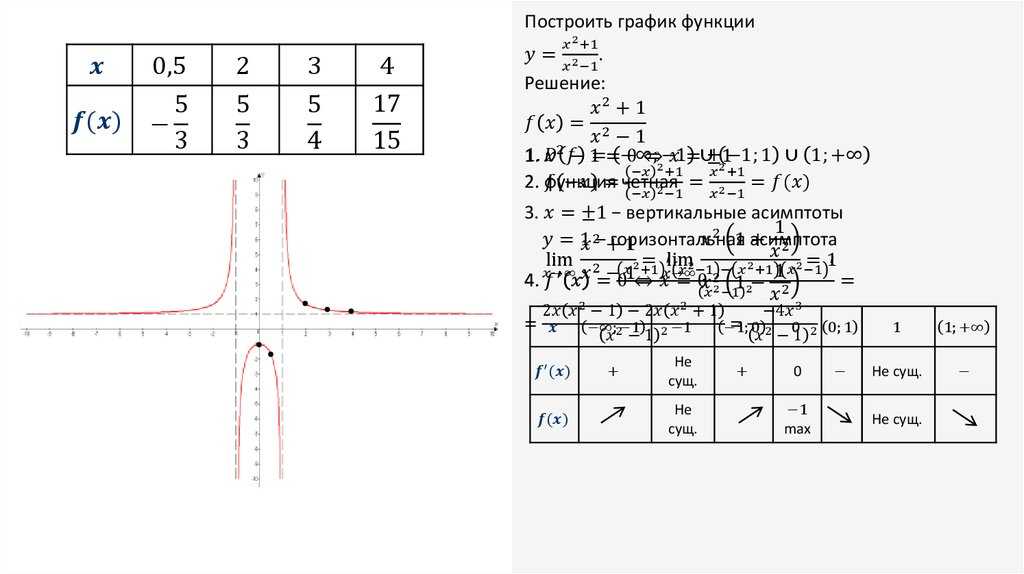 .хmax. Для того чтобы на экране появился символ промежутка («..» — две точки), необходимо нажать клавишу «;» либо щелкнуть на соответствующей пиктограмме m..n панели Векторы и матрицы. В Mathcad существует возможность строить график функции, не задавая предварительно промежуток изменения независимой переменной. По умолчанию этот промежуток принимается равным [-10,10].

Если на одном графике необходимо отобразить несколько функций, то их надо просто перечислить после первой функции в месте ввода возле оси Y, отделяя выражения функций запятыми.

8.2 Упражнения к теме 8.1

Построить график функции y = sin(x), х[0,2].
Добавить на предыдущий график функции y = cos(2x) и y = sin³(x).
Построить график функции y = -2^—^^х^, х[-10,10].
Построить график функции, соединяющий точки:

(хi,

уi) = (sin(2), sin(4)), i = 0, 2,…,N.

Пример выполнения упражнения 1. Присваиваем функции значение y := sin(x), задаем промежуток изменения независимой переменной от 0 до 2: х := 0,0.01..2, выбираем меню Добавить — подменю Графики — Х-У график, заполняем внизу х, по оси ординат — f(x):

Пример выполнения упражнения 4. Для построения графика функции, заданной параметрически, задаем число точек, аналитические выражения для пар чисел (хi, уi), выбираем меню Добавить — подменю Графики — Х-У график, заполняем внизу х_i, по оси ординат — y

8.3 Построение графиков поверхностей

Построение графиков поверхностей (трехмерных графиков или 3D-графиков) требует создания матрицы точек (аппликат) зависимости z(x,y), т.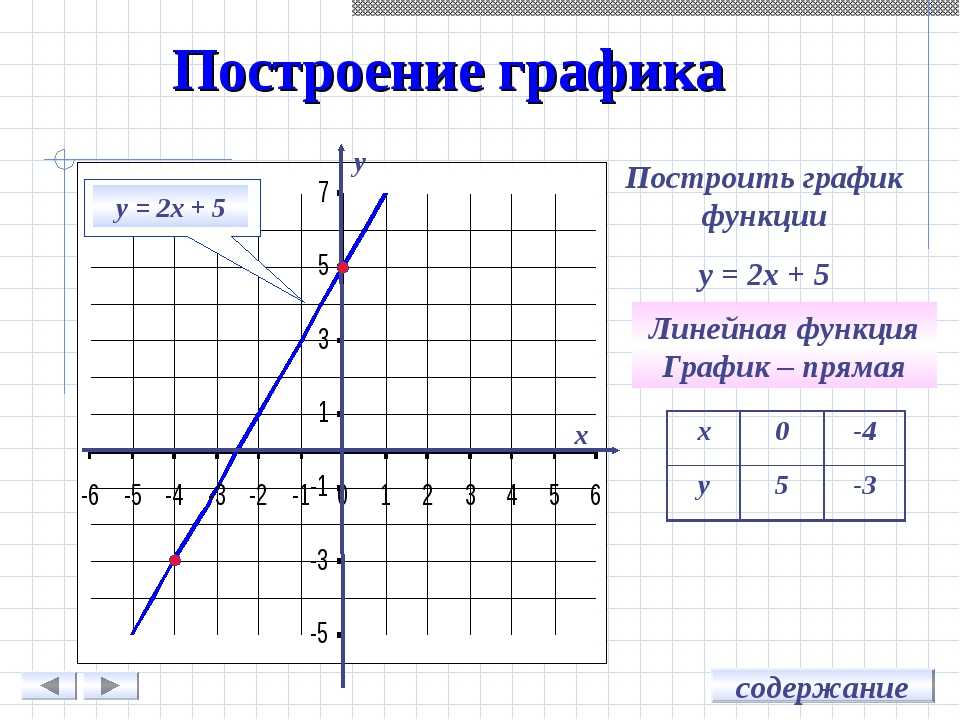

е. функции двух переменных.

Необходимо определить функцию двух переменных. Затем выбрать меню: Добавить — Графики — График 3D–разброса. На единственное место ввода под шаблоном вводим имя функции двух переменных. Выводим указатель мыши за пределы графика и щелкаем левой кнопкой.

Трехмерную фигуру можно вращать в пространстве при помощи мыши. Вид трехмерных фигур сильно зависит от того, под какими углами относительно осей X, Y и Z фигуру рассматривают. Нередко небольшие пики, впадины или лепестки фигуры просто не видны на фоне высоких пиков или глубоких впадин. Вращение фигуры эквивалентно ее просмотру с разных сторон.

Для вращения фигуры необходимо поместить указатель мыши в область графика, нажать левую кнопку мыши и, удерживая ее, начать перемещать мышь в том или ином направлении.

Если оперировать мышью при нажатой клавише CTRL, можно удалять объект от наблюдателя или приближать объект к наблюдателю. Если проделать те же действия с нажатой клавишей SHIFT, то после отпускания левой кнопки можно вообще наблюдать анимированную («живую») картину вращения объекта в любом заданном предварительно направлении. Для остановки вращения надо щелкнуть левой кнопкой мыши в области графика.

На одном графике можно строить несколько поверхностей. Для этого надо определить несколько функций двух переменных, описывающих поверхности, и ввести через запятую имена этих функций в месте ввода шаблона трехмерного графика.

После построения каждую фигуру можно форматировать отдельно.

Equation Grapher — Граф неявных функций

Этот бесплатный онлайн-график уравнений

предназначен для построения графиков общих уравнений G(x,y) = F(x,y) , где переменные x и y могут появляться обе части уравнения. С помощью графического редактора уравнений вы также можете построить графики неявных функций , стандартных и общих форм из конических сечений и кривых уровня .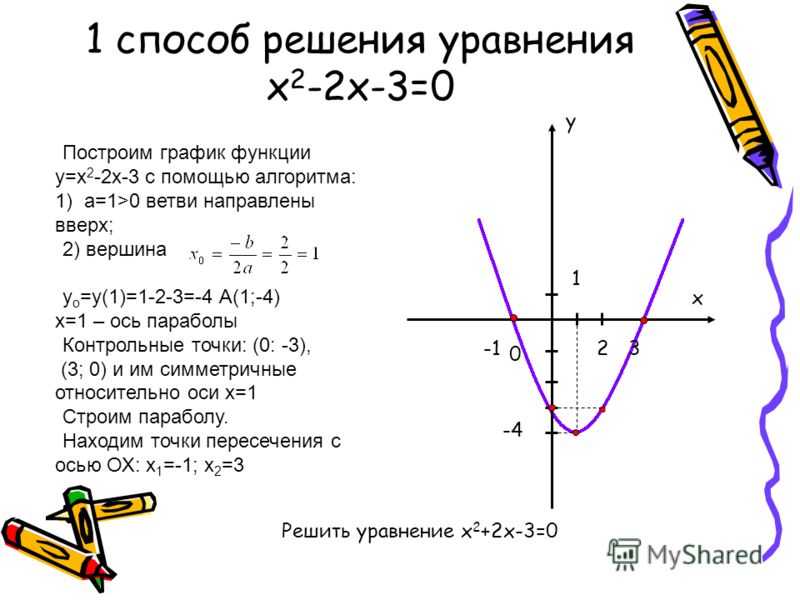

Ан график уравнений — это графический калькулятор , который рисует график любого уравнения формы G(x,y) = F(x,y) , где каждая сторона представляет собой выражение, которое может содержать x и y.

Устройство для построения графиков уравнений является более общим графическим инструментом, чем средство построения графиков функций

, которое только рисует график уравнений в форме y = f(x) , где правая часть представляет собой выражение в x только.

Графический калькулятор уравнений также можно использовать для построения графика неявно определенных функций .

Для графических уравнений знак равенства должен использоваться для ввода обеих частей уравнения. Это позволяет отображать, например, уравнения линий в точках-наклонах форм, уравнения конических сечений ( окружностей , парабол , гипербол и эллипсов ) и 30 кривых уровня4 как неявные функции .

Советы: по мере ввода:

пи заменяется на π .

МышьМатикс! Вы можете использовать мышь для поворота оси, перемещения и изменения масштаба

В дополнение к вводу данных — сначала нажав кнопку шестеренки — вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивного полярного графографа как изложены ниже.

Щелкните по оси (или рядом с ней) и переместите мышь. Это будет вращать ось . графики перерисованы в обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
Перетащите мышь на , переместите систему координат вместе с графиками.
Дважды щелкните на холсте, чтобы переместить исходную точку туда, где был сделан щелчок.
Удерживая клавишу Alt, щелкните по оси до изменить масштаб (увеличение в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.

Анимация вращения оси: Икс у ► ⬛

сообщение

f(x) =

f( ) =

⌨

4 Десятичные разряды

Graph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)

Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°:

⚙

РезультатыСкрыть

Наложение Прозрачный 92 грех (ху) = потому что (ху)

Уравнения — полярные

В данный момент недоступно.

РАД Полярный

🔍+ 1 🔍−

время построения графика (с)

Калькулятор загружается.
Пожалуйста, подождите….

Сделайте это прозрачным

Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осей

заголовок

. ..

Медленный Быстрый

Показать угловые оси Сделанный

Отключить программную клавиатуру

Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.

Графический редактор уравнений прост в использовании ; введите уравнение , например, 3x -2 y = x + 4y в любом поле выражения . Графический редактор уравнений отображает графики при вводе (по умолчанию).

Для графика двух или более уравнений в одной системе координат нажмите » для отображения мультиграфической панели . Панель мультиграфиков состоит из панелей выражений , который можно добавить или удалить по желанию, нажав + или × . на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
Вы можете установить точность графиков, выбрав нужный параметр из раскрывающегося списка Graph Fineness . Как правило, чем выше точность, тем больше времени требуется графическому редактору уравнений для построения графиков уравнений.
Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графиком уравнений . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.

Интересные кривые : Нарисуйте любое выражение из раздела Интересные графики , нажав на него. Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness 9.0010 как «+1» или выше.

При построении графика уравнений в форме y = f(x) ( функция ) рекомендуется использовать калькулятор построения графиков функций, который более точно рисует уравнения этого типа.

Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.

Измените толщину графиков с помощью предоставленного ползунка.
Выберите режим угла ( радиана – по умолчанию , градуса или градуса ).
Если вы отмените выбор График при вводе параметра , вам придется нажать График выбранных выражений , который затем появится в нижней части калькулятора, чтобы обновлять графики всякий раз, когда вы вносите какие-либо изменения в выражения или координаты. плоскость (т. е. переместить начало координат, повернуть оси и т. д.).
При необходимости отобразите элементы управления в верхней части графического редактора уравнений , которые позволяют запускать/приостанавливать и останавливать вращение любой или всех осей.
Графический редактор уравнений запоминает введенные вами выражения уравнений и извлекает их между посещениями. Вы можете очистить их, нажав кнопку Reset Calculator .

Чтобы эффективно использовать это онлайн Графический калькулятор уравнения используйте последние версии браузеров Chrome , Microsoft Edge , Firefox , Opera или Safari . В противном случае некоторые компоненты графического редактора уравнений могут не отображаться или работать.

Вставка 1 ^St производная Вставка 2 ^{и производная от}

Контрольные графики и бесплатный онлайн-калькулятор

При построении графиков функций с несколькими локальными функциями мне часто хочется объяснить часть поведения графика независимо от остальной части графика. Когда я начал преподавать пару десятков лет назад, процессор моего TI-81 был достаточно медленным, чтобы я мог наблюдать, как пиксели загораются последовательно. Я мог видеть, КАК был сформирован график. Сегодня процессоры явно намного быстрее. Мне нравится сила решения задач, которая дала мне и моим ученикам, но иногда мне не хватало возможности видеть графики функций по мере их развития.

Ниже я описываю происхождение идеи управления графом, как работает управление, а затем привожу примеры полиномов с несколькими корнями, рациональных функций с несколькими точками пересечения и/или вертикальными асимптотами, полярных функций, параметрического моделирования столкновений и графических производных. заданных кривых.

ПРЕДПОСЫЛКА: На прошлой неделе после школы мы с коллегой планировали модуль рациональной функции, чтобы иметь возможность создавать графики по частям, чтобы мы могли обсудить влияние каждой локальной функции. В прошлом мы «фальсифицируем» изображения калькулятора, рисуя графики функций параметрически и контролируя входные значения 9.0015 т . Неуклюжий и статичный, но это дало нам полезные кадры. Достаточно неплохо, но нам очень хотелось чего-то динамичного. Поскольку мы использовали ползунки в нашем программном обеспечении TI-nSpire, Geogebra и калькуляторе Desmos, решение, которое мы искали, было ближе, чем мы предполагали.

РЕАЛИЗАЦИЯ И ПОЧЕМУ ЭТО РАБОТАЕТ: На прошлой неделе мы обнаружили, что можем использовать для создания того, что хотим. Аргумент корня равен 1 для , что делает . Для аргумент корня равен -1, что делает число недействительным. Наше понимание заключалось в том, что умножение любой функции на соответствующую версию g не изменит результат f , если входное значение g положительное, но сделает произведение неграфическим из-за комплексных значений, если входное значение g отрицательное.

Если я сделаю ползунок для параметра и , то будет вывод 1 для всех . Это означает, что для любой функции только с реальными выходами будут реальные выходы (и реальный график) только для. Ага! Использование ползунка и позволило бы мне контролировать внешний вид моего графика слева направо.

ПРИМЕЧАНИЕ. Пока он находится в стадии разработки, я стал большим поклонником бесплатного онлайн-калькулятора Desmos после недавней презентации на факультете глобальной математики (присоединяйтесь к нашим 45-60-минутным онлайн-встречам каждый вторник в 21:00 по восточному времени!). Я использую Desmos для всех следующих графиков в этом посте, но, очевидно, подойдет любое программное обеспечение для построения графиков с возможностями ползунка.

ПРИМЕР 1: График , полином 6-й степени, чье конечное поведение соответствует , «колеблется» по оси x в точке -2, затем отскакивает от начала координат и, наконец, проходит через x — ось в точке 1.

Нажмите здесь, чтобы получить доступ к графику Desmos, который создал изображение выше. Затем вы можете манипулировать ползунком, чтобы наблюдать, как график качается, затем отскакивает и, наконец, проходит по оси x .

ПРИМЕР 2: График , полином 6-й степени, поведение которого в конце соответствует , «колеблется» по оси x в точке -2, затем отскакивает от начала координат и, наконец, проходит через ось x в 1.

Щелкните здесь, чтобы получить доступ к приведенному выше графику Desmos и управлять созданием графика рациональной функции с помощью ползунка.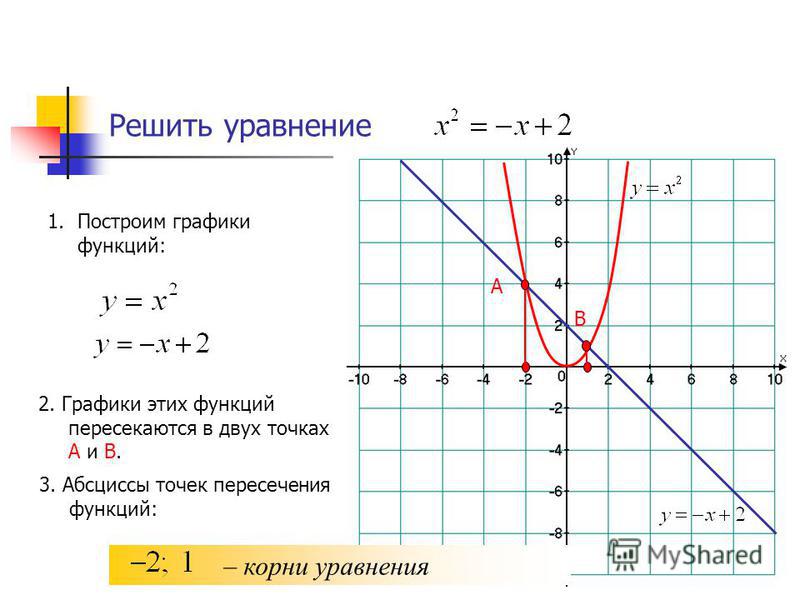

ПРИМЕР 3: Я считаю, что учащиеся лучше понимают полярный график, когда видят кривые, подобные лимакону, перемещающемуся между максимальным и минимальным кругами. Управление ползунком также позволяет пользователям видеть значения, при которых лимакон пересекает полюс. Вот график Desmos для графика ниже.

ПРИМЕР 4: Объект A покидает (2,3) и движется на юг со скоростью 0,29 единицы/сек. Объект B покидает (-2,1) и движется на восток со скоростью 0,45 единиц/сек. Пересечение их путей равно (2,1), но какой объект прибывает туда первым? Вот живая версия.

Хорошо, я знаю, что это слишком упрощенный пример, но вы получите представление о том, как управляющий ползунок работает с параметрически заданной функцией. $латекс \sqrt{\frac{\left | a-x \right |}{a-x}}$ должен быть только в одном из параметрических уравнений. Еще одним преимуществом ползункового подхода является простота, с которой пользователи могут определить значение t (или времени), когда каждая частица достигает точки пересечения или их оси пересекаются. Очевидно, что в данной задаче эти значения можно было бы определить алгебраически, но это не всегда верно, и такой графо-числовой подход всегда дает альтернативу алгебраическим методам при исследовании параметрических функций.

ПОКАЗАТЬ 1. Обратите внимание на простоту нотации Desmos для параметрических графов. Введите [r,s], где r — x-компонент параметрической функции, а s — y-компонент. Чтобы нарисовать точку, оставьте r и s постоянными. Легкий.

ПРИМЕР 5: При обучении математике я всегда прошу своих учеников рисовать графики производных функций, заданных в графической форме. Я всегда создаю эти графики по частям. В качестве примера этот график показывает и позволяет получить его производную постепенно с помощью ползунка.

ДОПОЛНИТЕЛЬНО 2–Кроме того, очень просто вводить производные функций в калькулятор Desmos. Введите «d/dx» перед именем или определением функции, и производная будет выполнена. Desmos — это не CAS, поэтому я уверен, что программа вычисляет производные численно.