Линейная функция — определение, основные свойства, график.
Если функция задана формулой , где и — некоторые числа, называется линейной функцией. Линейная функция областью определения имеет множество всех действительных чисел, потому что выражение имеет смысл при всех значениях . Все частные виды линейной функции можно записать общей формулой . Линейные функции изучаются в школьном курсе математики 7 класса. О том какие они бывают, как построить их графики мы поговорим в этой статье. Вы получите все ответы на тему линейной функции, потому что мы с вами разберем примеры определения ее вида, построения графика и его анализа. Почитать о функции, что это такое и как ее можно задать можно здесь.
Содержание
Определение линейной функции
Вот так выглядит график линейной функции:
Линейная функция y=kx+b и ее график
Примеры линейных функций:
- ,
- ,
Обратите внимание, что уравнение — описывает общий вид, есть и частные виды, линейной функции, например, (когда ) и , когда .
Частный случай линейной функции y=b
Частный вид линейной функции y=kx
Стоит заметить, что уравнение задает прямую пропорциональность между значением и аргументом . Прямая пропорциональность — это зависимость вида , она изучается в курсе алгебры.
Для построения графика линейной функции достаточно двух точек.
Коэффициенты k и b
Коэффициент характеризует угол, который образует прямая с положительным направлением оси . Поэтому коэффициент k линейной функции называется угловым коэффициентом.
Частный случай линейной функции y=x
- Если , то угол между графиком линейной функции и осью острый.
- Если , то угол между графиком линейной функции и осью тупой.
- Если , то прямая совпадает с осью .
Коэффициент — показывает сдвиг графика вдоль оси .
У коэффициентов и есть геометрический смысл. Коэффициент показывает длину отрезка, которую прямая отсекает по оси , начало отрезка находится в точке . Геометрический смысл коэффициента — тангенс угла наклона прямой линии к положительному направлению оси .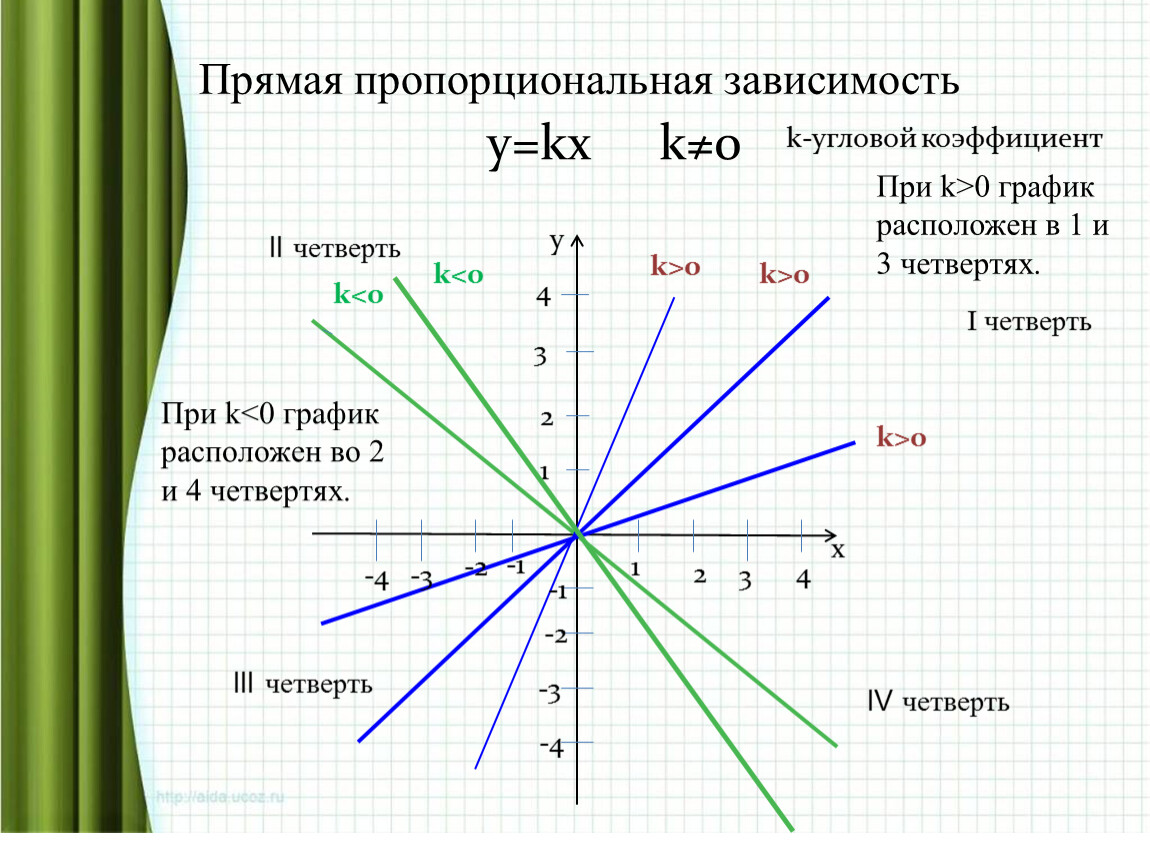
По данному коэффициенту можно определить угол наклона прямой линии, например, , это означает и . То есть угол наклона прямой к оси будет 450.
Примеры
Определите коэффициенты и функций и результаты запишите в таблицу.
| Линейная функция | Коэффициент | Коэффициент |
| 1 | 0 | |
| 3 | 5 | |
| 0 | 6 | |
| -1 | 3 | |
| 2 | -5 | |
| -3 | -1 |
Обратите внимание, что данная функция может быть задана и числом, например, , это означает, что угловой коэффициент равен нулю, то есть , а значит и прямая параллельна оси . Коэффициенты и могут принимать любые числовые значения, то есть могут быть и 0, и 1, и отрицательным числом.
Попробуем записать функцию y=kx+b, зная только значения коэффициентов.
Пример 1
Запишите линейную функцию, если известно, что , .
Решение: сначала запишем общий вид линейной функции: , теперь вместо и подставим указанные значения: . Упростим выражение и получим:
.
Ответ:
Пример 2
Запишите линейную функцию, если известны коэффициенты и .
Решение: .
Ответ: .
Область определения и область значений
Проанализируем и определим область определения линейной функции. Смотрим на уравнение, очевидно, что в это уравнение можно подставить любое значение . Это значит, что областью определения является вся числовая ось: .
Так как и может принимать любые значения, то мы можем говорить о том, что область значений линейной функции — все числа: .
График линейной функции
Если вы видите прямую линию — например, прямую дорогу или столб, дерево, то знайте — линии эти могут быть описаны с помощью функции, которая называется линейной.
Чтобы построить график функции необходимо и достаточно взять всего две точки. Построим таблицу координат точек:
| x | 0 | -b/k |
| y | b | 0 |
Таким образом, мы можем построить график любой линейной функции вида .
График прямой в общем виде
Примеры построения графика линейной функции
Пример 1
Построим график линейной функции .
Графиком функции является прямая линия. Для построения прямой достаточно взять две точки.
Возьмем точки и . Кстати, эти точки являются одновременно и точками пересечения графика с осями и соответственно.
Нарисуем координатные оси, покажем масштаб и отметим точки и , затем их соединим, получим прямую. Эта прямая и будет графиком функции .
График функции y=2x+1
Итак, мы научились с вами строить график функции, зная ее уравнение. Алгоритм построения графика линейной функции прост:
- Найти координаты двух точек, удовлетворяющих данному уравнению прямой.
Для этого берем произвольное значение аргумента и подставляем его в уравнение, вычисляем значение . Можно действовать и наоборот — задать определенное значение и решить уравнение относительно . - Рисуем координатные оси, указываем их направление, определяем масштаб.
- Наносим найденные точки на координатную плоскость.
- Проводим прямую, через две эти точки.
Для этого берем произвольное значение аргумента и подставляем его в уравнение, вычисляем значение . Можно действовать и наоборот — задать определенное значение и решить уравнение относительно .Совет: если точки взяты близко друг к другу, то при продлении прямой можно получить погрешность рисования — отклонение на несколько градусов, поэтому старайтесь брать точки подальше друг от друга, или же возьмите пару контрольных точек, опираясь на уравнение прямой линии.
Пример 2
Построим новый график линейной функции. Пусть нам дано уравнение: .
Находим две точки. Пусть , тогда подставим в формулу функции ноль вместо , получим: . Вторую точку возьмем немного подальше — пусть , тогда .
Итак, мы получили две точки: и . Построим график прямой.
График функции y=-x-2
Убывает или возрастает
Функция прямой является убывающей или возрастающей функцией? Вопрос не корректен.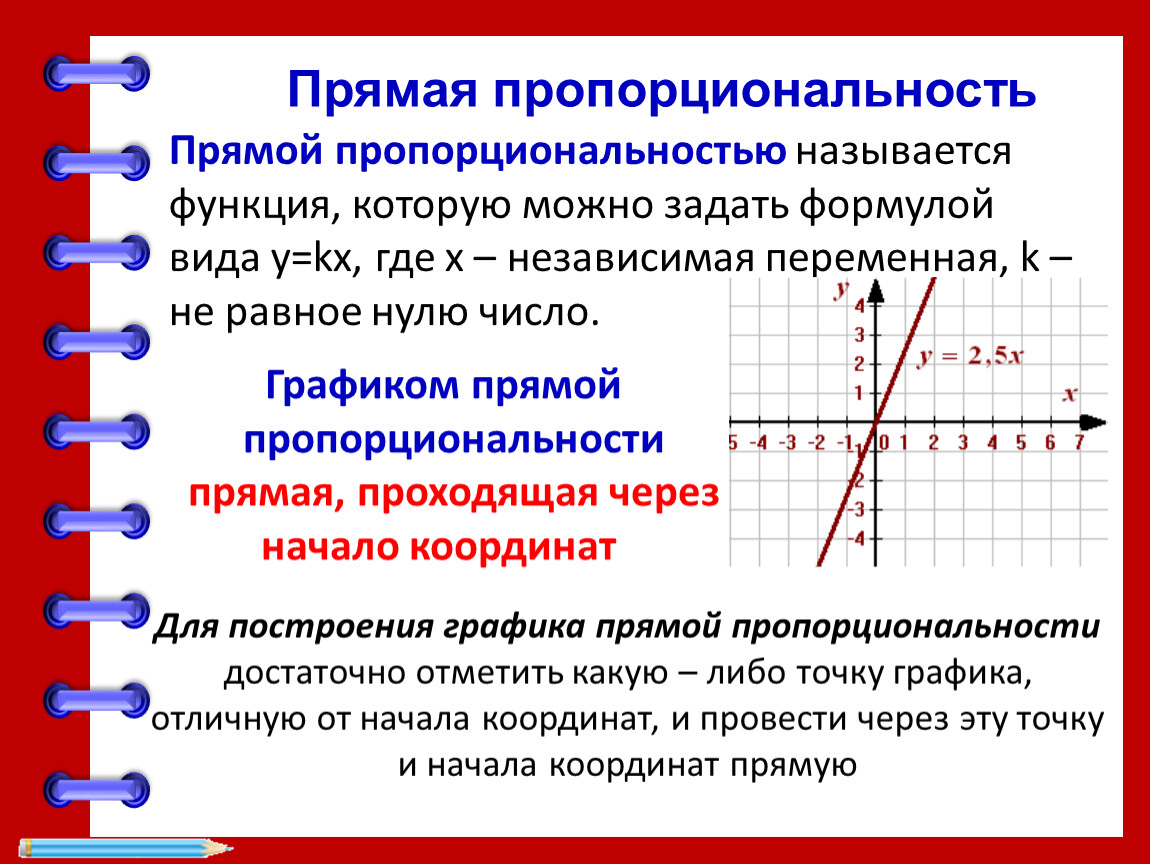
Все функции прямых разные, одни убывают, другие возрастают, надо обращать внимание при оценке убывания или возрастания функции на поведение ее при изменении аргумента. Существует такое правило:
Если при увеличении аргумента значение функции возрастает, то функция является возрастающей, если значение функции при возрастании аргумента уменьшается, то функция является убывающей. Давайте посмотрим как это выглядит на графике.
Перед вами два графика функции, — на каком графике функция убывает, а на каком возрастает, можно понять по тому увеличивается или уменьшается значение функции при движении в положительном направлении оси .
График возрастающей линейной функции
Теперь легко увидеть, почему ниже приведен график убывающей линейной функции:
График убывающей линейной функции
Как мы видим — при увеличении значения аргумента значение функции уменьшается.
Свойства линейной функции
Функция y = x называется линейной функцией, так как переменная x находится в первой степени.
Графиком такой функции будет прямая.
Построение графика функции y = x
Для того, чтобы построить график линейной функции нам необходимо задать две точки. Берем их произвольно. Пусть , тогда . И вторая точка , тогда .
Отмечаем эти точки на координатной плоскости и проводим через них прямую. Это и есть график функции y = x.
Свойства функции
Выпишем свойства функции y = x:
- Функция y = x является линейной, непрерывной и монотонно возрастающей на всем протяжении координатной плоскости, со скоростью 1, так как производная функции равна 1.
- Любое значение переменной будет равно такому же значению функции.
- График функции проходит через начало координат.
- График функции располагается в первой и четвертой четвертях.
- Функция принимает отрицательные значения при отрицательных значениях переменной и положительные значения при положительных значениях переменной.
- Функция y = x является нечетной, так как (условие нечетности функции).
Обратная функция
Обратная функция совпадает с функцией y (x)=x и тоже записывается y = x.
Данная функция также является осью симметрии для всех обратных функций. Графики обратных функций симметричны относительно оси симметрии y=x.
Линейная функция, ее свойства и график • СПАДИЛО
ОпределениеФункция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
| х | 0 | 3 |
| у |
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
| х | 0 | 3 |
| у | –1 | 5 |
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
| х | 0 | 2 |
| у | 4 | –2 |
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х.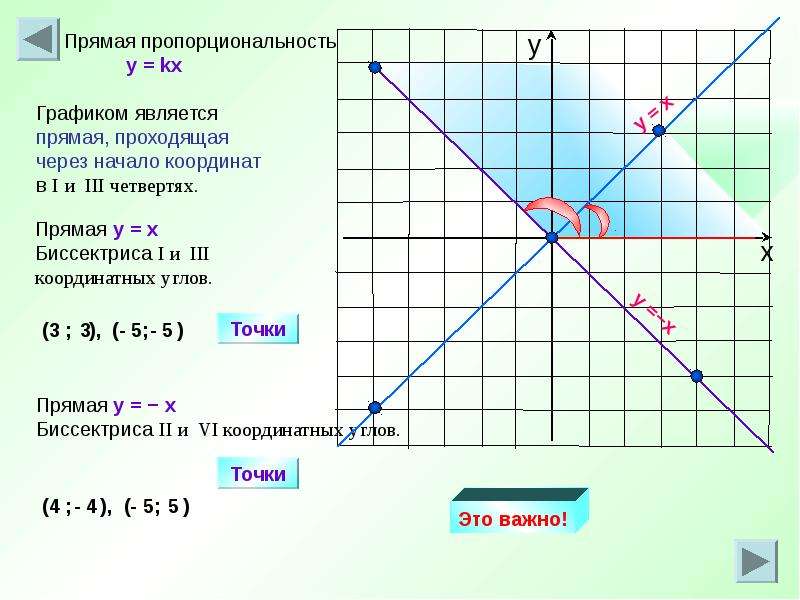
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106oНа рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля.
Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103oУстановите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.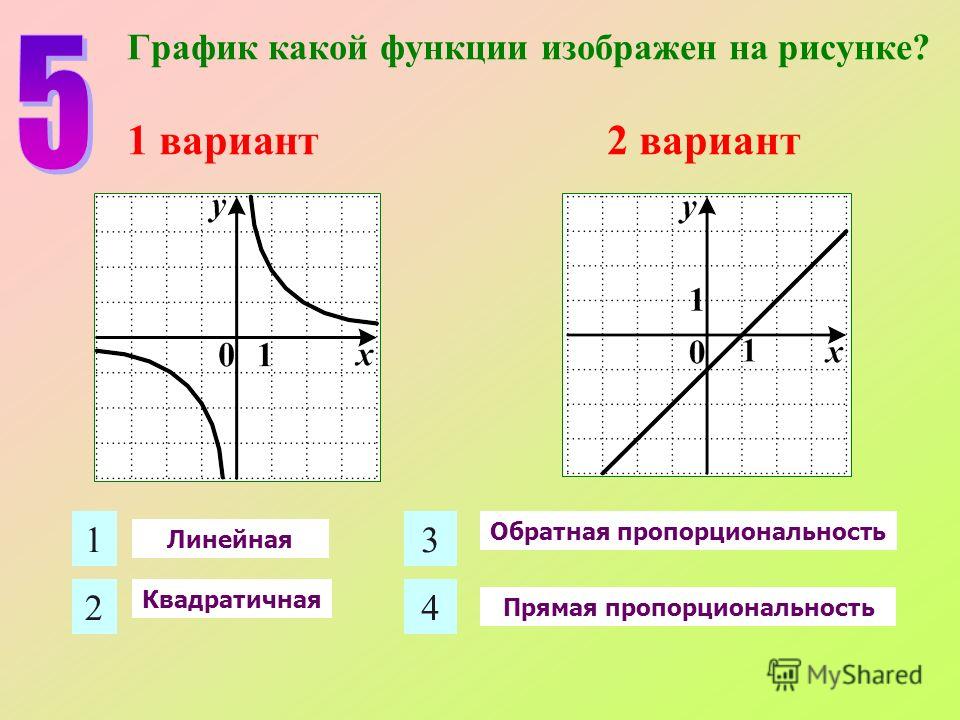
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 5.
Прямые графики — математика GCSE
Введение
Как построить линейный график
Таблица прямых графиков
Распространенные заблуждения
Практические вопросы по линейным графикам
Прямые графики Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как построить линейный график
Таблица прямых графиков
Распространенные заблуждения
Практикуйте прямые графики, вопросы
Прямые графики Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о прямолинейных графиках, в том числе о том, как рисовать прямолинейные графики формы y = mx + c, используя таблицу и пару координат.
Существуют также рабочие листы с линейными графиками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое линейный график?
Прямолинейный график — это визуальное представление линейной функции. Он имеет общее уравнение:
у=мх+с
Где m — уклон линии
А c — точка пересечения у.
у=2х+1
Здесь мы видим, что градиент = 2 , а точка пересечения с y происходит в точке (0,1) .
График этого уравнения выглядит следующим образом:
На графике выделено несколько важных значений, которые вы должны иметь возможность пометить на любом линейном графике.
К ним относятся:
- Помеченные оси для x и y .
- Четко нанесенные координаты.
- Одна прямая линия по всей сетке — необходимо использовать линейку.
- Точка пересечения с осью Y.
- Уравнение прямой.
Что такое линейный график?
1. Построение линейных графиков
Чтобы построить линейные графики , нам нужно подставить значения для x в уравнение для графика и вычислить соответствующие значения для y .
Мы часто помещаем эти значения в таблицу, чтобы сделать нашу работу более понятной. После того, как мы вычислили координаты, мы можем изобразить их в виде графика.
Пример
Заполните таблицу, чтобы построить график уравнения.
у=х+4| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| у=х+4 | 5 | 7 | 8 |
- Подставьте каждое заданное значение вместо x в общее уравнение прямой .
Здесь нам нужно подставить значения x в таблицу, чтобы вычислить значения y .
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| у=х+4 | у=-2+4 у=2 | у=-1+4 у=3 | у=0+4 у=4 | 5 | у=2+4 y=6 | 7 | 8 |
2 Нанесите полученные координаты на набор осей с метками
Поскольку координата записывается как (x,y) , из таблицы у нас теперь есть координаты (-2,2), (-1,3), (0,4), (1,5), (2 ,6), (3,7) и (4,8), которые мы можем построить:
3 Проведите прямую линию через все нанесенные координаты через всю область построения .
Главный совет: не забудьте пометить строку как уравнение в вопросе. Здесь мы обозначили прямую линию y = x + 4 .
Пошаговое руководство: Уравнение прямой
2. Набросок графика
Иногда нам нужен только набросок прямолинейного графика — нам не нужно, чтобы он был построен с той же точностью, как если бы мы вычисляли координаты.
Набросанный график должен включать определенную информацию, такую как помеченные оси, помеченная линия и точки, в которых линия пересекает оси.
Сравним плохой набросок с хорошим наброском прямой y=2x+1
Плохой набросок
Хотя линия имеет положительный градиент и пересекает ось y в одной точке, на графике предполагается, что существуют только положительные значения x . Также ничего на графике не помечено.
Хороший набросок
Основные детали, которые следует выделить на изображении выше:
- Помеченные оси x и y без шкалы
- Несколько четко нанесенных координат
- Одна прямая линия по всей сетке – необходимо использовать линейку
- Точка пересечения с осью Y
- Точка пересечения с осью x
- Уравнение прямой
3. Нахождение середины отрезка
Середина отрезка — это точка, которая находится ровно посередине между двумя точками.
Это одинаковое расстояние от каждой конечной точки отрезка прямой.
Мы находим середину отрезка, находя среднее значение координат x и среднее значение координат y двух конечных точек.
Например, для точек (4, 6) и (8, 2):
Среднее значение координат x =\frac{4+8}{2}=\frac{12}{2}=6
Среднее значение координат y =\frac{6+2}{2}=\frac{8}{2}=4
Таким образом, координаты средней точки равны (6, 4).
Пошаговое руководство: Как найти середину
4. Градиент линии
Градиент линии говорит нам, насколько крута линия. Он говорит нам, на сколько шагов поднимается линия при каждом пересечении. Следовательно, чем выше градиент, тем круче линия.
Если градиент отрицательный, линия идет вниз, а не вверх (слева направо).
Пример :
Вычислите уклон прямой линии на диаграмме.
- Укажите две координаты, лежащие на прямой.
Найдя две координаты, проходящие через углы квадратов сетки, мы получим координаты (0,1) и (4,7) .
2 Найдите изменение в y и изменение в х .
Изменение y равно y_2 − y_1 = 7 − 1 = 6 .
Изменение x равно x_2 − x_1 = 4 − 0 = 4 .
3Здесь
m=\frac{6}{4}=\frac{3}{2}
Итак, градиент линии равен m=\frac{3}{2} .
Пошаговое руководство: Градиент линии
5. y = mx + c
Общее уравнение для прямой линии : y=mx+c , где m — градиент, а c — у перехвата.
Мы можем найти уравнение прямой линии, найдя градиент и точку пересечения y, а затем используя эти значения в уравнении.
Пример :
Две координаты A (3,5) и B (5,11) лежат на одной прямой L. Используйте эти координаты, чтобы найти уравнение прямой L.
- Вычислить градиент линии .
m=\frac{y_2-y_1}{x_2-x_1}=\frac{11-5}{5-3}=\frac{6}{2}=3
Итак, градиент m = 3
2 Вычислить точку пересечения прямой линии по оси Y.
Когда y = 3x + c при A (3,5),
\begin{выровнено} 5&=3\умножить на 3+с\\\\ 5&=9+с\\\\ с&=-4 \end{выровнено}
Таким образом, точка пересечения y находится в точке (0,−4) .
3 Составьте уравнение прямой.
у=3х-4
Пошаговое руководство: y=mx+c
6. Параллельные и перпендикулярные линии
Параллельные линии 9о друг к другу.
Градиенты перпендикулярных линий умножаются вместе, чтобы получить -1 (они являются отрицательными обратными величинами).
Пример :
Покажите, что две прямые y = 6 — 4x и 4y = x перпендикулярны.
- Преобразуйте оба уравнения в форму y = mx + c .
Здесь мы имеем y = -4x + 6 и y = \frac{1}{4}x .
2 Укажите уклон каждой линии .
{{m}_{1}}=-4 и {{m}_{2}}=\frac{1}{4}
3 Перемножьте градиенты. Если они равны -1, две линии перпендикулярны.
-4\times\frac{1}{4}=\frac{-4}{4}=-1
Да, они перпендикулярны.
Пошаговое руководство: Параллельные и перпендикулярные линии
Изучение прямых графиков
Сводка линейных графиков
- Для линейных графиков есть линейная зависимость между значениями x и y, поэтому линия прямая и должна быть проведена с помощью линейки.
- Градиент определяет насколько крута линия , а точка пересечения y сообщает нам место, где прямая пересекает ось y .
- Каждая прямая может быть нарисована точно путем подстановки значений x в общее уравнение прямой линии y = mx + c или начерчена с соответствующей маркировкой.
- Мы можем рисовать прямые линии с положительным градиентом, с отрицательным градиентом, горизонтальные или вертикальные, параллельные и перпендикулярные.
Как построить линейный график
Чтобы построить линейный график:
- Подставьте каждое заданное значение x в общее уравнение прямой линии.
- Нанесите полученные координаты на набор осей с метками .
- Проведите прямую через все нанесенные координаты по всей области построения .
Рабочий лист с прямыми графиками
Получите бесплатный рабочий лист с прямыми графиками, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
ИксРабочий лист с прямыми графиками
Получите бесплатный рабочий лист с прямыми графиками, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Примеры линейных графиков
Пример 1: Дан график y = mx + c и таблица
Постройте график уравнения y=2x-3
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| у=-х+4 | -5 |
Подставьте каждое данное значение вместо x в общее уравнение прямой линии .
| х | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| у=2х-3 | у = (2 × -2) — 3 у = -4 — 3 у = -7 | -5 | у = (2 × 0) — 3 у = 0 — 3 у = — 3 | у = (2 × 1) — 3 у = 2 — 3 у = -1 | у = (2 × 2) — 3 у = 4 — 3 y = 1 |
Нанесите полученные координаты на набор помеченных осей .
Теперь у нас есть следующие координаты для построения на наборе осей:
(-2,-7), (-1,-5), (0,-3), (1,-1), ( 2,1).
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 2: Различные масштабы осей
Постройте график уравнения на наборе осей ниже.
у=\фракция{1}{2}х-2
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Здесь нам не нужно заполнять таблицу, поэтому нам нужно выбрать значения для x, которые появляются на наборе осей. Помните, что чем больше точек вы сможете нанести, тем больше вероятность того, что ваша прямая линия будет правильной. Здесь мы выберем значения x равными 0, 1 и 2.
Когда x = 0,
\begin{aligned} &y=(\frac{1}{2}\times{0})-2\\\\ &y=0-2\\\\ &y= -2 \end{aligned}
Итак, у нас есть координата (0,−2) .
Когда x = 1 ,
\begin{aligned} &y=(\frac{1}{2}\times{1})-2\\\\ &y=\frac{1}{2}- 2\\\\ &y=-1\frac{1}{2} \end{aligned}
Итак, у нас есть координата (1, -1\frac{1}{2}).
Когда x = 2 ,
\begin{aligned} &y=(\frac{1}{2}\times{2})-2\\\\\ &y=1-2\\\\ &y =-1 \end{выровнено}
Итак, у нас есть координата (2,−1).
Теперь у нас есть три координаты: (0,−2), (1,−1\frac{1}{2}) и (2,−1) .
Нанесите полученные координаты на набор осей с метками .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 3: Постройте прямую линию не в форме y = mx + c
Постройте график уравнения ниже на заданном наборе осей для -2\leq{x}\leq2.
2у-6=4х
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Сначала нам нужно изменить уравнение 2y = 4x + 6, чтобы сделать y субъектом. Это упростит вычисление значений y.
Чтобы сделать y субъектом:
Теперь мы можем подставить значения x в y = 2x + 3, чтобы найти соответствующую координату y.
Здесь мы нарисуем таблицу для y = 2x + 3 для диапазона значений -2\leq{x}\leq2.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| у | у = (2 × -2) +3 у = -4 + 3 у = -1 | у = (2 × -1) +3 у = -2 + 3 у = 1 | у = (2 × 0) +3 у = 0 + 3 у = 3 | у = (2 × 1) +3 у = 2 + 3 у = 5 | у = (2 × 2) +3 у = 4 + 3 y = 7 |
Нанесите полученные координаты на набор помеченных осей .
Теперь у нас есть координаты: (−2,−1), (−1,1), (0,3), (1,5) и (2,7) .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 4: Отрицательный градиент в форме y = mx + c
Заполните таблицу, чтобы построить график уравнения.
у=-4х+1
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 1 |
Подставьте каждое заданное значение вместо x в общее уравнение прямой .
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| г | г = (−4 × −2) + 1 у = 8 + 1 у = 9 | у = (-4 × -1) + 1 у = 4 + 1 у = 5 | 1 | у = (−4 × 1) + 1 у = -4 + 1 у = -3 | у = -4 × 2) + 1 у = -8 + 1 y = −7 |
Нанесите полученные координаты на набор помеченных осей .
Теперь у нас есть координаты: (−2,9), (−1,5), (0,1), (1,−3) и (2,−7) .
Проведите прямую через все нанесенные координаты по всей области построения .
Пример 5: Отрицательный градиент не в форме y = mx + c
Постройте график уравнения для -1\leq{x}\leq3.
3х+у=2
Подставьте каждое заданное значение x в общее уравнение прямой линии .
Сначала нам нужно изменить уравнение 3x + y = 2, чтобы сделать y субъектом.
Чтобы сделать y субъектом:
Теперь мы можем подставить значения x в y = −3x + 2, чтобы найти соответствующую координату y. Здесь мы нарисуем таблицу для y = −3x + 2 для диапазона значений -1\leq{x}\leq3.
| x | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| у 9 0127 | у = (−3 × −1) + 2 у = 3 + 2 у = 5 | у = (−3 × 0) + 2 у = 0 + 2 у = 2 | у = (−3 × 1) + 2 у = -3 + 2 у = -1 | у = (-3 × 2) + 2 у = -6 + 2 у = -4 | у = (-3 × 3) + 2 у = -9 + 2 y = -7 |
Нанесите полученные координаты на набор помеченных осей .
Теперь у нас есть следующие координаты линии 3x + y = 2: (-1,5), (0,2), (1,-1), (2,-4), (3,-7)
Проведите прямую через все нанесенные координаты по всей области построения .
Распространенные заблуждения
- Проведите линию через всю сетку
Прямая непрерывна.
Если вы соединяете координаты только на наборе осей, вы рисуете только часть линии. Убедитесь, что график расширен по всей сетке. Визуальное описание см. ниже:
- Метка осей одинаково
Масштаб на каждой оси линейный, что означает, что каждая единица имеет заданное расстояние. Когда вы записываете шкалу на набор осей, убедитесь, что каждая единица имеет такое же количество квадратов сетки, что и следующая, это очень важно вокруг начала координат. См. ниже визуальное представление нескольких заблуждений с маркировкой осей:
- Без использования линейки
Это не обязательно неправильное представление, но причина, по которой вы всегда должны использовать линейку, заключается в том, что вы рисуете одну прямую линию без разрывов, изгибов или кривых. Прямая линия есть прямая линия!
- Линия не прямая (случайные координаты)
Иногда вы сгенерировали координату, которая не лежит в ожидаемом положении на прямой.
Это может означать одно из двух: а) подстановка рассчитана неправильно, б) координата нанесена неправильно.
Чтобы решить эту проблему, посмотрите, где должна лежать координата, используя прямую линию, чтобы помочь вам, и проверьте построение координаты, а затем подстановку.
- Перепутать x и y значения
Координата на декартовой сетке имеет общий вид (x, y) . Убедитесь, что при создании координат значение x отображается первым в скобках, а затем значение y, которое было рассчитано.
Практические вопросы по линейным графикам
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −4 | −2 | 0 | −2 | 4 | 10 |
| х | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | 4 | 2 | 0 | 2 | 4 | 10 |
| х | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −8 | −2 | 4 | 10 |
| х | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −6 | −2 | 4 | 10 |
При x=-2
\begin{выровнено} &y=(6\times-2)-8\\ &у=-12-8\\ &у=-20 \end{выровнено}
При x=-1
\begin{выровнено} &y=(6\times-1)-8\\ &у=-6-8\\ &у=-14 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(6\times0)-8\\ &у=0-8\\ &у=-8 \end{выровнено}
Когда x=1
\begin{выровнено} &y=(6\times1)-8\\ &у=6-8\\ &у=-2 \end{выровнено}
При x= 2
\begin{выровнено} &y=(6\times2)-8\\ &у=12-8\\ &у=4 \end{выровнено}
При x= 3
\begin{выровнено} &y=(6\times3)-8\\ &у=18-8\\ &у=10 \end{выровнено}
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| у = 6х — 8 | −20 | −14 | −8 | −2 | 4 | 10 |
| x | −2 | −1 | 0 | 1 |
| у = 5х + 3 | −7 | −2 | 3 | 8 |
При x=-2
\begin{выровнено} &y=(5\times-2)+3\\ &у=-7 \end{выровнено}
При x=-1
\begin{выровнено} &y=(5\times-1)+3\\ &у=-2 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(5\times0)+3\\ &у=3 \end{выровнено}
При x=1
\begin{выровнено} &y=(5\times1)+3\\ &у=8 \end{выровнено}
\begin{выровнено} &x \quad \quad \quad \,-8 \quad \quad -4 \quad \quad 0 \quad \quad \;4 \quad \quad \;\,8\\ y=&-\frac{1}{4}x \quad \quad \; 2 \четверка \четверка \;\;\; 1 \quad \quad \, 0 \quad \;\;-1 \quad \;\; -2 \end{выровнено}
Чтобы вычислить координаты некоторых точек на этом графике, мы можем использовать значения x, которые легко делятся на 4 (т.
е. числа в таблице умножения на 4).
Когда x=-8
\begin{выровнено} &y=(-\frac{1}{4}\times{-8})\\ &у=2 \end{выровнено}
При x=-4
\begin{выровнено} &y=(-\frac{1}{4}\times{-4})\\ &у= 1 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(-\frac{1}{4}\times{0})\\ &у=0 \end{выровнено}
При x=4
\begin{выровнено} &y=(-\frac{1}{4}\times{4})\\ &у=-1 \end{выровнено}
При x=8
\begin{выровнено} &y=(-\frac{1}{4}\times{8})\\ &у=-2 \end{выровнено}
| x | −2 | −1 | 0 | 1 | 2 |
| 2у + 3х = 12 | 9 | 7,5 | 6 | 4,5 | 3 |
При x=-2
\begin{выровнено}
&y=(-1.
5\times-2)+6\\
&у=3+6\\
&у=9
\end{выровнено}
При x=-1
\begin{выровнено} &y=(-1.5\times-1)+6\\ &у=1,5+6\\ &у=7,5 \end{выровнено}
Когда x= 0
\begin{выровнено} &y=(-1.5\times0)+6\\ &у=0+6\\ &у=6 \end{выровнено}
Когда х=1
\begin{выровнено} &y=(-1.5\times1)+6\\ &у=-1,5+6\\ &у=4,5 \end{выровнено}
При x=2
\begin{выровнено} &y=(-1.5\times2)+6\\ &у=-3+6\\ &у=3 \end{выровнено}
y=-6x+3
y=6x-3
y=3x+6
y=3x-6
Общее уравнение прямой имеет вид y=mx+c, где m — градиент (так что это будет 3x ), а c — это точка пересечения y (так что это будет -6 ).
y=-4x+5
y=4x-3
y=2x+5
y=\frac{1}{4}x +5
Градиенты параллельных линий равны, поэтому любая линия с градиент 4 будет параллелен y=4x+5.
Прямые графики Вопросы GCSE
1. Обведите координату, лежащую на прямой 6x + 12y = 0
| (12,6) | (18,0) | (2,0) | (2,-1) | (-4,-2) |
(1 балл)
Показать ответ
(2,-1)
(1)
2. ( а) Две прямые пересекаются в точке P.
Вычислите координату точки P.
(b) Укажите уклон линии 2y=x+8
(5 баллов) 90 003
Показать ответ
(а)
Горизонтальная линия y=2
(1)
При y=2, 2 × 2=x+8
(1)
x= -4 и (-4,2)
(1 )
(б)
у=\фракция{1}{2}х+4
(1)
м=\фракция{1}{2}
(1)
3.
(a) Заполните таблицу для y=-6+4x
| x | −3 | −2 | −1 | 0 | 1 | 2 |
| г | −18 | −2 |
(b) Нарисуйте график линии y=-6+4x
( 9 0051 5 м ковчег)
Показать ответ
(a)
| x | −3 | −2 | −1 | 0 | 1 | 2 |
| г | −18 | −14 | −10 | −6 | −2 | 2 |
(2)
(б)
Все координаты нанесены правильно
(1)
Одна непрерывная прямая через все точки
(1)
Y-пересечение четко обозначено
(1)
Контрольный список для обучения
Теперь вы научились:
9 0071Все еще зависает?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе обучения математике GCSE.
Мы используем необходимые и необязательные файлы cookie, чтобы улучшить работу нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Принять
Уравнение прямой линии
Уравнение прямой обычно записывается так:
у = мх + б
(или «y = mx + c» в Великобритании, см. ниже)
Что это означает?
| Наклон или Градиент | y значение, когда x=0 (см. Пересечение Y) |
y = расстояние вверх
x = расстояние вдоль
м = уклон или уклон (насколько крута линия) 9000 3
б = значение y , когда x=0
Как найти «м» и «б»?
- b легко: просто посмотрите, где линия пересекает ось Y.
- м (Уклон) нуждается в расчете:
м = Изменение Y Изменение X
Зная это, мы можем составить уравнение прямой линии:
Пример 1
м = 2 1 = 2
b = 1 (значение y при x=0)
Подставляя это в y = mx + b получаем:
y = 2x + 1900 03
С помощью этого уравнения мы можем теперь …
… выбрать любое значение для x и найти соответствующее значение для y
Например, когда x равно 1:
y = 2× 1 + 1 = 3
Убедитесь сами, что x=1 и y=3 действительно находятся на прямой.
Или мы могли бы выбрать другое значение для x, например 7:
y = 2× 7 + 1 = 15
Таким образом, когда x=7, у вас будет y=15
Положительный или отрицательный наклон?
Двигаясь слева направо, велосипедист должен P проехать по положительному склону P Наклон:
Пример 2
м = −3 1 = −3
б = 0
Это дает нам:
y = −3x + 0
Нуль нам не нужен! Итак:
y = −3x
Пример 3: Вертикальная линия
Какое уравнение составляет вертикальная линия?
Наклон undefined .
.. и где он пересекает ось Y?
На самом деле это частный случай , и мы используем другое уравнение, не « y =…», а вместо этого мы используем « x =…».
Вот так:
х = 1,5
Каждая точка на прямой имеет координату x 1,5 ,
поэтому ее уравнение x = 1,5
Встань и беги
Иногда употребляются слова «вставать» и «бежать».
- Как высоко подняться
- Бежать — это как далеко
Таким образом, наклон «м» равен:
м = подъем прогон
Возможно, вам будет легче это запомнить.
Теперь поиграйте с графиком!Вы можете увидеть влияние различных значений 91 563 м 91 564 (наклон) и 91 563 b 91 564 (пересечение по оси y) на странице Explore the Straight Line Graph | .
Ваш комментарий будет первым