Графики функции, производной, первообразной — Умскул Учебник
На этой странице вы узнаете- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производнойПодготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.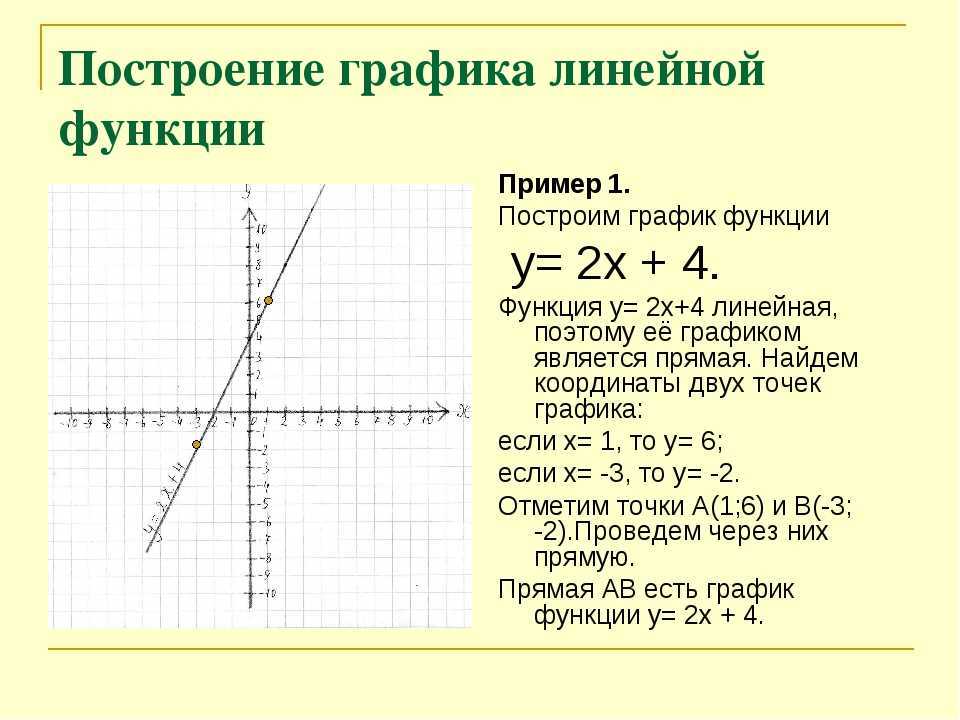
| Где проходит граница между теплом и холодом? Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной. Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах. |
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.

Эти зависимости можно отследить на любых графиках функции и ее производной.
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
В скольких из этих точек производная функции отрицательна?
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
Ответ: -2
| Почему успех фильма не всегда зависит от наличия экшн-сцен? Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой. Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются. |
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
Ответ: 9
| Чем кофе похож на функцию, ее первообразную и производную? Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток. Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная. Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной. |
- Графики функции, производной и первообразной связаны между собой.

- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.

- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
Построение графиков функций — презентация онлайн
Похожие презентации:
План построения графика функции с помощью производной
Исследование функции. Построение графиков
Применение производной
Применение производной к исследованию функции и построению графика функции
Схема исследования функции и построение графика
Исследование функций и построение графиков
Исследование функций и построение графиков с помощью производной
Исследование функции и построение ее графика
Точки перегиба функции, выпуклость графика функции
Исследование функций и построение графиков с помощью производной
Построение
графиков
функций
ДЗ
2.
 План построения графика функции с помощью производной1) Найти область определения функции и
План построения графика функции с помощью производной1) Найти область определения функции иопределить точки разрыва если они существуют
2) Выяснить является ли функция четно или
нечетной, проверить её на периодичность
3) Найти точки пересечения графика с осями
координат, если это возможно
4) Найти стационарные и критические точки
5) Найти точки экстремума функции и
промежутки монотонности
6) Определить промежутки вогнутости,
выпуклости и точки перегиба графика функции
7) Найти координаты ещё нескольких точек (для
большей точности)
3. Как найти промежутки выпуклости, вогнутости и точку перегиба графика функции
Промежутки выпуклости и вогнутостикривой можно находить с помощью
производной.
Теорема. (признак вогнутости и выпуклости)
Если вторая производная функции у=f(х) в
данном промежутке положительна, то
кривая вогнута в этом промежутке, а если
отрицательна – выпукла в этом
промежутке.
4.
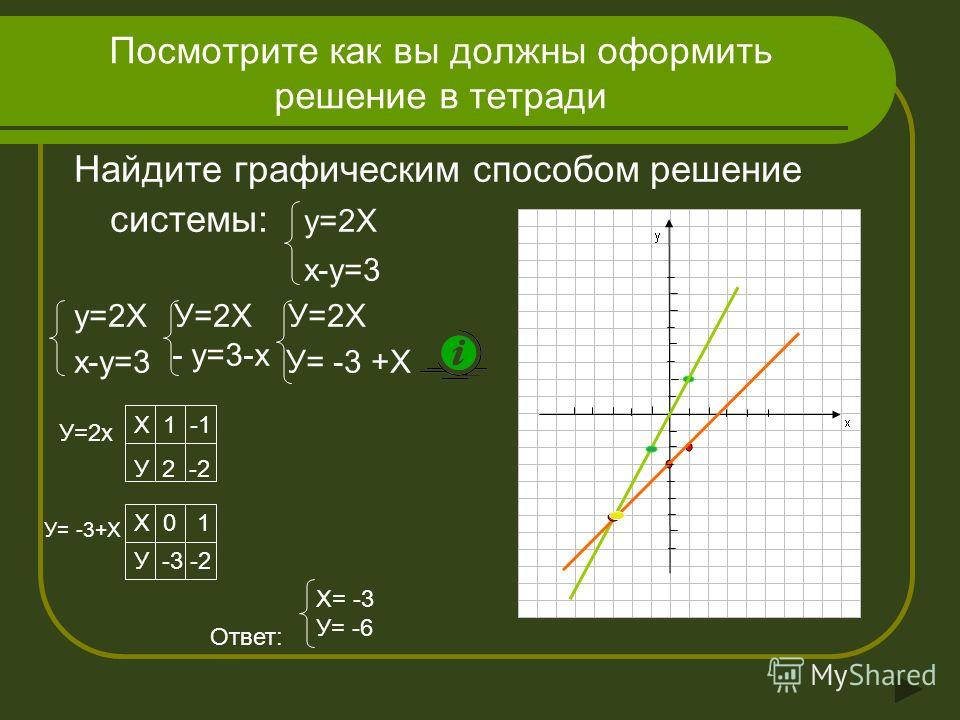 Для нахождения интервалов выпуклости графика функции используют следующий алгоритм:1) Находят f΄(х), а затем f ΄΄(х)
Для нахождения интервалов выпуклости графика функции используют следующий алгоритм:1) Находят f΄(х), а затем f ΄΄(х)2) Находят точки, в которых f ΄΄(х) = 0
3) Отмечают полученные точки на числовой
прямой и получают несколько
промежутков области определения
функции
4) Устанавливают знаки второй
производной в каждом из полученных
промежутков. Если f ΄΄(х) < 0, то на этом
промежутке кривая выпукла; если
f ΄΄(х)>0 — вогнута
Точкой перегиба кривой называется
такая точка, которая отделяет
выпуклую часть кривой от вогнутой её
части.
0
х0
Точкой перегиба кривой графика
функции будут те точки, в которых
f ΄΄(х) = 0 и при переходе через неё
вторая производная меняет знак.
6. Найти интервалы выпуклости и точку перегиба функции
Решение.y x 6x 4
Найдем у΄(х) и у΄΄(х):
у΄(х) = 4х³-12х => у΄΄(х) = 12х²-12=12(х²-1)
Найдём стационарные точки второго порядка,
т.е. у΄΄(х)=0 => 12(х²-1)=0 => х²-1=0 => х²=1
х = ±1 у΄΄(х)
4
2
—
+
-1
+
1
Значит: при х ϵ (-∞; -1) и (1;+ ∞ ) функция
вогнута, а при х ϵ (-1:1) – выпукла; точки
перегиба х= ±1
7.
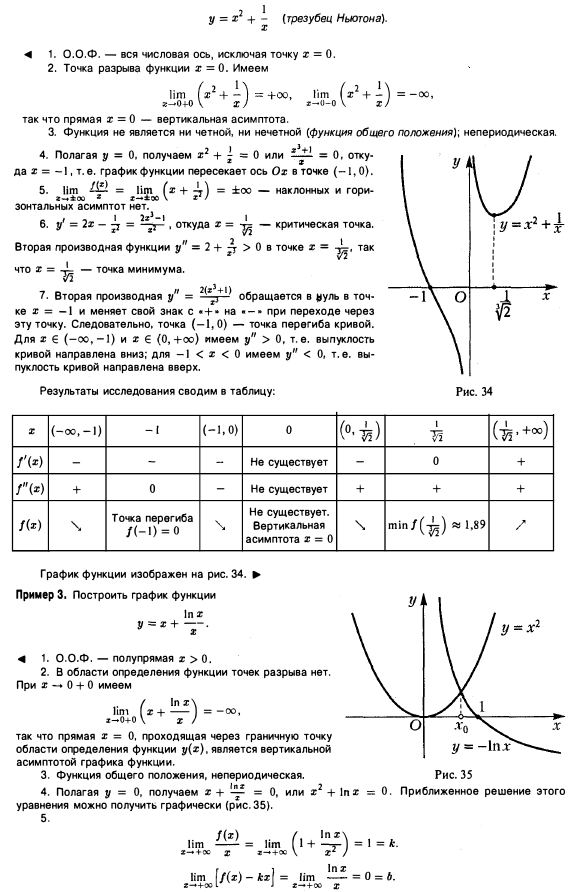 Например: исследовать функцию у = 2х³+3х² -1 и построить её графикРешение. D(у)= (-∞; +∞), четность не
Например: исследовать функцию у = 2х³+3х² -1 и построить её графикРешение. D(у)= (-∞; +∞), четность неопределена
Найдем стационарные точки:
т.к. у΄=6х²+6х=6х(х+1) => 6х(х+1)=0
тогда х=0 и х=-1 стационарные точки
Найдем точки экстремума:
f´(x) +
+
т.к.
f(x)
-1
и х=-1 – точка максимума
х= 0 – точка минимума
0
х
Найдем промежутки монотонности:
при x ϵ (-∞; -1] и [0; + ∞) — функция
возрастает
при x ϵ [-1; 0] — функция убывает
Найдем точки пересечения графика с
осями координат:
если х=0, то у=-1 => (0;-1)
если у=0, то х= -1 => (-1; 0)
Найдем ещё некоторые точки
(контрольные, дополнительные):
• т.к. х=-1 – точка максимума, то уmax=0
=> (-1; 0) -точка локального максимума
• т.к. х= 0 – точка минимума, уmin=-1
=> (0;-1) -точка локального минимума
• если х=1, то у=4 => (1;4)
• если х=-2, то у=-5 => (-2;-5)
Удобнее все эти данные заполнять в виде
таблицы.
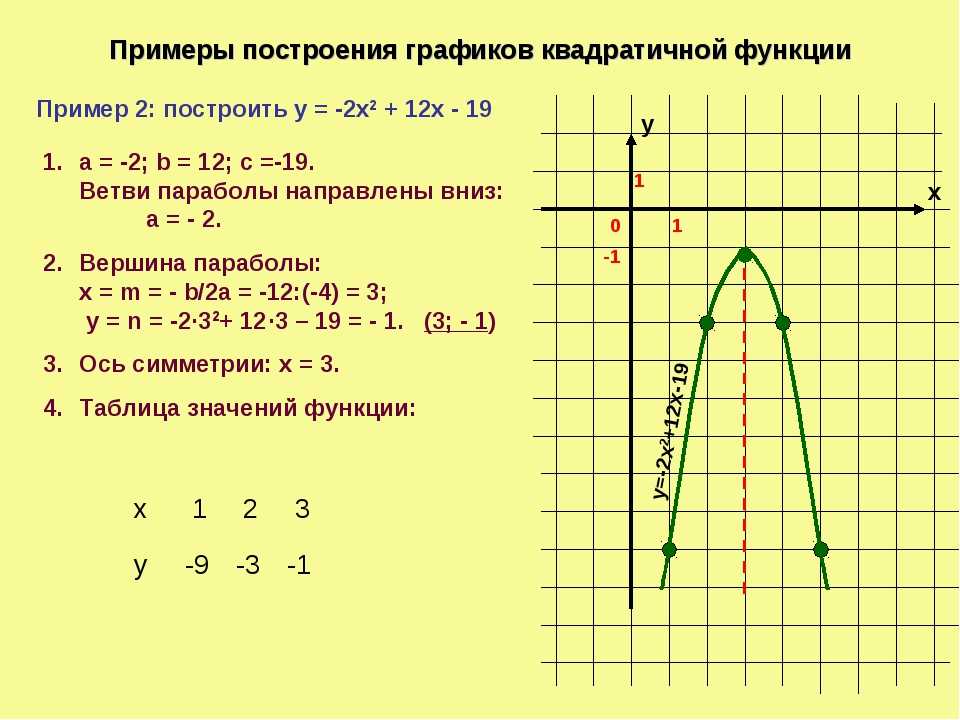
Составим таблицу:
х
(-∞;-1)
-1
f΄(х)
f(х)
+
↑
0
0
(-1;0)
max
(-1;0)
0
(0;+∞)
↓
0
-1
+
↑
(0;-1)
min
Найдем f ΄΄(х).
f΄΄(х) =(6х(х+1))΄=12х+6 = 6(2х+1)
f΄΄(х)=0 => 6(2х+1)=0 => х = -0,5 — точка перегиба
т.к. при х=-1(левее х=-0,5) f΄΄(х) <0,
а при х=-0,1(правее х=-0,5) f΄΄(х) >0
Найдем её координаты: (-0,5; ? ), если это не
трудно
Построим график
функции:
у
4
-2 -1 0
1
-5
х
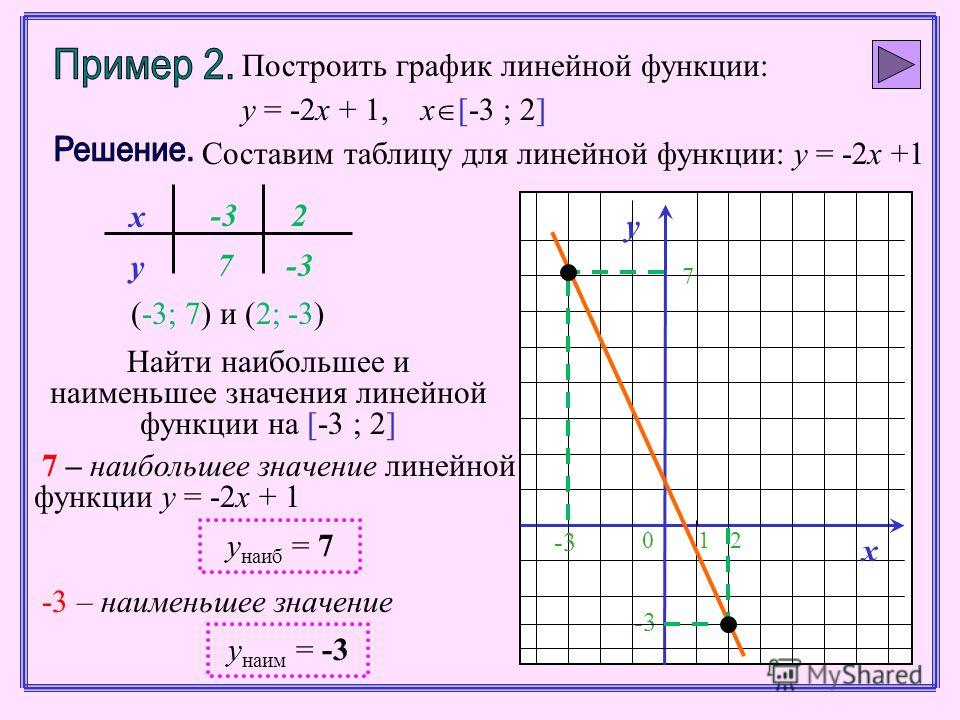
12. Исследовать функцию и построить её график
1) у = 3х² — х³2) у = — 9х + х³
3) у = х³ — 3х² + 2
4) у = — х³ + 6х² — 5
5) у = 3х³ + х² — 8х – 7
6) у = (х)/(1+х²)
Работа
с графиками
функций
№ 1.
По графику функции ответьте
на вопросы
1) Отметьте стационарные
точки.
2) Что можно сказать о
производной в точке х2?
3) Назовите точки экстремума.
4) Что можно сказать о
производной на (−∞; х2]?
5) Укажите промежутки
возрастания функции.
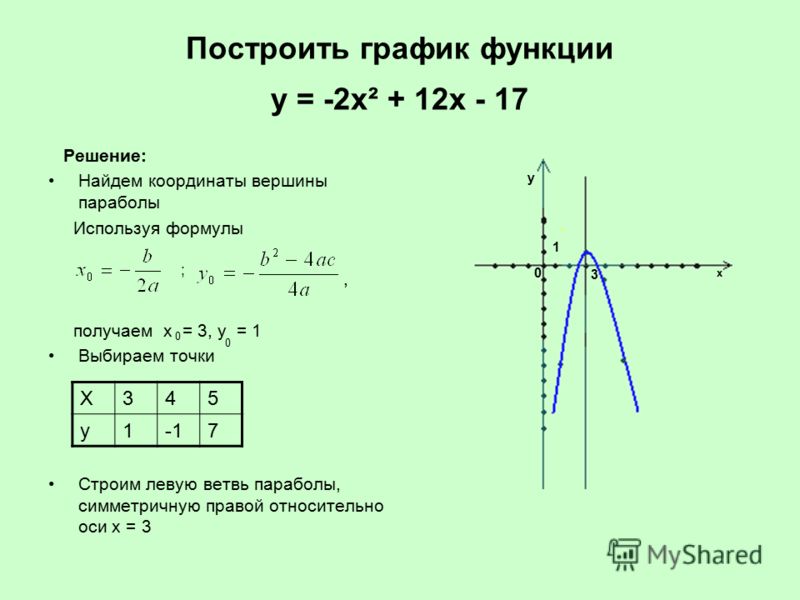
6) Отметьте критические точки
15. Проверим ответы
1. х1,х3,х42. не существует
3. х2,х3,х4
4. f′(х) ≤ 0
5. [х2; х3]U [х4;+∞)функция
возрастает
6. х2
16. № 2. Постройте график непрерывной функции у = f(х), определенной на [а;в], удовлетворяющей следующим условиям: а) а=-1, в=4,
f΄(х)>0 при -1<х<4, f(1)=0, f(4)=3б) а=0, в=5, f΄(х)<0 при 0<х<5, f(2)=0, f(3)=-2
График.
а)
3
-1
1
1
4
17. б) а=0, в=5, f΄(х)<0 при 0<х<5, f(2)=0, f(3)=-2
б) а=0, в=5, f΄(х)<0 при 0<х<5, f(2)=0, f(3)=-2График.
2
0
-2
1
3
5
18. № 3. По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет
максимум, имеет минимум.19. № 4. На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция?
20. № 5. Дан график производной некоторой функции.
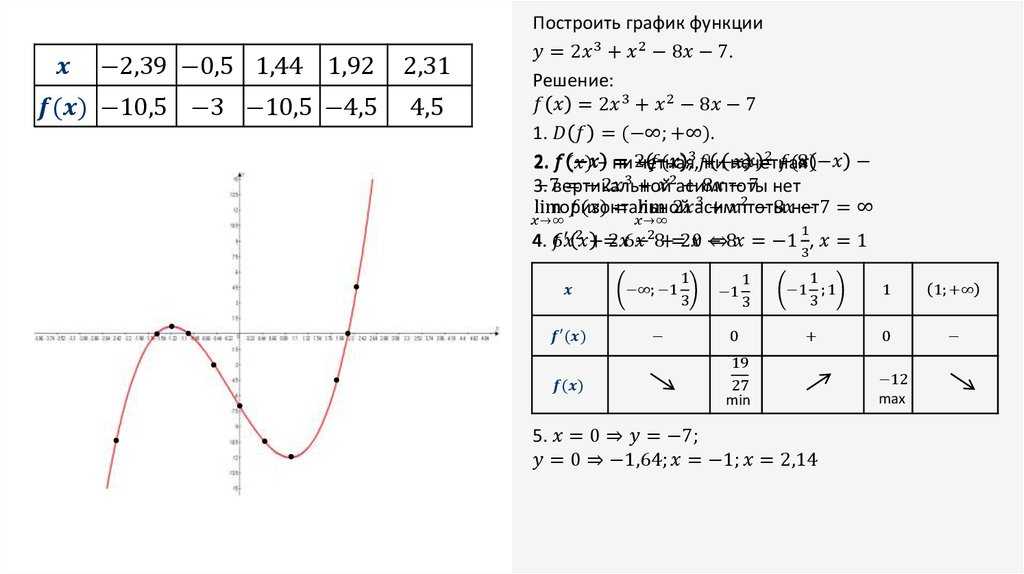 Определить промежутки, на которых функция убывает?
Определить промежутки, на которых функция убывает?21. Верно или не верно ? №1
1. График производной. Точки х= -1, х=1, х=2являются точками максимума.
2. Производная функции в точке хо равна 0,
значит хо — критическая точка.
3. Производная функции не существует в
точке хо, значит хо — критическая точка.
4. Критическая точка является точкой
экстремума.
5. Точка экстремума является
критической точкой.
6. Функция y(x) непрерывна в точке
x=4, причем y’ (x)>0 на (1;4) и y'(x)<0
на (4;7). Точка x=4 является точкой
минимума.
23. № 2. По данному графику функции определить верно или нет высказывание
уХ1
Х3
Х2
0
Х4
х
1) Точка х1 – точка минимума. Да
2) Точка х1 – точка перегиба.
Нет
3) В точках х2 и х4 касательная
Да
параллельна оси абсцисс
4) В точке х3 производной не
Да
существует.
5) Точка х4 – точка экстремума Да
Да
6) Точка х4 – точка минимума
7) Точка х4 – стационарная точка Да
8) Точка х3 – точка экстремума Нет
9) Точка х2 – точка максимума Да
25.
 Используемые ресурсы • А.Г. Мордкович «Алгебра и начала анализа»
Используемые ресурсы • А.Г. Мордкович «Алгебра и начала анализа»10-11 класс. Учебник,- М., Мнемозина, 2016
• А.Г. Мордкович «Алгебра и начала анализа»
10-11 класс. Задачник,- М., Мнемозина, 2016
• Л.И. Мартышова «Открытые уроки алгебры и
начала анализа» 9-11 классы, — М., ВАКО,
2012
English Русский Правила
Онлайн-калькулятор: Метод Эйлера
Исследование Математика
Этот онлайн-калькулятор реализует метод Эйлера, который является численным методом первого порядка для решения дифференциальных уравнений первой степени с заданным начальным значением.
Вы можете использовать этот калькулятор для решения дифференциальных уравнений первой степени с заданным начальным значением, используя метод Эйлера.
Для использования этого метода необходимо иметь дифференциальное уравнение вида
Вы вводите правую часть уравнения f(x,y) в поле y’ ниже.
Вам также потребуется начальное значение
и точка, для которой вы хотите аппроксимировать значение.
Последний параметр метода – размер шага – это буквально шаг по касательной для вычисления следующего приближения кривой функции.
Если вы знаете точное решение дифференциального уравнения в форме y=f(x) , вы также можете ввести его. В этом случае калькулятор также наносит решение вместе с аппроксимацией на график и вычисляет абсолютную ошибку для каждого шага аппроксимации.
Описание метода можно найти под калькулятором.
Euler method
Initial x
Initial y
Point of approximation
Step size
Exact solution (optional)
Calculation precision
Digits after the decimal point: 2
Differential equation
Приблизительное значение y
Приблизительное значение
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Во время загрузки и создания может происходить замедление работы браузера.
Метод Эйлера
Итак, предположим, что мы имеем следующее
Если мы вычислим
, то найдем производную y’ в начальной точке.
Для достаточно малых , мы можем аппроксимировать следующее значение y как
Или, короче,
И в общем случае
Продолжаем вычислять следующие значения y , используя это соотношение цель x точек.
Это суть метода Эйлера. это размер шага. Ошибка на каждом шаге (локальная ошибка усечения) примерно пропорциональна квадрату размера шага, поэтому метод Эйлера более точен, если размер шага меньше. Однако глобальная ошибка усечения является кумулятивным эффектом локальных ошибок усечения и пропорциональна размеру шага, поэтому метод Эйлера считается методом первого порядка.
Более сложные методы позволяют достичь более высокого порядка (и большей точности). Одна из возможностей состоит в том, чтобы использовать больше вычислений функций. Это иллюстрируется методом средней точки 9.0007
Одна из возможностей состоит в том, чтобы использовать больше вычислений функций. Это иллюстрируется методом средней точки 9.0007
URL, скопированный в буфер обмена
Аналогичные калькуляторы
- • Ипотечный кредит. 304 калькуляторы )
#дифференциация #дифференциация по Эйлеру Эйлер Математика Численные дифференциальные уравнения
PLANETCALC, метод Эйлера
Тимур 2020-12-16 10:29:26
Создать график онлайн и найти кратчайший путь или использовать другой алгоритм
Создать график и найти кратчайший путь. На странице помощи вы найдете обучающее видео.
График
Алгоритм создания
Вставьте свой алгоритм ниже и нажмите «Выполнить».Введите заголовок
Настройка матрицы смежности. Используйте запятую «,» в качестве разделителя
Используйте запятую «,» в качестве разделителя
Матрица мультиграфа содержит вес минимальных ребер между вершинами.
Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной
Настройте матрицу заболеваемости. Используйте запятую «,» в качестве разделителя.
Матрица неверна. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на проверку и в случае успеха он будет добавлен на сайт.
Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате матрицы смежности
.Невозможно создать график. Матрица заболеваемости имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате матрицы заболеваемости
. Невозможно создать график.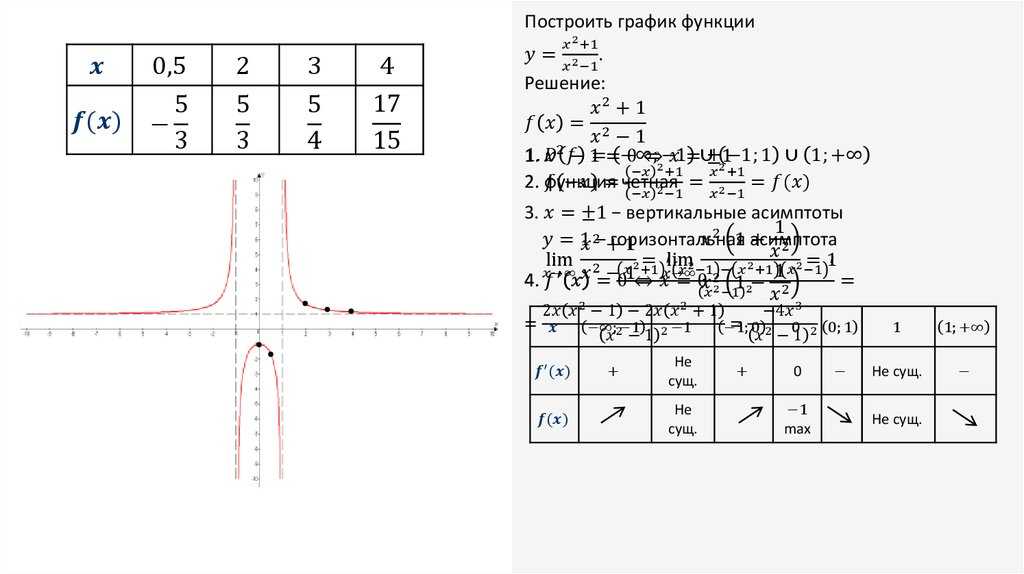 Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «помощь», чтобы открыть справку о формате 9.0007
Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «помощь», чтобы открыть справку о формате 9.0007
Какие функции мы должны добавить в первую очередь?
Наш сервис уже поддерживает следующие функции: Поиск кратчайшего пути с помощью алгоритма Дейкстры, Матрица смежности, Матрица инцидентности.
Непрозрачность
Выбор и перемещение объектов мышью или перемещение рабочей области.
Перетащите курсор для перемещения объектов
Выбор и перемещение объектов мышью или перемещение рабочей области.
Перетащите курсор для перемещения объектов
Щелкните в рабочей области, чтобы добавить новую вершину. Перечисление вершин
Выберите первую вершину ребра
Выберите вторую вершину ребра
Выберите начальную вершину кратчайшего пути
Выберите конечную вершину кратчайшего пути
Длина кратчайшего пути составляет %d
Путь не существует
Нажмите на объект, чтобы удалить
Добавить ребро
Режиссер
Ненаправленный
Матрица смежности
Сохранить
Отменить
самое низкое расстояние
Матрица заболеваемости
Сохранение графика
закрыть
Количество подключаемых компонентов
Количество слабо связанных компонентов
Что вы думаете о сайте?
Имя (электронная почта для обратной связи)
Обратная связь
Отправить
Чтобы задать нам вопрос или отправить нам комментарий, напишите нам по телефону
исправить матрицу
помощь
Матрица имеет неправильный формат
Сохранить изображение графика
Полный отчет
Краткий отчет
Граф не имеет эйлерова цикла
Граф имеет эйлеров цикл
Обработка. ..
..
Добавить вершину
Переименовать вершину
Переименовать
и
Редактировать вес
не имеет веса
Переименование группы
Проголосовать
Рекомендовать алгоритмы
Граф не имеет эйлерова пути
Граф имеет эйлеров путь
График минимальных расстояний
Проверить, чтобы сохранить
Показать матрицу расстояний
Матрица расстояний
Выберите источник максимального расхода
Выберите сток максимального расхода
Максимальный поток от %2 до %3 равен %1
Поток из %1 в %2 не существует
Источник
Раковина
Граф не имеет гамильтонова цикла
Граф имеет гамильтонов цикл
Граф не имеет гамильтоновой траектории
Граф имеет гамильтонов путь
Выбор начальной вершины обхода
Порядок обхода:
Изгиб кромки
Отменить
Сохранить график
По умолчанию
Вершинный стиль
Стиль кромки
Цвет фона
Мультиграф поддерживает не все алгоритмы
не имеет веса
Используйте Cmd⌘ для выбора нескольких объектов.
Используйте Ctrl для выбора нескольких объектов.
Группа перетаскивания.
Группа копирования
Удалить группу
Поиск в ширину
Раскраска графа
Найти подключенные компоненты
Поиск в глубину
Найти цикл Эйлера
Найти эйлеров путь
Алгоритм Флойда-Уоршалла
Упорядочить график
Найти цикл Гамильтона
Найти гамильтонов путь
Найти максимальный расход
Поиск минимального остовного дерева
Визуализация на основе веса
Радиус и диаметр графа поиска
Найти кратчайший путь с помощью алгоритма Дейкстры
Вычислить степень вершин
Вес минимального остовного дерева
При расчете мы не учитывали направление ребер.
График отключен
Выберите первый график для проверки изоморфности.

 Совпадут ли эти графики? Скорее всего, нет.
Совпадут ли эти графики? Скорее всего, нет. 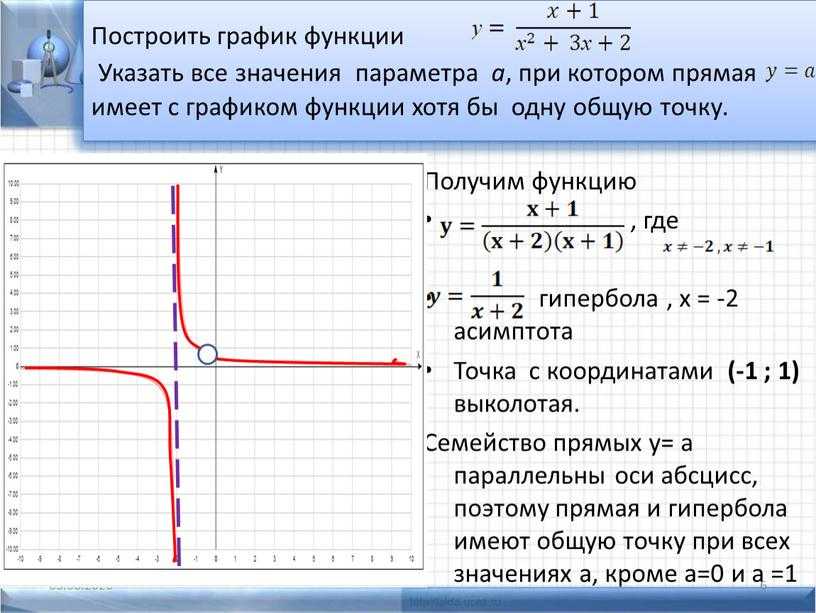
Ваш комментарий будет первым