Объем тела вращения вокруг оси Ox, Oy
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y1(x) и y2(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций yi(x) по переменной x
Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле
Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример. 2, y=0
2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:
И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:
б) Вычислим объем тела вращения вокруг оси Oy:
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.
Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:
Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:
б) Выполняем вычисление объема тела при вращении вокруг оси Oy:
Замена переменных помогает найти последний интеграл.
Пример 2.142 (2475) Найти объем тела, образованного вращением кривой
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Чтобы записать подинтегральную функцию найдем разницу квадратов заданных функций:
а)
б) для тела, образованного вращением вокруг оси Oy подинтегральная функция имеет вид
Из условия равенства функций y1(x)=y2(x) определяем пределы интегрирования
x1=0, |x|=a поэтому
Пределы интегрирования :
а)
б)
При :
поэтому принимая во внимание симметрию имеем неравенство .
а) Вычисляем объем тела вращения вокруг оси Ox:
б) Через следующий интеграл определяем объем тела вращения вокруг оси Oy:
Здесь нет сложных моментов при вычислении интеграла.
Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e— x, y=0,
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y2=e-2x;
б) x*y (x) =xe-x.
Запишем пределы интегрирования (известно за условием):
а) Находим объем тела вращения вокруг оси Ox:
б) Найдем объем тела вращения вокруг оси Oy:
Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.
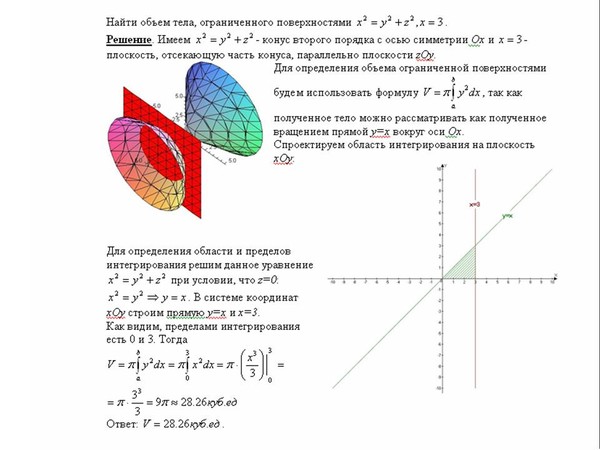
Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x2+(y-b)2=a2, , вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:
При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:
Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:
Внимательно разберите приведенный пример.
Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x2-xy+y2=a2, вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
— уравнение в канонической системы координат.
В приведенной системе координат уравнения эллипса имеет вид:
Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:
Найдем пределы интегрирования из условия равности функций y2(x)=y1(x):
или двукратный объем на интервале
Но тогда еще нужно отнять объем тела в пределах
(которая не принадлежит эллипсу) и ограничена первой кривой
и результат умножить на 2 (симметрия).
Последним шагом вычисляем объем тела вращения вокруг оси Ox:
Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.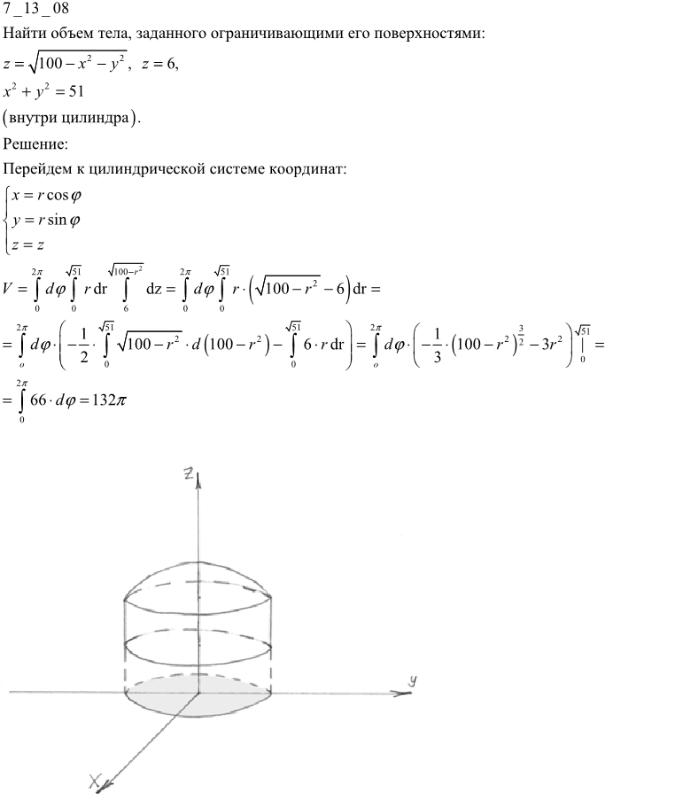
Пример 2.146 (2479) Найти объем тела, образованного вращением кривой вокруг оси Ox.
Решение: Запишем подинтегральную функцию:
y2(x)=e-2x*sin (x).
Установим пределы интегрирования: при , где k=0,1,2.
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:
Здесь вычислили интеграл дважды выполнив замену переменных:
тому
— это числовой ряд.
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b1=1, b2=e-4Pi, поэтому q=e— 4Pi, а сумма прогрессии равна
Пример 2480 Найти объем тела, образованного вращением кривой x=a (t — sin (t)), y=a (1 — cos (t)), , y=0.
а) вокруг оси Ox; б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Вычислим подинтегральную функцию и дифференциал по аргументу:
y2=a2(1-cos (t))2, dx=a(1-cos(t)) dt.
Пределы интегрирования известны из начального условия: tє[0;2pi].
Переходим к применению формул объемов:
а) Первым вычислим объем тела вращения вокруг оси Ox:
Здесь применили замену переменных и условие
б) Следующим найдем объем тела вращения вокруг оси Oy:
Его попробуйте расписать самостоятельно.
в) Последним вычислим объем тела вращения вокруг прямой y=2a:
Перейдем к новой системе координат по формулам y1=y-2a, x1=x.
Тогда искомый объем V=V1-V2, где V1 — объем колового цилиндра с высотой H=2pi*a и радиусом основы R=2a, поэтому объем цилиндра равен
куб. од.
Второй объем находим интегрированием
Как и в предыдущих задачах здесь использовали замену переменных под интегралом.
Напоследок находим разницу объемов
куб. од.
Объем тела, образованного вращением вокруг полярной оси плоской фигуры
Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
необходимо вычислить определенный интеграл по формуле
Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), , y=0
а) вокруг полярной оси;
б) вокруг прямой
Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию:
Пределы интегрирования записываем из начального условия:
а) Сначала найдем объем тела вращения вокруг полярной оси:
Для упрощения вычислений переходим к новой переменной под интегралом.
б) Перейдем к новым координатам с помощью формул: x1=y, y1=-x-a/4.
Определяем пределы интегрирования:
при росте угла от 0 к Pi/2 координата x1 растет от 0 к , при росте от Pi/2 к Pi переменная x1 спадает от к 0, поэтому пределы ограничены интервалом
Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид
Подстановкой в уравнение получим:
,
Найдем объем тела вращения вокруг прямой :
откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю получим
Здесь последние интегралы выражаются через факториалы
(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу
Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi (a>0)вокруг полярной оси.
Решение: Запишем подинтегральную функцию:
С пределами интегрирования проблем нет:
Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами:
Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.
Пример 2484.2 Найти объем тела, образованного вращением кривой phi=Pi*r3, phi=Pi, вокруг полярной оси.
Решение: Запишем подинтегральную функцию:
Пределы интегрирования:
Вычисляем объем тела вращения вокруг полярной оси:
Здесь синус вносим под дифференциал и выполняем интегрирование частями.
На данное время это все примеры, которые мы смогли подготовить для Вас по данной теме.
Вычисление тройных интегралов: теория и примеры
- Понятие тройного интеграла
- Вычисление тройного интеграла путём уменьшения кратности
- Расстановка пределов интегрирования при переходе к последовательности трёх интегралов
- Замена переменных в тройном интеграле и цилиндрические координаты
- Тройной интеграл в сферических координатах
- Приложения тройного интеграла
Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Записывается тройной интеграл так:
.
Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.
Вычислить тройной интеграл — значит найти число, равное объёму тела V или, что то же самое — области V.
Практически каждый может понять смысл вычисления тройного интеграла «на своей шкуре».
Точнее — «под шкурой», а ещё точнее — по своим органам дыхания — лёгким. Вне зависимости от того, знаете
ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол — пузырьковых образований,
оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так:
объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из
маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное
количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое «огромное количество малостей»
математически как раз и формулируется понятие тройного интеграла.
А состоит этот объём из
маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное
количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое «огромное количество малостей»
математически как раз и формулируется понятие тройного интеграла.
Почему именно тройной интеграл служит для нахождения объёма тела V? Пусть область V разбита на n произвольных областей Δvi, причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δvi — наоборот, уменьшать. Можем составить интегральную сумму вида
.
Если функция f(M) = f(x, y, z)
непрерывна, то будет существовать предел интегральных сумм вида, указанного выше.
В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V — областью интегрирования; x, y, z — переменными интегрирования, dv (или dx dy dz) — элементом объёма.
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Рассмотрим трёхмерную область V. Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z1(x, y) и z = z2(x, y). С боковых сторон (то есть по ширине) область ограничена поверхностями y
= y1(x) и y = y2(x). И, наконец, по глубине (если Вы смотрите на область в направлении оси Ox) — поверхностями x = a и x = bЧтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной.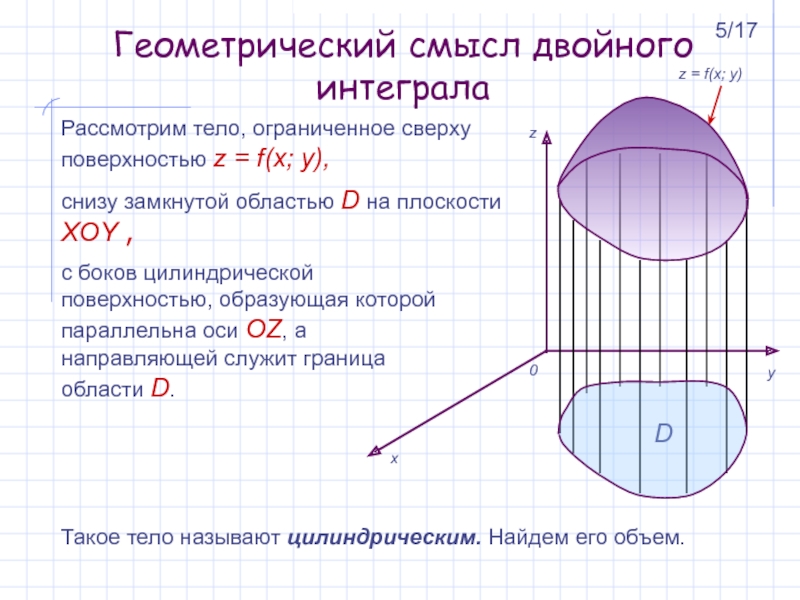 Она правильна тогда, когда прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Правильными
трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже —
прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.
Она правильна тогда, когда прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Правильными
трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже —
прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.
Чтобы наглядно представить отличие правильности от
неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На
рисунке ниже — пример неправильной области
Мы будем рассматривать только правильные области.
Итак, область V — правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула
Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению
внутреннего определённого интеграла по переменной z (при постоянных x и y) и
внешнего двойного интеграла по двумерной области D.
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:
.
Из этой записи уже однозначно видно, что:
- сначала нужно интегрировать функцию f(x, y, z) по переменной z, а в качестве пределов интегрирования взять уравнения z = z1(x, y) и z = z2(x, y) поверхностей ограничивающих область V снизу и сверху;
- получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов
интегрирования взять уравнения
- получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов
интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу
—
последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла. В нашем случае применяем формулу 10 из таблицы интегралов:
.
Вычислим второй интеграл — по переменной y (применяя формулу 7 из таблицы интегралов):
.
Теперь вычисляем самый внешний интеграл — по переменной x (применяя все ту же формулу 7):
.
Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
Пример 2. Вычислить тройной интеграл
,
где V — параллелепипед, ограниченный плоскостями x = − 1, x = + 1, y = 0, y = 1, z = 0, z = 2.
Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем интеграл «в серединке» — по переменной y. Получаем;
.
Теперь вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен -2.
Пример 3. Вычислить тройной интеграл
,
где V — пирамида, ограниченная плоскостью x + y + z = 1
и координатными плоскостями x = 0, y = 0, z = 0. Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y + z = 1, считая при этом, что z = 0 (так как линия расположена в плоскости xOy). Получаем: 1 − x.
Сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
Наконец, вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Пример 4. Вычислить тройной интеграл
,
где V — пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0, y = 0, z = 0.
Посмотреть правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Интеграл
Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление
интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к
последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».
Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V — эллипсоид
.
Решение. Пусть центр эллипсоида — начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу.
Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена
ниже плоскости xOy.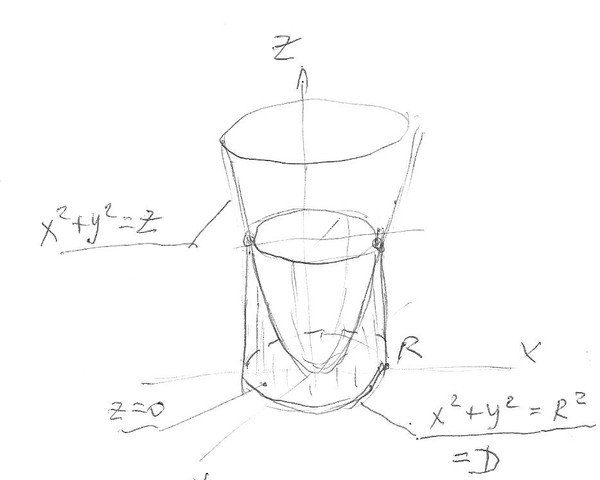 Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
.
Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:
.
Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:
.
Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:
.
Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:
.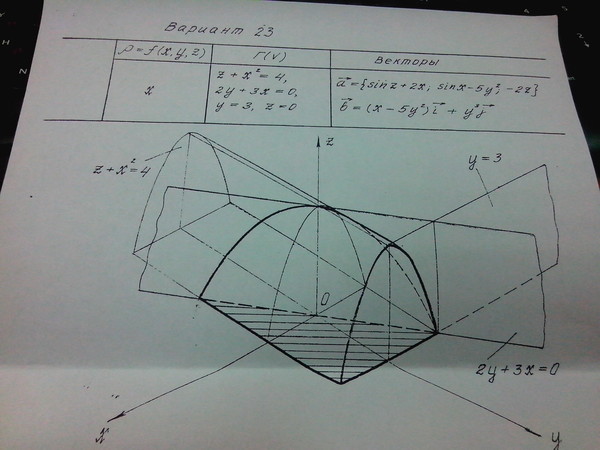
Что касается интегрирования по переменной x, то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a: x1 = − a и x2 = a.
Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:
,
где «игрек первое», «игрек второе», «зет первое» и «зет второе» — полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.
Следующие примеры — не такие страшные, как только что рассмотренный. При этом они предполагают
не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся.
Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся.
Пример 6. Вычислить тройной интеграл
,
если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.
Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.
В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной
интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования
снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили
фигуру набок и считаем, что смотрим на неё снизу.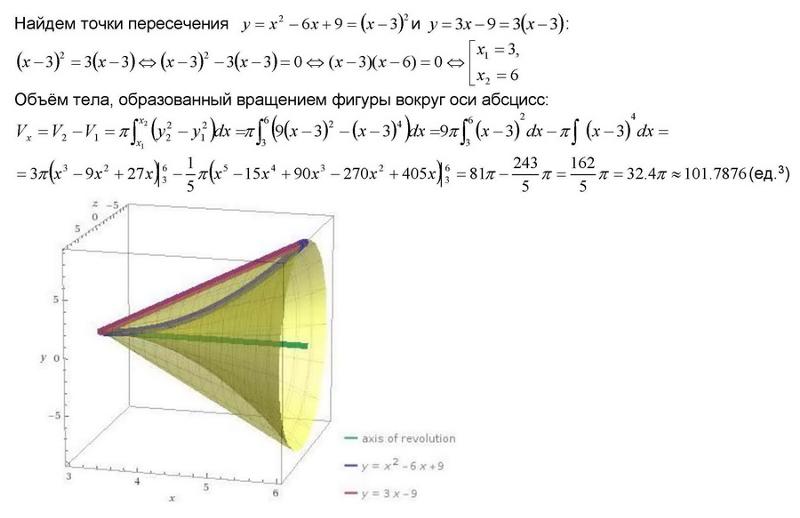 Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
.
Внимание! В этом примере самый внешний интеграл — не по переменной «икс», а по переменной «игрек», а «средний» — по переменной «икс»! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной x. Получаем:
Получаем:
.
Наконец, вычисляем самый внешний интеграл — по переменной y:
Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл
,
если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.
Нижние пределы интегрирования по всем переменным заданы в условии примера.
Найдём верхний предел интегирования по «иксу». Для этого выразим «икс» из четвёртого уравнения,
считая «игрек» равным нулю, а «зет» равным двум. Получаем x = 2.
Найдём верхний предел интегирования по «игреку». Для этого выразим «игрек» из того же четвёртого
уравнения, считая «зет» равным двум, а «икс» — переменной величиной. Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
.
Вычисляем самый внешний интеграл — по переменной x и окончательно находим данный тройной интеграл:
Ответ: данный тройной интеграл равен 2.
Если проекцией области интегрирования на какую-либо из координатных плоскостей
является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы
x = rcosφ,
y = rsinφ,
z = z.
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Пример 8. Вычислить тройной интеграл
переходом к цилиндрическим координатам, где V — область, ограниченная поверхностями и .
Решение. Так как область V на плоскость xOy проектируется в круг , то
координата φ изменяется в пределах от 0 до 2π, а координата r — от r=0 до r=1. Постоянному значению
в пространстве соответствует цилиндр .
Рассматривая пересечение этого цилиндра с областью V, получаем изменение
ординаты z от z = r² до z = 1.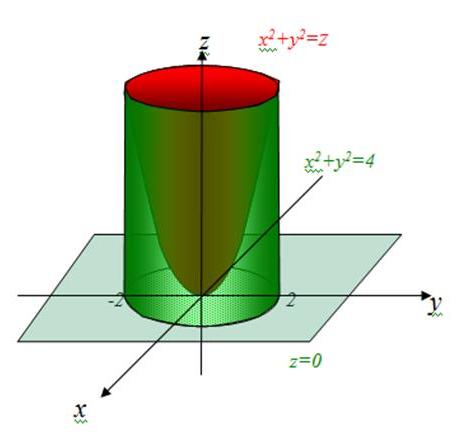 Переходим к цилиндрическим координатам и получаем:
Переходим к цилиндрическим координатам и получаем:
Ответ: данный тройной интеграл равен π/6.
Если область интегрирования в тройном интеграле представляет собой шар или часть шара, то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M характеризуют три величины (ρ, φ, θ), где ρ — расстояние от точки M до начала координат 0, φ — угол между вектором ON и положительным направлением оси Ox (N — проекция точки M на плоскость xOy), θ — угол между вектором OM и положительным направлением оси Oz.
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
x = ρsinθcosφ,
y = ρsinθsinφ,
z = ρcosθ.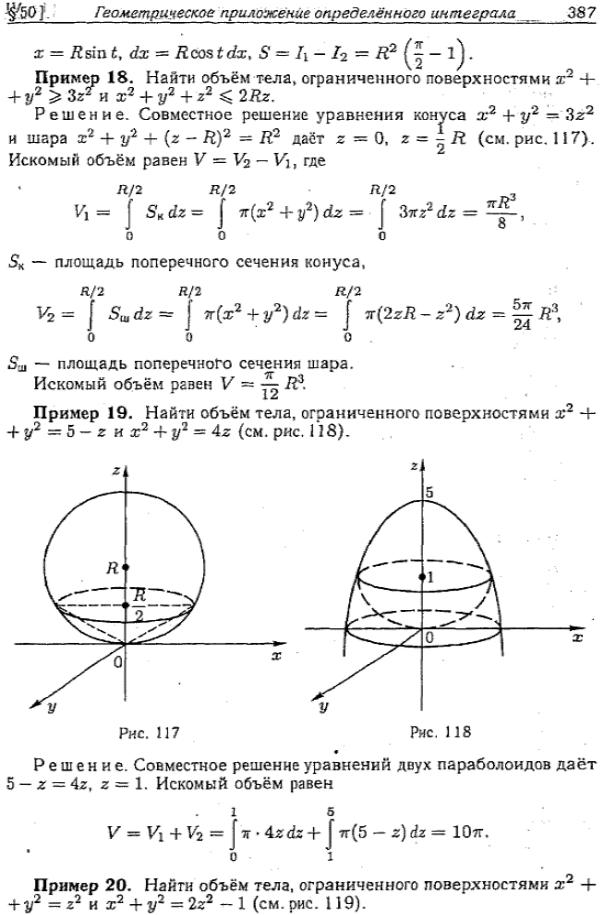
Элемент объёма в сферических координатах выражается следующим образом:
.
Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах — перейти к повторным интегралам (последовательности трёх определённых интегралов):
Пример 9. Вычислить тройной интеграл
переходом к сферическим координатам, где V — область, ограниченная неравенствами и .
Решение. Снизу область интегрирования ограничена конической поверхностью
, а сверху — сферой
. Так как область
интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную
функцию:
Перепишем подынтегральную
функцию:
Учитывая, что , получаем
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому
Итак, тройной интеграл вычислен. Так как все три интеграла — независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:
.
Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:
.
Статические моменты материального тела. Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам:
Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам:
Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:
Центр тяжести материального тела. Координаты центра массы C(xc, yc, zc) материального тела с плотностью ρ = ρ(x, y, z) определяются по формулам:
Пример 10. Вычислить объём тела, ограниченного поверхностями
,
,
.
Вычислить объём тела, ограниченного поверхностями
,
,
.
Решение. Одна их поверхностей — — цилиндрическая поверхность (образующая параллельна оси Oz), то есть проекция области на плоскость xOy совпадает с фигурой, которую ограничивает линия , или . Эта линия изображена на рисунке ниже.
Таким образом, записываем тройной интеграл в цилиндрических координатах и вычисляем его:
Ответ: объём тела равен 176 единиц объёма.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кратные и криволинейные интегралы
Кратные и криволинейные интегралы
- Вычисление двойных интегралов
- Двойные интегралы в полярных координатах
- Вычисление тройных интегралов
- Вычисление криволинейных интегралов
- Интегралы по замкнутому контуру, формула Грина
- Вычисление поверхностных интегралов
Поделиться с друзьями
Калькулятор площади поверхности| Определение
Создано Богной Шик и Ханной Памула, докторами наук
Отредактировано Стивеном Вудингом и Джеком Боуотером
Последнее обновление: 02 марта 2023 г.
- Что такое площадь поверхности? Определение площади поверхности
- Формула площади поверхности…
- Площадь поверхности сферы
- Площадь поверхности цилиндра
- Площадь поверхности конуса
- Площадь поверхности куба
- Площадь поверхности пирамиды
- Площадь поверхности прямоугольной призмы
- Площадь поверхности треугольной призмы
- Площадь поверхности тела
- Как рассчитать площадь поверхности сферы?
- Прочие вопросы
- Часто задаваемые вопросы
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел . Если вы когда-нибудь задавались вопросом, как найти площадь поверхности или что такое площадь боковой поверхности, этот калькулятор здесь, чтобы помочь вам. Площадь поверхности имеет гигантский список приложений в каждой области, например, в аэродинамике.
В этой статье вы найдете формулы площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной/треугольной призмы. Мы также объясним, как рассчитать площадь поверхности сферы в качестве примера.
Мы также объясним, как рассчитать площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности равна общей площади, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности можно разделить на сумму площадь основания и площадь боковой поверхности . Боковая поверхность – это площадь всех сторон объекта, исключая его основание и вершину. Это деление используется для форм, в которых существует очевидное различие между основанием и другой частью, например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основания (например, в кубе или параллелепипеде), и мы не используем его для гладких поверхностей, таких как сфера.
Формула площади поверхности…
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел. Формула зависит от типа твердого тела.
Формула зависит от типа твердого тела.
Площадь поверхности сферы:
A = 4πr², где r — радиус сферы.Площадь поверхности куба:
A = 6a², где a — длина стороны.Площадь поверхности цилиндра:
A = 2πr² + 2πrh, где r — радиус, а h — высота цилиндра.Площадь поверхности конуса:
A = πr² + πr√(r² + h²), где r — радиус, а h — высота конуса.Площадь поверхности прямоугольной призмы (коробки):
A = 2(ab + bc + ac), где a , b и c — длины трех сторон прямоугольного параллелепипеда.Площадь поверхности треугольной призмы:
A = 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c), где a , b и c — длины трех сторон основания треугольной призмы, а h — высота (длина) призмы.
Площадь поверхности пирамиды:
A = l × √(l² + 4 × h²) + l², где l — длина стороны квадратного основания и ч — высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы вычислить площадь поверхности сферы, все, что вам нужно знать, это радиус сферы или ее диаметр.
-
A = 4 × π × r², гдеr— радиус.
Как мы знаем, диаметр шара равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
-
A = 4 × π × (d / 2)² = π × d², гдеd— диаметр сферы.
Вывод этой формулы площади поверхности требует интегрирования. Если вам интересно, посмотрите это доказательство.
Площадь поверхности цилиндра
Чтобы узнать площадь поверхности цилиндра, необходимо иметь две величины: радиус (или диаметр) основания и высоту цилиндра. Общее уравнение как обычно — площадь основания раз высота . В нашем случае круг является основой.
Общее уравнение как обычно — площадь основания раз высота . В нашем случае круг является основой.
-
А = 2πr² + 2πrh
Откуда взялась эта формула? Вы можете написать уравнение для площади поверхности цилиндра как:
-
A = A(боковая) + 2 × A(основная)
Площадь основания найти легко — помним известную формулу площади круга: A(основание) = π × r² . Но какова форма площади боковой поверхности? Попробуйте представить, что мы его «разворачиваем». Вы признаете это? это прямоугольник ! Длина одной стороны — это высота цилиндра, а вторая — длина окружности в развернутом виде.
-
А(основание) = π × r² -
A(поперечный) = h × (2 × π × r)
Площадь поверхности конуса
Мы можем разделить площадь поверхности конуса на две части:
-
A = A(боковая) + A(основание), так как у нас есть только одно основание, напротив к цилиндру.
Основание снова равно площади круга A(основание) = π × r² , но происхождение площади боковой поверхности может быть не столь очевидным:
-
A(боковая) = π × r × √(r² + h²)
Давайте посмотрим на этот пошаговый вывод:
Раскатайте боковую поверхность до плоского состояния. Круговой сектор, являющийся частью окружности радиусом s ( s высота наклона конуса).
Для круга с радиусом s, длина окружности равна
2 × π × с. Длина дуги сектора равна2 × π × r.Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
A(поперечный) = (s × (длина дуги)) / 2 = (s × 2 × π × r) / 2 = π × r × sФормулу можно получить из пропорций, так как отношение площадей фигур такое же, как отношение длины дуги к длине окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (длина большого круга), поэтому:(площадь сектора) / (π × с²) = (2 × π × r) / (2 × π × с)(площадь сектора) = (π × с²) × (2 × π × r) / (2 × π × с)A(поперечный) = π × r × sЧтобы найти недостающий член этого отношения, вы также можете попробовать наш калькулятор отношений!
- Обычно у нас нет
sзадано значение, ноh, что равно высоте конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
r² + h²= s², извлекая квадратный корень, получаемs = √(r² + h²)Таким образом, формула площади боковой поверхности выглядит следующим образом:
A(поперечный) = π × r × √(r² + h²)
- Наконец, сложите площади основания и боковой части, чтобы найти окончательную формулу площади поверхности конуса :
-
A = A(поперечный) + A(основной) = π × r × s + π × r²заданоrиsили -
A = π × r × √(r² + h²) + π × r²учитываяrиh.
Площадь поверхности куба
Площадь поверхности куба проще всего представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
-
A = 6 × (боковая часть)
Так как площадь квадрата является произведением длины его сторон, окончательная формула для площади поверхности куба будет следующей:
-
A = 6 × l², гдеl— квадрат сторона
Площадь поверхности пирамиды
Пирамида представляет собой трехмерное тело с многоугольным основанием и треугольными боковыми гранями. Когда вы слышите пирамида , обычно предполагается, что обычная квадратная пирамида . Но в зависимости от формы основания, это могла быть и шестиугольная пирамида, и прямоугольная пирамида. Обычный означает, что он имеет основание правильного многоугольника и представляет собой правильную пирамиду (вершина прямо над центроидом его основания), а квадрат – означает, что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Когда вы слышите пирамида , обычно предполагается, что обычная квадратная пирамида . Но в зависимости от формы основания, это могла быть и шестиугольная пирамида, и прямоугольная пирамида. Обычный означает, что он имеет основание правильного многоугольника и представляет собой правильную пирамиду (вершина прямо над центроидом его основания), а квадрат – означает, что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
-
A = l × √(l² + 4 × h²) + l²гдеlсторона основания, аhвысота пирамиды
Опять же, мы можем разделить уравнение на:
A = A(основание) + A(сторона) = A(основание) + 4 × A(боковая сторона)
Основание имеет форму квадрата , так что A (основание) = l² . Для расчета площади боковой поверхности начнем с площади одной треугольной грани:
Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
с = √(а² + b²)Вычислите гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
c = √(h² + (l/2)²) = √(h² + l²/4)Площадь треугольника (в нашем случае это равнобедренный треугольник) можно вычислить как:
A = высота × основание / 2поэтомуA(боковая сторона) = √(h² + l²/4) × l / 2Итак, окончательная формула площади поверхности пирамиды:
A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)A = l² + l × √(4 × h² + l²)
Площадь поверхности прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, достаточно вычислить площади сторон прямоугольника:
-
A = 2 × (A1 + A2 + A3)
где:
-
A1 = длина × ширина -
A2 = Ш × В -
A3 = Д × В
Таким образом, окончательная формула:
-
A = 2 × (l × w + w × h + l × h)
Площадь поверхности треугольной призмы
Чтобы понять, откуда берется формула площади поверхности треугольной призмы, давайте посмотрим на этот вывод:
Часть площади боковой поверхности в этом случае легко вычислить.
 Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:A(боковой) = a × h + b × h + c × h = h × (a + b + c), который мы также можем записать вкратце как:
A(боковой) = h × P, гдеP— периметр базового треугольникаЗатем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дано. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A(основание) = 0,25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)))Окончательная формула площади поверхности треугольной призмы:
A = A (боковой) + 2 × A (базовый)A = h × (a + b + c) + 0,5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c) ))
Площадь поверхности тела
Вы можете рассчитать поверхность любого твердого тела, например, вашего тела — это не обязательно должна быть простая фигура из геометрии! Если вам интересно, какова площадь внешней поверхности человеческого тела, посмотрите этот калькулятор площади поверхности тела.
Как рассчитать площадь поверхности сферы?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие шаги:
Определить радиус сферы. Мы можем принять радиус 10 см.
Введите это значение в формулу:
А = 4πr²Рассчитать результат:
А = 4π × 10² = 1256 см²Вы также можете использовать онлайн-калькулятор площади поверхности, чтобы найти радиус сферы, если знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить его в см², дюймах², футах², м², а также в акрах и гектарах.
Если вы хотите найти объем любого из этих тел, воспользуйтесь нашим калькулятором объема.
Часто задаваемые вопросы
Как найти сторону куба по заданной площади?
Чтобы преобразовать площадь поверхности куба в длину его стороны, выполните следующие действия:
- Запишите площадь вашего куба.

- Разделите на шесть . Результатом является площадь одного лица.
- Возьмите квадратный корень из числа из шага 2.
- Это длина сторон вашего куба . Отличная работа!
Как найти радиус сферы по заданной площади?
Чтобы определить радиус сферы по площади ее поверхности:
- Запишите площадь поверхности сферы.
- Разделите на
4π ≈ 12,566. - Возьмите квадратный корень из :
√(Площадь / 4π). - Вот и все; это радиус! Вы можете проверить свой результат с помощью онлайн-калькулятора площади поверхности.
Какова площадь поверхности цилиндра с радиусом и высотой, равными 2 дюймам?
Ответ: 50,2655 в кв. . Чтобы получить этот результат, вспомните, что формула площади поверхности цилиндра:
Площадь = 2πr(r + h)
Подставляя r = h = 2 , получаем Площадь = 16π ≈ 50,2655 . Запомните единицы измерения! Так как
Запомните единицы измерения! Так как r и h находятся в в , площадь равна в кв .
Богна Шик и Ханна Памула, PhD
Радиус (r)
Площадь поверхности
Площадь поверхности
Посмотреть 23 похожих калькулятора 3D-геометрии 📦
Площадь полушарияКуб Cube Calc: найти v, a, d… еще 20
Калькулятор объема коробки 📐
Быстрая навигация:
- Формула объема коробки
- Как рассчитать объем коробки?
- Пример: определение объема прямоугольного ящика
- Расчет груза в кубических метрах / кубических футах
- Другие приложения
Объем прямоугольной коробки можно рассчитать, если известны три ее измерения: ширина, длина и высота. Тогда формула том коробка = ширина х длина х высота . Иллюстрация ниже:
Измерить стороны прямоугольной коробки или резервуара очень просто. Результат вычисления с использованием нашего калькулятора объема прямоугольного ящика или иным образом всегда будет в используемой единице длины, кубе. Убедитесь, что все измерения указаны в одних и тех же единицах, если вы выполняете расчеты вручную, а если используете наш калькулятор, обязательно выберите соответствующую метрику. Если вы измерили длину в дюймах, результат будет в кубических дюймах. Если длина указана в футах, результат будет в кубических футах, и так далее для ярдов 3 , миль 3 , мм 3 , см 3 , метров 3 .
Результат вычисления с использованием нашего калькулятора объема прямоугольного ящика или иным образом всегда будет в используемой единице длины, кубе. Убедитесь, что все измерения указаны в одних и тех же единицах, если вы выполняете расчеты вручную, а если используете наш калькулятор, обязательно выберите соответствующую метрику. Если вы измерили длину в дюймах, результат будет в кубических дюймах. Если длина указана в футах, результат будет в кубических футах, и так далее для ярдов 3 , миль 3 , мм 3 , см 3 , метров 3 .
Чтобы найти объем прямоугольного ящика или бака, нужно провести три измерения, а затем умножить их. В практических ситуациях у вас может быть план или инженерная схема, в которой даны все измерения, что значительно упрощает вашу задачу. Это довольно легко сделать в уме, если числа маленькие, но это быстро становится неудобным, если числа становятся большими, когда объем калькулятора, такого как выше, становится действительно полезным.
Следует отметить, что «объем коробки» может быть неточным термином, поскольку, если мы примем коробку за абстрактное математическое понятие, ее стенки будут иметь нулевую толщину, а сам ящик будет иметь нулевой объем. Однако в практических ситуациях мы обычно говорим об объеме с точки зрения пространства, ограниченного коробкой или резервуаром, и это то, что вычисляет приведенный выше калькулятор. Если это то, что вы рассчитываете и хотите знать, что он может вместить, обязательно измерьте его внутренние, а не внешние размеры, иначе вам нужно будет вычесть объем стен.
Пример: найдите объем прямоугольной коробки
Для вычисления объема любой коробки прямоугольной формы необходимо знать три измерения: длины двух сторон ее основания, а также высоту. Например, если две стороны основания имеют длину 3 дюйма и 6 дюймов соответственно, а высота коробки равна 2 дюймам, то с помощью уравнения объема коробки получается 3 x 6 x 2 = 18 x 2 = 36 дюймов.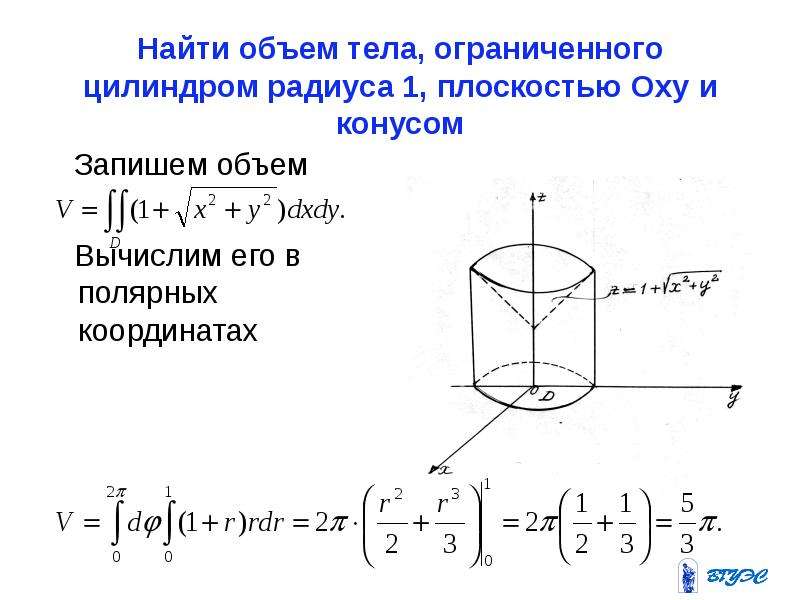 3 (куб. дюймы).
3 (куб. дюймы).
В качестве альтернативы можно указать площадь одной стороны коробки и высоту относительно этой стороны. В этом случае просто умножьте площадь на высоту. Например, если площадь основания коробки составляет 25 кв. футов, а сторона коробки, ортогональная к ней, имеет длину 4 фута, то объем коробки равен 25 х 4 = 100 куб. футов9.0003
Расчет груза в кубических метрах / кубических футахЧасто требуется рассчитать объем транспортных контейнеров, ящиков, ящиков, цистерн и других транспортных средств. Обычно у производителя есть техническая спецификация, или, по крайней мере, вы должны знать стандарт, на основе которого был произведен контейнер, с указанием минимально допустимых размеров.
Если вам нужен более специализированный калькулятор, который подскажет, сколько предметов при заданных размерах вы можете разместить, попробуйте наш калькулятор контейнеров и калькулятор поддонов.
Прочие области применения Прямоугольная коробка — одна из наиболее широко используемых форм тела в науке, технике и архитектуре благодаря хорошим конструктивным свойствам и устойчивости к силовым воздействиям с разных сторон.


 Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора: Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны: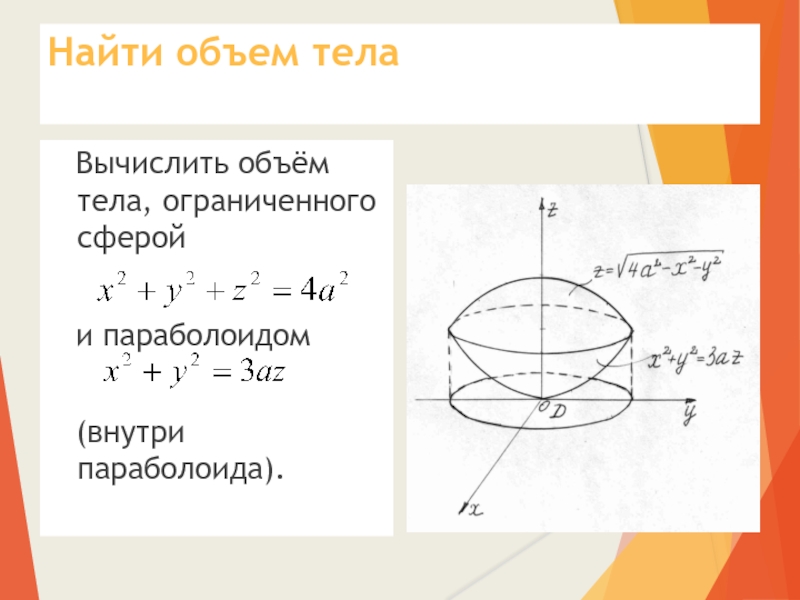
Ваш комментарий будет первым