Графики уравнений 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Системы уравнений
Урок: Графики уравнений
1. Тема урока, введение
Мы рассматриваем рациональное уравнение вида и системы рациональных уравнений вида
Мы говорили, что каждое уравнение в этой системе имеет свой график, если конечно имеются решения уравнений. Мы рассмотрели несколько графиков различных уравнений.
Сейчас мы систематически рассмотрим каждое из известных нам уравнений, т.е. выполним обзор по графикам уравнений.
2. График линейного уравнения
1. Линейное уравнение с двумя переменными
x, y – в первой степени; a,b,c – конкретные числа.
Пример:
Графиком этого уравнения является прямая линия.
Мы действовали равносильными преобразованиями – y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.
Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.
|
X |
0 |
|
|
Y |
1 |
0 |
В данном случае
Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если сли
Эта функция возрастает, т.е. с увеличением x увеличивается y. Мы получили два частных решения, а как записать множество всех решений?
Если точка имеет абсциссу x, то ордината этой точки
Значит, решением исходного уравнения является множество пар чисел
У нас было уравнение, мы построили график, нашли решения. Множество всех пар – сколько их? Бесчисленное множество.
Множество всех пар – сколько их? Бесчисленное множество.
3. График рационального уравнения
2.
Это рациональное уравнение,
Найдем y, равносильными преобразованиями получаем
Положим и получаем квадратичную функцию, ее график нам известен.
Пример: Построить график рационального уравнения.
Графиком является парабола, ветви направлены вверх.
Найдем корни уравнения:
Схематически изобразим график (Рис. 2).
С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.
У уравнения бесчисленное множество решений, т.е. бесчисленное множество пар , удовлетворяющих уравнению, но все А каким может быть x? Любым!
Если мы зададим любое x, то получим точку
Решением исходного уравнения является множество пар
4.
 График уравнения – гипербола
График уравнения – гипербола
3. Построить график уравнения
Необходимо выразить y. Рассмотрим два варианта.
Графиком функции является гипербола, функция не определена при
Функция убывающая.
Если
Если мы возьмем точку с абсциссой , то ее ордината будет равна
Решением исходного уравнения является множество пар
Построенную гиперболу можно сдвигать относительно осей координат.
Например, график функции – тоже гипербола – будет сдвинут на единицу вверх по оси ординат.
5. График уравнения окружности
4. Уравнение окружности
Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке радиус равен R (Рис. 4).
Рассмотрим конкретные примеры.
a.
Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:
– получили уравнение окружности с центром в .
Построим график уравнения (Рис. 5).
b. Построить график уравнения
Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.
График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т.е. двух прямых.
Построим его (Рис. 6).
Построим график функции Прямая будет проходить через точку (0; -1). Но как она пройдет – будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).
Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.
Координаты всех точек двух построенных прямых и являются решением уравнения.
6. Вывод
Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.
График кубической функции. Построить кубическую функцию. Кубическая парабола график.
- Альфашкола
- Статьи 3 + k\).
- Если \(k > 0\), то график сдвигается на \(k\) единиц вверх; если \(k < 0\), то график сдвигается на \(k\) единиц вниз.
- Если \(h > 0\),то график сдвигается на \(h\) единиц вправо; если \(h < 0\), то график смещается на \(h\) единиц влево.
- Если \(a < 0\), график переворачивается.
- Задачи на движение
- Подобие треугольников
- Как легко разделить на 0,5
- ЕГЭ по математике, базовый уровень.
 Планиметрия. Прямоугольный треугольник (вариант 4)
Планиметрия. Прямоугольный треугольник (вариант 4) - Как не умереть от скуки в детском лагере?
- Неуверенный ребенок: что мешает его самооценке и как помочь повысить
- Как объяснить ребёнку, что нет денег на дорогой подарок?
- Что такое парабола?
- Уравнение параболы в вершинной форме
- Фокус параболы и директриса
- Как использовать калькулятор уравнения параболы: пример калькулятор параболы, чтобы быть идеальным инструментом для вас. Он не только предоставит вам уравнение параболы как в стандартной форме , так и в форме вершины , но также вычислить для вас вершину параболы, фокус и директрису.

Что такое парабола?
источник: Wikimedia Парабола — это U-образная симметричная кривая . Его основное свойство состоит в том, что каждая точка, лежащая на параболе, равноудалена как от некоторой точки, называемой фокусом параболы, так и от прямой, называемой ее директрисой. Это также кривая, соответствующая квадратным уравнениям.
Ось симметрии параболы всегда перпендикулярна директрисе и проходит через точку фокусировки. Вершина параболы — это точка, в которой парабола делает самый крутой поворот; он находится на полпути между фокусом и директрисой.
Реальным примером параболы является траектория, прочерченная объектом, движущимся снарядом.
Уравнение параболы в форме вершины
Стандартная форма квадратного уравнения:
y = ax² + bx + c. Вы можете использовать этот калькулятор вершин, чтобы преобразовать это уравнение в вершинную форму, которая позволит вам найти важные точки параболы — ее вершину и фокус.
Уравнение параболы в его вершинной форме имеет вид
y = a(x - h)² + k, где:- a — То же, что и коэффициент a в стандартной форме;
- h — x-координата вершины параболы; и
- k — координата y вершины параболы.
Вы можете рассчитать значения h и k из следующих уравнений:
h = - b/(2a)k = c - b²/(4a)Фокус и директриса параболы
Калькулятор формы вершины параболы также находит фокус и директрису параболы. Все, что вам нужно сделать, это использовать следующие уравнения:
- Координата x фокуса:
x₀ = - b/(2a) - Координата Y фокуса:
y₀ = c - (b² - 1)/(4a); и - Уравнение директрисы:
y = c - (b² + 1)/(4a).
Как пользоваться калькулятором уравнения параболы: пример
Введите коэффициенты a, b и c стандартной формы вашего квадратного уравнения.
 Предположим, что уравнение
Предположим, что уравнение y = 2x² + 3x - 4, что означает, что a = 2, b = 3 и c = -4.Рассчитайте координаты вершины, используя приведенные выше формулы:
ч = - б/(2а) = -3/4 = -0,75k = c - b²/(4a) = -4 - 9/8 = -5,125Найдите координаты фокуса параболы. Координата x фокуса такая же, как у вершины (x₀ = -0,75), а координата y:
y₀ = c - (b² - 1)/(4a) = -4 - (9-1)/8 = -5Найдите директрису параболы. Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение:
y = c - (b² + 1)/(4a) = -4 - (9+1)/8 = -5,25
Если вы хотите узнать больше о понятиях координатной геометрии, мы рекомендуем проверить калькулятор средней скорости изменения и калькулятор прямой кишки.
Часто задаваемые вопросы
Что такое парабола?
Парабола представляет собой симметричную U-образную кривую, каждая точка которой равноудалена от директрисы и фокуса.

Как определить параболу?
Парабола определяется уравнением, которому удовлетворяет каждая точка кривой. Математически
y = ax² + bx + c.Как вычислить вершину параболы?
Для вычисления вершины параболы, заданной координатами (x, y):
Найдите координату x, используя формулу оси симметрии:
х₀ = - б/(2а)Найдите координату y, используя уравнение параболы:
y₀ = c - (b² - 1)/(4a)
Как рассчитать фокус параболы?
Чтобы вычислить фокус параболы, заданной координатами (x, y):
- Найдите координату y по формуле
y = c - (b² + 1)/(4a) - Найдите координату x, используя уравнение параболы.
Богна Шик и Войцех Сас, доктор философии
Что вводить?
Ориентация по параболе
Стандартная форма: y = ax² + bx + c Результаты
Показать результаты с использованием дробей?
Ознакомьтесь с 38 похожими калькуляторами координатной геометрии 📈
Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35
Калькулятор гиперболы — eMathHelp
Этот калькулятор найдет либо уравнение гиперболы по заданным параметрам, либо центр, фокусы, вершины, ко-вершины, длину (полу)большой оси, (полу)длину малой оси, латеральную прямую кишку, длину латеральной прямой кишки, фокусный параметр, фокусное расстояние, эксцентриситет, линейный эксцентриситет, директрисы, асимптоты, пересечения по оси x, пересечения по оси y, домен и диапазон введенной гиперболы.
 Кроме того, он будет отображать гиперболу. Шаги доступны.
Кроме того, он будет отображать гиперболу. Шаги доступны.Связанные калькуляторы: Калькулятор параболы, Калькулятор окружности, Калькулятор эллипса, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
Ваш ввод
Найти центр, фокусы, вершины, ко-вершины, длину большой оси, длину большой полуоси, длину малой оси, длину малой полуоси, латеральную прямую кишку, длину латеральной прямой кишки, фокальную параметр, фокусное расстояние, эксцентриситет, линейный эксцентриситет, директрисы, асимптоты, пересечения по оси x, пересечения по оси y, домен и диапазон гиперболы $$$x^{2} — 4 y^{2} = 36$$$.
 9{2}} = 3 \sqrt{5}$$$.
9{2}} = 3 \sqrt{5}$$$.Эксцентриситет равен $$$e = \frac{c}{a} = \frac{\sqrt{5}}{2}$$$.
Первый фокус $$$\left(h — c, k\right) = \left(- 3 \sqrt{5}, 0\right)$$$.
Второй фокус $$$\left(h + c, k\right) = \left(3 \sqrt{5}, 0\right)$$$.
Первая вершина $$$\left(h — a, k\right) = \left(-6, 0\right)$$$.
Вторая вершина $$$\left(h + a, k\right) = \left(6, 0\right)$$$.
Первая ковершина $$$\left(h, k — b\right) = \left(0, -3\right)$$$. 9{2}}{c} = \frac{12 \sqrt{5}}{5}$$$.
Первая асимптота: $$$y = — \frac{b}{a} \left(x — h\right) + k = — \frac{x}{2}$$$.
Вторая асимптота: $$$y = \frac{b}{a} \left(x — h\right) + k = \frac{x}{2}$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-6, 0\right)$$$, $$$\left(6, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов).
 9{2}}{4}$$$А.
9{2}}{4}$$$А. График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Первый фокус: $$$\влево(- 3 \sqrt{5}, 0\вправо)\приблизительно \влево(-6,708203932499369, 0\вправо)$$$A.
Второй фокус: $$$\влево(3\sqrt{5}, 0\вправо)\приблизительно \влево(6,708203932499369, 0\вправо)$$$A.
Первая вершина: $$$\left(-6, 0\right)$$$A.
Вторая вершина: $$$\left(6, 0\right)$$$A.
Первая ковершина: $$$\left(0, -3\right)$$$A.
Вторая ковершина: $$$\left(0, 3\right)$$$A.
Длина по главной (поперечной) оси: $$$12$$$A.
Длина большой полуоси: $$$6$$$A.
Длина малой (сопряженной) оси: $$$6$$$A.
Длина малой полуоси: $$$3$$$A.
Первая широкая прямая кишка: $$$x = — 3 \sqrt{5}\приблизительно -6,708203932499369$$$A.

Вторая широкая прямая кишка: $$$x = 3 \sqrt{5}\приблизительно 6,708203932499369$$$A.
Концы первой широкой прямой кишки: $$$\left(- 3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, -1,5\right) $$$, $$$\left(- 3 \sqrt{5}, \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, 1,5\right)$$$A.
Концы второй широкой прямой кишки: $$$\left(3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(6.708203932499369, -1.5\right)$$ $, $$$\left(3\sqrt{5}, \frac{3}{2}\right)\приблизительно \left(6.708203932499369, 1,5\справа)$$$А.
Длина латерального отдела прямой кишки: $$$3$$$A.
Параметр фокуса: $$$\frac{3 \sqrt{5}}{5}\приблизительно 1,341640786499874$$$A.
Эксцентриситет: $$$\frac{\sqrt{5}}{2}\приблизительно 1,118033988749895$$$A.
Линейный эксцентриситет: $$$3 \sqrt{5}\приблизительно 6,708203932499369$$$A.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Александр Николаевич Мельничук
Репетитор по математике
Стаж (лет)
Образование:
Приднестровский государственный университет им. Т.Г. Шевченко
Т.Г. Шевченко
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Подготовка к ОГЭ, ЕГЭ, любая проверочная работа по математике и физике, контрольные работы, экзамены.
Преподаю математику, физику школьникам на школьном уровне, знаком со многими форматами экзаменов по физике, в том числе ЕГЭ. Ученики, с которыми я работаю поступают на бюджет в разные вузы своих городов, а также Москвы и Санкт-Петербурга. С ЕГЭ по математике знаком хорошо. Я практикую разные методы преподавания в зависимости от того на каком уровне знаний находится ученик, что ученик хочет вспомнить, повторить или закрепить. Стараюсь понятно и доступно излагать не всегда простой материал.
Мне нравится объяснять материал, показывать как можно применить полученные знания на практике при решении бытовых, практических задач.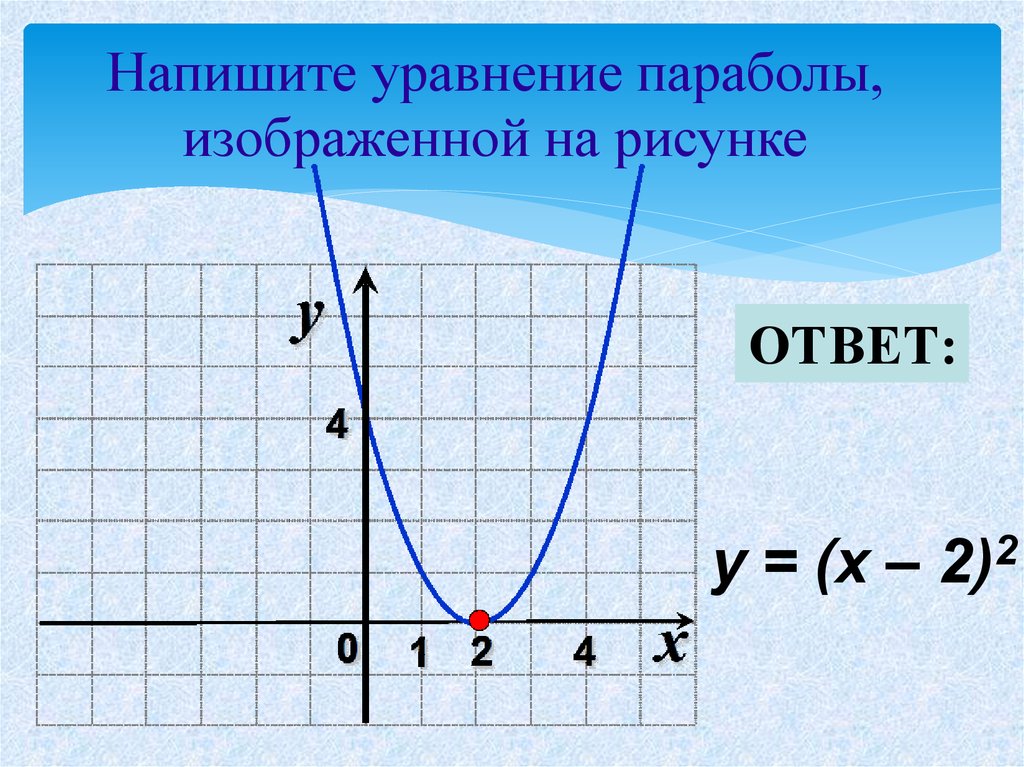
Денис Александрович Косвинцев
Репетитор по математике
Стаж (лет)
Образование:
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Курс информатики с 7 по 11 класс. Подготовка к ОГЭ и ЕГЭ (на не Microsoft-ПО). Практические занятия по программированию на Python, Pascal, C или Java и в офисном пакете LibreOffice. Индивидуальные программы обучения по выборочным темам.
Владислав Александрович Тарапатин
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 5-11 классы. Подготовка к ОГЭ, ЕГЭ, ВПР по русскому языку. Повышение общего уровня знаний. Всё обсудим и поможем. Если ученик будет выполнять то, что от него потребуется, хороший результат ему обеспечен.
Похожие статьи
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Калькулятор параболы
Создано Богной Шик и Войцехом Сас, доктором философии
Отзыв Стивена Вудинга и Джека Боуотера
Последнее обновление: 18 января 2022 г.
Содержание: Планиметрия. Прямоугольный треугольник (вариант 4)
Планиметрия. Прямоугольный треугольник (вариант 4)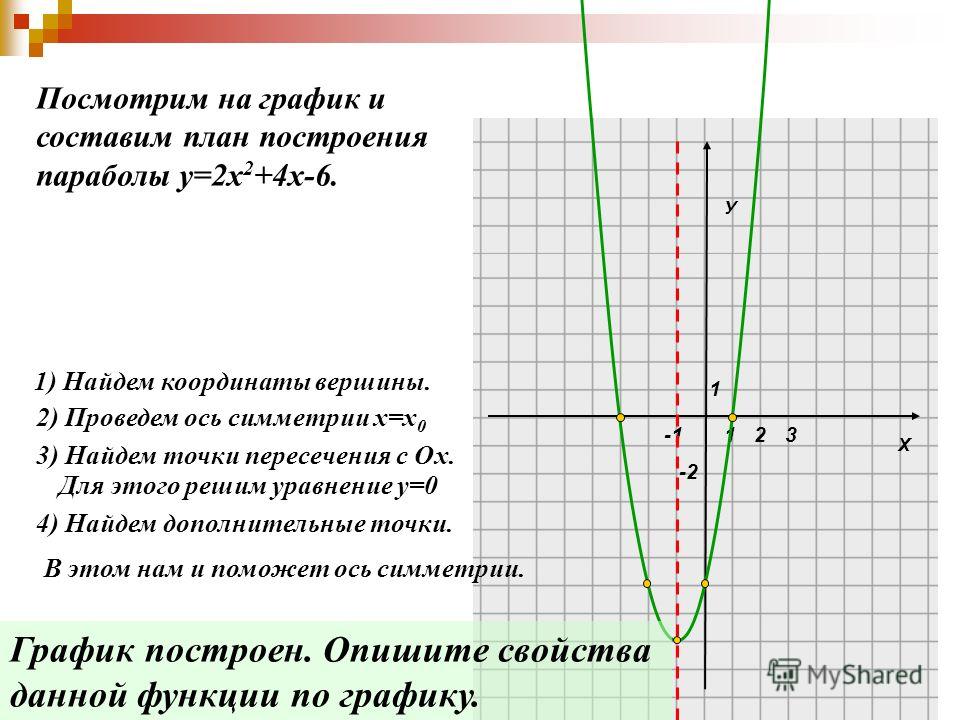

 Предположим, что уравнение
Предположим, что уравнение 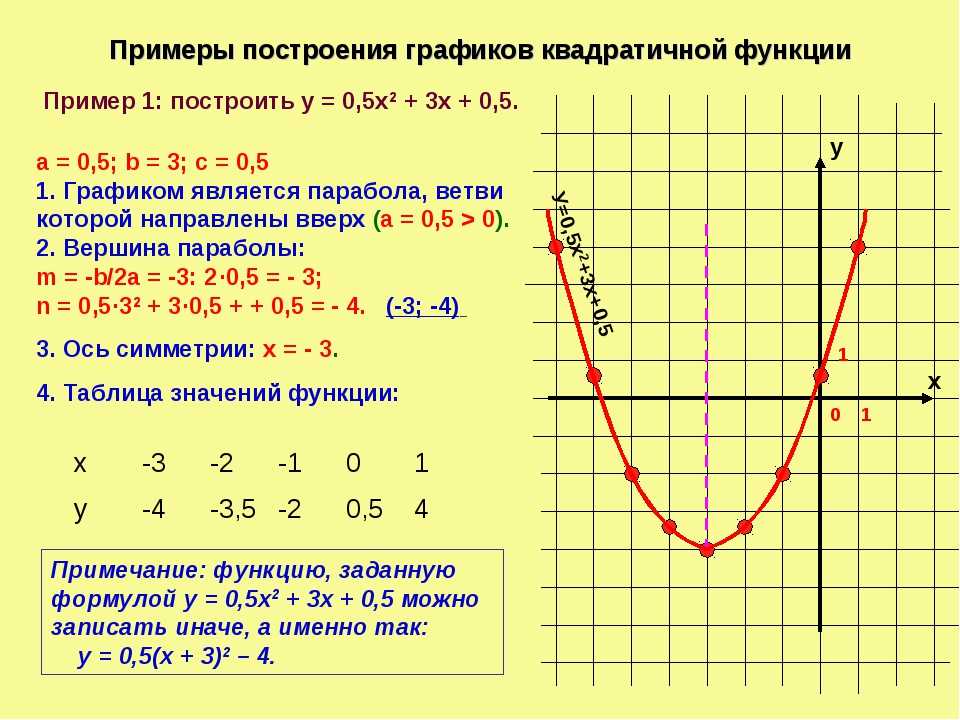
 Кроме того, он будет отображать гиперболу. Шаги доступны.
Кроме того, он будет отображать гиперболу. Шаги доступны. 9{2}} = 3 \sqrt{5}$$$.
9{2}} = 3 \sqrt{5}$$$. 9{2}}{4}$$$А.
9{2}}{4}$$$А. 
Ваш комментарий будет первым