Как только вы введете правильное квадратичное выражение, вы можете нажать на кнопку «Вычислить», и на экране появится окно график функции будет сгенерирован, показывая этапы вычисления вершина параболы и Ось симметрии а также .
Квадратичные функции занимают главенствующее место в базовой алгебре, поскольку они часто используются в контексте решения задачи
квадратные уравнения
и прикладные проблемы.
Как построить график квадратичной формы?
Построить график квадратичной функции просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы. Но все же парабол бесконечно много. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.
Шаги для нахождения графика квадратичной функции
- Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите ее
- Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c.
Обратите внимание, что a не может быть нулем - Шаг 3: Если a > 0, вы знаете, что график будет параболой, раскрывающейся вверх, тогда как если a < 0, вы знаете, что график будет параболой, раскрывающейся вниз
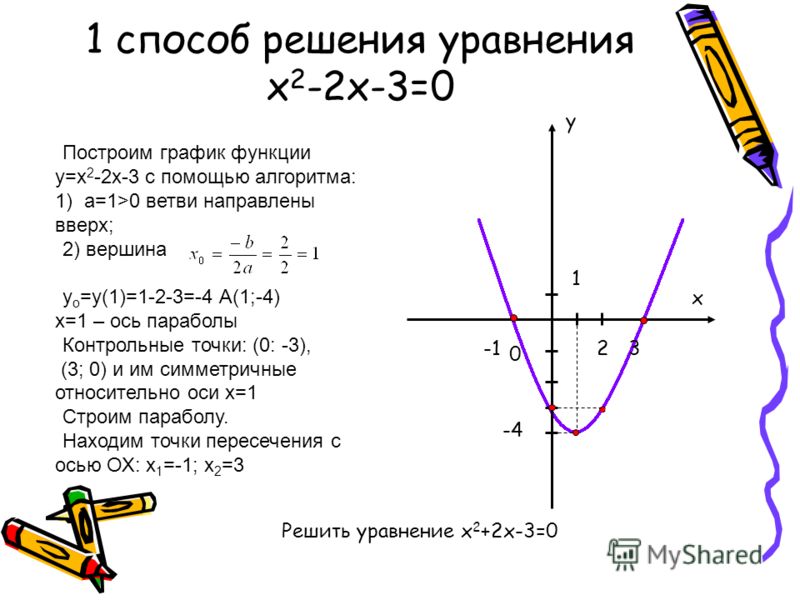
- Шаг 5: Обратите внимание, что x* = -b/(2a) — координата x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c — координата y вершины
Обратите внимание, что a не может быть нулем Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графике.
2 + bx + c = 0 \]
вы получите корни квадратного уравнения, а когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.
Особый случай имеет место, когда корни комплексные, в этом случае парабола не пересекает ось x.
Типы квадратичных графиков
Как мы уже говорили, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a < 0, параболы будут раскрываться вверх или вниз соответственно.
Другое различие типов парабол может быть для тех, которые «центрированы» (т.е
вершина
это происхождение), и те, которые не являются таковыми.
2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]
Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59}{16}\). Это означает, что точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).
Графически получается следующее:
Больше квадратичных калькуляторов
Большинство всех приложений в базовой алгебре основаны на решении некоторого рода
Квадратное уравнение
, поэтому у него есть сильная педагогическая цель узнать об этом.
квадратичная формула является одним из самых печально известных учебных предметов в математике. Дело не в том, что кубические или квартовые уравнения не существуют, а в том, что квадратные уравнения это те, которые мы можем легко объяснить.
Уравнение прямой по двум точкам
УчебаМатематика
Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой.
На этой странице вы найдете два калькулятора, которые строят уравнение прямой по координатам двух точек, принадлежащих этой прямой.
Первый калькулятор находит уравнение прямой с угловым коэффициентом, то есть уравнение в форме . Также он строит график и отдельно выводит угловой коэффициент и значение y в месте пересечения прямой с осью ординат.
Второй калькулятор находит параметрические уравнения прямой, то есть систему уравнений вида . Он также строит график и отдельно выводит направляющий вектор.
Формулы расчета можно найти под калькуляторами.
Уравнение прямой с угловым коэффициентом по двум точкам
Первая точка
Вторая точка
Уравнение прямой
Угловой коэффициент
Значение y в точке пересечения с осью ординат
Точность вычисления
Знаков после запятой: 2
Параметрическое уравнение прямой
Первая точка
Вторая точка
Параметрическое уравнение для x
Параметрическое уравнение для y
Направляющий вектор
Точность вычисления
Знаков после запятой: 2
Уравнение прямой с угловым коэффициентом
Найдем уравнение прямой с угловым коэффициентом по двум известным точкам и .
Нам надо найти угловой коэффициент a и y координату точки пересечения прямой с осью ординат b.
Мы можем составить следующие уравнения для двух точек относительно a и b
Вычитаем первое из второго
Откуда
b можно найти как
Таким образом, как только мы нашли а, для расчета b достаточно только подставить значения или в выражение выше.
Параметрическое уравнение прямой
Найдем параметрическое уравнение прямой по двум известным точкам и .
Нам надо найти компоненты направляющего вектора.
Этот вектор описывает величину и направление воображаемого движения по прямой от первой до второй точки.
Имея направляющий вектор, легко записать параметрические уравнения прямой
Обратите внимание, что если , то и если , то
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнения прямой, проходящей через две точки в трехмерном пространстве
- • Нахождение уравнений прямой, заданной пересечением двух плоскостей
- • Условия параллельности и перпендикулярности прямых на плоскости
- • Уравнение окружности по заданному центру и радиусу в различных формах
- • Решение системы двух уравнений первой степени с двумя неизвестными
- • Раздел: Математика ( 269 калькуляторов )
#математика #Прямая Математика Математикая направляющий вектор параметрическое уравнение параметрическое уравнение прямой прямая угловой коэффициент уравнение уравнение прямой уравнение прямой с угловым коэффициентом
PLANETCALC, Уравнение прямой по двум точкам
Timur2020-11-03 14:19:37
Калькулятор гиперболы — eMathHelp
Этот калькулятор найдет либо уравнение гиперболы по заданным параметрам, либо центр, фокусы, вершины, ко-вершины, (полу)длину большой оси, (полу)длину малой оси, латеральную прямую, длина латерального отдела прямой кишки (ширина фокуса), параметр фокуса, эксцентриситет, линейный эксцентриситет (фокусное расстояние), директрисы, асимптоты, точки пересечения x, точки пересечения y, домен и диапазон введенной гиперболы.
Связанные калькуляторы: Калькулятор параболы, Калькулятор окружности, Калькулятор эллипса, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже. 9{2}} = 3 \sqrt{5}$$$.
Эксцентриситет равен $$$e = \frac{c}{a} = \frac{\sqrt{5}}{2}$$$.
Первый фокус $$$\left(h — c, k\right) = \left(- 3 \sqrt{5}, 0\right)$$$.
Второй фокус $$$\left(h + c, k\right) = \left(3 \sqrt{5}, 0\right)$$$.
Первая вершина $$$\left(h — a, k\right) = \left(-6, 0\right)$$$.
Вторая вершина $$$\left(h + a, k\right) = \left(6, 0\right)$$$.
Первая ковершина $$$\left(h, k — b\right) = \left(0, -3\right)$$$. 9{2}}{c} = \frac{12 \sqrt{5}}{5}$$$.
Первая асимптота: $$$y = — \frac{b}{a} \left(x — h\right) + k = — \frac{x}{2}$$$.
Вторая асимптота: $$$y = \frac{b}{a} \left(x — h\right) + k = \frac{x}{2}$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-6, 0\right)$$$, $$$\left(6, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов). 9{2}}{4}$$$А.
График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Первый фокус: $$$\влево(- 3 \sqrt{5}, 0\вправо)\приблизительно \влево(-6,708203932499369, 0\вправо)$$$A.
Второй фокус: $$$\влево(3\sqrt{5}, 0\вправо)\приблизительно \влево(6,708203932499369, 0\вправо)$$$A.
Первая вершина: $$$\left(-6, 0\right)$$$A.
Вторая вершина: $$$\left(6, 0\right)$$$A.
Первая ковершина: $$$\left(0, -3\right)$$$A.
Вторая ковершина: $$$\left(0, 3\right)$$$A.
Длина по главной (поперечной) оси: $$$12$$$A.
Длина большой полуоси: $$$6$$$A.
Длина малой (сопряженной) оси: $$$6$$$A.
Длина малой полуоси: $$$3$$$A.
Первая широкая прямая кишка: $$$x = — 3 \sqrt{5}\приблизительно -6,708203932499369$$$A.
Вторая широкая прямая кишка: $$$x = 3 \sqrt{5}\приблизительно 6,708203932499369$$$A.
Концы первой широкой прямой кишки: $$$\left(- 3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, -1,5\right) $$$, $$$\left(- 3 \sqrt{5}, \frac{3}{2}\right)\приблизительно \left(-6,708203932499369, 1,5\right)$$$A.
Концы второй широкой прямой кишки: $$$\left(3 \sqrt{5}, — \frac{3}{2}\right)\приблизительно \left(6.708203932499369, -1.5\right)$$ $, $$$\left(3\sqrt{5}, \frac{3}{2}\right)\приблизительно \left(6.708203932499369, 1,5\справа)$$$А.
Длина латерального отдела прямой кишки (ширина фокуса): $$$3$$$A.
Параметр фокуса: $$$\frac{3 \sqrt{5}}{5}\приблизительно 1,341640786499874$$$A.
Эксцентриситет: $$$\frac{\sqrt{5}}{2}\приблизительно 1,118033988749895$$$A.
Линейный эксцентриситет (фокусное расстояние): $$$3 \sqrt{5}\приблизительно 6,708203932499369$$$A.
Первая направляющая: $$$x = — \frac{12 \sqrt{5}}{5}\приблизительно -5,366563145999495$$$А.
Вторая направляющая: $$$x = \frac{12 \sqrt{5}}{5}\примерно 5,366563145999495$$$A.
Первая асимптота: $$$y = — \frac{x}{2} = — 0,5 x$$$A.
Вторая асимптота: $$$y = \frac{x}{2} = 0,5 x$$$A.
x-отрезки: $$$\left(-6, 0\right)$$$, $$$\left(6, 0\right)$$$A.
y-пересечения: нет y-пересечения.
Домен: $$$\left(-\infty, -6\right] \cup \left[6, \infty\right)$$$A.
Диапазон: $$$\left(-\infty, \infty\right)$$$A.
Калькулятор эллипса — eMathHelp
Этот калькулятор найдет либо уравнение эллипса по заданным параметрам, либо центр, фокусы, вершины (большие вершины), ко-вершины (второстепенные вершины), (полу)длину большой оси, (полу)длина малой оси, площадь, окружность, латеральная прямая мышца, длина латеральной прямой кишки (ширина фокуса), фокальный параметр, эксцентриситет, линейный эксцентриситет (фокусное расстояние), директрисы, точки пересечения по оси X, точки пересечения по оси Y, домен и диапазон введенного эллипса. Кроме того, он будет отображать эллипс. Шаги доступны.
Связанные калькуляторы: Калькулятор параболы, Калькулятор окружности, Калькулятор гиперболы, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже. 9{2}} = \sqrt{5}$$$.
Эксцентриситет равен $$$e = \frac{c}{a} = \frac{\sqrt{5}}{3}$$$.
Первый фокус $$$\left(h — c, k\right) = \left(- \sqrt{5}, 0\right)$$$.
Второй фокус $$$\left(h + c, k\right) = \left(\sqrt{5}, 0\right)$$$.
Первая вершина $$$\left(h — a, k\right) = \left(-3, 0\right)$$$.
Вторая вершина $$$\left(h + a, k\right) = \left(3, 0\right)$$$.
Первая ковершина $$$\left(h, k — b\right) = \left(0, -2\right)$$$. 9{2}}{c} = \frac{9 \sqrt{5}}{5}$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-3, 0\right)$$$, $$$\left(3, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов).
y-отрезки: $$$\left(0, -2\right)$$$, $$$\left(0, 2\right)$$$
Домен $$$\left[h — а, ч + а\вправо] = \влево[-3, 3\вправо]$$$. 9{2}}{9}$$$А.
График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Первый фокус: $$$\влево(-\sqrt{5}, 0\вправо)\приблизительно \влево(-2,23606797749979, 0\вправо)$$$A.
Второй фокус: $$$\left(\sqrt{5}, 0\right)\приблизительно \left(2.23606797749979, 0\right)$$$A.
Первая вершина: $$$\left(-3, 0\right)$$$A.
Вторая вершина: $$$\left(3, 0\right)$$$A.
Первая ковершина: $$$\left(0, -2\right)$$$A.
Вторая ковершина: $$$\left(0, 2\right)$$$A.
Длина главной оси: $$$6$$$A.
Длина большой полуоси: $$$3$$$A.
Длина малой оси: $$$4$$$A.
Длина малой полуоси: $$$2$$$A.
Площадь: $$$6 \pi\ок. 18,849555921538759$$$A.
Окружность: $$$12 E\left(\frac{5}{9}\справа)\приблизительно 15,86543958929059$$$A.
Первая широкая прямая кишка: $$$x = — \sqrt{5}\приблизительно -2,23606797749979$$$A.
Вторая широкая прямая кишка: $$$x = \sqrt{5}\приблизительно 2,23606797749979$$$A.
Концы первой широкой прямой кишки: $$$\left(- \sqrt{5}, — \frac{4}{3}\right)\приблизительно \left(-2.23606797749979, -1.
3333333333333333\right)$ $$, $$$\left(-\sqrt{5}, \frac{4}{3}\right)\приблизительно \left(-2,23606797749979, 1,333333333333333\right)$$$A.
Конечные точки второй широкой прямой кишки: $$$\left(\sqrt{5}, — \frac{4}{3}\right)\приблизительно \left(2.23606797749979, -1.333333333333333\right)$$$, $$$\left(\sqrt{5}, \frac{4}{3}\right)\приблизительно \left(2.23606797749979, 1.3333333333333333\right)$$$A.
Длина латерального отдела прямой кишки (ширина фокуса): $$$\frac{8}{3}\приблизительно 2,666666666666667$$$A.
Параметр фокуса: $$$\frac{4 \sqrt{5}}{5}\приблизительно 1,788854381999832$$$A.
Эксцентриситет: $$$\frac{\sqrt{5}}{3}\приблизительно 0,74535599249993$$$А.
Линейный эксцентриситет (фокусное расстояние): $$$\sqrt{5}\приблизительно 2,23606797749979$$$A.
Первая направляющая: $$$x = — \frac{9 \sqrt{5}}{5}\приблизительно -4,024922359499621$$$A.
Ваш комментарий будет первым