 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Кривые второго порядка. Эллипс: формулы и задачи
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Определение эллипса. Эллипсом называется множество
всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами,
есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и
(- a, О), а ось ординат — в точках (b, О) и
(- b, О). Эти четыре точки называются вершинами эллипса. Отрезок
между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат —
малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b, то уравнение эллипса принимает вид . Это уравнение окружности радиуса a, а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a, если сжать её в a/b раз вдоль оси Oy.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса,
если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:
.Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
Число
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13. Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Окружность, круг, сегмент, сектор. Формулы и свойства
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
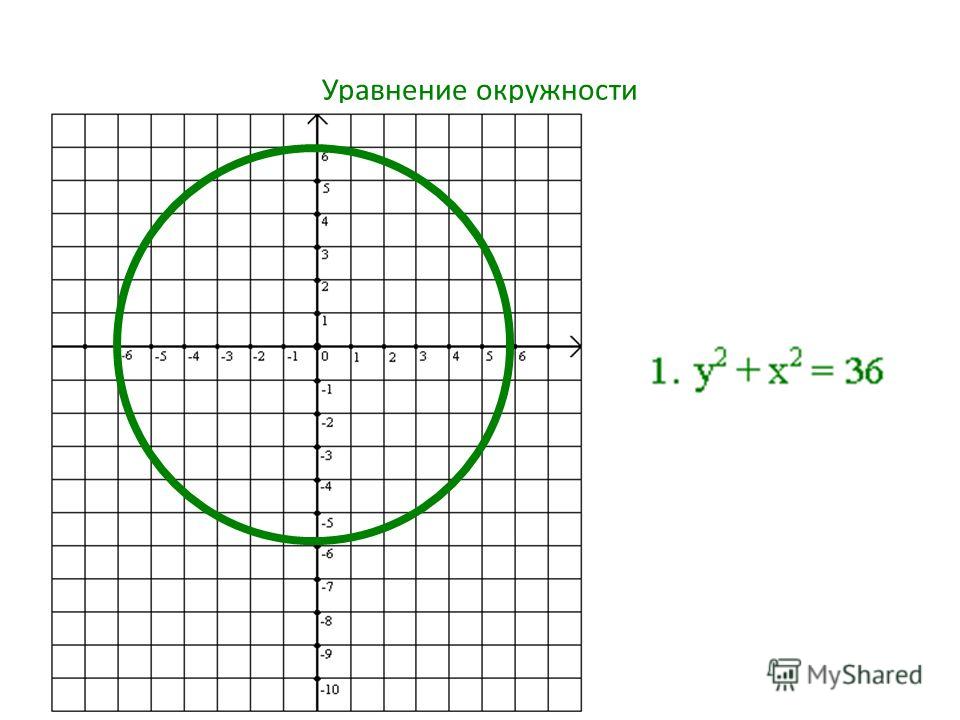
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
1. Длина хорды через центральный угол и радиус:AB = 2r sin α2
2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
1. Все вписанные углы, которые опираются на одну дугу — равны. 2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ.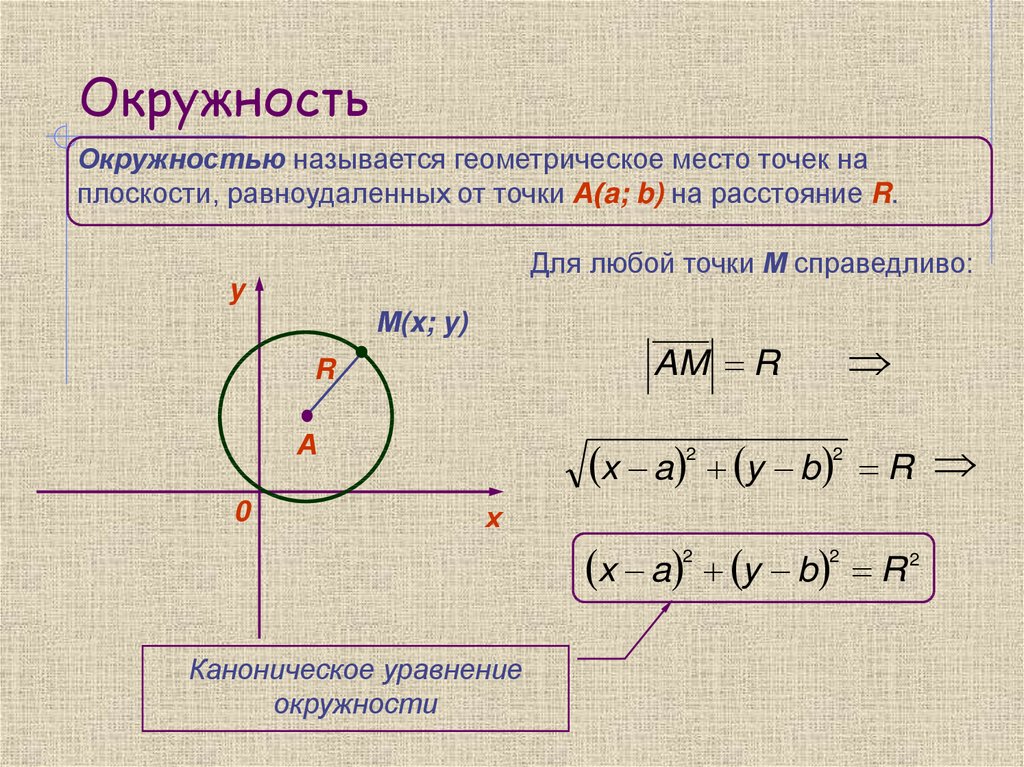 Эти системы:
Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
(2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
ОСОБЫЕ РЕШЕНИЯ:
1
Отметим на окружности точки, ордината которых равна 0:
2.
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.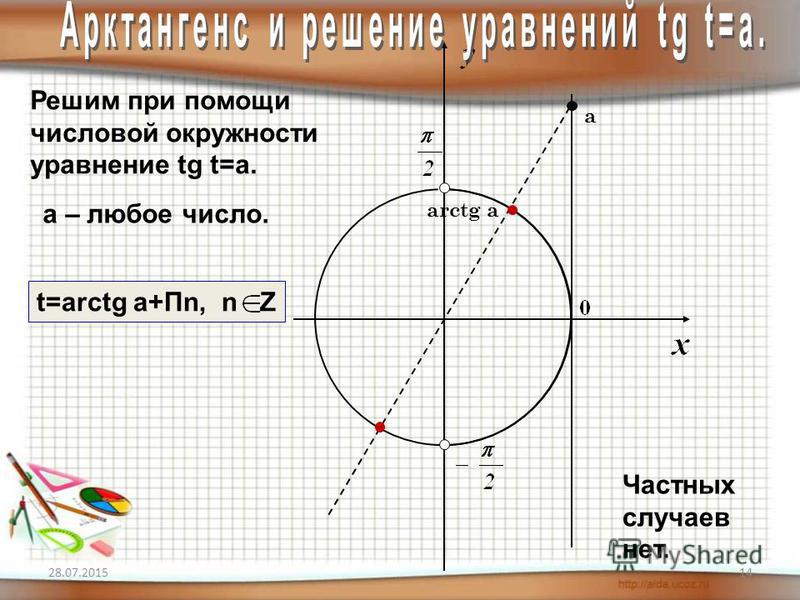
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
Найти центр и радиус окружности
Если окружность задана уравнением вида
найти центр (a;b) и радиус R такой окружности несложно.
Примеры.
Определить по уравнению окружности координаты её центра и радиуса:
Решение:
a=3, b=7, R²=4.
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
a=0, b=-3, R²=9.
Центр окружности — (0;-3), радиус R=3.
a=6, b=0, R²=5.
Центр — в точке (6;0), радиус R=√5.
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
Отсюда
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.
Примеры.
Найти координаты центра и радиус окружности:
Решение:
Группируем слагаемые
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
Аналогично
Таким образом,
Центром этой окружности является точка (-5;3), радиус R=7.
Центр окружности — точка (2,5;0), радиус R=1,5.
Разделим обе части уравнения на 3:
Далее — аналогично
Центр этой окружности лежит в точке
Уравнение плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т. д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через три точки
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M1, M2, M3 тогда и тольно тогда, когда векторы M1M2, M1M3 и компланарны. Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M1M2, M1M3, M1M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:
Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M1M2, M1M3, M1M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:
Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M1, M2, M3:
Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).
Решение.
Уравнение плоскости, проходящей через точки A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3) имеет следующий вид:
Подставляя координаты точек A, B, C в (1), получим:
Упростим:
Разложим определитель по первому столбцу:
Упростим выражение:
или
Ответ:
Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:
Уравнение плоскости, проходящей через одну точку и имеющий нормаль
nПример 2. Построить плоскость, проходящую через точку M0(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).
Построить плоскость, проходящую через точку M0(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).
Решение.
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормаль n(A, B, C) имеет следующий вид:
Подставляя координаты векторов M0 и n в (2), получим:
или
2 \ cdot \ pi $$A = площадь
C = окружность
r = радиус
d = диаметр
На диаграмме справа показано, когда использовать каждую из этих формул. 2 = 6,37 \\
& r = \ sqrt {6.37} \\
& r = 2,52
\ end {выровнен} $$
2 = 6,37 \\
& r = \ sqrt {6.37} \\
& r = 2,52
\ end {выровнен} $$
Теперь найдем окружность по формуле $ \ color {blue} {C = 2r \ pi} $.
$$ \ begin {выровнено} & \ color {синий} {C = 2 r \ pi} \\ & C = 2 \ cdot 2.52 \ cdot 3.14 \\ & C = 15,82 \ end {выровнен} $$ Калькулятор кругов— eMathHelp
Этот калькулятор найдет либо уравнение окружности по заданным параметрам, либо центр, радиус, диаметр, площадь, окружность (периметр), эксцентриситет, линейный эксцентриситет, точки пересечения по оси x, точки пересечения по оси Y, область значений и диапазон введенных значений. круг.3 (х).
 -1 (x)
-1 (x)Калькулятор уравнения круга
Независимо от вашего знания геометрии круга, уравнение круга может заставить вашу голову кружиться.В таком случае не волнуйтесь! Это стандартное уравнение калькулятора круга поможет вам определить радиус и координаты центра круга в мгновение ока. Если вам интересно, как найти уравнение круга, прокрутите вниз, и вы найдете объяснение формулы.
Если геометрическая форма, которую вы пытаетесь проанализировать, выглядит немного сжатой, вероятно, это эллипс. В таком случае сразу переходите к нашему калькулятору эллипсов!
Что такое стандартное уравнение окружности?
Стандартное уравнение окружности — это способ описать все точки, лежащие на окружности, всего одной формулой:
(x - A) ² + (y - B) ² = r²
(x, y) — координаты любой точки, лежащей на окружности окружности. Это означает, что пока вы знаете все константы, вы можете ввести любое значение
Это означает, что пока вы знаете все константы, вы можете ввести любое значение x , чтобы вычислить координаты любой произвольной точки на окружности.
(A, B) — координаты центральной точки . Просто будьте осторожны со знаками + и — здесь; например, окружность с уравнением вида (x - 3) ² + (y + 3) ² = 5² будет иметь центр в (3, -3) .
r² — это радиус окружности, возведенный в степень двойки.Чтобы найти радиус, просто извлеките квадратный корень из этого значения.
Наш калькулятор с уравнением круга находит не только эти значения, но также диаметр, длину окружности и площадь круга — и все это для экономии вашего времени!
Параметрическое уравнение окружности
Уравнение круга можно определить по-разному; не только в стандартной форме, показанной выше. Круг также можно описать как геометрическое место всех точек, удовлетворяющих уравнениям:
x = r * cos (α)
y = r * sin (α)
где
(x, y) — координаты любой точки на окружности, как и раньше;
r — радиус окружности, а
α — это параметр — угол, образуемый точкой в центре окружности.
Если вы переместите центр круга в координаты (A, B) , вы просто добавите их к координатам x и y, чтобы получить общее параметрическое уравнение круга:
x = A + r * cos (α)
y = B + r * sin (α)
Как и выше, будьте осторожны со знаками центральной точки.
Стандартное уравнение параметрического уравнения окружности
Чтобы продемонстрировать, что эти две формы формулы круга эквивалентны, давайте сделаем преобразование между ними:
- Исходя из параметрического уравнения, мы знаем, что
x = r * cos (t) , поэтому cos (t) = x / r
y = r * sin (t) , поэтому sin (t) = y / r
- Возьмем известное тригонометрическое тождество Пифагора:
sin² (t) + cos² (t) = 1
- Объедините тождество с параметрическими уравнениями:
(y / r) ² + (x / r) ² = 1
- Затем уберем круглые скобки:
y² / r² + x² / r² = 1
- И, наконец, умножьте на r² (пусть r = 1) и расположите элементы в правильном порядке.

x² + y² = 1
Вот и мы! Это стандартное уравнение круга.
Как найти уравнение окружности?
Хорошо, вы узнали о различных уравнениях круга. Но откуда они взялись? Давай выясним!
- Выберите центр
O = (A, B)вашего круга. Не выбирайте его как начало системы координат. - Нарисуйте круг с выбранным радиусом
r. - Укажите любую точку на окружности. Предположим, что координаты этой точки равны
P = (x, y). - Угол POC равен α.
Отлично, у нас есть все необходимые данные. Теперь нам нужно использовать только один геометрический закон или базовый элемент тригонометрии, чтобы связать данные значения вместе:
Используйте формулу расстояния :
√ [(x₂ - x₁) ² + (y₂ - y₁) ²] = r, поэтому√ [(x - A) ² + (y - B) ²] = rи возведите полученную формулу в квадрат, чтобы получить стандартное уравнение круга:(x - A) ² + (y - B) ² = r²Используйте теорему Пифагора :
r— гипотенуза прямоугольного треугольника POC, поэтому из теоремы Пифагора мы можем написать:| OC | ² + | CP | ² = r²Также мы знаем, что:
| OC | = | x - A || CP | = | y - B |Возвращаясь к первому уравнению, получаем:
| x - A | ² + | y - B | ² = r²как a² = (−a) ², приведенное выше уравнение работает для каждого квадранта, а не только для первого. Тогда уравнение можно упростить до стандартной формулы:
Тогда уравнение можно упростить до стандартной формулы:(x - A) ² + (y - B) ² = r²Использовать тригонометрию :
выразить стороны треугольника POC с помощью функций синуса и косинуса:
cos (α) = OC / r, поэтомуOC = r * cos (α)sin (α) = CP / r, поэтомуCP = r * sin (α)Координаты точки P могут быть выражены как:
x = A + OCиy = B + CP, поэтомуx = A + r * cos (α)y = B + r * sin (α)Два последних уравнения представляют собой параметрические уравнения окружности.
Теперь, когда вы знаете, как найти уравнение круга, попробуйте этот калькулятор!
Другая форма уравнения окружности
Довольно часто вы встретите другую форму уравнения окружности. Выглядит это так:
Выглядит это так:
x² + y² + Dx + Ey + F = 0
Это общая форма уравнения круга — такая же, как стандартная форма, но в развернутом виде. Отсюда можно получить стандартную форму, выполнив всего несколько простых операций — все, что вам нужно сделать, это выполнить следующие шаги!
- Начните с вашего общего уравнения, например:
x² + y² + 4x - 6y + 8 = 0
- Соедините x и y вместе:
(x² + 4x) + (y² - 6y) + 8 = 0
- Переместим константу в правую часть уравнения:
(x² + 4x) + (y² - 6y) = -8
- Теперь завершите квадрат для x.Для этого вам нужно взять половину четверки, возвести ее в квадрат и прибавить к обеим сторонам:
(x² + 4x + 4) + (y² - 6y) = -8 + 4
- Повторите предыдущий шаг, на этот раз завершив квадрат для y:
(x² + 4x + 4) + (y² - 6y + 9) = -8 + 4 + 9
- Упростите члены x и y в соответствии с формулами факторизации:
(x + 2) ² + (y - 3) ² = 5
Готово — это стандартная форма круга с центром в точке (-2, 3) и радиусом, равным √5 .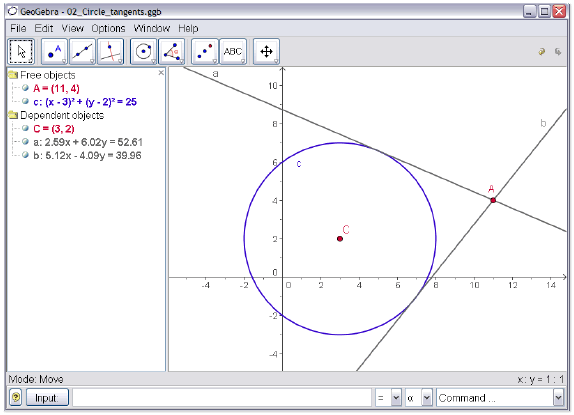
Естественно, вам не обязательно проходить весь этот процесс в одиночку. Вместо этого используйте это уравнение калькулятора круга!
Как использовать это уравнение калькулятора круга?
Если вы все еще не знаете, как использовать наш инструмент, взгляните на этот простой пример ниже.
- Предположим, вы хотите использовать стандартное уравнение для окружности . Итак, это первая часть калькулятора.
- Введите данные . Допустим, что параметры вашего уравнения окружности равны A = 7, B = -2 и C = 9.
- Тадаа! Калькулятор уравнения круга сделал свое дело! Инструмент покажет вам параметры в других формах уравнения, объясняя, каковы значения A и B (координаты центра круга), и дополнительно вычислит другие значения, такие как:
- радиус — что равно 3 для нашего круга,
- диаметр -6 в нашем случае
- область для нашего примера составляет 28,3, а
- Окружность окружности равна 18.
 85.
85.
В этом калькуляторе мы не указывали единицы измерения, так как во многих случаях они вам не нужны, потому что вы работаете с координатами. Если вам нужны единицы — например, дюймы, футы или сантиметры — просто добавьте их к полученным результатам. Не забывайте, что площадь круга будет иметь квадраты длины!
Нарисуйте круг — WebMath
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок
Завершение Квадрат: уравнения круга Техника выполнения
квадрат используется, чтобы превратить квадратичный в сумму возведенного в квадрат двучлена и
число: ( x a ) 2 + b . Но уравнения круга часто дается в общем формате ax 2 + по 2 + cx + dy + e = 0, Когда вам дадут эту общую форму уравнения и попросят найти центр и радиус круга, вам нужно будет «завершить квадрат », чтобы преобразовать уравнение в форму центрального радиуса.Этот урок объясняет, как сделать это преобразование. Авторские права Элизабет Стапель 2000-2011 Все права защищены
Завершение квадрата до
найти центр круга и радиус всегда работает таким образом. Предупреждение: не интерпретируйте неправильно
окончательное уравнение. Помните, что формула круга ( x h ) 2 + ( y k ) 2 = r 2 .Если вы получите уравнение типа ( x + 4) 2 + ( y + 5) 2 = 5,
вы должны держать прямо, что h и к вычитается из в форме центрального радиуса, так что у вас действительно есть ( x (4)) 2 + ( y (5)) 2 = 5.
То есть центр находится в точке (4,
5), а не в (4,
5).Будь осторожен с
знаки; не просто «зачитывай ответ», не задумываясь. В ходе вышеуказанного
процедуры, о единственной другой вещи, которая может быть проблемой, это забыть
знак на ступеньке, где вы умножаете на половину. Предупреждение: если вы уроните
отрицательный, вы получите неправильный ответ для координат центра,
так что будьте осторожны с этим.Не пытайтесь проделать этот шаг в уме: напишите
это из! Вот еще один пример о том, как завершение квадрата работает для круговых уравнений:
Верх | Вернуться к индексу
|
Общий вид уравнения круга
Общий вид уравнения круга — Математика Открытый справочник Круг можно определить как геометрическое место всех точек, удовлетворяющих уравнению(x-h) 2 + (y-k) 2 = r 2
где r — радиус окружности,а h, k — координаты его центра.
Попробуй это Перетащите точку C и обратите внимание, как h и k изменяются в уравнении. Перетащите P и обратите внимание, как квадрат радиуса изменяется в уравнении.
Напомним из
Основное уравнение круга,
что, когда центр круга находится в начале координат, формула Когда центр круга находится в другом месте, нам нужна более общая форма. Мы добавляем две новые переменные h и k, которые являются координатами центральной точки круга:
Мы добавляем две новые переменные h и k, которые являются координатами центральной точки круга:
(x-h) 2 + (y-k) 2 = r 2
Мы вычитаем их из x и y в уравнении, чтобы перевести («переместить») центр обратно в начало координат.Если вы сравните две формулы, вы увидите, что единственное различие состоит в том, что переменные h и k вычитаются из членов x и y. перед их возведением в квадрат:
| Базовый | (x) 2 + (y) 2 = r 2 |
| Общие | (x-h) 2 + (y-k) 2 = r 2 |
Пример
Когда мы видим уравнение круга, такое как мы знаем, что это круг радиуса 9 с центром в точках x = 3, y = –2.
- Радиус равен 9, потому что в формуле справа r 2 . 9 в квадрате равно 81.
- Координата y отрицательна, поскольку член y в общем уравнении равен (y-k) 2 .

В этом примере уравнение имеет (y + 2), поэтому k должно быть отрицательным: (y– (–2)) 2 становится (y + 2) 2 .
Если центр окружности находится в начале координат
Тогда уравнение немного проще. Поскольку центр находится в начале координат, h и k равны нулю.Таким образом, общая форма становится который упрощается до основной формы уравнения круга: Подробнее об этом см. Основное уравнение круга.
Параметрическая форма
Вместо использования теоремы Пифагора чтобы решить прямоугольный треугольник в круге выше, мы также можем решить его с помощью тригонометрии. Это дает так называемую параметрическую форму уравнения окружности, как описано в Параметрическое уравнение круга. Эта параметрическая форма особенно полезна в компьютерных алгоритмах, которые рисуют круги и эллипсы.Это описано в Алгоритм рисования кругов.
Что попробовать
- В апплете выше нажмите «Сброс» и «Скрыть детали».

- Перетащите точки C и P, чтобы создать новый круг.
- Напишите общую формулу получившегося круга.
- Нажмите «Показать подробности», чтобы проверить результат.
Связанные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
| ||||||||||||||||||||||||||||

 Тогда уравнение можно упростить до стандартной формулы:
Тогда уравнение можно упростить до стандартной формулы: 85.
85. Форма центрального радиуса уравнения окружности имеет формат ( x h ) 2 + ( y k ) 2 = r 2 ,
с центром в точке ( ч,
k ) и радиус
« r «.
Эта форма уравнения полезна, так как вы можете легко найти центр
и радиус.
Форма центрального радиуса уравнения окружности имеет формат ( x h ) 2 + ( y k ) 2 = r 2 ,
с центром в точке ( ч,
k ) и радиус
« r «.
Эта форма уравнения полезна, так как вы можете легко найти центр
и радиус.
 Группа y -материал
все вместе.
Группа y -материал
все вместе. Сделайте то же самое с y — срок
коэффициент.Преобразуйте левую часть в квадратную форму, и
упростить правую сторону.
Сделайте то же самое с y — срок
коэффициент.Преобразуйте левую часть в квадратную форму, и
упростить правую сторону. Всегда
выполняйте шаги в этом порядке, и каждое из ваших упражнений должно работать
отлично. (Кроме того, если вы привыкли всегда выполнять упражнения в
Таким же образом вы с большей вероятностью запомните процедуру на тестах.)
Всегда
выполняйте шаги в этом порядке, и каждое из ваших упражнений должно работать
отлично. (Кроме того, если вы привыкли всегда выполнять упражнения в
Таким же образом вы с большей вероятностью запомните процедуру на тестах.)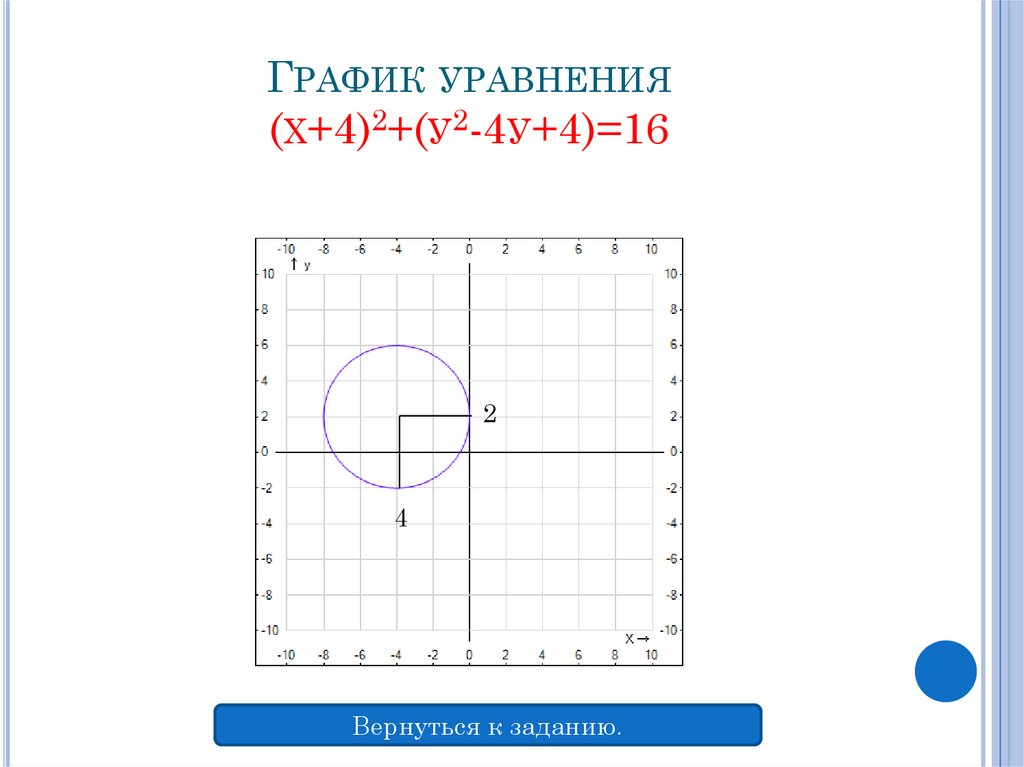 Также помните, что формула гласит: « r 2 »,
не « r «,
поэтому радиус в этом случае равен sqrt (5),
не 5.
Также помните, что формула гласит: « r 2 »,
не « r «,
поэтому радиус в этом случае равен sqrt (5),
не 5. «Завершение квадрата: уравнения круга». Пурпурная математика .
Доступно по номеру
«Завершение квадрата: уравнения круга». Пурпурная математика .
Доступно по номеру 


Ваш комментарий будет первым