Калькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара, объем шара онлайн.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
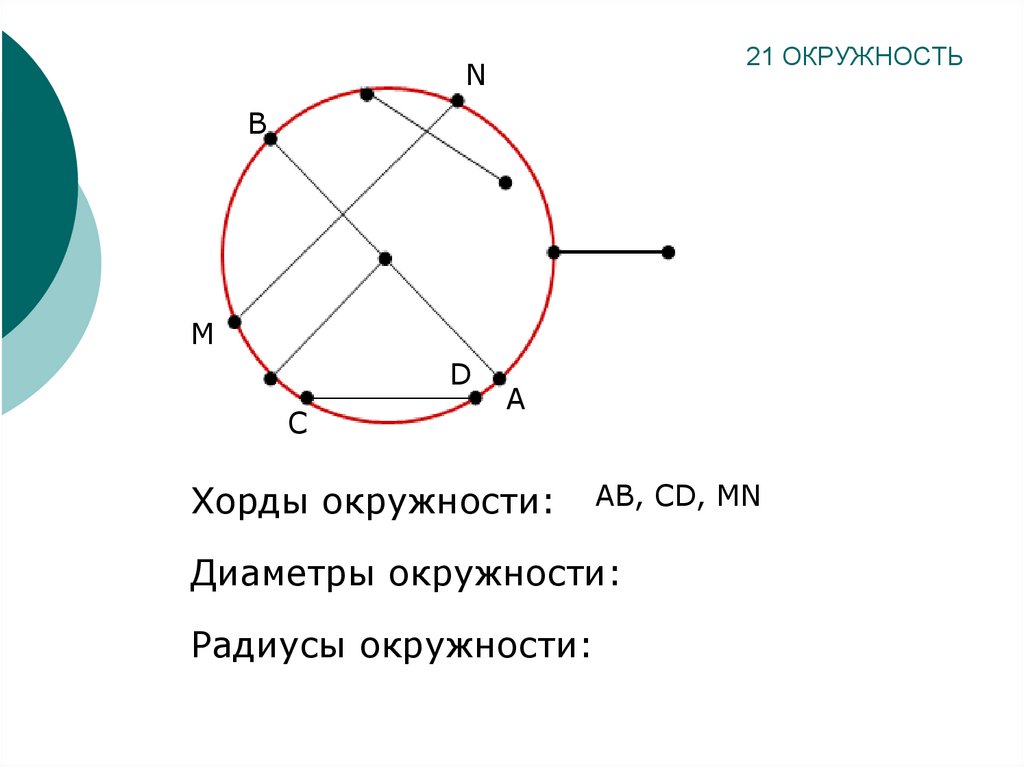
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR2. Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr3). Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга.
Рисование кривой или окружности — Служба поддержки Office
Рисование кривой
-
На вкладке Вставка в группе Иллюстрации нажмите кнопку Фигуры.
-
В разделе линиищелкните Кривая .
-
Щелкните место, где необходимо начать кривую, перетащите указатель для рисования кривой, а затем щелкните в место, где необходимо добавить кривую.
-
Чтобы завершить рисование фигуры, выполните одно из следующих действий:
-
Чтобы оставить фигуру незамкнутой, дважды щелкните в любой момент рисования.
-
Чтобы замкнуть фигуру, щелкните вблизи ее начальной точки.

Примечание: К замкнутой фигуре по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.
-
К началу страницы
Добавление овала или круга
-
На вкладке Вставка в группе элементов Иллюстрации нажмите кнопку Фигуры.
-
В разделе основные фигурыщелкните овал .
-
Щелкните в том месте, откуда следует начать круг.
 Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.
Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.Примечания:
-
-
Если вы хотите получить более сложную схему, например перекрывающиеся круги, организационную диаграмму или блок-схему, можно создать графический элемент SmartArt, а не рисовать каждую фигуру вручную.
-
К кругу или овалу по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.
 2-2Rρ\sin(φ) = 0 \]
2-2Rρ\sin(φ) = 0 \]И этого уравнения получается система
\[ \lvbig ρ = 0
ρ = 2R\sin(φ) \r.\]Первое уравнение системы описывает полюс окружности.
Второе описывает саму окружность в полярной системе координат.
В итоге получаем:
\[ ρ = 2R\sin(φ) \]
Построение окружности в полярной системе координат смещенной вверх относительно полюса
Окружность в полярных координатах
стр. 124 Решение высшей математики онлайн
‹— НазадОпределение 12.3 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Для эллипса можно дать еще несколько эквивалентных определений.
 Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью .
Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью .В отличие от окружности, записать в «удобном» виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.
Пусть и — фокусы эллипса. Начало системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось — перпендикулярно к этому отрезку (рис. 12.3).
Теорема 12.2 Пусть сумма расстояний от точки эллипса до фокусов равна , а расстояние между фокусами — . Тогда в выбранной системе координат эллипс имеет уравнение(12.  4)
4)
где(12.5)
Доказательство. Пусть — текущая точка эллипса. По определению эллипса . Из треугольника (рис. 12.3) видно, что , то есть , , и поэтому число существует.Рис.12.3.Фокусами в выбранной системе координат являются точки , . По формуле (10.4) для плоского случая находим
Тогда по определению эллипса Пренесем один из корней вправо и обе части возведем в квадрат: После того, как раскроем скобки и приведем подобные члены, приходим к выражению Разделим обе части этого уравнения на 4 и возведем в квадрат Раскроем скобку и приведем подобные члены Учитывая, что , имеем равенство Наконец, разделив обе части на , получим уравнение (12.
Уравнение (12.4) называется каноническим уравнением эллипса.
Прежде, чем нарисовать эллипс, выясним некоторые его свойства.
Предложение 12.1 Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси и , начало координат — центр симметрии. Доказательство. Можно было бы провести доказательство на основе определения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического аспекта мы проведем доказательство на основе уравнения (12.4).Пусть эллипс задан уравнением (12.4) и — какая-то точка эллипса. Тогда
(12.6)
Точка является точкой, симметричной точке относительно оси (рис. 12.4).Рис.12.4.Симметрия точек
12.4).Рис.12.4.Симметрия точекВычисляем значение левой части уравнения (12.4) в точке
В силу равенства (12.6) получаем следовательно, точка лежит на эллипсе. Точка является точкой симметричной точке относительно оси (рис. 12.4). Для нее аналогичным путем убеждаемся, что то есть является точкой эллипса. Наконец точка является симметричной точке относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.Проведем построение эллипса, заданного уравнением (12.4). Заметим, что из-за симметрии достаточно нарисовать часть эллипса, лежащую в верхней полуплоскости. Уравнение этой линии мы получим, выразив из уравнения (12.4) и взяв перед корнем знак » «,
Построим график этой функции. Область определения — отрезок , , при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция монотонно растет при изменении от до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график — выпуклый вверх.
Область определения — отрезок , , при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция монотонно растет при изменении от до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график — выпуклый вверх.Осталось не исследованным поведение кривой вблизи концов отрезка . Выразим из уравнения (12.4) переменное через : . Очевидно, что в точке эта функция имеет производную, то есть касательная к этому графику в точке существует. Легко проверить, что она параллельна оси . Из симметрии эллипса делаем вывод, что это гладкая кривая и строим ее с учетом полученных данных (рис. 12.5).
Рис.12.5.Эллипс Определение 12.4 Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии — центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины — большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса.
Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса. Если эллипс задан каноническими уравнениями, то его вершины имеют координаты , , , , большая полуось равна , малая полуось равна . Величина , являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины , а именно, .
Замечание 12.1 Уравнение (12.4) было получено в предположении, что и — различные точки, то есть . Тогда . Но кривую, определяемую уравнением (12.4), мы можем рассмотреть и в случае , . Уравнение (12.4) в этом случае после умножения на примет вид . Это — уравнение окружности радиуса с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда , , или, как иногда говорят математики, окружность является «вырожденным» эллипсом, у которого фокусы совпали.
Эксцентриситет эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса .
Если задано каноническое уравнение эллипса и требуется его построить, то для отображения качественных характеристик достаточно правильно отметить вершины эллипса и провести через них линию, похожую на кривую рис. 12.4, выдерживая симметрию и избегая образования углов на рисунке. Если же из рисунка предполагается получать числовую информацию о координатах его точек, то тогда построение следует проводить более точно. Нужно построить по точкам верхнюю половину эллипса как график функции , взяв для построения достаточно много точек, а нижнюю половину эллипса получить, используя его симметрию. С другим способом построения эллипса можно познакомиться в курсе черчения.
Эллипс обладает многими замечательными свойствами.
Рис.12.6.Отражение лучей света от эллипса Приведем без доказательства одно из них (рис. 12.6).
Приведем без доказательства одно из них (рис. 12.6).Данное свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то отразившись от самого эллипса, он обязательно пройдет через другой фокус. Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, то есть освещенность в обоих фокусах будет одинаковой.
Пример 12.3 Нарисуйте эллипс . Найдите его фокусы и эксцентриситет.Решение. Уравнение запишем в виде
(12.7)
Это уравнение не является каноническим уравнением эллипса, так как в соответствии с уравнением (12. 4) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (12.7) в координатах примет вид Это — каноническое уравнение эллипса при , . Делаем чертеж (рис. 12.8).Рис.12.8.Эллипс, заданный уравнением
4) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (12.7) в координатах примет вид Это — каноническое уравнение эллипса при , . Делаем чертеж (рис. 12.8).Рис.12.8.Эллипс, заданный уравнением Из соотношения (12.5) находим . Значит, фокусы в системе координат имеют координаты , , а в системе координат — координаты , . Эксцентриситет равен .
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Синус и косинус.
 Онлайн калькулятор
Онлайн калькуляторС помощю этого онлайн калькулятора можно найти синусы и косинусы угла, представленных как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Синус и косинус − теория, примеры и решения
Пусть задана прямоугольная система координат xOy и пусть на ней нарисована окружность радиусом 1 и с центром в начале координат. Рассмотрим единичный вектор лежащий на оси Ox. Положительным направлением поворота вектора относительно центра координат O принята считать поворот против часовой стрелки, а отрицательным направлнением − по часовой стрелке. Пусть некоторый вектор, совпадающий с вектором , совершивший поворот в положительном направлении совпадает с вектором (Рис.
 1).
1).Точку B назовем точкой, соответствующей углу α. Рассмотрим координаты x, y точки B. Абсцис x точки B называют косинусом угла α и обозначают cosα, а ординат y точки B называют синусом угла α и обозначают sinα. Таким образом
Так как мы рассматриваем окружность с радиусом R=1, то
а любая точка на кружности удовлетворяет следующему равенству:
Подставляя (1) и (2) в (3), получим:
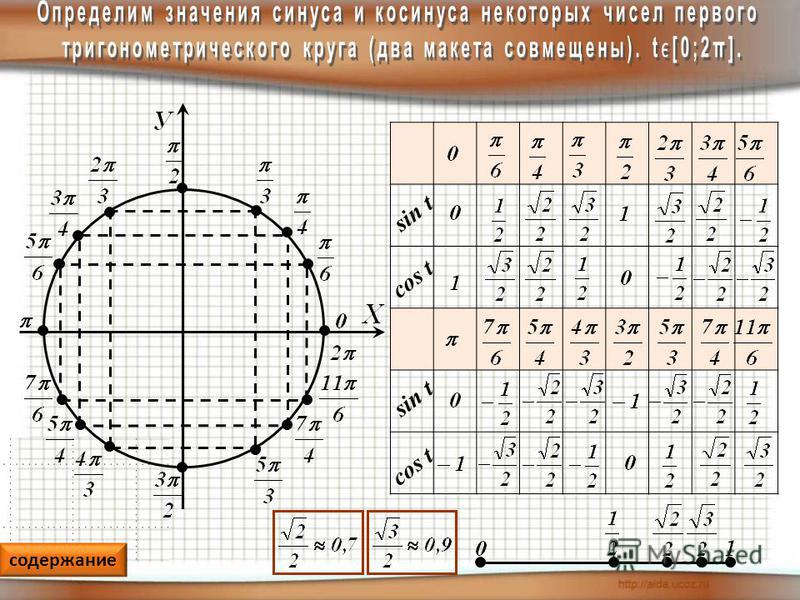
На рисунках Рис.2 и Рис.3 представлены некоторые углы единичной окружности в радианах и в градусах. Как преобразовать градусы в радианы и наоборот посмотрите на странице радианы и градусы онлайн.
Как видно из рисунков, оси OX и OY разделяют плоскость на 4 части. Эти части принято пронуменровать римскими числами I, II, III, IV. Каждая часть называется четвертью. На рисунке Рис.2 в каждой четверти окружность разделена на две части, а в Рис.3 − на три.
Пример 1.
 Найти синус и косинус угла, равного 45°(или радиан)( Рис.4).
Найти синус и косинус угла, равного 45°(или радиан)( Рис.4).Имеем прямоугольный треугольник OxB. Так как угол BOx=45°, то угол OBx=45°. Следовательно треугольник OBx равнобедренный, т.е.
Подставляя (5) в (3), получим:
То есть (учитывая (1) и (2))
В радианных мерах (6) примет следующий вид:
Пример 2. Найти синус и косинус угла, равного 60°(или радиан)( Рис.5).
Имеем прямоугольный треугольник OxB. Так как угол BOx=60°, то угол OBx=30°. Как известно из геометрии, катет, напротив угла 30° равен половине гипотенузы. Т.е.
Подставляя (8) в (3), получим:
В первой четверти x>0, y>0. Тогда, учитывая (1) и (2), решением будет:
или
Пример 3. Найти синус и косинус угла, равного 120°(или радиан)( Рис.6).
Имеем прямоугольный треугольник OxB. Так как угол BOx=120°, то ∠yOB=∠OBx=30°. Как известно из геометрии, катет, напротив угла 30° равен половине гипотенузы.
 Т.е.
Т.е.Подставляя (9) в (3), получим:
Во второй четверти x<0, y>0. Тогда, учитывая (1) и (2), решением будет:
или
С помощью вышеизложенных соображений можно построить таблицу синусов и косинусов некоторых углов.
Таблица 1.
Рассмотрим свойства синуса и косинуса.
Свойство 1. Для любого числа α справедливы равенства:
Доказательство. Пусть числу α соответствует точка P на окружности (Рис. 7). Тогда числу −α соответствует точка Q, симметричная точке P относительно оси абсцисс. Эти точки имеют одну и ту же абсциссу, следовательно . Такие точки имеют равные по модулю, но противоположные по знаку ординаты. Следовательно .
Свойство 2. Для любого числа α выполнены равенства (в радианах):
или (в градусах)
где k∈Z (k любое целое число).
Поскольку числам α и α+2πk в радианах соответствует одна и та же точка на числовой окружности, то справедливы равенства (12) и (13).
 Так как числам α и α+360k в градусах соответствует одна и та же точка на числовой окружности, то выполнены равенства (14) и (15).
Так как числам α и α+360k в градусах соответствует одна и та же точка на числовой окружности, то выполнены равенства (14) и (15).Свойство 3. Для любого значения α выполнены равенства (в радианах):
или (в градусах):
Например (в радианах):
или (в градусах):
Доказательство. Пусть числу α соответствует точка P на окружности. Тогда числу α+π (или α+180°) соответствует точка Q, симметричной точке P относительно начала координат (Рис. 8). Абсциссы этих точек равны по модулю но имеют противоположные знаки. Ординаты этих точек равны по модулю и имеют противоположные знаки. А это значит, что выполнены равенства (16),(17),(18),(19).
График функции синус (y=sin x)
Для построения графика функции синус, поставим в соответствие любому числу α, ординату соответствующей точки на единичной окружности (Рис.9).
Пусть точка M движется по окружности в положительном направлении (против часовой стрелки) начиная с точки A.
 вектор радиус точки M движется по окружности, начиная от точки A.
вектор радиус точки M движется по окружности, начиная от точки A.Вектор радиус точки M с осью OX имеет угол α. Увеличивая этот угол от нуля до π/2 ордината точки M увеличивается от 0 до 1. Далее, увеличивая этот угол от π/2 до π, ордината точки M уменьшается на от 1 до 0. Построим график функции синус на отрезке [0,π]. Так как привычнее запись функции в виде y=sin x, то вместо sin α мы будем использовать sin x, а y− это значение функции соответствующей точке x.
В декартовой прямоугольной системе координат, на оси OX отметим точки (можно взять π≈3 и тогда этим точкам будут соответствовать числа 0, 0.5, 1, 1.5, 2, 2.5, 3). Далее, используя таблицу 1, запишем соответствующие значения y.
Построим график:
Равенство (10) показывает, что функция синус симметрична относительно начала координат (т.е. нечетна). Тогда добавив построенной линии, линию, симметричную относительно начала коордиинат, получим:
Равентство (12)((14)) показывает, что синус периодичная функция с периодом 2π( 360°).
 Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:
Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:Область определения функции синус (−∞;+∞). Область значений: [−1;1].
График функции косинус (y=cos x)
Для построения графика функции косинус, поставим в соответствие любому числу α, абсциссу соответствующей точки на единичной окружности (Рис.13).
Пусть точка M движется по окружности в положительном направлении (против часовой стрелки) начиная с точки A.
Вектор радиус точки M с осью OX имеет угол α. Увеличивая этот угол от нуля до π/2 абсцисс точки M уменьшается от 1 до 0. Далее, увеличивая этот угол от π/2 до π, абсцисс точки M увеличивается от 0 до 1. Построим график функции косинус на отрезке [0,π]. Так как привычнее запись функции в виде y=cos x, то вместо cos α мы будем использовать cos x, а y− это значение функции соответствующей точке x.

В декартовой прямоугольной системе координат, на оси OX отметим точки (можно взять π≈3 и тогда этим точкам будут соответствовать числа 0, 0.5, 1, 1.5, 2, 2.5, 3). Далее, используя таблицу 1, запишем соответствующие значения y.
Построим график:
Равенство (11) показывает, что функция синус симметрична относительно оси ординат (т.е. четна). Тогда добавив построенной линии, линию, симметричную относительно оси ординат, получим:
Равентство (13)((15)) показывает, что косинус периодичная функция с периодом 2π( 360°). Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:
Область определения функции косинус (−∞;+∞). Область значений: [−1;1].
Окружность. Уравнение окружности
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.Примеры решения задач про уравнение окружности
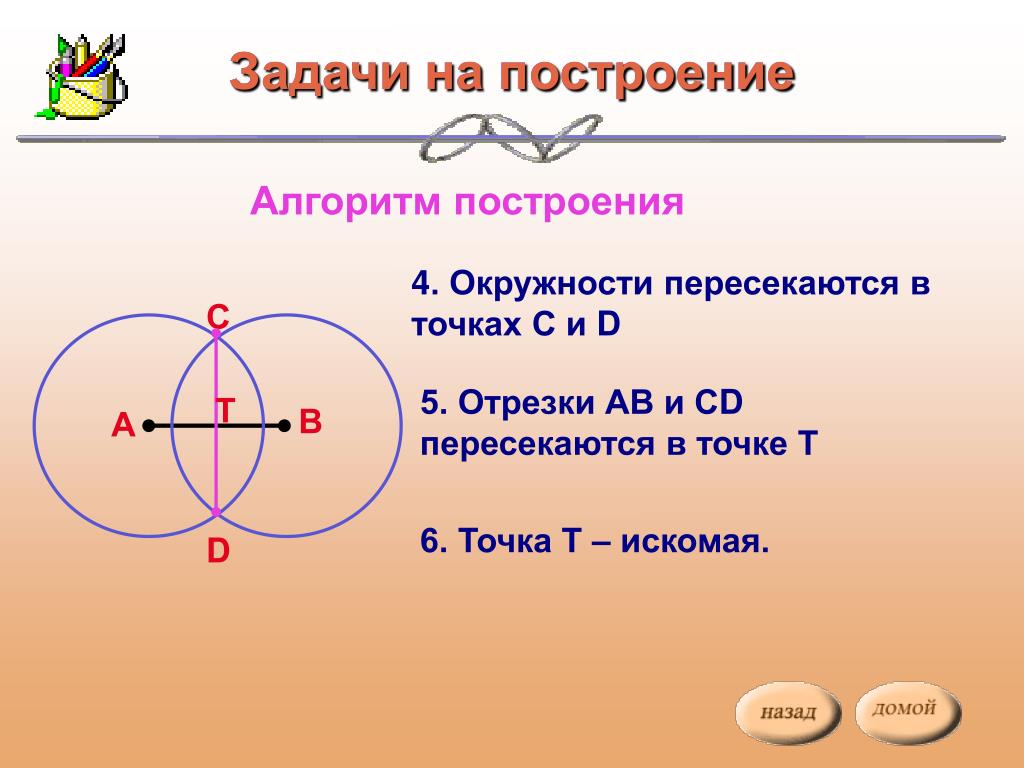
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.Решение.
Обратимся к формуле уравнения окружности:
R2 = (x-a)2 + (y-b)2Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3Получаем:
(x — 2)2 + (y — (-3))2 = 42
или
(x — 2)2 + (y + 3)2 = 16.
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2)2 + (y + 3)2 = 16.Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.В уравнение (x — 2)2 + (y + 3)2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3Проверим истинность полученного равенства
(x — 2)2 + (y + 3)2 = 16
(2 — 2)2 + (3 + 3)2 = 16
0 + 36 = 16 равенство неверноТаким образом, заданная точка не принадлежит заданному уравнению окружности.
Содержание главы:
Площадь геометрической фигуры | Описание курса | Задачи про окружностьWolframAlpha по-русски: Окружность в Wolfram|Alpha
? Как с помощью в Wolfram|Alpha построить окружность, если задано ее уравнение, если заданы координаты центра и радиус, если известны три точки, через которые проходит окружность? Как найти координаты точек пересечения окружности и прямой? Такие элементарные задачи Wolfram|Alpha решает легко.
Изображение окружности и основные сведения о ней Wolfram|Alpha выводит по запросу circle:
Если требуется просто крупное изображение окружности и ничего более, используйте запрос circle image:
Как построить окружность с заданными параметрами при помощи Wolfram|Alpha? Это можно сделать несколькими способами.
Во-первых, Wolfram|Alpha, естественно, сможет построить окружность по ее уравнению. Если нужно, можно будет найти, например, координаты центра окружности и ее радиус:
x^2+y^2-4x-6y-12=0 center, radiusЧтобы построить окружность, если известны координаты центра и радиус, нужно использовать запрос вида circle center (3,4) radius 5, или его упрощенный вариант:
circle (3,4) r=5
Пример: построить изображение единичной окружности с центром в начале координат.

сircle (0,0) r=1 image
Через три точки, не лежащие на одной прямой, можно провести единственную окружность. Чтобы построить окружность, проходящую через три точки, не лежащие на одной прямой, Wolfram|Alpha использует другой запрос. При этом система выводит не только изображение, но также уравнение окружности и ее основные параметры — координаты центра окружности (center), радиус (radius), диаметр (diameter), площадь (area), периметр (perimeter):
circle through (-2,1) (4,-2) (3,5)
Чтобы не только найти координаты центра окружности, но и обозначить центр на рисунке, используйте тот же запрос с параметром center:
circle through (-2,1) (4,-2) (3,5) center
Еще один способ построить окружность — задать координаты центра и одну точку, через которую проходит эта окружность:
circle center (2,1) through (4,3)
Вместе с окружностью в Wolfram|Alpha можно построить изображение другой линии.
 2-4x-6y-12=0, y=x
2-4x-6y-12=0, y=xЕсли же окружность и прямая заданы другим способом, то с помощью Wolfram|Alpha можно найти точки их пересечения, используя запрос intersection:
intersection circle (2,3) r=5, line (-3,-1) (4,6)
Наконец, вот еще один пример использования запроса intersection. На этот раз получим пересечение окружности и треугольника
intersection circle (2,3) r=5 and triangle (3,-3) (-4,3) (5,8)
Уравнения, радиуса и центра окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r 2 = (x — h) 2 + (y — k) 2
где,
- ч, к — координаты центра Окружности
- x, y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение:
Шаг: 1
Подставляем координаты точек в формулу
- (2 — h) 2 + (2 — k) 2 = r 2
- (2 — h) 2 + (4 — k) 2 = r 2
- (5 — h) 2 + (5 — k) 2 = r 2
Шаг: 2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
- 4 — 4 ч + ч 2 + 4 — 4 к + к 2 = 4 — 4 ч + ч 2 +16 — 8 к + к 2
- 8 — 4k = 20 — 8k
- к = 3
Шаг: 3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
- 4 — 4 ч + ч 2 + 4 — 4 к + к 2 = 25 — 10 ч + ч 2 + 25 — 10 к + к 2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6к + 6ч = 42
Подставив значение k = 3 в уравнение
Получаем координаты точки центра (h, k) = ( 4,3 )
Шаг: 4
Подставим значения h, k в формулу
- r 2 = (x — h) 2 + (y — k) 2
- r 2 = (2–4) 2 + (2–3) 2
- r 2 = (-2) 2 + (-1) 2
- r 2 = 5
- г = 2.
 24
24
Шаг: 5
Подставим значения h, k в уравнение окружности
(x — h) 2 + (y — k) 2
Уравнение окружности = (x — 4) 2 + (y — 3) 2
Ответ:
- Координаты точки центра окружности c (h, k) = c (4,3)
- Радиус окружности r = 2.24
- Уравнение окружения = (x — 4) 2 + (y — 3) 2 = (2.24) 2
Было ли это полезно?
Определить формулу окружности по трем точкам
Полученная формула окружности Рассмотрим частный пример расчета кривой второго порядка на плоскости по точкам
Напомним, что общее уравнение второго порядка выглядит так
Частные примеры кривой второго порядка это и парабола и гибербола и окружность и прямая линия.

Формула окружности с (a; b) и радиусом R имеет вид
или если мы раскроем скобки
из этого уравнения можно видеть что кривая второго окружности, если
Из этого же мы можем утверждать, что для построения окружности нам н ужно как минимум три точки , только три коэффицента неизвестны.
Бот, позволяет вам рассчитывать формулу окружности по заданным трем точкам.
Если бы бота не было, то Вам пришлось решать систему из трех переменных, что не очень удобно и трудоёмко.
Интересные факты
Эти два основных фактора: центр окружности и радиус окружности
определяют все коэффициенты кривой второго порядка.Центр окружности
Радиус окружности
Синтаксис
Так как это частный пример уже созданного бота то просто расскажем о нюансах
кп2 1 1 0 координаты точек
Где координаты точек есть представление в виде x: y (х-абсцисса, y-ордината)
Каждая координата точки должна разделиться как минимум одним пробелом.
 2 + (0) xy + (4.000000000) x + (-2.000000000) y + (-20.000000000) = 0
2 + (0) xy + (4.000000000) x + (-2.000000000) y + (-20.000000000) = 0 Или если раскроем скобки и уберем нулевые коээфиценты получим
или тоже самоеТо есть центр полученной окружности находится по координатам (-2: 1) и радиус 5 условных единиц.
Успехов в расчетах!
- Пересечение двух прямых.Угол и точка пересечения >>
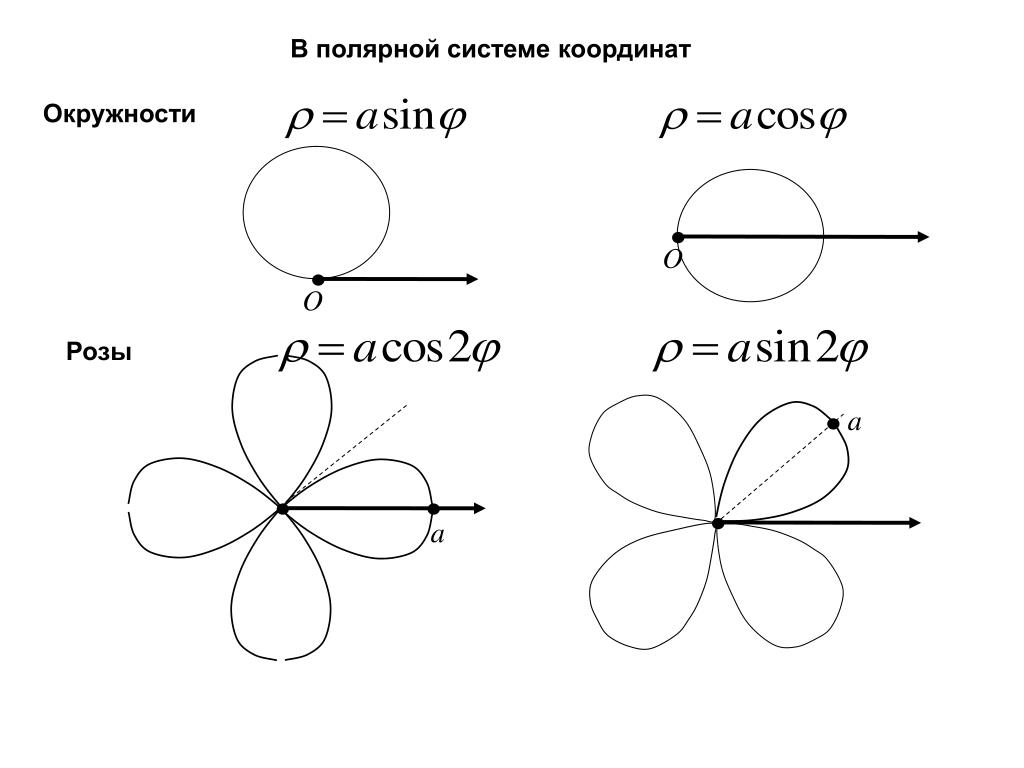
Окружность в полярных координатах | Формулы и расчеты онлайн
Уравнение окружения в полярных координатах выглядит очень просто
\ [ρ = R = \ const \]
Это уравнение показывает, что ρ вообще не зависит от угла φ.
Построение окружности по простому уравнению в полярной системе координат
Еще одно уравнение окружности в полярных координатах
Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.
 2-2Rρ \ cos (φ) = 0 \]
2-2Rρ \ cos (φ) = 0 \]И этого уравнения получается система
\ [\ lvbig ρ = 0
ρ = 2R \ cos (φ) \ r. \]Первое уравнение системы полюс окружности.
Второе изображение саму окружность в полярной системе координат.
В получаем:
\ [ρ = 2R \ cos (φ) \]
Построение окружности в полярной системе координат
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.2-2Rρ \ sin (φ) = 0 \]
И этого уравнения получается система
\ [\ lvbig ρ = 0
ρ = 2R \ sin (φ) \ r. \]Первое уравнение системы полюс окружности.
Второе изображение саму окружность в полярной системе координат.
В получаем:
\ [ρ = 2R \ sin (φ) \]
Построение окружности в полярной системе координат смещенной вверх относительно полюса
Окружность в полярных координатах
стр.  124
124Окружность. Уравнение окружности
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а линию — уравнением с двумя неизвестными, графиком которого эта линия является уравнением с двумя неизвестными, графиком которого эта линия является уравнением. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным своимством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности — это линия окружности.
Если окружность в системе координат, то все точки окружности удовлетворяют одному условию — расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а; б) , а координаты любой точки окружности (х; у) , то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей разных координат точки окружности и ее центра, это уравнение уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса равенство сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек задается уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у , определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с точкой в точке O (2; -3) и радиусом 4.Решение .
Обратимся к формуле уравнения окружности:
R 2 = (x-a) 2 + (y-b) 2Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3Получаем:
(x — 2) 2 + (y — (-3)) 2 = 4 2
или
(x — 2) 2 + (y + 3) 2 = 16.Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A (2; 3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16 .Решение .
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точку с заданными координатами, подставим координаты точки в уравнении заданной окружности.В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А (2; 3), то есть
x = 2
y = 3Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 -2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверноТаким образом, заданная точка не принадлежит заданному уравнению окружения.
Содержание главы:
Площадь геометрической фигуры | Описание курса | Задачи про окружностьКалькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара шара онлайн.
Калькулятор круга — это сервис, специально для расчета геометрических размеров фигур онлайн.
 Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг.Например: Вы знаете размер шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку выбрать. Сервис не только выдает результаты вычислений, но и формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда окружаете радиус, диаметр, длину (периметр круга), площадь круга и шара.
Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг.Например: Вы знаете размер шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку выбрать. Сервис не только выдает результаты вычислений, но и формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда окружаете радиус, диаметр, длину (периметр круга), площадь круга и шара.Вычислить радиус
Задача на вычисление значения радиуса — одна из самых распространенных.Вы можете определить значение любого другого оператора круга или шара. Наш сайт построен именно по такой схеме. Вне зависимости от того, какой вы выбираете исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра — самый простой вид расчета из тех, что умеет выполнять наш калькулятор.
 Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр значению радиуса умноженному на 2. Диаметр — важнейший параметр круга, который используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за секунды.
Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр значению радиуса умноженному на 2. Диаметр — важнейший параметр круга, который используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за секунды.Узнать длину окружности
Они представляют, как много вокруг нас, круглых объектов и какую роль они играют в нашей жизни.Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычислений длинны окружности очень проста: D = 2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга — как и все перечисленные перечисленные в этой статье характеристики диагностической современной цивилизации.
 Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычислений опять же нетрудная: S = PR 2 . Эта формула и наш онлайн-калькулятор поможет вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует выполнение вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычислений опять же нетрудная: S = PR 2 . Эта формула и наш онлайн-калькулятор поможет вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует выполнение вычислений и их молниеносное выполнение.Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах.S = 4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает возможность точно вычислить площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 квадратных километров. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления размера используйте формулу V = 4/3 (Pr 3 ).
 Она была при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы указан радиус, диаметр, диаметр, диаметр окружности, площадь круга или площадь шара. Так же вы можете применить его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы указан радиус, диаметр, диаметр, диаметр окружности, площадь круга или площадь шара. Так же вы можете применить его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.Решение высшей математики онлайн
‹- НазадОпределение 12.3 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух точек плоскости той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Для эллипса можно дать еще несколько эквивалентных определений.Желающие познакомиться с ними в более серьезных учебниках по аналитической геометрии.
 Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, которая образует острый угол с плоскостью.
Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, которая образует острый угол с плоскостью.В отличие от окружности, записать в «удобном» виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему так, чтобы его уравнение было достаточно простым.
Пусть и — фокусы эллипса. Начало системы расположим на середине отрезка. Ось направим вдоль этого отрезка, ось — перпендикулярно к этому отрезку (рис. 12.3).
Теорема 12.2 Пусть сумма расстояний от точки эллипса до фокусов равна, расстояние между фокусами -. Тогда в выбранной системе координат эллипс имеет уравнение(12,4)
где(12.  5)
5)
Доказательство . Пусть — текущая точка эллипса. По определению эллипса. Из треугольника (рис. 12.3) видно, что, то есть,, и поэтому число существует. Рис.12.3.Фокусами в выбранной системе координат являются точки,. По формуле (10.4) для плоского случая находим
Тогда по определению эллипса Пренесем один из корней вправо и обе части возведем в квадрат: После того, как раскроем скобки и приведем соответствующие элементы, приходим к выражению Разделим обе части этого уравнения на 4 и возведем в квадрат квадрат Раскроем скобку и приведем приведенное число, что, имеем равенство Наконец, разделив обе части на, получим уравнение (12.4).Уравнение (12.4) называется каноническим уравнением эллипса.
Прежде, чем нарисовать эллипс, естественно некоторые его свойства.
Предложение 12.1 Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центр симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии оси и, начало координат — центр симметрии. Доказательство .Можно было бы провести доказательство на основе уравнения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического мы проведем доказательство на основе уравнений (12.4).
Если эллипс задан каноническим уравнением (12.4), то его осями симметрии оси и, начало координат — центр симметрии. Доказательство .Можно было бы провести доказательство на основе уравнения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического мы проведем доказательство на основе уравнений (12.4).Пусть эллипс задан уравнением (12.4) и — какая-то точка эллипса. Тогда
(12,6)
Точка является точкой, симметричной точкой относительно оси (рис.12.4). Рис.12.4.Симметрия точекВычисляем значение левой части уравнения (12.4) в точке
В силу равенства (12.6) получаем, следовательно, точка лежит на эллипсе. Точка является точкой симметричной точки относительно оси (рис. 12.4). Другим путем убеждаемся, что есть точка эллипса. Наконец точка является симметричной точкой относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе.Итак, предложение доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью.
Наконец точка является симметричной точкой относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе.Итак, предложение доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью.Проведем построение эллипса, заданного уравнением (12.4). Заметим, что из-за симметрии достаточно нарисовать часть эллипса, лежащую в верхней полуплоскости. Уравнение этой линии мы получим, выразив из уравнения (12.4) и взяв перед корнем знак «»,
Построим график этой функции.Область определения — отрезок,, при увеличении переменного от 0 до функции монотонно убывает. В силу симметрии оси графика функция монотонно растет при изменении от до 0. Производственная определена во всех точках интервала и, следовательно, график гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала, следовательно, график — выпуклый вверх.
Осталось не исследованным исследованием кривой концов отрезка. Выразим из уравнения (12.4) переменное через:. Очевидно, что в точке эта функция имеет производную, то есть касательная к этому графику в точке существует. Легко проверить, что она параллельна оси. Из симметрии эллипса делаем вывод, что это гладкая кривая и строим ее с учетом полученных данных (рис. 12.5).
Рис.12.5.Эллипс Определение 12.4 Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии — центра эллипса, отрезок между двумя вершинами, называется фокусы, большой осью эллипса, половина его — окружности. большой полуосью эллипса.Отрезок между вершинами на оси симметрии, не фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса.Если эллипс задан каноническими уравнениями, то его вершины имеют координаты«, большая полуось равна, малая полуось равна. Величина, являющаяся половиной расстояния между фокусами, определяется из формулы (12.
Замечание 12.1 Уравнение (12.4) было получено в предположении, что и — различные точки, то есть. Тогда. Но кривую, определяемую уравнением (12.4), мы можем рассмотреть и в случае,. Уравнение (12.4) в этом случае после умножения на примет вид. Это — уравнение окружности радиуса с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда,,,,, или, как иногда говорят математики, окружность является «вырожденным» эллипсом, у которого фокусы совпадают. 5) для величины, а именно,.
5) для величины, а именно,.Эксцентриситет эллипса проверяет степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса.
Если задано каноническое уравнение эллипса и его построить, для отображения качественных характеристик достаточно правильно отметить вершины эллипса и провести через них линию, похожую на кривую рис.12.4, выдерживая симметрию и избегая образования углов на рисунке.
 После создания рисунка следует проводить более точно информацию о координатах его точек. Нужно построить по точкам верхнюю половину эллипса как график функции, взяв для построения много точек, используя его симметрию. С другими способами эллипса можно познакомиться в курсе черчения.
После создания рисунка следует проводить более точно информацию о координатах его точек. Нужно построить по точкам верхнюю половину эллипса как график функции, взяв для построения много точек, используя его симметрию. С другими способами эллипса можно познакомиться в курсе черчения.Эллипс обладает замечательными свойствами.Приведем без доказательства одно из них (рис. 12.6).
Рис.12.6.Отражение лучей света от эллипсаЭто свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то отразившись от самого эллипса, он обязательно пройдет через другой фокус. Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, есть освещенность в обоих фокусах будет одинаковой.
Пример 12.3 Нарисуйте эллипс. Найдите его фокусы и эксцентриситет.
Найдите его фокусы и эксцентриситет.Решение. Уравнение запишем в виде
(12.7)
Это уравнение является не каноническим уравнением эллипса, так как в соответствии с уравнением (12.4) в нем,,, а должно быть. Однако, если переобозначить оси, то есть положить, то уравнение (12.7) в координатах примет вид Это — каноническое уравнение эллипса при,. Делаем чертеж (рис. 12.8). Рис.12.8.Эллипс, заданный уравнениемИз соотношения (12.5) находим. Значит, фокусы в системе координат имеют координаты« а в системе координат — координаты,. Эксцентриситет равенство.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики онлайн, онлайн решение математики, высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, вектор алгебра онлайн, решение онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел, высшие производные, производная неявной функции
Кривые второго порядка — презентация онлайн
1.
1 Кривые второго порядка
Кривые второго порядка 2. Повторение
Какие линии на
плоскости вы можете
построить?
Какими уравнениями
эти линии можно
указать?
Выделить среди
приведенных условий
уравнения первого
порядка, уравнения
второго порядка.
y kx b
Кубическую параболу
у топор
BX
с
прямую
2
у х
n
параболу
k
y
х
гиперболу
23.Определение
Алгебраической кривой второго порядка
называется кривая Г, уравнение которой в
декартовой системы координат имеет вид:
Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0,
где не все коэффициенты А, В и С равны
одновременно нулю.
34. Виды кривых второго порядка
1. Окружность.
Определение:
Окружностью
называется
геометрическое
место точек
плоскости, одинаково
удаленных от одной
точки, называемой
центр.
М0 — центр окружности,
М0М — радиус
45. Уравнение окружности
Уравнение окружности с центром в точке
Мо (x0, y0) и радиуса R имеет вид:
(х х0) (у у0)
рэнд 2
2
2
Вывод
Пример 1: Написать уравнение окружности
с центром в точке С (3; 5) и радиусом R = 3.
Если центр окружности в начале системы
координат, то уравнение имеет вид:
2
2
2
х у2 К 2
Решение: (x 3) (y 5) 9
56.Вывод уравнения окружности
M (x; y), M 0 (x0; y0)
М 0 М (х х0) (у у0)
2
2
M 0M R
(х х0) (у у0)
рэнд 2
2
(х х0) (у у0)
рэнд 2
2
2
67. Окружность
Пример 2: Найти центр и радиус
окружности и построить ее
(х 3) (у 2) 100
2
2
Решение:
R = 10, M0 (-3; 2)
78. Окружность
Пример 3: Доказать, что уравнение задает
окружность, найти координаты центра и радиус,
построить окружность
х 2 х 4 у г 20 0
2
2
Решение:
R = 5, M0 (1; -2)
89.
Пример 4. Окружность
Окружность
Дана окружность x2 + y2-4x + 2y-15 = 0 и хорда
х + у-7 = 0. Найти длину этой хорды.
Решение:
1. Найти уравнение окружности.
2. Построить чертеж
3. Решить систему, найти точки пересечения
линий
4. Найти расстояние между двумя точками
910. Окружность
Пример 5.
Дана окружность (x + 2) 2+ (y + 3) 2 = 13 и
точка на ней с ординатой, равной
нулю. Найти ее абсциссу.
Пример 6.
Написать уравнение окружности,
проходящей через три точки А (0; 2),
В (1; 1), С (2, -2).
1011. Окружность
Пример 7.
Окружность обеих осей координат и
проходит через точку А (2; 9). Написать
уравнение этой окружности.
Пример 8.
Окружность оси оси Оy в точке А (0; -3) и
имеет радиус r = 2. Написать уравнение этой
окружности.
1112. Домашнее задание
Построить окружности:
(x + 3) 2+ (y-2) 2 = 16 и x2 + (y-4) 2 = 25
Найти координаты центра и длины
радиуса окружности x2 + y2-6x-8y = 0.
Составить уравнение окружности,
касающейся оси ОХ в начале
координаты и проходящей через точку
А (0; -8).
1213. Виды кривых второго порядка
2. Эллипс
Определение:
Эллипсом называется геометрическое место
точек плоскости, сумма расстояний от
каждой из которых до двух точек той
же плоскости, называемых фокусами, есть
величина постоянная и больше расстояния
между фокусами
1314.Эллипс
F1 и F2 — фокусы,
F1 (-c, 0), F2 (c, 0)
F1F2 — фокальной
расстояние
| F1F2 | = 2а
Пусть М (x; y) — точка
на эллипсе, то
MF1 = MF2
1415. Эллипс
Вывод уравнения эллипса:
F1M (x c) 2 (y 0) 2 (x c) 2 y 2
F2 M (x c) 2 (y 0) 2 (x c) 2 y 2
Тогда
(х в) 2 у 2 (х в) 2 у 2 2а
Раскроем скобки, упростим выражение:
1516. Эллипс
Уравнение эллипса:
2
2
х
y
1
2
2
b
Это уравнение называется
каноническим уравнением эллипса.
1617. Эллипс
Число а называется большой полуосью, b
— малой полуосью.
Точки А, А1, В, В1 называются вершинами
эллипса.
Точка О — центр эллипса.
Эксцентриситетом эллипса называется
отношение расстояния между его
фокусами к длине большей оси (а> b), т.е.
2с с
а б
2а а
2
2
1718. Эллипс
Располагается симметрично осей.
Ограничен прямыми х = ± а, y = ± b, т.е.
вписан в прямоугольник, стороны
которого параллельны координатным
осям и длины, равные 2а и 2b,
а диагонали пересекаются в начале
координат.
1819. Эллипс
Пример 1.
Дан эллипс 16×2 + 25y2 = 400. Определить длину
его осей, координаты вершин и фокусов, а
также имеет эксцентриситета.
Пример 2.
Написать каноническое уравнение эллипса,
если фокальное расстояние равно 8, и
эллипс проходит через точку М (0, -3)
1920.
Пример 3 Эллипс
Эллипс
Определить длину осей и координаты
фокусов эллипса 49×2 + 24y2 = 1176
Пример 4
Составить уравнение эллипса, если две
его вершины находятся в точках А (8; 0)
и А1 (-8; 0), а фокусы имеют
координаты (± 5; 0)
2021. Эллипс
Пример 5
Написать уравнение эллипса,
координаты фокусов которого (± 3; 0), а
длина большей оси равная 12.
Пример 6
Найти эксцентриситет эллипса
4×2 + 9y2 = 180
2122.Эллипс
Если координаты центра эллипса смещены
относительно центра, то уравнение
эллипса имеет вид:
(х х0) (у у0)
1
2
2
b
2
2
2223. Эллипс
Пример 7
Найти координаты центра, длины осей и
эксцентриситет эллипса:
(х 5) (у 2)
1
64
16
2
2
Построить эллипс
2324. Домашнее задание
Написать каноническое уравнение
эллипса, если даны длины его полуоси
а = 5 и б = 4.
Дан эллипс, определить его оси и
расстояние между фокусами:
2
2
х
y
1
36 9
2425. Виды кривых второго порядка
3. Гипербола.
Определение. Гиперболой называется
геометрическое место точек
плоскости, разность расстояний от
каждой из которых до двух данных
точек плоскости, называемых
фокусами, есть величина постоянная.
2526. Гипербола
F1, F2 — фокусы
гиперболы
F1F2 — фокальное
расстояние
F1 (-c, 0), F2 (c, 0)
2627.Вывод формулы уравнения гиперболы
F1M (x c) (y 0) (x c) y
2
2
2
2
F2 M (x c) 2 (y 0) 2 (x c) 2 y 2
Тогда
(х в) 2 у 2 (х в) 2 у 2 2а
Раскроем скобки, упростим выражение:
2728. Каноническое уравнение гиперболы
2
2
х
y
1
2
2
b
2829. Гипербола
Гипербола симметрична относительно оси
ОХ, оси ОY
Пересекает ось ОХ в точках А1 (-а, 0), А2 (а, 0)
— вершинах гиперболы.
О (0,0) — центр гиперболы
А1А2 — вещественная ось, В1В2 — мнимая
ось
F1M, F2M — фокальные радиусы гиперболы
2930. Гипербола
Эксцентриситетом гиперболы называется
отношение расстояния между фокусами к
длине вещественной оси, т.е.
2с с
а б
2а а
2
2
3031. Гипербола
Прямые y = ± b / a x называются
асимптотами гиперболы.
Если полуосей гиперболы
равны, т.е. а = б, то гипербола
называется равнобочной.
Асимптоты равнобочной гиперболы
имеют вид: y = ± x
3132. Гипербола
Пример 1.
Дана гипербола. Узнать,
лежит ли точка А (2; 1,5)
на какой-либо ее
астотимпе.
Пример 2.
Определить координаты
фокусов, длина осей и
эксцентриситет
гиперболы:
2
2
х
y
1
16 9
24×2-25y2 = 600
3233. Гипербола
Гипербола
называется
сопряженной, если
ее уравнение имеет
вид:
Гипербола
называется
равносторонней,
если a = b, т. е.
е.
2
2
х
y
2 1
2
b
х2 у2
2 1,
2
à
ò .å. х 2 у 2 1
3334. Гипербола
Пример 3
Написать уравнение гиперболы, если
б = 6, в = 13.
Пример 4.
Написать уравнение гиперболы, у
которой вещественная ось равна 8, а
расстояние между фокусами,
лежащими на оси ОХ, рано 10.
3435. Гипербола
Пример 5.
Найти острый угол между асимптотами
гиперболы 4х2-5у2 = 100.
Пример 6.
Написать уравнения асимптот, а также
найти применение эксцентриситета
гиперболы x2-2y2 = 6.
3536. Гипербола
Уравнение гиперболы со смещенным
центр:
(х х0) (у у0)
1
2
2
b
2
2
3637. Домашнее задание
1) Написать каноническое уравнение
гиперболы, если a = 6, b = 2.
2) Определить координаты фокусов,
длина осей и эксцентриситет
гиперболы 16y2-9×2 = 144.
3738. Виды кривых второго порядка
4. Парабола
Определение. Параболой называется
геометрическое место точек
плоскости, каждая из которых
одинаково удалена от точки,
называемой фокусом, и от прямого,
называемой директрисой.
3839. Парабола
F (p / 2,0) — фокус
Х = -p / 2 — уравнение
директрисы
О (0,0) — вершина
Уравнение
параболы:
y 2 пикселей
2
3940.Парабола
Парабола проходит через начало координат
Располагается справа от оси ОY, если p> 0
Парабола симметрична относительно оси
ОХ
Если уравнение имеет вид х2 = 2py, то ветви
параболы будут перемещаться вверх.
4041. Парабола
Пример 1
Построить параболу y2 = 6x
Пример 2
Дана парабола y2 = 12x. Найти координаты ее
фокуса и написать уравнение директрисы.
Пример 3.
Написать уравнение параболы с вершиной в
начало координат, зная, что фокус имеет
координаты F (4,0)
4142.

-
 Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.
Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.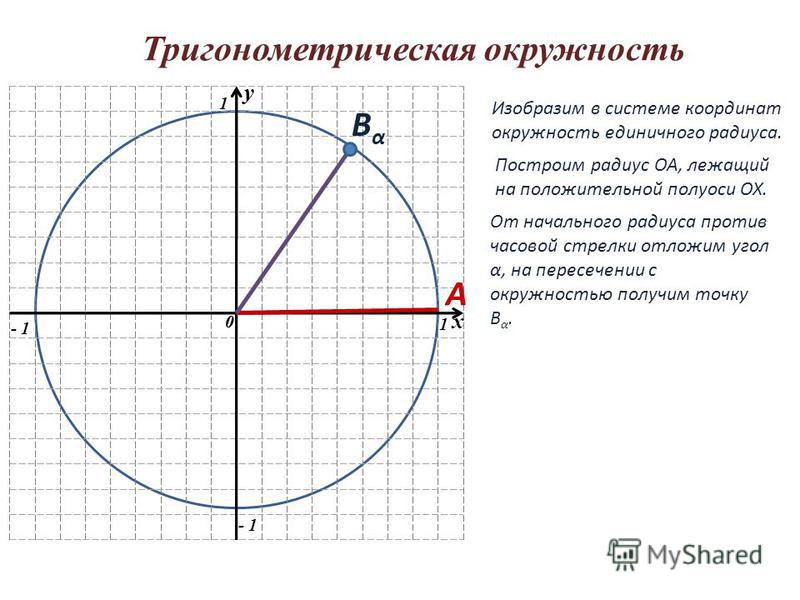 2-2Rρ\sin(φ) = 0 \]
2-2Rρ\sin(φ) = 0 \] Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью .
Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью . 4)
4)
 12.4).Рис.12.4.Симметрия точек
12.4).Рис.12.4.Симметрия точек Область определения — отрезок , , при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция монотонно растет при изменении от до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график — выпуклый вверх.
Область определения — отрезок , , при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция монотонно растет при изменении от до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график — выпуклый вверх.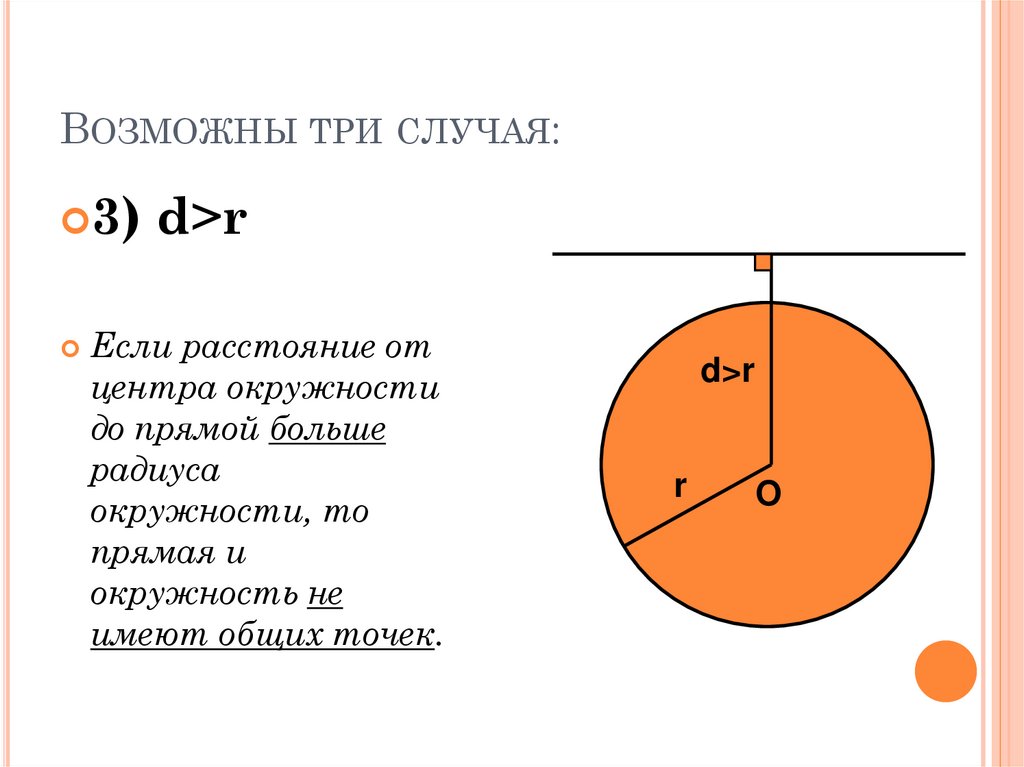 Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса.
Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса. 
 Приведем без доказательства одно из них (рис. 12.6).
Приведем без доказательства одно из них (рис. 12.6). 4) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (12.7) в координатах примет вид Это — каноническое уравнение эллипса при , . Делаем чертеж (рис. 12.8).Рис.12.8.Эллипс, заданный уравнением
4) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (12.7) в координатах примет вид Это — каноническое уравнение эллипса при , . Делаем чертеж (рис. 12.8).Рис.12.8.Эллипс, заданный уравнением  Онлайн калькулятор
Онлайн калькулятор 1).
1). Найти синус и косинус угла, равного 45°(или радиан)( Рис.4).
Найти синус и косинус угла, равного 45°(или радиан)( Рис.4). Т.е.
Т.е. Так как числам α и α+360k в градусах соответствует одна и та же точка на числовой окружности, то выполнены равенства (14) и (15).
Так как числам α и α+360k в градусах соответствует одна и та же точка на числовой окружности, то выполнены равенства (14) и (15). вектор радиус точки M движется по окружности, начиная от точки A.
вектор радиус точки M движется по окружности, начиная от точки A. Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:
Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево: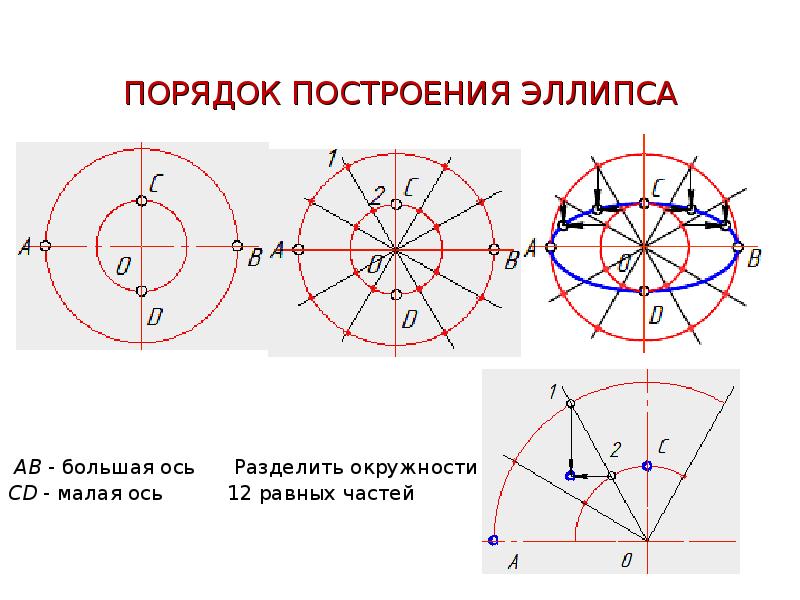




 2-4x-6y-12=0, y=x
2-4x-6y-12=0, y=x 24
24 
 2 + (0) xy + (4.000000000) x + (-2.000000000) y + (-20.000000000) = 0
2 + (0) xy + (4.000000000) x + (-2.000000000) y + (-20.000000000) = 0  2-2Rρ \ cos (φ) = 0 \]
2-2Rρ \ cos (φ) = 0 \] 124
124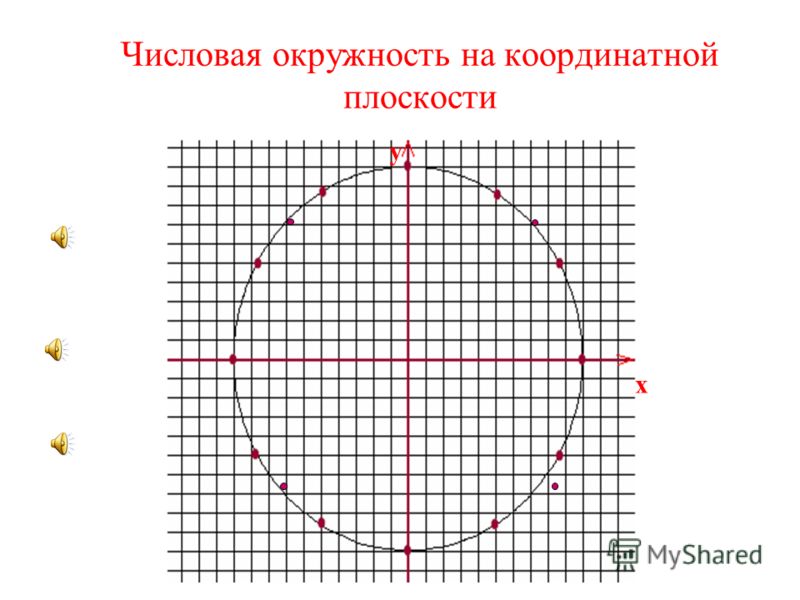


 Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг.Например: Вы знаете размер шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку выбрать. Сервис не только выдает результаты вычислений, но и формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда окружаете радиус, диаметр, длину (периметр круга), площадь круга и шара.
Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг.Например: Вы знаете размер шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку выбрать. Сервис не только выдает результаты вычислений, но и формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда окружаете радиус, диаметр, длину (периметр круга), площадь круга и шара. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр значению радиуса умноженному на 2. Диаметр — важнейший параметр круга, который используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за секунды.
Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр значению радиуса умноженному на 2. Диаметр — важнейший параметр круга, который используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за секунды.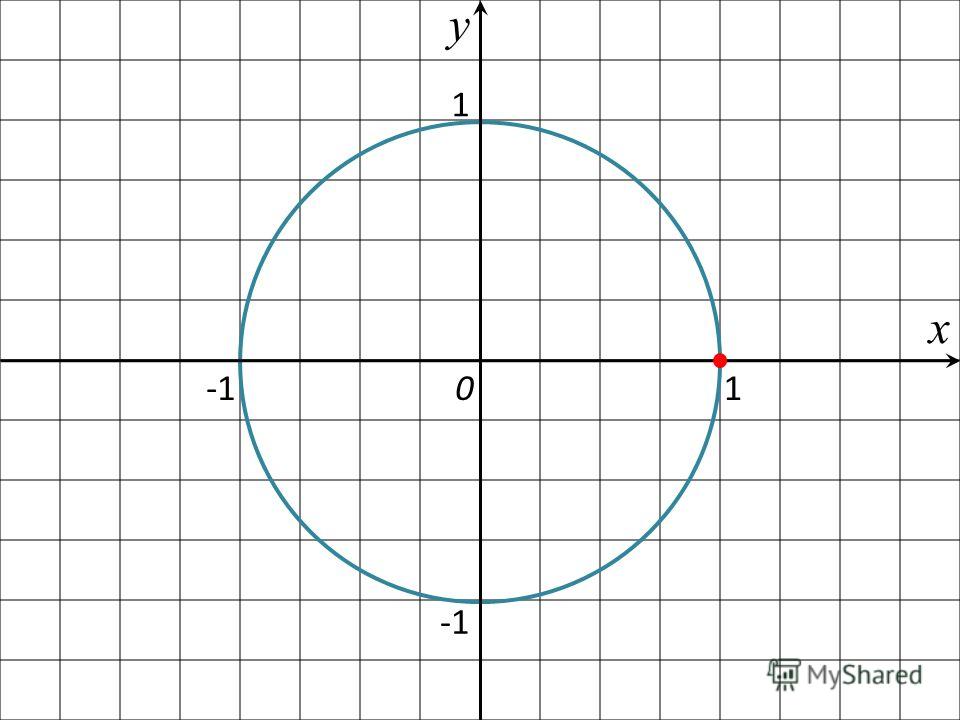 Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычислений опять же нетрудная: S = PR 2 . Эта формула и наш онлайн-калькулятор поможет вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует выполнение вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычислений опять же нетрудная: S = PR 2 . Эта формула и наш онлайн-калькулятор поможет вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует выполнение вычислений и их молниеносное выполнение.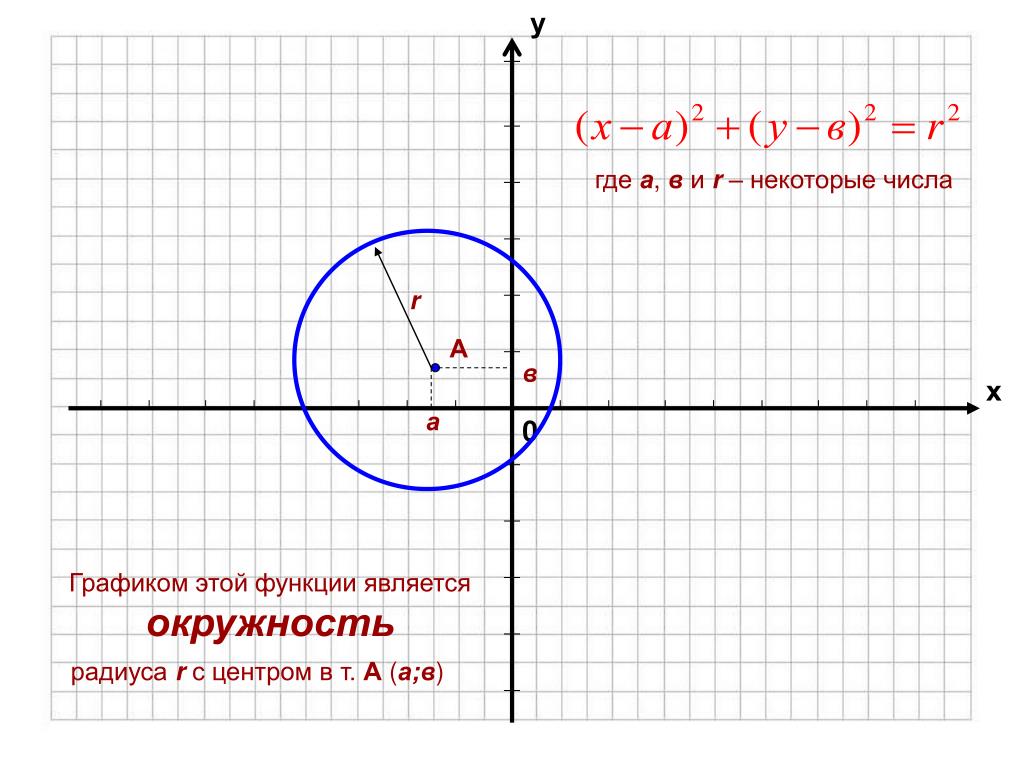 Она была при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы указан радиус, диаметр, диаметр, диаметр окружности, площадь круга или площадь шара. Так же вы можете применить его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы указан радиус, диаметр, диаметр, диаметр окружности, площадь круга или площадь шара. Так же вы можете применить его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, которая образует острый угол с плоскостью.
Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, которая образует острый угол с плоскостью. 5)
5) Если эллипс задан каноническим уравнением (12.4), то его осями симметрии оси и, начало координат — центр симметрии. Доказательство .Можно было бы провести доказательство на основе уравнения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического мы проведем доказательство на основе уравнений (12.4).
Если эллипс задан каноническим уравнением (12.4), то его осями симметрии оси и, начало координат — центр симметрии. Доказательство .Можно было бы провести доказательство на основе уравнения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического мы проведем доказательство на основе уравнений (12.4). Наконец точка является симметричной точкой относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе.Итак, предложение доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью.
Наконец точка является симметричной точкой относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе.Итак, предложение доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью.
 5) для величины, а именно,.
5) для величины, а именно,. После создания рисунка следует проводить более точно информацию о координатах его точек. Нужно построить по точкам верхнюю половину эллипса как график функции, взяв для построения много точек, используя его симметрию. С другими способами эллипса можно познакомиться в курсе черчения.
После создания рисунка следует проводить более точно информацию о координатах его точек. Нужно построить по точкам верхнюю половину эллипса как график функции, взяв для построения много точек, используя его симметрию. С другими способами эллипса можно познакомиться в курсе черчения. Найдите его фокусы и эксцентриситет.
Найдите его фокусы и эксцентриситет. Кривые второго порядка
Кривые второго порядка 
 Окружность
Окружность 

 Эллипс
Эллипс 
 е.
е. 

Ваш комментарий будет первым