Построить линию в полярной системе координат онлайн: Построить график в полярных координатах на плоскости

Содержание

Двойные интегралы в полярных координатах: теория и примеры

Что значит вычислить двойной интеграл полярных координатах?
Пределы интегрирования в повторных интегралах
Решения двойных интегралов в полярных координатах: примеры

Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ:

Что представляет собой элемент площади dxdy, выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const. Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы

φ и φ + dφ и линии окружности с радиусом r и r + dr. Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ. Поэтому элемент площади в полярных координатах выражается следующим образом:

dxdy = rdrdφ,

а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ, а внутренний — по радиусу r.

Вычислить двойной интеграл в полярных координатах

— значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D.

При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.

Случай первый

Полюс O является внутренней точкой области интегрирования D, область ограничена линией r = r(φ).

Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

Случай второй

Полюс O находится на границе области интегрирования

D, ограниченного линией r = r(φ), но не является угловой точкой.

Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

Случай третий

Полюс O находится на границе области интегрирования D, ограниченного линией r = r(φ), и является угловой точкой.

Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы α и β. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны

α и β, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый

Полюс O находится вне области интегрирования D.

Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы α и β, а область D ограничивают линии r = r1(φ) и r = r2(φ). Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β, а внутреннего интеграла — r1(φ) и r2(φ). Переход к повторным интегралам осуществляется следующим образом:

Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями , , .

Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.

Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D, приводим к полярным координатам:

Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):

Пример 2. В повторном интеграле

перейти к полярной системе координат.

Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x², а сверху — прямой y = 1. Область интегирования изображена на следующем чертеже.

При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1, в третьей области — от 0 до параболы.

Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1). В первой точке полярный угол составляет , во второй точке он составляет . Поэтому в первой области φ меняется от от 0 до , во второй области — от 0 до , в третьей области — от до π.

Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1: или . Найдём уравнение параболы y = x² в полярной системе координат:

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Пример 3. Вычислить в полярных координатах двойной интеграл

где область

D ограничена линией окружности .

Решение. Строим на чертеже область интегрирования.

Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a. В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности касается оси Oy, поэтому полярный угол в области интегрирования меняется от до . Подставим и в уравнение окружности и получим

Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:

Наконец, находим двойной интеграл в полярных координатах:

В полученном выражении второе слагаемое равно нулю, так как и sinπ, и sin(−π) равны нулю. Продолжая, получаем:

Пример 4. Вычислить плоской фигуры, которую ограничивают линии , , , .

Решение. Построим заданную фигуру на следующем рисунке.

Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:

Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:

Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями и .

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.

В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Кратные и криволинейные интегралы

Вычисление двойных интегралов

Двойные интегралы в полярных координатах
Вычисление тройных интегралов
Вычисление криволинейных интегралов
Интегралы по замкнутому контуру, формула Грина
Вычисление поверхностных интегралов

Поделиться с друзьями

Как построить линию в полярных координатах?

Собственно:

– Сначала нужно построить полярную систему координат: отметить полюс, изобразить полярную ось и указать масштаб. Впрочем, этот пункт можно выполнить позже.

– Определяем область определения функции – угловые секторы, в которых линия существует, и в которых нет. Тонко прочерчиваем соответствующие угловые направления (прямые и / или лучи, разграничивающие эти секторы). Лучше пунктиром.

– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.

– На следующем шаге следует прочертить угловые направления точек (тонкие прямые) и отметить на них найденные точки. Как это сделать с помощью каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил выше.

– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).

Отработаем алгоритм на более основательных типовых задачах:

Задача 120

Построить по точкам линию, заданную в полярной системе координат уравнением , рассматривая значения угла с интервалом в рад. Найти уравнение линии в прямоугольной системе координат.

Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
Неравенство опять же удобно решить графически. Мысленно либо на черновике изобразите график косинуса (см. Приложение Тригонометрия) и прямой . Что означает неравенство ? Оно означает, что нас устраивает та часть косинусоиды, которая не ниже прямой . График косинуса полностью удовлетворяет этому условию, поэтому может принимать любые значения, и нам предстоит «перепахать» весь круг от 0 до , причём, по условию сделать это требуется строго с интервалом в рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:

и так далее, пока не будет пройден весь оборот до «двух пи»…., но хочется ли вам сидеть с калькулятором… и ложкой? J Используйте Приложение Геометрический Калькулятор, который позволит буквально в пару щелчков вычислить все значения !
Вычисления, как правило, не расписывают подробно, а сразу заносят их результаты в таблицу:

Изобразим на чертеже полярную систему координат и угловые направления – тонкие прямые, соответствующие вышеуказанным углам. Здесь можно опять воспользоваться Геометрическим Калькулятором, где все направления уже прочерчены, но вы должны быть готовы к самым суровым обстоятельствам 🙂

Если у вас под рукой нет ни программы, ни транспортира, ни даже линейки, то используйте мой handmade-продукт – выполните этот чертёж, ориентируясь по клеточкам:

(углы проставлены для удобства, и на чистовике их записывать не надо)
До сих пор бережно храню этот листок бумаги, чтобы лет через 10-20 продать его антикварном аукционе J

… Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта. КИЛОбайта. При этом программисты умудрялись заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим больше двух десятилетий.

После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:

Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем,
а слишком малые значения для углов допустимо отметить и «на глазок».

Данная кривая называется кардиоидой. Найдём её уравнение в декартовой системе координат. Для этого используем знакомый приём – домножим обе части уравнения на «эр»:

И по формулам перехода к прямоугольным координатам , получим:

Перенесём «икс» налево и возведём обе части в квадрат:

Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, и обратите внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших порядков посвящены серьёзные исследования, и желающие без труда могут отыскать море информации по данной теме. Хорошая тема для курсовика, кстати, или реферата. Ну а я, как обычно, предлагаю полезную и здоровую пищу на каждый день:

Задача 121

Линия задана уравнением в полярной системе координат. Треба:

1) построить линию по точкам, придавая значения через интервал , начиная
с и заканчивая ;

2) найти уравнение линии в декартовой системе координат;

3) определить вид кривой.

Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения,
а нередко и чертыханья студента. Но только не того, кто прочитал эту книгу! Примерный образец оформления задачи в конце урока.

Рассмотрим ряд других важных особенностей решения:

Задача 122

Линия задана уравнением в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от до и придавая значения через промежуток ;

2) найти уравнение данной линии в прямоугольной системе координат;

3) назвать линию, найти координаты фокусов и эксцентриситет.

Решение: 1) найдём область определения: .
Заметьте, что ноль в знаменателе нас тоже не устраивает, и поэтому неравенство строгое. Перенесём косинус направо: и развернём избушку – к нам передом, а к лесу задом:

Неравенство несложно решить аналитически, но для лучшего понимания я опять воспользуюсь графическим методом. Мысленно или на черновике изобразим графики , при этом нас будет интересовать только один период – от до :

Условию удовлетворяет та часть синусоиды, которая расположена ПОД прямой .

То есть, в нашем распоряжении оказываются почти все значения угла за исключением «макушки», расположенной на симметричном отрезке .
Таким образом, . Арккосинус составляет примерно , поэтому из рассмотрения исключаем углы и . Заполним расчётную таблицу с прочерками в соответствующих ячейках:

Изобразим полярную систему координат и лучи , между которыми нет точек линии. Прочертим угловые направления найденных точек и с помощью циркуля сделаем засечки. Аккуратно соединим отмеченные точки линией (точки, соответствующие углам , не вместились на чертёж):
2) Найдём уравнение линии в прямоугольной системе координат. Судя по всему должна получиться гипербола. Избавляемся от дроби:

Используем формулы перехода

и дальнейшее знакомо из задач с линиями второго порядка:

– искомое уравнение.

3) Данная линия представляется собой гиперболу с центром симметрии в точке , действительной полуосью , мнимой полуосью .
Вы спрОсите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли сейчас говорить о целой гиперболе?». Не ошибочно! И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае всё получается ловко и очень хитро – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.

Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.

Вычислим значение и поправкой на параллельный перенос в точку найдём фокусы:

Эксцентриситет:

Готово. Педантичные люди могут ещё записать развёрнутый ответ.

Заключительное задание для самостоятельного решения:

Задача 123

Линия задана уравнением в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от до и придавая значения через промежуток ;

2) найти уравнение данной линии в прямоугольной системе координат и определить её вид;

3) привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.

Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз «налетал» – краем глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к каноническому виду выполнено строгим академическим способом.

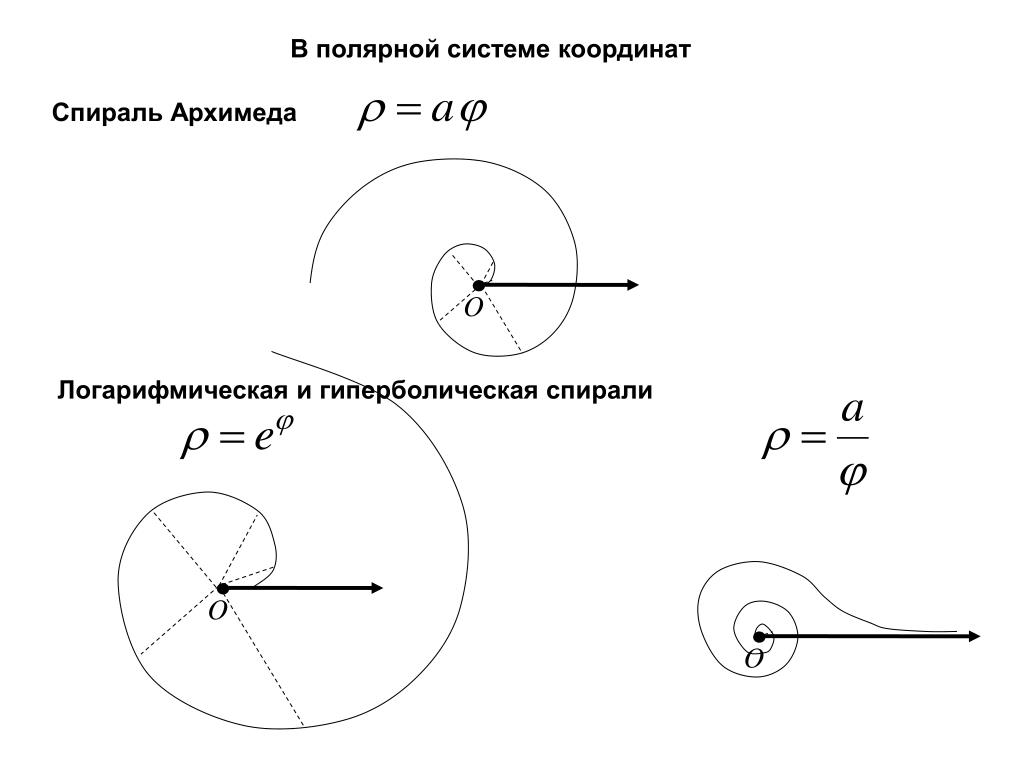
Когда удобно использовать полярные координаты? Ну, конечно, когда мы имеем дело со всевозможными окружностям, дугами, кругами, эллипсами, спиралями и т.д. А причина простА – уравнения получаются простые.

На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в воздушной навигации и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что «распиаренная» прямоугольная система координат как-то здесь совсем «не в тему».

5.1.1. Понятие плоскости в пространстве

4.5. Полярная роза

| Оглавление |

Автор: Aлeксaндр Eмeлин

Полярные координаты | Алгебра и тригонометрия
Цели обучения
В этом разделе вы будете:
Наносить точки с помощью полярных координат.
Преобразовать полярные координаты в прямоугольные.
Преобразовать прямоугольные координаты в полярные.
Преобразование уравнений между полярной и прямоугольной формами.
Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
На расстоянии более 12 км от порта парусник попадает в непогоду и сбивается с курса ветром силой 16 узлов (см. (рисунок)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Рисунок 1.
Построение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах[латекс]\,\влево(х,у\вправо)\,[/ латекс] в декартовой плоскости координат. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные [латекс]\,\левый(r,\тета\правый)\,[/латекс] и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью x-, которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата[latex]\,r\,[/latex] — это радиус или длина направленного отрезка прямой от полюса. Угол[латекс]\,\тета,[/латекс], измеренный в радианах, указывает направление[латекс]\,r.\,[/латекс]Мы двигаемся против часовой стрелки от полярной оси на угол[латекс]\ ,\theta ,[/latex]и измерьте направленный отрезок длины[latex]\,r\,[/latex]в направлении[latex]\,\theta .\,[/latex]Хотя мы сначала измерьте [латекс]\,\тета \,[/латекс], а затем [латекс]\,r,[/латекс] полярная точка записывается с помощью r -координата первая. Например, чтобы построить точку [латекс]\,\влево(2,\фракция{\пи} {4}\вправо),[/латекс] мы должны переместить[латекс]\,\фракция{\пи} {4 }\,[/latex]единицы в направлении против часовой стрелки, а затем длину 2 от полюса. Эта точка нанесена на сетку (рисунок).
Рис. 2.
Построение точки на полярной сетке полярная сетка.
Показать решение
Попробуй
Нанесите точку[латекс]\,\влево(2,\,\frac{\pi }{3}\вправо)\,[/латекс]в полярную сетку.
Показать решение
Нанесение точки в полярной системе координат с отрицательной составляющей на полярной сетке.
Показать решение
Попробуйте
Нанесите точки [латекс]\,\влево(3,-\frac{\pi }{6}\right)[/латекс]и[латекс]\,\влево(2,\frac{ 9\pi }{4}\right)\,[/latex]на той же полярной сетке.
Показать решение
Преобразование полярных координат в прямоугольные координаты
Когда задан набор полярных координат, нам может потребоваться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными [latex]\,x,\,y,\,r,\,[/latex] и [latex]\,\theta . [/latex]
[латекс]\begin{array}{l}\begin{array}{l}\\ \mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\ ,\theta \end{массив}\hfill \\ \mathrm{sin}\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta \hfill \end{массив }[/латекс]
При опускании перпендикуляра из точки плоскости на ось x- образуется прямоугольный треугольник, как показано на (Рисунок). Простой способ запомнить приведенные выше уравнения — представить [латекс]\,\mathrm{cos}\,\тета \,[/латекс] как примыкающую сторону к гипотенузе и [латекс]\,\mathrm{sin} \,\theta\,[/latex] как противоположная сторона гипотенузы.
Рисунок 5.
Преобразование полярных координат в прямоугольные
Преобразование полярных координат [латекс]\,\left(r,\,\theta \right)\,[/latex]в прямоугольные координаты[латекс ]\,\left(x,\,y\right),[/latex] пусть
[латекс]\mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\,\theta [/latex]
[латекс]\mathrm{sin }\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta [/latex]
How To
Учитывая полярные координаты, преобразовать в прямоугольные координаты.

Учитывая полярную координату [латекс]\,\влево(г,\тета \вправо),[/латекс] напишите[латекс]\,х=г\mathrm{cos}\,\тета \,[ /латекс] и [латекс]\,y=r\mathrm{sin}\,\тета .[/латекс]
Оценить [латекс]\,\mathrm{cos}\,\theta \,[/latex]и[латекс]\,\mathrm{sin}\,\theta .[/latex]
Умножьте [латекс]\,\mathrm{cos}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату x- прямоугольной формы.
Умножьте [латекс]\,\mathrm{sin}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату y- прямоугольной формы.
Запись полярных координат в виде прямоугольных координат
Запись полярных координат [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] в виде прямоугольных координат.
Показать решение
Запись полярных координат в виде прямоугольных координат
Запись полярных координат[латекс]\,\влево(-2,0\вправо)\,[/латекс]в виде прямоугольных координат.
Показать решение
Попробуйте
Запишите полярные координаты[латекс]\,\влево(-1,\фракция{2\пи }{3}\вправо)\,[/латекс]в виде прямоугольных координат.
Показать решение
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 9{2}\hfill \\ \mathrm{tan}\,\theta =\frac{y}{x}\,\hfill \end{array}[/latex]
Рис. 8.
Запись прямоугольных координат as Полярные координаты
Преобразовать прямоугольные координаты[латекс]\,\влево(3,3\вправо)\,[/латекс]в полярные координаты.
Показать решение
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки[латекс]\,\влево(-3\sqrt{2},\,\frac{5\pi }{4}\right)\,[/latex]и[латекс]\,\влево (3\sqrt{2},-\frac{7\pi }{4}\right)\,[/latex] совпадет с исходным решением [latex]\,\left(3\sqrt{2}, \,\frac{\pi }{4}\right).\,[/latex]Точка[латекс]\,\left(-3\sqrt{2},\,\frac{5\pi }{4 }\right)\,[/latex]обозначает движение против часовой стрелки на [latex]\,\pi ,\,[/latex], которое прямо противоположно [latex]\,\frac{\pi }{4}.\ ,[/latex]Радиус выражается как [латекс]\,-3\sqrt{2}.\,[/latex]Однако угол[латекс]\,\frac{5\pi }{4}\, [/latex] находится в третьем квадранте, и, поскольку [latex]\,r\,[/latex]отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и [латекс]\,\left(3\sqrt{2},\,\,\frac{\pi }{4}\right).\,[/latex]Точка [латекс]\ ,\left(3\sqrt{2},\,-\frac{7\pi }{4}\right)\,[/latex] — ход дальше по часовой стрелке на [latex]\,-\frac{7\ pi }{4},\,[/latex]из [латекса]\,\frac{\pi }{4}.\,[/latex]Радиус,[латекс]\,3\sqrt{2},\ ,[/латекс]то же самое.
Преобразование уравнений между полярной и прямоугольной формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
How To
Имея уравнение в полярной форме, постройте его график с помощью графического калькулятора.

Измените MODE на POL , представляя полярную форму.
Нажмите кнопку Y= , чтобы открыть экран, позволяющий ввести шесть уравнений: [латекс]\,{r}_{1},\,\,{r}_{2},\,\,. \,\,.\,\,.\,\,\,\,{r}_{6}.[/латекс]
Введите полярное уравнение, установите его равным [латекс]\,r.[/латекс]
Пресс ДИАГРАММА 9{2}\,[/latex] в полярной форме.
Показать решение
Идентификация и построение полярных уравнений путем преобразования в прямоугольные уравнения
Мы узнали, как преобразовывать прямоугольные координаты в полярные координаты, и мы увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Построение графика полярного уравнения путем преобразования в прямоугольное уравнение
Преобразуйте полярное уравнение[латекс]\,r=2\mathrm{sec}\,\theta \,[/латекс] в прямоугольное уравнение и нарисуйте соответствующий график.
Показать решение
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение[latex]\,r=\frac{3}{1-2\mathrm{cos}\,\theta }\,[/latex]в виде декартова уравнение.
Показать решение
Анализ
В этом примере правая часть уравнения может быть расширена, а уравнение еще больше упрощено, как показано выше. Однако уравнение нельзя записать в виде одной функции в декартовой форме. Мы можем захотеть записать прямоугольное уравнение в стандартной форме гиперболы. Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]
Попробуйте
Перепишите полярное уравнение[latex]\,r=2\mathrm{sin}\,\theta \,[/latex] в декартовой форме.
Показать решение
Переписать полярное уравнение в декартовой форме
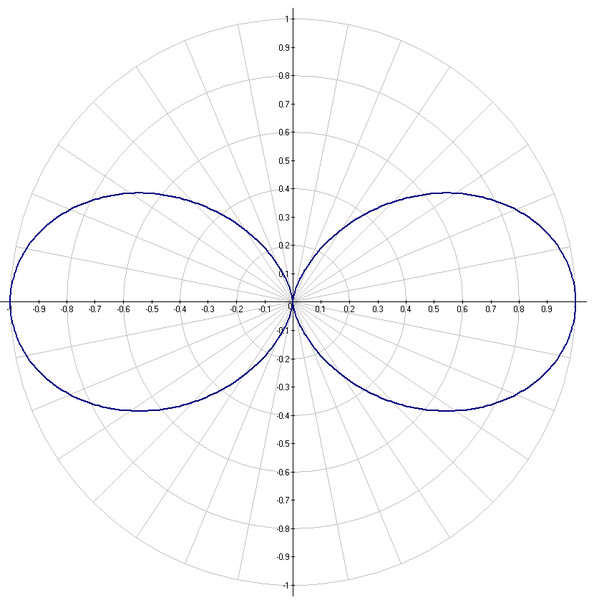
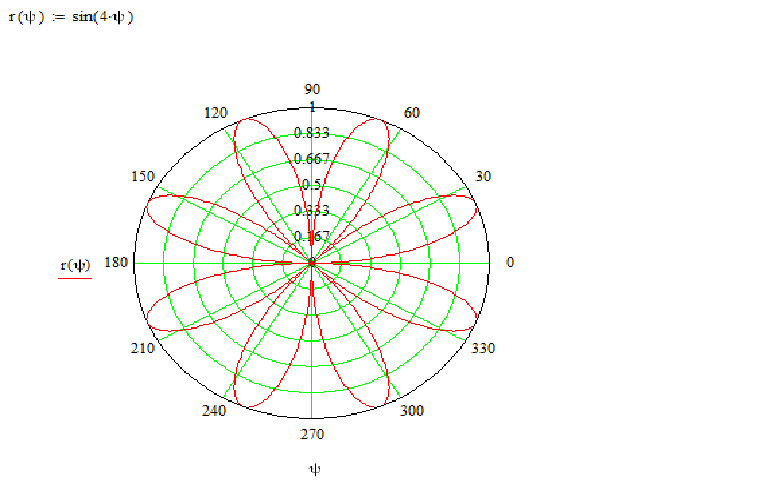
Переписать полярное уравнение[латекс]\,r=\mathrm{sin}\left(2\theta \right)\,[/latex]в декартовой форме.
Показать решение
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными координатами. 9{2}\hfill \\ \hfill & \mathrm{tan}\,\theta =\frac{y}{x}\hfill \end{массив}[/latex]
Ключевые понятия
Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или исходной точки.
Чтобы нанести точку в виде [латекс]\,\влево(r,\тета\вправо),\,\тета >0,\,[/латекс] переместите против часовой стрелки от полярной оси на угол [латекс]\,\theta ,\,[/латекс], а затем продлите направленный отрезок от полюса на длину [латекс]\,r\,[/латекс] в направлении [латекс]\,\тета .\,[/latex]Если [латекс]\,\тета \,[/латекс]отрицательно, двигайтесь по часовой стрелке и продолжайте направленный отрезок на длину [латекс]\,r\,[/латекс ] в направлении[латекс]\,\тета .[/латекс] См. (рисунок).
Если [латекс]\,r\,[/латекс]отрицательно, удлините направленный отрезок в направлении, противоположном [латекс]\,\тета .\,[/латекс]См. (рисунок).
Чтобы преобразовать полярные координаты в прямоугольные, используйте формулы [латекс]\,x=r\mathrm{cos}\,\theta \,[/latex] и [латекс]\,y=r\mathrm{sin} \,\theta .\,[/latex] См. (Рисунок) и (Рисунок).
Чтобы преобразовать прямоугольные координаты в полярные, используйте одну или несколько формул: [латекс]\,\mathrm{cos}\,\theta =\frac{x}{r},\mathrm{sin}\,\ theta =\frac{y}{r},\mathrm{tan}\,\theta =\frac{y}{x},\,[/latex]and[latex]\,r=\sqrt{{x} ^{2}+{y}^{2}}. \,[/latex] См. (рисунок).
Преобразование уравнений между полярной и прямоугольной формой означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. (Рисунок), (Рисунок) и (Рисунок).
Использование соответствующих замен позволяет переписать полярное уравнение как уравнение прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. (Рисунок), (Рисунок) и (Рисунок).
Упражнения по разделам
Вербальные
Чем полярные координаты отличаются от прямоугольных координат?
Показать решение
Чем полярные оси отличаются от осей x и y декартовой плоскости?
Объясните, как изображаются полярные координаты.
Показать решение
Как расположены точки [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(-3,\frac{\ pi }{2}\right)\,[/latex]связаны?
Объясните, почему точки [латекс]\,\left(-3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(3,-\frac{ \pi }{2}\right)\,[/latex] одинаковы.
Показать решение
Алгебраический
Для следующих упражнений преобразуйте заданные полярные координаты в декартовы координаты с помощью [латекс]\,r>0\,[/латекс]и[латекс]\,0\le \theta \le 2\pi . \,[/latex]Не забывайте учитывать квадрант, в котором находится данная точка, при определении[latex]\,\theta \,[/latex]для точки.
[латекс]\влево(7,\фракция{7\пи }{6}\вправо)[/латекс]
[латекс]\влево(5,\пи \вправо)[/латекс]
Показать решение
[латекс]\влево(6,-\frac{\pi }{4}\вправо)[/латекс]
[латекс]\влево(-3,\frac{\pi }{6}\вправо)[/латекс]
Показать решение
[латекс]\left(4,\frac{7\pi }{4}\right)[/latex]
В следующих упражнениях преобразуйте заданные декартовы координаты в полярные координаты с помощью [латекс]\,r> 0,\,\,0\le \theta <2\pi .\,[/latex]Не забудьте рассмотреть квадрант, в котором находится данная точка.
[латекс]\влево(4,2\вправо)[/латекс]
Показать решение
[латекс]\влево(-4,6\вправо)[/латекс]
9{2}=9x[/latex]
[latex]9xy=1[/latex]
Показать решение
Для следующих упражнений преобразуйте данное полярное уравнение в декартово уравнение. Если возможно, напишите в стандартной форме коники и определите представленное коническое сечение.
[латекс]r=3\mathrm{sin}\,\theta [/latex]
[латекс]r=4\mathrm{cos}\,\theta [/latex]
Показать решение
[латекс]r=\frac{4}{\mathrm{sin}\,\theta +7\mathrm{cos}\,\theta}[/latex]
[латекс]r=\frac{6} {\ mathrm {cos} \, \ theta +3 \ mathrm {sin} \, \ theta} [/ латекс] 9{2}=4[/latex]
Показать решение
[латекс]r=\frac{1}{4\mathrm{cos}\,\theta -3\mathrm{sin}\,\theta}[/latex]
[латекс]r=\frac{3 }{\mathrm{cos}\,\theta -5\mathrm{sin}\,\theta }[/latex]
Показать решение
Графический
Для следующих упражнений найдите полярные координаты точки.
Показать решение
Показать решение
Для следующих упражнений отметьте точки.
[латекс]\влево(-2,\frac{\pi }{3}\вправо)[/латекс]
Показать решение
[латекс]\влево(-1,-\frac{\pi }{2}\right)[/latex]
[латекс]\left(3.5,\frac{7\pi }{4}\right )[/latex]
Показать решение
[латекс]\влево(-4,\frac{\pi} {3}\вправо)[/латекс]
[латекс]\влево(5,\frac{\pi} {2}\вправо)[ /латекс]
Показать решение
[латекс]\left(4,\frac{-5\pi }{4}\right)[/latex]
[латекс]\left(3,\frac{5\pi }{6}\right )[/latex]
Показать решение
[латекс]\влево(-1,5,\фракция{7\пи }{6}\вправо)[/латекс] 9{2}=3x[/latex]
Показать решение
Для следующих упражнений преобразуйте уравнение из полярной формы в прямоугольную и постройте график на прямоугольной плоскости.
[латекс]r=6[/латекс]
[латекс]r=-4[/латекс]
Показать решение
[латекс]\theta =-\frac{2\pi }{3}[/latex]
[латекс]\theta =\frac{\pi }{4}[/latex]
Показать решение
[латекс]r=\mathrm{sec}\,\theta [/latex]
[латекс]r=-10\mathrm{sin}\,\theta [/latex]
Показать решение
[латекс]r=3\mathrm{cos}\,\theta [/латекс]
Технология
С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(2,-\frac{ \pi }{5}\right).\,[/latex]Округлите до тысячных.
Показать решение
С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(-3,\frac{3\pi }{7}\right).\,[/latex]Округлите до тысячных.
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(-7,8\вправо)\,[/латекс]в градусах. Округлить до тысячных.
Показать решение
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(3,-4\вправо)\,[/латекс]в градусах. Округлить до сотых.
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\левый(-2,0\правый)\,[/латекс]в радианах. Округлить до сотых.
Показать решение
Расширения
Описать график [латекс]\,r=a\mathrm{sec}\,\theta ;a>0.[/latex]
Описать график [латекс]\,r=a\ mathrm{sec}\,\theta ;a<0.[/latex]
Показать решение
Описать график [латекс]\,r=a\mathrm{csc}\,\theta ;a>0.[/latex]
Описать график [латекс]\,r=a\mathrm{csc }\,\theta ;a<0.[/latex]
Показать решение
Какие полярные уравнения дадут косую линию?
Для следующего упражнения постройте график полярного неравенства.
[латекс]r<4[/латекс]
Показать решение
[латекс]0\le \theta \le \frac{\pi }{4}[/latex]
[латекс]\theta =\frac{\pi }{4},\,r\,\ge \,2[/латекс]
Показать решение
[латекс]\theta =\frac{\pi }{4},\,r\,\ge -3[/latex]
[латекс]0\le \theta \le \frac{\pi }{ 3},\,r\,<\,2[/latex]
Показать решение
[латекс]\frac{-\pi }{6}<\theta \le \frac{\pi }{3},-3
Глоссарий
полярная ось
на полярной сетке, эквивалент положительной оси x- на прямоугольной сетке
полярные координаты
на полярной сетке координаты точки, помеченной угол поворота от полярной оси и [латекс]\,r\,[/латекс] представляет собой радиус или расстояние точки от полюса в направлении [латекс]\,\тета [/латекс]
полюс
происхождение полярной сетки
Как читать полярную диаграмму? — PlotDigitizer
Обновлено 2 года назад • 5 мин чтения
Полярные графики — это двумерная система координат, обычно используемая в навигации и изучении величин по направлениям. Как и в декартовой системе, полярная координата имеет две переменные (радиус и тета), однозначно определяющие точку.
Понимание полярных координат
Полярная система координат состоит из двух параметров: радиуса и тета. Радиус (r) — это расстояние между началом координат и точкой на полярном графике. Это ненаправленный параметр; это означает, что у него нет направления. Тета (θ), или более известная как угол, определяет угловое положение точки относительно базовой линии. В отличие от радиуса, тета направлена.
В декартовой системе координат мы определяем положение точки с помощью x и y, которые являются перпендикулярными расстояниями от обеих осей, тогда как в полярных координатах точка определяется с помощью r и θ.
В зависимости от направления измерения угла мы классифицируем полярные графики как против часовой стрелки и по часовой стрелке.
против часовой стрелки
Против часовой стрелки, как следует из названия, угол измеряется против часовой стрелки, противоположно тому, как движутся стрелки часов.
Всякий раз, когда мы измеряем угол, мы используем базовую линию, от которой измеряется угол. На приведенном ниже рисунке опорной линией является правая ось X. Мы начинаем измерять угол от этой линии, и угол равен 0 ° для всех точек на правой оси x.
Угол 90° для верхней оси Y. Точно так же угол составляет 180° и 270° для левой оси x и нижней оси y.
Центр является исходной точкой с нулевыми радиусами. Под углом 360° мы достигаем той же опорной линии, завершая весь круг.
Полярный график против часовой стрелки
На предыдущей диаграмме углы указаны как в градусах, так и в радианах.
По часовой стрелке
На полярной диаграмме по часовой стрелке углы измеряются в направлении стрелок часов, как показано на следующем рисунке.
Полярный график по часовой стрелке
Направления
Как упоминалось ранее, угол имеет направление. Если угол отрицательный, то направление измерения угла противоположно направлению графика.
На приведенной ниже полярной диаграмме 150° и −210° достигают одинакового положения. Угол -210° означает, что угол измеряется в направлении, противоположном направлению графика, то есть против часовой стрелки.
Углы 150° и -210° обозначают одно и то же положение.
Примеры полярных графиков
Давайте возьмем несколько основных примеров, чтобы лучше понять полярные графы.
Очки
На следующем графике есть несколько случайных точек. Мы хотим определить координаты (радиус, угол) каждого из них.
Полярный график с точками от P1 до P6
Точка P1 расположена на 30° и имеет радиус 3. Итак, координаты 3, 30°.
Таким же образом можно вычислить полярные координаты для остальных.
Полярные координаты точек от P1 до P6
Точка Радиус Угол
Р1 3 30° (или π/6)
Р2 4 150° (или 5π/6)
Р3 3 180° (или π)
Р4 4 240° (или 4π/3)
Р5 5 270° (или 3π/6)
Р6 2 330° (или 11π/6)
Уравнения
На следующей диаграмме есть линия и круг. Мы хотим определить уравнения этих кривых.
Полярная диаграмма с кругом и линией.
Линия проходит в начало координат и наклонена под углом 60° (или π/3). Итак, уравнение θ = π/3. Поскольку в уравнении нет члена радиуса, он не зависит от радиуса.
Окружность радиусом 3 с центром в начале координат. Итак, уравнение r = 3, и оно не зависит от тета.
То же самое уравнение в декартовой системе координат будет иметь вид y = tan(π/3) × x для прямой и x2 + y2 = 32 для окружности.
Это гораздо более простые уравнения; в большинстве уравнений будут присутствовать как r, так и θ.
Как читать и извлекать данные из полярного графика с помощью PlotDigitizer?
Вы можете читать и извлекать данные из полярного графика с помощью PlotDigitizer. PlotDigitizer — это программное обеспечение для извлечения данных, которое может извлекать данные из нескольких типов графиков, включая полярные. У него есть бесплатное онлайн-приложение. Другие графики: XY, троичные, круговая/бубликовая, гистограмма, столбец.
Вам необходимо выполнить несколько простых шагов. Мы возьмем следующий график в качестве примера нашего объяснения.
Полярный график
Шаг 1: Загрузка изображения полярного графика
Посетите https://plotdigitizer.com/app и загрузите или перетащите изображение.
Загрузите полярную диаграмму в PlotDigitizer
Шаг 2: Выбор типа диаграммы
По умолчанию используется тип графика XY, поэтому мы должны изменить его на полярный. Это может быть достигнуто с помощью меню выбора на панели окна.
Выбор типа графика в PlotDigitizer
Шаг 3: Калибровка графика
Теперь перетащите точку O в начало графика, поместите точку θ под любым известным углом. Здесь мы поместили θ на 30°. Переместите точку r на известный радиус.
Калибровка полярного графика
Введите значения θ и r на боковой панели. Здесь r = 15 и θ = 30°. Полярная диаграмма направлена против часовой стрелки, поэтому направление сохраняется против часовой стрелки.
Ввод значений точки r и точки θ
Можно использовать панель масштабирования (или лупу) для повышения точности разметки.