Задание по Excel № 2 » Построение графика кусочной функции»
Построить график кусочной функции на участке [a;b] с шагом 0,5.
№ Вар | Функция | [a;b] |
1. | [-7;7] | |
2. | [-7;7] | |
3. | [-5;5] | |
4. | [-5;5] | |
5. | ||
6. | [-7;7] | |
7. | [-10;10] | |
8. | [-10;10] | |
9. | [-4;10] a-коэф-т | |
10. | [-10;10] | |
11. | [-5;8] с-коэф-т | |
12. | [-4;4] a-коэф-т | |
13. | [-4;4] | |
14. | [-10;10] с-коэф-т | |
15. | [-10;10] d-коэф-т | |
16. | [-7;7] | |
17. | [-7;7] | |
18. | [-30;30] | |
19 | [-30;30] | |
20. | ||
21. | [-10;10] | |
22. | < | [-3;3] |
23. | [-10;10] | |
24. | [-10;10] | |
25. | [-5;6] a-коэф-т | |
26. | [-5;5] b-коэф-т | |
27. | [-10;10] | |
28. | [-8;8] d-коэф-т | |
29. | [-5;6] a-коэф-т | |
30. | [-7;7] d-коэф-т |
Получить матрицу значений функции в виде двумерной таблицы. Для этого задать изменение двух аргументов функции в виде числовых рядов, расположенных под прямым углом друг к другу. Вычислить значение функции для каждой пары аргументов. Шаг 0,1
x\y
-4
-3.5 -3
….
0
0.5
1
Z(x,y)
1.
 5
5…
Внимание! Формула для вычисления значения функции должна быть набрана один раз, затем скопирована.
Выполнить построение трехмерной поверхности. Сравнить получившийся результат с образцом.
№ | Уравнение и диапазон аргументов | Вид графика | № | Уравнение и диапазон аргументов | Вид графика |
1 | x=[-5;5] y=[-5;5] a=2 b=7 | 8 | x=[-2;2] y=[—2×p ; 2×p] a=2 | ||
2 | x=[-5;5] y=[-5;5] a=2 b=5 | 9 | x=[-1;1] y=[—2×p ; 2×p] a=10 b=2 | ||
3 | x=[-5 ; 5] y=[-2 ; 2] a=1. b=0.5 | x=[—p ; p] y=[—p ; p] a=2 | |||
4 | x=[-5;5] y=[-5;5] a=0.7 | 11 | x=[—p ; p] y=[—p ; p] a=0.5
| ||
5 |
x=[—2×p ; 2×p] y=[—2×p ; 2×p] a=2 b=5 | 12 | x=[—p ; p] y=[—p ; p] a=4 | ||
6 | x=[—p ; p] y=[—p ; p] a=3 | 13 | x=[-2;2] y=[-2;2] a=0. | ||
7 | x=[ —p ; p] y=[ —p ; p] a=3 | 14 | x=[-2;2] y=[-2;2] a=2 | ||
15 | x=[-2;2] y=[-2;2] a=2 | 22 | x=[0.01 ; 2×p] y=[0.01 ; 2×p] a=200 | ||
16 | x=[-5;5] y=[-5;5] a=2 b=1 | 23 | x=[0. y=[0.01 ; p] a=200 | ||
17 | x=[-5;5] y=[-5;5] a=0.3 | 24 | x=[-3’3] y=[-1;6] a=50 | ||
18 | x=[-5;5] y=[-5;5] a=0.3 | 25 | x=[-3;3] y=[-3;3] a=0.5 | ||
19 | x=[-5;5] y=[-5;5] a=5 | 26 | x=[-3;3] y=[-3;3] a=2 b=3 | ||
20 | x=[-5;5] y=[-5;5] a=0. |
| x=[—p/2 + 0.05] ; p/2 — 0.05] y=[—p/2 + 0.05] ; p/2 — 0.05] a=0.1 b=2 | ||
21 | x[0.1;1] y[0.1;1] a=0.1 | 28 | x[—p/4 + 0.05] ; p/4 — 0.05] y[—p/4 + 0.05] ; p/4 — 0.05] a=2 b=1 |
y=
Задание №1 по MathCAD «Двумерные графики, заданные в параметрическом виде, и графики, заданные в полярных координатах»
Задание:
1. Построить
два графика;
Построить
два графика;
2. Вывести таблицу значений функции, заданной в параметрическом виде;
3. При сдаче работы уметь:
перевести полярные координаты в декартовы;
отобразить несколько зависимостей на одном графике.
Указания к работе:
1. Для построения XY-графика, заданного в параметрическом виде необходимо:
указать диапазон и шаг изменения параметра в виде . Знак «:=» вводится с помощью английского знака «:». Символ «..» вводится с помощью символа «;»
№ Вар | Функция, заданная в параметрическом виде | Функция, заданная в полярных координатах |
1 | ||
2 | ||
3 | ||
4 | ||
5 | ||
6 | ||
7 | ||
8 | ||
9 | ||
10 | ||
11 | ||
12 | ||
13 | ||
14 | ||
15 | ||
16 | ||
17 | ||
18 | ||
19 | ||
20 | ||
21 | ||
22 | ||
23 | ||
24 | ||
26 | ||
27 | ||
28 | ||
29 |
задать зависимость ;
“Graph”à
“Create
XY-Plot”.
2. В полярной системе координат каждая точка задается углом и радиусом определенной длины. Длина радиуса находится в определенной зависимости от полярного угла. Для построения графика, заданного в полярных координатах необходимо:
указать диапазон и шаг изменения полярного угла в радианах , например ;
задать зависимость
“Graph”à “Create Polar Plot”.
Непрерывность функции в точке и на промежутке. С примерами
- Примеры и условия непрерывности функции. Непрерывность в точке и на промежутке
- Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение
- Что такое непрерывное изменение функции
- Основные свойства непрерывных функций
На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это
с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на
то что записываются как и
.
Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.
Графически функция непрерывна в точке , если её график не «разрывается» в этой точке. График такой непрерывной функции — показан на рисунке ниже.
Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:
1. Функция определена в точке .
2. Существует предел функции в точке ,
при этом правый и левый пределы равны: . Правый и левый
пределы вычисляются как предел вообще: в выражение функции
вместо икса подставляется то, к чему стремится икс, причём вместе с плюс нулём при правом пределе и с минус нулём
при левом пределе.
3. Предел функции в точке равен значению функции в этой точке:
А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому стремится икс, прибавляется или вычитается всего лишь нуль? Могут. Когда и почему — это объяснено на уроке о точках разрыва функции и их видах.
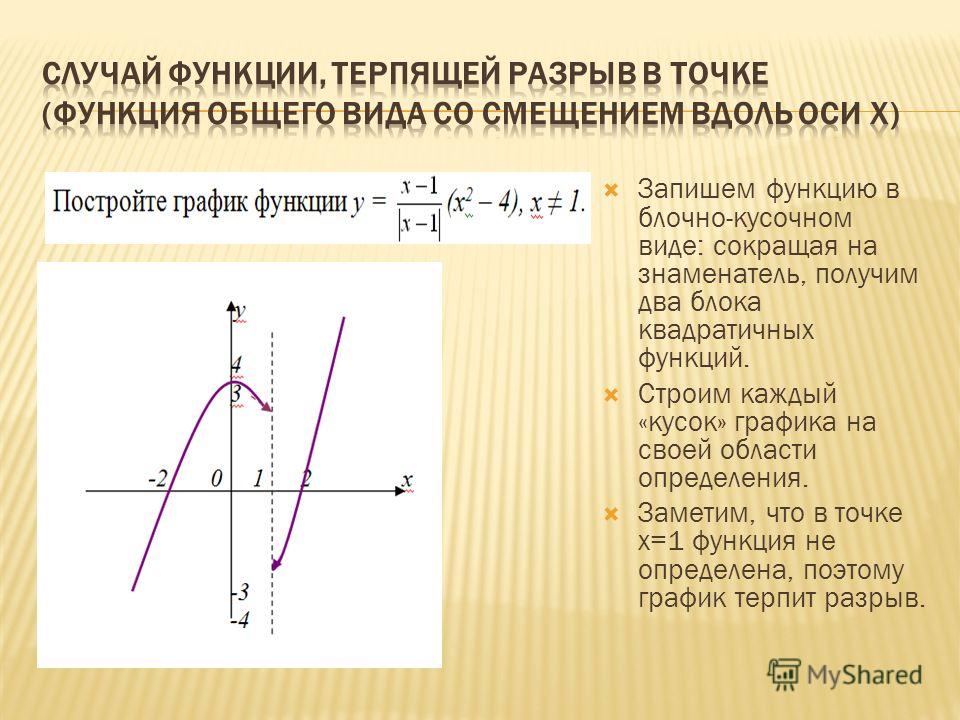
Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 — на рисунке ниже.
Пример 1. Функция f(x) определена следующим образом:
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0, x = 1, x = 3?
Решение. Проверяем все три условия непрерывности функции в каждой
граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из
граничных точек, следует из определения функции. Осталось проверить остальные два условия.
Проверяем все три условия непрерывности функции в каждой
граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из
граничных точек, следует из определения функции. Осталось проверить остальные два условия.
Точка x = 0. Найдём левосторонний предел в этой точке:
.
Найдём правосторонний предел:
.
Предел функции и значение функции в точке x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
.
Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0.
Точка x = 1. Найдём левосторонний предел в этой точке:
.
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 1
должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
Находим их:
.
Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1.
Точка x = 3. Найдём левосторонний предел в этой точке:
Найдём правосторонний предел:
Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
.
Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3.
Основной вывод: данная функция является непрерывной в каждой граничной точке.
Пример 2. Установить, непрерывна ли функция в точке x = 2.
Правильное решение и ответ.
Пример 3. Установить, непрерывна ли функция в точке x = 8.
Правильное решение и ответ.
Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .
Проиллюстрируем это непрерывное изменение функции на примере.
Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m, то есть l = f(m), m≥0.
Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l. Однако если масса
груза близка к пределу прочности
нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию
от точки подвеса до поверхности стола.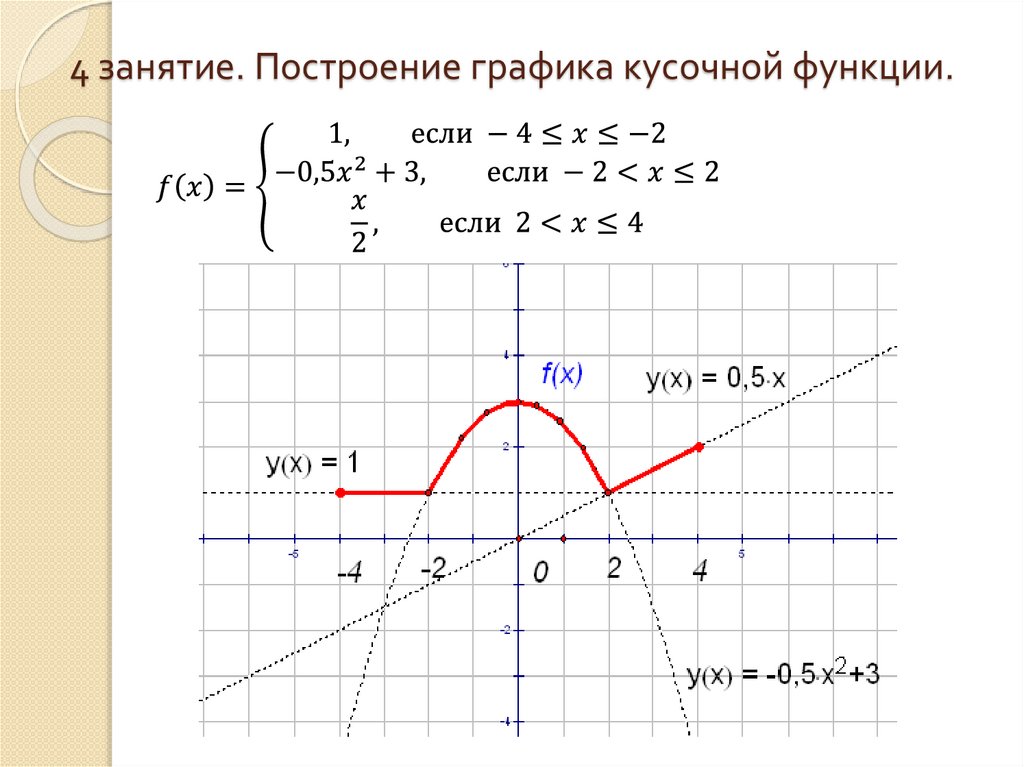 График функции l = f(m)
изображён на рисунке. На участке
этот график является непрерывной (сплошной) линией, а в точке
он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках,
кроме , функция l = f(m) непрерывна,
а в точке
она имеет разрыв.
График функции l = f(m)
изображён на рисунке. На участке
этот график является непрерывной (сплошной) линией, а в точке
он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках,
кроме , функция l = f(m) непрерывна,
а в точке
она имеет разрыв.
Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика.
Непрерывность функции на промежутке
Пусть функция y = f(x)
определена в интервале ]a, b[
и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в
интервале ]a, b[. Аналогично
определяется понятие непрерывности функции на промежутках вида
]- ∞, b[,
]a, + ∞[,
]- ∞, + ∞[.
Пусть теперь функция y = f(x)
определена на отрезке [a, b].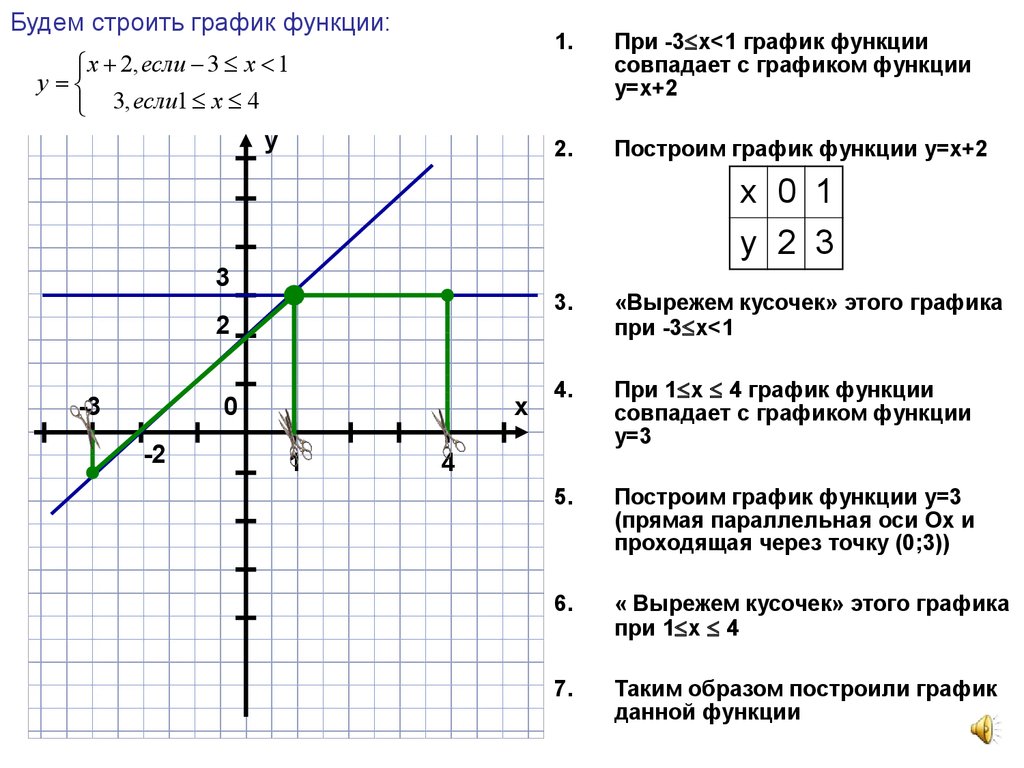 Разница между интервалом и отрезком: граничные точки интервала не входят в интервал,
а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой
односторонней непрерывности: в точке a, оставаясь на отрезке [a, b],
мы можем приближаться только справа, а к точке b —
только слева. Функция называется непрерывной на отрезке [a, b],
если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b.
Разница между интервалом и отрезком: граничные точки интервала не входят в интервал,
а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой
односторонней непрерывности: в точке a, оставаясь на отрезке [a, b],
мы можем приближаться только справа, а к точке b —
только слева. Функция называется непрерывной на отрезке [a, b],
если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b.
Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a, b], функция непрерывна на отрезке [0, b], функция непрерывна на любом отрезке, не содержащем точку a = 2.
Пример 4. Исследовать функцию
на непрерывность.
Решение. Проверяем первое условие. Функция не определена в точках — 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах
.
Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Найдём правосторонний предел при :
.
Очевидно, что значение в точке x = 2 должно быть равно ax:
Ответ: функция непрерывна на всей области определения при a = 1,5.
Нет времени вникать в решение? Можно заказать работу!
Пройти тест по теме Производная, дифференциал и их применение
Пройти тест по теме Предел
Пример 6. Определить, при каких значениях
параметров a и b непрерывна на всей области определения функция
Определить, при каких значениях
параметров a и b непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Следовательно, значение в точке должно быть равно 1:
.
Найдём левосторонний функции в точке :
.
Очевидно, что значение функции в точке должно быть равно :
Ответ: функция непрерывна на всей области определения при a = 1; b = -3.
К понятию непрерывной функции математика пришла, изучая в первую очередь
различные законы движения. Пространство и время бесконечны, и зависимость, например,
пути s от времени t, выраженная законом s = f(t),
даёт пример непрерывной функции f(t). Непрерывно
изменяется и температура нагреваемой воды, она также является непрерывной функцией от
времени: T = f(t).
В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.
1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.
2. Функция f(x), непрерывная на интервале [a, b], принимает все промежуточные значения между значениями в концевых точках, то есть, между f(a) и f(b). В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.
3. Если функция непрерывна на интервале, то на этом интервале она
достигает своего наибольшего и своего наименьшего значения: если m —
наименьшее, а M — наибольшее значение функции
на интервале [a, b], то найдутся
на этом отрезке такие точки и
, что
и
. Теорема,
в которой изложено это свойство, называется второй теоремой Вейерштрасса.
Теорема,
в которой изложено это свойство, называется второй теоремой Вейерштрасса.
Пример 7. Используя первое из приведённых выше свойств непрерывных функций, доказать, что уравнение имеет по меньшей мере один вещественный корень в интервале [1; 2].
Решение.
Пусть .
Вычислим значения функции при x = 1 и x = 2.
.
.
Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.
Следовательно, в интервале [1; 2] существует такое число a, при котором f(a) = 0. То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.
Установление непрерывности функции может быть как самостоятельной задачей,
так и частью Полного исследования функции и построения графика.
Пример 8. Есть ли у уравнения хотя бы один вещественный корень?
Решение.
Функция
определена на интервале .
Вычислим значения функции при x = 0 и .
.
.
Получили
и .
Следовательно, существует такое число a, при котором f(a) = 0. Ответ на вопрос задачи: уравнение имеет по меньшей мере один вещественный корень.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
Весь раздел «Исследование функций»
- Непрерывность функции
- Точки разрыва функции и их виды
- Экстремумы функции
- Наименьшее и наибольшее значения функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
Кусочная функция | Как построить график кусочных функций?
- Введение
- Примеры: как построить график кусочно-определяемой функции?
- Как с помощью калькулятора кусочных функций нарисовать ее график?
- Узнайте, как использовать Desmos Graphing Calculator для наброска кусочной функции
- Использование/применение кусочных функций
- Заключение
Некоторые функции определяются по-разному в разных частях своей области и, таким образом, более естественно выражаются в терминах более чем одной формулы. Назовем такую функцию кусочно-функция или кусочно-определенная функция . Кусочные функции будут нам полезны при изучении пределов, непрерывности и производной как примеры и контрпримеры функций, обладающих определенными свойствами.
Назовем такую функцию кусочно-функция или кусочно-определенная функция . Кусочные функции будут нам полезны при изучении пределов, непрерывности и производной как примеры и контрпримеры функций, обладающих определенными свойствами.
Если вы не находите достаточно времени, чтобы прочитать эту статью за одно чтение, не забудьте добавить эту страницу в закладки для дальнейшего насыщения, если вы не хотите пропустить этот полезный контент.
Примеры: как построить график кусочно-определяемой функции?Пример №1
Пусть f — функция, определяемая выражением;
\[ f(x) = \begin{case} х-1, \текст{ если } х <3 \\ 5, \text{ если } x =3 \\ 2x+1 , \text{ если } 3 < x \end{случаи} \]
Определить область определения и область значений f и начертить ее график .
Решение:-
Область определения f равна (-∞, +∞), на следующем рисунке показан график f;
состоит из части прямой y=x-1, для которой x<3, точки (3,5) и части прямой y = 2x+1, для которой 3 Определите область определения и область значений g и нарисуйте его кусочный график. Решение:- Область определения g равна (-∞, +∞), ниже приведен график функции; График содержит участок прямой y= 3x-2, для которого x<1, и участок параболы y = x 2 , для которого 1 ≤ x. Диапазон составляет (-∞, +∞). Пример №3 H — функция, определяемая формулой; \[ H(x) = \begin{case}
х+3, \текст{ если } х ≠ 3 \\
2 , \текст{ если } х = 3
\end{случаи}
\] Определите домен и область значений H и нарисуйте его график. Решение: — Поскольку H определено для всех x, его область определения равна (-∞, +∞), график показан ниже; Диапазон — это набор всех действительных чисел, кроме 6, поэтому с точки зрения набора мы можем выразить диапазон как ℝ-{6}. 92, \text{ если } х ≠ 2 \\
7 , \text{ если } х = 2
\end{случаи}
\] Определить область определения и область значений f и начертить ее график. Решение: — Поскольку f определено для всех x, домен равен (-∞, +∞). График ниже; состоит из точки (2, 7) и всех точек параболы y = x 2 кроме (2, 4). Диапазон равен [0, +∞). Пример №5 Определите область определения и диапазон функции абсолютного значения ‘f’, для которой f(x) = |x| и нарисуйте его график. Решение: — Из определения функции абсолютного значения |x|, f(x) определяется кусочно, как показано ниже, \[ f(x) = \begin{s }
х, \текст{ если } х ≥ 0 \\
-x , \text{ если } x < 0
\end{случаи}
\] Домен (-∞, +∞). один имеет наклон 1, а другой имеет наклон -1. Диапазон равен [0, +∞). Example#6 Кусочная функция f определяется как; \[ f(x) = \begin{case}
-2, \text{ если } x ≤ 3 \\
2 , \текст{ если } 3 < х
\end{случаи}
\] Определить домен и диапазон f и начертить его график. Решение:- Область определения g равна (-∞, +∞), ниже приведен график функции; 92 , \text{ если } x < 0 \\
3x + 1 , \text{ если } 0 ≤ x
\end{случаи}
\] Определить домен и диапазон f и начертить его график. Решение:- Область определения g равна (-∞, +∞), ниже приведен график функции; Это непрерывный график с диапазоном (-∞, +∞). Пример# 8 Кусочная функция f определяется как; \[ f(x) = \begin{case}
6x + 7 , \text{ если } x ≤ -2 \\
4 – х , \текст{ если } -2 < х
\end{случаи}
\] Определить домен и диапазон f и начертить его график. Решение:- Область определения g равна (-∞, +∞), ниже приведен график функции; Диапазон: (-∞, 6). Пример № 9 Нарисуйте график знаковая функция (или знаковая функция), обозначаемая как «знак» и определяемая кусочно, как показано ниже; \[ sign(x) = \begin{case}
-1 , \text{ если } x < 0 \\
0 , \текст{ если } х = 0 \\
1 , \текст{ если } 0 < х
\end{случаи}
\] знак х читается как «знак ‘х’». Решение: — Область определения знака x равна (-∞, +∞). Ниже приведен график знаковой (сигнум) функции; Диапазон содержит всего три целых числа, как указано в вопросе, то есть {-1, 0, 1}. 92} , \text{ если } -5 ≤ x≤ 5 \\
3-x , \text{ если } 5 Решение:- Область (-∞, +∞), вот как мы набросали график; И диапазон равен (-∞, -2) ∪ [0, 5]. Существуют различные доступные онлайн и загружаемые графические калькуляторы, которые облегчают пользователям набросок кусочных функций, некоторые из них, как показано ниже; Здесь я собираюсь подробно рассказать о том, как набросать график кусочных функций, используя Графический калькулятор Desmos ? В приведенном выше видео я выбрал несколько примеров, которые были решены и нарисованы вручную в этой статье, и ввел их кусочные определения с соответствующими областями, чтобы получить их график, I have picked Example#1 here and tried to substitute commands on Desmos interface , let’s try to understand step by step . ШАГ №1 ШАГ № 2 Поскольку «3» не входит в первую кусочную область «x < 3», это означает, что субъективный граф не содержит (3, 2), поэтому мы должны разработайте там «дырку» для этой цели; Первая кусочная обработка завершена. ШАГ №3 STEP#5 For more examples, you can watch my aforementioned video . Кусочные функции в дополнение к исчислению великодушно способствуют математическому моделированию различных повседневных задач реальной жизни, которые впоследствии оцениваются для получения оптимальных и точных решений. Я попытался собрать несколько примеров из области счетов, физики, биологии и т. \[ f(x) = \begin{case}
0, \text{ если } x < $10 000 \\
10\text{%} , \text{ если } 10 000 долларов США ≤ x≤ 20 000 долларов США \\
15\text{%} , \text{ если } x> 20 000 долларов
\end{случаи}
\] \[ C(x) = \begin{case}
7x, \text{ если } 0 Где C(x) — общая стоимость крышек, а «x» — количество заказанных крышек. \[ v(t) = \begin{case}
5t, \text{ если } 0 \le t < 15 \\
70 , \text{ если } 15 ≤ x< 50 \\
250-3t , \text{ если } т \geq 50
\end{случаи}
\] Кусочная функция действительно является отличительной чертой в области исчисления и глубоко вовлечена в концепции пределов, непрерывности, дифференциального и интегрального исчисления. Вне всякого сомнения, кусочные функции упростили многие сложные цели из Все, что мы изучаем в математике, имеет свое глубокое значение и существенный вклад в различные области реальной жизни, кусочная функция является ярким примером этого.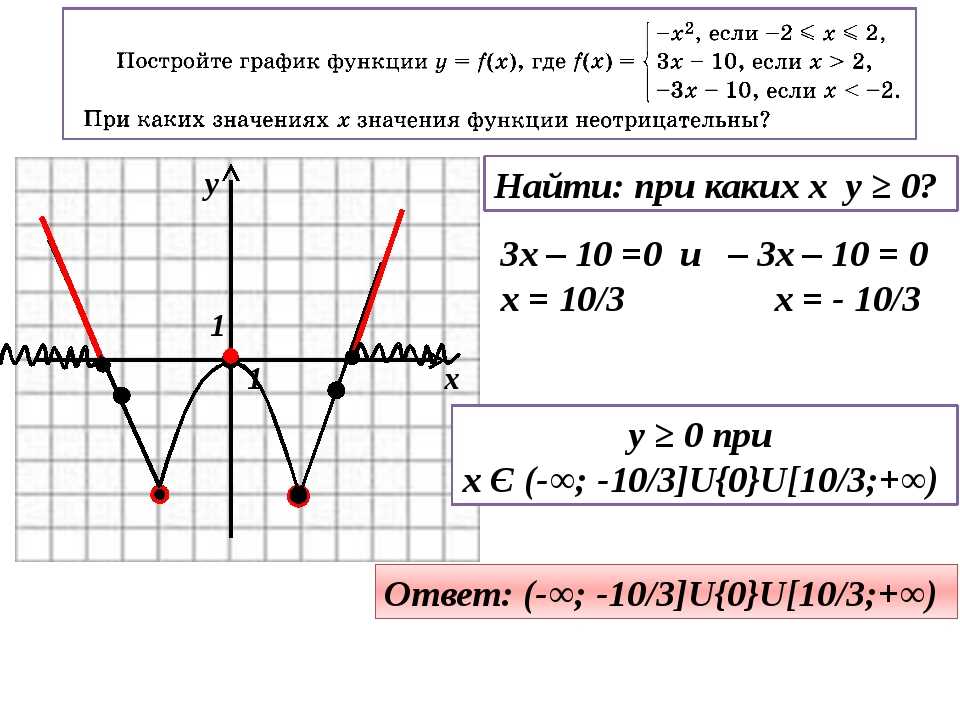
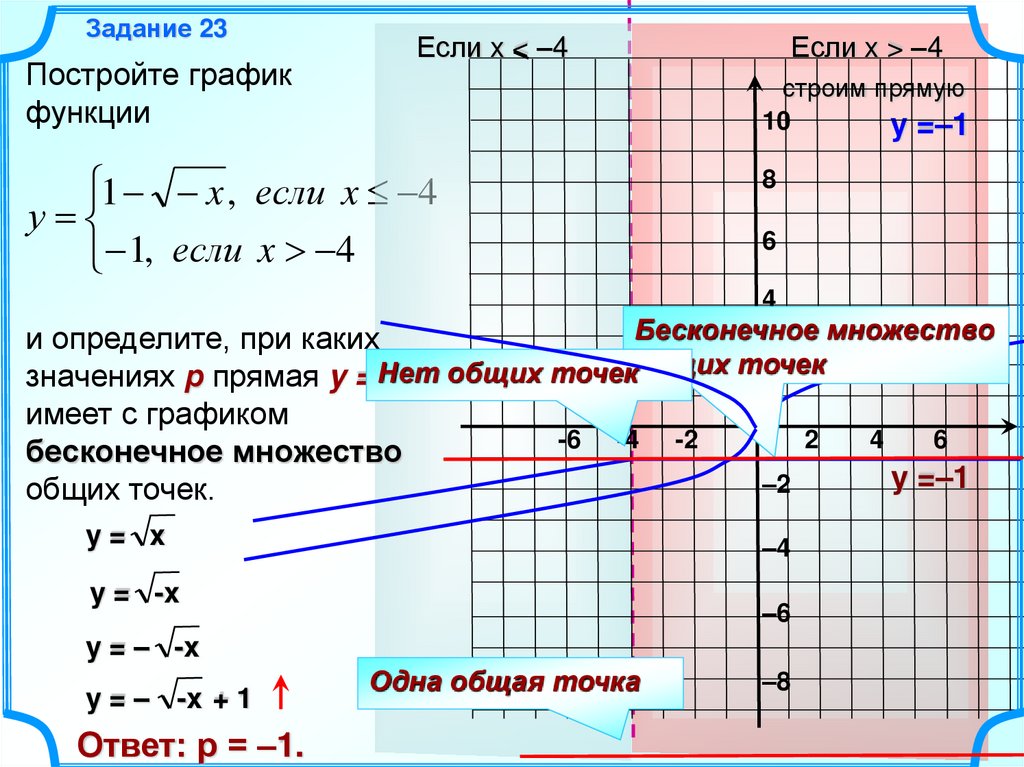 График «f» состоит из двух полупрямых, проходящих через начало координат и выше оси x.
График «f» состоит из двух полупрямых, проходящих через начало координат и выше оси x. 

Learn how to use Desmos Graphing Calculator to sketch a кусочная функция 
 д., которые помогут вам получить представление о приложениях и значении кусочных функций.
д., которые помогут вам получить представление о приложениях и значении кусочных функций. 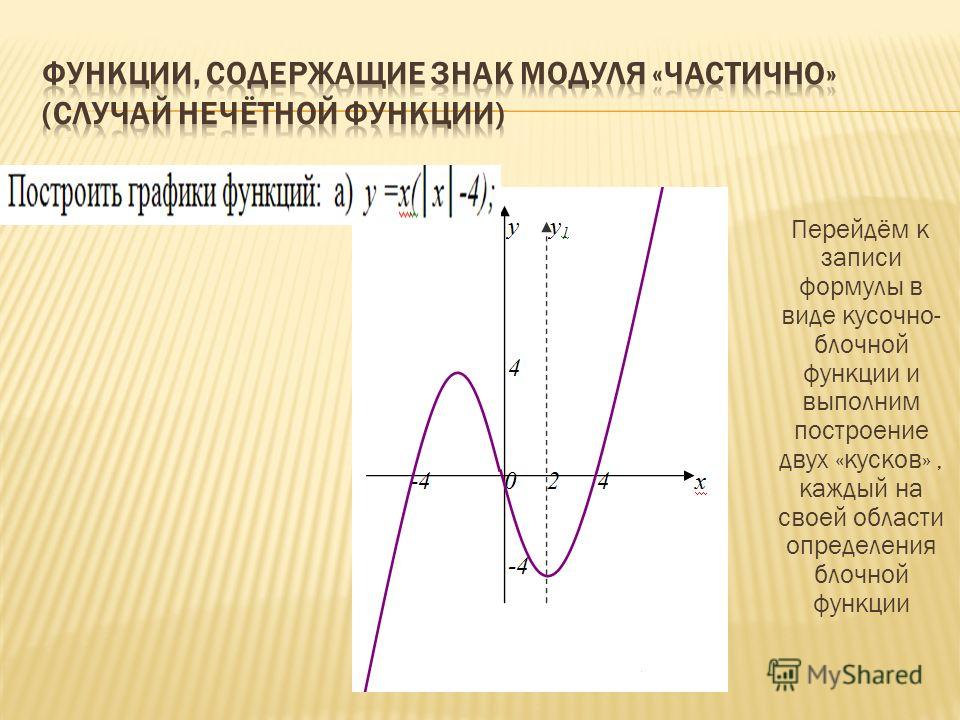




 5
5 5
5 5
5 01 ; 2×p]
01 ; 2×p] 1
1
Ваш комментарий будет первым