Задание по Excel № 2 » Построение графика кусочной функции»
Построить график кусочной функции на участке [a;b] с шагом 0,5.
№ Вар | Функция | [a;b] |
1. | [-7;7] | |
2. | [-7;7] | |
3. | [-5;5] | |
4. | [-5;5] | |
5. | ||
6. | [-7;7] | |
7. | [-10;10] | |
8. | [-10;10] | |
9. | [-4;10] a-коэф-т | |
10. | [-10;10] | |
11. | [-5;8] с-коэф-т | |
12. | [-4;4] a-коэф-т | |
13. | [-4;4] | |
14. | [-10;10] с-коэф-т | |
15. | [-10;10] d-коэф-т | |
16. | [-7;7] | |
17. | [-7;7] | |
18. | [-30;30] | |
19 | [-30;30] | |
20. | ||
21. | [-10;10] | |
22. | < | [-3;3] |
23. | [-10;10] | |
24. | [-10;10] | |
25. | [-5;6] a-коэф-т | |
26. | [-5;5] b-коэф-т | |
27. | [-10;10] | |
28. | [-8;8] d-коэф-т | |
29. | [-5;6] a-коэф-т | |
30. | [-7;7] d-коэф-т |
Получить матрицу значений функции в виде двумерной таблицы. Для этого задать изменение двух аргументов функции в виде числовых рядов, расположенных под прямым углом друг к другу. Вычислить значение функции для каждой пары аргументов. Шаг 0,1
x\y
-4
-3.5
-3
….
0
0.5
1
Z(x,y)
1.
 5
5…
Внимание! Формула для вычисления значения функции должна быть набрана один раз, затем скопирована.
Выполнить построение трехмерной поверхности. Сравнить получившийся результат с образцом.
№ | Уравнение и диапазон аргументов | Вид графика | № | Уравнение и диапазон аргументов | Вид графика |
1 | x=[-5;5] y=[-5;5] a=2 b=7 | 8 | x=[-2;2] y=[—2×p ; 2×p] a=2 | ||
2 | x=[-5;5] y=[-5;5] a=2 b=5 | 9 | x=[-1;1] y=[—2×p ; 2×p] a=10 b=2 | ||
3 | x=[-5 ; 5] y=[-2 ; 2] a=1. b=0.5 | x=[—p ; p] y=[—p ; p] a=2 | |||
4 | x=[-5;5] y=[-5;5] a=0.7 | 11 | x=[—p ; p] y=[—p ; p] a=0.5
| ||
5 |
x=[—2×p ; 2×p] y=[—2×p ; 2×p] a=2 b=5 | 12 | x=[—p ; p] y=[—p ; p] a=4 | ||
6 | x=[—p ; p] y=[—p ; p] a=3 | 13 | x=[-2;2] y=[-2;2] a=0. | ||
7 | x=[ —p ; p] y=[ —p ; p] a=3 | 14 | x=[-2;2] y=[-2;2] a=2 | ||
15 | x=[-2;2] y=[-2;2] a=2 | 22 | x=[0.01 ; 2×p] y=[0.01 ; 2×p] a=200 | ||
16 | x=[-5;5] y=[-5;5] a=2 b=1 | 23 | x=[0. y=[0.01 ; p] a=200 | ||
17 | x=[-5;5] y=[-5;5] a=0.3 | 24 | x=[-3’3] y=[-1;6] a=50 | ||
18 | x=[-5;5] y=[-5;5] a=0.3 | x=[-3;3] y=[-3;3] a=0.5 | |||
19 | x=[-5;5] y=[-5;5] a=5 | 26 | x=[-3;3] y=[-3;3] a=2 b=3 | ||
20 | x=[-5;5] y=[-5;5] a=0. |
| x=[—p/2 + 0.05] ; p/2 — 0.05] y=[—p/2 + 0.05] ; p/2 — 0.05] a=0.1 b=2 | ||
21 | x[0.1;1] y[0.1;1] a=0.1 | 28 | x[—p/4 + 0.05] ; p/4 — 0.05] y[—p/4 + 0.05] ; p/4 — 0.05] a=2 b=1 |
y=
Задание №1 по MathCAD «Двумерные графики, заданные в параметрическом виде, и графики, заданные в полярных координатах»
Задание:
1. Построить
два графика;
Построить
два графика;
2. Вывести таблицу значений функции, заданной в параметрическом виде;
3. При сдаче работы уметь:
перевести полярные координаты в декартовы;
отобразить несколько зависимостей на одном графике.
Указания к работе:
1. Для построения XY-графика, заданного в параметрическом виде необходимо:
указать диапазон и шаг изменения параметра в виде . Знак «:=» вводится с помощью английского знака «:». Символ «..» вводится с помощью символа «;»
№ Вар | Функция, заданная в параметрическом виде | Функция, заданная в полярных координатах |
1 | ||
2 | ||
3 | ||
4 | ||
5 | ||
6 | ||
7 | ||
8 | ||
9 | ||
10 | ||
11 | ||
12 | ||
13 | ||
14 | ||
15 | ||
16 | ||
17 | ||
18 | ||
19 | ||
20 | ||
21 | ||
22 | ||
23 | ||
24 | ||
26 | ||
27 | ||
28 | ||
29 |
задать зависимость ;
“Graph”à
“Create
XY-Plot”.
2. В полярной системе координат каждая точка задается углом и радиусом определенной длины. Длина радиуса находится в определенной зависимости от полярного угла. Для построения графика, заданного в полярных координатах необходимо:
указать диапазон и шаг изменения полярного угла в радианах , например ;
задать зависимость
“Graph”à “Create Polar Plot”.
Как построить кусочную функцию? – Обзоры Вики
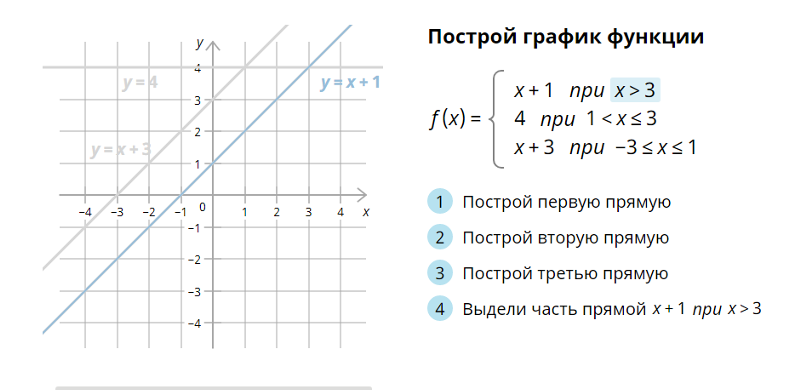
Что такое пример кусочной функции? Кусочная функция — это функция, которая определяется различными формулами или функциями для каждого заданного интервала. Это также в названии: шт. … Как видно из приведенного выше примера, F (X) является кусочной функцией, потому что она однозначно определена для трех интервалов: x > 0, x = 0 и x < 0.
Это также в названии: шт. … Как видно из приведенного выше примера, F (X) является кусочной функцией, потому что она однозначно определена для трех интервалов: x > 0, x = 0 и x < 0.
Во-вторых, что такое реальный пример кусочной функции? налоговые скобки являются еще одним реальным примером кусочных функций. Например, рассмотрим простую налоговую систему, в которой доходы до 10,000 10 долларов облагаются налогом по ставке 20, а любой дополнительный доход облагается налогом по ставке XNUMX%.
Как сделать кусочно на ТИ-84?
Как построить график кусочной функции на TI 83 Plus?
- График кусочно-определяемой функции на TI-83+
- Y= (Очистить функции)
- Мода.
 2, т.е. 27. f(-3) должна быть функцией связанного уравнения.
2, т.е. 27. f(-3) должна быть функцией связанного уравнения.Как вы решаете абсолютные уравнения?
Чтобы решить уравнение, содержащее абсолютное значение, выделите абсолютное значение на одной стороне уравнения. потом установить его содержимое равным положительное и отрицательное значение числа на другой стороне уравнения и решите оба уравнения.
Как решить кусочно-функциональную задачу?
Какая из них является примером линейной кусочной функции?
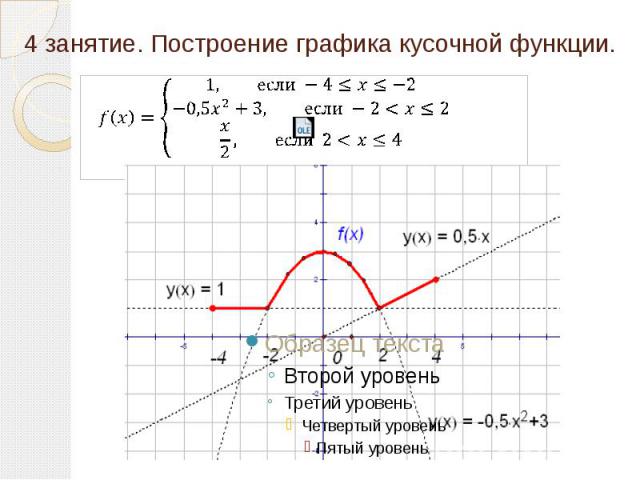
График непрерывной кусочно-линейной функции на компактном отрезке представляет собой ломаную цепь.
 Другие примеры кусочно-линейных функций включают функция абсолютного значения, пилообразная функция и функция пола.
Другие примеры кусочно-линейных функций включают функция абсолютного значения, пилообразная функция и функция пола.Как построить график на TI-84? Первым шагом в любой графической задаче является построение графика. На TI-83 и TI-84 это делается путем перехода к экрану функций с помощью нажатием кнопки «Y=» и вводом функции в один из линии. После ввода функции нажмите кнопку «ГРАФИК», и калькулятор нарисует для вас график.
Как построить график неравенств на TI-84 Plus CE 2020?
Какая последняя ОС для TI 84 Plus?
Самая последняя операционная система для TI-84 Plus и TI-84 Plus Silver Edition: 2.
 55MP. Примечание. Если вы обновляете контроллер TI-Nspire™ с клавиатурой TI-84, см. документ Обновление операционной системы TI-Nspire™.
55MP. Примечание. Если вы обновляете контроллер TI-Nspire™ с клавиатурой TI-84, см. документ Обновление операционной системы TI-Nspire™.Как поставить игры на TI 84 Plus? Как поставить игры на TI-84 Plus CE
- Шаг 1: Материалы для ворот. Все, что вам нужно, перечислено здесь:…
- Шаг 2: Загрузите и установите TI Connect CE. …
- Шаг 3: Загрузите игры. …
- Шаг 4: Извлеките файлы Games. …
- Шаг 5: Отправьте игры на свой калькулятор. …
- Шаг 6: Запустите игры. …
- Шаг 7: Играйте в свою игру!
Как построить график ступенчатой функции на TI 83?
Как построить график функции на TI-84 Plus? Настройка окна графика TI-84 Plus
- Нажмите [WINDOW] для доступа к оконному редактору.
- После каждой переменной окна введите числовое значение, подходящее для отображаемых функций.
 Нажимайте e после ввода каждого числа. …
Нажимайте e после ввода каждого числа. … - Нажмите [GRAPH], чтобы построить график функций.
9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Проект кусочно-функций — АЛГЕБРА И НЕ ТОЛЬКО
11.
 11.2017
11.20173 комментария
Я привык презирать обучение кусочным функциям. Вы знаете, когда идет дождь, и вы забыли свой зонт? Что вы делаете? Ну, ты бежишь со всех ног к своей машине, и как только ты садишься в нее, ты делаешь глубокий вдох и думаешь, я сделал это!.. но я довольно мокрый. Именно так я использую для обучения кусочным функциям. Я не был готов, я сделал это быстро, и результаты были невелики.
Пару лет назад я решил серьезно подумать о том, как лучше всего обучать кусочным функциям. Я провел небольшое исследование и решил удостовериться, что я рассказал о том, как оценивать, составлять графики и писать функции. В прошлом я просто сосредоточился на их графическом отображении и предполагал, что если студенты могут это делать, то они могут делать что угодно с кусочными функциями. Да, я знаю, принятие желаемого за действительное. Поэтому я создал урок, в котором четко охвачены эти три области. Затем я заставил своих детей погрузиться прямо в кусочные функции с проектом.
 Будем честными, после того одного урока они еще не любили кусочные функции. Этот проект был так же важен, как и урок, потому что он оживил кусочные функции.
Будем честными, после того одного урока они еще не любили кусочные функции. Этот проект был так же важен, как и урок, потому что он оживил кусочные функции.ЧАСТЬ A
Учащиеся строят график американских горок в зависимости от времени и высоты, используя линейную, абсолютную и квадратичную функции. Я говорю им, что они могут представить, что их график — это то же самое, что и американские горки, потому что это сделает их немного веселее. Однако мы знаем, что физика не обязательно допустит, чтобы это было правдой. (Спуск будет не таким быстрым, как в гору, как вы могли бы видеть в абсолютном значении или квадратичной функции).ЧАСТЬ B
Учащиеся пишут функцию, представляющую их график. Некоторые из моих учеников используют Desmos, чтобы проверить, совпадают ли их функция и график. Это действительно помогает убедиться, что все уравнения в кусочной функции верны, и если они неверны, они могут соответствующим образом скорректировать свой график. Другой способ — попросить их проверить на своем графическом калькуляторе. Конечно, всегда найдутся студенты, которые этого не сделают. Я использую Desmos при оценивании проекта и иногда вижу вот что…
Другой способ — попросить их проверить на своем графическом калькуляторе. Конечно, всегда найдутся студенты, которые этого не сделают. Я использую Desmos при оценивании проекта и иногда вижу вот что…УРА! Учитель => лицом к столу.
Хмммм….что-то не так.
УРА! Ты получил это!
ЧАСТЬ C
Поехали кататься….Для них это интересный способ проанализировать характеристики своей функции.
ЧАСТЬ D
Учащиеся создают ключ ответа для своей функции, который определяет атрибуты функции, которые будут использоваться в деятельности станции.СТАНЦИИ АКТИВНОСТЬ
Я не прошу учеников демонстрировать свои американские горки классу, потому что это не только утомительно, но и требует много времени. Вместо этого учащиеся обходят несколько американских горок и определяют домен, диапазон, интервалы увеличения/уменьшения, минимумы, максимумы и оценивают значения x. У них есть возможность увидеть другие американские горки и получить отзывы.
У них есть возможность увидеть другие американские горки и получить отзывы.ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ — ПОЕЗДКА
И, наконец, самое приятное! Вы можете взять своих учеников на экскурсию в парк развлечений. Студенты снимают на видео американские горки и рисуют график, относящийся к времени и высоте. Им нравится этот аспект проекта… день вдали от школы! Вот одно из видео с нашей экскурсии:Я знаю, о чем вы думаете… Я превратил 1-2 дня обучения в 5 дней. Правильно, у вас может не быть такого времени. Не беспокойся! Вы можете использовать те части проекта, которые лучше всего подходят для вас. Используйте видео выше вместо того, чтобы отправиться на экскурсию. Каждый год я нахожу способ получить как можно больше, потому что результаты потрясающие! На днях ко мне подошел новый преподаватель предварительного исчисления в этом году и сказал: «Вау, студенты из Алгебры 2 в прошлом году действительно знают кусочные функции».
 И я сказал: «Да, да», — с широкой улыбкой на лице. Некоторые вещи просто того стоят.
И я сказал: «Да, да», — с широкой улыбкой на лице. Некоторые вещи просто того стоят.Хотите попробовать этот проект со своими учениками БЕСПЛАТНО?
Подпишитесь на список рассылки Algebra and Beyond, который дает вам мгновенный доступ к бесплатной библиотеке ресурсов , где вы можете найти этот проект и многие другие ресурсы!ДА! Я хочу этот проект БЕСПЛАТНО!
Вы можете найти все ресурсы, упомянутые в этом посте здесь:
3 комментария
Здравствуйте,
Я ТАЙРА!Я образовательный блогер и разработчик учебных программ. Я с энтузиазмом отношусь к созданию творческих, всеобъемлющих и понятных ресурсов для учителей математики средних и старших классов. Моя цель – создать контент, который легко реализовать учителю и который поможет учащимся соединить знания с пониманием — по одному уроку за раз.
Ищете что-то конкретное?
НАЙТИ МЕНЯ ЗДЕСЬ
Категории
Все
Любимые вещи в классе
Бесплатные вещи
Графический калькулятор
Математические занятия
Математические проекты
Математические разминки
Реальная математика
Советы учителюАрхивы
февраль 2023 г.



 5
5 5
5 5
5 01 ; 2×p]
01 ; 2×p] 1
1 2, т.е. 27. f(-3) должна быть функцией связанного уравнения.
2, т.е. 27. f(-3) должна быть функцией связанного уравнения. Другие примеры кусочно-линейных функций включают функция абсолютного значения, пилообразная функция и функция пола.
Другие примеры кусочно-линейных функций включают функция абсолютного значения, пилообразная функция и функция пола. 55MP. Примечание. Если вы обновляете контроллер TI-Nspire™ с клавиатурой TI-84, см. документ Обновление операционной системы TI-Nspire™.
55MP. Примечание. Если вы обновляете контроллер TI-Nspire™ с клавиатурой TI-84, см. документ Обновление операционной системы TI-Nspire™. Нажимайте e после ввода каждого числа. …
Нажимайте e после ввода каждого числа. …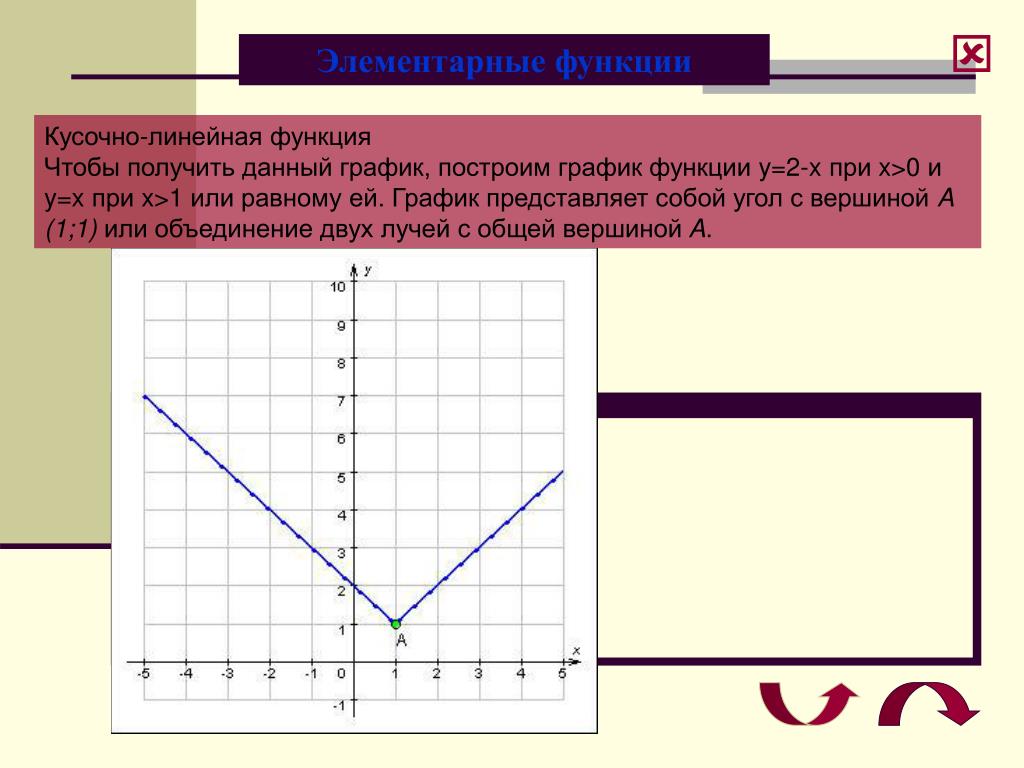 11.2017
11.2017 Будем честными, после того одного урока они еще не любили кусочные функции. Этот проект был так же важен, как и урок, потому что он оживил кусочные функции.
Будем честными, после того одного урока они еще не любили кусочные функции. Этот проект был так же важен, как и урок, потому что он оживил кусочные функции. Другой способ — попросить их проверить на своем графическом калькуляторе. Конечно, всегда найдутся студенты, которые этого не сделают. Я использую Desmos при оценивании проекта и иногда вижу вот что…
Другой способ — попросить их проверить на своем графическом калькуляторе. Конечно, всегда найдутся студенты, которые этого не сделают. Я использую Desmos при оценивании проекта и иногда вижу вот что… У них есть возможность увидеть другие американские горки и получить отзывы.
У них есть возможность увидеть другие американские горки и получить отзывы. И я сказал: «Да, да», — с широкой улыбкой на лице. Некоторые вещи просто того стоят.
И я сказал: «Да, да», — с широкой улыбкой на лице. Некоторые вещи просто того стоят.
Ваш комментарий будет первым