| 1. |
Параллельный перенос
Сложность: лёгкое |
1 |
| 2. |
Направление сдвига графика функции
Сложность: лёгкое |
1 |
3.
|
Формула функции
Сложность: лёгкое |
1 |
| 4. |
Уравнение параболы
Сложность: среднее |
2 |
5.
|
Значение функции
Сложность: среднее |
2 |
| 6. |
График функции
Сложность: среднее |
2 |
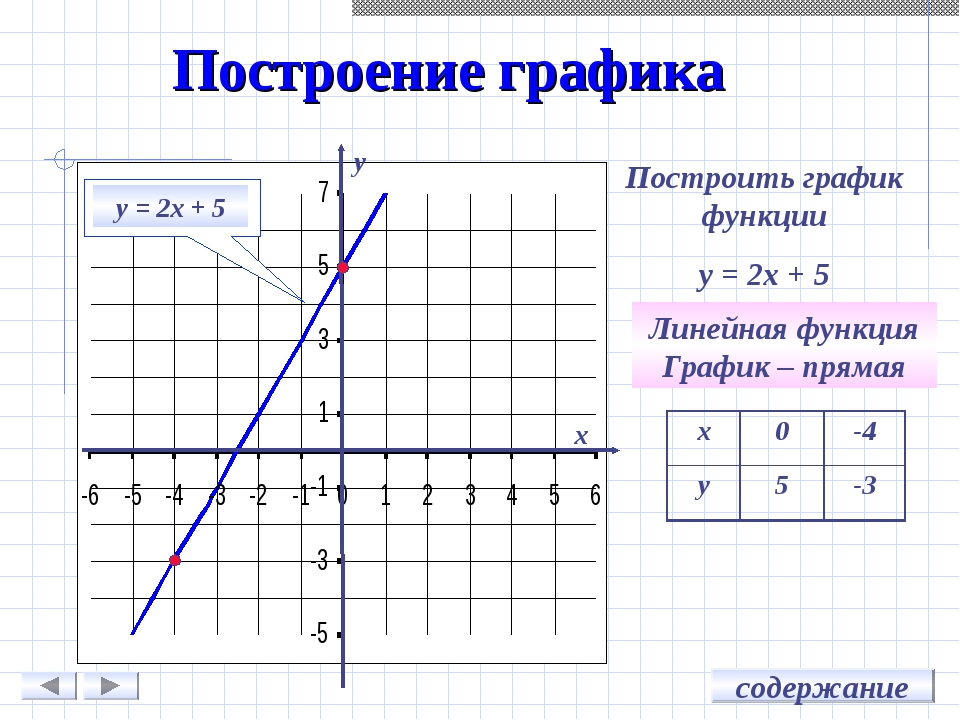
7.
|
Графическое решение уравнения
Сложность: сложное |
3 |
| 8. |
Система уравнений
Сложность: сложное |
1 |
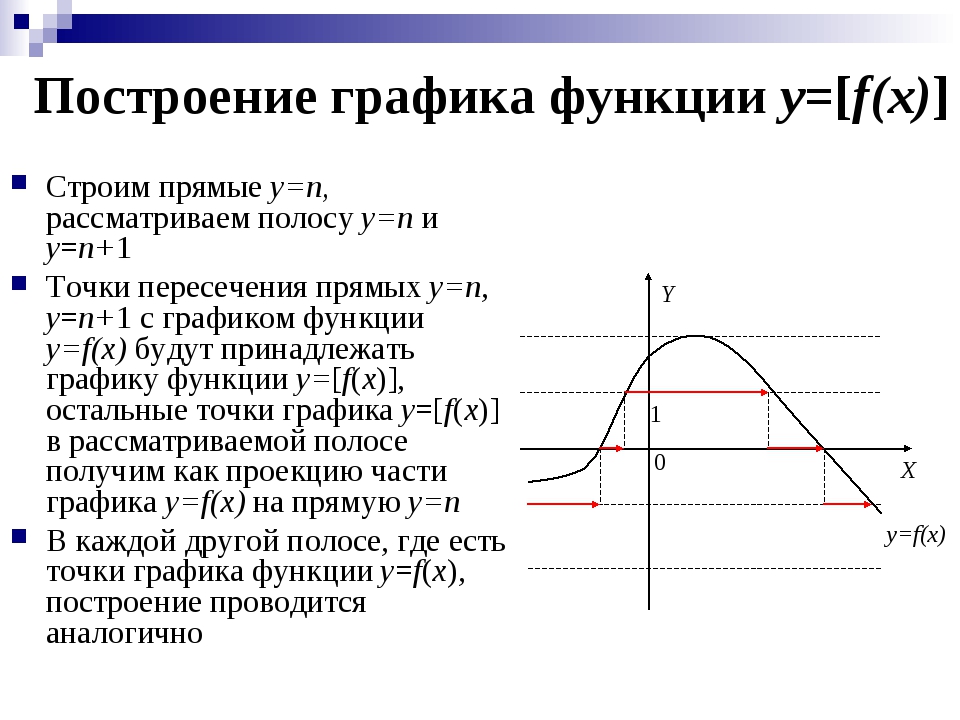
9.
|
Значение аргумента
Сложность: сложное |
3 |
Как построить график функции в Excel
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5.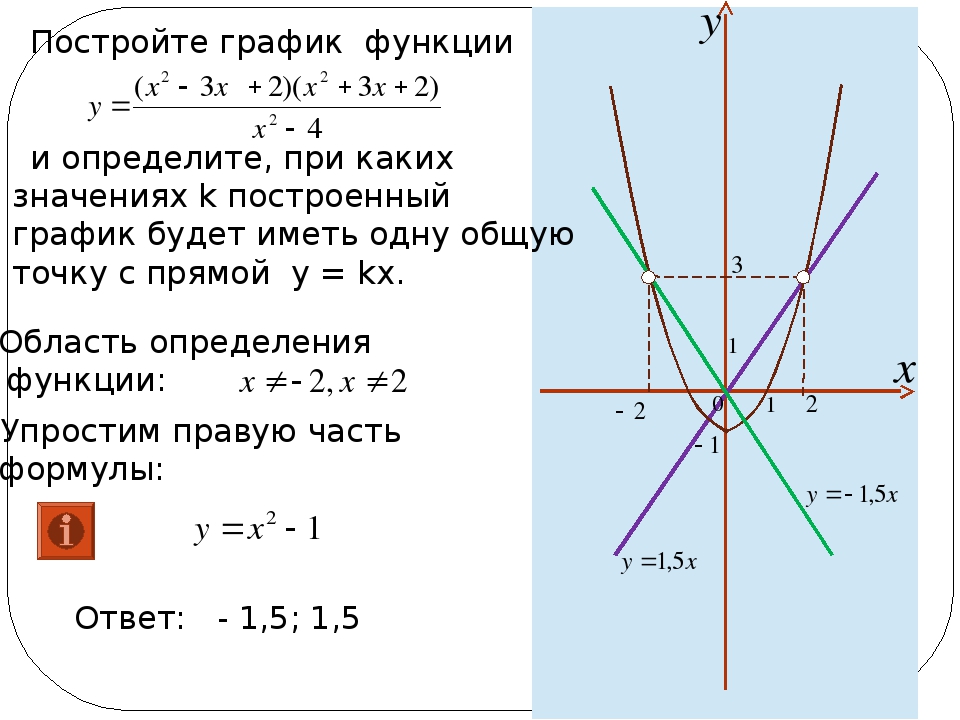 2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Оценить статью: Загрузка… Поделиться новостью в соцсетях
Об авторе: Олег Каминский
Вебмастер.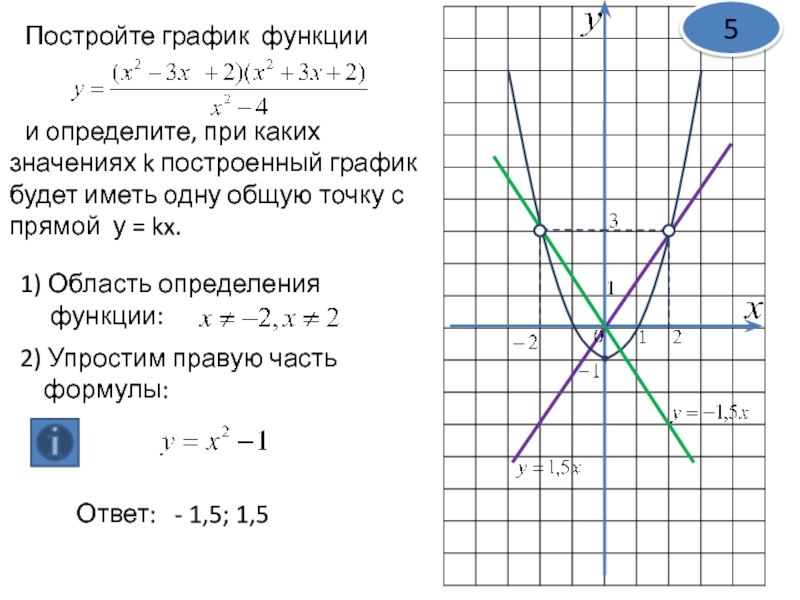 Высшее образование по специальности «Защита информации». Создатель портала comp-profi.com. Автор большинства статей и уроков компьютерной грамотности
Высшее образование по специальности «Защита информации». Создатель портала comp-profi.com. Автор большинства статей и уроков компьютерной грамотности
Построение графика с помощью элементарных преобразований.
Построение графика функции
y=f(kx) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; b=0)Рассмотрим сначала два частных случая при b=0,т.е. функция имеет вид y=f(kx) .
1. При |k|>1 график функции y=f(x) сжимается в |k| раз вдоль оси OX относительно оси OY.
2. При |k|<1 график функции y=f(x) растягивается в раз вдоль оси OX
Рассмотрим примеры:
| Построить график функции | Построить график функции |
Построение графика функции
y=f(x+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; k=1)При b>0 график функции y=f(x) сдвигается влево вдоль оси OX на b единиц.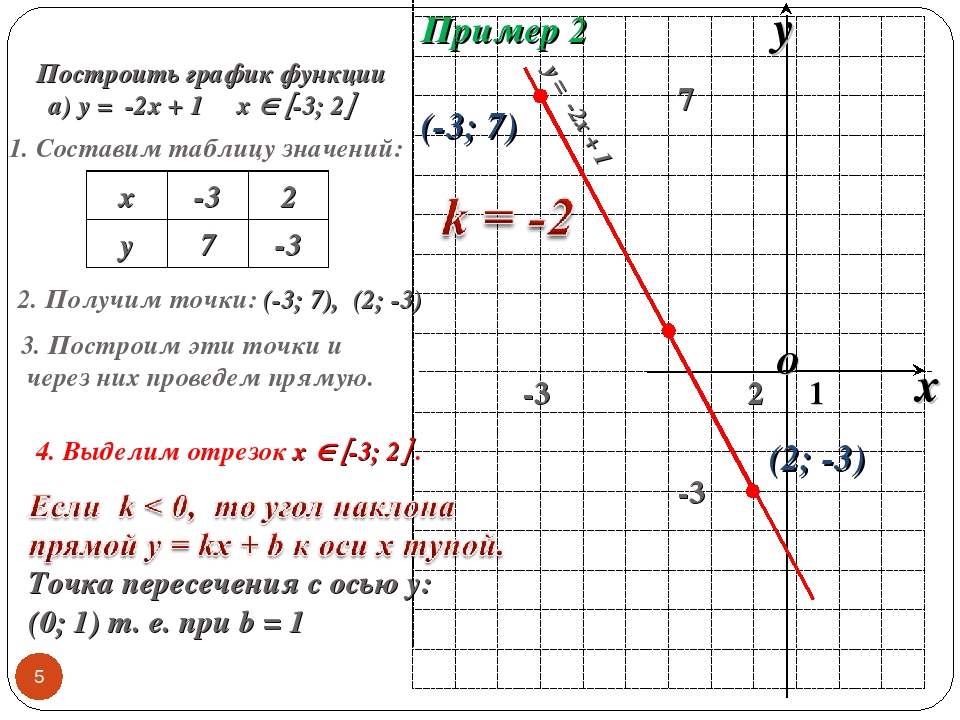
При b<0 график функции y=f(x) сдвигается вправо вдоль оси OX на |b| единиц
Рассмотрим примеры:
| Построить график функции ( b>0 ) | Построить график функции ( b<0 ) |
Построение графика функции
y=f(kx+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0)Рассмотрим общий случай : y=f(kx+b) .
Сначала вынесем коэффициент k за скобку: .
Именно число определяет сдвиг вдоль оси OX , а не b ,
как полагают некоторые абитуриенты.
Теперь строим график функции y=f(x) .
Затем строим график функции y=f(kx) , после чего сдвигаем полученный график вдоль оси OX на
единиц влево или вправо в зависимости от знака этого числа.
| Рассмотрим пример: построить график функции |
Построение графика функции
y=A·f(kx+b)+B с помощью элементарных преобразоаний графика функции y=f(x)Комбинируя методы построения графиков, рассмотренные в предыдущих случаях, можно по известному графику функции y=f(x) построить график функции y=A·f(kx+b)+B с помощью растяжений, сжатий по горизонтали и вертикали, параллельных переносов вдоль осей координат, а также симметрий относительно координатных осей тех графиков, которые получаются из первоначального графика последовательно применением подходящего преобразования.
Рассмотрим примеры.
| Построить график функции | Построить график функции |
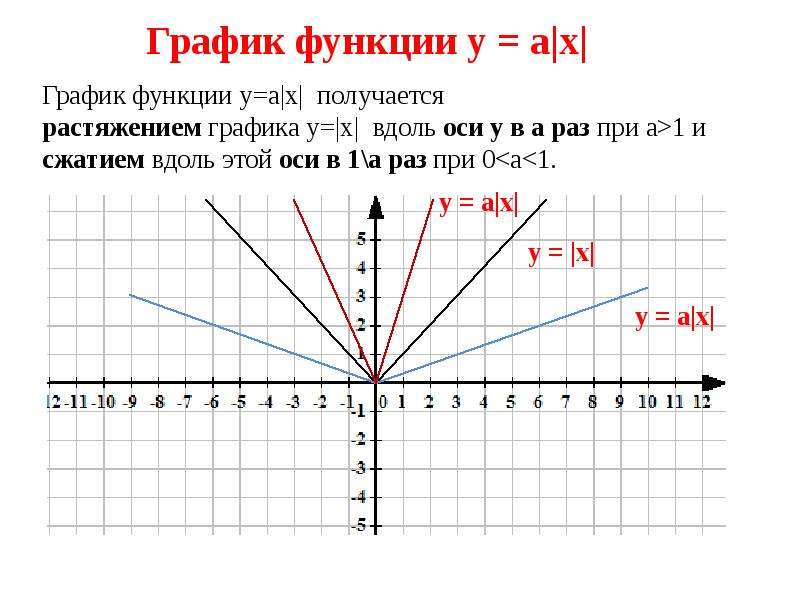
Графиком линейной функции является прямая линия. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y. Пример: В уравнении функции y=kx+b коэффициент k отвечает за наклон графика функции: если k>0, то график наклонен вправо если k<0, то график наклонен влево Коэффициент b отвечает за сдвиг графика вдоль оси OY: если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY если b<0, то график функции y=kx+b получается из графика функции y=kx сдвигом на b единиц вниз вдоль оси OY Заметим, что во всех этих функциях коэффициент k больше нуля, и все графики функций наклонены вправо. Во всех функциях b=3 — и мы видим, что все графики пересекают ось OY в точке (0;3) На этот раз во всех функциях коэффициент k меньше нуля, и все графики функций наклонены влево. Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3) Теперь во всех уравнениях функций коэффициенты k равны. И мы получили три параллельные прямые. Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках: График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3) График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат. График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2) Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b. Если k<0 и b>0, то график функции y=kx+b имеет вид: Если k>0и b>0, то график функции y=kx+b имеет вид:Если k>0 и b<0, то график функции y=kx+b имеет вид: Если k<0 и b<0, то график функции y=kx+b имеет вид: Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид: Ординаты всех точек графика функции y=b равны b Если b=0, то график функции y=kx проходит через начало координат: Это график прямой пропорциональности. Отдельно отмечу график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельную оси OY все точки которой имеют абсциссу x=a. Например, график уравнения x=3 выглядит так: Внимание! Уравнение x=a не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции. Условие параллельности двух прямых: График функции y=k_1{x}+b_1 параллелен графику функции y=k_2{x}+b_2, если k_1=k_2 Условие перпендикулярности двух прямых: График функции y=k_1{x}+b_1 перпендикулярен графику функции y=k_2{x}+b_2, если k_1*k_2=-1 или k_1=-1/{k_2} Точки пересечения графика функции y=kx+b с осями координат. С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. |
«Построение графиков функций у=ах²+n и у=а(х–m)²». 9-й класс
Цели: отрабатывать умение построения графиков функций у=ах2+n и у=а(х-m)2 с помощью параллельных переносов вдоль осей координат.
Задачи урока:
Образовательные:
- расширить сведения о свойствах квадратичной функции;
- повторить графики частных видов квадратичной функции – функций: у = ах2, у = ах2 + n, y = a (x – m)2;
- отработать алгоритмпостроения с помощью
преобразований графиков квадратичной функции.

Развивающие:
- развитие у учащихся аналитического мышления;
- развитие речи (расширение математического словаря).
Воспитательные:
- привитие практических умений и навыков по построению графиков;
- воспитание познавательной активности;
- воспитание ответственности;
- воспитание культуры диалога.
Тип урока: урок обобщения и систематизации.
Оборудование: компьютер, мультимедийная презентация, доска и мел.
Ход урока
I. Организационный момент (2 мин.)
Результаты выполнений самостоятельной работы по теме “Построение графиков функций у=ах2”.
II. Актуализация знаний учащихся (10 мин.)
1. Проверка домашнего задания. № 107 (б), № 108 (г).
Проверка домашнего задания. № 107 (б), № 108 (г).
2 ученика вызываются к доске, оформляют решение домашнего задания, в это время выполняется устная работа с классом.
№ 107 (б)
б) y= — x2 + 3 – квадратичная функция, графиком функции является парабола, a<0 —> ветви направлены вниз. Построим график функции, с помощью следующих преобразований:
1) y=x2 – строим параболу с помощью шаблона;
2) y= — x2 – график, симметричный (осевая симметрия) y=x2, относительно оси Ох;
3) y= — x2 + 3 – параллельный перенос вдоль оси Оу на 3 единичных отрезка (рисунок 1).
№ 108 (г)
г) y= — (x-3)2 – квадратичная функция, графиком функции является парабола, a < 0 —> ветви направлены вниз. Построим график функции, с помощью следующих преобразований:
1) y= x2 – строим параболу с помощью шаблона;
2) y= — x2 – график, симметричный (осевая симметрия) y= x2, относительно оси Ох;
3) y= — (x-3)2 – параллельный перенос вдоль
оси Оx на 3 единичных отрезка —> (рисунок 2).
2. Устный счет (Приложение 1, слайды 1-5).
III. Закрепление изученного материала (15 мин.)
Решение тренировочных упражнений:
1. № 109 (е), с подробным комментарием у доски.
Вспомогательные вопросы учащимся:
— как построить график функции у=а(х-m)2?
— какие виды преобразований графиков сегодня мы еще не повторяли? (Cужение и растяжение относительно осей координат)
е) у= -3(х+5)2 — квадратичная функция, графиком функции является парабола, a < 0 —> ветви направленны вниз. Построим график функции, с помощью следующих преобразований:
1) y= x2 – строим параболу с помощью шаблона;
2) y= — x2 – график, симметричный (осевая симметрия) y= x2, относительно оси Ох;
3) y= — 3x2 – растяжение графика от оси Ох в 3 раза;
4) у= -3(х+5)2 – параллельный перенос вдоль оси Оx на 5 единичных отрезка <— (рисунок 3)
2.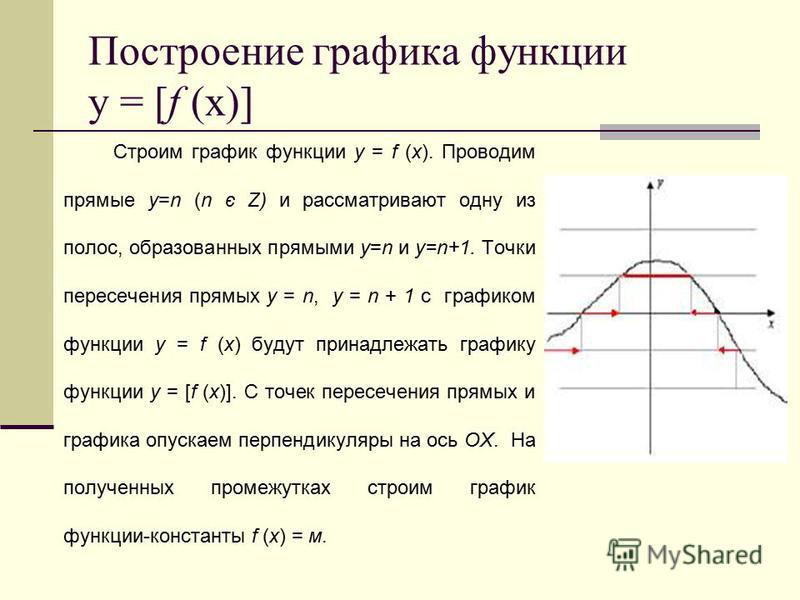 Задача с параметром: при каких значениях
параметра а парабола у = -х2+2 и прямая у =
х + а не имеют общих точек пересечения?
Задача с параметром: при каких значениях
параметра а парабола у = -х2+2 и прямая у =
х + а не имеют общих точек пересечения?
Учитель может вызвать сильного учащего к доске, или в зависимости от уровня класса – самостоятельно разобрать данное упражнение с подробным комментарием.
Вспомогательные вопросы учащимся:
— что значит, графики функций имеют общие точки пересечения?
— назовите коэффициенты получившегося квадратного уравнения?
— что значит, графики функций не имеют общих точек пересечения? Каким должен быть D уравнения?
Решение: Предположим, что данные линии имеют общую точку. Тогда ее координаты удовлетворяют системе уравнений:
Решим эту систему. Так как левые части уравнения равны, то можем приравнять и правые части:
Чтобы графики функций не имели общих точек
пересечения, данное квадратное уравнение не
должно иметь корней .
Изобразим графики функций схематически (рисунок 4):
Вариант 1
1. Как построить график ункции у = f(x) + n?
2. Постройте график функции.
а) у = -0,5x2 +2;
б) у = 2(x–1)2;
Вариант 2
1. Как построить график ункции у = f(x – m)?
2. Постройте график функции.
а) у = 2x2 – 1;
б) у = -0,5(x+2)2;
Ответ: при прямая у = х + а не имеет общих точек пересечения с параболой у = — х2+2
Замечание: обратить внимание учащихся на важность правильно записанного ответа; ответ должен быть подробным, отвечать целиком и полностью на вопрос задачи.
IV. Итоги урока (13 мин.)
1. Самостоятельная работ
2. Рефлексия (Приложение 1, слайд 6)
Лист рефлексии
| Подчеркните, пожалуйста, те состояния, которые Вы испытывали в процессе сегодняшнего урока: | |
| интерес беспокойство эмоциональный подъем |
скука удовольствие раздражение |
V. Домашнее задание (Приложение 1, слайд 7)
Домашнее задание (Приложение 1, слайд 7)
1. Построить в одной системе координат графики функций:
а) у=1/2х2;
б) у=-1/2(х-3)2;
2. Построить графики функций, указать координаты вершины параболы и направление ветвей:
а) y = -3x2+5;
б) y = 2(x-3)2
Приложение 2
Приложение 3
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида , где называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки».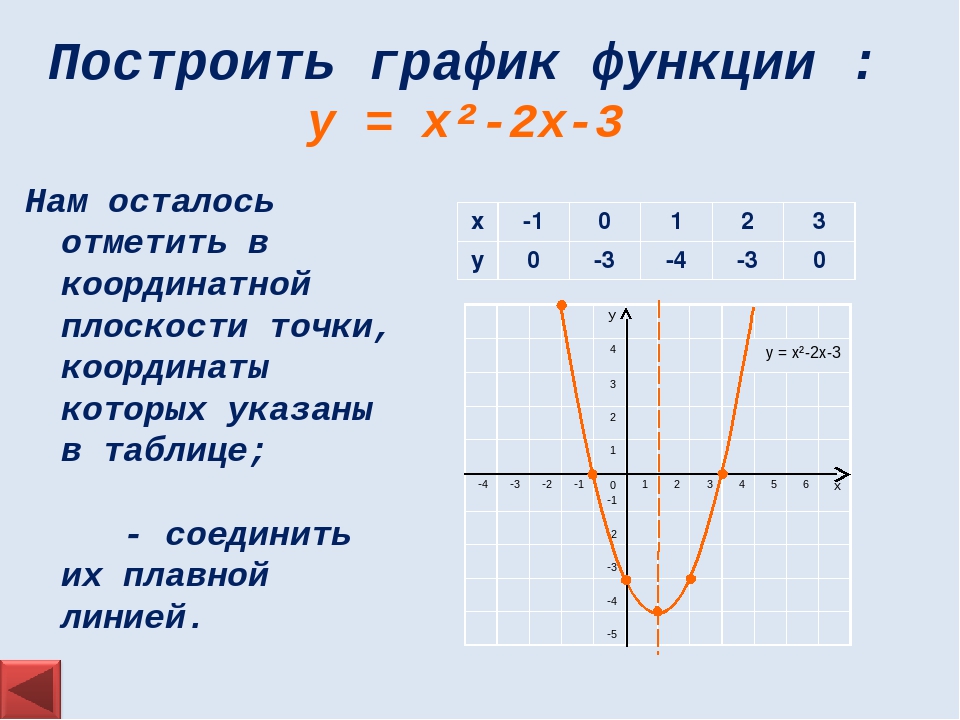 Чтобы найти координаты этих точек для функции , составим таблицу:
Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.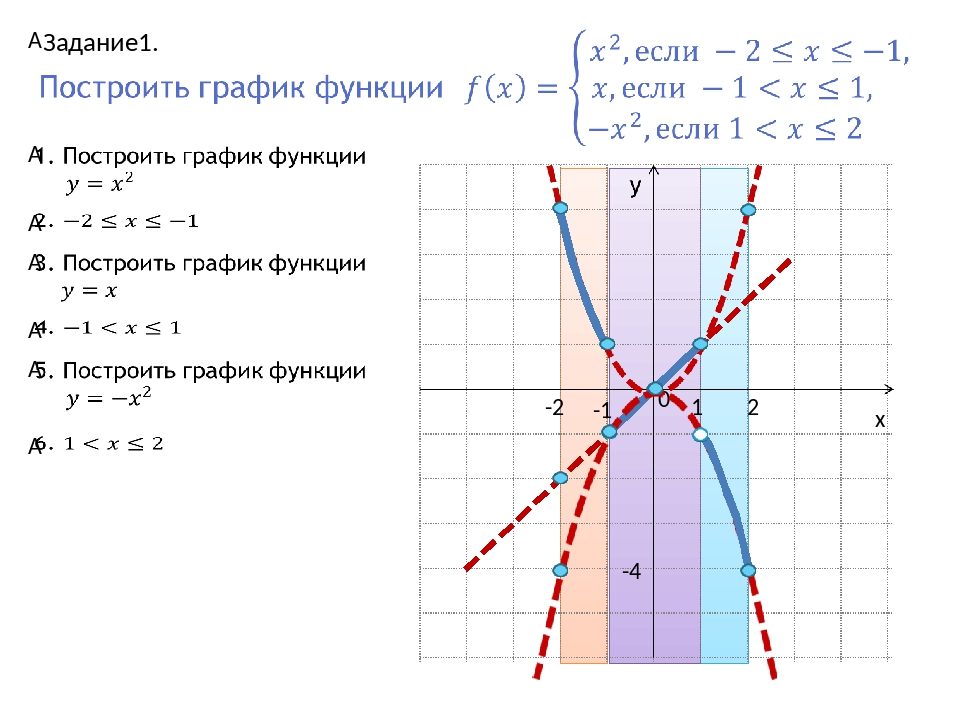
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Направление ветвей параболы.
Так как ,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2.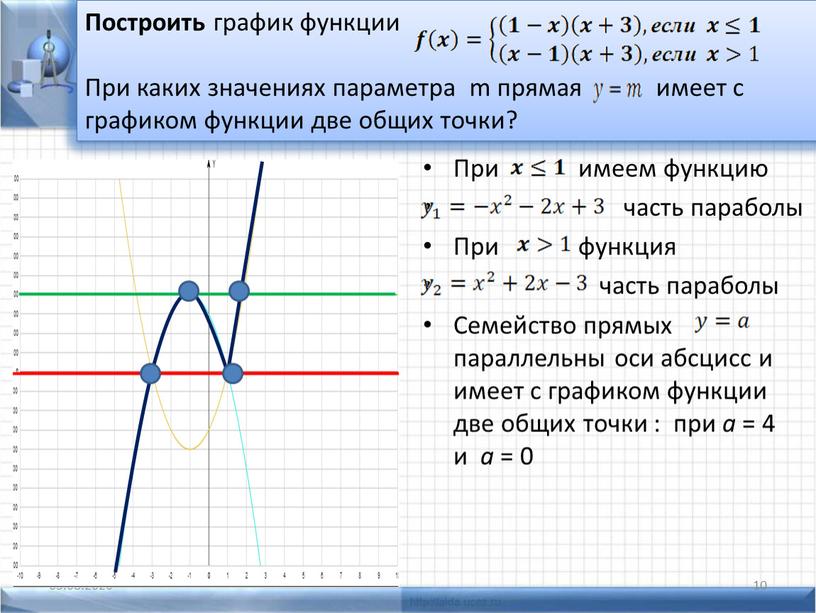 Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
или в уравнении квадратичной функции , и второй коэффициент — четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
- сначала построить график функции ,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,
— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Wolfram | Примеры альфа: домен и диапазон
Домен и диапазон
Найдите область и диапазон математического выражения.
Вычислить область определения функции:
Вычислить диапазон функции:
Укажите ограничение на независимую переменную:
Вычислить как домен, так и диапазон:
Вычислить область и диапазон функции нескольких переменных:
Другие примеры
Wolfram | Примеры альфа: приложения исчисления
Другие примеры
Асимптоты Вычислить горизонтальные, вертикальные или наклонные асимптоты.
Вычислить асимптоты функции:
Другие примеры
Другие примеры
Касательные и нормалиВычислить касательную линию к кривой или вычислить касательную плоскость или нормальную линию к поверхности.
Найдите касательную к графику функции в точке:
Найдите нормаль к кривой, заданной уравнением:
Другие примеры
Другие примеры
Бугорки и углы Вычислить и визуализировать куспиды и углы функции.
Найдите точки возврата на графике функции:
Найдите углы на графике функции:
Другие примеры
Другие примеры
Стационарные точки Вычисляйте и визуализируйте стационарные точки функции.
Найдите стационарные точки функции:
Найдите стационарные точки функции нескольких переменных:
Другие примеры
Другие примеры
Точки перегиба Вычислить и визуализировать точки перегиба функции.
Найдите точки перегиба функции:
Найдите точки перегиба в указанном домене:
Другие примеры
Другие примеры
Оптимизация Найдите глобальные и локальные экстремумы и стационарные точки функций или наложите ограничение на функцию и вычислите ограниченные экстремумы.
Свернуть или развернуть функцию:
Минимизируйте или максимизируйте функцию нескольких переменных:
Свернуть или развернуть функцию с ограничением:
Другие примеры
Другие примеры
Площадь между кривыми Вычисляет площади замкнутых областей, ограниченных областей между пересекающимися точками или областей между указанными границами.
Вычислите площадь, ограниченную двумя кривыми:
Укажите ограничения для переменной:
Другие примеры
Другие примеры
Длина дуги Вычислить длину дуги в различных системах координат и размерах.
Вычислите длину дуги кривой:
Другие примеры
Другие примеры
Поверхности и твердые тела революцииВычислите площадь поверхности вращения или объем тела вращения.
Вычислить свойства поверхности вращения:
Вычислить свойства твердого тела вращения:
Другие примеры
Другие примеры
Кривизна Вычисляет кривизну функций и параметризованных кривых в различных системах координат и измерениях.
Вычислите кривизну плоской кривой:
Вычислить кривизну пространственной кривой в точке:
Другие примеры
Другие примеры
Седловые точки Вычислить и визуализировать седловые точки функции.
Найдите седловые точки функции:
Найдите точку перевала, ближайшую к указанной точке:
Другие примеры
Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
Как построить график функции в Excel | Small Business
Математическая функция — это формула, которая принимает входные данные x, применяет к ним набор вычислений и производит выходные данные с именем y. Вычисляя функцию с большим количеством заданных интервалов, можно создать диаграмму рассеяния функции. В бизнесе это имеет множество применений.Например, вы можете построить график прибыли за вычетом затрат на различных уровнях продаж, или общие затраты можно оценить, нанеся на график постоянные затраты с разными приращениями переменных затрат.
Создайте заголовки для таблицы данных. Введите входную переменную в ячейку A1 и выходную переменную в ячейку B1. Если хотите, вы можете использовать математические стандарты «x» и «y» или использовать что-то более наглядное, например «продажи» и «прибыль».
Введите первый и второй интервалы входной переменной (например, «x» или «продажи»), которые вы будете использовать для построения графика функции.Например, если ваши интервалы представляют собой целые числа, вы можете начать с ввода «1» в ячейку A2 и «2» в ячейку A3. Выделите обе эти ячейки, а затем щелкните и перетащите маленький черный квадрат в правом нижнем углу области выбора вниз, пока у вас не будет столько значений, сколько вы хотите построить.
Введите знак равенства «=» в ячейку B2, а затем введите формулу сразу после него, не оставляя пробелов. Например, чтобы определить количество продаж определенного продукта для покрытия расходов, можно использовать:
= (A2 * 50) -3500
Замените «50» продажной ценой, а «3500» — ваши расходы.
Выберите ячейку B2, а затем перетащите, чтобы скопировать формулу вниз по столбцу тем же методом, который вы использовали на шаге 2. Убедитесь, что каждое из ваших значений x имеет соответствующую функцию справа от него. При этом столбец автоматически заполнится решениями для каждой функции на основе значения x в столбце A.
Выберите все ячейки, в которые вы ввели данные, включая заголовок.
Щелкните вкладку «Вставка», щелкните «Разброс» в области диаграмм, а затем выберите нужный тип графика.График появится на вашем листе.
Биография писателя
Уоррен Дэвис пишет с 2007 года, уделяя особое внимание индивидуальным проектам для онлайн-клиентов, таких как PsyT и Институт коучинга. Это было параллельно с исследованиями, веб-дизайном и ведением блогов. Пользователь Linux и игрок, Уоррен занимается боевыми искусствами в качестве хобби. Он имеет степень бакалавра и магистра психологии, а также дополнительную квалификацию в области статистики и бизнес-исследований.
Построение функции y = f (x) в Python (с Matplotlib)
В нашем предыдущем уроке мы узнали, как построить прямую линию или линейные уравнения типа $ y = mx + c $.2 здесь у = х ** 2 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [‘влево’]. set_position (‘центр’) ax.spines [‘дно’]. set_position (‘ноль’) ax.spines [‘правильно’]. set_color (‘нет’) ax. {3} $.3 здесь у = х ** 3 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [‘влево’]. set_position (‘центр’) ax.spines [‘дно’]. set_position (‘центр’) ax.spines [‘правильно’]. set_color (‘нет’) ax.spines [‘вверху’]. set_color (‘нет’) ax.xaxis.set_ticks_position (‘снизу’) ax.yaxis.set_ticks_position (‘влево’) # построить функцию plt.plot (x, y, ‘g’) # показать сюжет plt.show ()
Тригонометрические функции
Здесь мы строим тригонометрическую функцию $ y = \ text {sin} (x) $ для значений $ x $ между $ — \ pi $ и $ \ pi $.У метода linspace () интервал установлен от $ — \ pi $ до $ \ pi $.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
x = np.linspace (-np.pi, np.pi, 100)
# функция, которая здесь y = sin (x)
у = np.sin (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
Построим его вместе с еще двумя функциями, $ y = 2 \ text {sin} (x) $ и $ y = 3 \ text {sin} (x) $. На этот раз мы помечаем функции.
import matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
x = np.linspace (-np.pi, np.pi, 100)
# функция, которая здесь y = sin (x)
у = np.sin (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
топор.yaxis.set_ticks_position ('влево')
# построить график функций
plt.plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
И здесь мы строим вместе как $ y = \ text {sin} (x) $, так и $ y = \ text {cos} (x) $ через один и тот же интервал от $ — \ pi $ до $ \ pi $.
import matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
x = np.linspace (-np.pi, np.pi, 100)
# здесь функции y = sin (x) и z = cos (x)
у = np.sin (х)
z = np.cos (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.Икс')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
Графические рациональные функции
Рациональные функции имеют вид у знак равно ж Икс , куда ж Икс это рациональное выражение .
Вот некоторые из примеров рациональных функций:
у знак равно 1 Икс , у знак равно Икс Икс 2 — 1 , у знак равно 3 Икс 4 + 2 Икс + 5
Графики рациональных функций нарисовать сложно.Чтобы нарисовать график рациональной функции, вы можете начать с поиска асимптоты и перехватывает.
Этапы построения графиков рациональных функций:
- Найдите асимптоты рациональной функции, если таковые имеются.
- Нарисуйте асимптоты пунктирными линиями.
- Найди Икс -перехват (песок у -перехват рациональной функции, если таковая имеется.
- Найдите значения у для нескольких разных значений Икс .
- Постройте точки и нарисуйте плавную кривую, чтобы соединить точки. Убедитесь, что график не пересекает вертикальные асимптоты.
Пример:
Постройте график рациональной функции
у знак равно 4 Икс + 1 2 Икс + 1
Вертикальная асимптота рациональной функции равна Икс -значение, где знаменатель функции равен нулю.Приравняйте знаменатель к нулю и найдите значение Икс .
2 Икс + 1 знак равно 0 Икс знак равно — 1 2
Вертикальная асимптота рациональной функции равна Икс знак равно — 0,5 .
Эта функция имеет Икс -перехват в — 1 4 , 0 а также у -перехват в 0 , 1 .Найдите больше точек на функции и нанесите график функции.
Иногда перед построением графика данную рациональную функцию необходимо упростить. В этом случае, если есть какие-либо исключенные значения (где функция не определена), кроме асимптот, то есть дополнительный шаг, связанный с построением графика функции.
Чтобы представить неопределенную функцию, убедитесь, что функция не является непрерывной гладкой кривой при исключенном значении. Это исключенное значение обычно называют дырой в рациональной функции.
Например, рациональная функция у знак равно 4 Икс 2 + Икс 2 Икс 2 + Икс есть дыра в Икс знак равно 0 .
Обратите внимание, что графики рациональных функций удовлетворяют тест вертикальной линии .
: основы работы с графами — Справка | ArcGIS for Desktop
Визуальные и аналитические преимущества графика можно улучшить, добавив функцию.Функция применяет определенную математическую или статистическую операцию к значениям в серии данных и отображает результат в виде линии на графике.
Категории функций
В графических инструментах приложений ArcGIS for Desktop доступны 16 типов функций. Они делятся на две широкие категории: описательные и трендовые.
Описательная
Описательная функция — это функция, в которой одно значение вычисляется из всех значений в серии. Этот тип функции отображается в виде прямой линии на графике, представляющей вычисленное значение.
Описательные типы функций
| Тип функции | Описание |
|---|---|
Среднее | Простое среднее (среднее) значений. |
Счетчик | Количество значений в серии ( n ). |
Высокий | Наибольшее значение в серии. |
Низкий | Наименьшее значение в серии. |
Медиана | Среднее значение ряда. |
Режим | Значение режима серии. |
RMS | Среднеквадратичное значение для ряда. Общая формула для RMS: |
Стандартное отклонение | Мера разброса значений в ряду.Общая используемая формула: |
Дисперсия | Дисперсия — это разброс распределения значений в ряду, вычисляемый как среднее квадратичное отклонение каждого числа от его среднего. |
(где n — количество значений)
Тренд
Функции тренда показывают направление изменения значений.Функции трендов могут быть локальными или глобальными, и при добавлении к графику они действуют как глобальная сводка по диапазону значений данных.
| Типы функций | Описание |
|---|---|
Тренд | Линейная зависимость, отображаемая в виде прямой линии с определенным уклоном. |
Экспоненциальный тренд | Изогнутая линия, представляющая экспоненциальную зависимость. |
Другие тренды вычисляют локальную сводку для обобщения или сглаживания значений.
| Типы локальных сводок | Описание |
|---|---|
Скользящее среднее | Для каждого значения в серии среднее (простое или взвешенное) вычисляется для подмножества смежных значений. Это помогает лучше отличать долгосрочные тенденции от циклических. |
Экспоненциальное скользящее среднее | Подобно скользящему среднему, за исключением того, что оно взвешено так, что значениям в подмножестве, близком к вычисляемому, дается больший вес. |
Подгонка кривой | Сглаженная кривая генерируется из значений в серии путем применения полиномиальной функции Гаусса. Степень полинома используется для управления порядком (числом коэффициентов) используемого полинома. |
Сглаживание | Сглаженная кривая создается из значений в серии путем применения сплайн-функции к значениям. Чем выше коэффициент, тем более гладкой будет кривая (на основе компонента B-Spline Мартина ван Энгеланда). |
Другой тип тренда — Накопительный, который показывает совокупное количество значений:
Накопительное | Каждое значение добавляется к предыдущему значению, чтобы показать степень увеличения. |
 Причем, чем больше значение k, тем круче идет прямая.
Причем, чем больше значение k, тем круче идет прямая.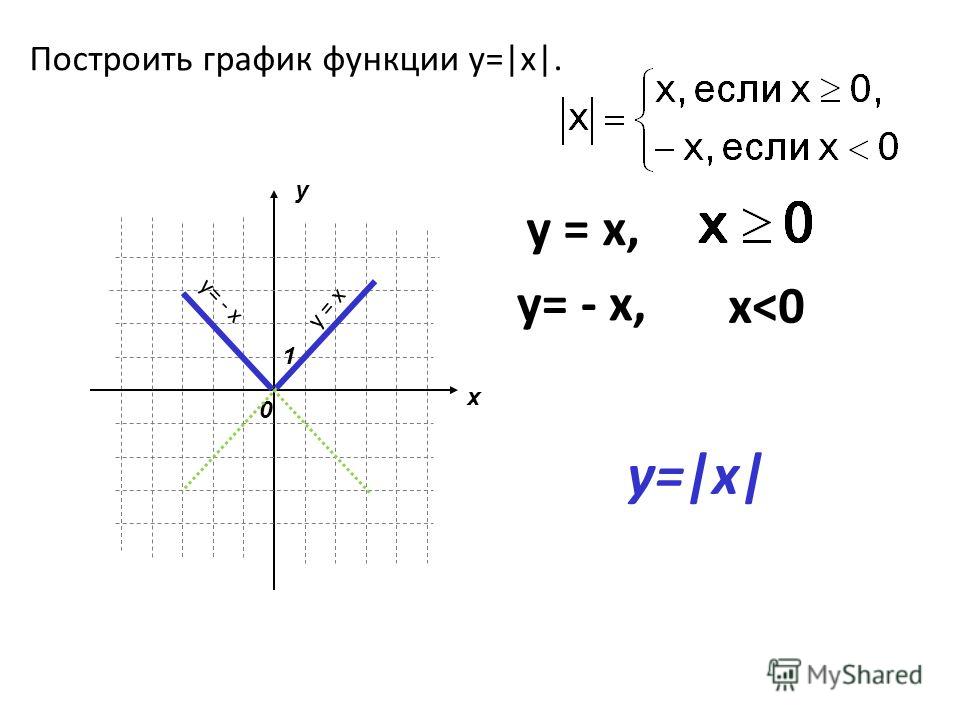
 Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
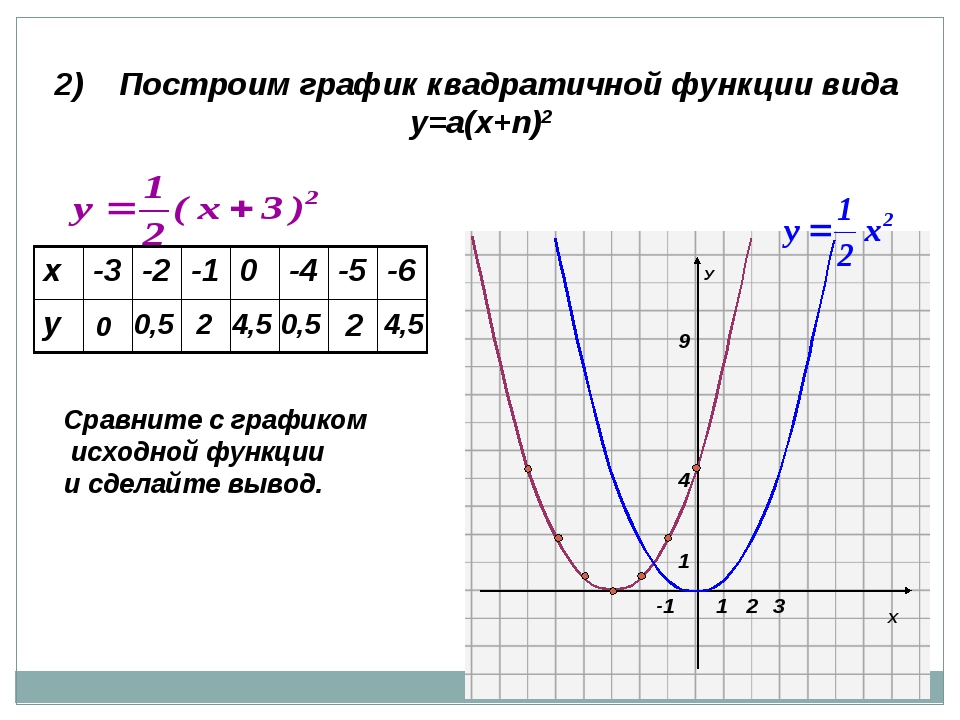
 Переходить от общего к частному намного проще, чем к конкретному.
Общее.
И это то, что мы делаем здесь, глядя на графики в целом, так что
потом
при необходимости вы можете применить его к чему-то конкретному. Мы также
пересмотреть
понятие домена и диапазона. На этот раз мы их найдем
смотрящий
на графике. Мы будем использовать обозначение интервалов для записи нашего
ответы. В некоторых случаях наш домен и / или диапазон будут недоступны
до бесконечности.
Думаю, вы готовы пойти дальше и построить график.
Переходить от общего к частному намного проще, чем к конкретному.
Общее.
И это то, что мы делаем здесь, глядя на графики в целом, так что
потом
при необходимости вы можете применить его к чему-то конкретному. Мы также
пересмотреть
понятие домена и диапазона. На этот раз мы их найдем
смотрящий
на графике. Мы будем использовать обозначение интервалов для записи нашего
ответы. В некоторых случаях наш домен и / или диапазон будут недоступны
до бесконечности.
Думаю, вы готовы пойти дальше и построить график.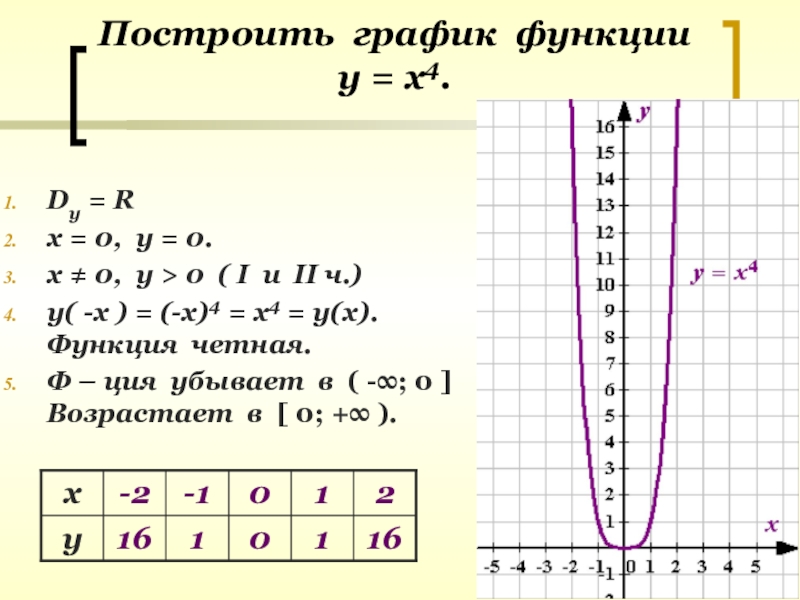 Если вам нужен обзор домена,
смело переходите к Учебник
30: Введение в функции.
Если вам нужен обзор домена,
смело переходите к Учебник
30: Введение в функции. Если вам нужен обзор ассортимента, смело переходите к руководству .
30: Введение в функции.
Если вам нужен обзор ассортимента, смело переходите к руководству .
30: Введение в функции. Найдите на
минимум четыре упорядоченных парных решения.
Найдите на
минимум четыре упорядоченных парных решения. 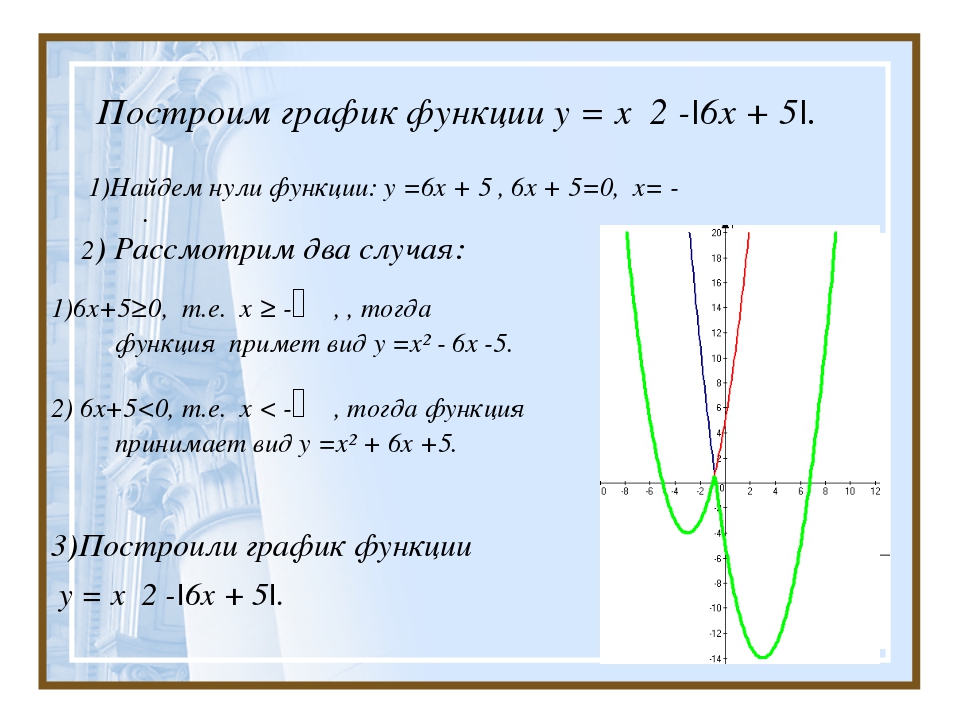
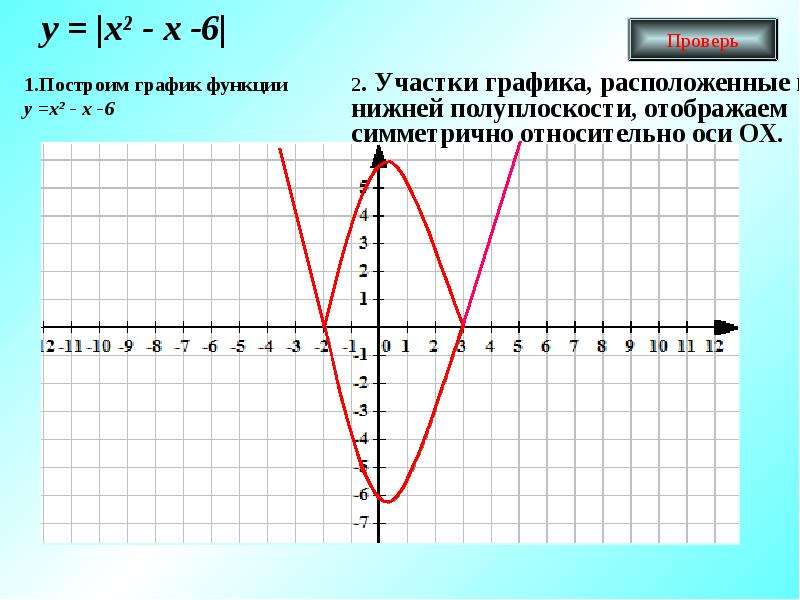 Также
использовать
график для определения области и диапазона функции.
Также
использовать
график для определения области и диапазона функции.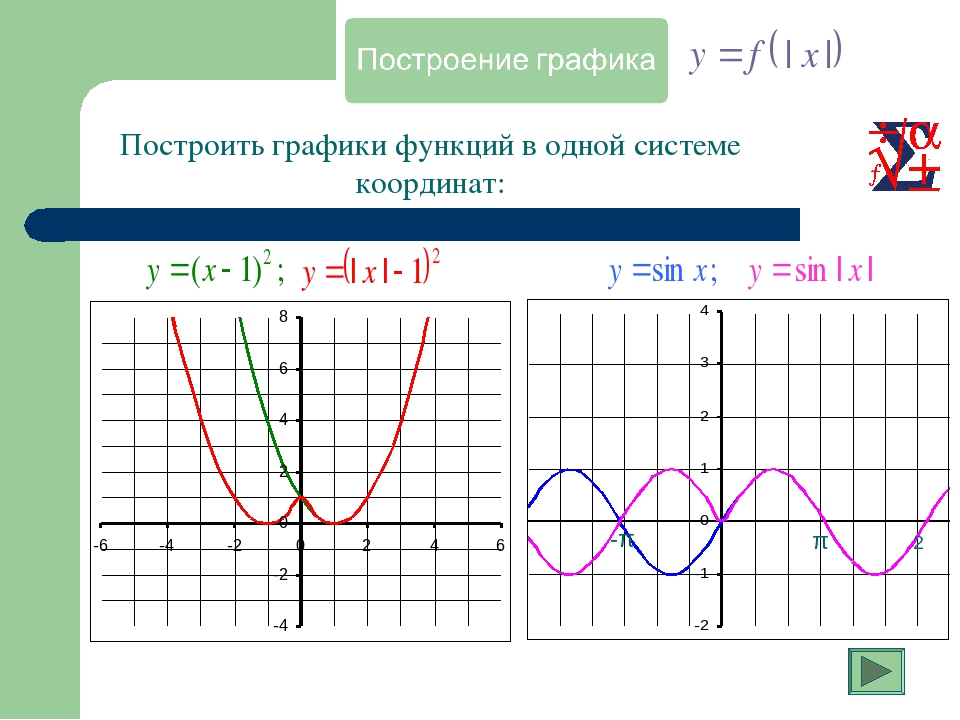
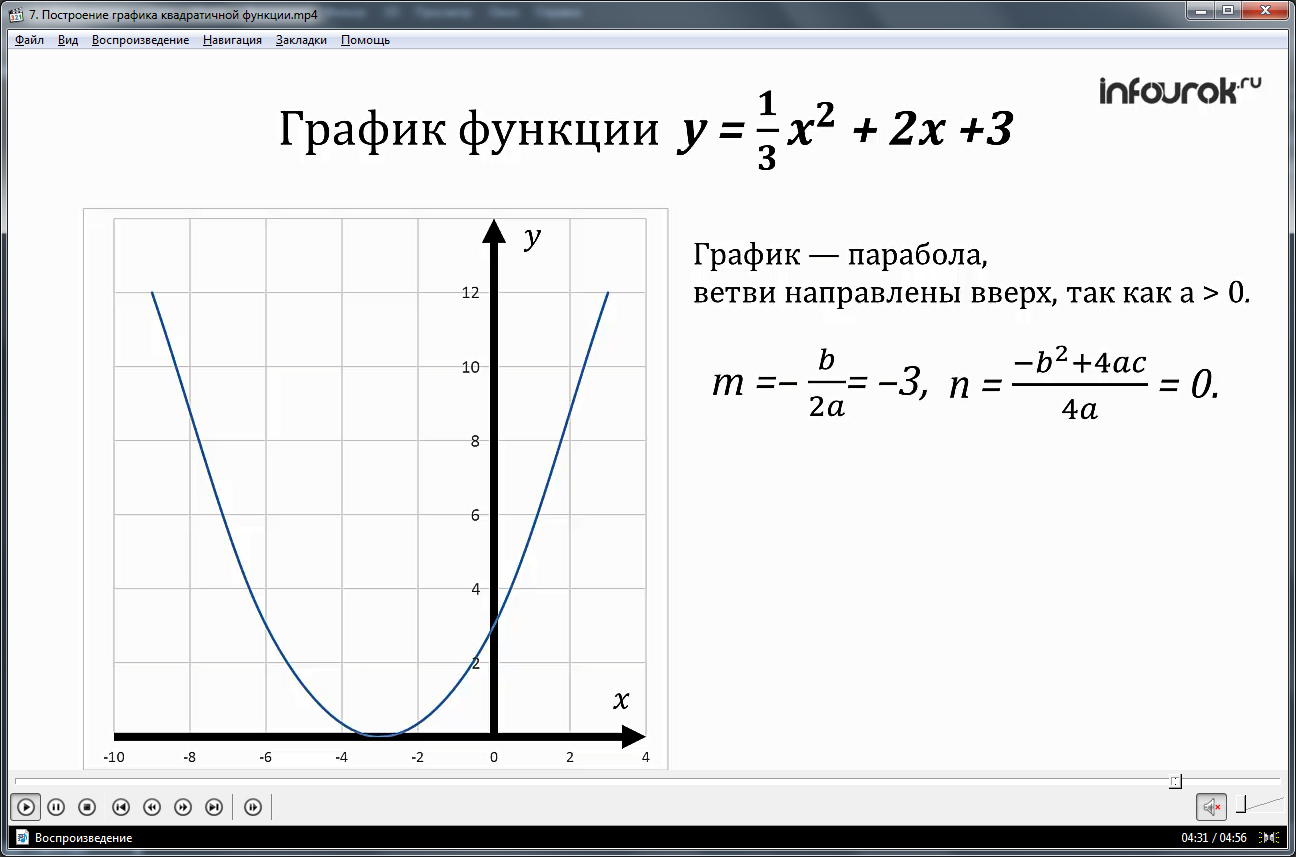 В терминах этого двумерного графа это
соответствует
со значениями x (по горизонтали
ось).
В терминах этого двумерного графа это
соответствует
со значениями x (по горизонтали
ось).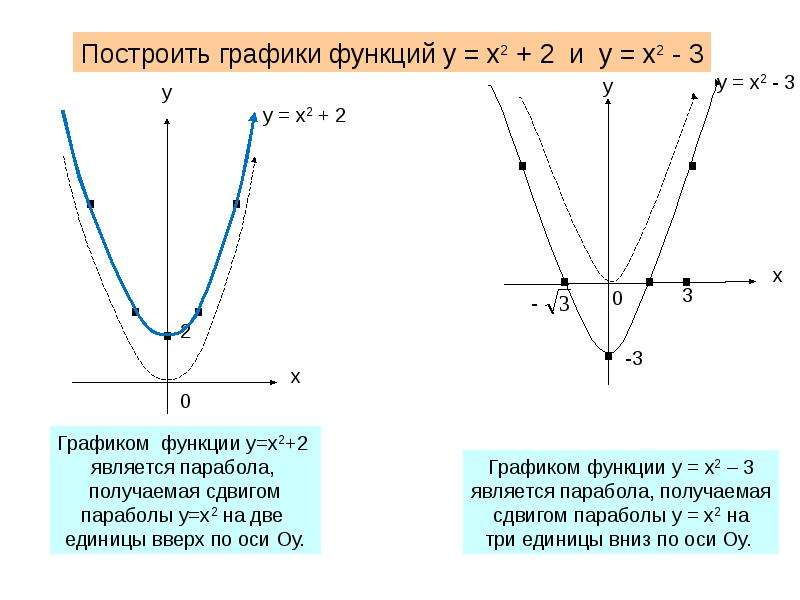
 Найдите на
минимум четыре упорядоченных парных решения.
Найдите на
минимум четыре упорядоченных парных решения.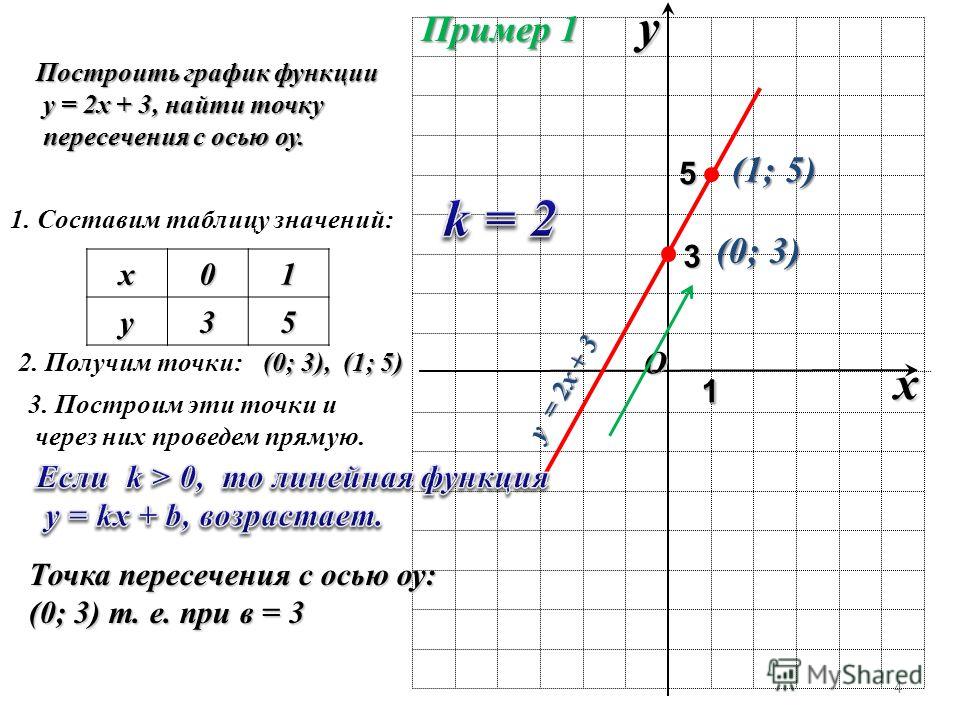
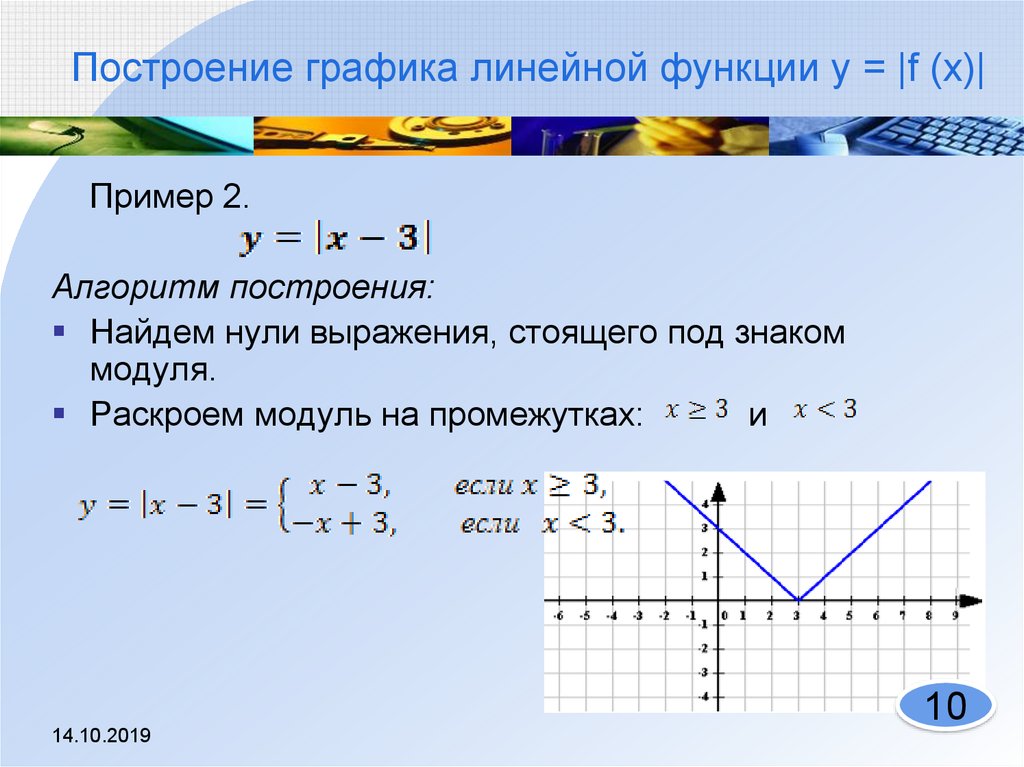 Также обратите внимание, что кривая
имеет
стрелка, идущая вправо, означает, что она будет продолжаться и продолжаться
навсегда
Направо.
Также обратите внимание, что кривая
имеет
стрелка, идущая вправо, означает, что она будет продолжаться и продолжаться
навсегда
Направо.
Ваш комментарий будет первым