Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
2 — вопрос №2616781 Лучший ответ по мнению автора
| |||||||||||||||||
10.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб
Помогите составить условия задачи, не решения, а условия.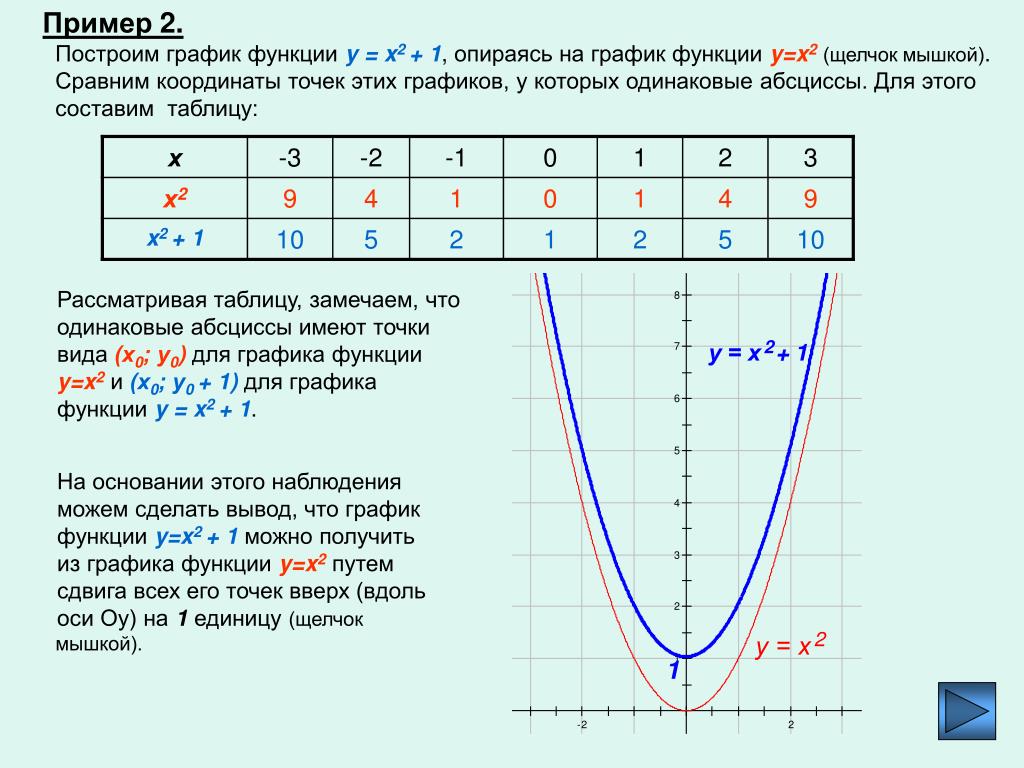
В школьный буфет привезли 36 кг яблок по 9 кг в каждом ящике, сколько ящиков привезли в буфет?
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Дан вектор m{1;2;2}.Найдите координаты единичного вектора е ,сонаправленного с вектором
Лексико-грамматический комментарий к слову по заочью и в очью
Пользуйтесь нашим приложением1.3.3.26. Точечная диаграмма
1.3.3.26. Точечная диаграмма| 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.3. Графические приемы: Алфавитный
| |||
| Цель: Проверка на родство | Точечная диаграмма (камеры
1983) выявляет отношения или связь между двумя
переменные. Такие отношения проявляются любым
неслучайная структура сюжета. Различные распространенные типы шаблонов
демонстрируются на примерах. | ||
| Пример графика: линейных отношений Между переменными Y и X | Этот образец участка данные трубопровода Аляски показывают линейная зависимость между двумя переменными, указывающая на то, что модель линейной регрессии может быть уместно. | ||
| Определение: Y против X | Точечная диаграмма представляет собой график значений Y в зависимости от
соответствующие значения X :
| ||
| вопросов | Диаграммы рассеяния могут дать ответы на следующие вопросы:
| ||
| Примеры |
| ||
| Объединение точечных диаграмм | Точечные диаграммы также можно объединять в несколько диаграмм на странице для
помочь понять структуру более высокого уровня в наборах данных с более чем
две переменные. Матрица диаграммы рассеяния генерирует все попарные диаграммы рассеяния на одной странице. участок кондиционирования, также называемый совместный график или подмножество графиков, генерирует точечные графики Y по сравнению с X зависит от значения третьей переменной. | ||
| Причинность не доказана ассоциацией | Точечная диаграмма раскрывает отношения в
данные. «Отношения» означают, что существует некоторая структурированная
связь (линейная, квадратичная и т. д.) между X и Y .
Заметьте, однако, что, хотя
Диаграммы рассеяния — полезный диагностический инструмент
для определения ассоциации, но если таковая
ассоциация существует, сюжет может подсказывать, а может и не подсказывать
лежащий в основе причинно-следственный механизм.
Точечная диаграмма никогда не может «доказать» причину и
эффект — в конечном счете только исследователь
(в зависимости от лежащей в основе науки/техники)
кто может заключить, что причинность действительно существует. | ||
| Появление | Самое популярное представление точечной диаграммы
Другие варианты формата точечной диаграммы включают
В обоих случаях полученный график называется разбросом. участок, хотя прежний (дискретный и несвязный) является личное предпочтение автора, так как ничего не попадает на экрана, кроме данных — нет интерполяционных артефакты, искажающие интерпретацию. | ||
| Связанные методы | Выполнить график последовательности Блок-график Блочный график | ||
| Практический пример | График рассеяния показан на
данные калибровки тензодатчика
тематическое исследование. | ||
| Программное обеспечение | Диаграммы рассеяния — это фундаментальный метод, который должен быть доступен в любой статистической программе общего назначения. Графики рассеяния также доступен в большинстве программ для работы с графикой и электронными таблицами. | ||
Как нанести размеры по оси Y | Смотритель
Все пользовательские данные, представленные на этой странице, предназначены для примера.
Визуализации Looker автоматически определяют, какие значения отображать по оси Y.
в зависимости от того, какие типы полей присутствуют в запросе. Например, если
который разбивает пользователей по имени и пользователей по возрасту для
10 самых высоких Orders Count визуализируются в виде гистограммы,
10 значений измерения для Имя пользователя и Возраст пользователя автоматически объединяются и разделяются тире (–) по оси X.
Что делать, если вы хотите разделить пользователей с возрастом и пользователей с именем , чтобы пользователей с возрастом на оси Y, а Имя пользователя и Количество заказов отображаются на оси X?
Два следующих решения показывают, как преобразовать измерение, например Users Age , в меру, чтобы ее можно было визуализировать на оси Y:
- Использование табличного расчета — создайте одноразовое решение прямо из Explore, не разрабатывая LookML.
- Создание показателя. Разработайте LookML, чтобы можно было повторно использовать выражение в будущих исследованиях без необходимости создания табличных вычислений.
Использование табличного расчета
Табличный расчет — это самый быстрый и простой способ нанести размер на ось Y. Вычисление обычно изображается в виде измерения, если в выражении не участвуют меры.
Вы можете заставить табличное вычисление вести себя как меру, включив меру в выражение вычисления. Главное — убедиться, что мера не повлияет на значение исходного измерения.
Чтобы использовать расчет таблицы для построения показателя по оси Y, выполните следующие действия:
- Если в запросе «Изучение» нет меры, добавьте любую меру (например, число), а затем скрывать это из визуализации. Если в вашем запросе уже есть мера, которую вы хотите включить в визуализацию, нет необходимости ее скрывать.
- Далее создадим табличный расчет:
- Для числового поля расчет будет следующим:
${mydimension} + (0 * ${mymeasure})Расчет сохраняет исходное значение размера путем умножения измерить на 0, - Для строкового поля вычисление будет включать два
логические функции,
if()иis_null()вместо этого:если (is_null ($ {mymeasure}), $ {string_dimension}, $ {string_dimension})Это выражение сообщает Looker всегда отображать значение размерности строки вместо измерять значения.
- Для числового поля расчет будет следующим:
- Скройте исходное измерение — в данном случае Users Age — из визуализации, поскольку табличное вычисление — мера Age — теперь представляет значения измерения в визуализации.
Чтобы различать значения в визуализации — в этом примере расчет таблицы мер Age и Orders Count показателей — вы можете использовать несколько типов vis на одном графике.
Например, вы можете визуализировать значений Orders Count в виде строки и значений Users Age в виде столбец, чтобы различать их после того, как Users Age нанесены на ось Y.
Создание показателя в LookML
Если вы планируете в будущем снова отобразить определенное измерение по оси Y, более устойчивым вариантом будет создание сумма мера или номер мера
в LookML, который превращает измерение, которое вы хотите отобразить, в меру.
Вместо того чтобы повторно создавать одно и то же табличное вычисление в Исследовании несколько раз, вы можете добавить поле в запрос из средства выбора поля.
Мера будет выглядеть примерно так:
мера: Measure_for_age { ## заменить новым именем
description: "Используйте это поле возраста для отображения возраста по оси Y"
тип: число ## или сумма
sql: ${возраст} ;; ## замените на свой размер
}
Добавление описания к мере может помочь пользователям понять предполагаемое использование поля. В этом случае мера_для_возраста является мерой типа номер , поскольку меры типа номер не выполняют никакого фактического агрегирования. Это означает, что мера для Age будет отображать те же значения, что и Users Age , потому что это мера типа number , которая не выполняет никакого агрегирования.
Ваш комментарий будет первым