2+n-72)=1/(n+9)Графики линейных уравнений: дополнительные примеры
T-ChartsPlotting & DrawingExamples
Purplemath
Во всех предыдущих упражнениях уравнения, которые нам давали, решались для одной из переменных, обычно и .
Иногда, однако, нам дают уравнения, которые не решены.
Содержание продолжается ниже
MathHelp.com
Графики линейных уравнений
В таком случае обычно проще всего сначала заняться алгеброй, чтобы решить уравнение (обычно для » y =»), чтобы упростить нашу жизнь. (Возможно, вы слышали, что это называется «решением буквальных уравнений».)
Не обязательно сначала выполнять алгебраические вычисления, но мы можем сначала решить уравнение, а затем просто «подключи и пыхни», или мы можем подключиться к уравнение, как указано, а затем решить для каждого значения плагина. Первое обычно значительно экономит время по сравнению со вторым.
- График 4 x — 3 y = 12
Я считаю, что для такого рода уравнений проще всего сначала найти » y =». Это особенно верно, если я использую графический калькулятор для заполнения своей T-диаграммы, потому что графические калькуляторы могут обрабатывать линейные уравнения только в том случае, если они имеют форму » y =».
Итак, чтобы облегчить себе жизнь, я сначала решу это уравнение алгебраически.
Для этого я вычту 12 из левой части и прибавлю −3 и на правую сторону. Тогда я разделю на 3 и упрощу. Наконец, я перестрою уравнение (поменяв местами стороны), чтобы получить и в левой части, где я привык. Вот эти шаги:
4 x — 12 = 3 y
4 х — 12 = 3 у
(4 х )/3 — (12)/3 = (3 у )/3
(4/3) х — 4 = у
Итак, я на самом деле нарисовал это уравнение: равно 3, проще всего выбрать x значений, кратных 3, чтобы знаменатель уравновешивался.
Вот моя Т-диаграмма…
…и вот мой график:
Они попросили график; Я дал им график, так что я сделал.
График −3
x = 6 y − 2
Сначала я решу уравнение для » y =»
Итак, после того, как я поменял местами стороны, чтобы привести значения в обычный формат, мое уравнение будет таким:
y = −(1/ 2) x + 1/3
Итак, вычисление точек сюжета для этого будет запутанным из-за всех дробей.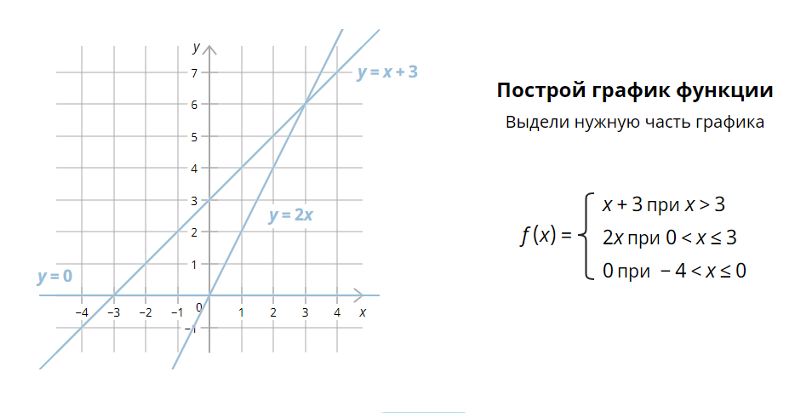
Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я буду делать все, что в моих силах, когда буду строить свои точки:
Из этих точек я строю свой график:
Обратите внимание, что этот график должен быть больше (с точки зрения минимального и максимального значений осей), чем тот, который я нарисовал раньше. Это потому, что точки были «беспорядочными», поэтому мне нужно было больше точек, и мне нужно было, чтобы эти точки были дальше друг от друга, чтобы убедиться, что моя линия верна. Это пример графика, для которого стоит потратить дополнительное время и быть осторожным!
Редко вы увидите графическое упражнение, в котором используются десятичные дроби. Преобразование в дроби может быть полезным, так как вы сможете увидеть, какие виды x — значения могут быть более полезными.
График
y = 0,4 x − 4
Десятичное число 0,4 совпадает с дробью
4/10 = 2/5.
y = (2/5) x − 4
Это говорит мне о том, что выбор x -значений, кратных 5, с большей вероятностью даст мне красивые, аккуратные сюжетные точки. Вот моя Т-диаграмма:
| х | г |
| −10 | (2/5)(-10) — 4 = -4 — 4 = -8 |
| −5 | (2/5)(-5) — 4 = -2 — 4 = -6 |
| 0 | (2/5)(0) — 4 = 0 — 4 = -4 |
| 5 | (2/5)(5) — 4 = 2 — 4 = -2 |
| 10 | (2/5)(10) — 4 = 4 — 4 = 0 |
| 15 | (2/5)(15) — 4 = 6 — 4 = 2 |
| 20 | (2/5)(20) — 4 = 8 — 4 = 4 |
Даже если я пропущу несколько точек на концах (что, я думаю, так и сделаю), это будет широкий график, по крайней мере, с точки зрения масштаба.
Взгляните еще раз на этот график выше; в частности, посмотрите на шкалы по двум осям. Весы помечены неодинаково, поэтому мне нужно было нанести на весы цифры. В противном случае можно было бы предположить, что шкалы равны -1, 0, 1, 2, 3 и так далее.
Вместо этого я нарисовал область графика, чтобы он соответствовал моему вкусу. (То есть я подгонял вещи так, чтобы они выглядели лучше, по моему личному мнению.) В результате мне нужно было пометить шкалы осей, чтобы избежать путаницы.
Не думайте, что вам нужно ограничивать каждую область графика значениями от −10 до 10. Если вы считаете, что ваш график становится слишком высоким или слишком широким, отрегулируйте масштаб соответствующим образом. Пока вы маркируете четко, вы можете нарисовать область графика в любом удобном для вас масштабе.
Какие существуют четыре способа графического отображения линейных уравнений?
Вместе с методом, показанным в этом уроке, существует четыре метода построения графика прямых линий.
- построение графика с помощью T-диаграммы (которая всегда работает и может быть полезна при принятии решения о том, как нарисовать область графика)
- построение графика по перехватам (что дает вам только две точки, так что это может быть немного сомнительно)
- график из у -перехват и наклон (если вы правильно поймете перехват, то наклон даст вам столько очков, сколько захотите)
- построение графиков с помощью переводов (что включает в себя каким-то образом определение правильного «эталонного» графика, а затем каким-то образом определение того, как перемещать этот график «правильным» образом)
Я бы использовал точки пересечения только в том случае, когда уравнение не было решено для y =; в этом случае вы должны подставить ноль для каждой из переменных по очереди и найти соответствующее значение другой переменной.
Я бы *никогда* не использовал переводы, особенно для таких простых вещей, как построение графиков линейных уравнений.
Ваш комментарий будет первым