Построение графика в полярных координатах. Контрольные онлайн
Построение графика в полярных координатах
Дано уравнение кривой в полярной системе координат .
Требуется:
а) построить кривую по точкам, придавая j значения из промежутка с шагом ;
б) записать уравнение этой кривой в декартовой прямоугольной системе координат, согласованной с полярной, и определить тип этой кривой. Решение а) Составим таблицу значений функции.
j | 0 | p/8 | p/4 | 3p/8 | p/2 | 5p/8 | 3p/4 | 7p/8 | p | 9p/8 | 5p/8 | 11p/8 | 3p/2 | 13p/8 | 7p/4 | 15p/8 |
r | 3 | 2,8 | 2,32 | 1,72 | 1,5 | 1,26 | 1,11 | 1,02 | 1 | 1,02 | 1,11 | 1,26 | 1,5 | 1,72 | 2,32 | 2,8 |
По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.
б) Перейдём к декартовой прямоугольной системе координат, пользуясь формулами , .
Заданное уравнение примет вид .
Преобразуем это уравнение: ,
, , , .
Выделив полные квадраты переменных и , получим или .
Использование excel для построения графиков функций заданных в параметрическом виде или в полярных координатах и графиков объемных функций цели урока
Бут Людмила Александровна
учитель информатики лицея №14 г.Жуковский
Использование Excel для построения графиков функций, заданных в параметрическом виде или в полярных координатах и графиков объемных функций.
Цели урока:
Образовательная:
Научить учащихся применять современное программное обеспечение в решении нестандартных задач;
Сформировать представление учащихся о способах построения объемных изображений средствами Excel.

Развивающая:
Продолжить развивать умения учащихся применять компьютер для решения конкретных задач из конкретной предметной области;
Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений.
Воспитательная:
Задачи урока:
Воспитательная. Развитие познавательного интереса, воспитание информационной культуры.
Учебная. Изучить и закрепить основные навыки работы с электронными таблицами.
Развивающая.
Развитие логического мышления, расширение кругозора.
Тип урока: Комбинированный — урок формирования и закрепления умений и навыков практического использования MS Excel.
План урока.
Организационная часть.

Повторение пройденного материала.
Обобщение и систематизация понятий для выполнения самостоятельной работы.
Самостоятельная работа.
Подведение итогов.
Домашнее задание.
Ход урока.
Вопросы для повторения:
Что такое относительная и абсолютная адресация?
Как протабулировать функцию, заданную в виде y=f(x)?
Как построить график функции, используя Мастер диаграмм?
На уроке мы рассмотрим особенности построения двух наиболее часто употребляемых в инженерной практике типов диаграмм – точечных (графиков) и поверхностных (или объемных).
Построение графиков функций, заданных в параметрическом виде или в полярной системе координат.
Параметрическое представление кривой на плоскости – это две функции, явно выражающие обе координаты x и y через значение некоторого производящего параметра:
Параметрические линии по форме
могут быть более разнообразными, чем
линии, описываемые одним уравнением.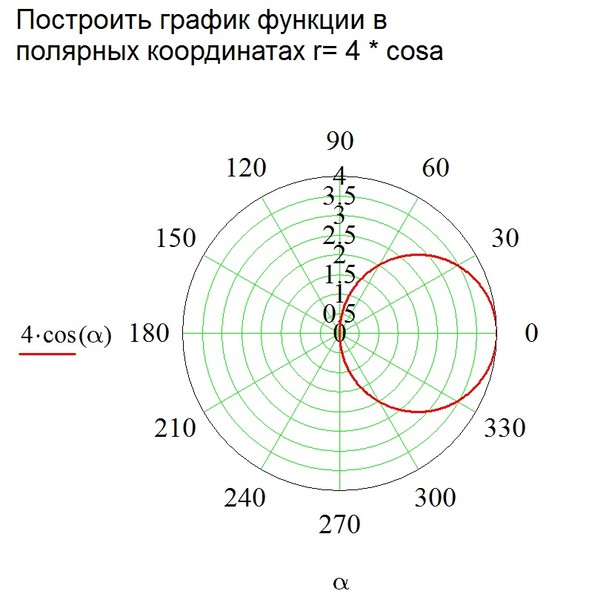 На них не распространяется ограничение
по многозначности, поэтому линии могут
быть самопересекающимися.
На них не распространяется ограничение
по многозначности, поэтому линии могут
быть самопересекающимися.
Для примера рассмотрим уравнение окружности с центром в начале координат и радиусом R.
.
Координаты точек окружности вычисляются по формулам:
.
Здесь центральный угол t является генерирующим параметром.
Для построения полной окружности радиуса R=100 составим таблицу, в которой значение параметра t меняется с шагом 0,1 от 0 до 2π.
Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная. Точечная диаграмма отображает взаимосвязь между числовыми значениями в нескольких рядах и представляет две группы чисел в виде одного ряда точек в координатах XY.
Получим диаграмму:
Полярные координаты и точки М на плоскости – это расстояние
=ОМ
от фиксированной точки О (полюса) до
точки М и угол
между
лучами ОМ и ОР (полярная ось).
Полярные координаты являются наиболее употребительными после декартовых. Это нелинейные координаты. При построении кривых, заданных в полярных координатах, полярные координаты переводят в декартовы. Если полюс имеет координаты (x0, y0), то формулы преобразования таковы:
Для функций, заданных в полярных координатах формула имеет вид
, где – полярный угол.
Таблица должна содержать данные для построения кривой в полярной системе координат. Затем надо перевести данные из полярных координат в декартовы. Данные для построения точечного графика должны быть представлены в декартовой системе координат.
Рассмотрим Архимедову спираль, ее уравнение в полярных координатах:
ρ = aφ, где а — постоянная.
Составим таблицу для a=2,
значение полярного угла меняется с
шагом 0,1 от 0 до 6π.
Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная.
Получим диаграмму:
Задания для самостоятельной работы:
Построить графики замечательных кривых:
Астроида | Кардиоида X=acost(1+cost) Y=asint(1+cost) или ρ=a (1+cosφ) | ||
n- лепестковая роза ρ= a sin mφ или ρ = a cos mφ | Лемниската Бернулли ρ2-a2cos(2φ)=0 |
Элементы диаграммы можно
видоизменять при помощи контекстного
меню, вызываемого правой кнопкой мыши. Видоизменение, как правило, состоит в
определении другого цвета для какого-то
элемента, нового типа линии или маркера.
Внести изменения можно, выбрав в
контекстном меню первый пункт – Формат соответствующего объекта и определив
нужные параметры.
Видоизменение, как правило, состоит в
определении другого цвета для какого-то
элемента, нового типа линии или маркера.
Внести изменения можно, выбрав в
контекстном меню первый пункт – Формат соответствующего объекта и определив
нужные параметры.
Построение графика объемной функции.
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей.
Поверхность будем рассматривать как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0.
Рассмотрим зависимость, которая описывает сферу радиуса R.
X2 +Y2+Z2=R2
Выразим z:
Поскольку z(x, y) является
функцией двух переменных, то ее график
будет объемным, т.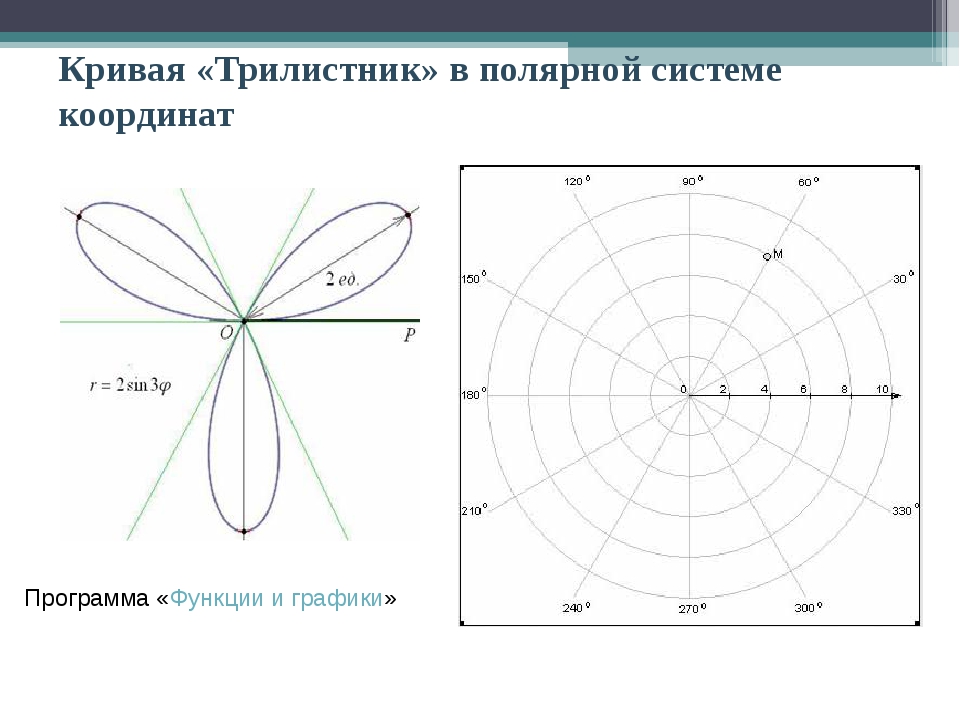 к. по двум осям (x, y)
будут откладываться значения аргументов,
а по третьей (z) – вычисленные значения
функции.
к. по двум осям (x, y)
будут откладываться значения аргументов,
а по третьей (z) – вычисленные значения
функции.
Сначала нужно создать таблицу значений функции в заданных диапазонах аргументов.
Если бы мы попытались сделать это известными способами, то нам потребовалось бы ввести большое множество значений аргументов, т. к. для каждого значения x пришлось бы ввести все значения диапазона y. При этом таблица имела бы очень большие размеры в длину или ширину. Однако можно построить таблицу по другому – в виде массива(матрицы): по строке отложить значения переменной x, а по столбцу – переменной y, а вычисленные значения функции – в ячейках на пересечении соответствующих значений аргументов. Это компактный способ представления данных.
Рассмотрим пример такой таблицы для R=3.
Значение квадрата радиуса вводится в ячейку B1.
В ячейки A3:A15
введите числа от -3 до 3 с шагом 0,5. 2). Для
того, чтобы все значения x
брались из строки 2, а все значения y
из столбца A нужно
использовать абсолютную адресацию.
Замена относительных адресов в формуле
на абсолютные производится с помощью
клавиши F4, которая при
выборе очередной ячейки при вводе
формулы нажимается несколько раз до
появления нужного вида адреса.
Распространяя формулы на диапазон
B3:O19, получим
следующую таблицу( в ней удалены сообщения
об ошибке в ячейках, где происходило
извлечение квадратного корня из
отрицательного числа).
2). Для
того, чтобы все значения x
брались из строки 2, а все значения y
из столбца A нужно
использовать абсолютную адресацию.
Замена относительных адресов в формуле
на абсолютные производится с помощью
клавиши F4, которая при
выборе очередной ячейки при вводе
формулы нажимается несколько раз до
появления нужного вида адреса.
Распространяя формулы на диапазон
B3:O19, получим
следующую таблицу( в ней удалены сообщения
об ошибке в ячейках, где происходило
извлечение квадратного корня из
отрицательного числа).
Будем использовать стандартную объемную поверхностную диаграмму.
Поверхностные диаграммы отображают два или несколько рядов данных в виде поверхности.
В отличие от остальных диаграмм, в этом случае Excel применяет различные цвета для выделения значений, а не рядов данных.
Для построения
графика выделим всю таблицу и выберем
тип диаграммы Поверхность. Так как
в таблице вычислены только положительные
значения z , то на диаграмме
будет изображена полусфера.
Получим объемный график.
Для видоизменения поверхностных диаграмм предоставляется больше возможностей. Вызвав через меню Диаграмма – Объемный вид диалоговое окно Формат трехмерной проекции, мы можем задать повороты в разных направлениях, перспективу, изменить высоту графика (задается в процентах от нормальной высоты), а также некоторые другие параметры.
Задания для самостоятельной работы:
Построить объемную диаграмму поверхностей второго порядка.
Эллиптический параболоид | ||
Гиперболический параболоид | ||
Вещественный конус | ||
Однополостной гиперболоид | ||
Двуполостной гиперболоид |
Требования к
выполнению заданий.
Каждое задание выполняется на отдельном листе книги. Таблицы и диаграммы должны быть полностью оформлены. Файл сохранить в Личной папке.
Лепестковая диаграмма в Excel в полярной системе координат
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.

График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.

* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.

Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Линия в полярной системе координат — построение графика в полярной системе координат.
 Связь между полярными и декартовыми координатами
Связь между полярными и декартовыми координатами
Краткая теория
В полярной системе координат точка задается полярным углом φ и полярным радиусом r.
φ — угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки)
r — расстояние от заданной точки до полюса
Если совместить начало декартовых координат с полюсом, а ось абсцисс с полярной осью, то между полярной и декартовой системой координат может быть установлена однозначная связь.
Пример решения задачи
Задача
Линия задана уравнением в полярной системе координат. Требуется:
- Построить линию по точкам начиная с до и придавая значения через промежуток ;
- Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
- По уравнению в
декартовой прямоугольной системе координат определить, какая это линия.

Решение
Построение линии по точкам
Построим линию по точкам, предварительно заполнив таблицу значений r и j:
| 1 | 0 | 1 | 9 | 0,556 |
| 2 | 0,924 | 8,772 | 0,570 | |
| 3 | 0,707 | 8,121 | 0,616 | |
| 4 | 0,383 | 7,148 | 0,699 | |
| 5 | 0,000 | 6,000 | 0,833 | |
| 6 | -0,383 | 4,852 | 1,031 | |
| 7 | -0,707 | 3,879 | 1,289 | |
| 8 | -0,924 | 3,228 | 1,549 | |
| 9 | -1 | 3 | 1,667 | |
| 10 | -0,924 | 3,228 | 1,549 | |
| 11 | -0,707 | 3,879 | 1,289 | |
| 12 | -0,383 | 4,852 | 1,031 | |
| 13 | 0,000 | 6,000 | 0,833 | |
| 14 | 0,383 | 7,148 | 0,699 | |
| 15 | 0,707 | 8,121 | 0,616 | |
| 16 | 0,924 | 8,772 | 0,570 | |
| 17 | 1 | 9 | 0,556 |
Используя данные
таблицы, строим линию.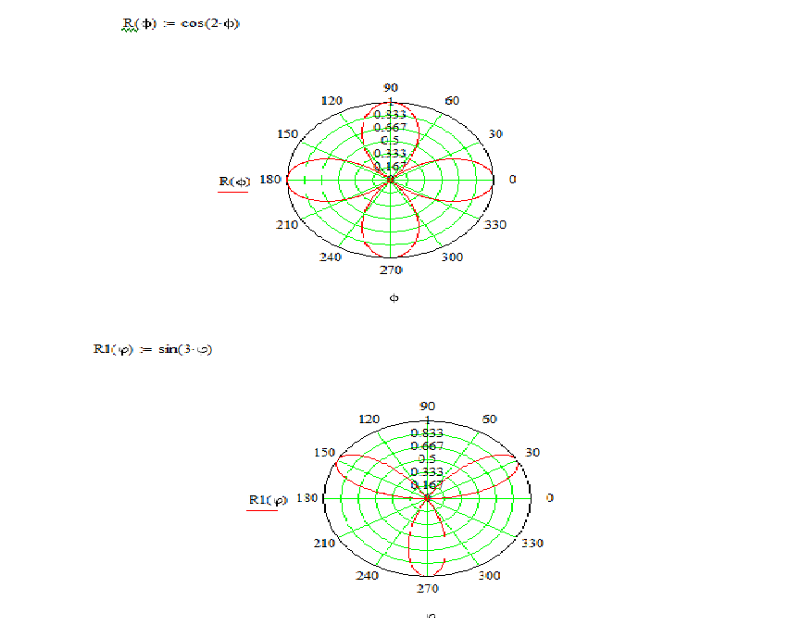
- Отмечаем полюс и указываем масштаб.
- С помощью транспортира прочерчиваем угловые направления
- Циркулем и линейкой отмечаем найденные точки
- Отложенные точки соединяем линией
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
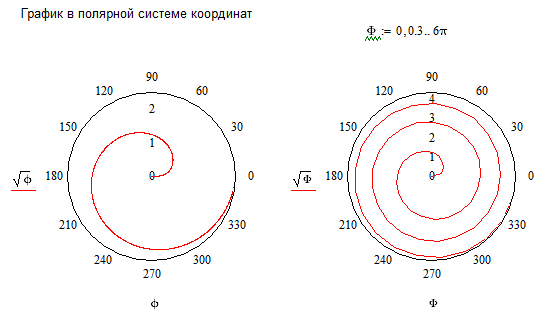
График в полярной системе координат имеет вид:
Уравнение линии в декартовой прямоугольной системе координат
Найдем уравнение данной линии в декартовой системе координат:
Подставляя в исходное уравнение в полярных координатах, получаем:
Полученная линия -эллипс
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.
Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.
Полярная система координат, построение графика, примеры — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Аналитическая геометрия
Это видео посвящено вопросу о том, что такое полярная система координат, построение графика, примеры. Вы уже наверняка знаете, что такое прямоугольная декартова система координат на плоскости. На одном из уроков эта тема уже рассматривалась. Она часто используется при решении многих задач и позволяет установить взаимно однозначное соответствие между точками плоскости и действительными числами. Но в некоторых случаях более эффективным является использование полярной системы координат. В этом видео уроке подробно рассказывается об этой системе. Вы узнаете, что такое полярная ось, полюс, полярный радиус, полярный угол, полярные координаты точки и многое другое. На приведенном примере вы узнаете, как построить график в полярной системе координат. Затем будет установлена связь между полярными и декартовыми координатами, т.е. по известным полярным координатам, при помощи формул, вычисляются координаты декартовой системы координат и наоборот. Во втором примере будет рассмотрена задача, в которой даны декартовы координаты точки, а требуется найти полярные координаты этой точки. Видео урок «Полярная система координат, построение графика, примеры» вы можете смотреть онлайн совершенно бесплатно. Удачи Вам!
В этом видео уроке подробно рассказывается об этой системе. Вы узнаете, что такое полярная ось, полюс, полярный радиус, полярный угол, полярные координаты точки и многое другое. На приведенном примере вы узнаете, как построить график в полярной системе координат. Затем будет установлена связь между полярными и декартовыми координатами, т.е. по известным полярным координатам, при помощи формул, вычисляются координаты декартовой системы координат и наоборот. Во втором примере будет рассмотрена задача, в которой даны декартовы координаты точки, а требуется найти полярные координаты этой точки. Видео урок «Полярная система координат, построение графика, примеры» вы можете смотреть онлайн совершенно бесплатно. Удачи Вам!
- Автор: alWEBra
- Длительность: 6:06
- Дата: 01.11.2013
- Смотрели: 479
- Рейтинг: 0.0/0
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Desmos — построение графиков | Knitting club // нитин клаб
Desmos — простой и мощный инструмент для построения графиков, онлайн графический калькулятор. Позволяет не только быстро нарисовать график функции по формуле, но отобразить табличные данные, изучить поведение функции при изменении параметров, решить систему уравнений или неравенств и многое другое.
Функция вписывается в левый столбец, а график моментально строится в правой части:
Здесь a — параметр, который можно изменять мышкой с помощью слайдера:
Кнопка слева от параметра включает анимацию.
Можно ввести несколько выражений (уравнений или неравенств), графики будут построены в одной системе координат.
А вот график в полярной системе координат:
Desmos умеет работать со списками, что позволяет одним кликом строить семейства функций:
Собственного поиска на сайте нет, поэтому для поиска среди опубликованных материалов используйте запрос google или яндекс вида «что искать site:desmos. com».
com».
Решим графически неравенство:
Как построить график по точкам? Добавляем таблицу и вводим координаты точек, затем соединяем точки линией.
График параметрического уравнения:
Живой график можно встроить на любой сайт или форум. Попробуйте подвигать точку:
Как вставить график на свой сайт:
на верхнем тулбаре есть кнопка Поделиться (Share graph) — она дает ссылку на график и три варианта — печать, embed и image.
* Печать — послать график в черно-белом варианте на принтер
* Export image — открывает картинку в новой вкладке, после чего ее можно сохранить, распечатать или скопировать адрес статичной картинки для вставки на сайт или документ. Есть выбор толщины линий.
* embed — генерирует html-код, который вставляет картинку 200×200 со ссылкой на график на сайте desmos или BBCode (форум должен поддерживать desmos)
Надписи. При добавлении точки в список выражений, например (2,3), вы автоматически добавляете возможность добавить надпись. Нужно установить чекбокс «Метка (Show Label)».
Нужно установить чекбокс «Метка (Show Label)».
Если указать текст — он будет отображаться рядом с точкой.
Если текст не указывать, то по умолчанию будут отображаться координаты точки.
Можно выбрать один из трех размеров надписи.
Создание динамических надписей (Dynamic Labels). Допустим, вы уже создали два параметра m и b. Теперь напечатайте ${m} или ${b} в любом поле ввода текста надписи. Вместо переменных будет показано числовое значение этих переменных. При изменении переменных надпись будет автоматически обновляться. Можно комбинировать переменные с текстом: y = ${m}x + ${b}.
Обратные кавычки в надписях используются как признак математического текста:
Данный сервис с успехом может применяться преподавателями как наглядное пособие при объяснении материала.
На сайте размещено руководство пользователя, перевод которого на русский язык давно не обновлялся. Предлагаем новый перевод руководства, в котором более подробно рассказано о параметрах, таблицах, списках, регрессиях.
Скачать руководство пользователя Desmos, перевод на русский язык от Knitting Club:
Скачать руководство — pcloud
Скачать руководство — ЯндексДиск
Обновление (апрель 2018). В графический калькулятор Desmos добавлена новая команда polygon — многоугольник:
Многоугольник может быть закрашенным и незакрашенным, с контуром или без контура. Можно настроить способ отображения вершин, или сделать их перетаскиваемыми:
Ссылки по теме

Построить график функции c помощью GeoGebra
В поисках решения, как же предложить всем желающим, создавать графики уравнения или строить произвольные графики функций, я перелопатил многое: искал скрипты, писал сам и пытался изучить язык metapost и научить гостей сайта, но в к конечном итоге я нашел ту «жемчужину» которая помогла мне.
Речь идет о бесплаьной программе Geogebra, сайт которого размещен по адресу http://www.geogebra.org/
Программа написана на Java, поэтому является кроссплатформенным решением, то работает как на Linux-совместимых ( Ubuntu, Red Hat и прочее), так и на Windows операционных системах.
Рабочее окно GeoGebra выглядит вот так
Функционал программы очень обширен, но в основном на 100% процентов эту программу будут использовать преподаватели для создания учебных материалов, студенты для создания дипломных работ, и школьники при защите курсовых или для понимания той или иной задачи.
Программа может строить:
— Многоугольники и рассчитывать площади
— Вектора и вычисления с ними
— поворот точки или фигуры вокруг начала координат или другой произвольной точки
— зеркальное отображени фигуры.
— биссектриссу угла
— много другое, вплоть до анимационных картинок для показания физических процессов.
Но самое главная возможность, на мой взгляд это построение графика любого уравнения от одного или двух переменных.
Рассмотрим примеры
Открываем GeoGebra и внизу в поле Ввод пишем уравнение третьей степени
и получаем следующее
Поставив точку на пересечении графика уравнения и оси абсцисс мы можем получить координаты
Точка А имеет координаты (-2.46:0)
То есть один из корней уравнения третьей степени будет иметь значение -2.46 и это легко проверяется подстановкой в исходное уравнение.
С помощью программы можно создавать более сложные графики как здесь
так и анимационные ролики, которые можно увидеть в форуме создателей GeoGebra.
Программа GeoGebra почему то незаслуженно забыта на российских просторах, и ни один из более менее популярных ресурсах, посвященных учебе, об этой программе не говорит.Хотя для возникновения интереса у школьников, для понимания геометрических а иногда и алгебраических задач это незаменимая программа.
Успехов в изучении программы!
- Построить ненаправленный граф по матрице >>
Полярные координаты, уравнения и графики — она любит математику
Этот раздел охватывает:
Обратите внимание, что мы говорим о преобразовании назад и вперед из полярной комплексной формы в прямоугольную комплексную форму здесь, в разделе тригонометрии и комплексной плоскости .
До сих пор мы построили точки с использованием прямоугольных (или декартовых ) координат , поскольку точки с тех пор, как мы движемся вперед и назад \ (x \) единиц, и вверх и вниз \ (y \) единицы измерения.
В системе полярных координат мы обходим начало координат или полюс на определенное расстояние и на определенный угол от положительного \ (x \) — ось:
Упорядоченные пары, называемые полярными координатами , имеют форму \ (\ left ({r, \ theta} \ right) \), где \ (r \) — количество единиц от начала координат или полюса ( если \ (r> 0 \)), как радиус круга, а \ (\ theta \) — угол (в градусах или радианах), образованный лучом на положительном \ (x \) — ось ( полярная ось ), против часовой стрелки .Если \ (r <0 \), точка равна единицам (например, радиусу) в противоположном направлении (через начало координат или полюс) угла \ (\ theta \). Если \ (\ theta <0 \), вы двигаетесь по часовой стрелке с углом, начиная с положительной оси \ (x \) — .
Чтобы построить точку, вы обычно сначала обводите вокруг положительной оси \ (x \) — градусов \ (\ theta \), а затем выходите из начала координат или полюса \ (r \) единиц (если \ (r \) отрицательное значение, пойти другим путем ( 180 ° ) \ (r \) единиц).
Вот полярный график с некоторыми точками. Обратите внимание, что мы обычно считаем с шагом 15 ° или \ (\ displaystyle \ frac {\ pi} {{12}} \).
Для точки \ (\ left ({r, \ theta} \ right) \) вы видите, как вы всегда идете против часовой стрелки (или по часовой стрелке , если у вас отрицательный угол ), пока вы не достигнете желаемого угла, а затем от центра \ (r \) единиц, если \ (r \) положительное значение ? Если \ (r \) равно отрицательному , вы идете в в противоположном направлении от угловых единиц \ (r \).\ circ} \ right) \) (сделать оба отрицательными). (Помните, что 240 ° и –120 ° , и 60 ° и –240 ° являются углами со-терминала ). Чтобы получить их, если первое число (\ (r \)) отрицательно, вы хотите пойти в противоположном направлении, а если угол отрицательный, вы хотите идти по часовой стрелке, а не против часовой стрелки от положительного \ (x \) — ось.
<
Возможно, вам будет предложено преобразовать координаты между полярной формой и прямоугольной формой .
Преобразование полярных координат в прямоугольные
Давайте сначала преобразуем из полярных координат в прямоугольные ; для этого мы используем следующие формулы, как видно из графика:
Это преобразование довольно прямолинейно:
\ (\ begin {array} {l} x \, \, = \, \, r \, \ cos \, \ theta \\ y \, \, = \, \, r \, \ sin \, \ theta \ end {array} \)
Преобразование прямоугольных координат в полярные
Преобразование от прямоугольных координат до полярных координат может быть немного сложнее, поскольку нам нужно проверить квадрант прямоугольной точки, чтобы получить правильный угол; квадранты должны совпадать.Функция {{-1}}} \) на калькуляторе возвращает ответы только в интервале \ (\ displaystyle \ left ({- \ frac {\ pi} {2}, \, \, \ frac {\ pi} { 2}} \ right) \)):
Обратите внимание, что при преобразовании из прямоугольного в полярный может быть несколько «ответов», поскольку полярные точки могут быть представлены разными способами (сопредельные углы, положительные или отрицательный «\ (r \)» и т. д.). Таким образом, обычно проще преобразовать полярное изображение в прямоугольное.
Примеры
Вот несколько примеров двустороннего преобразования; обратите внимание, вас могут попросить преобразовать обратно в полярные значения в градусов, или радиан. Для обратного преобразования в полярные значения убедитесь, что ответы находятся в диапазоне от 0 до 360 ° для градусов или от 0 до \ (2 \ pi \) для радианов. (И снова обратите внимание, что при обратном преобразовании в полярные координаты мы не всегда можем получить такое же представление, как полярная точка, с которой мы начали. {{- 1}}} \ left ({\ frac {3} {0}} \ right) = \ frac {\ pi} {2} \ text {(мы хотим, чтобы загар был} \\\ text {undefined, между 1-м и 2-м квадрантами)} \ end {массив} \)
\ (\ displaystyle \ left ({3, \ frac {\ pi} {2}} \ right), \ text {то же самое, что и} \ left ({3, — \ frac { {3 \ pi}} {2}} \ right) \)
Здесь мы переходим от прямоугольной к полярной и мы не можем получить угол от единичной окружности.{{-1}}} \ left ({\ frac {5} {{- 1}}} \ right) = — 1,373+ \ pi = 1,768 \ text {(2-й квадрант)} \)
\ (\ displaystyle \ left ({\ sqrt {{26}}, 1.768} \ right) \)
Обратите внимание, что вы также можете использовать « 2 nd APPS (ANGLE) » на графическом калькуляторе , чтобы сделайте эти преобразования, но вы не получите ответов с корнями в них (вы получите десятичные дроби, которые не являются «точными»). И вам нужно решить для \ (x \) и \ (y \) или \ (r \) и \ (\ theta \) отдельно, и использовать «, » над 7 для запятой. .
Убедитесь, что у вас есть калькулятор: ГРАДУСОВ или РАДИАНОВ (в РЕЖИМЕ ), в зависимости от того, с чем вы работаете.
Я считаю, что рисование полярных графиков — это комбинация части запоминания и знания того, как создавать полярные t -диаграммы .
Во-первых, вот таблица некоторых наиболее распространенных полярных графиков . Я включил t — диаграммы как в градусах, так и в радианах.
(Обратите внимание, что вы также можете поместить их в свой графический калькулятор , например, с радиан : РЕЖИМ: РАДИАН, ПОЛЯРНЫЙ и ОКНО: θ = [0, 2 π ], θstep = π /12 или π /6, X = [–10, 10], Y = [–6, 6] , а затем используя « Y = », чтобы ввести уравнение, или просто поместите на график и используйте ZOOM ZTRIG (опция 7 ). {2}} \).
Обратите внимание, что \ (r = -5 \) приведет к тому же графику.
| \ (r \) | θ ° | |
| 5 | 0 0 | |
| 5 | \ (\ displaystyle \ frac {\) | \ (\ displaystyle \ frac {\ pi} {2} |
| 5 | \ (\ pi \) 180 | |
| 5 | \ (\ displaystyle \ frac {{3 \ pi}} {2} \) 270 | |
| 5 | \ (2 \ pi \) 360 |
Смещенный круг
\ (r = 4 \ cos \ theta \)
Круг симметричный с \ (x \) — осью диаметром 4 .
Если отрицательное (например, \ (r = -4 \ cos \ theta \)), отразите по оси \ (y \) — так, чтобы она находилась слева.
| \ (r \) | θ ° |
| 4 | 0 0 |
| \ (2 \ sqrt {2} \ приблизительно 2,8 \) | \ ( \ frac {\ pi} {4} \) 45 |
| 0 | \ (\ displaystyle \ frac {\ pi} {2} \) 90 |
| \ (- 2 \ sqrt {2} \ приблизительно -2.8 \) | \ (\ displaystyle \ frac {{3 \ pi}} {4} \) 135 |
| –4 | \ (\ pi \) 180 |
Смещенная окружность
\ (r = -6 \ sin \ theta \)
Окружность, симметричная оси \ (y \) с диаметром 6 .
Так как это отрицательное значение , отразите по оси \ (x \), чтобы он оказался внизу.
(положительное значение будет выше оси \ (x \)).
| \ (r \) | θ ° |
| 0 | 0 0 |
| \ (- 3 \ sqrt {2} \ приблизительно -4,2 \) | \ displaystyle \ frac {\ pi} {4} \) 45 |
| –6 | \ (\ displaystyle \ frac {\ pi} {2} \) 90 |
| \ (- 3 \ sqrt {2 } \ приблизительно -4,2 \) | \ (\ displaystyle \ frac {{3 \ pi}} {4} \) 135 |
| 0 | \ (\ pi \) 180 |
Вот несколько полярных уравнений, которые приводят к строкам :
| Тип полярной функции | T-Chart | Graph |
н / д = не применимо; может быть что угодно | |||||||||||
Вертикальная линия \ (r = 3 \ sec \ theta \) Я помню, что эта линия вертикальная, поскольку она такая же, как \ (r \ cos \ тета = 3 \). Это то же самое, что \ (x = 3 \) в прямоугольной форме, которая представляет собой вертикальную линию . Если отрицательное (например, \ (r = -3 \ sec \ theta \)), отразите по оси \ (y \) — так, чтобы она находилась слева. |
und = undefined | |||||||||||||
Горизонтальная линия \ (r = -4 \ csc \ theta \) Я помню, что эта линия горизонтальная, поскольку она такая же, как \ (r \ sin \ theta = — 4 \). Это то же самое, что \ (y = -4 \) в прямоугольной форме, которая представляет собой горизонтальную линию . Так как это отрицательное значение , отразите по оси \ (x \), чтобы он оказался внизу. (положительное значение будет выше оси \ (x \)). |
|
Вот графики, которые мы называем Cardioids и Limacons . Они имеют вид \ (r = a + b \ cos \ theta \) или \ (r = a + b \ sin \ theta \).
Примечание : В отличие от своих прямоугольных эквивалентов, \ (r = a \ pm b \ cos \ theta \) и \ (r = -a \ pm b \ cos \ theta \) (то же самое с \ (r = a \) pm b \ sin \ theta \) и \ (r = -a \ pm b \ sin \ theta \)) — это один и тот же полярный граф! Попробуй!
Во-первых, Кардиоиды (сердца) ; обратите внимание, что эти и Limecon «Петли» касаются полюса (исходной точки) , а Limecon «Бобы» — нет:
| Тип полярной функции | T-Chart | График | |||||||||||
Кардиоидный или Сердце \ (\ begin {array} {l} r = a + b \ cos \ theta, \, \, \, a = b \ \ r = a + b \ sin \ theta, \, \, \, a = b \ end {array} \) \ (r = 3 + 3 \ cos \ theta \) Примечание: Я помню, что когда \ (a = b \), все в гармонии, как сердце. Сердце выходит на \ (3 + 3 = 6 \) по оси \ (x \) — и достигает 3 и –3 по \ (y \). Если cos равен отрицательным (например, \ (r = 3-3 \ cos \ theta \)), отразите по оси \ (y \) — так, чтобы она находилась слева. |
Обратите внимание, что \ (r = -3 + 3 \ cos \ theta \) будет такой же график. | ||||||||||||
Кардиоид или Сердце \ (\ begin {array} {l} r = a + b \ cos \ theta, \, \, \, a = b \\ r = a + b \ sin \ theta, \, \, \, a = b \ end {array} \) \ (r = 4-4 \ sin \ theta \) Примечание: я помню, что когда \ (a = b \), вещи находятся в гармонии, как сердце. Сердце выходит на \ (4 + 4 = 8 \) на оси \ (y \) — и достигает 4 и –4 на \ (x \). Так как sin отрицательное значение , отразите по оси \ (x \), чтобы он оказался внизу.(Положительное значение будет выше оси \ (x \)). |
Обратите внимание, что \ (r = -4-4 \ sin \ theta \) будет такой же график. |
Вот Limacons :
| Тип полярной функции | T-Chart | Graph 9207| 92 | \ (\ begin {array} {l} r = a + b \ cos \ theta, \, \, \, a \ (r = 3-5 \ cos \ theta \) Примечание: я помню, что когда \ (a \) на меньше , чем \ (b \) (\ (a (совпадение l ). Лимакон выходит на \ (3 + 5 = 8 \) на отрицательной оси \ (x \) — и достигает 3 и –3 на оси \ (y \) -. Он также попадает в цикл \ (5-3 = 2 \). Поскольку cos равен отрицательным , отразите по оси \ (y \), чтобы она находилась слева. (Позитив будет на правой стороне).
Обратите внимание, что \ (r = -3-5 \ cos \ theta \) составит такой же график. | ||||||||||||
Лимакон (Бин) \ (\ begin {array} {l} r = a + b \ cos \ theta, \, \, \, a> b \\ r = a + b \ sin \ theta, \, \, \, a> b \ end {array} \) \ (r = 4 + 3 \ sin \ theta \)
Примечание: я помню что когда b является наименьшим, это « b ean». Бин поднимается до \ (4 + 3 = 7 \) по оси \ (y \) — и достигает 4 и –4 по \ (x \).Он также попадает в \ (4-3 = 1 \) по отрицательной оси \ (y \). Если sin отрицательное (например, \ (r = 4-3 \ sin \ theta \)), отразите по оси \ (x \), чтобы она находилась внизу. |
Обратите внимание, что \ (r = -4 + 3 \ sin \ theta \) будет такой же график. |
Графики Роз образуют «лепестки» и имеют форму \ (r = a \ cos \ left ({b \ theta} \ right) \) или \ (r = a \ sin \ left ({b \ theta} \ right) \). Обратите внимание: поскольку у нас есть начальная точка для этих графиков и расстояние между лепестками, диаграмма t не очень полезна. (На графиках t я сделал угол \ (\ Delta \) таким же, как расстояние между лепестками).
Начнем с cos Графики Rose:
| Тип полярной функции | T-Chart | Graph | ||||||||||||||||||
| “ boldsymbol {b} \) ”равно , даже ) \ (r = a \ cos \ left ({b \ theta} \ right), \, \, r = a \ sin \ left ({b \ theta} \ right) \) \ (r = 7 \ cos \ left ({4 \ theta} \ right) \) Поскольку \ (b \) ( 4 ) равно , даже , мы имеют \ (2b \) лепестков, или 8 лепестков . При положительном cos, они начинаются с положительного \ (\ boldsymbol {x} \) -оси , и они равны \ (\ displaystyle \ frac {{360}} {8} \), или на 45 ° друг от друга, против часовой стрелки. Длина каждого лепестка равна \ (a \) ( 7 ). |
| |||||||||||||||||||
Rose («\ (\ boldsymbol {b} \)» равно odd ) \ (r = a \ cos \ left ({b \ theta} \ right), \, \ , r = a \ sin \ left ({b \ theta} \ right) \) \ (r = -6 \ cos \ left ({5 \ theta} \ right) \ ) Поскольку \ (b \) ( 5 ) равно нечетное , у нас есть лепестки \ (b \) или 5 лепестков (мы не умножаем на 2 ). При отрицательном cos они начинаются с отрицательного положительного \ (\ boldsymbol {x} \) -оси (отражаются над \ (\ boldsymbol {y} \) -осью ) и \ (\ displaystyle \ frac {{360}} {5} \) или 72 ° друг от друга против часовой стрелки. (Обратите внимание, что, поскольку диаграмма t начинается на положительной оси \ (\ boldsymbol {x} \), \ (r \) на диаграмме отрицательны). Длина каждого лепестка равна \ (a \) ( 6 ). |
|
И вот some sin Rose graphs:
| Тип полярной функции | T-Chart | Graph | ||||||||||||||||||||
\ bold ) ”Равно , даже ) \ (r = a \ cos \ left ({b \ theta} \ right), \, \, r = a \ sin \ left ({b \ theta} \ right) \) \ (r = 8 \ sin \ left ({4 \ thet a} \ right) \) Поскольку \ (b \) ( 4 ) равно , даже , у нас есть лепестки \ (2b \), или 8 лепестков . При положительном sin они начинаются в \ (\ displaystyle \ frac {{90}} {b} = \ frac {{90}} {4} = 22,5 \) градусах от положительного \ ( \ boldsymbol {x} \) — ось (запомните это), и они находятся \ (\ displaystyle \ frac {{360}} {8} \), или , разнесены на 45 ° против часовой стрелки. Длина каждого лепестка равна \ (a \) ( 8 ). |
| |||||||||||||||||||||
Rose («\ (\ boldsymbol { } \) ”Равно нечетное ) \ (r = a \ cos \ left ({b \ theta} \ right), \, \, r = a \ sin \ left ({b \ theta} \ right) \) \ (r = -6 \ cos \ left ({5 \ theta} \ right) \) Поскольку \ (b \) ( 5 ) равно нечетное , мы имеем \ (b \) лепестков, или 5 лепестков (на 2 не умножаем). С отрицательным sin, они начинаются с \ (\ displaystyle \ frac {{90}} {b} = \ frac {{90}} {5} = 18 \) градусов вниз на от положительного \ (\ boldsymbol {x} \) — ось (отражается над \ (x \) — осью) и находятся \ (\ displaystyle \ frac {{360}} {5} \), или 72 ° друг от друга против часовой стрелки. (Обратите внимание, что, поскольку диаграмма t начинается на положительной оси \ (x \), \ (r \) на диаграмме отрицательны). Длина каждого лепестка равна \ (a \) ( 6 ). |
|
Примечание. Для диаграммы роз вас могут попросить назвать порядок рисования лепестков .Один из способов сделать это — использовать угловые измерения \ (\ displaystyle 0, \, \ frac {\ pi} {4}, \, \ frac {{3 \ pi}} {4}, \, \ frac {{ 5 \ pi}} {4}, \, \ frac {{7 \ pi}} {4} \), решите относительно \ (r \) и соблюдайте порядок лепестков. Вы также можете использовать графический калькулятор , как показано выше, но уменьшите θstep , чтобы замедлить построение графика.
Примечание: вы также можете увидеть комбинацию из розы и лимакон в форме \ (r = a + b \ cos \ left ({k \ theta} \ right), \, \, r = a + b \ sin \ left ({k \ theta} \ right), \, \, k> 1 \).В этих случаях вы можете увидеть графики, которые не пересекаются в начале координат; попробуйте их на своем калькуляторе!
Вот еще пара полярных графиков ( спиралей и лемнискатов ), которые вы можете увидеть:
| Тип полярной функции | T-Chart | 0192 | ||||||||||
Spiral \ (r = a \ theta \) \ (r = 2 \ theta \) При заполнении диаграммы t используйте радианы. Чем меньше \ (r \), тем плотнее спираль. {2}} \ sin \ left ({2 \ theta} \ right)}} = \ sqrt {{49 \ sin \ left ({2 \ theta} \ right)} } \) При sin график идет \ (\ displaystyle \ frac {\ pi} {4} \). На графике 2 лепестков, и длина каждого лепестка равна \ (a \) ( 7 ). |
|
Вас могут попросить получить уравнение полярной функции из графика:
| Graph | Graph Get Polar |
| . | Мы видим, что график представляет собой узор Rose с нечетным числом лепестков , поэтому нам не нужно делить количество лепестков на 2 , чтобы получить \ (b \) в полярном графике роза. формула \ (r = a \ cos \ left ({b \ theta} \ right) \) или \ (r = a \ sin \ left ({b \ theta} \ right) \). Мы также видим, что лепестки имеют длину 4 единиц (\ (a \)) и не начинаются на оси \ (x \), поэтому мы имеем \ (r = 4 \ sin \ left ( {5 \ theta} \ right) \) или \ (r = a \ sin \ left ({b \ theta} \ right) \). С 5 лепестками и sin они должны начинаться на \ (\ displaystyle \ frac {{90}} {b} = \ frac {{90}} {5} = 18 \) градусов вверх от положительная \ (x \) — ось; так как они начинаются на 18 градусов ниже (отраженных) по оси \ (x \), график должен быть \ (r = -4 \ sin \ left ({5 \ theta} \ right) \) . |
| График представляет собой Bean ( Limacon — без петли), а не кардиоид или сердце, поскольку он не проходит через начало координат. График горизонтальный и отражается по оси \ (\ boldsymbol {y} \) -, поэтому мы имеем \ (r = a-b \ cos \ theta, \, \, \, a> b \). \ circ \) |
Вот другие типы вопросов, которые могут возникнуть при изучении полярных графиков:
| Вопрос о полярном уравнении | Решение |
| Для полярного графика роз \ (5 \ sin \ left ({10 \ theta} \ right) \): Найдите длину каждого лепестка, количество лепестков, расстояние между каждым лепестком и концом лепестка 1 st в квадранте I.\ circ} \ right) \), мы можем найти \ (a \): \ (\ displaystyle r = a \ theta; \, \, 6 = a60; \, \, a = \ frac {1} {{ 10}} \). Таким образом, полярное уравнение имеет вид \ (\ displaystyle r = \ frac {1} {{10}} \ theta \) или \ (\ displaystyle r = \ frac {\ theta} {{10}} \). | |
| Может ли роза иметь 14 лепестков? Объясните, почему да или почему нет. | Нет. Так как для розы, если количество педалей четное, у вас будет вдвое больше лепестков. Если количество лепестков нечетное, у вас точно такое количество лепестков.Так как дважды 7 равно 14 , а 7 нечетно, этого не может произойти. |
| Постройте график прямоугольного уравнения и полярного уравнения \ (r = -6 \ cos \ left ({5 \ theta} \ right) \). | Из раздела Преобразования триггерных функций мы узнали, что прямоугольный граф в форме \ (y = a \ cos b \ left ({xc} \ right) + d \) имеет амплитуду \ (\ left | a \ right | \) (и переворачивается по оси \ (x \) — есть отрицательное значение), имеет период \ (\ displaystyle \ frac {{2 \ pi}} {b} \), горизонтальный сдвиг \ (c \) и вертикальный сдвиг \ (d \).{2}} \ theta = 1 \ end {array} \) Вот несколько примеров; обратите внимание, что мы хотим найти \ (r \) , если сможем ; в случае квадратичных или более высоких степеней, это может включать перемещение всего в одну сторону и факторинг. {2}} \ left (1 \ right) = 49 \\\ подчеркивание {{r = \ pm 7}} \ end {array} \) |
| \ (y = -x \ ) | \ (\ begin {array} {c} r \ sin \ theta = -r \ cos \ theta \\ r \ sin \ theta + r \ cos \ theta = 0 \\ r \ left ({\ sin \ theta + \ cos \ theta} \ right) = 0 \ end {array} \) \ (\ displaystyle \ begin {array} {c} \ xcancel {{r = 0}} \, \, \, \, \ , \ text {или} \, \, \, \, \ sin \ theta = — \ cos \ theta \\\, \ tan \ theta = -1 \\\, \ underline {{\ theta = \ frac {{{\ theta = \ frac {{ 3 \ pi}} {4}}} \ end {array} \) |
Чтобы преобразовать полярных уравнений в прямоугольных уравнений , мы хотим избавиться от \ (r \) ‘ s и \ (\ theta \) и в ответе есть только \ (x \) и / или \ (y \).{2}}}}}} \)
Вот несколько примеров. Обратите внимание, что иногда нас могут попросить Заполнить квадрат , чтобы получить уравнение в форме круга; мы узнали, как это сделать, в разделах «Квадратичное разложение на множители » и «Завершение квадрата » здесь. {2}} = \ frac {{13}} {4}}} \ end {array} \)
Чтобы найти целое точки сечения для наборов полярных кривых, полезно рисовать кривые, а также решать их алгебраически. Чтобы решить алгебраически, мы просто устанавливаем \ (r \) вместе и решаем для \ (\ theta \).
Обратите внимание, что после того, как мы решим одну переменную (например, \ (\ theta \)), мы должны включить ее обратно в любое уравнение, чтобы получить другую координату (например, \ (r \)).
Мы также должны быть осторожны, поскольку есть точки « фантомов, » или « неуловимых », обычно на полюсе. Причина, по которой эти точки являются «фантомами», заключается в том, что, хотя мы не обязательно получаем их алгебраически, мы можем увидеть их на графике.Это потому, что с «\ (r \)», равным 0 , \ (\ theta \) действительно может быть чем угодно, поскольку мы не уходим на какое-либо расстояние.
Мы также увидим фантомные точки, когда одно из уравнений является «\ (r = \) константой», поскольку другой способ записать это — «\ (r = \) отрицательное значение этой константы».
Обратите внимание, что с «фантомными» точками оба уравнения не должны работать; Я знаю, это странно. Чтобы получить все эти неуловимые точки, вы вводите значение — в обе кривые, чтобы увидеть, какие дополнительные баллы вы получите.
Найдите точки пересечения следующих наборов полярных кривых (алгебраически), а также нарисуйте эскиз. Найдите пересечения, когда \ (\ theta \) находится между 0 и \ (\ boldsymbol {2 \ pi} \).
| Полярные уравнения | Точки пересечения | График |
| \ (\ begin {array} {l }\ r = — \ sin \ theta \ text {} \ text {} \ text {} \ text {} \ text {} \ text {} \ text {} \ text {} = \ соз \ тета \ конец {массив} \) | \ (\ Displaystyle \ begin {array} {c} — \ sin \ theta = \ cos \ theta; \, \, \, \, \, \, \ tan \ theta = -1 \\\ theta = \ frac {{3 \ pi}} {4} \, \, \ left ({r = \ cos \ left ({\ frac {{3 \ pi}} {4 }} \ right) = — \ frac {{\ sqrt {2}}} {2}} \ right) \ text {(duplicate)}, \, \, \, \, \ frac {{7 \ pi}} {4} \, \, \ left ({r = \ frac {{\ sqrt {2}}} {2}} \ right) \\\ underline {{\ left ({\ frac {{\ sqrt {2}) }} {2}, \ frac {{7 \ pi}} {4}} \ right), \, \, \ left ({0,0} \ right) \ text {(«фантомная» точка)}}} \ end {array} \) | |
| \ (\ begin {array} {l} r = \ cos \ theta \\ r = \ cos 2 \ theta \ end {array} \) | \ (\ displaystyle \ begin {array} {c} \ cos \ theta = \ cos 2 \ theta \\\ cos \ theta = 2 {{\ cos} ^ {2}} \ theta -1 \, \, \ text {(идентичность )} \\ 2 {{\ cos} ^ {2}} \ theta — \ cos \ theta -1 = 0; \, \, \, \, \, \, \ left ({2 \ cos +1} \ верно ) \ left ({\ cos \ theta -1} \ right) = 0 \\\ cos \ theta = — \ frac {1} {2} \, \, \, \, \, \, \, \, \ , \, \ cos \ theta = 1 \\\ theta = \ frac {{2 \ pi}} {3} \, \, \ left ({r = \ cos \ left ({\ frac {{2 \ pi} } {3}} \ right) = — \ frac {1} {2}} \ right), \, \, \ frac {{4 \ pi}} {3} \, \, \ left ({r = — \ frac {1} {2}} \ right), \, \, \, \ theta = 0 \, \, \ left ({r = 1} \ right) \\\ подчеркивание {{\ left ({- \ frac {1} {2}, \ frac {{2 \ pi}} {3}} \ right), \, \, \ left ({- \ frac {1} {2}, \ frac {{4 \ pi }} {3}} \ right), \, \, \, \ left ({1,0} \ right), \, \, \ left ({0,0} \ right) \ text {(«фантом» точка)}}} \ end {array} \) | |
| \ (\ begin {array} {c} r = 3 \\ r = -6 \ sin \ theta \ end {array} \) | \ (\ Displaystyle \ begin {array} {c} -6 \ sin \ theta = 3; \, \, \, \, \, \, \ sin \ theta = — \ frac {1} {2} \\ \ theta = \ frac {{7 \ pi}} {6} \, \, \ left ({r = 3} \ right), \, \, \, \, \ frac {{11 \ pi}} {6 } \, \, \ left ({r = 3} \ right) \\\\\ text {«Фантомные» точки: используйте} \, \, r = -3 \ text {, так как это} \! \! ‘ \! \! \ text {s тот же круг} \\\ text {as} \, \, r = 3.\, \, \, \, \, \, \, \, \, \, \, \, \, \, — 3 = -6 \ sin \ theta; \, \, \, \, \ theta = \ frac {\ pi} {6}, \, \, \ frac {{5 \ pi}} {6}, \\\ text {поэтому «фантомными точками» являются} \, \, \ left ({-3, \ frac {\ pi} {6}} \ right), \, \, \ left ({-3, \ frac {{5 \ pi}} {6}} \ right). \\\ underline {{\ left ( {3, \ frac {{7 \ pi}} {6}} \ right), \, \, \ left ({3, \ frac {{11 \ pi}} {6}} \ right), \, \ , \ left ({-3, \ frac {\ pi} {6}} \ right) \, \, \, \ left ({-3, \ frac {{5 \ pi}} {6}} \ right) }} \ end {array} \) | |
| \ (\ begin {array} {l} r = \ sin 2 \ theta \\ r = \ cos \ theta \ end {array} \) | \ (\ Displaystyle \ begin {array} {c} \ sin 2 \ theta = \ cos \ theta \\ 2 \ sin \ theta \ cos \ theta \, \, \ text {(identity)} = \ cos \ theta \ \ 2 \ sin \ cos \ theta — \ cos \ theta = 0; \, \, \, \ cos \ theta \ left ({2 \ sin \ theta -1} \ right) = 0 \\\ cos \ theta = 0 \, \, \, \, \, \, \, \, \, \, \ sin \ theta = \ frac {1} {2} \\\ theta = \ frac {\ pi} {2} \, \, \ left ({r = \ cos \ left ({\ frac {\ pi} {2}} \ right) = 0} \ right), \, \, \, \, \ frac {{3 \ pi} } {2} \, \, \ left ({r = 0} \ right) \, \, \, \ text {(duplicate)}, \, \\\ theta = \ frac {\ pi} {6} \ , \, \ left ({r = \ frac {{\ sqrt {3}}} {2}} \ right), \, \, \, \, \ frac {{5 \ pi}} {6} \, \, \ left ({r = — \ frac {{\ sqrt {3}}} {2}} \ right) \\\ подчеркивание {{\ left ({0, \ frac {\ pi} {2}} \ right), \, \, \, \ left ({\ frac {{\ sqrt {3}}} {2}, \ frac {\ pi} {6}} \ right), \, \, \ left ({- \ frac {{\ sqrt {3}}) } {2}, \ frac {{5 \ pi}} {6}} \ right)}} \ end {array} \) |
Также было бы полезно знать последовательность, в которой построены полярные графики; другими словами, от 0 до \ (2 \ pi \), какие части графиков рисуются раньше других графиков.(Проверьте это на графическом калькуляторе, где вы это увидите!)
Вы можете использовать t-диаграмму или , чтобы установить полярное уравнение на 0 , если график пересекает полюс, и контрольные точки между ними. Вот несколько примеров:
| Проблема и решение | T-Chart | Graph | ||||||||||||||||||
| Внутренний цикл для \ (2 + 4 \ cos \ theta \) между какими двумя значениями \ (\ theta \) образовалось? Решение: Найдите два случая, когда \ (r = 0 \), поскольку это до и после , график рисует свой внутренний цикл: \ (\ displaystyle 0 = 2 + 4 \ соз \ тета; \, \, \, \, \, \ соз \ тета = — \ гидроразрыва {1} {2} \) \ (\ displaystyle \ theta = \ frac {{2 \ pi}} { 3}; \, \, \, \, \, \ theta = \ frac {{4 \ pi}} {3} \) Поскольку конец внутреннего цикла находится в \ (\ left ({-2, \ pi} \ right) \) (то же самое, что \ (\ displaystyle \ left ({2,0 {} ^ \ circ} \ right) \)), и это находится между \ (\ displaystyle \ frac {{2 \ pi }} {3} \) и \ (\ displaystyle \ frac {{4 \ pi}} {3} \), внутренний цикл формируется, когда \ (\ displaystyle \ frac {{2 \ pi}} {3 } <\ theta <\ frac {{4 \ pi}} {3} \) |
| |||||||||||||||||||
| Крайний левый лепесток для \ (\ cos 2 \ theta \) нарисован между какими двумя значениями \ (\ theta \)? В каком порядке нарисованы лепестки? Решение: С этой задачей мы можем создать следующую диаграмму t и увидеть последовательность нарисованных лепестков.{2}} \ theta -1 \, \, \, \ text {(identity)} \, \, \, \, \, \ end {array} \) \ (\ displaystyle \ text {cos} \ theta \, \, \ text {=} \, \, \ pm \ sqrt {{\ frac {1} {2}}} = \ pm \ frac {{\ sqrt {2}}} {2} \) \ (\ Displaystyle \ theta = \ frac {\ pi} {4}; \, \, \, \, \, \ theta = \ frac {{3 \ pi}} {4}; \, \, \, \, \, \ theta = \ frac {{5 \ pi}} {4}; \, \, \, \, \, \ theta = \ frac {{7 \ pi}} {4} \) Таким образом, крайний левый ( 3 rd ) лепесток образуется, когда \ (\ displaystyle \ frac {{3 \ pi}} {4} <\ theta <\ frac {{5 \ pi}} {4 } \) |
|
Изучите эти правила , и практика, практика, практика!
Нажмите «Отправить» (стрелка справа от проблемы), чтобы решить эту проблему.Вы также можете ввести больше проблем или щелкнуть 3 точки в правом верхнем углу, чтобы просмотреть, например, проблемы.
Если вы нажмете «Нажмите, чтобы просмотреть шаги», вы перейдете на сайт Mathway , где вы можете зарегистрироваться для получения полной версии (шаги включены) программного обеспечения. Вы даже можете получить рабочие листы по математике.
Вы также можете перейти на сайт Mathway здесь, где вы можете зарегистрироваться, или просто использовать программное обеспечение бесплатно без подробных решений.Есть даже приложение Mathway для вашего мобильного устройства. Наслаждаться!
На Тригонометрия и комплексная плоскость — готово!
Калькулятор полярных координат
Этот калькулятор полярных координат представляет собой удобный инструмент, который позволяет преобразовывать декартовы координаты в полярные, а также наоборот. Это полезно только в 2D-пространстве — для 3D-координат вы можете обратиться к нашему калькулятору цилиндрических координат. Эта статья предоставит вам краткое объяснение обоих типов координат и формул для быстрого преобразования.
Декартовы и полярные координаты
Как вы, наверное, знаете, координаты используются для однозначного описания положения точки в пространстве. На всякий случай ограничимся 2D-пространством. Это означает, что у нас есть только два измерения: высота и ширина (без глубины), как на листе бумаги.
Декартова система координат создается путем рисования двух линий, перпендикулярных друг другу. Тогда точка, где они встречаются, называется началом системы координат. Координаты любой произвольной точки в пространстве — это расстояния между этой точкой и двумя линиями, обозначаемые осью x и осью y .
Полярная система координат, с другой стороны, не включает никаких перпендикулярных линий. Источником полярной системы является точка, называемая полюсом . Произвольный луч из этой точки выбран в качестве полярной оси . Чтобы найти полярные координаты данной точки, сначала нужно провести линию, соединяющую ее с полюсом. Тогда координаты точки — это длина этой линии r и угол θ , который она составляет с полярной осью.
Наш калькулятор полярных координат может конвертировать декартовы координаты в полярные.
Преобразование из декартовой системы в полярную
Предположим, вы знаете декартовы координаты точки, но хотите выразить их как полярные координаты. (Наш декартово-полярный калькулятор предполагает, что происхождение декартовой системы совпадает с полюсом полярной системы). Для преобразования необходимо использовать следующие формулы:
r = √ (x² + y²)
θ = arctan (y / x)
где
- (x, y) — декартовы координаты;
- (r, θ) — полярные координаты.
Полярные координаты подчиняются следующим ограничениям:
- r должно быть равно или больше 0;
- θ должно лежать в диапазоне (−π, π].
Преобразование полярной системы в декартовую
Также возможно, что вы знаете полярные координаты точки, но хотите найти декартовы координаты с помощью нашего калькулятора полярных координат. Для этого просто используйте следующие уравнения:
x = r * cos θ
y = r * sin θ
Вы можете заметить, что значение y / x — это наклон линии, соединяющей полюс и произвольную точку.
7. Полярные координаты
Для некоторых функций прямоугольные координаты (те, которые используют x — ось и y — ось) очень неудобны. В прямоугольные координаты, мы описываем точки как определенные расстояние по оси x и определенное расстояние по оси y — ось.
Но некоторые функции очень сложны, если мы используем прямоугольный система координат. Такие функции могут быть намного проще в полярная система координат , которая позволяет описывать и графически отображать определенные функции в очень удобном виде.
Полярные координаты работают примерно так же, как мы видели в тригонометрии (радианы и длина дуги, где мы использовали r и θ ) и в полярной форме комплексных чисел (где мы также видели r и θ ).
Векторы также используют ту же идею. [Подробнее см. В разделе «Векторы в двух измерениях».]
В полярных координатах мы описываем точки как определенные расстояние ( r ) от полюса (начало координат) и под определенным углом (θ) от положительной горизонтальной оси (называется полярной осью ).
Координаты точки в полярных координатах записываются как
( r , θ )
График точки ( r , θ ) выглядит следующим образом:
Пример 1
Точка, описываемая в полярных координатах как `(2, (3π) / 4)`, будет выглядеть так:
Мы используем полярную миллиметровую бумагу для рисования точек в полярных координатах.
ПРИМЕЧАНИЕ. Углы могут быть в градусах или радиан для полярных координат.
Пример 2
Постройте точки на следующей полярной сетка:
а) (2, 60 °)
б) (4, 165 °)
в) (3, 315 °)
Ответ
Преобразование полярных и прямоугольных координат
Преобразование полярных координат в прямоугольные — это та же идея, что и преобразование прямоугольной формы в полярной сформируйте в комплексных числах .
[Смотрите, как преобразовать прямоугольную и полярную формы в главе о комплексных числах.]
Из Пифагора имеем: r 2 = x 2 + y 2 и базовая тригонометрия дает нам:
`tan \ theta = y / x` x = r cos θ y = r sin θ
Значит, это то же самое, что и у нас со сложными числа.@) `в прямоугольные координаты.
Ответ
Используя калькулятор, имеем:
(4,27, 168 o ) полярный ≡ (-4,18, 0,888) прямоугольный
Нарисуйте , чтобы проверить свой ответ!
8. Кривые в полярных координатах
r = sin (2 θ ) — 1,7
Это реальный график с использованием полярных координат.
Хорошо, я допускаю добавление
глаз и улыбка. 🙂
В этом разделе мы построим графики с помощью компьютера.Вы также научитесь рисовать некоторые из них на бумаге, потому что это поможет вам понять, как работают графики в полярных координатах.
Не беспокойтесь о всей сложной алгебре во второй части ответов — это просто чтобы продемонстрировать, что полярные координаты для этих графиков намного проще, чем прямоугольные. Мы конвертируем их, используя то, что мы узнали в последнем разделе «Полярные координаты».
Полезный фон
Кривые в полярных координатах очень похожи на векторы.См .:
Векторные концепции
Примеры
Нарисуйте каждую из следующих функций, используя полярные координаты, а затем преобразуйте каждую в уравнение в прямоугольной форме. координаты.
Пример 1: r = 2 + 3 sin θ
(Этот полярный график называется лимакон от латинского слова «улитка».)
Ответ
Использование таблицы значений для построения кривых полярных координат
Если у нас нет компьютера и нам нужно набросать функцию на бумаге, нам нужно создать таблицу значений следующим образом:
| θ (градусы) | `0 °` | `30 °` | `60 °` | `90 °` | `120 °` | `150 °` | `180 °` |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `0` | `π / 6` | `π / 3` | `π / 2` | `(2π) / 3` | `(5π) / 6` | `π` |
r = 2 + 3 sin θ | `2` | `3.5` | `4.60` | `5` | `4.6` | `3.5` | `2` |
| θ (градусы) | `180 °` | `210 °` | `240 °` | `270 °` | `300 °` | `330 °` | `360 °` |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `π` | `(7π) / 6` | `(4π) / 3` | `(3π) / 2` | `(5π) / 3` | `(11π) / 6` | `2π` |
r = 2 + 3 sin θ | `2` | `0.5` | `-0,60` | `-1` | `-0,60` | `0,5` | `2` |
Первые 7 точек в этой таблице: (2, 0 ○ ), (3,5, 30 ○ ), (4.60, 60 ○ ), (5, 90 ○ ), (4.6, 120 ○ ), (3,5, 150 ○ ) и (2, 180 ○ ).
Наносим эти точки (они пронумерованы) на полярном графике. Я также указал стрелками направление, в котором вам нужно двигаться при соединении точек.
Напомним: Отрицательное значение « r » означает, что мы должны находиться на противоположной стороне от начала координат.
Вот полный график.
0 ° 30 ° 60 ° 90 ° 120 ° 150 ° 180 ° 210 ° 240 ° 270 ° 300 ° 330 ° 012345График r = 2 + 3 sin θ, лимон.
Преобразование в прямоугольную форму
Мы снова преобразуем нашу полярную функцию в прямоугольную форму, чтобы мы могли видеть, насколько проще полярная форма для некоторых функций.2` `= 0`
Обратите внимание, насколько полярная форма проще по сравнению с прямоугольная форма.
Вот еще пример лимакончика:
График r = 2 -2 sin θ , лимон.
Пример 2: r = 3 cos 2 θ
Ответ
Использование таблицы значений для построения этой кривой
Что делать, если вы не можете использовать компьютер для построения графика?
Вам необходимо создать таблицу значений, как показано ниже.Я поставил градусы и их эквиваленты в радианах.
| θ (градусы) | 0 ○ | 30 ○ | 60 ○ | 90 ○ | 120 ○ | 150 ○ | 180 ○ |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `0` | `π / 6` | `π / 3` | `π / 2` | `(2π) / 3` | `(5π) / 6` | `π` |
`r = 3 \ cos \ 2θ` | `3` | `1.5` | `-1,5` | `-3` | `-1,5` | `1,5` | `3` |
| θ (градусы) | 210 ○ | 240 ○ | 270 ○ | 300 ○ | 330 ○ | 360 ○ |
|---|---|---|---|---|---|---|
| θ (радианы) | `(7π) / 6` | `(4π) / 3` | `(3π) / 2` | `(5π) / 3` | `(11π) / 6` | `2π` |
`r = 3 \ cos \ 2θ` | `1.5` | `-1,5` | `-3` | `-1,5` | `1,5` | `3` |
Первые 7 точек из этой таблицы: (3, 0 °), (1,5, 30 °), (-1,5, 60 °), (-3, 90 °), (-1,5, 120 °), ( 1.5, 150 °) и (3, 180 °).
Размещение этих первых 7 точек на сетке полярных координат дает нам следующее:
Мы начинаем с точки 1 (3, 0 °) и перемещаемся по графику, увеличивая угол и изменяя расстояние от начала координат (определяется путем подстановки угла в r = 3 cos 2 θ .Я нарисовал стрелки, чтобы указать основное направление, в котором мы должны двигаться, чтобы добраться до следующей точки.
Напомним: Отрицательное значение « r » означает, что мы должны находиться на противоположной стороне от начала координат.
Я нанес только первые 7 точек выше, чтобы не усложнять график. Ясно, что нам нужно будет рассчитать больше, чем это количество точек, чтобы получить хороший набросок. (Вам понадобится как минимум вдвое больше точек, чем у меня в таблице выше — каждые 15 ° будет достаточно.)
Вот полный график.
0 ° 30 ° 60 ° 90 ° 120 ° 150 ° 180 ° 210 ° 240 ° 270 ° 300 ° 330 ° 0123График r = 3 cos (2θ).
[На приведенном выше графике углы указаны в радианах , где π радиан = 180 °. Чтобы узнать больше, см .: Радианы.]
Обратите внимание, что кривая полностью нарисована, когда θ принимает все значения от 0 до 2 π .
Преобразование полярных координат в прямоугольные
Далее, вот ответ на преобразование в прямоугольные координаты.
Почему? Мы преобразуем функцию, указанную в этом вопросе, в прямоугольные координаты, чтобы увидеть, насколько она проще при записи в полярных координатах.2) `
в прямоугольных координатах.
Мы видим, что наше уравнение в полярных координатах, r = 3 cos 2 θ , намного проще, чем его прямоугольный эквивалент.
Пример 3: r = sin θ — 1
(Его называют кардиоидным , потому что он имеет форму сердца. Это особый дело лимакон.)
Ответ
Нам нужно набросать `r = sin theta-1`.
Используя тот же процесс для предыдущих примеров, мы получаем:
График r = sin θ — 1, лимон.2` `= 0`
Пример 4: `r = 2,5`
Ответ
Нам нужно набросать `r = 2,5`
В этом примере мы не видим « θ » в функция нам дана. Это означает, что радиус r равен постоянный , нет независимо от того, какое значение принимает угол θ .
Вот график:
График r = 2,5, лимон.
Что такое эквивалент в прямоугольных координатах?
Мы преобразуем функцию, указанную в этом вопросе, в прямоугольные координаты, чтобы увидеть, насколько она проще при записи в полярных координатах.2 = 6,25`.
Итак, это дает нам: x 2 + y 2 = 6,25
Неудивительно, что это похоже на уравнение для круга, которое мы получили ранее в разделе «Круг».
Пример 5: r = 0,2 θ
Это интересная кривая, называемая спиралью Архимеда. По мере увеличения θ увеличивается и r .
Ответ
На этот раз мы строим график r = 0.2 θ в полярных координатах.
График r = 2,5, лимон.
Обратите внимание, что значение r всегда в 0,2 раза больше значения θ (конечно, мы находимся в радианах ).
См. Также Равноугольная спираль.
Позже мы узнаем, как найти длину спирали Архимеда.
Пример 6: r = sin (2 θ ) — 1,7
Это лицо, которое я нарисовал вверху страницы.Мы даже не будем пытаться найти эквивалент в прямоугольных координатах!
Вы можете поиграть с этим графиком в следующем интерактивном апплете.
Интерактивный график
Вы можете изучить приведенные выше графики с помощью этого интерактивного графика.
Используйте ползунок под графиком, чтобы обвести кривые.
Посмотрите, что произойдет, если вы выйдете за пределы нормальной области для этих графиков (то есть, когда `theta` меньше` 0` или больше `theta = 2pi`).
Измените функцию, используя поле выбора в верхней части графика.
Выберите функцию:
Авторские права © www.intmath.com
Приложение
Проверьте полярные координаты и кардиоидные микрофоны для применения полярных координат.
Исчисление II — Полярные координаты
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-6: Полярные координаты
До этого момента мы имели дело исключительно с декартовой (или прямоугольной, или x-y ) системой координат.Однако, как мы увидим, это не всегда самая простая система координат для работы. Итак, в этом разделе мы начнем рассматривать полярную систему координат.
Системы координат на самом деле не более чем способ определения точки в пространстве. Например, в декартовой системе координат точке задаются координаты \ (\ left ({x, y} \ right) \), и мы используем это для определения точки, начиная с начала координат и затем перемещая \ (x \) единицы. по горизонтали, за которыми следуют единицы \ (y \) по вертикали.Это показано на рисунке ниже.
Однако это не единственный способ определить точку в двухмерном пространстве. Вместо того, чтобы перемещаться по вертикали и горизонтали от начала координат, чтобы добраться до точки, мы могли бы вместо этого выйти прямо из начала координат, пока не коснемся точки, а затем определить угол, который эта линия составляет с положительной осью \ (x \). Затем мы могли бы использовать расстояние точки от начала координат и величину, необходимую для поворота от положительной оси \ (x \), в качестве координат точки.Это показано на рисунке ниже.
Координаты в этой форме называются полярными координатами .
Приведенное выше обсуждение может привести к мысли, что \ (r \) должно быть положительным числом. Однако мы также допускаем отрицательное значение \ (r \). Ниже приведен эскиз двух точек \ (\ left ({2, \ frac {\ pi} {6}} \ right) \) и \ (\ left ({- 2, \ frac {\ pi} {6}) } \верно)\).
Из этого эскиза мы видим, что если \ (r \) положительно, точка будет в том же квадранте, что и \ (\ theta \).С другой стороны, если \ (r \) отрицательно, точка окажется в квадранте точно противоположном \ (\ theta \). Также обратите внимание, что координаты \ (\ left ({- 2, \ frac {\ pi} {6}} \ right) \) описывают ту же точку, что и координаты \ (\ left ({2, \ frac {{7 \ pi}} {6}} \ right) \) делаю. Координаты \ (\ left ({2, \ frac {{7 \ pi}} {6}} \ right) \) говорят нам повернуть угол \ (\ frac {{7 \ pi}} {6} \ ) от положительной оси \ (x \) — это поставило бы нас на пунктирную линию на скетче выше, а затем отойдите на расстояние 2.
Это приводит к важному различию между декартовыми координатами и полярными координатами. В декартовых координатах для любой заданной точки существует ровно один набор координат. С полярными координатами это не так. В полярных координатах для данной точки существует буквально бесконечное количество координат. Например, все следующие четыре точки являются координатами одной и той же точки.
\ [\ left ({5, \ frac {\ pi} {3}} \ right) = \ left ({5, — \ frac {{5 \ pi}} {3}} \ right) = \ left ({ — 5, \ frac {{4 \ pi}} {3}} \ right) = \ left ({- 5, — \ frac {{2 \ pi}} {3}} \ right) \]Вот эскиз углов, используемых в этих четырех наборах координат.
Во второй паре координат мы повернулись по часовой стрелке, чтобы добраться до точки. Не следует забывать о вращении по часовой стрелке. Иногда это то, что нам нужно делать.
Последние две пары координат используют тот факт, что если мы окажемся в квадранте, противоположном точке, мы можем использовать отрицательный \ (r \), чтобы вернуться к точке, и, конечно, есть и против часовой стрелки, и вращение по часовой стрелке, чтобы добраться до угла.
Эти четыре точки представляют собой только координаты точки, не оборачиваясь вокруг системы более одного раза.Если мы позволим углу совершать столько полных оборотов вокруг системы осей, сколько мы хотим, тогда будет бесконечное количество координат для одной и той же точки. Фактически, точка \ (\ left ({r, \ theta} \ right) \) может быть представлена любой из следующих пар координат.
\ [\ left ({r, \ theta + 2 \ pi n} \ right) \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ left ({- r, \ theta + \ left ({2n + 1} \ right) \ pi} \ right), \ hspace {0.25in} \, \, \, \, \, {\ mbox {where}} n {\ mbox {- любое целое число}} {\ mbox {.}} \ ]Далее мы должны поговорить о происхождении системы координат.В полярных координатах начало отсчета часто называют полюсом . Поскольку на самом деле мы не удаляемся от начала координат / полюса, мы знаем, что \ (r = 0 \). Однако мы все еще можем вращаться вокруг системы на любой угол, который нам нужен, поэтому координаты начала / полюса равны \ (\ left ({0, \ theta} \ right) \).
Теперь, когда мы разобрались с полярными координатами, нам нужно подумать о преобразовании между двумя системами координат. Начнем со следующего наброска, напоминающего нам, как работают обе системы координат. {- 1}} \ left ({\ frac {y} {x}} \ right) \]
Мы должны быть осторожны с этим, потому что обратные касательные возвращают значения только в диапазоне \ (- \ frac {\ pi} {2} <\ theta <\ frac {\ pi} {2} \).{- 1}} \ left ({\ frac {y} {x}} \ right) \ end {align *} \]
Давайте быстро рассмотрим пример.
Пример 1 Преобразуйте каждую из следующих точек в заданную систему координат.- Преобразует \ (\ left ({- 4, \ frac {{2 \ pi}} {3}} \ right) \) в декартовы координаты.
- Преобразует \ (\ left ({- 1, -1} \ right) \) в полярные координаты.
Это преобразование достаточно просто. Все, что нам нужно сделать, это подставить точки в формулы.
\ [\ begin {align *} x & = — 4 \ cos \ left ({\ frac {{2 \ pi}} {3}} \ right) = — 4 \ left ({- \ frac {1} {2 }} \ right) = 2 \\ y & = — 4 \ sin \ left ({\ frac {{2 \ pi}} {3}} \ right) = — 4 \ left ({\ frac {{\ sqrt 3 }} {2}} \ right) = — 2 \ sqrt 3 \ end {align *} \]Итак, в декартовых координатах это точка \ (\ left ({2, — 2 \ sqrt 3} \ right) \).{- 1}} \ left (1 \ right) = \ frac {\ pi} {4} \]
Однако это неправильный угол. Это значение \ (\ theta \) находится в первом квадранте, а точка, которую мы поставили, находится в третьем квадранте. Как отмечалось выше, мы можем получить правильный угол, добавив к нему \ (p \). Следовательно, фактический угол равен
. \ [\ theta = \ frac {\ pi} {4} + \ pi = \ frac {{5 \ pi}} {4} \] Итак, в полярных координатах это точка \ (\ left ({\ sqrt 2, \ frac {{5 \ pi}} {4}} \ right) \).2} \ cos \ theta \ sin \ theta \ end {align *} \]
b Преобразование \ (r = — 8 \ cos \ theta \) в декартовы координаты. Показать решение
Это немного сложнее, но не намного. Во-первых, обратите внимание, что мы можем заменить прямо на \ (r \). Однако прямой замены косинуса, которая даст нам только декартовы координаты, нет. Если бы у нас был \ (r \) справа вместе с косинусом, мы могли бы сделать прямую замену. Итак, если \ (r \) с правой стороны было бы удобно, давайте поместим его туда, просто не забудьте поставить еще один и с левой стороны.2} & = 16 \ end {выровнять *} \]
Итак, это круг радиуса 4 с центром \ (\ left ({- 4,0} \ right) \).
Это подводит нас к последней теме этого раздела.
Графы общих полярных координат
Давайте определим несколько наиболее распространенных графиков в полярных координатах. Мы также рассмотрим несколько специальных полярных графиков.
Линии
Некоторые линии имеют довольно простые уравнения в полярных координатах.{- 1}} \ left ({\ frac {y} {x}} \ right) & = \ beta \\ \ frac {y} {x} & = \ tan \ beta \\ y & = \ left ({ \ tan \ beta} \ right) x \ end {align *} \]
Это линия, которая проходит через начало координат и составляет угол \ (\ beta \) с положительной осью \ (x \). Или, другими словами, это линия, проходящая через начало координат с наклоном \ (\ tan \ beta \).
Это достаточно легко преобразовать в декартовы координаты в \ (x = a \).Итак, это вертикальная линия.
Точно так же это преобразуется в \ (y = b \), и поэтому это горизонтальная линия.
В этом нет ничего особенного, кроме построения графика, так что вот оно.
Окружности
Давайте посмотрим на уравнения окружностей в полярных координатах.
- \ (г = а \).
Это уравнение гласит, что независимо от того, какой угол мы получили, расстояние от начала координат должно быть \ (a \). Если вы думаете об этом, это в точности определение круга радиуса \ (a \) с центром в начале координат.Итак, это круг радиуса \ (a \) с центром в начале координат. Это также одна из причин, по которой мы можем захотеть работать в полярных координатах. Уравнение окружности с центром в начале координат имеет очень хорошее уравнение, в отличие от соответствующего уравнения в декартовых координатах.
- \ (г = 2а \ соз \ тета \).
Мы рассмотрели конкретный пример одного из них, когда преобразовывали уравнения в декартовы координаты.Это круг радиуса \ (\ left | a \ right | \) и центра \ (\ left ({a, 0} \ right) \). Обратите внимание, что \ (a \) может быть отрицательным (как в нашем примере выше), поэтому на радиусе требуются полосы абсолютного значения. Однако их не следует использовать по центру.
- \ (г = 2b \ sin \ theta \).2}} \) и по центру \ (\ left ({a, b} \ right) \). Другими словами, это общее уравнение круга, центр которого не находится в начале координат.
Первый круг радиуса 7 с центром в начале координат. Второй — круг радиуса 2 с центром в \ (\ left ({2,0} \ right) \). Третий — круг радиуса \ (\ frac {7} {2} \) с центром в \ (\ left ({0, — \ frac {7} {2}} \ right) \).Вот график трех уравнений.
Обратите внимание, что для полного графика \ (r = a \) требуется диапазон \ (0 \ le \ theta \ le 2 \ pi \), а диапазон — только \ (0 \ le \ theta \ le \ pi \), чтобы построить график других кругов, представленных здесь. Вы можете проверить это с помощью быстрой таблицы значений, если хотите.
Кардиоиды и лимаконы
Их можно разделить на следующие три случая.
- Кардиоиды: \ (r = a \ pm a \ cos \ theta \) и \ (r = a \ pm a \ sin \ theta \).
У них есть диаграмма в форме сердца, которая всегда содержит начало координат. - Лимакон с внутренним циклом: \ (r = a \ pm b \ cos \ theta \) и \ (r = a \ pm b \ sin \ theta \) с \ (a Они будут иметь внутренний цикл и всегда будут содержать начало координат.
- Лимакон без внутреннего цикла: \ (r = a \ pm b \ cos \ theta \) и \ (r = a \ pm b \ sin \ theta \) с \ (a> b \).
Они не имеют внутреннего цикла и не содержат начало координат.
Все они будут отображены один раз в диапазоне \ (0 \ le \ theta \ le 2 \ pi \). Вот таблица значений для каждого, а также графики для каждого.
| \ (\ theta \) | \ (г = 5-5 \ грех \ тета \) | \ (г = 7-6 \ соз \ тета \) | \ (г = 2 + 4 \ соз \ тета \) |
|---|---|---|---|
| 0 | 5 | 1 | 6 |
| \ (\ Displaystyle \ frac {\ pi} {2} \) | 0 | 7 | 2 |
| \ (\ pi \) | 5 | 13 | -2 |
| \ (\ displaystyle \ frac {{3 \ pi}} {2} \) | 10 | 7 | 2 |
| \ (2 \ пи \) | 5 | 1 | 6 |
И последнее, что нам нужно сделать в этом разделе.На третьем графике в предыдущем примере у нас был внутренний цикл. Иногда нам нужно знать значение \ (\ theta \), для которого граф будет проходить через начало координат. Чтобы найти это, все, что нам нужно сделать, это приравнять уравнение к нулю и решить следующим образом:
\ [0 = 2 + 4 \ cos \ theta \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \, \, \, \, \, \ cos \ theta = — \ frac { 1} {2} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ theta = \ frac {{2 \ pi}} {3}, \ frac { {4 \ pi}} {3} \]8.4 Полярные координаты: Графики — Предварительное вычисление
Цели обучения
В этом разделе вы:
- Проверить полярные уравнения симметрии.
- Построение полярных уравнений путем нанесения точек.
Планеты движутся в космосе по эллиптическим периодическим орбитам вокруг Солнца, как показано на рисунке 1. Они находятся в постоянном движении, поэтому определение точного положения любой планеты возможно только на мгновение. Другими словами, мы можем зафиксировать только мгновенное положение планеты на .Это одно из применений полярных координат, представленных как (r, θ). (R, θ). Мы интерпретируем rr как расстояние от Солнца и θθ как угловой пеленг планеты или ее направление от фиксированной точки на Солнце. В этом разделе мы сосредоточимся на полярной системе и графиках, которые создаются непосредственно из полярных координат.
Рис. 1 Планеты движутся по эллиптическим траекториям, вращаясь вокруг Солнца. (кредит: модификация работы NASA / JPL-Caltech)
Проверка полярных уравнений на симметрию
Подобно тому, как прямоугольное уравнение, такое как y = x2y = x2, описывает взаимосвязь между xx и yy на декартовой сетке, полярное уравнение описывает взаимосвязь между rr и θθ на полярной сетке.Напомним, что пара координат (r, θ) (r, θ) указывает, что мы перемещаемся против часовой стрелки от полярной оси (положительная ось x ) на угол θ, θ и вытягиваем луч от полюса (начала координат). rr единиц в направлении θ.θ. Все точки, удовлетворяющие полярному уравнению, отображаются на графике.
Симметрия — это свойство, которое помогает нам распознать и построить график любого уравнения. Если уравнение имеет график, симметричный относительно оси, это означает, что если мы сложим график пополам по этой оси, часть графика на одной стороне будет совпадать с частью на другой стороне.Выполнив три теста, мы увидим, как применить свойства симметрии к полярным уравнениям. Далее мы будем использовать симметрию (в дополнение к нанесению ключевых точек, нулей и максимумов r) r) для определения графика полярного уравнения.
В первом тесте мы рассматриваем симметрию относительно прямой θ = π2θ = π2 ( y — ось). Мы заменяем (r, θ) (r, θ) на (−r, −θ) (- r, −θ), чтобы определить, эквивалентно ли новое уравнение исходному уравнению. Например, предположим, что нам дано уравнение r = 2sinθ; r = 2sinθ;
r = 2sinθ − r = 2sin (−θ) Заменим (r, θ) на (−r, −θ).−r = −2sinθIdentity: sin (−θ) = — sinθ.r = 2sinθ Умножим обе части на −1. R = 2sinθ − r = 2sin (−θ) Заменим (r, θ) на (−r, −θ). −r = −2sinθIdentity: sin (−θ) = — sinθ.r = 2sinθ Умножаем обе части на −1.Это уравнение демонстрирует симметрию относительно прямой θ = π2.θ = π2.
Во втором тесте мы рассматриваем симметрию относительно полярной оси (оси xx). Заменим (r, θ) (r, θ) на (r, −θ) (r, −θ) или (−r, π − θ) (- r, π − θ), чтобы определить эквивалентность между тестируемым уравнением и оригинал. Например, предположим, что нам дано уравнение r = 1−2cosθ.r = 1−2cosθ.
r = 1−2cosθr = 1−2cos (−θ) Заменить (r, θ) на (r, −θ) .r = 1−2cosθEven / Odd identityr = 1−2cosθr = 1−2cos (−θ) Заменить ( r, θ) с (r, −θ) .r = 1−2cosθEven / Odd identityГрафик этого уравнения демонстрирует симметрию относительно полярной оси.
В третьем тесте мы рассматриваем симметрию относительно полюса (начала координат). Мы заменяем (r, θ) (r, θ) на (−r, θ) (- r, θ), чтобы определить, эквивалентно ли тестируемое уравнение исходному уравнению. Например, предположим, что нам дано уравнение r = 2sin (3θ).r = 2sin (3θ).
r = 2sin (3θ) −r = 2sin (3θ) r = 2sin (3θ) −r = 2sin (3θ)Уравнение не прошло проверку на симметрию, но это не означает, что оно не симметрично относительно столб. Прохождение одного или нескольких тестов симметрии подтверждает, что симметрия будет отображаться в графе. Однако отсутствие проверки на симметрию не обязательно означает, что график не будет симметричным относительно линии θ = π2, θ = π2, полярной оси или полюса. В этих случаях мы можем подтвердить, что симметрия существует, нанеся точки отражения поперек кажущейся оси симметрии или полюса.Проверка симметрии — это метод, который упрощает построение графиков полярных уравнений, но его применение не идеально.
Тесты симметрии
Полярное уравнение описывает кривую на полярной сетке. График полярного уравнения можно оценить для трех типов симметрии, как показано на рисунке 2.
Рисунок 2 (a) График симметричен относительно прямой θ = π2θ = π2 ( y -ось), если заменить (r, θ) (r, θ) на (−r, −θ) (- r, −θ) дает эквивалентное уравнение.(b) График симметричен относительно полярной оси (ось x ), если заменить (r, θ) (r, θ) на (r, −θ) (r, −θ) или (−r, π − θ) (- r, π − θ) дает эквивалентное уравнение. (c) Граф является симметричным относительно полюса (начала координат), если замена (r, θ) (r, θ) на (−r, θ) (- r, θ) дает эквивалентное уравнение.Как к
Проверим на симметрию для полярного уравнения.
- Подставьте соответствующую комбинацию компонентов вместо (r, θ) 🙁 r, θ): (- r, −θ) (- r, −θ) вместо θ = π2θ = π2 симметрии; (r, −θ) (r, −θ) для симметрии полярной оси; и (−r, θ) (- r, θ) для симметрии относительно полюса.
- Если результирующие уравнения эквивалентны в одном или нескольких тестах, график дает ожидаемую симметрию.
Пример 1
Проверка симметрии полярного уравнения
Проверить симметрию уравнения r = 2sinθr = 2sinθ.
Решение
Тест на каждый из трех типов симметрии.
| 1) Замена (r, θ) (r, θ) на (−r, −θ) (- r, −θ) дает тот же результат.Таким образом, график симметричен относительно прямой θ = π2.θ = π2. | −r = 2sin (−θ) −r = −2sinθ Четно-нечетное тождествоr = 2sinθMultiplyby − 1Passed − r = 2sin (−θ) −r = −2sinθ Четно-нечетное identityr = 2sinθMultiplyby − 1Passed |
| 2) Замена θθ на −θ − θ не дает того же уравнения. Следовательно, график не проходит проверку и может быть или не быть симметричным относительно полярной оси. | r = 2sin (−θ) r = −2sinθ Четно-нечетное тождество r = −2sinθ ≠ 2sinθFailedr = 2sin (−θ) r = −2sinθ Четно-нечетное тождествоr = −2sinθ ≠ 2sinθFailed |
| 3) Замена rr на –r – r изменяет уравнение и не проходит проверку.Граф может быть или не быть симметричным относительно полюса. | −r = 2sinθ r = −2sinθ ≠ 2sinθFailed − r = 2sinθ r = −2sinθ ≠ 2sinθFailed |
Таблица 1
Анализ
Используя графический калькулятор, мы можем увидеть, что уравнение r = 2sinθr = 2sinθ представляет собой круг с центром в точке (0,1) (0,1) и радиусом r = 1r = 1, который действительно симметричен прямой θ = π2. θ = π2. Мы также можем видеть, что график не симметричен полярной оси или полюсу. См. Рисунок 3.
Рисунок 3
Попробуй # 1
Проверить уравнение на симметрию: r = −2cosθ.r = −2cosθ.
Построение полярных уравнений по точкам
Для построения графика в прямоугольной системе координат мы строим таблицу значений xx и yy. Для построения графика в полярной системе координат мы строим таблицу значений θθ и rr. Вводим значения θθ в полярное уравнение и вычислить относительную влажность. Однако использование свойств симметрии и нахождение ключевых значений θθ и rr означает, что потребуется меньше вычислений.
Нахождение нулей и максимумов
Чтобы найти нули полярного уравнения, мы решаем значения θθ, которые приводят к r = 0.r = 0. Напомним, что для нахождения нулей полиномиальных функций мы устанавливаем уравнение равным нулю, а затем решаем относительно x.x. Мы используем тот же процесс для полярных уравнений. Установите r = 0, r = 0 и решите относительно θ.θ.
Для многих форм, с которыми мы встретимся, максимальное значение полярного уравнения находится путем подстановки тех значений θθ в уравнение, которые дают максимальное значение тригонометрических функций.Рассмотрим r = 5cosθ; r = 5cosθ; максимальное расстояние между изгибом и опорой — 5 единиц. Максимальное значение функции косинуса равно 1, когда θ = 0, θ = 0, поэтому наше полярное уравнение — 5cosθ, 5cosθ, а значение θ = 0θ = 0 даст максимальное значение | r |. | R |.
Аналогично, максимальное значение синусоидальной функции равно 1, когда θ = π2, θ = π2, и если наше полярное уравнение r = 5sinθ, r = 5sinθ, значение θ = π2θ = π2 даст максимум | r | . | г |. Мы можем найти дополнительную информацию, вычислив значения rr, когда θ = 0.θ = 0.Эти точки будут пересечениями полярной оси, что может быть полезно при построении графика и идентификации кривой полярного уравнения.
Пример 2
Нахождение нулей и максимальных значений для полярного уравнения
Используя уравнение из примера 1, найдите нули и максимум | r || r | и, если необходимо, полярная ось пересекает r = 2sinθ.r = 2sinθ.
Решение
Чтобы найти нули, установите rr равным нулю и решите относительно θ.θ.
2sinθ = 0sinθ = 0θ = sin − 10θ = nπ, где n — целое число, 2sinθ = 0sinθ = 0θ = sin − 10θ = nπ, где n — целое числоПодставьте любое из значений θθ в уравнение.Мы будем использовать 0.0.
Точки (0,0) (0,0) и (0, ± nπ) (0, ± nπ) являются нулями уравнения. Все они совпадают, поэтому на графике видна только одна точка. Эта точка также является единственной точкой пересечения полярной оси.
Чтобы найти максимальное значение уравнения, посмотрите на максимальное значение тригонометрической функции sinθ, sinθ, которое возникает, когда θ = π2 ± 2kπθ = π2 ± 2kπ, что приводит к sin (π2) = 1.sin (π2) = 1 . Подставляем π2π2 вместо θ.θ.
r = 2sin (π2) r = 2 (1) r = 2r = 2sin (π2) r = 2 (1) r = 2Анализ
Точка (2, π2) (2, π2) будет максимальным значением на графике.Давайте нарисуем еще несколько точек, чтобы проверить график круга. См. Таблицу 2 и Рисунок 4.
| θθ | r = 2sinθr = 2sinθ | руб. |
|---|---|---|
| 0 | r = 2sin (0) = 0r = 2sin (0) = 0 | 00 |
| π6π6 | r = 2sin (π6) = 1r = 2sin (π6) = 1 | 11 |
| π3π3 | r = 2sin (π3) ≈1.73r = 2sin (π3) ≈1.73 | 1,731,73 |
| π2π2 | r = 2sin (π2) = 2r = 2sin (π2) = 2 | 22 |
| 2π32π3 | r = 2sin (2π3) ≈1.73r = 2sin (2π3) ≈1.73 | 1,731,73 |
| 5π65π6 | r = 2sin (5π6) = 1r = 2sin (5π6) = 1 | 11 |
| ππ | r = 2sin (π) = 0r = 2sin (π) = 0 | 00 |
Таблица 2
Рисунок 4
Попробуй # 2
Без преобразования в декартовы координаты, проверьте данное уравнение на симметрию и найдите нули и максимальные значения | r |: | r |: r = 3cosθ.г = 3cosθ.
Следственные круги
Теперь мы увидели уравнение круга в полярной системе координат. В последних двух примерах одно и то же уравнение использовалось для иллюстрации свойств симметрии и демонстрации того, как находить нули, максимальные значения и нанесенные точки, по которым построены графики. Однако круг — лишь одна из многих фигур в наборе полярных кривых.
Есть пять классических полярных кривых : кардиоиды , лиманов, лемнискаты, кривые розы и спирали Архимеда .Мы кратко коснемся полярных формул для круга, прежде чем перейти к классическим кривым и их вариациям.
Формулы уравнения окружности
Некоторые формулы, которые создают график круга в полярных координатах, задаются формулами r = acosθr = acosθ и r = asinθ, r = asinθ, где aa — диаметр круга или расстояние от полюса до самой дальней точки. по окружности. Радиус равен | a | 2, | a | 2 или половине диаметра. Для r = acosθ, r = acosθ центр равен (a2,0).(а2,0). Для r = asinθ, r = asinθ центром является (a2, π2). (A2, π2). На рисунке 5 показаны графики этих четырех кругов.
Рисунок 5
Пример 3
Построение графика полярного уравнения для окружности
Нарисуйте график r = 4cosθ.r = 4cosθ.
Решение
Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что график симметричен относительно полярной оси. Далее находим нули и максимум | r || r | для r = 4cosθ.r = 4cosθ. Сначала установите r = 0, r = 0 и решите относительно θθ.Таким образом, нуль возникает при θ = π2 ± kπ.θ = π2 ± kπ. Ключевой точкой для построения графика является (0, π2). (0, π2).
Чтобы найти максимальное значение r, r, обратите внимание, что максимальное значение функции косинуса равно 1, когда θ = 0 ± 2kπ.θ = 0 ± 2kπ. Подставляем θ = 0θ = 0 в уравнение:
r = 4cosθr = 4cos (0) r = 4 (1) = 4r = 4cosθr = 4cos (0) r = 4 (1) = 4Максимальное значение уравнения составляет 4. Ключевой точкой для построения графика является (4,0). (4,0).
Поскольку r = 4cosθr = 4cosθ симметрично относительно полярной оси, нам нужно только вычислить r -значений для θθ в интервале [0, [0, π].π]. Точки в верхнем квадранте затем могут быть отражены в нижний квадрант. Составьте таблицу значений, подобную Таблице 3. График показан на Рисунке 6 .
| θθ | 0 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | ππ |
| руб. | 4 | 3.46 | 2,83 | 2 | 0 | −2 | -2,83 | −3,46 | −4 |
Таблица 3
Рисунок 6
Исследование кардиоидов
Хотя в некоторых случаях перевод из полярных координат в декартовы координаты может показаться проще, построение классических кривых в полярной системе на самом деле менее сложно.Следующая кривая называется кардиоидной, так как она напоминает сердце. Эту форму часто включают в семейство кривых, называемых лимасонами, но здесь мы обсудим кардиоиду отдельно.
Формулы кардиоиды
Формулы, по которым строятся графики кардиоиды, имеют следующий вид: r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, a> 0, b> 0, b> 0 и ab = 1. ab = 1. Кардиоидный график проходит через полюс, как мы видим на Рисунке 7.
Рисунок 7
Как к
Дан полярное уравнение кардиоиды, нарисуйте ее график.
- Проверьте уравнение для трех типов симметрии.
- Найдите нули. Установите r = 0. r = 0.
- Найдите максимальное значение уравнения согласно максимальному значению тригонометрического выражения.
- Составьте таблицу значений для rr и θ.θ.
- Постройте точки и нарисуйте график.
Пример 4
Построение графика кардиоиды
Нарисуйте график r = 2 + 2cosθ.r = 2 + 2cosθ.
Решение
Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что график этого уравнения будет симметричным относительно полярной оси.Далее находим нули и максимумы. Полагая r = 0, r = 0, имеем θ = π + 2kπ.θ = π + 2kπ. Нуль уравнения находится в точке (0, π). (0, π). График проходит через эту точку.
Максимальное значение r = 2 + 2cosθr = 2 + 2cosθ возникает, когда cosθcosθ является максимальным, то есть когда cosθ = 1cosθ = 1 или когда θ = 0.θ = 0. Подставляем θ = 0θ = 0 в уравнение и решаем относительно r.r.
r = 2 + 2cos (0) r = 2 + 2 (1) = 4r = 2 + 2cos (0) r = 2 + 2 (1) = 4Точка (4,0) (4,0) является максимальное значение на графике.
Мы обнаружили, что полярное уравнение симметрично относительно полярной оси, но поскольку оно распространяется на все четыре квадранта, нам нужно построить значения в интервале [0, π].[0, π]. Затем верхняя часть графика отражается над полярной осью. Затем мы составляем таблицу значений, как в Таблице 4, а затем наносим точки и рисуем график. См. Рисунок 8.
| θθ | 00 | π4π4 | π2π2 | 2π32π3 | ππ |
| руб. | 4 | 3,41 | 2 | 1 | 0 |
Таблица 4
Рисунок 8
Исследование Лимасона
Слово limaçon на старофранцузском означает «улитка», имя, которое описывает форму графа.Как упоминалось ранее, кардиоида является членом семейства limaçon, и мы можем видеть сходство на графиках. Другие изображения в этой категории включают лимит с одной петлей и с двумя петлями (или с внутренней петлей). Лимасоны с одной петлей иногда называют ямчатыми, если 1 Формулы, по которым строится график однопетлевого лимака с ямочками, задаются следующим образом: r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, b> 0, a> 0, b > 0 и 1 Рисунок 9 Лимасоны с ямочками Дано полярное уравнение для лимака с одной петлей, нарисуйте график. Изобразите уравнение r = 4−3sinθ.r = 4−3sinθ. Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что оно не проходит все три теста на симметрию, что означает, что график может демонстрировать или не демонстрировать симметрию, поэтому мы не можем использовать симметрию, чтобы помочь нам построить график. Однако это уравнение имеет график, который явно демонстрирует симметрию относительно линии θ = π2, θ = π2, но не проходит все три теста на симметрию.Графический калькулятор сразу же продемонстрирует качество отражения графика. Затем мы находим нули и максимум и наносим на график точки отражения для проверки симметрии. Установка r = 0r = 0 приводит к тому, что θθ не определен. Что это значит? Как могло θθ быть неопределенным? Угол θθ не определен ни при каком значении sinθ> 1. sinθ> 1. Следовательно, θθ не определено, потому что не существует значения θθ, для которого sinθ> 1. sinθ> 1. Следовательно, граф не проходит через полюс. Возможно, график действительно пересекает полярную ось, но не на полюсе.Мы можем исследовать другие точки пересечения, вычислив rr, когда θ = 0.θ = 0. Итак, имеется хотя бы одна полярная ось перехватить в точке (4,0). (4,0). Далее, поскольку максимальное значение синусоидальной функции равно 1 при θ = π2, θ = π2, мы подставим θ = π2θ = π2
в уравнение и решите относительно r.r. Таким образом, r = 1.r = 1. Составьте таблицу координат, аналогичную таблице 5. Таблица 5 График показан на рисунке 10. Рисунок 10 Лимасон с одной петлей Это пример кривой, для которой составление таблицы значений критически важно для построения точного графика.Тесты на симметрию терпят неудачу; ноль не определен. Хотя может быть очевидно, что уравнение, включающее sinθsinθ, вероятно, симметрично относительно линии θ = π2, θ = π2, оценка большего количества точек помогает проверить правильность графика. Нарисуйте график r = 3−2cosθ.r = 3−2cosθ. Другой тип лимака, лимит внутренней петли , назван в честь петли, образованной внутри общей формы лимака. Он был обнаружен немецким художником Альбрехтом Дюрером (1471-1528), который раскрыл метод рисования лимасона с внутренней петлей в своей книге 1525 года Underweysung der Messing .Спустя столетие отец математика Блеза Паскаля, Этьен Паскаль (1588–1651), открыл его заново. Формулы, которые порождают лимасоны внутренней петли, задаются как r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, a> 0, b> 0, b> 0 и а <ба <б. График limaçon внутреннего цикла проходит через полюс дважды: один раз для внешнего цикла и один раз для внутреннего цикла. Графики см. На Рисунке 11. Рисунок 11 Нарисуйте график r = 2 + 5cosθ.г = 2 + 5cosθ. Проверяя симметрию, мы обнаруживаем, что график уравнения симметричен относительно полярной оси. Затем поиск нулей показывает, что при r = 0, r = 0, θ = 1,98. Θ = 1,98.
Максимум | r || r | находится, когда cosθ = 1cosθ = 1 или когда θ = 0.θ = 0. Таким образом, максимум находится в точке (7, 0). Несмотря на то, что мы нашли симметрию, ноль и максимум, нанесение большего количества точек поможет определить форму, и тогда появится узор. См. Таблицу 6. Таблица 6 Как и ожидалось, значения начинают повторяться после θ = π.θ = π. График показан на рисунке 12. Рисунок 12 Лимасон с внутренним контуром Лемниската — это полярная кривая, напоминающая символ бесконечности ∞∞ или цифру 8.Расположенная в центре полюса лемниската по определению симметрична. Формулы, образующие график лемнискаты, даются как r2 = a2cos2θr2 = a2cos2θ и r2 = a2sin2θr2 = a2sin2θ, где a ≠ 0.a ≠ 0. Формула r2 = a2sin2θr2 = a2sin2θ симметрична относительно полюса. Формула r2 = a2cos2θr2 = a2cos2θ симметрична относительно полюса, прямой θ = π2, θ = π2 и полярной оси. Графики см. На Рисунке 13. Рисунок 13 Нарисуйте график r2 = 4cos2θ.r2 = 4cos2θ. Уравнение демонстрирует симметрию относительно прямой θ = π2, θ = π2, полярной оси и полюса. Давай найдем нули. Сейчас это должно быть обычным делом, но мы подойдем к этому уравнению немного иначе, сделав замену u = 2θ.u = 2θ. А теперь найдем максимальное значение. Поскольку максимум cosu = 1 cosu = 1, когда u = 0, u = 0, максимум cos2θ = 1cos2θ = 1, когда 2θ = 0,2θ = 0. Таким образом, У нас есть максимум на (2, 0). Поскольку этот график симметричен относительно полюса, линии θ = π2, θ = π2 и полярной оси, нам нужно построить точки только в первом квадранте. Составьте таблицу, аналогичную таблице 7. Таблица 7 Нанесите точки на график, например, показанный на рисунке 14. Рисунок 14 Лемниската Выполнение такой замены, как u = 2θu = 2θ, является обычной практикой в математике, поскольку она может упростить вычисления. Однако мы не должны забывать заменять заменяющий член исходным членом в конце, а затем решать неизвестное. Некоторые точки на этом графике могут не отображаться при использовании функции Trace на графическом калькуляторе TI-84, а таблица калькулятора может показывать ошибку для тех же самых точек r.р. Это потому, что для этих значений θ.θ нет реальных квадратных корней. Другими словами, соответствующие r -значения 4cos (2θ) 4cos (2θ)
являются комплексными числами, потому что под корнем стоит отрицательное число. Следующий тип полярного уравнения дает форму лепестка, называемую кривой розы. Хотя графики выглядят сложными, простое полярное уравнение порождает закономерность. Формулы, которые создают график кривой розы, задаются как r = acosnθr = acosnθ и r = asinnθr = asinnθ, где a 0.а ≠ 0. Если nn четное, кривая имеет 2n2n лепестков. Если nn нечетное, кривая имеет nn лепестков. См. Рисунок 15. Рисунок 15 Нарисуйте график r = 2cos4θ.r = 2cos4θ. Проверяя симметрию, мы снова обнаруживаем, что тесты симметрии не раскрывают всей картины. График симметричен не только относительно полярной оси, но и относительно прямой θ = π2θ = π2 и полюса. Теперь найдем нули. Сначала сделаем замену u = 4θ.u = 4θ. Ноль равен θ = π8.θ = π8. Точка (0, π8) (0, π8) находится на кривой. Далее находим максимум | r |. | R |. Мы знаем, что максимальное значение cosu = 1cosu = 1 при θ = 0.θ = 0. Таким образом, Точка (2,0) (2,0) находится на кривой. График кривой розы обладает уникальными свойствами, которые раскрыты в Таблице 8. Таблица 8 Поскольку r = 0r = 0 при θ = π8, θ = π8, имеет смысл разделить значения в таблице на π8π8 единиц.Возникает определенная закономерность. Посмотрите на диапазон значений r : 2, 0, −2, 0, 2, 0, −2 и т. Д. Это представляет развитие кривой по одному лепестку за раз. Начиная с r = 0, r = 0, каждый лепесток простирается на расстояние r = 2, r = 2, а затем возвращается к нулю 2n2n раз, всего восемь лепестков. См. График на рисунке 16. Когда эти кривые нарисованы, лучше всего наносить точки по порядку, как в таблице 8. Это позволяет нам увидеть, как график достигает максимума (кончик лепестка), петляет, пересекая полюс, попадает в противоположный максимум, и петли обратно к полюсу.Действие продолжается до тех пор, пока не будут нарисованы все лепестки. Нарисуйте график r = 4sin (2θ) .r = 4sin (2θ). Нарисуйте график r = 2sin (5θ) .r = 2sin (5θ). График уравнения показывает симметрию относительно прямой θ = π2.θ = π2. Далее найдите нули и максимум. Мы хотим сделать замену u = 5θ.и = 5θ. Максимальное значение рассчитывается под углом, где sinθsinθ является максимум. Следовательно, Таким образом, максимальное значение полярного уравнения равно 2. Это длина каждого лепестка. Поскольку кривая для нечетных nn дает то же количество лепестков, что и n, n, на графике будет пять лепестков. См. Рисунок 17. Создайте таблицу значений, подобную Таблице 9. Таблица 9 Нарисуйте график r = 3cos (3θ).г = 3cos (3θ). Последнее полярное уравнение, которое мы обсудим, — это спираль Архимеда, названная в честь ее первооткрывателя, греческого математика Архимеда (ок. 287 г. до н. Э. — ок. 212 г. до н. Э.), Которому приписывают многочисленные открытия в области геометрии и механики. Формула, по которой строится график спирали Архимеда, имеет вид r = θr = θ
для θ≥0.θ≥0. При увеличении θθ rr
увеличивается с постоянной скоростью по постоянно расширяющемуся, нескончаемому спиралевидному пути.См. Рисунок 18. Рисунок 18 Нарисуйте график для спирали Архимеда над [0,2π], [0,2π]. Нарисуйте график r = θr = θ на [0,2π]. [0,2π]. Поскольку rr равно θ, θ, график спирали Архимеда начинается на полюсе в точке (0, 0).Хотя график намекает на симметрию, формальной симметрии в отношении прохождения тестов симметрии нет. Кроме того, нет максимального значения, если домен не ограничен. Создайте таблицу, такую как Таблица 10. Таблица 10 Обратите внимание, что значения r — это просто десятичная форма угла, измеренного в радианах. Мы можем видеть их на графике на Рисунке 19. Рисунок 19 Спираль Архимеда Область этой полярной кривой составляет [0,2π]. [0,2π]. В общем, однако, область определения этой функции — (−∞, ∞).(−∞, ∞). Изобразить уравнение спирали Архимеда довольно просто, хотя изображение кажется сложным. Нарисуйте график r = −θr = −θ на интервале [0,4π]. [0,4π]. В этом разделе мы исследовали ряд, казалось бы, сложных полярных кривых. На рисунках 20 и 21 представлены графики и уравнения для каждой из этих кривых. Рисунок 20 Рисунок 21 Опишите три типа симметрии в полярных графах и сравните их с симметрией декартовой плоскости. Какой из трех типов симметрии полярных графов соответствует симметрии относительно оси x , оси y и начала координат? Какие шаги необходимо выполнить при построении полярных уравнений? Опишите формы графиков кардиоидов, лимаконов и лемнискат. Какая часть уравнения определяет форму графика полярного уравнения? Для следующих упражнений проверьте уравнение на симметрию. r = 31 − cos2θr = 31 − cos2θ Для следующих упражнений нарисуйте полярное уравнение. Определите имя формы. r2 = 36cos (2θ) r2 = 36cos (2θ) r2 = 10cos (2θ) r2 = 10cos (2θ) r2 = 10sin (2θ) r2 = 10sin (2θ) Для следующих упражнений используйте графический калькулятор, чтобы нарисовать график полярного уравнения. r = 2sinθtanθ, r = 2sinθtanθ, циссоид r = 21 − sin2θr = 21 − sin2θ, гиппопед r = 2 − sin (2θ) r = 2 − sin (2θ) Для следующих упражнений используйте графическую утилиту для построения графика каждой пары полярных уравнений в области [0,4π] [0,4π], а затем объясните различия, показанные на графиках. r = θ, r = θ + sinθr = θ, r = θ + sinθ r = sinθ + θ, r = sinθ − θr = sinθ + θ, r = sinθ − θ r = 2sin (θ2), r = θsin (θ2) r = 2sin (θ2), r = θsin (θ2) r = sin (cos (3θ)) r = sin (3θ) r = sin (cos (3θ)) r = sin (3θ) В графической утилите: graph r = sin (165θ) r = sin (165θ) на [0 [0, 4π] 4π], [0 [0, 8π] 8π], [0 [0, 12π] 12π ] и [0 [0, 16π] .16π]. Опишите эффект увеличения ширины домена. В графической утилите: график и эскиз r = sinθ + (sin (52θ)) 3r = sinθ + (sin (52θ)) 3 на [0,4π]. [0,4π]. С помощью графической утилиты нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. С помощью графической утилиты нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. С помощью графической утилиты нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. Для следующих упражнений нарисуйте каждое полярное уравнение на одном и том же наборе полярных осей и найдите точки пересечения. r1 = 3 + 2sinθ, r2 = 2r1 = 3 + 2sinθ, r2 = 2 r1 = 6−4cosθ, r2 = 4r1 = 6−4cosθ, r2 = 4 r1 = 1 + sinθ, r2 = 3sinθr1 = 1 + sinθ, r2 = 3sinθ r1 = 1 + cosθ, r2 = 3cosθr1 = 1 + cosθ, r2 = 3cosθ r1 = cos (2θ), r2 = sin (2θ) r1 = cos (2θ), r2 = sin (2θ). r1 = sin2 (2θ) r1 = sin2 (2θ), r2 = 1 − cos (4θ) r2 = 1 − cos (4θ). r1 = 3, r2 = 2sin (θ) r1 = 3, r2 = 2sin (θ) r12 = sinθ, r22 = cosθr12 = sinθ, r22 = cosθ r1 = 1 + cosθr1 = 1 + cosθ, r2 = 1 − sinθr2 = 1 − sinθ Преобразуйте точку в декартовой плоскости в ее равные полярные координаты с помощью этого калькулятора полярных координат.Полярные координаты также имеют место в плоскости x-y, но представлены радиусом и углом, как показано на диаграмме ниже. Следующие формулы используются для преобразования полярных координат из декартовых координат. r = √ (x² + y²) θ = арктангенс (y / x) Полярные координаты выражаются двумя значениями.Один — это радиус, а другой — угол. Радиус является функцией координат x и y и является углом. Следующие формулы используются для расчета радиуса и угла. Как видно из формул, радиус является функцией квадратного корня из суммы квадратов координат x и y. Другими словами, длина радиуса действует как гипотенуза на треугольнике с длинами x и y. Угол, описывающий вращение радиуса, равен углу в треугольнике со сторонами x и y и гипотенузой r.Это также известно как опорный угол. Полярные координаты существуют уже тысячелетие. Происходит, как и большинство связанных с математикой концепций, через греческого ученого. В частности, греческий астроном хотел использовать функции для вычисления положения звезд. Угол в полярных координатах часто описывается греческой буквой тета и измеряется либо в градусах, либо в радианах. Радиус, обозначенный буквой r, обычно измеряется безразмерной единицей измерения, но можно использовать некоторые меры расстояния, такие как дюймы или метры. Полярные координаты — это способ отображения местоположения точки на 2-мерной плоскости с использованием радиуса круга и угла, отсчитываемого от оси x. Декартовы координаты — это способ отображения местоположения точки на двухмерной плоскости с использованием координат X и Y. Формулы для лимасонов с одной петлей
Как к
Пример 5
Построение графа однопетлевой Лимасон
Решение
θθ 00 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ 7π67π6 4π34π3 3π23π2 5π35π3 11π611π6 2π2π руб. 4 2.5 1,4 1 1,4 2,5 4 5,5 6,6 7 6,6 5,5 4 Анализ
Попробуй # 3
Формулы для лимасонов внутреннего контура
Пример 6
Построение графика внутренней петли Лимасон
Решение
θθ 00 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ 7π67π6 4π34π3 3π23π2 5π35π3 11π611π6 2π2π руб. 7 6.3 4,5 2 -0,5 -2,3 −3 -2,3 -0,5 2 4,5 6,3 7 Исследование лемнискат
Формулы лемнискат
Пример 7
Построение графика лемнискаты
Решение
θθ 0 π6π6 π4π4 руб. ± 2 ± 2 ± 2 ± 2 0 Анализ
Исследование кривых розы
Rose Curves
Пример 8
Построение графика кривой розы (
n четных) Решение
θθ 0 π8π8 π4π4 3π83π8 π2π2 5π85π8 3π43π4 руб. 2 0 −2 0 2 0 −2 Анализ
Попробуй # 4
Пример 9
Построение графика кривой розы (
n Odd) Решение
θθ 0 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ руб. 0 1 -1,73 2 -1,73 1 0 Попробуй # 5
Исследование спирали Архимеда
Спираль Архимеда
Как к
Пример 10
Набросок графика спирали Архимеда
Решение
θθ π4π4 π2π2 ππ 3π23π2 7π47π4 2π2π руб. 0.785 1,57 3,14 4,71 5,50 6,28 Анализ
Попробуй # 6
Сводка кривых
8.Упражнения из 4 частей
Устные
1. Графический
Технологии
Расширения
| Формула | Пример
Формула полярных координат
Определение полярных координат
Как рассчитать полярные координаты
Подробнее о полярных координатах
FAQ
Что такое полярные координаты?
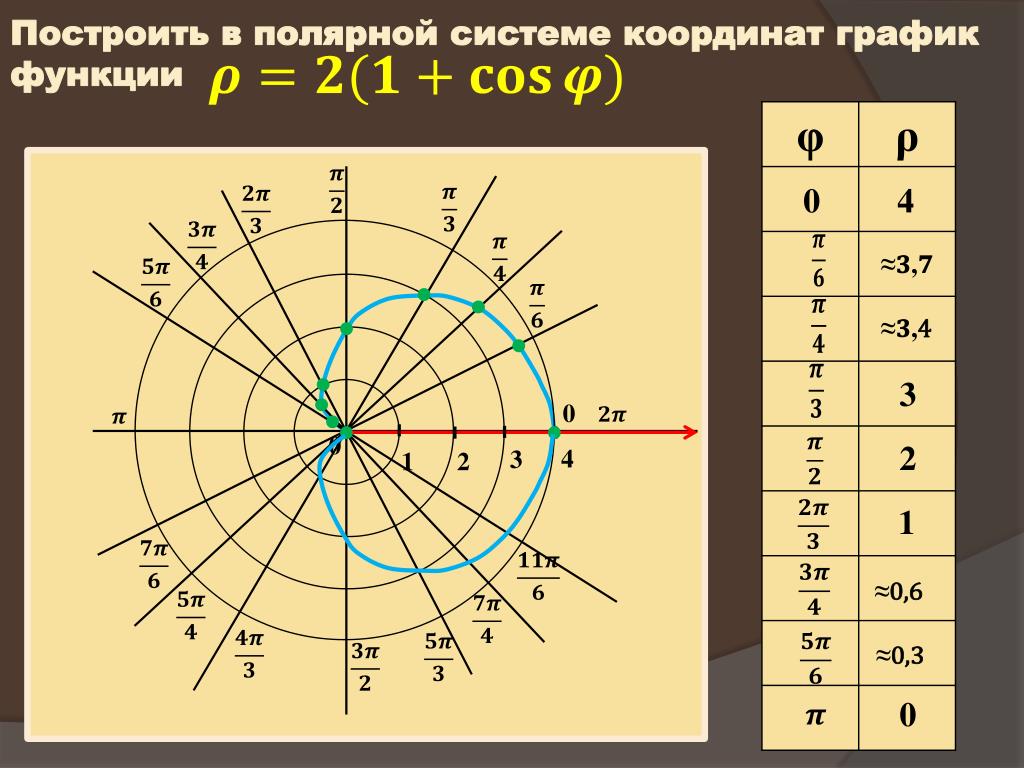
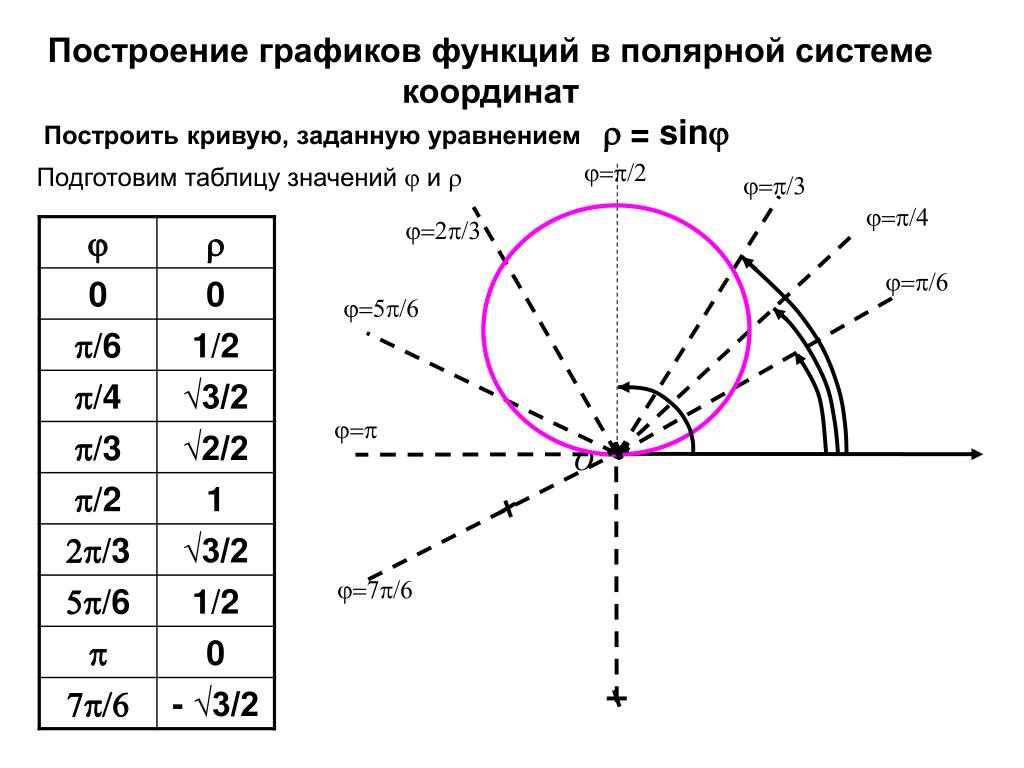

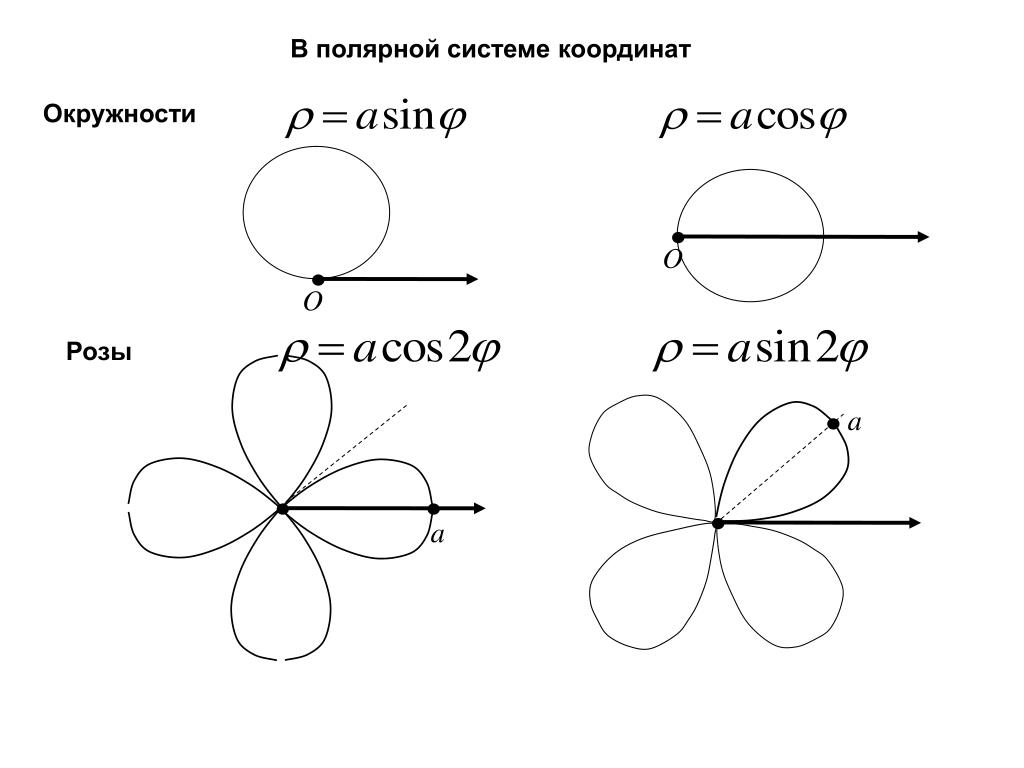


Ваш комментарий будет первым