Построить график степенной функции онлайн: Построение графика функции онлайн

Степенные функции, их свойства и графики. Степенные функции с рациональным показателем 11 класс онлайн-подготовка на

1. Основные понятия и определения

 

Напомним свойства и графики степенных функций с целым отрицательным показателем.

 

При четных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида – их четность, графики симметричны относительно оси ОУ.

Рис. 1. График функции

При нечетных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида – их нечетность, графики симметричны относительно начала координат.

 

Рис. 2. График функции

 

2. Функция с отрицательным рациональным показателем степени, графики, свойства

 

 

Напомним основное определение.

 

Степенью неотрицательного числа а с рациональным положительным показателем  называется число .

Степенью положительного числа а с рациональным отрицательным показателем  называется число .

Для  выполняется равенство:

Например: ;  – выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,

Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.

Например:

Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя – он нам известен (рисунок 3).

 

Рис. 3. График функции

График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при  корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).

Рис. 4. График функции

 

Рассмотрим еще одну функцию из семейства изучаемых функций.

Важно, что  по определению

Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).

Рис. 5. График функции

При построении графика исходной функции точка (1;1) остается, при  корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).

Рис. 6. График функции

Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции – функции с отрицательным рациональным показателем.

Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.

Область определения функции:

Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.

Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.

Функция выпукла вниз (рисунок 15.7)

На кривой взяты точки А и В, через них проведен отрезок, вся кривая находится ниже отрезка, данное условие выполняется для произвольных двух точек на кривой, следовательно функция выпукла вниз. Рис. 7.

Рис. 7. Выпуклость функции

 

3. Решение типовых задач

 

 

Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют.

 

Пример 1 – найти максимум и минимум функции на интервале [1;8):

вычислим значения функции в концах заданного промежутка:

Теперь мы можем выписать ответ на основании того, что функция монотонно убывает.

, минимального значения нет, так как правая граница не включена в интервал.

Пример 2 – построить и прочесть график функции:

Преобразуем заданную функцию по определению рациональной степени:

Не забудем указать, что по определению

Строим график функции , для нас это стандартная кривая, она проходит через точку (1;1), убывает. После этого сдвигаем полученный график на одну единицу вверх, точка (1;1) переходит в точку (1;2) (рисунок 8)

Читаем полученный график: если аргумент возрастает от нуля (не включая) до бесконечности, функция убывает от бесконечности до единицы (не включая).

Рис. 8. Построение графика функции

Пример 3 – построить и прочесть график функции:

Преобразуем заданную функцию по определению степени с рациональным показателем:

Нам известен график функции , построим его. Полученная кривая возрастает и проходит через точку (1;1), поскольку показатель степени больше единицы – кривая выпукла вниз. Сдвинем построенную кривую на две единицы вправо (получаем график функции ) и на одну единицу вверх – получаем искомый график (рисунок 9)

Прочтем полученный график:

При возрастании аргумента от двух до бесконечности функция возрастает от единицы до бесконечности.

Пример 4 – построить и прочесть график функции:

В данном случае функция задана кусочно.

Напомним, что такое модуль, раскроем его по определению:

Итак, строим график функции . Имеем две ветки:  и . После этого строим стандартную кривую  на интервале  (Рисунок 10)

Прочтем график построенной функции:

Если аргумент возрастает от минус бесконечности до нуля, функция убывает от бесконечности до нуля. Когда аргумент возрастает от нуля до единицы, функция также возрастает от нуля до единицы. Наконец, когда аргумент возрастает от единицы не включительно до плюс бесконечности, функция убывает от единицы не включительно до нуля не включительно.

Рис. 9. Построение графика функции

Рис. 10. График кусочно заданной функции

Пример 5 – найти значения параметра, при котором уравнение а) имеет хотя бы одно решение; б) имеет только одно решение:

График заданной функции мы уже построили в предыдущем примере. Теперь рассечем его семейством прямых  и найдем количество точек пересечения для каждого случая.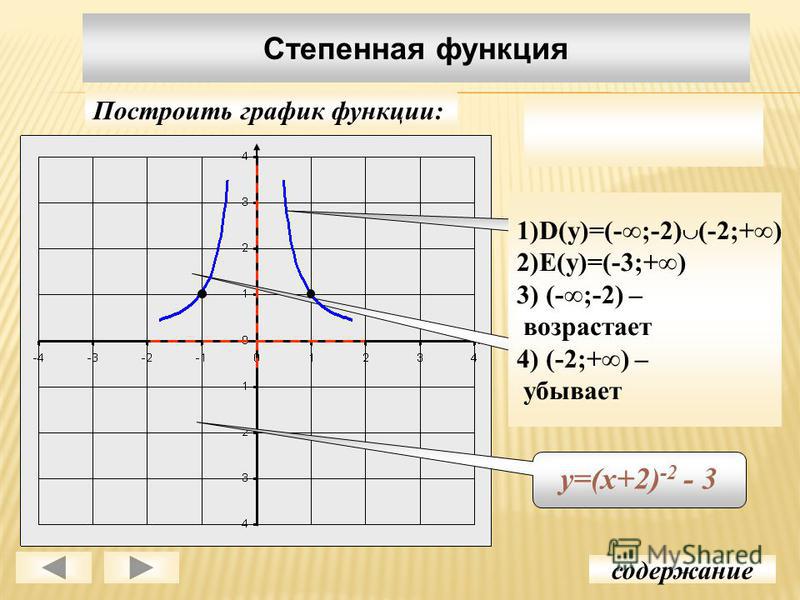

Выполним рассечение (рисунок 11).

Рис. 11. Рассечение графика прямыми

При  уравнение имеет три решения; при  уравнение имеет единственное решение

Ответ: при  уравнение имеет хотя бы одно решение, при  уравнение имеет единственное решение.

Итак, мы рассмотрели степенные функции, их свойства и графики. На следующем уроке мы перейдем к дифференцированию и интегрированию степенных функций.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Edu.glavsprav.ru (Источник).
3. Pm298.ru (Источник).

 

Домашнее задание

1. Найдите наибольшее и наименьшее значение функции  на интервале:

а) ; б) ; в) ; г)

2. Построить и прочесть график функции:

а) ; б); в);  г)

 

3. Решите уравнение с параметром:

 

Степенные функции, их свойства и графики

Степенные функции,
их свойства и
графики
Цель урока:
обобщить и систематизировать знания и умения
по теме «Степенные функции, их свойства и
графики»
Задачи:
видеть график степенной функции по формуле
определять по графику функцию
уметь анализировать график
уметь решать уравнения, неравенства, системы
уравнений с помощью графиков и свойств
степенной функции
развивать навыки мыслительной деятельности,
математической зоркости
умение работать в сообществе
Степенными функциями
называются функции вида
r
у = х , где r – заданное
рациональное число
y
у = х2
у = х4
у = х6
-1 0 1 2
x
Показатель r = 2n – чётное натуральное число
Показатель r = 2n – чётное натуральное число
у = х2 , у = х 4 , у = х6 , у = х 8 , …
у
D( y ) : x R
у = х2n
Е ( y) : у 0
0
График чётной функции
симметричен относительно
оси Оу.
х
Функция у=х2n чётная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке
[0; )
Показатель r = 2n-1
нечётное
натуральное число
y
у = х3
у = х5
у = х7
-1 0 1 2
x
Показатель r = 2n-1 – нечётное натуральное число
у = х3 , у = х 5 , у = х7 , у = х 9 , …
у
D( y ) : x R
Е ( y) : у R
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
х
Функция возрастает
на промежутке ;
График нечётной
функции симметричен
относительно начала
координат – точки О.
Показатель r — целое
отрицательное нечётное
число
y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x
Показатель r = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
( 2 n 1)
Функция у=х-(2n-1)
нечётная,
–(2n-1)
= –х–(2n-1)
х т.к. (–х)
1
y
х
1
Функция убывает на
2 n 1
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
y
у = х-2
у = х-4
у = х-6
-1 0 1 2
Показатель r –целое отрицательное
чётное число
x
Показатель r = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2 n
1
1
y 2n
х
х
Функция у=х2n чётная,
т. к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
y
у = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x
Показатель r – положительное дробное число,
0<r<1
Показатель r – положительное дробное число, 0 < 1r < 1
у
у = х0,3,
у = х0,7, у = х0,12,
у х 3…
D( y ) : x 0
у х
r
Е ( y) : у 0
Функция возрастает на
0
1
х промежутке
[0; )
y
у = х3,1
2, 5
у
1,5
х
у
=
х
=
D( y ) : x 0
Е ( y) : у 0
-1 0 1 2
Функция возрастает на
промежутке [0; )
Показатель r – положительное дробное
число, r >1
x
y
у = х-1,3
у = х-2,3
у = х-3,8
у = х-0,3
-1 0 1 2
Показатель
r – отрицательное
дробное число, r < 0
x
Показатель r – отрицательное дробное число 1
у
у=х
-1,3
,
у=х
-0,7
, у=х
-2,12
,
у х
3
…
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )
Графическое лото.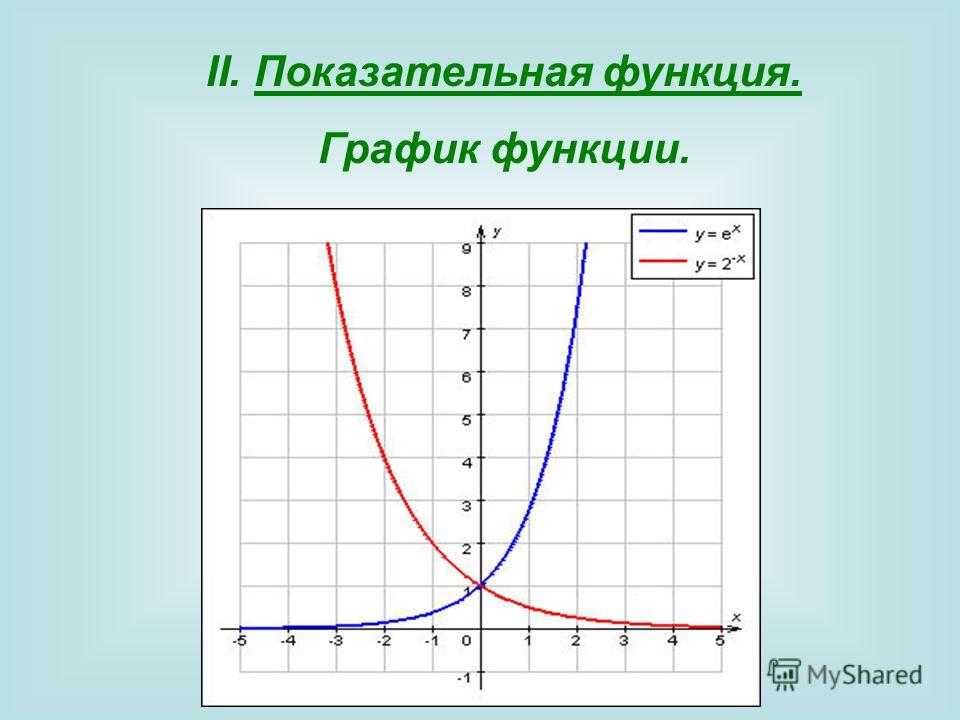
у
у
1
у
2
у
4
3
1
1
1
0
-1 0
у
1
х
1
у
5
х
1
1) у = х-0,7
6) у = х3,14
х
0
2) у = х-7
7) у = х8
0
1
у
1
1
х
3) у = х
8) у = 1
0
х
х
у
6
1
1
0
-1 0
1
1
7
1
х
4) у = х7
9) у = х-6
9
0
5) у = х0,6
8
1
х
ПРАВИЛЬНЫЙ ОТВЕТ:
796 514 283
у
у х
у
х
=
у
х
=
у
у х
0
1
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции у х
лежит выше (ниже) графика
функции у = х.
у
у х
у
х
=
у
х
=
у
у х
0
1
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у х
sin 450
лежит выше (ниже) графика
Пользуясь рисунком, найти промежутки, на которых
1
график функции
лежит выше (ниже) графика
у х
функции у = х.
у
х
=
у
0
1
х
Преобразования
графиков
степенных функций
Как построить график функции
y = f(x + l),
если известен график функции
y = f(x)
y
у = х-4
-1 0 1 2
у = (х – 2)-4
x
Как построить график функции
y = f(x) + m,
если известен график функции
y = f(x)
y
у = х-4
-1 0 1 2
у = х– 4 – 3
x
Как построить график функции
y = f(x + l) + m,
если известен график функции
y = f(x)
y
у = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x
y
у = (х-2)– 3– 1
у = х-3
-1 0 1 2
x
y
у = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x
Проверим свои знания:
Пройдем тестирование,
воспользовавшись ссылкой:
http://anketer.ru/vote/oBDZLxsxTh/
домашнее задание
п.9, № 9.16(б),
9.19 (а),
9.20 (б),
9.22(в).
п.9, № 9.16(г),
9.19 (б),
9.20 (г),
9.22(г).
видеть график степенной функции по формуле
определять по графику функцию
уметь анализировать график
уметь решать уравнения, неравенства, системы
уравнений с помощью графиков и свойств
степенной функции
развивать навыки мыслительной деятельности,
математической зоркости
умение работать в сообществе
Дружить наукам можно вечно,
Вселенная ведь бесконечна.
Спасибо всем вам за урок,
А главное, чтоб он был впрок!
Оцените свою работу на уроке
«5»
«4»
«3»
затрудняюсь
Напишите свою фамилию в тот
столбик, на какую оценку, по
Вашему мнению, Вы работали

Калькулятор степенной функции

Автор: Артуро Баррантес

Отзыв от Luis Hoyos

Последнее обновление: 20 января 2023 г.

Содержание:

• Что такое степенная функция в математике?
• Как вычислить степень любого числа?
• Другие полезные инструменты, такие как калькулятор степенной функции
• Часто задаваемые вопросы

Калькулятор степенной функции поможет вам получить любое число в степени положительного, отрицательного, нулевого или даже десятичного порядка. 9nf(x)=xn

, где x представляет собой основание, n — показатель степени, а f(x) — степенная функция. Показатель степени указывает, во сколько раз мы умножим основание. Например, если кто-то спросит: Сколько будет 2 в степени 30? . Нам придется умножить число 2 в тридцать раз. Звучит много, правда?

В таких случаях мы можем использовать наш калькулятор функций мощности. Следовательно, результат равен 1 073 741 824 . Но что, если мы столкнемся с проблемой, требующей 4 в степени 0 или степени -2? Эти и другие случаи мы рассмотрим в следующем разделе.

Как вычислить степень любого числа?

Что касается вычисления степени любого числа, мы будем использовать метод, описанный выше, но разделенный на три части:

• Когда показатель степени положителен: мы следуем тому же процессу, указанному выше для степенных функций. Пример: 4 в степени 4: 4 x 4 x 4 x 4 = 256 .

• Когда показатель степени отрицательный: Пример: Сколько будет 2 в степени -3.

  1. Узнать показатель степени. В этом случае: -3 . Следовательно, мы будем использовать - , чтобы преобразовать основание в его обратное значение.
  2. Напишите обратное основание. Если основание равно 2, мы используем 12\frac{1}{2}21​.
  3. Умножьте новое основание столько раз, сколько указывает показатель степени: 12×12×12=18\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \ frac{1}{8} 21​×21​×21​=81​.

• Когда показатель степени равен 0: любое число в степени 0 равно 1.

Другие полезные инструменты, такие как калькулятор функции мощности

Поскольку вы уже знаете, как работают степенные функции, вы можете взглянуть на другие связанные инструменты:

• Калькулятор экспоненты;
• степень числа 2; и
• Степень числа 10.

Часто задаваемые вопросы

Что есть в степени 0?

1. По соглашению, все, что в степени 0 равно 1. Итак, если кто-то спросит, чему равен 1 миллион в степени 0, вы ответите: просто 1.

Сколько будет 2 в степени 3?

Это 8 . Вы можете использовать инструмент Омникалькулятора: Калькулятор функции степени или:

1. Определите степень, в которую он возведен. В данном случае это 3.
2. Умножить три раза на основание: 2 * 2 * 2. В результате получится 8.

Чему равно 2 миллиона в степени 0?

Помните, всякий раз, когда кто-то спрашивает вас, что такое что-нибудь в степени 0, ответ будет 1.

Артуро Баррантес

f(x) = b ^x

Основание (b)

Показатель степени (x)

Степенная функция f(x)

Пошаговое решение

• Рассчитаем:
b 9011 9 х = f(x)

Ознакомьтесь с 14 похожими калькуляторами экспонент и логарифмов 🇪

AntilogИзменение базовой формулыКонденсированные логарифмы… Еще 11

Графическое представление функции exp(x)

Программное обеспечение для построения кривых онлайн , также известное как .графопостроитель , представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн.

Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. Построитель кривых особенно подходит для функционального исследования , позволяет получить графическое представление функции из уравнения кривой, его можно использовать для определения вариации, минимума, максимума функции.

Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.

Операторы, используемые в графическом калькуляторе для записи математических функций, следующие:

1. + Для сложения
2. — для вычитания
3. * Для умножения
9Для мощности
4. / Для отдела

Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :

• абс (абсолютное значение), график абсолютного значения
• арккос (арккосинус), арккосинус участка
• арксинус (арксинус), арксинус графика
• arctan (арктангенс), арктангенс графика
• ч (гиперболический косинус), построить гиперболический косинус
• косинус (косинус), график косинус
• косек (косеканс), косеканс участка
• котан (котангенс), котангенс участка
• coth (гиперболический котангенс), построить гиперболический котангенс
• cube_root (кубический корень), построить кубический корень
• эксп (экспоненциальная), экспоненциальный график
• ln (напировский логарифм), построить напьеровский логарифм
логарифм
• (логарифм), логарифм графика
• сек (секанс), секущая участка
• ш (гиперболический синус), построить гиперболический синус
• грех (синус), график синуса
• sqrt (квадратный корень), участок квадратный корень
• тангенс (тангенс), участок касательной
• -й (гиперболический тангенс), построить гиперболический тангенс
• абс. (абсолютное значение), график абсолютного значения
• арккос (арккосинус), арккосинус участка
• арксинус (арксинус), арксинус графика
• arctan (арктангенс), арктангенс графика
• ч (гиперболический косинус), построить гиперболический косинус
• косинус (косинус), график косинус
• косек (косеканс), косеканс участка
• котан (котангенс), котангенс участка
• coth (гиперболический котангенс), построить гиперболический котангенс
• cube_root (кубический корень), построить кубический корень
• эксп (экспоненциальная), экспоненциальный график
• ln (напировский логарифм), построить напьеровский логарифм
логарифм
• (логарифм), логарифм графика
• сек (секанс), секущая участка
• ш (гиперболический синус), построить гиперболический синус
• sin (синус), график синуса
• sqrt (квадратный корень), участок квадратный корень
• тангенс (тангенс), участок касательной
• -й (гиперболический тангенс), построить гиперболический тангенс

1. Графические функции онлайн

Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно , просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .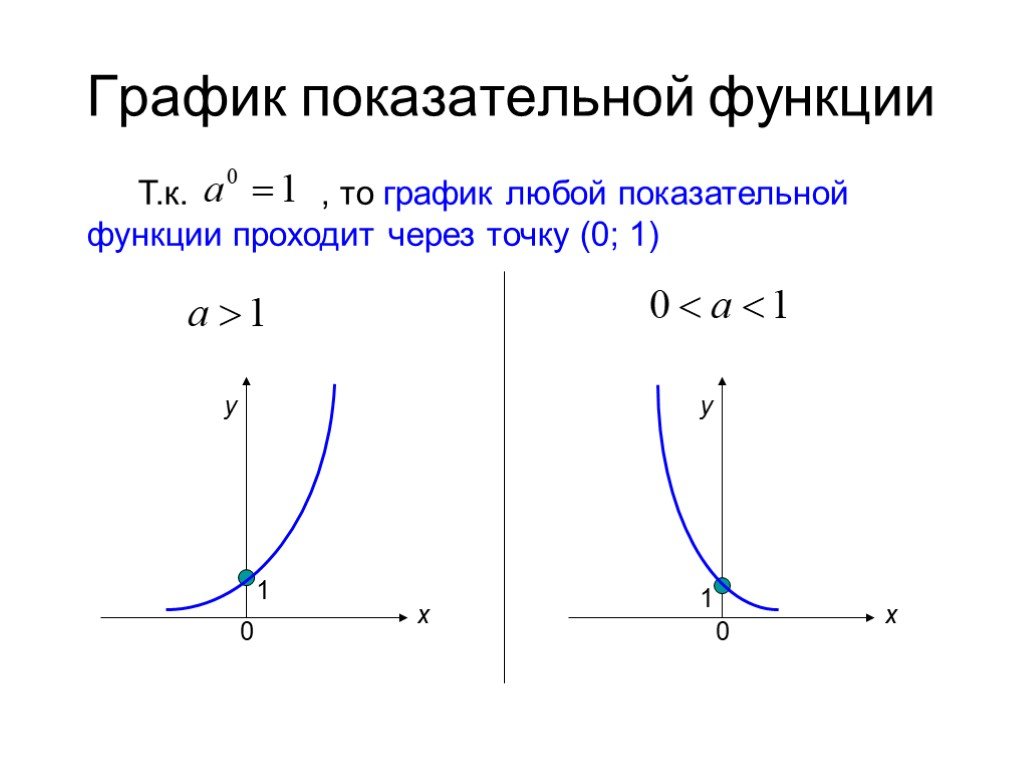

Переменная, которая будет использоваться для представления функций, — «x».

Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.

Кривые можно удалить из плоттера:

• Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
• Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.

Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.

онлайн-плоттер имеет несколько опций, позволяющих настроить график. Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов, чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.

1. Проведение касательной функции к точке

Онлайн-плоттер позволяет провести тангенс функции в точке сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.

2. График производной функции

Онлайн-плоттер позволяет вам построить производную функции для этого, вы просто рисуете нужную функцию, затем после того, как функция нарисована, нажмите на меню, на параметры, затем на появившуюся производную кнопку, затем строится производная функции.

9Построитель кривых 0019 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).

Построить параметрическую кривую онлайн

Плоттер позволяет рисовать параметрическую кривую , для этого вам просто нужно ввести абсциссу, ординату как функцию от t, затем нажмите кнопку «Построить параметрическую кривую», кривая автоматически отображается с двумя курсорами для отображения нужных точек.

Построить полярную кривую онлайн

Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.

Переместите курсор на кривую

Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.

Доступные графические опции

Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.

Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это, используйте область в правом нижнем углу графиков.

• Кнопка + позволяет увеличить масштаб кривых,
• — позволяет уменьшить масштаб кривых,
• Стрелки используются для перемещения кривых,

Экспорт кривых

Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков. Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение, также возможно скопировать изображение. Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.