Построить график системы уравнений онлайн: Отзывы, пожелания, предложения, критика сервиса построения графиков функций онлайн

Математический калькулятор с расширенными возможностями.

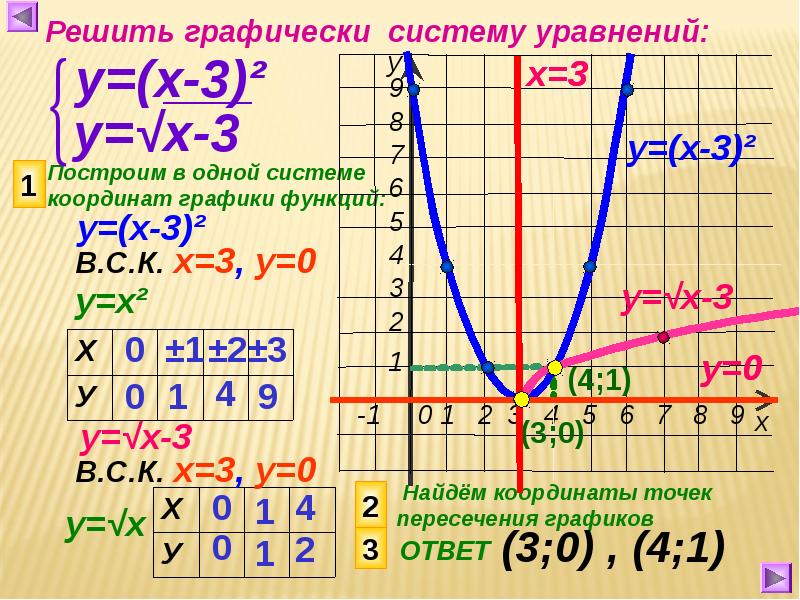
Математический калькулятор онлайн

Незаменимый помощник для студентов и инженеров, позволяющий производить вычисления начиная с элементарной линейной математики и заканчивая дифференциальными исчислениями и основами метафизики. Расчет тригонометрических функций, логарифмов, факториалов, решение квадратных уравнений в поле комплексных чисел, вычисления биномиальных коэффициентов, расчет матриц, конвертация величин и построение графиков. Стильный интерфейс бесплатного математического калькулятора прост и понятен, его не нужно устанавливать на компьютер, достаточно зайти на нашу страничку и можно комфортно им пользоваться. Удобный и простой инженерный калькулятор с богатым арсеналом возможностей для математических расчетов и между тем с приятным и понятным интерфейсом, способен выполнять практически любые арифметические действия и сложные математические вычисления. 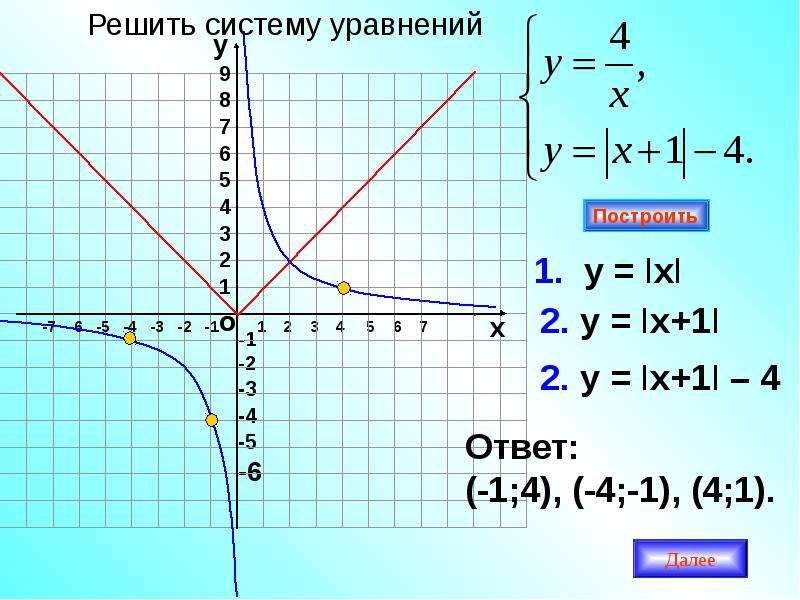Инженерный калькулятор позволяет использовать много разных математических функций: • решение гиперболических, тригонометрических и обратных тригонометрических функций: • возведение в степень и извлечение корней: • решение матриц и уравнений: • построение графиков и конвертертация величин: • вычисление логарифмов и экспоненты: • дифференцирование и интегрирование функций: • нахождение факториала, абсолютной величины числа, значения аргумента функции, биноминального коэффициента, наибольшего общего делителя, наименьшего общего кратного: • Использование мнимой единицы при расчётах комплексных чисел: • Выделение целой действительной части и исключение действительной части: • Разложение числа на простые множители. Инженерный калькулятор позволяет конвертировать физические величины разных систем измерений (масса, расстояние, время, компьютерные информационные единицы измерения и др. С возможностями нашего калькулятора вы сможете моментально перевести фунты в килограммы, мили в километры, секунды в часы и т.д. Для выполнения математических расчетов, просто введите последовательность математических выражений в соответствующее поле и для получения результата нажмите на кнопку со знаком равенства. Для построения графиков достаточно в поле ввода с помощью панели инструментов записать функцию и нажать на кнопку с изображением графика. Кнопка с надписью Unit предназначена для перехода в конвертер величин, для вычисления матриц нажмите на кнопку Matrix. В таблице указаны все клавиши (со значком * вызывается через дополнительную клавишу II) калькулятора и выполняемые ими операции. Клавиша Символ Операция pi pi Постоянная pi е е Число Эйлера % % Процент ( ) ( ) Открыть/Закрыть скобки , , Запятая sin sin(α) Синус угла cos cos(β) Косинус tan tan(y) Тангенс sinh sinh() Гиперболический синус cosh cosh() Гиперболический косинус tanh tanh() Гиперболический тангенс sin-1 asin() Обратный синус cos-1 acos() Обратный косинус tan-1 atan() Обратный тангенс sinh-1 asinh() Обратный гиперболический синус cosh-1 acosh() Обратный гиперболический косинус tanh-1 atanh() Обратный гиперболический тангенс x2 ^2 Возведение в квадрат х3 ^3 Возведение в куб xy ^ Возведение в степень 10x 10^() Возведение в степень по основанию 10 ex exp() Возведение в степень числа Эйлера √x sqrt(x) Квадратный корень 3√x sqrt3(x) Корень 3-ей степени y√x sqrt(x,y) Извлечение корня log2x log2(x) Двоичный логарифм log log(x) Десятичный логарифм ln ln(x) Натуральный логарифм logyx log(x,y) Логарифм I / II Сворачивание/Вызов дополнительных функций Unit Конвертер величин Matrix Матрицы Solve Уравнения и системы уравнений изображение графика Построение графиков * mod mod Деление с остатком * ! ! Факториал * i / j i / j Мнимая единица * Re Re() Выделение целой действительной части * Im Im() Исключение действительной части * |x| abs() Модуль числа * Arg arg() Аргумент функции * nCr ncr() Биноминальный коэффициент * gcd gcd() НОД * lcm lcm() НОК * sum sum() Суммарное значение всех решений * fac factorize() Разложение на простые множители * diff diff() Дифференцирование * Deg Градусы * Rad Радианы Теперь, когда вам понадобится калькулятор, приходите на сайт и используйте бесплатный научный калькулятор.

Построение графиков функций с помощью графической системы Desmos.Com/Calculator — Математика — Каталог статей

   Графики функций — одна из основных тем школьного курса алгебры. Умение строить графики как по точкам, так и с помощью геометрических преобразований является обязательным для каждого ученика средней школы.

   В данной статье пойдет речь о том, как учителю с помощью компьютера и сети Интернет облегчить ученикам задачу восприятия материала, связанного с графиками функций в любом классе.

    Содержание

---

«Графический калькулятор» Desmos

   Чтобы запустить систему построения графиков, необходимо просто зайти на страничку http://desmos.com/calculator. Система будет работать только в режиме онлайн, т.е. без Интернета ее использовать будет невозможно. Вот так выглядит приветственное окно системы для построения графиков Desmos:

Рис. 1. Приветственное окно системы

   Нажав на большую зеленую кнопку Start Fresh, можно строить график «с чистого листа». Если Вы нажмете на один из трех квадратиков ниже, Вы сможете просмотреть пример построения графиков функций, изображенных на них.

   Внимание! Для того, чтобы система у Вас запустилась и работала, необходимо, чтобы FlashPlayer был установлен в качестве плагина к Вашему браузеру. Иначе просто появится надпись «Flash Required» с иконкой Adobe Flash.

    После нажатия Start Fresh окно графического калькулятора будет выглядеть так:

Рис. 2. Окно системы Desmos для построения графиков функций

   Окно будет содержать в верхней части кнопки Undo (отменить последнее действие), Redo (повторить последнее действие), Clear (очистить все графики), Save and share (сохранить и опубликовать), Examples (примеры), Graph Settings (графические настройки).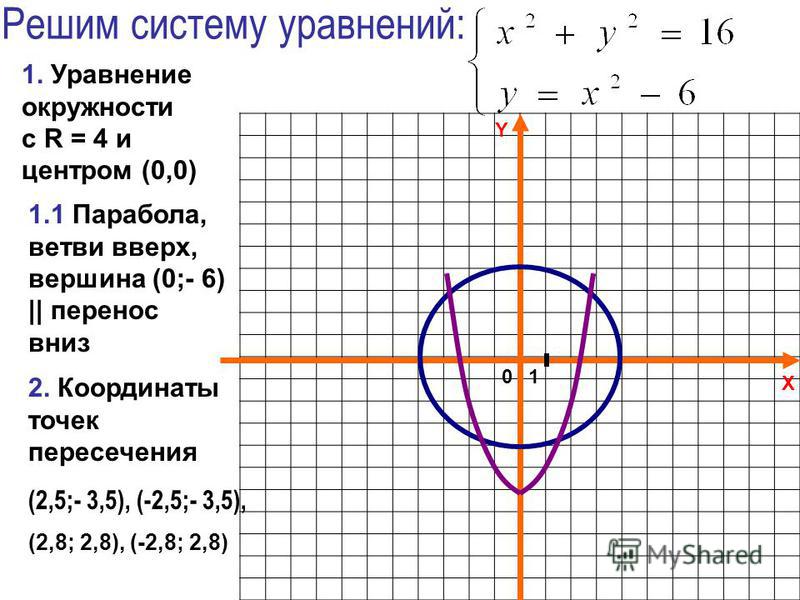

   В правой части находится панель для ввода уравнений (функций), графики которых будут построены затем в области построения (то бишь на координатной плоскости). Область построения занимает большую часть экрана.

   Чтобы изменить масштаб области построения, просто установите на нее курсор мыши, а затем подвигайте колесиком в ту или иную сторону.

   Чтобы переместить область построения, просто захватите ее мышью и протащите.

---

Построение графика функции

   Для того, чтобы построить график, необходимо воспользоваться полем для ввода функций (уравнений). Три важных совета:

   1. Вставлять уравнение в поле ввода не получится. Можно только вводить вручную.

   2. Символы y, x и другие должны набираться в английской раскладке клавиатуры. Вообще, данная система построения графиков англоязычная, но она очень проста для понимания.

   3. (комбинация клавиш Shift+6). Курсор автоматически перейдет в верхний регистр.

   Чтобы ввести основание логарифма (например, функцию y=log_0.5x), введите символ «_» (подчеркивания). Курсор автоматически перейдет в нижний регистр.

   Чтобы ввести модуль, используйте символ | (как обычно).

   Вот пример построенных графиков функций и уравнений в системе Desmos:

Рис. 3. Примеры построенных графиков в системе Desmos

---

Точки экстремума и нули функции

   Если просто навести мышью на любую точку уже построенного графика, то высветятся ее координаты. А к точкам экстремума и нулям функции курсор мышки вообще «примагничивается»:

Рис. 4. Точка максимума функции y=sin x (на нее навели мышкой)

   Внимание! Для того, чтобы при наведении мыши на график показывались координаты точек, этот самый график нужно предварительно выделить, то есть просто щелкнуть мышью по самой линии графика.

---

Демонстрация геометрических преобразований
графиков функций

   Система Desmos позволяет строить графики функций, которые содержат параметр. Например, можно в поле ввода ввести примерно следующее: y=(x — a)². Вместо а может стоять любая буква, и функция может содержать несколько параметров, например, y=k(x — a)²+b. При незаданном значении а график не построится, однако если вслед за этим ввести что-то типа а=5, то график будет построен при этом значении параметра (см. рис.5):

Рис. 5. Построение графика функции с параметром

   Как же можно демонстрировать геометрические преобразования графиков? Дело в том, что значение параметра а можно изменять. Если присмотреться, то снизу надписи «а=5» появляется ползунок под названием «adjust a«:

Рис. 6. Изменение параметра

   Так вот, если плавно перемещать ползунок в любую сторону, то график функции, уже построенный в координатной плоскости, начнет перемещаться вместе с ним (попробуйте!) Это дает возможность наглядной демонстрации различных геометрических преобразований графиков (особенно в сочетании с различными цветами):

Рис.7. Демонстрация геометрических преобразований

   Таким образом можно продемонстрировать геометрические преобразования графиков любых функций

школьного курса математики.

---

Как отметить точки и построить график по точкам

   Чтобы отметить точку на координатной плоскости, можно просто ввести ее координаты x и y в скобках через запятую. В одном поле ввода можно ввести несколько точек. Вот пример того, как можно построить график функции y=sqrt(x), предварительно нанеся точки на координатную плоскость:

Рис. 8. Пример того, как можно отметить точки на координатной плоскости

   Можно сказать, что данный пример иллюстрирует возможность имитации процесса построения графика на бумаге: сначала нанесли точки, а затем только провели график.

   Кстати, чтобы ввести символ квадратного корня, нужно просто набрать комбинацию sqrt(

   А можно просто возвести нужное число в степень 0,5.

---

Сохранение результатов в файл и в виде ссылки

   Система позволяет сохранять построенный график функции в виде графического файла. Вы можете, например, вставить его в свою презентацию или распечатать в качестве раздаточного материала, если не имеете возможности посадить учеников за компьютеры.

   Для сохранения файла нужно воспользоваться кнопкой  которая находится сверху. Внимание! В некоторых браузерах может наблюдаться «глюк», во избежание которого нажимать надо не на надпись «save & share», а на изображение дискеты.

   При нажатии кнопки может появиться ошибка сохранения (timeout). Всё-таки графический калькулятор находится на этапе тестирования. В этом случае — ничего не поделаешь — график сохранить можно только с помощью снимка экрана (то бишь кнопочкой PrintScreen).

   Если же ошибки не возникло, то появится такое окно:

Рис. 9. Окно сохранения построенного графика функции в Desmos

   С помощью этого окна Вы можете:

   1) поделиться Вашим графиком функции в Facebook или Twitter (кнопки Like, Send, Tweet)

   2) поставить на любом сайте ссылку на график функции типа этой (для этого нужно скопировать ссылку из текстового поля и вставить ее в HTML-страницу сайта)

   3) сохранить график функции в виде картинки (для этого нажмите на самую нижнюю ссылку Save graph as image (opens in a new a window), см. рис. 9). Откроется новое окно, в котором отобразится только график построенной Вами функции. Щелкнув правой кнопкой по картинке, можно выбрать команду «Сохранить изображение» (в зависимости от того, каким браузером Вы пользуетесь, название этой команды может отличаться):

Рис. 10. Сохранение графиков функций в виде графического файла

   Таким способом можно делиться ссылками на свои графики, сохранять свои файлы с графиками функций, а также проверять работы учеников (например, ученик может на компьютере построить график и сдать Вам либо ссылку на него, либо распечатанный график, либо график функции в электронном виде).

---

Встроенные примеры построения графиков

   Чтобы лучше понять принципы работы системы, вы можете просмотреть ряд примеров уже построенных графиков. Для этого нужно просто нажать на кнопку . Появится боковая панель, в которой можно будет путем простого нажатия на кнопку посмотреть примеры графиков функций и уравнений. Ниже приводится перевод на русский язык почти всей панели Examples:

Рис. 11. Панель Examples системы построения графиков Desmos

   Рекомендую ознакомиться с панелью Examples и посмотреть примеры построения графиков функций перед началом использования системы для преподавания в учебном заведении.

---

Графические настройки

   Для того, чтобы изменить графические настройки системы, существует кнопка . При нажатии на нее появляется панель графических настроек. Ниже приводится перевод на русский язык элементов управления графической панели:

Рис. 12. Панель графических настроек системы Desmos.Com

   С графическими настройками разобраться в принципе нетрудно, но необходимо прежде, чем использовать Desmos на уроках для демонстрации построения графиков. В следующем разделе отдельным пунктом разбирается важный вопрос графических настроек — как отобразить на осях координат числа (метки), выраженные через число pi.

---

Как сделать, чтобы по осям OX и OY отображались pi-координаты

   Как правило, чтобы построить график тригонометрической функции, по оси ОХ удобно отмечать абсциссы, выраженные через число pi (т.е. pi/2, pi, 3pi/2, 2pi и т.д.). В случае же построения графика обратной тригонометрической функции (арксинус, арккосинус, арктангенс, арккотангенс) бывает удобно отложить ординаты, выраженные через pi.

   Система Desmos позволяет легко эту возможность реализовать. Сначала нужно с помощью кнопки  открыть панель графических настроек (см. предыдущий пункт), а затем в самом низу поставить галочку напротив той оси, на которой нужно отображать pi-метки (см. рис. 13):

Рис. 13. Нижний раздел панели графических настроек — 
отображение pi-меток на осях

   Вот примеры построенных графиков с pi-метками на осях:

Рис. 14. Графики тригонометрических функций с pi-метками на оси ОХ

Рис. 15. Графики обратных тригонометрических функций
y=arcsin x и y=arccos x с pi-метками на оси ОY

---

Немного о keypad’e

   Keypad (англ. — «клавиатура») в системе Desmos — это такая небольшая панель, которая вылезает каждый раз, когда вы пытаетесь ввести уравнение для построения графика или для проведения расчетов. Вот так она выглядит:

Рис. 16. Keypad

   При желании можно пользоваться keypad’ом для ввода различных функций, констант или переменных. Мне лично хватает обычной клавиатуры, так что этой я не пользуюсь.

   Если навести на некоторые кнопки keypad’a мышкой, появляется всплывающая подсказка, которая показывает, что можно ввести с клавиатуры вместо нажатия этой кнопки. Так, вместо нажатия кнопки ln можно ввести с клавиатуры ln( и т.д.

---

Итоги и выводы

   Система Desmos для построения графиков на сегодняшний день является лучшей из тех, что попадались мне на глаза, для применения на уроках в школе. Она позволяет строить графики всех функций и уравнений из школьной программы, включая уравнения с модулем, тригонометрические функции и т.д. Система легко позволяет сохранять графики, в том числе в виде ссылок. Имеется большое количество примеров, по которым можно понять, как пользоваться системой, а также удобный и интуитивно понятный интерфейс управления.

   К некоторым недостаткам для применения в школах стран СНГ можно отнести во-первых, «англоязычность» системы, а во-вторых, «онлайновость». Использовать Desmos можно только в случае, если компьютер или компьютерный класс подключен к Интернету.

   В случае наличия подключенного к Сети компьютерного класса ученики могут строить графики функций самостоятельно. В случае наличия одного компьютера, подключенного к Интернет, имеет смысл задействовать проектор и демонстрировать на нем построение графиков функции по точкам или геометрические преобразования.

Построение графиков функции онлайн бесплатно

Как построить график функции

1. x — это е^х;

тригонометрические функции: синус sin, косинус cos, тангенс tan, котангенс cot. При этом аргумент функции должен обязательно стоять в скобках: sin(x), а не sin x.

обратные тригонометрические функции: арксинус аsin, арккосинус аcos, арктангенс аtan, арккотангенс аcot

модуль числа х обозначается как |x| или abs(x)

Системы линейных уравнений

Системы линейных уравнений (или линейные системы, как их иногда называют) определяются как наборы линейных уравнений, которые используют один и тот же набор переменных. Это означает, что в пределах систем линейных уравнений у вас есть два или более линейных уравнения с одинаковыми переменными. Это пример такой системы:

3x — 5y = 16

х — 3у = 8

В этом примере показана линейная система с двумя уравнениями и двумя переменными.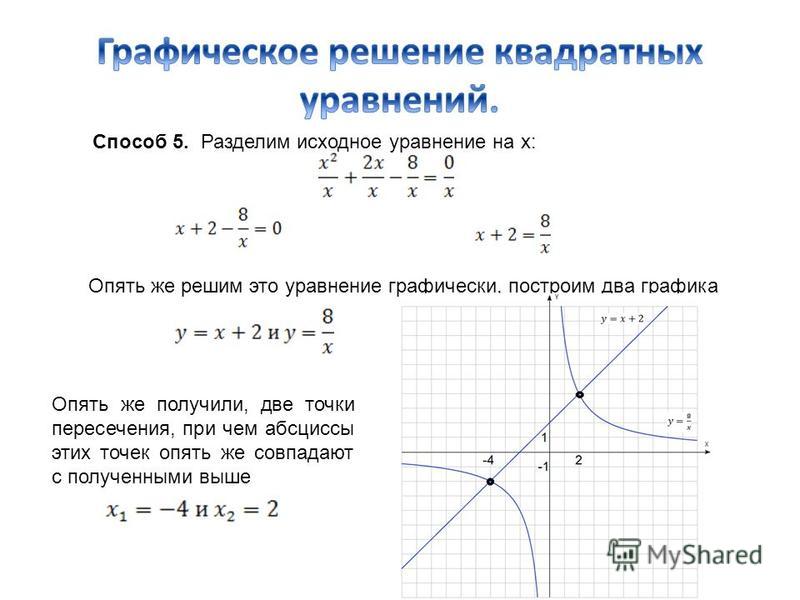 Количество уравнений в системе, как и количество переменных, не ограничено. Но количество решений меняется в зависимости от соотношения уравнений и переменных в системе. Если есть больше переменных, чем уравнений в линейной системе, такая система имеет бесконечно много решений или иногда уникальных разреженных решений. Такая система называется недоопределенной системой . Если в системе одинаковое количество уравнений и переменных, она имеет единственное уникальное решение. Но если в системе линейных уравнений больше уравнений, чем неизвестных, она не имеет решения.Такая система называется переопределенной системой .

Системы линейных уравнений являются важной частью линейной алгебры и играют важную роль в таких науках, как инженерия, физика, экономика, химия и информатика, а также в моделировании сложных систем.

Решение систем линейных уравнений

Существует несколько подходов к решению систем линейных уравнений. Самый простой способ — использовать метод под названием подстановка. Этот метод подходит для простейших типов линейных систем, и мы будем использовать этот метод для решения указанной выше системы.

Первый шаг, который вам нужно выполнить при использовании подстановки, — это решить одно из уравнений для, скажем, x в терминах y . Мы сделаем это со вторым уравнением, так как оно имеет только одно x .

х — 3у = 8

х = 8 + 3у

Теперь мы вставляем выражение для x в верхнее уравнение:

3 * (8 + 3y) — 5y = 16

24 + 9лет + -5лет = 16

17лет = 16–24

4y = -8 |: 4

г = -2

После этого мы просто вставляем значение y в любое из данных уравнений, и у нас будет значение x и координаты решения.Итак, давайте вставим значение x во второе уравнение:

х — 3 * (- 2) = 8

х + 6 = 8

х = 8–6

х = 2

Координаты решения: (2, -2).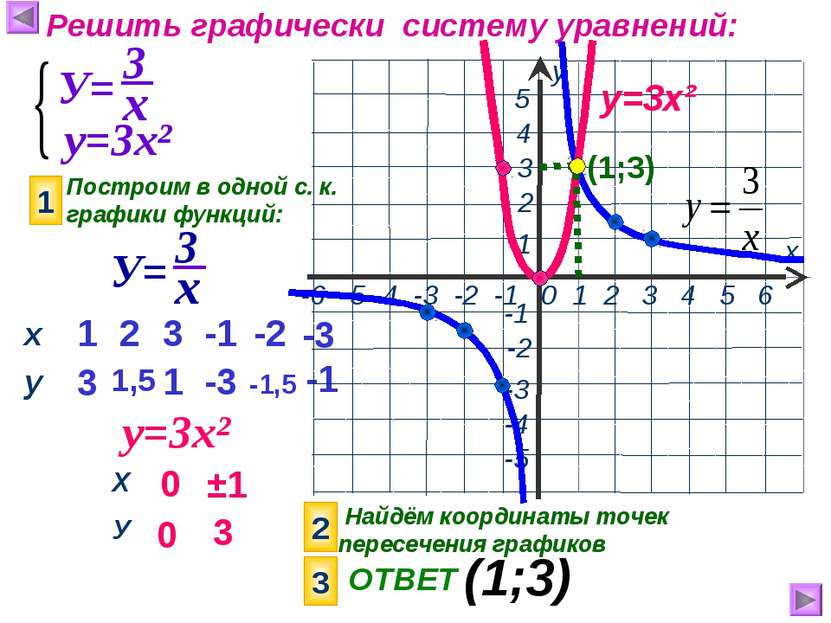 Решение — это единственная точка, в которой две линии (которые являются визуальным представлением данных уравнений в системе координат) пересекаются друг с другом.

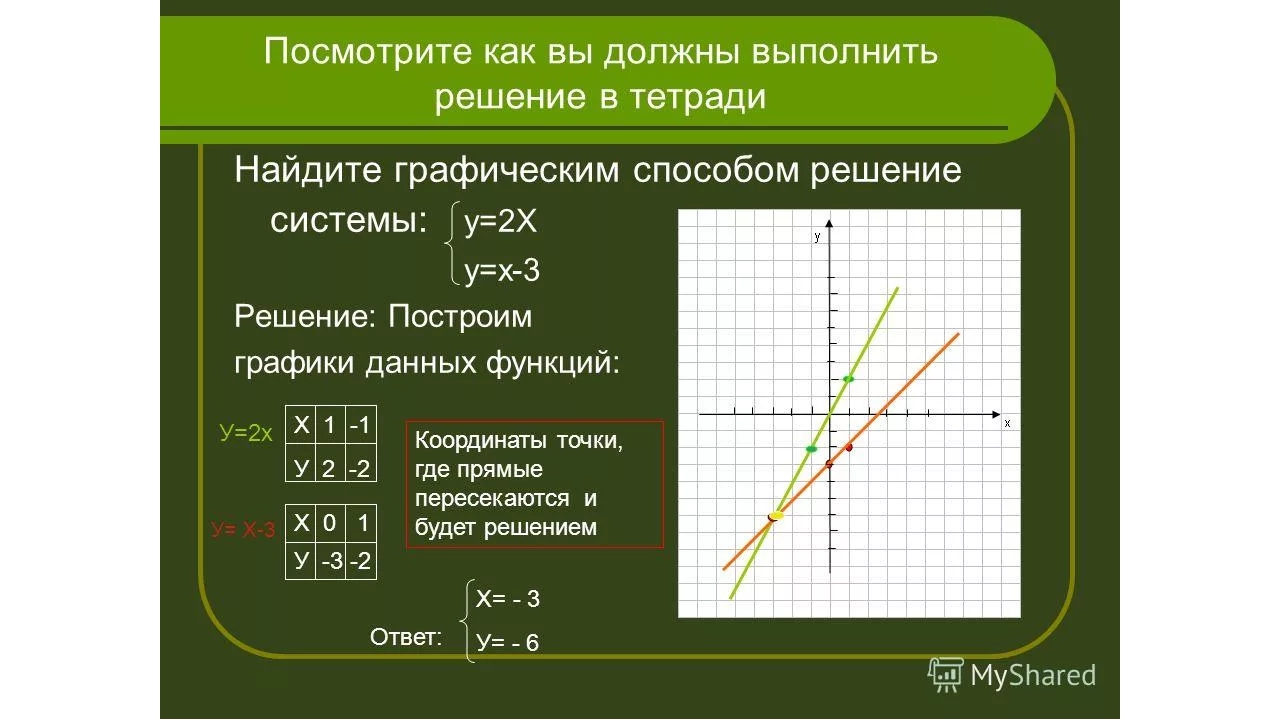
Построение графика системы линейных уравнений

Решение системы линейных уравнений может быть определено графически.Единственное, что вам нужно сделать, это нарисовать линии на основе заданных уравнений, а затем визуально определить точку, в которой линии пересекаются. Вы можете научиться делать это, щелкнув ссылку на нашу статью о построении графиков линейных уравнений.

Если вы хотите попрактиковаться в решении и построении графиков систем линейных уравнений, воспользуйтесь приведенными ниже таблицами по математике.

Графические системы линейных уравнений экзаменов для учителей

Название экзамена	Размер файла	Загрузки	Дата загрузки
Графические системы линейных уравнений
Графические системы линейных уравнений — Стандарт — очень просто	833. 1 кБ	10645	3 сентября 2019 г.
Графические системы линейных уравнений — Стандарт — easy	895.8 Кбайт	7886	3 сентября 2019 г.
Графические системы линейных уравнений — Стандарт — среда	809.8 Кбайт	9836	3 сентября 2019 г.
Графические системы линейных уравнений — Стандарт — Жесткий	464.2 Кбайт	5633	3 сентября 2019 г.
Графические системы линейных уравнений — Стандартные — очень сложные	464.3 кБ	4165	3 сентября 2019 г.
Графические системы линейных уравнений — наклон / пересечение — очень просто	833.1 Кбайт	10645	3 сентября 2019 г.
Графические системы линейных уравнений — наклон / пересечение — easy	895. 8 Кбайт	7886	3 сентября 2019 г.
Графические системы линейных уравнений — наклон / пересечение — средний	846 Кбайт	5084	3 сентября 2019 г.
Графические системы линейных уравнений — Наклон / Пересечение — жесткий	464.5 кБ	3814	3 сентября 2019 г.
Графические системы линейных уравнений — наклон / пересечение — очень сложно	464.6 Кбайт	3202	3 сентября 2019 г.
Системы линейных уравнений
Системы линейных уравнений — очень просто	461.3 Кбайт	7388	3 сентября 2019 г.
Системы линейных уравнений — easy	461.8 кБ	7320	3 сентября 2019 г.
Системы линейных уравнений — среда	462. 2 Кбайт	11117	3 сентября 2019 г.
Системы линейных уравнений — жесткие	462.4 Кбайт	8200	3 сентября 2019 г.
Системы линейных уравнений — очень сложные	462.7 Кб	7863	3 сентября 2019 г.

Графические системы рабочих листов линейных уравнений для студентов

Программное обеспечение для научного построения графиков, подбора нелинейных кривых, подбора нескольких пиков и анализа данных для ученых и инженеров

MagicPlot Поделиться этой страницей: Посетите нашу страницу в Facebook

Легкое приложение для анализа данных, построения графиков и нелинейной аппроксимации Подгонка нелинейной кривой Введите уравнение, визуально измените диапазон данных и выполнить подгонку. MagicPlot подтвержден с помощью Наборы данных NIST для тестирования алгоритмов подгонки. Импорт данных смарт-текста Используйте пункт меню «Импортировать текстовую таблицу», чтобы открыть свой . данные, сохраненные в текстовых файлах. Разделители столбцов и десятичные разделители распознаются автоматически. Многопиковый фитинг Наслаждайтесь созданием модели подгонки по часам и перемещение пиков и базовой линии с помощью мыши. Вычтите несколько пиков, чтобы увидеть остаток. Полностью настраиваемые графики Вы можете свободно изменять стиль кривой и стиль осей с помощью панели инструментов инспектора. Сюжеты журнального качества банка сохраняться в векторных форматах: EPS, PDF, SVG, EMF. Основной математический анализ Сглаживание, БПФ, интегрирование, дифференцирование, гистограммы, свертки, алгоритмы корреляции включены в меню «Обработка». Easy Data Exploration Исследуйте скрытые детали вашего участка с помощью навигации инструменты: Колесо мыши с Shift / Ctrl изменяет масштаб и прокручивает. Также доступен ручной инструмент. Пакетная обработка Самый простой способ обработать и уместить несколько данные точно так же, без скриптов.Фитинг результатов серии в сводной таблице параметров. Шаблоны стилей Отформатируйте одну фигуру и сохраните шаблон. Этот шаблон можно использовать для форматирования всего вашего цифры, включая названия и масштаб четных осей. Многоуровневая отмена и возврат Эксперимент с параметрами обработки данных, стили графика и нелинейная подгонка, зная, что вы можете отменить все и просмотреть историю. Для Windows, Mac OS X, Linux Запустите MagicPlot в любой операционной системе, в которой используется членами вашей рабочей группы. Бесплатно обмениваться проектами между различными ОС. Итак, что можно сделать с помощью MagicPlot? Рисунок из: Чербунин Р.В. et al. , Phys.Ред. B 84 , 041304 (R) (2011) © 2011 Американское физическое общество. Опубликовано с разрешения. MagicPlot — это все, что вам нужно от программы для повседневного построения графиков , но она работает быстрее и умнее «Еще одна привлекательность — очень чистый, понятный, легкий в освоении графический интерфейс, не вызывающий особых затруднений. Сама программа быстрая, отзывчивая и легкая. MagicPlot хорошо оборудован для быстрого исследования, с воплощением идей так быстро, как задумано.Инструменты хорошо реализованы и удивительно просты ». Из обзора MagicPlot Феликса Гранта в журнале Scientific Computing World Загрузите вашу версию MagicPlot С удовольствием исследуйте! © 2020 Magicplot Systems, LLC. | Конфиденциальность (мы используем файлы cookie) | сроки

Символическое решение системы уравнений: ключевое слово «Решить»

Примеры символьного расчета / 153

Mathcad вставляет результат справа от символа «→.Обратите внимание: если переменная была возведена в квадрат в исходном уравнении, вы можете получить обратно два результата, отображаемых в виде вектора.

На Рис. 13-10 показан пример.

Рисунок 13-10: Решение уравнений и поиск корней. При нахождении корней необязательно устанавливать выражение равным 0.

Совет Другой способ найти переменную — щелкнуть переменную, для которой вы хотите найти, и выбрать

Переменная> Решить в меню «Символика».

Одним из способов символического решения системы уравнений является использование того же ключевого слова решения, которое используется для решения одного уравнения с одним неизвестным.Чтобы решить систему из n уравнений относительно n неизвестных:

1. Наберите [Ctrl] M, чтобы создать вектор, содержащий n строк и 1 столбец.

2. Заполните каждый заполнитель вектора одним из n уравнений, составляющих систему. Убедитесь, что вы набрали [Ctrl] [=], чтобы ввести логический знак равенства.

3. Наберите [Ctrl] [Shift] [.] (Точка).

4. Введите решение и поставьте запятую в поле слева от символического знака равенства «→».

5. Наберите [Ctrl] M, чтобы создать вектор из n строк и 1 столбца.Затем введите переменные, которые вы решаете.

6. Нажмите [Enter].

Mathcad отображает n решений системы уравнений справа от символического знака равенства.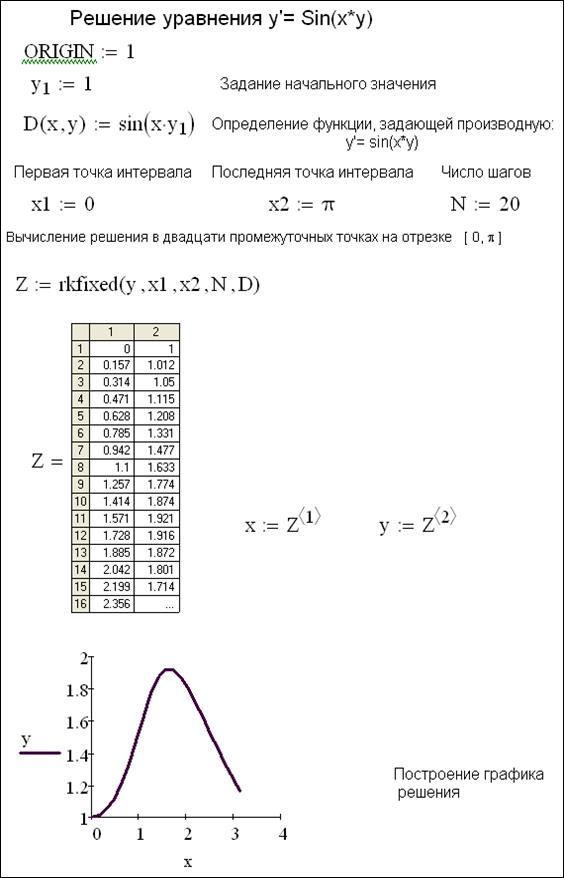 На рисунке 13-11 показан пример.

154 / Глава 13 Символьные вычисления

Используйте ключевое слово решения, нажав [Ctrl] [Shift] [.] (Точка)

Использование решающего блока. (Используйте [Ctrl] [=], чтобы ввести знак равенства.)

Рисунок 13-11: Два метода символьного решения системы уравнений.

Символическое решение системы уравнений: блок решения

Еще один способ символьного решения системы уравнений — использовать блок решения, аналогичный числовому блоку решения:

1. Введите слово «Дано» в математической области, указав, что далее следует система уравнений. Вы можете набирать Given в любой комбинации заглавных и строчных букв и любым шрифтом.

2. Введите уравнения под словом Дано. Обязательно введите [Ctrl] [=] в качестве логического знака равенства.

3. Введите функцию поиска с аргументами, соответствующими вашей системе уравнений. Эта функция описана в разделе «Решение и оптимизация линейных / нелинейных систем» на странице 104.

4. Нажмите [Ctrl] [.] (Точка). Mathcad отображает символический знак равенства «→».

5. Нажмите [Enter].

Mathcad отображает решения системы уравнений справа от символического знака равенства. На рисунке 13-11 показан пример.

Большинство рекомендаций для блоков численного решения, описанных ранее, применимы к символьному решению систем уравнений.Основное отличие состоит в том, что когда вы решаете уравнения символически, вы не вводите предполагаемые значения для решений.

Манипуляции с символической матрицей

Вы можете использовать Mathcad для поиска символьного транспонирования, инверсии или определителя матрицы с помощью встроенного оператора и символьного знака равенства. Чтобы найти транспонирование матрицы, например:

1. Поместите всю матрицу между двумя линиями редактирования, щелкнув [Пробел] один или несколько раз.

2. Нажмите [Ctrl] 1, чтобы вставить оператор транспонирования матрицы.

Примеры символьных вычислений / 155

3. Нажмите [Ctrl] [.] (Точка) для символьного знака равенства «→.»

4. Нажмите [Enter].

Mathcad возвращает результат справа от «→». На рис. 13-12 показано несколько примеров.

Рисунок 13-12: Операции с символической матрицей: транспонирование матрицы, поиск обратного и определение определителя.

Вы также можете найти транспонирование, инверсию или определитель матрицы, используя команды «Матрица» в меню «Символика».

Математические уравнения — EqWorld

Главный редактор Полянин Андрей Дмитриевич Мы желаем вам и вашей семье чудесного Рождества и счастливого, Здорового и успешного Нового 2021 года! Редакция журнала Александр В. Аксенов, Россия Джордж Блюман, Канада Франческо Калоджеро, Италия Питер А. Кларксон, Великобритания Роберт Конте, Франция Питер Г. Лич, Южная Африка Николай А. Кудряшов, Россия Уиллард Миллер, США Анатолий Г. Никитин, Украина Уильям Э. Шиссер, США Алексей И. Журов, Россия / Великобритания Даниэль И. Цвиллинджер, США Уравнения играют решающую роль в современной математике и образуют основа для математического моделирования многочисленных явлений и процессов в наука и техника. Международный научно-образовательный сайт EqWorld представляет обширную информация о решениях для различных классов обыкновенный дифференциал, частный дифференциал, интеграл, функциональный и другие математические уравнения.Он также описывает некоторые методы решения уравнений, включает интересные статьи, дает ссылки на математические веб-сайты и пакеты программного обеспечения, перечисляет полезные справочники и монографии, а также ссылки на научные издательства, журналы и т. д. включает динамический раздел Equation Archive, который позволяет авторам для быстрой публикации своих уравнений (дифференциальных, интегральных и др.) а также точные решения, первые интегралы и преобразования. Сайт EqWorld предназначен для исследователи, преподаватели университетов, инженеры и студенты со всего мира.Это содержит около 2000 веб-страниц, и их посещают более 3000 пользователей в день (из 200 стран мира). Все ресурсы, представленные на этом сайте, бесплатны для его пользователей. » Требуется решение обобщенного интегрального уравнения Абеля второго своего рода? Поставлен в тупик уравнением ФитцХью-Нагумо, которое может описывать теплопередачу а напряжение на клеточной мембране? Проверьте EqWorld … EqWorld собирает решения, которые были найдены в справочниках, журналах, и другие источники.На сайте представлены обыкновенные уравнения и уравнения в частных производных … » Наука, 2005 г. , том 308, выпуск 5727, стр. 1387 » … EqWorld предоставляет общие решения многих типов уравнений, которые ученые и инженеры наверняка столкнутся. На сайте также есть статьи и списки чтения. » Physics Today, июль 2005 г., стр. 35 Вам может быть интересно: А.Д. Полянин , г. Функциональное разделение переменных в нелинейных УЧП: общий подход, новые решения уравнений диффузионного типа, Математика , 2020, Vol. 8, №1, 90. А.Д. Полянин , Сравнение эффективности различных методов построения точных решений нелинейных уравнений в частных производных. Обобщения и новые решения, Математика , 2019, Т. 7, № 5, 386. Последнее обновление сайта: 9 января 2020 г.

Искать EqWorld

.