Построение с Matplotlib
Введение
Примеры
Простой сюжет в Matplotlib
Этот пример показывает , как создать простую синусоидальную кривую с использованием Matplotlib
# Plotting tutorials in Python # Launching a simple plot import numpy as np import matplotlib.pyplot as plt # angle varying between 0 and 2*pi x = np.linspace(0, 2.0*np.pi, 101) y = np.sin(x) # sine function plt.plot(x, y) plt.show()
Добавление дополнительных функций к простому графику: метки оси, заголовок, метки оси, сетка и легенда
В этом примере мы берем график с синусоидой и добавляем к нему больше функций; а именно заголовок, метки оси, заголовок, метки оси, сетка и легенда.
# Plotting tutorials in Python # Enhancing a plot import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2.0*np.pi, 101) y = np.sin(x) # values for making ticks in x and y axis xnumbers = np.linspace(0, 7, 15) ynumbers = np.linspace(-1, 1, 11) plt.plot(x, y, color='r', label='sin') # r - red colour plt.xlabel("Angle in Radians") plt.ylabel("Magnitude") plt.title("Plot of some trigonometric functions") plt.xticks(xnumbers) plt.yticks(ynumbers) plt.legend() plt.grid() plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend] plt.show()
Создание нескольких графиков на одной фигуре путем наложения, аналогичного MATLAB
В этом примере кривая синуса и кривая косинуса изображены на одном рисунке путем наложения графиков друг на друга.
# Plotting tutorials in Python
# Adding Multiple plots by superimposition
# Good for plots sharing similar x, y limits
# Using single plot command and legend
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.0*np.pi, 101)
y = np.sin(x)
z = np.cos(x)
# values for making ticks in x and y axis
xnumbers = np.linspace(0, 7, 15)
ynumbers = np.linspace(-1, 1, 11)
plt.plot(x, y, 'r', x, z, 'g') # r, g - red, green colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt. title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend(['sine', 'cosine'])
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend(['sine', 'cosine'])
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
Создание нескольких графиков на одном рисунке с использованием наложения графиков с отдельными командами графиков
Как и в предыдущем примере, здесь кривая синуса и косинуса строится на одном и том же рисунке с использованием отдельных команд построения. Это более Pythonic и может быть использовано для получения отдельных маркеров для каждого сюжета.
# Plotting tutorials in Python # Adding Multiple plots by superimposition # Good for plots sharing similar x, y limits # Using multiple plot commands # Much better and preferred than previous import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2.0*np.pi, 101) y = np.sin(x) z = np.cos(x) # values for making ticks in x and y axis xnumbers = np.linspace(0, 7, 15) ynumbers = np.linspace(-1, 1, 11) plt.plot(x, y, color='r', label='sin') # r - red colour plt.plot(x, z, color='g', label='cos') # g - green colour plt.xlabel("Angle in Radians") plt.ylabel("Magnitude") plt.title("Plot of some trigonometric functions") plt.xticks(xnumbers) plt.yticks(ynumbers) plt.legend() plt.grid() plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend] plt.show()
Графики с общей осью X, но с другой осью Y: с использованием twinx ()
В этом примере мы построим синусоидальную и гиперболическую синусоидальные кривые на одном графике с общей осью X, имеющей разные оси Y. Это достигается за счет использования команды TwinX ().
# Plotting tutorials in Python # Adding Multiple plots by twin x axis # Good for plots having different y axis range # Separate axes and figure objects # replicate axes object and plot curves # use axes to set attributes # Note: # Grid for second curve unsuccessful : let me know if you find it! :( import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 2.0*np.pi, 101) y = np.sin(x) z = np.sinh(x) # separate the figure object and axes object # from the plotting object fig, ax1 = plt.subplots() # Duplicate the axes with a different y axis # and the same x axis ax2 = ax1.twinx() # ax2 and ax1 will have common x axis and different y axis # plot the curves on axes 1, and 2, and get the curve handles curve1, = ax1.plot(x, y, label="sin", color='r') curve2, = ax2.plot(x, z, label="sinh", color='b') # Make a curves list to access the parameters in the curves curves = [curve1, curve2] # add legend via axes 1 or axes 2 object. # one command is usually sufficient # ax1.legend() # will not display the legend of ax2 # ax2.legend() # will not display the legend of ax1 ax1.legend(curves, [curve.get_label() for curve in curves]) # ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid # Global figure properties plt.title("Plot of sine and hyperbolic sine") plt.show()
Графики с общей осью Y и другой осью X с использованием twiny ()
В этом примере, график с кривыми , имеющими общую ось ординат , но разные оси х продемонстрирована с использованием метода 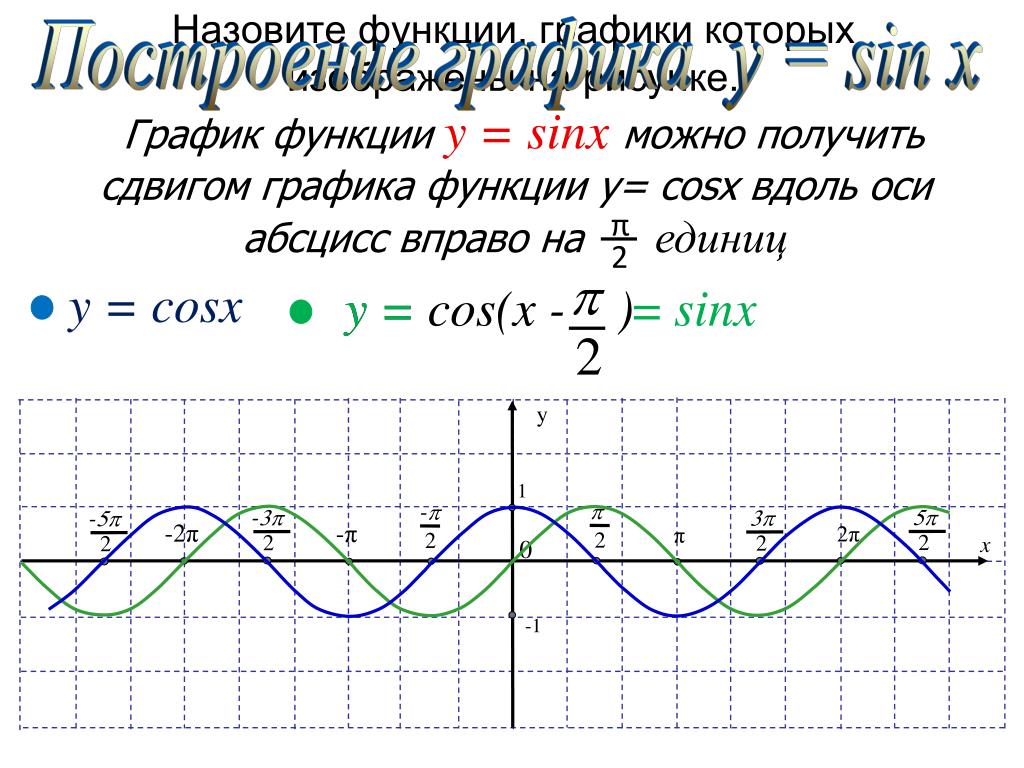 Кроме того, некоторые дополнительные функции, такие как заголовок, легенда, метки, сетки, метки осей и цвета, добавляются к графику.
Кроме того, некоторые дополнительные функции, такие как заголовок, легенда, метки, сетки, метки осей и цвета, добавляются к графику.
# Plotting tutorials in Python # Adding Multiple plots by twin y axis # Good for plots having different x axis range # Separate axes and figure objects # replicate axes object and plot curves # use axes to set attributes import numpy as np import matplotlib.pyplot as plt y = np.linspace(0, 2.0*np.pi, 101) x1 = np.sin(y) x2 = np.sinh(y) # values for making ticks in x and y axis ynumbers = np.linspace(0, 7, 15) xnumbers1 = np.linspace(-1, 1, 11) xnumbers2 = np.linspace(0, 300, 7) # separate the figure object and axes object # from the plotting object fig, ax1 = plt.subplots() # Duplicate the axes with a different x axis # and the same y axis ax2 = ax1.twiny() # ax2 and ax1 will have common y axis and different x axis # plot the curves on axes 1, and 2, and get the axes handles curve1, = ax1.plot(x1, y, label="sin", color='r') curve2, = ax2.plot(x2, y, label="sinh", color='b') # Make a curves list to access the parameters in the curves curves = [curve1, curve2] # add legend via axes 1 or axes 2 object. # one command is usually sufficient # ax1.legend() # will not display the legend of ax2 # ax2.legend() # will not display the legend of ax1 # ax1.legend(curves, [curve.get_label() for curve in curves]) ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid # x axis labels via the axes ax1.set_xlabel("Magnitude", color=curve1.get_color()) ax2.set_xlabel("Magnitude", color=curve2.get_color()) # y axis label via the axes ax1.set_ylabel("Angle/Value", color=curve1.get_color()) # ax2.set_ylabel("Magnitude", color=curve2.get_color()) # does not work # ax2 has no property control over y axis # y ticks - make them coloured as well ax1.tick_params(axis='y', colors=curve1.get_color()) # ax2.tick_params(axis='y', colors=curve2.get_color()) # does not work # ax2 has no property control over y axis # x axis ticks via the axes ax1.
tick_params(axis='x', colors=curve1.get_color()) ax2.tick_params(axis='x', colors=curve2.get_color()) # set x ticks ax1.set_xticks(xnumbers1) ax2.set_xticks(xnumbers2) # set y ticks ax1.set_yticks(ynumbers) # ax2.set_yticks(ynumbers) # also works # Grids via axes 1 # use this if axes 1 is used to # define the properties of common x axis # ax1.grid(color=curve1.get_color()) # To make grids using axes 2 ax1.grid(color=curve2.get_color()) ax2.grid(color=curve2.get_color()) ax1.xaxis.grid(False) # Global figure properties plt.title("Plot of sine and hyperbolic sine") plt.show()
Синтаксис
Параметры
Примечания
Как найти sin pi/3, и какие пути упрощения этой функции вам известны?
Маруф Убайдуллоева Математика- Ирина Селезнева Математика
Я всегда решаю подобные задачи методом подстановки значения pi, которое равно 180 градусам.
 Если 180
разделить на три, получим результат —
600. Значение синуса 600 по
таблицам функций будет равно корню из
3, деленному на 3. Это и есть решение вашей
задачи.
Если 180
разделить на три, получим результат —
600. Значение синуса 600 по
таблицам функций будет равно корню из
3, деленному на 3. Это и есть решение вашей
задачи. - Елена Бобкова Математика
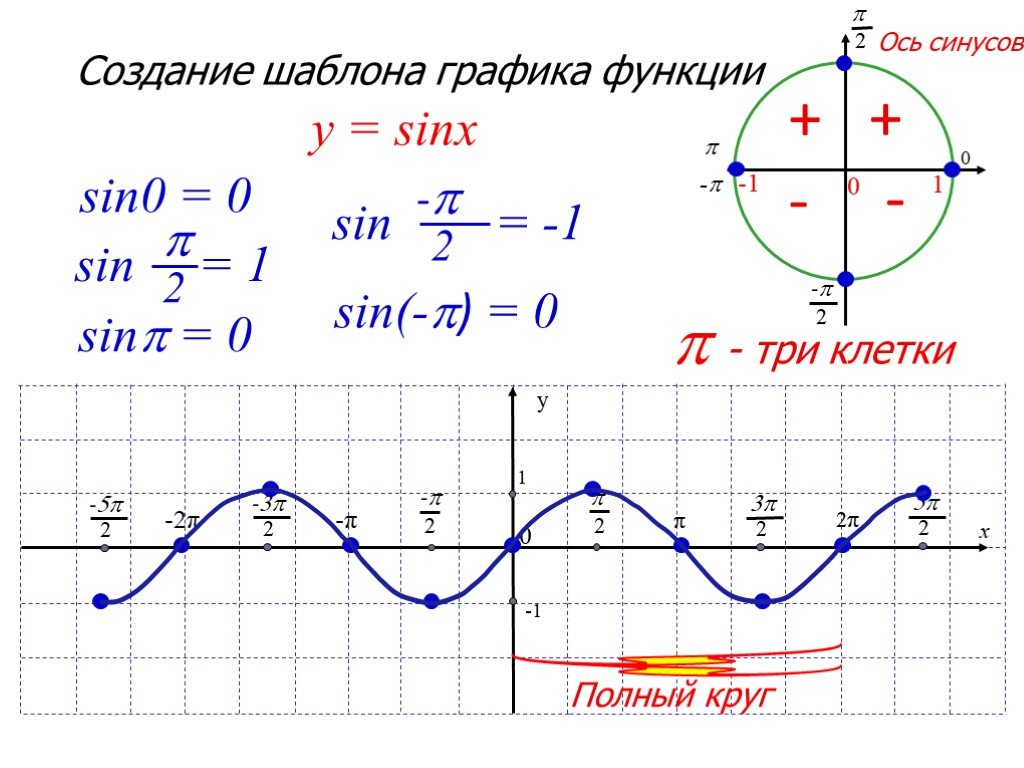
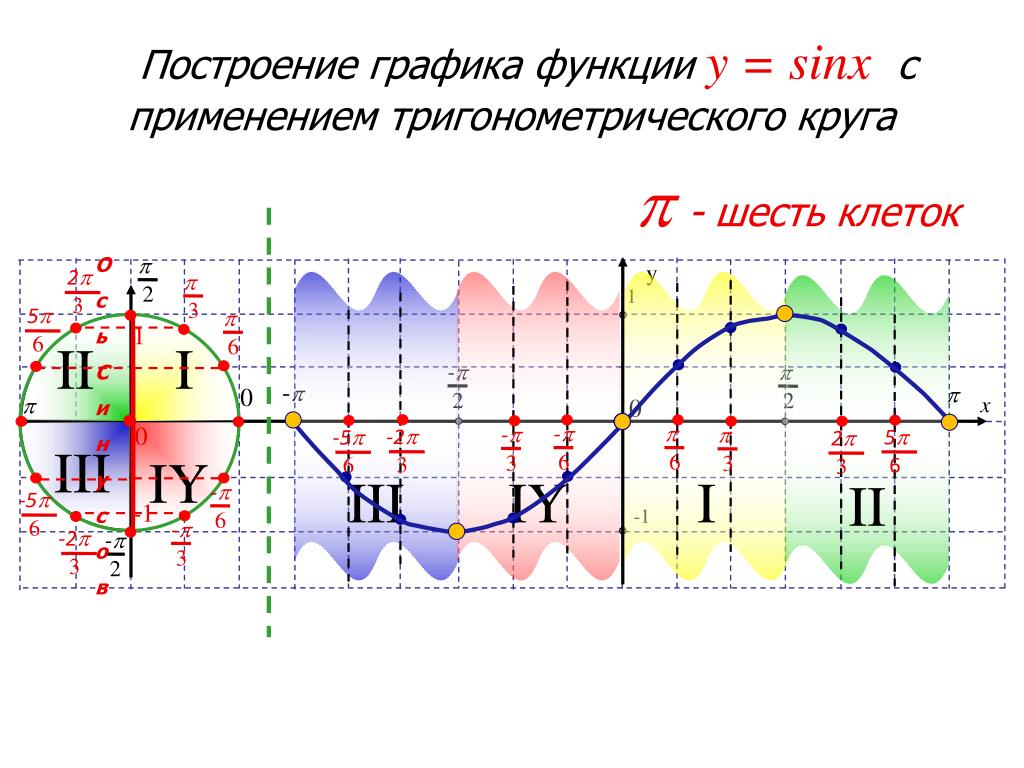
Еще один способ понять суть заданного значения – это построить график синусоиды. На оси синусоиды построенного графика необходимо найти значение, которое будет соответствовать pi/3. Когда вы нашли эту точку, то нужно от точки опустить перпендикуляр к оси Оу. Точка соприкосновения будет равна корню из 3/2, что и отвечает значению синуса pi/3.

- Василий Шариков Математика
Пользуйся калькулятором математическим или введи данные в онлайн калькулятор и получишь необходимый результат. Преимущество онлайн калькулятора – его мобильность.
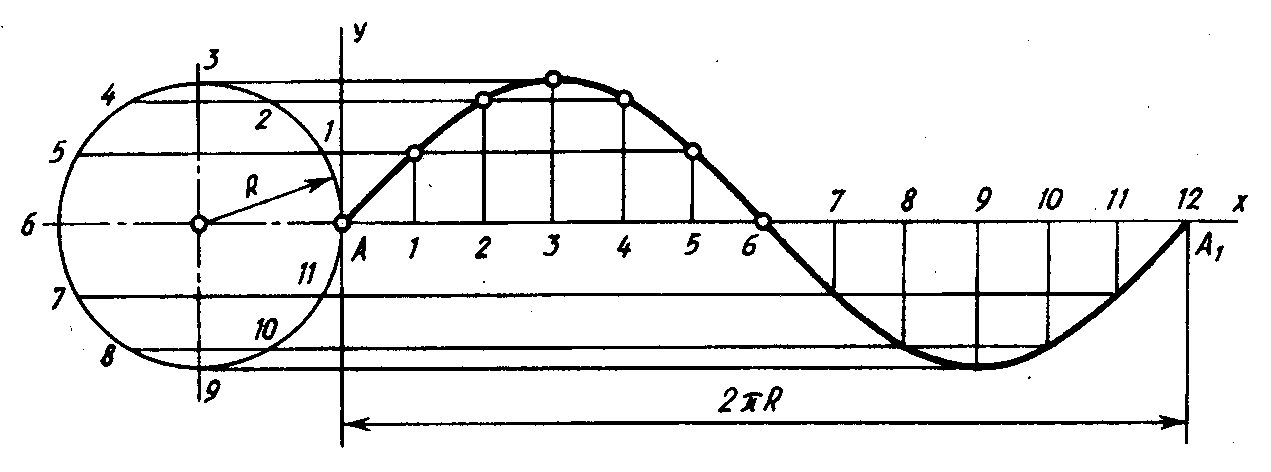
График синусоидальной функции
Горячая математика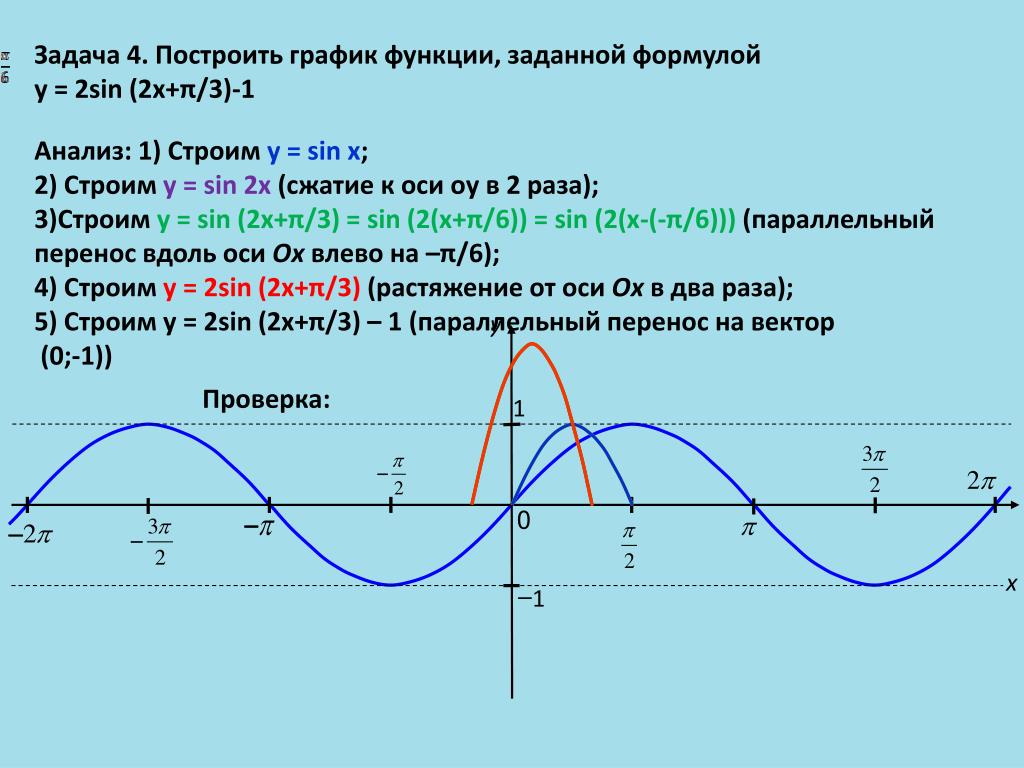 Эта угловая мера может быть либо задана в
градусов
или
радианы
. Здесь мы будем использовать радианы.
Эта угловая мера может быть либо задана в
градусов
или
радианы
. Здесь мы будем использовать радианы.График синус функция у «=» грех ( Икс ) выглядит так:
Свойства функции синуса, у «=» грех ( Икс )Домен : ( − ∞ , ∞ )
Диапазон : [ − 1 , 1 ] или − 1 ≤ у ≤ 1
у -перехват : ( 0 , 0 )
Икс -перехват : н π , где н является целым числом.
Период: 2 π
Непрерывность: непрерывно вкл.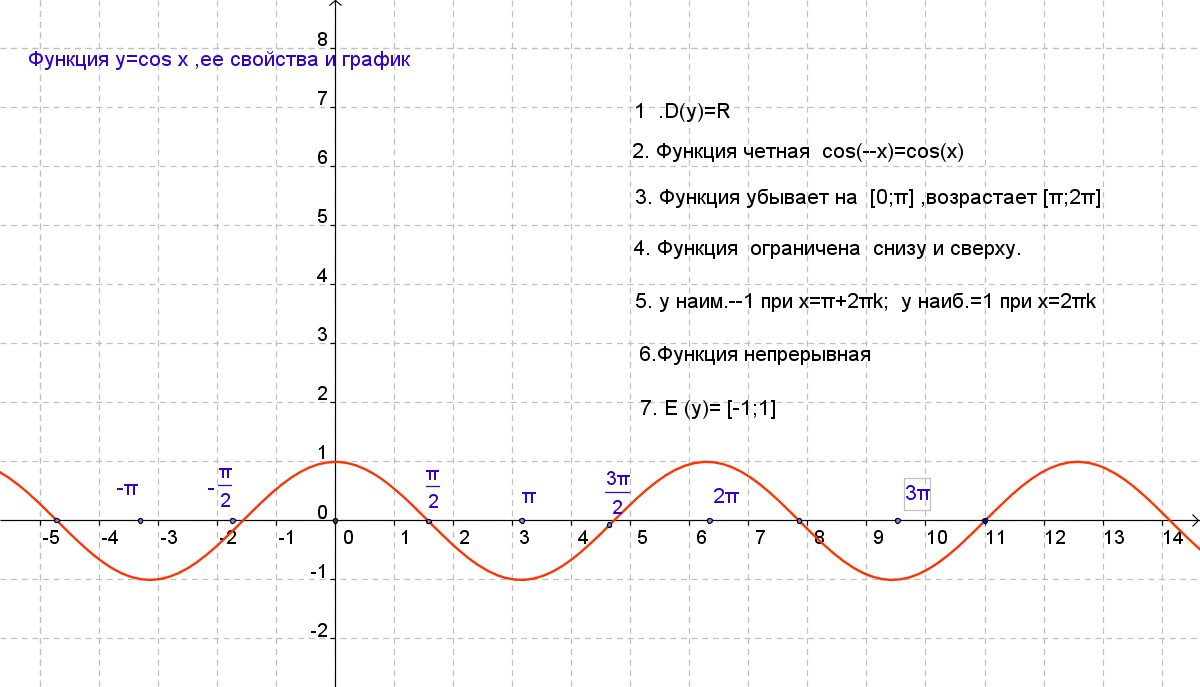 (
−
∞
,
∞
)
(
−
∞
,
∞
)
Симметрия: происхождение (нечетная функция)
Максимальное значение у «=» грех ( Икс ) происходит, когда Икс «=» π 2 + 2 н π , где н является целым числом.
Минимальное значение у «=» грех ( Икс ) происходит, когда Икс «=» 3 π 2 + 2 н π , где н является целым числом.
Амплитуда и период функции «с тех пор»Амплитуда графика у «=» а грех ( б Икс ) это величина, на которую она изменяется выше и ниже Икс -ось.
Амплитуда = | а |
Период синусоидальной функции – это длина кратчайшего интервала на
Икс
-ось, по которой повторяется график.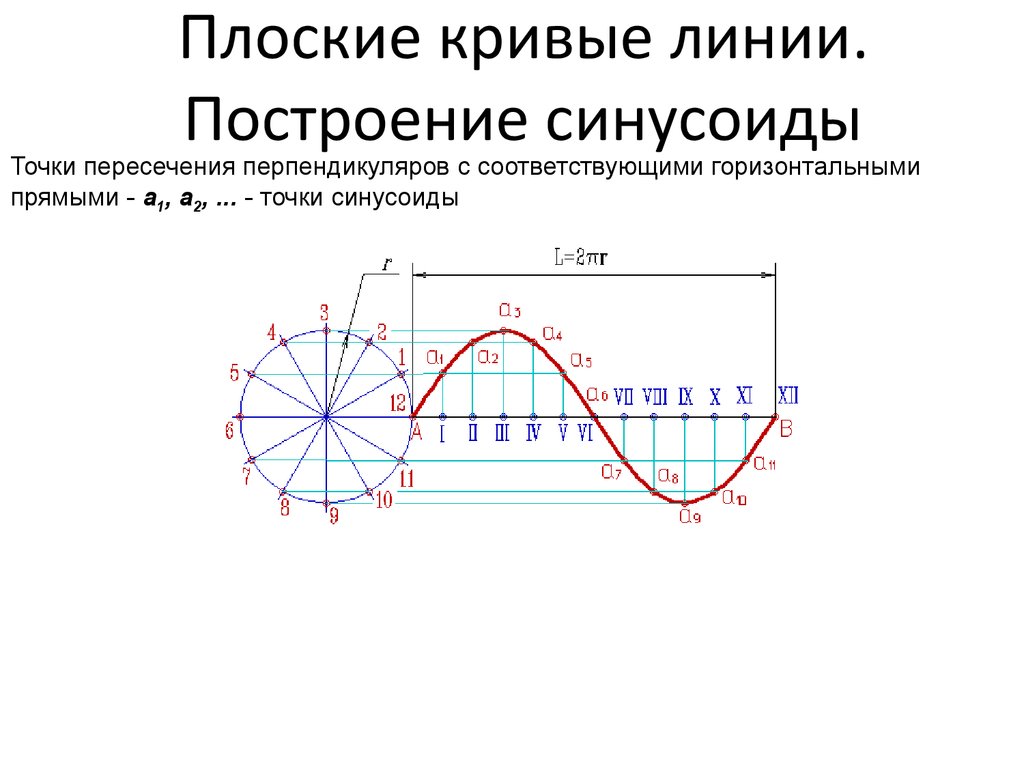
Период = 2 π | б |
Пример:
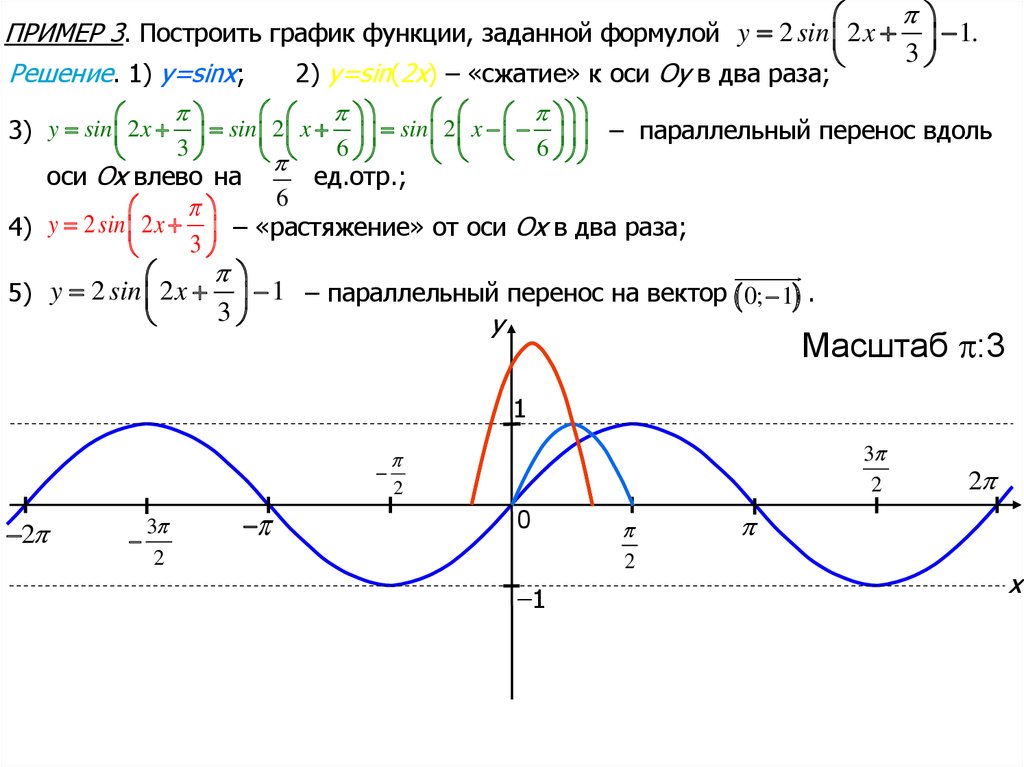
Нарисуйте графики у «=» грех ( Икс ) и у «=» 2 грех ( Икс ) . Сравните графики.
Для функции у «=» 2 грех ( Икс ) , график имеет амплитуду 2 . С б «=» 1 , график имеет период 2 π . Таким образом, он циклически повторяется один раз из 0 к 2 π с одним максимумом 2 , и один минимум − 2 .
Обратите внимание на графики
у
«=»
грех
(
Икс
)
и
у
«=»
2
грех
(
Икс
)
.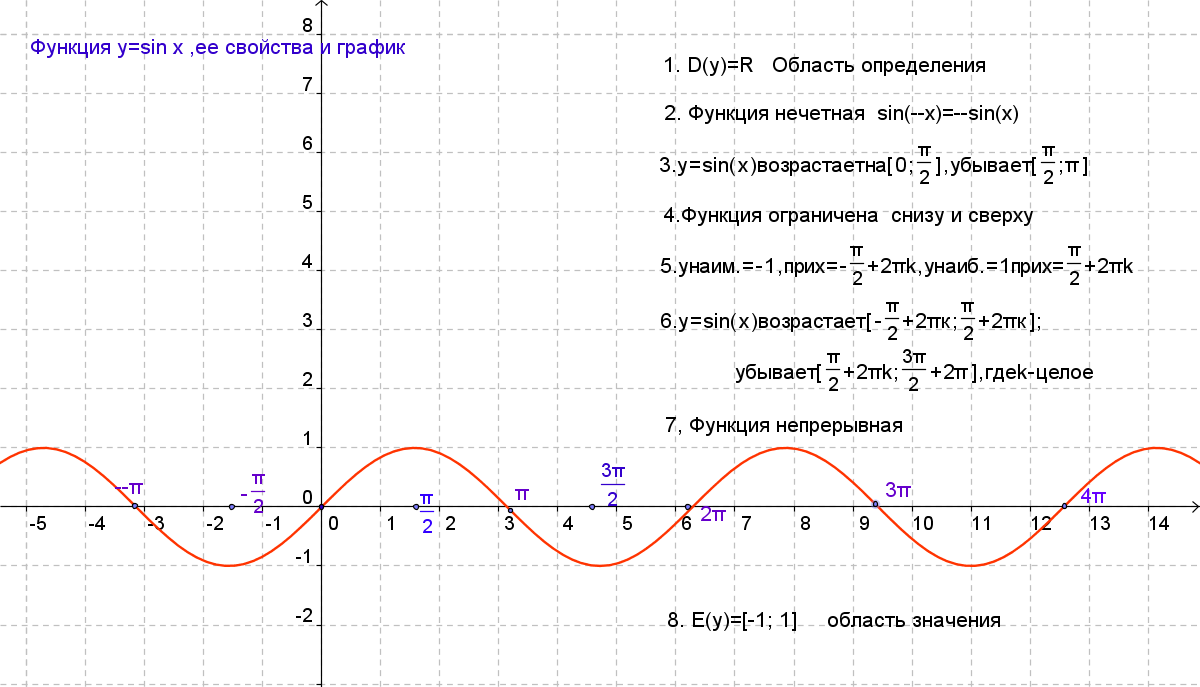 У каждого одинаковые
Икс
— перехватывает, но
у
«=»
2
грех
(
Икс
)
имеет амплитуду, в два раза превышающую амплитуду
у
«=»
грех
(
Икс
)
.
У каждого одинаковые
Икс
— перехватывает, но
у
«=»
2
грех
(
Икс
)
имеет амплитуду, в два раза превышающую амплитуду
у
«=»
грех
(
Икс
)
.
Также см Тригонометрические функции .
Определение, для чего используется, пример и причины
Что такое синусоида?
Синусоида – это геометрическая форма волны, которая периодически колеблется (движется вверх, вниз или из стороны в сторону) и определяется функцией y = sin x . Другими словами, это s-образная гладкая волна, которая колеблется выше и ниже нуля.
Синусоидальные волны используются в техническом анализе и торговле, чтобы помочь идентифицировать модели и пересечения, связанные с осцилляторами.
Ключевые выводы
- Синусоида представляет собой S-образную форму волны, определяемую математической функцией y = sin x.

- Графически изображается в виде двух полукруглых кривых, чередующихся выше и ниже центральной линии.
- В финансах участники рынка могут идентифицировать циклические паттерны или сигналы осцилляторов по синусоидальным функциям.
- Синусоида как инструмент технического анализа графиков основана на передовой математике и предназначена для определения того, находится ли рынок в тренде или в циклическом режиме.
- Синусоидальные волны являются основой анализа разложения Фурье.
Понимание синусоидальных волн
Индикатор синусоиды основан на предположении, что рынки движутся циклически. После количественной оценки цикла трейдер может попытаться использовать модель для разработки опережающего индикатора. Это работает очень хорошо, когда рынок действительно движется по циклу. Однако, когда рынок находится в тренде, эта система дает сбой (и к этому нужно приспосабливаться).
Изображение Сабрины Цзян © Investopedia 2020 Рынки чередуются между периодами цикличности и тренда. Циклические периоды характеризуются отскоком цены от уровней поддержки или сопротивления и неудачными прорывами или выбросами. Трендовые периоды характеризуются новыми максимумами или новыми минимумами и откатами, которые затем продолжаются в направлении тренда, пока не исчерпаются.
Циклические периоды характеризуются отскоком цены от уровней поддержки или сопротивления и неудачными прорывами или выбросами. Трендовые периоды характеризуются новыми максимумами или новыми минимумами и откатами, которые затем продолжаются в направлении тренда, пока не исчерпаются.
В техническом анализе часто используются осцилляторы, которые могут иметь синусоидальные характеристики. Осциллятор существует между двумя крайними значениями, а затем строит индикатор тренда с результатами. Затем аналитики используют индикатор тренда для обнаружения краткосрочных условий перекупленности или перепроданности. Когда значение осциллятора приближается к верхнему экстремуму, аналитики интерпретируют эту информацию как перекупленность актива, а когда оно приближается к нижнему экстремуму, аналитики считают актив перепроданным.
Дополнением к синусоидальной функции является косинус.
Синусоидальные волны как аналитические инструменты
Синусоидальная волна как инструмент технического анализа графиков основана на продвинутой математике и предназначена для определения того, находится ли рынок в тренде или в циклическом режиме. Это помогает трейдерам определить начало и конец трендового движения, а также возможные сдвиги тренда.
Это помогает трейдерам определить начало и конец трендового движения, а также возможные сдвиги тренда.
Этот опережающий индикатор также называется индикатором MESA и был разработан Джоном Элерсом на основе алгоритма , который изначально применялся для цифровой обработки сигналов. Он состоит из двух линий, называемых синусоидальной волной и ведущей волной. Когда цена находится в тренде, линии не пересекаются и обычно проходят параллельно и на расстоянии друг от друга.
Пересечения линий могут указывать на точки разворота и генерировать сигналы на покупку или продажу при правильных условиях. Индикатор также может сигнализировать о перекупленности или перепроданности рынка (т. е. о неоправданно высоком или неоправданно низком уровне), что может повлиять на преобладающий тренд. Независимо от того, используются ли они отдельно или в сочетании с другими методами или некоррелированными индикаторами (например, индикаторами на основе скользящих средних), синусоидальные волны очень полезны для трейдера.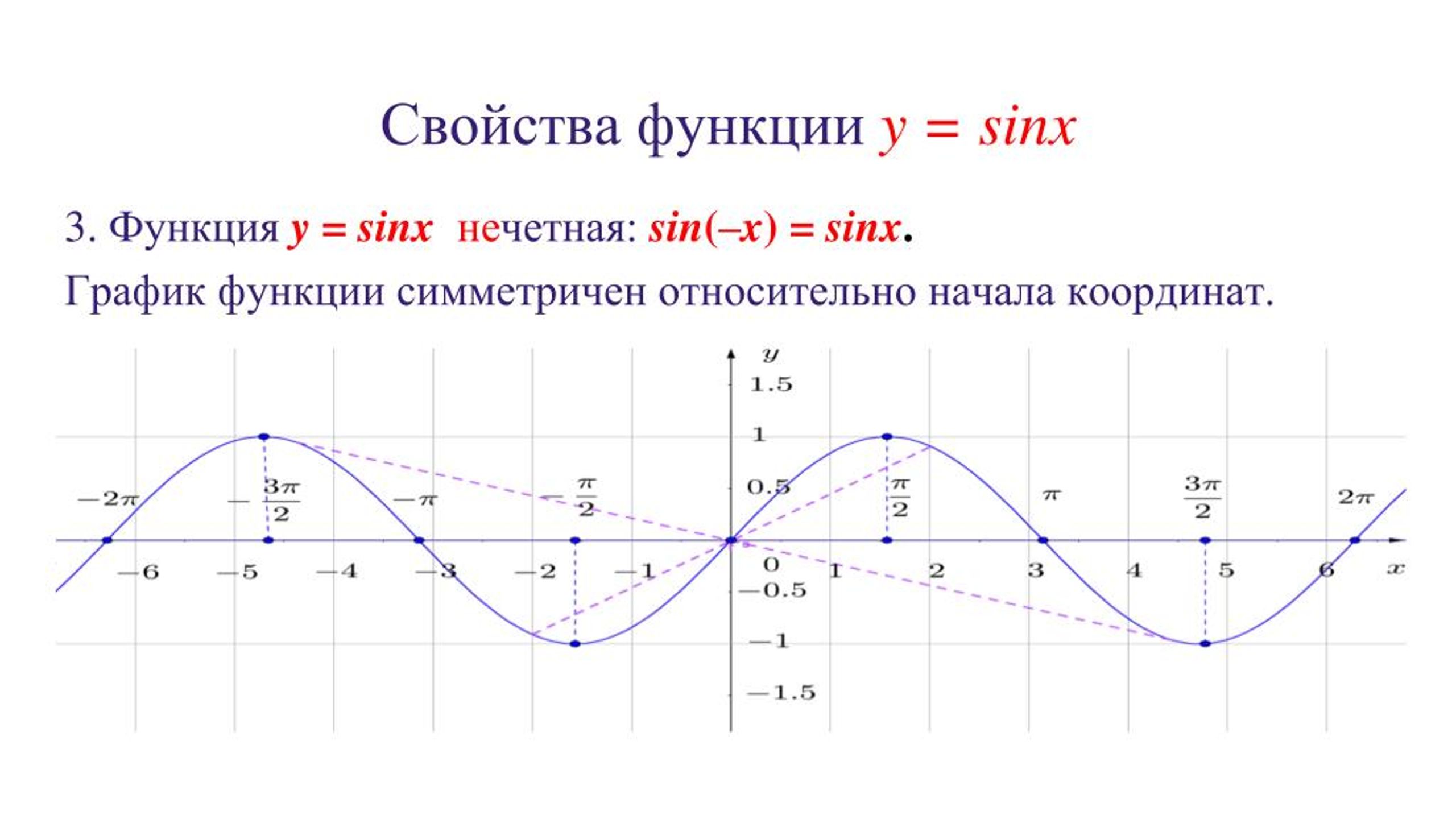
Композитный индекс запаздывающих индикаторов часто напоминает синусоиду, поскольку показатели, входящие в состав индекса (т. е. коэффициенты и процентные ставки), имеют тенденцию колебаться между диапазоном значений.
Например, инфляция всегда удерживается между указанными уровнями, и если / как только инфляция достигает или превышает указанный предел, процентные ставки будут скорректированы либо для увеличения, либо для уменьшения инфляции, чтобы она находилась в пределах целевого диапазона. Таким образом, по мере того, как уровень инфляции увеличивается, уменьшается или остается неизменным, процентные ставки будут колебаться вверх и вниз, чтобы контролировать нежелательный уровень инфляции.
Кто использует синусоидальные волны на рынках?
Технические трейдеры, использующие анализ Фурье, по своей сути используют синусоидальные волны для принятия торговых решений. Анализ Фурье — это метод, который по существу разбивает часть сложных данных временного ряда на ряд более простых компонентов, основанных на синусе или других тригонометрических функциях. Делая это, трейдер может лучше отделить сигнал от шума в данных.
Делая это, трейдер может лучше отделить сигнал от шума в данных.
Например, если трейдер считает, что инфляция циклична и представляет собой шум в истории цен на определенную потребительскую циклическую акцию, он может попытаться определить синусоидальную волну, которая соответствует модели инфляции, и удалить ее. В то время как специалисты по рынку применяли анализ Фурье, финансовые исследователи по-прежнему не убеждены в том, что это жизнеспособная или эффективная стратегия.
Как синусоида описывает волну?
Волна (будь то звуковая волна, океанская волна, радиоволна или любая другая) может быть описана по ее амплитуде (высоте или мощности) и частоте (насколько близко друг от друга пик каждой волны находится от следующей). При этом создается синусоида определенной высоты и частоты.
Как построить графики функций синуса и косинуса?
Косинусоидальная кривая изображается аналогично синусоидальной кривой, но не совпадает с ней по фазе. В частности, синусоида пересекает центральную линию с каждым интервалом пи (π), тогда как косинусоидальная волна достигает максимума с интервалом π и пересекает центральную линию с интервалом ½π (точки пика синусоиды).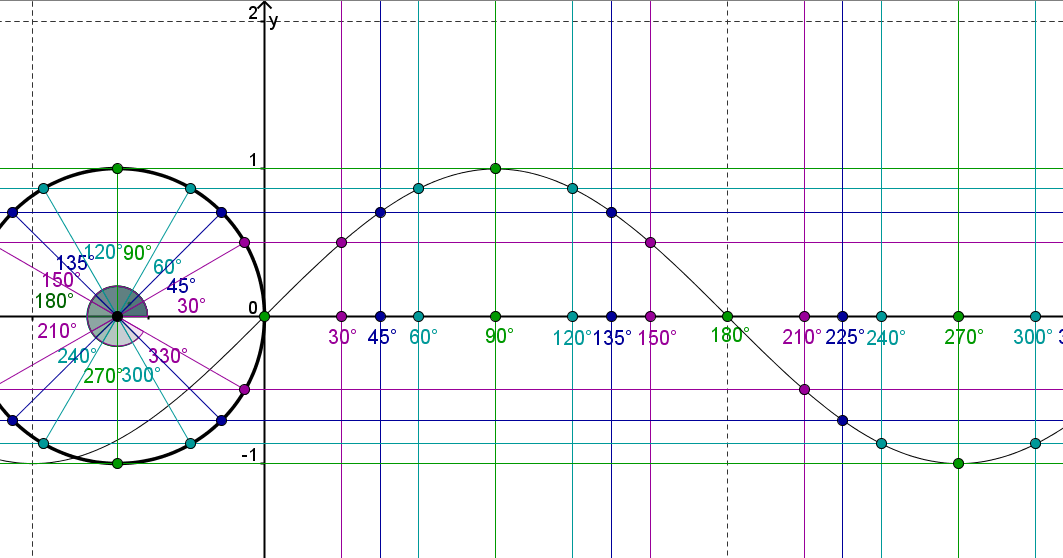
 plot(x, y, color='r', label='sin') # r - red colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
plot(x, y, color='r', label='sin') # r - red colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend(['sine', 'cosine'])
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend(['sine', 'cosine'])
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 plot(x, z, color='g', label='cos') # g - green colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
plot(x, z, color='g', label='cos') # g - green colour
plt.xlabel("Angle in Radians")
plt.ylabel("Magnitude")
plt.title("Plot of some trigonometric functions")
plt.xticks(xnumbers)
plt.yticks(ynumbers)
plt.legend()
plt.grid()
plt.axis([0, 6.5, -1.1, 1.1]) # [xstart, xend, ystart, yend]
plt.show()
 sinh(x)
# separate the figure object and axes object
# from the plotting object
fig, ax1 = plt.subplots()
# Duplicate the axes with a different y axis
# and the same x axis
ax2 = ax1.twinx() # ax2 and ax1 will have common x axis and different y axis
# plot the curves on axes 1, and 2, and get the curve handles
curve1, = ax1.plot(x, y, label="sin", color='r')
curve2, = ax2.plot(x, z, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
ax1.legend(curves, [curve.get_label() for curve in curves])
# ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# Global figure properties
plt.title("Plot of sine and hyperbolic sine")
plt.show()
sinh(x)
# separate the figure object and axes object
# from the plotting object
fig, ax1 = plt.subplots()
# Duplicate the axes with a different y axis
# and the same x axis
ax2 = ax1.twinx() # ax2 and ax1 will have common x axis and different y axis
# plot the curves on axes 1, and 2, and get the curve handles
curve1, = ax1.plot(x, y, label="sin", color='r')
curve2, = ax2.plot(x, z, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
ax1.legend(curves, [curve.get_label() for curve in curves])
# ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# Global figure properties
plt.title("Plot of sine and hyperbolic sine")
plt.show()
 plot(x2, y, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
# ax1.legend(curves, [curve.get_label() for curve in curves])
ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# x axis labels via the axes
ax1.set_xlabel("Magnitude", color=curve1.get_color())
ax2.set_xlabel("Magnitude", color=curve2.get_color())
# y axis label via the axes
ax1.set_ylabel("Angle/Value", color=curve1.get_color())
# ax2.set_ylabel("Magnitude", color=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# y ticks - make them coloured as well
ax1.tick_params(axis='y', colors=curve1.get_color())
# ax2.tick_params(axis='y', colors=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# x axis ticks via the axes
ax1.
plot(x2, y, label="sinh", color='b')
# Make a curves list to access the parameters in the curves
curves = [curve1, curve2]
# add legend via axes 1 or axes 2 object.
# one command is usually sufficient
# ax1.legend() # will not display the legend of ax2
# ax2.legend() # will not display the legend of ax1
# ax1.legend(curves, [curve.get_label() for curve in curves])
ax2.legend(curves, [curve.get_label() for curve in curves]) # also valid
# x axis labels via the axes
ax1.set_xlabel("Magnitude", color=curve1.get_color())
ax2.set_xlabel("Magnitude", color=curve2.get_color())
# y axis label via the axes
ax1.set_ylabel("Angle/Value", color=curve1.get_color())
# ax2.set_ylabel("Magnitude", color=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# y ticks - make them coloured as well
ax1.tick_params(axis='y', colors=curve1.get_color())
# ax2.tick_params(axis='y', colors=curve2.get_color()) # does not work
# ax2 has no property control over y axis
# x axis ticks via the axes
ax1.
 Если 180
разделить на три, получим результат —
600. Значение синуса 600 по
таблицам функций будет равно корню из
3, деленному на 3. Это и есть решение вашей
задачи.
Если 180
разделить на три, получим результат —
600. Значение синуса 600 по
таблицам функций будет равно корню из
3, деленному на 3. Это и есть решение вашей
задачи.
Ваш комментарий будет первым