matematikam ru построение графиков — ComputerMaker.info
Автор admin На чтение 3 мин.
Построение графиков онлайн с помощью нашего сервиса является простой задачей. Возможность построения одновременно сразу нескольких функций, помеченных разными цветами. Укажите пределы переменной и функции — и наш сервис быстро нарисует ваш график.
Построение графиков онлайн
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos. Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.
Преимущества построения графиков онлайн
- Визуальное отображение вводимых функций
- Построение очень сложных графиков
- Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
- Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
- Управление масштабом, цветом линий
- Возможность построения графиков по точкам, использование констант
- Построение одновременно нескольких графиков функций
- Построение графиков в полярной системе координат (используйте r и θ( heta) )
С нами легко в режиме онлайн строить графики различной сложности. 2-x/3 ).
2-x/3 ).
Чтобы построить трехмерный график в Excel , необходимо указать функцию f(x,y) , пределы по x и y и шаг сетки h .
Принципы и способы построения графика функции
Прикладное применение графика функции
Построить пирамиду ABCD по координатам можно здесь.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться. Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
© Контрольная работа РУ — калькуляторы онлайн
Как построить график в Excel по данным таблицы
При работе в Excel табличных данных часто не достаточно для наглядности информации. Для повышения информативности ваших данных советуем использовать графики и диаграммы в Эксель. В этой статье рассмотрим пример того, как построить график в Excel по данным таблицы.
Для повышения информативности ваших данных советуем использовать графики и диаграммы в Эксель. В этой статье рассмотрим пример того, как построить график в Excel по данным таблицы.
Кликните по кнопке ниже и мы пришлем Вам Excel файл с примером графика, построенного по данным таблицы на E-mail:
Видеоурок
Как построить простой график в Excel
Представим, что у нас есть таблица с ежемесячными данными среднего курса Доллара в течении года:
На основе этих данных нам нужно нарисовать график. Для этого нам потребуется:
- Выделить данные таблицы, включая даты и курсы валют левой клавишей мыши:
- На панели инструментов перейти во вкладку “Вставка” и в разделе “Диаграммы” выбрать “График”:
- Во всплывающем окне выбрать подходящий стиль графика. В нашем случае, мы выбираем график с маркерами:
- Система построила нам график:
Как построить график в Excel на основе данных таблицы с двумя осями
Представим, что у нас есть данные не только курса Доллара, но и Евро, которые мы хотим уместить на одном графике:
Для добавления данных курса Евро на наш график необходимо сделать следующее:
- Выделить созданный нами график в Excel левой клавишей мыши и перейти на вкладку “Конструктор” на панели инструментов и нажать “Выбрать данные”:
- Изменить диапазон данных для созданного графика.
 Вы можете поменять значения в ручную или выделить область ячеек зажав левую клавишу мыши:
Вы можете поменять значения в ручную или выделить область ячеек зажав левую клавишу мыши:
- Готово. График для курсов валют Евро и Доллара построен:
Если вы хотите отразить данные графика в разных форматах по двум осям X и Y, то для этого нужно:
- Перейти в раздел “Конструктор” на панели инструментов и выбрать пункт “Изменить тип диаграммы”:
- Перейти в раздел “Комбинированная” и для каждой оси в разделе “Тип диаграммы” выбрать подходящий тип отображения данных:
Ниже мы рассмотрим как улучшить информативность полученных графиков.
Как добавить название в график Эксель
На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:
- Нажать на графике левой клавишей мыши;
- Нажать на “зеленый крестик” в правом верхнем углу графика;
- Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:
- Над графиком появится поле с названием графика.
 Кликните по нему левой клавишей мыши и внесите свое название:
Кликните по нему левой клавишей мыши и внесите свое название:
Как подписать оси в графике Excel
Для лучше информативности нашего графика в Excel есть возможность подписать оси. Для этого:
- Щелкните левой клавишей мыши по графику. В правом верхнем углу графика появится “зеленый крестик”, нажав на который раскроются настройки элементов диаграммы:
- Щелкните левой клавишей мыши на пункте “Названия осей”. На графике под каждой осью появятся заголовки, в которые вы можете внести свой текст:
Как добавить подписи данных на графике Excel
Ваш график может стать еще более информативным с помощью подписи отображаемых данных.
На примере курсов валют мы хотим отобразить на графике стоимость курса Доллара и Евро помесячно. Для этого нам потребуется:
- Щелкнуть правой кнопкой мыши по линии графика, на которую хотим добавить данные. В раскрывающемся меню выбрать пункт “Добавить подписи данных”:
Система отобразила курс Доллара на линии графика, но наглядность данных это не улучшило, так как значения сливаются с графиком. Для настройки отображения подписи данных потребуется сделать следующие шаги:
Для настройки отображения подписи данных потребуется сделать следующие шаги:
- Кликните правой кнопкой мыши на любом значении линии графика. В всплывающем окне выберите пункт “Формат подписей данных”:
В этом меню вы сможете настроить положение подписи, а также из чего будет состоять подпись данных: из имени ряда, категории, значения и.т.д.
Помимо настроек расположения, в том же меню вы сможете настроить размер подписей, эффекты, заливку и.т.д:
Настроив все параметры у нас получился такой график курса валют:
Еще больше полезных приемов в работе с графиками, списками данных и функциями в Excel вы узнаете в практическом курсе “От новичка до мастера Excel“. Успей зарегистрироваться по ссылке!
Оператор |
Описание |
||||
| + — * : / () [] {} |
Сложение, вычитание, умножение, деление и группирующие символы. |
||||
| root(x,n) | Корень n-ой степени из x. Например: root(x,3) есть корень 3й степени из x. | ||||
| sqrt() | Квадратный корень. Эквивалентно root(аргумент,2) | ||||
| cbrt() | Кубический корень. Эквивалентно root(аргумент,3) | ||||
| logn(x,a) | Логарифм x пооснованию a | ||||
| ln() | Натуральный логарифм (с основанием е) | ||||
| lg() | Логарифм по основанию 10 (Десятичный логарифм), то же, что и logn(аргумент,10).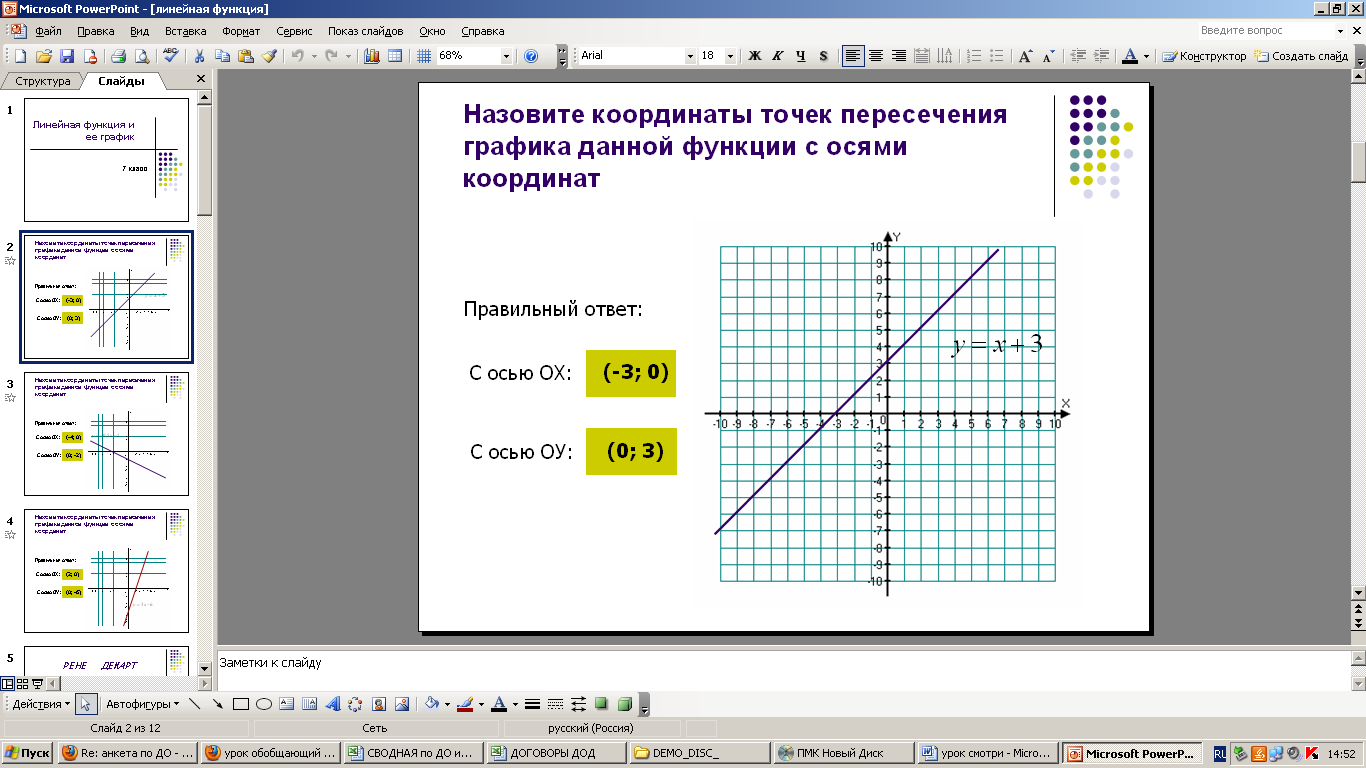 аргумент аргумент |
||||
| sin() | Синус | ||||
| cos() | Косинус | ||||
| tan() | Тангенс | ||||
| cot() | Котангенс | ||||
| sec() |
Секанс, определяется как 1/cos() | ||||
| csc() | Косеканс, определяется как 1/sin() | ||||
| asin() | Арксинус | ||||
| acos() | Арккосинус | ||||
| atan() | Арктангенс | ||||
| acot() | Арккотангенс | ||||
| asec() | Арксеканс, обратный секанс | ||||
| acsc() | Арккосеканс, обратный косеканс | ||||
| sinh() | Гиперболический синус, шинус | ||||
| cosh() | Гиперболический косинус, чосинус | ||||
| tanh() | Гиперболический тангенс | ||||
| coth() | Гиперболический котангенс | ||||
| sech() | Гиперболический секанс | ||||
| csch() | Гиперболический косеканс | ||||
| asinh() | Гиперболический арксинус, функция обратная |
||||
| acosh() | Гиперболический арккосинус, функция обратная cosh() | ||||
| atanh() | Гиперболический арктангенс, функция обратная tanh() | ||||
| acoth() | Гиперболический арккотангенс, функция обратная cotanh() | ||||
| asech() | Гиперболический арксеканс, функция обратная sech() | ||||
| acsch() | Гиперболический арккосеканс, функция обратная csch() | ||||
| gaussd(x,среднее,сигма) | Нормальное распределение (Распределение Гаусса). Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1. Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1. |
||||
| min(число1,число2) | Вычисляет наименьшее из 2х значений | ||||
| max(число1,число2) | Вычисляет наибольшее из 2х значений | ||||
| round() | Округляет аргумент до целого значения | ||||
| floor() | |||||
| ceil() | Округление вверх | ||||
| abs() или | | | Модуль (абсолютное значение) | ||||
| sgn() | Функция сигнум, определяет знак аргумента
|
||||
| rand | Случайное число от 0 до 1 |
как правильно выбрать диаграмму или график для годового отчета
Целевая аудитория вашей презентации либо отчета — инвесторы, руководство и просто люди — ожидают получить не ворох цифр, а уже сформулированные выводы либо понятно расставленные акценты. Возникает необходимость обратить внимание аудитории на факторы и обстоятельства, показать планы и стратегию.
Возникает необходимость обратить внимание аудитории на факторы и обстоятельства, показать планы и стратегию.
Но есть одна проблема — восприятие положительных и отрицательных результатов. При этом разные аудитории по-разному относятся даже к положительным. Например, журналисты могут скептически комментировать достижения. Акционеры склонны болезненно реагировать на убытки. И здесь необходим тонкий продуманный подход.
О неудачах и негативе можно рассказать очень скучно и нудно, а интересный и бодрый рассказ об успехах — подкрепить наглядной демонстрацией, включающей в себя презентацию с впечатляющими графиками. При этом правильно выбранная диаграмма может в корне изменить восприятие информации: если вы просто покажете, как рос доход компании в течение года, это будет не так впечатляюще, как если рядом будет показана динамика проседания вашего конкурента.
Одна из трудностей, которая существенно замедляет составление отчетов и аналитическую работу, заключается в подборе правильного типа диаграммы. Неверный ее выбор может вызвать путаницу в голове у зрителей или привести к ошибочной интерпретации данных.
Давайте посмотрим на инфографику о мировом производстве масла.
Инфографика Top Lead для компании Baker Tilly. Посмотреть в полном размере.
Здесь все — и объемы производства, экспорт, прогнозы, спрос, потребители и еще тонны информации. Эта инфографика вмещает в себя по сути огромный объем данных по целой отрасли. Тем не менее она проста в восприятии, и на графике четко видны определенные тенденции.
Чтобы создать диаграмму, которая объясняет и демонстрирует точную аналитику, сначала нужно понять причины, по которым вообще она может понадобиться. В этой статье мы рассмотрим пять вопросов, возникающих при выборе типа диаграммы. Затем мы дадим обзор 13 различных видов диаграмм, из которых можно выбрать самую подходящую.
1. Вам нужно сравнивать величины?
Графики идеально подходят для сравнения одного или нескольких наборов величин, и они могут легко отображать самые низкие и высокие показатели.
Для создания сравнительной диаграммы используйте следующие типы: гистограмма, круговая диаграмма, точечная диаграмма, шкала со значениями.
2. Вы хотите показать структуру чего-либо?
Например, вы хотите рассказать о типах мобильных устройств, которые используют посетители сайта или общий объем продаж, разбитый на сегменты.
Чтобы показать структуру, используйте следующие диаграммы: круговая диаграмма, гистограмма с накоплением, вертикальный стек, областная диаграмма, диаграмма-водопад.
3. Вы хотите понять, как распределяются данные?
Таблицы с распределением помогают понять основные тенденции и отметить, что выходит за рамки.
Используйте эти диаграммы: точечная диаграмма, линейная диаграмма, гистограмма.
4. Вы заинтересованы в анализе тенденций в определенном наборе данных?
Если вы хотите узнать больше о том, как цифры ведут себя в течение конкретного временного периода, есть типы диаграмм, которые очень хорошо это отображают.
Вам пригодятся: линейная диаграмма, двойная ось (столбец и линия), гистограмма.
5. Хотите лучше понять взаимосвязь между установленными значениями?
Взаимосвязанные графики подходят для того, чтобы показать, как одна переменная относится к другой или нескольким различным переменным. Это можно использовать, чтобы показать положительное, отрицательное или нулевое влияние на другую цифру.
Используйте для этого следующие диаграммы: точечная диаграмма, пузырьковая диаграмма, линейная диаграмма.
13 различных типов диаграмм для анализа и представления данныхЧтобы лучше понять каждый график и возможности его применения, рассмотрим все типы диаграмм.
ГистограммаГистограмма используется, чтобы показать сравнение между различными элементами, также она может сравнить элементы за определенный промежуток времени. Этот формат можно использовать для отслеживания динамики переходов на лендинг или количества клиентов за определенный период.
Этот формат можно использовать для отслеживания динамики переходов на лендинг или количества клиентов за определенный период.
Инфографика Top Lead для юридической компании AEQUO
Рекомендации по дизайну для столбчатых диаграмм
1. Подбирайте единую цветовую гамму и акцентируйте цветом места, которые хотите выделить как значимые моменты перелома или изменения с течением времени.
2. Используйте горизонтальные метки, чтобы улучшить читаемость.
3. Начните ось y с 0, чтобы правильно отразить значения на графике.
Горизонтальная гистограммаГистограмму — в основном горизонтальную столбчатую — следует использовать, чтобы избежать путаницы, когда одна полоска данных слишком длинная или в случае сравнения более 10 элементов. Этот вариант также может использоваться для визуализации отрицательных значений.
Инфографика Top Lead для интернет-издания Aggeek. Посмотреть в полном размере.
Рекомендации по дизайну для гистограмм
1. Подбирайте единую цветовую гамму и акцентируйте цветом места, которые хотите выделить как значимые точки перелома или изменения с течением времени.
2. Используйте горизонтальные метки, чтобы улучшить читаемость.
3. Начните ось Y с 0, чтобы правильно отразить значения на графике.
Линейная диаграммаЛинейная диаграмма отображает тенденции или прогресс и может использоваться для визуализации самых разных категорий данных. Ее следует использовать, когда вы создаете график, основанный на длительном сборе данных.
Инфографика Top Lead. Линейная диаграмма — снизу.
Рекомендации по дизайну для линейных диаграмм
1. Используйте сплошные линии.
2. Не рисуйте больше четырех линий, чтобы избежать появления визуальных отвлекающих факторов.
3. Используйте правильную высоту, чтобы линии занимали примерно 2/3 высоты оси Y.
Двухосевая диаграмма позволяет выстраивать данные с использованием двух осей — Х и Y. Используется несколько наборов данных, один из которых, например, — данные за период, а другой — лучше подходит для группировки по категориям. Таким образом можно продемонстрировать корреляцию или ее отсутствие между разными показателями.
Инфографика Top Lead для Growth Up. Диграмма с двойной осью — вверху.
Рекомендации по дизайну для диаграмм с двумя осями
1. Используйте левую ось Y для основной переменной, потому что для людей естественно сначала смотреть влево.
2. Используйте разные стили графиков, чтобы проиллюстрировать два набора данных.
3. Выберите контрастные цвета для сравниваемых наборов данных.
Областная диаграммаОбластная диаграмма в целом выглядит как линейная диаграмма, но пространство между осью Х и линией графика заполняется цветом или рисунком. Такой вариант подойдет для демонстрации отношений между частями одного целого, например, вклада отдельных торговых представителей в общий объем продаж за год. Это поможет проанализировать как всю картину в целом, так и информацию о тенденциях на отдельных участках.
Такой вариант подойдет для демонстрации отношений между частями одного целого, например, вклада отдельных торговых представителей в общий объем продаж за год. Это поможет проанализировать как всю картину в целом, так и информацию о тенденциях на отдельных участках.
Инфографика Top Lead для компании Baker Tilly. Сверху вниз: круговая диаграмма, две обласных диаграммы, круговые диаграммы.
Рекомендации по дизайну для диаграмм областей
1. Используйте полупрозрачные цвета.
2. Используйте не более четырех категорий, чтобы избежать путаницы.
3. Организовывайте данные с высокой частотой изменчивости в верхней части диаграммы, чтобы было легче воспринимать динамические изменения.
Штабельная диаграммаЕе можно использовать для сравнения большого количества различных составляющих. Например, частоту посещения нескольких сайтов и каждой страницы в отдельности.
Инфографика и верстка — Top Lead. Для «Нафтогаз України». Штабельная диаграмма — внизу слева. Посмотреть в полном размере.
Для «Нафтогаз України». Штабельная диаграмма — внизу слева. Посмотреть в полном размере.
Рекомендации по дизайну для штабельных диаграмм
1. Лучше всего использовать ее для иллюстрации отношений «часть-целое». Для большей наглядности выбирайте контрастные цвета.
2. Сделайте масштаб диаграммы достаточно большим, чтобы видеть размеры групп по отношению друг к другу.
Круговая диаграммаКруговая диаграмма отображает статическое число и то, как части складываются в целое — состав чего-либо. Круговая диаграмма показывает числа в процентах, и общая сумма всех сегментов должна равняться 100%.
Инфографика и верстка — Top Lead. Для «Нафтогаз України». Посмотреть в полном размере.
Рекомендации по дизайну для круговых диаграмм
1. Не добавляйте слишком много категорий, чтобы разница между срезами была хорошо заметна.
2. Убедитесь, что общая сумма всех частей составляет 100%.
3. Необходимо упорядочить части в соответствии с их размером.
Инфографика Top Lead для компании Baker Tilly. Посмотреть в полном размере.
Диаграмма-водопадДиаграмма-водопад используется для демонстрации того, как промежуточные значения — положительные и отрицательные — влияют на изначальное значение и приводят к окончательному результату. Примером может служить визуализация того, как общий доход компании зависит от различных отделов и превращается в конкретный объем прибыли.
Инфографика и верстка — Top Lead. Годовой отчет «Нафтогаз України». Диаграмма-водопад в верхней половине верстки. Посмотреть в полном размере.
Рекомендации по дизайну для водопадных диаграмм
1. Используйте контрастные цвета, чтобы выделить различия в наборах данных.
2. Выбирайте теплые цвета, чтобы показать рост, и холодные цвета — для падения.
Воронкообразная диаграммаДиаграмма-воронка отображает последовательность этапов и скорость завершения каждого из них. Ее можно использовать для отслеживания процесса продаж или взаимодействия пользователей с сайтом.
Ее можно использовать для отслеживания процесса продаж или взаимодействия пользователей с сайтом.
Инфографика Top Lead.
Рекомендации по дизайну для воронкообразных диаграмм
1. Масштабируйте размер каждой секции, чтобы точно отобразить объем набора данных.
2. Используйте контрастные цвета или оттенки одного цвета от самого темного до самого светлого по мере сужения воронки.
Есть еще несколько видов графиков — они используются не так часто, но тоже могут пригодиться для визуализации болььших объемов данных. Среди них:
Точечная диаграммаТочечная диаграмма показывает взаимосвязь между двумя различными переменными или демонстрирует распределяющие тенденции. Она подходит, если у вас много разных точечных данных, и вы хотите найти общее в наборе данных. Такая визуализация хорошо работает в поиске исключений или закономерности распределения данных.
Рекомендации по дизайну для точечных диаграмм
1. Включите больше переменных, таких как разные размеры, чтобы объединить больше данных.
Включите больше переменных, таких как разные размеры, чтобы объединить больше данных.
2. Начните ось Y с 0 для точного распределения данных.
3. Если вы используете линии тенденций, необходимо ограничиться максимум двумя, чтобы график был понятен.
Пузырьковая диаграммаПузырьковая диаграмма похожа на точечный график. Но только в том смысле, что она может показывает распределение и взаимосвязь. Существует третий набор данных, который обозначается размером круга.
Рекомендации по дизайну для пузырьковых диаграмм
1. Проводите градацию пузырьков по занимаемой ими площади, а не по диаметру.
2. Убедитесь, что метки четкие и хорошо видны.
3. Используйте только круги.
Шкала со значениямиТакой график показывает прогресс в достижении цели, сравнивает его по разным критериям и отображает результат как рейтинг или производительность.
Рекомендации по разработке дизайна для шкалы со значениями
1. Используйте контрастные цвета, чтобы показать динамику.
Используйте контрастные цвета, чтобы показать динамику.
2. Используйте один цвет в разных оттенках для оценки прогресса.
Тепловая картаТепловая карта показывает взаимосвязь между двумя элементами и предоставляет рейтинговую информацию. Информация о рейтинге отображается с использованием различных цветов или разной насыщенности.
Рекомендации по разработке дизайна для тепловой карты
1. Используйте базовый и четкий план карты, чтобы не отвлекать зрителей от данных.
2. Используйте разные оттенки одного цвета, чтобы показать изменения.
3. Избегайте использования нескольких шаблонов.
Вариантов дизайна может быть огромное количество.
Чтобы узнать больше о подготовке нефинансовых отчетов и послушать кейсы таких компаний как Coca-Cola, Kernel, Нова Пошта, 1+1 Media, Infopulse и других, регистрируйтесь на нашу онлайн-конференцию Corporate Reporting Conference 2020. Жмите на баннер, чтобы узнать подробности, а билеты покупайте прямо в Фейсбуке:
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов.
| ||||
Бесплатный онлайн построитель графиков Chart Creator
Если Вы собираетесь участвовать в конференции, научном докладе либо просто составляете какой-либо отчет, то без использования графиков, диаграмм и иных форм графического представления данных никак не обойтись. Можно написать сотни слов о тех или иных показателях и никто толком ничего не поймет )) А можно просто показать один единственный график, и все сразу становится на свои места!
Сегодня практически в любом приличном офисном пакете можно найти функцию построения графиков и диаграмм. Где-то этот функционал более удобный, где-то менее, но не об этом речь…
Я хочу рассказать Вам об одном сервисе, при помощи которого Вы сможете построить график онлайн, даже не имея на компьютере ни одного редактора. Достаточно только браузера и выхода в Интернет!
Достаточно только браузера и выхода в Интернет!
Chart Creator – построитель графиков онлайн. Идеальное решение для тех, кто хочет сделать диаграмму либо график быстро и удобно!
Интерфейс построителя графиков и принцип работы в нем настолько просты, что разберется абсолютно любой )). В поле «Data Name» вводите название и в поле «Data» в левую колонку вводите показатели, а в правую – их численные значения. Нажимайте кнопку «Draw» и график построен! ))
Вид графика можно изменить. Для этого нажимайте кнопку «Editor» и в закладке «Диаграммы» выбирайте нужный Вам тип графика либо диаграммы. Всего я насчитал 26 вариантов графического представления данных! По-моему неплохо для скромного веб-приложения ))
В закладке «Настройка» онлайн построителя графиков можно изменять параметры шрифтов:
- сделать жирным либо курсивом
- изменить размер, цвет, семейство
Также в этой закладке можно настроить ряд параметров представления графика:
- подписи осей
- сетки
- планки погрешностей
- формат чисел
- масштаб и т.
 п.
п.
Как видите, настроек онлайн сервиса вполне хватает для того, чтобы построить график не только на скорую руку )).
Что же делать дальше с построенным онлайн графиком либо диаграммой?
- Вы можете сделать скриншот экрана и вставить его в документ.
- Можно распечатать график, нажав кнопку «Print».
- Вы можете отослать ссылку на Ваше творение по почте либо скайпу (к примеру, своему шефу). В верхнем правом углу в небольшом окошке Вы найдете нужную ссылку.
- Можно быстро поделиться ссылкой в своем твиттере, нажав ссылку «Tweet» в том же верхнем углу экрана.
Друзья, как видите, построитель графиков онлайн Chart Creator неплохо справляется с возложенными на него функциями. Конечно, некоторым его функционала будет явно недостаточно, но как средство быстро построить график, когда нужного софта попросту нет под рукой, а время (или шеф) поджимает, по-моему данный вариант можно вполне рассматривать )).
Обновлено 08.
2019: Chart Creator больше не работает, к сожалению.
Автор статьи: Сергей Сандаков, 40 лет.
Программист, веб-мастер, опытный пользователь ПК и Интернет.
Построение графиков онлайн. Построение графиков онлайн Построить график функции у х3 6х2
Разделы: Математика
Тема: “Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)
Цель.
- Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
- Развить навыки построения графика функции, содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.
Решение.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).
4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2
= 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Алгоритм построения графика квадратной функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
2.у = |х| + 1. График функции на рисунке 3.
3. у = |х + 1|. График функции рисунке 4.
Вывод.
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.
2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в группах.
Группа 1. Построить графики функций:
а) у = х 2 — 6|x| + 3,
б) у = |х 2 — 6х + 3|.
Решение.
1.Построить график функции у = х 2 -6х+3.
2. Отобразить его симметрично относительно оси Оу.
График на рисунке 5.
б) 1. Построить график функции у = х 2 — 6х + 3.
2. Отобразить его симметрично относительно оси Ох.
График функции на рисунке 6.
Вывод.
1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.
Решение.
1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.
2. Полученный график отображаем симметрично относительно оси Ох.
График функции на рисунке 7.
Вывод.
График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.
1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х 2 + 6x + 3 при х
График функции на рисунке 9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х 2 + 6х + 3 при х 6.
2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.
График на рис.10.
Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.
(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
Группа 4.
Построить график функции:
а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.
Решение.
а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:
Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:
Строим каждый график на соответствующем интервале.
График функции на рисунке 12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно оси Ох.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.
Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.
3. Задание на дом.
Построить графики функций с различным расположением модуля:
1. у = х 2 + 4х + 2;
2. у = — х 2 + 6х — 4.
4. Рефлексивно – оценочный этап.
1.Оценки за урок складываются из отметок:
а) за работу в группе;
б) за самостоятельную работу.
2. Какой момент был наиболее интересен на уроке?
3. Трудное ли домашнее задание?
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.
Преимущества построения графиков онлайн
- Визуальное отображение вводимых функций
- Построение очень сложных графиков
- Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
- Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
- Управление масштабом, цветом линий
- Возможность построения графиков по точкам, использование констант
- Построение одновременно нескольких графиков функций
- Построение графиков в полярной системе координат (используйте r и θ(\theta))
С нами легко в режиме онлайн строить графики различной сложности.2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
3-осевой график Метод Excel: добавление третьей оси Y
Вы когда-нибудь хотели знать, как создать 3-осевой график в Excel? На днях я получил вопрос от Тодда, подписчика EngineerExcel.com. Он использует Excel для создания диаграмм положения кулачка, скорости и ускорения. Стандартный способ построения графика этих данных — включить все три кривые в одну диаграмму, как на изображении ниже, и он хотел создать такую кривую в Excel.
Создание трехосевого графика в Excel
Проблема в том, что все три кривые имеют очень разные масштабы, причем ускорение является наименьшим.Это затрудняет просмотр кривой ускорения на графике без уникальной оси. Поэтому он хотел узнать, есть ли способ создать в Excel трехосевой график. К сожалению, для его создания нет встроенных функций, но мы можем подделать один на , создав другую серию данных с постоянным значением x , как я сделал на изображении ниже.
Это не идеальное решение, но, насколько мне известно, это лучшее, что мы можем сделать в Excel с помощью доступного в настоящее время набора инструментов.
Выберите коэффициент масштабирования и масштабируйте данные
Excel позволяет нам добавить вторую ось к диаграмме рассеивания, мы будем использовать ее для скорости и ускорения.Однако нам нужно масштабировать данные об ускорении так, чтобы они заполняли область диаграммы. Для этого я ввел соответствующий коэффициент масштабирования в электронную таблицу и создал новый столбец масштабированных данных ускорения, умножив исходные данные ускорения на коэффициент масштабирования.
Определите положение для третьей оси Y
Третья ось Y (которая на самом деле будет серией данных) будет находиться в области диаграммы, поэтому в какой-то момент она должна пересекать ось X. Я выбрал значение 285 градусов, так как положение и, следовательно, скорость и ускорение равны нулю за этой точкой.Конечно, мы всегда можем изменить это позже.
Выберите данные для 3-х осевого графика в Excel
Затем я создал диаграмму, выбрав угол, положение, скорость и масштабированные данные ускорения. Я поместил данные о скорости и ускорении на вторичную ось диаграммы.
Масштабированные данные ускорения могли быть на первичной оси. В этом случае мне пришлось бы использовать другой коэффициент масштабирования.
Я также добавил немного цвета к осям и меткам осей для ясности.
Создание трех массивов для 3-осевой диаграммы
После вставки диаграммы я создал три массива:
- Массив значений оси X для третьей «оси Y» графика
- Массив немасштабированных значений, которые примерно одного порядка величины, но также полностью охватывают исходные данные ускорения. Например, диапазон данных ускорения был от ~ -0,0005 до ~ 0,0005. Поэтому я выбрал -0,001 и 0,001 в качестве пределов .
- Массив масштабированных (вычисленных) значений с использованием коэффициента масштабирования сверху.
Эти массивы использовались для создания третьей оси Y на следующем шаге.
Создайте третью «ось» с четвертой серией данных
Затем я добавил четвертую серию данных, чтобы создать трехосевой график в Excel.
Значения x для ряда были массивом констант, а значения y были немасштабированными значениями.
Я также изменил стиль линии, чтобы он соответствовал весу других линий сетки, добавил маркеры (такие, которые выглядят как знаки плюса) и изменил цвет линии и маркера в соответствии с серией данных (зеленый).
Добавить метки данных — выбрать диапазон меток данных
Ярлыки осейбыли созданы, щелкнув серию правой кнопкой мыши и выбрав «Добавить метки данных». По умолчанию Excel добавляет значения y для ряда данных. В данном случае это были масштабированные значения, которые не могли быть точными метками для оси (они соответствовали бы непосредственно вторичной оси).
Однако в Excel 2013 и более поздних версиях вы можете выбрать диапазон для меток данных. Для этой диаграммы это массив немасштабированных значений, который был создан ранее.
Итак, я щелкнул правой кнопкой мыши метки данных, затем выбрал «Форматировать метки данных».
Затем на панели задач «Форматирование меток данных» я установил флажок рядом с «Значения из ячеек».
Откроется небольшое диалоговое окно, в котором я могу выбрать диапазон. Я выбрал массив немасштабированных значений и нажал ОК.
Добавить текстовое поле для заголовка третьей оси
Наконец, я добавил текстовое поле рядом с осью и ввел заголовок.
Обновление диаграммы
Если данные когда-либо обновляются, просто изменить коэффициент масштабирования и / или положение оси X третьей оси Y.Просто измените значения на листе, и трехосевой график автоматически обновится в Excel.
График с тремя осями Y с помощью Chart Studio и Excel
Перейдите в рабочую область Chart Studio и войдите в свою бесплатную учетную запись Chart Studio. Перейдите в «Импорт», нажмите «Загрузить файл», затем выберите файл Excel для загрузки. Ваш файл Excel откроется в сетке Chart Studio. Для получения дополнительной информации о сетке Chart Studio см. Этот учебник
.Обозначьте свои столбцы, как мы сделали ниже.У вас будет три столбца по оси Y (стоимость, выпуск, дефект) и один столбец по оси X (дата). Выберите «Линейные графики» в меню «СДЕЛАТЬ ГРАФИК», а затем щелкните линейный график в левом нижнем углу.
Изначально ваш участок будет выглядеть примерно так.
Пройдите во всплывающее окно TRACES и войдите в Col2.Приготовьтесь добавить вторую ось Y. Щелкните «New Axis / Subplot…»
.Вы захотите применить новую ось Y к правой части графика.
Ваш график должен теперь выглядеть примерно так:
Теперь мы выполним аналогичный процесс для Col3.Вместо того, чтобы применять третью ось Y к правой стороне графика, выберите «свободный левый».
Ваш график должен теперь выглядеть примерно так:
Вы могли заметить, что ось Y занята линиями сетки.Откройте всплывающее окно AXES, затем Lines на панели инструментов, чтобы очистить его. Выберите первую и вторую оси Y и отключите линии сетки.
Затем убедитесь, что весь ваш диапазон оси Y начинается с 0. Откройте всплывающее окно Axes, затем Range и настройте его на 0. Сделайте это для всех осей Y.
Ваш график должен теперь выглядеть примерно так:
В легенде в правой части графика вы можете пометить свою трассу «Col2» «Стоимость», «Col3» — «Выход» и «Col4» — «Дефект».’
Теперь ваш участок должен выглядеть примерно так. Чтобы график находился в верхней части руководства, вам нужно немного изменить его стиль. Вы можете настроить «Линии / Маркеры» во всплывающем окне TRACES.
Мы дали нашему графику название. Мы также добавили цветные метки оси Y к нашим следам.Вы даже можете добавить «Тиковые префиксы» во всплывающем окне AXES и на вкладке «Ярлыки». Если вы чувствуете себя так тронутым, вы даже можете закодировать «галочки» на своих следах цветом. Наконец, мы связались с нашими исходными данными в области меток оси X.
Вы можете загрузить готовый график Chart Studio, чтобы встроить его в книгу Excel. Мы также рекомендуем включить ссылку Chart Studio на график в вашей книге Excel для быстрого доступа к интерактивной версии Chart Studio.Получите ссылку на свой график, нажав кнопку «Поделиться». Загрузите изображение графика Chart Studio, щелкнув ЭКСПОРТ на панели инструментов.
Чтобы добавить файл Excel в книгу, щелкните в том месте, куда вы хотите вставить изображение в Excel. На вкладке ВСТАВИТЬ в Excel в группе ИЛЛЮСТРАЦИИ щелкните ИЗОБРАЖЕНИЕ. Найдите загруженное изображение графика Chart Studio и дважды щелкните его.Обратите внимание, что мы также скопировали ссылку на график Chart Studio в ячейку для облегчения доступа к интерактивной версии Chart Studio.
Как построить график трех переменных в Excel
Анализ данных включает построение графиков, и графики XY являются одними из самых эффективных графиков. Вы можете использовать графики xy для построения и сравнения двух переменных, тренда и того, как они меняются друг с другом.Но что вы будете делать, если у вас есть три набора данных для построения на одном графике? Это может показаться странным, но в Excel есть множество возможностей. Из этого туториала Вы узнаете, как построить три переменных на одном графике, поэтому выполните следующие действия:
1. Откройте электронную таблицу Excel, введите данные в три столбца и назовите столбцы.
2. Выделите все и вставьте диаграмму. Линейная диаграмма xy более предпочтительна для этой задачи.
3. Сделать второстепенную ось несложно. Просто дважды щелкните одну из линий, чтобы открыть панель форматирования и изменить ее на дополнительную ось.
4. Сделать третью ось намного сложнее, поэтому мы сделаем две диаграммы. Продолжите, нажав Ctrl + D, чтобы продублировать диаграмму.
5. Щелкните и перетащите диаграммы, чтобы отделить их друг от друга. На одной из диаграмм удалите одну ось, оставив только одну, чтобы у вас было всего три оси.
Три оси должны иметь разные цвета, поэтому быстро удалите или измените цвета для облегчения идентификации.
7. На втором графике измените заливку на «без заливки».
8. Щелкните и перетащите вторую диаграмму на первую диаграмму, пока вертикальная и горизонтальная оси двух диаграмм не выровняются. Три оси будут отображаться четко, как если бы они были нанесены на один график.
9. Теперь второй график все еще нечеткий из-за линий сетки.Пора убрать линии сетки.
10. Щелкните и перетащите вторую диаграмму, чтобы разделить ее Перейти, чтобы заполнить и удалить линии сетки
11. Взгляните на вторую диаграмму, вы увидите заголовок. Он может не совпадать с первым графиком, поэтому удалите заголовок со второго графика — перейдите к заливке текста под опцией форматирования и измените значение на «без заливки».
12. Именование осей очень важно, особенно для облегчения идентификации.Назовите оси в соответствии с заголовками столбцов.
Перетащите и выровняйте две диаграммы вместе.
Это все, что есть о том, как нанести три переменные на один график. Надеюсь, вам понравился этот урок. Поделись, пожалуйста!
Нравится:
Нравится Загрузка …
Пузырьковая диаграмма с 3 переменными
Что такое пузырьковая диаграмма?
Пузырьковая диаграмма используется для визуализации данных в трех измерениях. Вместо того, чтобы отображать только две переменные (x и y) на традиционной диаграмме, пузырьковая диаграмма позволяет вам также добавить третью переменную.Первые переменные отображаются как координаты, а третьи — как размер пузыря.
Эту диаграмму можно использовать, когда у вас есть третье значение, которое можно использовать для определения относительного размера пузыря. Чем выше значение, тем больше будет размер пузыря.
Например, если у вас есть точечная диаграмма, которая показывает взаимосвязь между возрастом дома и его близостью к городу , и вы хотите добавить значение дома (третья переменная), тогда пузырьковая диаграмма приведет вас к этому.
Как создать пузырьковую диаграмму?
Этот график Excel с 3 переменными очень легко создать в Excel. Давайте посмотрим, как создать диаграмму рассеяния в Excel с 3 переменными с помощью нескольких примеров.
Загрузите книгу Excel и следуйте по ней:
Пример 1:
В таблице у вас есть возраст дома, близость к городу (в км) и стоимость дома. Итак, используя пузырьковую диаграмму с 3 переменными, вы можете построить возраст дома по оси X, близость к городу по оси Y и значение дома (3-я переменная ) как размер пузыря.
Выполните следующие шаги, чтобы понять, как создать пузырьковую диаграмму с 3 переменными:
ШАГ 1 : Выберите таблицу , в которой мы хотим создать диаграмму .
ШАГ 2 : перейдите к Вставить> Вставить точечную диаграмму или пузырьковую диаграмму> Пузырь .
ШАГ 3 : Щелкните Series1 и щелкните Delete , чтобы удалить его.
Горизонтальная ось также содержит отрицательные значения. Поскольку ось X представляет возраст дома, она не может быть отрицательной. Форматирование этой оси для ограничения значения негативов — хорошая идея, чтобы избежать путаницы.
ШАГ 4 : Щелкните правой кнопкой мыши по оси и выберите Format Axis , чтобы открыть Format Axis Panel .
ШАГ 5 : Под Параметры оси> Минимум> Установите значение 0.
Вот как будет выглядеть диаграмма:
Пример 2:
В этой таблице данных у вас есть данные по проекту, включая стоимость, прибыль и вероятность успеха.
Используя эти данные, давайте попробуем создать трехмерную пузырьковую диаграмму с 3 переменными!
ШАГ 1 : Выберите таблицу , в которой мы хотим создать диаграмму .
ШАГ 2 : перейдите к Вставить> Вставить точечную диаграмму или пузырьковую диаграмму> 3D-пузырь .
3Y-Y-YY-График СводкаИз этого туториала Вы узнаете, как создать график с тремя осями Y; одна левая ось Y и две правые оси Y. Что вы узнаете
Ступени
|
Видео: создание комбинированной диаграммы
Измените тип диаграммы для одного или нескольких рядов данных в диаграмме (графике) и добавьте дополнительную вертикальную ось (значения) в комбинированную диаграмму.
Создание комбинированной диаграммы со вторичной осью
В Excel 2013 вы можете быстро отобразить диаграмму, подобную приведенной выше, изменив диаграмму на комбинированную диаграмму.
Щелкните в любом месте диаграммы, которую вы хотите преобразовать в комбинированную диаграмму, чтобы отобразить CHART TOOLS .
Нажмите ДИЗАЙН > Изменить тип диаграммы .
На вкладке All Charts выберите Combo , а затем выберите диаграмму Clustered Column — Line on Secondary Axis .
Менее Выберите тип диаграммы и ось для серии данных , установите флажок Вторичная ось для каждой серии данных, которую вы хотите построить на дополнительной оси, а затем измените тип диаграммы на Линия .
Убедитесь, что все остальные серии данных показаны как Clustered Column .
Хотите больше?
Скопируйте диаграмму Excel в другую программу Office
Создайте диаграмму от начала до конца
Вы можете выделить различные типы данных, такие как Температура и Осадки, объединив два или более типов диаграмм в одну комбинированную диаграмму.
Различные типы данных часто имеют разные диапазоны значений, и с помощью комбинированной диаграммы вы можете включить дополнительную ось.
Выберите ячейки, которые хотите нанести на диаграмму.
Комбинированная диаграмма не является опцией Quick Analysis , поэтому мы нажимаем вкладку ВСТАВИТЬ на ленте, нажимаем кнопку Combo и выбираем вариант.
Я перемещаю диаграмму и меняю ее размер, чтобы с ней было легче работать.
Я даю диаграмме название.
Добавление дополнительной оси для осадков упростит понимание диаграммы.
Я дважды щелкаю линию осадков на диаграмме и выбираю Secondary Axis на панели задач.
Если бы мы добавили заголовки осей, это сделало бы диаграмму еще четче.
Нажмите кнопку ЭЛЕМЕНТЫ ДИАГРАММЫ , щелкните стрелку рядом с заголовком Axis Titles , выберите Primary Vertical и Secondary Vertical , щелкните поля заголовка и введите соответствующий текст.
Далее, Скопируйте график .
Добавить или удалить дополнительную ось на диаграмме в Excel
Примечание: Следующая процедура применима к Office 2013 и более новым версиям. Ищете шаги по Office 2010?
Выберите диаграмму, чтобы открыть ее. Инструменты для диаграмм .
Выберите Дизайн > Изменить тип диаграммы .
Выберите комбинацию > Столбец кластера — линия на вторичной оси .
Выберите Secondary Axis для серии данных, которую вы хотите отобразить.
Щелкните стрелку раскрывающегося списка и выберите Строка .
Выберите ОК .
Добавление или удаление дополнительной оси на диаграмме в Office 2010
Когда значения на двумерной диаграмме сильно различаются от ряда данных к ряду данных, или когда у вас есть смешанные типы данных (например, цена и объем), вы можете нанести один или несколько рядов данных на вторичную вертикаль (значение ) ось.Масштаб вторичной вертикальной оси отражает значения для связанных рядов данных.
После добавления дополнительной вертикальной оси к двухмерной диаграмме вы также можете добавить дополнительную горизонтальную ось (категории), которая может быть полезна на диаграмме xy (точечной диаграммы) или пузырьковой диаграмме.
Чтобы помочь различать ряды данных, нанесенные на вторичную ось, вы можете изменить их тип диаграммы.Например, в столбчатой диаграмме вы можете изменить ряд данных на вторичной оси на линейную диаграмму.
Важно: Для выполнения следующих процедур у вас должна быть существующая двухмерная диаграмма. Вторичные оси не поддерживаются в трехмерных диаграммах.
Добавить дополнительную вертикальную ось (Office 2010)
Вы можете нанести данные на вторичную вертикальную ось по одному ряду данных за раз.Чтобы нанести более одной серии данных на вторичную вертикальную ось, повторите эту процедуру для каждой серии данных, которую вы хотите отобразить на вторичной вертикальной оси.
На диаграмме щелкните ряд данных, который вы хотите отобразить на вторичной вертикальной оси, или выполните следующие действия, чтобы выбрать ряд данных из списка элементов диаграммы:
Щелкните диаграмму.
Появится окно «Инструменты диаграммы » , добавив вкладки Design , Layout и Format .
На вкладке Формат в группе Текущий выбор щелкните стрелку в поле Элементы диаграммы , а затем щелкните ряд данных, которые вы хотите построить вдоль вторичной вертикальной оси.
На вкладке Формат в группе Текущий выбор щелкните Формат выбора .
Отображается диалоговое окно Формат данных серии .
Примечание: Если отображается другое диалоговое окно, повторите шаг 1 и убедитесь, что вы выбрали ряд данных на диаграмме.
На вкладке Series Options в разделе Plot Series На нажмите Secondary Axis , а затем нажмите Close .
На диаграмме отображается дополнительная вертикальная ось.
Чтобы изменить отображение дополнительной вертикальной оси, выполните следующие действия:
На вкладке Макет в группе Оси щелкните Оси .
Щелкните Secondary Vertical Axis , а затем щелкните нужный параметр отображения.
Чтобы изменить параметры оси вторичной вертикальной оси, выполните следующие действия:
Щелкните правой кнопкой мыши вторичную вертикальную ось, а затем выберите Ось формата .
В разделе Параметры оси выберите параметры, которые вы хотите использовать.
Добавить дополнительную горизонтальную ось (Office 2010)
Для выполнения этой процедуры у вас должна быть диаграмма, отображающая вторичную вертикальную ось.Чтобы добавить дополнительную вертикальную ось, см. Добавление дополнительной вертикальной оси.
Щелкните диаграмму, на которой отображается дополнительная вертикальная ось.
Появится окно «Инструменты диаграммы » , добавив вкладки Design , Layout и Format .
На вкладке Макет в группе Оси щелкните Оси .
Щелкните Secondary Horizontal Axis , а затем щелкните нужный параметр отображения.
Изменение типа диаграммы ряда данных (Office 2010)
На диаграмме щелкните ряд данных, который нужно изменить.
Появится окно «Инструменты диаграммы » , добавив вкладки Design , Layout и Format .
Совет: Вы также можете щелкнуть правой кнопкой мыши ряд данных, выбрать Изменить тип диаграммы ряда , а затем перейти к шагу 3.
На вкладке Модель в группе Тип щелкните Изменить тип диаграммы .
В диалоговом окне Изменить тип диаграммы щелкните тип диаграммы, который вы хотите использовать.
В первом поле отображается список категорий типов диаграмм, а во втором поле показаны доступные типы диаграмм для каждой категории типов диаграмм. Дополнительные сведения о типах диаграмм, которые вы можете использовать, см. В разделе Доступные типы диаграмм.
Примечание: Вы можете изменить тип диаграммы только для одного ряда данных за раз. Чтобы изменить тип диаграммы для нескольких серий данных в диаграмме, повторите шаги этой процедуры для каждой серии данных, которую вы хотите изменить.
Удаление дополнительной оси (Office 2010)
Щелкните диаграмму, на которой отображается дополнительная ось, которую вы хотите удалить.
Появится окно «Инструменты диаграммы » , добавив вкладки Design , Layout и Format .
На вкладке Макет в группе Оси щелкните Оси , щелкните Вторичная вертикальная ось или Вторичная горизонтальная ось , а затем нажмите Нет .
Советы:
Вы также можете щелкнуть вторичную ось, которую хотите удалить, и затем нажать DELETE или щелкнуть правой кнопкой мыши вторичную ось и затем нажать Удалить .
Чтобы удалить второстепенные оси сразу после их добавления, нажмите Отменить на панели быстрого доступа или нажмите CTRL + Z.
Когда значения на диаграмме сильно различаются от ряда к ряду данных, вы можете нанести один или несколько рядов данных на вторичную ось. Вторичную ось также можно использовать как часть комбинированной диаграммы, когда у вас есть смешанные типы данных (например, цена и объем) на одной диаграмме.
На этом графике основная вертикальная ось слева используется для объемов продаж, а дополнительная вертикальная ось справа — для цен.
Выполните одно из следующих действий:
Добавить дополнительную ось
Этот шаг относится только к Word для Mac: в меню View щелкните Print Layout .
На диаграмме выберите ряд данных, которые вы хотите отобразить на вторичной оси, а затем щелкните вкладку Конструктор диаграммы на ленте.
Например, на линейной диаграмме щелкните одну из линий диаграммы, и все маркеры данных этой серии данных станут выделенными.
Щелкните Добавить элемент диаграммы > Оси > и выберите между Secondary Horizontal или Second Vertical .
 Вы можете поменять значения в ручную или выделить область ячеек зажав левую клавишу мыши:
Вы можете поменять значения в ручную или выделить область ячеек зажав левую клавишу мыши: Кликните по нему левой клавишей мыши и внесите свое название:
Кликните по нему левой клавишей мыши и внесите свое название: Строим график функций онлайн
Строим график функций онлайн

 Изобразить график функции y = log 2 |x|
Изобразить график функции y = log 2 |x|  Значит, вместо исходной функции y = -x 2 + 2|x| – 1
Значит, вместо исходной функции y = -x 2 + 2|x| – 1 9) .
9) .
 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .
 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

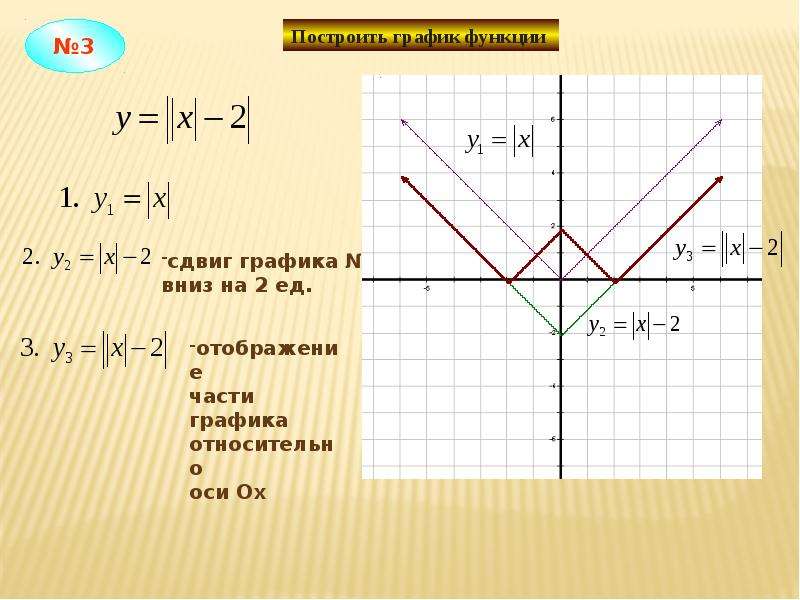 Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции. е. часть графика функции
е. часть графика функции если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) . е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .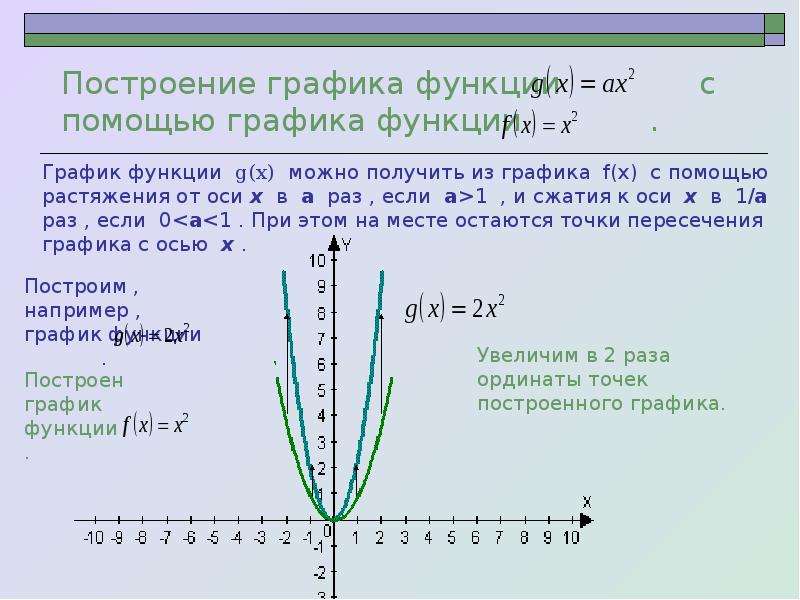 А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).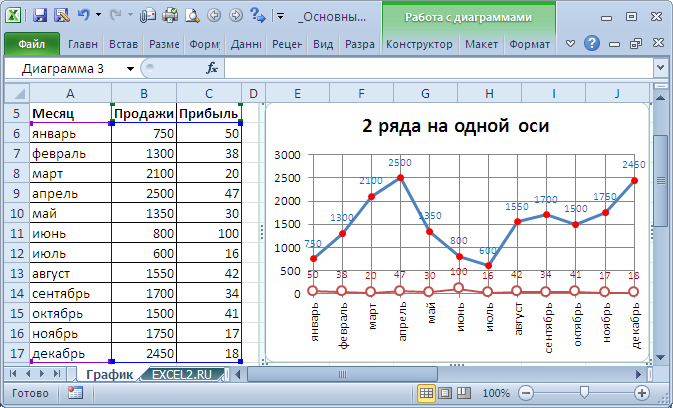 Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.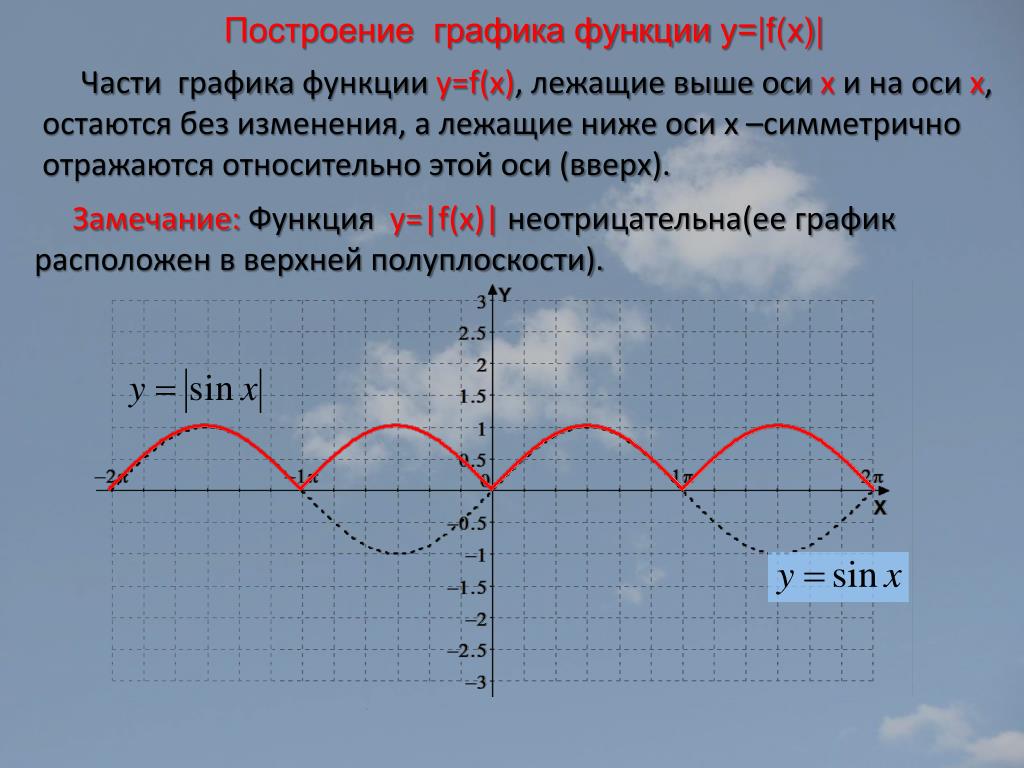 Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Здесь пример для y = 2 x (a = 2 > 1).
Здесь пример для y = 2 x (a = 2 > 1). Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2
Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2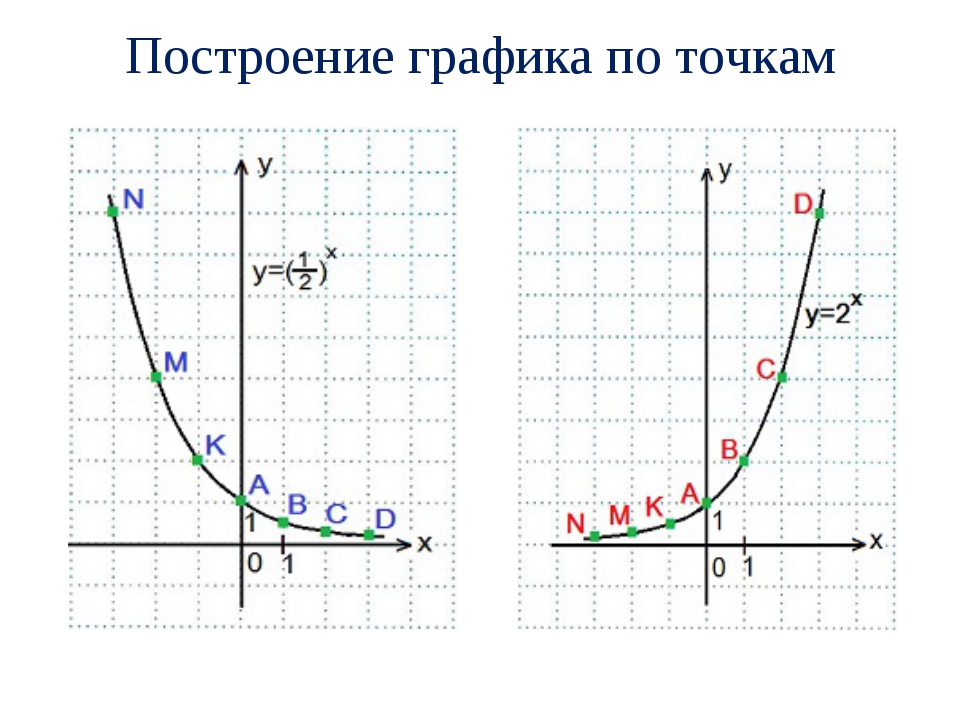
 п.
п. 2019: Chart Creator больше не работает, к сожалению.
2019: Chart Creator больше не работает, к сожалению.
Ваш комментарий будет первым