Урок 20. построение графиков функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №20. Построение графиков функций.
Перечень вопросов, рассматриваемых в теме
- Исследование функций;
- Построение графиков функций;
- Применение производной для решения графических задач.
Глоссарий по теме
Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.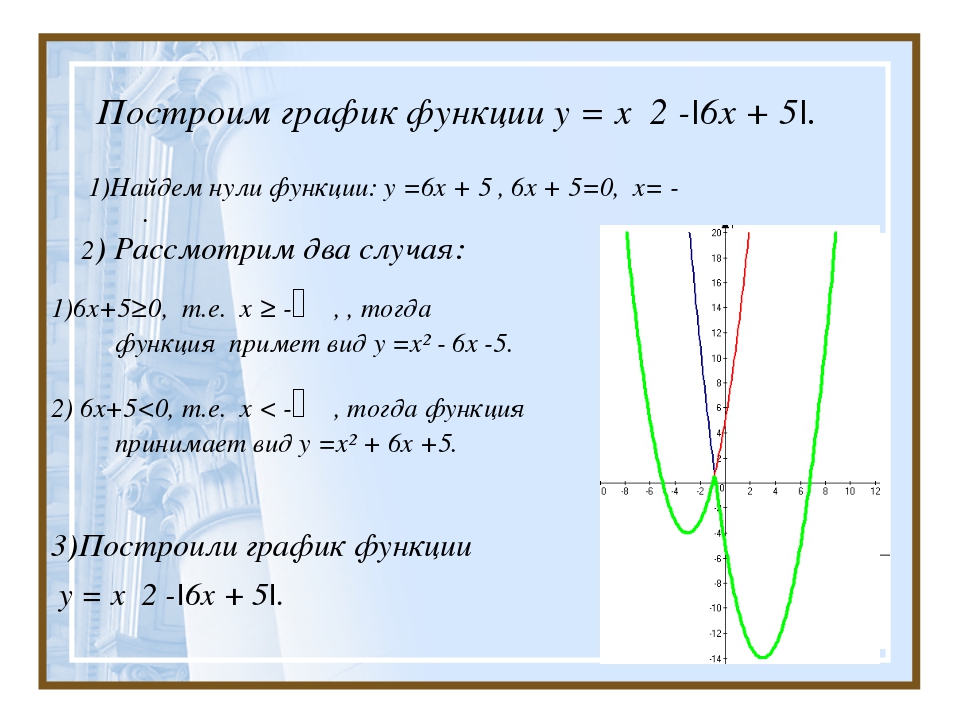
Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Максимум функции. Значение функции в точке максимума называют максимумом функции.
Минимум функции. Значение функции в точке минимума называют минимумом функции.
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.
Точка максимума функции.
Точку х0называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2 , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.
: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.
Полная схема построения графика функции:
- Найти область определения функции D(f).
- Исследовать функцию на четность (найти f(-x)).
- Найти асимптоты.
- Найти стационарные и критические точки.
- Найти промежутки монотонности.
- Найти интервалы выпуклости вверх и выпуклости вниз.
- Найти точки перегиба
- Составить таблицу значений функции для некоторых точек.
- По полученным данным построить график функции.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Постройте график функции у = х3 – 3х + 3, используя краткую схему построения. схему построения.
Решение:
1) D(y) = (-∞; +∞)
2) Функция не является ни четной, ни нечетной, т. к.
3) Асимптот нет
4) f’(x) = 3x2 – 3, f’(x) = 0 при х = 1, х = -1.
х = 1, х = -1 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.
6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.
Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.
7) Результаты исследования представим в виде таблицы.
x | (-∞; -1) | -1 | (-1; 1) | 1 | (1; +∞) |
f’(x) | + | 0 | — | 0 | + |
f(x) | 5 | 1 | |||
max | min |
8) Координаты некоторых точек:
9) По полученным данным строим график (рис.
Рисунок 1 – график функции у = х3 – 3х + 3
Пример 2. Постройте график функции, используя подробную схему построения. схему построения.
Решение:
1)
2) Функция не является ни четной, ни нечетной, т. к.
3) х = 1 – вертикальная асимптота
4) , f’(x) = 0 при х = 2, х = 0.
х = 2, х = 0 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки убывания.
Так как в точке х = 0 производная меняет знак с «+» на «-», то х = 0 – точка максимума.
Так как в точке х = 2 производная меняет знак с «-» на «+», то х = 2 – точка минимума.
х = 1 – не является точкой экстремума
6) Найдем интервалы выпуклости функции.
; при функция выпукла вверх.
; при функция выпукла вниз.
7) Результаты исследования представим в виде таблицы.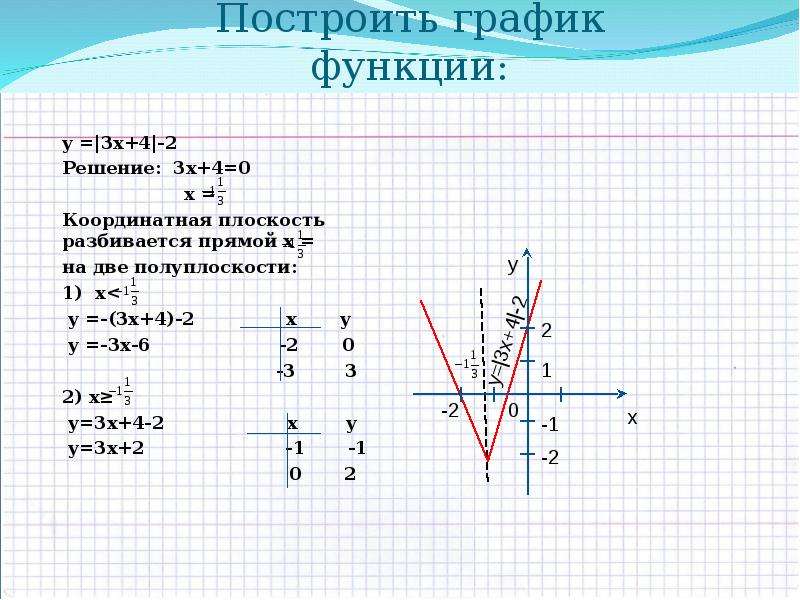
x | (-∞; 0) | 0 | (0; 1) | 1 | (1; 2) | 2 | (2; +∞) |
f’(x) | + | 0 | — | Не сущ. | — | 0 | + |
f’’(x) | — | — | Не сущ. | + | + | ||
f(x) | -4 | Не сущ. | 0 | ||||
max | min |
8) Координаты некоторых точек:
x | -1 | 0,5 | 1,5 | 3 |
f(x) | -4,5 | -4,5 | 0,5 | 0,5 |
9) По полученным данным строим график (рис.
2)
Рисунок 2 – график функции
Графики функций и поверхностей в Python Питон Matplotlib
Построение графиков с помощью модуля Matplotlib в Python Питон.
В этом уроке мы разберём, как строить графики функций с помощью модуля Matplotlib в Python Питон.
Matplotlib это библиотека для Python, предназначенная для визуализации данных. В данном уроке мы разберём построение графиков функций в Питон на плоскости и построение поверхности в трёхмерном пространстве. Зачастую, именно Matplotlib используется в научных исследованиях и конференциях для демонстрации полученных данных.
Для построения графиков нужно импортировать модуль 
Для удобного построения графиков так же нужно использовать библиотеку NumPy.
Matplotlib, как и NumPy, встроен в среду разработки Spyder, поэтому их можно импортировать без предварительной установки.
import numpy as np
import matplotlib.pyplot as plt
as np и as plt означает, что когда мы будем вызывать функции и процедуры из модулей, вместо названия модулей мы будем использовать np и plt.
Для построения графика функции в Python нужно задать саму функцию. Её можно задать с помощью лямбда-функции. Лямбда-функция — это краткий способ записи обычной функции в одну строчку. В этом уроке мы рассмотрим построение синусоиды на Питоне. Синусоида задаётся функцией f(x) = sin(x).
y = lambda x: np.sin(x)
y это обозначение функции (для её вызова мы будем использовать y(x)), lambda это ключевое слово, обозначающее начало задания лямбда-функции, x это аргумент, использующийся в функции, после двоеточия задаётся функция.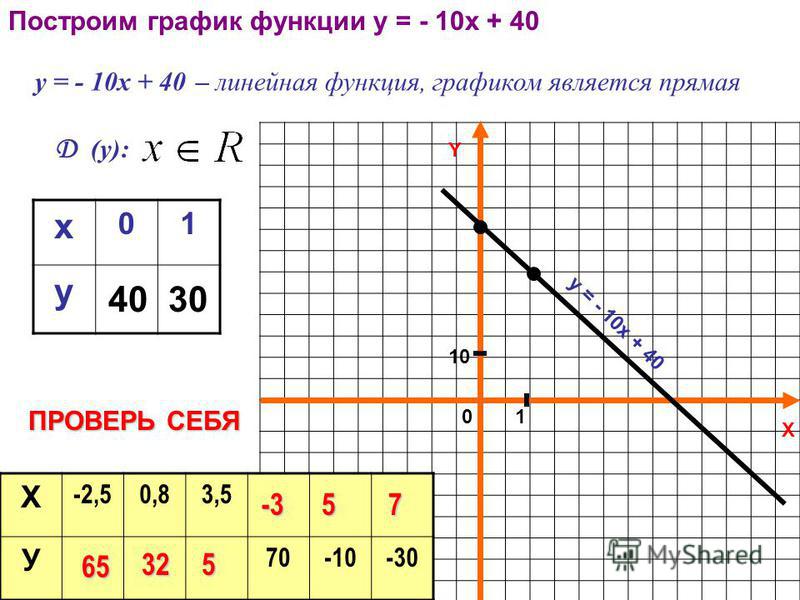
Так как в стандартном Python нет функции, возвращающей синус x, мы его задаём с помощью NumPy, его мы импортировали под именем np.
Все действия в Pyplot производятся на рисунках. Для построения графика функции в Python нужно сначала задать сетку координат. Сетка координат в python задается с помощью команды plt.subplots().
fig = plt.subplots()
Мы должны определить область значений, на которой мы будем строить график функции в
x = np.linspace(-3, 3, 100)
linspace создаёт массив с нижней границей -3 и верхней границей 3, в созданном массиве будет 100 элементов. Чем больше будет последнее число, тем больше значений функции будет рассчитываться, тем точнее будет отображаться график в Python.
После того, как мы создали систему координат, область построения, мы можем построить график в Питон.
Для построения графика фуекции в Python нужно использовать команду plt.plot(x, y(x)), где x это аргумент, y(x) это функция от x, заданная с помощью лямбда-выражения.
plt.plot(x, y(x))
После того, как мы построили график в Python, нужно показать его на рисунке. Для этого используется plt.show().
Полный код программы на python для рисования графика функции
# импортируем модули
import numpy as np
import matplotlib.pyplot as plt
# функция
y = lambda x: np.sin(x)
# создаём рисунок с координатную плоскость
fig = plt.subplots()
# создаём область, в которой будет
# — отображаться график
x = np.linspace(-3, 3,100)
# значения x, которые будут отображены
# количество элементов в созданном массиве
# — качество прорисовки графика
# рисуем график
plt.plot(x, y(x))
# показываем график
plt.
show()
Получим график синусоиды в python в отдельном окне
Отображение нескольких графиков на одном рисунке в Python
В одной области в python можно отобразить графики нескольких функций. Добавим aeyrwb. y=x и нарисуем ее совместно с синусоидой.
Для этого введем еще одну функцию с помощью lambda
y1=lambda x: x
Построим график этой функции
plt.plot(x,y1(x))
В итоге программа в Python для построения графиков двух функций в одном окне
# импортируем модули
import numpy as np
import matplotlib.pyplot as plt
# функция
y = lambda x: np.sin(x)
y1=lambda x: x
# создаём рисунок с координатную плоскость
fig = plt.subplots()
# создаём область, в которой будет
# — отображаться график
x = np.linspace(-3, 3,100)
# значения x, которые будут отображены
# количество элементов в созданном массиве
# — качество прорисовки графика
# рисуем график
plt.
2
от двух аргументов. Аргументы x и y, функция z.
f = lambda x, y: x ** 2 — y ** 2
Чтобы начать рисовать трехмерные поверхности в Python нужно сначал задать область построения с помощью функции plt.figure принимает параметр figsize(x, y), где x и y – ширина и высота рисунка в дюймах. Создадим рисунок в Python размером 12×6 дюймов для отображения графиков
fig = plt.figure(figsize = (12, 6))
В построенной области мы создадим рисунок, в котором будут отображено трёхмерное пространство с координатными осями и сама поверхность. В Питоне для этого используется fig.add_subplot().
ax = fig.add_subplot(1, 1, 1, projection = ‘3d’)
Функция в Python fig.add_subplot() разбивает область построения на клетки и задает в какой клетке рисовать трехмерный график. Так команда ax = fig.add_subplot(1, 1, 1, projection = ‘3d’) разбивает область построения на две клтки и в первую клетку будет отображаться трехмерный гарфик, благодаря аргументу projection = ‘3d’
Введём области отображения функции для каждого аргумента в Питон.
xval = np.linspace(-5, 5, 100)
yval = np.linspace(-5, 5, 100)
Нужно создать поверхность, которая будет отображаться на рисунке в Python. Для этого используется
surf = ax.plot_surface(x, y, z, rstride = 4, cstride = 4, cmap = cm.plasma)
Где x и y это принимаемые аргументы, z это получаемая функция, rstride и cstride отвечает за шаг прорисовки поверхности в Питон, чем меньше будут эти значения, тем более плавно будет выглядеть градиент на поверхности. С помощью cmap.plasma поверхность будет отображаться с цветовой схемой plasma. Например, существуют цветовые схемы, такие как viridis и magma. Полный список цветовых схем есть на сайте Matplotlib.
Пример программы на Python построение поверхности в трёхмерном пространстве# импортируем модули
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib import cm
import matplotlib.
pyplot as plt
# уравнение поверхности
f = lambda x, y: x ** 2 — y ** 2
# создаём полотно для рисунка
fig = plt.figure(figsize = (10, 10))
# создаём рисунок пространства с поверхностью
ax = fig.add_subplot(1, 1, 1, projection = ‘3d’)
# размечаем границы осей для аргументов
xval = np.linspace(-4, 4, 100)
yval = np.linspace(-4, 4, 100)
# создаём массив с xval столбцами и yval строками
# — в этом массиве будут храниться значения z
x, y = np.meshgrid(xval, yval)
# приравниваем z к функции от x и y
z = f(x, y)
# создаём поверхность
surf = ax.plot_surface(
# отмечаем аргументы и уравнение поверхности
x, y, z,
# шаг прорисовки сетки
# — чем меньше значение, тем плавнее
# — будет градиент на поверхности
rstride = 10,
cstride = 10,
# цветовая схема plasma
cmap = cm.
plasma)
Получим график трехмерной поверхности в цветовой гамме в специальном окне
Изменим параметры построения трехмерной поверхности, уменьшим размер сетик, сделаем поверхность более плавной и точной для этого уменьшаем параметры и сменим цветовую гамму на viridis
rstride = 2,
cstride = 2,
cmap = cm.viridis)
Получим график трехмерной поверхности в Python более точный и в другой цветовой гамме
Вернуться к содержанию курса python Следующая тема Классы в Питон
Поделиться:
Построение графиков — Sage Tutorial in Russian v9.2
Sage может строить двумерные и трехмерные графики.
Двумерные графики
В двумерном пространстве Sage может отрисовывать круги, линии и
многоугольники; графики функций в декартовых координатах; также графики
в полярных координатах, контурные графики и изображения векторных полей.
Некоторые примеры будут показаны ниже. Для более исчерпывающей информации
по построению графиков см.
Решение дифференциальных уравнений и Maxima,
а также документацию
Sage Constructions.
Данная команда построит желтую окружность радиуса 1 с центром в начале:
sage: circle((0,0), 1, rgbcolor=(1,1,0)) Graphics object consisting of 1 graphics primitive
Также можно построить круг:
sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True) Graphics object consisting of 1 graphics primitive
Можно создавать окружность и задавать ее какой-либо переменной. Данный пример не будет строить окружность:
sage: c = circle((0,0), 1, rgbcolor=(1,1,0))
Чтобы построить ее, используйте c.show() или show(c):
c.save('filename.png') сохранит график в файл.
Теперь эти „окружности“ больше похожи на эллипсы, так как оси имеют разный масштаб. Это можно исправить следующим образом:
sage: c.show(aspect_ratio=1)
Команда Хороший способ создания заполненных фигур — создание списка точек ( Напечатайте Можно добавить текст на график: Учителя математики часто рисуют следующий график на доске: не одну
ветвь arcsin, а несколько, т. Так как функция тангенса имеет больший интервал, чем синус, при
использовании той же техники для перевертывания тангенса требуется
изменить минимальное и максимальное значения координат для оси x: Sage также может строить графики в полярных координатах, контурные
построения и изображения векторных полей (для специальных видов функций).
Далее следует пример контурного чертежа: Sage также может быть использован для создания трехмерных графиков. Тип
урока: урок усвоения новых
знаний Оборудование
и материалы: компьютеры с
установленной программой, трафареты
параболы у=х2,
цветные маркеры. Цели урока: объяснить
правила построения графика
функции вида y=f(x+l),
если известен график функции y=f(x),
развивать умение строить графики
различных функций. Задачи
урока: Образовательные: экспериментальным путем (с
использованием ЭВМ) получить алгоритмы
построения графика функции вида
y=f(x+l),
если известен график функции y=f(x) научиться
применять полученные алгоритмы к
построению графиков с помощью трафарета закрепление
умений работать с операционной системой
Windows ХР Развивающие: формирование умений сравнивать,
обобщать изучаемые факты; развитие
у обучающихся самостоятельности в
мышлении и учебной деятельности; развитие
эмоций учащихся путем привлечения
наглядности и средств ТСО (компьютер). Воспитательные: воспитание коллективизма и
ответственности за общую работу; воспитание
взаимопомощи; воспитание
аккуратности (при выполнении построения
графиков функций). ХОД УРОКА 1.
Организационный момент. 2.
Актуализация знаний. Что
вы можете рассказать о функции у=х2? (Демонстрируется
слайд с изображением цветка.) Перед
вами ландыш. Данный рисунок выполнен с
помощью графика функции у=х2.
После изучения материала сегодняшнего
урока вы сами сможете нарисовать такой
рисунок, а проверить свои художества
можно, используя компьютер. 3.Сообщение
темы, цели урока. Организация восприятия
и осознания нового материала. Мы
с вами познакомились с графиками функций
у=кх2, у=. Какой
способ мы использовали для построения
графиков этих функций? (по
контрольным точкам). у=(х+3)2,
у=(х-2) 2 и у= по
точкам может занять очень много времени,
а мы сегодня научимся строить эти графики
быстро. Чем
отличаются данные функции от функций
у=х2 и
у=? Итак,
тема урока: “ Как
построить график функции у = f(x+l),
если известен график функции у = f(x)
”. На уроке мы должны экспериментальным
путем получить алгоритмы для построения
графиков квадратичных функций подобных
видов. Объяснение нового материала.
Практическая работа. Краткий
инструктаж по технике безопасности в
компьютерном классе. Нельзя
самостоятельно, без разрешения учителя,
включать и выключать компьютеры. Нельзя
касаться тыльной стороны компьютера
и проводов. Нельзя
работать мокрыми руками и во влажной
одежде. Нельзя
нажимать на клавиши ручкой или карандашом. Нельзя
ходить по классу, вставать со своего
рабочего места. В
случае неисправности компьютера или
при обнаружении запаха гари – подозвать
учителя. Учащиеся
проходят к компьютерам и садятся по 2-3
человека. Задание 1. Алгоритм работы:1.Впишите в окне имя
пользователя. 2.
Нажмите на кнопку «Вход» левой кнопкой
мыши. Выберите «Виртуальные лаборатории».
Щелкните левой кнопкой мыши «Лаборатория
«Графики функций»». 3.
На панели инструментов вызовите редактор
математических формул. 4.
а) Наберите формулу у=х2 и нажмите «ОК». б) Наберите формулу у=(х+2)2 и нажмите «ОК». в) Наберите формулу у=(х-3)2 и нажмите «ОК». Смените цвет графика
двойным щелчком левой кнопкой мыши. 5.
Какие изменения произошли с графиком
функции у=х2? Посмотрите
на значения l
и сделайте вывод: как, имея график функции
у=х2, построить
график функции у = f(x+l). Проверьте
свою гипотезу, построив графики функций: у=
, у = Разбор
происходит по тому же алгоритму работы. 6.
Точно так же обстоит дело и с графиками
функций у=аf(х+l) Алгоритм записывается в тетрадь Чтобы построить график функции
y= аf(х+l),
где l-заданное
положительное число, нужно сдвинуть
график функции у=ах2 вдоль оси х на l
единиц масштаба влево; чтобы построить
график функции y=af(x+l),
где l-заданное
отрицательное число, нужно сдвинуть
график функции у=ах2 вдоль оси х на l
единиц масштаба вправо. Итак,
мы получили алгоритмы для построения
графиков квадратичных функций. Как вы
считаете, будут ли полезны эти алгоритмы
в нашей работе, облегчат ли они нам
работу? 5.
Закрепление нового материала. 1) С помощью трафарета
функции у=х2 в одной системе координат постройте
графики функций. у = -(х + 4)2 у = - (х -1)2 2) Для закрепления материала учитель на
доске работает с помощью шаблона функции
у=х2.На
координатной плоскости шаблон переносится
в разные позиции относительно оси Ох
(вершина лежит на оси Ох в точках
-1,4,-5,3), а учащиеся называют функцию,
определяющую данный график. 3)Разобрать
задания: №394. График какой
функции получится, если гиперболу у
=7/х перенести: а) на 6 единиц масштаба влево
вдоль оси х; б) на 2 единицы масштаба вправо
вдоль оси х; в) на 4,7 единицы масштаба влево
вдоль оси х; г) на 7/8 единицы масштаба вправо
вдоль оси х. №395(а)Постройте
график функции и укажите, где она убывает,
где возрастает: у=2(х+1)2 №403(а). Решите
графически уравнение: (х-2)2=х № 400. Найдите
наибольшее и наименьшее значение функции
у= а)на отрезке [4;7]; б)на луче;
в) на луче;
г) на полуинтервале (3;7]. №405(а). Решите
графически уравнение: При наличии времени решить №
410 Постройте график функции у=х2 – 2х + 1 6. Подведение
итогов: Что нового вы узнали сегодня на
уроке? Какие были трудности? 7. Домашнее задание с.58-60(прочитать, выучить алгоритм
построения) №393, 396 (в,г), №404(г), №406(в) Приготовить шаблоны у=2х2 и у= Как построить график в Excel - задача несложная, но новичков порой сбивает с толку, какой тип диаграммы выбрать или как правильно построить таблицу данных. Итак, Excel предлагает два типа диаграмм для построения графика - Давайте построим сначала график, он строится очень просто, практически в одно-два касания. Используем данные о курсе доллара за декабрь 2013 г. Таблица данных Панель диаграмм Нажимаете кнопку "График". Виды графиков Среди них можно выбрать тот, что больше подходит для ваших целей. Но так как нам нужен просто ряд изменения по времени, то выбираем или первый график или аналогичный с маркерами. Я выбрал с маркерами, т.к. у нас не так много данных. График после первого этапа Перемещаем график Настройка подписей графика Я меняю название диаграммы, осей, легенду убираю, т.к. у нас одна кривая, легенда нужна для двух и больше, чтобы различать данные. Еще я добавлю основные линии по вертикали, так нагляднее. Остальное не критично. График с трендом В принципе, все. Виды точечных диаграмм График, построенный при помощи точечной диаграммы График функции Вторая таблица данных Окно выбора данных Корректировка данных рядов Можно поставить свое произвольное название ряда. Если вдруг Excel неверно взял какой-то ряд в качестве независимой или зависимой переменной, можно произвольно определить нужные диапазоны. Итоговый график Тут пятиминутное видео: Для большей инфы предлагаю посмотреть пример построения графика безубыточности. Эксель Практик «Глаза боятся, а руки делают» P.S. Понравилась статья? Подпишитесь на рассылку в правой части страницы (Бесплатный курс "Топ-10 инструментов Excel") и будьте в курсе новых событий. Графиком функции \(y=f\left(x \right)\) называется множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, т.е. точек \(M\left(x,f\left(x \right) \right)\). Для построения графиков функций со значениями аргумента и значениями функции, изменяющимися в широком диапазоне, удобно использовать логарифмический масштаб (от значения функции берется десятичный логарифм). Создание диаграмм и графиков - часть работы большинства людей - это один из лучших способов визуализировать данные в ясной, легко усваиваемой форме. (Ознакомьтесь с этим руководством, чтобы узнать больше о том, как создавать более качественные диаграммы.) Однако неудивительно, что некоторых людей немного пугает перспектива ковыряться в Microsoft Excel. Я вообще-то обожаю Excel, но я работаю в отделе маркетинга, так что это в значительной степени обязательное требование. Вот почему я подумал, что поделюсь полезным видеоуроком, а также некоторыми пошаговыми инструкциями для всех, кто съеживается при мысли о преобразовании электронной таблицы, полной данных, в диаграмму, которая на самом деле, знаете ли, означает что-то. Вот простые шаги, необходимые для построения диаграммы или графика в Excel. А если у вас мало времени, посмотрите видеоурок ниже. Имейте в виду, что существует много разных версий Excel, поэтому то, что вы видите в видео выше, может не всегда точно совпадать с тем, что вы увидите в своей версии.В приведенных ниже инструкциях я использовал Excel 2017 версии 16.9 для Max OS X . Мы рекомендуем вам следовать приведенным ниже письменным инструкциям и демонстрационным данным (или загружать их в формате PDF по ссылкам ниже), чтобы вы могли следовать их указаниям. Большинство кнопок и функций, которые вы увидите и прочитаете, очень похожи во всех версиях Excel. Загрузить демонстрационные данные | Инструкции по загрузке (Mac) | Скачать инструкцию (ПК) Во-первых, вам нужно ввести данные в Excel. Возможно, вы экспортировали данные из другого места, например, из маркетингового программного обеспечения или инструмента для проведения опросов. Или, может быть, вы вводите его вручную. В приведенном ниже примере в столбце A у меня есть список ответов на вопрос «Показал ли входящий маркетинг ROI?», А в столбцах B, C и D у меня есть ответы на вопрос: «Есть ли у вас у компании есть официальное соглашение о продажах и маркетинге? » Например, столбец C, строка 2 показывает, что 49% людей, имеющих SLA (соглашение об уровне обслуживания), также говорят, что входящий маркетинг продемонстрировал рентабельность инвестиций. В Excel у вас есть множество вариантов для создания диаграмм и графиков. (Чтобы узнать, какой тип диаграммы / графика лучше всего подходит для визуализации ваших данных, ознакомьтесь с нашей бесплатной электронной книгой Как использовать визуализацию данных для победы над аудиторией .) Данные, с которыми я работаю, лучше всего будут выглядеть на гистограмме, так что давайте сделаем ее. Чтобы создать гистограмму, выделите данные и включите заголовки осей X и Y. Затем перейдите на вкладку « Insert » и в разделе диаграмм щелкните значок столбца . В открывшемся раскрывающемся окне выберите нужный график. В этом примере я выбрал первый вариант двухмерного столбца - просто потому, что я предпочитаю плоскую графику трехмерному виду.См. Получившуюся гистограмму ниже. Если вы хотите переключить то, что отображается на осях X и Y, щелкните правой кнопкой мыши гистограмму, выберите « Select Data » и нажмите « Switch Row / Column ». Это изменит порядок того, какие оси несут какие части данных в списке, показанном ниже. Когда вы закончите, нажмите «ОК» внизу. Итоговый график будет выглядеть так: Чтобы изменить макет надписи и легенды, щелкните гистограмму, а затем перейдите на вкладку « Chart Design ». Здесь вы можете выбрать, какой макет вы предпочитаете для заголовка диаграммы, заголовков осей и легенды. В моем примере (показанном ниже) я выбрал вариант, который отображал более мягкие цвета полос и надписи под на диаграмме. Для дальнейшего форматирования легенды щелкните по ней, чтобы открыть боковую панель «Легенда формата », как показано ниже. Когда вы впервые создаете график в Excel, размер меток оси и легенды может быть немного маленьким, в зависимости от типа выбранного вами графика или диаграммы (столбик, круговая диаграмма, линия и т. Д.). Создав диаграмму, вы захотите усилить эти метки, чтобы они были удобочитаемыми. Чтобы увеличить размер меток графика, щелкните их по отдельности и, вместо того чтобы открывать новое окно формата, снова щелкните вкладку « Home » на верхней панели навигации Excel. Затем используйте раскрывающиеся поля типа и размера шрифта, чтобы по своему усмотрению расширить или сузить легенду диаграммы и метки осей. Чтобы изменить тип измерения, отображаемого на оси Y, щелкните проценты оси Y на диаграмме, чтобы открыть окно « Format Axis ». Здесь вы можете решить, хотите ли вы отображать единицы измерения, расположенные на вкладке Axis Options , или вы хотите изменить, будет ли ось Y отображать проценты до 2 знаков после запятой или до 0 знаков после запятой. Поскольку мой график автоматически устанавливает максимальный процент оси Y на 60%, я могу вручную изменить его на 100%, чтобы представить мои данные в более универсальном масштабе.Для этого я могу выбрать опцию « Максимум » - два поля ниже под « Границы » в окне оси формата - и изменить значение с 0,6 на 1 . Результирующий график будет изменен так, чтобы он выглядел так, как показано ниже (я увеличил размер шрифта по оси Y на вкладке «Главная», чтобы вы могли видеть разницу): Чтобы отсортировать данные, чтобы ответы респондентов отображались в обратном порядке, щелкните правой кнопкой мыши график и выберите «Выбрать данные», чтобы открыть то же окно параметров, которое вы вызывали на шаге 3 выше.На этот раз щелкните стрелки вверх и вниз, как показано ниже, чтобы изменить порядок данных на диаграмме. Если у вас есть более двух строк данных для настройки, вы также можете изменить их порядок в возрастающем или убывающем порядке. Для этого выделите все данные в ячейках над диаграммой, щелкните « Data » и выберите « Sort, », как показано ниже. Вы можете выбрать сортировку от наименьшего к наибольшему или от наибольшего к наименьшему, в зависимости от ваших предпочтений. А теперь самое интересное и легкое: присвоение имени графику. К настоящему времени вы, возможно, уже поняли, как это сделать. Вот простой разъяснитель. Сразу после создания диаграммы появится название «Заголовок диаграммы» или что-то подобное в зависимости от используемой версии Excel. Если у вас есть название, которое вам нравится, нажмите « Home » на верхней панели навигации и используйте параметры форматирования шрифта, чтобы выделить заголовок, которого он заслуживает.См. Эти варианты и мой окончательный график ниже: Довольно просто, правда? Ознакомьтесь с некоторыми дополнительными ресурсами ниже, чтобы получить дополнительную помощь по использованию Excel и разумной визуализации данных. Хотите еще больше советов по Excel? Прочтите этот пост о том, как добавить вторую ось на диаграмму Excel. Создать график Origin предоставляет библиотеку шаблонов. Начиная с Origin 2016, был добавлен более мощный «клонируемый» шаблон. Эти шаблоны предназначены для «умного построения», то есть вы можете клонировать график со сложной иерархией слоев или с исходными данными, которые нельзя указать простым выбором.См. Это руководство по построению графиков на основе пользовательских шаблонов графиков, чтобы узнать, как сохранять и использовать как стандартные, так и клонируемые шаблоны. Из этого туториала Вы узнаете, как: Используйте тот же рабочий лист из предыдущего примера. С помощью этого контекстного меню вы можете изменить данные X или Y текущего графика, чтобы они были другим столбцом в текущем проекте. Этим столбцом будет любой столбец, кроме текущего столбца данных X или Y, независимо от обозначения столбца. Вы также можете использовать контекстное меню Изменить рабочий лист , чтобы изменить текущие данные X и Y, чтобы они были столбцами с тем же индексом столбца на другом листе текущей книги, независимо от обозначения столбца и короткого имени столбца. Примечание: Вы также можете использовать диалоговое окно Layer Contents или Plot Setup для изменения входных данных. Тип графика по умолчанию для графика перетаскивания - Текущий , который совпадает с текущим активным графиком.Однако вы можете изменить параметр по умолчанию. Для этого щелкните «Предпочтение : параметры », перейдите на вкладку «График » и измените параметр « Перетащите график » в раскрывающееся меню. В этом разделе мы будем использовать кнопку Copy for Plotting на мини-панели инструментов , чтобы добавить новые графики к существующему графику. Диалоговое окно Layer Contents полезно в первую очередь для добавления или удаления графиков данных из графического слоя. Начиная с Origin 2016, вы можете переключать слои, не закрывая диалоговое окно, что упрощает добавление графиков или удаление графиков из многослойного графика.Чтобы продемонстрировать это, мы вернемся к трехслойному графику, который мы создали в первом упражнении этого руководства: В первом упражнении мы построили данные из листа S32-014-04. Диалоговое окно «Настройка графика» полезно для множества задач построения графиков, включая создание графиков, изменение типа графика, добавление графиков или удаление графиков с графика, группирование или разгруппирование графиков и редактирование диапазона графиков. На приведенном выше графике условные обозначения для каждого слоя идентичны друг другу.Вы можете удалить два из них. Или выполните настройки ниже в диалоговом окне Legend Update , чтобы просто показать одну легенду для всего окна графика. После применения настроек вы можете нажать Ctrl + двойной щелчок по тексту легенды для дальнейшего редактирования на месте; или вы можете щелкнуть правой кнопкой мыши поле легенды, чтобы выбрать Properties . Когда ваши данные включают столбец категориальных данных или несколько столбцов, характеризующих какую-то вложенную подгруппу данных, как и данные ниже , тогда вы можете отобразить свои данные как: Начиная с Origin 2017, вы представили график Trellis Plot, который имеет один слой, но с панелями M X N . Как видите, этот решетчатый график имеет только один слой, но с шестью панелями ( 2 × 3 ): 2 строки представляют переменную «Пол», Женский и Мужской ; три столбца представляют переменную «Город»: A , B и C . Помимо решетчатой диаграммы, вы также можете отобразить данные такого типа в виде сгруппированной диаграммы в виде прямоугольников / столбцов. Как вы можете видеть, столбец данных («Зарплата») был нанесен в виде сгруппированных прямоугольных диаграмм: две группы по «полу», женский и мужской ; внутри этих двух групп три подгруппы по «городу»: A , B и C . Origin предлагает опцию построения, Несколько панелей по метке , которая позволяет создавать многослойный график, каждый слой которого содержит несколько графиков, обозначенных одной и той же меткой. Ана Дафф Desmos - это открытый онлайн-инструмент с обширной числовой и визуальной универсальностью.Он позволяет пользователю строить и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, функции графиков и создавать модели регрессии из наборов данных, среди других возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент слайдера, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к конкретным компонентам. Перейдите на сайт Desmos.com и перейдите по ссылке «Начать построение графиков». Щелкните График без названия и введите название графика (доступно только зарегистрированным пользователям). Введите краткое описание действия: поместите курсор в строку 1, щелкните + Desmos позволяет пользователю явно указывать функцию (функции) и моделировать данные с помощью функции с использованием регрессии.Если вы используете упражнение как часть оценивания, попросите учащихся импортировать случайно сгенерированные данные (например, из документа Excel), чтобы в результирующих функциях была изменчивость. Позвольте результатам обучения направлять ваш набор инструкций. Обратите внимание, что задачи могут включать статическое и динамическое исследование модели, включая визуализацию изменений с помощью ползунка. Для лучшего прогресса задачи можно организовать по папкам и руководствоваться заметками инструктора, встроенными в график Desmos.Оба могут быть добавлены, щелкнув Раздел справки предоставляет большой банк подробных и интерактивных учебных ресурсов для новых и опытных пользователей Desmos. Учащиеся могут научиться создавать ползунки и таблицы, определять ограничения домена и диапазона и выполнять регрессию, следуя простым интерактивным турам, предоставляемым Desmos. Библиотека видеоуроков обширна и легко доступна для поиска, а Руководство пользователя Desmos предоставляет базовое руководство по инструментам Desmos. Нажмите на инструмент «Поделиться своим графиком», расположенный в верхнем левом углу. Созданная ссылка отправит студентов на график и позволит каждому студенту просматривать и изменять его отдельно от других пользователей, не затрагивая созданный вами график. Обратите внимание, что вы также можете использовать этот инструмент для сохранения изображения графика (за некоторыми исключениями) и встраивания его в другие платформы. Включите результаты исследований учащихся и извлеченные уроки в оценки с помощью инструмента «Поделитесь своим графиком», с помощью которого учащиеся обмениваются ссылками или изображениями своей работы внутри, непосредственно или как часть отдельного документа для отправки.Обратите внимание, что ссылка будет включать график в том виде, в котором он был на момент создания ссылки. Руководство пользователя Desmos Примеры изучения функций через Desmos в действии: Экичи, Селил и Плайли, Крис. «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Интернет. Годин, Шон. "В чем проблема? Ищу лжецов.Бюллетень - Ассоциация математиков Онтарио 56.4 (2018): 11–13. Интернет. Хойлс, Селия. «Преобразование математической практики учащихся и учителей с помощью цифровых технологий». Исследования в области математического образования. 20.3 1–20. Интернет. Набб, Кейт и Муравска, Жаклин. «Мотивация расчетов с помощью одного вопроса». ПРИМУС 29.10 (2019): 1140–1153. Интернет. Shahriari, Razieh et al. «Влияние использования технологий на понимание студентами математики и алгебры в колледже.”ProQuest Dissertations Publishing, 2019. Web. Ана Дафф - научный сотрудник факультета бизнеса и информационных технологий Технического университета Онтарио, где она преподает математические курсы первого года обучения. Ее исследовательский опыт связан с математикой, в которой она имеет докторскую степень. из Университета Оттавы. До Технологического университета Онтарио она преподавала математику в Оттавском университете, Королевском военном колледже Канады и Международной школе Белграда в Сербии. Она также имеет обширный опыт в разработке и управлении крупномасштабными программами мобилизации и обучения сообществ в Канаде и за рубежом в неправительственном и государственном секторах. TL; DR: Определите свои собственные функции, которые включают построение графиков на определенных осях со следующим синтаксисом: = None, ** plt_kwargs): Вы можете найти исходный репозиторий кода по адресу эта ссылка. В предыдущем посте я показал вам, как лучше организовать ваши фигуры. Мы увидели, как вы можете аккуратно отображать различные графики с помощью подзаголовков, как добавлять свободно плавающие оси и как легко создать мозаичную организацию ваших осей с помощью GridSpec. Поскольку в центре внимания этого поста была общая структура и представление общей фигуры, сами графики были довольно простыми, поскольку они использовали только одну предопределенную функцию matplotlib, такую как Здесь я покажу вам, как создавать свои собственные пользовательские функции построения графиков, которые можно легко использовать, вызывая их на ваших организованных графиках, используя что-то вроде следующего: Вместе с хорошей организацией подзаголовков, это поможет вам максимизировать статические графики на matplotlib (предвещая последующее руководство по динамическим графикам… ... возможно ...) и использовать информацию с разных графиков, чтобы поделиться исчерпывающей историей ваших данных. Первый шаг к тому, чтобы иметь возможность иметь серию настраиваемых графиков внутри вашей фигуры, - это возможность связать индивидуальный настраиваемый график с отдельными осями.Первый шаг - передать оси, по которым мы хотим построить график, нашей пользовательской функции. Это можно сделать просто так: Итак, что я там делал? Первая важная часть здесь - это аргумент Почему , мы видим, что если объект axes не был предоставлен в Давайте проверим это, сначала построив график без указания осей, а затем указав конкретные оси: Пока все хорошо; мы можем создать функцию для построения данных и связать ее с определенными осями нашего графика (она даже позаботится о себе, если оси не были предоставлены). А как насчет Если вы не привыкли работать с В стороне, однако, если вы действительно не видели этот тип обозначения звездочки раньше, использование одинарных звездочек Ни ошибок, ни проблем ... А что, если вы хотите сделать линию толще? Обычно в Это решит проблему. Но как насчет всех остальных возможных аргументов в .plot () . Записывать их все в нашей функции вместе со значениями по умолчанию было бы очень долго и не очень практично: Вот где используется нотация Например, если бы мы использовали нашу функцию построения графика как Таким образом, использование Ранее я упоминал, что Таким образом, не зная, сколько и какие настройки графика будут использоваться, мы можем передать их все той части нашей функции, которая будет выполнять построение графика. Мы можем увидеть это снова, используя нашу оригинальную функцию Тогда это позаботится об основном синтаксисе. После этого вы уже сможете приступить к созданию еще нескольких интересных сюжетов. Но прежде чем приступить к работе, нам нужно решить одну потенциальную проблему, с которой вы можете столкнуться при использовании Ответ состоит в том, что « Чем здесь отличается и как его использовать? Сначала посмотрите список возможных входов. Теперь вместо Если вы следовали моему объяснению о Использование их позже с двойной звездочкой ничем не отличается от исходного Давайте посмотрим, как мы будем использовать это: Итак, когда дело доходит до создания пользовательских функций, из которых вы можете строить график, предыдущего раздела должно быть достаточно, чтобы вы могли немного повеселиться со статикой. сюжеты.В этом следующем разделе я просто приведу вам пример сюжета с использованием настраиваемой функции, надеюсь, вдохновит вас на создание собственных сюжетов. Представьте, что вы хотите увидеть, как размер выборки из заданной случайной величины влияет на оценку лежащего в ее основе распределения вероятностей. Предположим, что у нас есть непрерывная случайная величина X, которая нормально распределена со средним значением μ (mu) и стандартным отклонением σ (сигма) (, т.е.X ∼N ( μ , σ ²)).Мы хотели бы знать, как на оценку плотности ядра scipy (kde) влияет размер нашей случайной выборки (сколько раз мы выбираем случайным образом из нашего нормального распределения), сравнивая ее с оценкой основного истинного распределения плотности вероятности (pdf) . Мы сделаем это, построив сами образцы, их kde и лежащий в их основе pdf для различных значений N. # генерировать pdf # сгенерировать kde # Построение графика Давайте разберем функцию пошагово: Сначала входные данные.Здесь вместо того, чтобы запрашивать массивы данных, мы будем создавать наши собственные данные из генератора случайных чисел Гаусса. Поэтому нам нужно запросить соответствующие статистические параметры μ и σ (среднее и стандартное отклонение соответственно для гауссовых распределений). Нам также нужно спросить, сколько образцов N нужно взять. Фактически мы будем перебирать различные значения N позже, чтобы увидеть влияние размера выборки на оценку. Идея состоит в том, чтобы построить образцы как точки разброса, а pdf и kde как обычные линейные графики.Таким образом, мы предоставим в качестве входных данных словарь для соответствующих параметров построения графика (ширина линии, размер маркера и т. Д.). Наконец, мы спросим оси фигуры, на которой мы хотим построить все три объекта. Первый раздел функции просто сгенерирует случайную гауссовскую выборку размера N из предоставленных статистических параметров. Вторая часть кода создаст пары x-y линейного графика, соответствующие pdf нормального распределения, заданного μ и σ.Мы ограничиваем диапазон PDF до ± 5 стандартных отклонений, так как все, что находится дальше с обеих сторон, в любом случае будет довольно маленьким. Третья часть кода сначала вычисляет kde нашего образца, а затем применяет его к тому же диапазону значений на оси x, что и наш pdf. Наконец, в четвертой части кода мы просто строим как диаграмму рассеяния все выбранные значения по оси x (на высоте 0), а pdf и kde как линейные графики. Все три, с соответствующими аргументами ключевого слова построения. И все! Надеюсь, вы научились добавлять возможности построения графиков в свои функции, правильно передавая соответствующие оси и аргументы ключевых слов. Это должно помочь вам иметь все более модульный код для быстрого исследования и визуализации ваших данных. Графики - это клей, который связывает преобразования воедино.Это единственная структура данных, которую бонобо может выполнять напрямую.
Графики должны быть ациклическими и содержать столько узлов, сколько может обрабатывать ваша система. Однако, хотя теоретически число
узлов может быть довольно большим, практические случаи обычно не превышают нескольких сотен узлов и даже это довольно высокий
число, с которым вы можете не так часто сталкиваться. В графе каждый узел изолирован и может взаимодействовать только с помощью своих очередей ввода и вывода. Для каждой входной строки
данный узел будет вызываться со строкой, переданной в качестве аргументов.Каждый результат или yield Значение будет помещено на узел
очередь вывода, и узлы, соединенные в графе, смогут ее обработать. Bonobo - это решение для построчной обработки потоков данных. Такая обработка потока данных дает следующие свойства: Первый пришел, первый вышел : если не указано иное, каждый узел будет получать строки из очередей FIFO, и, следовательно, порядок
строк будут сохранены.Это верно для каждого отдельного узла, но учтите, что если вы определяете «пузыри графа»
(где граф расходится в разных ветвях, а затем снова сходится), узел конвергенции получит FIFO строк из
каждая входная очередь, что означает, что порядок, существующий в точке расхождения, не останется верным в точке схождения. Параллелизм : каждый узел работает параллельно (по умолчанию с использованием независимых потоков). Это полезно, поскольку у вас нет
беспокоиться о блокировке звонков.Если поток ожидает, скажем, базы данных или сетевой службы, другие узлы
продолжит обработку данных, пока у них есть входные строки. Независимость : строки независимы друг от друга, что делает этот способ работы с потоками данных удобным для
построчная обработка данных, но также не идеальна для «сгруппированных» вычислений (когда результат зависит от нескольких
строка входных данных). Вы можете преодолеть это с помощью скользящих окон, если требуемый ввод - это соседние строки, но если вы
необходимо работать со всем набором данных сразу, вам следует подумать о другом программном обеспечении. Графики определены с использованием экземпляров TL; DR :… что угодно, при условии, что это callable () или итерабельно. При построении графика вы можете просто добавить свою функцию: Или используя новый синтаксис: Примечание Обратите внимание, что мы передаем объект функции, а не результат вызываемой функции. Распространенная ошибка
для вызова функции при построении графика, что не сработает и может быть утомительным для отладки. По соглашению мы используем объекты snake_cased, когда объект может быть напрямую передан графу, как эта функция. Некоторые функции являются фабриками для замыканий и, следовательно, ведут себя по-разному (так как вам нужно вызвать их, чтобы получить фактическое
объект можно использовать как преобразование.В этом случае мы используем CamelCase как соглашение, так как он ведет себя одинаково.
как класс. При построении графика вы можете добавить экземпляр своего объекта (или даже несколько экземпляров, в конечном итоге настроенных
иначе): Или используя новый синтаксис: В качестве удобного инструмента мы можем использовать итерации непосредственно в графике. Его можно использовать в качестве узлов-производителей (узлов,
обычно вызываются только один раз и производят данные) или, в случае генераторов, как преобразования. Затем добавьте его на график: Или используя новый синтаксис: Опять же, пока он вызываемый, вы можете использовать его как узел. Это означает, что встроенные функции python работают (подумайте о , напечатайте или стр. Верх …) Или используя новый синтаксис: Каждый узел графа будет выполняться изолированно от других узлов, и данные передаются от одного узла к другому.
далее с использованием очередей FIFO, управляемых платформой.Однако он прозрачен для конечного пользователя, и вы будете использовать только
аргументы функции (для входов) и возвращаемые / выходные значения (для выходов). Каждая входная строка узла вызывает один вызов вызываемого объекта этого узла. Каждый вывод преобразуется внутри как кортеж
структура данных (или, точнее, структура данных, подобная именованному кортежу), и для одного данного узла каждая выходная строка должна
имеют такую же структуру. Если вы вернете / отдадите что-то, что не является кортежем, бонобо создаст кортеж из одного элемента. Bonobo помогает вам определить поток данных в процессе разработки данных, а затем передает данные через ваш
вызываемые графы. Каждый вызов узла будет обрабатывать одну строку данных. Очереди, которые передают данные между узлами, представляют собой стандартную очередь python Каждый узел будет работать параллельно Стратегия выполнения по умолчанию использует потоки, и каждый узел будет работать в отдельном потоке. Выполнение узла отказоустойчиво. Если при вызове узла возникает исключение, то вызов этого узла будет прерван, но бонобо продолжит выполнение
со следующей строкой (после вывода трассировки стека и увеличения счетчика «ошибок» для контекста узла). Это позволяет выполнять задания ETL, которые игнорируют ошибочные данные и стараются изо всех сил обрабатывать допустимые строки набора данных. Однако некоторые ошибки фатальны. Если вы передадите кортеж из 2 элементов в узел, который принимает 3 аргумента, Bonobo вызовет График Направленный ациклический граф преобразований, который Бонобо может проверить и выполнить. Узел Преобразование в графе.Преобразования не имеют состояния и не знают, являются ли они
включены в график, несколько графиков или не включены вообще. Графики в Bonobo являются экземплярами Графики должны быть экземплярами Примечание Начиная с Bonobo 0.7 доступен новый синтаксис, который, по нашему мнению, является более мощным и читаемым, чем унаследованный. add_chain метод.Прежний API никуда не денется, и его совершенно безопасно использовать (на самом деле, новый синтаксис использует add_chain под капотом). Если это вариант для вас, мы предлагаем вам рассмотреть новый синтаксис. В переходный период мы задокументируем
оба, но новый синтаксис в конечном итоге станет стандартным. Или используя новый синтаксис: Результирующий график: Чтобы создать два или более расходящихся потока данных («вилок»), вы должны указать _input kwarg до add_chain . Или используя новый синтаксис: Результирующий график: Примечание Оба филиала будут получать одни и те же данные в одно и то же время. Чтобы объединить два потока данных, вы можете использовать _output kwarg в add_chain или использовать именованные узлы (см. Ниже). Или используя новый синтаксис: Результирующий график: Примечание Это не «соединение» или «декартово произведение». Любые данные, поступающие из b или g , будут проходить через нормализовать , один на
время. Думайте о ребрах графа как о каналах передачи данных. Использование приведенного выше кода для создания сходимостей часто приводит к коду, который трудно читать, потому что вам нужно определить «целевой» поток.
перед потоками, которые логически идут в начало графа преобразования.Чтобы преодолеть это, можно использовать
«Именованные» узлы. Обратите внимание, что присвоение имени цепочке - это то же самое, что присвоение имени первому узлу цепочки. При использовании нового синтаксиса нет необходимости давать имена узлам.Сообщите нам, если вы считаете иначе, создав проблему. Результирующий график: Вы также можете создавать отдельные узлы, и API предоставляет те же возможности на отдельных узлах. Поведение по умолчанию add_chain (или get_cursor ) заключается в подключении первого узла к специальному токену BEGIN , который
проинструктировать Bonobo вызвать подключенный узел один раз без параметра, чтобы запустить поток данных. Обычно это именно то, что вам нужно, но есть способы переопределить это, так как вы можете захотеть добавить «сиротские» узлы или цепочки в свой граф. В какой-то момент может потребоваться соединить два узла. Для этого можно использовать add_chain без узлов. Или используя новый синтаксис: Курсоры - это простые структуры, которые ссылаются на график, начальную и конечную точки.Их можно использовать для
управлять графиками с помощью оператора >> интуитивно понятным способом. Чтобы захватить курсор с графика, у вас есть разные варианты: Получив курсор, вы можете использовать его для добавления узлов, объединения его с другими курсорами и т. Д. Каждый раз, когда вы что-то вызываете
это должно привести к изменению курсора, вы получите новый экземпляр, поэтому старый курсор будет по-прежнему доступен, если вам нужно
Это. Есть два варианта выполнения графика (которые дают аналогичный результат, но нацелены на разные варианты использования). Вы можете использовать интерфейс командной строки bonobo, который является интерфейсом самого высокого уровня. Вы можете использовать API Python, который является более низким уровнем, но позволяет использовать бонобо из вашего собственного кода (например,
команда управления django). Если нет веских причин не делать этого, вы должны использовать bonobo run… для запуска графов преобразований, найденных в вашем питоне.
файлы исходного кода. Вы также можете запустить модуль Python: В каждом случае интерфейс командной строки bonobo будет искать экземпляр Если вы находитесь в контексте интерактивного терминала, для отображения будет использоваться Если вы находитесь в контексте записной книжки jupyter, он (попытается) использовать Чтобы интегрировать выполнение бонобо в любой другой код Python, вы должны использовать Мы предлагаем вам сначала пройти через руководство. Затем вы можете прочитать руководства, используя предложенный порядок или выбрав главу, которая вас интересует больше всего на
в один момент: Предупреждение Эта страница остается здесь по историческим причинам и может содержать устаревшую или неверную информацию. Существует обширная литература по алгоритмам графов, которые являются важными
часть дискретной математики.Графики также имеют практическое применение в
компьютерные алгоритмы. Наглядные примеры можно найти в управлении
сетей, но примеров предостаточно во многих других областях. Например,
отношения между вызывающим и вызывающим абонентами в компьютерной программе можно рассматривать как график
(где циклы указывают на рекурсию, а недостижимые узлы представляют собой мертвые
код). Немногие языки программирования обеспечивают прямую поддержку графиков как типа данных,
и Python не исключение. Однако графики легко построить из списков.
и словари.Например, вот простой график (я не могу использовать
рисунки в этих столбцах, поэтому я записываю дуги графа): Напишем простую функцию для определения пути между двумя узлами. Это
принимает в качестве аргументов график и начальный и конечный узлы.Он вернет
список узлов (включая начальный и конечный узлы), составляющих путь.
Если путь не может быть найден, возвращается None. Тот же узел не появится
более одного раза на возвращаемом пути (т.е. он не будет содержать циклов). В
алгоритм использует важную технику под названием с возвратом : он пытается
каждая возможность по очереди, пока не будет найдено решение. Обратите внимание, что хотя пользователь вызывает Эту функцию легко изменить, чтобы она возвращала список всех путей (без
циклов) вместо первого найденного пути: ОБНОВЛЕНИЕ : Эрик Копчинский отметил, что эти функции
не оптимально. Напротив, «эта программа работает с экспоненциальным временем,
в то время как find_shortest_path может выполняться за линейное время с использованием BFS [Breadth
Первый поиск]. Кроме того, линейная BFS проще: " Другой вариант - добавить дополнительную абстракцию данных: создать класс для
представляют собой графы, методы которых реализуют различные алгоритмы. Пока
это апеллирует к стремлению к структурированному программированию, но не делает
код более эффективный (наоборот). Это упрощает добавление
различные метки для узлов или дуг и добавлять алгоритмы, которые
метки во внимание (например,грамм. найти кратчайший маршрут между двумя городами на
карта). Это тоже будет темой другой колонки. Рисование рукописных или печатных уравнений с помощью Math Assistant в OneNote. Вы даже можете манипулировать переменными, чтобы увидеть визуальный эффект от изменений, превращая Math Assistant в мощного математического тренера. Сначала создайте уравнение, используя рукописный ввод или текст. На вкладке Draw напишите или введите свое уравнение. Используйте инструмент Lasso Select , чтобы нарисовать круг вокруг уравнения. Затем выберите Math . Это откроет панель Math Assistant. Из Выберите действие в раскрывающемся меню на панели Math выберите График в 2D или График с обеих сторон в 2D . Чтобы настроить график, созданный Math Assistant, выполните одно из следующих действий (если возможно): Щелкните (или нажмите и удерживайте), а затем перетащите график в любом направлении, чтобы переместить его положение. Щелкайте или касайтесь кнопок увеличительного стекла + и - так часто, как это необходимо, чтобы изменить значения параметров в уравнении путем увеличения или уменьшения масштаба. Примечание. Если вы используете OneNote на устройстве с сенсорным экраном, вы также можете настроить график пальцами. Используйте один палец, чтобы изменить положение графика, или увеличьте масштаб двумя пальцами, чтобы изменить уровень увеличения.В OneNote в Интернете вы можете использовать стрелки по бокам графика, чтобы изменить его положение. Щелкните или коснитесь значка с двойной стрелкой Сбросить , чтобы вернуть график в исходное состояние. Когда график будет выглядеть так, как вы хотите, щелкните или коснитесь Вставить на странице , чтобы разместить его как снимок экрана на текущей странице. Примечание. Чтобы изменить способ отображения графика (градусы, радианы, градиенты), щелкните или коснитесь Настройки , когда панель «Математика» открыта. В зависимости от типа графика могут быть доступны другие функции. Считывание значений x-y: Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote в Интернете щелкните строку, чтобы просмотреть значения. Управление параметрами: Если у вас есть уравнение с параметрами, например ax + b, используйте знаки плюс + и минус - под графиком, чтобы изменить значения a и b. Ключевые особенности графика: Math Assistant вычисляет интересную информацию о графике, такую как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике. Создавайте математические уравнения с помощью рукописного ввода или текста с помощью Math Assistant в OneNote Решайте математические уравнения с помощью Math Assistant в OneNote Типы задач, поддерживаемые Math Assistant Создайте практическую викторину по математикеshow(c, aspect_ratio=1) выполнит то же самое. Сохранить
картинку можно с помощью c.
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false) L в следующем примере), а затем использование команды polygon для
построения фигуры с границами, образованными заданными точками. К
примеру, создадим зеленый дельтоид:sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)),
....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2))
sage: p
Graphics object consisting of 1 graphics primitive
show(p, axes=false), чтобы не показывать осей на графике.sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)
е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)]
sage: line(v)
Graphics object consisting of 1 graphics primitive
sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)]
sage: show(line(v), xmin=-20, xmax=20)
sage: f = lambda x,y: cos(x*y)
sage: contour_plot(f, (-4, 4), (-4, 4))
Graphics object consisting of 1 graphics primitive
Трехмерные графики
2 - 1)
sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1))
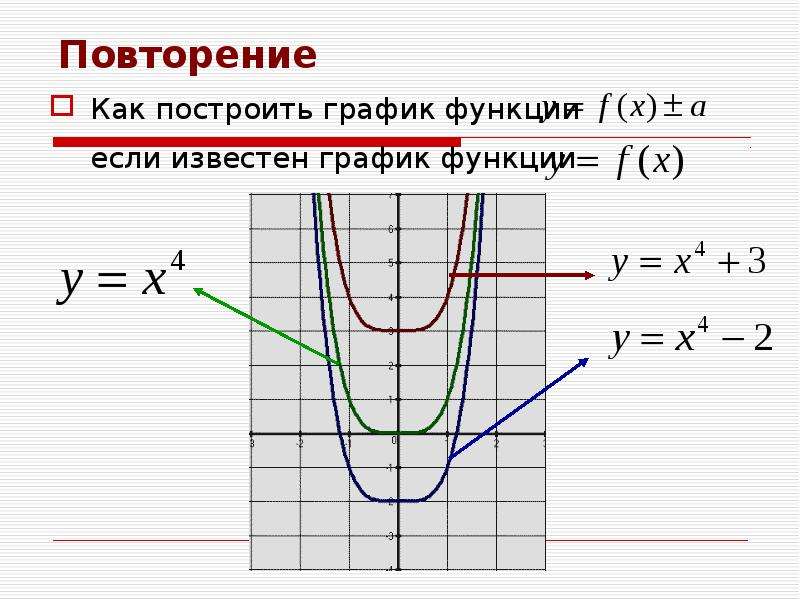
Graphics3d Object Урок по теме: «Как построить график функции у = f(x+l), если известен график функции у = f(X)»
Урок по теме: «Как
построить график функции у = f(x+l),
если известен график функции у = f(x)»
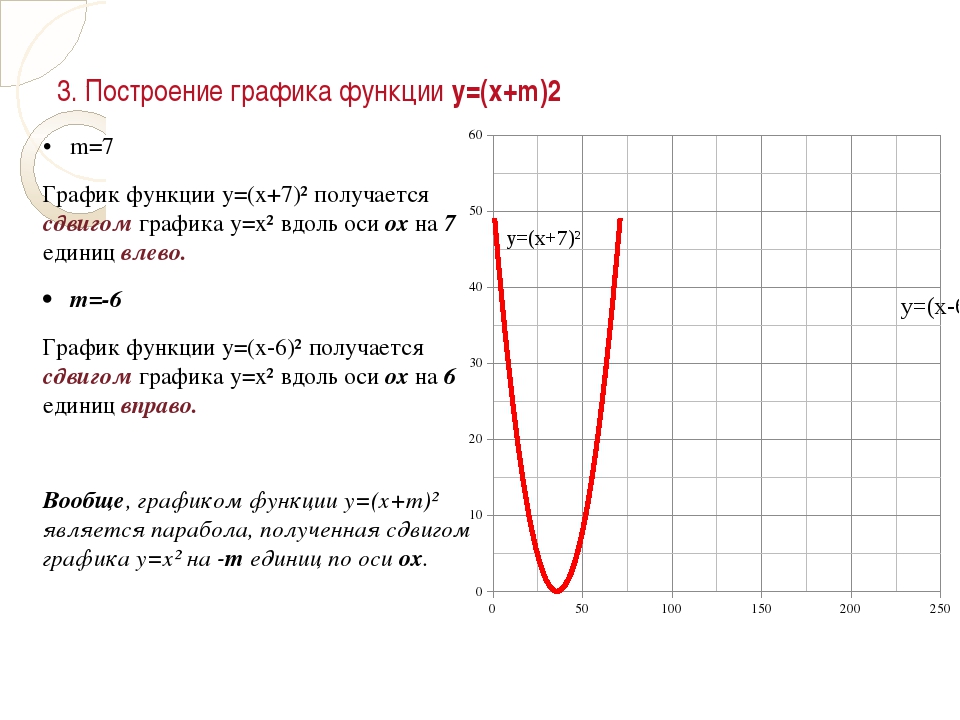
Построение таких графиков
Сегодня на уроке вам будет
помогать компьютер, и поэтому, еще одной
задачей нашего урока будет отработка
навыков работы с операционной системой
Windows ХР.
Смените цвет графика
двойным щелчком левой кнопкой мыши.
Построить график функции, провести ее полное исследование
Построить график функции, провести ее полное исследование
Часто при сдаче тестов по математике попадаются задания, в которых необходимо исследовать квадратичную функцию.
Вот типичный пример . Исследуем функцию, заданную формулой:исследование функции и построение графика
Область определения: множество всех действительных чисел Первая производная: Используем правило о том, что производная суммы равна сумме производных. На тестах по математике помним, что производная константы равна нулю. Воспользуемся правилом производной степени . Производная произведения константы и функции равна произведению константы на производную функции. Вторая производная: При сдаче тестов по математике вспоминает правило о том, что вторая производная - это производная от первой производной. Производная суммы равна сумме производных. Производная произведения константы и функции равна произведению константы на производную функции. Производная константы равна нулю. Когда вы решаете тесты по математике, в который нужно построить график функции, то необходимо найти точки пересечения с осью x: Нет Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.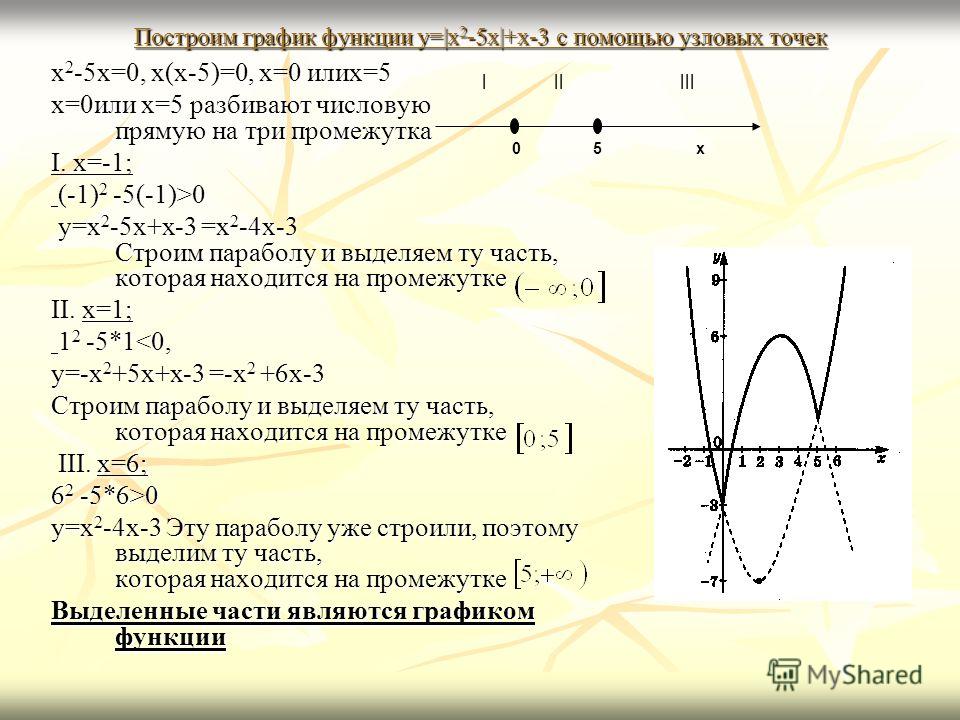
Находим дискриминант. Дискриминант отрицателен, значит, уравнение не имеет корней. Ответ: нет решений. Точки пересечения с осью
: Пусть Вертикальные асимптоты: нет Горизонтальные асимптоты: нет . Наклонные асимптоты: нет . стремится к бесконечности при x, стремящемся к бесконечности. стремится к бесконечности при x, стремящемся к бесконечности. Обязательно на тестах по математике найти критические точки: Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. Перенесем известные величины в правую часть уравнения. Разделим левую и правую часть уравнения на коэффициент при неизвестном. Сдавая тесты по математике, указываем правильный ответ: . Возможные точки перегиба: нет Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. Ответ: нет решений. Точки разрыва: нет Симметрия относительно оси ординат: нет Функция f(x) называется четной, если f(-x)f(x).
Раскрываем скобки. Выносим знак минус из произведения. Производим сокращение. Приводим подобные члены. Симметрия относительно начала координат: нет Функция f(x) называется нечетной, если f(-x)-f(x). Раскрываем скобки. Выносим знак минус из произведения. Производим сокращение. Приводим подобные члены. На тестах по математике надо указать тестовые интервалы: Относительные экстремумы: Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум (-2, 17) Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график. Указываем в своей работе множество значений функции: Наименьшее значение: y=17 Наибольшее значение: нетКак построить график в Excel
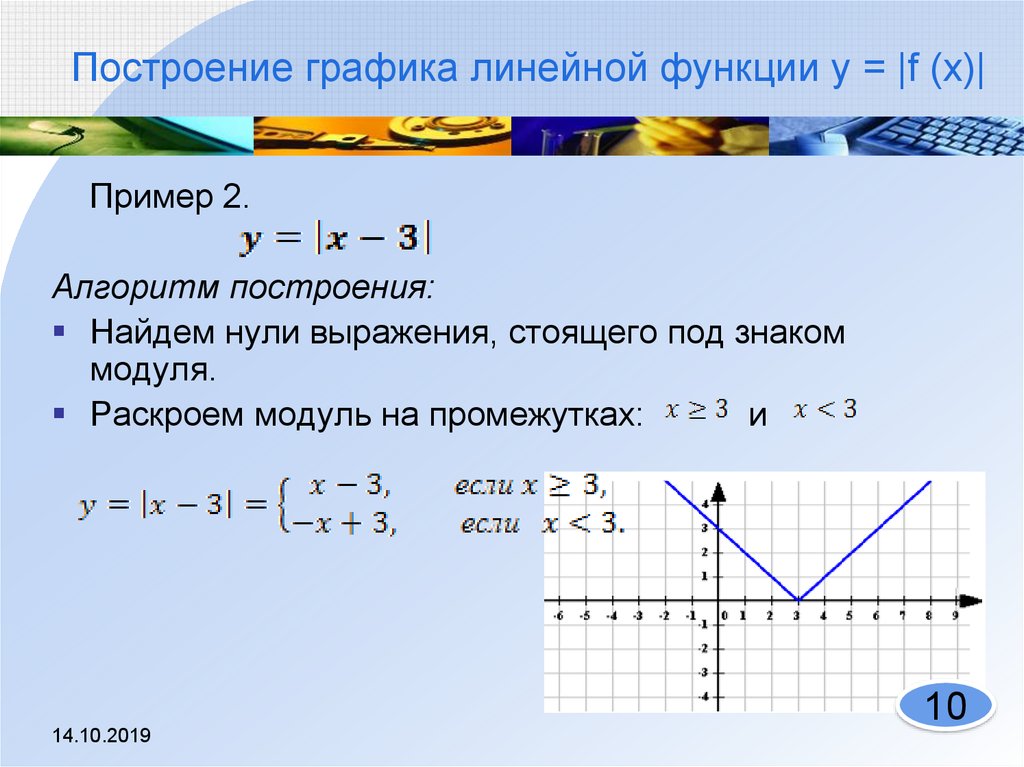2.Построение диаграммы "график"
Запись опубликована автором admin в рубрике Диаграммы.
к. тут еще много чего можно дорабатывать. Если вы хотите, чтобы график был у вас на листе, т.е., рядом с данными, то можно оставить так. Но я поменяю расположение листа. Правой кнопкой мыши тыкаем на диаграмму и выбираем "Переместить диаграмму".
2
Построить график функции | Решатели
Если каждому элементу \(x\in X\) по определенному правилу \(f\) поставлен в соответствие единственный элемент \(y\in Y\), то говорят, что на множестве \(X\) задана функция \(y=f\left(x \right)\) со значениями в множестве \(Y\).
Элементы \(x\in X\) называются значениями аргумента, а элементы \(y\in Y\) называются значениями функции. Множество \(X\) называется областью определения функции. Множество всех значений функции называется областью значений (областью изменений) этой функции.
С помощью нашего решебника вы можете построить график функции в обычном (линейном), в логарифмическом и смешанном (лог-линейном) масштабе. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку "Решить".
Построить график функции одной переменной
plot x^3 - 6x^2 + 4x + 12
graph sin t + cos (sqrt(3)t)
plot 4/(9*x^(1/4))
Построить график функции в указанной области определения
plot e^x from x=0 to 10
Построить график функции, принимающей действительные значения
real plot -(sqrt(25-y^2))
Построить график специальной функции
plot Ai(x)
Построить графики нескольких функций
plot sin x, cos x, tan x
plot x e^-x, x^2 e^-x, x=0 to 8
Построить график функции в логарифмическом масштабе
log plot e^x-x
Построить график функции в лог-линейном масштабе
log-linear plot x^2 log x, x=1 to 10
Построить график функции двух переменных
plot sin x cos y
Построить график функции в указанной области определения
plot (x^2)*(y^3), x=-1.
3 t)parametric plot (sin 10t, sin 8t), t=0..2pi
Как создать диаграмму или график в Excel [с видеоуроком]
Как построить график в Excel
1. Введите ваши данные в Excel.
2. Выберите один из девяти вариантов графика и диаграммы для создания.
Сюда входят столбчатые (или гистограммы), линейные, круговые, точечные и т. Д. Посмотрите, как Excel идентифицирует каждый из них на верхней панели навигации, как показано ниже: 3. Выделите данные и «Вставьте» нужный график.
4. При необходимости переключите данные на каждой оси.
5.Отрегулируйте макет и цвета ваших данных.
Здесь вы можете изменить цвет заливки легенды, что, в свою очередь, изменит цвет самих столбцов. Чтобы отформатировать другие части диаграммы, щелкните их по отдельности, чтобы открыть соответствующее окно Формат . 6. Измените размер легенды диаграммы и меток осей.
7. При необходимости измените параметры измерения оси Y.
8. При желании измените порядок данных.
9.Назовите свой график.
Чтобы изменить эту метку, нажмите «Заголовок диаграммы», чтобы появился курсор ввода. Затем вы можете свободно настроить заголовок вашей диаграммы. Дополнительные ресурсы для использования Excel и визуализации данных:
Справка в Интернете - Учебные пособия - Создание графика
Сводка
Вы можете создавать и изменять шаблоны самостоятельно и добавлять в коллекцию. Создать график в Origin так же просто, как выбрать нужные данные, а затем выбрать шаблон в меню или на панелях инструментов построения графиков. Диалоговое окно Plot Setup предлагает большую гибкость при создании графиков, например при выводе данных из нескольких книг или листов. Что вы узнаете
Быстрое создание графика путем выбора данных
Чтобы импортировать несколько ASCII, выберите CSV для Data Connector .
Изменить данные X / Y графика
Выберите пункт меню Select Column , чтобы указать столбец из текущей папки или текущего проекта. Добавить данные в существующий график и обновить легенду
Перетаскиванием
Установите Auto Legend Translation Mode на Custom . Введите @WS для Пользовательский формат легенды . Копирование для мини-панели инструментов печати
Диалог содержания слоя
В этом упражнении мы заменим данные из листа S32-014-04 данными из листа S21-235-07.
Теперь вы поменяли местами один набор данных для еще один. Создание графика с помощью настройки графика
Слой 1 выделен. Выберите Дельта температуры на средней панели, а затем нажмите кнопку Добавить . Поскольку вы уже выбрали три листа на шаге 3, это добавит все столбцы Delta Temperature из выбранных листов в слой 1.
Обратите внимание, что на каждом слое три графика данных автоматически сгруппированы.
Обратите внимание, что пользовательский формат легенды синтаксис @WS - это нотация подстановки LabTalk для имени рабочего листа, содержащего данные для каждого линейного графика.
.. из контекстного меню и выполнить дальнейшее расширенное редактирование в диалоговом окне Text Object . Построить сгруппированные данные как
Участок с решеткой
Появится диалоговое окно plot_group. Выберите col («Город») в качестве переменной горизонтальной группы и col («Пол») в качестве переменной вертикальной группы для панелей. Сгруппированный боксовый участок
Выделите col («Зарплата»), чтобы выбрать График> Категориальные: Групповые прямоугольные диаграммы - меню , чтобы открыть диалоговое окно plot_gdoxindexed. Выберите столбец («Пол») и столбец («Город») как Групповые столбцы . Графики по этикеткам
График должен выглядеть так: Изучение студентами функций и их графиков с помощью Desmos - Technology Tools for Teaching in Higher Education, The Practical Handbook Series
Преимущества обучения с использованием Desmos
Ресурсы
Шаг 1.Создайте учетную запись на Desmos.com (необязательно)
У вас есть возможность создать учетную запись и войти в систему, что позволит вам сохранять, называть и искать свою работу. Последующие шаги по реализации будут основаны на предположении, что вы вошли в свою учетную запись, чтобы воспользоваться этими функциями. Однако графические возможности Desmos не ограничиваются держателями учетных записей, и в этом случае можно сохранить доступ к своей работе, создав ссылку для общего доступа и сохранив ее на будущее. Шаг 2. Откройте Графический калькулятор Desmos и создайте график.
(Добавить элемент), затем примечание «» и добавьте описание в строку 1.
Шаг 3. Укажите функцию, функциональные компоненты или данные, моделируемые функцией
Шаг 4. Создайте набор инструкций
+ (Добавить элемент), затем папку или заметку.
Шаг 4. Предложите студентам изучить учебные материалы по графическим инструментам Desmos.
Шаг 5. Поделитесь графиком (ами) со своими учениками
Шаг 6. Включение Калькулятора Графа Десмоса в оценки
Цифровые ресурсы
Создание пользовательских функций построения графиков с помощью matplotlib | автор: Матиас Кальдерини
Краткое руководство, чтобы узнать, как создавать модульные функции, которые включают построение графиков с помощью matplotlib
если ax is None:
ax = plt.gca ()
ax.plot (x, y, ** plt_kwargs) ## пример графика здесь
return (ax) def multiple_custom_plots (x, y, ax = None, plt_kwargs = {}, sct_kwargs = {}):
, если ax is None:
ax = plt.gca ()
ax.plot (x, y, ** plt_kwargs) #example plot1
ax.scatter (x, y, ** sct_kwargs) #example plot2
return (ax) .график или .hist с параметрами по умолчанию. Однако часто в рамках красивой мозаичной структуры, которую вы узнали в предыдущем посте, вам нужно будет нарисовать собственный конкретный график, который объединяет информацию из различных типов основных функций построения графиков вместе с вызовами некоторых других генераторов данных или данных. функция обработки. Например, построение графика распределения случайных выборок с соответствующей теоретической функцией плотности сверху. fig, axes = plt.subplots (number_of_subplots)
для оси в осях:
my_custom_plotting_function (ax = ax, function_kwargs) def custom_plot (x, y, ax = None, ** plt_kwargs):
if ax is None:
ax = plt.gca ()
ax.plot (x, y, * * plt_kwargs) ## здесь пример сюжета
return (ax) ax . Если вы раньше использовали seaborn , возможно, вы уже знаете, как им пользоваться. По сути, ax будет принимать объект оси, на котором вы хотите построить.Это могут быть оси вспомогательного графика или простые свободно плавающие оси врезки. Идея состоит в том, что организационная часть сюжета будет обрабатываться вне этой функции, возможно, другой функцией. ax по умолчанию Но нет ? На этот вопрос лучше ответить строками:, если ax - None:
ax = plt.gca () ax , по умолчанию используется None и запускается этот , если Состояние .В этом случае, поскольку оси не были заданы, по умолчанию функция будет искать последние оси, использованные в текущем рисунке, или создавать их, если их нет, с помощью функции .gca (что означает получить текущий оси ) и используйте их в качестве осей для построения графика. В конце функции мы также возвращаем этот топор, если мы хотим использовать его для других настроек (не обязательно, но в некоторых случаях практично). # Без указания осей (по умолчанию None -> gca ())
plt.figure (figsize = (10, 5))
custom_plot ([1, 2], [10, 20])
plt.title ('Наш настраиваемый график без осей (по умолчанию .gca ())')
plt .xlabel ('x')
plt.ylabel ('y')
plt.show () # Предоставление осей
fig, axes = plt.subplots (2, figsize = (10, 5)) # Построение графика с наша функция
custom_plot ([2, 3], [4, 15], ax = axes [0])
axes [0] .set (xlabel = 'x', ylabel = 'y', title = 'Это наш пользовательский график по указанным осям ') # Пример графика для заполнения второго подзаголовка (не имеет отношения к нашей функции)
осей [1].hist (np.random.normal (size = 100))
axes [1] .set_title ('Этот график не имеет ничего общего с нашей функцией. Просто гистограмма некоторых случайных чисел') plt.tight_layout () # Это во избежание перекрытие меток и заголовков на графиках
plt.show () ** plt_kwargs ? ** kwargs (как в аргументах ключевого слова) в своих функциях (фактическое имя аргумента не имеет значения, вы можете назвать его ** kwargs , ** plt_kwargs , ** literally_anything_else , если вы поставите двойную звездочку «**»), это будет легче объяснить, сначала создав и используя новую функцию, в которой нет ** kwargs . * и двойных звездочек ** в python весьма полезно во многих ситуациях, будь то внутри или вне функций, и определенно стоит поискать в Google (возможно, даже написать об этом сообщение в блоге ... может быть ...). В любом случае, вернемся к нашему примеру custom_plot без ** kwargs : def no_kwargs_plot (x, y, ax = None):
, если ax is None:
ax = plt.gca ()
ax.plot (x, y) ## здесь пример графика
return (ax) plt.figure (figsize = (10, 5))
no_kwargs_plot ([1, 2], [10, 20])
plt.show () .plot () мы просто устанавливаем для аргумента linewidth более толстое значение. Мы могли бы добавить ширины линии к списку входных данных к no_kwargs_plot , а затем передать его .plot () следующим образом: def no_kwargs_plot (x, y, ax = None, linewidth = 1):
if ax Нет:
ax = plt.gca ()
ax.plot (x, y, linewidth) ## пример графика здесь def no_kwargs_plot (x, y, ax = None, linewidth = 1, other = 1, ...):
if ax is None:
ax = plt.gca ()
ax.plot (x, y, linewidth, other, ....) ## здесь пример графика ** ( * * kwargs ) становится полезным.При использовании со свободными элементами "ключ-значение", такими как бесхозные входы в нашей функции (те, которые не связаны с предопределенными аргументами x, y и ax в нашем случае) ** name упакует все эти элементы в словарь и сохраните их в переменной name . custom_plot (x = xdata, y = ydata, ax = axes [0], linewidth = 2, c = 'g') , то в результате получился бы словарь plt_kwargs будет {'ширина линии': 2, 'c': 'g'} .Если это все еще не совсем понятно, посмотрите на пример кода ниже, вывод (>>) и схему внизу: def print_kwargs_only (x, y, ax = None, ** plt_kwargs):
print (plt_kwargs) # чтобы распечатать словарь со всеми сиротами kwargsprint_kwargs_only (x = [1, 2], y = [10, 20], not_xyax = 1, random_orphan_kwarg = 'so lonely', linewidth = 2, c = 'g') >> { 'not_xyax': 1, 'random_orphan_kwarg': 'so lonely', 'linewidth': 2, 'c': 'g'} ** решает проблему включения всех возможных графических входных данных в нашу функцию без необходимости их явного предварительного определения и их готовности к использованию внутри словаря.Но как же используется этот словарь дополнительных аргументов ключевых слов? ** ведет себя как функция упаковки при использовании со свободными элементами. Когда вы используете ** в словаре (независимо от того, был ли он упакован с помощью ** или нет), ** фактически выполнит противоположное действие, которое он делал раньше: он распакует словарь на разные свободные элементы. В custom_function , когда мы пишем ** plt_kwargs внутри .plot () , , т.е. ax.plot (x, y, ** plt_kwargs) , мы фактически просим python взять словарь plt_kwargs и распаковать все его пары ключ-значение отдельно в .plot () работают как отдельные входы. custom_plot (вы могли заметить, что на этот раз я использовал оси, возвращаемые функцией, чтобы показать вам, как ее можно использовать): plt.figure (figsize = (10, 5))
out_ax = custom_plot ([1, 2], [10, 20], linewidth = 5, c = 'g')
out_ax.set (xlabel = 'xlabel', ylabel = 'ylabel', title = 'Проверка полезности ** kwargs')
plt.show () ** kwargs . То есть, что, если бы вы делали несколько графиков внутри функции custom_plot ? Например, что, если вы рисуете две линии, одна из которых должна быть пунктирной, а другая - сплошной.Как ** kwargs узнает, какие аргументы в какой заговор входят? ** kwargs упаковочная машина» больше не будет работать и ее нужно будет заменить, но « ** kwargs распаковочная машина» будет работать отлично. Что я имею в виду под Давайте определим новую функцию под названием multiple_custom_plots , чтобы прояснить ее: def multiple_custom_plots (x, y, ax = None, plt_kwargs = {}, sct_kwargs = {}):
if ax is None:
ax = plt.gca ()
ax.plot (x, y, ** plt_kwargs)
ax.scatter (x, y, ** sct_kwargs)
return (ax) ** kwargs у нас есть два новых аргумента, по одному для каждого из наших графиков. Также по умолчанию эти аргументы являются пустыми словарями. ** kwargs , надеюсь, это уже достаточно ясно для вас. Идея состоит в том, что, поскольку мы не можем попросить функцию автоматически упаковать все необязательные входные данные в один словарь (сейчас нам нужны два отдельных словаря), нам вместо этого придется предоставить каждый словарь параметров построения графиков самим, предварительно упакованным. custom_plot , поскольку использование ** в словаре по-прежнему означает, что мы хотим, чтобы его значения были распакованы. Мы используем пустые словари в качестве значений по умолчанию, потому что, если вы не предоставили словарь настроек, мы столкнемся с проблемами при попытке распаковать их (или их отсутствие) с помощью ** . Пустые словари, по сути, предназначены для того, чтобы ничего не распаковывать в функции, если ничего не предусмотрено. plot_params = {'linewidth': 2, 'c': 'g', 'linestyle': '-'}
scatter_params = {'c': 'red', 'marker': '+', 's': 100}
xdata = [1, 2]
ydata = [10, 20] plt.figure (figsize = (10, 5))
multiple_custom_plots (xdata, ydata, plt_kwargs = plot_params, sct_kwargs = scatter_params)
plt.show () def sample_plot (mu = 0, sigma = 1, N = 100, sct_kwargs = {}, pdf_kwargs = {} , kde_kwargs = {}, ax = None):
# сгенерировать образец
sample = np.random.normal (loc = mu, scale = sigma, size = N)
xrange = mu + 5 * sigma * np.linspace (-1, 1, 100)
pdf = stats.norm.pdf (xrange , loc = mu, scale = sigma)
rating = stats.gaussian_kde (sample)
kde = rating (xrange)
, если ax не равно None:
ax = plt.gca ()
ax .scatter (sample, np.zeros_like (sample), ** sct_kwargs)
ax.plot (xrange, pdf, ** pdf_kwargs)
ax.plot (xrange, kde, ** kde_kwargs)
return (xrange) # Параметры выборки
sample_sizes = (10, 20, 100, 250, 500, 2_000)
mean = 100
std = 15 # Параметры построения
scatter_params = {'alpha': 0.1, 'c': 'g', 's': 100, 'label': 'samples'}
pdf_params = {"linewidth": 2, 'c': 'k', 'label': 'pdf'}
kde_params = {"linewidth": 3, 'ls': '-', 'c': 'g', 'label': 'kde'} # Построение графика
fig, axes = plt.subplots (6, figsize = (15, 20))
для ax, n в zip (axes, sample_sizes):
sample_plot (mu = mean, sigma = std, N = n, ax = ax,
sct_kwargs = scatter_params, pdf_kwargs = pdf_params, kde_kwargs = kde_params)
ax.set_title (f'N = {n} ') axes [0] .legend ()
axes [-1] .set_xlabel (' Пример значения ', fontsize = 13)
plt.tight_layout ()
plt.savefig (' finalplot ')
plt.show () Графики - документация Bonobo 0.6.4
bonobo.Graph , как показано на предыдущем шаге учебного курса. Что можно использовать в качестве узла?
Функции
def get_item (id):
идентификатор возврата, items.get (id)
graph.add_chain (..., get_item, ...)
график >>... >> get_item >> ...
Классы
класс Foo:
...
def __call __ (self, id):
вернуть идентификатор, self.get (id)
graph.add_chain (..., Foo (), ...)
график >> ... >> Foo () >>...
Итерационные объекты (генераторы, списки,…)
def product (x):
для i в диапазоне (10)
вывести x, i, x * i
graph.add_chain (диапазон (10), продукт, ...)
график >> ассортимент (10) >> продукт >>...
Построен
graph.add_chain (диапазон (ord ("a"), ord ("z") + 1), chr, str.upper, print)
график >> диапазон (ord ("a"), ord ("z") + 1) >> chr >> str.upper >> print
Что происходит во время выполнения графа?
Недвижимость
типа first-in-first-out (FIFO). Отказоустойчивость
bonobo.errors.UnrecoverableTypeError , и как можно быстрее завершить выполнение текущего графика (завершение
выполнение других узлов, которые выполняются первыми, но не запускают новые, если есть оставшиеся входные строки). Определения
Графики построения
бонобо. График бонобо. График . Метод bonobo.Graph.add_chain () может принимать столько
позиционные параметры как хотите. импортный бонобо
graph = bonobo.Graph ()
graph.add_chain (a, b, c)
импортный бонобо
graph = bonobo.Graph ()
график >> a >> b >> c
Нелинейные графики
Расхождения / вилки
импортный бонобо
graph = bonobo.Graph ()
graph.add_chain (a, b, c)
graph.add_chain (f, g, _input = b)
импортный бонобо
graph = bonobo.Graph ()
график >> a >> b >> c
graph.get_cursor (b) >> f >> g
Схождение / слияние
импортный бонобо
graph = bonobo.Graph ()
# Здесь мы устанавливаем _input в значение None, поэтому нормализация не запустится сама по себе, а только после того, как получит ввод от других цепочек.
graph.add_chain (нормализовать, сохранить, _input = None)
# Добавляем две разные цепочки
graph.add_chain (a, b, _output = нормализовать)
graph.add_chain (f, g, _output = нормализовать)
импортный бонобо
graph = bonobo.Graph ()
# Здесь мы устанавливаем _input в значение None, поэтому нормализация не запустится сама по себе, а только после того, как получит ввод от других цепочек.graph.get_cursor (None) >> normalize >> store
# Добавляем две разные цепочки
график >> a >> b >> нормализовать
график >> f >> g >> нормализовать
Именованные узлы
импортный бонобо
graph = bonobo.Graph ()
# Здесь мы отмечаем _input как None, поэтому normalize не получит импульс "begin".
graph.add_chain (normalize, store, _input = None, _name = "load")
# Добавьте две разные цепочки, которые будут выводиться на узел "load"
graph.add_chain (a, b, _output = "load")
graph.add_chain (f, g, _output = "load")
импортный бонобо
graph = bonobo.Graph ()
# Создать узел без подключения, назовите его.
graph.add_node (foo, _name = "foo")
# Использовать его в другом месте в качестве источника данных.
graph.add_chain (..., _input = "foo")
# ... или как приемник данных.
graph.add_chain (..., _output = "foo")
Орфанные узлы / цепи
импортный бонобо
graph = bonobo.Graph ()
# использование add_node естественным образом добавит узел как "сиротский"
graph.add_node (а)
# использование add_chain с "None" в качестве ввода создаст цепочку-сирот
graph.add_chain (a, b, c, _input = None)
# используя новый синтаксис, вы можете использовать либо get_cursor (None), либо ярлык orphan ()
graph.get_cursor (Нет) >> a >> b >> c
#... используя ярлык ...
graph.orphan () >> a >> b >> c
Соединение двух узлов
импортный бонобо
graph = bonobo.Graph ()
# Создайте два "анонимных" узла
graph.add_node (а)
graph.add_node (б)
# Подключите их
graph.add_chain (_input = a, _output = b)
Курсоры
# самый очевидный способ получить курсор, его отправной точкой будет "BEGIN"
курсор = graph.get_cursor ()
# одно и то же, явно
курсор = graph.get_cursor (BEGIN)
# если вы попытаетесь использовать график с оператором `>>`, он создаст для вас курсор, начиная с "BEGIN"
cursor = graph >> ... # то же, что и `graph.get_cursor (BEGIN) >> ... `
# получаем курсор, указывающий ни на что
курсор = graph.get_cursor (Нет)
# ... или более читаемым способом
курсор = graph.orphan ()
c1 = graph.orphan ()
# добавляем узел, получаем новый курсор
c2 = c1 >> узел1
# создать сеть сирот
c3 = график.сирота () >> нормализовать
# соединяем цепочку с существующим курсором
c4 = c2 >> c3
Графики исполнения
Выполнение графика с помощью интерфейса командной строки
$ bonobo run -m my.own.etlmod
bonobo. График в вашем файле / модуле, создать сантехнику
необходимо выполнить и запустить его. bonobo.ext.console.ConsoleOutputPlugin . bonobo.ext.jupyter.JupyterOutputPlugin . Выполнение графика с использованием внутреннего API
bonobo.run () . Он ведет себя очень похоже на
CLI, и прочитав исходный код, вы сможете довольно легко понять его использование. Куда прыгать дальше?
шаблонов Python - реализация графиков
find_shortest_path как «почти оптимальный».
11.08.19: исправлено случайное использование find_graph () вместо find_path ()
Авторское право (c) 1998, 2000, 2003, 2019 Python Software Foundation.
Все права защищены.
Имеет лицензию PSF.
Графы - это сети, состоящие из узлов, соединенных ребрами или дугами. В
ориентированные графы, связи между узлами имеют направление и
называемые дугами; в неориентированных графах связи не имеют направления и
называются ребрами.В основном мы обсуждаем ориентированные графы. Алгоритмы в графах
включать поиск пути между двумя узлами, поиск кратчайшего пути между
два узла, определяющие циклы в графе (цикл - это непустой путь
от узла к самому себе), находя путь, который достигает всех узлов (знаменитый
"задача коммивояжера") и т. д. Иногда узлы или дуги
график имеют веса или связанные с ними затраты, и мы заинтересованы в
найти самый дешевый путь.
А -> В
А -> С
В -> С
B -> D
C -> D
D -> C
E -> F
F -> C
Этот граф имеет шесть узлов (A-F) и восемь дуг. Это может быть представлено
следующая структура данных Python:
graph = {'A': ['B', 'C'],
'B': ['C', 'D'],
'CD'],
'ОКРУГ КОЛУМБИЯ'],
'E': ['F'],
'F': ['C']}
Это словарь, ключи которого являются узлами графа.Для каждого ключа
соответствующее значение - это список, содержащий узлы, которые связаны
по прямой дуге от этого узла. Это почти так просто, как кажется (даже
проще, узлы могли быть представлены числами вместо имен, но
имена более удобны, и их можно легко заставить носить с собой
информация, например названия городов).
def find_path (график, начало, конец, путь = []):
путь = путь + [начало]
если начало == конец:
Обратный путь
если не график.has_key (начало):
return None
для узла в графе [начало]:
если узел не в пути:
newpath = find_path (граф, узел, конец, путь)
если newpath: вернуть newpath
return None
Пример выполнения (с использованием графика выше):
>>> find_path (график, 'A', 'D')
['A', 'B', 'C', 'D']
>>>
Второй оператор if необходим только в том случае, если есть узлы, которые
указаны как конечные точки для дуг, но не имеют исходящих дуг
сами по себе и вообще не указаны на графике.Такие узлы также могли
содержаться в графе с пустым списком исходящих дуг, но
иногда удобнее этого не требовать. find_path () с тремя аргументами,
он вызывает себя с четвертым аргументом: уже пройденным путем.
Значение по умолчанию для этого аргумента - пустой список, '[]', что означает отсутствие
узлы еще не пройдены. Этот аргумент используется, чтобы избежать циклов (
сначала if внутри цикла for).Аргумент 'путь' не изменяется:
присвоение «путь = путь + [начало]» создает новый список. Если бы у нас было
написали вместо этого "path.append (start)", мы бы изменили переменную
'path' в вызывающей программе с катастрофическими результатами. (Используя кортежи, мы могли бы
были уверены, что этого не произойдет, ценой необходимости написать
"path = path + (start,)", поскольку "(start)" не является одноэлементным кортежем - это
просто выражение в скобках.)
def find_all_paths (график, начало, конец, путь = []):
путь = путь + [начало]
если начало == конец:
Обратный путь]
если не график.has_key (начало):
возвращаться []
пути = []
для узла в графе [начало]:
если узел не в пути:
newpaths = find_all_paths (граф, узел, конец, путь)
для newpath в newpath:
paths.append (новый путь)
обратные пути
Пример выполнения:
>>> find_all_paths (график, 'A', 'D')
[['A', 'B', 'C', 'D'], ['A', 'B', 'D'], ['A', 'C', 'D']]
>>>
Другой вариант находит кратчайший путь:
def find_shortest_path (график, начало, конец, путь = []):
путь = путь + [начало]
если начало == конец:
Обратный путь
если не график.has_key (начало):
return None
кратчайший = Нет
для узла в графе [начало]:
если узел не в пути:
newpath = find_shortest_path (граф, узел, конец, путь)
если newpath:
если не самый короткий или len (новый путь)
>>> find_shortest_path (график, 'A', 'D')
['A', 'C', 'D']
>>>
Эти функции настолько просты, насколько это возможно.Тем не менее, они почти
оптимальный (для кода, написанного на Python). В других шаблонах Python
колонке, я постараюсь проанализировать их скорость бега и улучшить их
производительность за счет большего количества кода.
# Код от Эрика Копчинского
def find_shortest_path (график, начало, конец):
dist = {начало: [начало]}
q = deque (начало)
а len (q):
при = q.поплефт ()
для следующего на графике [at]:
если следующий не на расстоянии:
dist [next] = [dist [at], next]
q.append (далее)
return dist.get (конец)
Обратите внимание, что это возвращает путь в странном формате, например, [[['A'], 'B'], 'D'] . Особенно, len (find_shortest_path (graph, 'A', 'D')) даст
неправильный ответ (2, потому что внешний список имеет длину 2). Это
потому что добавление выполняется как [dist [at], next] вместо dist [at] + [next] .Второй метод будет использовать квадратичный
время и память, но все равно должно хватить для сравнительно небольших графиков;
в противном случае легко преобразовать список в правильный формат. Рисование графиков математических функций с помощью Math Assistant в OneNote
Расширенные возможности построения графиков
См. Также
Ваш комментарий будет первым