Функции и графики — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции).
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.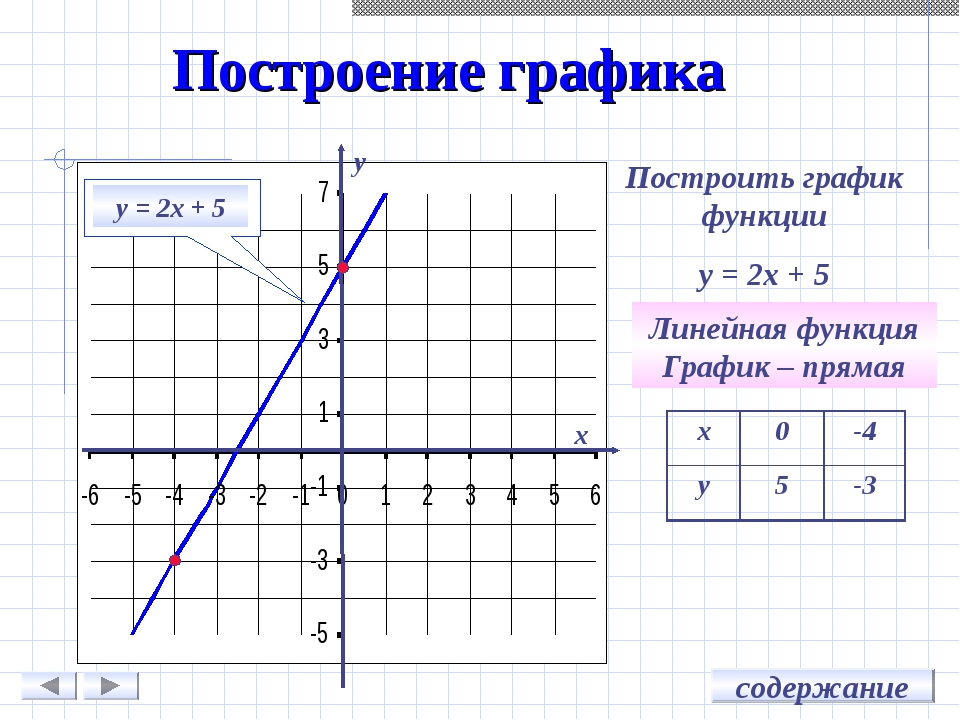
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению.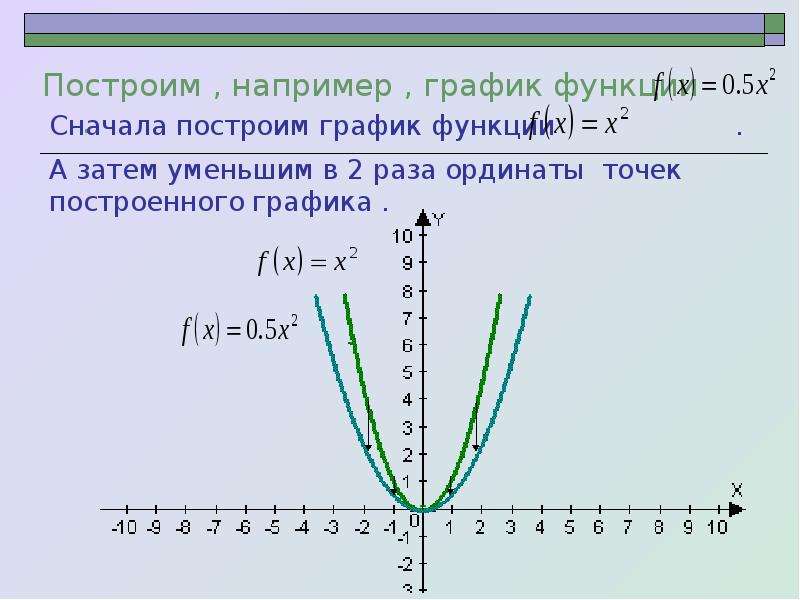 ..
..
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:
Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
График функции y
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Онлайн-калькулятор неопределенности измерений — Profilab.by
Расчет составляющей неопределенности измерений из-за построения градуировочного графика
Многие испытательные лаборатории при реализации различных методик выполнения измерений проводят калибровку (градуировку) оборудования (хроматографов, спектрофотометров) для выражения результатов измерений в установленных единицах измерений и обеспечения прослеживаемости своих измерений.
Калибровка (градуировка) связывает сигнал (отклик) используемого оборудования (например, оптическая плотность) с интересующей специалиста величиной (например, концентрация элемента в растворе).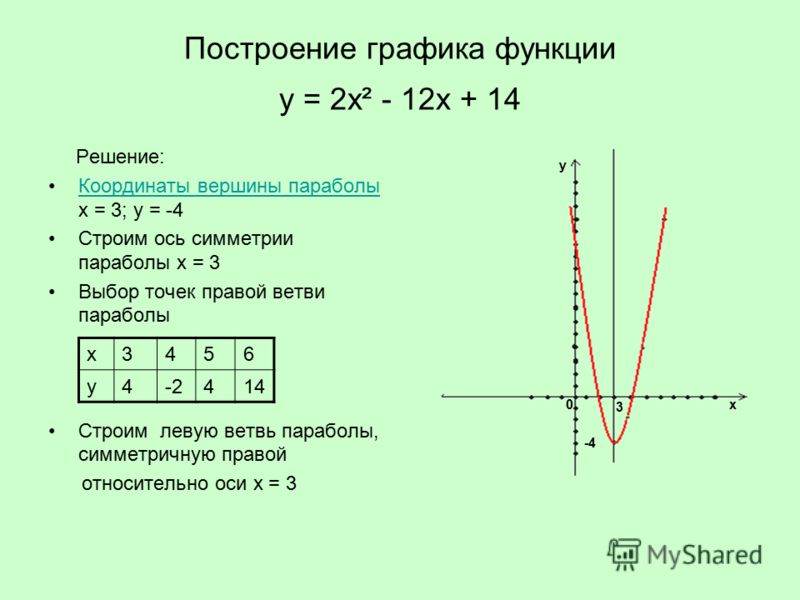
Наиболее часто используется простая линейная зависимость отклика оборудования от интересующей специалиста величины и применяется регрессионный анализ и метод наименьших квадратов для построения этой зависимости.
ВНИМАНИЕ!
Для удобства использования онлайн-калькулятора ознакомьтесь с видео инструкцией:
ОНЛАЙН-КАЛЬКУЛЯТОР
Перейти к калькулятору
Онлайн-калькулятор позволяет на основании введенных исходных данных: приписанных значений интересующей специалиста величины и измеренных откликов применяемого оборудования, построить и оценить параметры линейной регрессионной зависимости применяя метод наименьших квадратов, а также рассчитать составляющую неопределенности измерений, связанную с построением калибровочного (градуировочного) графика методом наименьших квадратов.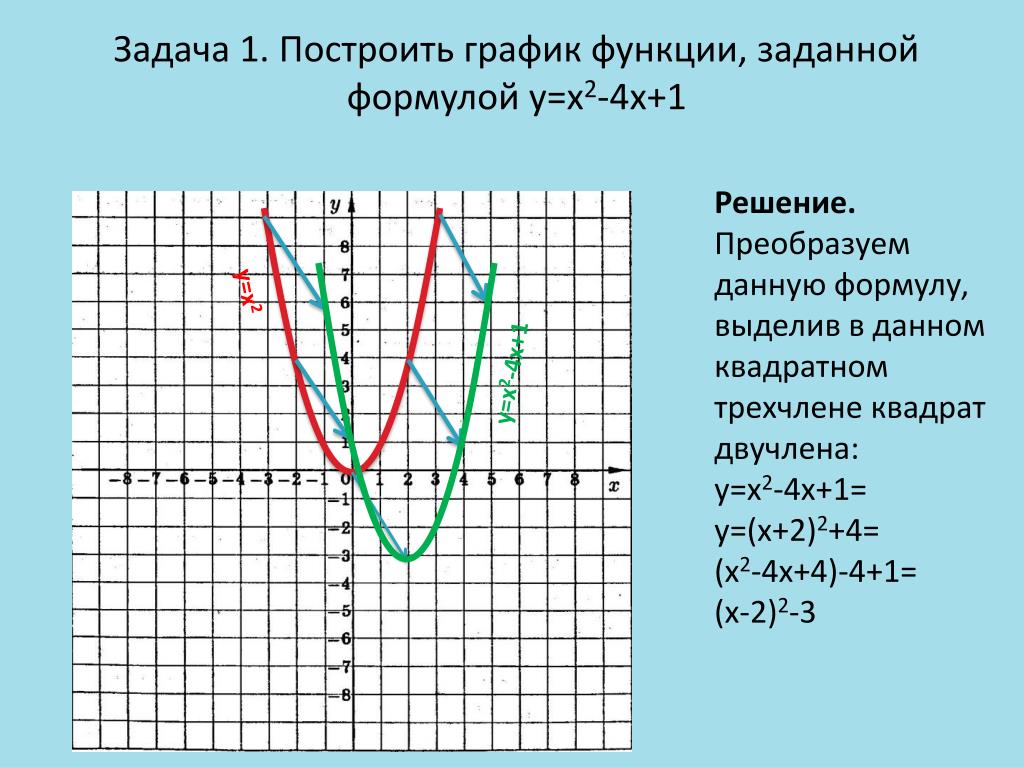
Расчет составляющей неопределенности измерений основан на подходе, изложенном в п. Е.4 (неопределенность от калибровки методом наименьших квадратов), EURACHEM/CITAC Guide Quantifying Uncertainty in Analytical Measurement, Third Edition, 2012.
Если вас интересует создание ОНЛАЙН-калькулятора расчета неопределенности измерений для конкретного вида измерений/испытаний, отправьте нам запрос.
Отправить заявку на создание онлайн-калькулятора неопределенности измеренийТакже информируем вас, что при заказе у нас Методики оценивания неопределенности вы получаете разработанную программу автоматизированного расчета неопределенности измерений величин согласно разработанным алгоритмам оценивания.
РАЗРАБОТКА/ВАЛИДАЦИЯ МЕТОДИК
Выполним работы по разработке Методик измерений
ПОДРОБНЕЕ ОБ УСЛУГЕ
РАЗРАБОТКА Методик оценивания неопределенности
В комплекте с автоматизированным расчетом
ПОДРОБНЕЕ ОБ УСЛУГЕ
ИЩЕТЕ ЧТО-ТО ДРУГОЕ?
Неопределенность измерения величин: основные принципы и подходы к оцениванию
Неопределенность измерения величин: основные принципы и подходы к оцениванию (при проведении химических и био-аналитических измерений)
Валидация/верификация методик выполнения измерений в рамках одной лаборатории. Метрологическая прослеживаемость измерений
Метрологическая прослеживаемость измерений
Математический феномен: формула, которая описывает всё
Чем ещё удивит математика? Вот как выглядит формула всего, и вот как это использовать в личных целях. Алгоритм с иллюстрациями.
Феноменальное неравенство
Посмотрите на одно занимательное число. Это классика. Возможно, вам знакомая.
48584506361897134235820959624942020445814005879832445494830930850619347047088099284506447 69865524364849997247024915119110411605739177407856919754326571855442057210445735883681829 82375413963433822519945219165128434833290513119319995350241375876523926487461339490687013 05622958132194811136853395355652908500238750928568926945559742815463865107300491067230589 33586052544096664351265349363643957125565695936815184334857605266940161251266951421550539 55451915378545752575659074054015792900176596796548006442782913148854825991472124850635268 6630476300
Через минуту поймёте, почему этот цифровой ряд вызывает чертовское любопытство. Он связан с одним фантастическим неравенством.
Он связан с одним фантастическим неравенством.
Формулу – в студию:
где ⌊ ⌋ – пол вещественного числа – округление до целой части в меньшую сторону, а mod — оператор остатка от деления.
Возьмите координатные оси x и y и для каждой точки в плоскости подставьте координаты x и y, тогда эта формула скажет, нужно ли окрашивать позицию. Неравенство показывает, какую часть пространства заполнить цветом.
Если вы построите диаграмму, то получите это:
Разве не поразительно, что график формулы выглядит как изображение её само́й?
Самореферентная формула Таппера правомерно занимает место в списке причудливых вещей математики. Впервые Джефф Таппер опубликовал её в 2001 году на конференции SIGGRAPH, когда демонстрировал собственную разработку – программу для рисования графиков GrafEq.
У внимательных в голове наверняка проскользнул вопрос: что за магическое k по оси y? С x область понятна – от 0 до 106. На самом деле,
На самом деле, k – то длинное число. То есть, по оси y мы забрались за облака. Когда абстрагируетесь от верхних и нижних значений и рассмотрите маленькую область от k до k + 17, вы увидите неравенство, по которому создали график.
Но потрясает в формуле Таппера не образование собственного изображения, а построение всего. Пройдитесь вдоль оси y, и увидите, как это неравенство сформирует каждый возможный рисунок из чёрных и белых пикселей размерами 106 на 17. Значит, изображения в рамках такого формата найдёте в определённых местах на графике. Не только формулу Таппера, но и всевозможные другие.
Например, мы отыскали такое значение числа k, при котором в формуле вместо символов остатка от деления появились смайлики:
А также приготовили вариант с Пакманом, поедающим формулу, и приведением:
Формула всего в действии
Настало время узнать, как из желаемой картинки получить заветное число.
В первую очередь возьмите изображение в пиксельном виде формата 106 на 17. Покажем на примере логотипа Библиотеки программиста:
Начинайте с левого нижнего угла и двигайтесь вверх. Если пиксель чёрный, то записывайте 1, в противном случае – 0. Когда подойдёте к концу первого столбца, переходите ко второму. Направление прежнее – снизу вверх.
На рассматриваемой картинке вначале будет масса нулей. В конечном счёте получим такое длинное двоичное число:
000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000011111111100000000000110011000 000000001000010000000000011001100000000000111110000000000000000000000000000000000000000000000 111111000000000000000100000000000000000100000000000000000000000000000111100000000000011001100 000000000100001000000000001000010000000000011001100000000000011110000000000000000000000000001 001111000000000110110011000000001001000010000000011011001100000000011111111000000000000000000 000000000000000000000000000000000000000001111111111111000111111111111111001111111111111110011 111111111111100111111111111111001111000000001110011110111111111100111111111111111001111000000 101110011111111111111100111111111111111001111000000001110011110011001111100111101111011111001 111001100111110011110000011111100111111111111111001111111111111110011111111111111100011111111 11111
Переведите результат в десятичную систему счисления и умножьте на 17.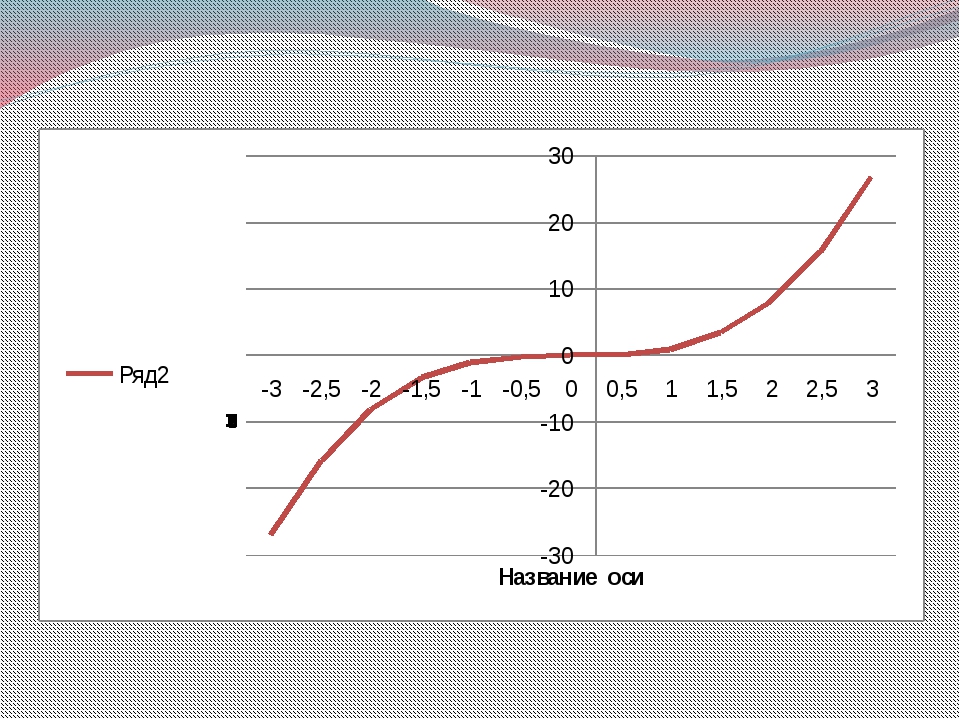 Поздравляем, вы получили значение
Поздравляем, вы получили значение k.
Для логотипа Библиотеки:
275920946718088023480723936896165056360565819683866987796214204083704967426367028838171010577 240995701759158859651200376151267820757234464431427249106688058522782455726480988406439648562 620760834048362915566450772662232356183743837870137689132679620381296484548019451375155482604 298164929327123340746339483037052696814767795015822491105174814111467113651849715266381480786 0373249589248
Осталось построить график.
С помощью этой формулы декодируют растровые изображения, зашифрованные в константе k. Так что смело воспроизводите картинки. Чтобы получить изображение, инвертируйте последовательность шагов алгоритма.
Бонус
С хардкором закончили. А что делать, когда нет желания провести выходные за переводом изображения в двоичное число? Используйте готовый инструмент, и эта процедура займёт минуту. Там вы загружаете изображение нужного формата или рисуете по клеточкам онлайн.
Источник
Какие картинки вам захотелось построить с помощью этой формулы?
Построение графиков в MathCad | Cl-Box
При решении задач в MathCad часто возникает необходимость построить график, будь то график функции или график по каким либо расчетным данным. В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.
- Построение графика функции в MathCad
1.1. Рассмотрим построение на примере функции sin, для этого введем в Маткад следующее (думаю как пользоваться инструментами ввода информации подробно рассматривать не надо, а если вдруг возникнут какие-либо трудности с вводом советую почитать статью Расчаты в MathCad ):
Не забываем что необходимо ставить не знак «равно» а именно знак «определения».
1.2. Теперь нам нужно создать сам график, для этого нажимаем на пункт меню Добавить, выбираем строку Графики, и в появившемся списке выбираем X—Y график
1. 3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
После ввоза названий полей кликаем в любой области вне поля графика
В итоге мы получаем готовый график функции синуса:
- Построение графика в MathCad по данным
2.1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:
2.2. Теперь повторяем действия указанные в пункте 1.2. этой статьи (т.е. добавляем график)
2.3. Как и в пункте 1.3. этой статьи заполняем название осей, только на этот раз у нас будут определители наших данных
2.4. При необходимости совместить два графика на одном делаем следующее: добавляем еще один блок данных, ставим курсор после определителя w в графике и нажимаем поставить запятую (напоминаю, что запятая на русской раскладке и на английской раскладке это разные клавиши, и так как мы работаем в Маткаде используя английскую раскладку нам нужна запятая именно английской раскладки), после этого вводим определитель во вторую (появившеюся) строку на нашем графике.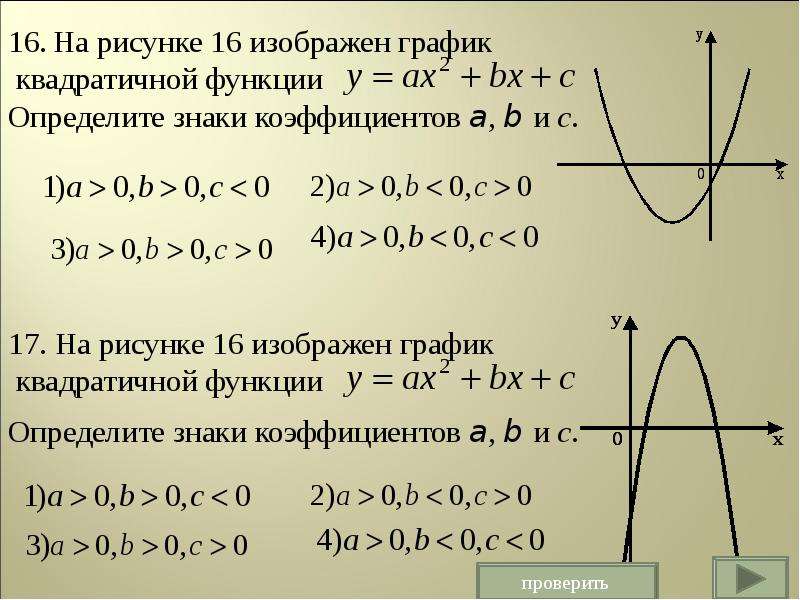
Теперь у нас получилось два пересекающихся графика (конечно же то как он будет выглядеть зависит от данных)
- Форматирование графика в MathCad
Созданный график по умолчанию очень бледный и Вам наверное захочется сделать его немого поярче.
3.1. На графике нажимаем ПКМ (правой клавишей мыши) и в контекстном меню выбираем пункт Формат…
В открывшемся диалоговом окне переходим на вкладку Графики
Тут мы видим табличку строка трассировка 1 соответствует первой кривой нашего графика, трассировка 2 соответственно второй. Столбик Линия соответствует типу линии на нашем графике (сплошная, прерывистая, точка-тире и т.п.). Столбик Линия Вес соответствует толщине нашей линии. И Цвет соответственно цвету. Я в своем примере изменю только толщину линии, и по второму графику тип линии с точек на пунктир для этого в двух верхних строках столбика Линия Вес поставлю цифру 2 и в столбике Линия поменяю тип линии, после чего нажму Применить
Вот что получилось:
Я думаю не надо объяснять как изменять размер графика, если это необходимо.
автор: Admin
Синусоида — онлайн построение графика
Следующий калькулятор служит для построения параметрической синусоиды в диапазоне от 0 до 2П.
при чем коэффициент k может задать сам пользователь.
Есть 3-и возможности введения коэффициентов: в радианах, градусах, пи радианах. По дефолту k = 1, а = 0, при этом функция графика выглядит так:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3. %2.%1%4 %6:%7
%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Строим график функции, заданный системой уравнений, в EXCEL. Примеры и описание
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью
Основы построения диаграмм в MS EXCEL
. О различии диаграмм Точечная и График см. статью
График vs Точечная диаграмма в MS EXCEL
.
статью
График vs Точечная диаграмма в MS EXCEL
.
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график
используя 2 ряда данных
.
Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график
используя 2 ряда данных
.
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Длительность технологического цикла онлайн
Данный сервис можно использовать для расчета длительности производственного цикла (аналитическим и графическим путем) при последовательном, параллельном и параллельно-последовательном движении деталей.Здесь будет показано решение
Длительность производственного цикла
Tц = Tтех + m*tMO + te
где Tтех — длительность технологического цикла, m — количество операций, tMO — среднее межоперационное время, te — длительность естественных процессов.

| Вид движений предметов труда | Формула |
| Последовательный | Tтех=n·m∑i=1tiCi |
| Параллельный | Tтех=(n—p)·timaxCi+p·m∑i=1tiCi |
| Параллельно-последовательный | Tтех=n·m∑i=1tiCi-(n—p)·m-1∑i=1(tkiCi) |
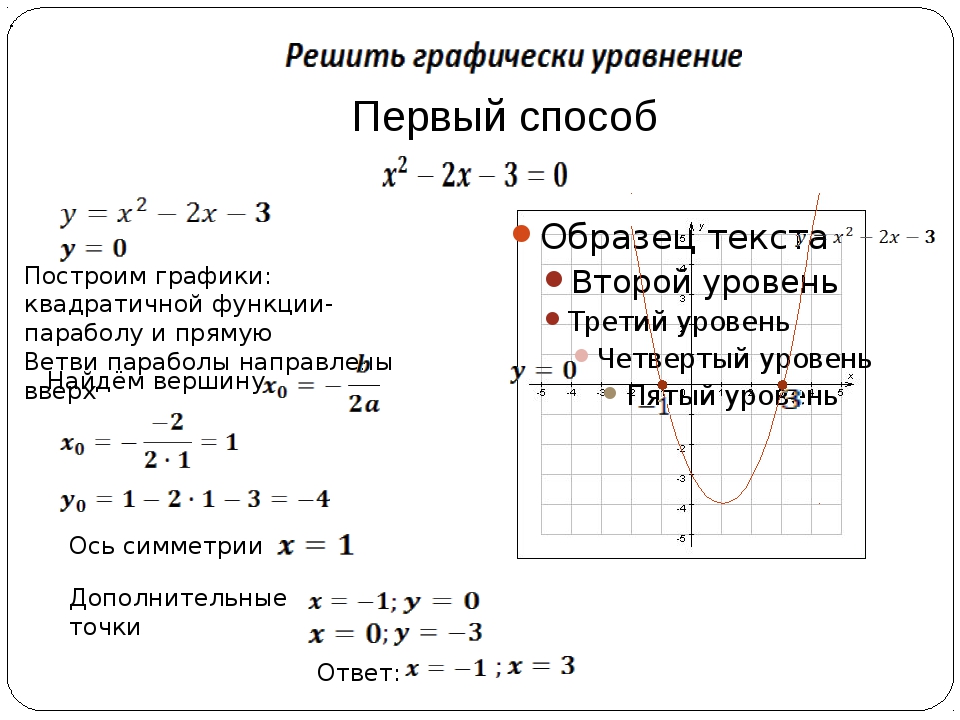 ; p – размер транспортной (передаточной) партии, шт; tki — наименьшая норма времени между k-й парой смежных операций с учетом количества единиц оборудования, мин.
; p – размер транспортной (передаточной) партии, шт; tki — наименьшая норма времени между k-й парой смежных операций с учетом количества единиц оборудования, мин.
Примеры задач
Пример №1. Определить длительность технологического цикла обработки партии деталей 50 шт. при последовательном виде движения её в производстве.Построить график последовательного процесса обработки.
Технологический процесс состоит из следующих операций:
| № операции | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Норма времени, мин. | 12 | 3 | 2 | 5 | 8 | 10 | 2.5 | 6 |
| Число станков на операции | 2 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
Решение.
Последовательный вид движения: Tтех=n·m∑i=1tiCi
Tц=800·(122+31+21+51+81+102+2,51+61)=800·37,5=30000 мин.
| Номер операции | ti | Ci | n·tiCi |
| 1 | 12 | 2 | 800*12/2 = 4800 |
| 2 | 3 | 1 | 800*3/1 = 2400 |
| 3 | 2 | 1 | 800*2/1 = 1600 |
| 4 | 5 | 1 | 800*5/1 = 4000 |
| 5 | 8 | 1 | 800*8/1 = 6400 |
| 6 | 10 | 2 | 800*10/2 = 4000 |
| 7 | 2.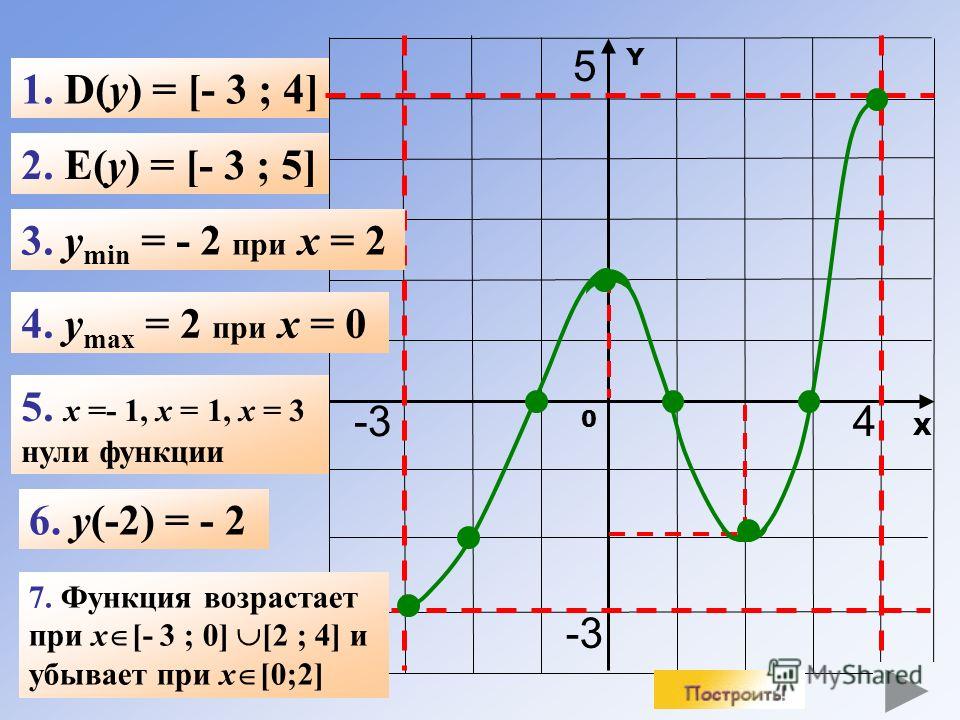 5 5 | 1 | 800*2.5/1 = 2000 |
| 8 | 6 | 1 | 800*6/1 = 4800 |
Пример №2. Построить графики циклов простого процесса при параллельном движении партии деталей.
Проверить правильность графического построения аналитическим расчётом длительности цикла при следующих условиях: величина партии деталей 200 шт., величина передаточной партии 20 шт. Нормы времени по операциям следующие:
| № операции | 1 | 2 | 3 | 4 | 5 | 6 |
| Норма времени, мин. | 1.7 | 2.1 | 0.9 | 4.3 | 2.8 | 0.7 |
 Работа производится в две смены (по 8 час.). Длительность цикла выразить в рабочих днях.
Работа производится в две смены (по 8 час.). Длительность цикла выразить в рабочих днях.
Решение.
Параллельный вид движения: Tтех=(n—p)·timaxCi+p·m∑i=1tiCi + m·tMO
Tц=(200-20)·4,31+20·(1,71+2,11+0,91+4,31+2,81+0,71)+6·2=774+250+12=1036 мин.
Переводим минуты в часы: Tц = 1036/60 = 17,27 час.
Переводим часы в дни: Tц=Tц часs·Tсм·f=17,272·8·1=1,08
| Номер операции | ti | Ci | n·tiCi |
| 1 | 1. 7 7 | 1 | 20*1.7 = 34 |
| 2 | 2.1 | 1 | 20*2.1 = 42 |
| 3 | 0.9 | 1 | 20*0.9 = 18 |
| 4 | 4.3 | 1 | 20*4.3 = 86 |
| 5 | 2.8 | 1 | 20*2.8 = 56 |
| 6 | 0.7 | 1 | 20*0.7 = 14 |
Пример №3. Построить графики цикла простого процесса при последовательном и параллельно-последовательном видах движения.
Построить графики цикла простого процесса при последовательном и параллельно-последовательном видах движения.
Проверить правильность графического построения аналитическим расчётом длительности цикла при следующих условиях: величина партии деталей 180 шт., величина передаточной партии 30 шт.
Нормы времени по операциям следующие:
| № операции | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Норма времени, мин. | 4.6 | 9.9 | 3.1 | 11.4 | 3.0 | 6.8 | 1 |
Решение.
Параллельно-последовательный вид движения: Tтех=n·m∑i=1tiCi-(n—p)·m-1∑i=1(tkiCi)
Среди смежных операций выбираем наименьшее:
min(4,6;9,9) = 4,6
min(9,9;3,1) = 3,1
min(3,1;11,4) = 3,1
min(11,4;3) = 3
min(3;6,8) = 3
min(6,8;1) = 1
Tц = 180·(4,6+9,9+3,1+11,4+3+6,8+1) — (180-30)·(4,6+3,1+3,1+3+3+1) + 7·60 = 7164-2670 + 420 = 4914 мин.
Переводим минуты в часы: Tц = 4914/60 = 81,9 час.
Переводим часы в дни: Tц=Tц часs·Tсм·f=81,92·8·1=5,12
| Номер операции | ti | Ci | n·tiCi |
| 1 | 4.6 | 1 | 30*4.6 = 138 |
| 2 | 9.9 | 1 | 30*9.9 = 297 |
| 3 | 3.1 | 1 | 30*3.1 = 93 |
| 4 | 11.4 | 1 | 30*11.4 = 342 |
| 5 | 3 | 1 | 30*3 = 90 |
| 6 | 6. 8 8 | 1 | 30*6.8 = 204 |
| 7 | 1 | 1 | 30*1 = 30 |
- предыдущий операционный цикл меньше последующего: Топi ≤ Топ(i+1)
Начало обработки на последующей операции возможно сразу после окончания обработки первой передаточной партии на предыдущей операции. - предыдущий операционный цикл больше последующего: Топi > Топ(i+1)
Необходимо передать последнюю транспортную партию и отложить вправо продолжительность её выполнения. Время обработки всех остальных деталей партии откладывается на графике влево. Начало обработки первой детали показывает тот момент, когда транспортный задел с предыдущей операции должен быть передан на данную операцию.
 310.10.10.10.360.360.360.360.360.360.090.090.090.210.210.210.210.210.210.03T = 5.12График цикла при параллельно-последовательном виде движения партий в производстве
310.10.10.10.360.360.360.360.360.360.090.090.090.210.210.210.210.210.210.03T = 5.12График цикла при параллельно-последовательном виде движения партий в производстве
Задание.
- Определите по исходным данным, представленным в табл., аналитическим и графическим путем длительность технологического цикла для изготовления партии изделия.
- Рассчитайте, как измениться цикл, если поменять местами операции 4 и 5?
Если вы не включите знак равенства, предполагается, что вы имеете в виду « = 0 »
Он не был хорошо протестирован, поэтому получайте удовольствие , но ему не доверяют .
Если возникнут проблемы, дайте мне знать.
Примечание: для завершения может потребоваться несколько секунд, потому что для этого требуется много вычислений.
Если вы просто хотите построить график функции в стиле «y = . ..», вы можете предпочесть Function Grapher и Calculator
..», вы можете предпочесть Function Grapher и Calculator
Масштабирование
Используйте ползунок масштабирования (влево увеличивает масштаб, вправо уменьшает).
Чтобы сбросить масштаб до исходных границ, нажмите кнопку Сбросить .
Перетаскивание
Щелкните и перетащите, чтобы переместить график. Если вы просто нажмете и отпустите (без перетаскивания), то место, на котором вы щелкнули, станет новым центром
.Примечание: на графиках использовано компьютерных расчетов . Округление может вызвать ошибки или значения могут быть полностью упущены.
Все функции
Операторы
| + | Оператор сложения | |
|---|---|---|
| – | Оператор вычитания | |
| * | Оператор умножения | |
| / | Оператор отдела | |
| ^ | Оператор экспоненты (степени) |
Функции
кв. | Квадратный корень значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| cos | Косинус значения или выражения | |
| желто-коричневый | тангенс значения или выражения | |
| asin | обратный синус (арксинус) значения или выражения | |
| acos | обратный косинус (arccos) значения или выражения | |
| атан | Арктангенс (арктангенс) значения или выражения | |
| синх | Гиперболический синус (sinh) значения или выражения | |
| cosh | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
эксп. | e (константа Эйлера) в степени значения или выражения | |
| пер. | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| круглый | Округлить до ближайшего целого числа. Примеры: округление (−2,5) = −2, округление (-0,1) = 0, округление (0,1) = 0, округление (2,5) = 3 | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или -1) значения или выражения | |
Константы
| пи | Константа π (3.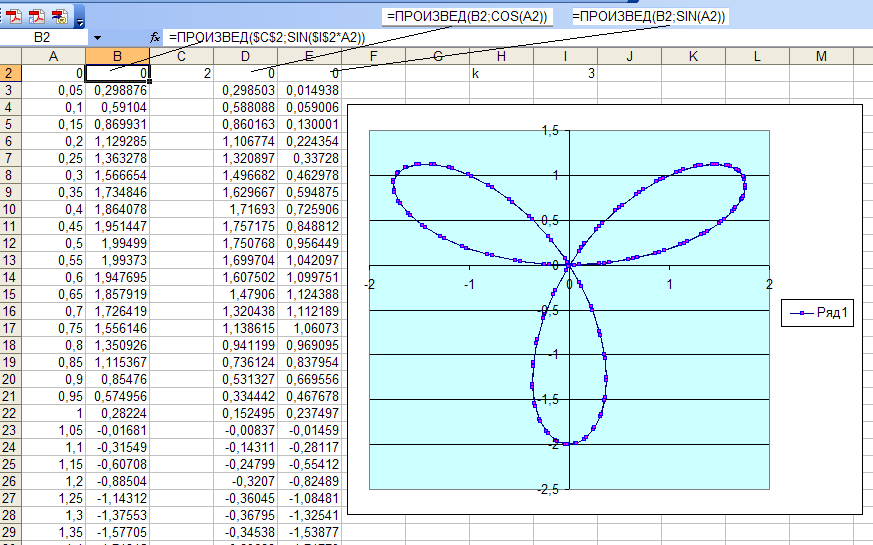 141592654 …) 141592654 …) | |
|---|---|---|
| e | Число Эйлера (2,71828 …), основание натурального логарифма |
Функция поиска уравнений по таблице точек
Поиск инструмента
Поиск по уравнениям функций
Инструмент для нахождения уравнения функции по ее точкам, ее координатам x, y = f (x) в соответствии с некоторыми методами интерполяции и алгоритмами поиска уравнений
Результаты
Функция поиска уравнений — dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Ответы на вопросы (FAQ)
Как найти уравнение кривой?
Чтобы найти уравнение на графике:
Метод 1 (подгонка): проанализируйте кривую (посмотрев на нее), чтобы определить, какой это тип функции (линейный, экспоненциальный, логарифмический, периодический и т.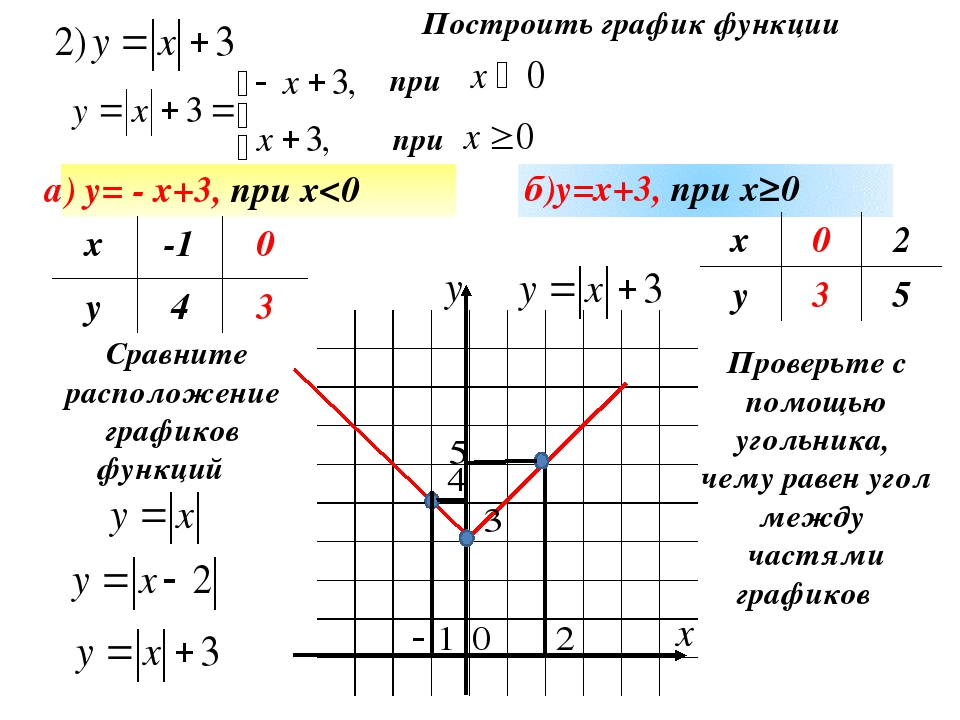 Д.)) и укажите некоторые значения в таблице, и dCode найдет функцию, которая ближе всего подходит к этим точкам.
Д.)) и укажите некоторые значения в таблице, и dCode найдет функцию, которая ближе всего подходит к этим точкам.
Метод 2 (интерполяция): из конечного числа точек есть формулы, позволяющие создать многочлен, который проходит точно через эти точки (см. Интерполяцию Лагранжа), указать значения определенных точек, и dCode вычислит проходящий полином по этим точкам. точки.
Как найти уравнение из набора точек?
Чтобы вывести уравнение функции из таблицы значений (или кривой), существует несколько математических методов.
Метод 1: обнаруживает замечательные решения , как и замечательные идентичности, иногда легко найти уравнение, анализируя значения (сравнивая два последовательных значения или идентифицируя определенные точные значения).
Пример: функция имеет для точек (пары $ (x, y) $) координаты: $ (1,2) (2,4), (3,6), (4,8) $, ординаты увеличиваются на 2, а абсциссы увеличиваются на 1, решение тривиально: $ f (x) = 2x $
Метод 2: использует функцию интерполяции , более сложный, этот метод требует использования математических алгоритмов, которые могут найти многочлены, проходящие через любые точки. Наиболее известными интерполяциями являются лагранжева интерполяция, ньютоновская интерполяция и интерполяция Невилля.
Наиболее известными интерполяциями являются лагранжева интерполяция, ньютоновская интерполяция и интерполяция Невилля.
NB: для данного набора точек существует бесконечное количество решений, потому что через определенные точки проходят бесконечные функции. dCode пытается предложить максимально упрощенные решения, основанные на аффинной функции или полиноме низкой степени (степени 2 или 3).
Как найти уравнение линии?
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Function Equation Finder».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «Function Equation Finder» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая «Функция» Функция Equation Finder (вычисление, преобразование, решение, дешифрование / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.), Без загрузки данных , скрипт, копипаст или доступ к API для «Function Equation Finder» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Д.), Без загрузки данных , скрипт, копипаст или доступ к API для «Function Equation Finder» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
уравнение, координата, кривая, точка, интерполяция, таблица
Ссылки
Источник: https: //www.dcode.fr / функция-уравнение-поиск
© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Таблица функций (2 переменные) Калькулятор
- Цель использования
- Назначение функций
[1] 2021/08/16 19:58 До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Мне нужно было быстро найти шаблон для [более сложных] линейных функций чтобы двигаться дальше по уравнению быстрее / точнее
- Комментарий / запрос
- что-то более четкое
[2] 2021/07/02 18:54 До 20 лет / Старшая школа / Университет / Аспирант / Не совсем /
- Цель использования
- Чтобы найти уравнение, необходимое с таблицей
- Комментарий / запрос
- Маршруты должны быть более точными, и должно быть больше вариантов, если мы хотим уравнение или что это такое.

[3] 2021/05/03 18:18 Моложе 20 лет / Начальная школа / Ученик средней школы / Не at All /
- Цель использования
- Чтобы мои расчеты выполнялись быстрее при выполнении домашнего задания.
[4] 2021/04/27 20:25 Моложе 20 лет / Средняя школа / Университет / аспирант / Не совсем /
- Цель использования
- Завершить таблицу с таблицей парабол по математике
- Комментарий / Запрос
- Меньше требований к калькулятору, я хочу найти y, а не выражение
[5] 2021/04/25 15:22 Моложе 20 лет / Начальная школа / Младший старшеклассник / Не совсем /
- Цель использования
- Нужна помощь с домашним заданием по математике.
- Комментарий / запрос
- Требуется уравнение таблицы функций.
[6] 2021/04/20 17:30 Меньше 20 лет / Начальная школа / Младший школьник / Немного /
- Цель использования
- Просто практика
- Комментарий / Запрос
- Мне нужно чтобы определить, какая функция (линейная, квадратичная или экспоненциальная) функционирует из таблиц.

[7] 2021.03.18 15:58 Моложе 20 лет / Начальная школа / Неполная средняя школа / Немного /
- Цель использования
- Определение, является ли функция линейной или нелинейной.
[8] 2021/03/15 15:48 До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Для домашнего задания по математике
- Комментарий / запрос
- Как я получу ответ?
[9] 2021/03/05 16:50 До 20 лет / Начальная школа / Неполная средняя школа / Немного /
- Цель использования
- онлайн-школа
- Комментарий / запрос
- как сделать я вижу, что это за функция
[10] 2021/02/18 17:15 До 20 лет / Старшая школа / Университет / аспирант / Немного /
Добавить символы-уравнения в графике Последнее обновление: 04.03.2021 Origin предоставляет три способа помочь пользователю вставить формулу или специальные символы в график.
Приложение LaTexКак использовать приложение LaTex
Чтобы отобразить уравнение LaTex в заголовке оси и легенде или в книгеЧтобы отобразить уравнение LaTex в заголовке и легенде оси
Вставить уравнениеКак использовать приложение Insert Equation
Текстовый инструмент с поддержкой UnicodeКак добавить уравнения или специальные символы с помощью текстового инструментаКакой шрифт следует использовать в математических уравнениях Для простых уравнений мы можем использовать текстовый инструмент с математическим шрифтом.
Как найти юникод нужных мне специальных символов
Ключевые слова: Unicode, ALT + X, греческий, ASCII, расширенный ASCII, ANSI, мю, пи, дельта, альфа, бета, эпсилон, лямбда, градусы, надстрочный индекс, подстрочный индекс, расширенный символ, escape-последовательность , надчеркнутый, тильда, точка, форматированный текст, ангстрем, математика, умляут, заголовок листа, подпись столбца, легенда |
Исчисление I — общие графики
Большинство людей вышло из класса алгебры, способного работать с функциями в форме \ (y = f (x) \).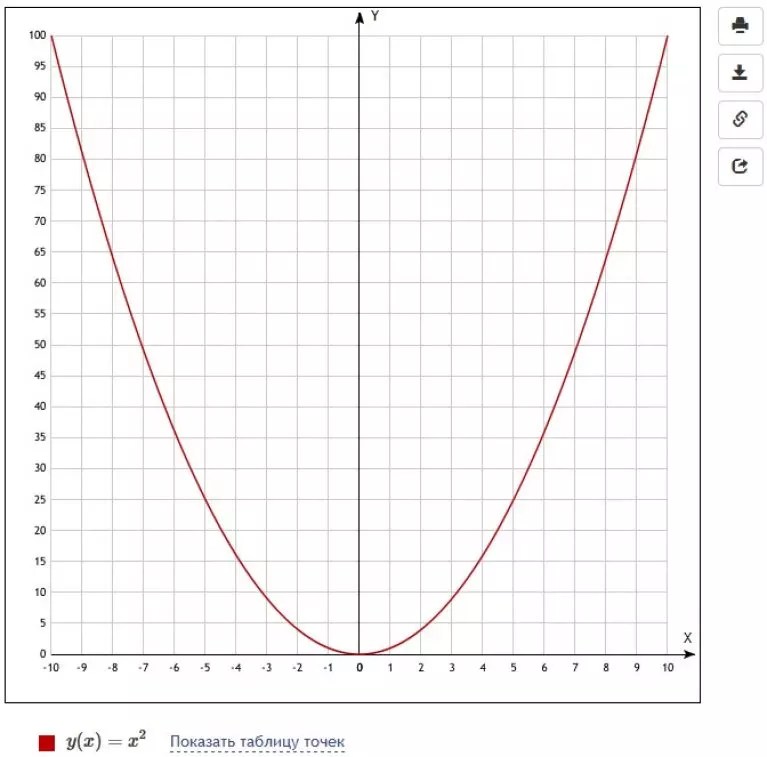 Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме. Итак, вам нужно привыкнуть к работе с функциями в таком виде.
Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме. Итак, вам нужно привыкнуть к работе с функциями в таком виде.
В этих функциях хорошо то, что если вы можете иметь дело с функциями в форме \ (y = f (x) \), то вы можете работать с функциями в форме \ (x = f (y) \) даже если вы не так хорошо с ними знакомы.
Давайте сначала рассмотрим уравнение.2} + на + c \]
Это общая форма этого вида параболы, и это будет парабола, которая открывается влево или вправо в зависимости от знака \ (a \). \ (Y \) — координата вершины задается как \ (y = — \ frac {b} {{2a}} \), и мы находим координату \ (x \), подставляя ее в уравнение. Итак, вы можете видеть, что это очень похоже на тип параболы, с которым вы уже привыкли иметь дело.
А теперь вернемся к примеру. Наша функция — парабола, которая открывается вправо (\ (a \) положительно) и имеет вершину в \ (\ left (-4,3 \ right) \).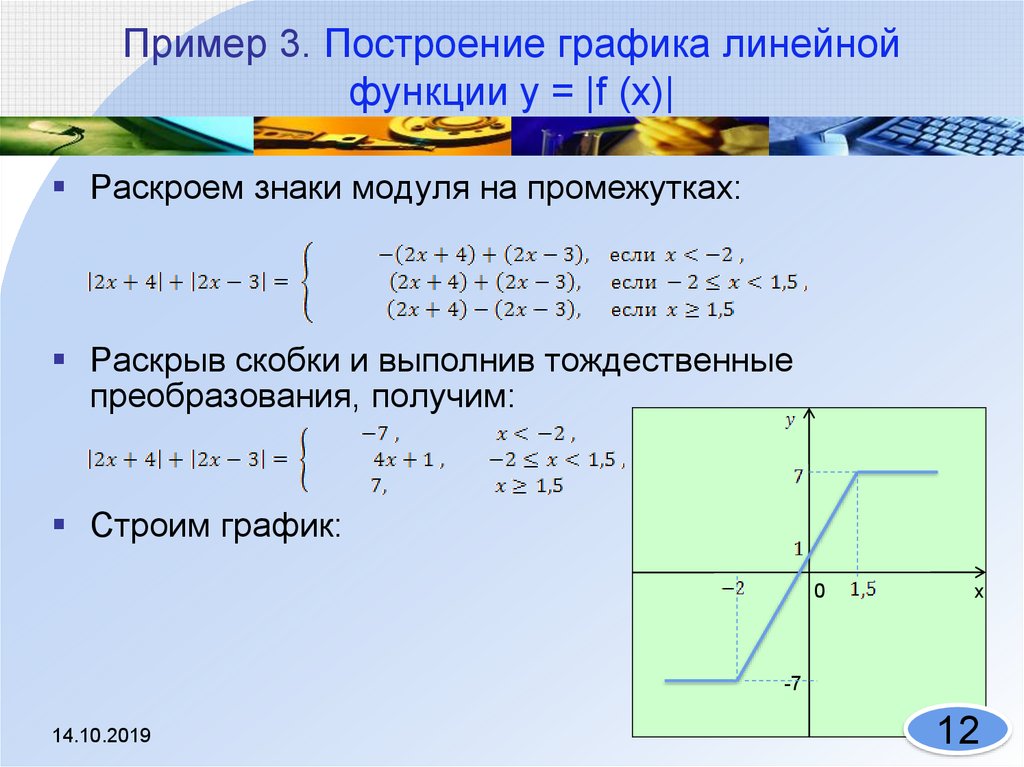 2} — 6y + 5 & = 0 \\ \ left ({y — 5} \ right) \ left ({y — 1} \ right) & = 0 \ end {align *} \]
2} — 6y + 5 & = 0 \\ \ left ({y — 5} \ right) \ left ({y — 1} \ right) & = 0 \ end {align *} \]
Итак, наша парабола будет иметь \ (y \) — точки пересечения в точках \ (y = 1 \) и \ (y = 5 \). Вот набросок графика.
Создавайте графики и сложные математические уравнения прямо из боковой панели Документов Google с помощью g (Math)
Если вы ищете самый простой способ вставки математических уравнений и графиков в свои документы Google, вот решение для вас.
Бывают случаи, когда вам просто нужно добавить немного математики в документ или построить график данных. По умолчанию Google Диск не предлагает ни одной из функций. Однако для того, чтобы найти инструмент, готовый взять на себя эту задачу, достаточно лишь немного покопаться в официальных надстройках.
Речь идет об инструменте g (Math). Теперь, прежде чем вы погрузитесь в это, предполагая, что оно будет создавать простые диаграммы из данных вашей электронной таблицы, это конкретное расширение является математическим и используется только для Google Docs. С его помощью вы можете:
С его помощью вы можете:
- Создавать графики и сложные математические вычисления прямо с боковой панели
- Использовать преобразование речи в математику в Chrome
- Использовать распознавание рукописного ввода для ввода выражений Используйте команды LaTex или готовые коды для создания математических формул, выходящих за рамки встроенного редактора формул
- | Точки графика
Когда вы создаете с помощью g (Math) и вставляете уравнение или график в документ, вы добавляете изображение. Это изображение (файл .png) будет включать связанную ссылку, которую вы можете открыть прямо в браузере.
Использование g (математика) требует понимания математики. Но любой, кому нужен такой инструмент, должен выполнить это предварительное требование.
Установка g (Math)
Как и следовало ожидать, поскольку это надстройка Google Docs, установка довольно проста. Вот шаги:
- Откройте свой Google Диск
- Откройте новый документ Google Docs
- Нажмите «Надстройки» | Получить надстройки
- Найдите g (Math)
- Наведите курсор на список, пока не появится кнопка + FREE
- Нажмите + FREE
- При появлении запроса нажмите Принять
Теперь вы готовы использовать g (Math) .
Использование
Если щелкнуть «Надстройки» | g (Математика) вы увидите подменю, которое позволяет вам выбирать из различных доступных опций (Рисунок A).
Рисунок A
Меню g (математика) в действии.
Изображение: Джек Уоллен
Давайте добавим в наш документ математическое выражение. Вот как это сделать:
- Нажмите «Дополнения» | g (математика) | Создание математического выражения
- Когда откроется боковая панель g (Math) (рисунок B), прокрутите вниз до Предварительно созданное форматирование и выражения
- Щелкните элементы, необходимые для создания формулы
- Прокрутите вверх до окна LaTex и отредактируйте формулу при необходимости
- Как только формула полностью соответствует вашим потребностям, поместите курсор в документ (там, где вы хотите формулу) и нажмите кнопку «Вставить».
Рисунок B
Боковая панель g (Math).
Изображение: Джек Уоллен
Формула появится в документе (Рисунок C).
Рисунок C
Формула добавлена из g (Math).
Изображение: Джек Уоллен
Если размер неправильный, вы можете щелкнуть изображение и, используя ручки перетаскивания, изменить размер по мере необходимости. Единственное предостережение при изменении размера — это, скорее всего, пикселирование изображения.Если вы обнаружите, что изображение слишком маленькое, удалите изображение (выберите его и нажмите «Удалить» на клавиатуре), вернитесь на боковую панель и увеличьте размер, введя ширину в пикселях. Использование этого метода увеличит размер, но имейте в виду, что если вы сделаете слишком большой, изображение все равно будет немного пикселизироваться.
Вы также можете использовать функцию «Преобразование речи в математику». Это переведет (и я могу добавить) то, что вы говорите, в математические уравнения. Чтобы использовать это, вам понадобится микрофон (конечно), который работает с Google Now в вашем браузере.Если это требование выполнено, все, что вам нужно сделать, это нажать кнопку микрофона в разделе «Преобразование речи в математику» и затем произнести необходимые математические выражения. Когда закончите, нажмите кнопку микрофона еще раз, чтобы остановить механизм Speech to Match.
Я обнаружил, что с помощью функции преобразования речи в математику необходимо добавить собственные замены. Например, при попытке добавить разделение слово «разделенный» всегда появляется как английский текст. Деление 12 на 2 не очень помогает в формуле. Чтобы обойти это, прокрутите вниз до раздела «Пользовательские замены» и введите разделенный в области «Разговорный текст» и / в качестве его замены.Как только вы это сделаете, функция «Преобразование речи в математику» переведет слово, разделенное на «/».
Если вы ищете самый простой способ вставки математики и графиков в свои документы Google, не ищите ничего, кроме g (Math).
Вы обнаружили, что в Документах Google отсутствуют функции? Если да, то какую функцию (или надстройку) вы бы хотели, чтобы Google воплотил в жизнь?
См. Также:
Рост и возможное падение графического калькулятора
Первый портативный графический калькулятор Casio FX-7000G появился в 1985 году.
С тех пор графические калькуляторы стали обычным — и спорным — инструментом для изучения математики. Эти устройства могут выполнять все вычисления научного калькулятора, а также графические уравнения, составлять таблицы функций и решать уравнения. Многие умеют проводить статистический анализ и даже некоторые расчеты.
Адвокаты утверждают, что калькуляторы предоставляют студентам доступ к более мощным математическим методам. Критики опасаются, что они могут повредить беглому владению учащимися базовой математикой и стандартными алгоритмами.
Сегодня некоторые учителя заменяют дорогие графические калькуляторы бесплатными приложениями, которые могут делать больше. Но даже после десятилетий использования графические технологии любого вида в классе по-прежнему вызывают споры.
Как преподаватели математики, мы думаем, что графический калькулятор изменил американские классы к лучшему. Независимо от того, продолжат ли учителя использовать эти инструменты или откажутся от них в пользу новых, графические технологии, вероятно, всегда будут иметь место в среднем математическом образовании.
Преподаватели математики часто говорят о двух видах понимания.
«Инструментальное понимание» приходит от усвоения процедуры или запоминания факта без реального понимания математики, лежащей в основе этого. Он знает как, но не знает почему. Поговорка «Не нам задаваться вопросом, почему, просто переверните и умножьте!» — который иногда используется для обучения делению на дроби — отражает такое понимание.
Первый научный графический калькулятор. 51764518 @ N02 / flickr, CC BY-SAНапротив, «реляционное понимание» — это своего рода связанное концептуальное понимание.Люди с пониманием отношений не просто знают, как инвертировать и умножать, они знают, почему такая процедура дает частное двух дробей.
Защитники графических калькуляторов в школе увидели многообещающую способность этого инструмента помочь ученикам развить взаимопонимание. В то время как калькулятор заботится о том, «как», учащиеся могут сосредоточиться на «почему».
Воздействие совершенно очевидно в программе вычислений Advanced Placement (AP), которая начала требовать графических калькуляторов в своих курсах и на экзаменах в 1995 году.До 1995 года вопросы экзамена по математическому анализу AP касались почти исключительно способности студентов использовать правила для нахождения производных и интегралов функций. После 1995 г. произошел заметный сдвиг от этого инструментального понимания к вопросам, требующим понимания отношений.
По мере развития экзаменов менялось и преподавание философии. Программа AP требовала, чтобы учителя использовали в своих курсах графические калькуляторы. Это было не только для того, чтобы студенты научились пользоваться калькулятором.Скорее, фокус обучения сместился, чтобы студенты могли изучать математику с помощью графического калькулятора.
Например, используя функции построения графиков и масштабирования графического калькулятора, учащиеся могут сравнивать и противопоставлять локальное и глобальное поведение таких функций, как y = x ² и y = x ² + 2. Увеличив масштаб, учащиеся могут увидеть, что в любой местности графики явно отличаются. Уменьшив масштаб, учащиеся могут увидеть, что в целом графики в основном идентичны.Благодаря такому исследованию студенты получили реляционное понимание бесконечных ограничений.
В локальной области (-6Результаты более чем трех десятилетий исследований очевидны. Графические калькуляторы положительно влияют на взаимопонимание учащихся и незначительно влияют на их инструментальное понимание.
Другой обзор, проведенный уважаемыми исследователями в области математического образования (но финансируемый компанией, производящей калькуляторы), пришел к аналогичному выводу.
Другими словами, ученики, которые используют графические калькуляторы в школе, знают как минимум столько же основных фактов и как минимум так же хорошо справляются со стандартными алгоритмами, как ученики, которые не используют графические калькуляторы.Однако студенты, использующие графические калькуляторы, имеют более глубокое понимание «почему» этих алгоритмов.
Конечно, есть много отдельных исследований, которые показывают незначительные или даже отрицательные эффекты графических калькуляторов. Но в целом, когда технология сочетается с соответствующими методиками обучения, результатом становится более полное и качественное изучение математики.
Сегодня онлайн-технологии и технологии на основе приложений, такие как Desmos и GeoGebra, призваны заменить роль автономных графических калькуляторов в школе.
Как и в случае с графическими калькуляторами, для того, чтобы эти новые технологии оказали положительное влияние на обучение учащихся, учителя должны адаптировать свои инструкции, изменив то, что они преподают, и то, как они учат.
Например, технологии могут помочь студентам соединить графические представления с алгебраическими уравнениями. Недавно мы наблюдали, как ученики седьмого класса в Миссуле, штат Монтана, делали это с помощью Desmos. Студенты изобразили три различных линейных уравнения, каждое с разными коэффициентами для члена x .На основе этого исследования студенты делали предположения о роли коэффициента и использовали приложение для проверки своих предположений — например, с помощью «ползунка» для динамического изменения коэффициента. Гибкость технологии также побуждала студентов задавать и исследовать свои собственные вопросы.
В приложении Desmos учащиеся могут проверять свои вопросы, динамически изменяя коэффициент с помощью ползунка. Дэвид ЭриксонНесмотря на то, что эти облачные инструменты и инструменты на основе приложений предоставляют мощные технологии бесплатно на смартфонах и других личных устройствах, дорогой графический калькулятор (который обычно стоит от 80 до 150 долларов США) продолжает оставаться неизменным в математических классах K-12, с годовой рост продаж единиц в 2015 и 2016 годах.
В последнее время в Интернете было много скандалов по поводу такого положения дел, и комментаторы были ошеломлены продолжающимся преобладанием графических калькуляторов по сравнению с недорогими или бесплатными приложениями. Дебаты даже вызвали реакцию президента Texas Instruments, доминирующей компании по производству графических калькуляторов в США
.Мы согласны со многими пунктами в пользу новых приложений. Но нет сомнений в том, что при правильном использовании технология построения графиков — будь то на калькуляторе, экране компьютера, планшете или смартфоне — является мощным инструментом, помогающим учащимся изучать математику.



 Обычно мы рекомендуем следующие три популярных математических шрифта
Обычно мы рекомендуем следующие три популярных математических шрифта
Ваш комментарий будет первым