Пример решения задачи: Исследование параметрически заданной функции. Построение графика ЗАДАНИЕ. Построить график функции y = y(x)
Математика (БкПл-100, БкК-100)
Математика (БкПл-100, БкК-100) М.П. Харламов 2009/2010 учебный год, 2-й семестр Лекция 5. Исследование функций с помощью производных 1 1. Понятие о производных высших порядков Опр. Пусть дана функция f(x)
ПодробнееПостроение графиков функций
Построение графиков функций 1. План исследования функции при построении графика 1. Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции:
ПодробнееУрок на тему: Построение графиков.

Урок на тему: Построение графиков. Ребята, мы с вами строили уже не мало графиков функций, например параболы, гиперболы, тригонометрических функций и другие. Давайте вспомним, как мы это делали? Мы выбирали
ВЗФЭИ. Контрольная работа 1
ВЗФЭИ. Контрольная работа Задача. По формулам Крамера решить систему уравнений: 5 4 5 6 7 0, 0, 0. Решение. Перенесем свободные члены в правую часть системы: 4 7, 5, 5 6. Решим систему методом Крамера.
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
ПодробнееМатематический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
ПодробнееМатематический анализ.
 Лекция 3.4
Лекция 3.4Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Модуль 3. Дифференциальное исчисление функций одной переменной
Подробнее6 Общая схема исследования функции
5 6 Общая схема исследования функции Исследование дважды дифференцируемой функции будем проводить по следующей схеме. Находим область определения функции D( f.. Определяем точки разрыва функции.. Находим
Подробнееприсутствие функций арксинуса вида arcsin f x
Практическая работа Полное исследование функции и построение графика Цель: закрепить навыки исследования функций и построения графиков Оборудование (приборы, материалы, дидактическое обеспечение): методические
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Введение в математический анализ Предел последовательности и функции. Раскрытие неопределенностей в пределах. Производная функции. Правила дифференцирования. Применение производной
Раскрытие неопределенностей в пределах. Производная функции. Правила дифференцирования. Применение производной
Образовательный портал «РЕШУ ЕГЭ» (
Применение производной к исследованию функций 1. На рисунке изображен график производной функции, определенной на интервале Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих
ПодробнееМатематика (БкПл-100)
Математика (БкПл-100) М.П. Харламов 011/01 учебный год Тема. Пределы, непрерывность, производные 1 Тема: Предел функции 1. Предел функции Пусть f(x) функция, определенная на множестве Х; А и а числа. Опр.
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
Подробнее«ИССЛЕДОВАНИЕ ФУНКЦИЙ»
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.
В.И. Иванов С.И. Васин
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
ПодробнееИССЛЕДОВАНИЕ ФУНКЦИЙ
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
ПодробнееКонтрольная работа T=3. Задание 1. [1, стр. 2]
Дана матрица Контрольная работа A 0 T= Задание [, стр ] Определите ее размерность Выпишите характеристики этой матрицы: прямоугольная, квадратная, симметричная, единичная, нулевая, треугольная, диагональная,
ПодробнееЧтение графиков функций
Материалы для выполнения внеаудиторной (домашней самостоятельной работы) нацеленные на устранение пробелов знаний и умений по дисциплине «Математика: алгебра и начала математического анализа, геометрия»
Подробнее~ 1 ~ «Признаки монотонности функции»
~ 1 ~ «Признаки монотонности функции» Теорема: Для того чтобы функция f(x), дифференцируемая на a,b возрастала (убывала) на a,b необходимо и достаточно, чтобы x a,b выполнялось неравенство f (x) 0 (f (x)
ПодробнееПостроение графиков функций
Построение графиков функций к о н с п е к т з а н я т и я y Александр Рубцов 8 октября 015 г.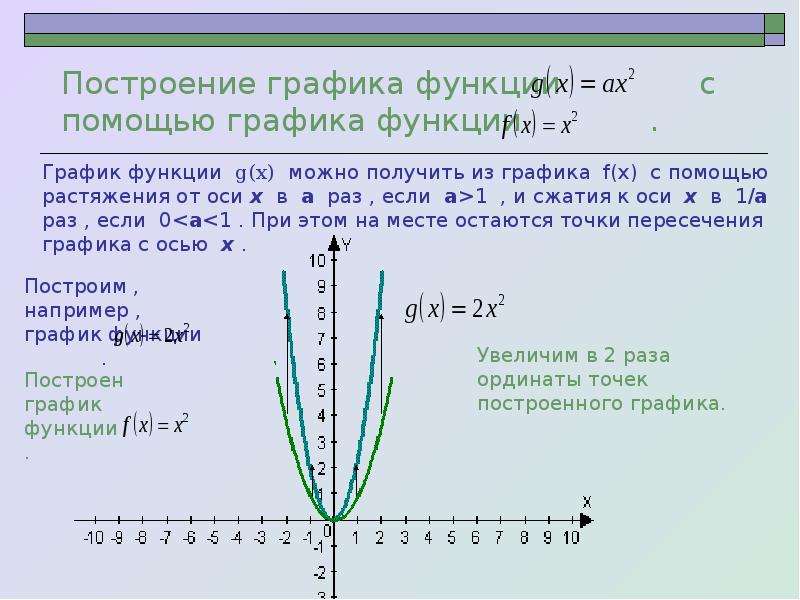
Примерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА класс (профиль) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
ПодробнееТема 39. «Производные функций»
Тема 39. «Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная
ПодробнееПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Пусть имеем функцию определенную на множестве X и пусть точка X — внутренняя точка те точка для которой существует окрестность X Возьмем любую точку и обозначим через называется
Подробнее.
 Преобразуем функцию:, если x
Преобразуем функцию:, если xВариант Найти область определения функции : + + + Неравенство + выполняется всегда Поэтому область определения данной функции определяется следующими неравенствами:, те, и, те Решением системы этих неравенств
ПодробнееПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
М и н и с т е р с т в о о б р а з о в а н и я и н а у к и Р о с с и й с к о й Ф е д е р а ц и и Федеральное государственное автономное образовательное учреждение высшего профессионального образования Национальный
Подробнееи построения их графиков
Применение производной для исследования функций и построения их графиков 1. Достаточные признаки монотонности функции. Достаточное условие возрастания функции Если f ( x ) > 0 в каждой точке интервала
ПодробнееДифференциальное исчисление
ФГОУ СПО ЛТК МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ Дифференциальное исчисление Ст Ленинградская 00г Предисловие Настоящее пособие написано в соответствии с программой по математике для студентов средни профессиональны
Подробнее16.
 2.Н. Производная.
2.Н. Производная.6..Н. Производная 6..Н. Производная. Оглавление 6..0.Н. Производная Введение…. 6..0.Н. Производная сложной функции…. 5 6..0.Н. Производные от функций с модулями…. 7 6..0.Н. Возрастание и убывание
ПодробнееПостроение графиков в пакете Maple
Министерство образования Ставропольского края
Государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ставропольский государственный педагогический институт»
Кафедра математики и информатики
Методические указания
к проведению практических занятий
Ставрополь 2013
Построение графиков в пакете Maple
/Сост.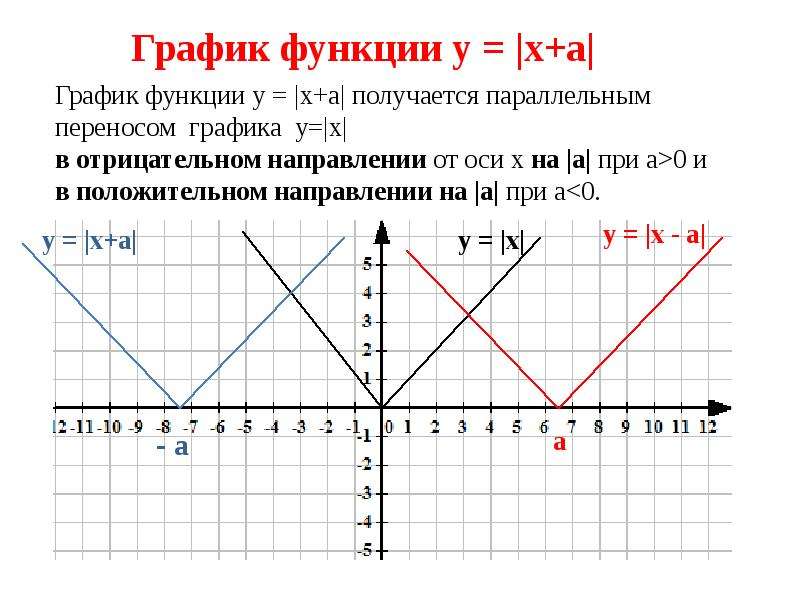 : А.А.Оленев, К.М. Сагдеев: СГПИ.
–Ставрополь, 2013. — __ с.
: А.А.Оленев, К.М. Сагдеев: СГПИ.
–Ставрополь, 2013. — __ с.
В работе рассмотрены приемы и методы построения различных графиков в пакете компьютерной математики Maple. Основное внимание уделено построению графиков, которые требуется строить при решении задач дисциплины «Математика». Методическая разработка будет полезна студентам всех специальностей дневного и заочного обучения СГПИ, применяющих при решении задач по математике систему компьютерной алгебры Maple.
Содержание
Введение …………………………………………………………………………………………………4
1. Графики на плоскости и в пространстве ……………………………………………….5
2. Функция plot построения графиков на плоскости ………………………………5
2.1. График явно заданной функции
. ……………………………………………………..5
……………………………………………………..5
2.2. Построение графика функции, заданной процедурой ………………………6
2.3. График параметрически заданной функции …………………………………….7
2.4. График функции, заданной параметрически процедурами ………………8
2.5. График, построенный по точкам, заданным декартовыми
координатами ……………………………………………………………………………………….9
2.6. Опции функции plot …………………………………………………………………..10
1) опция настройки осей координат ………………………………………………….10
2) опция задания цвета кривой графика …………………………………………….12
3) опция выбора системы координат
. ………………………………………………..12
………………………………………………..12
4) опция, учитывающая разрывы кривой графика ……………………………..12
5) опция, заполнения цветом области между кривой и осью абсцисс. ..14
6) опция, определяющая стиль построения линии графика ………………..14
7) опция, определяющая число точек, по которым строится график ….15
8) опция, определяющая соотношение равного масштаба на осях ……..15
9) опция, определяющая толщину линии …………………………………………..15
10) опция, определяющая размеры окна построения графика ……………15
3. Функция plot3d построения графиков в пространстве ……………………..15
3.1. График функции двух переменных ……………………………………………….16
3. 1. График поверхности, заданной
параметрически ……………………………17
1. График поверхности, заданной
параметрически ……………………………17
4. Пакет построения графиков plots ……………………………………………………19
4.1. График неявно заданной функции одной переменной ……………………20
4.2. Текстовые графики на плоскости ………………………………………………….21
4.3. Комбинированные графики …………………………………………………………..22
5. Графические построения при решении задач дисциплины «Математика»
……………………………………………………………………………………………………………..23
5.1. Исследование функций и построение их графиков ………………………..24
5.2. Построение графиков областей на плоскости, ограниченных
заданными кривыми
. …………………………………………………………………………..28
…………………………………………………………………………..28
5.3. Построение областей в пространстве, ограниченных заданными
поверхностями ……………………………………………………………………………………31
5.4. Построение графиков частичных сумм степенного ряда ………………..33
5.5. Построение графиков периодических функций и графиков
частичных сумм ряда Фурье ………………………………………………………………..34
6. Построение графика корреляционной таблицы …………………………………..37
Библиографический список …………………………………………………………………40
Введение
Необходимость построения графиков
функций, чертежей геометрических фигур
в тетради или на листах ватмана, возникает
при решении задач по алгебре и геометрии
в школе, при изучении различных разделов
дисциплины «Математика» в вузе. Кроме
того, потребность в таких построениях
возникает при научных исследованиях и
на производстве.
Кроме
того, потребность в таких построениях
возникает при научных исследованиях и
на производстве.
До появления компьютерной графики, построение графиков функций и чертежи фигур приходилось делать вручную, используя самые различные инструменты и приспособления, такие как линейки, циркули, кульманы и другие. При этом, нередко, для выполнения построений приходилось выполнять значительное количество предварительных расчетов и, если в этих расчетах появлялись ошибки, то всю работу приходилось переделывать заново.
Появление компьютеров и программ
компьютерной графики избавило от многих
рутинных расчетов и ручной работы,
которую надо было выполнить, чтобы
сделать графические построения. Теперь
любой человек, владеющий навыками
работы с компьютером и установленными
на нем программами компьютерной
графики, может построить самые сложные
графики и фигуры на экране компьютера
и затем, если нужно, распечатать их с
помощью принтера или плоттера.
Среди программ компьютерной графики существуют как простые графические программы, позволяющие строить простые фигуры и графики, так и мощные профессиональные программы технической графики среди которых можно отметить, например, программу AutoCad. К одной из лучших графических программ относится также программа Visio, входящая в настоящее время, в расширенный пакет семейства офисных программ Microsoft Office.
Возможности графических построений
имеют также и многие программы, не
являющиеся, по сути, графическими
программами. Рисунки, например, можно
выполнить прямо в текстовом редакторе
Word, а строить различные графики можно
в электронных таблицах Exel. Мощными
графическими возможностями обладают
также пакеты компьютерной математики
Maple, Mathematica, MathCad,MatLab. При
этом эти возможности сочетаются с
возможностями математических вычислений
и расчетов, чтобы наглядно представить
эти расчеты в виде фигур и графиков.
В данной работе рассматриваются возможности графических построений, которые можно выполнить в системе компьютерной математики Maple. Из огромного арсенала возможностей графических построений, которые можно сделать в этой программе, упор сделан на построение графиков и фигур, которые требуется выполнить при решении различных математических задач, встречающихся при изучении дисциплины «Математика».
Maxima — Руководства
Впервые было опубликовано в «Linux Format» №11 (85), ноябрь 2006 г.
«А рисовать вы тоже умеете?» — «Рисовать? Кого-нибудь привлечем»
Как мы уже говорили в прошлый раз, количество различных
функций в Maxima разработчики постарались свести к минимуму, а
широту размаха каждой конкретной функции, соответственно, к
максимуму. Соблюдается эта тенденция и в функциях построения
графиков: основных таких функций всего две, с очевидными, как
всегда, названиями — plot2d и plot3d (одно из значений слова plot — график, а
аббревиатуры 2d и 3d переводятся
как двумерный и трехмерный). Если говорить
точнее, возможности графической отрисовки не встроены в Maxima,
а реализованы посредством внешних программ, в чем и
прослеживается пресловутый Unix-way: «одна задача — одна
программа». По умолчанию, построением графиков
занимается
Если говорить
точнее, возможности графической отрисовки не встроены в Maxima,
а реализованы посредством внешних программ, в чем и
прослеживается пресловутый Unix-way: «одна задача — одна
программа». По умолчанию, построением графиков
занимается gnuplot, но кроме него есть
разрабатываемый вместе с Maxima и идущий в ее же
пакете openmath. Gnuplot необходимо установить
(вручную либо автоматически — как зависимость Maxima) из
пакета gnuplot-nox, либо
просто gnuplot, а для работы openmath нужен командный интерпретатор wish, входящий обычно
в пакет tk; и, начиная с версии 5.10.0, еще и
xMaxima.
Теперь кратко — о возможностях. Начнем
с plot2d. Кратчайший вариант ее вызова
такой: plot2d(выражение, [символ, начало, конец]),
где выражение задает функцию, график которой нужно построить,
символ — неизвестное (он, понятное дело, должен быть
единственным неопределенным символом, входящим в выражение), а
начало и конец задают отрезок оси Х для построения
графика; участок по оси Y в таком варианте записи
выбирается автоматически, исходя из минимума и максимума функции
на заданном промежутке. Обратите внимание, что неизвестное и
концы промежутка нужно задавать не тремя отдельными параметрами,
как, скажем, в
Обратите внимание, что неизвестное и
концы промежутка нужно задавать не тремя отдельными параметрами,
как, скажем, в integrate, а в виде списка. Это
связано с тем, что plot2d может принимать еще и
дополнительные аргументы — в таком случае они перечисляются
следом за таким списком, что исключает всякую путаницу.
После вызова функции plot2d в таком варианте
откроется окно gnuplot, в котором будет отображен
затребованный график. Никакой интерактивной работы с полученным
изображением gnuplot не предусматривает, кроме
автоматического его масштабирования при изменении размеров
окна. Насмотревшись вдоволь, можно закрыть окно с графиком
клавишей Q, либо, в случае работы с Maxima в
редакторе TeXmacs или wxMaxima, просто переключиться обратно в
интерфейс, оставив окно gnuplot открытым, и
продолжить работу:
В некоторых случаях автоматический подбор отображаемого
участка вертикальной оси может нас не устроить. Например, он
работает не очень хорошо, если функция имеет на заданном
промежутке точку разрыва, хотя бы один из односторонних пределов
в которой равен бесконечности: тогда промежуток по
оси
Например, он
работает не очень хорошо, если функция имеет на заданном
промежутке точку разрыва, хотя бы один из односторонних пределов
в которой равен бесконечности: тогда промежуток по
оси Y будет выбран слишком большим. Да и в других
случаях может понадобиться изменить умолчательное поведение. Для
этого предусмотрен такой вариант вызова
функции: plot2d(выражение, [символ, начало, конец],
[y, начало, конец]). Здесь буква y используется в качестве обозначения вертикальной оси, а
остальные два параметра имеют тот же смысл, что и выше.
Как видите, умолчательный вид графиков в gnuplot достаточно прост и даже аскетичен, но здесь можно очень и очень
многое менять с помощью дополнительных опций. Некоторые из
которых будут освещены чуть ниже, а остальные можно изучить по
документации к gnuplot.
Чтобы построить на одной и той же картинке одновременно два
графика (или больше), просто передайте
функции plot2d вместо отдельного выражения их
список:
Здесь [x, 0.01, 5] вместо [x, 0, 5] я написал «по привычке» — Maxima 5.9.x выдавала ошибку, если
заданная функция была не определена на одном из концов
интервала. В 5.10.0 мне эту ошибку воспроизвести не удалось; так
что есть основания полагать, что поведение в таких случаях
поправили.
Может plot2d строить и графики параметрически
заданных функций. Для этого используется список с ключевым
словом parametric: plot2d([parametric, x-выражение, y-выражение,
[переменная, начало, конец],
[nticks, количество]]). Здесь x-выражение и y-выражение задают зависимость координат от
параметра, то есть, по сути, это две функции
вида x(t), y(t), где
t — переменная параметризации. Эта же переменная должна
фигурировать в следующем аргументе-списке, а
параметры
Эта же переменная должна
фигурировать в следующем аргументе-списке, а
параметры начало, конец, как и в двух
других рассмотренных случаях, задают отрезок, в пределах
которого этот параметр будет изменяться. Последний
аргумент-список, с ключевым словом nticks, задает
количество кусочков, на которые будет разбит интервал изменения
параметра при построении графика. Этот аргумент опционален, но
на практике он нужен почти всегда: умолчательное
значение nticks равно 10; согласитесь,
редко бывает нужно в качестве графика получить ломаную из 10
отрезков. Вот пример построения графика параметрической
функции:
Кроме parametric, функция plot2d понимает еще одно ключевое
слово: discrete. Предназначено оно, как нетрудно
догадаться, для отображения на плоскости дискретных множеств;
точнее говоря, конечных наборов точек. По записи аргументов
такой вариант распадается еще на
два:
По записи аргументов
такой вариант распадается еще на
два: plot2d([discrete, x-список, y-список]) и plot2d([discrete, [x, y]-список]). В первом
варианте координаты задаются как два отдельных
списка [x1, x2, …, xn], [y1, y2, ,…, yn], а во
втором — как список пар координат отдельных
точек [[x1, y1], [x2, y2], …, [xn, yn]].
Если мы, к примеру, имеем набор статистических значений, зависящих от номера, мы можем отобразить его, задав в качестве x-координат сами эти номера, то есть натуральные числа:
По умолчанию множество отображается в виде ломаной с
вершинами в заданных точках; такое поведение можно изменить и
получить вывод, к примеру, в виде отдельных точек. Это
достигается использованием специальных опций, применимых как
к plot2d, так и к plot3d, поэтому
давайте перейдем к рассмотрению последней.
Придаем объем
Функция plot3d имеет два варианта вызова: один
для явного задания функции и один для параметрического. В обоих
случаях функция принимает три аргумента. Для явно заданной
функции: plot3d(выражение, [переменная1, начало, конец],
[переменная2, начало, конец]); аргументы
аналогичны plot2d, с той разницей, что здесь
независимых переменных две.
Построение нескольких поверхностей на одном графике не
поддерживается — потому, вероятно, что на таком рисунке
проблематично было бы что-либо разглядеть. Посему для
параметрически заданной функции ключевое слово parametric не
требуется: вызов с первым аргументом-списком уже не с чем
перепутать. График параметрически заданной функции строится
так: plot3d([выражение1, выражение2, выражение3],
[переменная1, начало, конец], [переменная2, начало, конец]),
где выражения отвечают, по порядку, x(u, v), y(u, v), z(u, v).
С помощью параметрической формы можно строить и пространственные кривые. Для этого просто нужно задать второй, фиктивный, параметр, чтобы Maxima не ругалась на неправильный синтаксис вызова функции:
И отсюда мы плавно переходим к опциям функций построения
графиков, посредством использованной выше
опции grid. Каждая опция имеет некоторое
умолчательное значение, а изменить его можно, добавив к
аргументам список
вида [имя-опции, значение]. Строго говоря,
рассмотренные выше y и nticks также
являются опциями; в предпоследнем примере мы задали
опции nticks значение 120, а в примере
перед ним в качестве значения опции y использовалась пара чисел 0, 5. В документации к
Maxima символ x, выступавший в примерах выше в
качестве обязательного параметра, также приводится как опция; на
самом деле опцией он является только в
случае parametric и действует тогда так же, как и
опция y, только по другой
оси. Опция
Опция grid, использованная выше, применима к
трехмерным графикам вместо опции nticks,
используемой для двумерных. Она, также как и y,
задается в виде двух целых значений, которые для поверхностей
задают размер ячеек сетки, в виде которой отображается
поверхность; первое число — вдоль оси X, второе —
вдоль оси Y; либо, в случае параметрического задания,
по первому и по второму параметру соответственно. Для кривых из
этих параметров действует только один, но писать нужно опять же
оба, дабы не нарушать синтаксис; и здесь этот параметр имеет в
точности тот же смысл, что nticks для кривых на
плоскости. Но перейдем к другим опциям.
С претензией на красоту
Первая опция, которую мы рассмотрим, задает формат вывода
результата; так она и
называется: plot_format. Формат может принимать
одно из четырех значений, первое из которых действует по
умолчанию: gnuplot, mgnuplot, openmath и ps. В умолчательном варианте
(значение
В умолчательном варианте
(значение gnuplot) данные для отображения
передаются напрямую программе gnuplot, которая сама
по себе имеет достаточно гибкое управление, и параметры ей можно
передавать прямо из Maxima с помощью дополнительных опций
функций plot2d/3d. Параметров этих
настолько много, что gnuplot могла бы стать темой
отдельной статьи; так что обращайтесь за ними к документации
по gnuplot. В противовес своим богатым
возможностям, gnuplot имеет перед следующими двумя
интерфейсами (если откровенно — скорее, лишь перед одним из них)
только один недостаток: она генерирует статичное изображение,
тогда как mgnuplot и openmath позволяют в реальном
времени масштабировать и передвигать картинку,
а plot3d — еще и вращать линию или поверхность в
разные стороны в пространстве.
Следующий вариант — mgnuplot — является
дополнительным интерфейсом к gnuplot, написанным на
Tcl/Tk, но динамика у него настолько «задумчивая», а остальные
возможности настолько бедны, что я не вижу смысла
останавливаться на нем подробнее.
И перехожу сразу к openmath. Он тоже не очень-то
поддается управлению, зато предоставляет хорошую
интерактивность, особенно ценную в трехмерном варианте: после
того, как объект сгенерирован, его можно масштабировать и очень
динамично вращать, разглядывая со всех сторон. Особенно это
помогает для сложных поверхностей, когда, глядя на статичную
«сетку» gnuplot, непросто понять форму
поверхности. Справедливости ради нужно отметить,
что gnuplot позволяет задавать точку обзора
трехмерного объекта в качестве одного из многочисленных
параметров, то есть хотя картинка и статична, но с какой стороны
на нее смотреть, мы можем указать произвольно.
Ну и последнее значение опции plot_format подталкивает Maxima к непосредственной генерации
PostScript-документа с изображением. Но и здесь надо сказать:
генерировать PostScript-вывод умеет и все тот
же gnuplot.
Большинство остальных опций относятся только к формату
вывода gnuplot. А мы рассмотрим еще одну
универсальную, пригодную для всех форматов и преобразующую не
результирующее изображение, а сам процесс построения графика;
точнее, систему координат. Называется эта
опция transform_xy, по умолчанию она
равна false. Передавать ей нужно выражение,
сгенерированное функцией make_transform([x, y, z],
f1(x, y, z), f2(x, y, z), f3(x, y, z)). Кроме того,
существует одно встроенное преобразование, известное
как polar_xy и
соответствующее make_transform([r, th, z], r*cos(th),
r*sin(th), z), то есть переходу к полярной цилиндрической
системе координат. В качестве примера
использования transform_xy приведу преобразование к
полярным сферическим координатам, раз уж во встроенном виде его
нет:
Обратите внимание: в первом аргументе-списке к make_transform
последним должен идти зависимый символ, то есть тот, который
будет выступать функцией от двух других.
Если вам нужно постоянно работать со сферическими
координатами, можете задать,
скажем, spherical_xy:make_transform([t, f, r],
r*sin(f)*sin(t), r*cos(f)*sin(t), r*cos(t)), и затем при
построении графиков писать [transform_xy,
spherical_xy]. Ветвитесь и повторяйтесь До сих пор мы двигались
только по прямой, а теперь поговорим о средствах «изменения
траектории»: условном операторе и циклах.
Начнем с условия. В Maxima, в отличие от большинства
«традиционных» процедурных и объектных языков программирования,
где существует так называемый условный оператор, привычная
связка if—then—else является не синтаксической конструкцией, а самым настоящим
оператором. По своему действию он больше всего похож на
тернарный оператор языка C, только с более «человеческим»
синтаксисом: if условие then выражение1 else выражение2. При
выполнении «условия» из двух «выражений» вычисляется только
первое и возвращается как результат оператора; в противном
случае выполняется только второе и оно же является значением
всего выражения if—then—else. Часть конструкции
Часть конструкции else выражение2, как и в большинстве
языков программирования, опциональна. Если ее нет, а условие
все-таки не выполнилось, результат оператора if будет равен false.
При этом, конечно же, никто вам не мешает использовать этот
оператор как обычную условную конструкцию, а возвращаемое
значение просто игнорировать. С другой стороны,
оператор if можно применять, например, для задания
рекурсивных последовательностей:
Немного о самих условиях, которые могут проверяться
оператором if. Условия >, <, >=, <= записываются и расшифровываются традиционно, так же как и логические
операторы and, or, not. А
вот о равенствах-неравенствах нужно сказать пару слов. Равенство
в Maxima есть двух видов: синтаксическое и
логическое. Знаком
Знаком = обозначается как раз первое, а
второе вычисляется с помощью функции equal(). Чтобы
не быть многословными, отличие синтаксического равенства от
логического продемонстрируем на примере; здесь дополнительно
используется предикат по имени is, которые
проверяет на истинность свой аргумент.
Ну и неравенств, соответственно, тоже существует два, с тем
же смыслом. Синтаксическое неравенство обозначается достаточно
непривычно — через #; видимо, этот символ
разработчики сочли наиболее визуально схожим со знаком ≠. Ну а
логическое неравенство обозначено
через notequal().
Конечно, кроме упомянутых сравнений в условном операторе
можно использовать любые предикаты, то есть функции,
возвращающие логические
значения true/false. Функций таких
достаточно много, но все они достаточно просты, поэтому не буду
тратить время на их описание: его можно почерпнуть в том же
объеме из документации.
Напоследок перейдем к циклам. Цикл в Maxima будто бы тоже один. Но он имеет столько различных вариантов, что назвать это все одним оператором цикла язык не поворачивается. Вот как выглядят основные разновидности:
for переменная:начало step шаг thru конец do выражениеfor переменная:начало step шаг while условие do выражениеfor переменная:начало step шаг unless условие do выражение
Первый прокручивает цикл, изменяя переменную с
заданным шагом от начала до конца; второй — от начала и пока
выполняется условие; третий — наоборот,
пока условие не выполняется. К примеру, мы можем
получить список из первых десяти членов последовательности из
позапрошлого примера:
Как видите, в качестве оператора цикл в простейшем его виде,
в отличие от условия, использовать смысла нет, так как его
возвращаемое значение всегда равно done. В этом
примере один из элементов циклического оператора не указан; шаг,
как видите, может быть опущен и по умолчанию равен
единице. Самое интересное в этом операторе то, что опустить
позволяется любую его часть, кроме
В этом
примере один из элементов циклического оператора не указан; шаг,
как видите, может быть опущен и по умолчанию равен
единице. Самое интересное в этом операторе то, что опустить
позволяется любую его часть, кроме do; и в том
числе в любых комбинациях. К примеру, опустив
кроме step еще и for, мы получаем из
этого же оператора традиционные циклы while и unless (второй и третий варианты). А проделав то
же самое с первым вариантом записи, получим цикл без счетчика
вида thru число do выражение, который
просто повторится заданное число раз. Можно, наоборот, опустить
условие окончания и получить цикл с индексной переменной, но
бесконечный. А оставив только do, получим самый
простой вариант бесконечного цикла. Из таких бесконечных циклов
можно выйти с помощью оператора return(выражение) (точнее, конечно, конструкции из двух операторов
вида if условие then return(выражение)), который
прервет выполнение цикла и вместо done вернет заданное
выражение. Естественно, оператор
Естественно, оператор return() можно
применять во всех видах циклов, а не только в бесконечных.
Но и это еще не все. Кроме всех уже рассмотренных вариаций,
цикл может принимать еще две ипостаси. Во-первых,
вместо step может использоваться
конструкция next выражение, смысл которой лучше
тоже продемонстрировать на примере
После next может стоять любое вычислимое
выражение относительно индекса цикла, и применяться эта
конструкция может во всех трех вариантах цикла
(thru/while/unless).
А «во-вторых» — это еще один отдельный вариант
цикла: for переменная in список do выражение; либо
расширенная
форма: for переменная in список условие do выражение. Здесь
цикл будет прокручен с переменной, изменяющейся по
всем элементам списка; плюс можно задать еще и
дополнительное условие на прерывание цикла. Вот
теперь мы с циклами действительно закончили. Как видите, все
достаточно разнообразно. Я, признаться, ничего, что здесь не
реализовано, и придумать не смог.
Вот
теперь мы с циклами действительно закончили. Как видите, все
достаточно разнообразно. Я, признаться, ничего, что здесь не
реализовано, и придумать не смог.
Но рассказ о циклах и условном операторе остается неполным,
пока я не рассказал о группировке выражений — ведь в обычном
варианте после then или do можно
написать всего одно из них. А группировка, или, как ее принято
называть, составной оператор, в Maxima — это опять-таки самый
настоящий оператор, который тоже, как и положено оператору,
возвращает некоторое значение. Обозначается он скобками, самыми
что ни на есть круглыми и обыкновенными; а разделяются
сгруппированные операторы/выражения внутри этих скобок не менее
обыкновенными запятыми. Возвращаемым значением составного
оператора является последнее вычисленное выражение.
С условным оператором, столь разнообразными циклами и
составным оператором мы уже можем, комбинируя их между собой и с
любыми другими функциями и выражениями Maxima, писать
полноценные программы с использованием богатого символьного
математического аппарата. Естественно, теперь нам захочется
сохранять эти программы в виде внешних файлов, чтобы не набирать
их каждый раз вручную, а подгружать одной короткой командой. Об
этом, а также о математических аналогах объявления переменных —
в завершающей статье цикла.
Естественно, теперь нам захочется
сохранять эти программы в виде внешних файлов, чтобы не набирать
их каждый раз вручную, а подгружать одной короткой командой. Об
этом, а также о математических аналогах объявления переменных —
в завершающей статье цикла.
Мы также поговорим о математических аналогах объявления переменных и рассмотрим практические примеры с применением уже достаточно богатого известного нам инструментария.
Построение графиков в электронной таблице Excel. Построить в электронной таблице Excel графики параметрически заданной функции при разных значениях
Построить в электронной таблице Excel графики параметрически заданной функции при разных значениях
конcтант а, b, l. Оси графика – х и y, которые зависят от аргумента t или j
| № | Название кривой | Вид графика | Параметрические уравнения | Диапазон аргумента | Кол-во граф. | Значения констант |
| Циклоида | x = a×(t — sin t) y = a×(1 — cos t) | t Î 0 ¸ 6×p Шаг 0,5 | a = 1; 1. 25; 1.5; 1.75; 2 25; 1.5; 1.75; 2 | |||
| Циклоида | x = a×(t — l×sin t) y = a×(1 — l×cos t) | t Î 0 ¸ 6×p Шаг 0,5 | a = 2 l = 0.4; 0.7; 1.0; 1.3; 1.6; 2.0 | |||
| Трохоида | x = a×t — b×sin t y = a — b×cos t | t Î 0 ¸ 10×p Шаг 0,1 | a = -1 b = 0.1; 1; 2; 3; 4 | |||
| Эпитрохоида | x = a×cos (l×t) — b×cos (t + l×t) y = a×sin (l×t) — b×sin (t + l×t) | t Î 0 ¸ 10×p Шаг 0,5 | a = 0; 1; 2; 3; 10; 15 b = 2 l = 0.25 | |||
| Гипотрохоида | x = a×cos (l×t) — b×cos (t — l×t) y = a×sin (l×t) — b×sin (t — l×t) | t Î 0 ¸ 10×p Шаг 0,5 | a = 0; 1; 2; 3; 10; 15 b = 2 l = 0.25 | |||
| Декартов лист | x = a×t / (1 + t3) y = a× t2 / (1 + t3) | t Î -6 ¸ 6 t ¹ -1 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | |||
| Циссоида Диоклеса | x = a× t2 / (1 + t2) y = a× t3 / (1 + t2) | t Î -6 ¸ 6 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | |||
| Строфоида | x = a× (t2 — 1) / (t2 + 1) y = a×t×(t2 — 1) / (t2 + 1) | t Î -6 ¸ 6 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | |||
| Конхоида Никомеда | x = a + b×cos t y = a×tg t + b×sin t | t Î 0 ¸ 10 t ¹ p/2 Шаг 0,01 | a = 2 b = 1; 10; 30; 50; 90 | |||
| Улитка Паскаля | x = a×cos2 t + b×cos t y = a× cos t ×sin t + b×sin t | t Î 0 ¸ 2×p Шаг 0,1 | a = 1; 2; 3; 4; 5; 6 b = 3 | |||
| Эпициклоида | x = (a + b)×cos j — a×cos[(a + b)×j/a] y = (a + b)× sin j — a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1 b = 1; 2; 3; 4; 5; 6 | |||
| Эпициклоида | x = (a + b)×cos j — l×a×cos[(a + b)×j/a] y = (a + b)× sin j — l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 10×p Шаг 0,2 | a = 3; b = 4 l = 0. 5; 0.7; 1; 1.5; 2; 3 5; 0.7; 1; 1.5; 2; 3 | |||
| Эпициклоида | x = (a + b)×cos j — l×a×cos[(a + b)×j/a] y = (a + b)× sin j — l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1; b = 4 l = 0.5; 1; 1.5; 2; 4; 6 | |||
| Эпициклоида | x = (a + b)×cos j — l×a×cos[(a + b)×j/a] y = (a + b)× sin j — l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 7; b = 4 l = 0.5; 1; 2; 4; 6; 8 | |||
| Гипоциклоида | x = (b — a)×cos j — a×cos[(b — a)×j/a] y = (b — a)× sin j — a ×sin[(b — a)×j/a] | j Î -2×p ¸ 2×p Шаг 0,1 | a = 1 b = 1.5; 2.5; 3; 3.5; 4; 5 | |||
| Гипоциклоида | x = (b — a)×cos j — a×cos[(b — a)×j/a] y = (b — a)× sin j — a ×sin[(b — a)×j/a] | j Î 0 ¸ 6×p Шаг 0,5 | a = 1.5; 2; 2.5; 3; 3,5; 4 b = 1 | |||
| Гипоциклоида | x = (b — a)×cos j — l×a×cos[(b — a)×j/a] y = (b — a)× sin j — l×a ×sin[(b — a)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1; b = 4 l = 0. 5; 1; 1.5; 2; 3; 4 5; 1; 1.5; 2; 3; 4 | |||
| Гипоциклоида | x = (b — a)×cos j — l×a×cos[(b — a)×j/a] y = (b — a)× sin j — l×a ×sin[(b — a)×j/a] | j Î 0 ¸ 10×p Шаг 0,2 | a = 5; b = 2 l = 0.2; 0.5; 0.7; 1; 1.5; 2 | |||
| Спираль | x = a×t×cos t y = b×t×sin t | t Î 0 ¸ 10×p Шаг 0,5 | a = 2 b = -2; -1; 1; 2; 3; 4 | |||
| Гиперболич. спираль | x = (a×cos t) / t y = (b ×sin t) / t | t Î -6 ¸ 6 t ¹ 0 Шаг 0,1 | a = 2 b = 1; 2; 3; 4; 5 | |||
| Гиперболич. спираль | x = (a×cos t) / t y = (b ×sin t) / t | t Î 0.5 ¸ 20 Шаг 0,5 | a = 3 b = 1; 2; 3; 4; 5 | |||
| Астроида | x = a×cos3 (t / 4) y = b ×sin3 (t / 4) | t Î 0 ¸ 8×p Шаг 0,1 | a = 2 b = 1; 2; 3; 4; 5 | |||
| Астроида | x = a×cos3 (t – b) y = a ×sin3 t | t Î 0 ¸ 8×p Шаг 0,2 | a = 2 b = 0; 1; 2; 3; 4 | |||
| Астроида | x = a×cos3 (b×t ) y = a ×sin3 t | t Î 0 ¸ 8×p Шаг 0,1 | a = 2 b = 0. 5; 1; 1.5; 3; 3.5 5; 1; 1.5; 3; 3.5 | |||
| Эвольвента | x = a×cos t + a×t ×sin t y = a ×sin t + a×t×cos t | t Î -10 ¸10 Шаг 0,5 | a = -2; -1; 1; 2 | |||
| Эвольвента | x = a×cos t + a×t ×sin t y = a ×sin t + a×t×cos t | t Î 0 ¸20 Шаг 0,5 | a = -2; -1; 1; 2 | |||
| Эллипс | x = a×cos t y = b ×sin t | t Î 0 ¸ 2×p Шаг 0,5 | a = 7 b = 1; 4; 7; 10; 13 | |||
| Эллипс | x = a×cos(c + t) y = b ×sin(c — t) | t Î 0 ¸ 2×p Шаг 0,11 | a = 3 b = 2 b = 1; 2; 3; 4; 5 |
FX-9860G / FX-9860G SD | Вычисления на калькуляторах | Научные и графические калькуляторы | Продукция
Графические калькуляторы FX-9860G / FX-9860G SD
Если Вы уже приобрели калькулятор CASIO серии fx-ES PLUS или fx-ES, ниже приведенные примеры вычислений помогут понять принцип работы калькулятора и научиться выполнять основные виды вычислений.
Меню с пиктограммами
Более чем 1000 функций разделены по режимам для того, чтобы в них не запутаться. Удобное меню с пиктограммами позволяет сделать выбор очень быстро и наглядно.
Режим калькулятора
В режиме калькулятора Вы можете производить как простые расчеты, так и задействовать функции, присущие самому продвинутому научному калькулятора. При этом, ввод выражения производится в том же виде, что и в учебнике.
Режим решения уравнений
Благодаря этому встроенному режиму Вы можете получить корни квадратного и кубического уравнения, а также системы
линейных уравнений до 61ти переменных. Все эти уравнения имеют фиксированный вид и Вы просто вводите коэффициенты и получаете корни. Произвольное уравнение можно решить методом подбора.
Произвольное уравнение можно решить методом подбора.
Пример: решить уравнение 2X + 5X – 7 = 0
Выбор типа уравнения:
— с одной переменной
— система уравнений
— режим подбора
Выбор степени уравнения:
— вторая
— третья
Ввод коэффициентов
а, b, c
Расчет корней
Ответ: x = 1, x = 13.5
Построение графиков
Вы всегда можете построить график любой функции, или нескольких функций, одновременно, при этом они будут отображаться разными линиями. Также, возможно построение неравенств.
Пример: построить графики функций f(X) = X . 2X и f(X) = 0.5X + 1
Ввод функций
Выбор масштаба
Построение графиков
Исследование графиков
Исследование графиков
Графики можно не только построить, но и исследовать, перемещать и масштабировать.
Пример: исследовать график функции f(X) = X² — 2X, найти минимальное значение, проверить проходит ли он через точку (0; 0), увеличить область координаты (0; 0).
Нахождение
минимального
значения
Проверка пересечения
с точкой (0; 0)
Выделение области
для увеличения
Одновременное
отображение графика
и его увеличенной области
Графические решения
Благодаря этой функции Вы можете найти точки пересечения графика с осью Х и Y, а также точки пересечения двух и более графиков.
Пример: найти корни уравнения X³ — 2X = 0, решить систему уравнений
Y = X³ — 2X; Y = 0. 5X + 1
5X + 1
Ввод функции
f(X) = X³ — 2X
Поиск корней
уравнения X³ — 2X = 0
Ввод функции
f(X) = 0.5X + 1
Поиск точек пересечения
функции f(X) = X³ — 2X и
функции f(X) = 0.5X + 1
Построение неравенств
Построение графиков не ограничивается прямоугольными координатами и равенствами. Вы также можете построить неравенства и сменить координаты на полярные или построить график параметрической функции.
Графическое интегрирование
Построив график функции, Вы можете найти ее интеграл. Для этого нужно указать нижний и верхний пределы, после чего Вы получите графическое и численное решение.
Динамические графики
Для того, чтобы понять свойства функции необходимо знать как она видоизменяется с изменением коэффициентов. Для того, чтобы не строить несколько графиков сразу, существует функция динамических графиков.
Пример: исследовать, как изменяется функция f(X)=AX² при 0,2
Ввод функции f(X)=AX²
Задание параметров
коэффициенту А
Установка скорости
отображения
Отображение графика
в динамике
Табличный процессор
При помощи табличного процессора Вы сможете работать с большим количеством цифр (массивами данных). Например, Вы сможете быстро найти среднее арифметическое, суммировать большое количество чисел, производить статистические расчеты. При этом данные можно загружать из MS Excel.
Пример: найти среднее арифметическое чисел 10, 14, 17, 12, 18, 25, 15, 22, отсортировать значения по возрастанию. Построить гистограмму на основе этих данных.
Ввод значений в
таблицу
Расчет среднего
значения
Сортировка по
возрастанию
Построение гистограммы
Решатель примеров онлайн
Введите в форму ниже уравнение, функцию или неравенство и подобное и нажмите Enter
Синтаксис программы:
Графики
Чтобы построить график функции, необходимо использовать оператор plot, например plot x^3-6x^2+4x+12 или plot sin x + cos (sqrt(3)x)
График функции с заданной областью определения plot e^x from x=0 to 10
График функции двух переменных с заданной областью определения plot x^2 y^3, x=-1.3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x3 -2x +1.
Оператор partial fractions разложит отношение многочленов в сумму простейших дробей.
minimize минимизирует функцию, а maximize максимизирует
Число «Пи» записывается, как pi
Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan
Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0
Производные и интегралы
Чтобы найти предел, необходимо в начале функции подставить lim, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity).8
Оператор factor раскладывает число на множители
! выводит факториал, например 123!
Оператор gcd выводит наибольший общий делитель, например gcd 164, 88 выводит наибольший общий делитель чисел 164 и 88
Как построить график функции в Wolfram|Alpha
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если не задавать область значений х?
Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Сравните:
Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.
Одновременно в Wolfram | Alpha можно строить графики нескольких функций.
Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:
Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:
Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:
Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных.2 cos(x) для x от -6 до 6 и y от -2 до 2
Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:
Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Опубликовано в блоге Web in Math
Parametric Equation Grapher — Open Omnia
Введите параметрическую кривую. Используйте t в качестве переменной.
См. Примеры
ПОМОЩЬ
Используйте предоставленную клавиатуру для ввода параметрических кривых. Используйте t в качестве переменной. Щелкните «PLOT», чтобы построить кривые, которые вы ввели.
Вот несколько примеров того, что вы можете ввести.
Вот как вы используете кнопки
долларов США| УЧАСТОК | Строит введенные кривые. | |
| ПРОЗРАЧНЫЙ | Удаляет весь текст в текстовом поле. | |
| DEL | Удаляет последний элемент перед курсором. | |
| триг | Показывает тригонометрические функции. | |
| ◀ | Переместите курсор влево. | |
| ▶ | Переместите курсор вправо.{□} {□} | N-й корень. |
| (□) | Круглая скобка. | |
| журнал | База 10. | |
| пер. | Натуральное бревно (база д). | |
| | $ □ $ | | Абсолютное значение. |
параметрических уравнений: графики | Precalculus II
Цели обучения
К концу этого раздела вы сможете:
- Графические плоские кривые, описываемые параметрическими уравнениями путем нанесения точек.\ circ [/ latex] к горизонтали. Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пройдет, используя параметрические уравнения . В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда.
Рис. 1. Параметрические уравнения могут моделировать траекторию полета снаряда.(Источник: Пол Крехер, Flickr)
Построение параметрических уравнений по точкам
Вместо графического калькулятора или компьютерной программы построения графиков, нанесение точек на график для представления графика уравнения является стандартным методом. Пока мы тщательно вычисляем значения, точечное построение очень надежно.
Практическое руководство. Для пары параметрических уравнений нарисуйте график с помощью точек.
- Создайте таблицу с тремя столбцами: [latex] t, x \ left (t \ right), \ text {и} y \ left (t \ right) [/ latex].{2} +1 [/ латекс] [латекс] y \ left (t \ right) = 2 + t [/ латекс] [латекс] -5 [/ латекс] [латекс] 26 [/ латекс] [латекс] -3 [/ латекс] [латекс] -4 [/ латекс] [латекс] 17 [/ латекс] [латекс] -2 [/ латекс] [латекс] -3 [/ латекс] [латекс] 10 [/ латекс] [латекс] -1 [/ латекс] [латекс] -2 [/ латекс] [латекс] 5 [/ латекс] [латекс] 0 [/ латекс] [латекс] -1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 3 [/ латекс] [латекс] 2 [/ латекс] [латекс] 5 [/ латекс] [латекс] 4 [/ латекс] [латекс] 3 [/ латекс] [латекс] 10 [/ латекс] [латекс] 5 [/ латекс] [латекс] 4 [/ латекс] [латекс] 17 [/ латекс] [латекс] 6 [/ латекс] [латекс] 5 [/ латекс] [латекс] 26 [/ латекс] [латекс] 7 [/ латекс]
График представляет собой параболу с вершиной в точке [latex] \ left (1,2 \ right) [/ latex], открывающуюся вправо.См. Рисунок 2.
Рисунок 2
Анализ решения
По мере того, как значения [latex] t [/ latex] меняются в положительном направлении от 0 до 5, нанесенные на график точки очерчивают верхнюю половину параболы. Когда значения [latex] t [/ latex] становятся отрицательными, они отслеживают нижнюю половину параболы. Ограничений по домену нет. Стрелки указывают направление согласно возрастающим значениям [латекс] t [/ латекс]. График не представляет функцию, так как он не пройдет проверку вертикальной линии.График состоит из двух частей: положительные значения для [latex] t [/ latex] и отрицательные значения для [latex] t [/ latex].
Попробуй 1
Нарисуйте график параметрических уравнений [латекс] x = \ sqrt {t}, y = 2t + 3,0 \ le t \ le 3 [/ latex].
Решение
Пример 2: Построение графика тригонометрических параметрических уравнений
Постройте таблицу значений для заданных параметрических уравнений и нарисуйте график:
[латекс] \ begin {массив} {l} \\ \ begin {array} {l} x = 2 \ cos t \ hfill \\ y = 4 \ sin t \ hfill \ end {array} \ end {array} [/ латекс]
Решение
Создайте таблицу, подобную приведенной ниже, используя угловую меру в радианах в качестве входных данных для [latex] t [/ latex] и оценивая [latex] x [/ latex] и [latex] y [/ latex].Использование углов с известными значениями синуса и косинуса для [latex] t [/ latex] упрощает вычисления.
[латекс] t [/ латекс] [латекс] x = 2 \ cos t [/ латекс] [латекс] y = 4 \ sin t [/ латекс] 0 [латекс] x = 2 \ cos \ left (0 \ right) = 2 [/ latex] [латекс] y = 4 \ sin \ left (0 \ right) = 0 [/ латекс] [латекс] \ frac {\ pi} {6} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {\ pi} {6} \ right) = \ sqrt {3} [/ latex] [латекс] y = 4 \ sin \ left (\ frac {\ pi} {6} \ right) = 2 [/ latex] [латекс] \ frac {\ pi} {3} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {\ pi} {3} \ right) = 1 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {\ pi} {3} \ right) = 2 \ sqrt {3} [/ latex] [латекс] \ frac {\ pi} {2} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {\ pi} {2} \ right) = 0 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {\ pi} {2} \ right) = 4 [/ latex] [латекс] \ frac {2 \ pi} {3} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {2 \ pi} {3} \ right) = — 1 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {2 \ pi} {3} \ right) = 2 \ sqrt {3} [/ latex] [латекс] \ frac {5 \ pi} {6} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {5 \ pi} {6} \ right) = — \ sqrt {3} [/ latex] [латекс] y = 4 \ sin \ left (\ frac {5 \ pi} {6} \ right) = 2 [/ latex] [латекс] \ pi [/ латекс] [латекс] x = 2 \ cos \ left (\ pi \ right) = — 2 [/ латекс] [латекс] y = 4 \ sin \ left (\ pi \ right) = 0 [/ латекс] [латекс] \ frac {7 \ pi} {6} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ sqrt {3} [/ latex] [латекс] y = 4 \ sin \ left (\ frac {7 \ pi} {6} \ right) = — 2 [/ latex] [латекс] \ frac {4 \ pi} {3} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {4 \ pi} {3} \ right) = — 1 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {4 \ pi} {3} \ right) = — 2 \ sqrt {3} [/ latex] [латекс] \ frac {3 \ pi} {2} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {3 \ pi} {2} \ right) = 0 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {3 \ pi} {2} \ right) = — 4 [/ latex] [латекс] \ frac {5 \ pi} {3} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {5 \ pi} {3} \ right) = 1 [/ latex] [латекс] y = 4 \ sin \ left (\ frac {5 \ pi} {3} \ right) = — 2 \ sqrt {3} [/ latex] [латекс] \ frac {11 \ pi} {6} [/ латекс] [латекс] x = 2 \ cos \ left (\ frac {11 \ pi} {6} \ right) = \ sqrt {3} [/ latex] [латекс] y = 4 \ sin \ left (\ frac {11 \ pi} {6} \ right) = — 2 [/ latex] [латекс] 2 \ pi [/ латекс] [латекс] x = 2 \ cos \ left (2 \ pi \ right) = 2 [/ latex] [латекс] y = 4 \ sin \ left (2 \ pi \ right) = 0 [/ латекс] На рисунке 3 показан график.
Рисунок 3
По симметрии, показанной в значениях [latex] x [/ latex] и [latex] y [/ latex], мы видим, что параметрические уравнения представляют собой эллипс . Эллипс отображается в направлении против часовой стрелки, как показано стрелками, указывающими увеличение значений [латекс] t [/ латекс].
Анализ решения
Мы видели, что параметрические уравнения могут быть построены на графике по точкам. Однако графический калькулятор сэкономит время и выявит нюансы на графике, которые могут быть слишком утомительными, чтобы обнаружить их, используя только ручные вычисления.
Обязательно измените режим на калькуляторе на параметрический (PAR). Для подтверждения в окне [latex] Y = [/ latex] должно отображаться
[латекс] \ begin {array} {c} {X} _ {1T} = \\ {Y} _ {1T} = \ end {array} [/ latex]
вместо [латекс] {Y} _ {1} = [/ latex].
Попробуй 2
Изобразите параметрические уравнения: [латекс] x = 5 \ cos t, y = 3 \ sin t [/ latex].
Решение
Пример 3: Графическое отображение параметрических уравнений и прямоугольной формы вместе
Изобразите параметрические уравнения [латекс] x = 5 \ cos t [/ latex] и [latex] y = 2 \ sin t [/ latex].Сначала постройте график, используя точки данных, сгенерированные из параметрической формы . Затем изобразите прямоугольную форму уравнения. Сравните два графика.
Решение
Создайте таблицу значений, как в таблице ниже.
[латекс] t [/ латекс] [латекс] x = 5 \ cos t [/ латекс] [латекс] y = 2 \ sin t [/ латекс] [латекс] \ text {0} [/ latex] [латекс] x = 5 \ cos \ left (0 \ right) = 5 [/ латекс] [латекс] y = 2 \ sin \ left (0 \ right) = 0 [/ латекс] [латекс] \ text {1} [/ латекс] [латекс] x = 5 \ cos \ left (1 \ right) \ приблизительно 2.7 [/ латекс] [латекс] y = 2 \ sin \ left (1 \ right) \ приблизительно 1,7 [/ латекс] [латекс] \ text {2} [/ латекс] [латекс] x = 5 \ cos \ left (2 \ right) \ приблизительно -2,1 [/ латекс] [латекс] y = 2 \ sin \ left (2 \ right) \ приблизительно 1,8 [/ латекс] [латекс] \ text {3} [/ latex] [латекс] x = 5 \ cos \ left (3 \ right) \ приблизительно -4,95 [/ латекс] [латекс] y = 2 \ sin \ left (3 \ right) \ приблизительно 0,28 [/ латекс] [латекс] \ text {4} [/ латекс] [латекс] х = 5 \ соз \ влево (4 \ вправо) \ приблизительно -3.3 [/ латекс] [латекс] y = 2 \ sin \ left (4 \ right) \ приблизительно -1,5 [/ латекс] [латекс] \ text {5} [/ латекс] [латекс] x = 5 \ cos \ left (5 \ right) \ приблизительно 1,4 [/ латекс] [латекс] y = 2 \ sin \ left (5 \ right) \ приблизительно -1,9 [/ латекс] [латекс] -1 [/ латекс] [латекс] x = 5 \ cos \ left (-1 \ right) \ приблизительно 2,7 [/ латекс] [латекс] y = 2 \ sin \ left (-1 \ right) \ приблизительно -1,7 [/ латекс] [латекс] -2 [/ латекс] [латекс] x = 5 \ cos \ left (-2 \ right) \ приблизительно -2.1 [/ латекс] [латекс] y = 2 \ sin \ left (-2 \ right) \ приблизительно -1,8 [/ латекс] [латекс] -3 [/ латекс] [латекс] x = 5 \ cos \ left (-3 \ right) \ приблизительно -4,95 [/ латекс] [латекс] y = 2 \ sin \ left (-3 \ right) \ приблизительно -0,28 [/ латекс] [латекс] -4 [/ латекс] [латекс] x = 5 \ cos \ left (-4 \ right) \ приблизительно -3,3 [/ латекс] [латекс] y = 2 \ sin \ left (-4 \ right) \ приблизительно 1,5 [/ латекс] [латекс] -5 [/ латекс] [латекс] x = 5 \ cos \ left (-5 \ right) \ приблизительно 1.4 [/ латекс] [латекс] y = 2 \ sin \ left (-5 \ right) \ приблизительно 1,9 [/ латекс] Постройте значения [latex] \ left (x, y \ right) [/ latex] из таблицы. См. Рисунок 4.
Рисунок 4
Затем преобразуйте параметрические уравнения в прямоугольную форму. Для этого мы решаем [латекс] t [/ латекс] в [латексе] x \ left (t \ right) [/ latex] или [латексе] y \ left (t \ right) [/ latex], и затем подставьте выражение для [латекс] t [/ латекс] в другое уравнение. Результатом будет функция [latex] y \ left (x \ right) [/ latex] при решении для [latex] t [/ latex] как функции [latex] x [/ latex] или [latex] x \ left (y \ right) [/ latex] при решении для [latex] t [/ latex] как функции [latex] y [/ latex].{2}} {4} = 1 \ end {array} [/ latex]
Анализ решения
На рисунке 5 данные параметрических уравнений и прямоугольного уравнения нанесены вместе. Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график.
Рисунок 5
Пример 4: Построение графиков параметрических и прямоугольных уравнений в системе координат
Постройте параметрические уравнения [латекс] x = t + 1 [/ latex] и [latex] y = \ sqrt {t}, t \ ge 0 [/ latex] и прямоугольный эквивалент [латекс] y = \ sqrt { x — 1} [/ latex] в той же системе координат.
Решение
Создайте таблицу значений для параметрических уравнений, как мы делали в предыдущем примере, и граф [latex] y = \ sqrt {t}, t \ ge 0 [/ latex] на той же сетке, как на рисунке 6.
Рисунок 6
Анализ решения
При ограничении домена [latex] t [/ latex], мы наносим только положительные значения [latex] t [/ latex]. Параметрические данные показаны синим цветом, а график прямоугольного уравнения — красным. И снова мы видим, что эти две формы пересекаются.
Попробовать 3
Нарисуйте график параметрических уравнений [латекс] x = 2 \ cos \ theta \ text {и} y = 4 \ sin \ theta [/ latex] вместе с прямоугольным уравнением на той же сетке.
Решение
Приложения параметрических уравнений
Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время.Однако параметрические уравнения показывают, как значения x и y изменяются в зависимости от t , как местоположения движущегося объекта в конкретный момент времени.
Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в восходящем направлении, образуя угол [латекс] \ тета [/ латекс] к горизонтали, с начальной скоростью [латекс] {v} _ {0} [/ latex ], и на высоте [латекс] ч [/ латекс] над горизонтом.{2} [/ латекс]. Уравнение для [latex] x [/ latex] дает горизонтальное расстояние, а уравнение для [latex] y [/ latex] дает вертикальное расстояние. \ круг \ справа) \ справа) t \ hfill \ end {array} [/ latex]
Вертикальное положение определяется с помощью параметрического уравнения для [латекс] y [/ латекс].{\ circ} \ right) \ right) t + 3 \ hfill & \ hfill \\ y = 0 \ hfill & \ text {Set} y \ left (t \ right) = 0 \ text {и решите квадратное уравнение}. \ hfill \\ t = 6.2173 \ hfill & \ hfill \ end {array} [/ latex]
Когда [latex] t = 6,2173 [/ latex] секунды, мяч упал на землю. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.)
- Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, касается ли мяч стены, нам нужно вычислить, насколько высок мяч, когда x = 400 футов. \ circ \ right) \ right) t \ hfill \\ \ text {} t = 4.\ circ \ right) \ right) \ left (4.04 \ right) +3 \ hfill \\ \ text {} y = 141.8 \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. Рисунок 7.
Рисунок 7
Ключевые понятия
- Когда есть третья переменная, третий параметр, от которого зависят [latex] x [/ latex] и [latex] y [/ latex], можно использовать параметрические уравнения.
- Чтобы построить график параметрических уравнений путем нанесения точек, составьте таблицу с тремя столбцами, обозначенными [латекс] t, x \ left (t \ right) [/ latex] и [latex] y \ left (t \ right) [/ latex] .Выберите значения для [latex] t [/ latex] в порядке возрастания. Постройте последние два столбца для [latex] x [/ latex] и [latex] y [/ latex].
- При построении параметрической кривой путем нанесения точек отметьте соответствующие значения t и покажите стрелки на графике, указывающие ориентацию кривой.
- Параметрические уравнения позволяют отображать направление или ориентацию кривой на графике. Уравнения, которые не являются функциями, можно изобразить в виде графиков и использовать во многих приложениях, связанных с движением.{2} + \ left ({v} _ {0} \ sin \ theta \ right) t + h [/ latex]. Начальная скорость обозначается как [латекс] {v} _ {0} [/ latex]. [latex] \ theta [/ latex] представляет начальный угол объекта при броске, а [latex] h [/ latex] представляет высоту, на которой объект перемещается.
Упражнения по разделам
1. Какие два метода используются для построения графиков параметрических уравнений?
2. В чем отличие параметрических уравнений точечного построения от декартовых уравнений?
3.{2} -1 \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] [латекс] -3 [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 3 [/ латекс] 7.{2} \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] -3 [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] 8.[латекс] \ begin {case} x \ left (t \ right) = 2 + t \ hfill \\ y \ left (t \ right) = 3 — 2t \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 3 [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] 9.[латекс] \ begin {case} x \ left (t \ right) = — 2 — 2t \ hfill \\ y \ left (t \ right) = 3 + t \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] -3 [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] 10.{3} \ hfill \\ y \ left (t \ right) = t + 2 \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] 11.{2} \ hfill \\ y \ left (t \ right) = t + 3 \ hfill \ end {case} [/ latex]
[латекс] t [/ латекс] [латекс] -2 [/ латекс] [латекс] -1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] x [/ латекс] [латекс] y [/ латекс] Для следующих упражнений нарисуйте кривую и укажите ее ориентацию.
12. [латекс] \ begin {case} x \ left (t \ right) = t \\ y \ left (t \ right) = \ sqrt {t} \ end {case} [/ latex]
13. [латекс] \ begin {case} x \ left (t \ right) = — \ sqrt {t} \\ y \ left (t \ right) = t \ end {case} [/ latex]
14. [латекс] \ begin {case} x \ left (t \ right) = 5- | t | \\ y \ left (t \ right) = t + 2 \ end {case} [/ latex]
15. [латекс] \ begin {case} x \ left (t \ right) = — t + 2 \\ y \ left (t \ right) = 5- | t | \ end {case} [/ latex]
16. [латекс] \ begin {case} x \ left (t \ right) = 4 \ text {sin} t \ hfill \\ y \ left (t \ right) = 2 \ cos t \ hfill \ end {case } [/ латекс]
17.{2}}, 0
31. [латекс] x \ left (t \ right) = — t, y \ left (t \ right) = \ sqrt {t}, t \ ge 0 [/ латекс]
32. [латекс] x = -2 \ cos t, y = 6 \ sin t, 0 \ le t \ le \ pi [/ латекс]
33. [латекс] x = — \ sec t, y = \ tan t, — \ frac {\ pi} {2}
В следующих упражнениях используйте параметрические уравнения для целых чисел a и b :
[латекс] \ begin {case} x \ left (t \ right) = a \ cos \ left (\ left (a + b \ right) t \ right) \\ y \ left (t \ right) = a \ cos \ left (\ left (ab \ right) t \ right) \ end {case} [/ latex]
34.График в области [латекс] \ left [- \ pi, 0 \ right] [/ latex], где [latex] a = 2 [/ latex] и [latex] b = 1 [/ latex], и включает ориентацию .
35. График в домене [latex] \ left [- \ pi, 0 \ right] [/ latex], где [latex] a = 3 [/ latex] и [latex] b = 2 [/ latex], и включить ориентацию.
36. График в домене [latex] \ left [- \ pi, 0 \ right] [/ latex], где [latex] a = 4 [/ latex] и [latex] b = 3 [/ latex], и включить ориентацию.
37. График в домене [latex] \ left [- \ pi, 0 \ right] [/ latex], где [latex] a = 5 [/ latex] и [latex] b = 4 [/ latex], и включить ориентацию.{2} [/ latex] и [latex] x \ left (t \ right) [/ latex] линейны
45. Напишите параметрические уравнения круга с центром [латекс] \ влево (0,0 \ вправо) [/ латекс], радиусом 5 и ориентацией против часовой стрелки.
46. Напишите параметрические уравнения эллипса с центром [латекс] \ влево (0,0 \ вправо) [/ латекс], большой осью длины 10, малой осью длины 6 и ориентацией против часовой стрелки.
Для следующих упражнений используйте графическую утилиту для построения графика в окне [latex] \ left [-3,3 \ right] [/ latex] с помощью [latex] \ left [-3,3 \ right] [/ latex] в домене [latex] \ left [0,2 \ pi \ right) [/ latex] для следующих значений [latex] a [/ latex] и [latex] b [/ latex], включая ориентацию.
[латекс] \ begin {case} x \ left (t \ right) = \ sin \ left (at \ right) \\ y \ left (t \ right) = \ sin \ left (bt \ right) \ end { case} [/ latex]
47. [латекс] a = 1, b = 2 [/ латекс]
48. [латекс] a = 2, b = 1 [/ латекс]
49. [латекс] a = 3, b = 3 [/ латекс]
50. [латекс] a = 5, b = 5 [/ латекс]
51. [латекс] a = 2, b = 5 [/ латекс]
52. [латекс] a = 5, b = 2 [/ латекс]
Для следующих упражнений посмотрите на графики, которые были созданы с помощью параметрических уравнений вида [латекс] \ begin {cases} x \ left (t \ right) = a \ text {cos} \ left (bt \ right) \ hfill \\ y \ left (t \ right) = c \ text {sin} \ left (dt \ right) \ hfill \ end {case} [/ latex].Используйте параметрический режим графического калькулятора, чтобы найти значения [latex] a, b, c [/ latex] и [latex] d [/ latex] для построения каждого графика.
53.
54.
55.
56.
Для следующих упражнений используйте графическую утилиту для построения графиков заданных параметрических уравнений.
- [латекс] \ begin {case} x \ left (t \ right) = \ cos t — 1 \\ y \ left (t \ right) = \ sin t + t \ end {case} [/ latex]
- [латекс] \ begin {case} x \ left (t \ right) = \ cos t + t \\ y \ left (t \ right) = \ sin t — 1 \ end {case} [/ latex]
- [латекс] \ begin {case} x \ left (t \ right) = t- \ sin t \\ y \ left (t \ right) = \ cos t — 1 \ end {case} [/ latex]
57.Постройте график всех трех наборов параметрических уравнений в области [latex] \ left [0,2 \ pi \ right] [/ latex].
58. Постройте график всех трех наборов параметрических уравнений в области [latex] \ left [0,4 \ pi \ right] [/ latex].
59. Постройте график всех трех наборов параметрических уравнений в области [латекс] \ left [-4 \ pi, 6 \ pi \ right] [/ latex].
60. Кажется, что график каждой системы параметрических уравнений «ползет» по одной из осей. Что контролирует, по какой оси ползет график?
61.{2} + 10t + 5. \ Text {} [/ latex] Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту как функцию горизонтального положения.
Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Учитывайте положение дротика в любое время [латекс] т [/ латекс]. Пренебрегайте сопротивлением воздуха.
65. Найдите параметрические уравнения, моделирующие проблемную ситуацию.
66. Найдите все возможные значения [latex] x [/ latex], которые представляют ситуацию.
67. Когда дротик упадет на землю?
68. Найдите максимальную высоту дротика.
69. В какое время дротик достигнет максимальной высоты?
Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений. Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене.
70. Эпициклоида: [латекс] \ begin {cases} x \ left (t \ right) = 14 \ cos t- \ cos \ left (14t \ right) \ hfill \\ y \ left (t \ right) = 14 \ sin t + \ sin \ left (14t \ right) \ hfill \ end {case} [/ latex] на домене [latex] \ left [0,2 \ pi \ right] [/ latex].
71. Гипоциклоида: [латекс] \ begin {case} x \ left (t \ right) = 6 \ sin t + 2 \ sin \ left (6t \ right) \ hfill \\ y \ left (t \ right) = 6 \ cos t — 2 \ cos \ left (6t \ right) \ hfill \ end {case} [/ latex] в домене [latex] \ left [0,2 \ pi \ right] [/ latex].
72. Гипотрохоид: [латекс] \ begin {cases} x \ left (t \ right) = 2 \ sin t + 5 \ cos \ left (6t \ right) \ hfill \\ y \ left (t \ right) = 5 \ cos t — 2 \ sin \ left (6t \ right) \ hfill \ end {case} [/ latex] в домене [latex] \ left [0,2 \ pi \ right] [/ latex].
73. Роза: [латекс] \ begin {case} x \ left (t \ right) = 5 \ sin \ left (2t \ right) \ sin t \ hfill \\ y \ left (t \ right) = 5 \ sin \ left (2t \ right) \ cos t \ hfill \ end {case} [/ latex] в домене [latex] \ left [0,2 \ pi \ right] [/ latex].
Calculus II — Параметрические уравнения и кривые
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, т.е. вы, вероятно, используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-1: Параметрические уравнения и кривые
До этого момента (как в исчислении I, так и в исчислении II) мы рассматривали почти исключительно функции в форме \ (y = f \ left (x \ right) \) или \ (x = h \ left (y \ right) ) \) и почти все формулы, которые мы разработали, требуют, чтобы функции были в одной из этих двух форм.2}} & \ hspace {0,15 дюйма} & \ left ({{\ mbox {left side}}} \ right) \ end {align *} \]
К сожалению, мы обычно работаем над всем кругом или просто не можем сказать, что будем работать только над его частью. Даже если мы можем сузить круг вопросов до одной из этих частей, работать с функцией все равно будет довольно неприятно.
Есть также очень много кривых, которые мы даже не можем записать в виде единого уравнения, используя только \ (x \) и \ (y \).Итак, чтобы справиться с некоторыми из этих проблем, мы вводим параметрических уравнений . Вместо определения \ (y \) в терминах \ (x \) (\ (y = f \ left (x \ right) \)) или \ (x \) в терминах \ (y \) (\ (x = h \ left (y \ right) \)) мы определяем как \ (x \), так и \ (y \) в терминах третьей переменной, называемой параметром, следующим образом:
\ [x = f \ left (t \ right) \ hspace {0,5 дюйма} y = g \ left (t \ right) \]Эта третья переменная обычно обозначается как \ (t \) (как мы это делали здесь), но, конечно, это не обязательно.Иногда мы ограничиваем значения \ (t \), которые мы будем использовать, а в других случаях — нет. Это часто будет зависеть от проблемы и от того, что мы пытаемся сделать.
Каждое значение \ (t \) определяет точку \ (\ left ({x, y} \ right) = \ left ({f \ left (t \ right), g \ left (t \ right)} \ right ) \), которую мы можем построить. Набор точек, который мы получаем, позволяя \ (t \) быть всеми возможными значениями, является графиком параметрических уравнений и называется параметрической кривой .
Чтобы визуализировать, что такое параметрическая кривая, представьте, что у нас есть большой резервуар с водой, который находится в постоянном движении, и мы бросаем в резервуар шарик для пинг-понга. Точка \ (\ left ({x, y} \ right) = \ left ({f \ left (t \ right), g \ left (t \ right)} \ right) \) будет представлять местоположение мяч для пинг-понга в резервуаре в момент времени \ (t \), и параметрическая кривая будет отражать все положения шара для пинг-понга. Обратите внимание, что это не всегда правильная аналогия, но она полезна на начальном этапе, чтобы помочь визуализировать, что такое параметрическая кривая.2} + t \ hspace {0,5 дюйма} y = 2t — 1 \] Показать решение
На данный момент наш единственный вариант для построения параметрической кривой — это выбрать значения \ (t \), вставить их в параметрические уравнения и затем построить точки. Итак, давайте добавим несколько \ (t \) ‘s.
\ (т \) \ (х \) \ (г \) -2 2 -5 -1 0 -3 \ (- \ frac {1} {2} \) \ (- \ frac {1} {4} \) -2 0 0 -1 1 2 1 Первый вопрос, который следует задать на этом этапе, — как мы узнали, что использовать значения \ (t \), которые мы использовали, особенно третий вариант? К сожалению, на данный момент нет реального ответа на этот вопрос.Мы просто выбираем \ (t \), пока не будем достаточно уверены, что получили хорошее представление о том, как выглядит кривая. Именно эта проблема с выбором «хороших» значений \ (t \) делает этот метод построения параметрических кривых одним из худших вариантов. Иногда у нас нет выбора, но если у нас есть выбор, мы должны его избегать.
В следующих примерах мы обсудим альтернативный метод построения графиков, который поможет объяснить, как были выбраны эти значения \ (t \).
У нас есть еще одна идея, которую нужно обсудить, прежде чем мы нарисуем кривую.Параметрические кривые имеют направление движения . Направление движения задается увеличением \ (t \). Итак, при построении параметрических кривых мы также включаем стрелки, показывающие направление движения. Мы часто будем указывать значение \ (t \), которое дало определенные точки на графике, а также чтобы прояснить значение \ (t \), которое дало эту конкретную точку.
Вот эскиз этой параметрической кривой.
Итак, похоже, у нас есть парабола, которая открывается вправо.
Прежде чем мы закончим этот пример, есть несколько важный и тонкий момент, который мы должны обсудить в первую очередь. Обратите внимание, что мы включили часть эскиза справа от точек, соответствующих \ (t = — 2 \) и \ (t = 1 \), чтобы указать, что там есть части эскиза. Если бы мы просто остановили набросок в этих точках, мы указываем, что не было части кривой справа от этих точек, и она явно будет. Мы просто не вычисляли ни одну из этих точек.
Это может показаться неважным, но, как мы увидим в следующем примере, это более важно, чем мы думаем.
Прежде чем приступить к более простому способу построения наброска этого графика, давайте сначала рассмотрим вопрос об ограничениях для параметра. В предыдущем примере у нас не было ограничений на параметр. Без ограничений для параметра график будет продолжаться в обоих направлениях, как показано на скетче выше.
Однако у нас часто бывают ограничения на параметр, и это влияет на эскиз параметрических уравнений.2} + t \ hspace {0,5 дюйма} y = 2t — 1 \ hspace {0,5 дюйма} — 1 \ le t \ le 1 \] Показать решение
Обратите внимание, что единственное отличие здесь — наличие ограничений на \ (t \). Все эти ограничения говорят нам, что мы не можем брать какое-либо значение \ (t \) за пределы этого диапазона. Следовательно, параметрическая кривая будет только частью приведенной выше кривой. Вот параметрическая кривая для этого примера.
Обратите внимание, что с этим скетчем мы начали и остановили скетч прямо на точках, исходящих из конечных точек диапазона \ (t \) ‘s.Сравните это с эскизом в предыдущем примере, где у нас была часть эскиза справа от «начальной» и «конечной» точек, которые мы вычислили.
В этом случае кривая начинается в \ (t = — 1 \) и заканчивается в \ (t = 1 \), тогда как в предыдущем примере кривая действительно не начиналась в самых правых точках, которые мы вычислили. В наших набросках мы должны четко понимать, начинается ли / заканчивается ли кривая прямо в точке, или эта точка была просто первой / последней, которую мы вычислили.
Пришло время взглянуть на более простой метод построения эскиза этой параметрической кривой. Этот метод использует тот факт, что во многих, но не во всех случаях мы можем фактически исключить параметр из параметрических уравнений и получить функцию, включающую только \ (x \) и \ (y \). Иногда мы будем называть это алгебраическим уравнением , чтобы отличить его от исходных параметрических уравнений. При использовании этого метода возникнут две небольшие проблемы, но их будет легко решить.2} + t \ hspace {0,5 дюйма} y = 2t — 1 \] Показать решение
Один из самых простых способов удалить параметр — просто решить одно из уравнений для параметра (в данном случае \ (t \)) и подставить его в другое уравнение. 2} + y + \ frac {3} {4} \]
Конечно, из наших знаний алгебры мы можем видеть, что это парабола, которая открывается вправо и будет иметь вершину в точке \ (\ left ({- \ frac {1} {4}, — 2} \ right) \) .
Мы не будем заморачиваться с наброском для этого, поскольку мы уже набросали его один раз, и смысл здесь был больше в том, чтобы в любом случае исключить параметр.
Прежде чем мы закончим этот пример, давайте быстро рассмотрим одну проблему.
В первом примере мы просто, казалось бы, случайным образом выбрали значения \ (t \) для использования в нашей таблице, особенно третье значение. На самом деле не было очевидной причины для выбора \ (t = — \ frac {1} {2} \).Однако, вероятно, это наиболее важный выбор \ (t \), поскольку именно он дает вершину.
Реальность такова, что при написании этого материала мы сначала решили эту задачу, а затем вернулись и решили первую задачу. Построение точек — это обычно способ, которым большинство людей сначала учатся строить графики, и он действительно иллюстрирует некоторые важные концепции, такие как направление, поэтому имело смысл сначала сделать это в примечаниях. Однако на практике этот пример часто выполняется первым.2} + t} \\ {- 2 = 2t — 1} \ end {array} \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,5 дюйма} \ begin {array} {ll} {t = — \ frac {1 } {2} \, \, \, \ left ({{\ mbox {двойной корень}}} \ right)} \\ {t = — \ frac {1} {2}} \ end {array} \]
Итак, как мы видим, значение \ (t \), которое даст обе эти координаты, равно \ (t = — \ frac {1} {2} \). Обратите внимание, что параметрическое уравнение \ (x \) дало двойной корень, а этого часто не происходит. Часто из этого уравнения мы получали два разных корня. На самом деле, нет ничего необычного в том, чтобы получить несколько значений \ (t \) из каждого уравнения.
Однако мы можем сказать, что будут значения \ (t \), которые встречаются в обоих наборах решений, и это \ (t \), которые мы хотим для этой точки. В конце концов мы увидим пример, где это происходит, в следующем разделе.
Теперь из этой работы мы видим, что если мы используем \ (t = — \ frac {1} {2} \), мы получим вершину, и поэтому мы включили это значение \ (t \) в таблицу в примере 1. Как только мы получили это значение \ (t \), мы выбрали два целых значения \ (t \) с каждой стороны, чтобы завершить таблицу.
Как мы увидим в последующих примерах в этом разделе, определение значений \ (t \), которые дадут конкретные баллы, — это то, что нам нужно будет делать на довольно регулярной основе. Однако, как показал этот пример, это довольно просто. Все, что нам нужно, это решить (обычно) довольно простое уравнение, которое к этому моменту не должно быть слишком сложным.
Создание эскиза параметрической кривой после исключения параметра кажется довольно простым.Все, что нам нужно сделать, это изобразить уравнение, которое мы нашли, исключив параметр. Однако, как уже отмечалось, у этого метода есть две небольшие проблемы. Первый — это направление движения. Уравнение, включающее только \ (x \) и \ (y \), НЕ будет указывать направление движения параметрической кривой. Однако, как правило, эту проблему легко решить. Давайте быстро посмотрим на производные параметрических уравнений из последнего примера. Их,
\ [\ begin {align *} \ frac {{dx}} {{dt}} & = 2t + 1 \\ \ frac {{dy}} {{dt}} & = 2 \ end {align *} \]Теперь все, что нам нужно сделать, это вспомнить наши знания по Исчислению I.Очевидно, что производная \ (y \) по \ (t \) всегда положительна. Вспоминая, что одна из интерпретаций первой производной — это скорость изменения, мы теперь знаем, что по мере увеличения \ (t \) \ (y \) также должно увеличиваться. Следовательно, мы должны двигаться вверх по кривой снизу вверх по мере увеличения \ (t \), поскольку это единственное направление, которое всегда будет давать увеличение \ (y \) при увеличении \ (t \).
Обратите внимание, что производная \ (x \) не так полезна для этого анализа, поскольку она будет как положительной, так и отрицательной, и, следовательно, \ (x \) будет как увеличиваться, так и уменьшаться в зависимости от значения \ (t \).Это не очень помогает с направлением, поскольку следование кривой в любом направлении будет показывать как увеличение, так и уменьшение \ (x \).
В некоторых случаях только одно из уравнений, например, в этом примере, задает направление, в то время как в других случаях можно использовать любое из них. Также возможно, что в некоторых случаях для определения направления потребуются обе производные. Это всегда будет зависеть от индивидуального набора параметрических уравнений.
Вторая проблема с исключением параметра лучше всего проиллюстрирована на примере, поскольку мы столкнемся с этой проблемой в остальных примерах.
Пример 4 Постройте параметрическую кривую для следующего набора параметрических уравнений. Четко укажите направление движения. \ [x = 5 \ cos t \ hspace {0,5 дюйма} y = 2 \ sin t \ hspace {0,5 дюйма} 0 \ le t \ le 2 \ pi \] Показать решениеПрежде чем мы приступим к устранению параметра для этой проблемы, давайте сначала обратимся к еще раз, почему просто выбирать \ (t \) и наносить точки на график не очень хорошая идея.
Учитывая диапазон значений \ (t \) в формулировке задачи, давайте воспользуемся следующим набором \ (t \) ’.
\ (т \) \ (х \) \ (г \) 0 5 0 \ (\ frac {\ pi} {2} \) 0 2 \ (\ pi \) -5 0 \ (\ frac {{3 \ pi}} {2} \) 0 -2 \ (2 \ pi \) 5 0 Вопрос, который нам нужно задать сейчас, заключается в том, достаточно ли у нас точек, чтобы точно нарисовать график этого набора параметрических уравнений? Ниже приведены некоторые эскизы некоторых возможных графиков параметрического уравнения, основанного только на этих пяти точках.
Учитывая природу синуса / косинуса, вы могли бы исключить ромб и квадрат, но нельзя отрицать, что это графики, проходящие через заданные точки. Последний график тоже немного глуп, но он показывает график, проходящий через заданные точки.
Опять же, учитывая природу синуса / косинуса, вы, вероятно, можете догадаться, что правильный график — это эллипс.Однако на данный момент это все, что нужно сделать. Догадка. На самом деле ничто не говорит однозначно о том, что параметрическая кривая представляет собой эллипс только из этих пяти точек. В этом опасность построения параметрических кривых на основе нескольких точек. Если мы не знаем заранее, какой график будет, мы на самом деле просто делаем предположение.
Итак, в общем, нам следует избегать нанесения точек на эскиз параметрических кривых. {- 1}} \ left ({\ frac {x} {5}} \ right) \ hspace {0.{- 1}} \ left ({\ frac {x} {5}} \ right)} \ right) \]
Вы видите проблему с этим? Это определенно легко сделать, но у нас больше шансов правильно построить график исходных параметрических уравнений путем нанесения точек, чем при построении этого графика!
Есть много способов исключить параметр из параметрических уравнений, и решение для \ (t \) обычно не лучший способ сделать это. Хотя часто это легко сделать, в большинстве случаев мы получаем уравнение, с которым практически невозможно справиться.2}}} {4} \]
Итак, теперь мы знаем, что у нас будет эллипс.
А теперь продолжим пример. Мы определили, что параметрические уравнения описывают эллипс, но мы не можем просто набросать эллипс и покончить с ним.
Во-первых, то, что алгебраическое уравнение было эллипсом, на самом деле не означает, что параметрическая кривая представляет собой полный эллипс. Всегда возможно, что параметрическая кривая является только частью эллипса.Чтобы определить, какую часть эллипса будет покрывать параметрическая кривая, давайте вернемся к параметрическим уравнениям и посмотрим, что они говорят нам о любых ограничениях на \ (x \) и \ (y \). Основываясь на наших знаниях о синусе и косинусе, мы имеем следующее:
\ [\ begin {align *} & — 1 \ le \ cos t \ le 1 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} — 5 \ le 5 \ cos t \ le 5 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0.25in} \, \, — 5 \ le x \ le 5 \\ & — 1 \ le \ sin t \ le 1 \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} — 2 \ le 2 \ sin t \ le 2 \, \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \, \, — 2 \ le y \ le 2 \ конец {выравнивание *} \]Итак, начав с синуса / косинуса и «построив» уравнение для \ (x \) и \ (y \) с помощью основных алгебраических манипуляций, мы получим, что параметрические уравнения накладывают указанные выше ограничения на \ (x \) и \ (у \). В этом случае это также полные ограничения на \ (x \) и \ (y \), которые мы получаем, построив график полного эллипса.
Это вторая потенциальная проблема, о которой говорилось выше.Параметрическая кривая не всегда может прослеживать полный график алгебраической кривой. Мы всегда должны находить ограничения на \ (x \) и \ (y \), налагаемые на нас параметрической кривой, чтобы определить, какая часть алгебраической кривой на самом деле нарисована параметрическими уравнениями.
Таким образом, в этом случае мы теперь знаем, что получаем полный эллипс из параметрических уравнений. Прежде чем мы продолжим рассмотрение остальной части примера, будьте осторожны, чтобы не всегда просто предполагать, что мы получим полный график алгебраического уравнения.Определенно бывают случаи, когда мы не можем получить полный график, и нам нужно будет провести аналогичный анализ, чтобы определить, какую часть графика мы на самом деле получаем. Позже мы увидим пример этого.
Также обратите внимание, что любые ограничения на \ (t \), указанные в постановке задачи, также могут повлиять на то, какую часть графика алгебраического уравнения мы получим. Однако в этом случае, основываясь на таблице значений, которые мы вычислили в начале задачи, мы можем видеть, что действительно получаем полный эллипс в диапазоне \ (0 \ le t \ le 2 \ pi \).Однако это не всегда так, поэтому обратите внимание на любые ограничения на \ (t \), которые могут существовать!
Далее нам нужно определить направление движения параметрической кривой. Вспомните, что все параметрические кривые имеют направление движения, а уравнение эллипса просто ничего не говорит нам о направлении движения.
Чтобы получить направление движения, заманчиво просто использовать таблицу значений, которую мы вычислили выше, чтобы получить направление движения.В этом случае мы могли бы предположить (и да, это все — предположение), что кривая идет против часовой стрелки. Мы были бы правы. В этом случае мы были бы правы! Проблема в том, что таблицы значений могут вводить в заблуждение при определении направления движения, как мы увидим в следующем примере.
Следовательно, лучше не использовать таблицу значений для определения направления движения. Чтобы правильно определить направление движения, мы будем использовать тот же метод определения направления, который мы обсуждали после примера 3.Другими словами, мы возьмем производную параметрических уравнений и воспользуемся нашими знаниями Исчисления I и триггера для определения направления движения.
Производные параметрических уравнений равны,
\ [\ frac {{dx}} {{dt}} = — 5 \ sin t \ hspace {0,5 дюйма} \ frac {{dy}} {{dt}} = 2 \ cos t \]Теперь, в точке \ (t = 0 \), мы находимся в точке \ (\ left ({5,0} \ right) \), и давайте посмотрим, что произойдет, если мы начнем увеличивать \ (t \).Увеличим \ (t \) с \ (t = 0 \) до \ (t = \ frac {\ pi} {2} \). В этом диапазоне значений \ (t \) мы знаем, что синус всегда положителен, и поэтому из производной уравнения \ (x \) мы можем видеть, что \ (x \) должно уменьшаться в этом диапазоне значений \ (t \)
Это, однако, не помогает нам определить направление параметрической кривой. Начиная с \ (\ left ({5,0} \ right) \), независимо от того, движемся ли мы по часовой стрелке или против часовой стрелки, \ (x \) должен будет уменьшаться, поэтому мы действительно ничего не узнали из \ (x \) производная.
С другой стороны, нам поможет производная от параметрического уравнения \ (y \). Опять же, когда мы увеличиваем \ (t \) от \ (t = 0 \) до \ (t = \ frac {\ pi} {2} \), мы знаем, что косинус будет положительным, и поэтому \ (y \) должен быть увеличивается в этом диапазоне. Однако это может произойти только в том случае, если мы движемся против часовой стрелки. Если бы мы двигались по часовой стрелке от точки \ (\ left ({5,0} \ right) \), мы могли бы увидеть, что \ (y \) пришлось бы уменьшаться!
Следовательно, в первом квадранте мы должны двигаться против часовой стрелки.Перейдем ко второму квадранту.
Итак, теперь мы находимся в точке \ (\ left ({0,2} \ right) \), и мы увеличим \ (t \) с \ (t = \ frac {\ pi} {2} \) до \ (т = \ пи \). В этом диапазоне \ (t \) мы знаем, что косинус будет отрицательным, а синус — положительным. Следовательно, из производных параметрических уравнений мы можем видеть, что \ (x \) все еще уменьшается, и \ (y \) теперь также будет уменьшаться.
В этом квадранте производная \ (y \) ничего не говорит нам, поскольку \ (y \) просто должен уменьшаться, чтобы перейти от \ (\ left ({0,2} \ right) \).Однако для уменьшения \ (x \), как мы знаем, в этом квадранте, направление все еще должно двигаться против часовой стрелки.
Сейчас мы находимся в \ (\ left ({- 5,0} \ right) \), и мы увеличим \ (t \) с \ (t = \ pi \) до \ (t = \ frac {{3 \ пи}} {2} \). В этом диапазоне \ (t \) мы знаем, что косинус отрицателен (и, следовательно, \ (y \) будет уменьшаться), а синус также отрицателен (и, следовательно, \ (x \) будет увеличиваться). Поэтому продолжим движение против часовой стрелки.
Для квадранта 4 мы начнем с \ (\ left ({0, — 2} \ right) \) и увеличим \ (t \) от \ (t = \ frac {{3 \ pi}} { 2} \) в \ (t = 2 \ pi \). В этом диапазоне \ (t \) мы знаем, что косинус положительный (и, следовательно, \ (y \) будет увеличиваться), а синус отрицателен (и, следовательно, \ (x \) будет увеличиваться). Итак, как и в предыдущих трех квадрантах, мы продолжаем двигаться против часовой стрелки.
На этом этапе мы охватили диапазон \ (t \), который был указан в постановке задачи, и в течение всего диапазона движение было в направлении против часовой стрелки.
Теперь мы можем полностью набросать параметрическую кривую, вот и эскиз.
Хорошо, это был действительно длинный пример. Большинство проблем такого типа не такие продолжительные. Нам просто нужно было многое обсудить в этом, чтобы мы могли выделить пару важных идей. Остальные примеры в этом разделе не займет много времени.
Теперь давайте взглянем на другой пример, который проиллюстрирует важную идею о параметрических уравнениях.
Пример 5 Постройте параметрическую кривую для следующего набора параметрических уравнений. Четко укажите направление движения. \ [x = 5 \ cos \ left ({3t} \ right) \ hspace {0,5 дюйма} y = 2 \ sin \ left ({3t} \ right) \ hspace {0,5 дюйма} 0 \ le t \ le 2 \ Пи \] Показать решениеОбратите внимание, что единственное различие между этими параметрическими уравнениями и уравнениями в примере 4 состоит в том, что мы заменили \ (t \) на 3 \ (t \). Здесь мы можем удалить параметр таким же образом, как и в предыдущем примере.2}}} {4} \]
Итак, мы получили тот же эллипс, что и в предыдущем примере. Также обратите внимание, что мы можем провести такой же анализ параметрических уравнений, чтобы определить, что у нас точно такие же ограничения на \ (x \) и \ (y \). А именно
\ [- 5 \ le x \ le 5 \ hspace {0,5 дюйма} \ hspace {0,25 дюйма} — 2 \ le y \ le 2 \]Начинает казаться, что изменение \ (t \) на 3 \ (t \) в тригонометрических уравнениях никоим образом не изменит параметрическую кривую.Однако это неверно. Кривая действительно меняется небольшим, но важным образом, который мы вскоре обсудим.
Прежде чем обсуждать то небольшое изменение, которое 3 \ (t \) вносит в кривую, давайте обсудим направление движения этой кривой. Несмотря на то, что мы сказали в последнем примере, что выбор значений \ (t \) и подключение к уравнениям для поиска точек для построения графика — плохая идея, давайте сделаем это любым способом.
Учитывая диапазон значений \ (t \) из условия задачи, следующий набор выглядит как хороший выбор для использования \ (t \).
\ (т \) \ (х \) \ (г \) 0 5 0 \ (\ frac {\ pi} {2} \) 0 -2 \ (\ pi \) -5 0 \ (\ frac {{3 \ pi}} {2} \) 0 2 \ (2 \ pi \) 5 0 Итак, единственное изменение в этой таблице значений / точек из последнего примера — это все ненулевые значения \ (y \) изменили знак.При быстром взгляде на значения в этой таблице может показаться, что кривая в этом случае движется по часовой стрелке. Но так ли это? Напомним, мы говорили, что эти таблицы значений могут вводить в заблуждение, когда используются для определения направления, и поэтому мы их не используем.
Посмотрим, верно ли наше первое впечатление. Мы можем проверить наше первое впечатление, выполнив производную работу, чтобы получить правильное направление. Давайте работать с параметрическим уравнением \ (y \), так как \ (x \) будет иметь ту же проблему, что и в предыдущем примере.Производная параметрического уравнения \ (y \) равна,
\ [\ frac {{dy}} {{dt}} = 6 \ cos \ left ({3t} \ right) \]Теперь, если мы начнем с \ (t = 0 \), как в предыдущем примере, и начнем увеличивать \ (t \). При \ (t = 0 \) производная явно положительна, и поэтому увеличение \ (t \) (по крайней мере, вначале) заставит \ (y \) также увеличиться. Единственный способ сделать это — если кривая изначально идет против часовой стрелки.
Теперь мы могли бы продолжить рассмотрение того, что происходит при дальнейшем увеличении \ (t \), но когда мы имеем дело с параметрической кривой, которая представляет собой полный эллипс (как эта), а аргумент триггерных функций имеет вид nt для любой константы \ (n \) направление не изменится, поэтому, как только мы знаем начальное направление, мы знаем, что оно всегда будет двигаться в этом направлении. Обратите внимание, что это верно только для параметрических уравнений в той форме, которая у нас есть. В последующих примерах мы увидим, что для различных типов параметрических уравнений это может быть неверно.
Хорошо, из этого анализа мы видим, что кривая должна быть начерчена против часовой стрелки. Это прямо противоречит нашему предположению из таблиц значений выше, и поэтому мы можем видеть, что в этом случае таблица, вероятно, привела бы нас в неправильном направлении. Итак, еще раз, таблицы, как правило, не очень надежны для получения практически любой реальной информации о параметрической кривой, кроме нескольких точек, которые должны быть на кривой. В остальном таблицы редко бывают полезными и, как правило, не рассматриваются в дальнейших примерах.
Итак, почему наша таблица дала неверное представление о направлении? Хорошо напомним, что мы упоминали ранее, что 3 \ (t \) приведет к небольшому, но важному изменению кривой по сравнению с просто \ (t \)? Давайте посмотрим, что это за изменение, поскольку оно также даст ответ на вопрос, что «пошло не так» с нашей таблицей значений.
Начнем с \ (t = 0 \). В \ (t = 0 \) мы находимся в точке \ (\ left ({5,0} \ right) \), и давайте спросим себя, какие значения \ (t \) возвращают нас в эту точку.В Примере 3 мы видели, как определять значения \ (t \), которые ставят нас в определенные точки, и здесь будет работать тот же процесс с небольшими изменениями.
Вместо того, чтобы смотреть на уравнения \ (x \) и \ (y \), как мы это делали в этом примере, давайте просто посмотрим на уравнение \ (x \). Причина этого в том, что мы отметим, что на эллипсе есть две точки, координата которых будет равна нулю \ (y \): \ (\ left ({5,0} \ right) \) и \ (\ слева ({- 5,0} \ right) \). Если мы установим координату \ (y \) равной нулю, мы найдем все \ (t \), которые находятся в обеих этих точках, когда нам нужны только значения \ (t \), которые находятся в \ ( \ left ({5,0} \ right) \).{- 1}} \ left (1 \ right) = 0 + 2 \ pi n \ hspace {0.25in} \, \, \, \ to \ hspace {0.25in} \, \, \, \, \, \ , t = \ frac {2} {3} \ pi n \, \, \, \, \, \, n = 0, \ pm 1, \ pm 2, \ pm 3, \ ldots \ end {align *} \]
Не забывайте, что при решении тригонометрического уравнения нам нужно добавить «\ (+ 2 \ pi n \)», где \ (n \) представляет количество полных оборотов против часовой стрелки (положительное значение \ ( n \)) и по часовой стрелке (отрицательное \ (n \)), которое мы поворачиваем от первого решения, чтобы получить все возможные решения уравнения.
Теперь давайте подставим несколько значений \ (n \), начиная с \ (n = 0 \). В этом случае нам не нужно отрицательное \ (n \), поскольку все они приведут к отрицательному \ (t \), а те выходят за пределы диапазона \ (t \), который мы были указаны в формулировке задачи. Тогда первые несколько значений \ (t \) равны
. \ [\ begin {align *} n & = 0 \ hspace {0,25 дюйма}: \ hspace {0,25 дюйма} t = 0 \\ n & = 1 \ hspace {0,25 дюйма}: \ hspace {0,25 дюйма} t = \ гидроразрыв {{2 \ pi}} {3} \\ n & = 2 \ hspace {0.25 дюймов}: \ hspace {0,25 дюйма} t = \ frac {{4 \ pi}} {3} \\ n & = 3 \ hspace {0,25 дюйма}: \ hspace {0,25 дюйма} t = \ frac {{6 \ pi}} {3} = 2 \ pi \ end {align *} \]На этом мы можем остановиться, так как все дальнейшие значения \ (t \) будут выходить за пределы диапазона \ (t \), указанного в этой задаче.
Итак, о чем это нам говорит? В Примере 4, когда аргументом было просто \ (t \), эллипс был начерчен ровно один раз в диапазоне \ (0 \ le t \ le 2 \ pi \). Однако, когда мы меняем аргумент на 3 \ (t \) (и помня, что кривая всегда будет отслеживаться против часовой стрелки для этой задачи), мы проходим через «начальную» точку \ (\ left ( {5,0} \ right) \) в два раза больше, чем в предыдущем примере.
Фактически, эта кривая прослеживается три разных раза. Первая трассировка завершается в диапазоне \ (0 \ le t \ le \ frac {{2 \ pi}} {3} \). Вторая трассировка завершается в диапазоне \ (\ frac {{2 \ pi}} {3} \ le t \ le \ frac {{4 \ pi}} {3} \), а третья и последняя трассировка завершается в диапазон \ (\ frac {{4 \ pi}} {3} \ le t \ le 2 \ pi \). Другими словами, изменение аргумента с \ (t \) на 3 \ (t \) увеличивает скорость трассировки, и кривая теперь будет трассироваться три раза в диапазоне \ (0 \ le t \ le 2 \ pi \ )!
Вот почему таблица производит неправильное впечатление.Скорость трассировки увеличилась, что привело к неправильному впечатлению от точек в таблице. Таблица, кажется, предполагает, что между каждой парой значений \ (t \) четверть эллипса прослеживается по часовой стрелке, тогда как на самом деле она выводит три четверти эллипса против часовой стрелки.
Вот последний набросок кривой и обратите внимание, что он не сильно отличается от предыдущего. Единственные различия — это значения \ (t \) и различные точки, которые мы включили.Мы включили еще несколько значений \ (t \) в различных точках, чтобы проиллюстрировать, где находится кривая для различных значений \ (t \), но в целом они действительно не нужны.
Итак, в последних двух примерах мы видели два набора параметрических уравнений, которые каким-то образом давали один и тот же график. Тем не менее, поскольку они вычерчивали график разное количество раз, нам действительно нужно думать о них как о разных параметрических кривых, по крайней мере, в некотором роде.Это может показаться различием, о котором нам не нужно беспокоиться, но, как мы увидим в следующих разделах, это может быть очень важным различием. В некоторых из следующих разделов нам понадобится кривая, которая будет начерчена ровно один раз.
Прежде чем мы перейдем к другим проблемам, давайте кратко рассмотрим, что происходит при изменении \ (t \) на nt в такого рода параметрических уравнениях. Когда мы имеем дело с параметрическими уравнениями, включающими только синусы и косинусы, и оба они имеют один и тот же аргумент, если мы изменим аргумент с \ (t \) на nt , мы просто изменим скорость, с которой выполняется трассировка кривой.2}}} {4} \]
В данном случае алгебраическое уравнение представляет собой параболу, которая открывается влево.
Однако нам нужно быть очень, очень осторожными при построении эскиза этой параметрической кривой. Мы НЕ получим всю параболу. Набросок параболы алгебраической формы будет существовать для всех возможных значений \ (y \). Однако параметрические уравнения определили как \ (x \), так и \ (y \) в терминах синуса и косинуса, и мы знаем, что их диапазоны ограничены, и поэтому мы не получим все возможные значения \ (x \ ) и \ (y \) здесь.2} t \ le 1 & \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} & 0 \ le x \ le 1 \\ — 1 \ le \ cos t \ le 1 & \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} & — 2 \ le 2 \ cos t \ le 2 & \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} & — 2 \ le y \ le 2 \ end {array} \]
Итак, из этого ясно, что мы получим только часть параболы, которая определяется алгебраическим уравнением. Ниже приведен краткий набросок части параболы, которую будет охватывать параметрическая кривая.
Чтобы закончить набросок параметрической кривой, нам также необходимо направление движения кривой. Однако, прежде чем мы перейдем к этому, давайте переместимся вперед и определим диапазон значений \ (t \) для одной трассы. Для этого нам нужно знать \ (t \), которые помещают нас в каждую конечную точку, и мы можем следовать той же процедуре, которую мы использовали в предыдущем примере. Единственная разница в том, что на этот раз давайте будем использовать параметрическое уравнение \ (y \) вместо \ (x \), потому что координаты \ (y \) двух конечных точек кривой различны, тогда как координаты \ (x \) одинаковы.{- 1}} \ left ({- 1} \ right) = \ pi + 2 \ pi n, \ hspace {0.25in} n = 0, \ pm 1, \ pm 2, \ pm 3, \ ldots \ end {выровнять*}\]
Итак, мы видим, что мы будем в нижней точке на,
\ [t = \ ldots, — 3 \ pi, — \ pi, \ pi, 3 \ pi, \ ldots \]Итак, если мы начнем, скажем, с \ (t = 0 \), мы находимся в верхней точке и увеличиваем \ (t \), мы должны двигаться по кривой вниз, пока не достигнем \ (t = \ pi \) в этот момент мы сейчас находимся в нижней точке.Это означает, что мы проведем кривую ровно один раз в диапазоне \ (0 \ le t \ le \ pi \).
Однако это не единственный диапазон, по которому можно проследить кривую. Обратите внимание, что если мы будем увеличивать \ (t \) от \ (t = \ pi \), теперь нам придется возвращаться вверх по кривой, пока мы не достигнем \ (t = 2 \ pi \), и теперь мы снова наверху. точка. Увеличение \ (t \) снова, пока мы не достигнем \ (t = 3 \ pi \), вернет нас вниз по кривой, пока мы снова не достигнем нижней точки, и т. Д. .Из этого анализа мы можем получить еще два диапазона \ (t \) для одной трассы,
\ [\ pi \ le t \ le 2 \ pi \ hspace {0,5 дюйма} 2 \ pi \ le t \ le 3 \ pi \]Как вы, вероятно, видите, существует бесконечное количество диапазонов \ (t \), которые мы могли бы использовать для одного следа кривой. Любой из них был бы приемлемым ответом на эту проблему.
Обратите внимание, что в процессе определения диапазона \ (t \) для одной трассы нам также удалось определить направление движения для этой кривой.В диапазоне \ (0 \ le t \ le \ pi \) мы должны были пройти вниз по кривой, чтобы добраться от верхней точки в \ (t = 0 \) до нижней точки в \ (t = \ pi \) . Однако в точке \ (t = 2 \ pi \) мы снова находимся в верхней точке кривой, и чтобы попасть туда, мы должны двигаться по пути. Мы не можем просто перепрыгнуть на верхнюю точку или выбрать другой путь, чтобы добраться туда. Все путешествие необходимо совершать по намеченному пути. Это означает, что нам пришлось вернуться вверх по пути. Дальнейшее увеличение \ (t \) возвращает нас обратно по пути, затем снова вверх по пути и т. Д. .
Другими словами, этот путь нарисован в обоих направлениях, потому что мы не налагаем никаких ограничений на \ (t \) ’, и поэтому мы должны предположить, что мы используем все возможные значения \ (t \). Если бы мы наложили ограничения на то, какие \ (t \) использовать, мы действительно могли бы двигаться только в одном направлении. Однако это будет результатом только диапазона \ (t \), который мы используем, а не самих параметрических уравнений.
Обратите внимание, что нам действительно не нужно было проделывать вышеуказанную работу, чтобы определить, идет ли кривая в обоих направлениях.в этом случае. Оба параметрических уравнения \ (x \) и \ (y \) включают синус или косинус, и мы знаем, что обе эти функции колеблются. Это, в свою очередь, означает, что и \ (x \), и \ (y \) также будут колебаться. Единственный способ сделать это на данной кривой — это провести кривую в обоих направлениях.
Будьте осторожны с приведенными выше рассуждениями о том, что колебательный характер синуса / косинуса заставляет кривую прослеживаться в обоих направлениях. Его можно использовать только в этом примере, потому что «начальная» и «конечная» точки кривых находятся в разных местах.Единственный способ добраться от одной из «конечных» точек кривой до другой — вернуться назад по кривой в противоположном направлении.
Сравните это с эллипсом в примере 4. В этом случае синус / косинус также присутствовал в параметрических уравнениях. Однако кривая прослеживалась только в одном направлении, а не в обоих направлениях. В Примере 4 мы строили график полного эллипса, и поэтому независимо от того, где мы начинаем рисовать график, мы в конечном итоге вернемся к «начальной» точке, даже не отслеживая никакую часть графика.В примере 4, когда мы обрисовываем полный эллипс, оба \ (x \) и \ (y \) фактически колеблются между своими двумя «конечными точками», но сама кривая не проходит в обоих направлениях, чтобы это произошло.
В принципе, мы можем использовать колебательный характер синуса / косинуса только для определения того, что кривая идет в обоих направлениях, если кривая начинается и заканчивается в разных точках. Если начальная / конечная точка совпадает, тогда нам обычно нужно пройти через аргумент полной производной, чтобы определить фактическое направление движения.
Итак, чтобы закончить эту проблему, ниже приведен эскиз параметрической кривой. Обратите внимание, что мы поместили стрелки направления в обоих направлениях, чтобы четко указать, что он будет прослеживаться в обоих направлениях. Мы также добавили несколько значений \ (t \), чтобы помочь проиллюстрировать направление движения.
К этому моменту мы видели примеры, которые могли бы проследить весь график, который мы получили, исключив параметр, если бы мы взяли достаточно большой диапазон \ (t \) ‘s.Однако в предыдущем примере мы увидели, что это не всегда так. Более чем возможно иметь набор параметрических уравнений, которые будут непрерывно отслеживать только часть кривой. Обычно мы можем определить, произойдет ли это, ища ограничения на \ (x \) и \ (y \), которые накладываются на нас параметрическим уравнением.
Мы часто будем использовать параметрические уравнения для описания пути объекта или частицы. Давайте посмотрим на это на примере.2} \ left ({2t} \ right) \]
Полностью опишите путь этой частицы. Для этого нарисуйте путь, определив пределы для \ (x \) и \ (y \) и указав диапазон значений \ (t \), для которых путь будет прослеживаться ровно один раз (при условии, что он трассирует более один раз конечно).
Показать решениеУдаление параметра на этот раз будет немного другим. На этот раз у нас есть только косинусы, и мы воспользуемся этим в наших интересах. Мы можем решить уравнение \ (x \) для косинуса и подставить его в уравнение для \ (y \).2} \ left ({2t} \ right) \ le 2 & \ hspace {0,25 дюйма} & 1 \ le y \ le 2 \ end {array} \]
Итак, мы снова обрисовываем только часть кривой. Вот быстрый набросок части параболы, которую будет охватывать параметрическая кривая.
Теперь, как мы обсуждали в предыдущем примере, поскольку параметрические уравнения \ (x \) и \ (y \) включают косинус, мы знаем, что и \ (x \), и \ (y \) должны колебаться, и поскольку «начало »И« конечные »точки кривой не совпадают, единственный способ колебания \ (x \) и \ (y \) — это движение кривой в обоих направлениях.
Чтобы решить проблему, все, что нам нужно сделать, это определить диапазон \ (t \) для одной трассы. Поскольку «конечные» точки на кривой имеют одинаковое значение \ (y \) и разные значения \ (x \), мы можем использовать параметрическое уравнение \ (x \) для определения этих значений. Вот эта работа.
\ [\ begin {array} {ll} \ begin {align} x = 3: \\ \\ \\ \ end {align} & \ begin {align *} 3 & = 3 \ cos \ left ({2t} \ справа) \\ 1 & = \ cos \ left ({2t} \ right) \\ 2t & = 0 + 2 \ pi n \ hspace {0.25 дюймов} \, \ to \ hspace {0,25 дюйма} t = \ pi n \ hspace {0,25 дюйма} \, \, \, n = 0, \ pm 1, \ pm 2, \ pm 3, \ ldots \ end { выровнять *} \ конец {массив} \] \ [\ begin {array} {ll} \ begin {align} x = -3: \\ \\ \\ \\ \ end {align} & \ begin {align *} — 3 & = 3 \ cos \ left ( {2t} \ right) \\ — 1 & = \ cos \ left ({2t} \ right) \\ 2t & = \ pi + 2 \ pi n \ hspace {0,25 дюйма} \, \ to \ hspace {0,25 дюйма } t = \ frac {1} {2} \ pi + \ pi n \ hspace {0.25in} \, \, \, n = 0, \ pm 1, \ pm 2, \ pm 3, \ ldots \ end { выровнять *} \ конец {массив} \]Итак, мы будем в правой конечной точке в \ (t = \ ldots, — 2 \ pi, — \ pi, 0, \ pi, 2 \ pi, \ ldots \), а мы будем в левом конце укажите на \ (t = \ ldots, — \ frac {3} {2} \ pi, — \ frac {1} {2} \ pi, \ frac {1} {2} \ pi, \ frac {3} { 2} \ пи, \ ldots \).Итак, в этом случае существует бесконечное количество диапазонов значений \ (t \) для одной трассы. Вот несколько из них.
\ [- \ frac {1} {2} \ pi \ le t \ le 0 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} 0 \ le t \ le \ frac {1} {2} \ pi \ hspace { 0,25 дюйма} \ hspace {0,25 дюйма} \ frac {1} {2} \ pi \ le t \ le \ pi \]Вот окончательный набросок траектории частицы с несколькими значениями \ (t \) на нем.
Здесь следует сделать небольшое предупреждение.Из-за заложенных в них идей мы сконцентрировались на параметрических кривых, которые повторяли части кривой более одного раза. Однако не стоит слишком зацикливаться на мысли, что это всегда будет происходить. Многие, если не большинство параметрических кривых могут быть построены только один раз. Первый из них, который мы рассмотрели, является хорошим примером этого. Эта параметрическая кривая никогда не повторится ни на одной своей части.
Перед тем, как продолжить, в этом разделе необходимо обсудить еще одну тему. До сих пор мы начали с параметрических уравнений и устранили параметр для определения параметрической кривой.2}}} = 1 \]
набор параметрических уравнений для него будет,
\ [x = a \ cos t \ hspace {1.0in} y = b \ sin t \]Этот набор параметрических уравнений будет обводить эллипс, начинающийся в точке \ (\ left ({a, 0} \ right) \), и прослеживать его против часовой стрелки, и только один раз будет прослеживаться в диапазоне \ ( 0 \ le t \ le 2 \ pi \). Это довольно важный набор параметрических уравнений, поскольку он постоянно используется в некоторых предметах, связанных с эллипсами и / или кругами.
Каждую кривую можно параметризовать более чем одним способом. Любой из следующих параметров также параметризует тот же эллипс.
\ [\ begin {align *} x & = a \ cos \ left ({\ omega \, t} \ right) \ hspace {0,5in} & y & = b \ sin \ left ({\ omega \, t} \ right) \\ x & = a \ sin \ left ({\ omega \, t} \ right) \ hspace {0.5in} & y & = b \ cos \ left ({\ omega \, t} \ right) \\ x & = a \ cos \ left ({\ omega \, t} \ right) \ hspace {0.5in} & y & = — b \ sin \ left ({\ omega \, t} \ right) \ end {выровнять*}\]Наличие символа \ (\ omega \) изменит скорость вращения эллипса, как мы видели в примере 5.Также обратите внимание, что последние два очерчивают эллипсы с направлением движения по часовой стрелке (вы можете проверить это). Также обратите внимание, что все они не начинаются в одном и том же месте (если мы думаем о \ (t = 0 \) как о начальной точке).
Конечно, существует множество других параметризаций эллипса, но вы поняли идею. Важно помнить, что каждая параметризация будет отслеживать кривую один раз с потенциально другим диапазоном \ (t \) ‘s. Каждая параметризация может вращаться с разными направлениями движения и может начинаться в разных точках.
Вы можете обнаружить, что вам нужна параметризация эллипса, который начинается в определенном месте и имеет определенное направление движения, и теперь вы знаете, что с некоторой работой вы можете написать набор параметрических уравнений, которые дадут вам поведение, которое ты после.
Теперь давайте запишем пару других важных параметризаций, и все комментарии о направлении движения, начальной точке и диапазоне \ (t \) для одной трассы (если применимо) по-прежнему верны.
Во-первых, поскольку круг — это не что иное, как частный случай эллипса, мы можем использовать параметризацию эллипса, чтобы получить параметрические уравнения для окружности с центром в начале радиуса \ (r \). Один из возможных способов параметризации круга:
\ [x = r \ cos t \ hspace {1.0in} y = r \ sin t \]Наконец, даже если может показаться, что для этого нет никаких причин, мы также можем параметризовать функции в форме \ (y = f \ left (x \ right) \) или \ (x = h \ left (y \ right) \).В этих случаях мы параметризуем их следующим образом:
\ [\ begin {align *} x & = t \ hspace {1.0in} & x & = h \ left (t \ right) \\ y & = f \ left (t \ right) \ hspace {1.0in} & y & = t \ end {выровнять *} \]На данный момент может показаться не очень полезным выполнять параметризацию такой функции, но есть много случаев, когда на самом деле будет проще или даже может потребоваться работать с параметризацией вместо самой функции .К сожалению, почти все эти случаи встречаются в курсе Calculus III.
Графики — Алгебра и тригонометрия
Дальнейшие применения тригонометрии
Цели обучения
В этом разделе вы будете:
- Графические плоские кривые, описываемые параметрическими уравнениями путем нанесения точек.
- Графические параметрические уравнения.
Это конец девятого иннинга с двумя аутами и двумя игроками на базе.Хозяева проигрывают с разницей в два раунда. Бэттер раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом примерно к горизонту. Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрические уравнения. В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда.
Рис. 1. Параметрические уравнения могут моделировать траекторию полета снаряда. (Источник: Пол Крехер, Flickr)Совместное построение графиков параметрических уравнений и прямоугольной формы
Постройте параметрические уравнения и сначала постройте график, используя точки данных, сгенерированные из параметрической формы. Затем изобразите прямоугольную форму уравнения. Сравните два графика.
Анализ
На (Рисунок) данные параметрических уравнений и прямоугольного уравнения нанесены вместе.Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график.
Рисунок 5.Попробуй
Нарисуйте график параметрических уравнений вместе с прямоугольным уравнением на той же сетке.
[show-answer q = ”fs-id1165137807092 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137807092 ″]График параметрических уравнений выделен красным цветом, а график прямоугольного уравнения нарисован синими точками поверх параметрических уравнений.
[/ hidden-answer]
Приложения параметрических уравнений
Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время. Однако параметрические уравнения показывают, как значения x и y меняются в зависимости от t , как местоположения движущегося объекта в конкретный момент времени.
Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в направлении вверх, образуя угол к горизонтали, с начальной скоростью и на высоте выше горизонтали.
Путь объекта, движущегося под наклоном к горизонтали, с начальной скоростью и на высоте над горизонтом, определяется как
, где учитывается влияние силы тяжести, а — начальная высота объекта.В зависимости от единиц измерения, участвующих в задаче, useorThe уравнение допускает расстояние по горизонтали, а уравнение для дает расстояние по вертикали.
Нахождение параметрических уравнений для описания движения бейсбольного мяча
Решите проблему, указанную в начале этого раздела. Попадает ли тесто в выигрышную игру? Предположим, что мяч ударяется с начальной скоростью 140 футов в секунду под углом к горизонтали, при этом происходит контакт на высоте 3 футов над землей.
- Найдите параметрические уравнения для моделирования траектории бейсбольного мяча.
- Где мяч через 2 секунды?
- Как долго мяч находится в воздухе?
- Это хоумран?
[скрытый-ответ a = ”fs-id1165137453386 ″]Используйте формулы, чтобы составить уравнения. Горизонтальное положение находится с помощью параметрического уравнения для Таким образом,
Таким образом,Подставьте 2 в уравнения, чтобы найти горизонтальное и вертикальное положение мяча.
Через 2 секунды мяч оказывается на расстоянии 198 футов от бокса бьющего и на высоте 137 футов над землей.
Чтобы рассчитать, как долго мяч находится в воздухе, мы должны выяснить, когда он ударится о землю или когда. Таким образом,
Через секунду мяч коснулся земли. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.)
Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, проходит ли мяч через стену, нам нужно вычислить высоту мяча, когда x = 400 футов. Итак, мы установим x = 400, найдем и введем в
Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. (Рисунок).
Рисунок 7.[/ hidden-answer]
Упражнения по разделам
Устный
Какие два метода используются для построения графиков параметрических уравнений?
[show-answer q = ”fs-id1165135194726 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135194726 ″]точек с помощью стрелки ориентации и графического калькулятора
[/ hidden-answer]
В чем отличие параметрических уравнений точечного построения от декартовых уравнений?
Почему на некоторых графиках нарисованы стрелки?
[show-answer q = ”fs-id1165137758269 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137758269 ″]Стрелки показывают ориентацию, направление движения согласно возрастающим значениям
[/ hidden-answer]
Назовите несколько распространенных типов графиков параметрических уравнений.
Почему параметрические графики важны для понимания движения снаряда?
[show-answer q = ”fs-id1165137715148 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137715148 ″]Параметрические уравнения показывают различные вертикальные и горизонтальные движения во времени.
[/ hidden-answer]
Графический
Для следующих упражнений нарисуйте каждый набор параметрических уравнений в виде таблицы значений. Включите ориентацию на графике.
[show-answer q = ”fs-id1165135188326 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135188326 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134583390 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134583390 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135237047 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135237047 ″] [/ скрытый-ответ]Для следующих упражнений нарисуйте кривую и укажите ее ориентацию.
[show-answer q = ”fs-id1165134069188 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134069188 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137417002 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137417002 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137936702 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137936702 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134081386 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134081386 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137805783 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137805783 ″] [/ скрытый-ответ]Для следующих упражнений нарисуйте уравнение и укажите ориентацию.Затем напишите декартово уравнение.
[show-answer q = ”fs-id1165135149887 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135149887 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135512730 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135512730 ″] [/ скрытый-ответ] [show-answer q = ”fs-id11651323 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651323 ″] [/ скрытый-ответ]Для следующих упражнений нарисуйте уравнение и укажите ориентацию.
[show-answer q = ”211246 ″] Показать решение [/ show-answer]
[hidden-answer a = ”211246 ″] [/ hidden-answer] [show-answer q = ”fs-id1165135252162 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135252162 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137680409 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137680409 ″] [/ скрытый-ответ]В следующих упражнениях используйте параметрические уравнения для целых чисел a и b :
График по домену и включению ориентации.
График по домену где и, включая ориентацию.
[show-answer q = ”fs-id1165137409296 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137409296 ″] [/ скрытый-ответ]График по домену где и, включая ориентацию.
График по домену где и, включая ориентацию.
[show-answer q = ”fs-id1165137551247 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137551247 ″] [/ скрытый-ответ]Ifis 1 более чем описывает влияние значений andhave на график параметрических уравнений.
Опишите график ifand
[show-answer q = ”fs-id1165135189746 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135189746 ″]Произойдет 100 возвратно-поступательных движений.
[/ hidden-answer]
Что произойдет, если на 1 больше, чем Опишите график.
Если параметрические уравнения и имеют график горизонтальной параболы, раскрывающейся вправо, что изменит направление кривой?
[show-answer q = ”fs-id1165135499919 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135499919 ″]Возьмем противоположное уравнению.
[/ hidden-answer]
Для следующих упражнений опишите график системы параметрических уравнений.
и линейный
и линейный
[show-answer q = ”fs-id1165135609231 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135609231 ″]Парабола открывается.
[/ hidden-answer]
и линейный
Напишите параметрические уравнения круга с центральным радиусом 5 и направлением против часовой стрелки.
[show-answer q = ”fs-id1165135352460 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135352460 ″][/ hidden-answer]
Напишите параметрические уравнения эллипса с большой центральной осью длиной 10, малой осью длиной 6 и ориентацией против часовой стрелки.
Для следующих упражнений используйте графическую утилиту, чтобы построить график в области окна для следующих значений и, а также включить ориентацию.
[show-answer q = ”fs-id1165132960728 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165132960728 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134386554 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134386554 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165133349420 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165133349420 ″] [/ скрытый-ответ]Расширения
Объект подбрасывается в воздух с вертикальной скоростью 20 футов / с и горизонтальной скоростью 15 футов / с.Высота объекта может быть описана уравнением, в то время как объект движется по горизонтали с постоянной скоростью 15 футов / с. Напишите параметрические уравнения для положения объекта, а затем избавьтесь от времени, чтобы записать высоту как функцию горизонтального положения.
[show-answer q = ”fs-id1165132079269 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165132079269 ″][/ hidden-answer]
Скейтбордист, едущий по ровной поверхности с постоянной скоростью 9 футов / с, подбрасывает в воздух мяч, высоту которого можно описать уравнением. Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту в виде функция горизонтального положения.
Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Учитывайте положение дротика в любое время и не обращайте внимания на сопротивление воздуха.
Найдите параметрические уравнения, моделирующие проблемную ситуацию.
[show-answer q = ”fs-id1165134371099 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134371099 ″][/ hidden-answer]
Найдите все возможные значения, которые представляют ситуацию.
Когда дротик упадет на землю?
[show-answer q = ”fs-id1165135445722 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135445722 ″]примерно 3,2 секунды
[/ hidden-answer]
Найдите максимальную высоту дротика.
В какое время дротик достигнет максимальной высоты?
[show-answer q = ”fs-id1165135444043 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135444043 ″]1,6 секунды
[/ hidden-answer]
Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений.Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене.
Эпициклоида: в домене.
Гипоциклоида: в домене.
[show-answer q = ”fs-id1165134569130 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134569130 ″] [/ скрытый-ответ]Гипотрохоид: в домене.
Роза: на домене.
[show-answer q = ”fs-id1165134134026 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134134026 ″] [/ скрытый-ответ]8.3 — Параметрические уравнения
8.3 — Параметрические уравненияВ прошлом мы работали с прямоугольными уравнениями, то есть уравнениями, включающими только x и y, чтобы их можно было изобразить в декартовой (прямоугольной) системе координат.
У нас также был пример зависимости высоты свободно падающего тела от времени в секундах t. Эта функция была квадратичной функцией. Если объект не уронили или не бросили прямо в воздух, также будет горизонтальная составляющая его положения.Горизонтальная составляющая — это простая функция расстояния (d = rt).
Путь падающего объекта
y (t) = -16t 2 — v 0 t + y 0
х (т) = г т
v 0 = начальная вертикальная скорость
y 0 = начальная высота
r = горизонтальная скорость
t = время в секундах
Обратите внимание, что обе эти функции, вертикальная высота и горизонтальное расстояние зависит от времени.Итак, чтобы полностью Чтобы описать путь объекта, нам понадобятся два уравнения. Один для вертикального компонента и один для горизонтального составная часть. Обе эти функции являются функциями третья переменная, т.
Это дает нам параметрические уравнения. Параметр просто независимая переменная в функции.
Построение плоской кривой
Плоская кривая получается, когда упорядоченные пары (x (t), y (t)) отображаются на графике для всех значений t на некотором интервал.
Один из способов нарисовать плоскую кривую — составить таблицу значений.Параметр t имеет несколько значения, перечисленные для него, и соответствующие значения для x (t) и y (t) вычисляются. Затем заказанный пары строятся, а кривая проводится между построенными парами.
Ориентация или направление
При рисовании плоской кривой «направление увеличения t» или «ориентация» кривой обозначается маленькими стрелками, указывающими, в каком направлении кривая продвигается, когда стоимость параметр t увеличивается.
Графический калькулятор
Графический калькулятор прекрасно справляется с графическим отображением параметрических уравнений.Вы должны, однако сообщите калькулятору, что вы хотите графически отображать параметрические уравнения, а не обычные функции. Для этого переведите калькулятор в параметрический режим, нажав [РЕЖИМ] и выбирая опцию [PAR]. Не забудьте сбросить калькулятор обратно на [УДОВОЛЬСТВИЕ] для режима функций. когда вы закончите с параметрическими уравнениями. Находясь в меню режима, вы можете установите калькулятор в режим [РАДИАН] вместо режима [ГРАДУСЫ]. Они используются для тригонометрические функции, которые мы не будем использовать, но они влияют на то, как клавиши масштабирования Работа.
После настройки вашего калькулятора для параметрического режима, обратите внимание, что когда вы нажимаете клавишу Y =, вы не больше у 1 =. Теперь у вас есть пара уравнений, x и y, которые являются функциями t. Просто введите параметрические уравнения для x и y. Обратите внимание, что ключ, который вы использовали для X также обозначается T. В параметрическом режиме вместо X автоматически появляется буква T.
Параметры окна
Теперь у вас будет три дополнительных окна, которых у вас не было раньше.Tmin, Tmax и Tstep. Tmin — наименьшее значение параметра, который вы хотите использовать. Если у вас нет веская причина не делать этого (например, в домене указано t> = 0), обязательно используйте отрицательные значения для Tmin. Tmax — наибольшее значение параметра, который вы хотите использовать. Если у вас нет веской причины не делать этого, используйте положительное значение Tmax. Другими словами, убедитесь, что T может взять на себя оба положительные и отрицательные значения. Tstep — это изменение T, и оно должно быть разумным. для диапазона значений T вы указали.
TMin = -5, TMax = 5 и TStep = 0,1 обычно являются хорошими начальными значениями. Если вы обнаружите, что график не отображается, вы мая необходимость чтобы изменить эти значения.
Внимание! Zoom Standard сбросит настройки на T. Если вы сделаете стандартное масштабирование, ваш T будет находиться в диапазоне от 0 до 2 пи (в в радианах) на пи / 24 и от 0 до 360 (в градусном режиме) на 7,5. Ни один из них не содержит отрицательных значений и может не отображать весь график.
Направление увеличения t — это направление, в котором калькулятор рисует кривую. в.Обозначьте это стрелками, направленными вдоль кривой.
Удаление параметра
Другой способ нарисовать плоскую кривую — исключить параметр. Шаги к устранению параметр прост.
- Решите одно из параметрических уравнений относительно t.
- Подставить вместо t другое параметрическое уравнение.
На шаге 1 вы должны решить относительно t в более простом уравнении. Легче решить не всегда означает меньшую степень.Если у вас есть t 2 и t 3 , решить для t в t 3 (если возможно). При выполнении Таким образом, вы избегаете положительной / отрицательной ситуации, когда извлекаете квадратный корень из t.
Не всегда может быть необходимо полностью решить для t. Это ценно когда один из членов появляется в других уравнениях.
Пример 1
Исключить параметр из x = 3t 2 — 4 и y = 2t.
Функция y определенно является более простой функцией для определения t, и когда вы это сделаете, вы получите t = y / 2.
Подставьте это в уравнение x для t, и вы получите x = 3 (y / 2) 2 — 4. Упростите, чтобы получить x = 3/4 y 2 — 4.
Пример 2
Рассмотрим систему уравнений x = e t и y = e 3t .
Если бы вы решили эту проблему, используя шаги, перечисленные выше, вы бы предприняли x = e t уравнение и решите его относительно t, чтобы получить t = ln x. Затем подставьте это в уравнение y = e 3t , чтобы получить y = e 3ln x .С использованием свойства логарифмов, вы бы переместили 3 в степень на x а затем функции e и ln инвертируют, оставляя вас с y = x 3 .
Теперь подумайте об этом. y = e 3t = (e t ) 3 . Поскольку x = e t , замените e t на x. у = (х) 3 или просто y = x 3 . Не было необходимости спускаться до t.
Еще одно замечание по поводу этой проблемы. Поскольку x и y являются экспоненциальными функциями, диапазон на каждом из них — положительные реалы.Однако это теряется, когда вы упрощаете до y = x 3 . Обязательно наложите ограничение на домен x, чтобы он был таким же, как оригинал. Это ограничение будет x> 0.
Справка в Интернете — Справка по Origin
PD-Dialog-3DParaFunc-Tab
Матрица значений Z создается одновременно при создании 3D-графика параметрической функции.
Сетка
Когда вы строите трехмерный функциональный график, Origin сначала создает матрицу, на основе которой строится график.Укажите размеры матрицы в поле редактирования «Столбцы и строки». Это определит плотность трехмерной поверхностной сетки.
Масштаб
Параметр
Укажите параметр для графика.
От и до
Укажите начало и конец диапазонов u и v.
X (u, v), Y (u, v) и Z (u, v)
Введите здесь формулу параметра X, Y и Z.
Общие математические и статистические функции распределения доступны при нажатии кнопки треугольника справа от текстовых полей X (u, v), Y (u, v) и Z (u, v).Для получения подробной информации об этих функциях, пожалуйста, прочтите встроенные функции LabTalk.
Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Вы также можете вызвать любую из встроенных функций Origin, даже если они недоступны из раскрывающегося меню треугольной кнопки или из любых функций, которые вы определили.
Если вы нажмете кнопку «Показать в отдельном окне» под кнопкой треугольника, откроется диалоговое окно с более широким полем ввода и панелью «Предварительный просмотр».На панели предварительного просмотра отображается матрица, рассчитанная по заданной вами формуле. Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода.
Определение
Определите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом.
Показать скрипт LabTalk
Установите этот флажок, чтобы определять переменные с помощью сценариев LabTalk.Если вы уже определили некоторые переменные в таблице Definition , установите этот флажок, чтобы отобразить эквиваленты этих определений в сценариях LabTalk.
Помимо встроенных или определяемых пользователем функций, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Введенные здесь сценарии будут выполняться до определения формулы.
Существует быстрый способ загрузить сценарий условного управления или цикла, когда вы выполняете сценарий в поле Before Formula Script .Щелкните правой кнопкой мыши на поле Before Formula Script , чтобы выбрать Conditional / Loop в нижней части контекстного меню, а затем выберите нужную условную структуру или цикл во всплывающем меню. Синтаксис будет добавлен к курсору с простыми комментариями.
График функции выхода
Раскрывающийся список опций в нижнем левом углу используется для указания способа вывода кривой функционального графика: Создать новый график , Добавить в активный график или Добавить в активный график и изменить масштаб .
Примечание: Этот флажок доступен только при активном окне 3D-графика. Если активное окно не является окном 3D-графика, оно создаст график 3D-функции в новом окне графика. Построение параметрических уравнений на TI-83 + и TI-84 +
Мы в Calcblog надеемся, что у вас были отличные зимние каникулы! До сих пор мы публиковали учебные пособия по построению графиков в прямоугольных / декартовых и полярных координатах, но есть и другие способы задания функций.Один из них является функцией параметра или так называемого «параметрического» уравнения.
Это может быть полезно, например, для записи координат X и Y объекта как функции параметра T для времени. У нас могут быть следующие уравнения:
Заглянув в учебник физики, можно сказать, что эти уравнения описывают координаты частицы со скоростью по оси X 5 футов в секунду, начинающейся с высоты 10 футов в воздухе и подверженной земному притяжению. Построим это на нашем калькуляторе.
Сначала нажмите MODE, чтобы перейти в меню режима, и с помощью клавиш со стрелками выберите PAR. Нажмите Ввод.
Во-вторых, нажмите Y =, чтобы перейти к экрану ввода уравнения. Введите соответствующие уравнения X и Y.
В-третьих, нажмите ОКНО, чтобы перейти к экрану окна. Это одна из самых важных частей процесса. Помимо установки нормальных пределов отображения, вы также должны указать минимальное значение T, максимальное значение T и шаг для построения точек.Если вы укажете слишком большое значение Tstep, ваш график будет выглядеть неровным или даже вводящим в заблуждение. Если вы укажете слишком маленький размер, для построения графика вашего уравнения может потребоваться больше времени.
- Создайте таблицу с тремя столбцами: [latex] t, x \ left (t \ right), \ text {и} y \ left (t \ right) [/ latex].{2} +1 [/ латекс] [латекс] y \ left (t \ right) = 2 + t [/ латекс] [латекс] -5 [/ латекс] [латекс] 26 [/ латекс] [латекс] -3 [/ латекс] [латекс] -4 [/ латекс] [латекс] 17 [/ латекс] [латекс] -2 [/ латекс] [латекс] -3 [/ латекс] [латекс] 10 [/ латекс] [латекс] -1 [/ латекс] [латекс] -2 [/ латекс] [латекс] 5 [/ латекс] [латекс] 0 [/ латекс] [латекс] -1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 1 [/ латекс] [латекс] 0 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 1 [/ латекс] [латекс] 2 [/ латекс] [латекс] 3 [/ латекс] [латекс] 2 [/ латекс] [латекс] 5 [/ латекс] [латекс] 4 [/ латекс] [латекс] 3 [/ латекс] [латекс] 10 [/ латекс] [латекс] 5 [/ латекс] [латекс] 4 [/ латекс] [латекс] 17 [/ латекс] [латекс] 6 [/ латекс] [латекс] 5 [/ латекс] [латекс] 26 [/ латекс] [латекс] 7 [/ латекс]
Ваш комментарий будет первым