Уравнение окружности по заданному центру и радиусу в различных формах
УчебаМатематикаГеометрия
Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Радиус
Стандартное уравнение окружности
Общее уравнение окружности
Параметрическое уравнение окружности
Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе.
Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнение окружности, проходящей через три заданные точки
- • Нахождение центра и радиуса окружности по общему уравнению окружности
- • Треугольник. Описанная окружность
- • Треугольник. Вписанная окружность
- • Уравнение прямой по двум точкам
- • Раздел: Геометрия ( 96 калькуляторов )
#алгебра #Уравнение окружности Алгебра Геометрия Общее окружность Параметрическое Стандартное уравнение
PLANETCALC, Уравнение окружности по заданному центру и радиусу в различных формах
Timur2021-10-05 12:01:17
| 1 | Упростить | квадратный корень из s квадратный корень из s^7 | |
| 2 | Упростить | кубический корень из 8x^7y^9z^3 | |
| 3 | Упростить | arccos(( квадратный корень из 3)/2) | |
| 4 | Risolvere per ? | sin(x)=1/2 | |
| 5 | Упростить | квадратный корень из s квадратный корень из s^3 | |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени из x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) |
— eMathHelp
Этот калькулятор найдет либо уравнение окружности по заданным параметрам, либо центр, радиус, диаметр, окружность (периметр), площадь, эксцентриситет, линейный эксцентриситет, точки пересечения по осям x, точки пересечения с y, домен и диапазон введенных значений. круг. Кроме того, он будет отображать круг. Шаги доступны.
Связанные калькуляторы: Калькулятор параболы, Калькулятор эллипса, Калькулятор гиперболы, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
{2} = 9{2} = 9 \pi$$$.
Эксцентриситет и линейный эксцентриситет окружности равны $$$0$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-3, 0\right)$$$, $$$\left(3, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов).
y-отрезков: $$$\left(0, -3\right)$$$, $$$\left(0, 3\right)$$$ 9{2} — 9 = 0$$$А.
График: см. графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Радиус: $$$3$$$A.
Диаметр: $$$6$$$A.
Окружность: $$$6 \pi\приблизительно 18,849555921538759$$$A.
Площадь: $$$9 \pi\ок. 28,274333882308139$$$A.
Эксцентриситет: $$$0$$$A.
Линейный эксцентриситет: $$$0$$$A.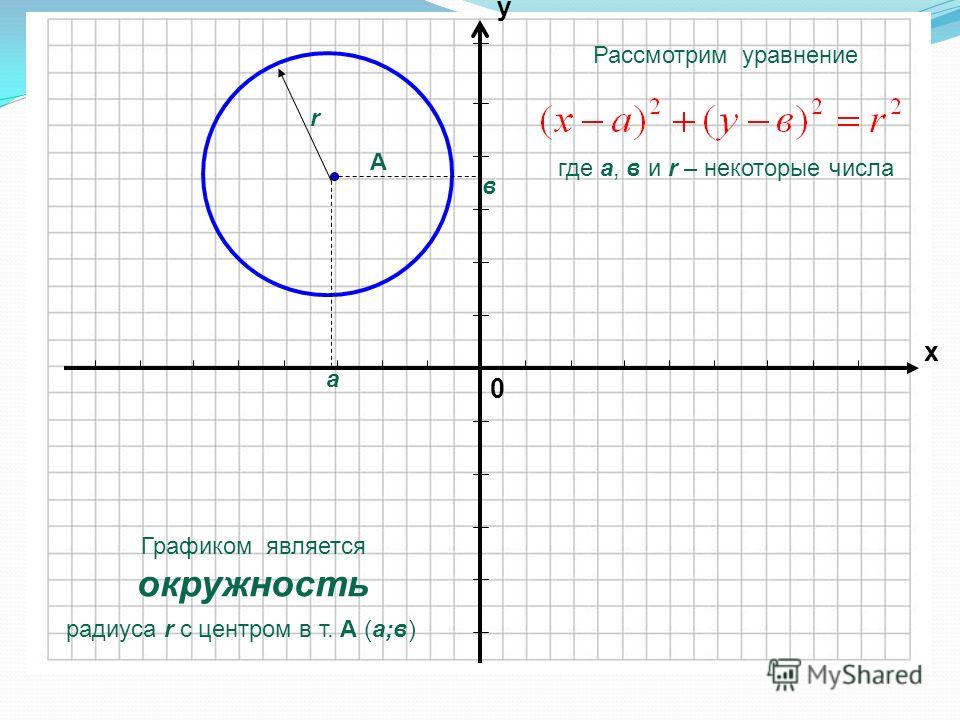
точек пересечения: $$$\влево(-3, 0\вправо)$$$, $$$\влево(3, 0\вправо)$$$A.
y-отрезки: $$$\left(0, -3\right)$$$, $$$\left(0, 3\right)$$$A.
Домен: $$$\left[-3, 3\right]$$$A.
Диапазон: $$$\влево[-3, 3\вправо]$$$A.
Уравнение окружности Калькулятор
Создано Bogna Szyk и Hanna Pamula, PhD
Отредактировано Jack Bowater
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое стандартное уравнение окружности?
- Параметрическое уравнение окружности
- Стандартное уравнение к параметрическому уравнению окружности
- Как найти уравнение окружности?
- Другая форма уравнения окружности
- Как использовать это уравнение калькулятора окружности?
Неважно, насколько хорошо вы разбираетесь в геометрии круга, от уравнения круга у вас может закружиться голова. Если это так, не волнуйтесь! Это стандартное уравнение калькулятора окружности поможет вам определить радиус окружности и координаты центра в мгновение ока.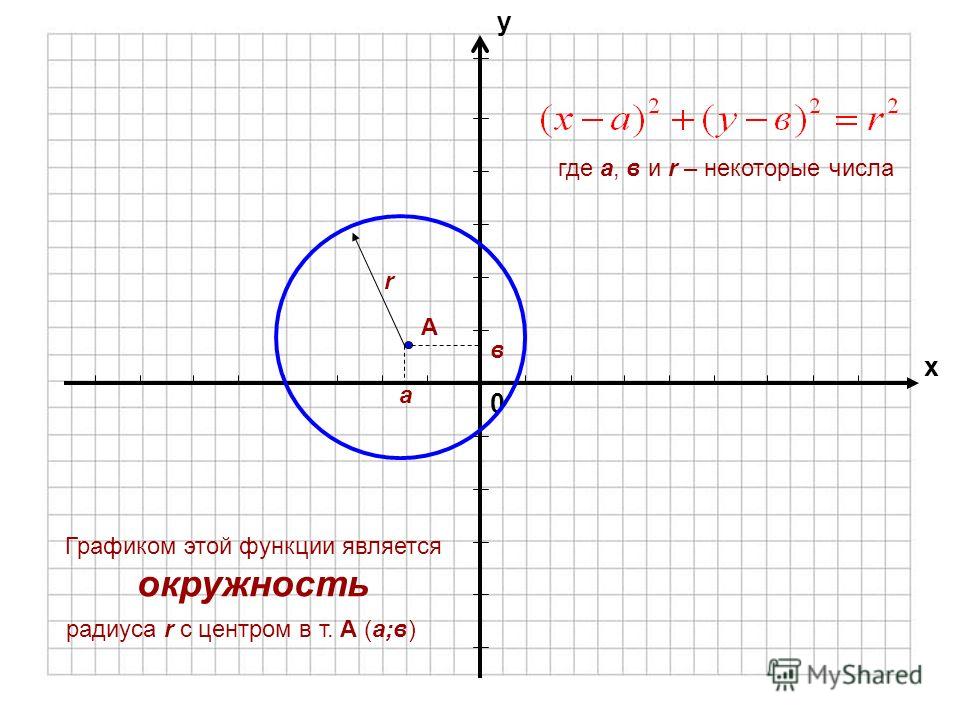
Если вам интересно, как найти уравнение окружности, прокрутите вниз, и вы найдете объяснение формулы.
Если геометрическая фигура, которую вы пытаетесь проанализировать, выглядит немного сплющенной, вероятно, это эллипс. В таком случае отправляйтесь прямо к нашему калькулятору эллипса!
🔎 Если вы новичок в кругах, вам могут быть полезны другие, более простые инструменты, такие как окружность и площадь круга , окружность до диаметра или квадратных метров круга и круг калькуляторы длины.
Что такое стандартное уравнение окружности?
Стандартное уравнение окружности — это способ описать все точки, лежащие на окружности, с помощью всего одной формулы: 92r2 — это радиус круга, возведенный в степень двойки, поэтому, чтобы найти радиус, возьмите квадратный корень из этого значения.
Наш калькулятор уравнения круга находит не только эти значения, но также диаметр, длину окружности и площадь круга — все для экономии вашего времени!
Параметрическое уравнение окружности
Уравнение окружности можно определить по-разному; не только в стандартной форме, показанной выше.
х=rcos(α)y=rsin(α)\маленький \начать{выравнивать*} х &= г \cos(\alpha)\\[.5em] у &= г \ грех (\ альфа) \end{align*}xy=rcos(α)=rsin(α)
где:
(x,y)(x,y)(x,y) — Координаты любой точки на окружности, как и раньше;
rrr – Радиус окружности; и
α\alphaα – Угол, образуемый точкой в центре окружности.
Если сместить центр круга на (A, B) координат, вы просто добавите их к координатам x и y, чтобы получить общее параметрическое уравнение окружности:
x=A+rcos(α)y=B+rsin(α)\small \начать{выравнивать*} x &= A + r \cos(\alpha)\\[.5em] y &= B + r \sin(\alpha) \end{align*}xy=A+rcos(α)=B+rsin(α)
Как и выше, вы должны быть осторожны со знаками центральной точки.
Стандартное уравнение в параметрическое уравнение окружности
Чтобы продемонстрировать, что эти две формы формулы окружности эквивалентны, давайте сделаем преобразование между ними.
92 = 1 x2+y2=1
Вот и мы! Это стандартное уравнение окружности.
Как найти уравнение окружности?
Итак, вы узнали о различных уравнениях окружности. Но откуда они? Давай выясним!
- Выберите центр круга, O=(A,B)O = (A, B)O=(A,B). Не выбирайте его в качестве начала системы координат.
- Нарисуйте окружность с выбранным радиусом rrr.
- Выберите любую точку на окружности. Предположим, что координаты этой точки равны P=(x,y)P = (x,y)P=(x,y). 92 (x−A)2+(y−B)2=r2
- Использовать тригонометрию :
Выразить стороны треугольника POC с помощью функций синуса и косинуса:
cos(α)=OC/r ⟹ OC=rcos(α)sin(α)=CP/r ⟹ CP=rsin(α)\small\quad\ \ \начать{выравнивать*} \cos(\alpha) &= OC / r \подразумевает \\[.5em]OC &= r\cos(\alpha)\\[1em] \sin(\alpha) &= CP / r \подразумевает \\[.5em]CP &= r\sin(\alpha) \end{align*} cos(α)OCsin(α)CP=OC/r⟹=rcos(α)=CP/r⟹=rsin(α)
Координаты точки P могут быть выражены как:
x=A+OC & y=B+CP⇓x=A+rcos(α)y=B+rsin(α)\small\quad\ \ \начать{выравнивать*} x = A + OC\ \ &\&\ \ y = B + CP\\[.
Два последних уравнения представляют собой параметрические уравнения окружности.
Теперь, когда вы знаете, как найти уравнение окружности, попробуйте этот калькулятор!
Другая форма уравнения окружности 92 = 5 (x+2)2+(y−3)2=5
Готово — это стандартная форма круга с центром в точке (−2,3)(-2, 3)( −2,3) и радиусом, равным 5\sqrt55.
Естественно, вам не нужно проходить весь этот процесс самостоятельно. Вместо этого используйте это уравнение калькулятора окружности!
Как пользоваться калькулятором уравнения окружности?
Если вы все еще не знаете, как использовать наш инструмент, взгляните на этот простой пример ниже.
Предположим, вы хотите использовать стандартное уравнение окружности . Итак, это первая часть калькулятора.
Введите данные .
- Использовать тригонометрию :
Ваш комментарий будет первым