Взаимно обратные функции — презентация онлайн
Если функция у = f ( х ) принимает каждое своё значениеу только при одном значении х, то эту функцию называют
обратимой.
Пусть у = f(x) – обратимая функция. Тогда каждому у из множества значений
функции соответствует одно определённое число х из области её
определения, такое, что f(x) = y. Это соответствие определяет функцию х от у,
которую обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g(x) (у = f -1(x)) называют обратной к функции у = f(x).
1
у
х 2
Пример:
Найти функцию, обратную данной
Решение:
1
у
х 2
1
х 2
у
1
х 2
у
Ответ:
1
f ( x) 2
x
1
1
у 2
х
у = f -1(x).
у
у
у
у 2
1
х 2
1
х
2
0
2
х
0
1. D(у)=(-∞;2)∪(2;+∞)
1. D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
х
1.
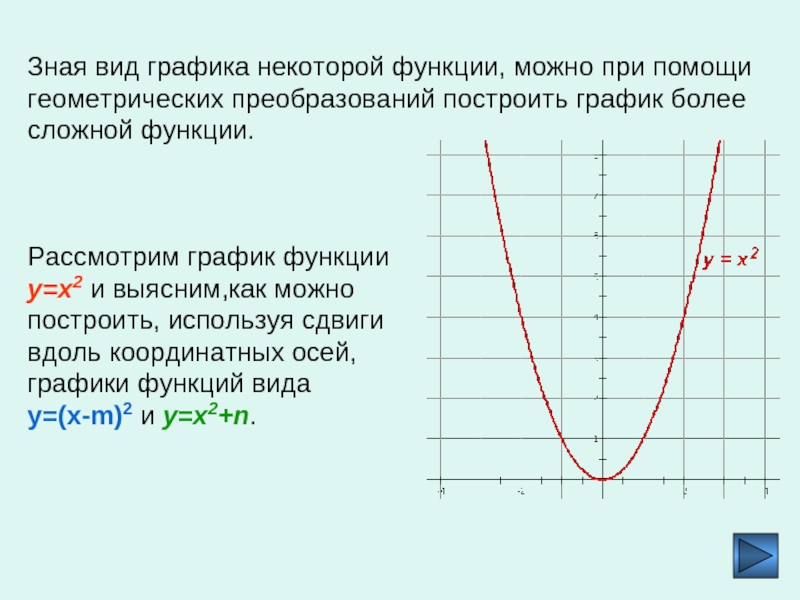
совпадает с множеством значений исходной f, а
множество значений обратной функции f -1
совпадает с областью определения исходной
функции f:
D(f -1) = E(f), E(f -1) = D(f).
2. Монотонная функция является обратимой:
если функция f возрастает, то обратная к ней
функция f -1 также возрастает;
если функция f убывает, то обратная к ней
функция f -1 также убывает.
3. Если функция имеет обратную, то график
обратной функции симметричен графику данной
функции относительно прямой у = х.
у
у=f(x)
y=x2,х
3
-2
0
у
у=g(x)
3
0
х
х
-2
у х
1. D(y)=(-∞;0]
1. D(y)=[0;+∞)
1. D(f)=R
1. D(g)=R
2. E(y)=[0;+∞)
2. E(y)=(-∞;0]
2. E(f)=R
2. E(g)=R
3. убывающая
3. убывающая
3. возрастающая 3. возрастающая
Пример:
Построить график функции, обратной данной.
у х3
Дано: у = х3
у
у 3 х
Построить функцию,
обратную к данной.
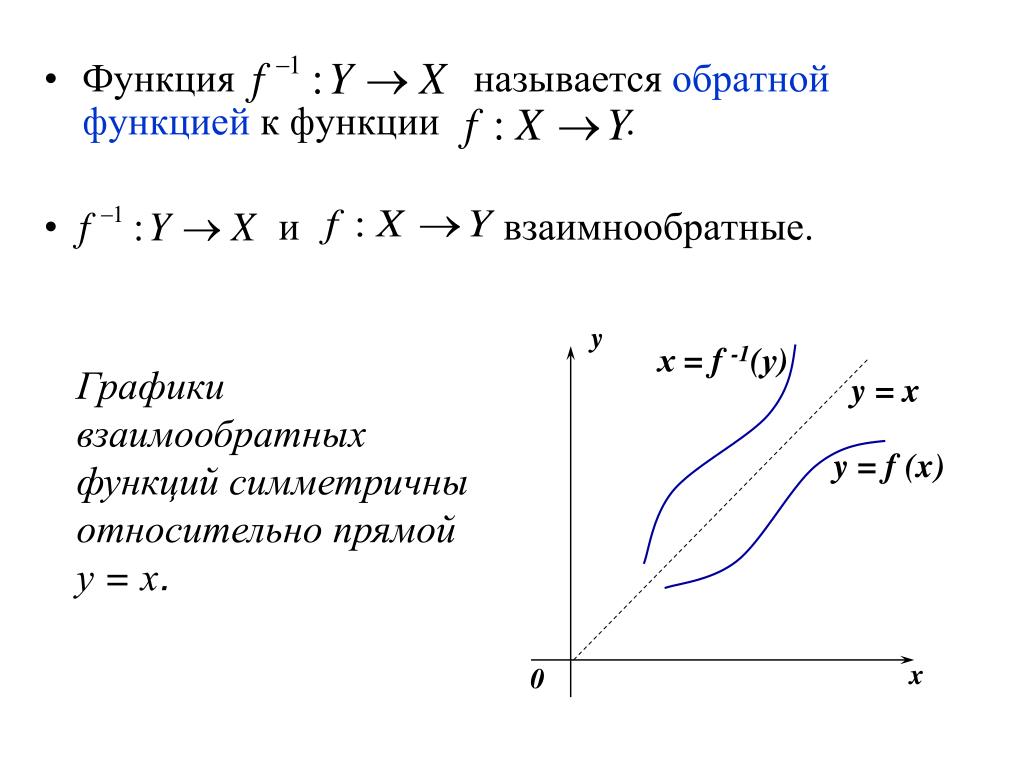
Решение:
х3 у
х 3 у у 3 х
0
х
Обратная функция | Алгебра
Что такое обратная функция? Как найти функцию, обратную данной?
Определение.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.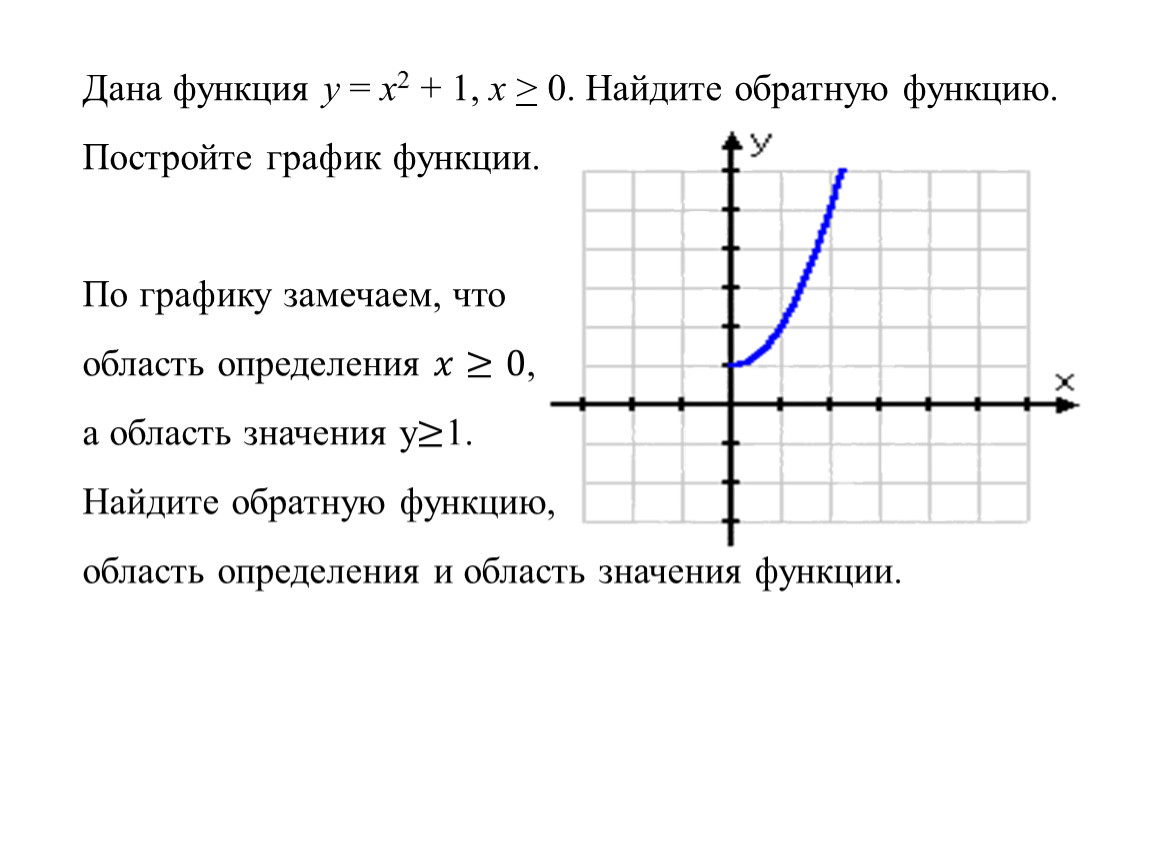
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.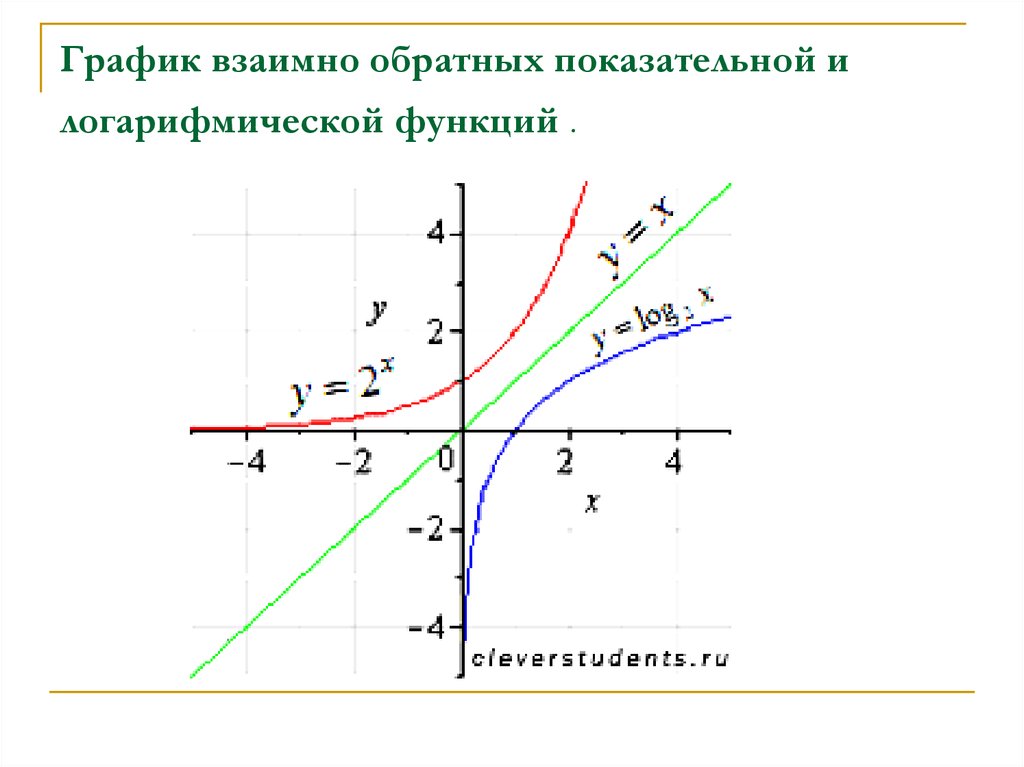
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
1) x=y².
2)
Так как y≥0, то
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
Взаимно обратные функции: алгоритм вывода формулы, примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
§34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X \xrightarrow{f} Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.
С другой стороны, мы можем рассмотреть обратное отображение $Y \xrightarrow{g} X$, заданное той же таблицей. {-1}$ называют обратной функцией к f.
{-1}$ называют обратной функцией к f.
Например: аналитическое выражение для функции $X \xrightarrow{f} Y$, заданной таблицей $y = f(x) = \frac{x}{2}$. Обратное соответствие $Y \xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X \xrightarrow{f} Y$ и $Y \xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = \frac{x}{2}$
Шаг 1. 2+1$
2+1$
Шаг 2. Находим y из полученной формулы: $y = \sqrt{\frac{x-1}{2}}$ — искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = \frac{x+4}{5}$ — искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = \frac{-x+2}{3}$ — искомая обратная функция
в) y = 4x+1, где $-1 \le x \le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = \frac{x-1}{4}$
Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac{x-1}{4} \le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$
Итак, искомая обратная функция: $y = \frac{x-1}{4}$, где -3 $\le x \le 21$
г) $y=- \frac{1}{2} x+7$, где $2 \le x \le 9$
Меняем аргумент и значение: $x=-\frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция
Пример 2. 2+3$
2+3$
Область определения: $x \ge 1$
Область значений: $y \ge 3$
Взаимно обратные функции, основные определения, свойства, графики
Понятие обратной функции
Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Для чего вообще нам нужно понятие обратных функций?
Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений.
Нахождение взаимно обратных функций
Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Пример 1Условие: какая функция будет обратной для y=3x+2?
Решение
Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив x через y.
Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:
y=13x-23
Ответ: функция y=13x-23 будет обратной для y=3x+2.
Обе взаимно обратные функции можно отобразить на графике следующим образом:
Мы видим симметричность обоих графиков относительно y=x. Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Пример 2Условие: определите, какая функция будет обратной для y=2x.
Решение
Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
Ответ: y=log2x.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
В этом пункте мы перечислим основные свойства функций y=f(x) и x=g(y), являющихся взаимно обратными.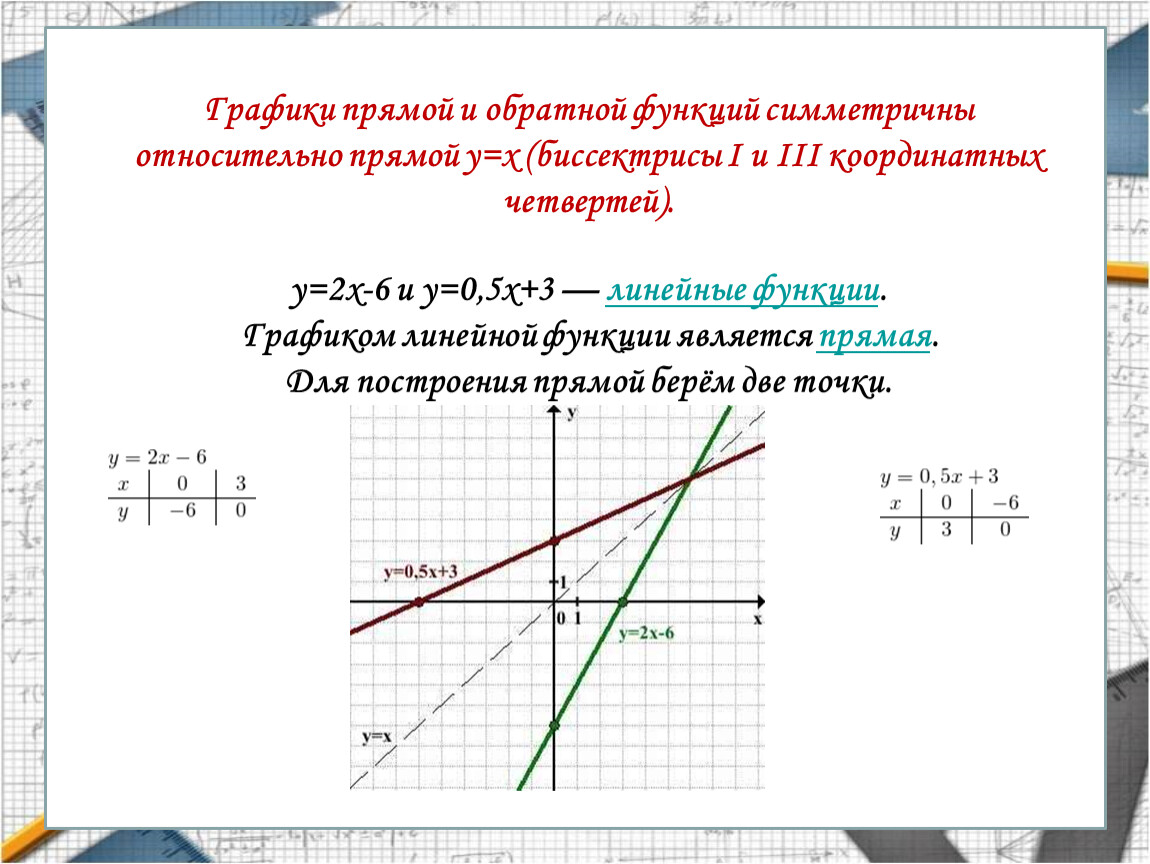
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 1- Первое свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
- Второе свойство вытекает из первого: область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
- Графики функций, являющихся обратными, будут симметричными относительно y=x.
- Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).
Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифм не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте, что это верно только при положительном y.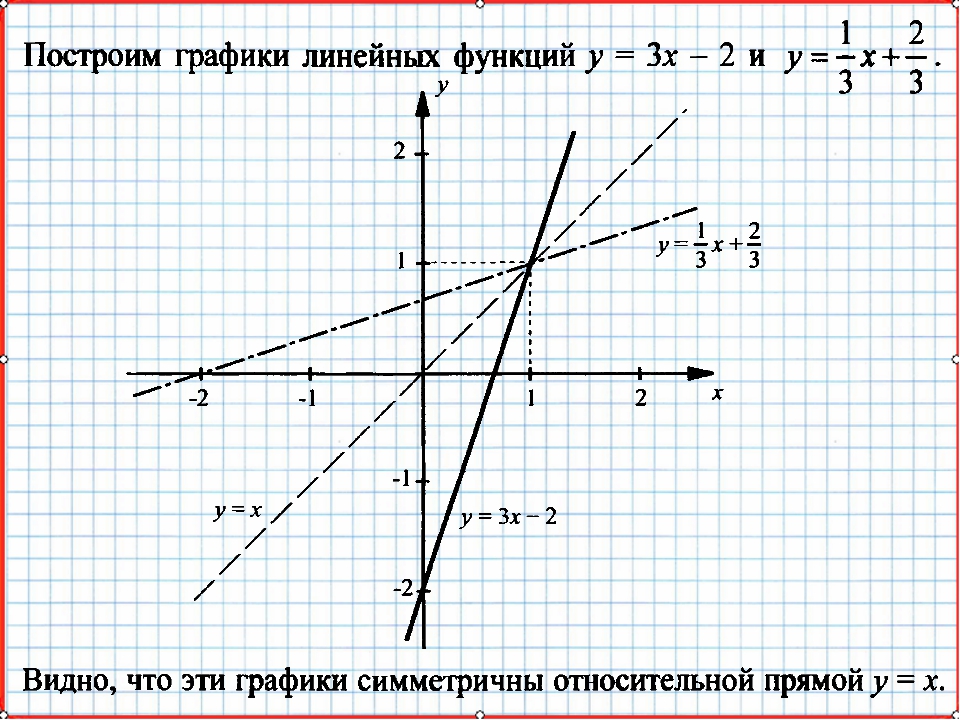
А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.
Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись
arcsinsin7π3=arcsinsin2π+π3==по формулепривидения=arcsinsinπ3=π3
А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!
Графики взаимно обратных функций
- Основные взаимно обратные функции: степенные
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Заменим буквы и получим соответственно y=xa и x=y1a.
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
- Основные взаимно обратные функции: показательные и логарифмические
Возьмем a,которое будет положительным числом, не равным 1.
Графики для функций с a>1 и a<1 будут выглядеть так:
- Основные взаимно обратные функции: тригонометрические и обратные тригонометрические
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
График главной ветви косинуса и арккосинуса выглядит так:
График главной ветви арктангенса и тангенса:
График главной ветви арккотангенса и котангенса будет таким:
Если же вам требуется построить обратные ветви, отличные от главных, то обратную тригонометрическую функцию при этом мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Понятие функции. Способы задания функции
Понятие функции является одним из важнейших понятий математики и её приложений. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Пусть X и Y — какие-то множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с помощью функции y = f(x)
множество X отображается в множество
Y. Поэтому функцию называют также отображением.
Кстати, будет полезным
открыть в новом окне материал Свойства и графики элементарных функций.
Поэтому функцию называют также отображением.
Кстати, будет полезным
открыть в новом окне материал Свойства и графики элементарных функций.
Например, авиапассажиры сидят в креслах салона пассажирского самолёта. Пусть X — множество пассажиров, а Y — множество кресел салона. Тогда возникает соответствие f : каждому пассажиру x∈X сопоставляется то кресло y = f(x), в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью
определения которой является множество X пассажиров,
а областью значений — множество f(X)
занимаемых ими кресел. Если заполнены не все кресла Y,
то множество значений функции будет подмножеством Y,
не совпадающим со всем множеством Y.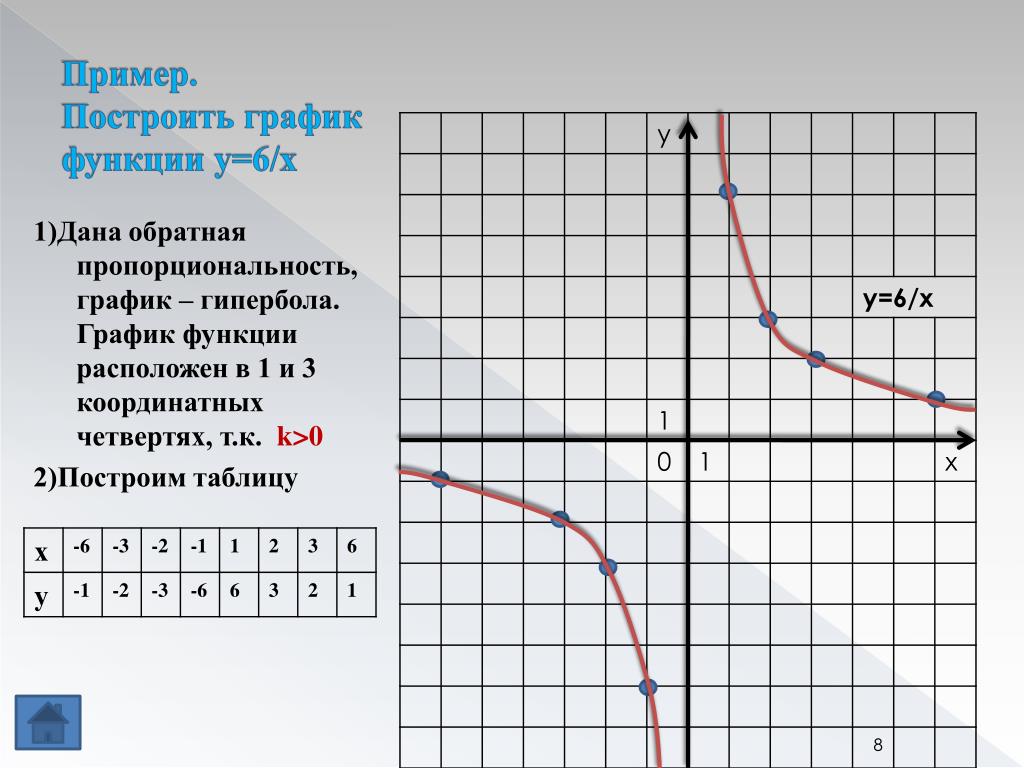
Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.
В математическом анализе часто X обозначают как D (область определения функции), а Y как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел). На сайте есть урок Как найти область определения функции.
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от
икса или f(x). И это неслучайно. Функции составляют бОльшую
часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также
широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления
в функции.
И это неслучайно. Функции составляют бОльшую
часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также
широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления
в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и L = {l, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.
Решение. Итак, множество A содержит
5 элементов, а множество L — 3 элемента. Если мы
поставим стрелки, ведущие от каждого элемента множества L к
элементам множества A, то некоторым элементам L
будут соответствовать более одного элемента A. Такое
соответствие не является функцией по определению. Но если мы проведём стрелки от элементов
A к элементам L,
то некоторым элементам A будут соответствовать одни и те
же элементы L, но при этом каждому элементу A
будет соответствовать не более одного элемента L. Такое
соответствие не противоречит определение функции, следовательно, ответ на вопрос задания —
положительный.
Такое
соответствие не является функцией по определению. Но если мы проведём стрелки от элементов
A к элементам L,
то некоторым элементам A будут соответствовать одни и те
же элементы L, но при этом каждому элементу A
будет соответствовать не более одного элемента L. Такое
соответствие не противоречит определение функции, следовательно, ответ на вопрос задания —
положительный.
Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией:
Пример 2. Даны множества A = {70, 140, 30, 48} и В = {35, 15, 12}. Установить между элементами множеств соответствие, заданное правилом «элемент A можно нацело поделить на элемент В«. Будет ли такое соответствие функцией?
Решение. Между элементами множеств A и В устанавливается следующее соответствие:
Это соответствие является функцией, так как каждому элементу из множества
A соответствует не более одного элемента из множества
В.
Аналитическое задание функции.
Функция задана аналитически, если функциональная зависимость выражена в виде формулы, которая указывает совокупность тех математических операций, которые должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение функции.
При аналитическом задании функции указывают область определения, либо не указывают. В первом случае функция задаётся в виде y = f(x), x∈D, где D — область определения функции, во втором случае — в виде y = f(x). Во втором случае областью определения функции считается наибольшее множество, на котором имеет смысл формула, которой задана функция, то есть наибольшее множество аргумента, которое приводит к действительным значениям функции.
Важно, что функцию не следует отождествлять с формулой, с помощью
которой она задана.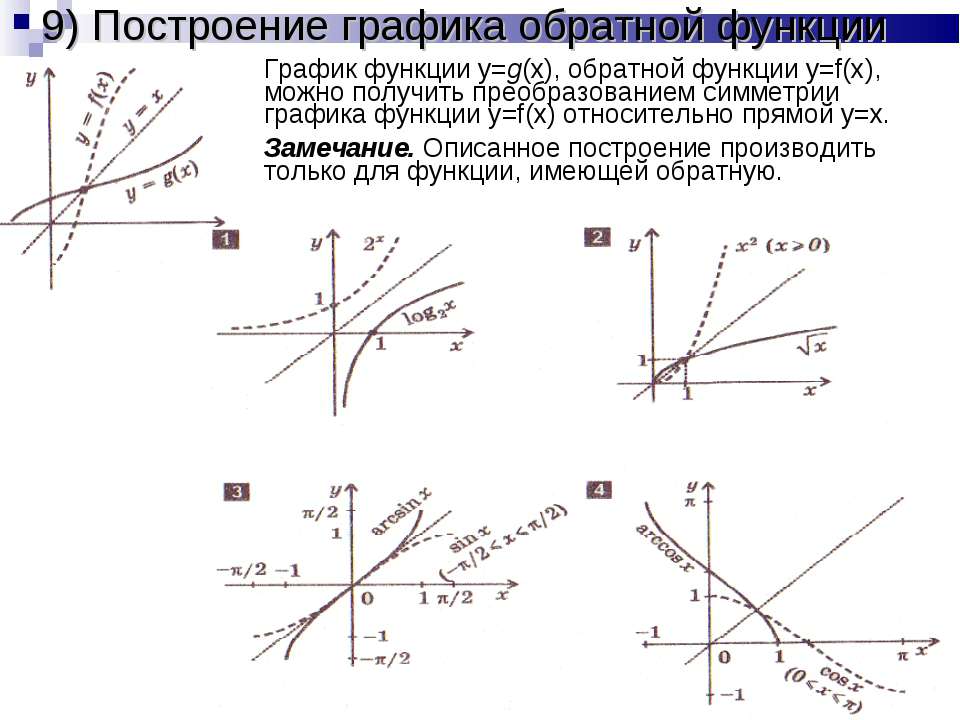 Например, функции y = x², x∈]-∞,+∞[ и
y = x², x∈[2, 4],
выраженные одной и той же формулой y = x²,
так как они имеют разные области определения.
Например, функции y = x², x∈]-∞,+∞[ и
y = x², x∈[2, 4],
выраженные одной и той же формулой y = x²,
так как они имеют разные области определения.
Наоборот, одна и та же функция может быть задана разными формулами на различных участках области определения. Пусть, например,
Здесь две формулы задают одну функцию, определённую на всей числовой прямой. При x≤0 значения этой функции определяются по первой формуле, а при x>0 — по второй.
Аналитический способ задания функции удобен тем, что значения функции можно вычислить при любых значениях аргумента. Недостатком этого способа задания функции является его малая наглядность.
Графический способ задания функции
График функции даёт наглядное представление о её свойствах.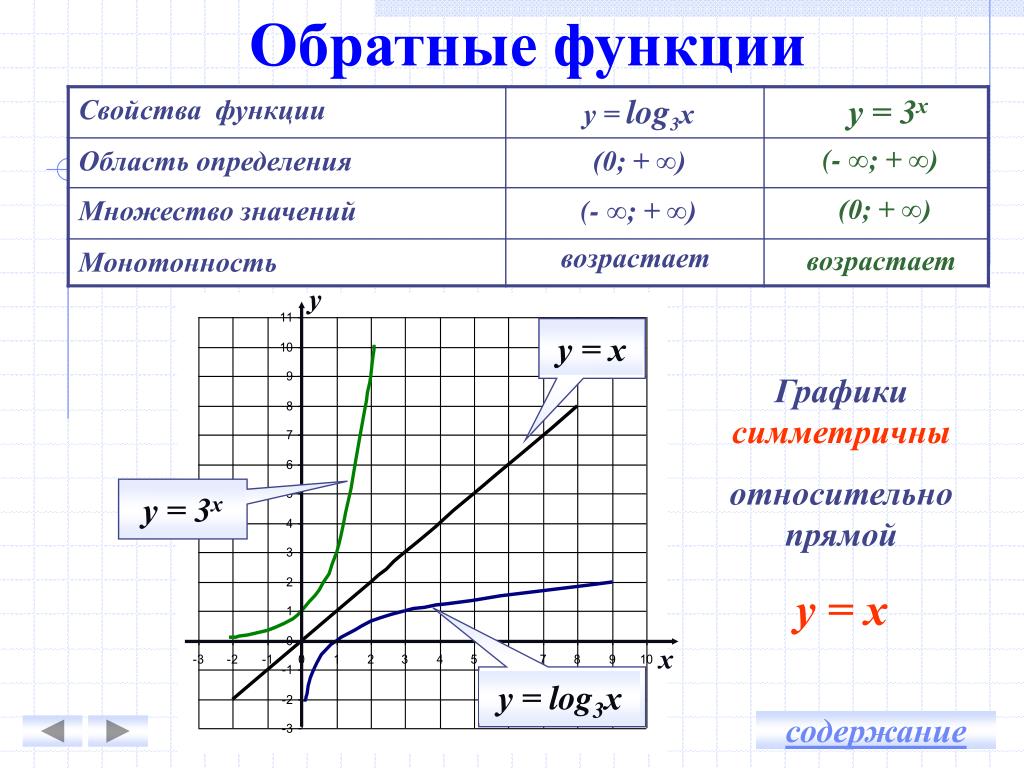 Например,
график линейной функции y = kx + b
— прямая линия, график квадратичной функции y = ax² + bx + c —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Например,
график линейной функции y = kx + b
— прямая линия, график квадратичной функции y = ax² + bx + c —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Графический способ задания функции помимо геометрического изображения функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически. Задать функцию графически — это значит построить её график. Это часто делают самопишущие приборы. Например, в медицине электрокардиограф строит электрокардиограмму — кривую изменения электрических импульсов сердечной мышцы.
Графиком числовой функции y = f(x)
называется множество точек плоскости с координатами (x; f(x)),
абсциссы которых — числа из области определения функции, а ординаты — соответствующие значения
функции.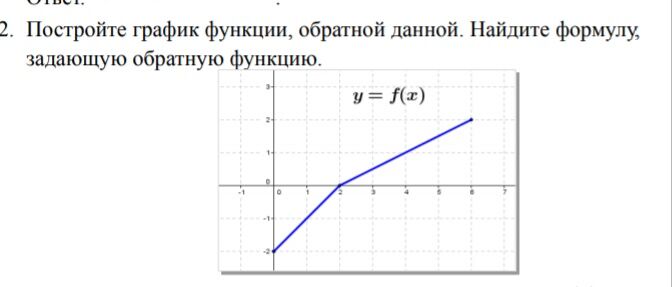
Не всякое множество точек координатной плоскости, даже не всякая линия может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая, параллельная оси 0y, пересекает её не более чем в одной точке.
Пример 4. На рисунке ниже — график параболы, заданной уравнением y² = 2x. Является ли этот график графиком функции?
Решение. График параболы, заданной уравнением y² = 2x, не является графиком функции, поскольку прямая, параллельная оси 0y, пересекает его в двух точках при всех значениях x, кроме x = 0. Заданное уравнение эквивалентно двум уравнениям , каждое из которых определяет функцию. Графиком функции служит верхняя половина параболы, а графиком функции — её нижняя половина.
Табличный способ задания функции
При табличном способе задания функции рядом с числовым значением аргумента
записывается соответствующее значение функции.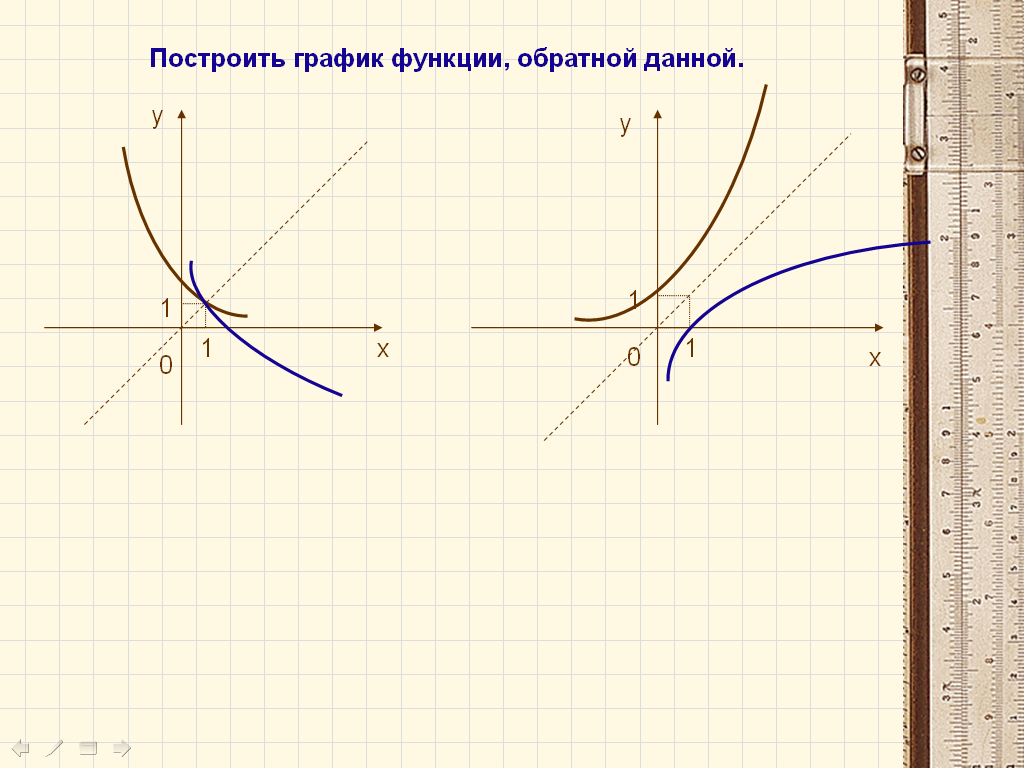 Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены.
Если функция y зависит от переменной u, то есть y = f(u), а u, в свою очередь, является какой-либо функцией от независимой переменной x, то есть u = g(x), то переменная y называется функцией от функции или сложной функцией от x.
Это записывается в виде
y = f(u), u = g(x)
или
y = f[g(x)].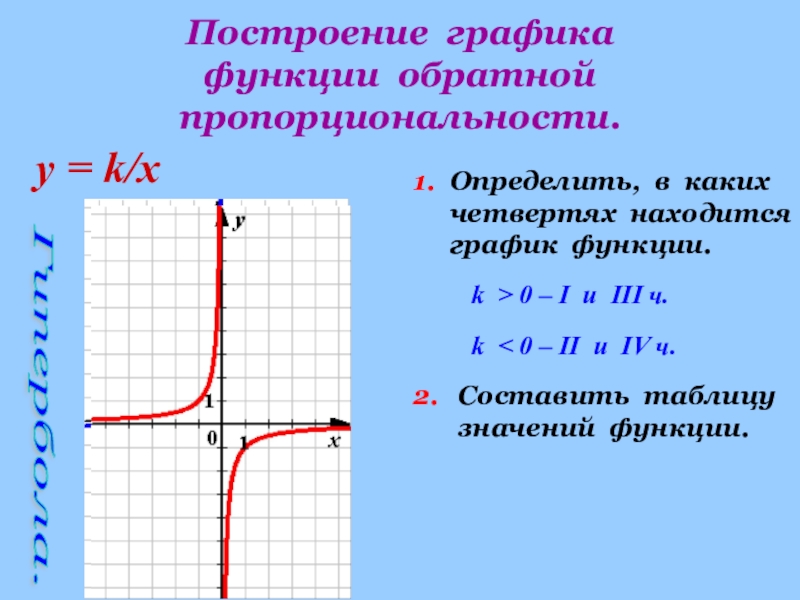
Таким образом, сложной называется функция, аргументом которой является не независимая переменная, а некоторая функция от неё.
Область определения сложной функции — это множество тех значений x из X, для которых соответствующие значения u принадлежат области определения U функции y = f(u). Ни для каких других значений x сложная функция не имеет смысла.
Из определения следует, что сложная функция y = f[g(x)]
может быть представлена в виде цепочки простых функций y = f(u), u = g(x).
Переменную u принято называть промежуточным аргументом
в отличие от независимой переменной x. Цепочка,
составляющая сложную функцию, может состоять не только из двух, но и из большего числа
звеньев.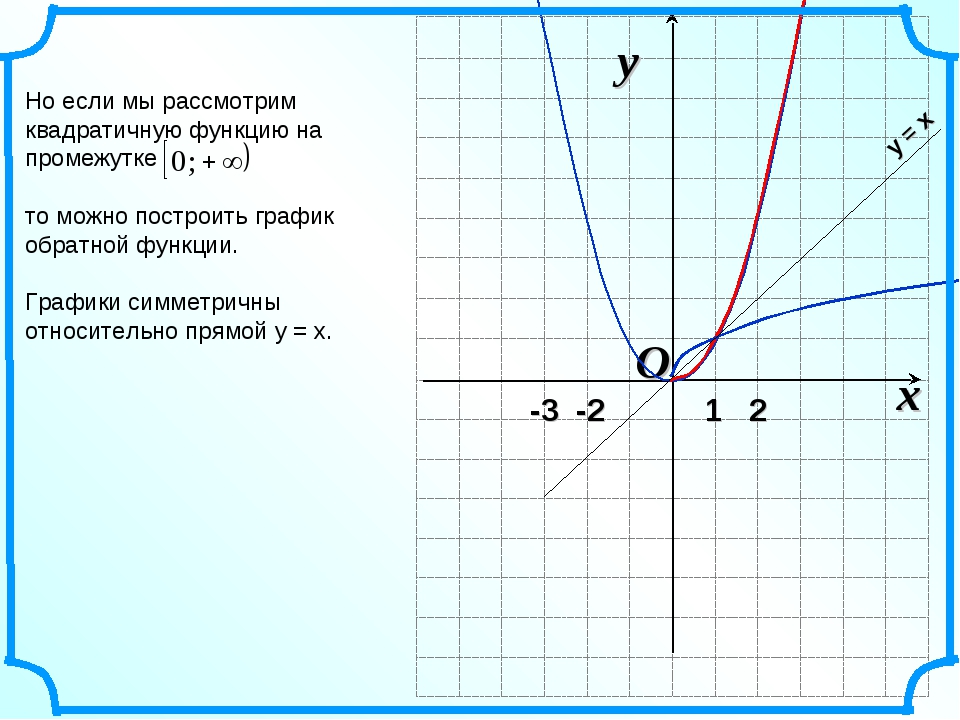
Например, функция состоит из трёх звеньев: , , .
Пример 5. Представить сложную функцию в виде звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:
Пример 6. Представить сложную функцию в виде звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:
Если функция y задана уравнением вида f(x, y) =0, не разрешённым относительно y, то она называется неявной функцией аргумента x (Что такое разрешить уравнение относительно одной из переменных — в примере 8).
Пусть задана некоторая функция y = f(x),
т.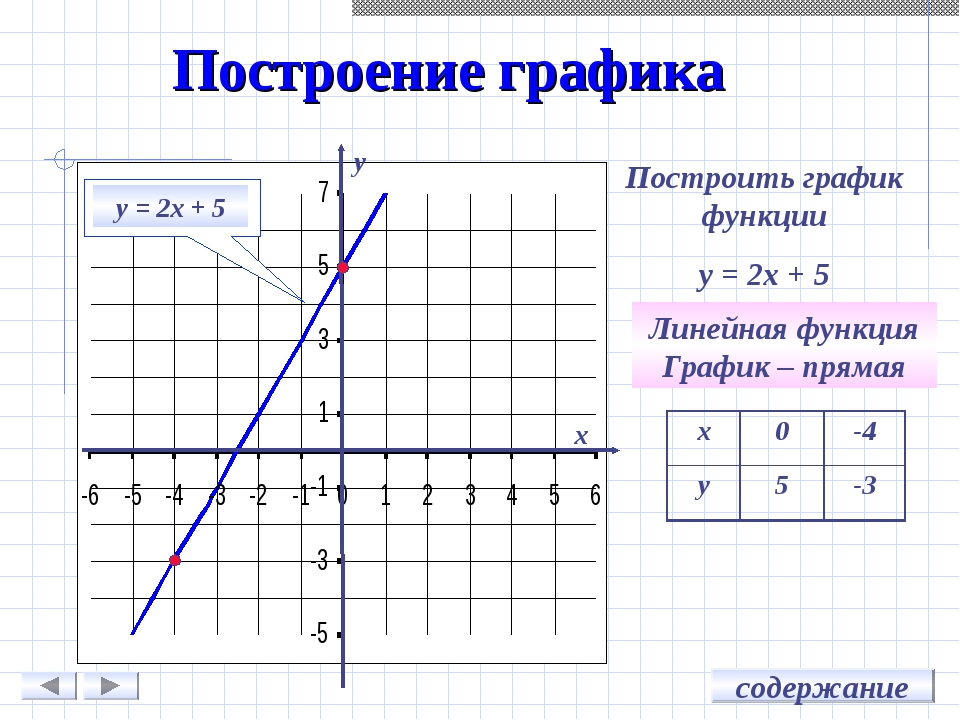 е. некоторое соответствие между множествами D(f)
(область определения) и E(f)
(множество значений). Если обратное соответствие есть функция,
т. е. каждому значению y∈E(f)
соответствует одно единственное значение x∈E(f),
то её называют обратной функцией по отношению к функции f(x).
е. некоторое соответствие между множествами D(f)
(область определения) и E(f)
(множество значений). Если обратное соответствие есть функция,
т. е. каждому значению y∈E(f)
соответствует одно единственное значение x∈E(f),
то её называют обратной функцией по отношению к функции f(x).
В этом случае уравнение y = f(x) определяет x как неявную функцию от y. Если это уравнение разрешимо относительно x, то получим явное выражение обратной функции: x = g(y).
Пример 7. Будет ли функцией соответствие, обратное функции ? А соответствие, обратное функции ?
Решение. Соответствие, обратное функции, заданной в первом условии, также является функцией:
.
Соответствие, обратное функции, заданной во втором условии, не является функцией, так как , то есть значениям икса, кроме нуля, соответствуют два значения игрека.
Весь раздел «Исследование функций»
Взаимно обратные функции
1 0 к л а с с
Функции и их графики
(обобщающее повторение по пройденному материалу)
Какой из графиков соответствует графику функции
у= х ?
у
у
у
у
1.
3.
х
х
х
х
2.
у
4.
у
х
х
Какой из графиков соответствует графику функции у=х 3 ?
1.
3.
2.
4.
Какой из графиков соответствует графику функции ?
3.
1 .
4.
2.
Какой из графиков соответствует графику
функции ?
1.
3.
4.
2.
Какой график соответствует функции?
у
у
а
б
2
2
1
1
х
х
— 1
— 1
— 2
1
1
0
0
— 1
— 2
— 2
у
г
у
в
2
1 группа: ответ а) объясняют почему
1
2
х
— 1
1
0
1
х
— 1
— 2
0
1
— 2
— 1
— 2
Какой график соответствует функции ?
у
у
а
б
2
2
1
1
х
— 1
1
0
— 2
х
— 2
— 1
1
— 1
0
— 1
— 2
— 2
у
в
у
г
2 группа: ответ а)
2
2
1
1
х
— 2
— 1
— 1
1
0
х
— 1
1
0
-2
— 2
Какой график соответствует функции ?
у
б
2
у
а
2
— 1
— 3
х
0
х
3
1
0
у
у
г
в
3 группа: ответ а)
х
— 1
— 3
х
0
0
1
3
— 2
— 2
Какой график соответствует функции ?
у
а
у
б
2
х
0
2
— 2
0
х
— 2
в
у
г
у
4 группа: ответ а)
2
2
х
х
0
-2
2
0
Какой функции соответствует график? 1 . у = х 3 2 . 3 . у = х 4 4 . у = х -2 5 . 6 . у = х -1
у = х 3 2 . 3 . у = х 4 4 . у = х -2 5 . 6 . у = х -1
у
г
в
у
у
у
б
а
х
х
х
х
д
е
у
у
х
х
1
г
2
е
3
а
4
5
д
б
6
в
Графическое лото.
у
у
1
у
2
у
4
3
1
1
1
х
0
1
0
х
1
-1
0
х
-1
1
1
0
х
у
у
у
5
у
6
8
1
7
1
1
1
1
х
0
х
0
1
9
1
0
х
1
0
х
№ 1 1) у = х -0,7 2) у = х -7 3) у = х 4) у = х 7 5) у = х 0,6
6) у = х 3,14 7) у = х 8 8) у = 1 9) у = х -6
№ 2
1) у = х -8 2) у = х 6 3) у = х 4) у = х 9 5) у = х 2,04
6) у = х 0,3 7) у = х -5 8) у = 1 9) у = х -0,2
Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определённому правилу f число у , то, говорят, что на этом множестве определена функция.
y
y = f ( x )
E ( f )
0
х
x
D ( f )
Укажите область определения данной
на графике функции
D(y)=(-:0) U(0;+)
Укажите область определения данной
на графике функции
D(y)= [-4;2]
Укажите область значений данной на графике функции
Е (y)=(- ; 2 ) U( 2 ;+)
Обратная
Задача.
Дано: у = f (x), у.
Найти значение х при заданном значении у .
Задача.
Прямая
Дано: у = f ( x ), x .
Найти значение у при заданном значении х .
Дано: у = 3 х + 1
Найти: у ( -2 )
Решение:
у ( -2 ) = 3 · (- 2) + 1 = — 5
Ответ: у ( -2 ) = — 5
Дано: у = — 7 х + 3 ,5 , у (х) = — 11, 2
Найти: х
Решение:
— 11,2 = — 7 х + 3 ,5
7 х = 14,7
х = 2 , 1
Ответ: у ( -11,2 ) = 2 ,1
Рассмотрим функцию зависимости скорости движения тела, брошенного вверх с начальной скоростью от времени движения t
Обратимая функция
Найти: t — ?
Решение:
, т. е.
е.
Обратная функция к v ( t )
Если функция у = f ( х ) принимает каждое своё значение у только при одном значении х , то эту функцию называют обратимой.
Обратимые функции
Необратимая функция
Пусть у = f ( x ) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f ( x ) = y . Это соответствие определяет функцию х от у , которую обозначим х = g ( y ). Поменяем местами х и у : у = g ( x ).
Функцию у = g ( x ) называют обратной к функции у = f ( x ).
Найти функцию, обратную данной у = g ( x )
(1)
Дано:
Решение:
Ответ:
(2)
Если функция (2) обратна к функции (1), то такие функции называют взаимно-обратными.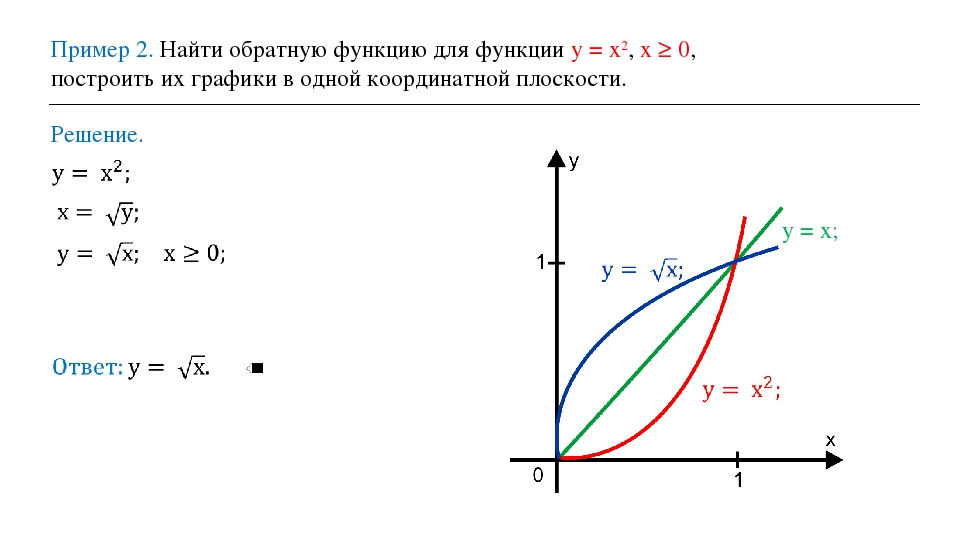
у
у
2
0
0
2
х
х
Найти область определения и множество значений для данных функций.
- D (у)= (- ∞ ;2) ∪ (2;+ ∞ )
- Е(у)=(- ∞ ;0) ∪ (0;+ ∞ )
- D (у)= (- ∞ ;0) ∪ (0;+ ∞ )
2. Е(у)= (-∞;2)∪(2;+∞)
- Область определения обратной функции g(x) совпадает с множеством значений исходной функции f ( x ), а множество значений обратной функции g(x) совпадает с областью определения исходной функции f(x) :
D( g(x) ) = E( f(x )), E( g(x )) = D( f(x )).
- Монотонная функция является обратимой:
- если функция f (x) возрастает, то обратная к ней функция g (x) также возрастает;
- Если функция f (x) убывает, то обратная к ней функция g (x) также убывает.

Дано: у = х 3
Решение:
Построить график данной функции, выразите формулу функции обратной данной и постройте её график.
у
0
х
Решение:
Дано: у = х 3
Построить график данной функции, выразите формулу функции обратной данной и постройте её график.
у
0
х
3. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у = х.
у
у = х
(х 0 ;у 0 )
у 0
(у 0 ;х 0 )
х 0
0
х
у
у
у= f(x)
y=x 2 ,х
у= g (x)
3
0
3
0
-2
х
х
-2
- D(f)=R
- E(f)=R
- возрастающая
- D(y)=(- ∞;0]
- E(y)=[0;+ ∞)
- убывающая
- D(y)=[0;+ ∞)
- E(y)=(- ∞;0]
- убывающая
- D( g )=R
- E( g )=R
- возрастающая
Построить график функции, обратной данной.
у
у
1
1
1
х
1
0
х
0
Обучающая самостоятельная работа
II вариант
I вариант
- Найти функцию, обратную к данной:
- Найти функцию, обратную к данной:
у=-7х+2 .
2. Найти область определения и множество значений функции, обратной к данной:
у=4х-3 .
3. Построить график функции, обратной к данной:
у=-4х+3 .
2. Найти область определения и множество значений функции, обратной к данной:
у=5х-1 .
3. Построить график функции, обратной к данной:
.
.
у
у
3
.
.
3
х
0
-2
1
-2
1
х
0
Ответы
II вариант
I вариант
№ 1 796 514 238
№ 2 215 694 738
2. D(y)=(- ; +)
Е (y)=(- ; +)
3.
2. D(y)=(- ; +)
Е (y)=(- ; +)
3.
3-х
2-х
4
7
.
.
у
у
3
.
.
3
.
.
1
-2
1
-2
0
х
0
х
Задание на дом:
изучить стр. 46-50,
решить № 132, № 133, № 134
по желанию №129(4),184(2)
- На уроке я научился(лась)………………………….
- На уроке мне интересно было …………………….
- Трудно было ………………………………………….
- Знания, полученные на уроке, я могу использовать …………………………………………
Р е ф л е к с и я:
График обратной пропорциональности
Предположим, что функция задана формулой у = 12/х. Область определения рассматриваемой функции представляет собой множество всех чисел, отличных от нуля. Построим график рассматриваемой функции. Для этого нам необходимо найти значения у, которые соответствуют некоторым положительным значениям х и противоположным им отрицательным значениям:
| х | -12 | -8 | -6 | -5 | -4 | -3 | -2 | -1,5 | -1 | 1 | 1,5 | 2 | 3 | 4 | 5 | 6 | 8 | 12 |
| y | -1 | -1,5 | -2 | -2,4 | -3 | -4 | -6 | -8 | -12 | 12 | 8 | 6 | 4 | 3 | 2,4 | 2 | 1,5 | 1 |
В координатной плоскости построим точки, координаты которых мы получили.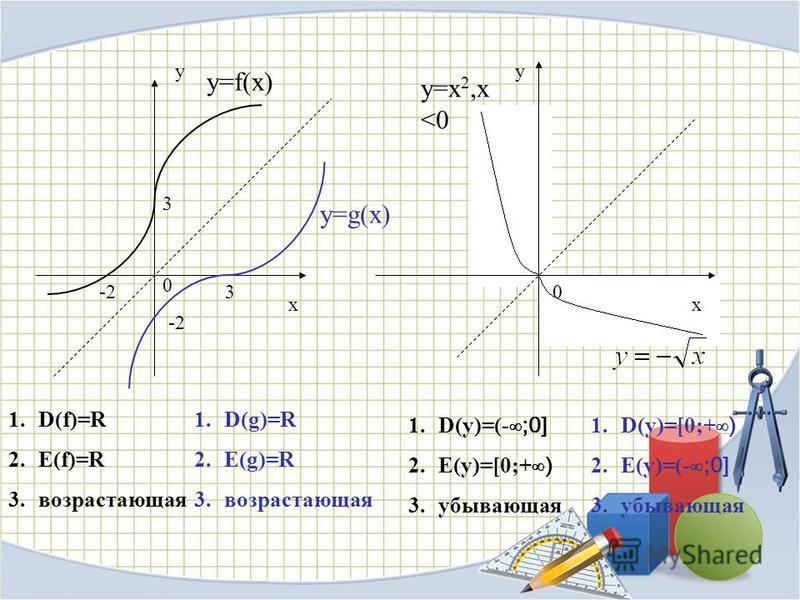 Уменьшая шаг вычислений, можно найти новые точки графика, расположенные все более и более плотно.
Уменьшая шаг вычислений, можно найти новые точки графика, расположенные все более и более плотно.
Число 0 не входит в область определения функции, поэтому на графике не будет точек с абсциссой 0, т.е. график не пересекает ось у. Т.к. нет ни одного такого значения х, при котором у был бы равен 0, то график также не будет пересекать и ось х.
Положительным значениям х будут соответствовать положительные значение у. Чем больше положительное значение х, тем меньше соответствующее ему значение у: например, если х = 120, то у = 0,1; если х = 24000, то у = 0,0005. Следовательно, чем больше положительная абсцисса точки графика, тем ближе эта точка расположена к оси абсцисс. Чем ближе положительное значение х к нулю, тем больше соответствующее ему значение у: например, х = 0,03, то у = 400; х = 0,000001, то у = 12000000.
Противоположным значениям х соответствует противоположные значения у. Каждая точка графика с отрицательными координатами симметрична относительно начала координат точке графика с положительными координатами.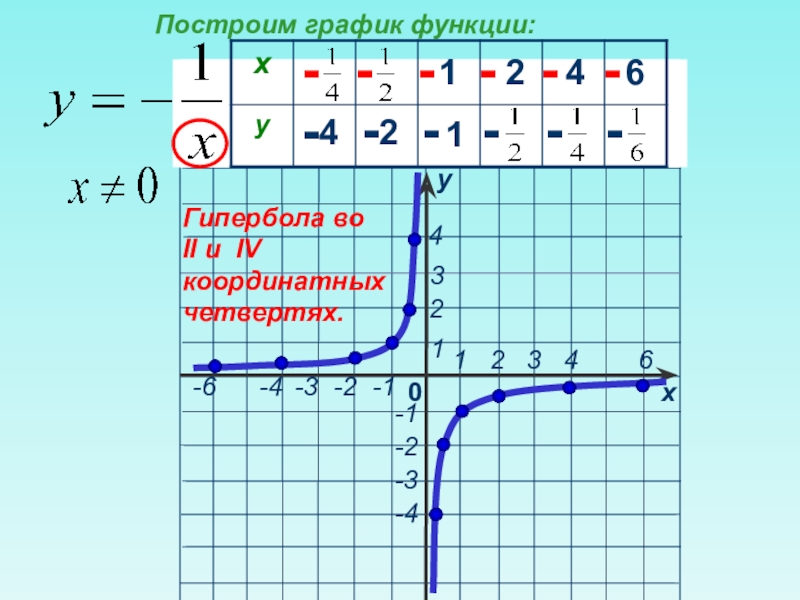
График функции, заданной формулой у = 12/х, будет состоять из двух ветвей, расположенных в первом и третьем координатных углах.
Если функция задана формулой вида у = k/х и k < 0, то положительным значениям х будут соответствовать отрицательные значения у, и наоборот, отрицательным значениям х будут соответствовать положительные значения у. Т.о., график функции, заданной формулой у = -12/х, будет представлять собой кривую, состоящую из двух ветвей, расположенных во втором и четвертом координатных углах.
В общем, график функции, заданной формулой у = k/х, где k ≠ 0, есть кривая, состоящая их двух ветвей; подобную кривую принято называть гиперболой.
Если область определения функции, заданной формулой у = k/х, состоит не из всех отличных от нуля чисел, то ее графиком служит подмножество точек гиперболы.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.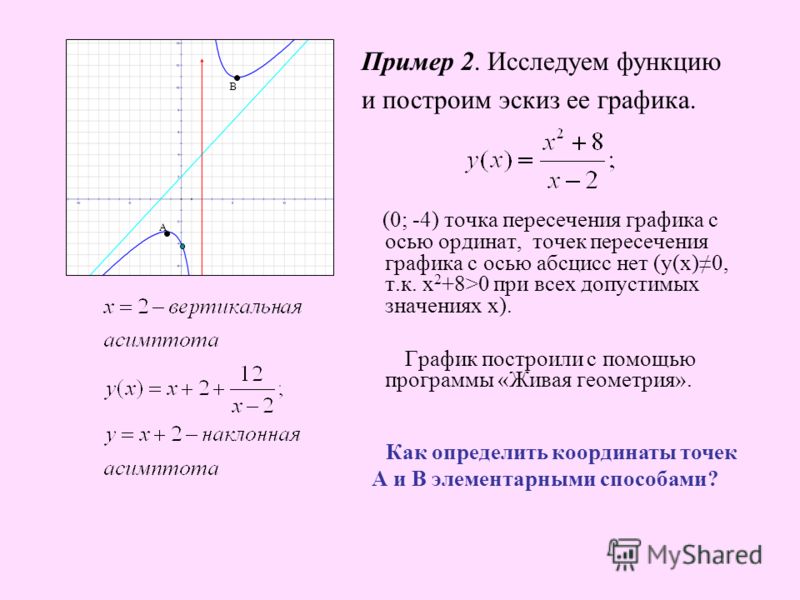
Калькулятор обратной функции — Найдите обратную функцию с шагом
Воспользуйтесь этим бесплатным онлайн-калькулятором обратной функции, который поможет вам определить обратную функцию любой заданной функции с помощью пошагового решения. Однако инверсия конкретной функции может быть или не быть функцией. Здесь вы можете увидеть, как найти обратную функцию, обратный график и многое другое.
Давайте нырнем!
Что такое обратные функции?В математике обратная функция — это функция (f), которая инвертирует конкретную функцию.Обратная функция ( f ) представлена как f -1 .
f (y) = x ⇔ f −1 (x) = y
Калькулятор обратной функции определяет обратную функцию, заменяет функцию другой переменной, а затем находит другую переменную посредством взаимного обмена.
Однако онлайн-калькулятор составных функций позволяет вам определять композицию функций из введенных значений функций.{-1} (г) $
Что совпадает с графиком уравнения:
$$ y = f (x) $$
Уравнение x = f (y) определяет график f, за исключением того, что роли y и x поменялись местами. Таким образом, график обратной функции (f -1 ) может быть получен из графика функции (f) путем переключения положения осей y и x.
Как вычислить обратную функцию (пошагово):Вычислить обратную функцию ( f -1 ) данной функции, выполнив следующие шаги:
- Сначала возьмем функцию f (y), имеющую y в качестве переменной.
- Теперь рассмотрим, что x — это функция для f (y)
- Затем поменяйте местами переменные y и x, тогда результирующая функция будет x и
- Решите уравнение y относительно x и найдите значение x.
Чтобы вам было удобно, калькулятор обратной функции сделает все эти вычисления за вас за доли секунды.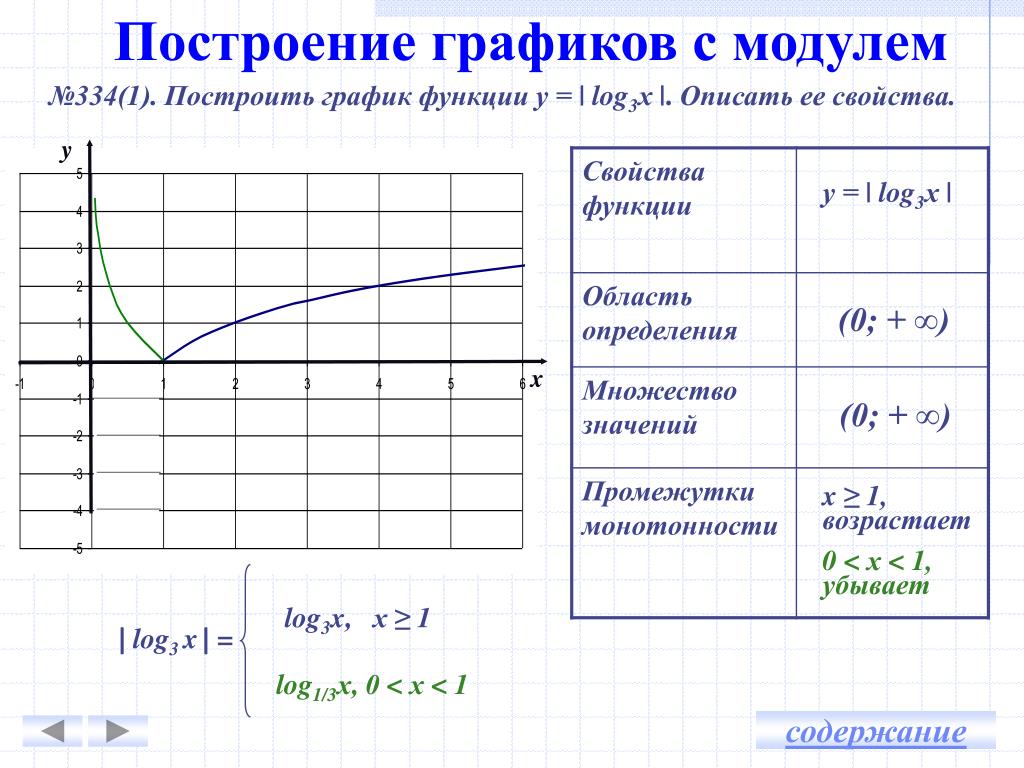
Пример:
Вычислить обратные функции x = y + 11 / 13y + 19?
Ответ:
Замените переменные y и x, чтобы найти обратную функцию f -1 :
$$ y = x + 11 / 13x + 19 $$
$$ y (13x + 19) = x + 11 $$
$$ 13xy + 19y — x = 11 $$
$$ x (13лет — 1) = 11–19лет $$
$$ x = 11 — 19лет / 13лет — 1 $$
Следовательно, функция, обратная y + 11 / 13y + 19, равна 11 — 19y / 13y — 1.
Однако онлайн-калькулятор квадратной формулы помогает решить данное квадратное уравнение, используя формулу квадратного уравнения.
Как работает калькулятор обратной функции?Онлайн-инверсия калькулятора функции находит инверсию введенной функции с помощью следующих шагов:
Ввод:- Прежде всего, введите функцию f (x).
- Нажмите кнопку «Рассчитать».
- Калькулятор обратной функции дает обратную функцию конкретной функции.

- Затем замените переменные и отобразите пошаговое решение для введенной функции.
Обратные функции — это функции, которые никогда не возвращают исходные значения, но обратные функции всегда возвращают исходные значения. Взаимные функции представлены как f (x) -1 или 1 / f (x). Тогда как обратные функции обозначаются f -1 (x).
Как обратная функция используется для преобразования температуры?Обратные функции, используемые для обратного преобразования Цельсия (C) в градусы Фаренгейта (F) и наоборот:
Для преобразования Фаренгейта (F) в Цельсия (C):
f (F) = 5/9 * (F — 32)
Обратная функция от Цельсия до Фаренгейта: f -1 (C) = (C * 9/5) + 32
Что обратное 1 / x?Предположим, что:
$$ f (y) = 1 / y = x $$
Заменить переменные y и x:
$$ y = 1 / x $$
$$ f ^ {- 1} (y) = 1 / x $$
Заключение: Онлайн-калькулятор обратной функции предоставляет пошаговое решение для преобразования функций в соответствии с заданными значениями. Хотя вы можете вычислить обратную функцию вручную с помощью уравнения обратной функции, это увеличивает неоднозначность, поэтому этот удобный калькулятор обратных функций быстро дает 100% безошибочные результаты.
Хотя вы можете вычислить обратную функцию вручную с помощью уравнения обратной функции, это увеличивает неоднозначность, поэтому этот удобный калькулятор обратных функций быстро дает 100% безошибочные результаты.
Из источника Википедии: Инверсии и композиция, Нотация, Самообращение, График инверсии, Инверсии и производные.
Из источника Paul Online Notes: Обратные функции, Нахождение инверсии функции, Частичные инверсии, Левая и правая инверсия.
Из источника Quest Calculus: ПРОИЗВОДНЫЕ ОБРАТНЫХ ФУНКЦИЙ, Цепное правило, Двусторонние инверсии, Прообразы.
Алгебра — обратные функции
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-7: Обратные функции
В последнем примере из предыдущего раздела мы рассмотрели две функции \ (f \ left (x \ right) = 3x — 2 \) и \ (g \ left (x \ right) = \ frac {x} {3 } + \ frac {2} {3} \) и увидел, что
\ [\ left ({f \ circ g} \ right) \ left (x \ right) = \ left ({g \ circ f} \ right) \ left (x \ right) = x \], и, как указано в этом разделе, это означает, что это особые функции.Посмотрим, что делает их такими особенными. Рассмотрим следующие оценки.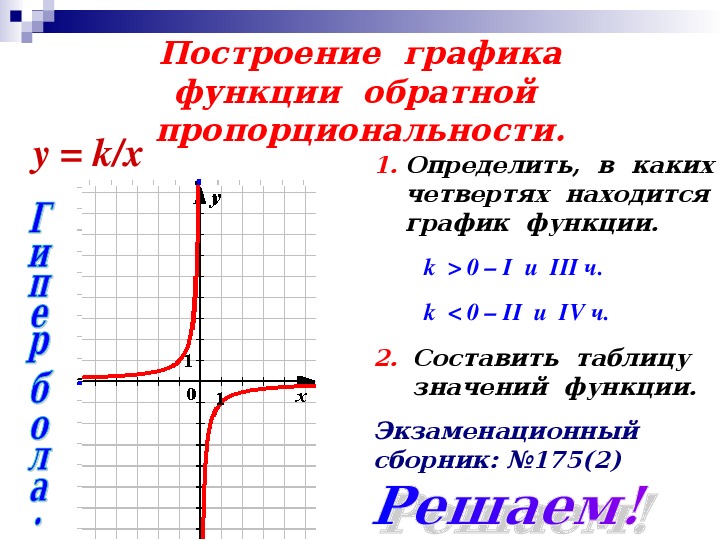
В первом случае мы подключили \ (x = — 1 \) к \ (f \ left (x \ right) \) и получили значение -5. Затем мы развернулись и подключили \ (x = — 5 \) к \ (g \ left (x \ right) \) и получили значение -1, число, с которого мы начали.
Во втором случае мы сделали нечто подобное. Здесь мы подключили \ (x = 2 \) к \ (g \ left (x \ right) \) и получили значение \ (\ frac {4} {3} \), мы развернулись и вставили это в \ ( f \ left (x \ right) \) и получил значение 2, которое снова является числом, с которого мы начали.
Обратите внимание, что здесь мы действительно выполняем некоторую композицию функций. Первый случай действительно,
\ [\ left ({g \ circ f} \ right) \ left ({- 1} \ right) = g \ left [{f \ left ({- 1} \ right)} \ right] = g \ left [ {- 5} \ right] = — 1 \]и второй случай действительно
\ [\ left ({f \ circ g} \ right) \ left (2 \ right) = f \ left [{g \ left (2 \ right)} \ right] = f \ left [{\ frac {4} {3}} \ right] = 2 \]Также обратите внимание, что оба они согласуются с формулой композиций, которые мы нашли в предыдущем разделе.Мы возвращаем из оценки функции число, которое мы изначально вставили в композицию.
Итак, что здесь происходит? В некотором смысле мы можем думать об этих двух функциях как об отмене того, что другой сделал с числом. В первом случае мы вставили \ (x = — 1 \) в \ (f \ left (x \ right) \), а затем вставили результат этой оценки функции обратно в \ (g \ left (x \ right) \) и каким-то образом \ (g \ left (x \ right) \) отменил то, что \ (f \ left (x \ right) \) сделал с \ (x = — 1 \), и вернул нам оригинал \ (x \), с которой мы начали.
Пары функций, которые демонстрируют такое поведение, называются обратными функциями . Прежде чем формально определять обратные функции и обозначения, которые мы собираемся использовать для них, нам нужно получить определение.
Функция называется взаимно однозначной , если никакие два значения \ (x \) не дают одинаковых \ (y \). Это довольно простое определение «один-к-одному», но для того, чтобы показать, что это означает, используется пример функции, которая не является взаимно-однозначной.2} \) во взаимно однозначную функцию, если мы ограничимся \ (0 \ le x <\ infty \). Иногда это можно сделать с помощью функций.
Демонстрация того, что функция является индивидуальной, часто бывает утомительным и трудным процессом. По большей части мы будем предполагать, что функции, с которыми мы будем иметь дело в этом разделе, взаимно однозначны. Однако нам нужно было поговорить о взаимно-однозначных функциях, поскольку только однозначные функции могут быть обратными.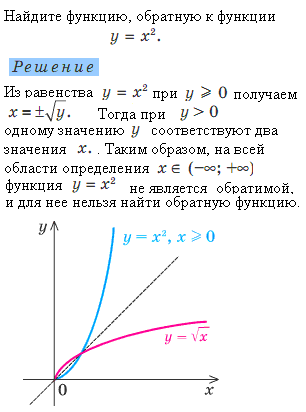 {- 1}} \ left (x \ right) \).{- 1}} \ circ f} \ right) \ left (x \ right) = x \) верны. Для всех функций, которые мы собираемся рассмотреть в этом разделе, если одна из них истинна, то другая также будет истинной. Однако есть функции (однако они выходят далеко за рамки этого курса), для которых может быть истинным только одно из них. Это вызвано тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять и то, и другое.
{- 1}} \ left (x \ right) \).{- 1}} \ circ f} \ right) \ left (x \ right) = x \) верны. Для всех функций, которые мы собираемся рассмотреть в этом разделе, если одна из них истинна, то другая также будет истинной. Однако есть функции (однако они выходят далеко за рамки этого курса), для которых может быть истинным только одно из них. Это вызвано тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять и то, и другое.
Давайте поработаем несколько примеров.{- 1}} \ left (x \ right) \). Показать решение
Теперь мы уже знаем, что является обратным к этой функции, поскольку мы уже поработали с ней. Однако было бы неплохо начать именно с этого, поскольку мы знаем, что должны получить. Это будет хорошей проверкой процесса.
Итак, приступим. Сначала заменим \ (f \ left (x \ right) \) на \ (y \).
\ [y = 3x — 2 \] Затем замените все \ (x \) на \ (y \), а все y, на \ (x \).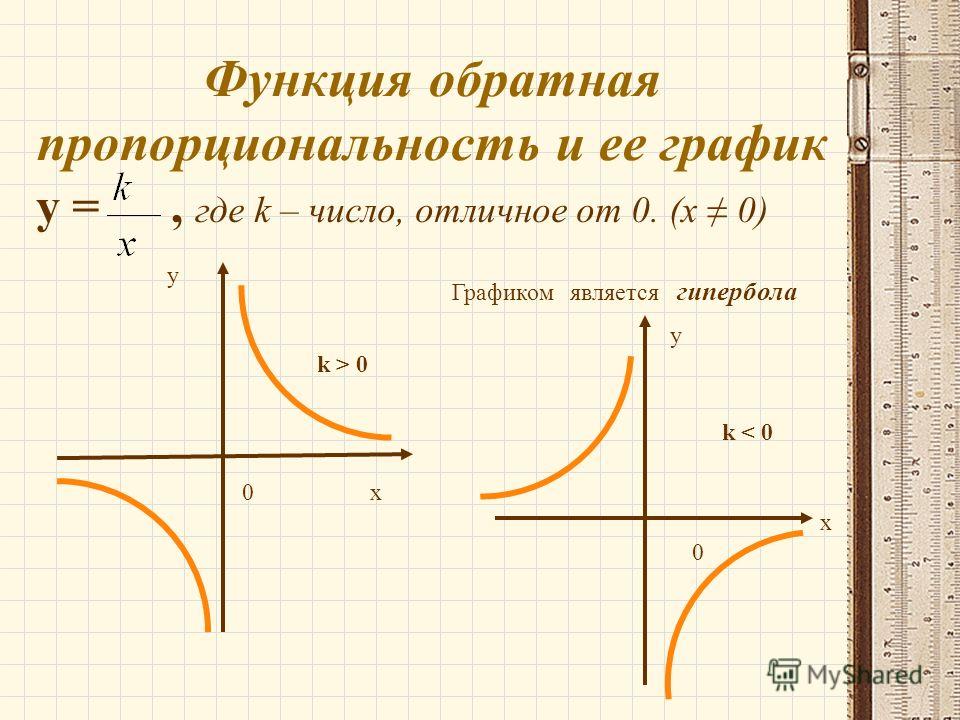 {- 1}} \ left (x \ right) = \ frac {{4 + 5x}} {{2x — 1}} \]
{- 1}} \ left (x \ right) = \ frac {{4 + 5x}} {{2x — 1}} \]
Наконец, нам нужно провести проверку.{- 1}}} \ right) \ left (x \ right) & = \ frac {{2x — 1}} {{2x — 1}} \, \, \ frac {{\ frac {{4 + 5x} } {{2x — 1}} + 4}} {{2 \ left ({\ frac {{4 + 5x}} {{2x — 1}}} \ right) — 5}} \\ & = \ frac { {\ left ({2x — 1} \ right) \ left ({\ frac {{4 + 5x}} {{2x — 1}} + 4} \ right)}} {{\ left ({2x — 1} \ right) \ left ({2 \ left ({\ frac {{4 + 5x}} {{2x — 1}}} \ right) — 5} \ right)}} \\ & = \ frac {{4 + 5x + 4 \ left ({2x — 1} \ right)}} {{2 \ left ({4 + 5x} \ right) — 5 \ left ({2x — 1} \ right)}} \\ & = \ frac {{4 + 5x + 8x — 4}} {{8 + 10x — 10x + 5}} \\ & = \ frac {{13x}} {{13}} \\ & = x \ end {align *} \]
Вау.Это было много работы, но в конце концов все получилось. Мы сделали всю нашу работу правильно, и у нас действительно есть обратное.
Есть еще одна последняя тема, которую нам нужно быстро обсудить, прежде чем мы покинем этот раздел. Существует интересная взаимосвязь между графиком функции и обратным ей.
Существует интересная взаимосвязь между графиком функции и обратным ей.
Вот график функции и обратной из первых двух примеров. Мы не будем рассматривать последний пример, поскольку это функция, о которой мы еще не говорили.
В обоих случаях мы можем видеть, что график инверсии является отражением фактической функции относительно линии \ (y = x \). Так всегда будет с графиками функции и обратной ей.
1.4 Обратные функции — Объем исчисления 1
Цели обучения
- Определите условия, при которых функция имеет инверсию.
- Используйте тест горизонтальной линии, чтобы распознать однозначное соответствие функции.
- Найдите обратное значение заданной функции.
- Постройте график обратной функции.
- Вычислить обратные тригонометрические функции.
Обратная функция отменяет операцию, выполняемую определенной функцией. Другими словами, что бы ни делала функция, обратная функция отменяет это. В этом разделе мы формально определяем обратную функцию и формулируем необходимые условия для существования обратной функции. Мы исследуем, как найти обратную функцию, и изучаем взаимосвязь между графиком функции и графиком обратной.Затем мы применяем эти идеи для определения и обсуждения свойств обратных тригонометрических функций.
В этом разделе мы формально определяем обратную функцию и формулируем необходимые условия для существования обратной функции. Мы исследуем, как найти обратную функцию, и изучаем взаимосвязь между графиком функции и графиком обратной.Затем мы применяем эти идеи для определения и обсуждения свойств обратных тригонометрических функций.
Начнем с примера. Учитывая функцию и результат, нас часто интересует, какое значение или значения были сопоставлены. Например, рассмотрим функцию. Поскольку любой выход, мы можем решить это уравнение, чтобы найти, что вход. Это уравнение определяется как функция от. Обозначив эту функцию как и написав, мы увидим, что для любого в домене. Таким образом, эта новая функция «отменила» то, что делала исходная функция.Функция с этим свойством называется функцией, обратной исходной функции.
Обратите внимание, что читается как «инверсия f». Здесь -1 не используется как показатель степени и. (Рисунок) показывает взаимосвязь между доменом и диапазоном и доменом и диапазоном.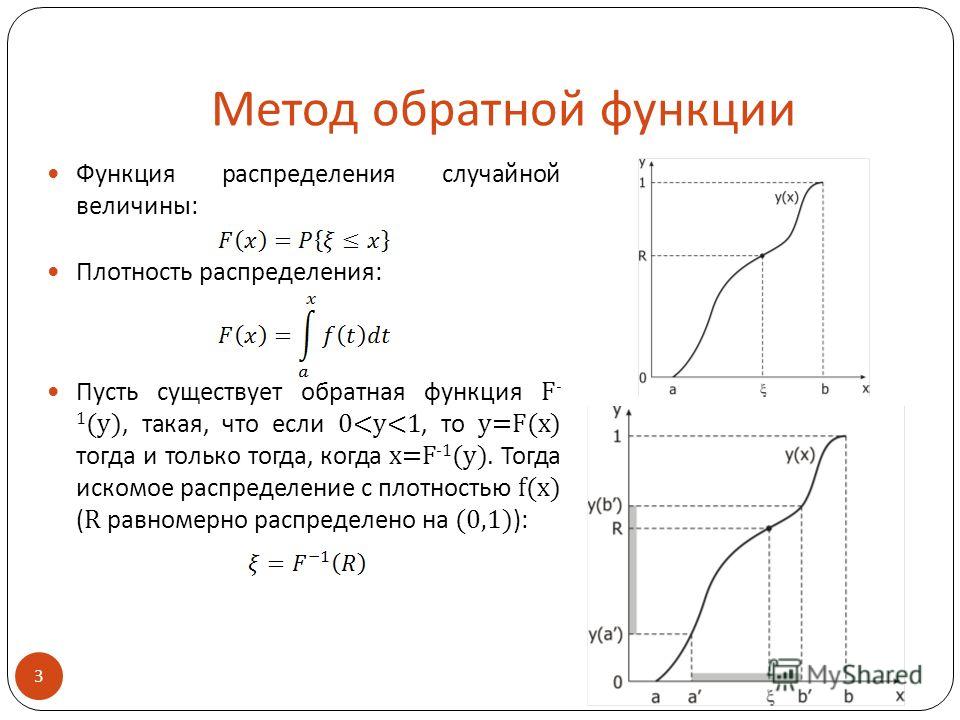
Напомним, что функция имеет ровно один выход для каждого входа. Следовательно, чтобы определить обратную функцию, нам нужно сопоставить каждый вход ровно с одним выходом. Например, давайте попробуем найти обратную функцию для.Решая уравнение для, мы приходим к уравнению. Это уравнение не описывается как функция от, потому что для каждого существует два решения этого уравнения. Проблема с попыткой найти обратную функцию для состоит в том, что два входа отправляются на один и тот же выход для каждого выхода. Обсуждаемая ранее функция не имела этой проблемы. Для этой функции каждый вход был отправлен на другой выход. Функция, которая отправляет каждый вход на другой выход , называется функцией «один-к-одному».
Определение
Мы говорим, что a является взаимно однозначной функцией if when.
Один из способов определить, является ли функция взаимно однозначной, — взглянуть на ее график. Если функция взаимно однозначна, то два входа не могут быть отправлены на один и тот же выход.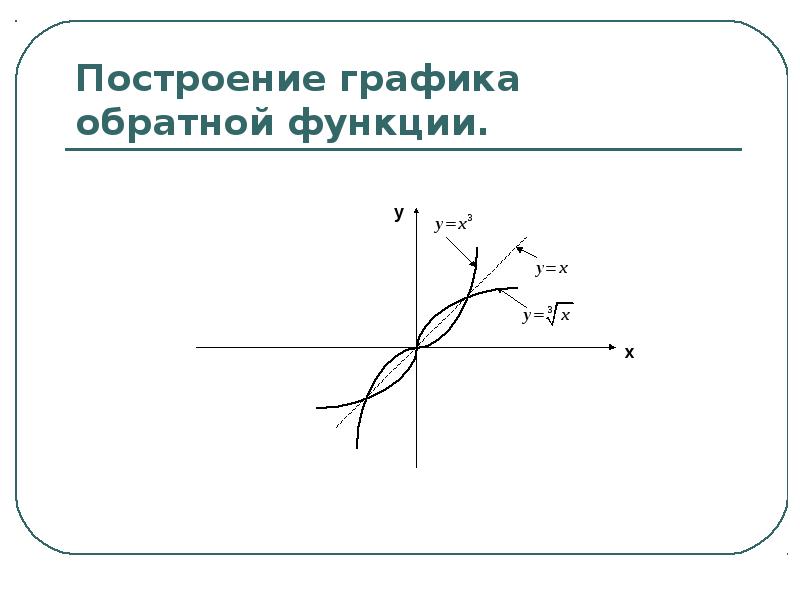 Следовательно, если мы проведем горизонтальную линию в любом месте плоскости, согласно тесту горизонтальной линии , она не может пересекать график более одного раза. Отметим, что тест горизонтальной линии отличается от теста вертикальной линии.Тест вертикальной линии определяет, является ли график графиком функции. Тест горизонтальной линии определяет, является ли функция взаимно однозначной ((рисунок)).
Следовательно, если мы проведем горизонтальную линию в любом месте плоскости, согласно тесту горизонтальной линии , она не может пересекать график более одного раза. Отметим, что тест горизонтальной линии отличается от теста вертикальной линии.Тест вертикальной линии определяет, является ли график графиком функции. Тест горизонтальной линии определяет, является ли функция взаимно однозначной ((рисунок)).
Правило: Тест горизонтальной линии
Функция взаимно однозначна тогда и только тогда, когда каждая горизонтальная линия пересекает график не более одного раза.
Рисунок 2. (a) Функция не является взаимно однозначной, потому что она не проходит тест горизонтальной линии. (b) Функция взаимно однозначна, потому что она проходит тест горизонтальной линии.Определение того, является ли функция взаимно однозначной
Соответствует ли функция на следующем изображении однозначно?
Шесть основных тригонометрических функций периодичны, поэтому они не взаимно однозначны.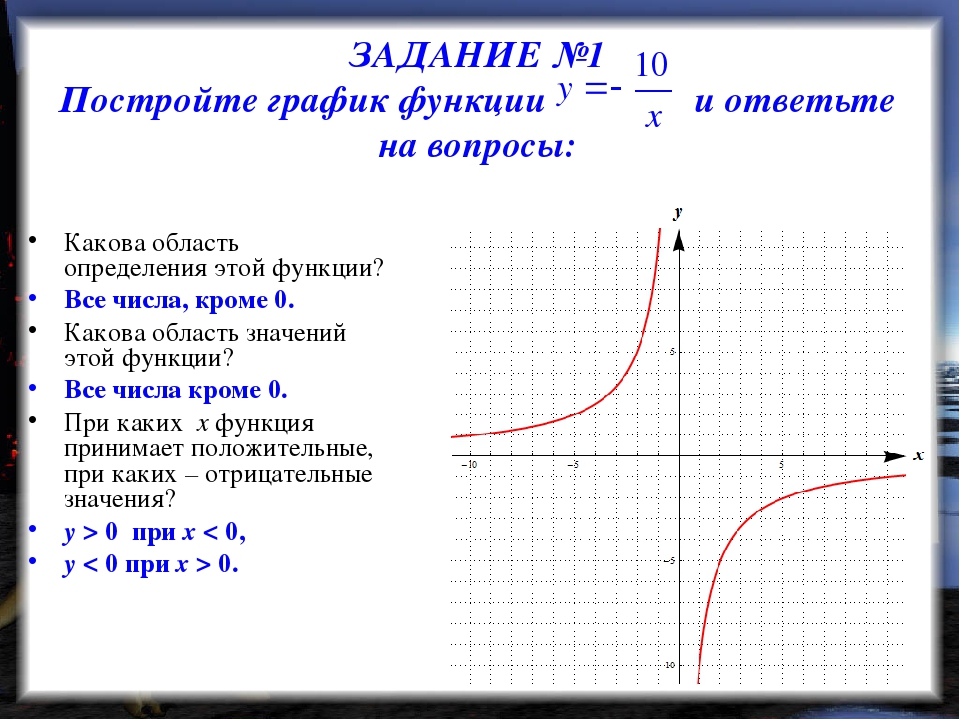 Однако, если мы ограничим область определения тригонометрической функции интервалом, в котором она взаимно однозначна, мы можем определить ее обратную. Рассмотрим синусоидальную функцию ((рисунок)). Синусоидальная функция взаимно однозначна на бесконечном количестве интервалов, но стандартное соглашение заключается в ограничении области до интервала.Таким образом, мы определяем обратную синусоидальную функцию в области так, что для любого в интервале обратная синусоидальная функция сообщает нам, какой угол в интервале удовлетворяет. Точно так же мы можем ограничить области действия других тригонометрических функций, чтобы определить i и обратные тригонометрические функции , которые являются функциями, которые сообщают нам, какой угол в определенном интервале имеет указанное тригонометрическое значение.
Однако, если мы ограничим область определения тригонометрической функции интервалом, в котором она взаимно однозначна, мы можем определить ее обратную. Рассмотрим синусоидальную функцию ((рисунок)). Синусоидальная функция взаимно однозначна на бесконечном количестве интервалов, но стандартное соглашение заключается в ограничении области до интервала.Таким образом, мы определяем обратную синусоидальную функцию в области так, что для любого в интервале обратная синусоидальная функция сообщает нам, какой угол в интервале удовлетворяет. Точно так же мы можем ограничить области действия других тригонометрических функций, чтобы определить i и обратные тригонометрические функции , которые являются функциями, которые сообщают нам, какой угол в определенном интервале имеет указанное тригонометрическое значение.
Определение
Обратная функция синуса, обозначенная или arcsin, и функция обратного косинуса, обозначенная или arccos, определены в области следующим образом:
Функция обратного тангенса, обозначенная или arctan, и функция обратного котангенса, обозначенная или arccot, определены в области следующим образом:
Обратная функция косеканса, обозначенная или arccsc, и обратная функция секанса, обозначенная или arcsec, определены в области следующим образом:
Для построения графиков обратных тригонометрических функций мы используем графики тригонометрических функций, ограниченных областями, определенными ранее, и отображаем графики относительно линии ((Рисунок)).
Перейдите на следующий сайт, чтобы получить больше сравнений функций и их обратных.
При оценке обратной тригонометрической функции выходным значением является угол. Например, чтобы оценить, нам нужно найти такой угол, чтобы. Ясно, что многие углы обладают этим свойством. Однако, учитывая определение, нам нужен угол, который не только решает это уравнение, но и лежит в интервале.Делаем вывод.
Теперь рассмотрим композицию тригонометрической функции и ее обратной. Например, рассмотрим два выражения и. Для первого упрощаем следующим образом:
.Для второго у нас
. Предполагается, что обратная функция «отменяет» исходную функцию, так почему же нет? Вспоминая наше определение обратных функций, функция и ее обратная функция удовлетворяют условиям для всех в области и для всех в области, так что же здесь произошло? Проблема в том, что обратная синусоидальная функция является обратной синусоидальной функции , ограниченной синусоидальной функцией , определенной в домене.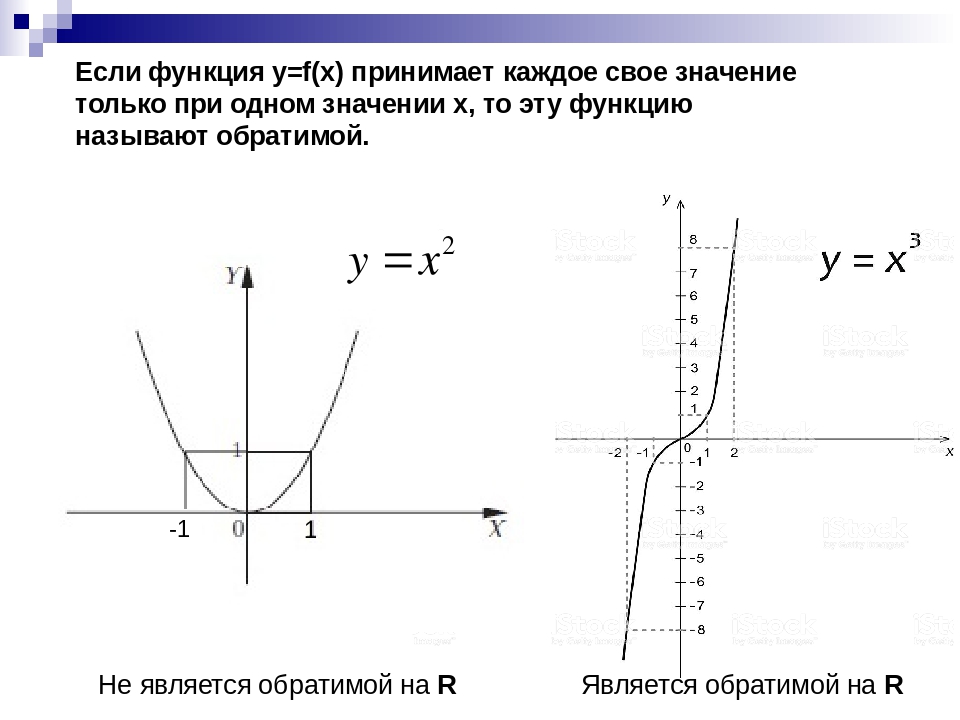 Следовательно, для в интервале верно, что. Однако для значений вне этого интервала уравнение не выполняется, даже если оно определено для всех действительных чисел.
Следовательно, для в интервале верно, что. Однако для значений вне этого интервала уравнение не выполняется, даже если оно определено для всех действительных чисел.
А что? Есть ли у этого похожая проблема? Ответ: нет . Поскольку область значений — это интервал, мы заключаем, что if и выражение не определено для других значений. Подводя итог,
и
.Аналогично для функции косинуса
и
.Подобные свойства сохраняются и для других тригонометрических функций и их обратных.
Вычисление выражений, включающих обратные тригонометрические функции
Оцените каждое из следующих выражений.
Максимальное значение функции
Во многих областях науки, техники и математики полезно знать максимальное значение, которое может получить функция, даже если мы не знаем ее точное значение в данный момент. Например, если у нас есть функция, описывающая прочность балки крыши, мы хотели бы знать максимальный вес, который балка может выдержать без разрушения. Если у нас есть функция, описывающая скорость поезда, мы бы хотели узнать его максимальную скорость, прежде чем он соскочит с рельсов. Безопасный дизайн часто зависит от знания максимальных значений.
Если у нас есть функция, описывающая скорость поезда, мы бы хотели узнать его максимальную скорость, прежде чем он соскочит с рельсов. Безопасный дизайн часто зависит от знания максимальных значений.
Этот проект описывает простой пример функции с максимальным значением, которое зависит от двух коэффициентов уравнения. Мы увидим, что максимальные значения могут зависеть от нескольких факторов, помимо независимой переменной.
- Рассмотрим график функции (рисунок). Опишите его общую форму.Это периодически? Откуда вы знаете? Рисунок 6. График.
С помощью графического калькулятора или другого графического устройства оцените — и — значения максимальной точки для графика (первая такая точка, где). Может быть полезно выразить -значение как кратное.
- Теперь рассмотрим другие графики вида для различных значений и. Нарисуйте график, когда и, и найдите — и -значения для максимальной точки. (Не забудьте выразить -значение как кратное, если возможно.
 ) Переехала?
) Переехала? - Повторите для. Есть ли какое-либо отношение к тому, что вы нашли в части (2)?
- Заполните следующую таблицу, добавив несколько собственных вариантов для и:
- Попытайтесь выяснить формулу для -значений.
- Формула для значений немного сложнее. Самые полезные моменты из таблицы. ( Подсказка : Рассмотрим обратные тригонометрические функции.)
- Если вы нашли формулы для частей (5) и (6), покажите, что они работают вместе.То есть замените найденную формулу -значение и упростите ее, чтобы получить формулу -значение, которую вы нашли.
В следующих упражнениях используйте тест горизонтальной линии, чтобы определить, является ли каждый из данных графиков взаимно однозначным.
1.2.
3.
4.
5.
6.
Для следующих упражнений: a. найти обратную функцию, и b. найти область определения и диапазон обратной функции.
найти обратную функцию, и b. найти область определения и диапазон обратной функции.
7.
Решение
а. б. Домен:, Диапазон:
8.
9.
Решение
а. б. Домен: все действительные числа, Диапазон: все действительные числа
10.
11.
Решение
а. , б. Домен:, Диапазон:
12.
Для следующих упражнений используйте график, чтобы нарисовать график его обратной функции.
13.Решение
14.15.
Решение
16.В следующих упражнениях используйте композицию, чтобы определить, какие пары функций являются обратными.
17.
Решение
Это обратное.
18.
19.
Решение
Это не наоборот.
20.
21.
Решение
Это обратное.
22.
23.
Решение
Это обратное.
24.
Оцените функции для следующих упражнений. Укажите точное значение.
25.
Решение
26.
27.
Решение
28.
29.
Решение
30.
31.
[show-answer q = ”461959 ″] Показать ответ [/ show-answer][hidden-answer a = ”461959 ″]
32.
33.
Решение
34. Функция конвертирует градусы Фаренгейта в градусы Цельсия.
Функция конвертирует градусы Фаренгейта в градусы Цельсия.
- Найти обратную функцию
- Для чего используется обратная функция?
Решение
а. б. Обратная функция определяет расстояние от центра артерии, по которому кровь течет со скоростью. c. 0,1 см; 0,14 см; 0,17 см
36. Функция, которая преобразует размеры одежды в Соединенных Штатах Америки в размеры одежды в Европе, задается выражением.
- Найдите европейские размеры одежды, соответствующие размерам 6, 8, 10 и 12 в США.
- Найдите функцию, которая преобразует европейские размеры одежды в американские.
- Используйте деталь b. чтобы найти размеры платьев в США, соответствующие 46, 52, 62 и 70.
37. [T] Стоимость удаления токсина из озера моделируется функцией
, где — стоимость (в тысячах долларов), а — количество токсина в небольшом озере (измеряется в частях на миллиард [ppb]). Эта модель действительна только тогда, когда количество токсина меньше 85 частей на миллиард.
Эта модель действительна только тогда, когда количество токсина меньше 85 частей на миллиард.
- Найдите стоимость удаления 25 частей на миллиард, 40 частей на миллиард и 50 частей на миллиард токсина из озера.
- Найдите обратную функцию. c. Используйте часть b. чтобы определить, сколько токсина удаляется за 50 000 долларов.
Решение
а. 31 250 долл. США, 66 667 долл. США, 107 143 долл. США b. c. 34 частей на миллиард
38. [T] Гоночный автомобиль ускоряется со скоростью, заданной в
.,
где — скорость (в футах в секунду) в момент времени.
- Найдите скорость автомобиля за 10 секунд.
- Найдите обратную функцию.
- Используйте деталь b. чтобы определить, сколько времени требуется автомобилю, чтобы достичь скорости 150 футов / сек.
42. [T] Глубина (в футах) воды в доке меняется с приливом и отливом. Моделируется функцией
,
где — количество часов после полуночи. Определить первый раз после полуночи, когда глубина составляет 11,75 фута.
Определить первый раз после полуночи, когда глубина составляет 11,75 фута.
43. [T] Объект, движущийся в простом гармоническом движении, моделируется функцией
,
где измеряется в дюймах и измеряется в секундах.Определите первый раз, когда пройденное расстояние составляет 4,5 фута.
Решение
44. [T] В местной картинной галерее есть портрет 3 фута высотой, который висит на 2,5 футах над уровнем глаз среднего человека. Угол обзора можно смоделировать с помощью функции
.,
где — расстояние (в футах) от портрета. Найдите угол обзора, когда человек находится в 4 футах от портрета.
45. [T] Используйте калькулятор для вычисления и.Объясните результаты каждого.
46. [T] Используйте калькулятор для вычисления и. Объясните результаты каждого.
Находка
Обратная функция (стр. Разделы: Определение / Инвертирование графика, обратная функция — это функция ?, Нахождение обратного, доказательство обратного Обычный метод поиск обратного — это вариант метода, который я собираюсь использовать ниже.Какой бы метод вы ни использовали, убедитесь, что вы выполняете точно такие же шаги в один и тот же порядок каждый раз, поэтому вы запомните эти шаги, когда получите к тесту.
Вот как процесс работ:
Если вам нужно найти домен и диапазон, посмотрите на исходную функцию и ее график. Домен оригинала функция — это набор всех допустимых значений x ; в этом случае функция была простым полиномом, поэтому область определения «все реальные числа». Диапазон исходной функции — все y -значения вы передадите график; в этом случае прямая линия продолжается всегда в любом направлении, поэтому диапазон также представляет собой «все действительные числа».Чтобы найти домен и диапазон обратного, просто поменяйте местами домен и диапазон от исходной функции.
Обычно считается
приемлемо для построения приведенного выше графика, проведите по нему горизонтальную линию,
дважды пересекает график, а затем произнесите что-то вроде «Обратный
этой функции не является функцией из-за горизонтальной линии
Тестовое задание». Как это будет выглядеть когда я пытаюсь найти обратное алгебраически? Вертикаль Line Test говорит что у меня не может быть двух и с общим значением x .То есть каждый x должен иметь УНИКАЛЬНЫЙ соответствующий y ценить. Но посмотрите, что происходит, когда я пытаюсь найти « x = «:
Ну я решил для « x знак равно
но я не получил УНИКАЛЬНЫЙ « x знак равноВместо этого я показал, что любое заданное значение x фактически будет соответствовать двум различным значениям y ,
один от плюса к квадратному корню, а другой от
«минус». Каждый раз, когда вы придумываете знак «», вы можете быть уверены, что обратное не функция.
Эта функция будет иметь обратное, что
тоже функция. Практически каждый раз, когда они задают вам проблему, где
они постарались ограничить домен, вы должны позаботиться
с алгеброй и нарисуйте красивую картинку, потому что, вероятно, обратное
— это функция, но, вероятно, потребуются дополнительные усилия, чтобы показать это.
(« x > 1 «ограничение
исходит из того, что x находится внутри квадратного корня. Так обратное — y = sqrt ( x 1), x > 1, и эта инверсия также является функцией.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>
|
Калькулятор обратной функции — Бесплатные онлайн-калькуляторы
Калькулятор обратной функции — это онлайн-инструмент для вычисления обратной функции любой заданной функции.{-1} \).
О калькуляторе обратной функции
Ввод
Входы калькулятора:
- Функция, для которой требуется найти обратную
Шаги
Калькулятор обратной функции— это удобный инструмент. Ниже приведен подробный пошаговый процесс поиска инверсии любой функции.
- Введите любую функцию в соответствующее поле ввода напротив текста « Обратная функция для »
- Нажмите кнопку «Отправить», чтобы сформулировать обратную функцию.
 {- 1} _ {x} = id_ {x} \) .{3} +3 \)
{- 1} _ {x} = id_ {x} \) .{3} +3 \)Оформить заказ Больше калькуляторов здесь
Калькулятор обратной функции
Калькулятор обратной функциипоможет вам определить обратные значения, предоставив входные данные для функций. Обратные функции — это функции, которые могут обращать другие функции. Другое название этого — антифункция. Это можно выразить так:
f (x) = y ⇔ f — 1 (y) = x
Как пользоваться калькулятором обратной функции?С помощью этого онлайн-калькулятора очень просто найти обратные функции.Для любой функции вы можете найти обратное, выполнив следующие действия.
Шаг 1: Введите любую функцию в поле ввода с текстом «Обратная функция для».
Шаг 2: В нижней части калькулятора нажмите кнопку «Отправить».
Шаг 3: Откроется отдельное окно, в котором вы можете вычислить обратное значение данной функции.
Калькулятор обратной функции
Как найти обратную функцию?Обратное значение любой функции можно найти, заменив функциональную переменную другой переменной, а затем решив для другой переменной, заменив ее другой переменной.
 Для лучшего понимания вот пример.
Для лучшего понимания вот пример.Пример: Обратить выражение f (x) = y = 3x — 2
Решение: Во-первых, замените f (x) на f (y).
Теперь уравнение y = 3x — 2 превратится в
х = 3у — 2
Решить задачу для y,
у = (х + 2) / 3
Это дает y = (x + 2) / 3 как обратное значение y = 3x — 2.
Обратная функция: что это такое?Обратные функции, или антифункции, определяются как функции, которые могут быть преобразованы в другую функцию.По сути, если какая-либо функция принимает входной x и преобразует его в выходной y, ее обратная функция будет делать то же самое. В случае функции, обозначенной «f» или «F», обратная функция будет обозначена «f-1» или «F-1». Будьте осторожны, чтобы не путать (-1) с экспонентами или обратными величинами.
В случае обратных функций f (x) = y только тогда и только тогда, когда g (y) = x
Чтобы найти угол, для которого функция синуса дает значение, тригонометрия использует функцию обратного синуса.
Определение Другими словами, sin-1 (1) = sin-1 (sin 90) = 90 градусов.Следовательно, sin 90 градусов равен 1.
Другими словами, sin-1 (1) = sin-1 (sin 90) = 90 градусов.Следовательно, sin 90 градусов равен 1.Операция выполняет операцию со значениями, а затем создает выходные данные на основе этих операций. Обратные функции согласуются с полученным результатом, работают и возвращают исходную функцию.
Обратные функции возвращают исходное значение, которое является выходом функции.
Если вы рассматриваете f и g как функции, f (g (x)) = g (f (x)) = x. Исходное значение функции получается через обратное.
Пример: f (x) = 2x + 5 = y
Тогда g (y) = (y-5) / 2 = x является обратным к f (x).
Примечание:
- Обратная связь, созданная заменой независимой переменной переменной, которая зависит от указанного уравнения, которое может быть или не быть функцией.
- f-1 (x) обозначает обратную функцию, если обратная функция является самой собой.
Обратные графики изображают две вещи: одна — функция, а другая — обратная функция, на линии y = x.
 На этой линии, проходящей через начало координат, имеется значение уклона 1. Это может быть выражено как;
На этой линии, проходящей через начало координат, имеется значение уклона 1. Это может быть выражено как;у = ф-1 (х)
, что равно; х = е (у)
Отношение y = f (x) несколько похоже на график f, за исключением того, что части x и y поменяны местами. Мы должны поменять местами x и y на осях, если мы хотим нарисовать график f-1.
Как найти обратную функцию?Обычно инверсии вычисляются путем замены координат x и y.Инверсии не обязательно являются функциями, но это отношения.
Чтобы гарантировать, что его обратная функция также будет функцией, исходная функция должна быть взаимно однозначной функцией. Функция называется взаимно однозначной, только если каждый второй элемент соответствует первому значению (значения x и y используются только один раз).
Используя тест горизонтальной линии, вы можете определить, является ли функция взаимно однозначной. Функция является взаимно однозначной, если горизонтальная линия пересекает ее в одной области и наоборот.
Типы обратной функции
Обратные функции включают тригонометрические функции, рациональные функции, гиперболические функции и логарифмические функции. Ниже приведены некоторые из наиболее распространенных функций в обратном порядке.
Обратные некоторые из наиболее распространенных функцийОбратные тригонометрические функции
Получая длину дуги, необходимую для получения определенного значения, обратные тригонометрические функции также известны как функции дуги.Этими функциями являются арксинус (sin-1), арккосинус (cos-1), арктангенс (tan-1), арксеканс (sec-1), арккосеканс (cosec-1) и арккотангенс (cot-1).
Обратная рациональная функция
f (x) — рациональная функция вида P (x) / Q (x), где Q (x) ≠ 0. Обратные функции можно найти, выполнив следующие шаги. Следующий пример также может помочь вам лучше понять концепцию.
Шаг 1: Заменить f (x) = y
Шаг 2: Поменять местами x и y
Шаг 3: Решите для y через x
Шаг 4: Замените y на f-1 (x), и получится функция, обратная функции.

Обратные гиперболические функции
Это обратные функции гиперболических функций, как и обратные тригонометрические функции. Sinh-1, cosh-1, tanh-1, csch-1, coth-1 и sech-1 — это шесть основных обратных гиперболических функций. Если вы хотите узнать больше об этих функциях, обратитесь к формуле обратной гиперболической функции.
Обратные логарифмические функции и обратные экспоненциальные функции
Функции, обратные экспоненциальным функциям, являются функциями натурального логарифма.Чтобы лучше понять обратные экспоненциальные функции и логарифмические функции, просмотрите следующий пример. Получите лучшее представление о том, как отвечать на похожие вопросы, и, следовательно, научитесь решать проблемы.
Пример обратных функцийПример 1: Найти обратную функцию функции f (x) = ln (x — 2)
Решение: Сначала замените f (x) на y
Итак, y = ln (x — 2)
Заменить уравнение экспоненциальным образом, x — 2 = ey
Теперь, решая для x,
х = 2 + ey
Теперь заменим x на y и, таким образом, f-1 (x) = y = 2 + ey
Пример 2: Решение: f (x) = 2x + 3, при x = 4
Решение: У нас,
f (4) = 2 × 4 + 3
ф (4) = 11
А теперь давайте подадим заявку на реверс 11.

ф-1 (11) = (11 — 3) / 2
ф-1 (11) = 4
Волшебным образом мы снова получаем 4.
Следовательно, f-1 (f (4)) = 4
Итак, когда мы применяем функцию f и ее обратную сторону, f-1 снова возвращает исходное значение, то есть f-1 (f (x)) = x.
Пример 3: Найдите обратное для функции f (x) = (3x + 2) / (x-1)
Решение: Сначала замените f (x) на y, и функция примет вид
у = (3х + 2) / (х-1)
Заменяя x на y, получаем
х = (3у + 2) / (у-1)
Теперь решите y через x:
х (у — 1) = 3у + 2
=> ху — х = 3у +2
=> ху — 3у = 2 + х
=> у (х — 3) = 2 + х
=> у = (2 + х) / (х — 3)
Итак, y = f-1 (x) = (x + 2) / (x-3)
ЗаключениеЭтот калькулятор функции инвертирования проведет вас через процесс инвертирования функций.Уравнение обратной функции может быть вычислено вручную, но оно по своей сути увеличивает неопределенность, поэтому этот удобный калькулятор обратной функции быстро предоставляет вам 100% безошибочные результаты.
Часто задаваемые вопросы о калькуляторе обратной функции
Что такое обратная функция?
Функция, возвращающая исходное значение, из которого был рассчитан результат, известна как обратная функция. В случае функции f (x), которая дает выходной y, обратный y, f-1 (y), даст значение x.
Как найти обратную функцию?
Предположим, что f (x) = 2x + 3 — функция.
Пусть f (x) = 2x + 3 = y
у = 2х + 3
х = (у-3) / 2 = ф-1 (у)
Это величина, обратная f (x).
Являются ли обратная функция и обратная функция одинаковыми?
Вопреки распространенному мнению, обратные функции и обратные — это не одно и то же. F-1 (x) — это функция, обратная функции, поскольку она возвращает исходное значение, из которого был рассчитан результат.В то время как обратная функция задается как 1 / f (x) или f (x) -1
Например, f (x) = 2x = y
f-1 (y) = y / 2 = x, является обратным к f (x).

Но, 1 / f (x) = 1 / 2x = f (x) -1 является обратной функцией функции f (x).
Что обратное 1 / x?
Пусть f (x) = 1 / x = y
Тогда обратным f (x) будет f-1 (y).
ф-1 (у) = 1 / х
Как решить функцию обратной тригонометрии?
Если нам нужно найти обратную тригонометрическую функцию sin x = ½, то значение x равно углу, синусоидальная функция которого равна ½.
Как известно, грех 30 ° = ½.
Следовательно, sin x = ½
x = sin-1 (½) = sin-1 (sin 30 °) = 30 °
В чем разница между обратной и обратной функцией?
Обратная функция никогда не возвращает исходные значения, а обратная функция всегда возвращает их. В качестве обратных функций 1 / f (x) представляется как f (x) -1. F-1 (x) — обозначение обратных функций.
Как обратная функция используется для преобразования температуры?
Обратные функции, используемые для обратного преобразования Цельсия (C) в градусы Фаренгейта (F) и наоборот:
Чтобы преобразовать градусы Фаренгейта (F) в градусы Цельсия (C): f (F) = 5/9 * (F — 32)
Обратная функция от Цельсия до Фаренгейта: f-1 (C) = (C * 9/5) + 32
Сообщение навигации
обратных функций
обратных функцийСодержание: Эта страница соответствует § 1.7 (стр. 150) текста.
Предлагаемые задачи из текста
с.158 # 1-4, 5, 8, 9, 12, 13, 15, 18, 21, 22, 27, 31, 34, 37, 46, 48, 51, 71, 74, 83
Определение обратной функции
Графики обратных функций
Существование инверсии
Поиск инверсий
Определение обратной функции
Прежде чем определять инверсию функции, нам нужно иметь правильный мысленный образ функции.
Рассмотрим функцию f (x) = 2x + 1. Мы знаем, как вычислить f при 3, f (3) = 2 * 3 + 1 = 7. В этом разделе это помогает думать о f как о преобразовании 3 в 7, а f превращает 5 в 11 и т. д.
Теперь, когда мы думаем о f как о «действующем» на числа и преобразовывающем их, мы можем определить обратное к f как функция, которая «отменяет» то, что сделала f. Другими словами, функция, обратная f, должна вернуть 7 к 3, и вернем -3 к -2 и т. Д.
Пусть g (x) = (x — 1) / 2.Тогда g (7) = 3, g (-3) = -2 и g (11) = 5, поэтому кажется, что g отменяет то, что сделал f, по крайней мере для этих трех значений. Чтобы доказать, что g является обратным к f, мы должны показать, что это верно для любого значения x в область f. Другими словами, g должен вернуть f (x) к x для всех значений x в области определения f. Итак, g (f (x)) = x должно выполняться для всех x в области определения f. Чтобы проверить это условие, убедитесь, что формула для g (f (x)) упрощается до x.
г (f (x)) = g (2x + 1) = (2x + 1 -1) / 2 = 2x / 2 = x.
Это упрощение показывает, что если мы выберем любое число и позволим f действовать им, то применение g к результату восстанавливает наш оригинальный номер. Нам также нужно увидеть, что этот процесс работает в обратном порядке, или что f также отменяет то, что делает g.
f (g (x)) = f ((x — 1) / 2) = 2 (x — 1) / 2 + 1 = x — 1 + 1 = x.
Обозначив f -1 как обратное к f, мы только что показали, что g = f -1 . (1/3)
Используйте калькулятор для вычисления значений f (g (4)) и g (f (-3)). g является обратной величине f, но из-за округления ошибка, калькулятор может не вернуть точное значение, с которого вы начали. Попробуйте f (g (-2)). Ответы будут отличаться для разные компьютеры. Однако на нашей тестовой машине f (g (4)) вернул 4; g (f (-3)) вернул 3; но, f (g (-2)) вернул -1.9999999999999991, что довольно близко к -2.
Калькулятор может дать нам хорошее представление о том, что g является обратной величиной f, но мы не можем проверить все возможные значения. из х.
(b) Докажите, что g является обратным к f, упростив формулы для f (g (x) и g (f (x)).
Вернуться к содержанию
Графики обратных функций
Мы видели примеры отражений в плоскости. Отражение точки (a, b) относительно оси x равно (a, -b), а отражение (a, b) вокруг оси y равно (-a, b). Теперь мы хотим поразмышлять о прямой y = x.
Отражением точки (a, b) относительно прямой y = x является точка (b, a) .Пусть f (x) = x 3 + 2. Тогда f (2) = 10 и точка (2,10) находится на графике f. Обратное к f должно возьмите 10 обратно к 2, то есть f -1 (10) = 2, поэтому точка (10,2) находится на графике f -1 . Смысл (10,2) — отражение на прямой y = x точки (2,10). Тот же аргумент можно сделать для всех пунктов графики f и f -1 .
График f -1 — это отражение относительно линии y = x графика f.
Вернуться к содержанию
Наличие инверсии
Некоторые функции не имеют обратных функций. Например, рассмотрим f (x) = x 2 . Есть два числа что f принимает значение 4, f (2) = 4 и f (-2) = 4. Если бы f имел обратный, то тот факт, что f (2) = 4, означал бы, что Функция, обратная f, возвращает 4 к 2. С другой стороны, поскольку f (-2) = 4, функция, обратная f, должна привести 4 к -2.Следовательно, не существует функции, обратной f.
Посмотрите на ту же задачу с точки зрения графиков. Если бы у f был обратный, то его график был бы отражением график функции f относительно прямой y = x. График f и его отражение относительно y = x показаны ниже.
Обратите внимание, что отраженный график не проходит тест вертикальной линии, так что это не график функции.
Это обобщает следующим образом: функция f имеет обратную тогда и только тогда, когда ее график отражается относительно line y = x, результат — график функции (проходит тест вертикальной линии).Но это можно упростить. Прежде чем отображать график, мы можем сказать, пересечется ли какая-либо вертикальная линия более одного раза, посмотрев как горизонтальные линии пересекают исходный график!
Тест горизонтальной линии
Пусть f — функция.
Если какая-либо горизонтальная линия пересекает график f более одного раза, то f не имеет обратной.
Если ни одна горизонтальная линия не пересекает график f более одного раза, то f действительно имеет обратный.
Свойство иметь обратное очень важно в математике, и у него есть название.
Определение : Функция f является взаимно однозначной тогда и только тогда, когда f имеет инверсию.
Следующее определение эквивалентно, и оно чаще всего дается для однозначного определения.
Альтернативное определение : функция f является взаимно однозначной , если для каждого a и b в своем домене, f (a) = f (b) влечет a = b.(1/3) (кубический корень из x). Ответ
Вернуться к содержанию
Поиск инверсий
Пример 1. Сначала рассмотрим простой пример f (x) = 3x + 2 .
График f представляет собой линию с наклоном 3, поэтому он проходит тест горизонтальной линии и имеет инверсию.
Чтобы вычислить f для числа x, необходимо выполнить два шага. Сначала мы умножаем x на 3, затем прибавляем 2.
Считая обратную функцию отменой того, что сделала f, мы должны отменить эти шаги в обратном порядке.
Шаги, необходимые для оценки f -1 , состоят в том, чтобы сначала отменить добавление 2 путем вычитания 2. Затем мы отменим умножение на 3 путем деления на 3.
Следовательно, f -1 (x) = (x — 2) / 3.
Этапы нахождения обратной функции f.
- Заменить f (x) на y в уравнении, описывающем функцию.
- Поменять местами x и y. Другими словами, замените каждый x на y и наоборот.
- Решить для y.
- Заменить y на f -1 (x).
Пример 2. f (x) = 6 — x / 2Шаг 1 у = 6 — х / 2. Шаг 2 х = 6 — у / 2. Шаг 3 х = 6 — у / 2. у / 2 = 6 — х.
y = 12 — 2x.
Шаг 4 f -1 (x) = 12 — 2x. Шаг 2 часто сбивает студентов с толку. Мы могли бы пропустить шаг 2 и найти x вместо y, но тогда мы бы получили с формулой в y вместо x. Формула будет такой же, но переменная будет другой. Избегать это мы просто меняем местами x и y перед тем, как решить.
Пример 3. f (x) = x 3 + 2
Это функция, с которой мы работали в упражнении 1. Из ее графика (показанного выше) мы видим, что у нее есть обратный. (Фактически, обратное ему было дано в упражнении 1.)
Шаг 1 y = x 3 + 2. Шаг 2 х = у 3 + 2. Шаг 3 х — 2 = у 3 .(1/3). Упражнение 3:
График f (x) = 1-2x 3 , чтобы увидеть, что у него есть обратное.

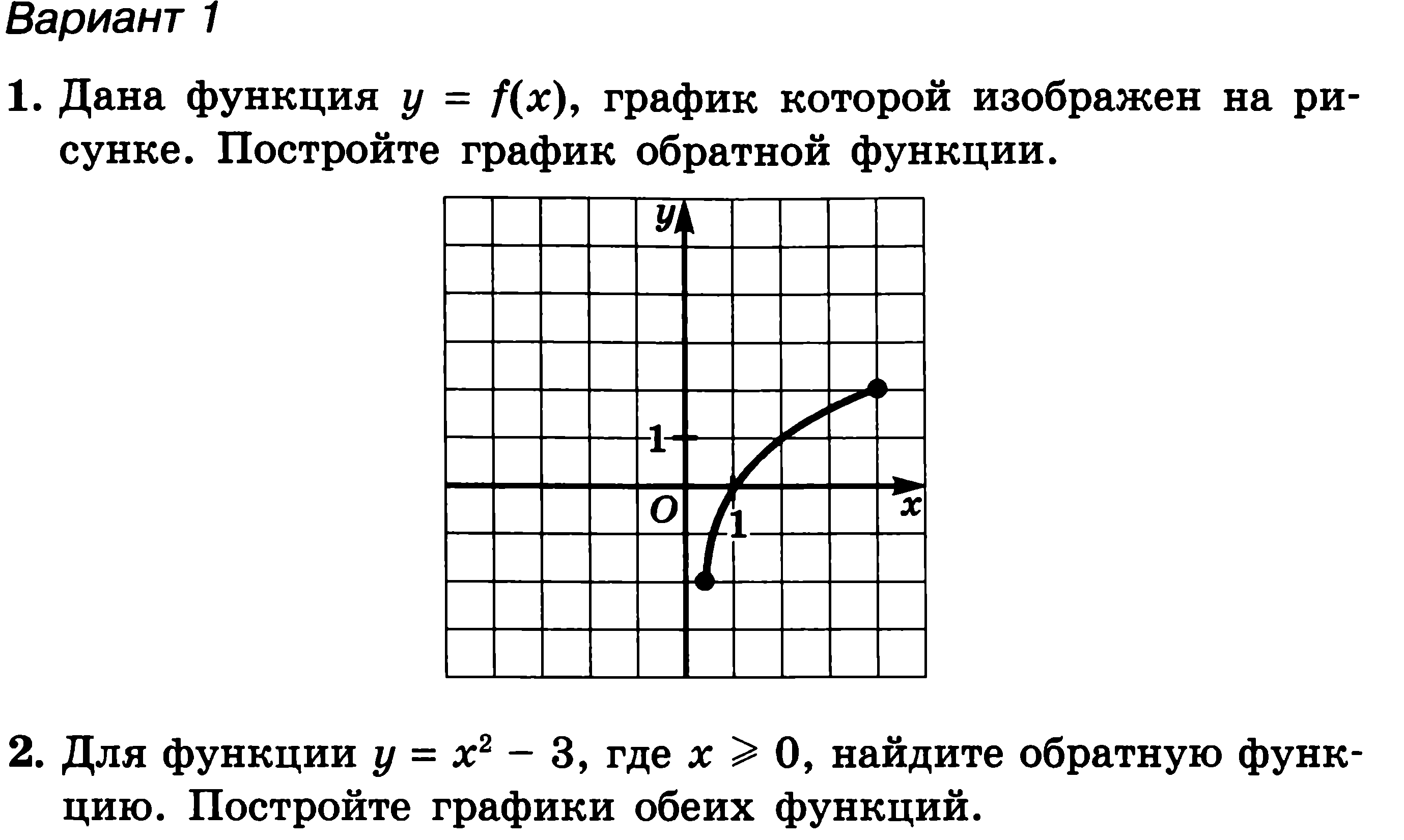
 ) Переехала?
) Переехала?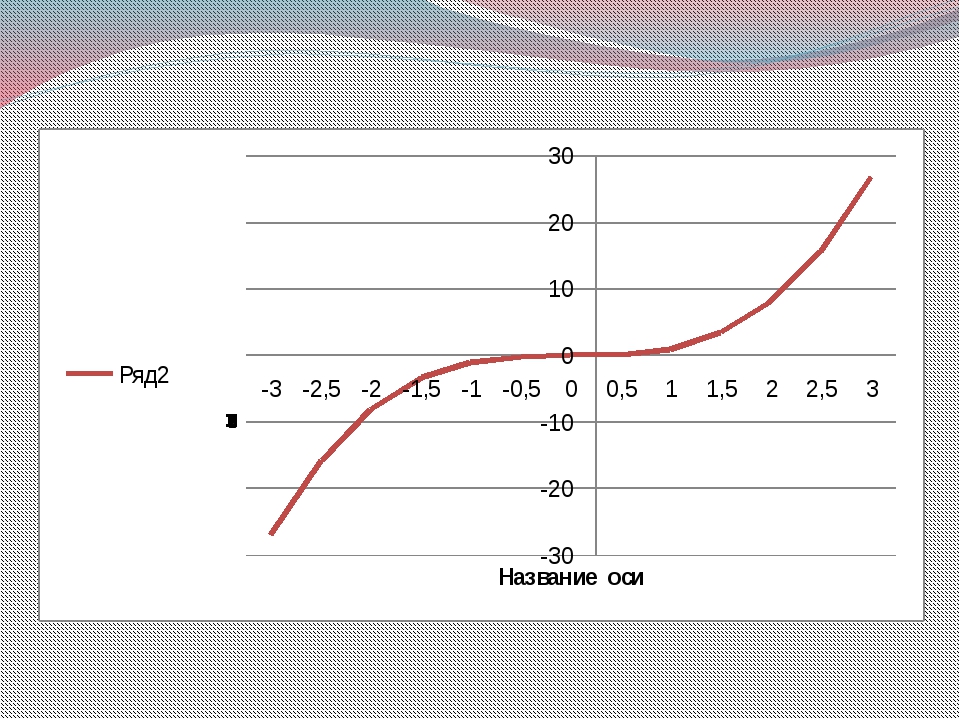 3 из 7)
3 из 7) 
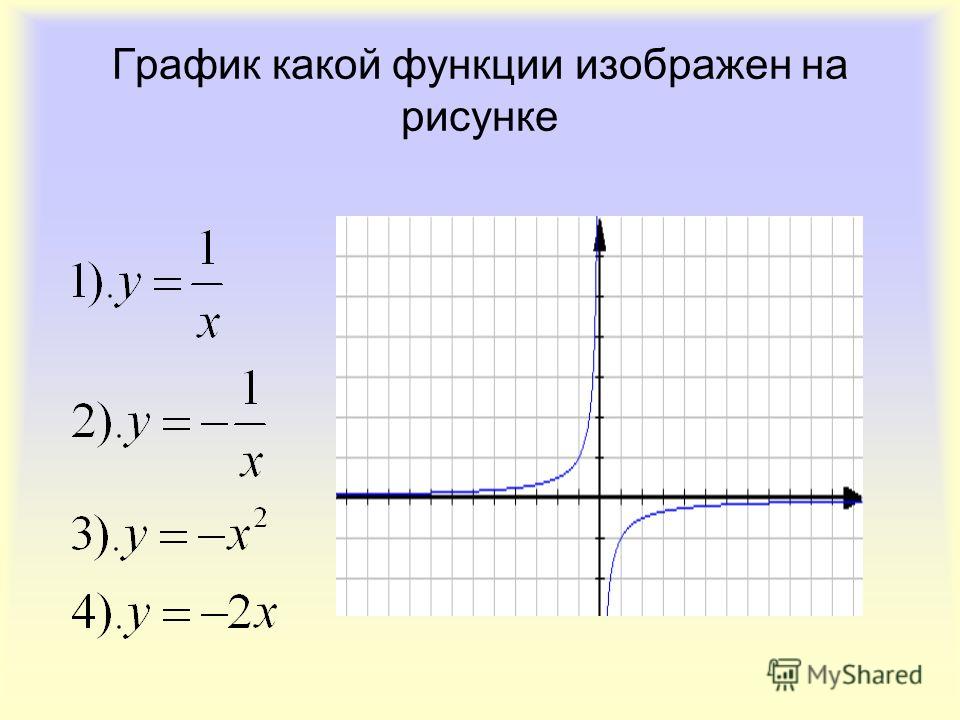 Но некоторые учителя все равно хотят изучать алгебру. Быть уверенным
чтобы уточнить у учителя, какой ответ будет приемлемым
— и сделайте это перед тестом ! авторское право
Элизабет Стапель 2000-2011 Все права защищены
Но некоторые учителя все равно хотят изучать алгебру. Быть уверенным
чтобы уточнить у учителя, какой ответ будет приемлемым
— и сделайте это перед тестом ! авторское право
Элизабет Стапель 2000-2011 Все права защищены
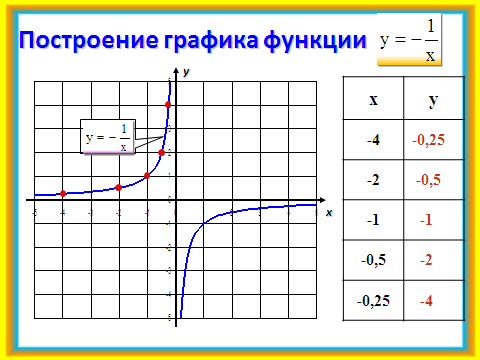 В этом случае, поскольку домен x < 0 и
диапазон (из графика) равен 1 < y ,
то обратный будет иметь область 1 < x и
диапазон y < 0. Вот
как выглядит алгебра:
В этом случае, поскольку домен x < 0 и
диапазон (из графика) равен 1 < y ,
то обратный будет иметь область 1 < x и
диапазон y < 0. Вот
как выглядит алгебра: )
)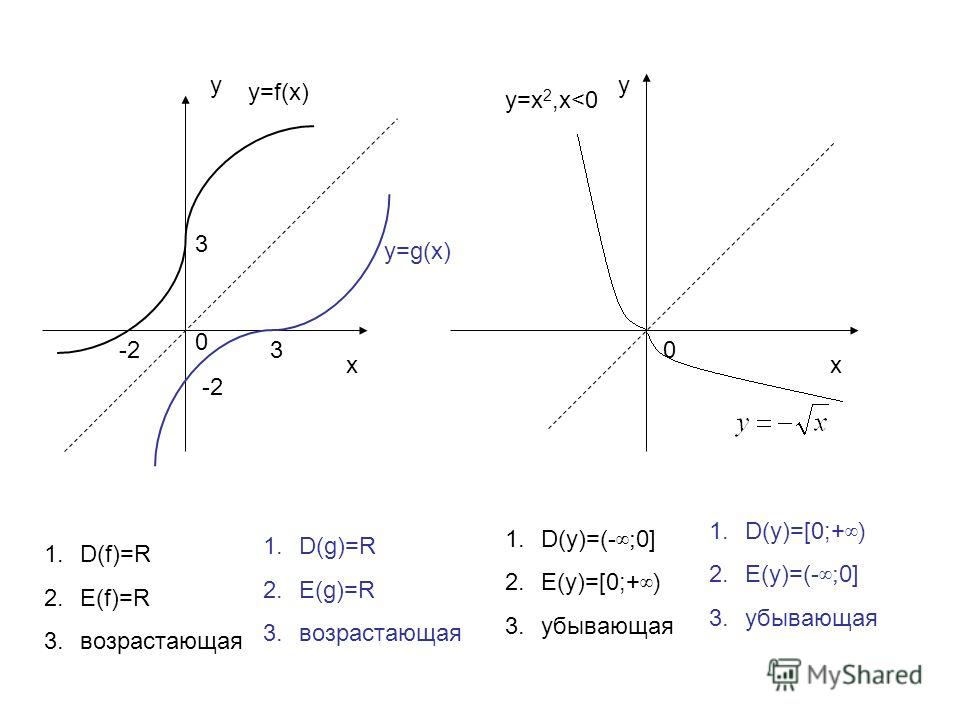 «Нахождение обратной функции». Пурпурная математика .
Доступно по номеру
«Нахождение обратной функции». Пурпурная математика .
Доступно по номеру 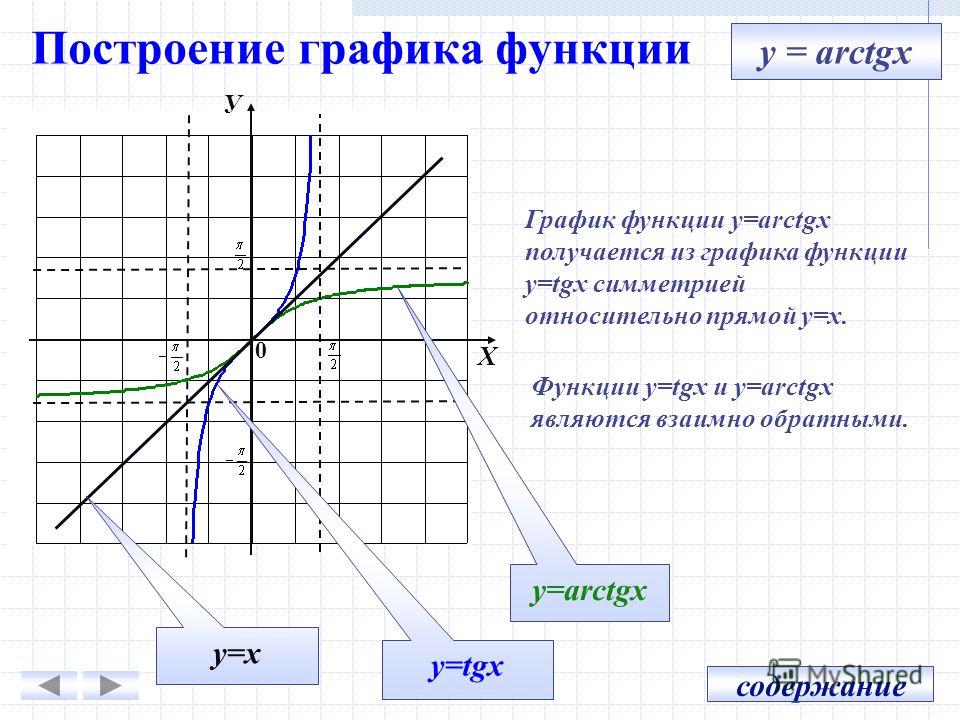 {- 1} _ {x} = id_ {x} \) .{3} +3 \)
{- 1} _ {x} = id_ {x} \) .{3} +3 \) Для лучшего понимания вот пример.
Для лучшего понимания вот пример. Другими словами, sin-1 (1) = sin-1 (sin 90) = 90 градусов.Следовательно, sin 90 градусов равен 1.
Другими словами, sin-1 (1) = sin-1 (sin 90) = 90 градусов.Следовательно, sin 90 градусов равен 1. На этой линии, проходящей через начало координат, имеется значение уклона 1. Это может быть выражено как;
На этой линии, проходящей через начало координат, имеется значение уклона 1. Это может быть выражено как;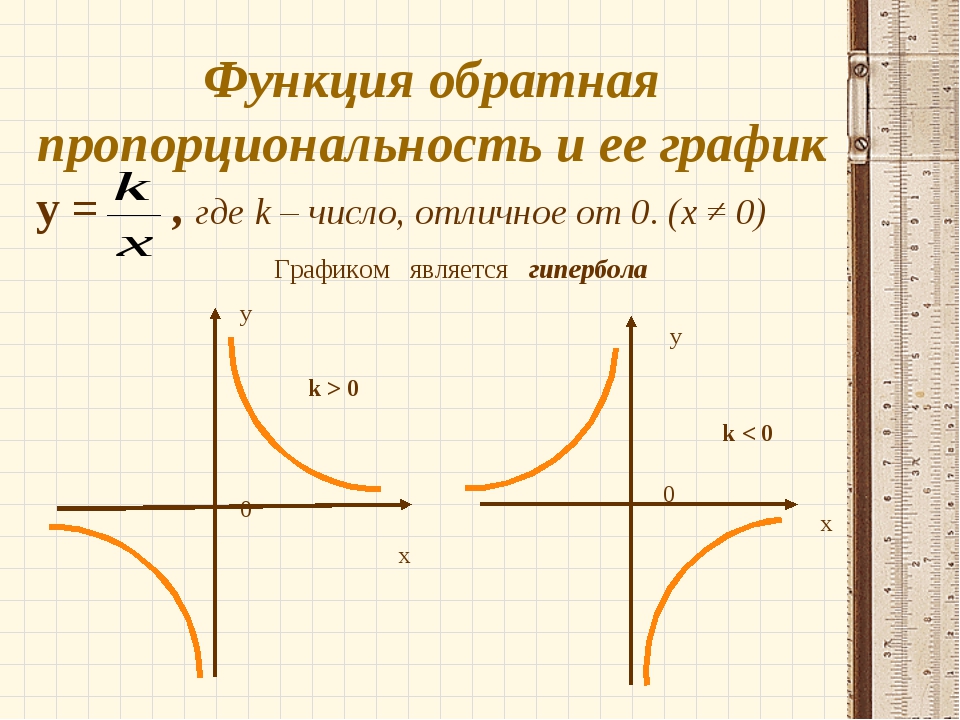
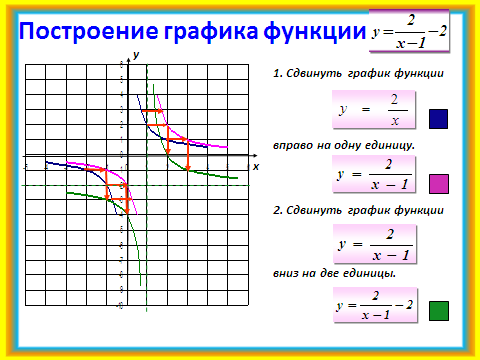
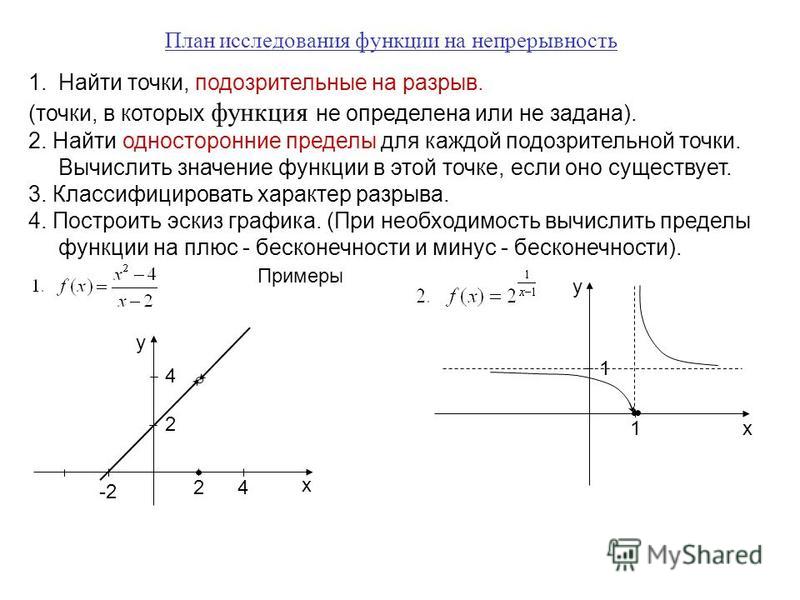


Ваш комментарий будет первым