Построить график неявной функции онлайн: График неявной функции · онлайн

графики, легенда, формат даты и сохранение

Модуль pyplot — это коллекция функций в стиле команд, которая позволяет использовать matplotlib почти так же, как MATLAB. Каждая функция pyplot работает с объектами Figure и позволяет их изменять. Например, есть функции для создания объекта Figure, для создания области построения, представления линии, добавления метки и так далее.

pyplot является зависимым от состояния (stateful). Он отслеживает статус объекта Figure и его области построения. Функции выполняются на текущем объекте.

Простой интерактивный график

Для знакомства с библиотекой matplotlib и с самим pyplot начнем создавать простой интерактивный график. В matplotlib эта операция выполняется очень просто. Достаточно трех строчек кода.

Но сначала нужно импортировать пакет pyplot и обозначить его как plt.

import matplotlib.pyplot as plt

В Python конструкторы обычно не нужны. Все определяется неявно. Так, при импорте пакета уже создается экземпляр plt со всеми его графическими возможностями, который готов к работе. Нужно всего лишь использовать функцию plot() для передачи функций, по которым требуется построить график.

Поэтому достаточно передать значения, которые нужно представить в виде последовательности целых чисел.

plt.plot([1,2,3,4])

[]

В этом случае генерируется объект Line2D. Это линия, представляющая собой линейный тренд точек, нанесенных на график.

Теперь все настроено. Осталось лишь дать команду показать график с помощью функции

show().

plt.show()

Результат должен соответствовать показанному на изображении. Он будет отображаться в окне, которое называется plotting window с панелью инструментов. Прямо как в MATLAB.

Окно графика

В этом окне есть панель управления, состоящая из нескольких кнопок.

Код в консоли IPython передается в консоль Python в виде набора команд:

import matplotlib. pyplot as plt
plt.plot([1,2,3,4])
plt.show()

Если же вы используете IPython QtConsole, то могли заметить, что после вызова plot() график сразу отображается без необходимости вызывать show().

Если функции plt.plot() передать только список или массив чисел, matplotlib предположит, что это последовательность значений

y на графике и свяжет ее с последовательностью натуральных чисел x: 0, 1, 2, 3, ….

Обычно график представляет собой пару значений (x, y), поэтому, если нужно определить его правильно, требуется два массива: в первом будут значения для оси x, а втором — для y. Функция plot() принимает и третий аргумент, описывающий то, как нужно представить точку на графике.

Свойства графика

На последнем изображении точки были представлены синей линией. Если не указывать явно, то график возьмет настройку функции plt.plot() по умолчанию:

• Размер осей соответствует диапазону введенных данных
• У осей нет ни меток, ни заголовков
• Легенды нет
• Соединяющая точки линия синяя

Для получения настоящего графика, где каждая пара значений (x, y) будет представлена в виде красной точки, нужно поменять это представление.

Если вы работаете в IPython, закройте окно, чтобы вернуться в консоль для введения новых команд. Затем нужно будет вызывать функцию show(), чтобы увидеть внесенные изменения.

plt.plot([1,2,3,4],[1,4,9,16],'ro')
plt.show()

Если же вы используете Jupyter QtConsole, то для каждой введенной команды будет появляться новый график.

в будущем в примерах средой разработки будет выступать IPython QtConsole.

Можно определить диапазон для осей x и y, задав значения в список [xmin, xmax, ymin, ymax] и передав его в качестве аргумента в функцию axis().

в IPython QtConsole для создания графика иногда нужно ввести несколько строк команд. Чтобы график при этом не генерировался с каждым нажатием Enter (перевод на новую строку), необходимо нажимать Ctrl + Enter. А когда график будет готов, остается лишь нажать Enter дважды.

Можно задать несколько свойств. Одно из них — заголовок, который задается через функцию title().

plt.axis([0,5,0,20])
plt.title('My first plot')
plt.plot([1,2,3,4],[1,4,9,16],'ro')
plt.show()

На следующем изображении видно, как новые настройки делают график более читаемым. Так, конечные точки набора данных теперь распределены по графику, а не находятся на краях. А сверху есть заголовок.

matplotlib и NumPy

Даже matplot, которая является полностью графической библиотекой, основана на NumPy. Вы видели на примерах, как передавать списки в качестве аргументов. Это нужно как для представления данных, так и для того, чтобы задавать границы осей. Внутри эти списки конвертируются в массивы NumPy.

Таким образом можно прямо добавлять в качестве входящих данных массивы NumPy. Массив данных, обработанный pandas, может быть использован matplotlib без дальнейшей обработки.

В качестве примера рассмотрим, как перенести на один график три тренда. Возьмем функцию sin из модуля math. ‘,t,y3,’ys’) plt.show()

Как видно на прошлом изображении, график представляет три разных тренда с помощью разных цветов и меток. В таких случаях когда тренд функции очевиден, график является не самой подходящим представлением — лучше использовать линии. Чтобы разделить их не только цветами, можно использовать паттерны, состоящие из комбинаций точек и дефисов.

plt.plot(t,y1,'b--',t,y2,'g',t,y3,'r-.')
plt.show()

если вы не пользуетесь IPython QtConsole со встроенной matplotlib или работаете с этим кодом в обычной сессии Python, используйте команду plt.show() в конце кода для получения объекта графика со следующего изображения.

Использование kwargs

Объекты, которые создают график, имеют разные характеризующие их атрибуты. Все они являются значениями по умолчанию, но их можно настроить с помощью аргументов-ключевых слов — kwargs.

Эти ключевые слова передаются в качестве аргументов в функции. В документации по разным функциям библиотеки matplotlib они всегда упоминаются последними вместе с kwargs. Например, функция plot() описана следующим образом.

matplotlib.pyplot.plot(*args, **kwargs)

В качестве примера с помощью аргумента linewidth можно поменять толщину линии.

plt.plot([1,2,4,2,1,0,1,2,1,4], linewidth=2.0)
plt.show()

Работа с несколькими объектами Figure и осями

До сих пор во всех примерах команды pyplot были направлены на отображение в пределах одного объекта. Но matplotlib позволяет управлять несколькими

Figure одновременно, а внутри одного объекта можно выводить подграфики.

Работая с pyplot, нужно помнить о концепции текущего объекта Figure и текущих осей (графика на объекте).

Дальше будет пример с двумя подграфиками на одном Figure. Функция subplot(), помимо разделения объекта на разные зоны для рисования, используется для фокусировки команды на конкретном подграфике.

Аргументы, переданные subplot(), задают режим разделения и определяют текущий подграфик. Этот график будет единственным, на который воздействуют команды. Аргумент функции subplot() состоит из трех целых чисел. Первое определяет количество частей, на которое нужно разбить объект по вертикали. Второе — горизонтальное разделение. А третье число указывает на текущий подграфик, для которого будут актуальны команды.

Дальше будут отображаться тренды синусоиды (синус и косинус), и лучше всего разделить полотно по вертикали на два горизонтальных подграфика. В график передают числа 211 и 212.

t = np.arange(0,5,0.1)
y1 = np.sin(2*np.pi*t)
y2 = np.sin(2*np.pi*t)
plt.subplot(211)
plt.plot(t,y1,'b-.')
plt.subplot(212)
plt.plot(t,y2,'r--')
plt.show()

Теперь — то же самое для двух вертикальных подграфиков. Передаем в качестве аргументов 121 и 122.

t = np.arange(0.,1.,0.05)
y1 = np.sin(2*np.pi*t)
y2 = np.cos(2*np.pi*t)
plt.subplot(121)
plt. plot(t,y1,'b-.')
plt.subplot(122)
plt.plot(t,y2,'r--')
plt.show()

Добавление элементов на график

Чтобы сделать график более информативным, недостаточно просто представлять данные с помощью линий и маркеров и присваивать диапазон значений с помощью двух осей. Есть и множество других элементов, которые можно добавить на график, чтобы наполнить его дополнительной информацией.

В этом разделе добавим на график текстовые блоки, легенду и так далее.

Добавление текста

Вы уже видели, как добавить заголовок с помощью функции title(). Два других текстовых индикатора можно добавить с помощью меток осей. Для этого используются функции

xlabel() и ylabel(). В качестве аргумента они принимают строку, которая будет выведена.

количество команд для представления графика постоянно растет. Но их не нужно переписывать каждый раз. Достаточно использовать стрелки на клавиатуре, вызывая раннее введенные команды и редактируя их с помощью новых строк (в тексте они выделены жирным).

Теперь добавим две метки на график. Они будут описывать тип значений на каждой из осей.

plt.axis([0,5,0,20])
plt.title('My first plot')
plt.xlabel('Counting')
plt.ylabel('Square values')
plt.plot([1,2,3,4],[1,4,9,16],'ro')
plt.show()

Благодаря ключевым словам можно менять характеристики текста. Например, можно поменять заголовок, выбрав другой шрифт и увеличив его размер. Также можно менять цвета меток осей, чтобы акцентировать внимание на заголовке всего графика.

plt.axis([0,5,0,20])
plt.title('My first plot', fontsize=20, fontname='Times New Roman')
plt.xlabel('Counting', color='gray')
plt.ylabel('Square values',color='gray')
plt.plot([1,2,3,4],[1,4,9,16],'ro')
plt.show()

Но в matplotlib можно делать даже больше: pyplot позволяет добавлять текст в любом месте графика. Это делается с помощью специальной функции text().

text(x,y,s, fontdict=None, **kwargs)

Первые два аргумента — это координаты, в которых нужно разметить текст. s — это строка с текстом, а fontdict (опционально) — желаемый шрифт. Разрешается использовать и ключевые слова.

Добавим метку для каждой точки графика. Поскольку первые два аргумента в функции являются координатами, координаты всех точек по оси

y немного сдвинутся.

plt.axis([0,5,0,20])
plt.title('My first plot', fontsize=20, fontname='Times New Roman')
plt.xlabel('Counting', color='gray')
plt.ylabel('Square values',color='gray')
plt.text(1,1.5,'First')
plt.text(2,4.5,'Second')
plt.text(3,9.5,'Third')
plt.text(4,16.5,'Fourth')
plt.plot([1,2,3,4],[1,4,9,16],'ro')
plt.show()

Теперь у каждой точки есть своя метка.

Поскольку matplotlib — это графическая библиотека, созданная для использования в научных кругах, она должна быть способна в полной мере использовать научный язык, включая математические выражения. matplotlib предоставляет возможность интегрировать выражения LaTeX, что позволяет добавлять выражения прямо на график. 2$’, fontsize=20, bbox={‘facecolor’:’yellow’,’alpha’:0.2}) plt.grid(True) plt.plot([1,2,3,4],[1,4,9,16],’ro’) plt.legend([‘First series’]) plt.show()

По умолчанию легенда добавляется в правом верхнем углу. Чтобы поменять это поведение, нужно использовать несколько аргументов-ключевых слов. Так, для выбора положения достаточно передать аргумент loc со значением от 0 до 10. Каждая из цифр обозначает один из углов. Значение 1 — значение по умолчанию, то есть, верхний правый угол. В следующем примере переместим легенду в левый верхний угол, чтобы она не пересекалась с точками на графике.

Код положения	Положение
0	лучшее
1	Верхний правый угол
2	Верхний левый угол
3	Нижний левый угол
4	Нижний правый угол
5	Справа
6	Слева по центру
7	Справа по центру
8	Снизу по центру
9	Сверху по центру
10	По центру

Тут важно сделать одну ремарку. ‘) plt.plot([1,2,3,4],[0.5,2.5,4,12],’b*’) plt.legend([‘First series’,’Second series’,’Third series’], loc=2) plt.show()

Сохранение графиков

В этом разделе разберемся, как сохранять график разными способами. Если в будущем потребуется использовать график в разных Notebook или сессиях Python, то лучший способ — сохранять графики в виде кода Python. С другой стороны, если они нужны в отчетах или презентациях, то подойдет сохранение в виде изображения. Можно даже сохранить график в виде HTML-страницы, что пригодится при работе в интернете.

Сохранение кода

Как уже стало понятно, объем кода, отвечающего за представление одного графика, постоянно растет. Когда финальный результат удовлетворяет, его можно сохранить в файле .py, который затем вызывается в любой момент.

Также можно использовать команду %save [имя файла] [количество строк кода], чтобы явно указать, сколько строк нужно сохранить. Если весь код написан одним запросом, тогда нужно добавить лишь номер его строки.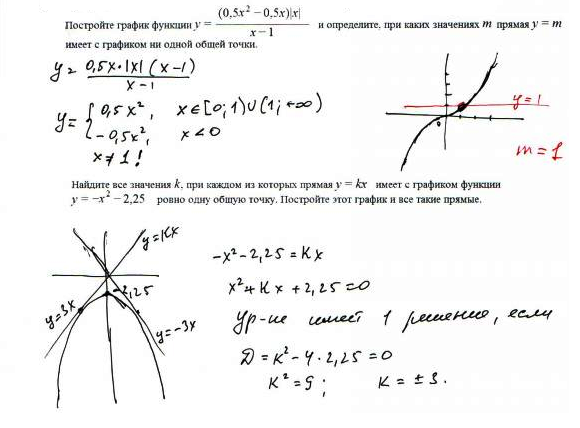 ‘) plt.plot([1,2,3,4],[0.5,2.5,4,12],’b*’) plt.legend([‘First series’,’Second series’,’Third series’], loc=2) plt.show()

Позже, когда вы откроете сессию IPython, у вас уже будет готовый график и его можно редактировать с момента сохранения этой командой:

ipython qtconsole --matplotlib inline -m my_first_chart.py

Либо его можно загрузить заново в один запрос в QtConsole с помощью команды %load.

%load my_first_chart.py

Или запустить в уже активной сессии с помощью %run.

%run my_first_chart.py

в определенных случаях последняя команда будет работать только после ввода двух предыдущих.

Сохранение сессии в HTML-файл

С помощью IPython QtConsole вы можете конвертировать весь код и графику, представленные в текущей сессии, в одну HTML-страницу. Просто выберите File → Save to HTML/XHTML в верхнем меню.

Будет предложено сохранить сессию в одном из двух форматов: HTML и XHTML. Разница между ними заключается в типе сжатия изображения. Если выбрать HTML, то все картинки конвертируются в PNG. В случае с XHTML будет выбран формат SVG.

В этом примере сохраним сессию в формате HTML в файле my_session.html.

Дальше программа спросит, сохранить ли изображения во внешней директории или прямо в тексте. В первом случае все картинки будут храниться в папке my_session_files, а во втором — будут встроены в HTML-код.

Сохранение графика в виде изображения

График можно сохранить и виде файла-изображения, забыв обо всем написанном коде. Для этого используется функция savefig(). В аргументы нужно передать желаемое название будущего файла. Также важно, чтобы эта команда шла в конце, после всех остальных (иначе сохранится пустой PNG-файл).

plt.axis([0,5,0,20])
plt.title('My first plot', fontsize=20, fontname='Times New Roman')
plt.xlabel('Counting', color='gray')
plt.ylabel('Square values',color='gray')
plt. ')
plt.plot([1,2,3,4],[0.5,2.5,4,12],'b*')
plt.legend(['First series','Second series','Third series'], loc=2)
plt.savefig('my_chart.png')

Файл появится в рабочей директории. Он будет называться my_chart.png и включать изображение графика.

Обработка значений дат

Одна из основных проблем при анализе данных — обработка значений дат. Отображение даты по оси (обычно это ось x) часто становится проблемой.

Возьмем в качестве примера линейный график с набором данных, который включает 8 точек, где каждая представляет точку даты на оси x в следующем формате: день-месяц-год.

import datetime
import numpy as np
import matplotlib.pyplot as plt
events = [datetime.date(2015,1,23), 
          datetime.date(2015,1,28),
          datetime.date(2015,2,3),
          datetime.date(2015,2,21),
          datetime.date(2015,3,15),
          datetime.date(2015,3,24),
          datetime.date(2015,4,8),
          datetime.date(2015,4,24)]
readings = [12,22,25,20,18,15,17,14]
plt. plot(events,readings)
plt.show()

Автоматическая расстановка отметок в этом случае — настоящая катастрофа. Даты сложно читать, ведь между ними нет интервалов, и они наслаиваются друг на друга.

Для управления датами нужно определить временную шкалу. Сперва необходимо импортировать matplotlib.dates — модуль, предназначенный для работы с этим типом дат. Затем указываются шкалы для дней и месяцев с помощью MonthLocator() и DayLocator(). В этом случае форматирование играет важную роль, и чтобы не получить наслоение текста, нужно ограничить количество отметок, оставив только год-месяц. Такой формат передается в качестве аргумента функции DateFormatter().

Когда шкалы определены (один — для дней, второй — для месяцев) можно определить два вида пометок на оси x с помощью set_major_locator() и set_minor_locator() для объекта xaxis. Для определения формата текста отметок месяцев используется set_major_formatter.

Задав все эти изменения, можно получить график как на следующем изображении.

import matplotlib.dates as mdates
months = mdates.MonthLocator()
days = mdates.DayLocator()
timeFmt = mdates.DateFormatter('%Y-%m')
events = [datetime.date(2015,1,23), 
          datetime.date(2015,1,28),
          datetime.date(2015,2,3),
          datetime.date(2015,2,21),
          datetime.date(2015,3,15),
          datetime.date(2015,3,24),
          datetime.date(2015,4,8),
          datetime.date(2015,4,24)]
readings = [12,22,25,20,18,15,17,14]
fig, ax = plt.subplots()
plt.plot(events, readings)
ax.xaxis.set_major_locator(months)
ax.xaxis.set_major_formatter(timeFmt)
ax.xaxis.set_minor_locator(days)
plt.show()

Область определения функции двух переменных

Цели работы:

• повторить и систематизировать нахождение области определения функции, закрепить это понятие и наглядно представить в координатной плоскости и в пространстве;
• рассмотреть аналитические и геометрические методы не изолированно друг от друга, а в тесной взаимосвязи. Это позволит облегчить переход от стандартных решений конкретных математических задач к нестандартным;
• воспитание интереса к математике и мультимедиа, активности, мобильности; восприятие компьютера, как инструмента обучения;
• использование компьютера для нахождения области определения и построения графиков с помощью графического редактора 3D Grapher 1.2, Copyright © 2000-2002 RomanLab Software и формирование информационной компетентности учащихся.

Определение функции двух переменных

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

A= – функция трех переменных.

Способы задания функций нескольких переменных

Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции. Наиболее часто функция задается аналитически — это явное задание функции или неявное задание

Например, — это явно заданная функция двух переменных; уравнение задает неявно две функции двух переменных.

Область определения функции

Непрерывное множество пар значений независимых переменных , при которых функцияопределена, называется областью определения функции.

Область определения называется замкнутой областью, если она включает в себя свою границу; открытой областью, если она не включает в себя свою границу; ограниченной областью, если может быть помещена в круг конечного радиуса.

Геометрически изобразить область определения функции можно только для функций:

• одной переменной – на прямой ,
• двух переменных – на плоскости ,
• трех переменных– в пространстве .

Геометрическое изображение самой функции возможно только для функции двух переменных.

Графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область D, которая является областью определения функции.

На рис. изображена поверхность графика функции и ее область определения.

В курсе учебного материала 9-го класса мы рассматриваем следующие задания на нахождение и построение области определения функции.

ПРИМЕРЫ

Найти область определения функции

Решение. Областью определения данной функции является вся плоскость, т. к. нет ограничений на переменные x и y.

2. Найти область определения функции .

Решение. Данная функция определена, когда xy > 0, т.е. в тех точках координатной плоскости, в которых знаки координат x и y - одинаковы. Это будут точки, лежащие в I и III координатных четвертях, т.е. множество точек, удовлетворяющих условиям:

и

3. Найти область определения функции .

Решение. Данная функция определена при условии, когда

т.е. . Это множество точек, лежащих внутри круга с центром в начале координат, радиус которого равен 2.

Изобразить на координатной плоскости Оху область определения функции .

Решение. Подкоренное выражение должно быть неотрицательно, т.е. следовательно, . Геометрическим решением неравенства служит полуплоскость, расположенная выше прямой и сама прямая.

5. Найти область определения функции и изобразить её графически.

.

Решение. Областью определения функции является множество точек плоскости, координаты которых удовлетворяют системе неравенств:

6. Изобразить на координатной плоскости Оху область определения функции

Решение. Эта функция определена, когда подкоренное выражение неотрицательно, т.е. Данным соотношениям удовлетворяют координаты всех точек, находящихся внутри кольца, образованного двумя окружностями с центрами в начале координат и радиусами R=3, R=4.

7. Изобразить на координатной плоскости Оху область определения функции

.

Решение. Учащиеся не могут найти область определения данной функции аналитически, но с помощью графического редактора 3D Grapher 1.2 это выполняется легко.

В Приложении приведено ещё несколько примеров, с решениями, для учащихся девятых классов.

Для учащихся 10-11 классов мы предлагаем систему упражнений по нахождению и построению области определения функции двух переменных. При этом отрабатываются свойства логарифмических, тригонометрических и обратных тригонометрических функций. Данные упражнения можно использовать при изучении нового материала, при повторении, при решении уравнений и неравенств.

Найти и изобразить на плоскости область определения функции

Решение. Область определения функции есть пересечение областей определения слагаемых функции. Для первой функции подкоренное выражение должно быть неотрицательным, т.е. Если значение логарифмической функции неотрицательно, то выражение, стоящее под знаком логарифма, должно быть больше или равно единице, т.е. отсюда . Это неравенство задает нам множество точек плоскости, лежащих вне окружности с центром в начале координат, радиуса 2, включая и точки данной окружности.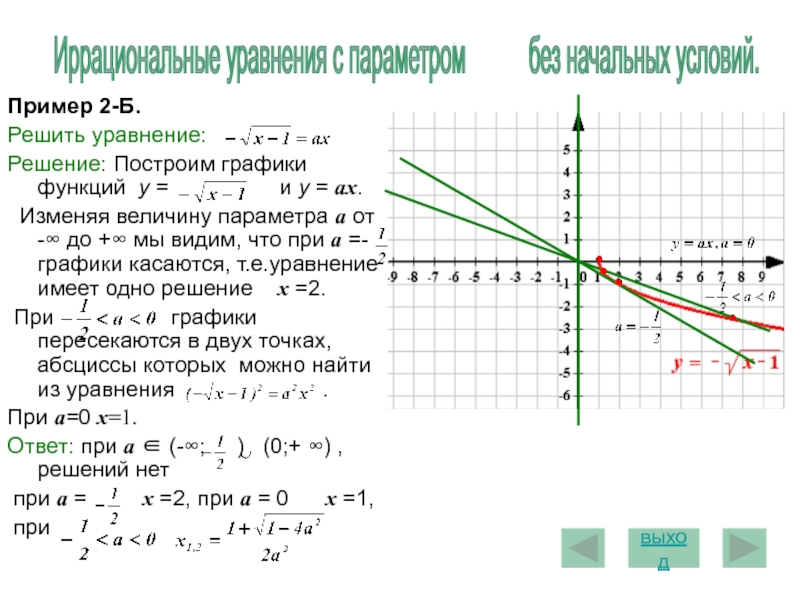 Вторая функция определена при Следовательно, Имеем две параболы с вершиной в начале координат . Поэтому полученное неравенство задает нам часть плоскости, заключенную между этими параболами, включая границы без начала координат. Третья функция определена при

Областью определения данной функции является общая часть найденных областей определения слагаемых.

Покажите на координатной плоскости xOy область определения функции

.

Решение. Ограничения для функции имеют вид:

3. Изобразить область определения функции

Решение. Эта функция определена при , т.е.

Областью определения является часть плоскости, расположенная между двумя прямыми.

4. Найти область определения функции .

Решение. Областью определения функции является решение неравенства. Поэтому нужно решить неравенство

Решая данное неравенство, получим Это область, заключенная между двумя параболами и .

5. Построить область определения функции

Решение. Область определения данной функции определяется системой неравенств:

Первое неравенство определяет круг с центром в точке (-2;0) и радиусом равным 2 за исключением его границы:

Второе неравенство определяет I и III координатные четверти, за исключением осей.

В Приложении приведено ещё несколько примеров, с решениями, для учащихся десятых и одиннадцатых классов.

Рассмотрим задание С5, используя функцию двух переменных.

Найдите все значения параметра а, при которых система , имеет ровно два решения.

Решение. Из второго уравнения находим y =. Первое уравнение принимает вид .

Пусть . В этом случае уравнение имеет единственное решение .

Запишем второе уравнение в виде = 0. Его дискриминант равен 4 , и он положителен, поскольку . Уравнение имеет два различных корня и Значит, в этом случае система имеет ровно два решения и .

Пусть теперь 1. В этом случае уравнение если и имеет корни, то только больше единицы Но тогда дискриминант уравнения = 0 отрицателен. Решений нет.

Ответ: .

С помощью графического редактора задаем функцию двух переменных , Находим значения а, при которых функция обращается в ноль.

На рисунке видно, что решением является интервал от 0 до 1.

При подготовке учащихся к итоговой аттестации мы сталкиваемся с тем, что задания уровня С5 решаются тяжело и не сразу. А ведь это функция двух переменных! Оперирование геометрическими образами упрощает решение задач с параметрами, а в некоторых случаях геометрический подход часто является единственно возможным методом решения. В сборнике ЕГЭ-2011 предложено задание.

Найдите все значения а, такие, что для любого х выполняется неравенство.

Решение. Рассмотрим функцию

Если то убывает.

Если то возрастает.

Значит, наименьшее значение функции равно или , или . Поэтому решение задачи получаем из решения системы

Решений нет.

Ответ: .

C помощью графического редактора мы построили график функции и определили значение параметра а при . График функции в системе координат выглядит следующим образом.

Приложение 1

Приложение 2

Приложение 3

Список источников и литературы.

1. Математика (математический анализ): учебно-методическое пособие для студентов нематематических специальностей / О.Ю. Ватюкова, Е.Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд., Волгоград: Волгоградское научное издательство, 2009. – 238с.
2. Дифференциальное исчисление функций нескольких переменных: типовой расчет по высшей математике / Сост. : А. В. Анкилов, Н. Я. Горячева, Т. Б. Распутько.- Ульяновск: УлГТУ, 2004.-32 с.
3. ЕГЭ 2011. Математика. Типовые тестовые задания / И.Р. Высоцкий, Д.Д. Гущин, П.И.Захаров, В.С. Панферов, и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: Издательство “Экзамен”, 2011.-63с.
4. Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.- сост. И.Р.Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: АСТ: Астрель, 2010.-93с.
5. Мордкович А.Г. Алгебра . 9 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений / А.Г.Мордкович, П.В.Семенов .—11-е изд., стер. -М.: Мнемозина, 2009.-224 с.
6. Смирнова И.М. Геометрия. 10-11 кл.: Учеб. для общеобразоват. учреждений (гуманитарный профиль).- М.: Мнемозина,2004. -223с.

График явных и неявных уравнений

Последнее обновление: 9 февраля 2023 г. Вернон Моррис

Был большой интерес к лицензированию метакалькулятора. Наша компания Engaging Edu лицензировала различные виды интеллектуальной собственности за последние несколько лет, и в последнее время наши научные/графические расчеты пользуются большим спросом — будь то компании, которые хотят ее купить, или компании, которые хотят ее лицензировать.

Повторяющаяся проблема в процессе лицензирования приложения заключается в том, как обрабатывать серверные запросы графического калькулятора, но прежде чем двигаться дальше, давайте удостоверимся, что мы определили две важные «математические» фразы: 92 = 25 (окружность с радиусом 5)

sin(x) = cos(y) (прикольный график, у которого нет названия)

Зачем проводить различие между этими двумя типами уравнений?

Потому что графически отображать неявные уравнения намного сложнее и требует больших вычислительных ресурсов. С другой стороны, явных уравнений относительно прямолинейны в графическом виде и не требуют такого же уровня мощности ЦП.

Например, ваш типичный графический калькулятор Texas Instruments уровня средней школы может выполнять только явные уравнения (даже TI-89, я думаю, может только графически отображать явные уравнения).

А как насчет мета-калькулятора?

Может отображать явные уравнения и неявные; однако, чтобы иметь возможность выполнять всю сложную математику, необходимую для неявного построения графиков, мы не можем полагаться на ваш браузер, который, вероятно, зависнет, если попытается обработать определенные графики. Вместо этого приложение отправляет запрос нашему серверному приложению.

Однако нет необходимости использовать сервер для явных уравнений. Одно из улучшений, которое мы планировали внедрить этой осенью, — это графическое отображение явных в вашем браузере — улучшение, которое может только ускорить процесс, поскольку приложению не нужно будет взаимодействовать с сервером, а сервер также будет получать меньше запросов. так что он мог бы посвятить свои числа тем уравнениям, которые этого требуют.

Поэтому в этом месяце мы работаем над тем, чтобы перенести отображение явных уравнений в ваш браузер! Изменение, которое, как я полагаю, останется незамеченным тысячами пользователей, ежедневно рисующих уравнения; тем не менее, эти небольшие улучшения в сочетании начинают создавать ощутимо более производительное приложение. (Natural-cure.org)

У нас есть различные комплексные калькуляторы, которые вы можете использовать онлайн бесплатно. Вы можете выбрать калькулятор t-теста, график, матрицу, стандартное отклонение, статистику и научные калькуляторы. Проверьте это здесь.

Калькулятор неявной дифференциации с шагами

Содержание

Получите виджет!

Знакомство с калькулятором производных. Добавьте этот инструмент на свой сайт для простых и эффективных расчетов производных.

Обратная связь

Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!

Доступно в приложении

Загрузите приложение «Калькулятор потери веса» для своего мобильного телефона.

Гугл игры Магазин приложений

Знакомство с калькулятором неявной дифференциации?

Калькулятор неявного дифференцирования — это онлайн-инструмент, с помощью которого можно вычислить любую производную функцию через x и y. Калькулятор неявной производной с шагами позволяет новичкам легко научиться этому быстро, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.

Интегрирование и дифференцирование обратны друг другу. Вы можете найти полезные калькуляторы интеграции на этом веб-сайте, а также полезные блоги.

Что такое неявное дифференцирование?

В исчислении слово неявный используется для функций, которые могут быть выражены как через x, так и через y. Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается путем

Отдельного дифференцирования каждого члена

Выражения производной зависимой переменной в виде символа

Решения полученного выражения для символа.

Формула, используемая калькулятором неявной дифференциации 92 \right) = \frac{d}{dx} (1) $

Преимущества использования калькулятора неявных функций

Всегда лучше использовать онлайн-инструмент, чем ручной метод. Вот некоторые из главных преимуществ калькулятора dy/dx с шагами:

1. Он экономит ваше время, которое вы тратите на ручные вычисления.
2. Неявные калькуляторы просты и удобны в использовании.
3. Обеспечивает точные и пошаговые результаты.
4. Вы можете увидеть график и возможные промежуточные шаги неявного дифференцирования.
5. Калькулятор неявных производных с пошаговыми инструкциями поможет вам попрактиковаться в Интернете, чтобы закрепить свои понятия.

Преимущества использования калькулятора dy dx

Всегда полезно и разумно использовать калькулятор второй неявной производной с шагами для обучения и практики. Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:

1. Он экономит ваше время, затрачиваемое на ручные вычисления.
2. Этот неявный калькулятор с шагами прост и удобен в использовании.
3. Вы можете попрактиковаться, чтобы закрепить свои концепции неявной дифференциации.
4. Дает пошаговые точные результаты.
5. Вы можете найти график и возможные промежуточные шаги неявного дифференцирования.
6. Для использования калькуляторов производных неявных функций не требуется никакой платы или подписки.

Как пользоваться калькулятором неявной дифференциации?

Наш калькулятор неявного дифференцирования с шагами очень прост в использовании. Просто выполните следующие действия, чтобы получить точные результаты. Эти шаги:

1. Введите функцию в основной ввод или загрузите пример.
2. Выберите переменную, относительно которой вы хотите оценить.
3. Подтвердите в предварительном просмотре правильность функции или переменной.
4. Нажмите на кнопку «РАССЧИТАТЬ», чтобы получить пошаговый ответ.

Часто задаваемые вопросы

Является ли неявное дифференцирование тем же, что и частичное дифференцирование?

При неявном дифференцировании функция дифференцируется по одной переменной, но в конце другая переменная исчезает.