Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение. Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о логарифмической функции и логарифмах и некоторые методы решения логарифмических уравнений.
Примеры подробного решения >>
ln(b) или log(b) или log(e,b)- натуральный логарифм числа blog(10,b) — десятичный логарифм числа b
log(a,b) — логарифм b по основанию a
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x4 = 81
По определению арифметического корня имеем \( x = \sqrt[4]{81} = 3 \)
Задача 2. Решить уравнение 3x = 81
Запишем данное уравнение так: 3x = 34, откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том,
что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3.
Но уже, например, уравнение 3x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень.
Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение ax = b, где a > 0, \( a \neq 1 \), b > 0, имеет единственный корень. Этот корень называют
логарифмом числа b no основанию a и обозначают logab
Например, корнем уравнения 3x = 81 является число 4, т.е. log381 = 4.
Определение. Логарифмом положительного числа b по основанию a, где a > 0, \( a \neq 1 \), называется показатель степени, в которую надо возвести число a, чтобы получить b
Например:
\( \log_3 \frac{1}{9} = -2 \), так как \( 3^{-2} = \frac{1}{9} \)
log77 = 1, так как 71 = 7
Определение логарифма можно записать так:
Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.
Вычислить log64128
Обозначим log64128 = х. По определению логарифма 64x = 128. Так как 64 = 26, 128 = 27,
то 2 6x = 27, откуда 6x = 7, х = 7/6.
Ответ log64128 = 7/6
Вычислить \( 3^{-2\log_3 5} \)
Используя свойства степени и основное логарифмическое тождество, находим
Решить уравнение log3(1-x) = 2
По определению логарифма 32 = 1 — x, откуда x = -8
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
1) loga(bc) = logab + logac
3) logabr = r logab
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log10b
Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо logeb
Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \dots + \frac{1}{1 \cdot 2 \cdot 3 \cdot \dots \cdot n} + \dots $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.
Для этого используется формула замены основания логарифма:
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$
Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, \( a \neq 1 \)
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0
5) Если a > 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0
Если 0 ax принимает положительные значения при 0
отрицательные при х > 1.
Ось Oy является вертикальной асимптотой графика функции y = logax


Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Теорема. Если logax1 = logax2 где a > 0, \( a \neq 1 \), x1 > 0, x2 > 0, то x1 = x2
Логарифмическая функция y = logax и показательная функция y = ax, где a > 0, \( a \neq 1 \), взаимно обратны.
Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х2 + 4х + 3 = 8, т.е. х2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого
уравнения.
Ответ x = 1
Решить уравнение lg(2x2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x2 — 4x + 12) = lg(x2 + 3x)
откуда
2x2 — 4x + 12 = x2 + 3x
x2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x 1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Введите график функции
Исследуем график функции y=f(x), для этого задайте функцию f(x).
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:

- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
| Основные функции
модуль x: abs(x)
| 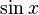 : sin[x] или Sin[x] : sin[x] или Sin[x]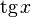 : tan[x] или Tan[x] : tan[x] или Tan[x]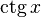 : cot[x] или Cot[x] : cot[x] или Cot[x]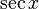 : sec[x] или Sec[x] : sec[x] или Sec[x]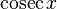 : csc[x] или Csc[x] : csc[x] или Csc[x]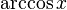 : ArcCos[x] : ArcCos[x]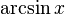 : ArcSin[x] : ArcSin[x]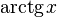 : ArcTan[x] : ArcTan[x]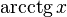 : ArcCot[x] : ArcCot[x]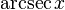 : ArcSec[x] : ArcSec[x]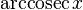 : ArcCsc[x] : ArcCsc[x]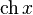 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 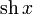 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]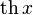 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]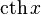 : coth[x] или Coth[x] : coth[x] или Coth[x]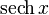 : sech[x] или Sech[x] : sech[x] или Sech[x]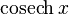 : csch[x] или Csch[е] : csch[x] или Csch[е]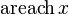 : ArcCosh[x] : ArcCosh[x]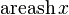 : ArcSinh[x] : ArcSinh[x]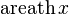 : ArcTanh[x] : ArcTanh[x]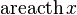 : ArcCoth[x] : ArcCoth[x]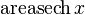 : ArcSech[x] : ArcSech[x]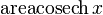 : ArcCsch[x] : ArcCsch[x] |
Вычисление логарифма числа онлайн | umath.ru
Онлайн калькулятор логарифмов
Калькулятор вычисляет логарифм числа онлайн. Можно вводить как десятичные дроби (в качестве разделителя для десятичных дробей можно использовать как точку, так и запятую), так и обычные (например, если нужно вычислить логарифм 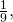 то в поле «число» можете смело писать 1/9).
то в поле «число» можете смело писать 1/9).
Помните, что операция взятия логарифма определена только для положительных чисел, а основание логарифма должно быть положительным и не должно равняться единице.
Что такое логарифм числа?
Примеры
Пример 2. Вычислить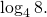
Решение. Воспользуемся следующим свойством логарифмов:
![\[\log_{a^{\alpha}}{b^{\beta}} = \frac{\beta}{\alpha}\log_a{b}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-dedd0477895656027b8c3f5ea44a1ee9_l3.png)
Получаем:
![\[\log_4 8 = \log_{2^2}{2^3} = \frac{3}{2}\log_2 2.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-3b4e2cd5f0c103ec094891b1fddd507a_l3.png)
Так как 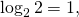 то
то 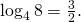
Как видите, всё очень просто!
Логарифм числа  по основанию 10 называют десятичным и обозначают
по основанию 10 называют десятичным и обозначают 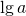 , а логарифм числа
, а логарифм числа  по основанию
по основанию  называют натуральным и обозначают
называют натуральным и обозначают 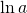 .
.
Про свойства логарифмов читайте здесь.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
Введите график функции
Важно phi должно лежать в правильном промежутке, иначе график не сможет построиться
Построим график функции в полярных координатах r=r(φ),
где 0 <= φ <= 2π,
но вы можете задать свои границы φ.
Задайте также полярную функцию r(φ).
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Логарифмический график

Хочу рассказать об одной важной вещи, которую должен знать каждый начинающий инвестор.
Сразу скажу, что когда я сам начинал инвестировать, я не знал об этом. Речь идет о логарифмическом графике, позволяющем объективно оценить долгосрочный рост активов.
Приведу определение логарифмического графика из Википедии:
«Логарифмический масштаб (шкала) — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах»
Если вы не учились на физ-мате, для вас это наверняка звучит как полная белиберда, собственно, как и для меня. Поэтому объясню своими словами.
Есть два вида графиков: линейный и логарифмический.
Первый вы все знаете: у него вертикальная шкала растет линейно, например, 0, 10, 20, 30, 40 и т.д. Т.е. шкалу задает величина между нулем и первым значением (абсолютный прирост в единицах, в примере – 10 единиц).
Со вторым интереснее: здесь рост нелинейный (геометрический), например, 0, 10, 20, 40, 80 и т.д. Тут шкалу задает относительный (процентный) прирост. В моем примере это рост в каждом периоде на 100%.
Разница в том, что логарифмический график более адекватно показывает относительный прирост. Т.е. в моем примере выше с логарифмическим графиком каждый год (пусть 0 — цена в первый год, 10 — во второй, 20 — в третий и т.д.) цена росла на 100%. И на графике это будет прямой трендовой линией.
Если этот же актив поместить на линейный график, то сначала будет казаться, что он почти не растет, а к концу мы увидим невероятный рост. Будет складываться ощущение, что актив перекуплен и вот-вот должен рухнуть.
Чтобы наглядно это увидеть я привел несколько сравнений линейных и логарифмических графиков одних и тех же активов. Я взял данные по S&P 500, Татнефти и Новатэку и McDonald’s из Investing.com.




Если на графиках Татнефти и Новатэка эффект выражен не так сильно ввиду недолгого периода существования Московской биржи (хотя тоже существенен), то на американских графиках (S&P 500 и McDonald’s) разница очевидна. Посмотрите на McDonald’s: на линейном графике кажется, как будто люди с ума сошли: покупают невероятно выросший актив. В то же время складывается ощущение, что раньше McDonald’s вообще не рос и не представлял инвестиционной привлекательности (до 1990 года).
Если же посмотреть на логарифмический график McDonald’s, то мы увидим, что сейчас темп роста, наоборот, замедлился в процентном отношении. Именно этот график показывает правдивую картину. McDonald’s давно уже стал зрелой компанией, и он физически не может расти быстрее, потому что и так занимает огромную долю рынка. Он может только поддерживать стабильный, устойчивый рост.
Поэтому если вы придерживаетесь, что называется, long-term investments, т.е. долгосрочных инвестиций, то обязательно смотрите на логарифмический график, чтобы объективно оценить тренд и темпы роста цен на активы на длинных периодах времени.
https://www.instagram.com/long_term_investments/
Создать график и найти кратчайший путь. На странице справки вы найдете обучающее видео.
Настройка матрицы смежности. Используйте запятую «,» в качестве разделителя
Мультиграфная матрица содержит вес минимальных ребер между вершинами.
Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной
Настройка матрицы заболеваемости.Используйте запятую «,» в качестве разделителя.
Матрица неверна. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на проверку и в случае успеха будет добавлен на сайт.
Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «справка», чтобы открыть справку о формате матрицы смежности
.Невозможно создать график. Матрица заболеваемости имеет неправильный формат.Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате Матрица инцидентности
.Выбор и перемещение объектов мышью или перемещение рабочей области.
Перетащите курсор для перемещения объектов
Выбор и перемещение объектов мышью или перемещение рабочей области.
Перетащите курсор для перемещения объектов
Нажмите в рабочую область, чтобы добавить новую вершину. Перечисление вершин
Выберите первую вершину ребра
Выберите второй вершин ребра
Выберите начальную вершину кратчайшего пути
Выберите конечную вершину кратчайшего пути
Самая короткая длина пути составляет% d
Путь не существует
Нажмите на объект, чтобы удалить
Добавить ребро
Направлено
Ненаправленный
Матрица смежности
Сохранить
Отмена
самое низкое расстояние
Матрица заболеваемости
Сохранение График
закрыть
Количество подключенных компонентов
Количество слабо связанных компонентов составляет
Что вы думаете о сайте?
Имя (электронная почта для обратной связи)
Обратная связь
Отправить
Чтобы задать нам вопрос или отправить нам комментарий, напишите нам на
исправить матрицу
помощь
Матрица имеет неправильный формат
Сохранить графическое изображение
Полный отчет
Краткий отчет
График не имеет эйлерова цикла
График имеет цикл Эйлера
Обработка…
Добавить вершину
Переименовать вершину
переименовать
и
Редактировать вес
не имеет веса
переименование группы
Голосовать
Рекомендовать алгоритмы
Граф не имеет эйлерова траектории
Граф имеет эйлерову траекторию
График минимальных расстояний
Проверить, чтобы сохранить
Показать матрицу расстояний
Матрица расстояний
Выберите источник максимального потока
Выберите мойку максимального потока
Максимальный поток от% 2 до% 3 равен% 1
Поток из% 1 в% 2 не существует
Источник
Мойка
График имеет не гамильтонов цикл
График имеет гамильтонов цикл
График не имеет гамильтонова пути
Графикимеет гамильтонов путь
Выберите начальную вершину обхода
Заказ прохождения:
Кромочный изгиб
Отменить
Сохранить график
По умолчанию
Vertex Style
Edge Style
Цвет фона
Multigraph поддерживает не все алгоритмы
не имеет веса
Используйте Cmd⌘ для выбора нескольких объектов.
Используйте Ctrl для выбора нескольких объектов.
Перетащите группу.
Копировать группу
Удалить группу
Поиск в ширину
Граф раскраски
Найти подключенные компоненты
Поиск в глубину
Найти цикл Эйлера
Найти Эйлерова дорожка
Алгоритм Флойда – Варшалла
Организовать график
Найти гамильтонов цикл
Найти гамильтонову дорожку
Найти Максимальный поток
Поиск минимального остовного дерева
Визуализация на основе веса
Поиск по графику радиуса и диаметра
Найти кратчайший путь, используя алгоритм Дейкстры
Рассчитать степень вершин
,Графический калькулятор— Draw Curve
× Программное обеспечение для построения графиков онлайн , также известное как графопостроитель , это онлайн-построитель кривых , который позволяет строить функции онлайн. Просто введите выражение в соответствии с x функции, которая будет построена, используя обычные математические операторы. Построитель кривой особенно подходит для исследования функции , это позволяет получитьОнлайн-плоттер также способен рисовать параметрические кривые и нарисуйте полярные кривые, что касается функций, то достаточно ввести выражение для представления в соответствии с параметром t.
Операторы, которые будут использоваться в графическом калькуляторе для написания математических функций, следующие:
- + за добавление
- — для вычитания
- * для умножения
- ^ Для власти
- / Для подразделения
Это программное обеспечение для построения кривых позволяет использовать следующие обычные математические функции :
- абс (абсолютное значение), график абсолютной величины
- арккос (арккосин), сюжет арккозина
- арксин (арксинус), сюжет арксинус
- арктан (арктангенс), сюжет арктангенс
- ч (гиперболический косинус), сюжет гиперболического косинуса
- cos (косинус), сюжет косинус
- котан (котангенс), участок котангенс
- кот (гиперболический котангенс), сюжет гиперболический котангенс
- кубический корень (корень куба), сюжет кубический корень
- exp (экспоненциальный), сюжет экспоненциальный
- ln (логарифм напьера), сюжет напиерианский логарифм
- log (логарифм), сюжетный логарифм
- ш (гиперболический синус), сюжет гиперболического синуса
- грех (синус), сюжет синус
- кв.м (квадратный корень), сюжет квадратный корень
- загар (тангенс), касательная графика
- -й (тангенс гиперболический), построение гиперболического тангенса
- Сюжетные функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно , просто введите выражение функции для построения графика и нажмите кнопку Добавить, графическое представление функции появляется мгновенно, есть возможность повторить операцию для графика других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — это «x».
С помощью курсора можно получить координаты точек на кривой . Для этого нажмите на кривую, чтобы появился курсор, а затем перетащите ее вдоль кривой, чтобы увидеть ее координаты.
Кривые могут быть удалены из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку «Удалить все» в меню.
Можно изменить кривую, присутствующую на графике, выбрав ее, отредактировав ее выражение и нажав на кнопку редактирования.
Онлайновый построитель кривых имеет несколько опций, которые позволяют настраивать график. Чтобы получить доступ к этим параметрам, нажмите кнопку параметров.Затем можно определить границы графиков, Чтобы подтвердить эти изменения, необходимо снова нажать кнопку «Параметры».
- Нарисуйте касательную функции к точке
- Участок производной функции
Онлайн-плоттер позволяет нарисовать касательную функции в точке , чтобы сделать это, вы просто строите желаемую функцию, а затем, когда функция нарисована, нажмите на меню, параметры, а затем кнопка тангенса, которая появляется на экране, тангенс затем рисуется, можно изменить точку касательной, что приводит к перерисовке касательной.Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции , чтобы сделать это, вы просто строите желаемую функцию, затем после того, как функция нарисована, нажмите на меню, на опции, а затем на производную кнопку, которая появляется, производная функции затем наносится на график.
Построитель кривой также можно использовать для вычисления производной функции и на участок это для этой цели, Вы должны построить желаемую функцию, а затем, когда функция нарисована, выберите ее, нажав на нее, красный курсор появляется на кривой. Затем нажмите на меню, на опции, а затем на производную кнопку «выражение», которая появляется на экране, производная функции затем строится и вычисляется.(«Выражение» представляет выражение, которое должно быть выведено и нанесено на график).
Плоттер позволяет нарисовать параметрическую кривую , чтобы сделать это, вам просто нужно ввести абсциссу, ординату как функцию t, затем нажмите на кнопку «построить параметрическую кривую», кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривой может использоваться для построения полярной кривой . Для этого просто введите выражение полярной кривой как функцию от t, затем нажмите кнопку «построить полярную кривую», кривая автоматически отобразится с двумя курсорами, чтобы отобразить нужные точки.
Можно перемещаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и переместить его по графику, координаты X и Y отображаются под графиком.
Можно изменить область сюжета, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического отображения.
Графический калькулятор предлагает возможность масштабирования и перемещения области графика. Сделать это, используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб на кривых,
- — позволяет уменьшить масштаб на кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт выполняется как изображение в формате PNG.Для этого вам необходимо перейти в меню графика, затем в подменю экспорта графиков. Затем калькулятор отображает кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение, также возможно скопировать изображение. Чтобы вернуться к нормальному отображению калькулятора, используйте кнопку «Выход из режима изображения».
,plot — Алгоритм построения 2d xy графа
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Загрузка…
- Авторизоваться зарегистрироваться
текущее сообщество
Wolfram | Примеры Alpha: Графика и графика
функции
График функции одной переменной в виде кривой на плоскости.
Построить функцию одной переменной:
Укажите явный диапазон для переменной:
Составьте реальную функцию:
Постройте функцию в логарифмическом масштабе:
Участок в логарифмическом масштабе:
Дополнительные примеры
3D Сюжеты
Постройте функцию двух переменных как поверхность в трехмерном пространстве.
Постройте функцию из двух переменных:
Укажите явные диапазоны для переменных:
Дополнительные примеры
уравнения
Постройте набор решений уравнения с двумя или тремя переменными.
Постройте решение уравнения с двумя переменными:
,
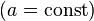
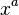 : x^a
: x^a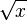 : Sqrt[x]
: Sqrt[x]![\sqrt[n]{x}](/800/600/https/upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n)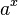 : a^x
: a^x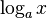 : Log[a, x]
: Log[a, x]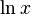 : Log[x]
: Log[x]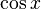 : cos[x] или Cos[x]
: cos[x] или Cos[x]
Ваш комментарий будет первым