Калькулятор логарифмов и антилогарифмов онлайн
Логарифмирование — это операция, обратная возведению в степень. Если вы задаетесь вопросом, в какую степень нужно возвести 2, чтобы получить 10, то вам на помощь придет логарифм.
Обратная операция для возведения в степень
Возведение в степень — это повторяющееся умножение. Для возведения двойки в третью степень нам потребуется вычислить выражение 2 × 2 × 2. Обратная операция для умножения — это деление. Если верно выражение, что a × b = c, то обратное выражение b = a / c так же верно. Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако ab не равно ba, за исключением единственного случая, когда 22 = 42. В выражении ab = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Понятие логарифма
Давайте попробуем решить простое уравнение вида 2x = 16. Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Теперь попробуем решить 2x = 20. Сколько раз нужно умножить двойку на саму себя, что бы получить 20? Это сложно, ведь 24 = 16, а 25 = 32. Рассуждая логически, корень этого уравнения располагается между 4 и 5, причем ближе к 4, возможно 4,3? Математики не терпят приблизительных вычислений и хотят знать точный ответ. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.
Выражение log2 20 читается как логарифм 20 по основанию 2. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.
Таким элегантным способом вы можете решить любое простое показательное уравнение. Например, для уравнений:
- 4x = 125, x = log4 125;
- 12x = 432, x = log12 432;
- 5x = 25, x = log5 25.
Последний ответ x = log5 25 математикам не понравится. Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 52 = 25. Поэтому для уравнения вида 5x = 25, x = 2.
Десятичный логарифм
Десятичный логарифм — это функция по основанию 10. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Натуральный логарифм
Натуральный логарифм — это функция по основанию e. В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
В какую степень нужно возвести число e, чтобы получить 10? Ответом был бы loge 10, но математики обозначают натуральный логарифм как ln, поэтому ответ будет записан как ln10. Тоже самое с выражениями loge 35 и loge 40, верная форма записи которых – ln34 и ln40.
Антилогарифм
Антилогарифм — это число, которому соответствует значение выбранного логарифма. Простыми словами, в выражении loga b антилогарифмом считается число ba. Для десятичного логарифма lga, антилогарифм равен 10a, а для натурального lna антилогарифм равняется ea. По сути, это тоже возведение в степень и обратная операция для логарифмирования.
Физический смысл логарифма
Нахождение степеней — чисто математическая задача, но для чего нужны логарифмы в реальной жизни? В начале развития идеи логарифмирования данный математический инструмент использовался для сокращения объемных вычислений. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Логарифмы нашли применение и в сфере изображения графических процессов. Если требуется нарисовать график функции, которая принимает значения 1, 10, 1 000 и 100 000, то маленькие значения будут невидны и визуально они сольются в точку около нуля. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.
Физический же смысл логарифмирования — это описание временных процессов и изменений. Так, логарифм по основанию 2 позволяет определить, сколько требуется удвоений начального значения для достижения определенного результата.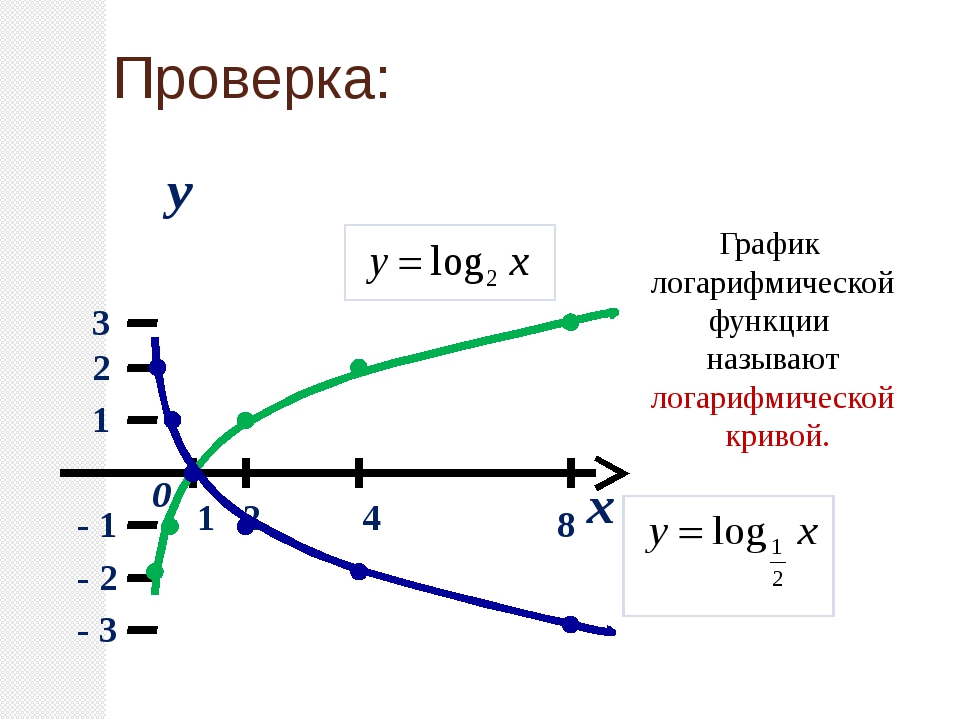 Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Наша программа представляет собой сборник из четырех онлайн-калькуляторов, которые позволяют вычислить логарифм по любому основанию, десятичную и натуральную логарифмическую функцию, а также десятичный антилогарифм. Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.
Примеры из реальной жизни
Школьная задача
Как было сказано выше, иррациональные значения по типу log2 345 не требуют дополнительных преобразований, и такой ответ полностью удовлетворит учителя математики. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:
- log7 65 — иррациональное число;
- log3 243 — целое число 5;
- log5 95 — иррациональное;
- log8 512 — целое число 3;
- log2 2046 — иррациональное.

Таким образом, значения log3 243 и log8 512 вам потребуется переписать как 5 и 3 соответственно.
Потенцирование
Потенцирование — это нахождение антилогарифма числа. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:
- для n = 1 antlog = 10;
- для n = 1,5 antlog = 31,623;
- для n = 2,71 antlog = 512,861.
Непрерывный рост
Натуральный логарифм позволяет описывать процессы непрерывного роста. Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.
Поиск количества удесятирений
Допустим, за 30 лет количество персональных компьютеров увеличилось с 250 000 до 1 миллиарда. Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.
Заключение
Несмотря на сложность логарифмов и нелюбовь детей к ним в школьные годы, этот математический инструмент находит широкое применение в науке и статистике. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.
Логарифмическая функция
Основные сведения
Логарифмической функцией называется функция вида y = logax, где a > 0 и a ≠ 1.
График функции имеет следующий вид:
Рассмотрим свойства функции:
- Областью определения функции является множество всех положительных чисел D(y) = (0; +∞).
- Множеством значений функции являются все действительные числа R.
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.
- Функция непереодическая.
- Нули функции: функция пересекает координатную ось Ox в точке (1; 0).
- При a > 1 функция возрастает, при 0 < a < 1 функция убывает.
Примеры решения задач
Задание 1.
В одной координатной плоскости построить графики функций:
- y = log
- y = log3x
- y = log5x
- y = log10x
Решение.
Для начала построим график функции y = log2x. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = log2x возрастает на всей области определения D(y)=R+, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем больше основание a (если a > 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задание 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y.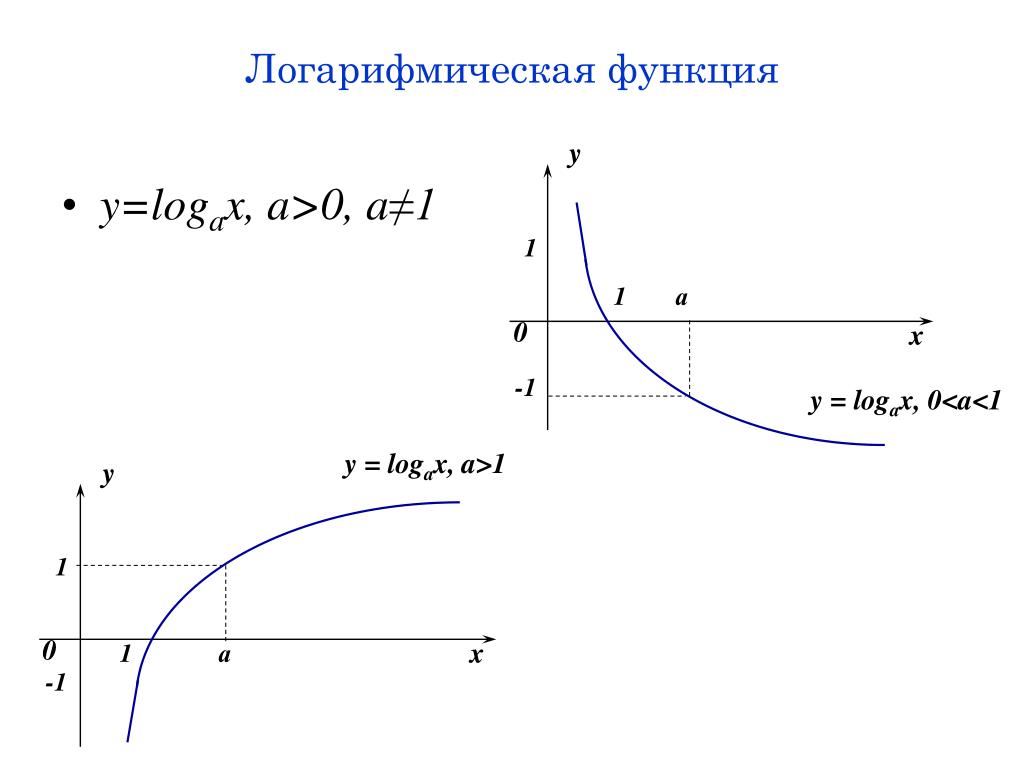 Функция убывает на всей своей области определения: D(y) = R, так как основание функции 0 < < 1.
Функция убывает на всей своей области определения: D(y) = R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. С осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем меньше основание a (если 0 < a < 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти обасть определеления функции:
- y = logπ(2x-4)
- y = log2((x-1)(x+5))
Решение
1. y = logπ(2x-4).
Область определения данной функции задается следующим неравенством:
2x-4 > 0
Решим это линейное неравенство:
2x > 4 → x > 2
2. y = log2((x-1)(x+5)).
Логарифм определен, если подлогарифмическая функция является положительной, то есть искомая область определения: D(y): (x-1)(x+5) > 0.
Решим полученное уравнение методом интервалов. Для этого найдем нули каждого из сомножителей:
x-1 = 0 → x = 1
x+5 = 0 → x = -5
Наносим их на координатную прямую и определяем знак неравенства на каждом из полученных промежутков.
Поскольку решаем неравенство со знаком «>», то оставляем промежутки со знаком «+», т. е D(y): (-∞; -5)U(1; +∞).
Ответ: D(y): (-∞; -5)U(1; +∞).
Логарифмическая функция. Преобразования графика логарифмической функции(11 класс)
Разработка урока обобщения и систематизации знаний в 11 классе по теме « Логарифмическая функция.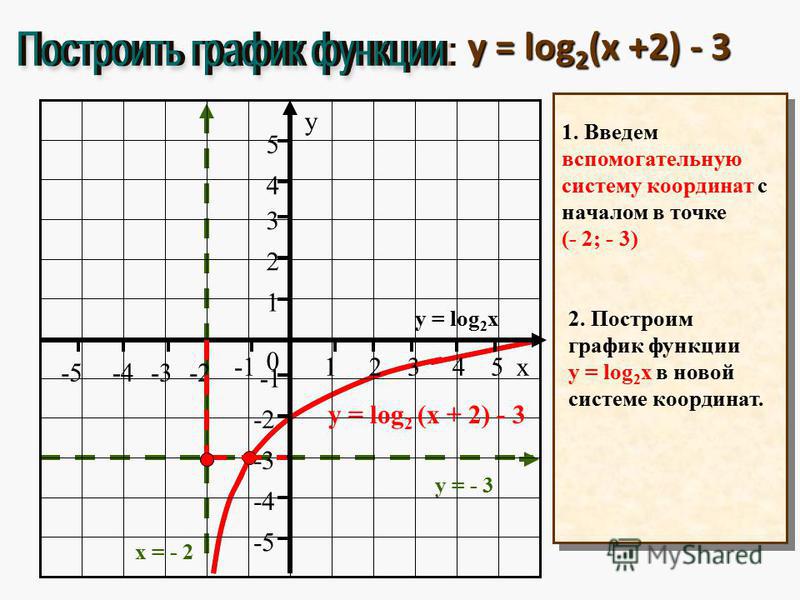 Преобразования графика логарифмической функции»
Преобразования графика логарифмической функции»
Этап урока
Время, мин.
Приёмы и методы
Содержание деятельности
Организация начала урока
1
словесный
Приветствует, проверяет готовность к уроку, организует внимание
Подготовка учащихся: сообщение темы (проблемы). Исторический материал и связь с окружающим миром – для развития интереса к предмету
5
Словесный, фронтальная беседа, словесно-наглядный с применением презентаций учащегося
Предлагает план работы на уроке.
Учащиеся с помощью презентации рассказывают о связи логарифмической функции с окружающим миром
Проверка готовности к уроку по материалу предыдущего урока (самими учащимися)
5
Индивидуальный интерактивный тест с последующей самопроверкой
Предъявляет задания.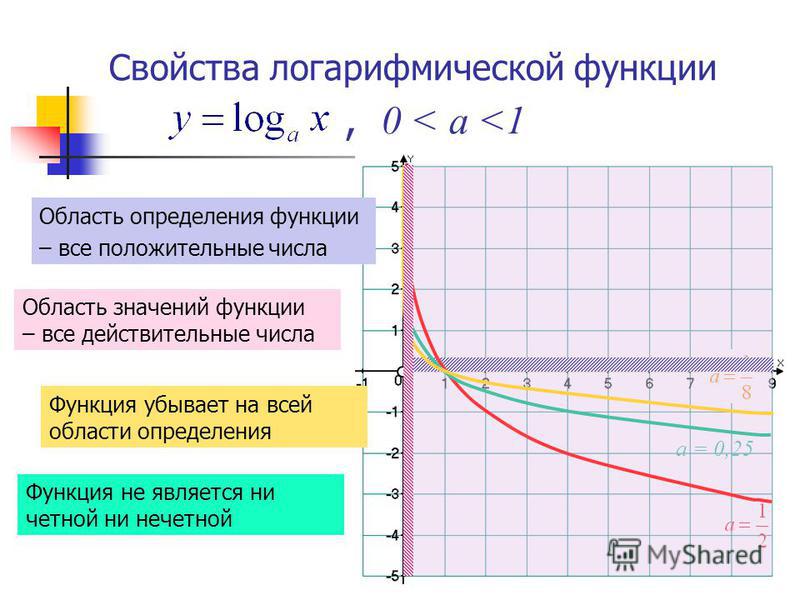
Обобщение отдельных фактов, понятий
Построение графика логарифмической функции путем несложных преобразований
5
Фронтальный анализ, словесно-наглядный с применением презентаций Самостоятельная работа с проверкой
Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку, демонстрируя параллельный перенос с помощью презентации
Обобщение отдельных фактов, понятий
Построение графика логарифмической функции путем сложных преобразований
10
Фронтальный анализ и обобщение
Самостоятельная работа с проверкой
Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку с помощью документ- камеры
Применение построений графиков при решении уравнений и неравенств
12
Работа у доски, самостоятельная работа
Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку
Подведение итогов урока. Рефлексия
Рефлексия
2
Словесный анализ, фронтальная
Задает вопросы, отвечая на которые учащиеся анализируют свою работу
Тема урока
Логарифмическая функция. Преобразования графика логарифмической функции
Цель урока (учебная, развивающая, воспитательная)
Образовательные: совершенствовать навыки построения графиков сложных логарифмических функций; уметь применять их при графическом решении уравнений и неравенств.
Развивающие:
Развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизаций
Сознательного восприятия учебного материала
Развитие математической речи учащихся, потребности к самообразованию
Способствовать развитию исследовательской деятельности учащихся
Воспитательные:
Чувства ответственности, уверенности в себе, воспитание культуры общения
Тип урока
Комбинированный
Основные термины и понятия для изучения
Логарифм, свойства логарифма, логарифмическая функция, ее свойства
Оборудование
Ноутбуки персональные, документ-камера, карточки с заданиями, листы оценивания, презентации, интерактивный тест.
Формы работы
Фронтальная, индивидуальная.
Методические приемы мотивации обучения
Использование ИКТ, презентации составленные учащимися
Методические приемы проверки домашнего задания
Интерактивный тест
Межпредметные связи
Выступление ученика с демонстрацией материала по презентации «Логарифмическая функция в окружающем нас мире»
Тема: Логарифм, его свойства, логарифмическая функция, ее свойства и график
«В науке нет широкой столбовой дороги, и только тот достигнет ее сияющих вершин, кто, не страшась усталости, карабкается по ее каменистым тропам»
(Маркс)
Цели урока:
Образовательные: совершенствовать навыки построения графиков логарифмических функций; уметь применять их при графическом решении уравнений и неравенств.
Развивающие:
Развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизаций
Сознательного восприятия учебного материала
Развитие математической речи учащихся, потребности к самообразованию
Способствовать развитию исследовательской деятельности учащихся
Воспитательные:
Воспитание познавательной активности
Чувства ответственности, уверенности в себе, воспитание культуры общения
Ресурсы урока: Карточки с заданиями, интерактивный тест, презентации, лист оценивания.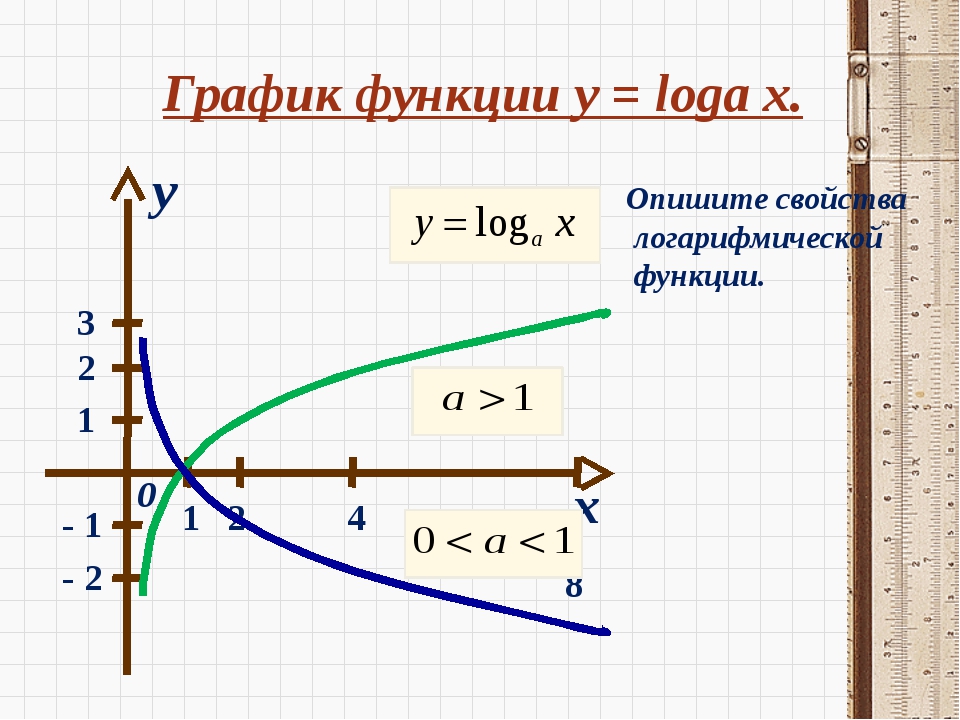
Тип урока: Комбинированный
Форма урока: Классно-урочная
Форма работы: фронтальная, индивидуальная.
Технология: Личностно-ориентированная; информационно-коммуникативная
План урока:
Организационный момент (сообщение темы урока, цель урока, что должны знать и уметь).
Осуществление межпредметных связей (сообщение учащегося)
Обобщение ранее изученного материала. Проверка готовности к изучению материала (индивидуальное тестирование).
Изучение и закрепление нового материала
Применение нового материала
Подведение итогов.
Ход урока:
Организационный момент (приветствие, проверка готовности учащихся к уроку).
Тема сегодняшнего нашего урока «Логарифмическая функция.
 Преобразование графика».
Преобразование графика».Наша цель научиться строить графики логарифмических функций с помощью преобразований и применять их в решении уравнений и неравенств.
Будем работать по следующему плану:
Узнаем о связи логарифмической функции с окружающим миром.
Проверка готовности к уроку с помощью тестирования
Построение графиков логарифмической функции +самостоятельная работа
Графическое решение уравнений и неравенств + самостоятельная работа
На уроке вы должны быть активными, так как ваша оценка за урок будет складываться из количества баллов набранных вами за урок. Критерии оценок посмотрите в листах оценивания.
Осуществление межпредметных связей (сообщение учащегося)
Обобщение ранее изученного материала. Проверка готовности к изучению материала (индивидуальное тестирование). Вопросы по тестированию есть? При рассмотрении примеров были ли у вас трудности?
Изучение и закрепление нового материала
Напомните как построить график графики функций y = log 3(x), y = log 0,3(x)
Как получить графики функции y = log 3(x – 1) , y = log 0,3(x)+3. Учитель обсуждает с учащимися сделанные выводы и дает задание построить самостоятельно графики функций y = log 3(x-3), y = log 3(x)+2, y = log 3(x +4) – 2. Ученики комментируют построение и проверяют с помощью презентации.
Учитель обсуждает с учащимися сделанные выводы и дает задание построить самостоятельно графики функций y = log 3(x-3), y = log 3(x)+2, y = log 3(x +4) – 2. Ученики комментируют построение и проверяют с помощью презентации.
А как построить графики следующих функций y = log 3(ǀxǀ), y =ǀlog 3(ǀxǀ)ǀ, y = ǀlog 3(ǀxǀ)ǀ
Обсуждается способ построения каждой функции, общие и отличительные черты в построении. Строятся графики на доске. Учитель предлагает учащимся самостоятельно построить графики следующих функций по выбору y = log 3(ǀx-2ǀ),, y = ǀ-log 3(ǀ-xǀ)ǀ-2. Комментируют построение и проверяют с помощью документ-камеры.
Применение нового материала
Выполнение у доски №29(а), 30(б), 31(б), 47(а), 48(б). Учащиеся обсуждают, делают выводы и выполняют самостоятельно на выбор задания
(x + 3) 2= log 2(x-2), (x + 3) 2˃ log 2(x-2), (x + 3) 2≥log 2(x-2)
или -2= log 2(x-2), -2 ˃ log 2(x-2), -2≥ log 2(x-2). Комментируют решение и проверяют с помощью документ-камеры.
Комментируют решение и проверяют с помощью документ-камеры.
Подведение итогов. Объявление оценок.
Десятичный логарифм и его свойства
Определение и формулы десятичного логарифма
Этот логарифм является решением показательного уравнения . Иногда (особенно в зарубежной литературе) десятичный логарифм обозначается еще как , хотя первые два обозначения присущи и натуральному логарифму.
Первые таблицы десятичных логарифмов были опубликованы английским математиком Генри Бригсом (1561-1630) в 1617 г. (поэтому иностранные ученые часто называют десятичные логарифмы еще бригсовыми), но эти таблицы содержали ошибки. На основе таблиц (1783 г.) словенского и австрийского математики Георга Барталомея Веги (Юрий Веха или Веховец, 1754-1802) в 1857 г. немецкий астроном и геодезист Карл Бремикер (1804-1877) опубликовал первое безошибочное издание. При участии русского математика и педагога Леонтия Филипповича Магницкого (Телятин или Теляшин, 1669-1739) в 1703 г. в России были изданы первые таблицы логарифмов. Десятичные логарифмы широко применялись для вычислений.
в России были изданы первые таблицы логарифмов. Десятичные логарифмы широко применялись для вычислений.
Свойства десятичных логарифмов
Этот логарифм обладает всеми свойствами, присущими логарифму по произвольному основанию:
1. Основное логарифмическое тождество:
2. .
3. .
4. .
5. .
6. .
7. Переход к новому основанию:
8. .
9. .
Функция десятичного логарифма — это функция . График этой кривой часто называют логарифмикой.
Свойства функции y=lg x
1) Область определения: .
2) Множество значений: .
3) Функция общего вида.
4) Функция непериодическая.
5) График функции пересекается с осью абсцисс в точке .
6) Промежутки знакопостоянства: для та для .
7) Функция возрастает на всей области определения.
8) Точек минимума/максимума нет.
9) График:
Производная логарифма натурального
Интеграл от натурального логарифма
Ряд Маклорена
| Понравился сайт? Расскажи друзьям! | |||
Интересные факты про логотипы известных компаний
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos .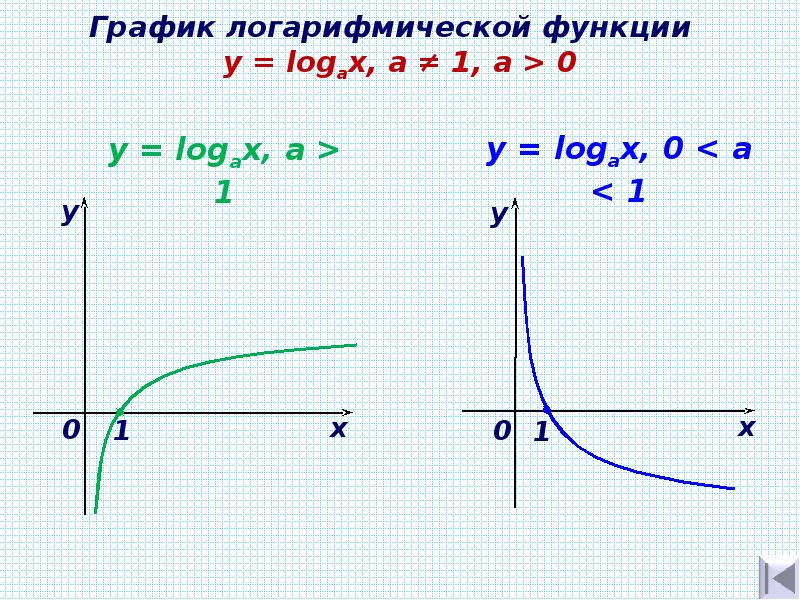 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .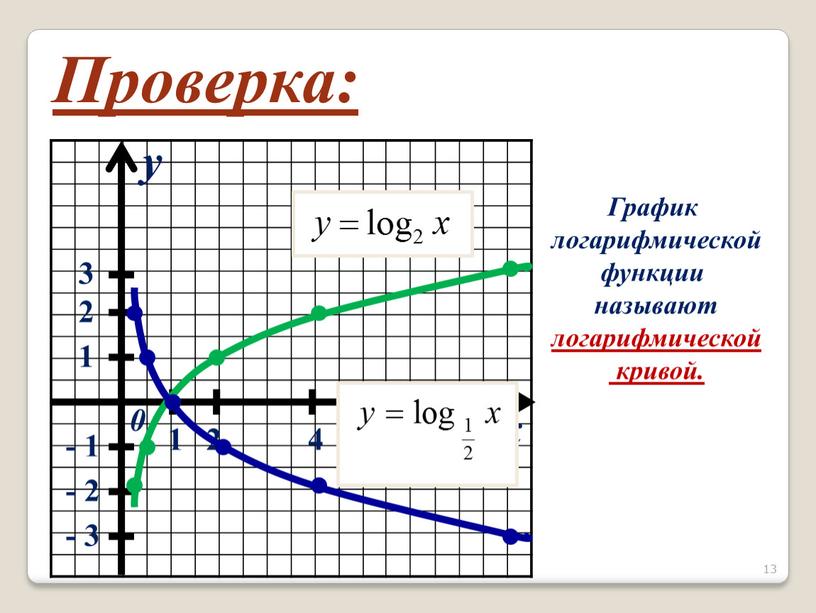
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис.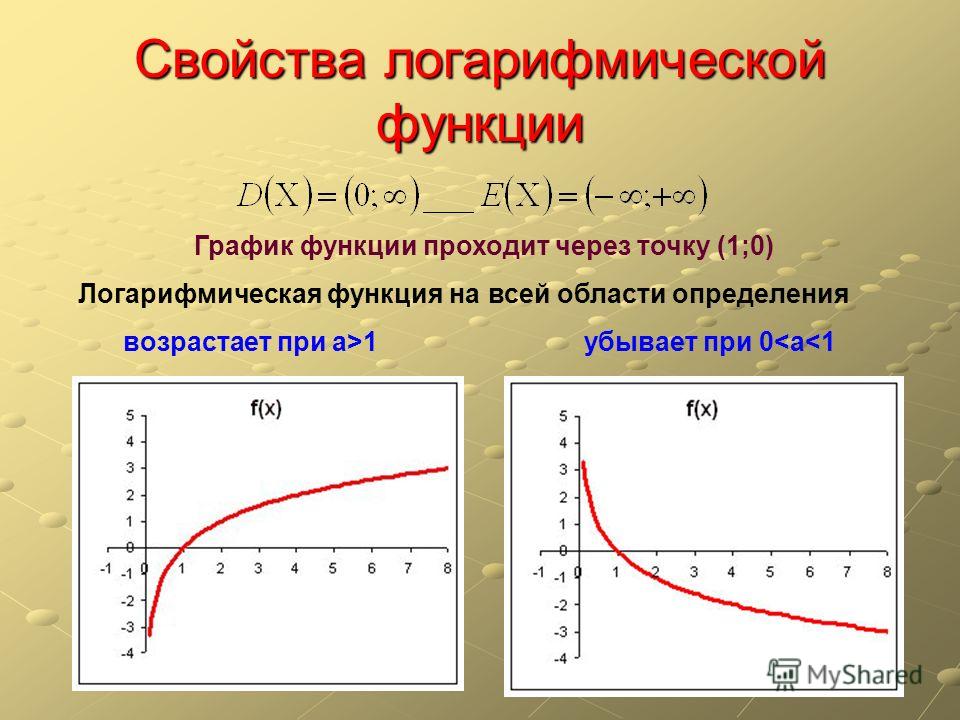 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).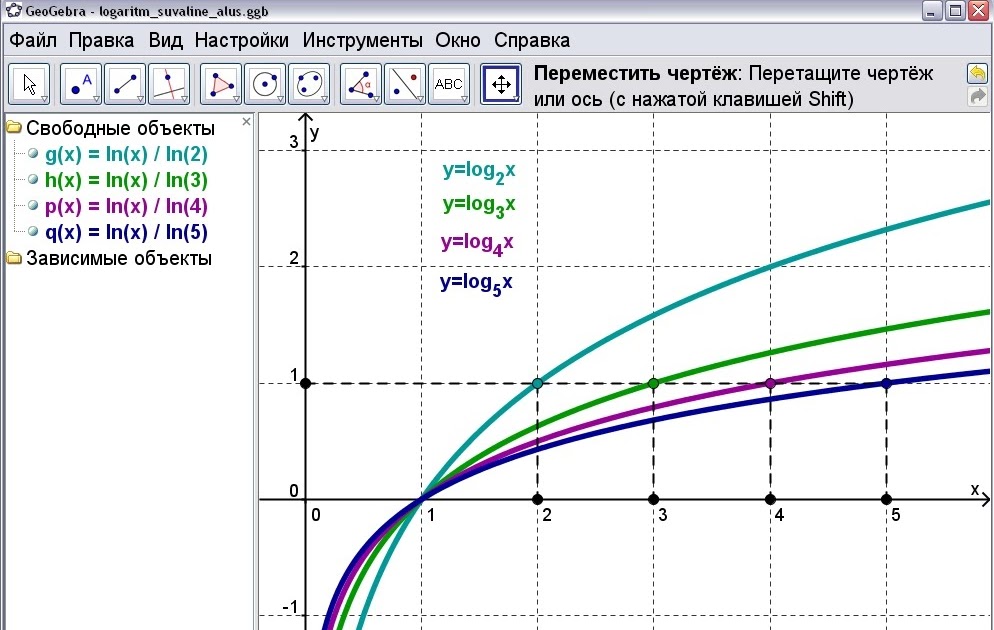
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.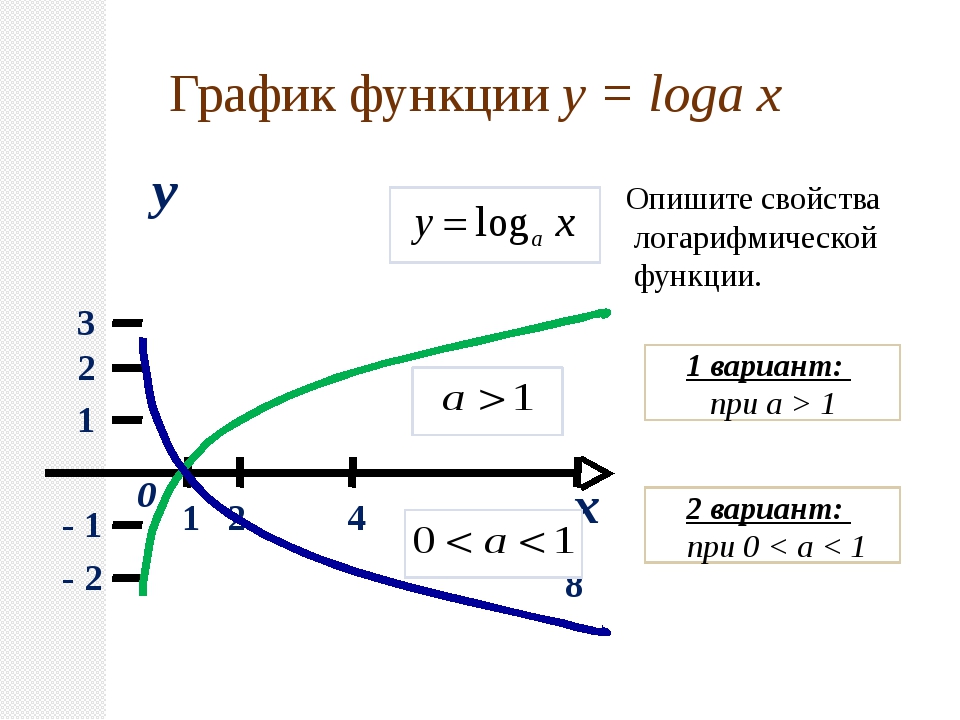
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.
Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.
Также задается и область построения.
Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.
Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.
Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.
Построение графика функции онлайн
ТОП-4 лучших сервиса для построения графиков онлайн
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.
- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т.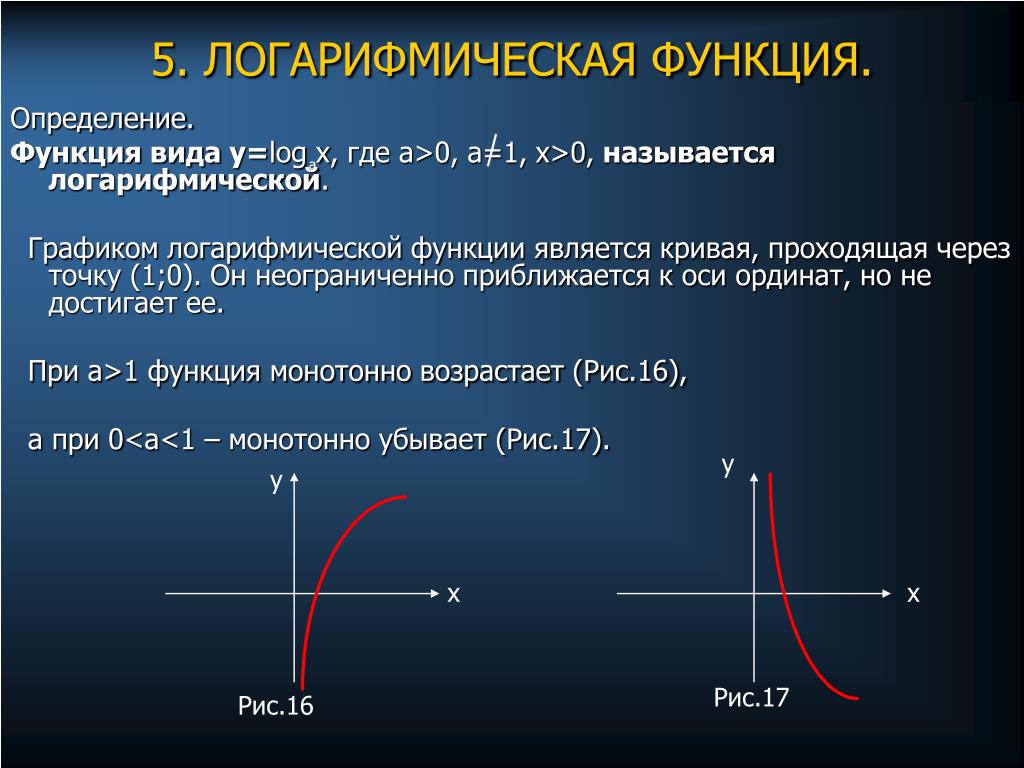 д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
1 2 cos x 2 график
Вы искали 1 2 cos x 2 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 2 x 4 график, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 2 cos x 2 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2 cos x 2 график,1 2 x 4 график,1 2 x график,1 2 график,1 2 х график,1 2x график,1 3 x график,1 ln x график,1 x 2 график,1 x 2 график функции,1 x 3 график,1 x 3 график функции,1 x 4 график,1 x в квадрате график,1 x график,1 x график функции,1 y график,1 график,1 корень из х график,1 постройте график функции y,1 х 1 4 построить график функции,1 х 2 график,1 х 3 график,1 х в квадрате график,1 х график,1 х график функции,1 х2 график,2 1 x построить график,2 arctg x график,2 ln x график,2 x 3 график,2 x график,2 x график функции,2 график,2 х 1 график,2x 1 2 график,2x 1 график,2x 2 1 график,2x 2 график,2x 2 график функции,2x 3 график,2x x 2 график,2x x 2 график функции,2x y 2 график,2x y 4 график,2x график,2x график функции,2×2 график,2х график,3 sin x график,3 x график,3 х график,3 х график функции,3d график онлайн,3d графики онлайн,3x 2 график,3x y 2 график,3x график,3д график онлайн,4 2 построить график,4 x 2 график,4 x 2 график функции,4 x график,4 x2 график,4 в степени х график,4 х 2 график,4 х в квадрате график,4 х график,4x x 2 график,4x x 2 график функции,5 x график,6 x график,8 x график,a x график,arctg 2 x график,arctg 2x график,cos x 1 график,cos x 2 график,cos2x 1 график,e x график,e y график,e график,f y 2 x 2,graph online,lgx график,ln x 1 график,online graph,sin 1 x график,sin 2 x график,sin 3 x график,sin x 1 2 график,sin x 1 график,sin x 2 график,sin x 3 график,sin2x график,sinx x график,sqrt x график,tg 2 x график,x 0 y 0 график,x 0 y 0 график функции,x 0 график,x 1 2 график,x 1 2 график построить,x 1 3 график,x 1 x 2x график,x 1 в квадрате график,x 1 график,x 1 график функции,x 2 1 график,x 2 2x 3 график,x 2 2x график,x 2 2x график функции,x 2 3 график,x 2 3x 2 график,x 2 3x 2 график функции,x 2 4 график,x 2 5 график,x 2 a 2 график,x 2 y 1 график,x 2 y 2 0 график,x 2 y 2 1 график,x 2 y 2 2x график,x 2 y 2 4 график,x 2 y 2 5 график,x 2 y 2 a 2 график,x 2 y 2 график,x 2 y 3 график,x 2 график,x 2 график функции,x 2x 2 график,x 3 1 график,x 3 2 график,x 3 2 график функции,x 3 x 1 график функции,x 3 график,x 4 x 1 график функции,x 4 график,x 4 график функции,x 4 функция,x 5 график,x 5 график функции,x 6 график,x 6 график функции,x a 2 y 2 a 2 график,x a график,x arctg x график,x e график,x e график функции,x log x график,x ot y,x sinx график,x sqrt y график,x y 0 график,x y 1 построить график,x y 2 график,x y 3 график,x y 4 график,x y 5 график,x y 6 график,x y ru,x y график,x y построить,x y построить график,x в 2 степени график,x в 4 степени график,x в квадрате график,x в степени 2 график,x в степени 3 график,x в степени 4 график,x график,x график функции,x от y,x у 2 график,x2 4 график,x3 1 график,x3 график,x3 график функции,x4 график,xy график,y 0 5x 2 график,y 0 x 0 график функции,y 0 x график,y 0 x график функции y,y 0 график,y 0 график функции,y 1 2 cos 2 x график,y 1 2 x график,y 1 2 график,y 1 2 график функции,y 1 2x 2 график функции,y 1 2x график функции,y 1 2×2 график функции,y 1 3 x 2 график,y 1 3 x 2 график функции,y 1 3x 2 график,y 1 4 x,y 1 4 x график,y 1 4x,y 1 4x 2 график,y 1 4x график,y 1 5 x график,y 1 5 x график функции,y 1 5x график,y 1 9x,y 1 9x график,y 1 x 1 построить график,y 1 x 2 5,y 1 x 2 график,y 1 x 2 график функции,y 1 x 3 график,y 1 x 4,y 1 x график,y 1 x график функции,y 1 x построить график,y 1 график,y 1 график функции,y 1 х 2,y 10 x график,y 2 1 график,y 2 2x график,y 2 3 в степени x,y 2 3x построить график,y 2 4x график,y 2 5x график функции,y 2 x 1 график функции,y 2 x 3 график,y 2 x 3 график функции,y 2 x график,y 2 x график функции,y 2 в степени x 3,y 2 график,y 2 график функции,y 2 х график,y 2 х график функции,y 2 ч y ч 2,y 2sin3x график,y 2x 1 график функции,y 2x 2 x 1,y 2x 3 x 1,y 2x 3 график функции,y 2x 3 построить график функции,y 2x x,y 2x x 2 график,y 2x график,y 2x график функции,y 2x построить график,y 2×2 2,y 2×2 график функции,y 3 2x график,y 3 sin x график,y 3 x 2 график,y 3 x 2 график функции,y 3 x график,y 3 x график функции,y 3 в степени x 2,y 3 график,y 3sin2x график,y 3x 1 график,y 3x 1 график функции,y 3x 2 график,y 3x 2 график функции,y 3x 2 построить график функции,y 3x 6 график,y 3x x 2,y 4 1 x,y 4 x,y 4 x 1,y 4 x 1 2,y 4 x 1 2 график,y 4 x 2 график,y 4 x 2 график функции,y 4 x график,y 4 x график функции,y 4 x построить график,y 4 x построить график функции,y 4 x2 график,y 4 в степени x,y 4 в степени x график функции,y 4 в степени x график функции y,y 4 график,y 4x,y 4x 1,y 4x 1 2,y 4x 2 график,y 4x 2 график функции,y 4x x 2 график,y 4x график,y 4x график функции,y 5 2x график функции,y 5 x,y 5 x 2 построить график,y 5 x график,y 5 x график функции,y 5 x построить график функции,y 5x график функции,y 6 x график,y 7 x,y 7 x график,y 9 x график,y 9 x график функции,y 9 x график функции y,y a x график,y cos x 1 график,y cos x 2 график,y cos3x 2 график,y e график,y sin3x график,y sinx в квадрате график,y sqrt x график,y sqrt x график функции y,y x 0,y x 0 5,y x 1 2 график,y x 1 2 график функции,y x 1 4,y x 1 в квадрате график функции,y x 1 график функции,y x 1 построить график,y x 10 график,y x 10 построить график функции,y x 2 3 график,y x 2 4 построить график,y x 2 4x 5 построить график данной функции по графику определить,y x 2 x 3 график,y x 2 график,y x 2 график функции,y x 2 построить график,y x 2 построить график функции,y x 2 постройте график,y x 3 2 график,y x 3 4,y x 3 4 график,y x 3 4x,y x 3 5,y x 3 x 0,y x 3 x построить график,y x 3 график построить,y x 3 график функции как построить,y x 3 построить график,y x 4,y x 4 1,y x 4 2 график функции,y x 4 3,y x 4 x,y x 4 x построить график,y x 4 график,y x 4 график функции,y x 4 построить график функции,y x 5,y x 5 0,y x 5 x,y x 5 график,y x 5 график функции,y x 5 построить график функции,y x 6,y x 6 1,y x 6 график,y x 6 построить график,y x 6 постройте график,y x 7,y x 7 график,y x 7 график функции,y x 8 график,y x 9,y x 9 график функции,y x a график,y x r,y x ru,y x sgn x,y x x2,y x y 2 0 график функции,y x в 3 степени график,y x в 6 степени график,y x в квадрате построить график,y x в степени 2,y x в степени 2 3,y x график,y x график функции,y x график функций,y x как построить график,y x как построить график функции,y x построить график,y x постройте график,y x решение,y x2 2 график функции,y x2 3 график функции,y x2 3x график,y x2 график,y x2 график функции,y x2 построить график функции,y x4,y x4 y 1,y x4 график функции,y x5,y x5 график функции,y x6,y x6 график,y x6 график функции,y от x,y х 2 график,y х 2 график функции,y х 2 х 3,y х 4 график,yotx графики онлайн,z x y график,генератор графиков,генератор графиков функций,гипербола онлайн,граф решишь,график,график 1,график 1 2 x,график 1 2 х,график 1 2x,график 1 2x 2,график 1 3 x,график 1 sin x,график 1 x,график 1 x 2,график 1 x 3,график 1 x в квадрате,график 1 корень из х,график 1 х,график 1 х 2,график 1 х 3,график 1 х в квадрате,график 1 х2,график 2 tg x,график 2 x,график 2 x 3,график 2 в степени x,график 2 синус х,график 2 х,график 2cos2x,график 2x,график 2x 1,график 2x 2,график 2x 2 1,график 2x 3,график 2x x 2,график 2×2,график 2х,график 3 2 x,график 3 2x,график 3 x,график 3 x 1,график 3 x 2,график 3 х,график 3x,график 3x 2,график 4 x,график 4 x 2,график 4 в степени х,график 4 х,график 4 х 2,график 4 х в квадрате,график 4x x 2,график 4x y 2,график 5 x,график 6 x,график a x,график arctg 1 x,график arctg 2x,график arctg x 2,график cos 2 x,график e x,график e y,график lgx,график ln 1 x,график sin 1 x,график sin 2 x,график sin x построить график,график sin3x,график sinx x,график sqrt x,график tg 2 x,график x,график x 0,график x 1 2,график x 1 3,график x 2,график x 2 1,график x 2 2x,график x 2 3,график x 2 4,график x 2 y 2 0,график x 3,график x 3 1,график x 3 2,график x 4,график x 4 2,график x 5,график x 6,график x a,график x e,график x e y,график x sqrt y,график x y,график x y 0,график x y 2,график x y 8,график x y a,график x y z,график x в 2 степени,график x в степени 2,график x в степени 3,график x2 4,график x3,график x3 1,график x4,график xy,график y,график y 0,график y 1,график y 1 2,график y 1 2 x,график y 1 2x,график y 1 2×2,график y 1 3 x 2 x,график y 1 3x 2,график y 1 4 x,график y 1 5 x,график y 1 x,график y 1 x 2,график y 1 x 4,график y 10 x,график y 2,график y 2 1,график y 2 2x,график y 2 2x 1,график y 2 3x,график y 2 5 x,график y 2 cos x,график y 2 x 1,график y 2 x 3,график y 2 корень x,график y 2 х,график y 2cos x,график y 2x,график y 2x x 2,график y 2x x2,график y 3 2x,график y 3 x,график y 3 x 2,график y 3 в степени x 2,график y 3 корень x,график y 3sin2x,график y 3x,график y 3x 2,график y 4,график y 4 x,график y 4 x 2,график y 4 x 3,график y 4 x2,график y 4x,график y 4x 1,график y 4x 2,график y 4x x 2,график y 5 2x,график y 5 x,график y 7 x,график y 8 x,график y 9 x,график y e,график y sqrt x,график y tg 2 x,график y tg 2x,график y x,график y x 0,график y x 1 x 5,график y x 1 в квадрате,график y x 10,график y x 2,график y x 2 3,график y x 3 2,график y x 4,график y x 4 и y x 4,график y x 5,график y x 5 2,график y x 6,график y x 7,график y x 8,график y x a,график y x в 3 степени,график y x в 7 степени,график y x в квадрате 1,график y x2,график y х 2,график z x y,график в полярной системе координат онлайн,график в полярных координатах онлайн,график в пространстве онлайн,график в трехмерном пространстве онлайн,график гиперболы онлайн построить,график е,график зависимости онлайн построить,график икс в степени икс,график калькулятор,график квадратичной функции онлайн,график квадратичной функции построить онлайн,график комплексной функции онлайн,график координат,график корень из х 1,график косинус 3х,график кусочной функции онлайн,график логарифма онлайн,график логарифмической функции онлайн,график математика,график нарисовать,график начертить,график неявной функции онлайн,график окружности онлайн,график окружности онлайн построить,график онлайн,график онлайн 3d,график онлайн в полярной системе координат,график онлайн в полярных координатах,график онлайн в пространстве,график онлайн в трехмерном пространстве,график онлайн квадратичной функции,график онлайн неявной функции,график онлайн по точкам,график онлайн по уравнению,график онлайн по формуле,график онлайн по функции,график онлайн построение,график онлайн построить,график онлайн построить x y z,график онлайн построить по точкам,график онлайн построить по уравнению,график онлайн построить с модулем,график онлайн с модулем,график онлайн трехмерный,график онлайн функция,график онлайн чертить,график параболы онлайн,график параметрической функции онлайн,график по точкам онлайн,график по уравнению онлайн,график по формуле онлайн,график по функции,график по функции онлайн,график построение,график построение онлайн,график решить,график с корнем онлайн с,график с модулем онлайн,график с модулем онлайн построить,график сайт,график синус х 2,график системы уравнений онлайн,график степенной функции онлайн,график строить,график строить онлайн,график тригонометрической функции онлайн,график у 1,график у 1 2 х,график у 1 2х,график у 1 2х2,график у 1 x,график у 1 корень из х,график у 1 х,график у 1 х 2,график у 2,график у 2 x,график у 3 x,график у 3 х,график у 3х,график у 4 х,график у x,график у x 2,график у х,график у х 1,график у х 1 х 3,график у х 2 5,график у х 4,график у х 5,график у х 7,график у х 8,график у х в степени 2,график у х2 1,график уравнения y 2 x 2,график уравнения онлайн,график функции,график функции 1 2 x,график функции 1 2 х,график функции 1 cos x 1,график функции 1 x,график функции 1 x 2,график функции 1 x 3,график функции 1 x 4,график функции 1 x в квадрате,график функции 1 корень из х,график функции 1 х,график функции 1 х 2,график функции 1 х 3,график функции 1 х в квадрате,график функции 2 1 х,график функции 2 3 x,график функции 2 x,график функции 2 x 1,график функции 2 x 3,график функции 2 y 1 x,график функции 2 х 1,график функции 2x,график функции 2x 2 x,график функции 3 1 х,график функции 3 x,график функции 3 x 1,график функции 3 x 2,график функции 3 х,график функции 4 x,график функции 4 x 2,график функции 4 в степени х,график функции 4 х,график функции 4 х 2,график функции 5 x,график функции sin 1 x,график функции x,график функции x 1,график функции x 1 2,график функции x 1 3,график функции x 1 в квадрате,график функции x 2,график функции x 2 1,график функции x 2 3,график функции x 2 4x,график функции x 2 y 2,график функции x 2 y 2 4,график функции x 2 y 2 9,график функции x 2 y 2 9 график,график функции x 2x 2,график функции x 3,график функции x 3 1,график функции x 3 2,график функции x 3 sin y,график функции x 3 x 1 x,график функции x 3 x 2 1,график функции x 4,график функции x 4 2,график функции x 5,график функции x 6,график функции x e,график функции x y,график функции x y 0 x,график функции x y 1,график функции x y 5,график функции x y a,график функции x3,график функции y 0,график функции y 0 x 0,график функции y 1,график функции y 1 2,график функции y 1 2x,график функции y 1 3 x 2,график функции y 1 3x в квадрате,график функции y 1 4x в квадрате,график функции y 1 x 4,график функции y 1 x в квадрате,график функции y 2,график функции y 2 1,график функции y 2 3x,график функции y 2 x,график функции y 2 x 1,график функции y 2 x 3,график функции y 2 x2,график функции y 2x,график функции y 2x 2,график функции y 2x 3,график функции y 2×2,график функции y 2×2 1,график функции y 3,график функции y 3 2x,график функции y 3 x,график функции y 3 x 2,график функции y 3x 2,график функции y 4 x,график функции y 4 x 2,график функции y 4 в x степени,график функции y 4x 2,график функции y 5,график функции y 5 2x,график функции y 5 x,график функции y 5 x 2,график функции y 5x,график функции y 5x 2,график функции y 5x 4,график функции y 6 2x,график функции y lg x,график функции y tg 2x,график функции y x,график функции y x 1,график функции y x 1 2,график функции y x 1 4,график функции y x 1 x 2,график функции y x 1 в квадрате,график функции y x 10,график функции y x 2 3,график функции y x 2 3 x 2x,график функции y x 2 5,график функции y x 2 x 0,график функции y x 3 2,график функции y x 3 4,график функции y x 3 как построить,график функции y x 4,график функции y x 4 2,график функции y x 4 3,график функции y x 5,график функции y x 6,график функции y x 7,график функции y x 9,график функции y x sqrt x 2,график функции y x в квадрате 1,график функции y x как построить,график функции y x2,график функции y x2 1,график функции y x2 3,график функции y x4,график функции y x5,график функции y x6,график функции y х,график функции в полярных координатах онлайн,график функции двух переменных онлайн,график функции двух переменных онлайн построить,график функции как выглядит,график функции калькулятор,график функции калькулятор онлайн,график функции нарисовать,график функции одна вторая икс в квадрате,график функции онлайн,график функции онлайн x y z,график функции онлайн двух переменных,график функции онлайн калькулятор,график функции онлайн неявной,график функции онлайн по точкам,график функции онлайн построение,график функции онлайн построить,график функции онлайн построить по точкам,график функции онлайн построить с корнем,график функции онлайн построить с модулем,график функции онлайн построить с решением,график функции онлайн с модулем,график функции онлайн с решением,график функции параметрической онлайн,график функции по,график функции по точкам онлайн,график функции по точкам онлайн построить,график функции построение,график функции построение онлайн,график функции решение,график функции решить онлайн,график функции с модулем онлайн,график функции с решением онлайн,график функции синус 2х,график функции строить онлайн,график функции у,график функции у 1 2 х,график функции у 1 2х,график функции у 1 х 2,график функции у 1 х в квадрате,график функции у 2,график функции у 2 x,график функции у 3,график функции у 3 x,график функции у 4х в квадрате,график функции у x,график функции у x 1,график функции у x 2,график функции х,график функции х 1,график функции х 1 2,график функции х 2 1,график функции х 2 y,график функции х 3 2,график функции х 4,график функции х 4 2,график функции х 4 х 2,график функции х y,график функции х y 2,график функции х в 4 степени,график функции х в квадрате минус х,график функции х в квадрате х,график функции х делить на х,график функции х у,график функций,график функций онлайн,график функция онлайн,график х,график х 0,график х 1,график х 1 2,график х 1 в квадрате,график х 2,график х 2 1,график х 2 3,график х 2 y 2,график х 3,график х 3 1,график х 3 2,график х 4,график х y 2,график х в квадрате,график х в квадрате 1,график х в квадрате 4,график х в степени 2,график х в степени 4,график х е х,график х и у,график х у,график х у 4,график х у z,график х2 1,график х3,график чертить онлайн,график экспоненты в степени минус х,графика онлайн,графика точками,графики,графики x 2 y 2,графики y 2 x,графики в полярной системе координат онлайн,графики в полярных координатах онлайн,графики онлайн,графики онлайн 3d,графики онлайн в полярной системе координат,графики онлайн в полярных координатах,графики онлайн по точкам,графики онлайн полярная система координат,графики онлайн построение,графики онлайн построение по точкам,графики онлайн построение по уравнению,графики онлайн трехмерные,графики по точкам онлайн,графики по точкам онлайн построение,графики построение,графики построение онлайн,графики построить,графики построить онлайн,графики рисовать онлайн,графики строить,графики строить онлайн,графики уравнений онлайн,графики функции онлайн,графики функций x 2 y 2,графики функций калькулятор,графики функций онлайн,графики функций онлайн калькулятор,графики функций онлайн построение,графики функций онлайн с модулем,графики функций онлайн с решением,графики функций построение,графики функций построение онлайн,графики функций построить,графики функций с модулем онлайн,графики функций строить онлайн,графики чертить,графический калькулятор онлайн,графический онлайн калькулятор,графическое решение уравнений онлайн,графік,графік функції y 2 x,графік функції y x 2,графік функції онлайн,графіки,графіки онлайн,графопостроитель онлайн,дослідити функцію та побудувати її графік онлайн,е график,е х график,изобразите график функции,изобразить график функции онлайн,изоклины онлайн построение,икс в степени икс график,инженерная графика онлайн построение,используя график функции y f x постройте график функции,используя график функции построить график функции,исследовать график функции онлайн,исследовать график функции онлайн с решением,исследовать и построить график функции онлайн,исследовать функцию и построить график онлайн решение калькулятор,как выглядит график,как выглядит график x 2 y 2,как выглядит график функции,как начертить график функции,как построить x y,как построить y x,как построить график x y,как построить график x y 2,как построить график y 2 x,как построить график y x,как построить график y x 2,как построить график функции x 2 y,как построить график функции x y,как построить график функции x y 2,как построить график функции x y 3,как построить график функции y,как построить график функции y x,как построить график функции y x 2,как построить график функции по уравнению,калькулятор график,калькулятор график функции,калькулятор графика функции,калькулятор графики функций,калькулятор графиков,калькулятор графиков онлайн,калькулятор графиков функций,калькулятор графиков функций онлайн,калькулятор графиков функций онлайн с решением,калькулятор графический онлайн,калькулятор для построения графиков функций,калькулятор онлайн график функции,калькулятор онлайн графиков,калькулятор онлайн построить график функции,калькулятор построения графиков функций,калькулятор построения графиков функций онлайн,калькулятор построить график функции,калькулятор функции график,калькулятор функции онлайн,калькулятор функций,калькулятор функций графики,калькулятор функций графики онлайн,калькулятор функций онлайн,квадратичная функция онлайн,конструктор графиков,конструктор графиков онлайн,конструктор онлайн функций,конструктор функций онлайн,координатная плоскость онлайн,координатная плоскость онлайн рисовать,координатная прямая онлайн,косинус 3х график,косинус х 2 график,лучший построитель графиков,лучший построитель графиков онлайн,математика график,математикам ру построение графика,найти график функции,нарисовать график,нарисовать график онлайн,нарисовать график онлайн вручную,нарисовать график онлайн по точкам,нарисовать график по точкам онлайн,нарисовать график функции,нарисовать график функции онлайн,нарисовать онлайн функцию,нарисовать функцию онлайн,начертите график,начертить график,начертить график онлайн,начертить график онлайн по точкам,начертить график по точкам онлайн,начертить график функции онлайн,неравенства график онлайн,окружность построить онлайн,онлайн 3d график,онлайн гипербола,онлайн график,онлайн график в полярной системе координат,онлайн график квадратичной функции,онлайн график логарифма,онлайн график логарифмической функции,онлайн график по таблице,онлайн график по точкам,онлайн график по уравнению,онлайн график по формуле,онлайн график построение,онлайн график с модулем,онлайн график функции,онлайн график функции z x y,онлайн график функции с модулем,онлайн графика,онлайн графики,онлайн графики в полярных координатах,онлайн графики в пространстве,онлайн графики по точкам,онлайн графики с модулем,онлайн графики уравнений,онлайн графики функции,онлайн графики функций построить,онлайн графіки,онлайн калькулятор график функции,онлайн калькулятор графики функций,онлайн калькулятор графиков,онлайн калькулятор графиков функций,онлайн калькулятор графиков функций с решением,онлайн калькулятор для функций,онлайн калькулятор построения графиков функций,онлайн калькулятор построить график функции,онлайн калькулятор функции,онлайн калькулятор функций,онлайн квадратичная функция,онлайн конструктор графиков,онлайн конструктор функций,онлайн координатная плоскость,онлайн координатная прямая,онлайн описать функцию,онлайн парабола,онлайн побудова графіків,онлайн побудова графіків функцій,онлайн построение,онлайн построение гиперболы,онлайн построение график функции,онлайн построение графика,онлайн построение графика в полярной системе координат,онлайн построение графика в полярных координатах,онлайн построение графика квадратичной функции,онлайн построение графика функции,онлайн построение графиков,онлайн построение графиков 3d,онлайн построение графиков в полярных координатах,онлайн построение графиков в трехмерной системе координат,онлайн построение графиков зависимости,онлайн построение графиков неравенств,онлайн построение графиков онлайн в полярной системе координат онлайн,онлайн построение графиков по точкам,онлайн построение графиков по уравнению,онлайн построение графиков по физике,онлайн построение графиков с двумя переменными,онлайн построение графиков с корнем,онлайн построение графиков с корнями,онлайн построение графиков с модулем,онлайн построение графиков сложных функций,онлайн построение графиков тригонометрических функций,онлайн построение графиков уравнений,онлайн построение графиков функции,онлайн построение графиков функций,онлайн построение графиков функций x y z,онлайн построение графиков функций по уравнению,онлайн построение графиков функций с модулем,онлайн построение графиков функций с решением,онлайн построение графов,онлайн построение квадратичной функции,онлайн построение кривых,онлайн построение логарифмических графиков,онлайн построение нескольких графиков в одной системе координат,онлайн построение окружности,онлайн построение параболы,онлайн построение синусоиды,онлайн построение тригонометрических графиков,онлайн построение тригонометрических функций,онлайн построение фигур,онлайн построение функций,онлайн построения графиков,онлайн построитель,онлайн построитель графиков,онлайн построитель графиков функций,онлайн построитель функций,онлайн построить график квадратичной функции,онлайн построить графики функций,онлайн постройка графика,онлайн постройка графиков,онлайн постройка графиков функций,онлайн программа для построения графиков,онлайн программа построения графиков,онлайн решение графика функции,онлайн решение графиков,онлайн решение графиков функций,онлайн решение графических уравнений,онлайн решение квадратичной функции,онлайн решение параболы,онлайн решение функций,онлайн решение функция,онлайн решить график функции,онлайн рисование графиков,онлайн система координат,онлайн составить график функции,онлайн составление графика,онлайн составление графиков,онлайн строим график,онлайн строим графики,онлайн строитель графиков,онлайн строитель графиков функций,онлайн строитель функций,онлайн строительство графиков,онлайн строить график функции,онлайн строить графики функций,онлайн трехмерная система координат,онлайн функции,онлайн функция,онлайн функция график,онлайн функция решение,онлайн чертить график,онлайн черчение графиков,описать график функции онлайн,описать функцию онлайн,определить функцию по графику онлайн,парабола онлайн,парабола онлайн построение,парабола построение онлайн,параболы онлайн построение,по графику определить функцию онлайн,по математике графики,по формуле построить график,побудова графіків,побудова графіків онлайн,побудова графіків функцій,побудова графіків функцій онлайн,побудувати графік,побудувати графік онлайн,побудувати графік функції,побудувати графік функції онлайн,побудувати графік функції онлайн розв язок,побудуйте графік функції,полярная система координат графики онлайн,построение 3д графиков онлайн,построение в полярных координатах онлайн,построение график,построение график онлайн,построение график функции,построение график функции онлайн,построение графика,построение графика в полярной системе координат онлайн,построение графика в полярных координатах онлайн,построение графика квадратичной функции онлайн,построение графика онлайн,построение графика онлайн в полярных координатах,построение графика онлайн по точкам,построение графика онлайн по функции,построение графика по точкам,построение графика по точкам онлайн,построение графика по функции онлайн,построение графика функции,построение графика функции онлайн,построение графика функции онлайн с решением,построение графики,построение графики функций,построение графиков,построение графиков xyz онлайн,построение графиков в полярной системе координат онлайн,построение графиков в полярной системе координат онлайн с решением,построение графиков в полярных координатах онлайн,построение графиков в пространстве онлайн,построение графиков в трехмерной системе координат онлайн,построение графиков в трехмерном пространстве онлайн,построение графиков зависимости онлайн,построение графиков на миллиметровке онлайн,построение графиков неравенств онлайн,построение графиков онлайн,построение графиков онлайн 3д,построение графиков онлайн xyz,построение графиков онлайн в полярной системе координат,построение графиков онлайн в полярных координатах,построение графиков онлайн в пространстве,построение графиков онлайн в трехмерной системе координат,построение графиков онлайн на миллиметровке,построение графиков онлайн неравенств,построение графиков онлайн по таблице,построение графиков онлайн по точкам,построение графиков онлайн по точкам на миллиметровке,построение графиков онлайн по уравнению,построение графиков онлайн по физике,построение графиков онлайн с двумя переменными,построение графиков онлайн с корнем,построение графиков онлайн с корнями,построение графиков онлайн с модулем,построение графиков онлайн с параметром,построение графиков онлайн с решением,построение графиков онлайн трехмерных,построение графиков по таблице онлайн,построение графиков по точкам,построение графиков по точкам онлайн,построение графиков по уравнению онлайн,построение графиков по физике онлайн,построение графиков полярных онлайн,построение графиков с двумя переменными онлайн,построение графиков с корнем онлайн,построение графиков с корнями онлайн,построение графиков с модулем онлайн,построение графиков с параметром онлайн,построение графиков сложных функций онлайн,построение графиков тригонометрических онлайн,построение графиков тригонометрических функций онлайн,построение графиков уравнений онлайн,построение графиков функции,построение графиков функции онлайн,построение графиков функции онлайн с решением,построение графиков функции с решением онлайн,построение графиков функций,построение графиков функций онлайн,построение графиков функций онлайн x y z,построение графиков функций онлайн по уравнению,построение графиков функций онлайн с модулем,построение графиков функций онлайн с подробным решением,построение графиков функций онлайн с решением,построение графиков функций по уравнению онлайн,построение графиков функций с модулем онлайн,построение графиков функций с решением онлайн,построение графов онлайн,построение квадратичной функции онлайн,построение кривых онлайн,построение логарифмических графиков онлайн,построение нескольких графиков в одной системе координат онлайн,построение нескольких графиков онлайн,построение обратной функции онлайн,построение окружности онлайн,построение онлайн,построение онлайн кривых,построение параболы онлайн,построение параболы онлайн по квадратному уравнению,построение параболы по квадратному уравнению онлайн,построение параметрических графиков онлайн с решением,построение полярных графиков онлайн,построение пространственных графиков онлайн,построение синусоиды онлайн,построение сложных графиков онлайн,построение сложных графиков функций онлайн,построение точек онлайн по координатам,построение точек по координатам онлайн,построение трехмерных графиков онлайн,построение тригонометрических графиков онлайн,построение тригонометрических функций онлайн,построение уравнений онлайн,построение функции,построение функции онлайн,построение функций,построение функций онлайн,построения графиков онлайн,построитель графиков,построитель графиков онлайн,построитель графиков функций,построитель графиков функций онлайн,построитель онлайн,построитель функций,построитель функций онлайн,построить y x 2 x 1,построить гиперболу онлайн,построить гиперболу онлайн по уравнению,построить гиперболу по уравнению онлайн,построить график,построить график 1 x 2,построить график 3d,построить график x 3 x 2,построить график x f y,построить график x sin x,построить график x y,построить график x y 1,построить график x y z онлайн,построить график x y в квадрате,построить график y,построить график y 1 x,построить график y 2 2x,построить график y 2 x,построить график y 2 x 3,построить график y 2x,построить график y 3 2 x,построить график y 4 x,построить график y cos2x,построить график y x,построить график y x 1,построить график y x 2,построить график y x 3,построить график y x 4,построить график y x 4 2,построить график y x 5,построить график y x 6,построить график в полярной системе координат онлайн,построить график в полярных координатах онлайн,построить график в трехмерном пространстве онлайн,построить график зависимости онлайн,построить график зависимости онлайн по точкам,построить график зависимости по точкам онлайн,построить график квадратичной функции онлайн,построить график квадратичной функции онлайн с решением,построить график логарифмической функции онлайн,построить график неявной функции онлайн,построить график обратной функции онлайн,построить график окружности онлайн,построить график онлайн,построить график онлайн x y z,построить график онлайн в полярной системе координат,построить график онлайн в трехмерном пространстве,построить график онлайн неявной функции,построить график онлайн окружности,построить график онлайн по данным таблицы,построить график онлайн по координатам,построить график онлайн по таблице,построить график онлайн по таблице онлайн,построить график онлайн по точкам,построить график онлайн по точкам x y,построить график онлайн по точкам на миллиметровке,построить график онлайн по точкам онлайн,построить график онлайн по уравнению,построить график онлайн по уравнению онлайн,построить график онлайн по функции,построить график онлайн с модулем,построить график параметрической функции онлайн,построить график по данным таблицы онлайн,построить график по координатам онлайн,построить график по таблице онлайн,построить график по точкам,построить график по точкам онлайн,построить график по уравнению онлайн,построить график по уравнению функции,построить график по функции онлайн,построить график с корнем онлайн с,построить график с модулем онлайн,построить график системы уравнений онлайн,построить график тригонометрической функции онлайн,построить график тригонометрической функции онлайн с решением,построить график у 2 х,построить график у 4 х,построить график у x 2 3 x 2,построить график у х 1 2,построить график у х 2,построить график у х 3,построить график у х 4,построить график уравнения,построить график уравнения онлайн,построить график уравнения онлайн с решением,построить график функции,построить график функции 1 x 1,построить график функции 1 x 2,построить график функции 1 y 2x,построить график функции 1 у 3 х,построить график функции 2 5 x 2,построить график функции 2 5x 2,построить график функции x 1 2,построить график функции x 2 1,построить график функции x 3 2x 2 x 3,построить график функции x f y,построить график функции x y,построить график функции x y 4,построить график функции y,построить график функции y 1 2 x 2,построить график функции y 1 2x 2,построить график функции y 1 2×2,построить график функции y 1 x,построить график функции y 1 x 3,построить график функции y 2 3 x,построить график функции y 2 3x,построить график функции y 2 5x,построить график функции y 2 x 3,построить график функции y 2 x 5,построить график функции y 2x 3,построить график функции y 2x 4 x 2 1 решение,построить график функции y 3 2x,построить график функции y 3 x 2,построить график функции y 3x в квадрате,построить график функции y 4 x,построить график функции y 4 x 1,построить график функции y 5 2x,построить график функции y 5 x 2,построить график функции y 5x 2,построить график функции y 8 x,построить график функции y cos x 1,построить график функции y x,построить график функции y x 1,построить график функции y x 1 2,построить график функции y x 1 2 3,построить график функции y x 1 4,построить график функции y x 1 x 2,построить график функции y x 1 x 3,построить график функции y x 10,построить график функции y x 2,построить график функции y x 2 3,построить график функции y x 3,построить график функции y x 3 2,построить график функции y x 4 2,построить график функции y x 4 x,построить график функции y x 5,построить график функции y x 7,построить график функции y x 8,построить график функции y x cos x,построить график функции y x sin x,построить график функции в полярной системе координат онлайн,построить график функции в трехмерном пространстве онлайн,построить график функции двух переменных онлайн,построить график функции калькулятор,построить график функции онлайн,построить график функции онлайн в полярной системе координат,построить график функции онлайн в трехмерном пространстве,построить график функции онлайн калькулятор,построить график функции онлайн по точкам,построить график функции онлайн по уравнению,построить график функции онлайн по уравнению онлайн,построить график функции онлайн по уравнению с решением,построить график функции онлайн с корнем,построить график функции онлайн с модулем,построить график функции онлайн с подробным решением,построить график функции онлайн с подробным решением 9 класс,построить график функции онлайн с решением,построить график функции онлайн с решением 10 класс,построить график функции онлайн с таблицей точек,построить график функции по модулю онлайн,построить график функции по точкам онлайн,построить график функции по уравнению,построить график функции по уравнению онлайн,построить график функции с корнем онлайн,построить график функции с модулем онлайн,построить график функции с модулем онлайн с подробным решением,построить график функции у,построить график функции у 1 х,построить график функции у 1 х 2,построить график функции у 2 х,построить график функции у х,построить график функции у х в квадрате,построить график функции х в квадрате,построить график функции х у,построить график функции х у 4,построить график функции х у 5,построить график функций,построить график функций онлайн с решением,построить график функций с решением онлайн,построить график х у 2,построить графики,построить графики онлайн,построить графики онлайн по точкам,построить графики по точкам онлайн,построить графики функций,построить графики функций в одной системе координат,построить графики функций онлайн,построить графики функций онлайн с решением,построить и исследовать график функции онлайн,построить и прочитать график функции,построить интегральную кривую онлайн,построить интегральные кривые онлайн,построить калибровочный график онлайн,построить кривую заданную уравнением в полярной системе координат онлайн,построить кривую онлайн,построить кривые по заданным уравнениям онлайн с решением,построить линии уровня функции онлайн,построить несколько графиков на одном онлайн,построить область ограниченную линиями онлайн,построить окружность онлайн,построить онлайн график в полярных координатах,построить онлайн график логарифмической функции,построить онлайн график с модулем,построить онлайн график функции по точкам,построить онлайн график функций,построить онлайн фигуру,построить параболу онлайн,построить параболу онлайн по уравнению,построить параболу по уравнению онлайн,построить по точкам график зависимости онлайн,построить прямую онлайн,построить прямую онлайн по уравнению,построить прямую по уравнению онлайн,построить тригонометрический график онлайн,построить функции онлайн,построить функцию,построить функцию онлайн,построить функцию онлайн с решением,построить функция онлайн,построить эллипс онлайн,построить эскиз графика функции онлайн,построй график функции,постройка графика,постройка графика онлайн,постройка графика онлайн по точкам,постройка графика по точкам онлайн,постройка графика функции,постройка графика функции онлайн,постройка графиков,постройка графиков онлайн,постройка графиков функций онлайн,постройте график,постройте график x y,постройте график y 2 x,постройте график y x,постройте график y x 2,постройте график y x 6,постройте график онлайн,постройте график уравнений,постройте график уравнения 2×2 y 4x 3,постройте график функции,постройте график функции x 3,постройте график функции x y 2 y 0 x,постройте график функции y,постройте график функции y 1 2,постройте график функции y 1 3 x 2,постройте график функции y 1 3x 2,постройте график функции y 1 4x,постройте график функции y 1 6x,постройте график функции y 1 x,постройте график функции y 2,постройте график функции y 2 3 x,постройте график функции y 2 корень 3 степени из x,постройте график функции y 2x,постройте график функции y 3 4 x 1,постройте график функции y 3 х 1,постройте график функции y x,постройте график функции y x 1,постройте график функции y x 1 2,постройте график функции y x 1 x 3 x 4,постройте график функции y x 10,постройте график функции y x 2 x 3 x 1,постройте график функции y x 3,постройте график функции y x 3 2,постройте график функции y x 5,постройте график функции y х 2,постройте график функции игрек равен,постройте график функции игрек равно,постройте график функции онлайн,постройте график функции онлайн с решением,постройте график функции у,постройте график функции у 1 4х2,постройте график функции у 1 x,постройте график функции х у,постройте график функций,постройте график функций y,постройте графики,постройте графики функций,преобразование графиков функций онлайн,преобразование функции онлайн,программа для построения графиков онлайн,программа для построения графиков функций онлайн,программа онлайн для построения графиков,программа онлайн построения графиков,программа построения графиков онлайн,программа построения графиков функций онлайн,прямая у х,прямоугольная система координат онлайн,решение y 1 x,решение график функции,решение графика функции онлайн,решение графиков,решение графиков онлайн,решение графиков функций,решение графиков функций онлайн,решение графиков функций онлайн с решением,решение графических уравнений онлайн,решение квадратичной функции онлайн,решение онлайн графика функции,решение онлайн графиков функций,решение онлайн квадратичной функции,решение онлайн функции,решение параболы онлайн,решение функции онлайн,решение функции онлайн с решением и графиком,решение функций онлайн,решение функций онлайн с решением,решение функций онлайн с решением и графиком,решение функция онлайн,решите графически уравнение онлайн,решите уравнение графически онлайн,решить график,решить график функции онлайн,решить график функции онлайн с решением,решить графически уравнение онлайн,решить графически уравнение онлайн с решением,решить онлайн график функции,решить онлайн функцию,решить уравнение графически онлайн,решить функцию онлайн,решить функцию онлайн с решением и построить график онлайн,рисование графиков онлайн,рисовать графики онлайн,рисовать онлайн графики,сайт для построения графиков,сайт для построения графиков функций,сайт построения графиков функции,свойства функции онлайн,сделать график онлайн,сделать график онлайн по данным,сделать график онлайн по точкам,сделать график по точкам онлайн,синусоида график онлайн,система координат онлайн,создание графиков онлайн,составить график функции онлайн,составить онлайн график функции,составление графика онлайн,составление графиков онлайн,составление онлайн графика,составление онлайн графиков,строение графика функции онлайн,строим график,строим графики онлайн,строим онлайн график,строитель графиков,строитель графиков онлайн,строитель графиков функций онлайн,строитель функций онлайн,строительство графиков онлайн,строить график,строить график онлайн,строить график функции онлайн,строить графики,строить графики онлайн,строить графики функций онлайн,трехмерная система координат онлайн,трехмерная система координат онлайн построение,трехмерная система координат онлайн построение по точкам,трехмерные графики онлайн,трехмерный график онлайн,тригонометрические графики онлайн,у 1 2х график,у 1 2х график функции,у 1 2х2 график,у 1 3х2 график,у 1 x график функции,у 1 график,у 1 график функции,у 1 корень из х график,у 1 х 2 график,у 1 х 2 график функции,у 1 х 3 график,у 1 х в квадрате график функции,у 1 х график,у 1 х2 график функции,у 2 x 2 график,у 2 x 2 график функции,у 2 x график,у 2 график,у 2 график функции,у 2 х 1 график,у 2 х построить график,у 2х 1 построить график,у 3 x график,у 3 x график функции,у 3 в степени х график,у 3 график,у 3 график функции,у 3 х 2 график,у 3 х график,у 3 х построить график функции,у 3х график,у 4 х 2 график функции,у 4 х построить график,у 5 х 2 график,у 5 х график,у x 2 график,у x график,у x график функции,у график функции,у х 1 2,у х 1 2 график,у х 1 график,у х 2 1 график,у х 2 построить график,у х 4,у х 4 2 график,у х 4 3,у х 4 график,у х 5 график функции,у х 6 график,у х в 2 степени график,у х в степени 2 график,у х график,у х построить график функции,у х2 1 график,функции график построение,функции калькулятор,функции онлайн,функции онлайн калькулятор,функции онлайн построить,функции онлайн с решением,функции решение онлайн,функция 1 3x 2,функция 1 x график,функция 2 x,функция 3 x,функция 4 x,функция x 1 график,функция x 2 график,функция x 4,функция x 5,функция y 1 2x в квадрате,функция y 5 x,функция y x 4,функция y x 5,функция график онлайн,функция квадратичная онлайн,функция онлайн,функция онлайн график,функция онлайн построить,функция онлайн решение,функция по точкам онлайн,функция построить онлайн,функция решение онлайн,х 0 график,х 1 в квадрате график,х 1 в квадрате график функции,х 1 график,х 1 х 2 построить график,х 2 1 график,х 2 4 график,х 2 4 график функции,х 2 y 2 1 график,х 2 y 4,х 2 график,х 3 1 график,х 3 график,х 4 график,х 4 график функции,х 4 функция,х y 2 график,х y график,х y график функции,х в квадрате 1 график,х в квадрате 4 график,х в степени 2 график,х график,х и у график,х у z график,х у график,х2 1 график,чертить график онлайн,чертить графики,черчение графиков онлайн.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2 cos x 2 график,1 2 x 4 график,1 2 x график,1 2 график,1 2 х график,1 2x график,1 3 x график,1 ln x график,1 x 2 график,1 x 2 график функции,1 x 3 график,1 x 3 график функции,1 x 4 график,1 x в квадрате график,1 x график,1 x график функции,1 y график,1 график,1 корень из х график,1 постройте график функции y,1 х 1 4 построить график функции,1 х 2 график,1 х 3 график,1 х в квадрате график,1 х график,1 х график функции,1 х2 график,2 1 x построить график,2 arctg x график,2 ln x график,2 x 3 график,2 x график,2 x график функции,2 график,2 х 1 график,2x 1 2 график,2x 1 график,2x 2 1 график,2x 2 график,2x 2 график функции,2x 3 график,2x x 2 график,2x x 2 график функции,2x y 2 график,2x y 4 график,2x график,2x график функции,2×2 график,2х график,3 sin x график,3 x график,3 х график,3 х график функции,3d график онлайн,3d графики онлайн,3x 2 график,3x y 2 график,3x график,3д график онлайн,4 2 построить график,4 x 2 график,4 x 2 график функции,4 x график,4 x2 график,4 в степени х график,4 х 2 график,4 х в квадрате график,4 х график,4x x 2 график,4x x 2 график функции,5 x график,6 x график,8 x график,a x график,arctg 2 x график,arctg 2x график,cos x 1 график,cos x 2 график,cos2x 1 график,e x график,e y график,e график,f y 2 x 2,graph online,lgx график,ln x 1 график,online graph,sin 1 x график,sin 2 x график,sin 3 x график,sin x 1 2 график,sin x 1 график,sin x 2 график,sin x 3 график,sin2x график,sinx x график,sqrt x график,tg 2 x график,x 0 y 0 график,x 0 y 0 график функции,x 0 график,x 1 2 график,x 1 2 график построить,x 1 3 график,x 1 x 2x график,x 1 в квадрате график,x 1 график,x 1 график функции,x 2 1 график,x 2 2x 3 график,x 2 2x график,x 2 2x график функции,x 2 3 график,x 2 3x 2 график,x 2 3x 2 график функции,x 2 4 график,x 2 5 график,x 2 a 2 график,x 2 y 1 график,x 2 y 2 0 график,x 2 y 2 1 график,x 2 y 2 2x график,x 2 y 2 4 график,x 2 y 2 5 график,x 2 y 2 a 2 график,x 2 y 2 график,x 2 y 3 график,x 2 график,x 2 график функции,x 2x 2 график,x 3 1 график,x 3 2 график,x 3 2 график функции,x 3 x 1 график функции,x 3 график,x 4 x 1 график функции,x 4 график,x 4 график функции,x 4 функция,x 5 график,x 5 график функции,x 6 график,x 6 график функции,x a 2 y 2 a 2 график,x a график,x arctg x график,x e график,x e график функции,x log x график,x ot y,x sinx график,x sqrt y график,x y 0 график,x y 1 построить график,x y 2 график,x y 3 график,x y 4 график,x y 5 график,x y 6 график,x y ru,x y график,x y построить,x y построить график,x в 2 степени график,x в 4 степени график,x в квадрате график,x в степени 2 график,x в степени 3 график,x в степени 4 график,x график,x график функции,x от y,x у 2 график,x2 4 график,x3 1 график,x3 график,x3 график функции,x4 график,xy график,y 0 5x 2 график,y 0 x 0 график функции,y 0 x график,y 0 x график функции y,y 0 график,y 0 график функции,y 1 2 cos 2 x график,y 1 2 x график,y 1 2 график,y 1 2 график функции,y 1 2x 2 график функции,y 1 2x график функции,y 1 2×2 график функции,y 1 3 x 2 график,y 1 3 x 2 график функции,y 1 3x 2 график,y 1 4 x,y 1 4 x график,y 1 4x,y 1 4x 2 график,y 1 4x график,y 1 5 x график,y 1 5 x график функции,y 1 5x график,y 1 9x,y 1 9x график,y 1 x 1 построить график,y 1 x 2 5,y 1 x 2 график,y 1 x 2 график функции,y 1 x 3 график,y 1 x 4,y 1 x график,y 1 x график функции,y 1 x построить график,y 1 график,y 1 график функции,y 1 х 2,y 10 x график,y 2 1 график,y 2 2x график,y 2 3 в степени x,y 2 3x построить график,y 2 4x график,y 2 5x график функции,y 2 x 1 график функции,y 2 x 3 график,y 2 x 3 график функции,y 2 x график,y 2 x график функции,y 2 в степени x 3,y 2 график,y 2 график функции,y 2 х график,y 2 х график функции,y 2 ч y ч 2,y 2sin3x график,y 2x 1 график функции,y 2x 2 x 1,y 2x 3 x 1,y 2x 3 график функции,y 2x 3 построить график функции,y 2x x,y 2x x 2 график,y 2x график,y 2x график функции,y 2x построить график,y 2×2 2,y 2×2 график функции,y 3 2x график,y 3 sin x график,y 3 x 2 график,y 3 x 2 график функции,y 3 x график,y 3 x график функции,y 3 в степени x 2,y 3 график,y 3sin2x график,y 3x 1 график,y 3x 1 график функции,y 3x 2 график,y 3x 2 график функции,y 3x 2 построить график функции,y 3x 6 график,y 3x x 2,y 4 1 x,y 4 x,y 4 x 1,y 4 x 1 2,y 4 x 1 2 график,y 4 x 2 график,y 4 x 2 график функции,y 4 x график,y 4 x график функции,y 4 x построить график,y 4 x построить график функции,y 4 x2 график,y 4 в степени x,y 4 в степени x график функции,y 4 в степени x график функции y,y 4 график,y 4x,y 4x 1,y 4x 1 2,y 4x 2 график,y 4x 2 график функции,y 4x x 2 график,y 4x график,y 4x график функции,y 5 2x график функции,y 5 x,y 5 x 2 построить график,y 5 x график,y 5 x график функции,y 5 x построить график функции,y 5x график функции,y 6 x график,y 7 x,y 7 x график,y 9 x график,y 9 x график функции,y 9 x график функции y,y a x график,y cos x 1 график,y cos x 2 график,y cos3x 2 график,y e график,y sin3x график,y sinx в квадрате график,y sqrt x график,y sqrt x график функции y,y x 0,y x 0 5,y x 1 2 график,y x 1 2 график функции,y x 1 4,y x 1 в квадрате график функции,y x 1 график функции,y x 1 построить график,y x 10 график,y x 10 построить график функции,y x 2 3 график,y x 2 4 построить график,y x 2 4x 5 построить график данной функции по графику определить,y x 2 x 3 график,y x 2 график,y x 2 график функции,y x 2 построить график,y x 2 построить график функции,y x 2 постройте график,y x 3 2 график,y x 3 4,y x 3 4 график,y x 3 4x,y x 3 5,y x 3 x 0,y x 3 x построить график,y x 3 график построить,y x 3 график функции как построить,y x 3 построить график,y x 4,y x 4 1,y x 4 2 график функции,y x 4 3,y x 4 x,y x 4 x построить график,y x 4 график,y x 4 график функции,y x 4 построить график функции,y x 5,y x 5 0,y x 5 x,y x 5 график,y x 5 график функции,y x 5 построить график функции,y x 6,y x 6 1,y x 6 график,y x 6 построить график,y x 6 постройте график,y x 7,y x 7 график,y x 7 график функции,y x 8 график,y x 9,y x 9 график функции,y x a график,y x r,y x ru,y x sgn x,y x x2,y x y 2 0 график функции,y x в 3 степени график,y x в 6 степени график,y x в квадрате построить график,y x в степени 2,y x в степени 2 3,y x график,y x график функции,y x график функций,y x как построить график,y x как построить график функции,y x построить график,y x постройте график,y x решение,y x2 2 график функции,y x2 3 график функции,y x2 3x график,y x2 график,y x2 график функции,y x2 построить график функции,y x4,y x4 y 1,y x4 график функции,y x5,y x5 график функции,y x6,y x6 график,y x6 график функции,y от x,y х 2 график,y х 2 график функции,y х 2 х 3,y х 4 график,yotx графики онлайн,z x y график,генератор графиков,генератор графиков функций,гипербола онлайн,граф решишь,график,график 1,график 1 2 x,график 1 2 х,график 1 2x,график 1 2x 2,график 1 3 x,график 1 sin x,график 1 x,график 1 x 2,график 1 x 3,график 1 x в квадрате,график 1 корень из х,график 1 х,график 1 х 2,график 1 х 3,график 1 х в квадрате,график 1 х2,график 2 tg x,график 2 x,график 2 x 3,график 2 в степени x,график 2 синус х,график 2 х,график 2cos2x,график 2x,график 2x 1,график 2x 2,график 2x 2 1,график 2x 3,график 2x x 2,график 2×2,график 2х,график 3 2 x,график 3 2x,график 3 x,график 3 x 1,график 3 x 2,график 3 х,график 3x,график 3x 2,график 4 x,график 4 x 2,график 4 в степени х,график 4 х,график 4 х 2,график 4 х в квадрате,график 4x x 2,график 4x y 2,график 5 x,график 6 x,график a x,график arctg 1 x,график arctg 2x,график arctg x 2,график cos 2 x,график e x,график e y,график lgx,график ln 1 x,график sin 1 x,график sin 2 x,график sin x построить график,график sin3x,график sinx x,график sqrt x,график tg 2 x,график x,график x 0,график x 1 2,график x 1 3,график x 2,график x 2 1,график x 2 2x,график x 2 3,график x 2 4,график x 2 y 2 0,график x 3,график x 3 1,график x 3 2,график x 4,график x 4 2,график x 5,график x 6,график x a,график x e,график x e y,график x sqrt y,график x y,график x y 0,график x y 2,график x y 8,график x y a,график x y z,график x в 2 степени,график x в степени 2,график x в степени 3,график x2 4,график x3,график x3 1,график x4,график xy,график y,график y 0,график y 1,график y 1 2,график y 1 2 x,график y 1 2x,график y 1 2×2,график y 1 3 x 2 x,график y 1 3x 2,график y 1 4 x,график y 1 5 x,график y 1 x,график y 1 x 2,график y 1 x 4,график y 10 x,график y 2,график y 2 1,график y 2 2x,график y 2 2x 1,график y 2 3x,график y 2 5 x,график y 2 cos x,график y 2 x 1,график y 2 x 3,график y 2 корень x,график y 2 х,график y 2cos x,график y 2x,график y 2x x 2,график y 2x x2,график y 3 2x,график y 3 x,график y 3 x 2,график y 3 в степени x 2,график y 3 корень x,график y 3sin2x,график y 3x,график y 3x 2,график y 4,график y 4 x,график y 4 x 2,график y 4 x 3,график y 4 x2,график y 4x,график y 4x 1,график y 4x 2,график y 4x x 2,график y 5 2x,график y 5 x,график y 7 x,график y 8 x,график y 9 x,график y e,график y sqrt x,график y tg 2 x,график y tg 2x,график y x,график y x 0,график y x 1 x 5,график y x 1 в квадрате,график y x 10,график y x 2,график y x 2 3,график y x 3 2,график y x 4,график y x 4 и y x 4,график y x 5,график y x 5 2,график y x 6,график y x 7,график y x 8,график y x a,график y x в 3 степени,график y x в 7 степени,график y x в квадрате 1,график y x2,график y х 2,график z x y,график в полярной системе координат онлайн,график в полярных координатах онлайн,график в пространстве онлайн,график в трехмерном пространстве онлайн,график гиперболы онлайн построить,график е,график зависимости онлайн построить,график икс в степени икс,график калькулятор,график квадратичной функции онлайн,график квадратичной функции построить онлайн,график комплексной функции онлайн,график координат,график корень из х 1,график косинус 3х,график кусочной функции онлайн,график логарифма онлайн,график логарифмической функции онлайн,график математика,график нарисовать,график начертить,график неявной функции онлайн,график окружности онлайн,график окружности онлайн построить,график онлайн,график онлайн 3d,график онлайн в полярной системе координат,график онлайн в полярных координатах,график онлайн в пространстве,график онлайн в трехмерном пространстве,график онлайн квадратичной функции,график онлайн неявной функции,график онлайн по точкам,график онлайн по уравнению,график онлайн по формуле,график онлайн по функции,график онлайн построение,график онлайн построить,график онлайн построить x y z,график онлайн построить по точкам,график онлайн построить по уравнению,график онлайн построить с модулем,график онлайн с модулем,график онлайн трехмерный,график онлайн функция,график онлайн чертить,график параболы онлайн,график параметрической функции онлайн,график по точкам онлайн,график по уравнению онлайн,график по формуле онлайн,график по функции,график по функции онлайн,график построение,график построение онлайн,график решить,график с корнем онлайн с,график с модулем онлайн,график с модулем онлайн построить,график сайт,график синус х 2,график системы уравнений онлайн,график степенной функции онлайн,график строить,график строить онлайн,график тригонометрической функции онлайн,график у 1,график у 1 2 х,график у 1 2х,график у 1 2х2,график у 1 x,график у 1 корень из х,график у 1 х,график у 1 х 2,график у 2,график у 2 x,график у 3 x,график у 3 х,график у 3х,график у 4 х,график у x,график у x 2,график у х,график у х 1,график у х 1 х 3,график у х 2 5,график у х 4,график у х 5,график у х 7,график у х 8,график у х в степени 2,график у х2 1,график уравнения y 2 x 2,график уравнения онлайн,график функции,график функции 1 2 x,график функции 1 2 х,график функции 1 cos x 1,график функции 1 x,график функции 1 x 2,график функции 1 x 3,график функции 1 x 4,график функции 1 x в квадрате,график функции 1 корень из х,график функции 1 х,график функции 1 х 2,график функции 1 х 3,график функции 1 х в квадрате,график функции 2 1 х,график функции 2 3 x,график функции 2 x,график функции 2 x 1,график функции 2 x 3,график функции 2 y 1 x,график функции 2 х 1,график функции 2x,график функции 2x 2 x,график функции 3 1 х,график функции 3 x,график функции 3 x 1,график функции 3 x 2,график функции 3 х,график функции 4 x,график функции 4 x 2,график функции 4 в степени х,график функции 4 х,график функции 4 х 2,график функции 5 x,график функции sin 1 x,график функции x,график функции x 1,график функции x 1 2,график функции x 1 3,график функции x 1 в квадрате,график функции x 2,график функции x 2 1,график функции x 2 3,график функции x 2 4x,график функции x 2 y 2,график функции x 2 y 2 4,график функции x 2 y 2 9,график функции x 2 y 2 9 график,график функции x 2x 2,график функции x 3,график функции x 3 1,график функции x 3 2,график функции x 3 sin y,график функции x 3 x 1 x,график функции x 3 x 2 1,график функции x 4,график функции x 4 2,график функции x 5,график функции x 6,график функции x e,график функции x y,график функции x y 0 x,график функции x y 1,график функции x y 5,график функции x y a,график функции x3,график функции y 0,график функции y 0 x 0,график функции y 1,график функции y 1 2,график функции y 1 2x,график функции y 1 3 x 2,график функции y 1 3x в квадрате,график функции y 1 4x в квадрате,график функции y 1 x 4,график функции y 1 x в квадрате,график функции y 2,график функции y 2 1,график функции y 2 3x,график функции y 2 x,график функции y 2 x 1,график функции y 2 x 3,график функции y 2 x2,график функции y 2x,график функции y 2x 2,график функции y 2x 3,график функции y 2×2,график функции y 2×2 1,график функции y 3,график функции y 3 2x,график функции y 3 x,график функции y 3 x 2,график функции y 3x 2,график функции y 4 x,график функции y 4 x 2,график функции y 4 в x степени,график функции y 4x 2,график функции y 5,график функции y 5 2x,график функции y 5 x,график функции y 5 x 2,график функции y 5x,график функции y 5x 2,график функции y 5x 4,график функции y 6 2x,график функции y lg x,график функции y tg 2x,график функции y x,график функции y x 1,график функции y x 1 2,график функции y x 1 4,график функции y x 1 x 2,график функции y x 1 в квадрате,график функции y x 10,график функции y x 2 3,график функции y x 2 3 x 2x,график функции y x 2 5,график функции y x 2 x 0,график функции y x 3 2,график функции y x 3 4,график функции y x 3 как построить,график функции y x 4,график функции y x 4 2,график функции y x 4 3,график функции y x 5,график функции y x 6,график функции y x 7,график функции y x 9,график функции y x sqrt x 2,график функции y x в квадрате 1,график функции y x как построить,график функции y x2,график функции y x2 1,график функции y x2 3,график функции y x4,график функции y x5,график функции y x6,график функции y х,график функции в полярных координатах онлайн,график функции двух переменных онлайн,график функции двух переменных онлайн построить,график функции как выглядит,график функции калькулятор,график функции калькулятор онлайн,график функции нарисовать,график функции одна вторая икс в квадрате,график функции онлайн,график функции онлайн x y z,график функции онлайн двух переменных,график функции онлайн калькулятор,график функции онлайн неявной,график функции онлайн по точкам,график функции онлайн построение,график функции онлайн построить,график функции онлайн построить по точкам,график функции онлайн построить с корнем,график функции онлайн построить с модулем,график функции онлайн построить с решением,график функции онлайн с модулем,график функции онлайн с решением,график функции параметрической онлайн,график функции по,график функции по точкам онлайн,график функции по точкам онлайн построить,график функции построение,график функции построение онлайн,график функции решение,график функции решить онлайн,график функции с модулем онлайн,график функции с решением онлайн,график функции синус 2х,график функции строить онлайн,график функции у,график функции у 1 2 х,график функции у 1 2х,график функции у 1 х 2,график функции у 1 х в квадрате,график функции у 2,график функции у 2 x,график функции у 3,график функции у 3 x,график функции у 4х в квадрате,график функции у x,график функции у x 1,график функции у x 2,график функции х,график функции х 1,график функции х 1 2,график функции х 2 1,график функции х 2 y,график функции х 3 2,график функции х 4,график функции х 4 2,график функции х 4 х 2,график функции х y,график функции х y 2,график функции х в 4 степени,график функции х в квадрате минус х,график функции х в квадрате х,график функции х делить на х,график функции х у,график функций,график функций онлайн,график функция онлайн,график х,график х 0,график х 1,график х 1 2,график х 1 в квадрате,график х 2,график х 2 1,график х 2 3,график х 2 y 2,график х 3,график х 3 1,график х 3 2,график х 4,график х y 2,график х в квадрате,график х в квадрате 1,график х в квадрате 4,график х в степени 2,график х в степени 4,график х е х,график х и у,график х у,график х у 4,график х у z,график х2 1,график х3,график чертить онлайн,график экспоненты в степени минус х,графика онлайн,графика точками,графики,графики x 2 y 2,графики y 2 x,графики в полярной системе координат онлайн,графики в полярных координатах онлайн,графики онлайн,графики онлайн 3d,графики онлайн в полярной системе координат,графики онлайн в полярных координатах,графики онлайн по точкам,графики онлайн полярная система координат,графики онлайн построение,графики онлайн построение по точкам,графики онлайн построение по уравнению,графики онлайн трехмерные,графики по точкам онлайн,графики по точкам онлайн построение,графики построение,графики построение онлайн,графики построить,графики построить онлайн,графики рисовать онлайн,графики строить,графики строить онлайн,графики уравнений онлайн,графики функции онлайн,графики функций x 2 y 2,графики функций калькулятор,графики функций онлайн,графики функций онлайн калькулятор,графики функций онлайн построение,графики функций онлайн с модулем,графики функций онлайн с решением,графики функций построение,графики функций построение онлайн,графики функций построить,графики функций с модулем онлайн,графики функций строить онлайн,графики чертить,графический калькулятор онлайн,графический онлайн калькулятор,графическое решение уравнений онлайн,графік,графік функції y 2 x,графік функції y x 2,графік функції онлайн,графіки,графіки онлайн,графопостроитель онлайн,дослідити функцію та побудувати її графік онлайн,е график,е х график,изобразите график функции,изобразить график функции онлайн,изоклины онлайн построение,икс в степени икс график,инженерная графика онлайн построение,используя график функции y f x постройте график функции,используя график функции построить график функции,исследовать график функции онлайн,исследовать график функции онлайн с решением,исследовать и построить график функции онлайн,исследовать функцию и построить график онлайн решение калькулятор,как выглядит график,как выглядит график x 2 y 2,как выглядит график функции,как начертить график функции,как построить x y,как построить y x,как построить график x y,как построить график x y 2,как построить график y 2 x,как построить график y x,как построить график y x 2,как построить график функции x 2 y,как построить график функции x y,как построить график функции x y 2,как построить график функции x y 3,как построить график функции y,как построить график функции y x,как построить график функции y x 2,как построить график функции по уравнению,калькулятор график,калькулятор график функции,калькулятор графика функции,калькулятор графики функций,калькулятор графиков,калькулятор графиков онлайн,калькулятор графиков функций,калькулятор графиков функций онлайн,калькулятор графиков функций онлайн с решением,калькулятор графический онлайн,калькулятор для построения графиков функций,калькулятор онлайн график функции,калькулятор онлайн графиков,калькулятор онлайн построить график функции,калькулятор построения графиков функций,калькулятор построения графиков функций онлайн,калькулятор построить график функции,калькулятор функции график,калькулятор функции онлайн,калькулятор функций,калькулятор функций графики,калькулятор функций графики онлайн,калькулятор функций онлайн,квадратичная функция онлайн,конструктор графиков,конструктор графиков онлайн,конструктор онлайн функций,конструктор функций онлайн,координатная плоскость онлайн,координатная плоскость онлайн рисовать,координатная прямая онлайн,косинус 3х график,косинус х 2 график,лучший построитель графиков,лучший построитель графиков онлайн,математика график,математикам ру построение графика,найти график функции,нарисовать график,нарисовать график онлайн,нарисовать график онлайн вручную,нарисовать график онлайн по точкам,нарисовать график по точкам онлайн,нарисовать график функции,нарисовать график функции онлайн,нарисовать онлайн функцию,нарисовать функцию онлайн,начертите график,начертить график,начертить график онлайн,начертить график онлайн по точкам,начертить график по точкам онлайн,начертить график функции онлайн,неравенства график онлайн,окружность построить онлайн,онлайн 3d график,онлайн гипербола,онлайн график,онлайн график в полярной системе координат,онлайн график квадратичной функции,онлайн график логарифма,онлайн график логарифмической функции,онлайн график по таблице,онлайн график по точкам,онлайн график по уравнению,онлайн график по формуле,онлайн график построение,онлайн график с модулем,онлайн график функции,онлайн график функции z x y,онлайн график функции с модулем,онлайн графика,онлайн графики,онлайн графики в полярных координатах,онлайн графики в пространстве,онлайн графики по точкам,онлайн графики с модулем,онлайн графики уравнений,онлайн графики функции,онлайн графики функций построить,онлайн графіки,онлайн калькулятор график функции,онлайн калькулятор графики функций,онлайн калькулятор графиков,онлайн калькулятор графиков функций,онлайн калькулятор графиков функций с решением,онлайн калькулятор для функций,онлайн калькулятор построения графиков функций,онлайн калькулятор построить график функции,онлайн калькулятор функции,онлайн калькулятор функций,онлайн квадратичная функция,онлайн конструктор графиков,онлайн конструктор функций,онлайн координатная плоскость,онлайн координатная прямая,онлайн описать функцию,онлайн парабола,онлайн побудова графіків,онлайн побудова графіків функцій,онлайн построение,онлайн построение гиперболы,онлайн построение график функции,онлайн построение графика,онлайн построение графика в полярной системе координат,онлайн построение графика в полярных координатах,онлайн построение графика квадратичной функции,онлайн построение графика функции,онлайн построение графиков,онлайн построение графиков 3d,онлайн построение графиков в полярных координатах,онлайн построение графиков в трехмерной системе координат,онлайн построение графиков зависимости,онлайн построение графиков неравенств,онлайн построение графиков онлайн в полярной системе координат онлайн,онлайн построение графиков по точкам,онлайн построение графиков по уравнению,онлайн построение графиков по физике,онлайн построение графиков с двумя переменными,онлайн построение графиков с корнем,онлайн построение графиков с корнями,онлайн построение графиков с модулем,онлайн построение графиков сложных функций,онлайн построение графиков тригонометрических функций,онлайн построение графиков уравнений,онлайн построение графиков функции,онлайн построение графиков функций,онлайн построение графиков функций x y z,онлайн построение графиков функций по уравнению,онлайн построение графиков функций с модулем,онлайн построение графиков функций с решением,онлайн построение графов,онлайн построение квадратичной функции,онлайн построение кривых,онлайн построение логарифмических графиков,онлайн построение нескольких графиков в одной системе координат,онлайн построение окружности,онлайн построение параболы,онлайн построение синусоиды,онлайн построение тригонометрических графиков,онлайн построение тригонометрических функций,онлайн построение фигур,онлайн построение функций,онлайн построения графиков,онлайн построитель,онлайн построитель графиков,онлайн построитель графиков функций,онлайн построитель функций,онлайн построить график квадратичной функции,онлайн построить графики функций,онлайн постройка графика,онлайн постройка графиков,онлайн постройка графиков функций,онлайн программа для построения графиков,онлайн программа построения графиков,онлайн решение графика функции,онлайн решение графиков,онлайн решение графиков функций,онлайн решение графических уравнений,онлайн решение квадратичной функции,онлайн решение параболы,онлайн решение функций,онлайн решение функция,онлайн решить график функции,онлайн рисование графиков,онлайн система координат,онлайн составить график функции,онлайн составление графика,онлайн составление графиков,онлайн строим график,онлайн строим графики,онлайн строитель графиков,онлайн строитель графиков функций,онлайн строитель функций,онлайн строительство графиков,онлайн строить график функции,онлайн строить графики функций,онлайн трехмерная система координат,онлайн функции,онлайн функция,онлайн функция график,онлайн функция решение,онлайн чертить график,онлайн черчение графиков,описать график функции онлайн,описать функцию онлайн,определить функцию по графику онлайн,парабола онлайн,парабола онлайн построение,парабола построение онлайн,параболы онлайн построение,по графику определить функцию онлайн,по математике графики,по формуле построить график,побудова графіків,побудова графіків онлайн,побудова графіків функцій,побудова графіків функцій онлайн,побудувати графік,побудувати графік онлайн,побудувати графік функції,побудувати графік функції онлайн,побудувати графік функції онлайн розв язок,побудуйте графік функції,полярная система координат графики онлайн,построение 3д графиков онлайн,построение в полярных координатах онлайн,построение график,построение график онлайн,построение график функции,построение график функции онлайн,построение графика,построение графика в полярной системе координат онлайн,построение графика в полярных координатах онлайн,построение графика квадратичной функции онлайн,построение графика онлайн,построение графика онлайн в полярных координатах,построение графика онлайн по точкам,построение графика онлайн по функции,построение графика по точкам,построение графика по точкам онлайн,построение графика по функции онлайн,построение графика функции,построение графика функции онлайн,построение графика функции онлайн с решением,построение графики,построение графики функций,построение графиков,построение графиков xyz онлайн,построение графиков в полярной системе координат онлайн,построение графиков в полярной системе координат онлайн с решением,построение графиков в полярных координатах онлайн,построение графиков в пространстве онлайн,построение графиков в трехмерной системе координат онлайн,построение графиков в трехмерном пространстве онлайн,построение графиков зависимости онлайн,построение графиков на миллиметровке онлайн,построение графиков неравенств онлайн,построение графиков онлайн,построение графиков онлайн 3д,построение графиков онлайн xyz,построение графиков онлайн в полярной системе координат,построение графиков онлайн в полярных координатах,построение графиков онлайн в пространстве,построение графиков онлайн в трехмерной системе координат,построение графиков онлайн на миллиметровке,построение графиков онлайн неравенств,построение графиков онлайн по таблице,построение графиков онлайн по точкам,построение графиков онлайн по точкам на миллиметровке,построение графиков онлайн по уравнению,построение графиков онлайн по физике,построение графиков онлайн с двумя переменными,построение графиков онлайн с корнем,построение графиков онлайн с корнями,построение графиков онлайн с модулем,построение графиков онлайн с параметром,построение графиков онлайн с решением,построение графиков онлайн трехмерных,построение графиков по таблице онлайн,построение графиков по точкам,построение графиков по точкам онлайн,построение графиков по уравнению онлайн,построение графиков по физике онлайн,построение графиков полярных онлайн,построение графиков с двумя переменными онлайн,построение графиков с корнем онлайн,построение графиков с корнями онлайн,построение графиков с модулем онлайн,построение графиков с параметром онлайн,построение графиков сложных функций онлайн,построение графиков тригонометрических онлайн,построение графиков тригонометрических функций онлайн,построение графиков уравнений онлайн,построение графиков функции,построение графиков функции онлайн,построение графиков функции онлайн с решением,построение графиков функции с решением онлайн,построение графиков функций,построение графиков функций онлайн,построение графиков функций онлайн x y z,построение графиков функций онлайн по уравнению,построение графиков функций онлайн с модулем,построение графиков функций онлайн с подробным решением,построение графиков функций онлайн с решением,построение графиков функций по уравнению онлайн,построение графиков функций с модулем онлайн,построение графиков функций с решением онлайн,построение графов онлайн,построение квадратичной функции онлайн,построение кривых онлайн,построение логарифмических графиков онлайн,построение нескольких графиков в одной системе координат онлайн,построение нескольких графиков онлайн,построение обратной функции онлайн,построение окружности онлайн,построение онлайн,построение онлайн кривых,построение параболы онлайн,построение параболы онлайн по квадратному уравнению,построение параболы по квадратному уравнению онлайн,построение параметрических графиков онлайн с решением,построение полярных графиков онлайн,построение пространственных графиков онлайн,построение синусоиды онлайн,построение сложных графиков онлайн,построение сложных графиков функций онлайн,построение точек онлайн по координатам,построение точек по координатам онлайн,построение трехмерных графиков онлайн,построение тригонометрических графиков онлайн,построение тригонометрических функций онлайн,построение уравнений онлайн,построение функции,построение функции онлайн,построение функций,построение функций онлайн,построения графиков онлайн,построитель графиков,построитель графиков онлайн,построитель графиков функций,построитель графиков функций онлайн,построитель онлайн,построитель функций,построитель функций онлайн,построить y x 2 x 1,построить гиперболу онлайн,построить гиперболу онлайн по уравнению,построить гиперболу по уравнению онлайн,построить график,построить график 1 x 2,построить график 3d,построить график x 3 x 2,построить график x f y,построить график x sin x,построить график x y,построить график x y 1,построить график x y z онлайн,построить график x y в квадрате,построить график y,построить график y 1 x,построить график y 2 2x,построить график y 2 x,построить график y 2 x 3,построить график y 2x,построить график y 3 2 x,построить график y 4 x,построить график y cos2x,построить график y x,построить график y x 1,построить график y x 2,построить график y x 3,построить график y x 4,построить график y x 4 2,построить график y x 5,построить график y x 6,построить график в полярной системе координат онлайн,построить график в полярных координатах онлайн,построить график в трехмерном пространстве онлайн,построить график зависимости онлайн,построить график зависимости онлайн по точкам,построить график зависимости по точкам онлайн,построить график квадратичной функции онлайн,построить график квадратичной функции онлайн с решением,построить график логарифмической функции онлайн,построить график неявной функции онлайн,построить график обратной функции онлайн,построить график окружности онлайн,построить график онлайн,построить график онлайн x y z,построить график онлайн в полярной системе координат,построить график онлайн в трехмерном пространстве,построить график онлайн неявной функции,построить график онлайн окружности,построить график онлайн по данным таблицы,построить график онлайн по координатам,построить график онлайн по таблице,построить график онлайн по таблице онлайн,построить график онлайн по точкам,построить график онлайн по точкам x y,построить график онлайн по точкам на миллиметровке,построить график онлайн по точкам онлайн,построить график онлайн по уравнению,построить график онлайн по уравнению онлайн,построить график онлайн по функции,построить график онлайн с модулем,построить график параметрической функции онлайн,построить график по данным таблицы онлайн,построить график по координатам онлайн,построить график по таблице онлайн,построить график по точкам,построить график по точкам онлайн,построить график по уравнению онлайн,построить график по уравнению функции,построить график по функции онлайн,построить график с корнем онлайн с,построить график с модулем онлайн,построить график системы уравнений онлайн,построить график тригонометрической функции онлайн,построить график тригонометрической функции онлайн с решением,построить график у 2 х,построить график у 4 х,построить график у x 2 3 x 2,построить график у х 1 2,построить график у х 2,построить график у х 3,построить график у х 4,построить график уравнения,построить график уравнения онлайн,построить график уравнения онлайн с решением,построить график функции,построить график функции 1 x 1,построить график функции 1 x 2,построить график функции 1 y 2x,построить график функции 1 у 3 х,построить график функции 2 5 x 2,построить график функции 2 5x 2,построить график функции x 1 2,построить график функции x 2 1,построить график функции x 3 2x 2 x 3,построить график функции x f y,построить график функции x y,построить график функции x y 4,построить график функции y,построить график функции y 1 2 x 2,построить график функции y 1 2x 2,построить график функции y 1 2×2,построить график функции y 1 x,построить график функции y 1 x 3,построить график функции y 2 3 x,построить график функции y 2 3x,построить график функции y 2 5x,построить график функции y 2 x 3,построить график функции y 2 x 5,построить график функции y 2x 3,построить график функции y 2x 4 x 2 1 решение,построить график функции y 3 2x,построить график функции y 3 x 2,построить график функции y 3x в квадрате,построить график функции y 4 x,построить график функции y 4 x 1,построить график функции y 5 2x,построить график функции y 5 x 2,построить график функции y 5x 2,построить график функции y 8 x,построить график функции y cos x 1,построить график функции y x,построить график функции y x 1,построить график функции y x 1 2,построить график функции y x 1 2 3,построить график функции y x 1 4,построить график функции y x 1 x 2,построить график функции y x 1 x 3,построить график функции y x 10,построить график функции y x 2,построить график функции y x 2 3,построить график функции y x 3,построить график функции y x 3 2,построить график функции y x 4 2,построить график функции y x 4 x,построить график функции y x 5,построить график функции y x 7,построить график функции y x 8,построить график функции y x cos x,построить график функции y x sin x,построить график функции в полярной системе координат онлайн,построить график функции в трехмерном пространстве онлайн,построить график функции двух переменных онлайн,построить график функции калькулятор,построить график функции онлайн,построить график функции онлайн в полярной системе координат,построить график функции онлайн в трехмерном пространстве,построить график функции онлайн калькулятор,построить график функции онлайн по точкам,построить график функции онлайн по уравнению,построить график функции онлайн по уравнению онлайн,построить график функции онлайн по уравнению с решением,построить график функции онлайн с корнем,построить график функции онлайн с модулем,построить график функции онлайн с подробным решением,построить график функции онлайн с подробным решением 9 класс,построить график функции онлайн с решением,построить график функции онлайн с решением 10 класс,построить график функции онлайн с таблицей точек,построить график функции по модулю онлайн,построить график функции по точкам онлайн,построить график функции по уравнению,построить график функции по уравнению онлайн,построить график функции с корнем онлайн,построить график функции с модулем онлайн,построить график функции с модулем онлайн с подробным решением,построить график функции у,построить график функции у 1 х,построить график функции у 1 х 2,построить график функции у 2 х,построить график функции у х,построить график функции у х в квадрате,построить график функции х в квадрате,построить график функции х у,построить график функции х у 4,построить график функции х у 5,построить график функций,построить график функций онлайн с решением,построить график функций с решением онлайн,построить график х у 2,построить графики,построить графики онлайн,построить графики онлайн по точкам,построить графики по точкам онлайн,построить графики функций,построить графики функций в одной системе координат,построить графики функций онлайн,построить графики функций онлайн с решением,построить и исследовать график функции онлайн,построить и прочитать график функции,построить интегральную кривую онлайн,построить интегральные кривые онлайн,построить калибровочный график онлайн,построить кривую заданную уравнением в полярной системе координат онлайн,построить кривую онлайн,построить кривые по заданным уравнениям онлайн с решением,построить линии уровня функции онлайн,построить несколько графиков на одном онлайн,построить область ограниченную линиями онлайн,построить окружность онлайн,построить онлайн график в полярных координатах,построить онлайн график логарифмической функции,построить онлайн график с модулем,построить онлайн график функции по точкам,построить онлайн график функций,построить онлайн фигуру,построить параболу онлайн,построить параболу онлайн по уравнению,построить параболу по уравнению онлайн,построить по точкам график зависимости онлайн,построить прямую онлайн,построить прямую онлайн по уравнению,построить прямую по уравнению онлайн,построить тригонометрический график онлайн,построить функции онлайн,построить функцию,построить функцию онлайн,построить функцию онлайн с решением,построить функция онлайн,построить эллипс онлайн,построить эскиз графика функции онлайн,построй график функции,постройка графика,постройка графика онлайн,постройка графика онлайн по точкам,постройка графика по точкам онлайн,постройка графика функции,постройка графика функции онлайн,постройка графиков,постройка графиков онлайн,постройка графиков функций онлайн,постройте график,постройте график x y,постройте график y 2 x,постройте график y x,постройте график y x 2,постройте график y x 6,постройте график онлайн,постройте график уравнений,постройте график уравнения 2×2 y 4x 3,постройте график функции,постройте график функции x 3,постройте график функции x y 2 y 0 x,постройте график функции y,постройте график функции y 1 2,постройте график функции y 1 3 x 2,постройте график функции y 1 3x 2,постройте график функции y 1 4x,постройте график функции y 1 6x,постройте график функции y 1 x,постройте график функции y 2,постройте график функции y 2 3 x,постройте график функции y 2 корень 3 степени из x,постройте график функции y 2x,постройте график функции y 3 4 x 1,постройте график функции y 3 х 1,постройте график функции y x,постройте график функции y x 1,постройте график функции y x 1 2,постройте график функции y x 1 x 3 x 4,постройте график функции y x 10,постройте график функции y x 2 x 3 x 1,постройте график функции y x 3,постройте график функции y x 3 2,постройте график функции y x 5,постройте график функции y х 2,постройте график функции игрек равен,постройте график функции игрек равно,постройте график функции онлайн,постройте график функции онлайн с решением,постройте график функции у,постройте график функции у 1 4х2,постройте график функции у 1 x,постройте график функции х у,постройте график функций,постройте график функций y,постройте графики,постройте графики функций,преобразование графиков функций онлайн,преобразование функции онлайн,программа для построения графиков онлайн,программа для построения графиков функций онлайн,программа онлайн для построения графиков,программа онлайн построения графиков,программа построения графиков онлайн,программа построения графиков функций онлайн,прямая у х,прямоугольная система координат онлайн,решение y 1 x,решение график функции,решение графика функции онлайн,решение графиков,решение графиков онлайн,решение графиков функций,решение графиков функций онлайн,решение графиков функций онлайн с решением,решение графических уравнений онлайн,решение квадратичной функции онлайн,решение онлайн графика функции,решение онлайн графиков функций,решение онлайн квадратичной функции,решение онлайн функции,решение параболы онлайн,решение функции онлайн,решение функции онлайн с решением и графиком,решение функций онлайн,решение функций онлайн с решением,решение функций онлайн с решением и графиком,решение функция онлайн,решите графически уравнение онлайн,решите уравнение графически онлайн,решить график,решить график функции онлайн,решить график функции онлайн с решением,решить графически уравнение онлайн,решить графически уравнение онлайн с решением,решить онлайн график функции,решить онлайн функцию,решить уравнение графически онлайн,решить функцию онлайн,решить функцию онлайн с решением и построить график онлайн,рисование графиков онлайн,рисовать графики онлайн,рисовать онлайн графики,сайт для построения графиков,сайт для построения графиков функций,сайт построения графиков функции,свойства функции онлайн,сделать график онлайн,сделать график онлайн по данным,сделать график онлайн по точкам,сделать график по точкам онлайн,синусоида график онлайн,система координат онлайн,создание графиков онлайн,составить график функции онлайн,составить онлайн график функции,составление графика онлайн,составление графиков онлайн,составление онлайн графика,составление онлайн графиков,строение графика функции онлайн,строим график,строим графики онлайн,строим онлайн график,строитель графиков,строитель графиков онлайн,строитель графиков функций онлайн,строитель функций онлайн,строительство графиков онлайн,строить график,строить график онлайн,строить график функции онлайн,строить графики,строить графики онлайн,строить графики функций онлайн,трехмерная система координат онлайн,трехмерная система координат онлайн построение,трехмерная система координат онлайн построение по точкам,трехмерные графики онлайн,трехмерный график онлайн,тригонометрические графики онлайн,у 1 2х график,у 1 2х график функции,у 1 2х2 график,у 1 3х2 график,у 1 x график функции,у 1 график,у 1 график функции,у 1 корень из х график,у 1 х 2 график,у 1 х 2 график функции,у 1 х 3 график,у 1 х в квадрате график функции,у 1 х график,у 1 х2 график функции,у 2 x 2 график,у 2 x 2 график функции,у 2 x график,у 2 график,у 2 график функции,у 2 х 1 график,у 2 х построить график,у 2х 1 построить график,у 3 x график,у 3 x график функции,у 3 в степени х график,у 3 график,у 3 график функции,у 3 х 2 график,у 3 х график,у 3 х построить график функции,у 3х график,у 4 х 2 график функции,у 4 х построить график,у 5 х 2 график,у 5 х график,у x 2 график,у x график,у x график функции,у график функции,у х 1 2,у х 1 2 график,у х 1 график,у х 2 1 график,у х 2 построить график,у х 4,у х 4 2 график,у х 4 3,у х 4 график,у х 5 график функции,у х 6 график,у х в 2 степени график,у х в степени 2 график,у х график,у х построить график функции,у х2 1 график,функции график построение,функции калькулятор,функции онлайн,функции онлайн калькулятор,функции онлайн построить,функции онлайн с решением,функции решение онлайн,функция 1 3x 2,функция 1 x график,функция 2 x,функция 3 x,функция 4 x,функция x 1 график,функция x 2 график,функция x 4,функция x 5,функция y 1 2x в квадрате,функция y 5 x,функция y x 4,функция y x 5,функция график онлайн,функция квадратичная онлайн,функция онлайн,функция онлайн график,функция онлайн построить,функция онлайн решение,функция по точкам онлайн,функция построить онлайн,функция решение онлайн,х 0 график,х 1 в квадрате график,х 1 в квадрате график функции,х 1 график,х 1 х 2 построить график,х 2 1 график,х 2 4 график,х 2 4 график функции,х 2 y 2 1 график,х 2 y 4,х 2 график,х 3 1 график,х 3 график,х 4 график,х 4 график функции,х 4 функция,х y 2 график,х y график,х y график функции,х в квадрате 1 график,х в квадрате 4 график,х в степени 2 график,х график,х и у график,х у z график,х у график,х2 1 график,чертить график онлайн,чертить графики,черчение графиков онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
Где можно решить любую задачу по математике, а так же 1 2 cos x 2 график Онлайн?
Решить задачу 1 2 cos x 2 график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Натуральный логарифм, функция ln x
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.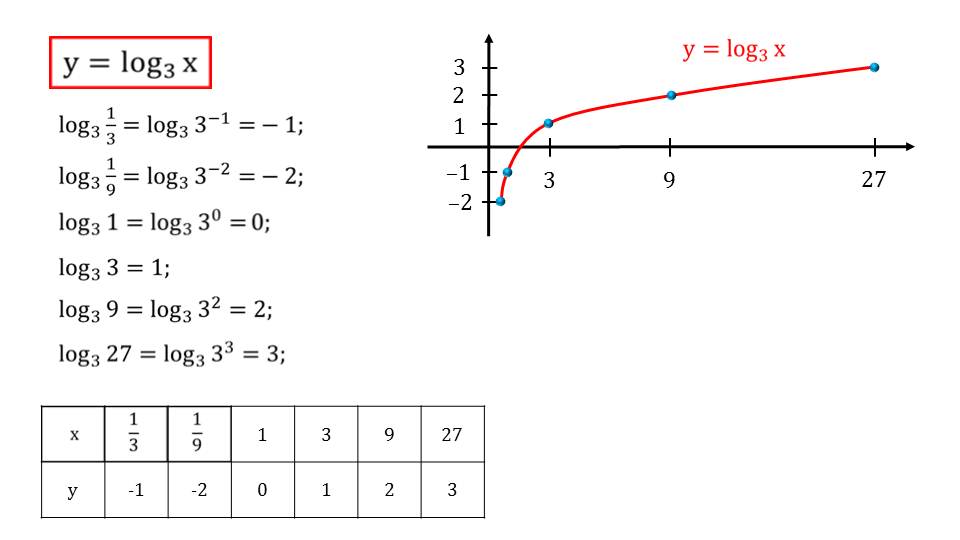
Определение
- Натуральный логарифм
- – это функция y = ln x, обратная к экспоненте, x = e y, и являющаяся логарифмом по основанию числа е: ln x = loge x.
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x.
Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045…;
.
График натурального логарифма ln x
График функции y = ln x.
График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.
Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).
При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма.
При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
| Область определения | 0 < x + ∞ |
| Область значений | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет |
| + ∞ | |
| – ∞ |
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм».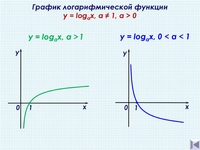
Обратная функция
Обратной для натурального логарифма является экспонента.
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям:
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z:
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.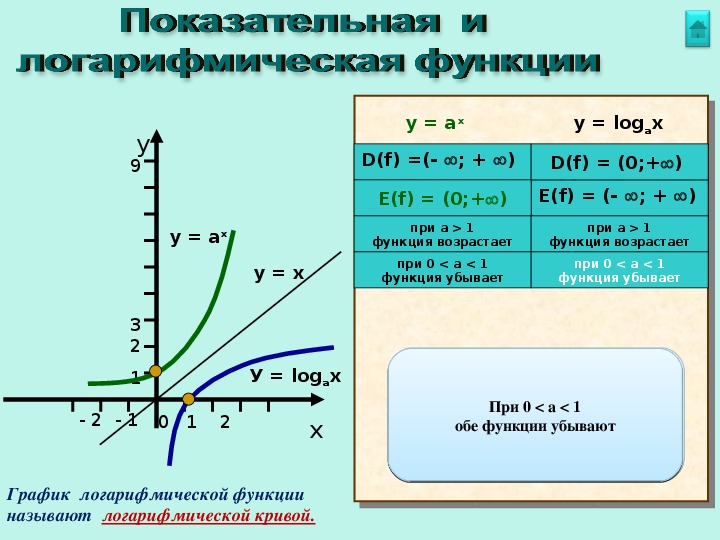 Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
графическое представление функции log (x)
× Программа для построения графиков , также известная как графопостроитель ,
представляет собой онлайновый плоттер кривых , который позволяет строить графики функций онлайн.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Графопостроитель особенно подходит для исследования функций ,
он позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума и максимума функции. Для мощности
Для мощности
Это программное обеспечение для построения графиков позволяет использовать следующие обычные математические функции :
- абс (абсолютное значение), абсолютное значение графика
- arccos (арккосинус), сюжет арккосинус
- арксин (арксинус), сюжет арксинус
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), сюжетный косинус
- котан (котангенс), котангенс участка
- котангенс (гиперболический котангенс), гиперболический котангенс графика
- cube_root (корень куба), Построить кубический корень
- exp (экспонента), сюжет экспоненциальный
- ln (наперский логарифм), график наперского логарифма
- лог (логарифм), логарифм графика
- ш (гиперболический синус), график гиперболический синус
- sin (синус), сюжетный синус
- sqrt (квадратный корень), квадратный корень из участка
- тангенс (тангенс), касательная к сюжету
- -я (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию до построить другие кривые онлайн .
Для представления функций используется переменная «x».
Можно получить координаты точек кривой с помощью курсора. Для этого щелкните кривую, чтобы появился курсор, а затем перетащите ее вдоль кривой, чтобы увидеть ее координаты.
Кривые можно снять с плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку «Удалить все» в меню.
Можно изменить кривую, присутствующую на графике, выбрав ее, отредактировав ее выражение, а затем нажав на кнопке редактирования.
Онлайн-плоттер имеет несколько опций, которые позволяют настраивать график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров.Затем можно определить границы графиков,
чтобы подтвердить эти изменения, необходимо еще раз нажать кнопку «Параметры».
- Проведите касательную функции к точке
- График производной функции
Онлайн-плоттер позволяет нарисовать касательную функции в точке , чтобы сделать это, вы просто нарисуете желаемую функцию, а затем, когда функция будет нарисована, щелкните меню, параметры, а затем кнопку касательной, которая появляется на экране, затем рисуется касательная, можно изменить точку касательной, что приведет к перерисовке касательной.Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет построить график производной функции для этого,
вы просто рисуете желаемую функцию, а затем после того, как функция нарисована,
нажмите на меню, на опции, затем на производную кнопку, которая появляется,
затем строится производная функции.
Графопостроитель может также использоваться для вычисления производной функции и участок для этого, вы должны построить желаемую функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, красный курсор появится на кривой. Затем нажмите на меню, на опции, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции.(«Выражение» представляет выражение, которое будет выведено и нанесено на график).
Плоттер позволяет построить параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения желаемых точек.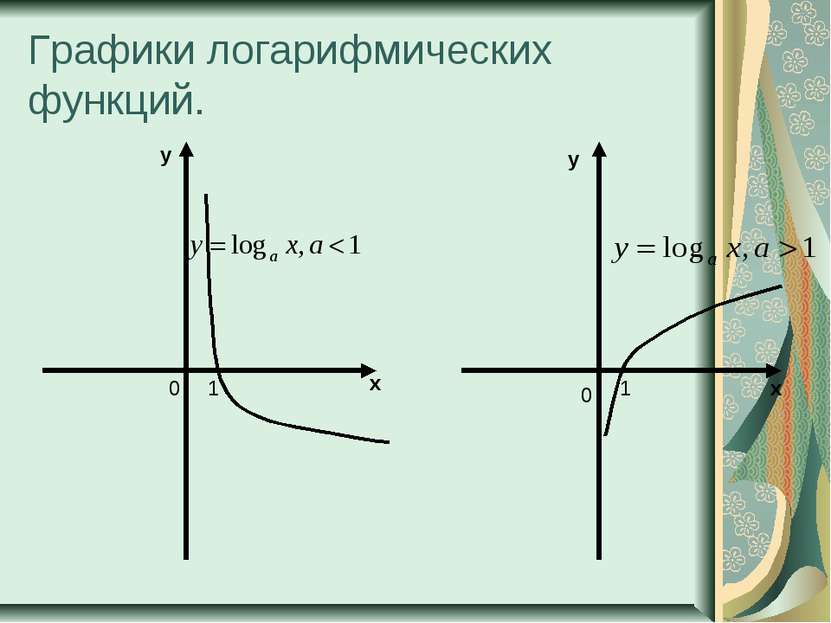
Графопостроитель может использоваться для построения полярной кривой . Для этого просто введите выражение полярной кривой как функцию от t, затем нажмите кнопку «построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения желаемых точек.
Есть возможность перемещаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо войти в меню, затем нажать на опции,
После этого можно изменить пределы графического отображения.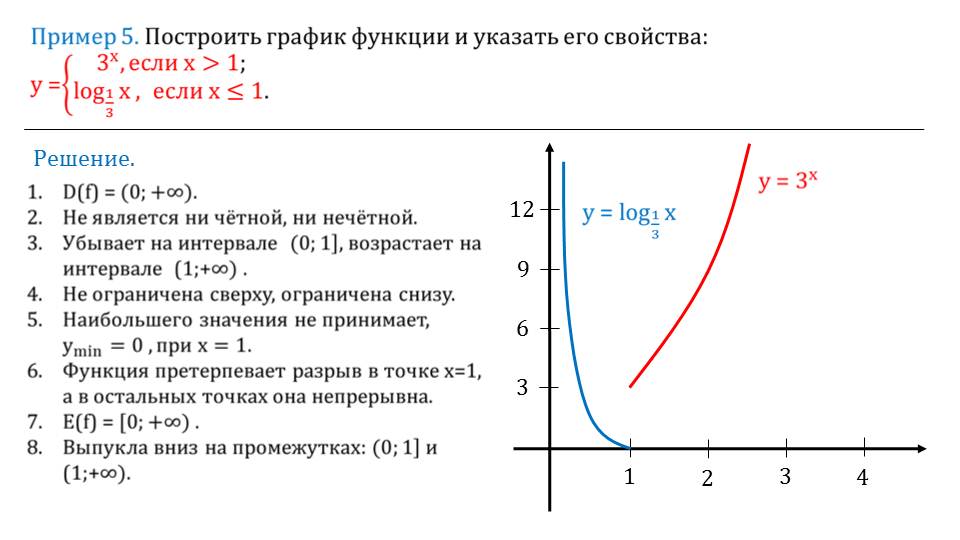
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это, используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Построенные кривые можно экспортировать с помощью графического калькулятора , экспорт выполняется как
изображение в формате PNG.Для этого вам нужно перейти в меню графика, затем в подменю экспорта графиков.
Калькулятор затем отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно копирование изображения. Чтобы вернуться к нормальному отображению калькулятора, используйте кнопку «Выйти из режима изображения».
Чтобы вернуться к нормальному отображению калькулятора, используйте кнопку «Выйти из режима изображения».
онлайн — журнал функций
Описание:
Функция журнала вычисляет логарифм числа в режиме онлайн.
войти в онлайнОписание:
Логарифм Функция определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, он отмечает журнал .
Калькулятор логарифма позволяет вычислить этого типа логарифма онлайн .
- Вычисление логарифма
- Производная от логарифма
- Первообразная логарифма
- Пределы логарифма
Для вычисления логарифма числа просто введите число и примените
функция log .Таким образом, для из расчета логарифм числа 1, необходимо ввести
журнал (`1`) или
непосредственно 1, если журнал кнопок уже появляется, возвращается результат 0.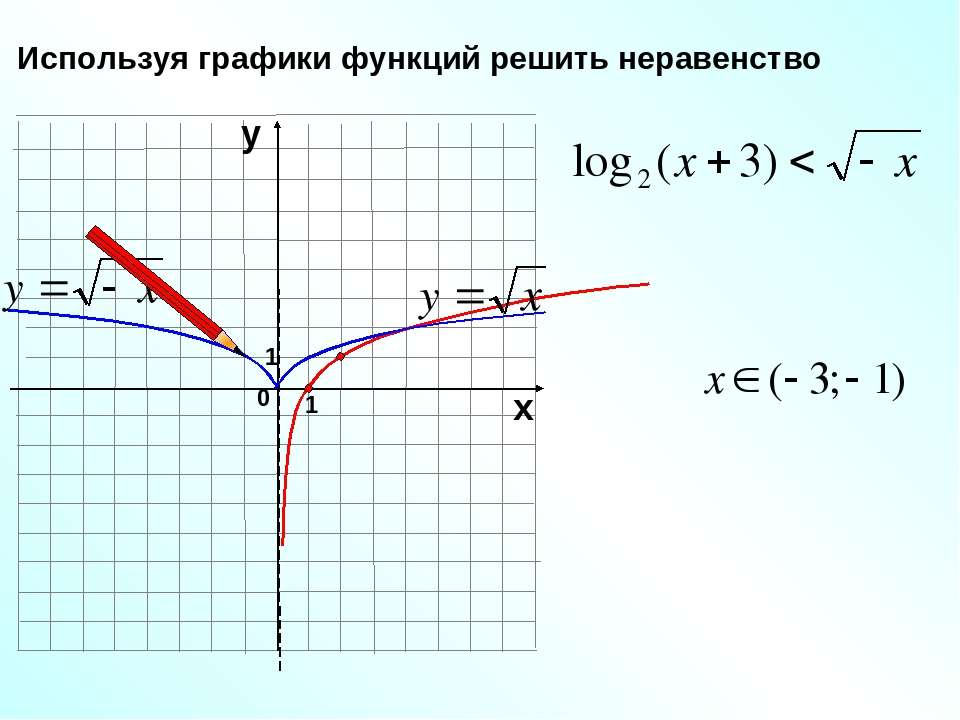
Производная логарифма равна `1 / (x * ln (10))`.
Первообразная логарифма равна `(x * ln (x) -x) / ln (10)`.
- Пределы логарифма существуют в «0» и «+ oo»:
- Функция логарифмирования имеет предел в «0», который равен «-oo».
- Функция логарифмирования имеет предел в «+ oo», который равен «+ oo».
Функция журнала вычисляет логарифм числа в режиме онлайн.
Синтаксис:
log (x), x — это число.Примеры:
log (1), возвращает 0Логарифм производной:
Чтобы дифференцировать логарифм функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции логарифма
Производная от log (x) — это производная_вычислителя (`log (x)`) = `1 / (ln (10) * x)`
Логарифм первообразной:
Калькулятор первообразных позволяет вычислить первообразную логарифмической функции.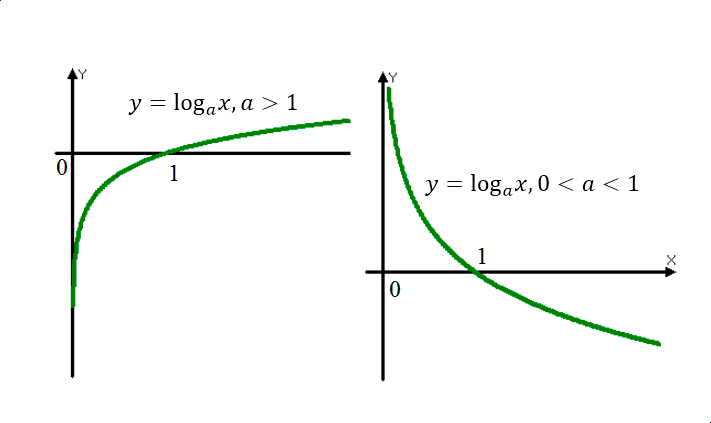
Первообразная от log (x) — это первообразная_производной (`log (x)`) = `(x * log (x) -x) / ln (10)`
Предельный логарифм:
Калькулятор пределов позволяет вычислять пределы логарифмической функции.
Предел для log (x) — limit_calculator (`log (x)`)
Графический логарифм:
Графический калькулятор может построить логарифмическую функцию в интервале ее определения.
Вычислить онлайн с логарифмом Создание графов логарифмических функций
— MathCracker.com
Инструкции: Этот создатель графика логарифмических функций позволяет вам построить логарифмическую функцию или сравнить график двух логарифмических функций.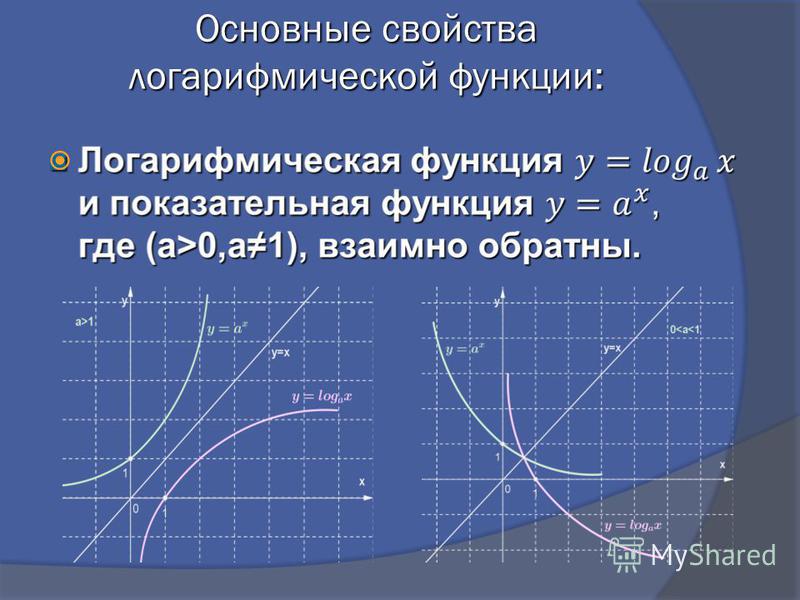 Вам необходимо предоставить базу \ (b \) каждой из функций \ (f (x) = \ log_b x \).
Вам необходимо предоставить базу \ (b \) каждой из функций \ (f (x) = \ log_b x \).
Построитель графиков логарифмических функций
Этот конструктор графиков позволяет построить график двух логарифмических функций и, при желании, оценить эти две функции при нескольких значениях.Икс\).
С точки зрения их графиков, график логарифмической функции и соответствующая экспоненциальная обратная функция симметричны относительно прямой линии 45 o .
Как построить график экспоненциальной функции
Показательная функция указанной выше формы будет иметь характерную экспоненциальную форму, и ее общий вид будет зависеть от того, является ли коэффициент \ (r \) положительным или отрицательным.
Для положительной скорости \ (r \) у нас будет экспоненциальный рост, а для отрицательной скорости \ (r \) будет экспоненциальный спад.
Какая польза от логарифмической бумаги?
Логарифмическая бумага — это особый тип бумаги, в которой масштаб изменен таким образом, что теперь логарифмические функции отображаются в виде линейных функций. У них было свое время, в настоящее время графические устройства (подобные этому) легко доступны и делают логарифмическую бумагу довольно устаревшей.
У них было свое время, в настоящее время графические устройства (подобные этому) легко доступны и делают логарифмическую бумагу довольно устаревшей.
Как вы оцениваете логарифмическую функцию?
Часто вам нужно оценить логарифмическую функцию, чтобы пройти через две точки, и для этой цели вам будут даны две точки, и вы решите систему для оценки требуемых параметров, чтобы логарифмическая функция проходила через эти точки. точки.
В случае, если у вас есть какие-либо предложения или вы хотите сообщить о неисправности решателя / калькулятора, пожалуйста, не стесняйтесь связаться с нами .
Графики Логарифмические функции: Введение (стр. 1 из 3) По характеру логарифма,
большинство лог-графиков имеют одинаковую форму, похожую на квадратный корень
график:
График квадрата
корень начинается с точки (0,
0), а затем гаснет
Направо.
Довольно просто
экспоненты графа. Для построения графика «вручную», мне сначала нужно помнить, что логи не определены для негатива x или для x = 0.Из-за этого ограничение на домен (входные значения) журнала, я даже не буду пытаться найти y -значения для, скажем, x = 3 или x = 0. Вместо этого я начать с x = 1 и работать с там, используя определение журнала.
Вышеуказанное дает мне точку (1, 0) и некоторые точки вправо, но что мне делать для значений x между 0 и 1? В этом интервале мне нужно мыслить категориями отрицательных сил и обратных величин.Так же, как левая «половина» экспоненциальной функции имела несколько точек захвата (остальные находятся слишком близко к оси x ), так что нижняя «половина» функции журнала имеет несколько графических точки, остальные расположены слишком близко к оси y . Но я могу найти несколько: С 2 1 = 1 / 2 = 0,5,
затем журнал 2 (0. Начиная с 2 2 = 1 / 4 = 0,25, затем журнал 2 (0,25) = 2 и (0,25, 2) находится на графике. Начиная с 2 3 = 1 / 8 = 0,125, затем журнал 2 (0,125) = 3 и (0,125, 3) находится на графике. Следующее степень 2 (как x движется в этом направлении) 1 / 16 = 2 4 , но значение x за точку (0,0625, 4) кажется слишком маленьким чтобы повозиться, так что я оставлю пункты, которые я уже нашел.
Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
| ||
Графические логарифмические функции
Функция у знак равно журнал б Икс является обратной функцией экспоненциальная функция у знак равно б Икс .
Рассмотрим функцию у знак равно 3 Икс . Это можно изобразить как:
График обратной функции любой функции — это отражение графика функции относительно линии
у
знак равно
Икс
. Итак, график логарифмической функции
у
знак равно
журнал
3
(
Икс
)
что является обратной функцией
у
знак равно
3
Икс
является отражением приведенного выше графика относительно линии
у
знак равно
Икс
.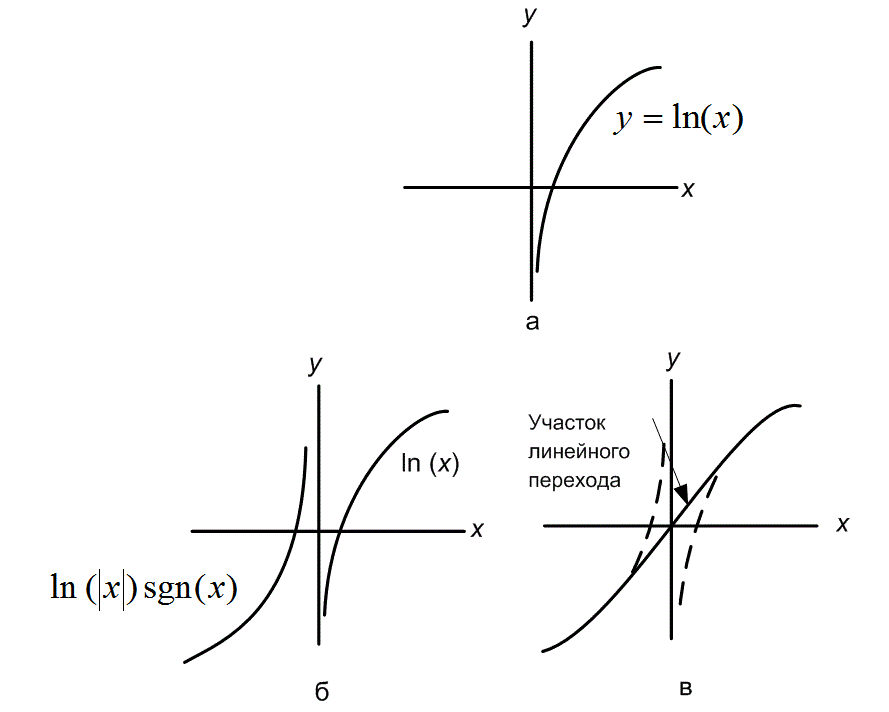
Икс 1 9 1 3 1 3 9 27 81 год у знак равно журнал 3 Икс — 2 — 1 0 1 2 3 4
Область определения функции — это набор всех положительных действительных чисел.
Если база не записана, предположим, что журнал является базовым. 10 .
Икс 1 1000 1 100 1 10 1 10 100 1000 у знак равно журнал Икс — 3 — 2 — 1 0 1 2 3
Логарифмическая функция,
у
знак равно
журнал
б
(
Икс
)
, можно сдвинуть
k
единиц по вертикали и
час
единиц по горизонтали с уравнением
у
знак равно
журнал
б
(
Икс
+
час
)
+
k
.
Вертикальный сдвиг
Если k > 0 , график сдвинется вверх.
Если k < 0 , график сместится вниз.
Горизонтальный сдвиг
Если час > 0 , график сдвинется влево.
Если час < 0 , график сдвинется вправо.
Рассмотрим логарифмическую функцию у знак равно [ журнал 2 ( Икс + 1 ) — 3 ] . Это можно получить, переведя родительский граф у знак равно журнал 2 ( Икс ) Пару раз.
Рассмотрим график функции
у
знак равно
журнал
2
(
Икс
)
.
поскольку час знак равно 1 , у знак равно [ журнал 2 ( Икс + 1 ) ] это перевод у знак равно журнал 2 ( Икс ) на одну единицу влево.
Сейчас же,
k
знак равно
—
3
.График
у
знак равно
[
журнал
2
(
Икс
+
1
)
]
будет перемещен
3
единицы вниз, чтобы получить
у
знак равно
[
журнал
2
(
Икс
+
1
)
]
—
3
.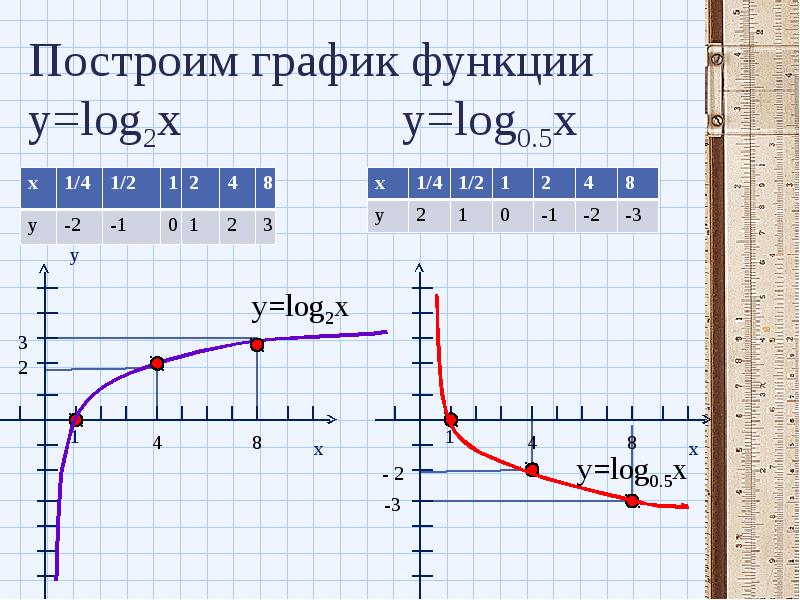
Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел.Это связано с тем, что для отрицательных значений соответствующее экспоненциальное уравнение не имеет решения. Например, 3 Икс знак равно — 1 не имеет реального решения, поэтому журнал 3 ( — 1 ) не определено.
Итак, как насчет такой функции, как у знак равно журнал 4 ( — Икс ) ?
Это определено только для отрицательных значений Икс .
Найдите значения функции для нескольких отрицательных значений Икс . Для упрощения расчета вы можете использовать экспоненциальную форму уравнения, 4 у знак равно — Икс .
Икс — 1 — 2 — 4 — 8 — 16 — 32 у знак равно журнал 4 ( — Икс ) или 4 у знак равно — Икс 0 1 2 1 1 1 2 2 2 1 2
Постройте точки и соедините их плавной кривой.
Вы можете видеть, что график является отражением графика функции у знак равно журнал 4 ( Икс ) о у -ось.
7. Логарифмические и полулогарифмические графики
М. Борна
На полулогарифмическом графике одна ось имеет логарифмический масштаб, а другая ось имеет линейный масштаб.
В логарифмических графиках обе оси имеют логарифмический масштаб.
Идея здесь в том, что мы используем оси полулогарифмического или логарифмического графика, чтобы нам было легче увидеть детали для малых значений y , а также больших значений y .
Вы можете увидеть несколько примеров полулогарифмических графиков на этом графике рейтинга трафика YouTube.
См. Также давление воздуха и Распределения Zipf далее на этой странице.
Полулогарифмические графы
В следующем наборе осей вертикальный масштаб равен , логарифмический (равный масштаб между степенями 10) и горизонтальный масштаб равен , линейный (даже пробелы между числами).
На оси y нет отрицательных чисел, так как мы можем найти только логарифм положительных чисел.
0-1-265432160504030201010012yxПолулогарифмические оси.
ПРИМЕЧАНИЕ. Числа на оси y становятся слишком близко друг к другу около каждой интегральной степени 10, поэтому они были удалены для удобства чтения.
Пример 1: График y = x
Давайте посмотрим, как выглядит простой график `y = x` на разных типах осей.
а.`y = x` на линейных осях
На обычных линейных осях график `y = x` представляет собой прямую линию, проходящую через` (-2, -2) `,` (-1, -1) `,` (0,0) `,` (1,1) `,` (2,2) `и т. Д.
123456-1-2-3-41234567-1-2-3xyГрафик y = x на линейных осях (lin-lin).
г. `y = x` на полулогарифмических осях (вертикальная ось логарифмическая, горизонтальная ось линейная)
На полулогарифмической оси график y = x представляет собой кривую, а не прямую линию. Он по-прежнему проходит через `(1,1)`, `(2,2)`, `(3,3)` и т. Д., Но вы заметите, что нет отрицательных значений для `y` (и поэтому в этом случае , также нет отрицательных значений для `x`), поскольку мы не можем найти логарифм отрицательного числа.
Д., Но вы заметите, что нет отрицательных значений для `y` (и поэтому в этом случае , также нет отрицательных значений для `x`), поскольку мы не можем найти логарифм отрицательного числа.
График y = x на полулогарифмической (логарифмической) оси.
Я отметил точки `(1,1)`, `(2,2)`, `(3,3)`, `(4,4)` `(5,5)`, `(6, 6) `на кривой.
г. `y = x` на полулогарифмических осях (линейный по вертикальной оси, логарифмический по горизонтальной оси)
012345678910-11010.10.01yxТочки вдоль кривой `y = x` на осях lin-log.
Я выделил на кривой точки `(1,1)`, `(2,2)`, `(3,3)` до `(10,10)`.
Обратите внимание, что на линейно-логарифмической кривой нет отрицательных значений для `x`.
Примеры полулогарифмических графиков
(а) Графики движения
Популярность сайта imeem.com в 2006/7 г. очень быстро росла. Вот график этого роста Alexa с использованием линейной горизонтальной шкалы (годы) и логарифмической вертикальной шкалы для рейтинга популярности (где ранг = 1 означает самый популярный).
имеем впоследствии был куплен MySpace.
Ранг имеем с течением времени.
(б) Финансовые графики
В финансовой отрасли используются полулогарифмические шкалы для облегчения чтения диаграмм.См. В качестве примера этот график цен на золото.
Пример 2: Переменная экспонента
Мы провели несколько наблюдений в эксперименте по росту микробной популяции при различных температурах и получили следующие данные:
| T (° C) | −2 | -1 | 0 | 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п. | 0.x` с использованием осей lin-log. В этом примере нет большого преимущества в использовании этого последнего типа полулогарифмического графика, поскольку мы не видим много деталей для значений меньше, чем `1`. Лог-лог-графики Логарифмические графики используют логарифмическую шкалу как для вертикальной, так и для горизонтальной осей. Теперь мы можем видеть еще больше деталей для небольших значений x и y , однако мы не можем включить отрицательные температуры по горизонтальной оси. Пример 4: Переменная, возведенная в дробную степеньГрафик y = x 1/2 с использованием всех 4 типов осей (прямоугольная, оба типа полулогарифмического и логарифмического). Эта функция эквивалентна `y = sqrt (x)`. Ответ Прямоугольные оси участокИспользуя прямоугольных осей , мы можем увидеть, что график y = x 1/2 представляет собой половину параболы на своей стороне (т.е.е. ось параболы горизонтальна): График y = sqrt (x) на линейных осях. Мы видели эту кривую раньше, в разделе «Парабола». Примечание 1: Детализация рядом с `(0, 0)` не так хороша при использовании прямоугольной сетки. Примечание 2: Кривая проходит через `(0, 0)`, `(1, 1)`, `(4, 2)` и `(9, 3)`. В каждом случае значение y является квадратным корнем из значения x , чего и следовало ожидать. Давайте теперь посмотрим на кривую, используя полулогарифмических графика. Вертикальная логарифмическая ось, линейная горизонтальная ось00.40.30.20.143211012345678910yxГрафик y = sqrt (x) на полулогарифмической (логарифмической) оси. Теперь у нас есть намного лучшая детализация для маленьких y . Наименьшее значение y , которое показывает график, равно «y = 0,1». Мы можем пойти ниже этого, но не можем показать «y = 0», поскольку логарифм «0» не определен. Мы видим, что кривая по-прежнему проходит через `(1, 1)`, `(4, 2)` и `(9, 3)`. Линейная вертикальная ось, логарифмическая горизонтальная ось Точки вдоль кривой `y = sqrt (x)` с использованием осей lin-log. Логарифмическая вертикальная ось, логарифмическая горизонтальная ось (логарифм) график10 -1 10 0 10 1 1010.1yxТочки вдоль кривой `y = sqrt (x)` на логарифмических осях. Мы видим, что график y = x 1/2 представляет собой прямую линию при построении по осям log-log. И снова наша кривая проходит через `(1, 1)`, `(4, 2)` и `(9, 3)` (обозначены точками на графике), как и должно быть. Приложение 1: Давление воздуха1. За счет откачки давление воздуха в баке снижается на 18%. каждую секунду. Таким образом, дан процент давления воздуха, остающегося в момент t. по п. = 100 (0,82) т . Участок п. против т для 0 < т <30 с на (а) прямоугольная система координат (б) полулогарифмическая система.t` на полулогарифмических осях. Приложение 2: Распределения Zipf Рассмотрим самые распространенные слова в английском языке. Распределение Zipf — это наблюдение, сравнивающее ранг и частоту вхождений слов.В общем, слово с рангом k имеет частоту, примерно пропорциональную «1 / k». Другими словами, второе по частоте употребление слово встречается примерно на 1/2 раза чаще, чем самое распространенное слово. Точно так же третье по частоте слово встречается примерно на 1/3 чаще, чем самое распространенное слово. РаспространениеZipf происходит естественным образом во многих ситуациях, например в:
а. Общеупотребительные английские словаЦипф первоначально разработал свой закон в ответ на наблюдение, что частота слов обратно пропорциональна рангу каждого слова. Например, в следующей таблице перечислены 20 наиболее употребительных английских слов. Таблица основана на Brown Corpus , тщательном изучении миллиона слов из самых разных источников, включая газеты, книги, журналы, художественную литературу, правительственные документы, комедийные и академические публикации. Наиболее распространенное слово «the» встречается около «70 000» раз (или «7%» из миллиона подсчитанных слов). Следующее по рейтингу слово, «of», встречается примерно в 3,6% случаев (или примерно в 1/2 раза чаще, чем слово с самым высоким рейтингом). Третьим по популярности слово было «и» с частотой «2,8%», или примерно «1/3» частоты наиболее ранжированного слова.
(Первые 20 слов Коричневого корпуса, опубликованные в 1967 г.Этот Корпус — это подсчет того, как часто один миллион слов использовался в различных книгах, газетах и других публикациях. Я включил «Теоретическое распределение Zipf», основанное на слове с n -м ранжированием, которое встречается примерно в 1 / n раз чаще, чем слово с наивысшим рейтингом. Это дает нам гиперболу, с которой мы встречались раньше.) Построим график того, что мы наблюдали: Темно-синие точки данных представляют 20 наиболее часто встречающихся английских слов (первые несколько помечены).0,94 = 15412, ` `…` Степень «0,94» получается из наблюдения наилучшей линии соответствия частот слов. (Я просто пробовал и ошибался в Excel, пока не нашел, что закрывающий элемент подходит.) Есть довольно большой разрыв в образце для слов «to», «a» и «in», но он успокаивается и после этого становится довольно последовательным. Теперь мы наносим верхние 2000 английских слов и используем шкалу log-log (логарифм ранга для горизонтальной оси и логарифм частоты для вертикальной оси). Мы видим, что есть удивительно стабильный результат для 2000 наиболее употребляемых английских слов. К вашему сведению, последние несколько слов в списке из 2000 слов: 1992-й аппарат
1993-е поведение
1994-е пробеги
1995-й улучшенный
1996-е игры
1997-й культурный
1998-е много
1999-я миля
2000 компоненты
г.Веб-сайты и дистрибутив ZipfМы также наблюдаем распространение Zipf, когда речь идет о популярности страниц на веб-сайтах. Например, из выборки из 500 000 просмотров страниц в Interactive Mathematics наиболее часто посещаемой страницей была домашняя страница с 27 855 просмотрами. Следующей по популярности страницей была «Введение в алгебру» с примерно половиной просмотров. Страница с 3-м рейтингом имела около 1/3 просмотров самой популярной страницы. Для 500 самых популярных страниц сайта у нас есть следующий лог-лог-график просмотров страниц: Теоретическое распределение Ципфа (розовая линия) получается следующим образом.0,67 = 8835 ` После того, как страница заняла 200-е место, шаблон распадается, но, что интересно, с 300-й по 500-ю страницу все еще существует постоянная взаимосвязь между рейтингом и частотой. См. Также Zipf Distributions, log-log графики и Site Statistics в блоге IntMath. Логарифмический график в масштабе — MATLAB loglog Цвет заливки маркера, заданный как Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.
Кроме того, вы можете указать несколько общих цветов по имени. В этой таблице перечислены названные цвета параметры, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию, которые MATLAB использует во многих типах графиков.
|
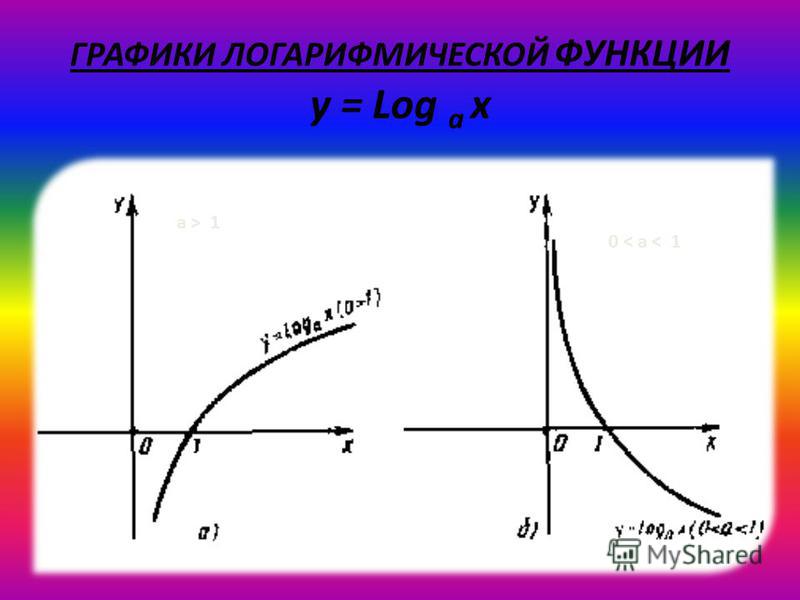
 Преобразование графика».
Преобразование графика».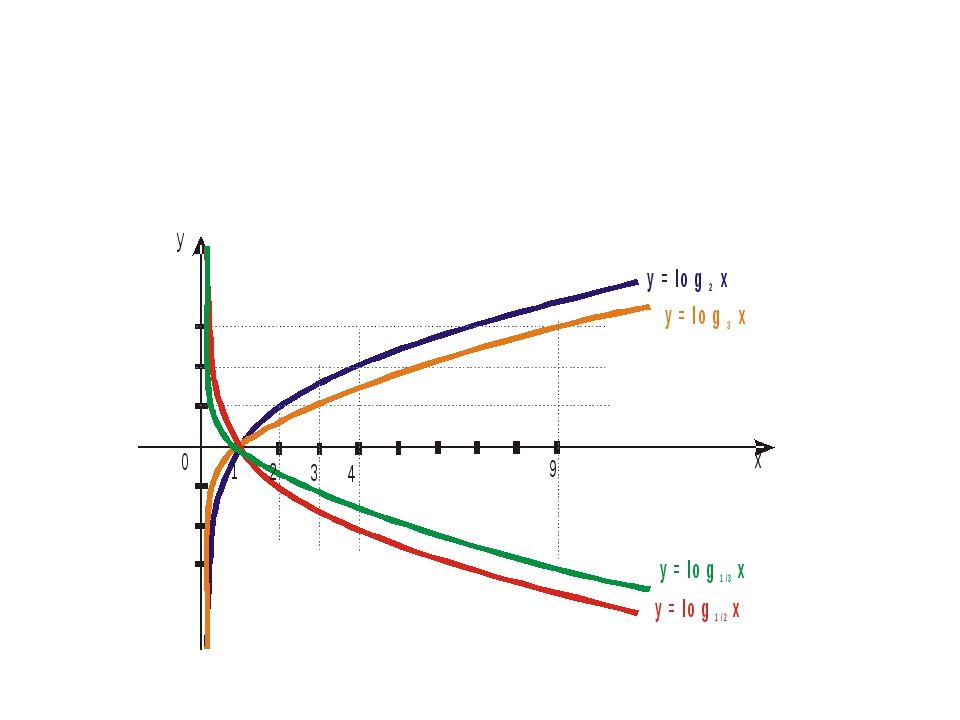
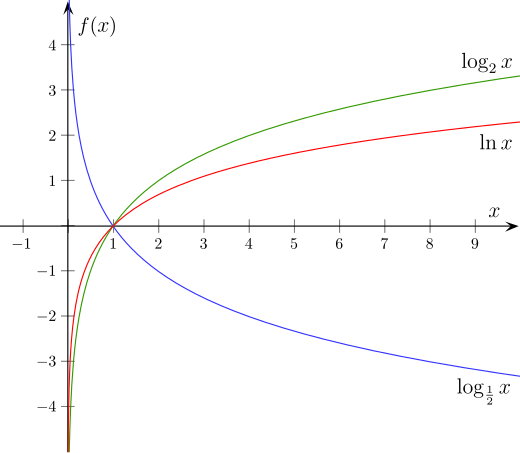 С другой стороны, график журнала проходит через (1,
0), уходя в
вправо, но также скользит вниз по положительной стороне оси y .
Помня, что журналы — это обратное
экспонент,
эта форма для лог-графика имеет смысл: график журнала,
будучи инверсией экспоненты, было бы просто «перевернуть»
графика экспоненты:
С другой стороны, график журнала проходит через (1,
0), уходя в
вправо, но также скользит вниз по положительной стороне оси y .
Помня, что журналы — это обратное
экспонент,
эта форма для лог-графика имеет смысл: график журнала,
будучи инверсией экспоненты, было бы просто «перевернуть»
графика экспоненты: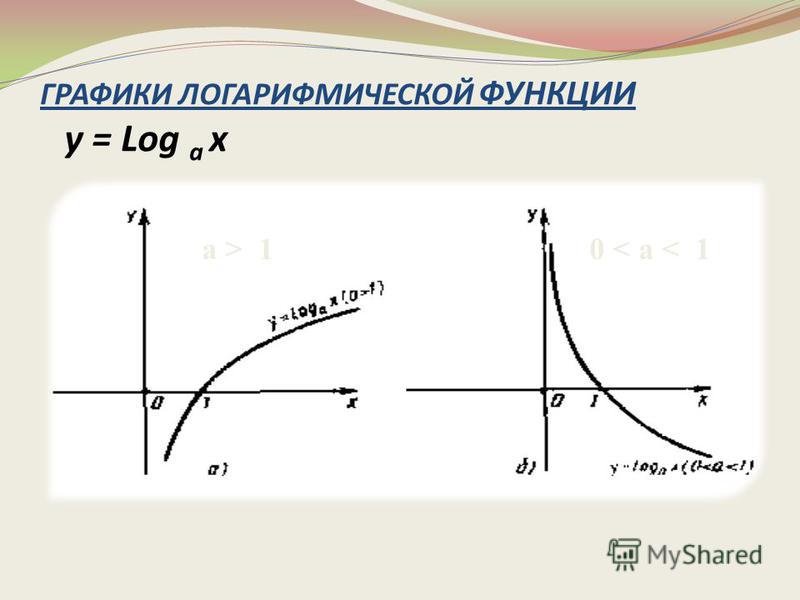 Например, к графику y = 2 х ,
вы просто вставляете некоторые значения для x ,
вычислить соответствующие y -значения,
и нанесите точки. Но как построить график журналов? Есть два
опции. Вот это
первое: Авторское право
Элизабет Стапель 2002-2011 Все права защищены
Например, к графику y = 2 х ,
вы просто вставляете некоторые значения для x ,
вычислить соответствующие y -значения,
и нанесите точки. Но как построить график журналов? Есть два
опции. Вот это
первое: Авторское право
Элизабет Стапель 2002-2011 Все права защищены
 5)
= 1 и (0,5,
1) находится на графике.
5)
= 1 и (0,5,
1) находится на графике. «Графические логарифмические функции: Введение». Purplemath .
Доступно по номеру
«Графические логарифмические функции: Введение». Purplemath .
Доступно по номеру  T` на журнальной бумаге (т.Т` по осям бревна.
T` на журнальной бумаге (т.Т` по осям бревна.
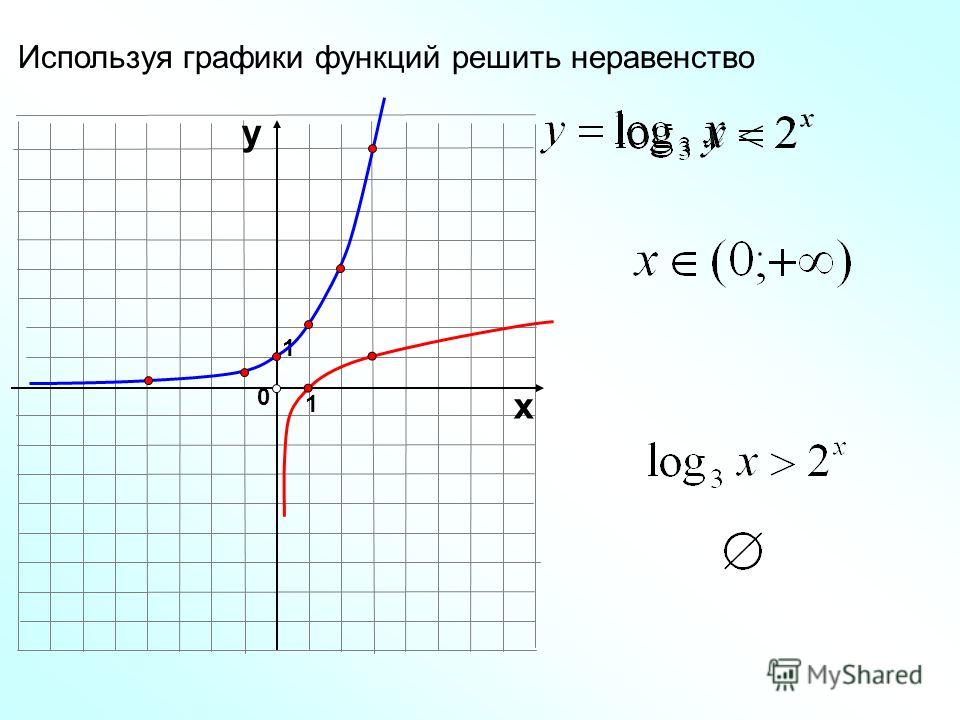
 Оказывается, существует взаимосвязь между рангом появления слова и частотой его использования. Эту связь наблюдал Джордж Кингсли Зипф в первой половине 20 века.
Оказывается, существует взаимосвязь между рангом появления слова и частотой его использования. Эту связь наблюдал Джордж Кингсли Зипф в первой половине 20 века.
 8872
8872 7176
7176 [Источник таблицы больше не доступен, но похож на Corpus of Contemporary American English.]
[Источник таблицы больше не доступен, но похож на Corpus of Contemporary American English.]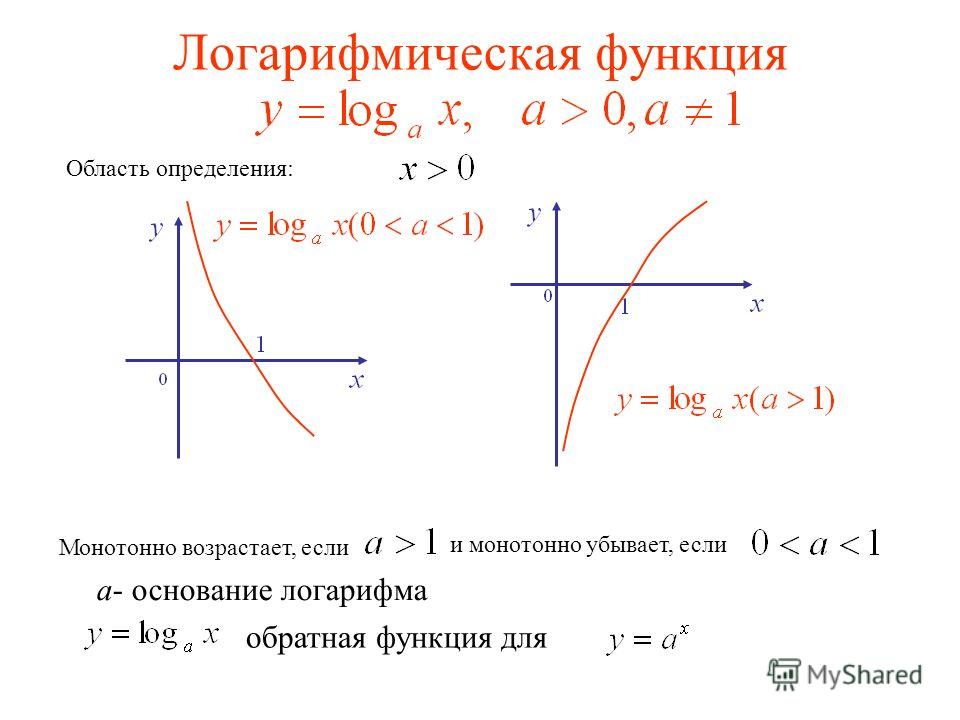 Если распределение дает нам прямую линию в логарифмическом масштабе, то мы можем сказать, что это распределение Zipf.
Если распределение дает нам прямую линию в логарифмическом масштабе, то мы можем сказать, что это распределение Zipf.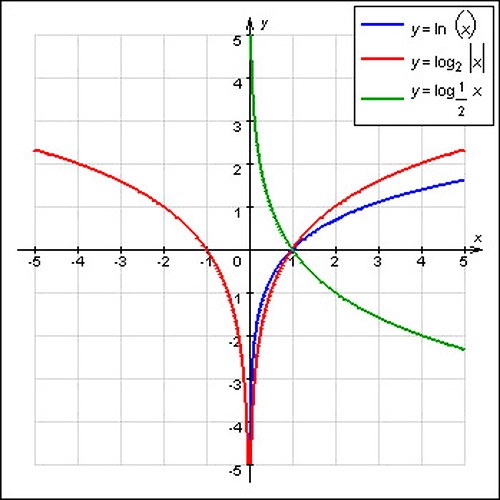
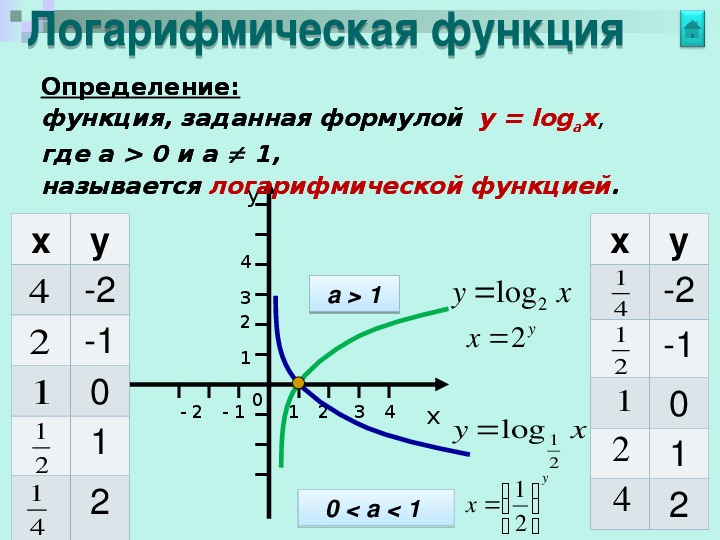

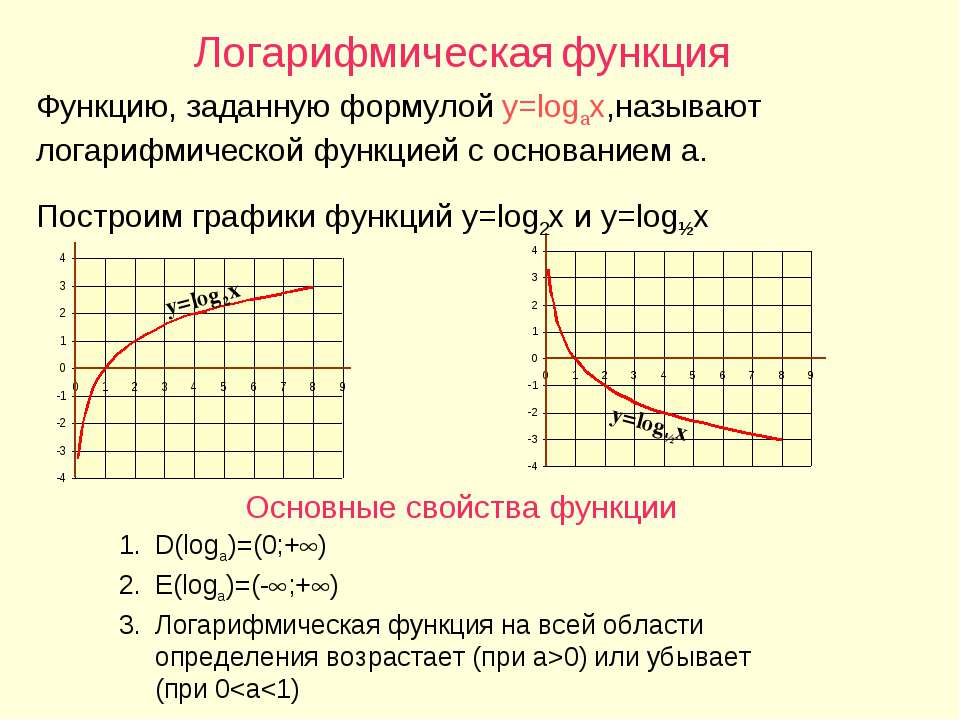
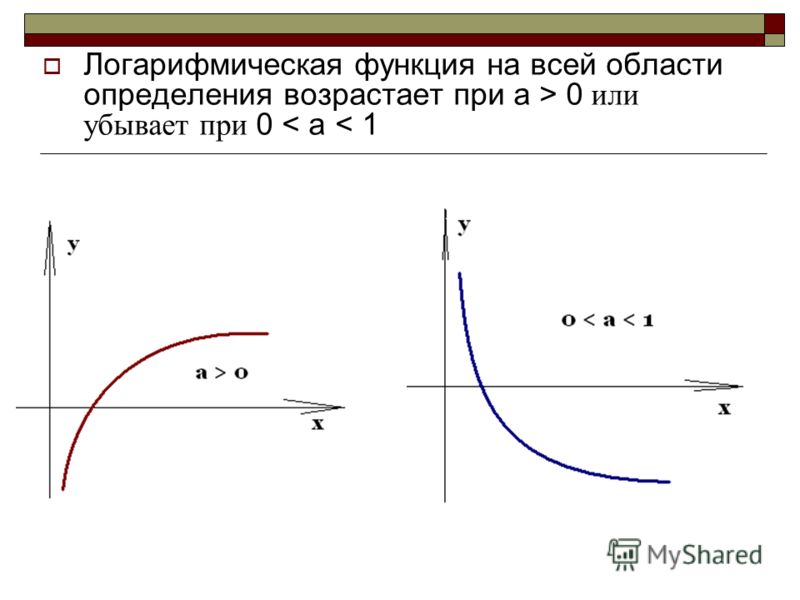
Ваш комментарий будет первым