Построить график линейной функции онлайн: IIS 7.0 Detailed Error — 404.11

Y 4 x 4 xy график. Построение графиков онлайн. Построение графика линейной функции

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения.

2) Построить ось симметрии x=-1. y.

Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.

В итоге мы получим табличку:

Теперь можно приступать к созданию графика.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

Появиться пустая область диаграмм. 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.

Рассмотрим это на примере функции у=1/х .

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом

0,2 :

Находим значения функции от каждого аргумента х аналогично примерам выше.

На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно

Получаем график функции y=1/x

В дополнение привожу видео — где показан порядок действий, описанный выше.

В следующей статье расскажу как создать 3-мерные графики в Excel.

Спасибо за внимание!

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению

y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции

y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .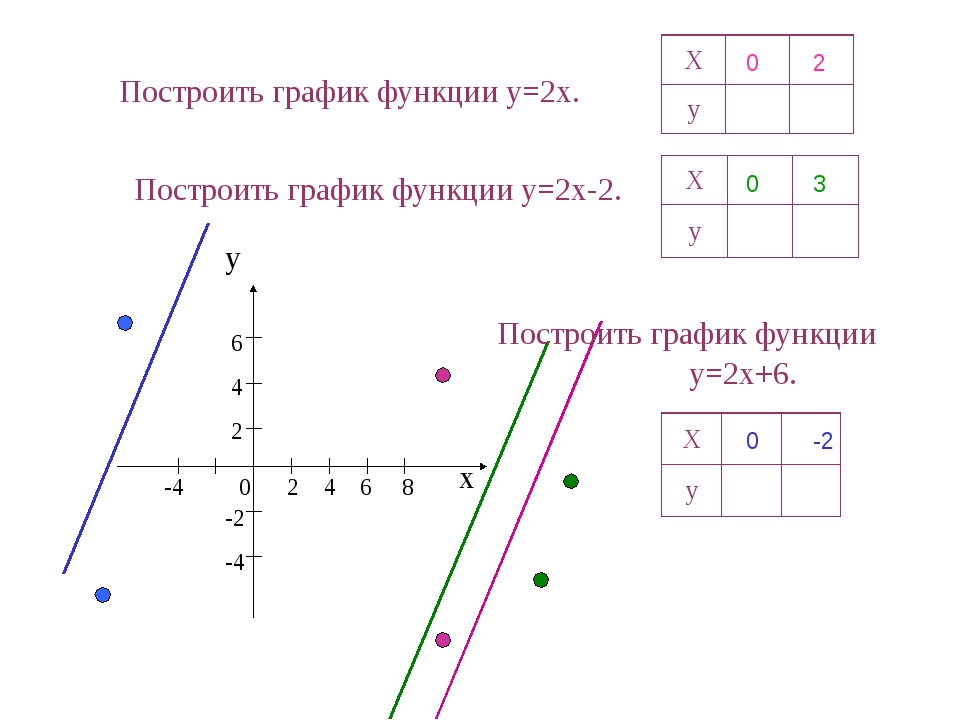

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу

х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.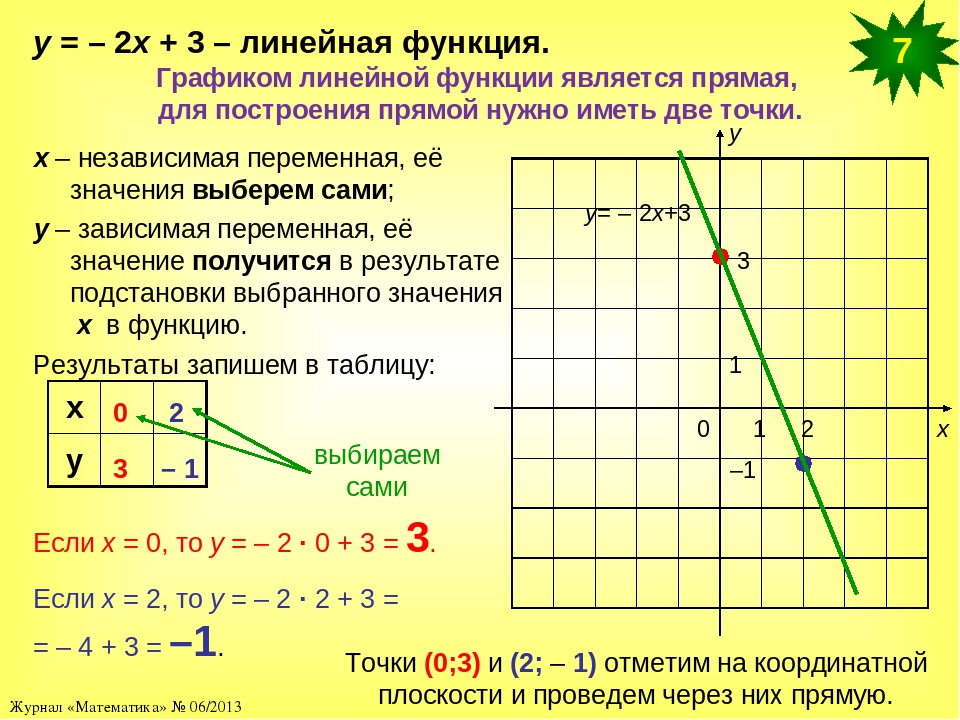

Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции

y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

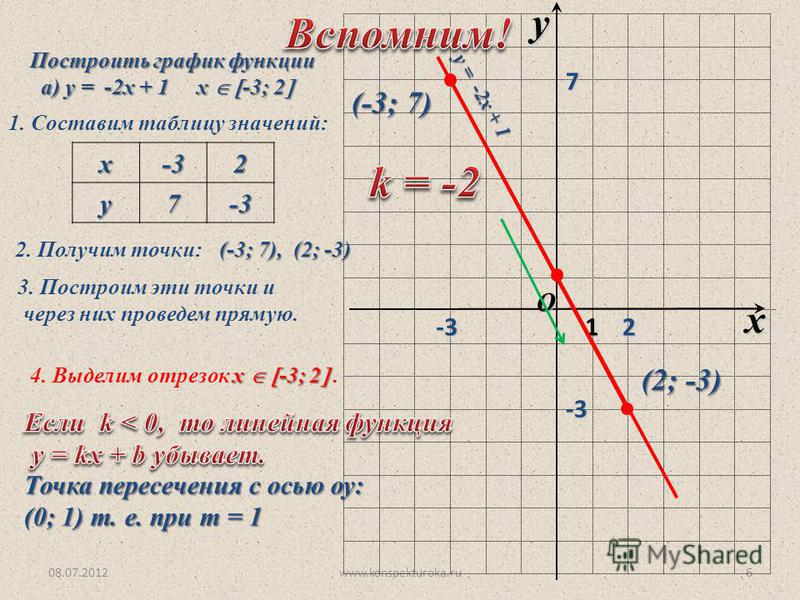
Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции

у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции

у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Решение функций | Онлайн калькулятор

Область определения функции найти область определения функции онлайн	Четность и нечетность функции калькулятор предназначен для определения четности и нечетности функции
Точки пересечения графика функции с осью определения точек пересечения графика функции с осями координат	Асимптоты функции нахождение асимптот графика функции онлайн
Разложить на слагаемые методом неопределенных коэффициентов	Периодичность функции онлайн калькулятор для определения периодичности
Точки перегиба графика функции и интервалы его выпуклости и вогнутости онлайн	Построение графиков кусочно-непрерывных функций
Найти градиент функции u=f(x,y,z)	Полное исследование функции и построение графика
Промежутки знакопостоянства функции найти интервалы знакопостоянства	Найти нули функции они же точки пересечения
Найти критические точки и интервалы монотонности	Оригинал функции по ее изображению обратное преобразования Лапласа онлайн
Найти изображения функций интегральное преобразование Лапласа онлайн	Найти сумму ряда по формуле общего члена ряда
Угол наклона прямой вычислить угол наклона	Угловой коэффициент прямой рассчитать угловой коэффициент
Найти экстремумы функции онлайн калькулятор	Найти максимум функции достаточно задать функцию, чтобы получить значения максимума
Найти минимум функции одно из необходимых условий наличия минимума	Точки разрыва функции функция в этих точках не является непрерывной
Построить график функции провести исследование графика функции	Решение пределов функции решать пределы любых функций онлайн
Уравнение касательной к графику функции составить и решить уравнение касательно	Тригонометрические функции найти как косинусы и синусы угла, так и решить выражения
Значения тригонометрических функций функции относятся к простейшим	Формула прямой, функции график функции
Разложение функции в ряд Тейлора раскладывается в степенной ряд по степеням	Разложение функции в ряд Маклорена любое число раз и в некоторой окрестности
Разложение функции в ряд Фурье абсолютно любую четную функцию можно разложить в ряды Фурье	Формула общего члена последовательности нахождение формулы
Прямая перпендикулярная прямой найти прямую перпендикулярной прямой	Построить график в полярных координатах на плоскости
Прямая перпендикулярная прямой найти прямую перпендикулярной прямой	Построить график в полярных координатах на плоскости
Вычислить площадь фигуры в полярных координатах	Интерполяция полиномами построить полином по точкам
Вычисление значений функции переменной	Найти наибольшее значение функции на отрезке в заданном интервале
Найти наименьшее значение функции на отрезке в заданном интервале	Точки экстремума найти точки экстремума функции
Множество значений функции найти область значений фукции	Интервалы монотонности функции найти нули производной
Найти наибольшее и наименьшее значение функции на отрезке	Стационарные точки функции производная функции равна 0 или не существует
Найти угловые точки графика функции

График линейной функции в 7 классе, определения, понятия, урок по алгебре

Дата публикации: 09 апреля 2017.

График линейной функции

График функции – это такое понятие в математике, которое дает наглядное геометрическое представление о функции.

Графиком линейной функции всегда является прямая. Как проще всего её построить?

Возьмем линейную функцию с двумя переменными, например, ax + by + с =0, где b ≠ 0.

Определим, чему равен y?
by = -ax — c

y = -$\frac{a}{b}x — \frac{c}{b}$.

Введём обозначения: k = -$\frac{a}{b}$ и m = — $\frac{c}{b}$.

Получаем запись нашего уравнения y = kx + m. Это уравнение называется линейным уравнением c двумя переменными, о таких уравнениях мы уже рассказывали.
Здесь х – независимая переменная; у – зависимая переменная.

Как мы уже говорили, графиком линейной функции y = kx + m является прямая.
Построим график этой функции. Для примера, возьмём уравнение y = x + 2.

Составим небольшую таблицу.
Х      0      2
У      2      4

Отметим эти точки на координатной плоскости и получим вот такой график.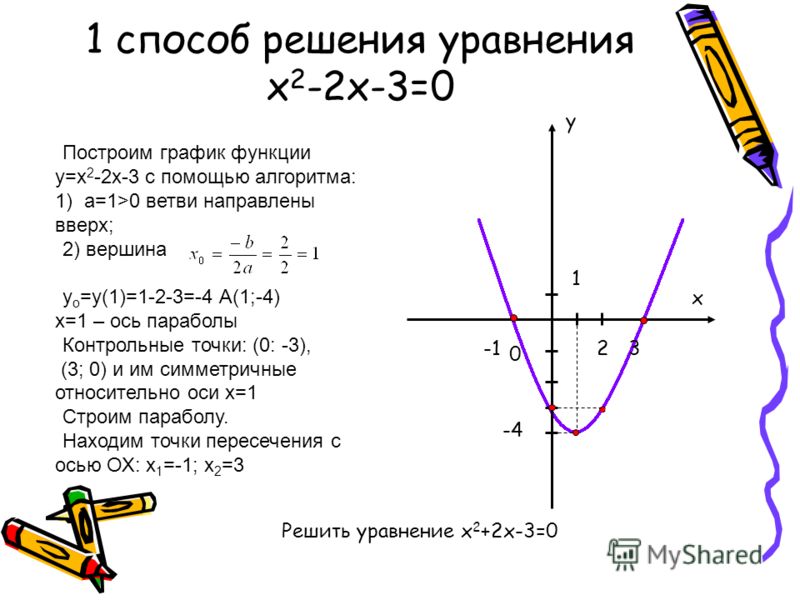

Давайте посмотрим, как на практике можно использовать график функции? Рассчитаем, на сколько дней хватит запаса яблок, если известно первоначальное количество яблок и количество яблок, которое магазин продает каждый день?

Задача.
На складе магазина находится 60 кг яблок. Каждый день магазин продает 12 кг этих фруктов. Сколько кг яблок останется на складе магазина через 2 дня, через 3 дня, через 5 дней?

Решение.
Построим математическую модель задачи: y= 60 — 12x.

Составим таблицу.
Х      2      3
У     36     24

По этим точкам построим график.
По графику можно предположить, какое количество яблок будет находится на складе магазина в любой день (от 1 до 5). Нужно помнить, что количество фруктов не может быть отрицательным.

Методическое пособие «Использование сервиса GeoGebra-онлайн при изучении графика линейной функции в 7 классе»

 

 

 

 

 

 

 

 

 

 

 

Методическое пособие

 

«Использование сервиса GeoGebra-онлайн при изучении графика линейной функции в 7 классе»

 

 

 

 

 

Составитель:

Учитель математики МБОУ

«ФМЛ»

Соловьева Марина Владимировна

 

 

 

 

 

 

 

 

 

 

2020г.

             

Введение.

В школьной программе по алгебре с 7 класса начинается изучение темы «Функции»: в 7 классе изучаются линейные функции, их свойства и графики, а в 8 – обратные пропорциональные, квадратичные и графики функций y=√х. Однако к концу 9 класса у учащихся не формируется система знаний по данной теме. Связано это с тем, что у учащихся слабо развито абстрактное мышление, плохо формируется владение терминологией, использование калькуляторов приводит к потере вычислительных навыков. Так как в современных образовательных программах сокращается количество часов в преподавании математики, учителям хватает времени только на рассмотрение элементарных заданий. Между тем итоговая аттестация в 9-м классе предполагает до 30% заданий по теме «Функции». В связи с обозначенными проблемами возникла необходимость использовать компьютер при построении графиков различных функций,

Практическая значимость работы заключается в том, что ученики решают стандартные математические задачи нестандартным способом – применяя современные компьютерные технологии.

И в самом деле — информационные технологии становятся неотъемлемой частью жизни современного человека. Владение информационными технологиями ставится в один ряд с такими качествами, как умение читать и писать. Поэтому школьников необходимо не только знакомить с  ИКТ технологиями, но и учить применять эти технологии в свой деятельности, способствуя тем самым формированию у них  ИКТ-компетентности. Одним из основных положений нового Федерального образовательного  стандарта  является формирование универсальных учебных действий (УУД), как важнейший результат реализации стандарта. Это положение в свою очередь также обусловлено потребностями современной цивилизации. В то же время, использование ИКТ принципиальным образом увеличивает возможности для такого формирования. Можно сказать, что без применения ИКТ формирование УУД в объемах и измерениях, очерченных стандартом, невозможно. Тем самым ИКТ-компетентность становится фундаментом для формирования УУД в современной массовой школе.

 Этим достигается и мотивационная цель – пробуждение интереса, показ необходимости знаний по математике и информатики в реальной жизни, а разработки и проведение систем уроков по построению графиков функций при помощи ПК, положив в основу личностно-ориентированное обучение, помогли учащимся лучше освоить ПК: строить графики элементарных математических функций с помощью сервиса GeoGebra-онлайн.

GeoGebra — самая популярная в мире бесплатная математическая программа. С помощью обучающей программы по математике, можно будет выполнить множество полезных вещей: анализировать функции, строить графики, решать задачи, работать с функциями и т. д.

Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т. п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.

Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения.

Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач. Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике.

В данной работе представлены практические работы:

— по построению и исследованию графиков линейной функции; — по решению систем линейных уравнений графическим методом.

Данные работы можно выполнять индивидуально – как домашнее задание, использовать для фронтальной работы, когда учитель выполняет построения на компьютере, а учащиеся по построенным графикам выполняют какие-то задания, можно выполнять во время урока в компьютерном или мобильном классе, а также с помощью гаджетов. Данные работы представлены как пошаговые инструкции для учащихся.

Конечно же, изучить линейную функцию только средствами ИКТ невозможно. Нужно разумно сочетать использование средств ИКТ и традиционных методов. Очень удобно использовать сервис GeoGebra для проверки решений традиционным методом. 

             

Практическая работа № 1. 

Построение и исследование графика линейной функции.

Задание 1:построить график функции у = х + 3, найдите точки пересечения данной функции с осями координат. 

1.                  Зайдите на сайт https://www.geogebra.org .

2.                  Нажмите        на        кнопку            START           CALCULATOR.

 

3.                  Откроется данное окно. Колесиком мыши мы можем менять масштаб координатной сетки. А, удерживая нажатой левую кнопку мыши, мы можем передвигать координатную плоскость.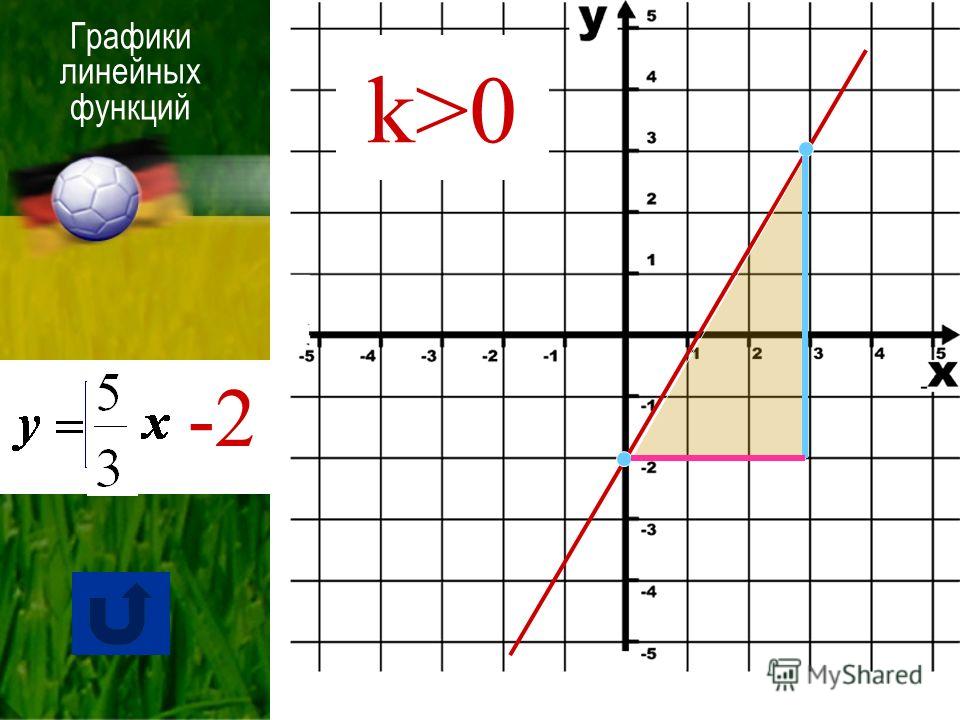

 

 

 

 

 

 

5.                   Появится график  данной функции, который выглядит так: 

 

 

 

6.                   Если нажать левой кнопкой мыши на данный график, то появится меню с

настройками: . С помощью него мы можем поменять: цвет линии, тип линии и вывести подпись. На графике. Также выделяются точки пересечения графика с осями координат.

7.                   Изменить        настройки      графика также можно нажав, на три точки справа от формулы. Справа появится окно настроек.

 

8.                   Нажмем левой кнопкой мыши на график и выделим его. Увидим, что при этом выделяются точки пересечения с осями. Можно просто определить их координаты 

 

 

Задание 2.Функция задана формулой у = — 2х + 5. Найдите а) значение функции, если значение аргумента равно: -4; 3,5; 0; б) значение аргумента, при котором значение функции равно: 9; — 5; 0; в) значение аргумента, при котором функция принимает положительные значения.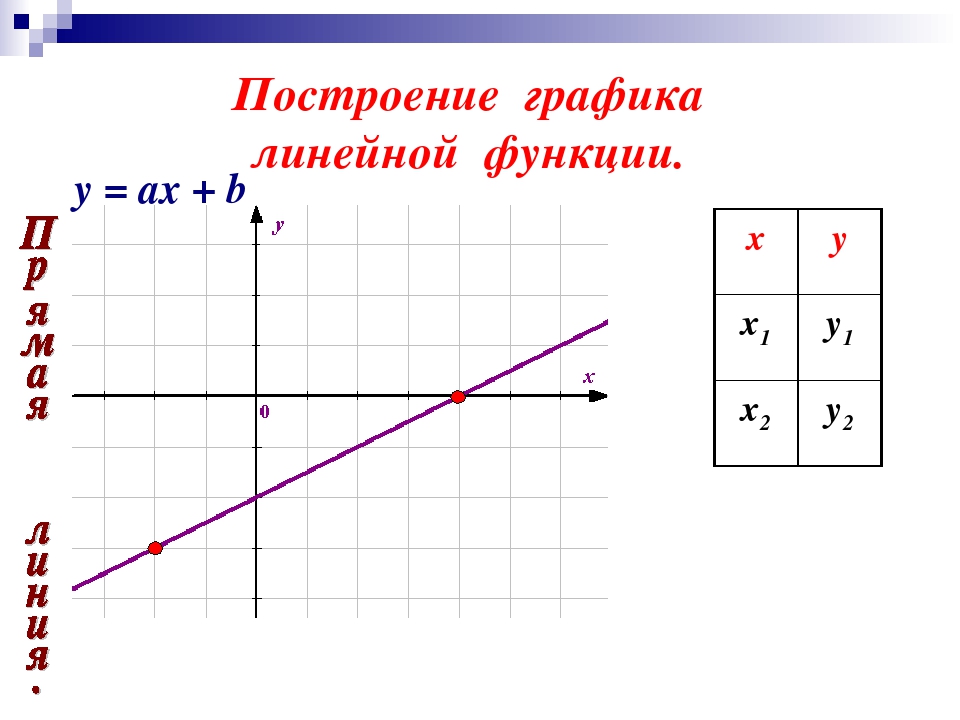

1.                   Построим график функции у = -2х + 5. Смотри задание выше.

2.                   В верхней строке переключитесь из режима Калькулятор на режим Фигуры

3.                   В режиме Фигуры выберите фигуру Точка и поставьте ее в любое место нашего графика. Подвигайте её – она движется только по графику.

4.                   Переключитесь обратно в режим Калькулятор и вы увидите в окошке слева координаты данной точки

 

5.                   Для выполнения задания под буквой а) передвигаем нашу точку так, чтобы значение аргумента (абсцисса точки) было равно -4 (для удобства можно менять масштаб). И смотрим, чему равна ордината данной точки (это и будет значение функции). Видим, что если значение аргумента равно -4, то значение функции равно 13.

 

Передвигая точку, аналогично ищем значение функции для других значений аргумента. И точно также выполняем задание под буквой б): передвигаем нашу точку так, чтобы значение функции было равно 9. И смотрим, чему равна абсцисса данной точки. Видим, что если значение функции равно 9, то значение аргумента равно -2.

 

6.                   Для выполнения задания под буквой в) найдем значения х, при которых функция принимает положительные значения. Это будет там, где график расположен выше оси Ох. Увеличим колесиком масштаб, чтобы увидеть точно точку пересечения графика с осью Ох. Видим, что это точка (2,5; 0). Видим, что график находится выше оси Ох для х <

2,5.      Ответ:     функция      принимает     положительные      значения      для      х      <       2,5.

 

 

Задание для самостоятельной работы: Функция задана формулой у = 10х — 3. Найдите а) значение функции, если значение аргумента равно: -5; 6; 0; б) значение аргумента, при котором значение функции равно: 7; -18; 0; в) значение аргумента, при котором функция принимает неположительные значения.

 

                 

Практическая работа № 2.  

Исследование графика линейной функции. Взаимное расположение графиков.

Задание 1.

1.                   Постройте на одной координатной плоскости в Geogebra онлайн графики следующих функций (как это делать описано выше): у=3, у=-6, у=2, у=-4, у=0. Выделите данные графики разными цветами и подпишите их (чтобы было нагляднее).

Сделайте выводы (заполните пропуски):

                Графиком     функции      у=а      (где      а     –      любое      число)      является       прямая

____________________________ оси Ох. 

Графиком функции у=0  является прямая ____________________________ с осью

Ох. 

Запишите этот вывод в тетрадь  или словарик.

 

2.                   Постройте на одной координатной плоскости в Geogebra онлайн графики следующих функций (как это делать описано выше): х=4, х=-3, х=5, х=-7, х=0. Выделите данные графики разными цветами и подпишите их (чтобы было нагляднее).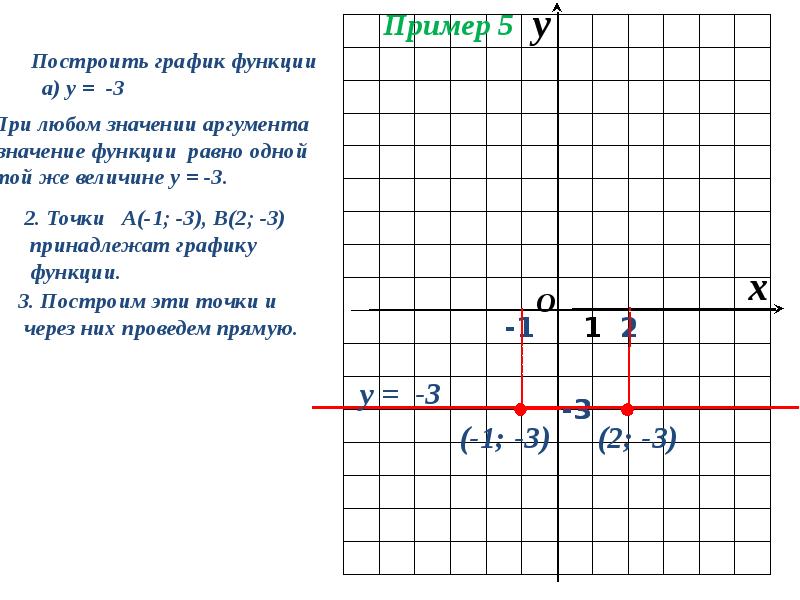

Сделайте выводы (заполните пропуски):

                Графиком     функции     ух=а     (где     а     –      любое     число)     является       прямая

____________________________ оси Оу. 

Графиком функции х=0  является прямая ____________________________ с осью

Оу. 

Запишите этот вывод в тетрадь  или словарик.

 

Задание 2.

Постройте на одной координатной плоскости в Geogebra онлайн графики следующих функций (как это делать описано выше): y=2х+5, у=2х – 4, у=2х, у=2х-1,5. Выделите их красным цветом.

                Что       вы       заметили?       Сделайте       вывод:       графики       данных         функций

______________________.

Достройте на этой же координатной плоскости графики следующих функций: y=3х6, у=3х – 1, у=3х. Выделите их зеленым цветом.

                Что       вы       заметили?       Сделайте       вывод:       графики       данных         функций

______________________.

Достройте на этой же координатной плоскости графики следующих функций: y=х-4, у=5х+2. Выделите их другими цветами.  Заполните таблицу:

Сделайте вывод и запишите его в тетрадь или словарик.

                Графики                 линейной                 функции                 параллельны,                   если

_______________________________________

             

Практическая работа № 3. 

Решение систем линейных уравнений графическим методом.

Задание 1.Решить систему линейных уравнений .

1.                   Постройте на одной координатной плоскости в Geogebra онлайн графики следующих функций (как это делать описано выше): 2х+3у=5 и 3х-у=-9.

2.                  

Кликните мышью на точку пересечения этих графиков и на экране вы увидите координаты этой точки – это и будет решением данной системы

 

Замечание:

Этот метод удобен тем, что не надо выражать у, как бы мы это делали, если бы строили графики в тетради.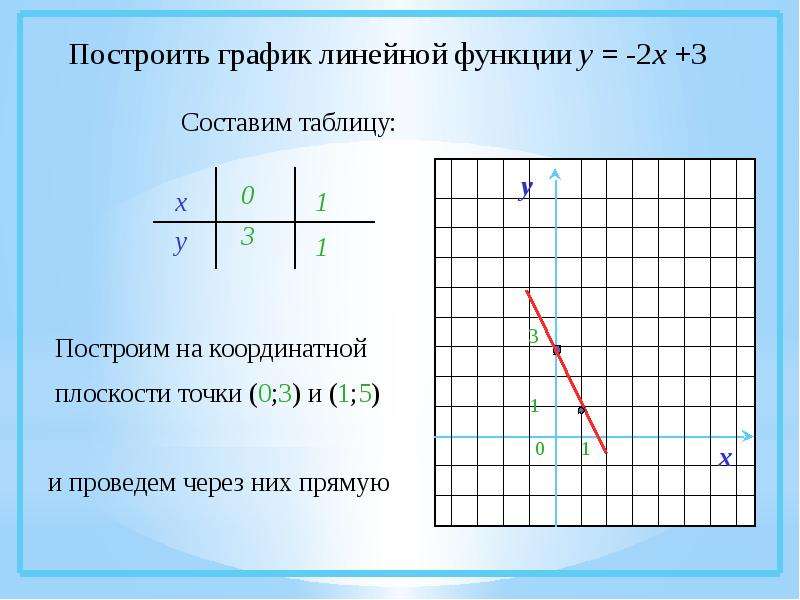 И его удобно использовать для проверки решения.

 

Задания для самостоятельной работы:

Решите системы линейных уравнений: 

1);     2) ;     3)  

 

 

 

             

Практическая работа №4. Решение задачи с параметром.

Задание 1.При каком значении а графики функций y=x-1 и у=ах-2 имеют общие точки.

1.       В окошке для ввода формул введем формулы: y=x-1 и у=ах-2. И нажмите Enter.

 

 

 

 

 

 

2.       В зоне ввода формул вы увидите следующее:

 

Мы видим бегунок, который меняет значение параметра а, и при этом график функции меняется. Сейчас значение параметра мы можем менять от -5 до 5. Но это можно изменить, кликнув на эти границы. Меняя значение параметра, мы видим, что при а=1, графики параллельны и не имеют общих точек. В остальных случаях графики

 

 

Таким образом, делаем вывод: графики функций y=x-1 и у=ах-2 имеют общие точки при всех а1.

 

Задание 2. При каком значении m график функции y=-5x+m проходит через точку

А(-1,2; 3).

1.                  В окошке для ввода формул введем формулы: y=-5x+m. И настроим параметр m так, чтобы он менялся от -5 до 5 с шагом 0,1. 

 

2.                  Построим       точку А.        Для      этого Режим

 

             

 

Графики линейной функции, содержащей модуль

1. Графики линейной функции, содержащей модуль.

2. I. Графики функций вида y = |kx+b|

Для построения графика функции y=|kx+b|
надо сохранить ту часть графика функции
y=kx+b, точки которой находятся на оси Ох
или выше этой оси, и симметрично отразить
относительно оси Ох ту часть графика
функции y=kx+b, которая расположена
ниже оси Ох.

3. Построение графика

y
1
у х 3
2
1. Построим
график функции
1
у х 3
2
х
0
4
у
-3
-1
2. 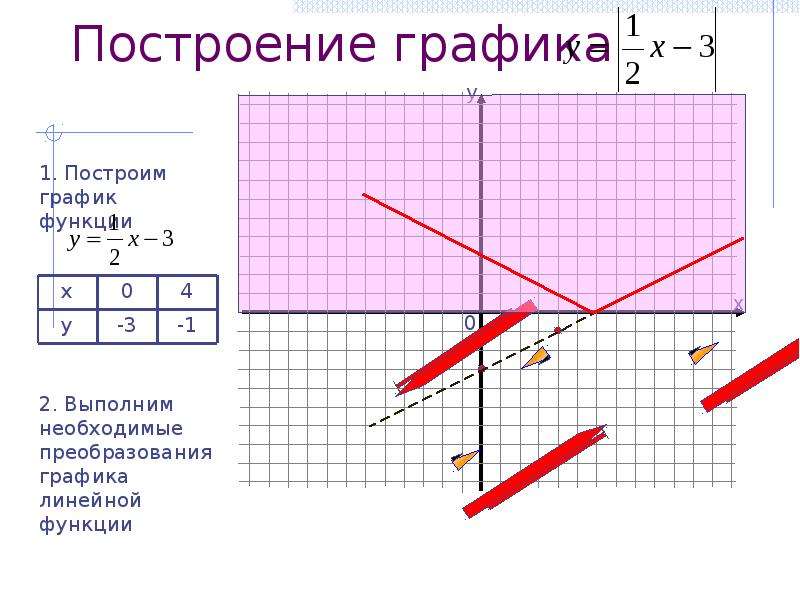Выполним
необходимые
преобразования
графика линейной
функции
0
x

4. II. Графики функций вида y= k|x|+b

Для построения графика функции
y= k|x|+b надо сохранить ту часть
графика функции y=kx+b, точки которой
находятся на оси Оу или справа от неё, и
симметрично отразить эту часть
относительно оси Оу.

5. Построение графика функции

у 3 x 2
y
1. Построить
график функции
у 3х 2
х
0
2
у
-2
4
x
0
2. Выполним
необходимые
преобразования
графика линейной
функции

6. Устная работа

y
3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6

7. Устная работа

y
Укажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3

8.

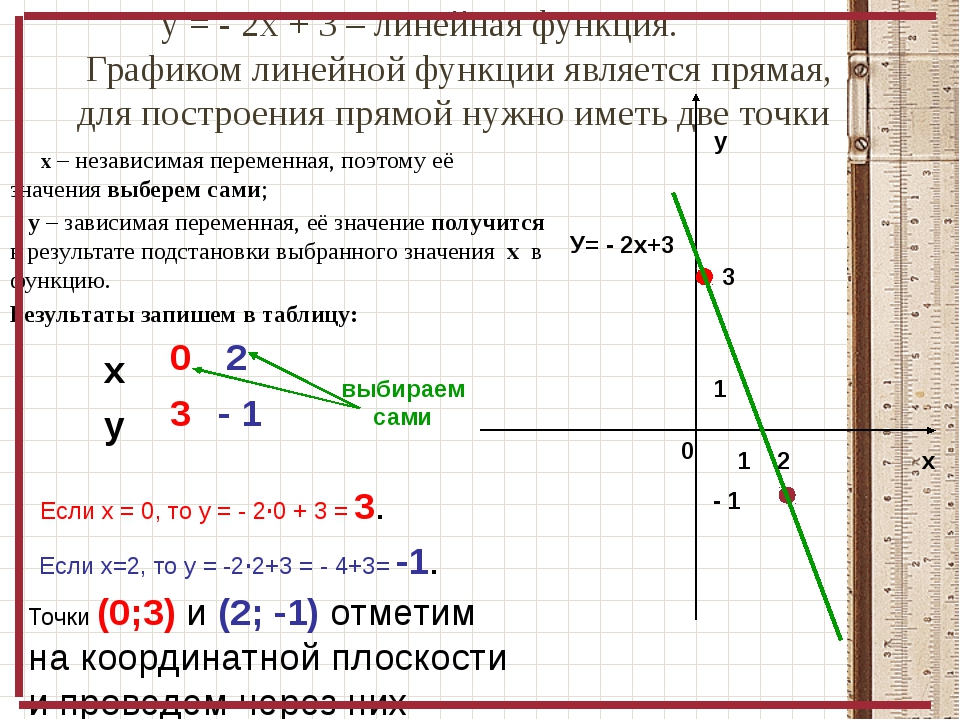Устная работа y
На рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5

9. Устная работа

y
3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6

10. Устная работа

y
Укажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3

11. Устная работа

y
На рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5

12. Построение графика функции

1
у
х 2
1
2
1
1. 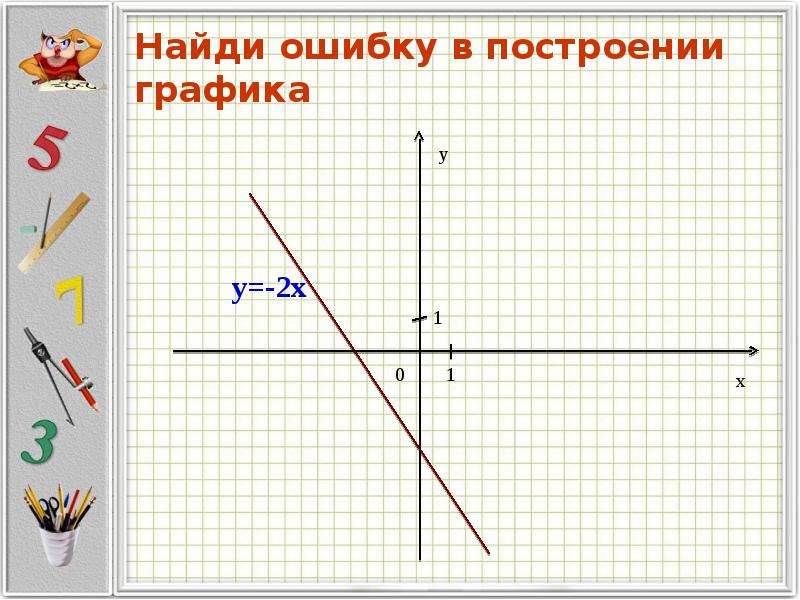у х 2
2. у х 2
2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
Первый вариант выполняет построения №1, второй вариант — №2.

13. Проверка работы I варианта

1
у х 2
2
х
0
4
у
-2
0
у
1
х 2
2
1
у х 2
2
y
x
0
1

14. Проверка работы II варианта

1
у х 2
2
х
0
4
у
-2
0
1
у х 2
2
1
у х 2
2
y
x
0 1
Исследуйте число решений
у 2 х 2 4х 24
2
b
уравнения
y
у 2х 4 2
y b
у 2х 4 2
Горизонтальная
прямая, проходящая
через точку с
ординатой b.
Ответ: если b
b=0, то уравнение имеет два корня; если 0
уравнение имеет четыре корня; если b=2, то
уравнение
имеет
три корня;
если
то
уравнение
Если
Если
Если
0
b>2
b
уравнение
то
то
уравнение
уравнение
имеет
корней
имеет
дваb>2,
корня
четыре
не
имеет.
корня.
Если
Если
b=2,
b=0,
то
то
уравнение
уравнение
имеет
имеет
три
два
корня.
корня.
имеет два корня.
x

16. При каком значении b уравнение имеет единственное решение

При каком значении b уравнение 3х 6 2 х b
имеет единственное решение
1. у 3х 6
y
2. у 2 х b
Ответ: при
b>-3
исходное
уравнение
имеет
единственно
е решение.
x
-3

18. Домашнее задание

у 2х 4
y
1
0
1
x

График линейной функции — презентация онлайн

1. Линейная функция и её график

2. Повтори:

• Линейной функцией называется
функция вида у=kх+b, где k,b-числа,
х-независимая переменная( аргумент),
у-зависимая переменная (функция).

3. Какие из функций

1.
2.
3.
4.
5.
6.
7.
2у=3:х-2
у=3-5х
у+х=0
у=1,4х-3
у=х
у=5
у=1/2х являются линейными?
Проверь себя: 2,3,4,5,6

5.

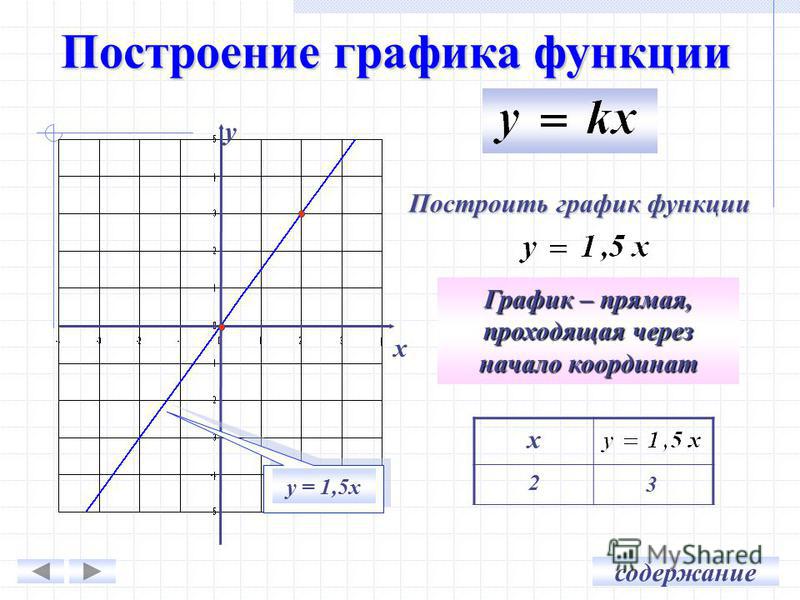Алгоритм построения графика линейной функции Чтобы построить график линейной функции нужно:
Задать два значения
аргумента х (любых, выбираем сами!!!;
Найти два соответствующих значения
функции у;
Построить точки в системе координат;
Провести через них прямую линию.

6. Построить график функции у=-2х+2

• Решение:
• Построение
у
У=-2х+2
х
0
-2
у
2
6
х
у= -2х+2

7. Задание

• Найдите значение линейной функции у=2х-1 при
заданном значении аргумента х=0;2;4;-1.
Алгоритм выполнения:
т.к. значение аргумента (х) задано, то
1. Вместо х подставляем конкретное значение
2. Вычисляем значение у.
Х=0 У=2*0-1=-1.
Х=2 у= 2*2-1=3
Х=4 у=2*4-1=7
х=-1 у= 2*(-1)-1=-2-1=-3
Задание
• Функция задана у=2х-1 Найдите значение аргумента
при заданном значении функции у=11,-3, 0
Алгоритм выполнения:
т.к. дано значение функции (у), значит
1. Вместо у подставляем конкретное значение
2. Решаем уравнение, что найти значение х.
У=11
2х-1=11
2х=11+1
2х=12
х=12/2
х=6
У=-3
2х-1=-3
2х=-3+1
2х=-2
х=-2/2
х=-1
У=0
2х-1=0
2х=0+1
2х=1
х=1/2
х=0,5

9. Постройте график линейной функции у=-3-х и у = — х

уу
• У = -3 – х
х
0
3
у
-3
-6
У= — х — 3
у= -3-х
у=-х
х
х
у= — х
х
0
6
у
0
-6

10. Постройте график линейной функции у = х – 3 и у = х

• у=х–3
у
х
0
3
у
-3
0
У=х-3
У=х
х
У=х-3
у= х
х
0
6
у=у х
0
6

11. Построить график линейной функции у= kх+b при k=0 , b=5 т.е. у=5

у
У=5
х

12. Ответить устно на вопросы:

• Что называется линейной функцией?
• Что является графиком линейной функции?
• Сколько точек нужно взять, чтобы построить
прямую?
• Как называется переменная х и
переменная у?

13.

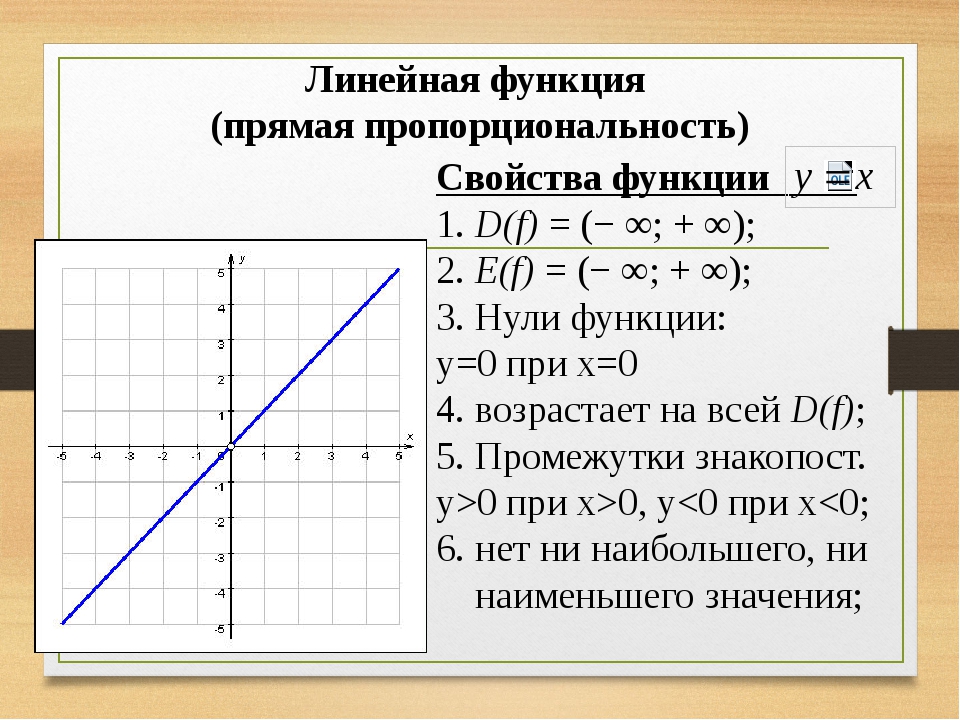Домашнее задание• №854(1,2), 858 (1;2), 856

График линейной функции (7 класс). Построение по двум точкам — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Элементарные функции

---

Онлайн урок «График линейной функции (7 класс). Построение по двум точкам» посвящен вопросу о том, как быстро и просто выполнить построение графика линейной функции. Пусть задана функция y = kx + b, где k и b являются действительными числами. Это линейная функция и её графиком является прямая. Частные случаи. Предположим, что b равно нулю. Тогда, на графике, все прямы будут проходить через начало координат. Классическим примером является функция y = x, В этом случае график функции будет биссектрисой первого и третьего углов координат. При значении коэффициента k отличного от нуля, на графике функции изменится угол между прямой и осями координат. Теперь рассмотрим случай, при котором коэффициент k будет равен нулю, а число b отлично от нуля. При построении графика такой функции, прямая будет всегда параллельна оси OX. Давайте рассмотрим конкретный пример построения графика линейной функции. Строить мы будем график функции y = -2x + 1. Для того, чтобы быстро его построить, необходимо и достаточно найти всего две точки. Т.е. вместо x нужно подставить произвольное число и найти значение y. Таким образом, мы найдем координаты двух точек и без труда выполним построение графика Видео урок «График линейной функции (7 класс). Построение по двум точкам» вы можете смотреть онлайн абсолютно бесплатно. Успехов!

---

• Автор: alWEBra
• Длительность: 2:43
• Дата: 20.04.2013
• Смотрели: 3462
• Рейтинг: 5.0/1

---

---

---

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

Бесплатный калькулятор для линейных функций

Что такое линейная функция?

Линейная функция — это функция, график которой представляет собой линию. Общий вид линейной функции таков, где m — наклон, а b — пересечение оси y. Вот пример:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht.Hol dir einen neuen. : P Корни в -1,333 пересечение оси Y в (0 | 4)

График линейной функции всегда представляет собой линию.

Слово, похожее на линейную функцию, — это линейная корреляция.

Каков наклон линейной функции?

Наклон линейной функции соответствует числу перед x. Он говорит, как могут единицы вы должны идти вверх / вниз, если вы идете на одну единицу вправо. Пример:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht. Hol dir einen neuen. : P Корни в 2,5 пересечение оси Y в (0 | -5)

Мы видим, что эта функция имеет наклон. Если мы переместимся на один квадрат вправо от любой точки на графике, мы должны пройти два квадрата вверх, чтобы снова оказаться на графике.

Другой пример, на этот раз с отрицательным наклоном:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht. Hol dir einen neuen. : P Корни в 1,333 пересечение оси Y в (0 | 4)

Эта линейная функция имеет наклон. Это означает, что всякий раз, когда мы идем на один квадрат вправо, нам нужно пройти на три квадрата вниз, чтобы снова оказаться на графике.

Что такое отрезок оси Y линейной функции?

Линия пересечения Y — это номер в конце функции.Как следует из названия, в нем указано, где функция пересекает ось Y. Если вы посмотрите на графики функций, вы увидите, что пересекает ось Y в точке, пересекает ось Y в точке.

Как рассчитать уравнение прямой из точки и наклона?

Вы должны вставить точку в уравнение, то есть одну координату для x, а другую для f (x). Вот пример: Предположим, мы знаем, что наша функция имеет наклон и проходит через (-2 | 5).

Как вычислить уравнение линейной функции из двух заданных точек?

Сначала мы должны вычислить наклон m, подставив координаты x и y точек в формулу.Это означает: вы вычисляете разность y-координат и делите ее на разность x-координат. Вот пример:
Как видим, сначала был рассчитан уклон. Чтобы найти уравнение функции, вы должны вставить точку и получить уравнение, которое дает точку пересечения оси Y.

Можно посмотреть еще примеры?

Конечно. Просто введите свои примеры выше, и они будут рассчитаны сразу, шаг за шагом. (Это идея Mathepower: Вы не просто смотрите на некоторые уже сделанные объяснения, но и получаете объяснение своих собственных расчетов!)

Уравнение прямой по двум точкам

Эти онлайн-калькуляторы находят уравнение прямой по двум точкам.
Первый калькулятор находит линейное уравнение в форме пересечения наклона, то есть. Он также выводит параметры наклона и пересечения и отображает линию на графике.
Второй калькулятор находит линейное уравнение в параметрической форме, то есть. Он также выводит вектор направления и отображает линию и вектор направления на графике.

Вы можете найти теорию под калькуляторами.

Уравнение наклона и пересечения линии из 2 точек

Первая точка

xy

Вторая точка

xy

Вычислить

Линейное уравнение

Наклон

Пересечение

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

Уравнение параметрической линии из 2 точек

Первая точка

xy

Вторая точка

xy

Вычислить

Уравнение для x

Уравнение для y

Вектор направления

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

Уравнение линии наклона-пересечения

Найдем угловую форму линейного уравнения по двум известным точкам и.
Нам нужно найти наклон a и точку пересечения b .
Для двух известных точек у нас есть два уравнения относительно a и b

Вычтем первое из второго

А оттуда

Обратите внимание, что b можно выразить так:

Итак, если у нас есть a , легко вычислить b , просто вставив или в выражение выше.

Параметрические линейные уравнения

Выясним параметрическую форму линейного уравнения по двум известным точкам и.
Нам нужно найти компоненты вектора направления , также известного как вектор смещения .

Этот вектор количественно определяет расстояние и направление воображаемого движения по прямой от первой точки до второй точки.

Когда у нас есть вектор направления от к, наши параметрические уравнения будут иметь вид

Обратите внимание, что если, то и если, то

Написание и построение графиков линейных функций — математический класс [2021]

Выражение линейной функции с помощью уравнения

Линейная функция представлена ​​уравнением:

y = mx + b , где:

y = координата y

m = наклон кривой

x = координата x

b = точка пересечения y, или точка пересечения оси y на графике

Давайте посмотрим, как мы можем использовать уравнение для график линейной функции. Как бы мы изобразили y = 2 x + 3? Уравнение говорит нам, что наклон линии (m) = 2, и она пересекает ось y (b) в точке 3. Чтобы построить график функции, нам нужно иметь несколько упорядоченных пар. Лучший способ получить эти точки — создать таблицу значений , которая показывает нам точки, которые находятся на линии. При создании таблицы значений всегда полезно использовать некоторые положительные и отрицательные значения для x , чтобы вы могли понять, как ведет себя линия.Предположим, что мы хотим построить график значений, когда x равно -2, -1, 0, 1 и 2. Таблица значений будет:

Теперь, когда у нас есть упорядоченные пары или значение для x и y , мы можем изобразить уравнение y = 2x + 3, нанеся эти пары на график.

Из графика видно, что линия пересекает ось y в точке 3 или в точке (0, 3) и что наклон линии вверх и вправо, что указывает на положительный наклон.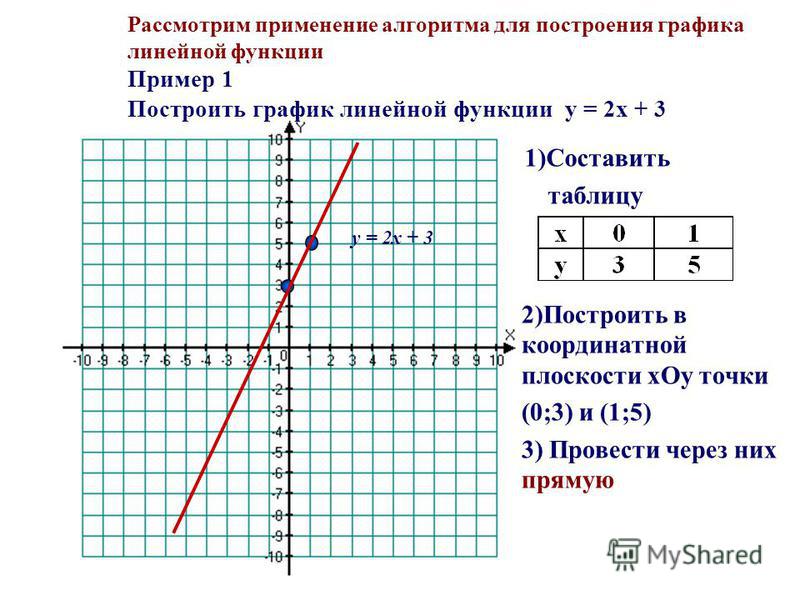 Это согласуется с нашим уравнением: y = 2 x +3, поскольку наклон прямой в этом уравнении равен +2. Мы также можем отметить, что все упорядоченные пары, которые мы вычислили в нашей таблице значений , также находятся на графике, в частности, (-2, -1), (-1, 1), (0, 3), ( 1, 5) и (2, 7).

Написание линейной функции из графика

Давайте попробуем начать с графика и написать уравнение, которое с ним связано. Чтобы записать линейную функцию в виде y = m x + b, нам потребуется определить наклон линии:

• уклон (м)
• y -перехват (б)

Из графика видно, что наклон линии отрицательный, потому что линия идет вниз и вправо.Похоже, что точка пересечения оси y (b) графика равна 2, что представлено точкой (0,2). Теперь нам нужно определить наклон линии. Для этого мы должны использовать как минимум две точки от линии. Выберем (-2, 4) и (0, 2). Мы можем использовать любые две точки, поскольку наклон — прямая линия. Для расчета уклона используем следующую формулу:

Используя наши две точки и подставив их в формулу, мы получаем:

m = (4-2) / (-2-0)

m = 2 / -2

m = -1

Теперь мы знаем, что наклон (m) = -1, а точка пересечения по оси y (b) равна 2.Когда мы сложим все вместе, уравнение для линии на графике будет:

y = m x + b

y = -1 x + 2

Написание линейной функции из информации в словесной задаче

Иногда мы можем выразить словесную задачу как линейную функцию. Предположим, Мэтт отправляется в школьную поездку, которая стоит 300 долларов за аренду автобуса плюс 20 долларов за каждого ученика, который путешествует на автобусе. Чтобы Мэтт выразил эту взаимосвязь как линейную функцию, ему необходимо определить, какая из переменных является зависимой, а какая независимой. В этой ситуации стоимость поездки зависит от того, сколько студентов поедет в нее, поэтому стоимость поездки должна быть зависимой переменной, y , а количество студентов — независимой переменной, x . Мы можем записать уравнение для этой связи как:

y = 20 x + 300

Если мы предположим, что в поездку отправятся 50 студентов, то поездка будет стоить 1300 долларов: (20 долларов x 50) + 300. Взаимосвязь между количеством студентов и стоимостью поездки является линейной, поскольку стоимость будет увеличиваться по мере того, как в поездку отправляется больше студентов.Когда это соотношение изображено на графике, это будет прямая линия.

Краткое содержание урока

Линейная функция , которая показывает взаимосвязь между двумя переменными и всегда приводит к прямой линии при построении графика, может быть выражена в виде графика, используя наклон и метод пересечения y , как уравнение, когда график предоставляется или из информации, заданной в словесной задаче.

В линейной функции одна из переменных независимая , что означает, что она не зависит от другой переменной и представлена ​​как y .Другая переменная, представленная как x , — это зависимая , что означает, что ее значение зависит от независимой переменной.

Уравнение линейной функции выражается следующим образом: y = m x + b, где m — наклон линии или ее крутизна, b представляет собой точку пересечения y или точку пересечения графика y — ось и x и y представляют точки на графике.

При построении линейной функции мы должны вычислить как минимум две точки, чтобы можно было провести линию между ними.Чтобы создать эти точки, мы можем использовать таблицу значений , где мы указываем значения для x , а затем используем уравнение нашей линейной функции для решения относительно y .

Рассчитайте линейную регрессию и график разброса и линию наилучшего соответствия

Что такое простая линейная регрессия?

Простая линейная регрессия — это способ описать взаимосвязь между двумя переменными с помощью уравнения прямой линии, называется линией наилучшего соответствия, которая наиболее точно моделирует эти отношения.

Обычная форма линейного уравнения для двух переменных x и y:
`y = mx + b`
, где m и b обозначают константы. Происхождение названия & quote; linear & quote; происходит из-за того, что множество решений такого уравнения образует прямую на плоскости. В этом конкретном уравнении константа m определяет наклон или градиент этой линии, а постоянный член «b» определяет точку, в которой линия пересекает ось y, иначе известный как Y-пересечение.{n} x_i} {n} `
, где суммирование снова производится по всему набору данных

линия наилучшего соответствия (линия тренда) — линия на диаграмме рассеяния, которую можно провести рядом с точками для большей четкости показывать тенденция между двумя наборами данных.

• Линия лучшего, которая быстро поднимается слева направо, называется положительная корреляция .
• Линия лучших, которая быстро падает слева направо, называется отрицательной корреляцией
• Сильная положительная и отрицательная корреляции имеют данные указывает очень близко к линии наилучшего соответствия. {n} x_i} {n}`

  `b = \ frac {[SUMY] — [SLOPE] \ times [SUMX]} {[NCOUNT]} `

  ` b = [INTERCEPT] `

  Регрессия / Линейное уравнение наилучшего соответствия,

  `y = m \ timesx + b`

  ` y = [SLOPE] \ timesx + ([INTERCEPT]) `

  Диаграмма рассеяния
  и линия наилучшего соответствия

  Стандартное отклонение

  Также полезно иметь меру средней неопределенности измерений, которая выражается в стандартном отклонении:
  Отклонение измерения x_i от среднего составляет d_i = x_i — \ bar {x} `

  Неопределенности наклона и точки пересечения

  Наклон и точка пересечения вычисляются на основе значений данных, с которыми связаны неопределенности.2 = [SDBSQ] `

  `\ sigma_b = \ pm [SDB]`

  Построение графиков линейных уравнений с помощью TI-83 +

  Это упражнение разработано, чтобы помочь вам познакомиться с графическим калькулятором. В нем вы научитесь составлять графики уравнений линий, изменять окно, находить точки пересечения и работать с табличной функцией калькулятора.

  1. Начните с включения калькулятора.
  2. Если у вас нет пустого экрана, нажмите кнопку 2 ^nd , затем QUIT (переключение РЕЖИМА).
  3. Нажмите кнопку Y = .
  4. Если есть уравнение, сохраненное в Y ₁ , нажмите кнопку CLEAR . Повторите для Y ₂ и любых других значений, для которых сохранено уравнение.
  5. Наведите курсор на строку Y ₁ и введите 2 +3, затем Enter. Теперь у вас есть уравнение y = 2x + 3, введенное в компьютер.
  6. Нажмите кнопку ZOOM . Выберите вариант 6 для ZStandard . Это дает вам координатную плоскость со значениями x и y от –10 до 10.
  7. Нажмите кнопку 2 ^nd , затем ТАБЛИЦА (сдвиг ГРАФИКА ), чтобы увидеть таблицу значений для вашего уравнения.
  8. Нарисуйте таблицу с 6 значениями для x и y ниже.
     
  9. Нажмите кнопку ГРАФИК, чтобы снова увидеть линию и нарисуйте то, что вы видите на калькуляторе, на координатной плоскости ниже.
  10. Повторите процесс с уравнением 4x + y = -5.
      
  11. Повторите процесс с уравнением.
  12. Вы получили линию? ______________ Как вы думаете, что с этим случилось?
  13. Нажмите кнопку ОКНО .Измените значения, чтобы они отражали значения в таблице справа.
  14. Нажмите кнопку GRAPH . Нарисуйте уравнение ниже. Обязательно измените масштаб на миллиметровой бумаге.
      
  15. Определите, какие значения необходимы для отображения пересечений по осям x и y графика y = 5x + 60
      
      
  16. Введите уравнение y = (2x — 6) / 3 дюйма Y ₁ . Нажмите 2 ^nd , затем TBLSET (сдвиг WINDOW). Измените TblStart = на -6 и Δ TBl = на 3.Нажмите 2 ^nd , затем ТАБЛИЦА , чтобы просмотреть значения для x и y. Запишите свою таблицу ниже.
      
  17. Нарисуйте диаграмму выше.
  18. Почему в скобках числа 16 должно быть 2x -6?
  19. Почему мы выбрали Δ TBl = равным 3?

  Версия этого упражнения для печати см. В разделе Построение графиков линейных уравнений с помощью TI83 +.

  Калькулятор линейных графиков — Онлайн-калькулятор линейных графиков

  Что такое калькулятор линейных графиков?

  Линейный график — это графическое представление прямой линии, которая представлена ​​уравнением вида ‘y = mx + c’ .Онлайн-вычислитель линейных графиков Cuemath — это бесплатный онлайн-инструмент, который за несколько секунд рисует линейный график, проходящий через две точки.

  Как пользоваться калькулятором линейного графика?

  Выполните шаги, указанные ниже, чтобы нарисовать линейный график линии, проходящей через две точки.

  • Шаг 1 — Введите значения x1, x2, y1, y2.
  • Шаг 2 — Щелкните « Draw », чтобы нарисовать линейный график, проходящий через эти точки.
  • Шаг 3 — Щелкните « Reset », чтобы очистить поля и ввести новые точки.

  Как нарисовать линейный график?

  Чтобы построить линейный график, выполните следующие действия:

  • Выберите две точки (x1, y1), (x2, y2), чтобы нарисовать линейный график.
  • Отметьте две точки на графике, используя их координаты x и y .
  • Затем с помощью линейки соедините две точки линией, проходящей через эти точки.

  Уравнение прямой можно найти, подставив обе точки в линейное уравнение y = mx + c. Наклон «m» и вертикальное пересечение «c» можно найти с помощью обоих уравнений, полученных из двух точек.

  Давайте на примере научимся рисовать линейный график.

  Решенный пример:

  Нарисуйте линейный график, проходящий через точки A (1,2) и B (2,3).

  Решение:

  На первом этапе мы должны отметить две точки A и B на миллиметровой бумаге.Чтобы отметить точку A, переместитесь на 1 единицу в сторону положительной оси x от исходной точки (0,0), затем на 2 единицы вверх. Чтобы отметить точку B, переместитесь на 2 единицы в направлении положительной оси x от исходной точки (0,0), а затем на 3 единицы вверх.

  Отметив две точки A и B, с помощью линейки нарисуйте линию, проходящую через две точки.

  Теперь воспользуйтесь калькулятором линейного графика и нарисуйте график следующих точек.

  1) (2,3), (3,4)

  2) (5,6), (7,2)

  Статьи по теме:

  Построение нелинейных уравнений и систем с помощью программы «Пошаговое решение математических задач»

  
  ЦЕЛИ

  • Графические уравнения
  • Графические уравнения методом точечной печати
  • Определение пересечений и симметрии графа
  • Графические уравнения с использованием графических калькуляторов
  • Решение задач с помощью графиков
    

  Как мы уже видели, такие иллюстрации, как диаграммы рассеяния и линии наилучшего синицы играют важную роль, помогая нам исследовать взаимосвязь между две величины. В случае, когда отношение между двумя величинами равно описывается уравнением с двумя переменными, часто желательно представить это геометрическая связь с графом. Мы повторяем определение, данное ранее.

  График уравнения
  График уравнения в переменных x и y состоит из всех точек в плоскость zy, координаты которой (x, y) удовлетворяют уравнению.

  Построение точечных графиков
  Обычный метод получения эскиза графика уравнения в двух переменная состоит в том, чтобы сначала построить несколько точек, лежащих на графике, а затем соедините точки плавной кривой.2

  Раствор

  Поскольку данное уравнение ясно показывает, как значения y связаны со значениями x, кажется разумным начать с присвоения x нескольких разных чисел а затем найдите соответствующие значения y, чтобы получить точки, лежащие на графике. Затем мы строим эти точки и соединяем их плавной кривой. См. Рисунок I.
  

  Обратите внимание, что на эскизе показаны не все точки на графике, но они видны. установить постоянный образец.Если на эскизе графика уравнения отображается достаточно графика, чтобы зритель мог «видеть» остальную часть графика как продолжением установленного шаблона мы часто называем эскиз завершенным. Так, при поиске такого эскиза один из подходов, который может быть использован, — это построить достаточное количество точек, чтобы узор стал очевидным, а затем соедините точки плавной кривой. Однако не всегда понятно, сколько очков достаточно. Некоторые знания о данном уравнении и его характеристиках ожидание графика уравнения, безусловно, полезно.Например, мы знаем, что график любого уравнения
  вида y = mx + b представляет собой прямую линию. Часто графическая утилита может быть очень полезно, так как позволяет очень быстро и в большом количестве наносить точки. А пока мы исследуем некоторые свойства графика уравнения, которое можно получить из алгебраического анализа уравнения. Позже мы вернуться к идее использования графической утилиты для получения эскиза графа уравнения.

  Пересечения и симметрия
  Точки, если таковые имеются, в которых график касается или пересекает одну из координат оси называются перехватчиками.Координата X точки, в которой график касается или пересекает ось x, называется пересечением по оси x. точка, в которой график касается или пересекает ось Y, называется пересечением по оси Y, см. Рисунок 2.
  
  

  ПРИМЕР 2

  Поиск точек пересечения — Определите точки пересечения по оси x и y для графика, приведенного в Рисунок 3.

  Решение На графике мы видим, что есть два пересечения по оси Y: — 3 и 4. По аналогии. есть три точки пересечения по оси x: — 3, 1 и 4.

  
  Переходы графика уравнения часто могут быть расположены алгебраически с помощью используя тот факт, что точки на оси x имеют нулевые координаты y, а точки по оси Y имеют нулевые координаты x.

  .