Подробнее про Параметрическое представление
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x) - функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) - знак числа:
sign(x) - для теории вероятности:
функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x) - Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.
5, не 7,5
5, не 7,5Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
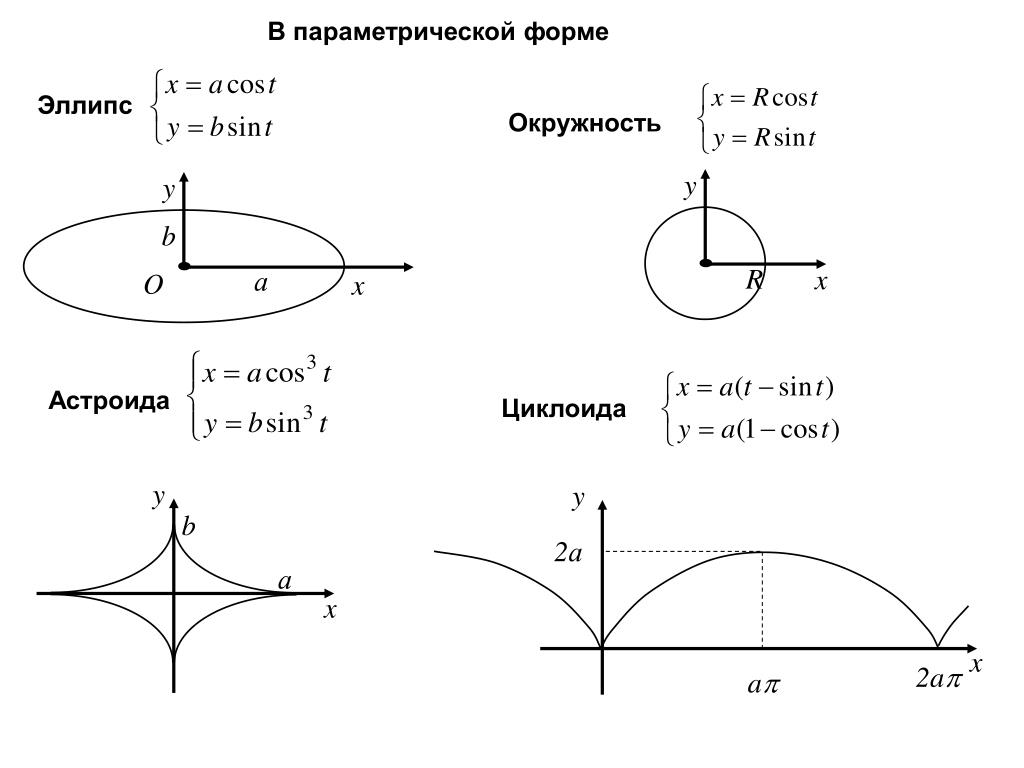
Параметрические уравнения
Параметрические уравнения
Линии
Напомним, что линия имеет уравнение
у = мх + б
Предположим, что один самолет
движется вдоль линии
y
= 2x + 3
в то время как другой самолет движется по
строка
г
= 3x — 2
Можете ли вы сказать, сталкиваются ли самолеты? Даже
хотя линии пересекаются, сами уравнения не говорят нам,
произойдет столкновение в воздухе. Уметь математически моделировать
В этом сценарии мы используем параметрическое уравнение. Введем переменную
t для времени и запишите x и y как функцию
т.
Рассмотрим два набора уравнений:
x(t) = t, y(t) = 2t + 1
x(t) = 2t, y(t) = 4t + 1
Они описывают одну и ту же прямую, но вторая движется в два раза быстрее.
Определение x = x(t), y = у(т) называется параметрически определенный 9кривая 0055 и функции х = х(т) и у = у(т) называются параметрических уравнения для кривой. |
Нахождение параметрических уравнений для линии по двум точкам
Пример:
Найдите параметрические уравнения для прямой, проходящей через
точки (3,2) и (4,6) так, что при t = 0 мы находимся в точке
(3,2) и
при t = 1 мы находимся в точке (4,6).
Решение:
Запишем символически:
(x,y) = (1 — t) (3, 2)+ (t) (4, 6)
= (3 — 3t + 4t, 2 — 2t + 6t)
= (3 + т, 2 + 4т)
так что
х(т) =
3 + т
и y(t)
= 2 + 4t
Функции
Если y = f (x) является функцией x, мы можем написать параметрические уравнения, написав
х =
t и y
= f(t).
Парабола
y = x 2
возможно
представлены параметрическими уравнениями:
х =
т
и г
= т 2
круга
Рассмотрим круг с центром в точке (0,0) и радиусом 2. Мы можем написать его параметрически как
х(т) =
2cos(t)
и г
= 2sin(t)
Мы видим, что круг рисуется против часовой стрелки.
Мы можем нарисовать такой же круг, как
.
х(т) =
2cos(-t)
и y(t)
= 2sin(-t)
теперь круг рисуется по часовой стрелке. Мы также можем написать
х(т) =
2 кос(т 2 )
и y = 2 sin(t 2 )
теперь круг начинается медленно и ускоряется.
Классный пример
График
x(t) = 11cost — 6cos(11/6 t)
и y(t) = 11sin(t) — 6sin(11/6
т)
изображен ниже:
Удаление параметра
Если кривая задана параметрическими уравнениями, нас часто интересуют нахождение уравнения для кривой в стандартной форме:
г = f(x)
Пример
Рассмотрим параметрические уравнения
х(т) = т 2 и y(t) =
sin(t) для t >
0
Чтобы найти обычный вид уравнения, мы решаем для t:
т =
отсюда
у = грех()
это уравнение.
Пример
Удалите параметр для
х(т) =
е т и y(t) = e 2t + 1
Решение
Пишем:
y(t) = (e
Отсюда
у = х 2 + 1
Перекрестки
Пусть
х 1 (т)
= 2t + 1
и у 1 (т)
= 4t 2
и
х 2 (т)
= 3t и
у 2 (т) = 3т
Они пересекаются? Если так то есть c
2c + 1 = 3c
и
4c 2 = 3c
первое уравнение дает нам, что
с = 1
Подставляем это во второе уравнение
у нас есть
4 = 3
что говорит нам о том, что они не пересекаются. Пересекаются ли их графики?
Если это так, то существуют c и k такие, что
2c + 1 = 3k
и
4c 2 = 3k
Отсюда мы видим, что
2с + 1 = 4с 2
или что
4c 2 – 2c – 1 =
0
Решаем получить две точки пересечения
следовательно их графики перехватываются.
Их графики показаны справа.
Назад на страницу полярных и параметрических уравнений
Назад на домашнюю страницу Math 107
Назад на домашнюю страницу математического факультета
электронная почта Вопросы и предложения
Параметрические уравнения и полярные координаты: Параметрические уравнения
До сих пор нарисованные нами графики определялись одним уравнением: функция с две переменные, x и y . Однако в некоторых случаях полезно ввести третью переменную, называемую параметром, и выразить x и y через параметр. Это приводит к двум уравнениям, называемым параметрическими уравнениями.
Пусть f и g — непрерывные функции (функции, графики которых представляют собой сплошные кривые) переменной
параметр t должен быть ограничен определенным интервалом, в течение которого функции f и g определены.Параметр может иметь положительные и отрицательные значения. Обычно плоская кривая рисуется по мере увеличения значения параметра. Направление плоской кривой по мере увеличения параметра называется ориентацией кривой. Ориентация плоской кривой может быть представлена стрелками, проведенными вдоль кривой. Изучите график ниже. Он определяется параметрическими уравнениями x = cos( t ), y = sin( t ), 0≤ t < 2 Π . Рисунок %: плоская кривая, определяемая параметрическими уравнениями Кривая такая же, как определено прямоугольным уравнением x 2 + y 2 = 1. Это единичный круг. Проверьте значения x и y в таких ключевых точках, как t = , Π и . Обратите внимание на ориентацию кривая: против часовой стрелки.
Единичная окружность является примером кривой, которую можно легко нарисовать с помощью
параметрические уравнения.
Одним из преимуществ параметрических уравнений является то, что
их можно использовать для построения кривых, которые не являются функциями, например единичный круг.
Еще одним преимуществом параметрических уравнений является то, что параметр можно использовать для представляют собой что-то полезное и, следовательно, предоставляют нам дополнительную информацию о графике. Часто плоская кривая используется для отслеживания движения объекта. через определенный промежуток времени. Предположим, что положение частицы дается приведенными выше уравнениями,
Полезно уметь преобразовывать прямоугольные уравнения в параметрические. уравнения. Преобразование из прямоугольного в параметрическое может быть сложным, и требует некоторого творчества. Здесь мы обсудим, как преобразовать параметрический в прямоугольные уравнения.
Процесс преобразования параметрических уравнений в прямоугольное уравнение таков: обычно называется удалением параметра. Во-первых, вы должны решить для параметр в одном уравнении. Затем подставьте прямоугольное выражение вместо параметр в другом уравнении и упростить. Изучите пример ниже, в что параметрические уравнения х = 2 t — 4, y = t + 1, — аау < t < аау преобразуются в прямоугольное уравнение.
параметрический
| х = 2 т — 4, у = т + 1 |
| т = |
| у = + 1 |
| у = х + 3 |
Решая параметр в одном параметрическом уравнении и подставляя в другого параметрического уравнения было найдено эквивалентное ему прямоугольное уравнение.
Ваш комментарий будет первым