Построить график функции y: Построение графиков функций онлайн

Содержание

График функции y=f(x)+b | Алгебра

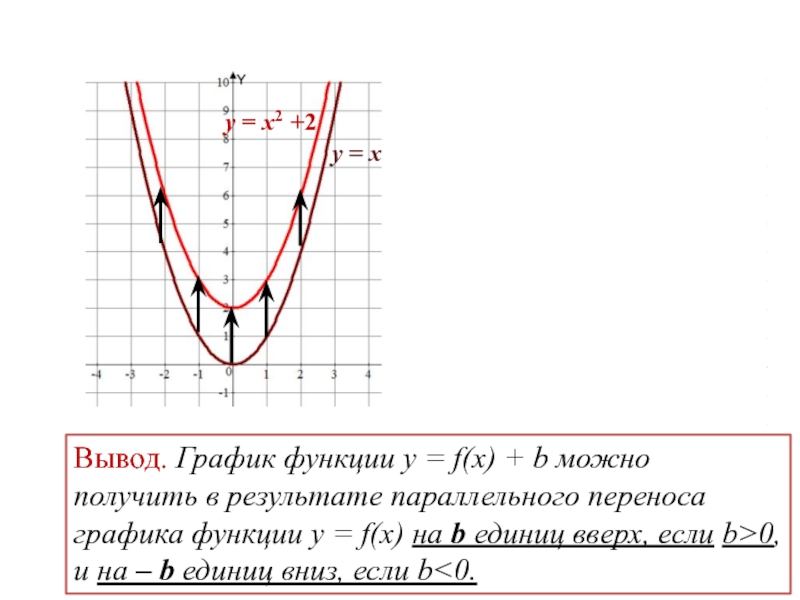
График функции y=f(x)+b (b>0) можно получить из графика функции y=f(x) с помощью параллельного переноса (сдвига) вдоль оси Oy на b единиц вверх.

При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y+b) графика функции y=f(x)+b (то есть абсцисса (координата x) каждой точки остается без изменения, а ордината (координата y ) увеличивается на b.

Один из вариантов преобразования — осуществить параллельный перенос начала отсчёта, точки O(0;0), в точку O1(0;b) и построить график y=f(x) с началом отсчёта от точки O1.

Примеры.

1) График функции y=x²+3 может быть получен из графика функции y=x² с помощью параллельного переноса вдоль оси Oy на 3 единицы вверх.

Строим параболу y=x². Затем переносим каждую из основных точек на 3 единицы вверх.

y=x²+3 из y=x²

Можно перенести только вершину параболы, точку (0; 0), на 3 единицы вверх, в точку (0; 3), и от новой вершины строить параболу y=x² (1 единица вправо, 1 — вверх; 1 единица влево, 1 — вверх; 2 единицы вправо, 2 — вверх и т.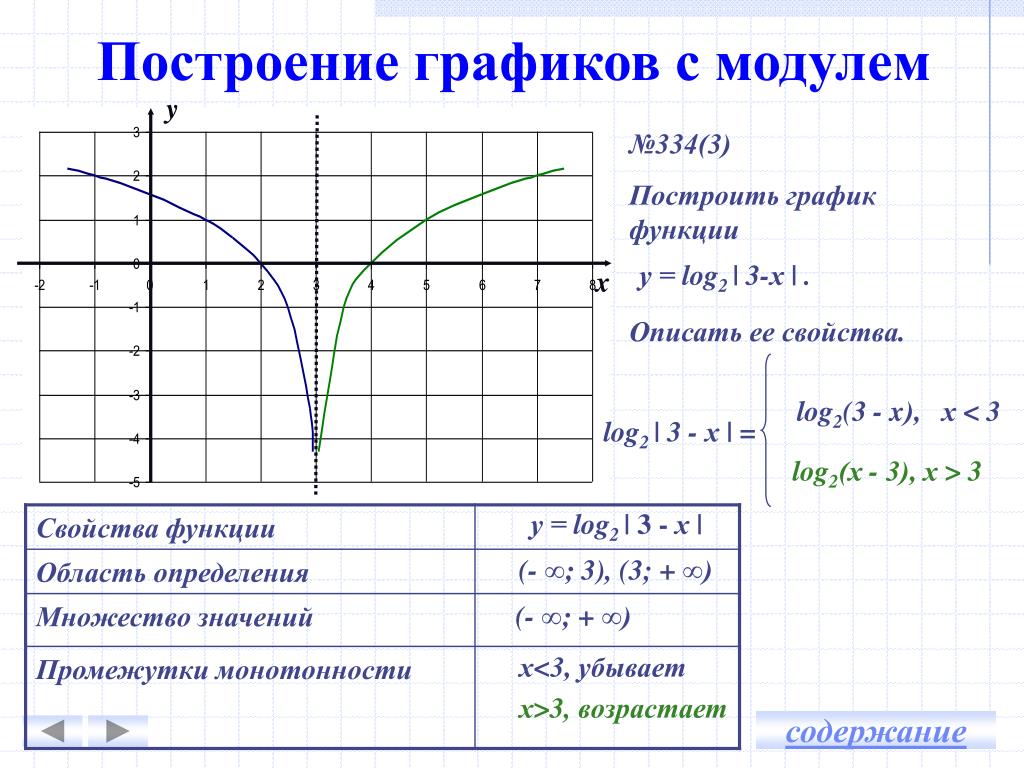

д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).

1) График функции y=x³+2 может быть получен из графика функции y=x³ с помощью параллельного переноса вдоль оси Oy на 2 единицы вверх.

Можно обойтись без построения начального графика y=x³, достаточно обозначить его основные точки, и выполнить параллельный перенос каждой из них на 2 единицы вверх.

y=x³+2 из y=x³

3) График функции y=√x+4 может быть получен из графика функции y=√x параллельным переносом на 4 единицы вверх вдоль оси Oy.

Строим график функции y=√x по основным точкам. Затем переносим каждую из этих точек вверх на 4 единицы.

Через полученные точки проводим ветвь параболы:

В следующих раз рассмотрим рассмотрим построение графиков вида y=f(x)-b.

Преобразование графиков позволяет на основе графиков элементарных функций получать графики сложных функций. Умение преобразовывать графики в алгебре пригодится не только при изучении функций, но и при решении уравнений и неравенств, в частности, при решении заданий с параметрами.

Открытая Математика. Функции и Графики. Параллельный перенос

Пусть имеется график функции y = f (x). Зададимся целью построить график функции y = f₁ (x), где f₁ (x) = f (x) + B. Ясно, что области определения этих функций совпадают. Пусть A (x₀; y₀) – точка на графике функции y = f (x). Соответствующая ей точка A′ (x₀; y₁) с той же абсциссой имеет координаты A′ (x₀; y

0 + B). Точка A′ получается из точки A сдвигом на B вертикально вверх, если B > 0, и на |B| вниз, если B < 0. Обобщая это рассуждение на все точки, приходим к выводу, что график функции y = f (x) + B получается из графика функции y = f (x) параллельным переносом вдоль оси OY на B вверх, если B > 0, и на |B| вниз, если B < 0.

Алгебраически для каждой точки графика это можно записать системой {x′=x,y′=y+B, где x и y – координаты какой-либо точки старого графика, x′ и y′ – соответствующей ей точки нового.

Аналогичным образом можно построить график функции y = f (x – b). Точка A′ (x′; y′) нового графика имеет такую же ординату, как и точка A (x; y), если x′ = x + b. Таким образом, чтобы построить точку

A′, нужно сместить точку A вправо, если b > 0, и влево, если b < 0.

Параллельный перенос графиков

График функции y = f (x – b) получается из графика функции y = f (x) параллельным переносом вдоль оси OX на b вправо, если b > 0, и на |b| влево, если b < 0.

Алгебраически это записывается системой: {x′=x+by′=y

Область определения функции, соответствующей новому графику, также смещается на a по отношению к области определения функции, задающей старый график.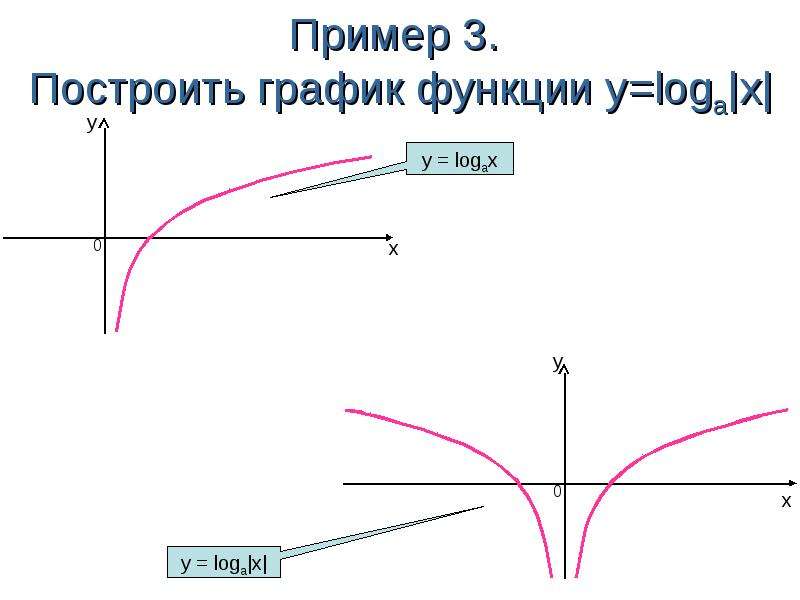

В общем случае график функции y = f (x – b) + B получается из графика функции y = f (x) параллельным переносом, при котором начало координат O (0, 0) переходит в точку O′ (b, B). Обычно находят точку O′ и проводят через нее вспомогательные координатные оси, относительно которых строят график функции

y = f (x).

Построение графика функции y = a(x–m)² + n

Цель урока: рассмотреть параллельный перенос (сдвиг вдоль оси Ох и оси Оу) графика функции у = ах²

Ход урока.
Сообщение темы и цели урока.
Повторение свойств и графика функции у = ах²
Изучение нового материала. На предыдущем уроке были рассмотрены два важнейших преобразования графика функции у = f(x).
График функции у = -f(x) получается из графика функции у = f(x) с помощью симметрии относительно оси абсцисс.

График функции у = аf(x) получается из графика функции у = f(x) растяжением вдоль оси ординат в а раз при а > 1 и сжатием в раз при 0 < а < 1.

Эти преобразования пригодны для любых функций (как изученных, так и еще не рассмотренных).
Слайд 1. Рассмотрим еще два важнейших преобразования графика функции у = f(x) – построение графиков функции у = f(x) + n и y = f(x-m).
Слайд 2. График функции у = ах² + n получается из графика функции у = ах² с помощью параллельного переноса (сдвига) вдоль оси Оу на |n| единиц: вверх, если n > 0 и вниз, если n < 0.
Слайд 3. График функции у = а(х-m)² получается из графика функции у = ах² с помощью параллельного переноса (сдвига) вдоль оси Ох на |m| единиц: вправо, если m > 0 и влево, если m < 0.
Слайды 4-5. График функции у = а(х-m)² + n получается из графика функции у = ах² с помощью двух последовательно выполненных преобразований, причем эти сдвиги можно выполнять в любом порядке.

Слайд 6. Устная работа: проговорить последовательность преобразований.
Слайд 7. Рассмотреть (повторить выделение полного квадрата из квадратного трехчлена) приведение функции у = ах² + вх + с к виду у = а(х-m) + n и построения с помощью преобразований.
Итоги урока. Контрольные вопросы.
Алгоритм построения графика функции у = -ах².

Как построить график функции у = ах² при а > 0 ?

Как построить график функции у = ах² + n ?

Как построить график функции у = а(х-m)² ?

Выполнение заданий из учебника.

Задание на дом. (На усмотрение учителя).
Выражение графика или функция — MATLAB fplot
Цвет заливки маркера, заданный как 'auto' , триплет RGB, шестнадцатеричный цвет код, название цвета или короткое название. 'auto' значение использует то же color как свойство
MarkerEdgeColor .
Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB — это трехэлементный вектор-строка, элементы которого укажите интенсивность красного, зеленого и синего компоненты цвета.Интенсивности должны быть в диапазон [0,1] ; например, [0,4 0,6 0,7].
Шестнадцатеричный цветовой код — это вектор символов или строка. скаляр, который начинается с хеш-символа ( # ) за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться с
0 до F .В значения не чувствительны к регистру. Таким образом, цветовые коды '# FF8800' , '# ff8800' , '# F80' и '# f80' эквивалентны.
Вы также можете указать некоторые общие цвета по имени. В этой таблице перечислены названные цвета параметры, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
'w'
Название цвета Краткое название Триплет RGB Шестнадцатеричный код цвета Внешний вид
'красный'
'r' [1 0 0] '# FF0000'
'зеленый' 'g' [0 1 0] '# 00FF00'
'синий' 'b' [0 0 1] '# 0000FF'
'голубой 'c' [0 1 1] '# 00FFFF'
'пурпурный' 'm' [1 0 1] '# FF00FF'
'желтый' 'y' [1 1 0] '# FFFF0066
'черный' 'k' [0 0 0] '# 000000'
'белый66 [1 1 1] '#FFFFFF'
'none' Неприменимо Неприменимо Неприменимо N o цвет
Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию, которые MATLAB использует во многих типах графиков.
0,8500 0,3250 0,0980] 4940 0,1840 0,5560]
Триплет RGB Шестнадцатеричный код цвета Внешний вид
[0 0,4470 0,7410] '# 0072BD'
'# D95319'
[0,9290 0,6940 0,1250] '# EDB120'
'# 7E2F8E'
[0,4660 0,6740 0,1880] '# 77AC30'
1

'# 4DBEEE'
[0,6350 0,0780 0,1840] '# A2142F'
Пример: [0. 3 0,2 0,1]
Пример: «зеленый»
Пример: '# D2F9A7'
Графические логарифмические функции
Функция у знак равно бревно б Икс является обратной функцией экспоненциальная функция у знак равно б Икс .
Рассмотрим функцию у знак равно 3 Икс .Это можно изобразить как:
График обратной функции любой функции — это отражение графика функции относительно линии у знак равно Икс . Итак, график логарифмической функции у знак равно бревно 3 ( Икс ) что является обратной функцией у знак равно 3 Икс является отражением приведенного выше графика относительно линии у знак равно Икс .
Икс 1 9 1 3 1 3 9 27 81 год у знак равно бревно 3 Икс — 2 — 1 0 1 2 3 4
Область определения функции — это набор всех положительных действительных чисел.
Если база не записана, предположим, что журнал является базовым. 10 .
Икс 1 1000 1 100 1 10 1 10 100 1000 у знак равно бревно Икс — 3 — 2 — 1 0 1 2 3
Логарифмическая функция, у знак равно бревно б ( Икс ) , можно сдвинуть k единиц по вертикали и час единиц по горизонтали с уравнением у знак равно бревно б ( Икс + час ) + k .
Вертикальный сдвиг
Если k > 0 , график сдвинется вверх.
Если k < 0 , график сместится вниз.
Горизонтальный сдвиг
Если час > 0 , график сдвинется влево.
Если час < 0 , график сдвинется вправо.
Рассмотрим логарифмическую функцию у знак равно [ бревно 2 ( Икс + 1 ) — 3 ] . Это можно получить, переведя родительский граф у знак равно бревно 2 ( Икс ) Пару раз.
Рассмотрим график функции у знак равно бревно 2 ( Икс ) .
С час знак равно 1 , у знак равно [ бревно 2 ( Икс + 1 ) ] перевод у знак равно бревно 2 ( Икс ) на одну единицу влево.
Теперь, k знак равно — 3 .График у знак равно [ бревно 2 ( Икс + 1 ) ] будет перемещен 3 единицы вниз, чтобы получить у знак равно [ бревно 2 ( Икс + 1 ) ] — 3 .
Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел.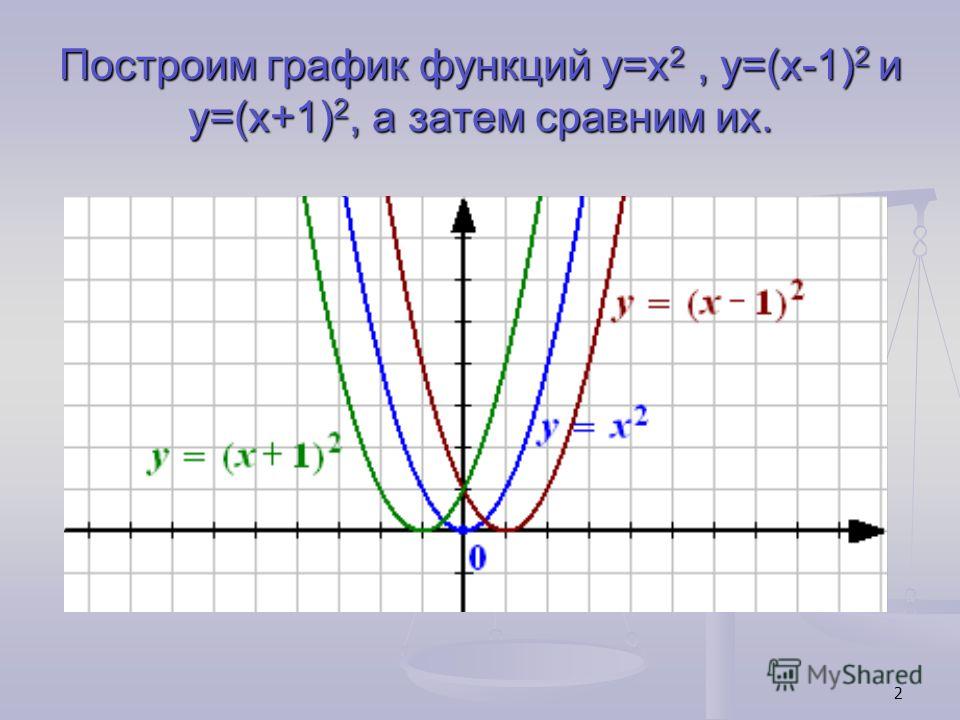 Это связано с тем, что для отрицательных значений соответствующее экспоненциальное уравнение не имеет решения. Например, 3 Икс знак равно — 1 не имеет реального решения, поэтому бревно 3 ( — 1 ) не определено.
Итак, как насчет такой функции, как у знак равно бревно 4 ( — Икс ) ?
Это определено только для отрицательных значений Икс .
Найдите значения функции для нескольких отрицательных значений Икс . Для упрощения расчета вы можете использовать экспоненциальную форму уравнения, 4 у знак равно — Икс .
Икс — 1 — 2 — 4 — 8 — 16 — 32 у знак равно бревно 4 ( — Икс ) или 4 у знак равно — Икс 0 1 2 1 1 1 2 2 2 1 2
Постройте точки и соедините их плавной кривой.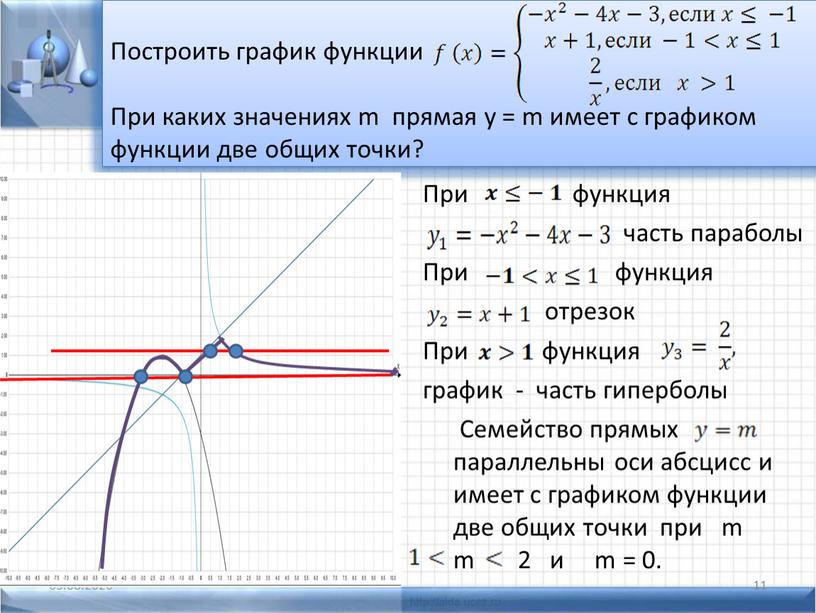
Вы можете видеть, что график является отражением графика функции у знак равно бревно 4 ( Икс ) о у -ось.
Онлайн-справка — Быстрая справка
Графические функции
Последнее обновление: 04.09.2019
Создание новой функциональной диаграммы
Origin поддерживает построение четырех видов функций: 2D-функции, 2D-параметрические функции, 3D-функции и 3D-параметрические функции.
Нажмите Файл: Новое: График функции
или
Нажмите кнопку функционального графика на стандартной панели инструментов.

Когда вы выбрали график функции из меню, откроется диалоговое окно, позволяющее вам определить функцию.

Чтобы построить 3D параметрическую функцию, вы можете выбрать меню File: New: Function Plot: 3D Parametric Function Plot , чтобы открыть диалоговое окно Create 3D Parametric Function Plot . В этом диалоговом окне введите сетку сетки , установите масштаб для двух параметров, введите параметрические уравнения для переменных X, Y и Z, а затем определите константы, которые можно использовать в определении функции в нижней таблице, если нужный. Нажмите ОК, чтобы получить график. См. Больше [образцы 3D-функций]
Примечание: После построения функции вы можете переопределить или настроить график функции на вкладке Функция диалогового окна Plot Details , которое можно открыть, дважды щелкнув график функции в окне графика.
Добавить график функции к существующему графику
При активном окне графика щелкните File: New: Function Plot или щелкните кнопку графика функции на стандартной панели инструментов, как описано выше.
Выберите Добавить в активный график в раскрывающемся списке внизу диалогового окна.
Примечание: Если вы выберете 3D-график функции, когда активным окном графика является 2D, этот раскрывающийся список не будет отображаться.

Альтернативный метод добавления графика функции к существующему графику
При активном графике щелкните Insert: Function Plot or Insert: Parametric Plot .
Примечание: В более старых версиях это находится в разделе График: добавить график функции .
Ключевые слова: график математических функций, трехмерный график параметрической функции, двухмерный график параметрической функции, график функции, сетка
Требуется минимальная исходная версия: 9.0SR0
Построение математических функций — Как строить математические функции в Python?
Привет, народ! В этом уроке мы узнаем, как построить математические функции с помощью Python. Итак, приступим.
Предварительные требования
Для построения различных математических функций с использованием Python нам потребуются следующие две библиотеки Python:
1.
NumPy
NumPy — это библиотека Python, которая поддерживает многомерные массивы и матрицы и предлагает широкий спектр математические функции для работы с массивами и матрицами NumPy.Это одна из самых фундаментальных библиотек для научных вычислений. Мы можем установить NumPy на наш локальный компьютер, используя следующую команду.
> python -m pip install numpy
2. Matplotlib
Matplotlib — это библиотека Python, которая широко используется для различных типов построения графиков. Используя Matplotlib, мы можем очень легко строить статические и интерактивные визуализации. Мы можем установить Matplotlib на наш локальный компьютер, используя следующую команду.
> python -m pip install matplotlib
Шаги для построения математических функций
Сначала импортируйте numpy и matplotlib.Модуль pyplot в основной программе Python (.py) или Jupyter Notebook (. ipynb) с помощью следующих команд Python.
импортировать numpy как np импортировать matplotlib.pyplot как plt
Для всех графиков мы будем выполнять почти те же шаги, за исключением использования конкретной математической функции NumPy в соответствующих графиках.
1. График (y = x) Функция идентичности
x = np.arange (0, 11, 1) у = х print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title ("Функция идентичности") plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [0 1 2 3 4 5 6 7 8 9 10] Значения y: [0 1 2 3 4 5 6 7 8 9 10]
График функции идентичности
2. График (y = a.x
² + b.x ² + c) Квадратичная функция
x = np.arange (-11, 11, 1) а = 2 b = 9 с = 10 у = а * (х ** 2) + Ь * х + с print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title ("Квадратичная функция") plt. xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [-11-10-9-8-7-6-5-4-3-2-1 0 1 2 3 4 5 6 7 8 9 10] Значения y: [153 120 91 66 45 28 15 6 1 0 3 10 21 36 55 78 105 136 171 210 253 300]
График квадратичной функции
3. График (y = a.x
³ + b.x ² + c.x + d) Кубическая функция
x = np.arange (-11, 11, 1) а = 2 б = 3 с = 4 d = 9 y = a * (x ** 3) + b * (x ** 2) + c * x + d print ('Значения x:', x) print ('Значения y:', y) plt.сюжет (x, y) plt.title («Кубическая функция») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [-11-10-9-8-7-6-5-4-3-2-1 0 1 2 3 4 5 6 7 8 9 10] Значения y: [-2334-1731-1242-855-558-339-186-87-30-3 6 9 18 45 102 201 354 573 870 1257 1746 2349]
График кубической функции
4. График (y = ln (x) или log
_e (x)) Функция натурального логарифма
x = np. аранж (1, 11, 0,001) у = np.log (х) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title («Функция натурального логарифма») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [1. 1.001 1.002 ... 10.997 10.998 10.999] Значения y: [0.00000000e + 00 9.99500333e-04 1.99800266e-03 ... 2.39762251e + 00 2.39771344e + 00 2.39780436e + 00]
График функции натурального логарифма
5. График (y = log
₁₀ x) Функция общего / десятичного логарифма
x = np.аранж (1, 11, 0,001) у = np.log10 (х) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title («Функция десятичного логарифма») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [1. 1.001 1.002 ... 10.997 10.998 10.999] Значения y: [0.00000000e + 00 4.34077479e-04 8.67721531e-04 ... 1.04127423e + 00 1. 04131372e + 00 1.04135320e + 00]
График функции десятичного логарифма
6. График (y = e
^x) Естественная экспоненциальная функция
x = np.аранж (-11, 11, 0,01) у = np.exp (x) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title ("Естественная экспоненциальная функция") plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [-11. -10,99 -10,98 ... 10,97 10,98 10,99] Значения y: [1.67017008e-05 1.68695557e-05 1.703e-05 ... 5.81045934e + 04 5.86885543e + 04 5.92783841e + 04]
График естественной экспоненциальной функции
7. График (y = a
^x) Общая экспоненциальная функция
x = np.аранж (-11, 11, 0,01) а = 8 у = а ** х print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title («Общая экспоненциальная функция») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [-11. -10,99 -10,98 ... 10,97 10,98 10,99] Значения y: [1.16415322e-10 1.18861455e-10 1.21358987e-10 ... 8.07043896e + 09 8.24001604e + 09 8.41315629e + 09]
График общей экспоненциальной функции
8. График (y = знак (x)) Функция Signum
x = np.аранж (-11, 11, 0,001) y = np.sign (x) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title ("Функция Signum") plt.xlabel («Значения x») plt.ylabel ("Значения y)") plt.show ()
Выход:
Значения x: [-11. -10,999 -10,998 ... 10,997 10,998 10,999] Значения y: [-1. -1. -1. ... 1. 1. 1.]
Signum Function Plot
9. Plot (y = a.sin (b.x + c)) Синусоидальная функция в Python
x = np.arange (-11, 11, 0.001) а = 5 б = 3 с = 2 у = а * нп.грех (Ь * х + с) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title («Синусоидальная функция») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show ()
Выход:
Значения x: [-11. -10,999 -10,998 ... 10,997 10,998 10,999] Значения y: [2.02018823 2.0332.04759397 ... -2.10016104 -2.11376421 -2.12734835]
Синусоидальная функция График 10. График (y = sinc (x)) Функция Sinc x = np.arange (-11, 11, 0.01) у = np.sinc (х) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title ("функция Sinc") plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show () Выход: Значения x: [-11. -10,99 -10,98 ... 10,97 10,98 10,99] Значения y: [1.41787526e-16 9.09768439e-04 1.82029537e-03 ... 2.73068428e-03 1.82029537e-03 9.09768439e-04] График функции Sinc 11. График (y = cosh (x)) Гиперболическая функция x = np.arange (-11, 11, 0.001) у = np.cosh (х) print ('Значения x:', x) print ('Значения y:', y) plt.plot (x, y) plt.title («Гиперболическая функция») plt.xlabel («Значения x») plt.ylabel ("Значения y") plt.show () Выход: Значения x: [-11. -10,999 -10,998 ... 10,997 10,998 10,999] Значения y: [29937.07086595 29907.14875865 29877.2565585 ... 29847.39423524 29877.25655813 29907.14875828] График функции гиперболического косинуса Подведение итогов В этом руководстве мы узнали, как строить графики различных типов математических функций с использованием библиотек Numpy и Matplotlib.Надеюсь, вы поняли процесс построения различных математических функций и готовы экспериментировать самостоятельно. Спасибо за прочтение! Следите за новостями, чтобы узнать о потрясающих учебных ресурсах по программированию на Python. GraphPad Prism 9 Curve Fitting Guide Prism предлагает график для функционального анализа, но на самом деле он не анализирует какие-либо данные. Скорее, он генерирует кривые на основе выбранного вами уравнения и вводимых вами параметров. Как построить график функции 1. Начните с любой таблицы или графика данных, щелкните "Анализировать", откройте папку "Создать кривую" и выберите "Построить график функции". 2. На первой вкладке (Функция) выберите уравнение, начальное и конечное значения X и количество кривых, которые вы хотите построить. 3. На второй вкладке (Параметры) выберите, хотите ли вы также построить первую производную, вторую производную или интеграл функции. «Кривая» на самом деле представляет собой набор координат X и Y, которые определяют серию точек, которые соединяются, образуя кривую. Вы можете выбрать количество отрезков линии, которые будут определять кривую. Нет особых причин для изменения значения по умолчанию (150), если только вы не хотите построить только часть кривой на некоторых графиках, и в этом случае вам следует увеличить это значение. 4. На третьей вкладке (Значения параметров) введите значения параметров (или щелкните значок крючка для анализа крючка или информационных констант). Советы по построению функции Построение семейства кривых Если вы решили построить более одной кривой (выбор на первой вкладке), остальная часть диалогового окна работает немного иначе. Вам нужно, чтобы один параметр в уравнении изменялся от кривой к кривой. Не определяйте это в уравнении. Вместо этого определите значения на третьей вкладке. Вы также захотите пометить столбцы вычисляемой таблицы. Есть два способа сделать это. Укажите внизу второй вкладки (Параметры), хотите ли вы пометить каждую кривую вручную (введите метки в верхней части третьей вкладки) или вы хотите, чтобы каждый столбец был помечен с использованием значения одного из параметров. Последнее обычно имеет больше смысла и проще. Если вам нужно сделать что-то более сложное, помните, что вы можете написать уравнение, чтобы некоторые строки применялись только к определенным наборам данных.Поместите перед строкой, которая относится только к столбцу A и т. Д. В верхней части третьей вкладки перечислены все кривые, которые вы создадите. Выберите одну или несколько из этих кривых (или нажмите «выбрать все»), а затем введите значения параметров ниже. Часто вам нужно сначала щелкнуть «выбрать все» и ввести большинство параметров. Затем щелкайте по одной кривой за раз и введите значение параметра, который варьируется между кривыми. Отображение каждой кривой на отдельном графике По умолчанию Prism создает график, содержащий все кривые на одном графике.Если вы хотите, чтобы каждая кривая была на своем графике, перейдите к таблице результатов, найдите раскрывающееся меню «Создать» на панели инструментов (выглядит как зеленый знак плюса) и выберите «Новый график существующих данных ...». В появившемся диалоговом окне выберите создание одного графика для каждого набора данных (в данном контексте набор данных представляет собой кривую). Если вы планируете увеличить масштаб и построить только часть кривой Кривая по умолчанию определяется как 150 линейных сегментов. Это создает плавную кривую. Но если вы затем измените диапазон значений X, показанный на графике, будет видна только часть этих линейных сегментов, а кривая может показаться грубой.Чтобы решить эту проблему, вернитесь в диалоговое окно параметров на вкладку «Параметры» и увеличьте количество сегментов линии до гораздо большего значения. Объединение двух кривых на одном графике Приведенный ниже график объединяет две построенные функции на одном графике. В первый раз, когда я построил график функции, я выбрал распределение Гаусса с X в диапазоне от -3 до 3. Я установил среднее значение 0,0, стандартное отклонение 1,0 и амплитуду 100,0 (произвольно, поскольку я скрыл эту ось). . Затем я повторил этот анализ, но на этот раз установил диапазон X от 1.3 до 3,0. Я поместил обе кривые на один график (Изменить ... Добавить наборы данных - помните, что кривая, сгенерированная этим анализом, является "набором данных" для Prism). Для более короткой кривой я решил создать заливку области. BioMath: тригонометрические функции В этом разделе мы исследуем графики шести тригонометрических функций, начиная с графика функции косинуса. Построение графика y = cos x Чтобы нарисовать график y = cos x , мы можем составить таблицу значений, которые мы можем вычислить ровно: Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них: Поскольку область определения функции косинуса - это все действительные числа, мы помещаем стрелки на график, чтобы указать, что график точно повторяется в обоих направлениях. Тот факт, что функция косинуса повторяется, означает, что она периодическая . В в частности, y = cos x периодичен с периодом 2π. Это означает, что если точка ( x , y ) лежит на графике, то точка ( x +2 k π, y ) также будет лежать на графике, где k - любое целое число. Например, ( x + 2π, y ) и ( x - 2π, y ) оба будут лежать на графике. График y = sin x Чтобы нарисовать график y = sin x , мы можем составить таблицу значений, которые мы можем вычислить. ровно: Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них: Поскольку область определения синусоидальной функции - это действительные числа, мы помещаем стрелки на graph, чтобы указать, что график точно повторяется в обоих направлениях.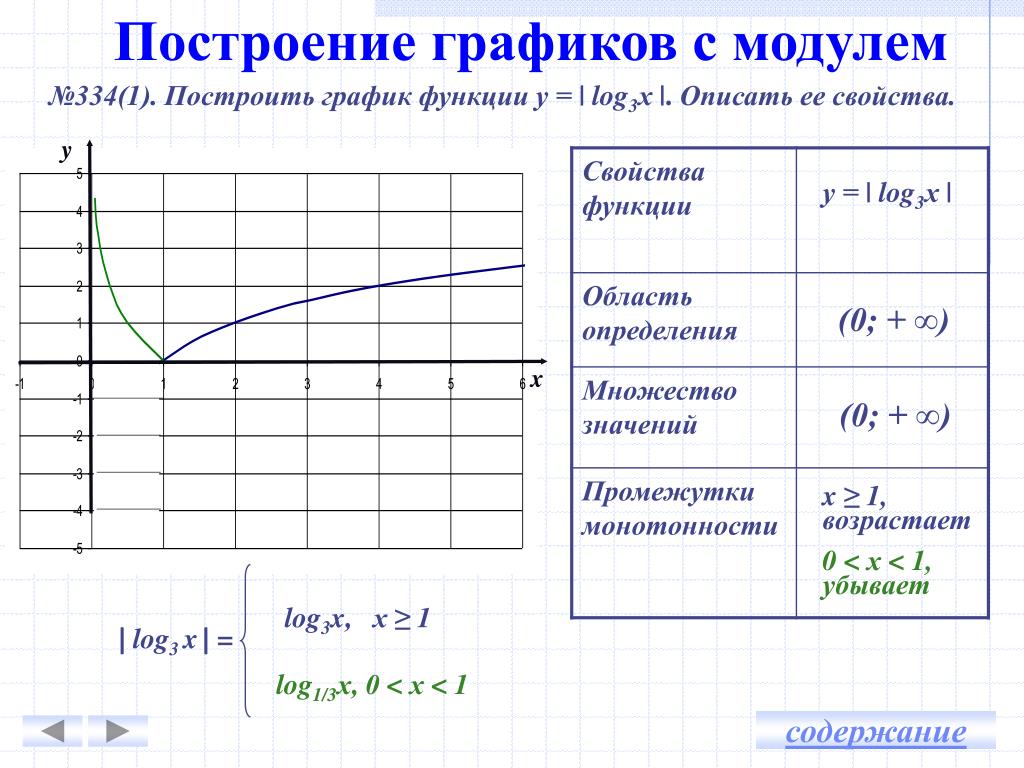 Нравиться функция косинуса, функция синуса также периодична 2π. График y = tan x Чтобы нарисовать график y = tan x , мы можем составить таблицу значений, которые мы можем вычислить. ровно: Обратите внимание, что теперь у нас есть несколько неопределенных функциональных значений; графически эти соответствуют вертикальным асимптотам.Мы можем набросать y = tan x следующим образом: На приведенном выше графике пунктирными линиями обозначены вертикальные асимптоты. Мы размещаем стрелки на графике, чтобы указать, что функция возрастает до ∞. Например, tan x → ∞ как x → (π / 2) ^-. (т.е. поскольку x приближается к π / 2 слева) и загар x → −∞ как x → (π / 2) ^- (т. е. поскольку x приближается к π / 2 справа). В отличие от функций синуса и косинуса, касательная функция π периодична. То есть, если точка ( x , y ) лежит на графике y = tan x , то будет точка ( x + k π, y ), где k любое целое число. График y = sec x , y = csc x, и y = детская кроватка x Напомним, что функции секанса, косеканса и котангенса являются обратными величинами функций косинуса, синуса и тангенса соответственно.Вы с меньшей вероятностью встретите эти графики при изучении наук о жизни. Мы включаем эти графики для полноты картины. Преобразование y = cos x и y = sin x Теперь мы рассмотрим графические преобразования y = cos x и y = sin x . Мы можно записать преобразованные функции косинуса и синуса следующим образом: y = a cos ( b ( x - d )) + c , y = a sin ( b ( x - d )) + c . Звоним | a | амплитуда функции. Амплитуда - это расстояние от минимальное функциональное значение к максимальному функциональному значению, деленному на 2.В период вышеуказанных функций равен 2π / b (обратите внимание, когда b = 1, период равен 2π). Когда моделирование определенной величины или явления с помощью функции синуса или косинуса, амплитуда и период - две важные характеристики, определяющие поведение. Ты можете обратиться к разделу преобразований, чтобы изучить другие преобразования ближе.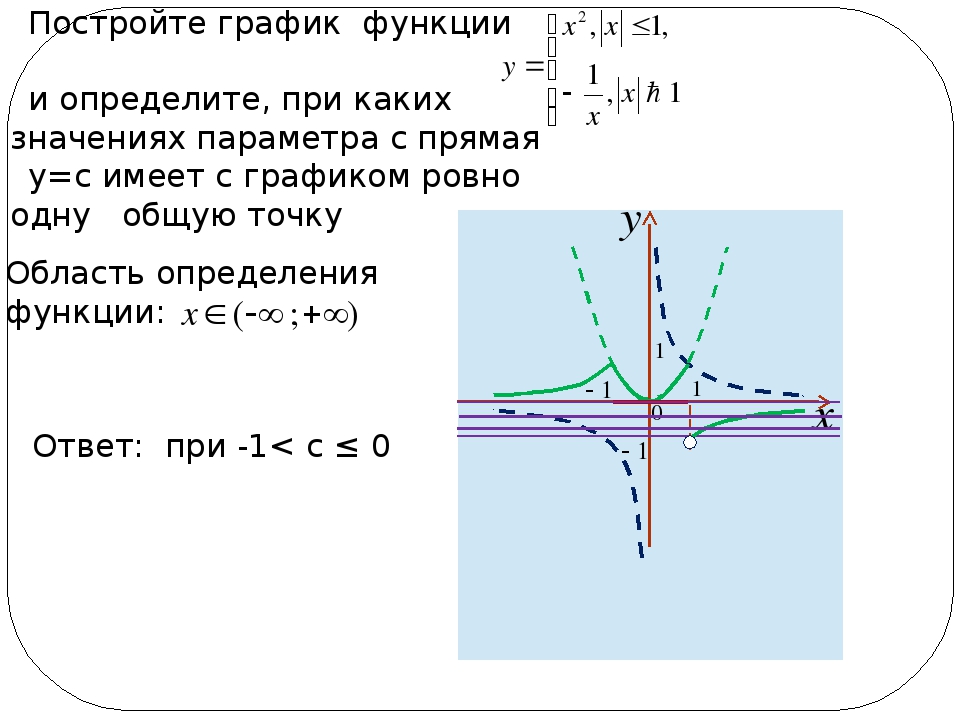 ***** В следующем разделе мы представим тригонометрические тождества. Личности Графические функции абсолютных значений | Purplemath Purplemath Принятие абсолютного значения отрицательного числа делает его положительным. По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу T-диаграмму при построении графиков функций абсолютных значений.Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график. Например, предположим, что ваш класс проходит следующую викторину: MathHelp. com Один из других учеников делает то, что обычно делает: он выбирает только положительные значения x для своей Т-диаграммы: Затем он набирает свои очки: Эти точки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график.В частности, они не содержат никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений что-то означают . В результате ученик забывает учесть эти столбцы и рисует ошибочный график: НЕПРАВИЛЬНЫЙ ОТВЕТ! Аааааи . .. он просто завалил викторину. Но вы более осторожны.Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Итак, вы выбираете значения x , которые ставят «минус» внутри абсолютного значения, и выбираете еще несколько точек. Ваш T-график выглядит примерно так: Затем вы наносите свои очки: ... и, наконец, вы соединяете точки: У вас есть правильный график: Правильный ответ! Ааааанд.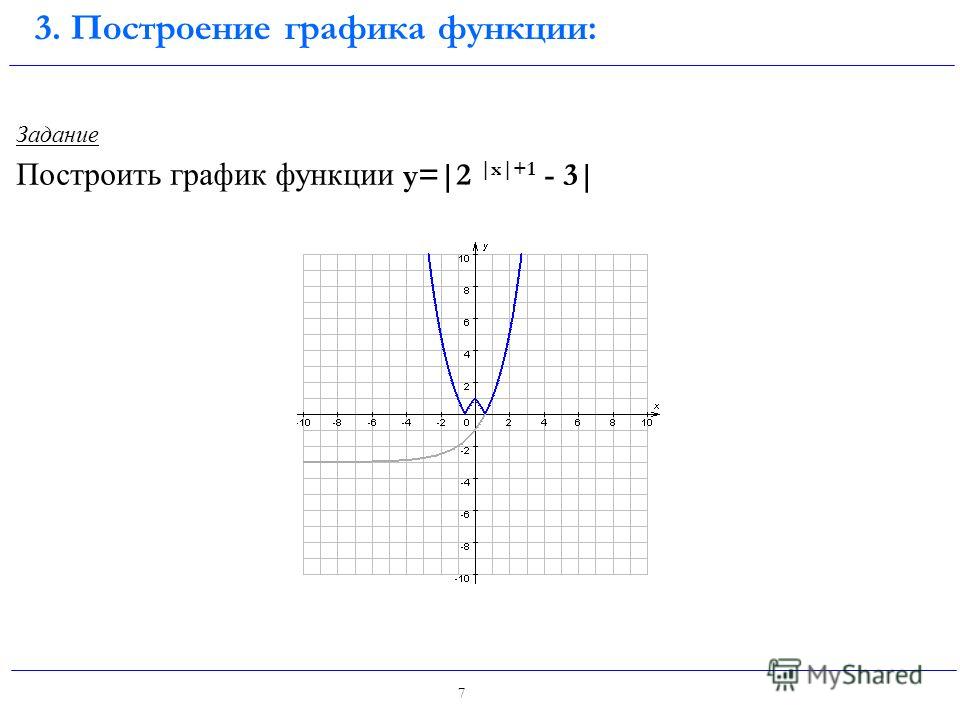 .. вы только что успешно прошли тест. Хорошая работа! Хотя графики абсолютных значений имеют тенденцию выглядеть так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает в себя абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон значений x , потому что три соседних значения x почти наверняка не дадут вам достаточно информации, чтобы нарисовать достоверную картину. Примечание. Полоски абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (то есть положительные или нулевые). В результате буква «V» на приведенном выше графике появилась там, где знак внутри был равен нулю. Когда x было меньше –2, выражение x + 2 было меньше нуля, и столбцы абсолютных значений перевернули эти «минусовые» значения из-под оси x наверх.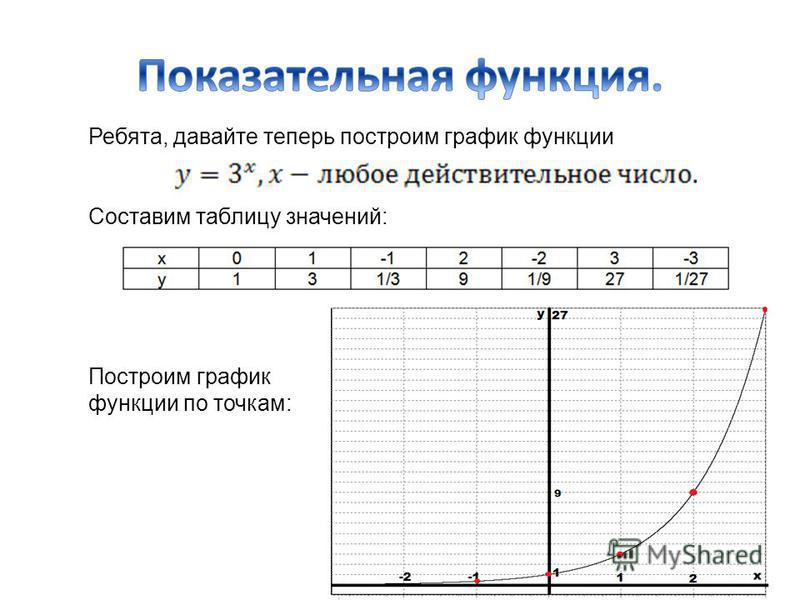 Когда x равняется –2, аргумент (то есть выражение внутри столбцов) равен нулю.Для всех значений x справа от –2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не меняли. Другими словами, графически столбцы абсолютных значений заняли этот график: ... и перевернул «минус» (зеленым на графике) снизу оси x наверх. Замечание, где аргумент столбцов абсолютного значения будет равен нулю, может быть полезным для проверки правильности построения графика. Эта функция почти такая же, как и предыдущая. Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, когда x = 0, поэтому я должен ожидать увидеть локоть в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютных значений, я ожидаю, что мой график будет выглядеть как обычный график абсолютных значений (представляющий собой букву «V» с коленом в начале координат), но смещенный вверх на две единицы. . Сначала я заполню свою Т-диаграмму, выбирая по ходу некоторые отрицательные значения x : Затем нарисую точки и заполню график: Партнер Поскольку столбцы абсолютных значений всегда показывают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x .Но могут: График y = - | x + 2 | Эта функция является своего рода противоположностью первой функции (выше), потому что в выражении абсолютного значения в правой части уравнения стоит «минус». Из-за этого «минуса» все положительные значения, представленные столбцами абсолютных значений, будут переключены на отрицательные значения.Другими словами, я должен ожидать, что этот график будет иметь изгиб в точке (–2, 0), как и первый график выше, но остальная часть графика будет перевернута вверх дном, чтобы оказаться ниже оси x . Сначала я заполню свою Т-диаграмму: Потом делаю свой график: Также не предполагайте, что какой-либо график абсолютных значений всегда будет находиться только на одной стороне оси x .Графики могут пересекаться: График y = - | x | + 2 Моя Т-диаграмма: .

График функции y=f(x)+b | Алгебра

Открытая Математика. Функции и Графики. Параллельный перенос

Построение графика функции y = a(x–m)² + n

Выражение графика или функция — MATLAB fplot

Графические логарифмические функции

Онлайн-справка — Быстрая справка

Создание новой функциональной диаграммы

Добавить график функции к существующему графику

Построение математических функций — Как строить математические функции в Python?

Предварительные требования

1.

2. Matplotlib

Шаги для построения математических функций

1. График (y = x) Функция идентичности

2. График (y = a.x

3. График (y = a.x

4. График (y = ln (x) или log

5. График (y = log

6. График (y = e

7. График (y = a

8. График (y = знак (x)) Функция Signum

9. Plot (y = a.sin (b.x + c)) Синусоидальная функция в Python

10. График (y = sinc (x)) Функция Sinc

11. График (y = cosh (x)) Гиперболическая функция

Подведение итогов

GraphPad Prism 9 Curve Fitting Guide

Советы по построению функции

Построение семейства кривых

Отображение каждой кривой на отдельном графике

Если вы планируете увеличить масштаб и построить только часть кривой

Объединение двух кривых на одном графике

BioMath: тригонометрические функции

Графические функции абсолютных значений | Purplemath

Purplemath

MathHelp.

График

График

`Ваш комментарий будет первым`

`Добавить комментарий Отменить ответ`

Название цвета	Краткое название	Триплет RGB	Шестнадцатеричный код цвета	Внешний вид
`'красный'`	`'r'`	`[1 0 0]`	`'# FF0000'`
`'зеленый'`	`'g'`	`[0 1 0]`	`'# 00FF00'`
`'синий'`	`'b'`	`[0 0 1]`	`'# 0000FF'`
`'голубой`	`'c'`	`[0 1 1]`	`'# 00FFFF'`
`'пурпурный'`	`'m'`	`[1 0 1]`	`'# FF00FF'`
`'желтый'`	`'y'`	`[1 1 0]`	`'# FFFF0066`
`'черный'`	`'k'`	`[0 0 0]`	`'# 000000'`
`'белый66`	`[1 1 1]`	`'#FFFFFF'`
`'none'`	Неприменимо	Неприменимо	Неприменимо	N o цвет

Триплет RGB	Шестнадцатеричный код цвета	Внешний вид
`[0 0,4470 0,7410]`	`'# 0072BD'`			`'# D95319'`
`[0,9290 0,6940 0,1250]`	`'# EDB120'`		`'# 7E2F8E'`
`[0,4660 0,6740 0,1880]`	`'# 77AC30'`	`1`
`'# 4DBEEE'`
`[0,6350 0,0780 0,1840]`	`'# A2142F'`