Построение графиков функций онлайн
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн.
|
|
Значение |
|---|---|
-
|
вычитание |
*
|
умножение |
/
|
деление |
^n
|
возведение в степень: x^n — x в степени n |
^(1/n)
|
корень степени n: x^(1/n) |
()
|
скобки |
| |
|
скобки модуля: |x| |
Список функций
| Имя | Описание | |
|---|---|---|
log2(x)
|
логарифм по основанию 2 от x | |
lg(x) или log10(x)
|
логарифм по основанию 10 от x | |
log(x;b)
|
логарифм x по основанию b log(x;3) | |
ln(x)
|
натуральный логарифм (логарифм по основанию e (2. x
|
экспонента от х (e в степени x) |
sqrt(x)
|
квадратный корень из x | |
sign(x)
|
функция знака: -1 если x<0, 1 если x>0 и 0 если x=0 | |
| Тригонометрические функции | ||
sin(x)
|
синус х | |
cos(x)
|
косинус х | |
tg(x)tan(x)
|
тангенс х | |
ctg(x) или
cot(x)
|
котангенс х | |
arcsin(x) или
asin(x)
|
арксинус х | |
arccos(x) или
acos(x)
|
арккосинус х | |
arctg(x) или
atan(x)
|
арктангенс х | |
arcctg(x) или
acot(x)
|
арккотангенс х | |
sinh(x) или
sh(x)
|
гиперболический синус х | |
cosh(x) или
ch(x)
| гиперболический косинус х | |
tanh(x) или
th(x)
|
гиперболический тангенс х | |
coth(x) или
cth(x)
|
гиперболический котангенс х | |
asinh(x)
|
гиперболический арксинус х | |
acosh(x)
|
гиперболический арккосинус х | |
atanh(x)
|
гиперболический арктангенс х | |
acoth(x)
|
гиперболический арккотангенс х | |
Встроенные константы
| Имя | Описание |
|---|---|
pi
|
Пи = 3,14. ..
|
e
|
e = 2,71828… число Эйлера |
Построение графика функции по точкам. Практикум по математическому анализу. Урок 6
Высшая математика / Практикум по математическому анализу
Наглядное графическое изображение функциональной зависимости между двумя переменными и можно получить, рассматривая значения этих переменных как координаты точек на плоскости.
Графиком функции, заданной уравнением , называется совокупность всех точек плоскости, координаты которых удовлетворяют этому уравнению.
Обычно график функции представляет некоторую плоскую линию.
Построение графика аналитически заданной функции по точкам выполняется в следующем порядке:
1) по данному аналитическому выражению функции составляется таблица соответствующих друг другу значений переменных;
2) выбирается система координат с подходящими единицами масштаба для каждой переменной.
Обычно применяется прямоугольная система координат и одна общая единица масштаба для обеих координатных осей;
3) строятся точки, координатами которых являются соответствующие друг другу значения аргумента и функции, содержащиеся в таблице;
4) полученные точки соединяются плавной линией.
Построенный этим способом график функции будет тем точнее, чем больше значений переменных содержится в таблице, чем больше точек будет нанесено на координатную плоскость.
Построение графика функции упрощается, если она является четной, нечетной или периодической. График четной функции симметричен относительно оси ; график нечетной функции симметричен относительно начала координату график периодической функции получается путем повторения части ее графика, соответствующей одному периоду.
Пример 1. Построить графики функций:
1) на отрезке [—2; 4];
2) на отрезке [—5; 5];
3) на отрезке ;
4) на отрезке [-6; 5];
5) между точками пересечения с осью .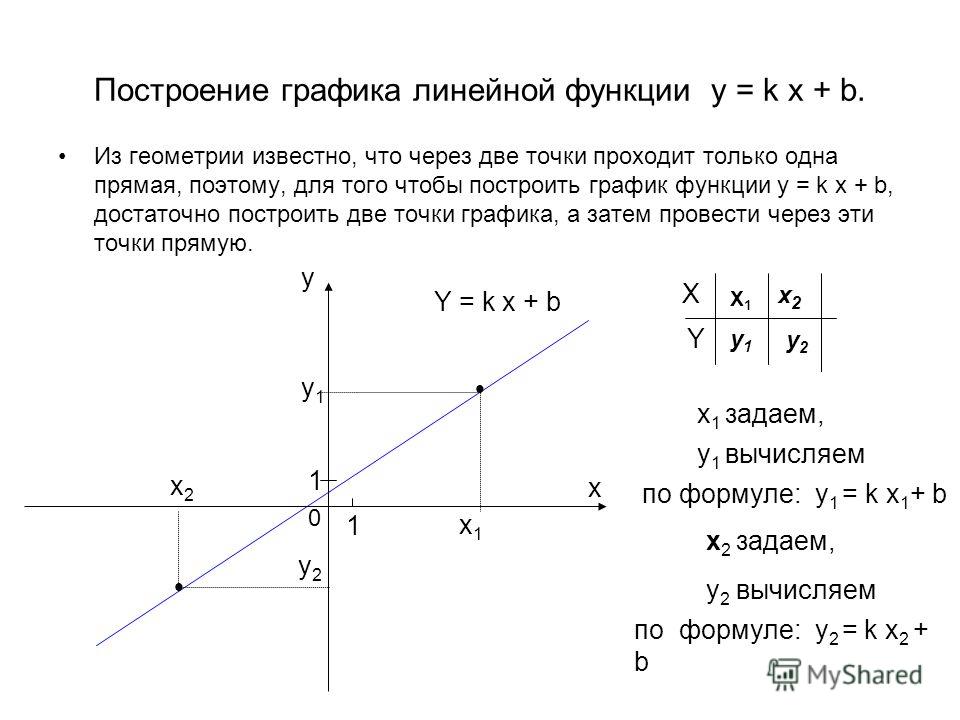
Решение. 1) В условии задачи указано, что независимой переменной можно придавать только значения, заключенные на отрезке [—2; 4]. Учитывая это, составим следующую таблицу, беря для простоты только целые значения и вычисляя из данного уравнения соответствующие значения :
Рис.1
Введем прямоугольную систему координат, как показано на рис. 1, с одинаковыми единицами масштаба, которые указаны числовыми пометками на координатных осях.
Построим точки, откладывая содержащиеся в таблице значения аргумента по оси абсцисс, а значения функции по оси ординат. Соединим полученные точки плавной кривой, которая и будет графиком данной функции. Эта кривая называется параболой.
Вообще графиком всякой квадратной функции является парабола, ось симметрии которой параллельна оси .
2) Функция — нечетная, так как для нее . Для значений аргумента, отличающихся только по знаку, значения нечетной функции будут также отличаться только по знаку.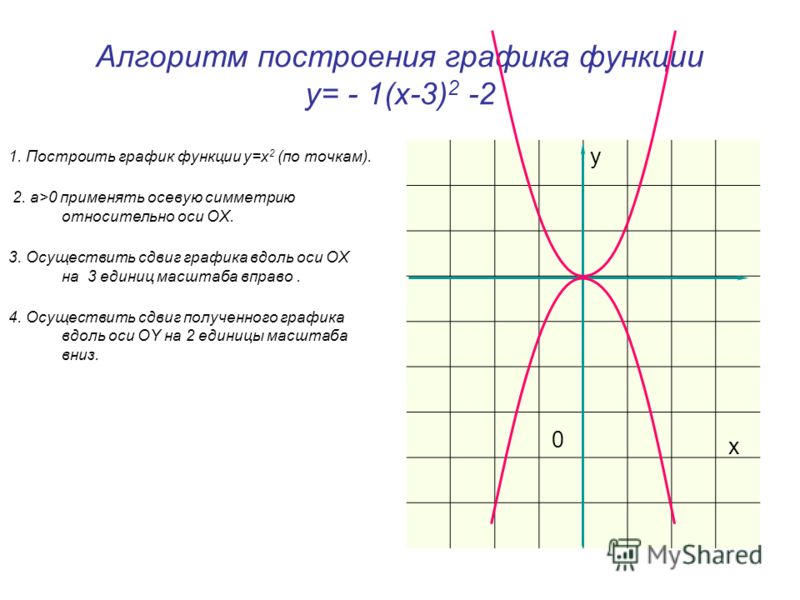
Поэтому при составлении таблицы здесь достаточно вычислить изданного уравнения значения функции только для положительных значений аргумента. Значения функции для отрицательных значений аргумента получим путем простои перемены знаков.
Выберем систему координат с одинаковыми масштабами на координатных осях (рис.2).
Построим точки для каждой пары числовых значений и , которые содержатся в строках таблицы. Соединяя эти точки плавной кривой, получим график, симметричный относительно начала координат.
Рис.2
3) Функция является четной, так как при перемене знака у любого значения аргумента значение этой функции не изменяется, . Поэтому здесь при составлении таблицы достаточно вычислить значения функции только для положительных значений аргумента; значения функции для отрицательных значений аргумента будут те же.
Составив таблицу, замечаем, что значения аргумента есть числа 1-го порядка, тогда как значения функции — числа 3-го порядка. Поэтому для построения соответствующих точек берем разные масштабы абсцисс и ординат; они показаны числовыми пометками на координатных осях (рис.
3).
Рис.3
График данной четной функции симметричен относительно оси ординат.
4) Составим таблицу значений функции для значений аргумента , заключенных на отрезке [—6; 5].
Затем строим точки и, соединяя их сплошной линией, получим искомый график (рис.4).
Данная функция не является четной или нечетной. Поэтому ее график не симметричен ни относительно оси , ни относительно начала координат.
Рис.4
5) Абсциссы точек пересечения графика данной функции с осью найдем из данного уравнения, зная, что в этих точках ордината . При , откуда . Далее составляем таблицу значений данной четной функции на отрезке [—4; 4] и строим ее график (рис.5).
Рис.5
Когда приближается к нулю слева или справа, значения функции и ординаты ее графика неограниченно возрастают. При функция не имеет никакого числового значения, ее график состоит из двух отдельных бесконечных ветвей.
youtube.com/embed/Qqi557_8mUY» frameborder=»0″ allowfullscreen=»»> Тегиграфик нечетной функцииграфик функцииграфик четной функциипостроить график функцииграфических функций — Как графические функции?
Графические функции — это процесс построения графика (кривой) соответствующей функции. Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.
Давайте посмотрим процесс графического отображения функций вместе с примерами.
| 1. | Что подразумевается под графическими функциями? |
| 2. | Основные графические функции |
| 3. | График сложных функций |
| 4. | Графические функции с помощью преобразований |
5. | Часто задаваемые вопросы о графических функциях |
Что подразумевается под графическими функциями?
Графические функции рисует кривую, представляющую функцию на координатной плоскости. Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2.
Возьмем любую точку на этой прямой, скажем, (-1, 3). Подставим (-1, 3) = (x, y) (т. е. x = -1 и y = 3) в функцию f(x) = -x + 2 (заметим, что ее можно записать как y = — х + 2). Затем
3 = -(-1) + 2
3 = 1 + 2
3 = 3, таким образом, (-1, 3) удовлетворяет функции.
Таким же образом можно попробовать взять разные точки и проверить, удовлетворяют ли они функции. Каждая точка на линии (обычно называемая «кривой») удовлетворяет этой функции. Рисование таких кривых, представляющих функции, известно как графическое отображение функций.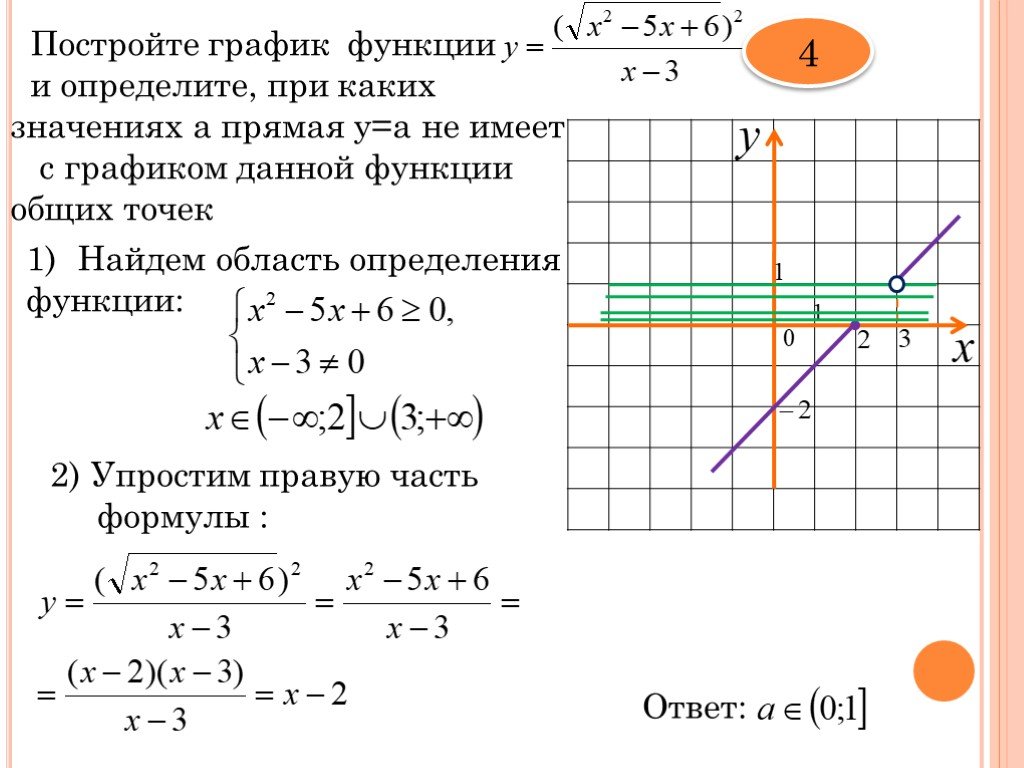
Основные функции построения графиков
Графики основных функций, таких как линейные функции и квадратичные функции, очень просты. Основная идея графических функций
- Определение формы, если возможно. Например, если это линейная функция вида f(x) = ax + b, то ее график будет линией; если это квадратичная функция вида f(x) = ax 2 + bx + c, то это парабола.
- нахождение на нем некоторых точек путем подстановки некоторых случайных значений x и нахождение соответствующих значений y путем подстановки каждого значения в функцию.
Вот несколько примеров.
Графики линейных функций
Построим график той же линейной функции, что и в предыдущем разделе (f(x) = -x + 2). Для этого мы создаем таблицу значений, взяв несколько случайных чисел для x, скажем, x = 0 и x = 1. Затем подставьте каждое из них в y = -x + 2, чтобы вычислить значения y.
| х | и |
|---|---|
| 0 | -0 + 2 = 2 |
| 1 | -1 + 2 = 1 |
Таким образом, на прямой есть две точки (0, 2) и (1, 1).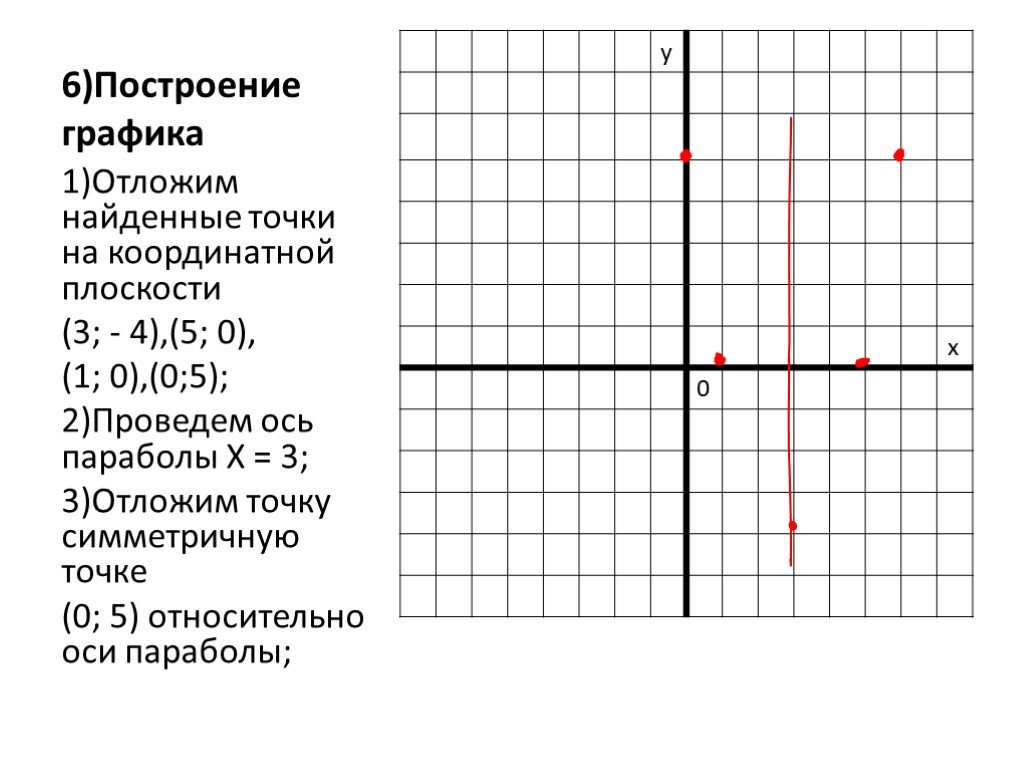
Если мы нанесем их на график и соединим их прямой линией (продолжив линию с обеих сторон), мы получим ее график, как показано в предыдущем разделе.
График квадратичных функций
Для построения графика квадратичной функции мы можем найти на ней несколько случайных точек. Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.
Пример: График квадратичной функции f(x) = x 2 — 2x + 5.
Решение:
Сравнение с f(x) = ax 2 , a + c + bx = 1, b = -2 и c = 5.
Координата x вершины: h = -b/2a = -(-2)/2(1) = 1.
Координата y есть, f(1) = 1 2 — 2(1) + 5 = 4.
Следовательно, вершина (1, 4).
Возьмем два случайных числа по обе стороны от 1 (координата x вершины) и создадим таблицу.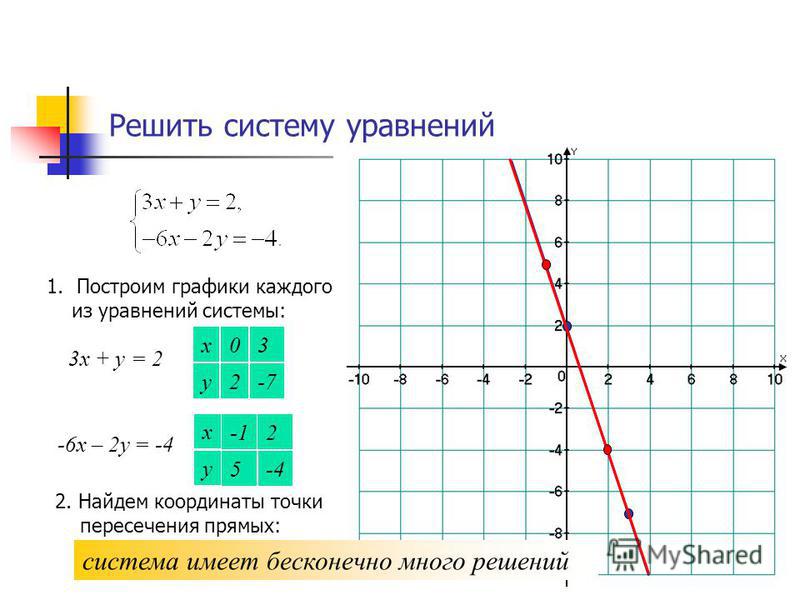
Затем мы можем вычислить координаты y с помощью функции.
| х | и |
|---|---|
| -1 | (-1) 2 — 2(-1) + 5 = 8 |
| 0 | 0 2 — 2(0) + 5 = 5 |
| Вершина: 1 | 4 |
| 2 | 2 2 — 2(2) + 5 = 5 |
| 3 | 3 2 — 2(3) + 5 = 8 |
Теперь мы нанесем точки (-1, 8), (0, 5), (1, 4), (2, 5) и (3, 8) на лист графика, соединим их, и продлите кривую с обеих сторон.
График сложных функций
Графические функции сравнительно просты, если каждый их домен и диапазон представляет собой набор всех действительных чисел. Но это НЕ относится ко всем типам функций. Есть некоторые сложные функции, для которых необходимо учитывать домен, диапазон, асимптоты и дыры при их построении.
Самые популярные такие функции:
- Рациональные функции. Его родительская функция имеет форму f(x) = 1/x (которая называется обратной функцией).
- Экспоненциальные функции. Его родительская функция имеет вид f(x) = a x .
- Логарифмические функции. Его родительская функция имеет вид f(x) = log x.
Просто представьте, как выглядят графики родительских функций каждой из этих функций.
В каждом из этих случаев за графических функций , мы выполняем следующие шаги:
- Найдите область определения и диапазон функции и помните об этом при построении кривой.
- Найдите точки пересечения x и y и нанесите их на график.
- Определите отверстия, если они есть.
- Найдите асимптоты (вертикальную, горизонтальную и наклонную) и нарисуйте их пунктирными линиями, чтобы мы могли разбить график по этим линиям и убедиться, что график их не касается.
- Постройте таблицу значений, взяв несколько случайных чисел для x (по обе стороны от точки пересечения x и/или по обе стороны от вертикальной асимптоты), рассчитайте соответствующие значения y.
- Нанесите точки из таблицы и соедините их, учитывая асимптоты, домен и диапазон.
Давайте посмотрим, как построить график функции в различных случаях, используя описанные выше шаги.
График рациональных функций
Построим график рациональной функции f(x) = (x + 1) / (x — 2). Мы следуем вышеуказанным шагам и рисуем график этой функции.
График экспоненциальных функций
Рассмотрим экспоненциальную функцию f(x) = 2 -x + 2. Мы построим ее график, используя те же шаги, что и упомянутые выше.
- Его областью определения является множество всех действительных чисел (R), а его диапазон равен y > 2. Чтобы узнать, как их найти, нажмите здесь.
- Не имеет вертикальных асимптот. Но у него есть горизонтальная асимптота при y = 2, .
- Он не имеет x-перехватов. Его y-пересечение равно (0, 3).
- Без отверстий.
- У нас нет данных о VA или x-intercept. Пока у нас есть только одно значение (0, 3). Итак, давайте возьмем несколько случайных чисел по обе стороны от x = 0 и составим таблицу.
х и -2 2 -(-2) + 2 = 6 -1 2 -(-1) + 2 = 4 0 3 (г-целое) 1 2 -1 + 2 = 2,5 2 2 -2 + 2 = 2,25 - Нанесем всю информацию на график.
Итак, давайте возьмем несколько случайных чисел по обе стороны от x = 0 и составим таблицу.Графики логарифмических функций
Мы построим график логарифмической функции, скажем, f(x) = 2 log 2 x — 2. Теперь мы построим ее график, выполнив действия, описанные ранее.
Точно так же вы можете увидеть, как построить график нелинейных функций, функции тождества, функции модуля, полиномиальной функции, функции нуля, функции наибольшего целого числа, постоянной функции, тригонометрических функций, функции дробной части и т.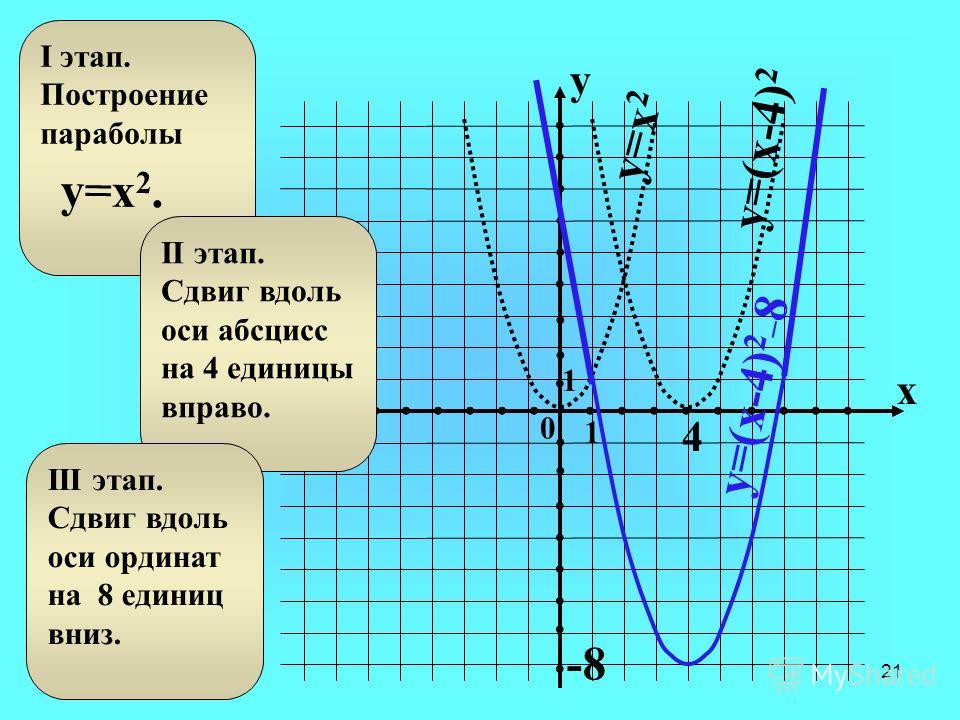
д., нажав на соответствующие ссылки.
Графические функции с помощью преобразований
Мы можем построить графики функций, применяя преобразования к графикам родительских функций. Вот родительские функции нескольких важных типов функций.
- Линейная функция: f(x) = x
- Квадратичная функция: f(x) = x 2
- Кубические функции: f(x) = x 3
- Функция квадратного корня: f(x) = √x
- Функция кубического корня: f(x) = ∛x
- Функция абсолютного значения: f(x) = |x|
- Обратная функция: f(x) = 1/x
- Экспоненциальная функция: f(x) = a x , 0 < a < 1
- Логарифмическая функция: f(x) = log x
Нам нужно иметь представление о том, как выглядит график каждой из этих родительских функций (нажав на соответствующие ссылки). Затем мы можем применить следующие преобразования для построения графика данной функции.
| Трансформация | Изменение графика |
|---|---|
| f(x) + с | Сдвигает график функции c единиц вверх. |
| ф(х) — с | Сдвигает график функции c единиц вниз. |
| ф(х + с) | Сдвигает график функции c единиц влево. |
| ф(х — в) | Смещает график функции c единиц вправо. |
| -ф(х) | Отражает график функции по оси X (в перевернутом виде). |
| ф(-х) | Отражает график функции по оси Y (т. е. левая и правая части меняются местами). |
| ф(акс) | Горизонтальное расширение с коэффициентом 1/a. |
| а ф(х) | Вертикальное расширение в a. |
Чтобы подробно понять, как построить график функций с помощью преобразований, нажмите здесь.
Важные примечания по графическим функциям:
- f(ax) ≠ a f(x). Оба могут иметь разные значения.
- Значение x, используемое для построения графика любой функции f(x), может быть целым числом, действительным числом или десятичным числом.
- График функции никогда не должен касаться асимптот.
- Не выбирайте значения x в таблице, которых НЕТ в домене функции.
☛ Похожие темы:
- Калькулятор графических функций
- Введение в графику
- Визуализация функций с помощью графиков
Часто задаваемые вопросы о графических функциях
Как графически отображать функции?
Для графических функций нам нужно построить его асимптоты, его точки пересечения x и y, дыры и несколько точек на нем, построив таблицу значений. Затем просто присоединитесь к точке, не касаясь асимптот и сохраняя примечание области определения и диапазона функции.
Какие этапы построения графика линейной функции?
Шаги построения графика линейной функции приведены ниже:
- Убедитесь, что линейная функция имеет форму y=mx+b.
- Теперь b откладывается по оси Y.
- м переводится в дробь.
- Теперь линия продлевается от b с использованием наклона.
- Линию можно продолжить, используя m в качестве направляющего фактора.
Альтернативный вариант:
Любые две точки на прямой определяют линию. Итак, чтобы нарисовать линейную функцию, нам нужно всего лишь две точки на ней. Чтобы отобразить это, просто создайте таблицу значений с двумя столбцами x и y, возьмите несколько случайных чисел для x и вычислите соответствующие значения y, подставив каждое из них в функцию. Затем просто нанесите точки на график, соедините их линией и бесконечно продлите линию с обеих сторон.
Как построить график кусочной функции?
Кусочная функция определяется по-разному (с помощью разных уравнений) на разных интервалах. Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.
Как идентифицировать функции с помощью графиков?
Вот несколько приемов для определения функций по графикам:
- Если график представляет собой линию, то это линейная функция, имеющая вид f(x) = ax + b.
- Если график имеет форму идеальной буквы U или перевернутой буквы U, то он является квадратичной функцией и имеет вид f(x) = ax 2 + bx + c.
- Если на графике есть две кривые, симметричные относительно наклонной линии, то это рациональная функция, которая обычно имеет вид f(x) = (ax + b) / (cx + d).
- Если график имеет форму V или перевернутой буквы V, то это функция абсолютного значения и имеет вид f(x) = a |bx + c| + д.
- Если график состоит из нескольких горизонтальных линий, то он представляет собой функцию нижнего или верхнего предела.
- Если график с одной кривой возрастает или убывает с вертикальной асимптотой, то это логарифмическая функция.
- Если график с одной кривой возрастает или убывает с горизонтальной асимптотой, то это экспоненциальная функция.
- Если на графике несколько волн, это может быть одна из тригонометрических функций:
Функция синуса
Функция косинуса
Функция тангенса
Функция косеканса
Функция секанса
Функция котангенса
Как узнать, является ли график функцией?
Функция всегда проходит тест вертикальной линии.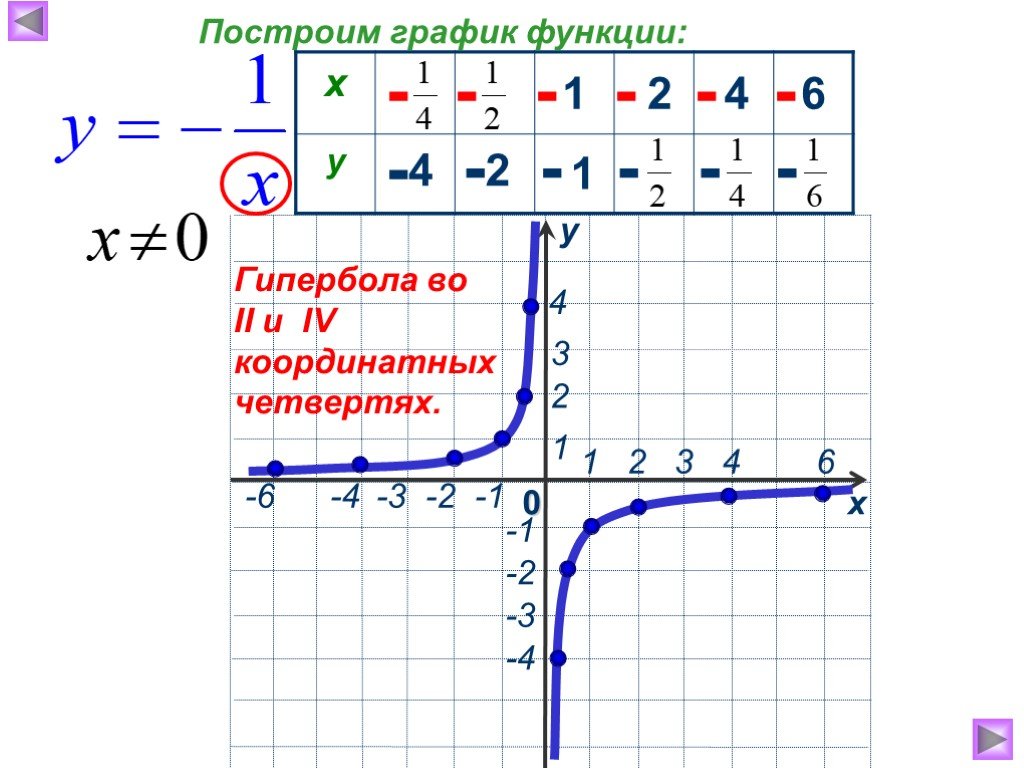
Чтобы использовать этот тест, просто возьмите вертикальную линию (или просто вертикальную палочку) и проведите ее по графику слева направо по горизонтали. Ни в какой момент времени линия не должна пересекать график более чем в одной точке, чтобы график представлял функцию.
Как использовать график для решения уравнения?
Сначала определите тип функции, взглянув на график. Возьмем его общее уравнение. Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
Как нарисовать график уравнения?
Чтобы нарисовать график уравнения функции, сделайте следующее:
- Нанесите различные точки уравнения.
- Соедините точки и сформируйте кривую. Полученная таким образом кривая является графиком данного уравнения.
Как построить график функций точек перегиба
Все ресурсы по исчислению 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Исчисление 1 Помощь » Функции » Графические функции » Точки » Точки перегиба » Как построить график функций точек перегиба
Найдите точки перегиба .
Возможные ответы:
Правильный ответ:
Объяснение:
Точки перегиба могут возникать только тогда, когда вторая производная равна нулю или не определена. Здесь у нас есть
.
Таким образом, возможные точки перегиба возникают в и . Однако, чтобы получить точку перегиба, мы должны убедиться, что знак второй производной отличается по обе стороны от точки. Здесь у нас есть
.
Следовательно, обе точки перегиба
Сообщить об ошибке
Ниже приведен график . Сколько у него точек перегиба?
Возможные ответы:
Недостаточно информации
Правильный ответ:
3
3
Объяснение: Возможные точки перегиба возникают, когда .
Это происходит при трех значениях . Однако, чтобы быть точкой перегиба, знак должен быть разным по обе стороны от критического значения. Следовательно, только являются критическими точками.
Сообщить об ошибке
Найти точки перегиба для функции .
Возможные ответы:
Нет точек перегиба.
и
и
Правильный ответ:
Объяснение:
Точка перегиба находится там, где график (или изображение) функции изменяет вогнутость. Чтобы найти это алгебраически, мы хотим найти, где вторая производная функции меняет знак с отрицательного на положительный или наоборот. Итак, находим вторую производную заданной функции
Первая производная с использованием правила степени
равна
и вторая производная
Затем мы находим, где эта вторая производная равна .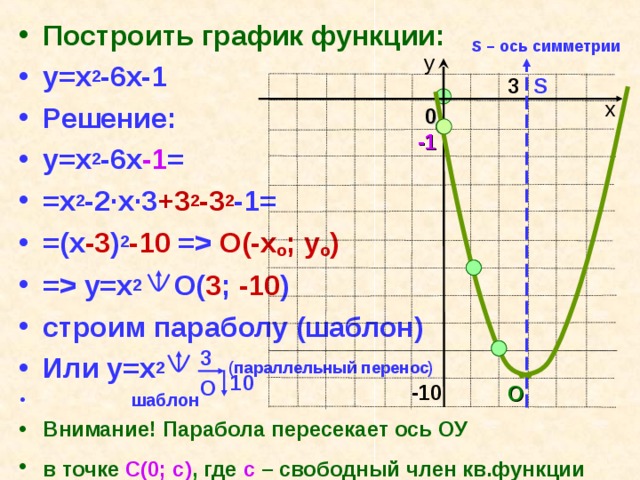
когда .
Затем мы смотрим, меняет ли знак вторая производная в этой точке. Как графически, так и алгебраически мы можем видеть, что функция действительно меняет знак в точке и только в точке , так что это наша точка перегиба.
Сообщить об ошибке
Найти все точки перегиба
.
Возможные ответы:
Точек перегиба нет.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти используя степенное правило, .
Теперь устанавливаем и находим.
Чтобы убедиться, что это истинная точка перегиба, нам нужно подставить значение, которое меньше ее, и значение, которое больше ее, во вторую производную. Если вокруг точки происходит смена знака, то это истинная точка перегиба.
Пусть
Теперь пусть
Поскольку вокруг точки знак меняется с положительного на отрицательный, мы можем заключить, что это точка перегиба.
Сообщить об ошибке
Найти все точки перегиба
Возможные ответы:
Нет точек перегиба.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти используя степенное правило .
Теперь, чтобы найти точки перегиба, нам нужно установить .
.
Теперь мы можем использовать квадратное уравнение.
Напомним, что квадратное уравнение имеет вид
,
, где a,b,c относятся к коэффициентам уравнения .
В данном случае a=12, b=0, c=-4.
Таким образом, возможные точки заражения
.
Теперь, чтобы проверить, являются ли точки перегиба или какие из них, нам нужно подставить значение выше и ниже каждой точки. Если есть смена знака, то точка является точкой перегиба.
Для проверки подключим.
Следовательно, это точка перегиба.
Теперь давайте проверим с .
Следовательно также является точкой перегиба.
Сообщить об ошибке
Найти все точки заражения
.
Возможные ответы:
Точек перегиба нет.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти с помощью степенного правила.
Теперь давайте помножим.
Теперь, чтобы найти точки перегиба, нам нужно установить .
.
Из этого уравнения мы уже знаем одну из точек перегиба, .
Чтобы вычислить остальные точки перегиба, мы можем использовать квадратное уравнение.
Напомним, что квадратное уравнение имеет вид
, где a,b,c относятся к коэффициентам уравнения
.
В данном случае a=20, b=0, c=-18.
Таким образом, другие 2 точки заражения
Чтобы убедиться, что все они являются точками перегиба, нам нужно подставить значения выше и ниже каждого значения и посмотреть, меняется ли знак.
Давайте подключим
Поскольку в каждой точке происходит смена знака, все они являются точками перегиба.
Сообщить об ошибке
Найти точки перегиба
.
Возможные ответы:
Нет точек перегиба.
Правильный ответ:
Точек перегиба нет.
Пояснение:
Чтобы найти точки перегиба, нам нужно найти
Теперь устанавливаем.
.
Это последнее утверждение говорит, что никогда не будет. Таким образом, точек перегиба нет.
Сообщить об ошибке
Найдите точки перегиба следующей функции:
Возможные ответы:
Правильный ответ: 62
Объяснение:
Точками перегиба данной функции являются значения, при которых вторая производная функции равна нулю.
Первая производная функции равна
, а производная этой функции (вторая производная исходной функции) равна
.
Обе производные были найдены с использованием степенного правила
.
Решение , .
Чтобы убедиться, что эта точка является истинной точкой перегиба, нам нужно подставить значение, которое меньше точки, и значение, которое больше точки, во вторую производную. Если между двумя числами есть смена знака, то рассматриваемая точка является точкой перегиба.
Подключаем,
.
Теперь подключите
.
Следовательно, это единственная точка перегиба функции.
Сообщить об ошибке
Найти все точки перегиба
.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти все точки перегиба, мы сначала находим, используя правило степени дважды, .
Теперь устанавливаем.
.
Теперь факторизуем левую часть.
Из этого мы видим, что есть одна точка перегиба в .
Для точки перегиба давайте найдем x для уравнения в скобках.
Отчет о ошибке
Найдите все точки перегиба:
Возможные ответы:
Нет точек интуиции.
Ваш комментарий будет первым